| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Оптимизация числа узлов и их размещения при независимом положении абонентов
В общем случае трудно выделить области локализации групп абонентов. Таким образом, задача состоит в выборе не только местоположения узлов, но и их числа. Увеличение числа узлов приводит к сокращению затрат на соединительные линии, однако при этом линейно возрастают суммарные затраты на оборудование и эксплуатацию совокупности узлов. Таким образом, существует некоторый оптимум числа узлов и координат их размещения на территории, занимаемой абонентами.
Пусть множество абонентов проектируемой сети включает  объектов, размещенных на некоторой ограниченной территории. Затраты, необходимые для создания и эксплуатации одного узла, равны 3, а
объектов, размещенных на некоторой ограниченной территории. Затраты, необходимые для создания и эксплуатации одного узла, равны 3, а  — затраты на создание линии связи от
— затраты на создание линии связи от  абонента до
абонента до  центра коммутации, если последний размещен в точке с координатами
центра коммутации, если последний размещен в точке с координатами  . К каждому узлу могут быть подключены не более
. К каждому узлу могут быть подключены не более  абонентов.
абонентов.
Тогда формальная постановка задачи размещения узлов будет состоять в следующем: найти число узлов  и координаты каждого из них
и координаты каждого из них  оптимальные по критерию
оптимальные по критерию

при ограничениях  Опраничением является также область возможного размещения узлов.
Опраничением является также область возможного размещения узлов.
В настоящее время целый ряд практических оптимизационных задач решается эвристическими методами [2, 24, 25], обеспечивающими достаточную точность результатов при незначительных сложности и трудозатратах. Для решения сформулированной задачи может быть использован алгоритм, основанный на идеях  тода наискорейшего спуска. Сущность алгоритма состоит в следующем. Территория района создания сети разбивается на квадраты, и от
тода наискорейшего спуска. Сущность алгоритма состоит в следующем. Территория района создания сети разбивается на квадраты, и от

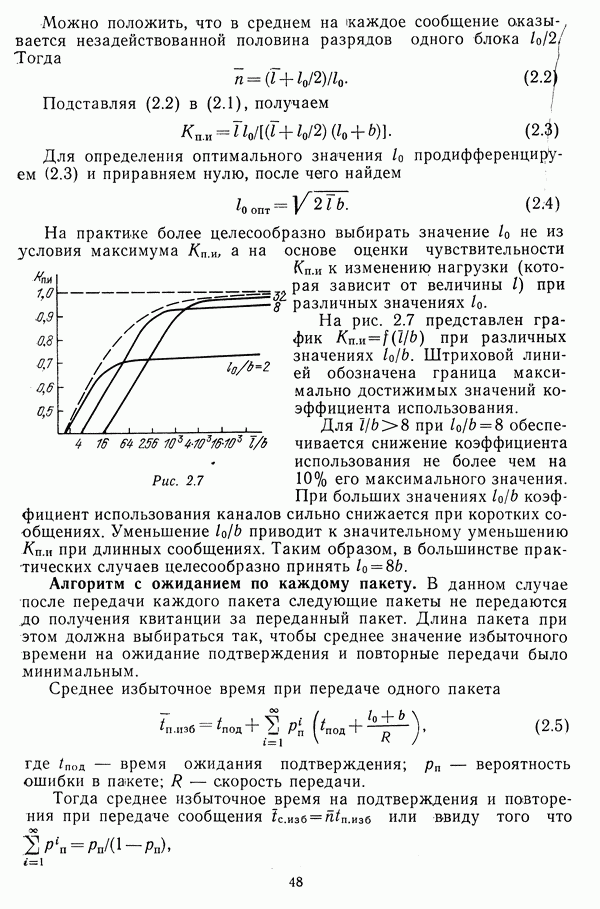
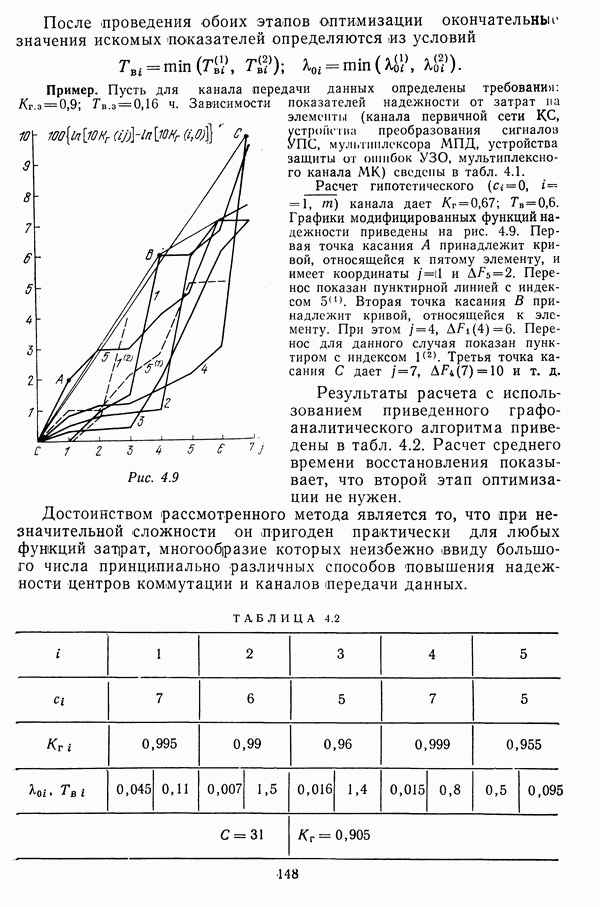
Рис. 4.2
непрерывной системы координат переходят к дискретной системе коордииат точек  Далее последовательно для различного числа узлов
Далее последовательно для различного числа узлов  производится их оптимальное размещение с оценкой суммарных затрат. Увеличение числа узлов М прекращается, как только прекратится снижение суммарных затрат. Полученные «три этом значение М и координаты каждого из узлов будут оптимальными.
производится их оптимальное размещение с оценкой суммарных затрат. Увеличение числа узлов М прекращается, как только прекратится снижение суммарных затрат. Полученные «три этом значение М и координаты каждого из узлов будут оптимальными.
Для каждого значения М алгоритм предусматривает такое пошаговое изменение координат узлов, при котором имеет место наибольшая скорость снижения затрат на соединительные линии абонентов в каждом фиксированном (положении узлов. Предполагается, что подключение абонентов в каждом фиксированном положении узлов осуществляется оптимальным образом.
Алгоритм включает следующую последовательность шагов:
Шаг 0. Ввод исходных данных:
массив дискретных координат области;
затраты на создание и эксплуатацию узла в точке с координатами 
затраты на соединительные линии как функция длины 
Присвоение начальных значений переменным:  — число узлов;
— число узлов;  - суммарные затраты на узлы и соединительные линии:
- суммарные затраты на узлы и соединительные линии:
Шаг 1. Формирование случайного варианта размещения М узлов —  (случайный выбор координат
(случайный выбор координат  — затраты на соединительные линии при варианте размещения узлов
— затраты на соединительные линии при варианте размещения узлов 
Шаг 2. Сдвиг одного из узлов в одном из направлений. (Для очередного  или
или  где
где  — шаги координатной сетки.)
— шаги координатной сетки.)
После сдвига образуется вариант размещения  (массив из М точек).
(массив из М точек).
Шаг 3. Определение затрат на соединительные линии при оптимальном подключении к узлам, размещенным по варианту 
Шаг 4. Если  то
то  иначе
иначе  Далее переход к шагу 5.
Далее переход к шагу 5.
Шаг 5. Сделано ли 4 М сдвигов? Если да, то переход к шагу 6, иначе переход к шагу 2.
Шаг 6. Вычисление суммарных затрат для текущего числа узлов М: 
Шаг 7. Если  то
то  и переход к шагу I, иначе вывод множества координат
и переход к шагу I, иначе вывод множества координат  и распределение абонентов по узлам.
и распределение абонентов по узлам.
Останов.
Точность результатов решения и объем вычислений определяются шагом квантования координат. Для небольших районов расстояние между объектами по заданным координатам может быть определено по теореме Пифагора. Для сетей большого масштаба более точные результаты дают формулы из сферической геометрии

где у — угловое расстояние, 
В приведенном алгоритме на шаге 3 решается внутренняя задача оптимального подключения абонентов к фиксированному набору узлов, которая состоит в определении такого набора переменных  из множества возможных наборов
из множества возможных наборов  при котором достигается
при котором достигается

при ограничениях  и
и 
Выполнение условия (4.23) является задачей целочисленного линейного программирования, которая может быть решена, например, методом «ветвей и границ» [40].
Решение сформулированной задачи может быть получено специальным обходом матрицы затрат [42] размерности  элементами которой являются
элементами которой являются  Цель такого обхода — выбор одного элемента в каждой
Цель такого обхода — выбор одного элемента в каждой  (ограничение 1) и не более
(ограничение 1) и не более  элементов в каждом столбце (ограничение 2).
элементов в каждом столбце (ограничение 2).
Вначале в первой строке выбирается наименьший элемент и включается в набор  содержащий один элемент и удовлетворяющий ограничениям. Далее то же повторяется для второй строки и проверяется выполнение ограничений. Если ограничения выполняются, то в состав
содержащий один элемент и удовлетворяющий ограничениям. Далее то же повторяется для второй строки и проверяется выполнение ограничений. Если ограничения выполняются, то в состав  включается выбранный элемент второй строки. Если в данной строке отсутствует элемент минимальной стоимости, удовлетворяющий ограничениям, эта строка пропускается. Пройдя таким образом все строки, получим набор элементов, (которые не нарушают ограничений и каждый из которых наименьший в своей строке.
включается выбранный элемент второй строки. Если в данной строке отсутствует элемент минимальной стоимости, удовлетворяющий ограничениям, эта строка пропускается. Пройдя таким образом все строки, получим набор элементов, (которые не нарушают ограничений и каждый из которых наименьший в своей строке.
Далее находим в первой пропущенной строке наименьший элемент и вычисляем прирост стоимости. Так как столбец, в котором выбран этот элемент, уже содержит  элементов, то один из них необходимо удалить и найти в данном столбце другой наименьший элемент. Новый элемент может привести к нарушению ограничения.
элементов, то один из них необходимо удалить и найти в данном столбце другой наименьший элемент. Новый элемент может привести к нарушению ограничения.
Таким образом, возникает чередующаяся цепочка введений и удалений элементов при отслеживании дополнительных затрат. Наконец, выбирается цепочка наименьшей стоимости и производится переход к следующей строке, в которой еще не выбран элемент. Ниже приводится пример использования изложенного метода [43].
Пример. Пусть  Элементы, выбранные на очередном шаге, обводятся кружками.
Элементы, выбранные на очередном шаге, обводятся кружками.


На шаге 3 все строки матрицы имеют по одному, а каждый столбец не более двух отмеченных элементов, т. е. ограничения выполнены. Общие затраты составляют 21 единицу. В решении оказался неиспользованным четвертый узел. Таким образом, при исходных данных задачи для получения оптимального решения четвертый узел следует исключить.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1 ОБЩАЯ ХАРАКТЕРИСТИКА СЕТЕЙ ПЕРЕДАЧИ ИНФОРМАЦИИ АСУ
- 1.1. СЕТЬ СВЯЗИ КАК ПОДСИСТЕМА СИСТЕМЫ УПРАВЛЕНИЯ
- 1.2. ПРИНЦИПЫ ПОСТРОЕНИЯ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ
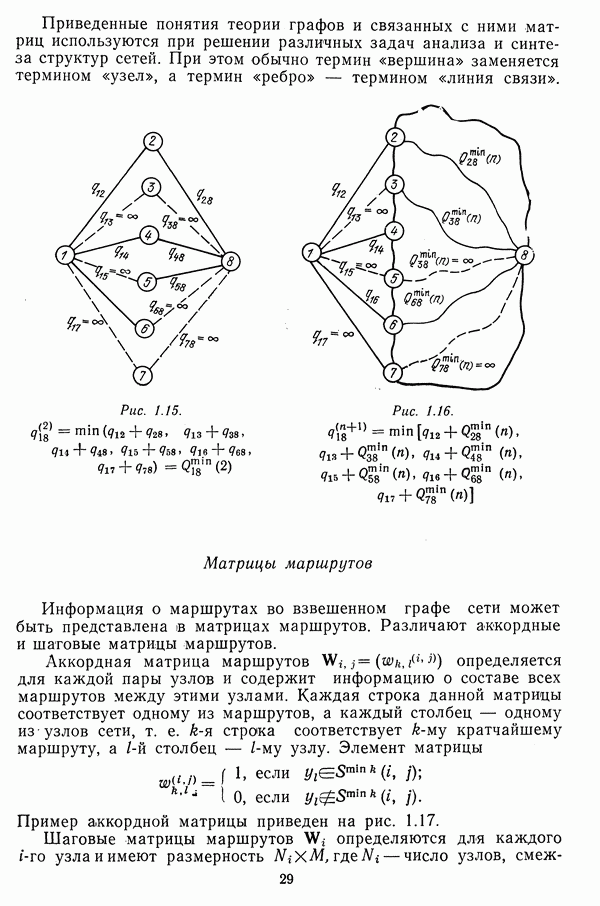
- 1.3. ПРЕДСТАВЛЕНИЕ СТРУКТУР СЕТЕЙ
- Кратчайшие маршруты во взвешенных графах
- Матрицы, определяющие структуру сетей
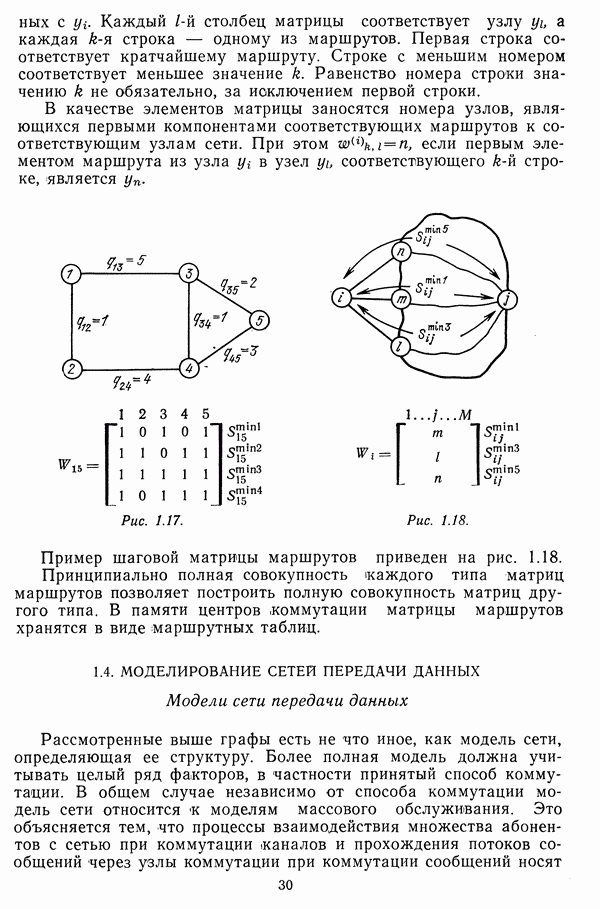
- Матрицы маршрутов
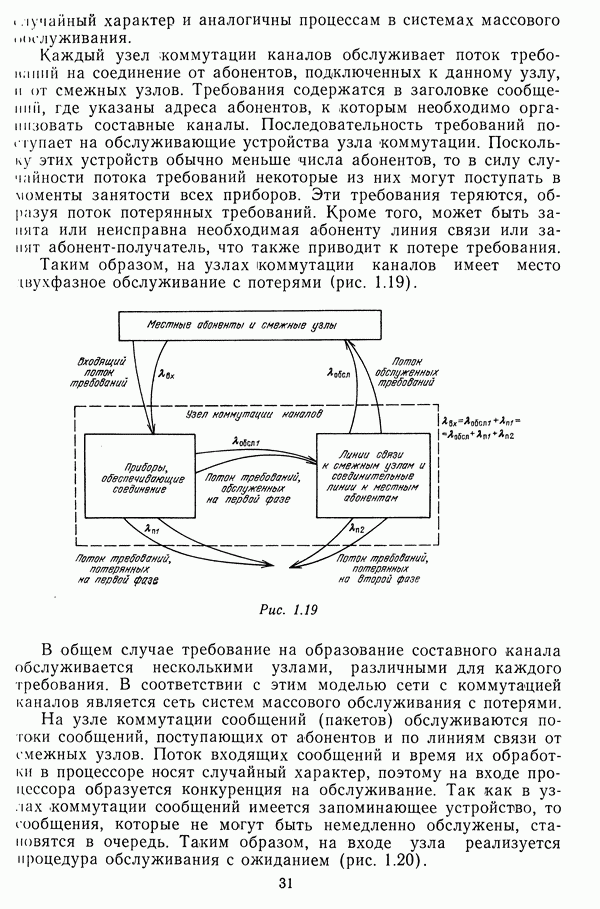
- 1.4. МОДЕЛИРОВАНИЕ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ
- Математические модели, используемые при расчете сетей
- Потоки в сетях передачи данных
- ГЛАВА 2. ПРИНЦИПЫ ФУНКЦИОНИРОВАНИЯ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ
- 2.1. СТРУКТУРА ФУНКЦИОНАЛЬНОГО ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ
- 2.2. ФОРМАЛИЗАЦИЯ СООБЩЕНИИ В СЕТЯХ ПЕРЕДАЧИ ДАННЫХ
- 2.3. АДРЕСОВАНИЕ СООБЩЕНИЙ
- 2.4. ПРОЦЕДУРЫ ВЫБОРА МАРШРУТОВ
- 2.5. РЕГУЛИРОВАНИЕ ПОТОКОВ СООБЩЕНИЙ ПО ПРИОРИТЕТАМ
- 2.6. УПРАВЛЕНИЕ В СЕТЯХ ПЕРЕДАЧИ ДАННЫХ
- Глава 3. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ МАРШРУТИЗАЦИИ И УПРАВЛЕНИЯ В СЕТЯХ ПЕРЕДАЧИ ДАННЫХ
- 3.2. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДЕТЕРМИНИРОВАННЫХ ПРОЦЕДУР ВЫБОРА МАРШРУТОВ
- 3.3. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ПОИСКОВЫХ ПРОЦЕДУР ВЫБОРА МАРШРУТОВ
- 3.4. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ КВАЗИСЛУЧАИНЫХ ПРОЦЕДУР ВЫБОРА МАРШРУТОВ
- 3.5. ФИЗИЧЕСКИЕ ВЕРСИИ ВЕСОВ ЭЛЕМЕНТОВ СЕТИ
- 3.6. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ УПРАВЛЕНИЯ ВНЕШНИМИ ПОТОКАМИ СООБЩЕНИЙ
- Глава 4. ВОПРОСЫ ПРОЕКТИРОВАНИЯ СЕТЕЙ ПЕРЕДАЧИ ИНФОРМАЦИИ АСУ
- 4.1. ЗАДАЧИ СИСТЕМНОГО ПРОЕКТИРОВАНИЯ СЕТЕЙ
- 4.2. РАЗМЕЩЕНИЕ УЗЛОВ КОММУТАЦИИ
- Оптимизация числа узлов и их размещения при независимом положении абонентов
- Размещение узлов для связи с мобильными абонентами
- Размещение центра управления сетью
- 4.3. СИНТЕЗ СТРУКТУРЫ СЕТИ
- Синтез структуры сети минимальной стоимости при заданной связности
- 4.4. РАСЧЕТ МОЩНОСТИ ЛИНИИ СВЯЗИ СЕТИ
- Оптимизация мощности линий связи при произвольном виде функций затрат
- Методика выбора каналов передачи данных для линий связи с заданной мощностью
- 4.5. ОПТИМИЗАЦИЯ ПАРАМЕТРОВ ЖИВУЧЕСТИ ЭЛЕМЕНТОВ СЕТИ
- 4.6. ВЫБОР ПАРАМЕТРОВ НАДЕЖНОСТИ ЭЛЕМЕНТОВ СЕТИ
- Методы вычисления вероятности связности сети
- Выбор параметров надежности центров коммутации
- Аналитическая оптимизация внутренних показателей надежности элементов сети
- Оптимизация внутренних показателей надежности при произвольном виде функций затрат
- СПИСОК ЛИТЕРАТУРЫ