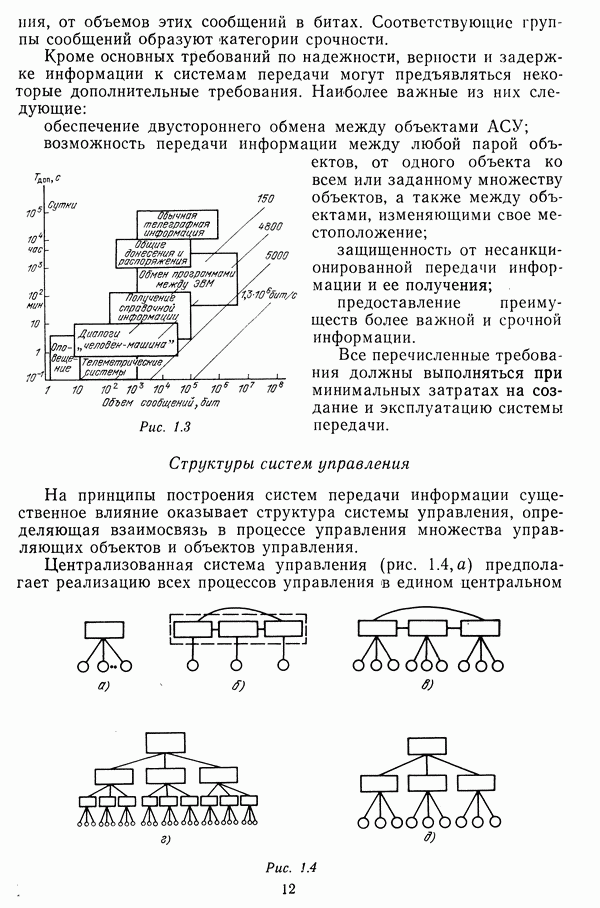
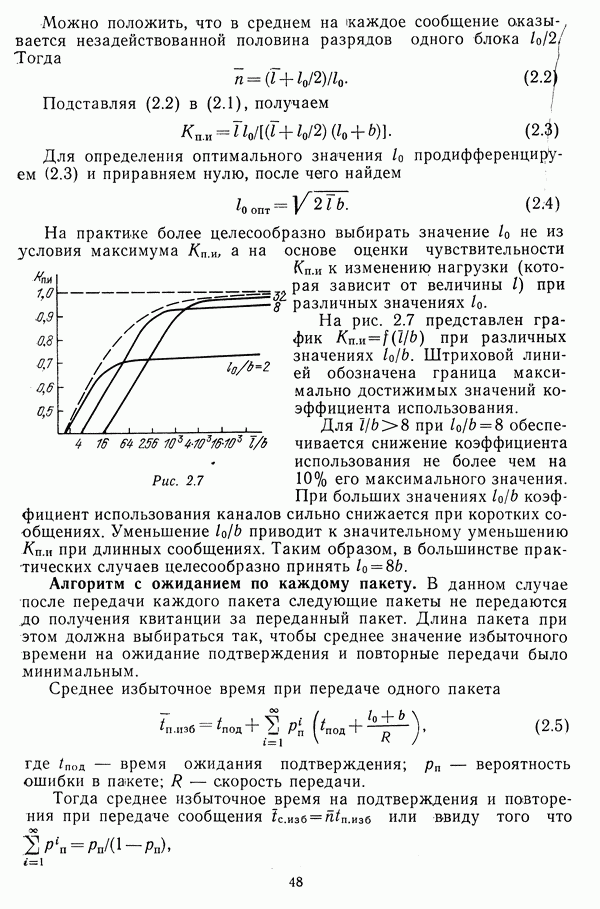
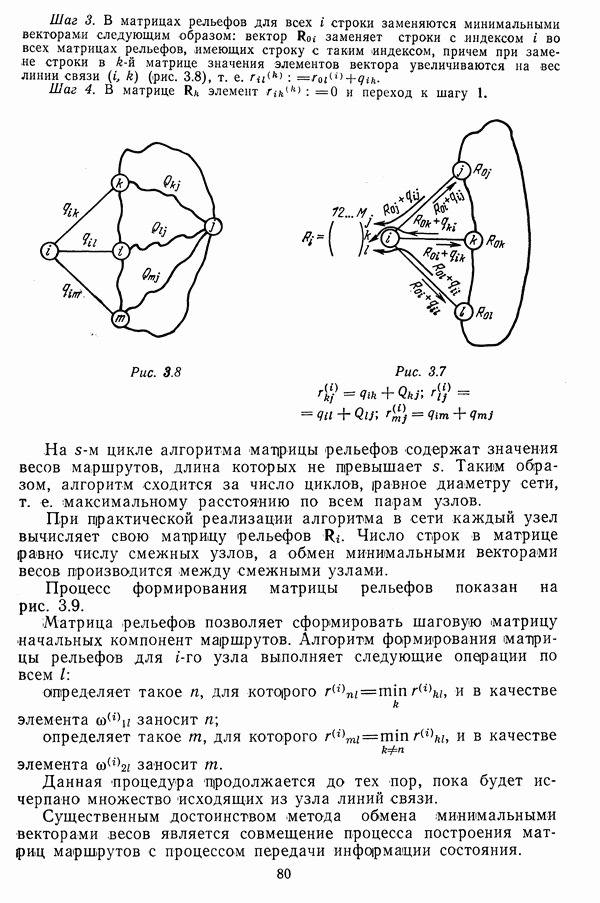
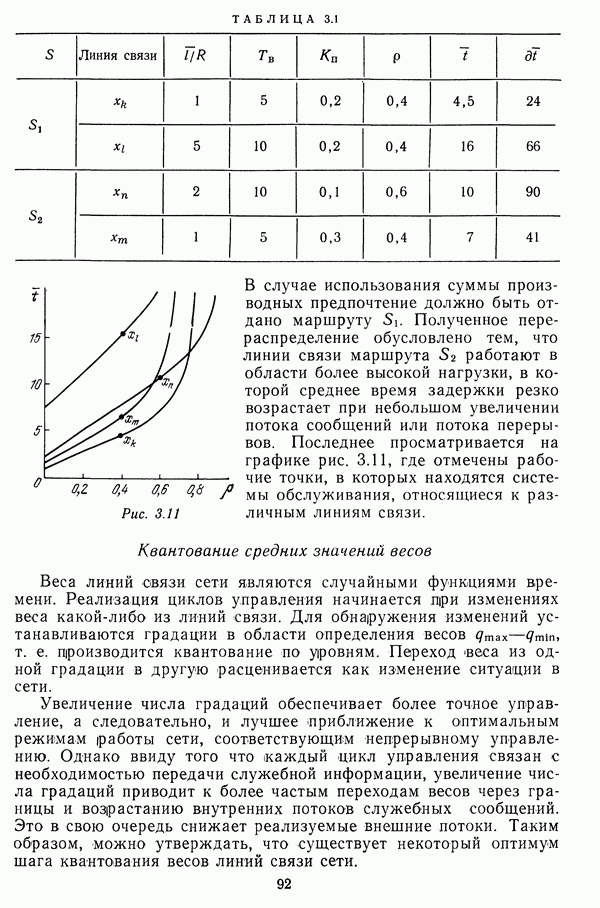
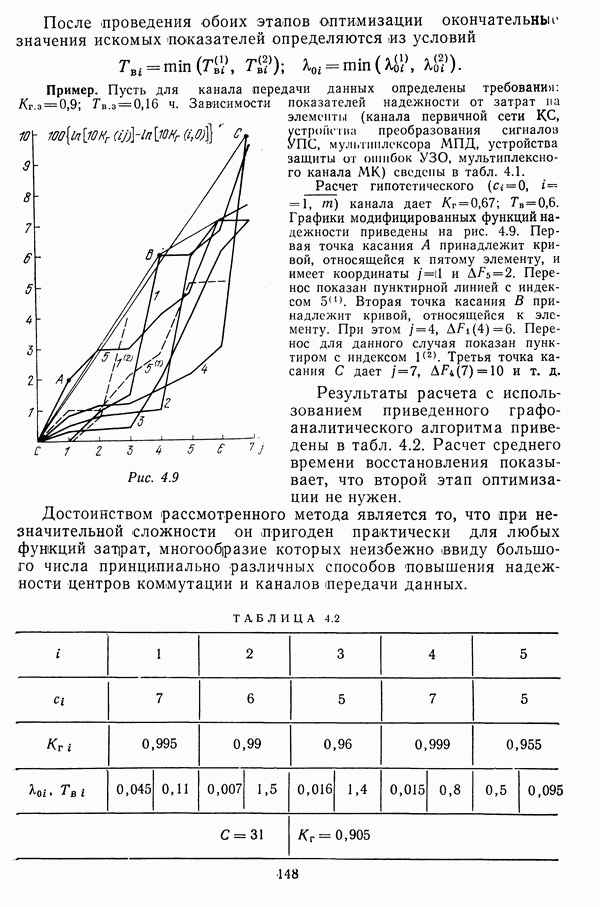
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Синтез структуры сети минимальной стоимости при заданной связности
Если при синтезе структуры сети имеется информация о затратах, необходимых для создания линий связи между парами узлов, то в качестве критерия оптимальности структуры следует использовать минимум затрат при ограничениях, налагаемых на связность 
Синтез в этом случае осуществляется следующим образом.
Пусть  множество структур в множестве структур на М узлах
множество структур в множестве структур на М узлах  каждая из которых содержит
каждая из которых содержит  линий связи. Необходимо найти такое подмножество
линий связи. Необходимо найти такое подмножество  для которого
для которого

и выполняется ограничение

где С — минимальная реберная связность сети.
Из множества  должна быть выбрана структура
должна быть выбрана структура  для которой выполняется условие
для которой выполняется условие

где  — затраты на создание и эксплуатацию линий связи
— затраты на создание и эксплуатацию линий связи 
Известно, что условию (4.34) при ограничении (4.35) отвечают реберно-критические структуры связности т. Число таких структур больше  что делает прямой перебор для поиска
что делает прямой перебор для поиска  неэффективным.
неэффективным.
Содержание излагаемого метода, являющегося эвристическим, состоит в совместном решении задач (4.34) и (4.35) путем синтеза структуры как суперпозиции последовательности независимых гамильтоновых циклов.
Соответствующий алгоритм для четных  включает следующие шаги.
включает следующие шаги.
Шаг 0. Ввод исходных данных: 
Шаг 1. Поиск минимального гамильтонова цикла 
Шаг 2. Если  то останов, иначе переход к шагу 3.
то останов, иначе переход к шагу 3.
Шаг  и переход к шагу 1.
и переход к шагу 1.
При нечетном значении  после окончания алгоритма каждый узел дополнительно соединяется с наиболее удаленным узлом, имеющим степень менее
после окончания алгоритма каждый узел дополнительно соединяется с наиболее удаленным узлом, имеющим степень менее 
В алгоритме может быть учтено ограничение по суммарным допустимым затратам. С этой целью после построения каждого очередного гамильтонова цикла должны подсчитываться суммарные затраты. Если они превышают допустимые, то требования по связности не могут быть выполнены.
Поиск минимального гамильтонова цикла сводится к решению задачи коммивояжера, относящейся к классу задач целочисленного программирования. Применительно к рассматриваемому случаю приемлемо использование эвристического алгоритма построения минимального гамильтонова цикла [24]. Основная эвристика при этом состоит в том, что маршрут, проходящий через счетное множество узлов, расположенных достаточно компактно, оказывается наиболее коротким, если двигаться от периферии к центру или, наоборот, по кривой, близкой к спирали.
Условие компактности множества узлов проверяется следующим образом. Упорядочиваются все  значений
значений  ассоциируется с расстоянием между узлами
ассоциируется с расстоянием между узлами  и перенумеровываются в
и перенумеровываются в  возрастания
возрастания  Далее находится среднее значение расстояния
Далее находится среднее значение расстояния

и среднее значение разности между 

Если  то множество узлов компактно.
то множество узлов компактно.
Чтобы организовать обход узлов по опирали, необходимо определить ее «центр. Для этого определим  и будем считать, что центр опирали лежит на полпути, т. е. в точке
и будем считать, что центр опирали лежит на полпути, т. е. в точке  Теперь обозначим узлы, для которых определено
Теперь обозначим узлы, для которых определено  соответственно
соответственно  и
и  Сравнивая значение
Сравнивая значение  со значением
со значением  для
для  и
и  находим узел
находим узел  расположенный от
расположенный от  на расстоянии, наименее отличающемся от
на расстоянии, наименее отличающемся от  То же самое проделывается для узла
То же самое проделывается для узла 
Если узлы с номерами  совпадают или расстояние между ними находится в пределах 10% среднего расстояния, то можно считать
совпадают или расстояние между ними находится в пределах 10% среднего расстояния, то можно считать  или
или  центром спирали.
центром спирали.
Обход узлов, начиная с  или
или  можно осуществлять по следующему алгоритму.
можно осуществлять по следующему алгоритму.
Шаг 1. Примем в качестве начальной точки узел  и присвоим ему номер один. Затем просматриваются все значения
и присвоим ему номер один. Затем просматриваются все значения  из узла
из узла  и выбираются два наименьших:
и выбираются два наименьших: 
Шаг 2. Из двух наименьших расстояний выбирается одно, обеспечивающее  и После этого узел
и После этого узел  исключается из дальнейшего рассмотрения на шаге 1. Узлу с номером I присваивается номер 2.
исключается из дальнейшего рассмотрения на шаге 1. Узлу с номером I присваивается номер 2.
Шаг 3. Для  повторяется процедура шагов 1 и 2.
повторяется процедура шагов 1 и 2.
Шаг 4. Обход узлов множества заканчивается при выполнении условия 
В результате реализации алгоритма получается упорядоченная последовательность узлов, которая образует гамильтонов цикл, минимальный с точностью около 5%. Выполнение алгоритма требует примерно в 20 раз меньшего машинного времени, чем метод «ветвей и праниц».
Синтез структуры сети по вероятностным показателям живучести
Одна из возможных методик синтеза структуры сети по вероятностным показателям базируется на обычно приемлемом предположении о том, что при одинаковой защищенности более короткая линия связи имеет меньшую вероятность выхода из строя. При этом задача синтеза формулируется следующим образом: найти структуру  для которой
для которой

где  — множество структур, для которых
— множество структур, для которых  — вероятность выживания структуры
— вероятность выживания структуры  — требования по вероятности выживания;
— требования по вероятности выживания;  — длина линии связи
— длина линии связи 
Получаемая при решении данной задачи сеть, как правило, наиболее экономична из всех сетей с заданной живучестью.
Исходными данными для синтеза являются расстояния между узлами сети и оценку вероятности поражения для линий связи в зависимости от длины. Синтез состоит в выполнении следующего алгоритма [28].
Шаг 0. Синтезируется минимальное дерево 

где  — полносвязный граф сети.
— полносвязный граф сети.
Шаг 1. Промежуточному минимальному графу  ставится в соответствие
ставится в соответствие 
Шаг 2. Производится оценка живучести структуры 
Шаг 3. Проверяется выполнение требований по живучести. Если  , то осуществляется переход к шагу 7, иначе к шагу 5.
, то осуществляется переход к шагу 7, иначе к шагу 5.
Шаг 4. Находится граф 
Шаг 5. Если граф  связный, то находится его минимальное дерево
связный, то находится его минимальное дерево  в противном случае находятся минимальные деревья в каждом из несвязных подграфов:
в противном случае находятся минимальные деревья в каждом из несвязных подграфов: 
Шаг 6. Найденные минимальные деревья суммируются с промежуточным минимальным графом  и осуществляется переход к шагу 2.
и осуществляется переход к шагу 2.
Шаг 7. Минимальному графу присваивается полученный промежуточный минимальный граф  и процесс синтеза оканчивается.
и процесс синтеза оканчивается.
Проверка связности графа может производиться, например, на основе алгоритма построения дерева (Дийкстры, Флойда). Наиболее известный метод синтеза кратчайшего дерева — алгоритм Прима. (Необходимо иметь в виду, что кратчайшее дерево в общем случае не соответствует дереву кратчайших маршрутов 
Алгоритм Прима базируется на двух принципах:
всякий изолированный узел сети должен быть соединен с ближайшим узлом;
всякий изолированный фрагмент сети должен быть соединен с ближайшим фрагментом или изолированным узлом кратчайшей линией связи.
Фрагментом сети называется промежуточная подсеть, образуемая в процессе синтеза.
Сеть с М узлами связывается кратчайшим деревом после  операций применения приведенных принципов, так как на каждом шаге число изолированных узлов уменьшается на единицу.
операций применения приведенных принципов, так как на каждом шаге число изолированных узлов уменьшается на единицу.
В формализованном виде алгоритм Прима включает следующую последовательность шагов.
 Поставить в соответствие фрагменту множество, включающее единственный произвольный узел
Поставить в соответствие фрагменту множество, включающее единственный произвольный узел  и найти узел
и найти узел  для которого выполняется условие
для которого выполняется условие 

Шаг 1. Найти  для которых справедливо условие
для которых справедливо условие 
Шаг 2. Включить в множество узлов и линий связи фрагмента узел  и линию связи
и линию связи 
Шаг 3. Если множество Ф содержит М узлов, то процесс синтеза сети окончен, иначе осуществляется переход к шагу 2 для нового множества узлов и линий связи, входящих в фрагмент.
Алгоритм Прима (позволяет построить минимальное дерево на заданном фиксированном множестве узлов. В ряде случаев, расширяя множество узлов путем введения вспомогательных узлов, можно получить дополнительное сокращение суммарной длины дерева [8].
Структуру любого дерева можно представить как совокупность треугольников. Так, структура, изображенная на рис. 4.6, включает треугольники  Для уменьшения длины линий связи, связывающих заданное множество узлов, с помощью вспомогательных узлов используются следующие положения из тригонометрии:
Для уменьшения длины линий связи, связывающих заданное множество узлов, с помощью вспомогательных узлов используются следующие положения из тригонометрии:

Рис. 4.6

Рис. 4.7
в остроугольных треугольниках кратчайшей сетью, близкой к минимально возможной, является сеть, построенная с помощью одного вспомогательного узла, расположенного на медиане наименьшего угла при удалении от противолежащей углу стороны на расстояние, равное ее длине, деленной на 
в треугольниках, один из углов которых равен или больше 120°, кратчайшей связывающей сетью является сеть, построенная двумя сторонами, составляющими тупой угол (рис. 4.7).
Из элементарной математики известно, что в треугольнике со сторонами  с величины углов (против этих сторон соответственно равны:
с величины углов (против этих сторон соответственно равны:

где  — полупериметр, а
— полупериметр, а 
Таким образом, зная расстояния между узлами в каждом треугольнике минимального дерева, можно определить, возможна ли дополнительная минимизация его длины с помощью
дополнительных узлов. Целесообразность использования вспомогательных узлов  получаемым при этом выигрышем в суммарной длине сети и возможностью создания дополнительных узлов.
получаемым при этом выигрышем в суммарной длине сети и возможностью создания дополнительных узлов.
На практике может использоваться эвристический метод синтеза структуры сети. Данный метод предусматривает после построения кратчайшего дерева итеративное добавление линий связи с оценкой после каждого шага вероятности выживания сети. Включение новых линий связи осуществляется эвристически при соблюдении следующих рекомендаций:
включаемая линия должна образовывать цикл как можно большей длины;
линия должна быть как можно более короткой.
В процессе синтеза структуры сети приходится неоднократно оценивать вероятность связности сети, промежуточных вариантов и фрагментов. Наиболее характерные методы оценки приводятся ниже.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1 ОБЩАЯ ХАРАКТЕРИСТИКА СЕТЕЙ ПЕРЕДАЧИ ИНФОРМАЦИИ АСУ
- 1.1. СЕТЬ СВЯЗИ КАК ПОДСИСТЕМА СИСТЕМЫ УПРАВЛЕНИЯ
- 1.2. ПРИНЦИПЫ ПОСТРОЕНИЯ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ
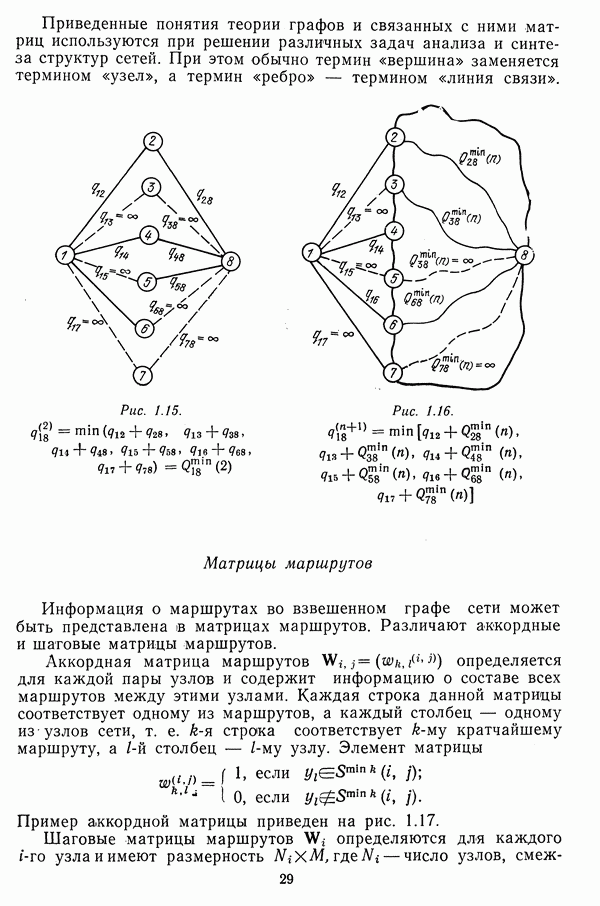
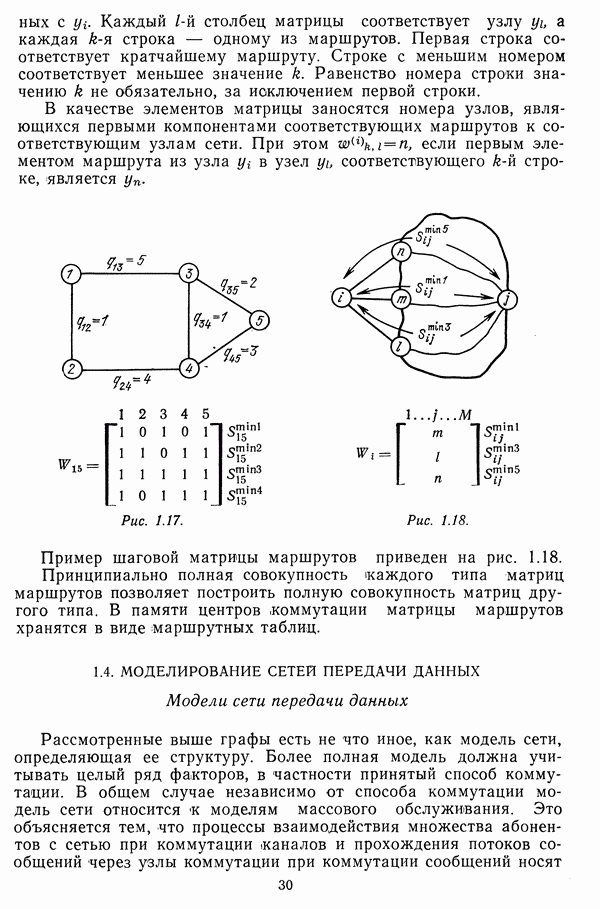
- 1.3. ПРЕДСТАВЛЕНИЕ СТРУКТУР СЕТЕЙ
- Кратчайшие маршруты во взвешенных графах
- Матрицы, определяющие структуру сетей
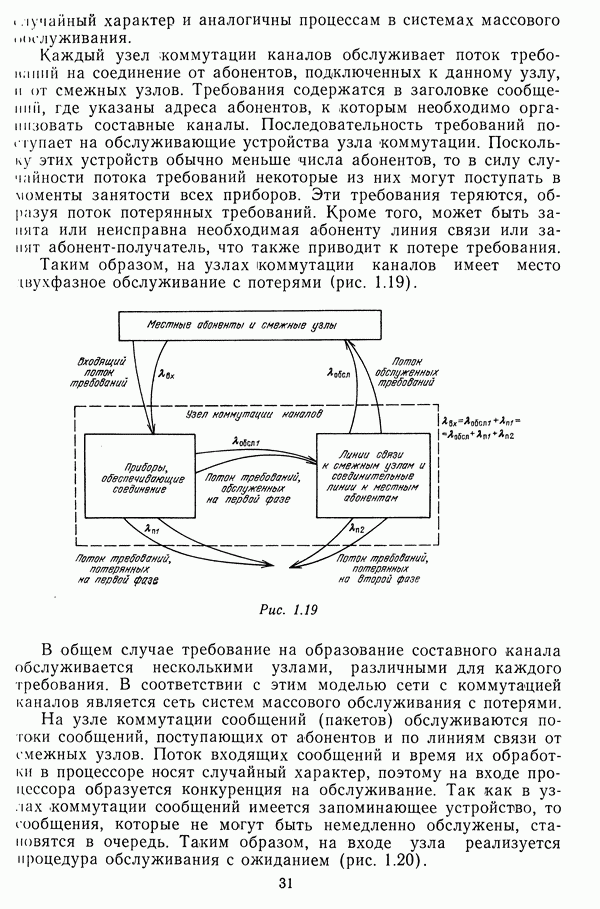
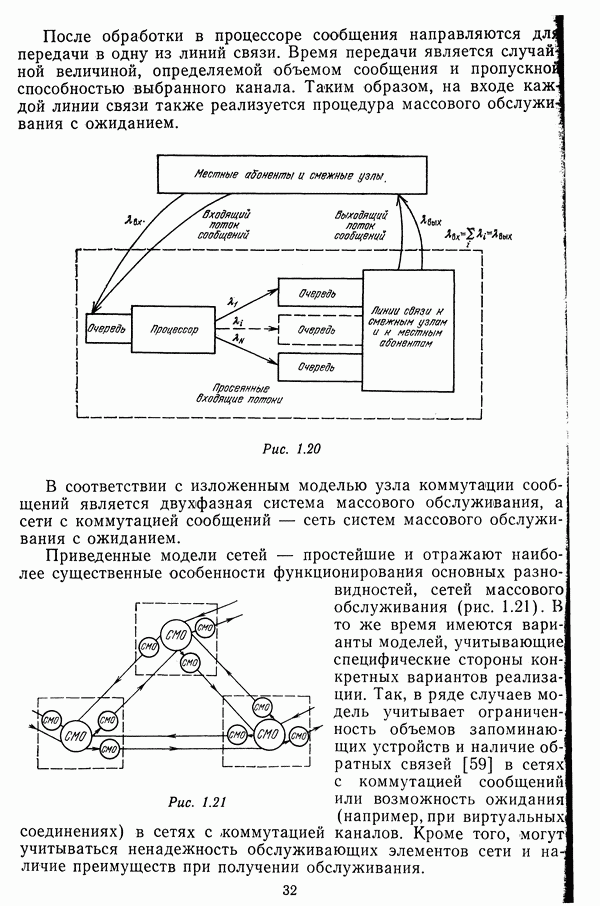
- Матрицы маршрутов
- 1.4. МОДЕЛИРОВАНИЕ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ
- Математические модели, используемые при расчете сетей
- Потоки в сетях передачи данных
- ГЛАВА 2. ПРИНЦИПЫ ФУНКЦИОНИРОВАНИЯ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ
- 2.1. СТРУКТУРА ФУНКЦИОНАЛЬНОГО ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ
- 2.2. ФОРМАЛИЗАЦИЯ СООБЩЕНИИ В СЕТЯХ ПЕРЕДАЧИ ДАННЫХ
- 2.3. АДРЕСОВАНИЕ СООБЩЕНИЙ
- 2.4. ПРОЦЕДУРЫ ВЫБОРА МАРШРУТОВ
- 2.5. РЕГУЛИРОВАНИЕ ПОТОКОВ СООБЩЕНИЙ ПО ПРИОРИТЕТАМ
- 2.6. УПРАВЛЕНИЕ В СЕТЯХ ПЕРЕДАЧИ ДАННЫХ
- Глава 3. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ МАРШРУТИЗАЦИИ И УПРАВЛЕНИЯ В СЕТЯХ ПЕРЕДАЧИ ДАННЫХ
- 3.2. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДЕТЕРМИНИРОВАННЫХ ПРОЦЕДУР ВЫБОРА МАРШРУТОВ
- 3.3. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ПОИСКОВЫХ ПРОЦЕДУР ВЫБОРА МАРШРУТОВ
- 3.4. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ КВАЗИСЛУЧАИНЫХ ПРОЦЕДУР ВЫБОРА МАРШРУТОВ
- 3.5. ФИЗИЧЕСКИЕ ВЕРСИИ ВЕСОВ ЭЛЕМЕНТОВ СЕТИ
- 3.6. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ УПРАВЛЕНИЯ ВНЕШНИМИ ПОТОКАМИ СООБЩЕНИЙ
- Глава 4. ВОПРОСЫ ПРОЕКТИРОВАНИЯ СЕТЕЙ ПЕРЕДАЧИ ИНФОРМАЦИИ АСУ
- 4.1. ЗАДАЧИ СИСТЕМНОГО ПРОЕКТИРОВАНИЯ СЕТЕЙ
- 4.2. РАЗМЕЩЕНИЕ УЗЛОВ КОММУТАЦИИ
- Оптимизация числа узлов и их размещения при независимом положении абонентов
- Размещение узлов для связи с мобильными абонентами
- Размещение центра управления сетью
- 4.3. СИНТЕЗ СТРУКТУРЫ СЕТИ
- Синтез структуры сети минимальной стоимости при заданной связности
- 4.4. РАСЧЕТ МОЩНОСТИ ЛИНИИ СВЯЗИ СЕТИ
- Оптимизация мощности линий связи при произвольном виде функций затрат
- Методика выбора каналов передачи данных для линий связи с заданной мощностью
- 4.5. ОПТИМИЗАЦИЯ ПАРАМЕТРОВ ЖИВУЧЕСТИ ЭЛЕМЕНТОВ СЕТИ
- 4.6. ВЫБОР ПАРАМЕТРОВ НАДЕЖНОСТИ ЭЛЕМЕНТОВ СЕТИ
- Методы вычисления вероятности связности сети
- Выбор параметров надежности центров коммутации
- Аналитическая оптимизация внутренних показателей надежности элементов сети
- Оптимизация внутренних показателей надежности при произвольном виде функций затрат
- СПИСОК ЛИТЕРАТУРЫ