| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Методы вычисления вероятности связности сети
Задача вычисления вероятности связности сети является по своей природе комбинаторной и связана с необходимостью перебора вариантов, число которых быстро возрастает при увеличении
размеров сети. Совокупность методов решения этой задачи может быть разбита на аналитические, методы предельных оценок и методы Монте-Карло. Ниже приводятся наиболее характерные методы из этих групп.
Метод перебора подграфов. Если каждой линии связи поставить в соответствие двоичную переменную  причем
причем  при наличии линии связи и
при наличии линии связи и  при выходе линии из строя, то каждое из
при выходе линии из строя, то каждое из  состояний сети можно представить
состояний сети можно представить  -мерным двоичным вектором.
-мерным двоичным вектором.
При заданных вероятностях исправности линий связи  вероятность состояния сети определяется следующим образом:
вероятность состояния сети определяется следующим образом:

Введя переменную

можно записать соотношение для вычисления вероятности связности сети:

Практически вычисления сводятся к перебору всех  двоичных векторов и проверке на каждом шаге связности подграфов, соответствующих каждому из них.
двоичных векторов и проверке на каждом шаге связности подграфов, соответствующих каждому из них.
Изложенный метод весьма прост для расчетов на ЭВМ, но для больших сетей нереализуем из-за объема вычислений. Последний может быть уменьшен, если не рассматривать варианты, для которых 
Асимптотические оценки вероятности связности. При сравнении вариантов структуры сети могут быть использованы асимптотические оценки нижней и верхней границ вероятности связности. Нижняя граница [17]

Максимум определяется по множеству базисных сечений. Верхняя оценка [16]

При использовании граничных оценок вероятности связности сети следует соблюдать определенную осторожность, так как разброс получаемых значений может быть в зависимости от конкретной структуры различным. В связи с этим, прежде чем выбрать, максимум граничного значения в качестве критерия оптимальности в задаче оптимизации надежности, целесообразно произвести пробный расчет исследуемой структуры при усредненных значениях надежности элементов. Если Рентах и  отличаются незначительно, то граничные значения являются приемлемым показателем для критерия оптимальности.
отличаются незначительно, то граничные значения являются приемлемым показателем для критерия оптимальности.
При использовании граничных методов значительно сокращается объем вычислений.
Метод Монте-Карло. Отмеченные недостатки методов, относящихся к предыдущим группам, делают наиболее предпочтительным использование для оценки вероятности связности метода Монте-Карло. Данный метод при значительной простоте реализующего алгоритма позволяет получить результаты сколь угодно высокой точности практически для любой реализуемой структуры сети.
В качестве исходных данных составляется вектор  Далее производится определенное число экспериментов в каждом из которых генерируется
Далее производится определенное число экспериментов в каждом из которых генерируется  случайных чисел
случайных чисел  с заданным законом распределения и строится матрица смежностей. Если оказывается, что
с заданным законом распределения и строится матрица смежностей. Если оказывается, что  то соответствующий элемент матрицы смежности принимается равным 0, в противном случае — 1. Таким образом, образуется некоторый случайный подграф сети
то соответствующий элемент матрицы смежности принимается равным 0, в противном случае — 1. Таким образом, образуется некоторый случайный подграф сети 
После проведения всех  экспериментов с проверкой связности в каждом из них вычисляется вероятность связности
экспериментов с проверкой связности в каждом из них вычисляется вероятность связности

где  определяется (4.68).
определяется (4.68).
Точность получаемого значения  определяется числом проведенных экспериментов [24]:
определяется числом проведенных экспериментов [24]:

где  — требуемая точность результатов; а — вероятность обеспечения заданной точности результатов.
— требуемая точность результатов; а — вероятность обеспечения заданной точности результатов.
Для определения связности подграфов целесообразно использовать метод Дийкстры. Отсутствие в дереве весов кратчайших маршрутов элементов, равных бесконечности, свидетельствует о связности структуры сети.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1 ОБЩАЯ ХАРАКТЕРИСТИКА СЕТЕЙ ПЕРЕДАЧИ ИНФОРМАЦИИ АСУ
- 1.1. СЕТЬ СВЯЗИ КАК ПОДСИСТЕМА СИСТЕМЫ УПРАВЛЕНИЯ
- 1.2. ПРИНЦИПЫ ПОСТРОЕНИЯ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ
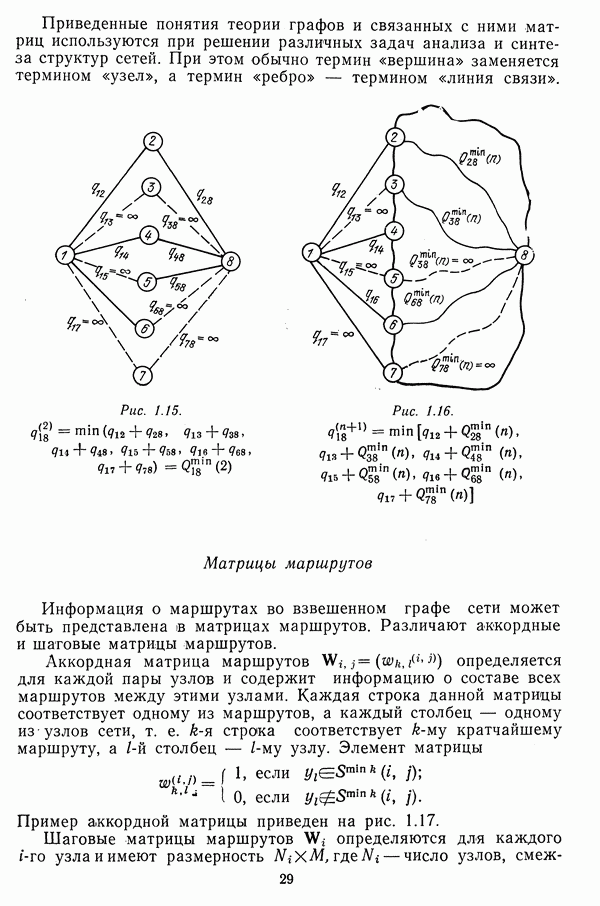
- 1.3. ПРЕДСТАВЛЕНИЕ СТРУКТУР СЕТЕЙ
- Кратчайшие маршруты во взвешенных графах
- Матрицы, определяющие структуру сетей
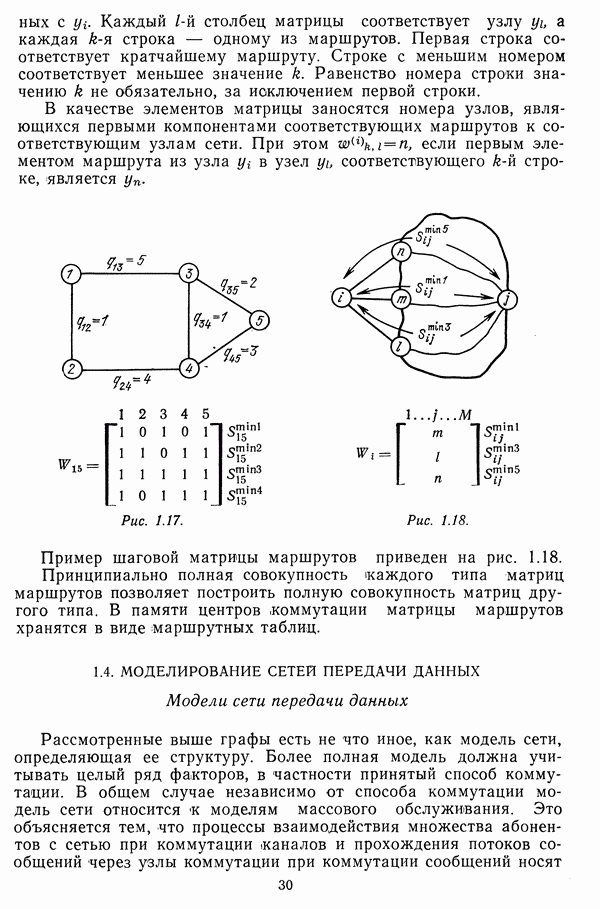
- Матрицы маршрутов
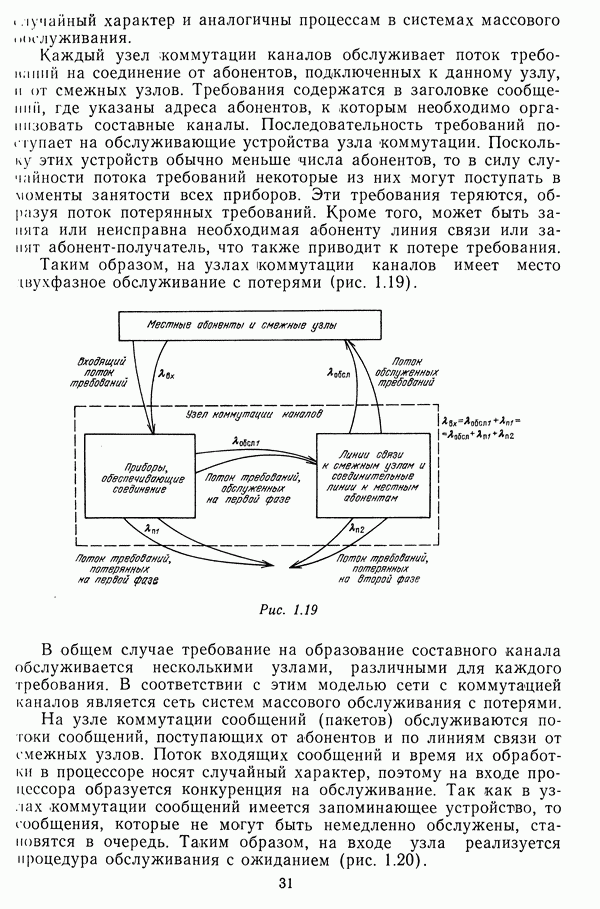
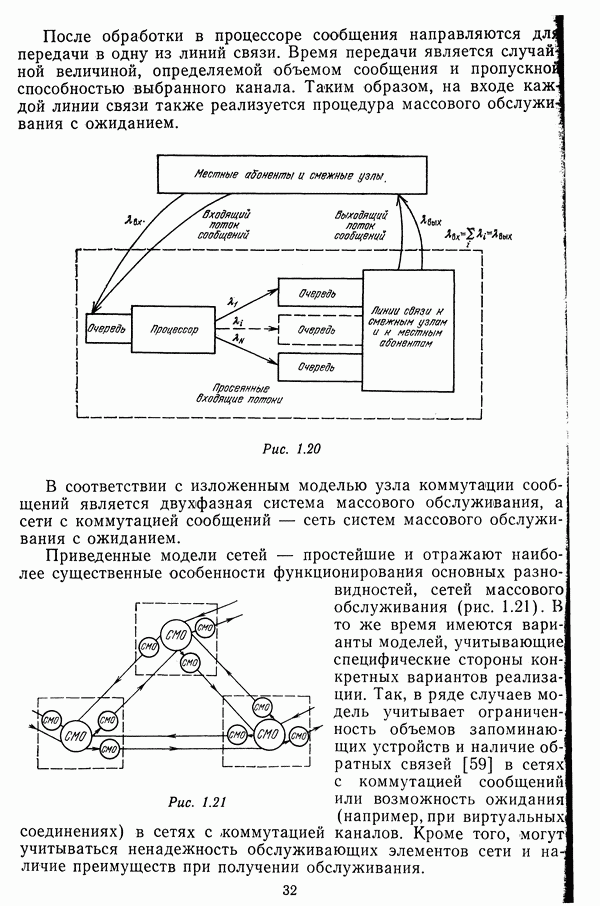
- 1.4. МОДЕЛИРОВАНИЕ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ
- Математические модели, используемые при расчете сетей
- Потоки в сетях передачи данных
- ГЛАВА 2. ПРИНЦИПЫ ФУНКЦИОНИРОВАНИЯ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ
- 2.1. СТРУКТУРА ФУНКЦИОНАЛЬНОГО ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ
- 2.2. ФОРМАЛИЗАЦИЯ СООБЩЕНИИ В СЕТЯХ ПЕРЕДАЧИ ДАННЫХ
- 2.3. АДРЕСОВАНИЕ СООБЩЕНИЙ
- 2.4. ПРОЦЕДУРЫ ВЫБОРА МАРШРУТОВ
- 2.5. РЕГУЛИРОВАНИЕ ПОТОКОВ СООБЩЕНИЙ ПО ПРИОРИТЕТАМ
- 2.6. УПРАВЛЕНИЕ В СЕТЯХ ПЕРЕДАЧИ ДАННЫХ
- Глава 3. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ МАРШРУТИЗАЦИИ И УПРАВЛЕНИЯ В СЕТЯХ ПЕРЕДАЧИ ДАННЫХ
- 3.2. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДЕТЕРМИНИРОВАННЫХ ПРОЦЕДУР ВЫБОРА МАРШРУТОВ
- 3.3. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ПОИСКОВЫХ ПРОЦЕДУР ВЫБОРА МАРШРУТОВ
- 3.4. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ КВАЗИСЛУЧАИНЫХ ПРОЦЕДУР ВЫБОРА МАРШРУТОВ
- 3.5. ФИЗИЧЕСКИЕ ВЕРСИИ ВЕСОВ ЭЛЕМЕНТОВ СЕТИ
- 3.6. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ УПРАВЛЕНИЯ ВНЕШНИМИ ПОТОКАМИ СООБЩЕНИЙ
- Глава 4. ВОПРОСЫ ПРОЕКТИРОВАНИЯ СЕТЕЙ ПЕРЕДАЧИ ИНФОРМАЦИИ АСУ
- 4.1. ЗАДАЧИ СИСТЕМНОГО ПРОЕКТИРОВАНИЯ СЕТЕЙ
- 4.2. РАЗМЕЩЕНИЕ УЗЛОВ КОММУТАЦИИ
- Оптимизация числа узлов и их размещения при независимом положении абонентов
- Размещение узлов для связи с мобильными абонентами
- Размещение центра управления сетью
- 4.3. СИНТЕЗ СТРУКТУРЫ СЕТИ
- Синтез структуры сети минимальной стоимости при заданной связности
- 4.4. РАСЧЕТ МОЩНОСТИ ЛИНИИ СВЯЗИ СЕТИ
- Оптимизация мощности линий связи при произвольном виде функций затрат
- Методика выбора каналов передачи данных для линий связи с заданной мощностью
- 4.5. ОПТИМИЗАЦИЯ ПАРАМЕТРОВ ЖИВУЧЕСТИ ЭЛЕМЕНТОВ СЕТИ
- 4.6. ВЫБОР ПАРАМЕТРОВ НАДЕЖНОСТИ ЭЛЕМЕНТОВ СЕТИ
- Методы вычисления вероятности связности сети
- Выбор параметров надежности центров коммутации
- Аналитическая оптимизация внутренних показателей надежности элементов сети
- Оптимизация внутренних показателей надежности при произвольном виде функций затрат
- СПИСОК ЛИТЕРАТУРЫ