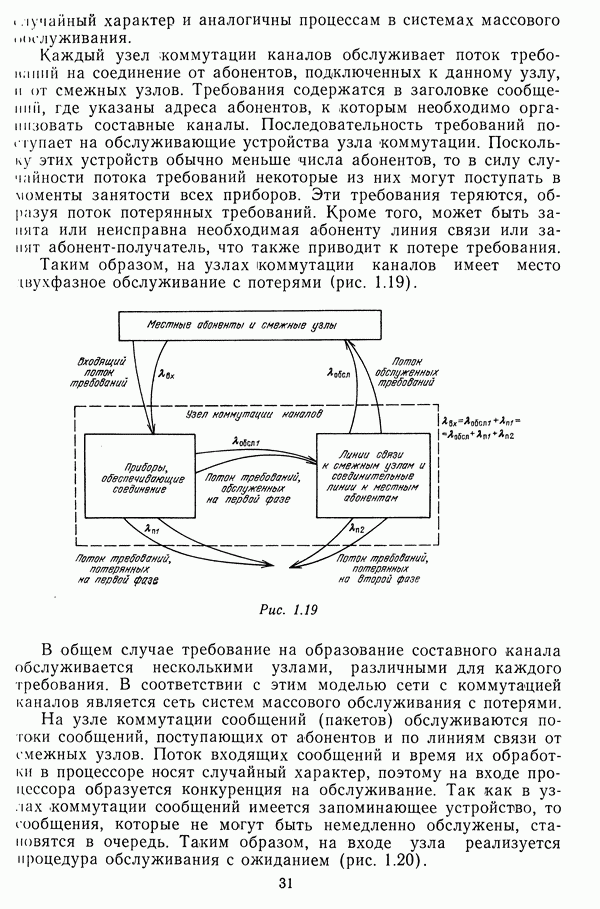
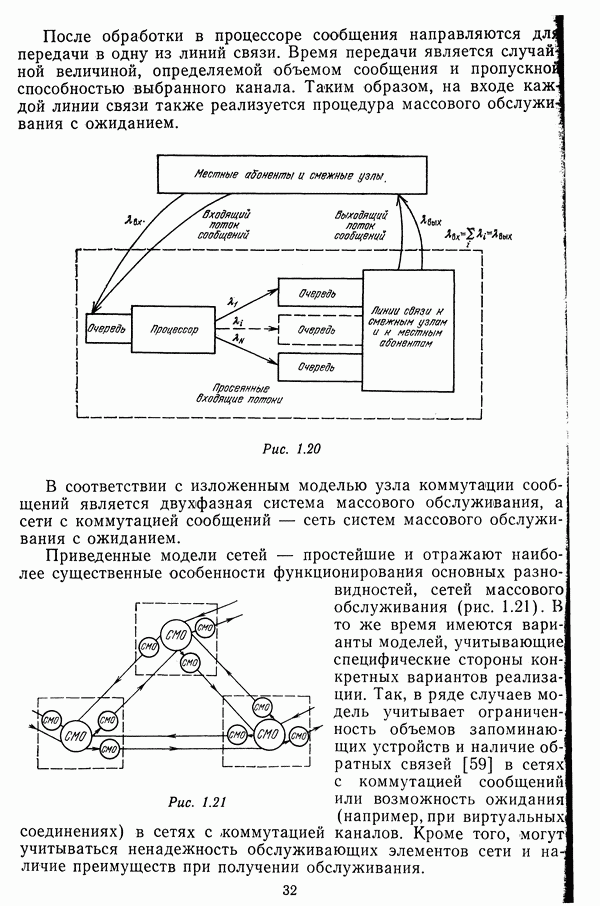
Матрицы, определяющие структуру сетей

Структура сети может быть задана матрицей смежностей или матрицей инциденций. Матрицей смежностей называется матрица размерности элементы которой

Для графа на рис. 1.12 матрица смежностей имеет вид

Матрицей инциденций называется матрица размерности элементы которой

Матрица инциденций для графа на рис. 1.12 имеет вид

Между матрицами смежности и инциденций одного и того же графа существует взаимно-однозначное соответствие

где — транспонированная матрица инциденций; I — единичная матрица размерности

На основе матрицы смежностей можно определить ряд характеристик структуры сети.

Теорема. Элемент степени матрицы смежностей равен числу маршрутов длины из вершины в у

Следствие 1. Расстояние между вершинами равно наименьшему из целых чисел для которых элемент степени матрицы А отличен от нуля.

Следствие 2. Элемент матрицы равен степени вершины у и т. е.

В некоторых случаях используется матрица связности или достижимости, в которой элемент если между вершинами имеется, по крайней мере, один маршрут. Для связного графа матрица связности является единичной матрицей.

Таким образом, если структура сети задана матрицей смежностей, то можно путем вычислений определить, имеется ли хотя бы один маршрут между любой парой узлов.

При ограничении на длину маршрута можно рассматривать матрицу ограниченной связности. В этой матрице элемент если имеется хотя бы один маршрут длины не больше допустимой между узлами

При решении ряда сетевых задач используют матрицы циклов и матрицы сечений. В матрице циклов каждая строка соответствует циклу в графе, а каждый столбец — одному из ребер. В матрице простых сечений каждая строка соответствует сечению в графе, а каждый столбец — также одному из ребер. Таким образом, если в одной из этих матриц элемент то ребро входит соответственно в цикл или сечение.

Для представления взвешенных графов обычно используются не матрицы смежностей, а матрицы весов размерности Элементы данной матрицы равны: весу ребра для смежных вершин бесконечности для несмежных вершин нулю при

Применительно к матрице весов представляет интерес следующая теорема.

Теорема. Если операцию суммирования заменить операцией а операцию умножения — операцией суммирования, то элемент степени матрицы весов равен весу кратчайшего маршрута между и у среди всех маршрутов между этими вершинами длиною

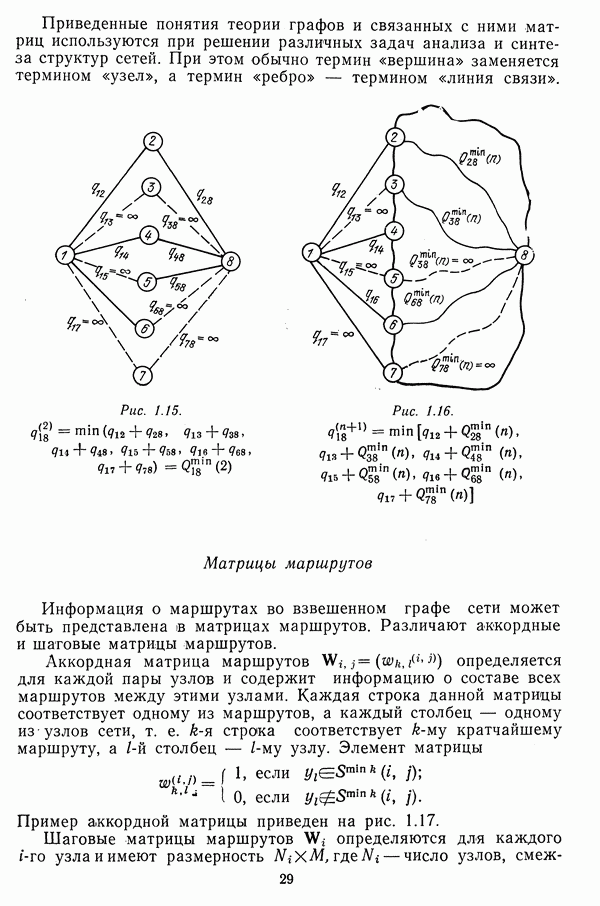
Доказательство. Элемент второй степени матрицы весов

После преобразования операций

где — вес кратчайшего маршрута между вершинами среди всех маршрутов длиной 2 (рис. 1.15).

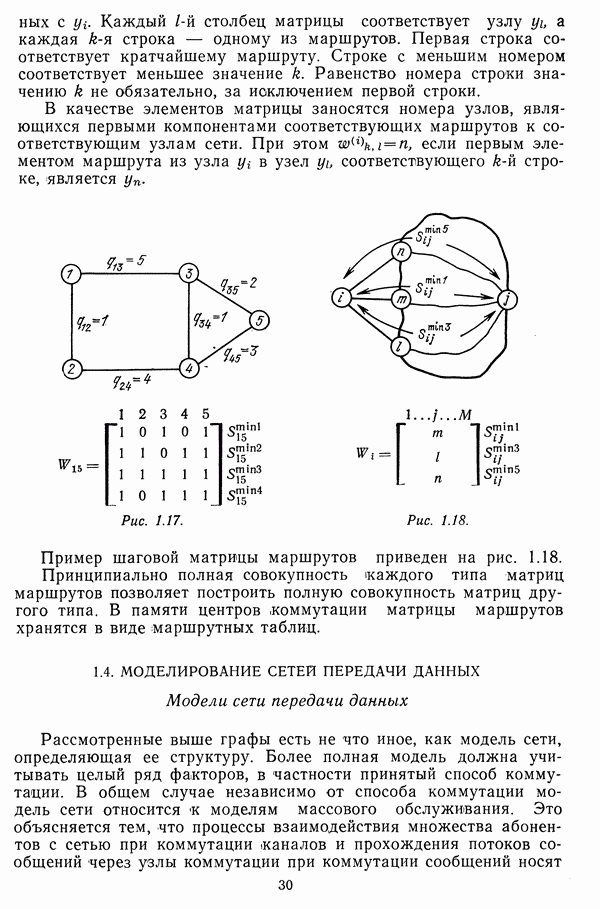
Элемент третьей степени матрицы весов

или после преобразования операций суммирования в операцию

где — вес кратчайшего маршрута из вершины в у среди всех маршрутов длиной 3. Далее по индукции получим (рис. 1.16)

что и требовалось доказать.

Приведенные понятия теории графов и связанных с ними матриц используются при решении различных задач анализа и синтеза структур сетей. При этом обычно термин «вершина» заменяется термином «узел», а термин «ребро» — термином «линия связи».

Рис. 1.15.

Рис. 1.16.