| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.5. ФИЗИЧЕСКИЕ ВЕРСИИ ВЕСОВ ЭЛЕМЕНТОВ СЕТИ
Критерии кратчайших маршрутов
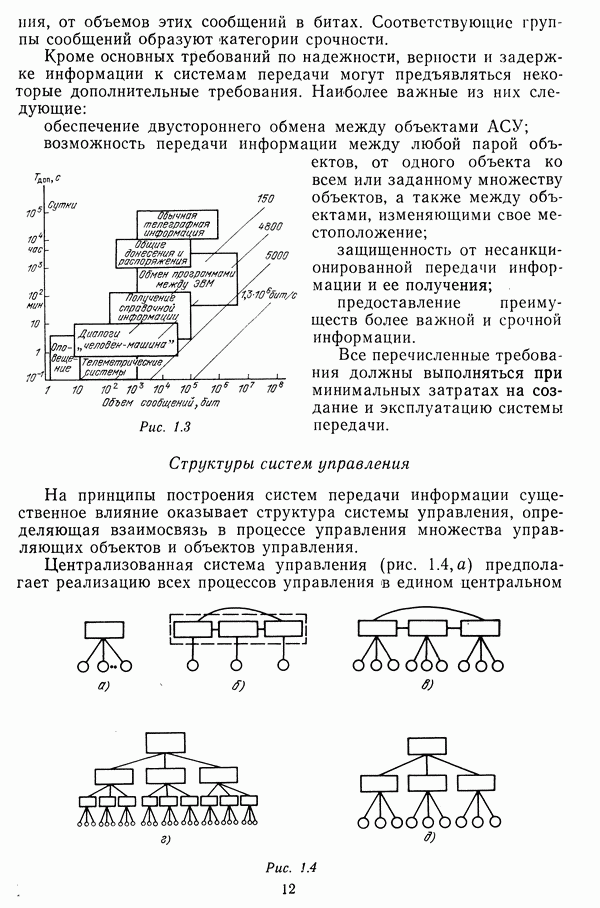
Понятие кратчайшего маршрута является условным и определяется выбранным критерием. В свою очередь критерий кратчайшего маршрута зависит от показателя, используемого в качестве весов элементов сети. Все многообразие возможных критериев образует три класса.
К первому классу отнесем критерии, основанные на аддитивных показателях таких, как длины линий связи, стоимости передачи сообщений, параметры задержки. При этом критерий кратчайшего маршрута

где  маршрут между некоторой шарой узлов;
маршрут между некоторой шарой узлов;  — множество всех таких маршрутов.
— множество всех таких маршрутов.
Второй класс образуют критерии, основанные на мультипликативных показателях, обычно вероятностного содержания. Сюда относятся: коэффициент исправного действия; вероятность безошибочной передачи; вероятность своевременной доставки. Для этого класса обобщенная запись имеет следующий вид:

Для упрощения критерий второго класса обычно приводят к эквивалентному критерию вида (3.13) путем логарифмирования:

К третьему классу относится критерий максимина, физическим параметром для которого является, например, пропускная способность элементов сети. Записывается данный критерий следующим образом:

При этом кратчайшим будем маршрут, имеющий максимальную пропускную способность, которая для каждого маршрута определяется минимальной пропускной способностью входящих в него линий связи. Данный критерий не приводится к общему виду
(3.13), что необходимо учитывать при его использовании в задачах маршрутизации.
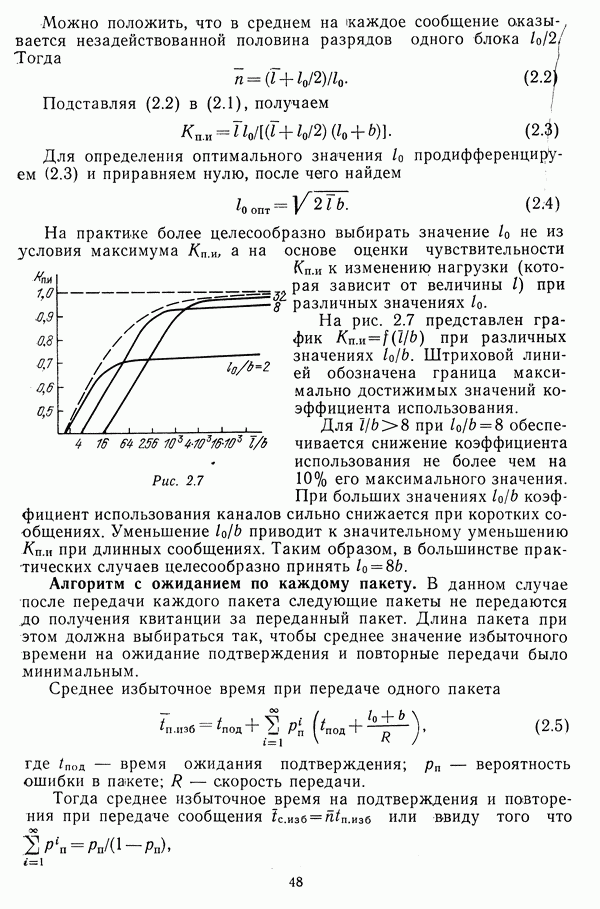
В сетях с коммутацией каналов в качестве критерия кратчайшего маршрута обычно выбираются минимум длины, максимум надежности или минимум вероятности ошибки. Сети с коммутацией сообщений (пакетов) в большинстве случаев базируются на временных версиях весов. Соответствующие характеристики будут рассмотрены в следующих разделах.
Виртуальное время ожидания
Виртуальное время ожидания является фактическим временем ожидания для некоторого сообщения, поступившего в конкретный момент времени.
При отсутствии перерывов процесса передачи виртуальное время ожидания  есть величина детерминированная и полностью определяется числом сообщений в очереди в момент измерения
есть величина детерминированная и полностью определяется числом сообщений в очереди в момент измерения  их объемами
их объемами  и пропускной способностью линии связи:
и пропускной способностью линии связи:

Перерывы в процессе передачи, обусловленные особенностями алгоритмов защиты от ошибок, отказами и обслуживанием приоритетных сообщений, приводят к тому, что реальное значение виртуального времени ожидания становится случайным:  где
где  — случайная составляющая, определяемая числом перерывов в процессе передачи и их длительностью.
— случайная составляющая, определяемая числом перерывов в процессе передачи и их длительностью.
Полагая, что перерывы являются событиями взаимонезависимыми, можно записать функцию распределения  для двух ситуаций. Первая ситуация предполагает рабочее состояние процесса передачи в момент измерения. Для этого случая
для двух ситуаций. Первая ситуация предполагает рабочее состояние процесса передачи в момент измерения. Для этого случая

Во второй ситуации момент измерения приходится на интервал перерыва процесса передачи:

В выражениях (3.17) и  — вероятность того, что за интервал времени
— вероятность того, что за интервал времени  произойдет
произойдет  нарушений процесса передачи;
нарушений процесса передачи;  — функция распределения
— функция распределения  в случае возникновения
в случае возникновения  перерывов.
перерывов.
Известно, что при простейшем потоке событий их число на заданном интервале распределено по закону Пуассона, а время до наступления  события подчиняется гамма-распределению с параметром
события подчиняется гамма-распределению с параметром  Исходя из этого можно записать:
Исходя из этого можно записать:

где  неполная гамма-функция, а
неполная гамма-функция, а  среднее время перерывов.
среднее время перерывов.
Таким образом, функция распределения случайной составляющей виртуального времени ожидания в двух ситуациях, соответствующих моменту измерения, будет иметь следующий вид:

где  — соответственно неполная гамма-функция и модифицированная функция Бесселя нулевого порядка.
— соответственно неполная гамма-функция и модифицированная функция Бесселя нулевого порядка.
При вычислениях по полученным соотношениям необходимо использовать таблицы значений  ограничиваясь первыми членами в соотношении для
ограничиваясь первыми членами в соотношении для 
Окончательно функция распределения  при коэффициенте готовности линии передачи
при коэффициенте готовности линии передачи  будет определяться выражением
будет определяться выражением

Найденная функция распределения позволяет, определив непосредственно детерминированную составляющую виртуального времени ожидания, оценить с некоторой вероятностью случайную составляющую. Вычисления могут производиться путем итераций.
При использовании в качестве веса виртуального времени ожидания слабо учитывается статистика процесса в системе обслуживания. Для учета и текущей ситуации, и статистического поведения системы может быть использована оценка  где
где  — среднее время ожидания сообщения в системе.
— среднее время ожидания сообщения в системе.
Прогнозируемое время ожидания
При известных характеристиках времени ожидания в системах обслуживания сети в качестве весов можно использовать прогнозируемое время ожидания, вычисляемое на основе измерения последовательности значений виртуального времени ожидания.
Для случая, когда процесс носит стационарный характер и известна функция распределения времени ожидания со средним  и дисперсией
и дисперсией  такая оценка может быть получена на основе линейного предсказания. Наилучший алгоритм линейного предсказания обеспечивает минимум среднеквадратической ошибки.
такая оценка может быть получена на основе линейного предсказания. Наилучший алгоритм линейного предсказания обеспечивает минимум среднеквадратической ошибки.
Если обозначить случайное время ожидания некоторого  сообщения
сообщения  прогнозируемую оценку времени ожидания
прогнозируемую оценку времени ожидания  сообщения
сообщения  а его действительное время ожидания
а его действительное время ожидания  то проблема предсказания будет состоять в построении правила, при котором обеспечивается минимум математического ожидания значения
то проблема предсказания будет состоять в построении правила, при котором обеспечивается минимум математического ожидания значения  Такая оценка может быть получена на
Такая оценка может быть получена на
основе информации о времени ожидания некоторого числа предшествующих сообщений.
Соответствующий алгоритм приведен в  и определяется соотношением
и определяется соотношением

где 

 — нагрузка системы.
— нагрузка системы.
При вычисленных коэффициентах  и известных параметрах
и известных параметрах  алгоритм будет состоять в измерении значения
алгоритм будет состоять в измерении значения  для каждого очередного поступающего сообщения и накоплении полученных значений путем взвешенного суммирования. Значение
для каждого очередного поступающего сообщения и накоплении полученных значений путем взвешенного суммирования. Значение  по сути является виртуальным временем ожидания.
по сути является виртуальным временем ожидания.
Получаемая при реализации данного алгоритма погрешность прогнозирования

В случае, когда последовательность  имеет марковский характер, алгоритм упрощается, так как в этом случае для прогноза может быть использовано только последнее измеренное значение виртуального времени ожидания. При этом оценка
имеет марковский характер, алгоритм упрощается, так как в этом случае для прогноза может быть использовано только последнее измеренное значение виртуального времени ожидания. При этом оценка

Соответствующий алгоритм состоит в определении значения  и вычислении по приведенному соотношению. Получаемая в данном случае погрешность
и вычислении по приведенному соотношению. Получаемая в данном случае погрешность

Глубина прогноза  должна выбираться таким образом, чтобы погрешность оценки обеспечивала целесообразность прогнозирования.
должна выбираться таким образом, чтобы погрешность оценки обеспечивала целесообразность прогнозирования.
Производная среднего времени задержки сообщений
В качестве весов линий связи может использоваться среднее время задержки, которое для пуассоновско-экспоненциальной системы с учетом ненадежности обслуживающего прибора
определяется соотношением (3.8). Данное соотношение получено на основе результата для системы с абсолютным приоритетом и конечным источником приоритетных требований путем интерпретации приоритетных заявок перерывами связи. Интенсивность обслуживания при этом выражается через средний объем сообщений  и пропускную способность линии связи. Процесс перерывов связи характеризуется коэффициентом простоя и средней длительностью перерывов.
и пропускную способность линии связи. Процесс перерывов связи характеризуется коэффициентом простоя и средней длительностью перерывов.
Все перечисленные параметры можно определить путем статистических измерений. Из формулы  видно, что среднее время задержки является существенно нелинейной функцией
видно, что среднее время задержки является существенно нелинейной функцией 
Потоки сообщений и потоки перерывов связи на практике не являются строго стационарными, т. е. на отдельных интервалах могут иметь приращения различного знака. При этом будут получать приращения также 
В связи с нелинейностью функции  приращения
приращения  могут привести к различной реакции в статистическом поведении системы в зависимости от их исходных значений. Таким образом, при упорядочении маршрутов по критерию минимума
могут привести к различной реакции в статистическом поведении системы в зависимости от их исходных значений. Таким образом, при упорядочении маршрутов по критерию минимума  возможны решения, которые будут далеки от оптимального в случае отклонения показателей нагрузки в надежности.
возможны решения, которые будут далеки от оптимального в случае отклонения показателей нагрузки в надежности.
Исходя из этого (целесообразно в качестве веса линий связи дать не само значение  а скорость её изменения при изменении параметров нагрузки и надежности. Такой подход без учета параметров надежности был предложен в [12], где в качестве веса линий связи используется производная среднего времени задержки.
а скорость её изменения при изменении параметров нагрузки и надежности. Такой подход без учета параметров надежности был предложен в [12], где в качестве веса линий связи используется производная среднего времени задержки.
С учетом параметров надежности аналогичный показатель получим, если найдем частные производные выражения (3.8):

— и сложим их. Тогда для вычисления веса будем иметь следующее соотношение:

Использование полученного показателя в качестве веса позволяет при упорядочении маршрутов отдавать предпочтение маршрутам, которые менее критичны к изменению интенсивности потоков сообщений и отказов.
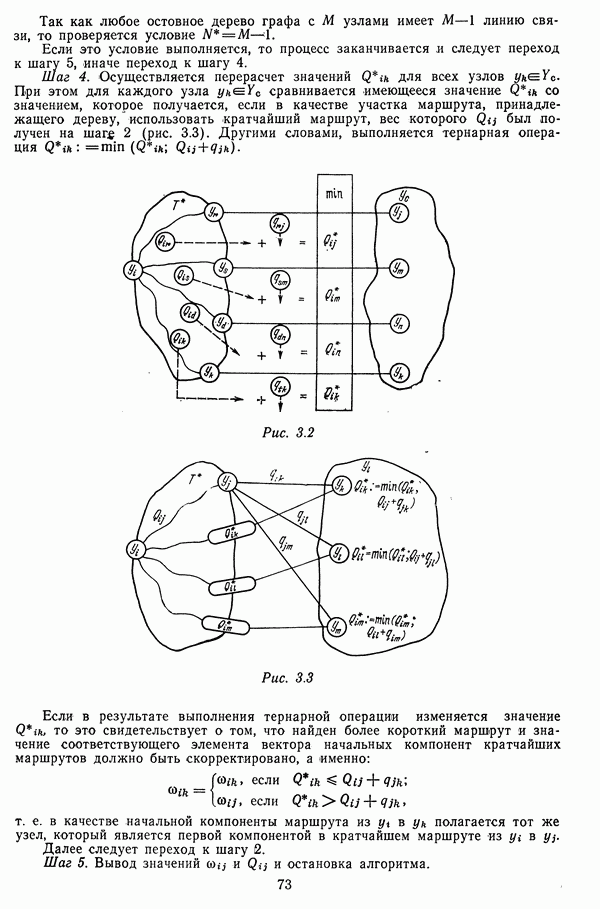
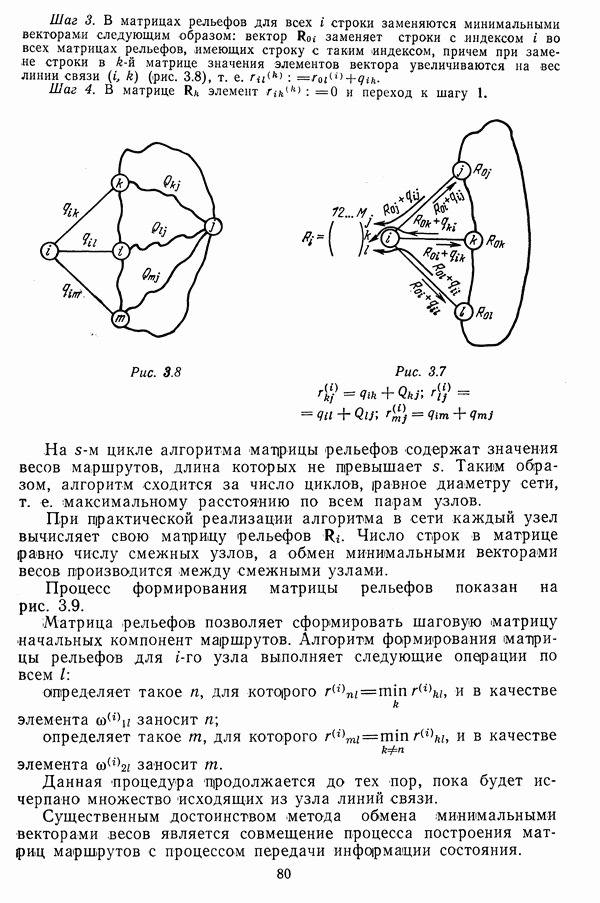
В качестве примера рассмотрим следующую ситуацию. Пусть необходимо установить отношение предпочтения между двумя маршрутами:  Первичные параметры линий и результаты расчетов весов сведены в табл. 3.1.
Первичные параметры линий и результаты расчетов весов сведены в табл. 3.1.
Из таблицы видно, что при выборе в качестве веса линий связи среднего времени задержки кратчайшим является маршрут 
ТАБЛИЦА 3.1 (см. скан)

Рис. 3.11
В случае использования суммы производных предпочтение должно быть отдано маршруту  Полученное перераспределение обусловлено тем, что линии связи маршрута
Полученное перераспределение обусловлено тем, что линии связи маршрута  работают в области более высокой нагрузки, в которой среднее время задержки резко возрастает при небольшом увеличении потока сообщений или потока перерывов. Последнее просматривается на графике рис. 3.11, где отмечены рабочие точки, в которых находятся системы обслуживания, относящиеся к различным линиям связи.
работают в области более высокой нагрузки, в которой среднее время задержки резко возрастает при небольшом увеличении потока сообщений или потока перерывов. Последнее просматривается на графике рис. 3.11, где отмечены рабочие точки, в которых находятся системы обслуживания, относящиеся к различным линиям связи.
Квантование средних значений весов
Веса линий связи сети являются случайными функциями времени. Реализация циклов управления начинается при изменениях веса какой-либо из линий связи. Для обнаружения изменений устанавливаются градации в области определения весов  т. е. производится квантование по уровням. Переход «веса из одной градации в другую расценивается как изменение ситуации в сети.
т. е. производится квантование по уровням. Переход «веса из одной градации в другую расценивается как изменение ситуации в сети.
Увеличение числа градаций обеспечивает более точное управление, а следовательно, и лучшее приближение к оптимальным режимам работы сети, соответствующим непрерывному управлению. Однако ввиду того что каждый цикл управления связан с необходимостью передачи служебной информации, увеличение числа градаций приводит к более частым переходам весов через границы и возрастанию внутренних потоков служебных сообщений. Это в свою очередь снижает реализуемые внешние потоки. Таким образом, можно утверждать, что существует некоторый оптимум шага квантования весов линий связи сети.
При равномерном квантовании по уровням непрерывного процесса изменения весов линий связи среднеквадратическая ошибка определяемых значений

где  квантования;
квантования;  — случайная величина ошибки, распределенная равномерно на интервале кванта.
— случайная величина ошибки, распределенная равномерно на интервале кванта.
Усредненное влияние числа градаций на качество функционирования сети можно оценить по снижению реализуемых внешних потоков.
Пусть  -интенсивность внешних потоков при идеальном (непрерывном) управлении. Тогда квантование весов и соответствующее отклонение от оптимального распределения внутренних потоков обусловливают снижение
-интенсивность внешних потоков при идеальном (непрерывном) управлении. Тогда квантование весов и соответствующее отклонение от оптимального распределения внутренних потоков обусловливают снижение  на
на

где  — среднее значение весов.
— среднее значение весов.
Усредненную величину потока служебных сообщений в зависимости от числа уровней квантования можно определить следующим образом:

где  — средняя длительность интервала между соседними экстремальными значениями
— средняя длительность интервала между соседними экстремальными значениями  и средняя разность между этими значениями соответственно.
и средняя разность между этими значениями соответственно.
Величина  характеризует снижение допустимых внешних потоков из-за передачи служебных сообщений. Общее снижение реализуемых потоков
характеризует снижение допустимых внешних потоков из-за передачи служебных сообщений. Общее снижение реализуемых потоков

Для определения оптимального значения  продифференцируем (3.34) и приравняем нулю:
продифференцируем (3.34) и приравняем нулю:

Отоюда

Из последнего соотношения видно, что частая шкала квантования может применяться в мощных сетях, в которых потоки служебных сообщений практически не влияют на внешние параметры, а изменение весов во времени носит инерционный характер.
При наличии достаточных статистических данных по характеру процесса изменения весов линий связи сети может оказаться целесообразным использовать неравномерную шкалу квантования. Во
всяком случае при разработке программного обеспечения управления потоками желательно предусмотреть возможность перехода на переменную шкалу.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1 ОБЩАЯ ХАРАКТЕРИСТИКА СЕТЕЙ ПЕРЕДАЧИ ИНФОРМАЦИИ АСУ
- 1.1. СЕТЬ СВЯЗИ КАК ПОДСИСТЕМА СИСТЕМЫ УПРАВЛЕНИЯ
- 1.2. ПРИНЦИПЫ ПОСТРОЕНИЯ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ
- 1.3. ПРЕДСТАВЛЕНИЕ СТРУКТУР СЕТЕЙ
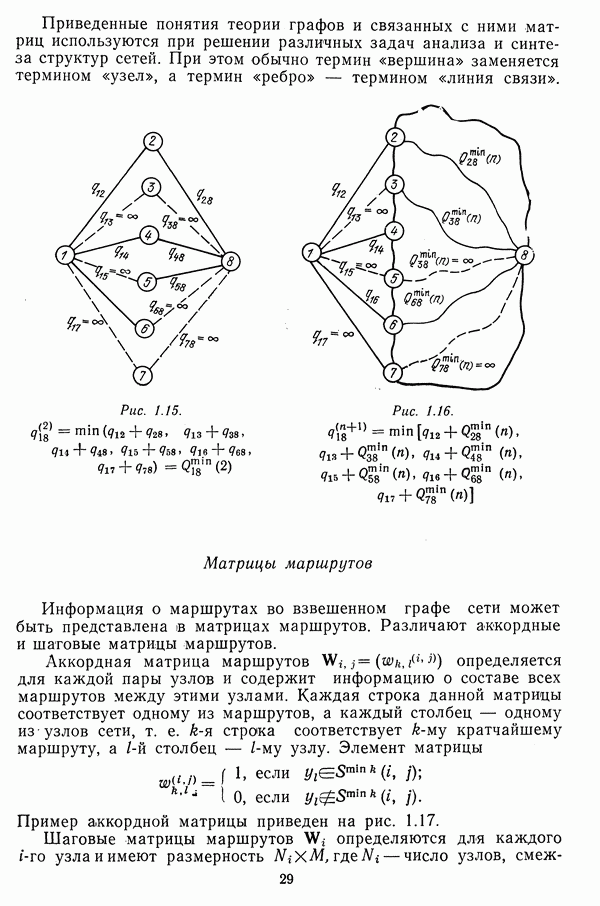
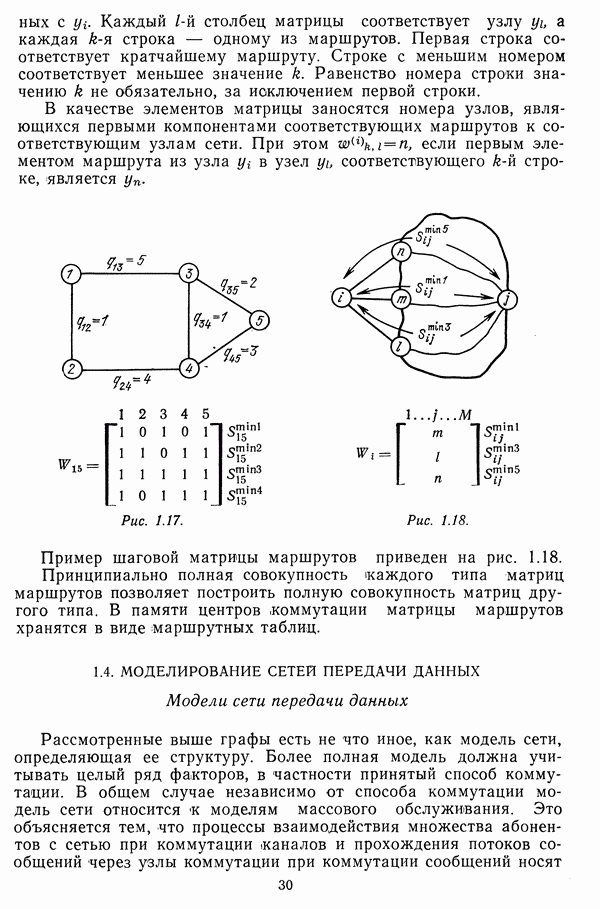
- Кратчайшие маршруты во взвешенных графах
- Матрицы, определяющие структуру сетей
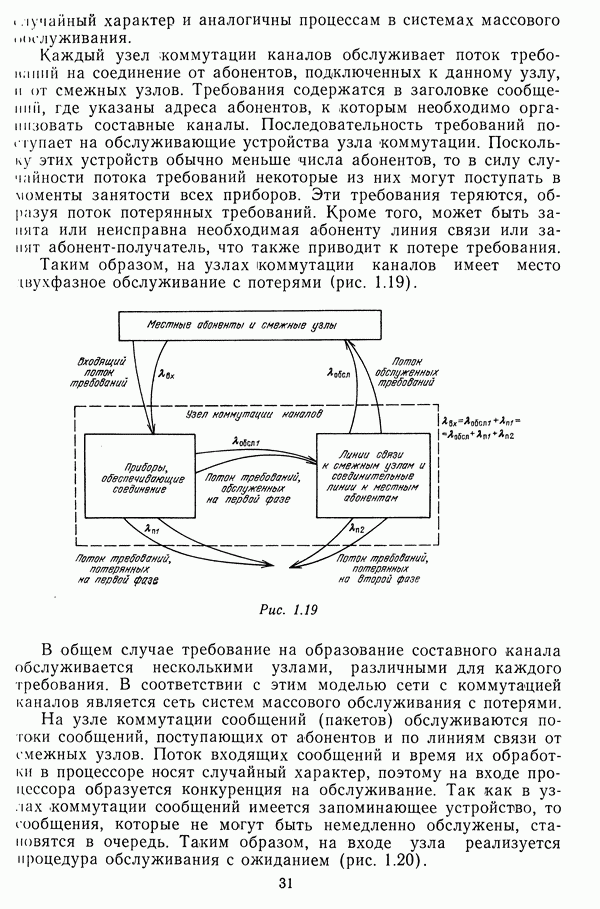
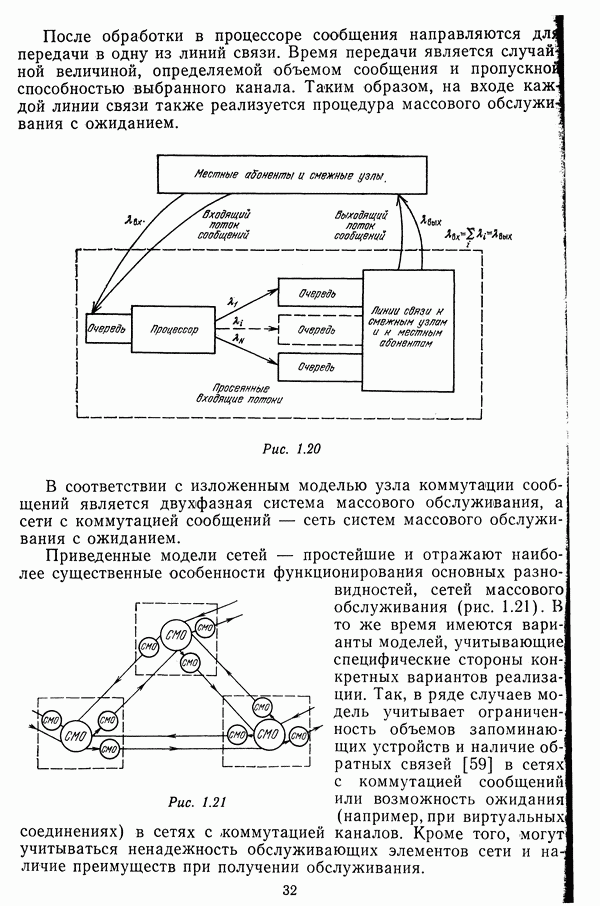
- Матрицы маршрутов
- 1.4. МОДЕЛИРОВАНИЕ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ
- Математические модели, используемые при расчете сетей
- Потоки в сетях передачи данных
- ГЛАВА 2. ПРИНЦИПЫ ФУНКЦИОНИРОВАНИЯ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ
- 2.1. СТРУКТУРА ФУНКЦИОНАЛЬНОГО ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ
- 2.2. ФОРМАЛИЗАЦИЯ СООБЩЕНИИ В СЕТЯХ ПЕРЕДАЧИ ДАННЫХ
- 2.3. АДРЕСОВАНИЕ СООБЩЕНИЙ
- 2.4. ПРОЦЕДУРЫ ВЫБОРА МАРШРУТОВ
- 2.5. РЕГУЛИРОВАНИЕ ПОТОКОВ СООБЩЕНИЙ ПО ПРИОРИТЕТАМ
- 2.6. УПРАВЛЕНИЕ В СЕТЯХ ПЕРЕДАЧИ ДАННЫХ
- Глава 3. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ МАРШРУТИЗАЦИИ И УПРАВЛЕНИЯ В СЕТЯХ ПЕРЕДАЧИ ДАННЫХ
- 3.2. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДЕТЕРМИНИРОВАННЫХ ПРОЦЕДУР ВЫБОРА МАРШРУТОВ
- 3.3. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ПОИСКОВЫХ ПРОЦЕДУР ВЫБОРА МАРШРУТОВ
- 3.4. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ КВАЗИСЛУЧАИНЫХ ПРОЦЕДУР ВЫБОРА МАРШРУТОВ
- 3.5. ФИЗИЧЕСКИЕ ВЕРСИИ ВЕСОВ ЭЛЕМЕНТОВ СЕТИ
- 3.6. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ УПРАВЛЕНИЯ ВНЕШНИМИ ПОТОКАМИ СООБЩЕНИЙ
- Глава 4. ВОПРОСЫ ПРОЕКТИРОВАНИЯ СЕТЕЙ ПЕРЕДАЧИ ИНФОРМАЦИИ АСУ
- 4.1. ЗАДАЧИ СИСТЕМНОГО ПРОЕКТИРОВАНИЯ СЕТЕЙ
- 4.2. РАЗМЕЩЕНИЕ УЗЛОВ КОММУТАЦИИ
- Оптимизация числа узлов и их размещения при независимом положении абонентов
- Размещение узлов для связи с мобильными абонентами
- Размещение центра управления сетью
- 4.3. СИНТЕЗ СТРУКТУРЫ СЕТИ
- Синтез структуры сети минимальной стоимости при заданной связности
- 4.4. РАСЧЕТ МОЩНОСТИ ЛИНИИ СВЯЗИ СЕТИ
- Оптимизация мощности линий связи при произвольном виде функций затрат
- Методика выбора каналов передачи данных для линий связи с заданной мощностью
- 4.5. ОПТИМИЗАЦИЯ ПАРАМЕТРОВ ЖИВУЧЕСТИ ЭЛЕМЕНТОВ СЕТИ
- 4.6. ВЫБОР ПАРАМЕТРОВ НАДЕЖНОСТИ ЭЛЕМЕНТОВ СЕТИ
- Методы вычисления вероятности связности сети
- Выбор параметров надежности центров коммутации
- Аналитическая оптимизация внутренних показателей надежности элементов сети
- Оптимизация внутренних показателей надежности при произвольном виде функций затрат
- СПИСОК ЛИТЕРАТУРЫ