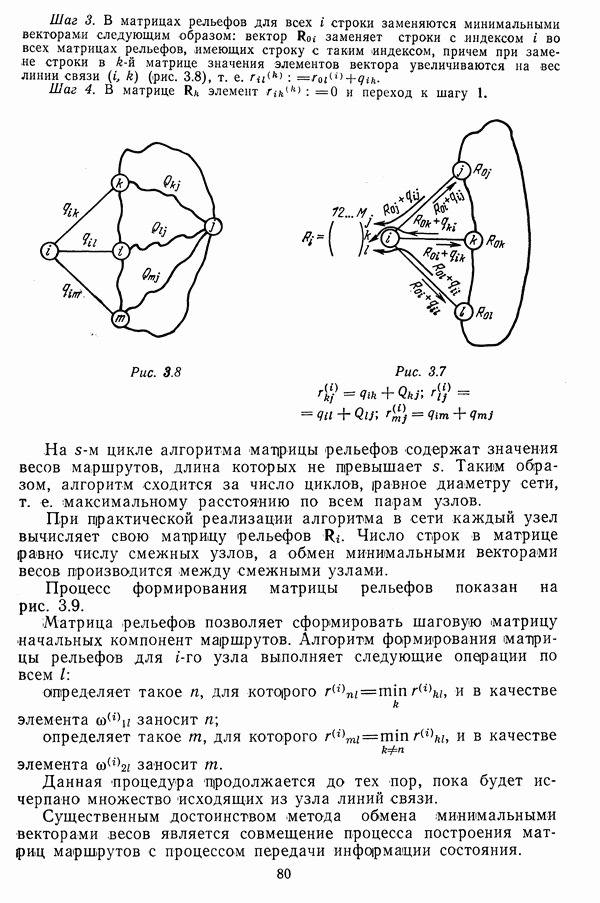
4.2. РАЗМЕЩЕНИЕ УЗЛОВ КОММУТАЦИИ

Выбор местоположения узлов для обслуживания группирующихся абонентов

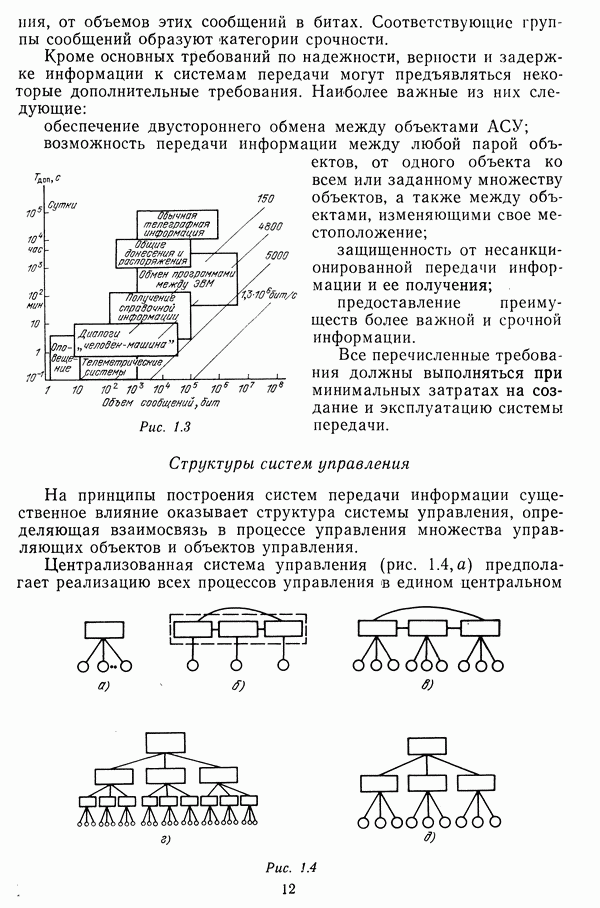
Группы стационарных абонентов часто локализуются в ограниченных районах, а узлы сети выполняют функции как коммутационных, так и оконечных узлов. В связи с этим положение

узлов в первом приближении определяется положением групп абонентов.

Располагая узел в районе локализации абонентов, следует выбирать такую точку, в которой обеспечивается минимум суммарных затрат соединительные линии от множества абонентов данного района. Пусть —затраты «а создание и эксплуатацию или аренду соединительной линии от абонента до узла коммутации, расположенного в точке с координатами тогда оптимальными будут такие значения при которых обеспечивается

-При произвольном виде функций для вычисления может быть использован эвристический подход, основанный на допущении о том, что оптимальная точка расположения узла находится внутри области локализации абонентов. Это допущение позволяет ограничить размерность задачи.

Излагаемый ниже решающий алгоритм основан на сочетании направленного поиска и метода Монте-Карло. Использование последнего заключается в том, что задача натравленного поиска решается неоднократно из выбранных случайным образом начальных точек. Это позволяет уменьшить вероятность получения локальных оптимумов в решении. Предварительный этап решения состоит в очерчивании на карте области с границами где — номера абонентов группы, и ее дискретизации с некоторым шагом Рассмотрим последовательность шагов алгоритма.

Шаг 0. Ввод исходных данных:

значения затрат для дискретных координатных точек

число реализаций

Шаг 1. Выбрать случайные значения

Шаг 2. Вычислить

Шаг 3. Произвести сдвиги точки в пределах ограниченной области:

Шаг 4. Вычислить:

Шаг 5. Если то перейти к шагу 7, иначе к шагу 6.

Шаг 6. Произвести сдвиг или в направлении минимального возрастания затрат и перейти к шагу 2.

Шаг 7.

Шаг 8. Проверить число реализаций. Если то перейти к шагу 9, иначе к шагу 1.

Шаг 9. Вывод значений

Число требуемых реализаций, так же как и шаг дискретизации, определяется требуемой точностью.

В большинстве случаев затраты на соединительные линии являются функцией их длины Тогда в качества исходных данных вместо вводится функция а вычислению затрат при рассмотрении вариантов размещения узла предшествует определение расстояний до него от каждого из абонентов.

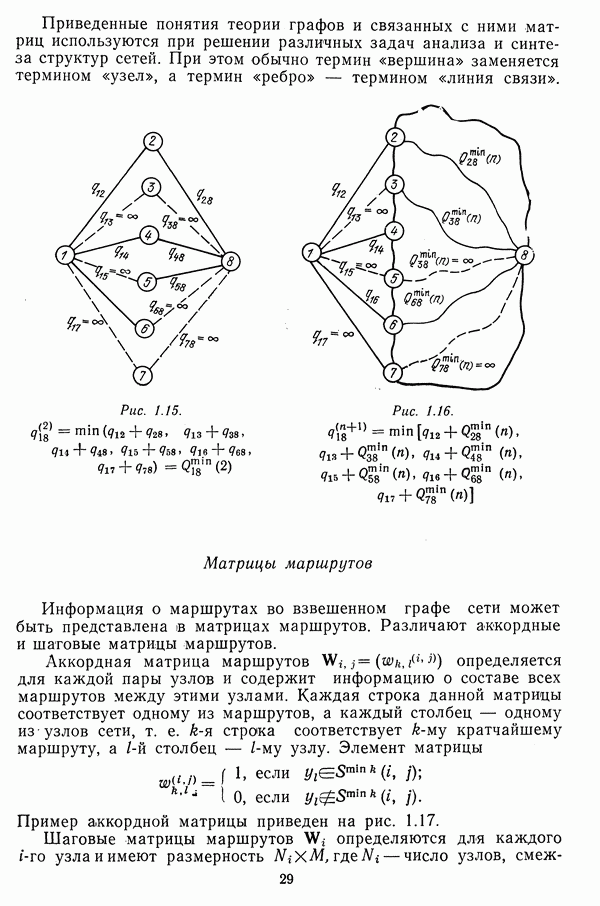
Рис. 4.1

Районы локализации абонентов, как правило, охватывают сравнительно небольшие пространства, поэтому при определении расстояния от абонента до точки с координатами можно не учитывать кривизну поверхности Земли и использовать теорему Пифагора

где — <координаты абонента (рис. 4.1).

Тривиальное аналитическое решение получается, если на ограниченном участке функцию затрат удается аппроксимировать квадратичной функцией длины. Тогда критерий оптимальности будет

где — константа, имеющая смысл нормированных затрат.

После подстановки в последнее соотношение (4.17) получим

Найдя частные производные выражения под знаком по и приравняв их нулю, получим соотношения, определяющие координаты узла, при которых суммарные затраты на построение соединительных линий минимальны:

Значение равно затратам на строительство одиппцы длины соединительной линии к абоненту.

Изложенный алгоритм может быть использован при сшптие топологии любой системы, имеющей (централизованную структуру.