| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 5. ГРАФЫ ПРЕОБРАЗОВАНИЙ. ОРБИТЫ. ЦИКЛИЧЕСКАЯ ФОРМА ЗАПИСИ ПЕРЕСТАНОВОК
Стрелочные схемы — графы преобразований заданного множества — можно строить иначе, чем схемы произвольных отображений. Обозначим каждый элемент множества М точкой на плоскости так, чтобы разным элементам отвечали разные точки. Точки обозначим теми же самыми символами, что и соответствующие элементы множества М. Две точки - соединим стрелкой в направлении от а к b тогда и только тогда, когда для элементов а, b выполняется условие  . Так получим граф преобразования
. Так получим граф преобразования  Ясно, что он определяет преобразование однозначно. Наоборот, если не обращать внимание на форму стрелок и размещение точек на плоскости, то каждому преобразованию будет отвечать вполне определенный граф.
Ясно, что он определяет преобразование однозначно. Наоборот, если не обращать внимание на форму стрелок и размещение точек на плоскости, то каждому преобразованию будет отвечать вполне определенный граф.
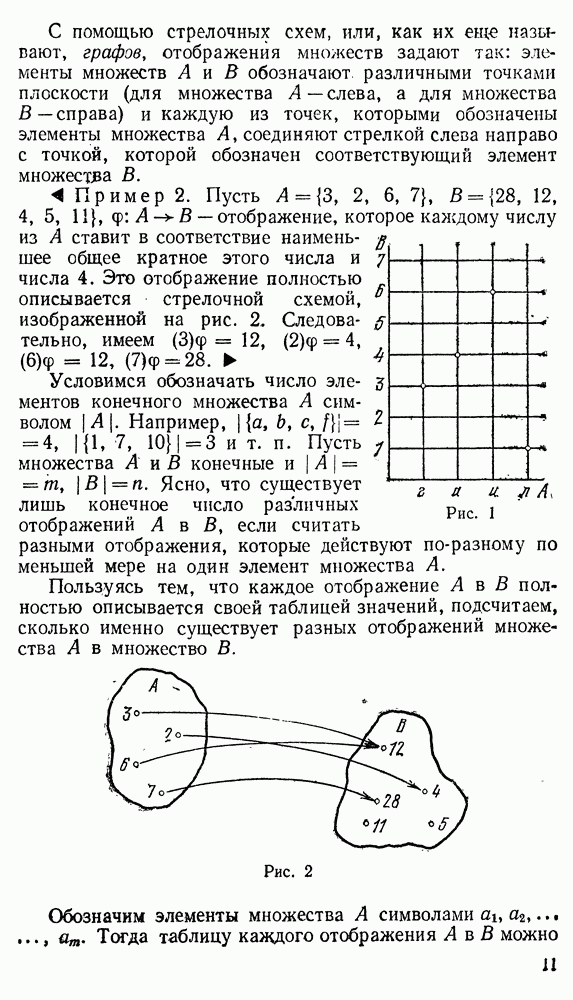
Примеры. 1. Пусть преобразование  множества М = {1, 2, 3, 4, 5, 6} задано таблицей
множества М = {1, 2, 3, 4, 5, 6} задано таблицей

Обозначим каждое число из М точкой на плоскости, например, так, как на рис. 9. Поскольку  точки I и 3 соединим стрелкой в направлении от точки 1 к точке 3. Аналогично построим стрелки, которые выходят из точек 2, 3, 4, 5, 6 (рис. 10). Это и есть граф преобразования
точки I и 3 соединим стрелкой в направлении от точки 1 к точке 3. Аналогично построим стрелки, которые выходят из точек 2, 3, 4, 5, 6 (рис. 10). Это и есть граф преобразования 
2. Пусть  — тождественное преобразование множества
— тождественное преобразование множества  По определению, для каждого
По определению, для каждого  . Так что граф преобразования
. Так что граф преобразования  будет такой, как на рис. 11.
будет такой, как на рис. 11.

Рис. 9

Рис. 10

Рис. 11

Рис. 12
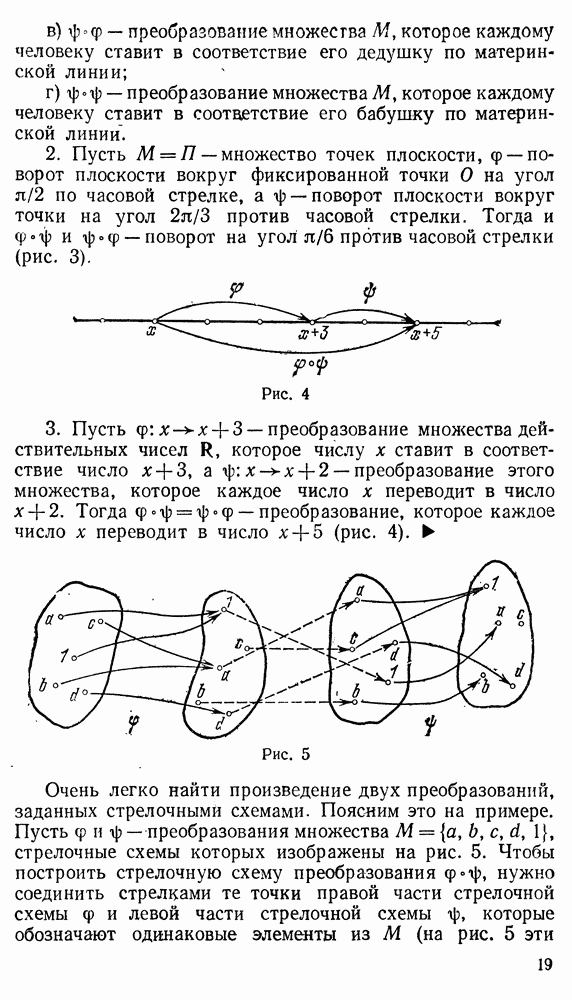
3. Пусть  — постоянное преобразование множества
— постоянное преобразование множества  , которое каждому элементу ЬМ ставит в соответствие фиксированный элемент
, которое каждому элементу ЬМ ставит в соответствие фиксированный элемент  т. е. для каждого ЬМ имеем
т. е. для каждого ЬМ имеем

В этом случае на графе преобразования  каждая точка b соединена с фиксированной точкой а стрелкой, которая заканчивается в а (рис. 12).
каждая точка b соединена с фиксированной точкой а стрелкой, которая заканчивается в а (рис. 12).
4. Пусть  ,
,  — преобразование множества Z, которое каждому целому числу
— преобразование множества Z, которое каждому целому числу  ставит в соответствие число
ставит в соответствие число  . В этом случае граф преобразования полностью построить не удается, но можно изобразить определенную часть его так, чтобы стало понятным строение графа в целом (рис. 13).
. В этом случае граф преобразования полностью построить не удается, но можно изобразить определенную часть его так, чтобы стало понятным строение графа в целом (рис. 13).
5. Если М — конечное множество и преобразование  является перестановкой на множестве М, то из каждой вершины графа
является перестановкой на множестве М, то из каждой вершины графа  выходит одна и только одна стрелка и в каждую вершину обязательно входит стрелка, причем только одна.
выходит одна и только одна стрелка и в каждую вершину обязательно входит стрелка, причем только одна.
В частности, если  — перестановка на множестве М:
— перестановка на множестве М:

то ее граф будет такой, как на рис. 14.
Граф произвольного преобразования  состоит из одной (рис. 10, 12) или нескольких (рис. 14) не связанных между собой частей, каждая из которых составляет одно целое. При этом отдельная связная часть графа преобразования
состоит из одной (рис. 10, 12) или нескольких (рис. 14) не связанных между собой частей, каждая из которых составляет одно целое. При этом отдельная связная часть графа преобразования  может состоять лишь из одной точки с «петлей», т. е. со стрелкой, которая выходит из этой точки и заканчивается в ней.
может состоять лишь из одной точки с «петлей», т. е. со стрелкой, которая выходит из этой точки и заканчивается в ней.

Рис. 13
Если а — такая точка, то для соответствующего элемента  справедливо равенство
справедливо равенство

Такие элементы называются неподвижными точками преобразования  Если для элемента
Если для элемента  выполняется условие
выполняется условие

то а называется подвижной точкой преобразования  На графе подвижные точки — это точки без петель.
На графе подвижные точки — это точки без петель.

Рис. 14
Например, на рис. 14 точки 1, 2, 3, 4, 5, 6 — подвижные, а точка 7 — неподвижная точка преобразования 
Количество подвижных точек преобразования является одной из важных его характеристик, которая называется степенью этого преобразования. Единственным преобразованием степени нуль является тождественное преобразование; постоянное преобразование множества из  элементов имеет степень
элементов имеет степень 
Пусть  — некоторое преобразование множества М и а — произвольный элемент из М. Последовательность
— некоторое преобразование множества М и а — произвольный элемент из М. Последовательность

элементов из М называется орбитой элемента а для преобразования  .
.
В общем случае множество  элементов орбиты (1) является подмножеством множества М. В частности, может случиться, что
элементов орбиты (1) является подмножеством множества М. В частности, может случиться, что 
Рассмотрим детально строение орбит, когда М — конечное множество,  . Очевидно, в этом случае элементы в последовательности (1), начиная с некоторого места, будут повторяться. Пусть
. Очевидно, в этом случае элементы в последовательности (1), начиная с некоторого места, будут повторяться. Пусть  — наименьшее число такое, что
— наименьшее число такое, что

Ясно, что элементы  также встречаются среди элементов
также встречаются среди элементов  . Поэтому
. Поэтому  и легко понять, что граф преобразования
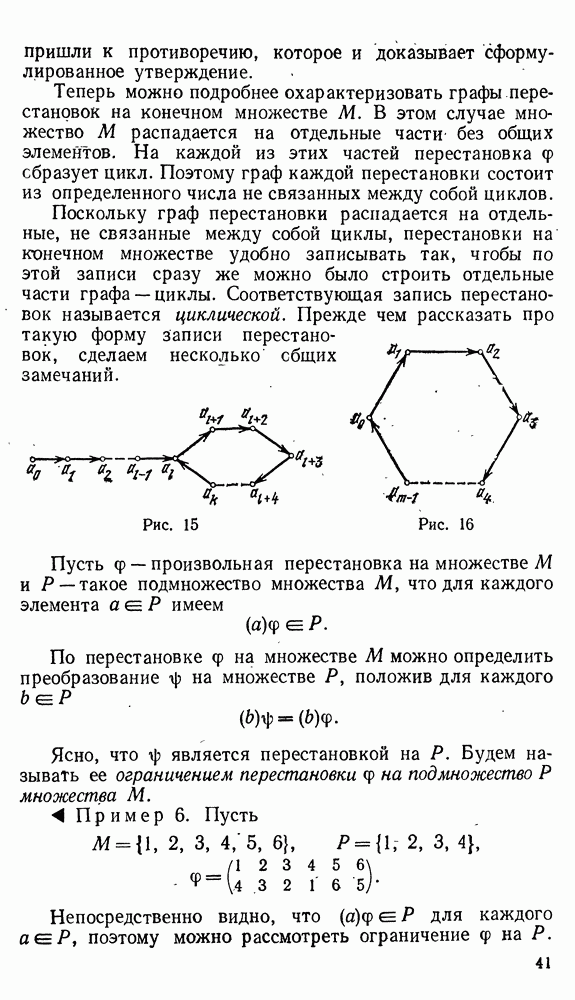
и легко понять, что граф преобразования  будет такой, как на рис. 15.
будет такой, как на рис. 15.
Если  преобразование
преобразование  не является перестановкой, потому что в точке
не является перестановкой, потому что в точке  заканчиваются две стрелки. Для
заканчиваются две стрелки. Для  преобразование имеет граф, который называется циклом (рис. 16), и в этом случае оно, очевидно, будет перестановкой. Эта перестановка действует на элементы из М так:
преобразование имеет граф, который называется циклом (рис. 16), и в этом случае оно, очевидно, будет перестановкой. Эта перестановка действует на элементы из М так:

Такая перестановка называется циклической или просто циклом и обозначается

Число  есть длина цикла. Циклы длины 2 называются транспозициями.
есть длина цикла. Циклы длины 2 называются транспозициями.
Если элементы орбиты  не исчерпывают все множество М, то графы (рис. 15, 16) не полностью характеризуют преобразование. Тогда нужно рассмотреть орбиты других элементов, которые не вошли в
не исчерпывают все множество М, то графы (рис. 15, 16) не полностью характеризуют преобразование. Тогда нужно рассмотреть орбиты других элементов, которые не вошли в  Разные орбиты для заданного преобразования могут иметь общие вершины (рис. 12), но для перестановки разные орбиты очерчивают не связанные части ее графа.
Разные орбиты для заданного преобразования могут иметь общие вершины (рис. 12), но для перестановки разные орбиты очерчивают не связанные части ее графа.
Действительно, пусть  — разные орбиты перестановки
— разные орбиты перестановки  Допустим, что
Допустим, что  имеют общие элементы. Идя в порядке возрастания номеров, выберем первый элемент
имеют общие элементы. Идя в порядке возрастания номеров, выберем первый элемент  который равняется определенному элементу
который равняется определенному элементу  . Тогда
. Тогда  Значит,
Значит,  и преобразование
и преобразование  не является перестановкой.
не является перестановкой.
Мы пришли к противоречию, которое и доказывает сформулированное утверждение. Теперь можно подробнее охарактеризовать графы перестановок на конечном множестве М. В этом случае множество М распадается на отдельные части без общих элементов. На каждой из этих частей перестановка  образует цикл. Поэтому граф каждой перестановки состоит из определенного числа не связанных между собой циклов.
образует цикл. Поэтому граф каждой перестановки состоит из определенного числа не связанных между собой циклов.
Поскольку граф перестановки распадается на отдельные, не связанные между собой циклы, перестановки на конечном множестве удобно записывать так, чтобы по этой записи сразу же можно было строить отдельные части графа — циклы. Соответствующая запись перестановок называется циклической. Прежде чем рассказать про такую форму записи перестановок, сделаем несколько сбщих замечаний.

Рис. 15

Рис. 16
Пусть  — произвольная перестановка на множестве М и Р — такое подмножество множества М, что для каждого элемента
— произвольная перестановка на множестве М и Р — такое подмножество множества М, что для каждого элемента  имеем
имеем

По перестановке  на множестве М можно определить преобразование
на множестве М можно определить преобразование  на множестве Р, положив для каждого
на множестве Р, положив для каждого 

Ясно, что является перестановкой на Р. Будем называть ее ограничением перестановки  на подмножество Р множества М.
на подмножество Р множества М.
Пример 6. Пусть

Непосредственно видно, что  для каждого
для каждого  поэтому можно рассмотреть ограничение
поэтому можно рассмотреть ограничение  на Р.
на Р.
Это будет перестановка

Обратно, если имеем перестановку  на множестве
на множестве  , то можно определить перестановку
, то можно определить перестановку  на множестве М, положив для каждого элемента
на множестве М, положив для каждого элемента  :
:

То есть на элементы из Р перестановка  действует так же, как перестановка а все остальные элементы из М оставляет на месте. Будем называть перестановку
действует так же, как перестановка а все остальные элементы из М оставляет на месте. Будем называть перестановку  расширением перестановки
расширением перестановки  на множество М.
на множество М.
Пример 7. Пусть

и

Тогда расширением  на М является перестановка
на М является перестановка

Назовем две перестановки на множестве М взаимно простыми, если их множества подвижных точек не имеюх общих элементов.
Взаимно простыми будут, например, перестановки

ибо множеством подвижных точек для  является
является  для
для 
В отличие от перестановок общего вида, произведение взаимно простых перестановок не зависит от порядка множителей.
Действительно, пусть  — взаимно простые перестановки и а — произвольный элемент множества М. Если а — подвижная точка для перестановки
— взаимно простые перестановки и а — произвольный элемент множества М. Если а — подвижная точка для перестановки  , то положим
, то положим  элементы а, b — неподвижные точки для
элементы а, b — неподвижные точки для  ибо
ибо  . Поэтому имеем
. Поэтому имеем

т. е. в этом случае 
Если а — неподвижная точка перестановки  то положим
то положим  (если а является неподвижной точкой и для перестановки
(если а является неподвижной точкой и для перестановки  , то
, то  ) и аналогично получим, что элементы а, с не меняются под действием перестановки
) и аналогично получим, что элементы а, с не меняются под действием перестановки  а поэтому
а поэтому

Так что и в этом случае перестановки  действуют на элемент
действуют на элемент  одинаково, а это и означает, что
одинаково, а это и означает, что

Таблицу произведения двух взаимно простых перестановок  составить очень просто. Для этого во втором ряду таблицы
составить очень просто. Для этого во втором ряду таблицы  нужно записать на своих местах (т. е. на тех местах, на которых они стоят в таблицах для
нужно записать на своих местах (т. е. на тех местах, на которых они стоят в таблицах для  ) все подвижные точки перестановок
) все подвижные точки перестановок  , а остальные места заполнить неподвижными точками. Например,
, а остальные места заполнить неподвижными точками. Например,

Пусть теперь  — произвольная перестановка на множестве М. Разобьем М на части
— произвольная перестановка на множестве М. Разобьем М на части  каждая из которых является орбитой некоторого элемента из М. Это разбиение имеет такие свойства:
каждая из которых является орбитой некоторого элемента из М. Это разбиение имеет такие свойства:
а) каждый элемент из М принадлежит одному из подмножеств 
б) если  то
то  не имеют общих элементов;
не имеют общих элементов;
в) для каждого  ; (i есть один из номеров
; (i есть один из номеров  ) элемент
) элемент  также принадлежит
также принадлежит 
По последнему свойству можно рассмотреть ограничение  перестановки
перестановки  на каждое из подмножеств М;
на каждое из подмножеств М;  есть, очевидно, циклическая перестановка на
есть, очевидно, циклическая перестановка на  Она определяется перестановкой
Она определяется перестановкой  однозначно.
однозначно.
В свою очередь, каждую из перестановок  можно расширить на все множество М. Обозначим это расширение через
можно расширить на все множество М. Обозначим это расширение через  Далее такие перестановки также будем называть циклическими и обозначать их так, как и обычные циклы. Следовательно, перестановка будет циклической в этом понимании тогда и только тогда, когда она имеет граф такого вида, как на рис. 17.
Далее такие перестановки также будем называть циклическими и обозначать их так, как и обычные циклы. Следовательно, перестановка будет циклической в этом понимании тогда и только тогда, когда она имеет граф такого вида, как на рис. 17.
Очевидно, множество подвижных точек каждой из перестановок  совпадает с множеством
совпадает с множеством  по свойству в) перестановки
по свойству в) перестановки  взаимно просты. Пользуясь приведенным выше правилом для умножения взаимно простых перестановок, получаем
взаимно просты. Пользуясь приведенным выше правилом для умножения взаимно простых перестановок, получаем

Поскольку перестановки  — попарно взаимно простые, это произведение не зависит от порядка множителей. Таким образом, доказана такая
— попарно взаимно простые, это произведение не зависит от порядка множителей. Таким образом, доказана такая
Теорема. Каждую перестановку на конечном множестве М можно разложить в произведение взаимно простых циклов, причем это разложение однозначно с точностью до порядка множителей.

Рис. 17
Набор чисел  , являющихся длинами циклов, на которые разложена данная перестановка, называется ее типом и обозначается
, являющихся длинами циклов, на которые разложена данная перестановка, называется ее типом и обозначается 
Пример 8. Разложить в произведение циклов перестановку

Находим разные орбиты для  Имеем
Имеем

Так что орбиты определяют подмножества  Ограничениями перестановки
Ограничениями перестановки  на эти множества будут такие перестановки:
на эти множества будут такие перестановки:

Расширениями этих перестановок на множество М будут перестановки

Поэтому можно записать

Последняя запись однозначно определяет перестановку лишь тогда, когда известно, на каком множестве она действует.
Упражнения
1. Может ли произвольный граф быть графом какого-нибудь преобразования?
2. Перестановка задана графом, Как построить граф обратной перестановки?
3. Указать правило для нахождения графа произведения преобразований, каждое из которых задано своим графом, не строя таблиц этих преобразований.
4. Построить графы преобразований, заданных таблицами:

5. Каждая перестановка, граф которой связан, циклична, Доказать это.
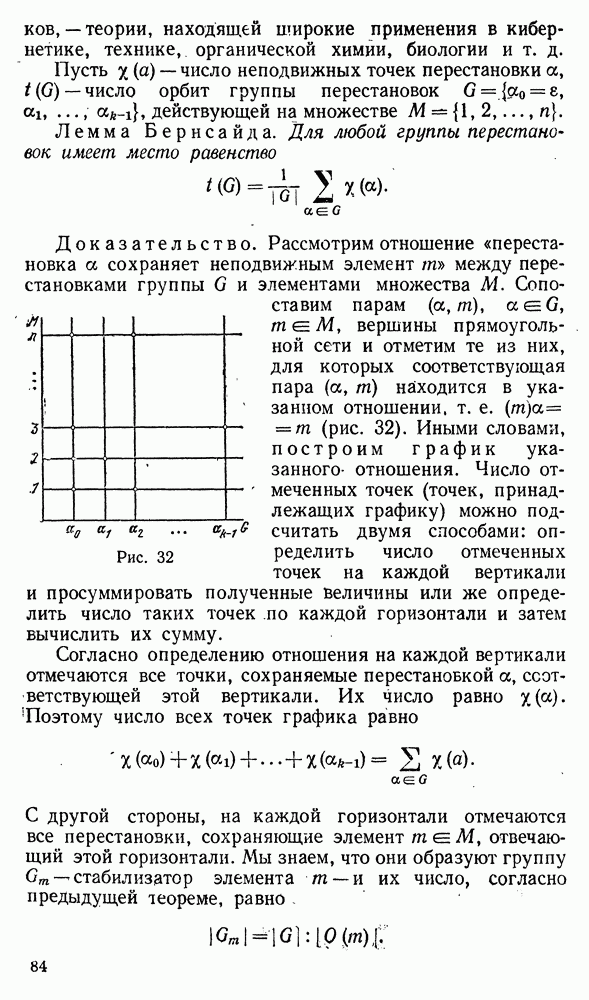
6. Длиной орбиты называется число ее элементов. Найти наибольшее и наименьшее значения сумм длин разных орбит для преобразований множества из  элементов.
элементов.
7. Преобразование  множества М будет перестановкой тогда и только тогда, когда сумма длин разных ее орбит равняется
множества М будет перестановкой тогда и только тогда, когда сумма длин разных ее орбит равняется  Доказать это.
Доказать это.
8. Пусть  — произвольное преобразование множества М. Существует такое множество
— произвольное преобразование множества М. Существует такое множество  и такое натуральное число к, что
и такое натуральное число к, что  для каждого
для каждого  и ограничение
и ограничение  на Р есть перестановка. Доказать это.
на Р есть перестановка. Доказать это.
9. Разложить в произведение взаимно простых циклов и найти типы таких перестановок:

10. Описать общий вид графа про звольного преобразования (так, как это сделано для перестановок).
11. Сколько существует перестановок на множестве из  элементов, которые имеют заданный тип
элементов, которые имеют заданный тип  (ясно, что
(ясно, что  ).
).
12. В группе  найти число перестановок каждого возможного типа.
найти число перестановок каждого возможного типа.
13. Определить тип перестановки, - характеризующей расположение тридцати физкультурников после двукратной перегруппировки (см, упражнение 12 § 3),
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- § 1. СУПЕРПОЗИЦИЯ ФУНКЦИЙ
- § 2. ПРЕОБРАЗОВАНИЯ
- 1. Отображение на все множество.
- 2. Взаимно однозначное отображение.
- 3. Взаимно однозначное отображение на все множество.
- § 3. УМНОЖЕНИЕ ПРЕОБРАЗОВАНИЙ
- Упражнения
- § 4. ГРУППА ПЕРЕСТАНОВОК И ПОЛУГРУППА ПРЕОБРАЗОВАНИЙ
- § 5. ГРАФЫ ПРЕОБРАЗОВАНИЙ. ОРБИТЫ. ЦИКЛИЧЕСКАЯ ФОРМА ЗАПИСИ ПЕРЕСТАНОВОК
- § 6. ПОРЯДОК ПЕРЕСТАНОВКИ
- § 7. ОБРАЗУЮЩИЕ СИММЕТРИЧЕСКОЙ ГРУППЫ
- Упражнения
- § 8. ПОДГРУППЫ СИММЕТРИЧЕСКИХ ГРУПП. ГРУППЫ ПЕРЕСТАНОВОК
- § 9. ГРУППЫ СИММЕТРИЙ
- 1. Группа симметрий правильного треугольника.
- 2. Группа симметрий квадрата.
- 3. Группа симметрий правильного n-угольника
- 4. Группа симметрий многоугольника, изображенного на рис. 26
- 5. Группа симметрий тетраэдра.
- 6. Группа симметрий куба.
- 7. Группа симметрий октаэдра.
- Упражнения
- § 10. ТЕОРЕМА КЭЛИ
- § 11. ТЕОРЕМА ЛАГРАНЖА
- § 12. ОРБИТЫ ГРУППЫ ПЕРЕСТАНОВОК. ЛЕММА БЕРНСАЙДА
- § 13. КОМБИНАТОРНЫЕ ЗАДАЧИ
- § 14. ДЕЙСТВИЕ ПЕРЕСТАНОВКИ НА МНОГОЧЛЕН
- § 15. ЧЕТНЫЕ И НЕЧЕТНЫЕ ПЕРЕСТАНОВКИ. ЗНАКОПЕРЕМЕННАЯ ГРУППА
- § 16. СИММЕТРИЧЕСКИЕ И ЧЕТНОСИММЕТРИЧЕСКИЕ МНОГОЧЛЕНЫ
- § 17. О РЕШЕНИИ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
- § 18. ИГРА «В ПЯТНАДЦАТЬ»
- § 19 ПЕРЕСТАНОВОЧНЫЕ КОНСТРУКЦИИ
- § 20. ВЕНГЕРСКИЙ ШАРНИРНЫЙ КУБИК
- § 21. ДРУГИЕ ИГРЫ
- ОТВЕТЫ, УКАЗАНИЯ, РЕШЕНИЯ
- СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ