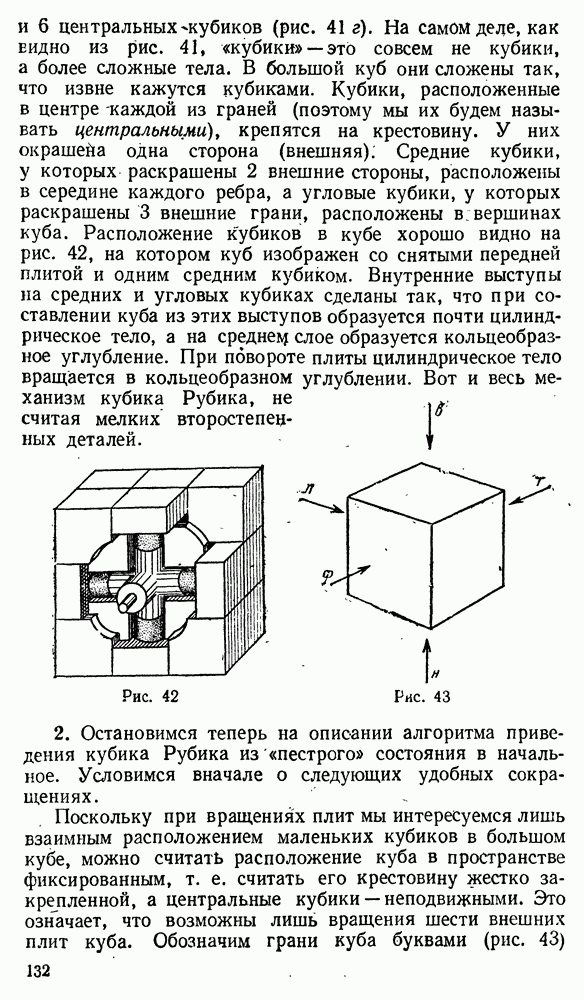
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
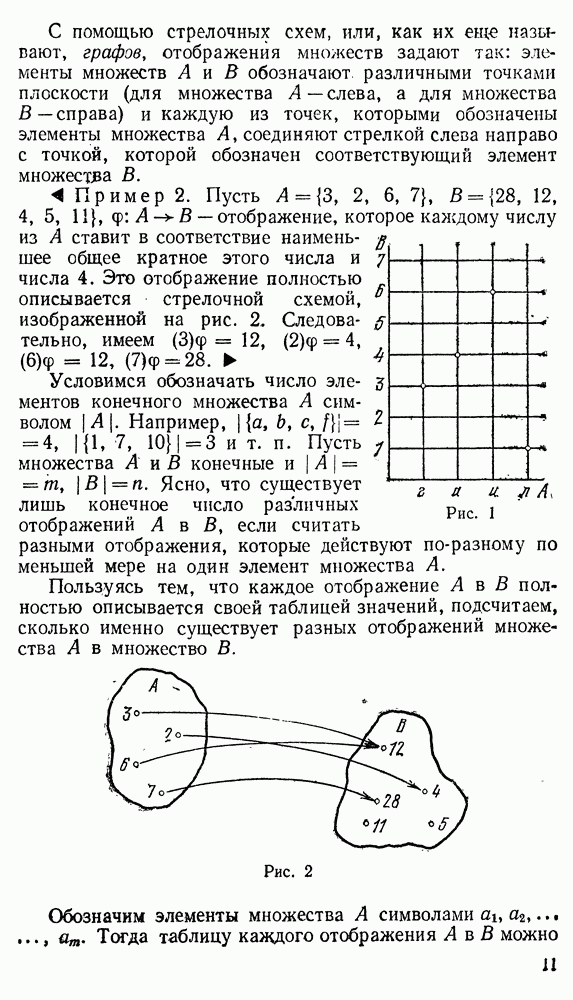
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5. Группа симметрий тетраэдра.
Тетраэдр (рис. 27) имеет 4 оси симметрии  порядка, проходящие через его вершины 1, 2, 3, 4 и центры противолежащих граней. Вокруг каждой оси, кроме тождественного, возможны еще два вращения. Им соответствуют такие перестановки:
порядка, проходящие через его вершины 1, 2, 3, 4 и центры противолежащих граней. Вокруг каждой оси, кроме тождественного, возможны еще два вращения. Им соответствуют такие перестановки:

Кроме того, имеется 3 оси симметрии  порядка, проводящие через середины А, В, С, D, Е, F скрещивающихся ребер.
порядка, проводящие через середины А, В, С, D, Е, F скрещивающихся ребер.
Поэтому имеется еще 3 (по числу  скрещивающихся ребер) нетождественных преобразования, которым соответствуют перестановки:
скрещивающихся ребер) нетождественных преобразования, которым соответствуют перестановки:

Итак, вместе с тождественным преобразованием получаем 12 перестановок. При указанных преобразованиях тетраэдр самосовмещается, поворачиваясь в пространстве; его точки при этом не изменяют своего положения относительно друг друга. Совокупность выписанных 12 перестановок замкнута относительно умножения, поскольку последовательное выполнение вращений тетраэдра снова будет вращением. Таким образом, получаем, группу, которая называется группой вращений тетраэдра.
При других преобразованиях пространства, являющихся самосовмещениями тетраэдра, внутренние точки тетраэдра передвигаются относительно друг друга. А именно: тетраэдр имеет 6 плоскостей симметрии, каждая из которых проходит через одно из его ребер и середину противолежащего ребра. Симметриям относительно этих плоскостей отвечают следующие транспозиции на множестве вершин тетраэдра:

Уже на основании этих данных можно утверждать, что группа всевозможных симметрий тетраэдра состоит из 24 преобразований. В самом деле, каждая симметрия, самосовмещая тетраэдр в целом, должна как-то переставлять его вершины, ребра и грани. В частности, как уже было сказано, в данном случае симметрии можно характеризовать перестановками вершин тетраэдра. Поскольку тетраэдр имеет 4 вершины, его группа симметрий не может состоять больше чем из 24 преобразований. Иными словами, она либо совпадает с симметрической группой 54, либо является ее подгруппой. Выписанные выше симметрии тетраэдра относительно плоскостей определяют всевозможные транспозиции на множестве его вершин.
Поскольку эти транспозиции порождают симметрическую группу  , получаем требуемое. Таким образом, любая перестановка вершин тетраэдра определяется некоторой его симметрией. Однако этого нельзя сказать о произвольной перестановке ребер тетраэдра. Если условиться обозначать каждое ребро тетраэдра той же буквой, что и его середину, то, скажем, перестановки на множестве ребер
, получаем требуемое. Таким образом, любая перестановка вершин тетраэдра определяется некоторой его симметрией. Однако этого нельзя сказать о произвольной перестановке ребер тетраэдра. Если условиться обозначать каждое ребро тетраэдра той же буквой, что и его середину, то, скажем, перестановки на множестве ребер

отвечают соответственно двум вращениям вокруг оси  и вращению вокруг оси АВ. Выписав перестановки на множестве А, В, С, D, Е, для всех преобразований симметрии, получим некоторую подгруппу симметрической группы
и вращению вокруг оси АВ. Выписав перестановки на множестве А, В, С, D, Е, для всех преобразований симметрии, получим некоторую подгруппу симметрической группы  , состоящую из 24 перестановок. Группа перестановок вершин тетраэдра и группа перестановок его ребер — разные группы перестановок, поскольку они действуют на разных множествах. Но за ними «видна» одна и та же группа — группа преобразований пространства, оставляющих тетраэдр на месте! В следующем параграфе для описания такой ситуации мы введем специальное понятие — изоморфизм групп, а о группах, «похожих» друг на друга в указанном смысле, будем говорить, что они изоморфны.
, состоящую из 24 перестановок. Группа перестановок вершин тетраэдра и группа перестановок его ребер — разные группы перестановок, поскольку они действуют на разных множествах. Но за ними «видна» одна и та же группа — группа преобразований пространства, оставляющих тетраэдр на месте! В следующем параграфе для описания такой ситуации мы введем специальное понятие — изоморфизм групп, а о группах, «похожих» друг на друга в указанном смысле, будем говорить, что они изоморфны.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- § 1. СУПЕРПОЗИЦИЯ ФУНКЦИЙ
- § 2. ПРЕОБРАЗОВАНИЯ
- 1. Отображение на все множество.
- 2. Взаимно однозначное отображение.
- 3. Взаимно однозначное отображение на все множество.
- § 3. УМНОЖЕНИЕ ПРЕОБРАЗОВАНИЙ
- Упражнения
- § 4. ГРУППА ПЕРЕСТАНОВОК И ПОЛУГРУППА ПРЕОБРАЗОВАНИЙ
- § 5. ГРАФЫ ПРЕОБРАЗОВАНИЙ. ОРБИТЫ. ЦИКЛИЧЕСКАЯ ФОРМА ЗАПИСИ ПЕРЕСТАНОВОК
- § 6. ПОРЯДОК ПЕРЕСТАНОВКИ
- § 7. ОБРАЗУЮЩИЕ СИММЕТРИЧЕСКОЙ ГРУППЫ
- Упражнения
- § 8. ПОДГРУППЫ СИММЕТРИЧЕСКИХ ГРУПП. ГРУППЫ ПЕРЕСТАНОВОК
- § 9. ГРУППЫ СИММЕТРИЙ
- 1. Группа симметрий правильного треугольника.
- 2. Группа симметрий квадрата.
- 3. Группа симметрий правильного n-угольника
- 4. Группа симметрий многоугольника, изображенного на рис. 26
- 5. Группа симметрий тетраэдра.
- 6. Группа симметрий куба.
- 7. Группа симметрий октаэдра.
- Упражнения
- § 10. ТЕОРЕМА КЭЛИ
- § 11. ТЕОРЕМА ЛАГРАНЖА
- § 12. ОРБИТЫ ГРУППЫ ПЕРЕСТАНОВОК. ЛЕММА БЕРНСАЙДА
- § 13. КОМБИНАТОРНЫЕ ЗАДАЧИ
- § 14. ДЕЙСТВИЕ ПЕРЕСТАНОВКИ НА МНОГОЧЛЕН
- § 15. ЧЕТНЫЕ И НЕЧЕТНЫЕ ПЕРЕСТАНОВКИ. ЗНАКОПЕРЕМЕННАЯ ГРУППА
- § 16. СИММЕТРИЧЕСКИЕ И ЧЕТНОСИММЕТРИЧЕСКИЕ МНОГОЧЛЕНЫ
- § 17. О РЕШЕНИИ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
- § 18. ИГРА «В ПЯТНАДЦАТЬ»
- § 19 ПЕРЕСТАНОВОЧНЫЕ КОНСТРУКЦИИ
- § 20. ВЕНГЕРСКИЙ ШАРНИРНЫЙ КУБИК
- § 21. ДРУГИЕ ИГРЫ
- ОТВЕТЫ, УКАЗАНИЯ, РЕШЕНИЯ
- СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ