Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
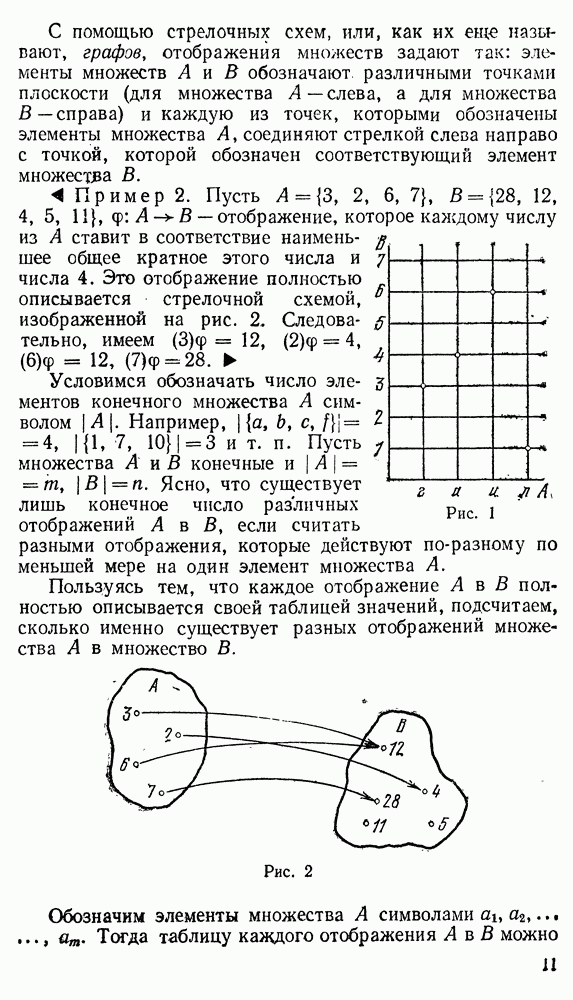
§ 9. ГРУППЫ СИММЕТРИЙОдним из наиболее употребляемых примеров групп и, в частности, групп перестановок, являются группы, которыми «измеряется» симметричность геометрических фигур как плоских, так и пространственных. В этом параграфе мы приведем соответствующие примеры. Рассмотрим сначала симметрию плоских фигур. Плоская фигура может иметь ось симметрии (одну или несколько) — прямую, которая разбивает ее на две части (рис. 21), каждая из которых является зеркальным отражением другой. В этом случае фигура называется симметричной относительно прямой. Другим типом симметрии является симметрия относительно точки (рис. 22), которая называется центром симметрии, а фигура — центральносимметричной. Это понятие естественным образом обобщается. А именно: будем говорить, что точка О есть центр симметрии
Рис. 21
Рис. 22
Рис. 23 Каждому типу симметрии соответствует преобразование симметрии — преобразование множества точек плоскости, определяемое этим типом. Так, если О — центр симметрии Опишем эти группы в случае, когда рассматриваемая фигура является правильным многоугольником.
|
 |
Оглавление
|
порядка для фигуры М, если фигура М совмещается с собой при поворотах на углы, кратные 
Например, на рис. 23 изображена фигура, имеющая центр симметрии порядка 3.
порядка, то соответствующим преобразованием симметрии является преобразование вращения всех точек плоскости вокруг точки О на угол 
(см. пример 8 § 2). Для определенности будем считать, что поворот осуществляется против движения часовой стрелки. А то, что некоторая фигура симметрична, означает, что она самосовмещается при соответствующем преобразовании симметрии. Таким образом, обозрение всех симметрий фигуры равносильно обозрению всех преобразований плоскости, при которых она самосовмещается. Понятно, что эти преобразования являются биекциями. Поэтому множество всех таких преобразований относительно умножения преобразований образует группу, которая является как бы мерой степени симметричности данной фигуры. Преобразования симметрии многих плоских фигур естественно описываются перестановками, т. е. их симметричность «намеряется» некоторыми группами перестановок.