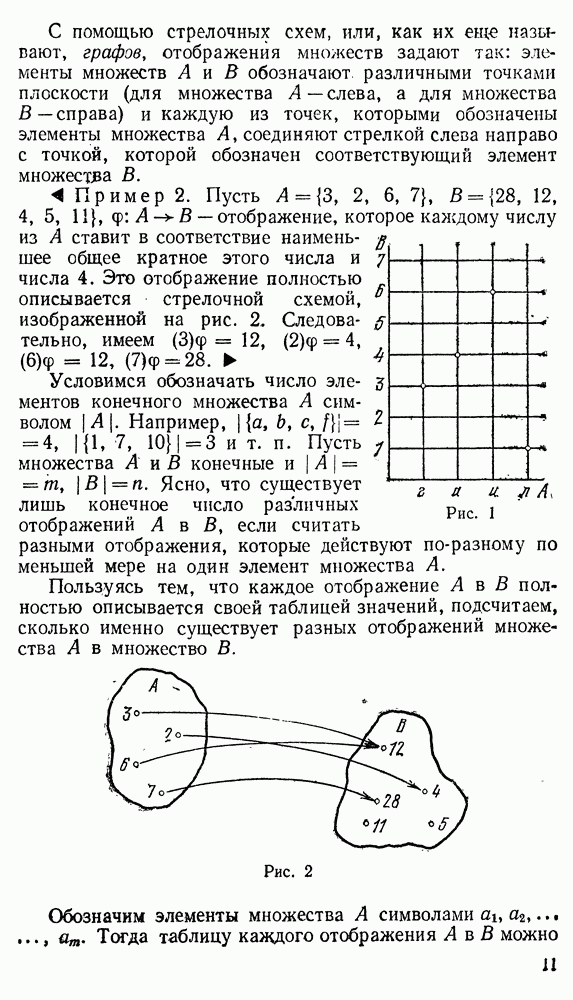
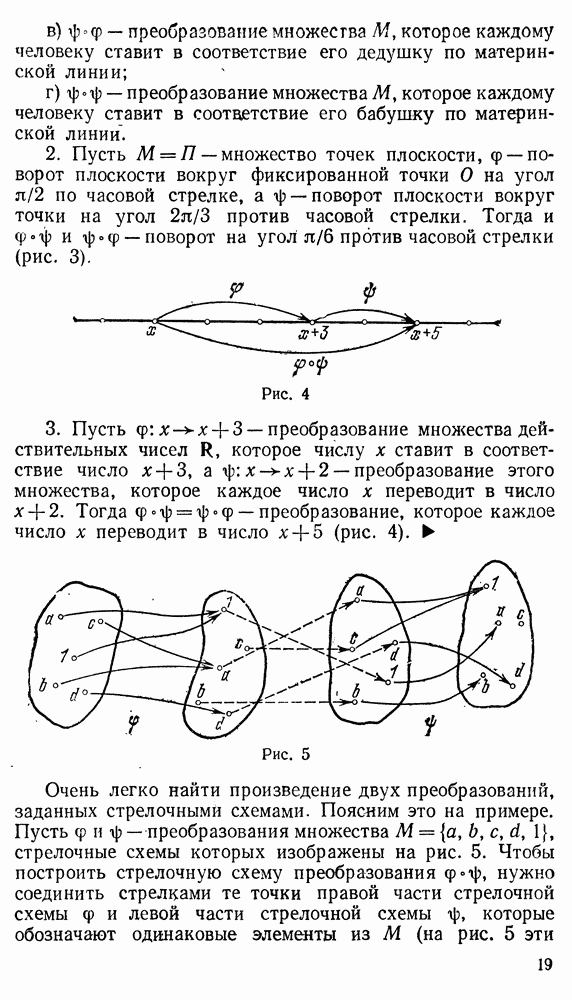
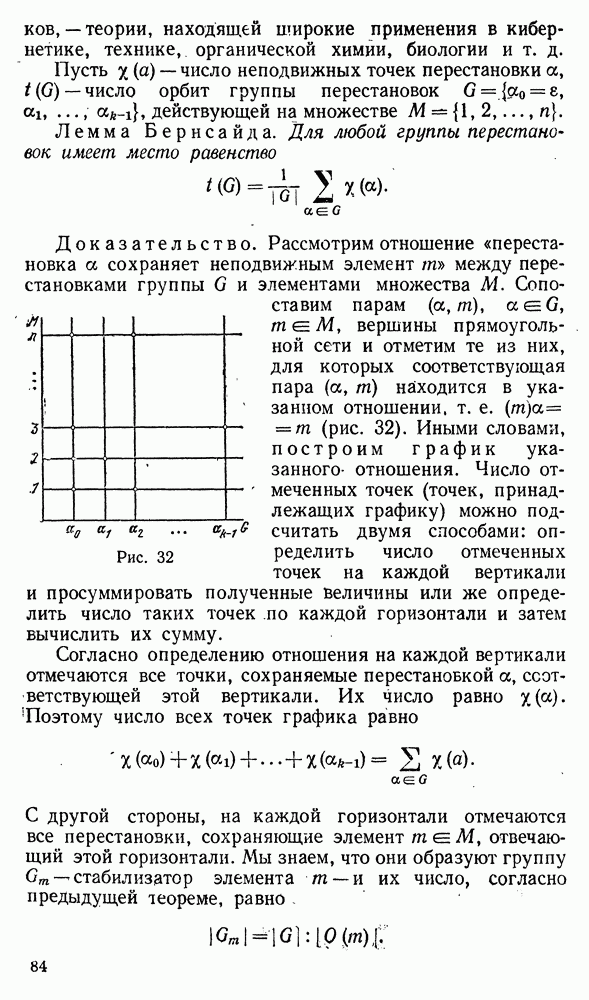
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 11. ТЕОРЕМА ЛАГРАНЖА
Пусть  — группы перестановок, причем
— группы перестановок, причем  , т. е. как принято говорить, Н является подгруппой группы G. Одной из первых теорем теории групп является теорема, устанавливающая связь между порядками групп G и Н, доказанная в несколько иных терминах Лагранжем еще в конце XVIII столетия.
, т. е. как принято говорить, Н является подгруппой группы G. Одной из первых теорем теории групп является теорема, устанавливающая связь между порядками групп G и Н, доказанная в несколько иных терминах Лагранжем еще в конце XVIII столетия.
Эта простая по идее доказательства теорема очень часто применяется как в самой теории групп, так и во всех приложениях, одно из которых мы рассмотрим ниже.
Теорема Лагранжа. Если Н — подгруппа группы G, то ее порядок является делителем порядка 
Доказательство. Пусть  — все перестановки, содержащиеся в группе
— все перестановки, содержащиеся в группе  — все перестановки из Н (т. е.
— все перестановки из Н (т. е.  ). Если
). Если  то утверждение теоремы справедливо, поэтому предположим, что
то утверждение теоремы справедливо, поэтому предположим, что  собственная подгруппа G). В силу этого предположения существует перестановка
собственная подгруппа G). В силу этого предположения существует перестановка  такая, что
такая, что  . Рассмотрим ряд перестановок
. Рассмотрим ряд перестановок

Все перестановки этого ряда различны: если бы для каких-то  имело место равенство
имело место равенство  , то, умножив его правую и левую части на
, то, умножив его правую и левую части на  мы получили бы равенство
мы получили бы равенство  . Кроме того, ни одна из них не содержится в подгруппе
. Кроме того, ни одна из них не содержится в подгруппе  если бы для какого-то номера i имело место включение
если бы для какого-то номера i имело место включение  то это означало бы, что для какого-то
то это означало бы, что для какого-то  Из этого равенства имеем
Из этого равенства имеем  , а так как
, а так как  - группа перестановок, то
- группа перестановок, то  что противоречит выбору этой перестановки.
что противоречит выбору этой перестановки.
Если перестановками группы Н и ряда (1) исчерпаны все перестановки из G, то  и все доказано. В противном случае найдется такая перестановка
и все доказано. В противном случае найдется такая перестановка  что
что  не содержится в ряде (1). Определим для нее ряд перестановок
не содержится в ряде (1). Определим для нее ряд перестановок

Аналогично проверяется, что а) все перестановки ряда (2) различны; б) они не содержатся в Н; в) ни одна из них не встречается среди перестановок ряда (1).
Если перестановками из подгруппы Н и рядов (1) и (2) исчерпываются все элементы группы G, то  доказано. В противном случае продолжаем процесс выбора перестановок у и построения рядов вида (1) и (2) дальше. Так как группа G конечная, то на каком-то, например на
доказано. В противном случае продолжаем процесс выбора перестановок у и построения рядов вида (1) и (2) дальше. Так как группа G конечная, то на каком-то, например на  шаге все перестановки из G будут исчерпаны.
шаге все перестановки из G будут исчерпаны.
Иными словами, все их можно расположить таким образом:

при этом все перестановки в каждой из строк различны и любые 2 строки не имеют общих элементов. Поскольку общее число элементов в (3) равно  (порядок группы G), а число элементов в каждой строке равно
(порядок группы G), а число элементов в каждой строке равно  (порядок
(порядок  группы Н), то имеем равенство
группы Н), то имеем равенство  , т. е.
, т. е.  является делителем
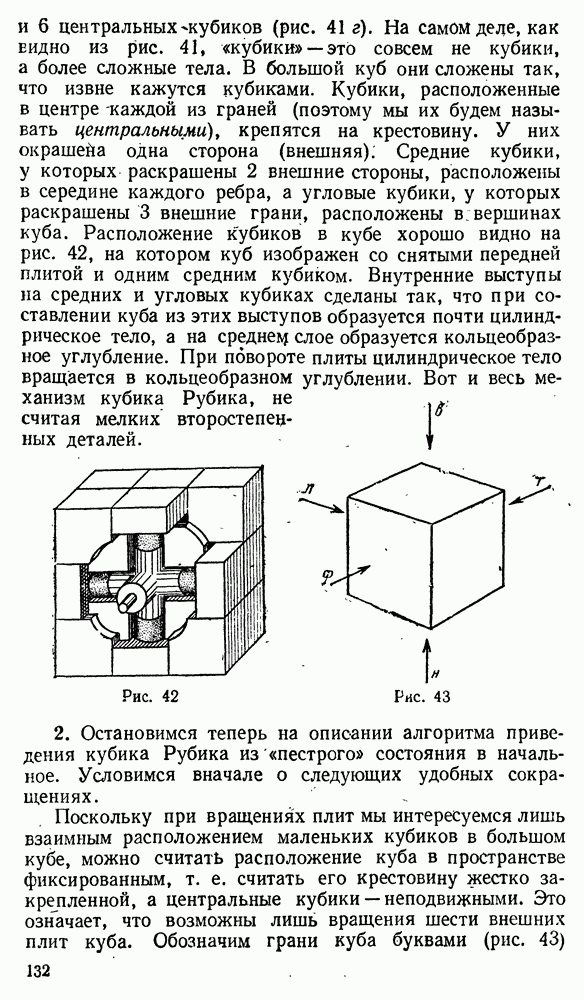
является делителем  и теорема доказана.
и теорема доказана.
Число k называют индексом подгруппы Н в группе G и обозначают  . Из доказательства теоремы Лагранжа мы получаем, что имеет место равенство
. Из доказательства теоремы Лагранжа мы получаем, что имеет место равенство

Так как порядок циклической подгруппы, порожденной перестановкой  совпадает с порядком перестановки а, то из теоремы Лагранжа получаем, что порядок любой перестановки из G — делитель
совпадает с порядком перестановки а, то из теоремы Лагранжа получаем, что порядок любой перестановки из G — делитель 
Теорема Лагранжа позволяет также существенно упростить решение задачи описания всех подрупп данной, группы. Например, если порядок группы G есть простое число, то в G нет нетривиальных собственных подгрупп (согласно теореме Лагранжа).
Собственные подгруппы из  могут состоять из двух и трех перестановок (делители числа
могут состоять из двух и трех перестановок (делители числа  поэтому непосредственную проверку, о которой идет речь в задаче из § 8, можно опустить. А ведь эта проверка длинная, так как есть
поэтому непосредственную проверку, о которой идет речь в задаче из § 8, можно опустить. А ведь эта проверка длинная, так как есть  подмножество из
подмножество из  состоящее из 4 или 5 элементов. Даже на этих двух примерах видно,
состоящее из 4 или 5 элементов. Даже на этих двух примерах видно,  насколько существенным может быть применение теоремы Лагранжа.
насколько существенным может быть применение теоремы Лагранжа.
Упражнения
1. Множества перестановок, стоящие в рядах таблицы (3), называются правыми (так как  умножается справа) классами смежности, а таблицу (3) естественно назвать таблицей разложения группы G на правые классы смежности по подгруппе Н. Вполне аналогично можно построить таблицу разложения группы G на левые классы смежности по подгруппе
умножается справа) классами смежности, а таблицу (3) естественно назвать таблицей разложения группы G на правые классы смежности по подгруппе Н. Вполне аналогично можно построить таблицу разложения группы G на левые классы смежности по подгруппе  Построить таблицы разложения группы 5 на класеы смежности как правые, так и левые по подгруппе
Построить таблицы разложения группы 5 на класеы смежности как правые, так и левые по подгруппе  по подгруппе
по подгруппе 
2. Доказать, что вращения правильного шестиугольника вокруг центра на углы, кратные  образуют подгруппу в группе всех его симметрий. Составить таблицы разложения на правые и левые классы смежности группы симметрий шестиугольника по подгруппе всех вращений. Обобщить это на случай произвольного
образуют подгруппу в группе всех его симметрий. Составить таблицы разложения на правые и левые классы смежности группы симметрий шестиугольника по подгруппе всех вращений. Обобщить это на случай произвольного  -угольника.
-угольника.
3. Если Н — подгруппа индекса 2 в группе G, то правые и левые классы смежности по этой подгруппе совпадают. Докажите.
4. Пусть  — решение
— решение  — натуральные) уравнения
— натуральные) уравнения

( — произвольное натуральное). Тогда
— произвольное натуральное). Тогда  является делителем
является делителем  Докажите.
Докажите.
5. Выпишите все числа, которые, согласно теореме Лагранжа, могут быть порядками элементов в группе  Существуют ли в группе
Существуют ли в группе  перестановки таких порядков?
перестановки таких порядков?
6. Тот же вопрос для группы 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- § 1. СУПЕРПОЗИЦИЯ ФУНКЦИЙ
- § 2. ПРЕОБРАЗОВАНИЯ
- 1. Отображение на все множество.
- 2. Взаимно однозначное отображение.
- 3. Взаимно однозначное отображение на все множество.
- § 3. УМНОЖЕНИЕ ПРЕОБРАЗОВАНИЙ
- Упражнения
- § 4. ГРУППА ПЕРЕСТАНОВОК И ПОЛУГРУППА ПРЕОБРАЗОВАНИЙ
- § 5. ГРАФЫ ПРЕОБРАЗОВАНИЙ. ОРБИТЫ. ЦИКЛИЧЕСКАЯ ФОРМА ЗАПИСИ ПЕРЕСТАНОВОК
- § 6. ПОРЯДОК ПЕРЕСТАНОВКИ
- § 7. ОБРАЗУЮЩИЕ СИММЕТРИЧЕСКОЙ ГРУППЫ
- Упражнения
- § 8. ПОДГРУППЫ СИММЕТРИЧЕСКИХ ГРУПП. ГРУППЫ ПЕРЕСТАНОВОК
- § 9. ГРУППЫ СИММЕТРИЙ
- 1. Группа симметрий правильного треугольника.
- 2. Группа симметрий квадрата.
- 3. Группа симметрий правильного n-угольника
- 4. Группа симметрий многоугольника, изображенного на рис. 26
- 5. Группа симметрий тетраэдра.
- 6. Группа симметрий куба.
- 7. Группа симметрий октаэдра.
- Упражнения
- § 10. ТЕОРЕМА КЭЛИ
- § 11. ТЕОРЕМА ЛАГРАНЖА
- § 12. ОРБИТЫ ГРУППЫ ПЕРЕСТАНОВОК. ЛЕММА БЕРНСАЙДА
- § 13. КОМБИНАТОРНЫЕ ЗАДАЧИ
- § 14. ДЕЙСТВИЕ ПЕРЕСТАНОВКИ НА МНОГОЧЛЕН
- § 15. ЧЕТНЫЕ И НЕЧЕТНЫЕ ПЕРЕСТАНОВКИ. ЗНАКОПЕРЕМЕННАЯ ГРУППА
- § 16. СИММЕТРИЧЕСКИЕ И ЧЕТНОСИММЕТРИЧЕСКИЕ МНОГОЧЛЕНЫ
- § 17. О РЕШЕНИИ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
- § 18. ИГРА «В ПЯТНАДЦАТЬ»
- § 19 ПЕРЕСТАНОВОЧНЫЕ КОНСТРУКЦИИ
- § 20. ВЕНГЕРСКИЙ ШАРНИРНЫЙ КУБИК
- § 21. ДРУГИЕ ИГРЫ
- ОТВЕТЫ, УКАЗАНИЯ, РЕШЕНИЯ
- СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ