2. Взаимно однозначное отображение.

Отображение называется взаимно однозначным или инъекцией, если разные элементы множества Л переводятся этим отображением в разные элементы множества В: для каждых из вытекает

Примеры. 6. Отображение множества целых чисел Z в множество всех четных чисел определим так: положим для каждого Это отображение — инъекция, так как из вытекает

7. Пусть А — множество всевозможных двухэлементных подмножеств множества действительных чисел R, В — множество приведенных квадратных уравнений. Каждому элементу множества А поставим в соответствие уравнение из В, для которого числа а, b являются корнями.

Как вытекает из теоремы Виета, такое отображение будет инъективным.

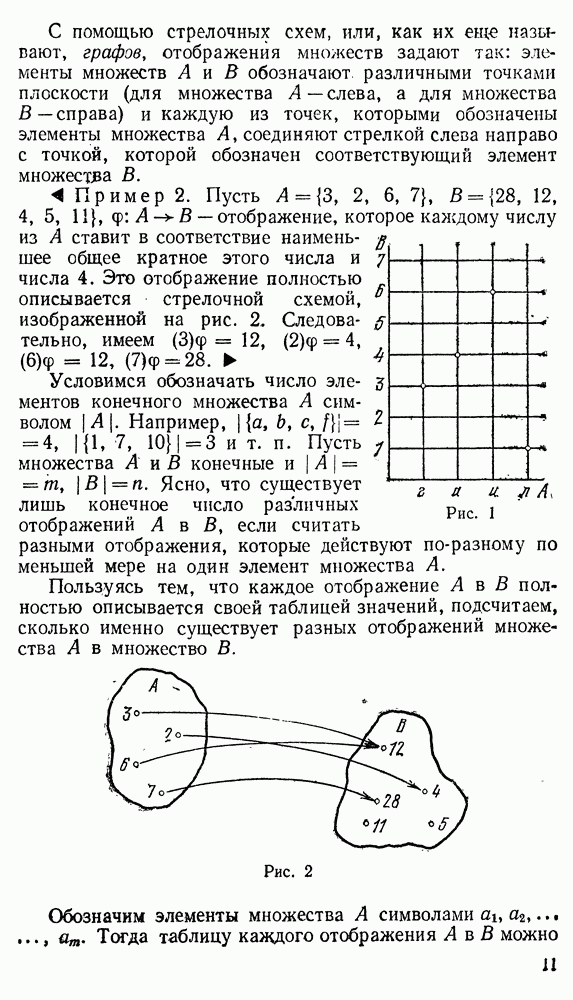
В нижнем ряду таблицы инъективного отображения в отличие от таблиц произвольных отображений, каждый элемент множества В встречается лишь один раз. Следовательно, на каждой горизонтальной прямой графика инъекции обозначено не более одной вершины сетки, а при стрелочном изображении инъекции в каждую точку, которой обозначается элемент множества В, входит не более чем одна стрелка.

Если множества А и В конечны и существует инъекция множества А в множество В, то, очевидно, должно выполняться неравенство