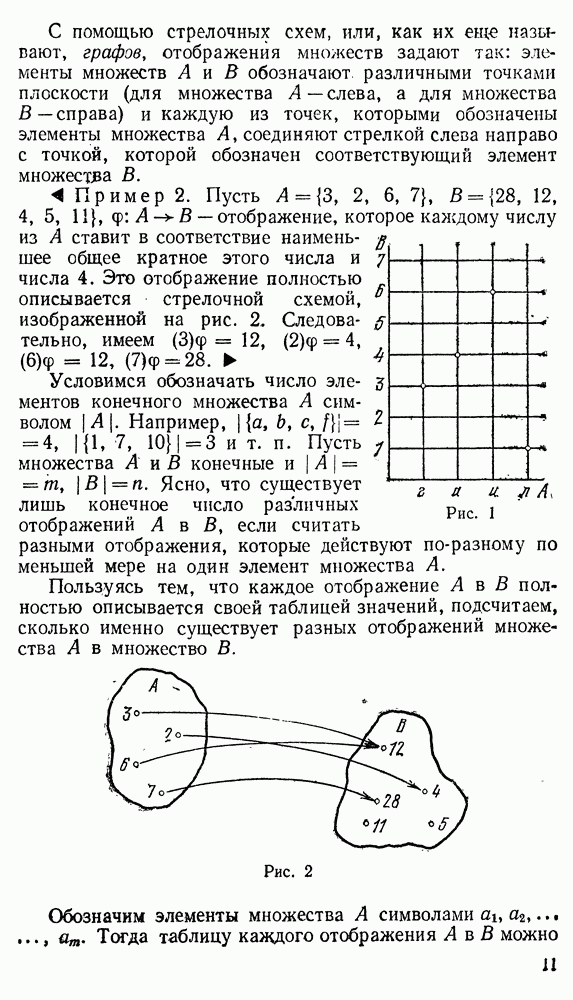
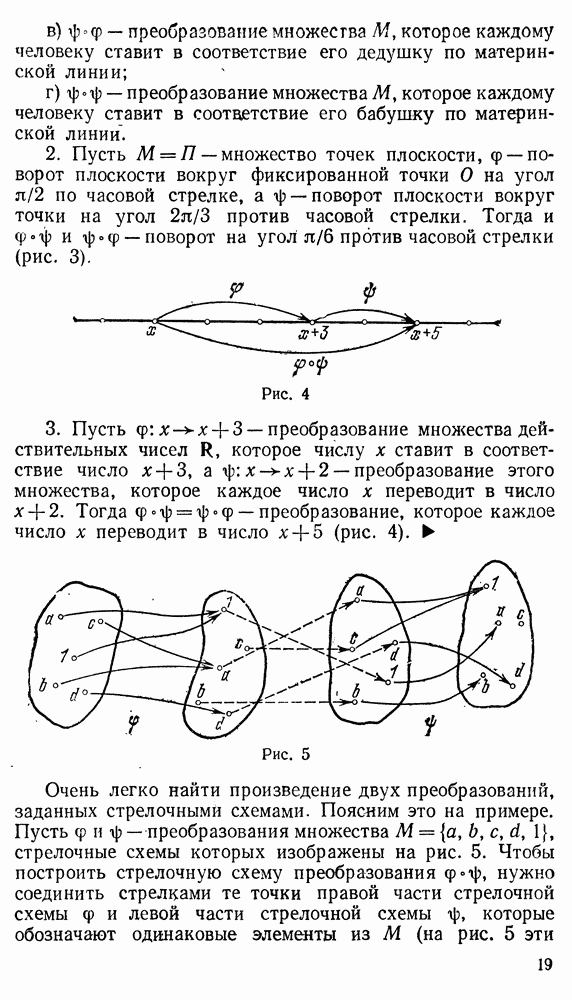
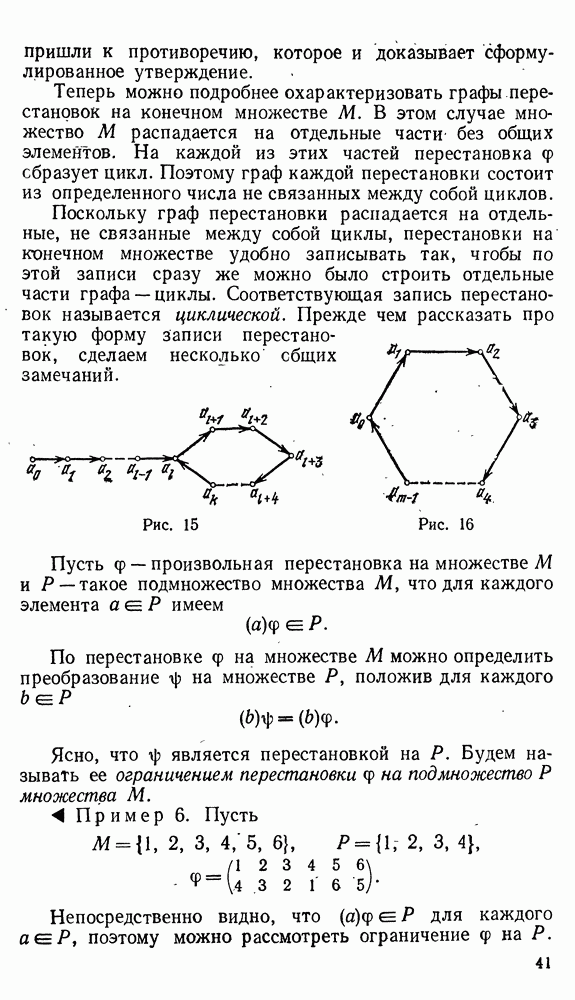
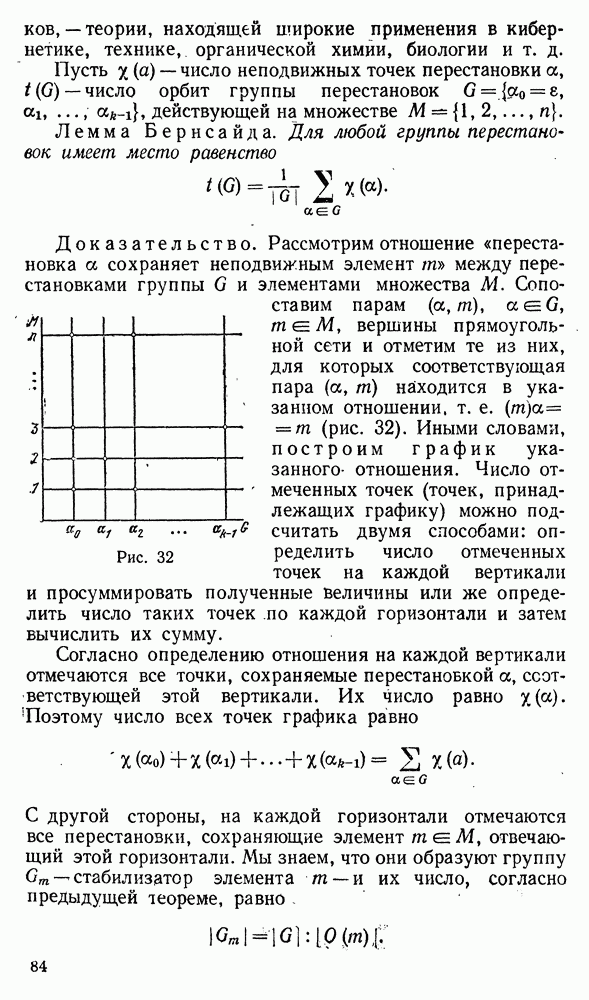
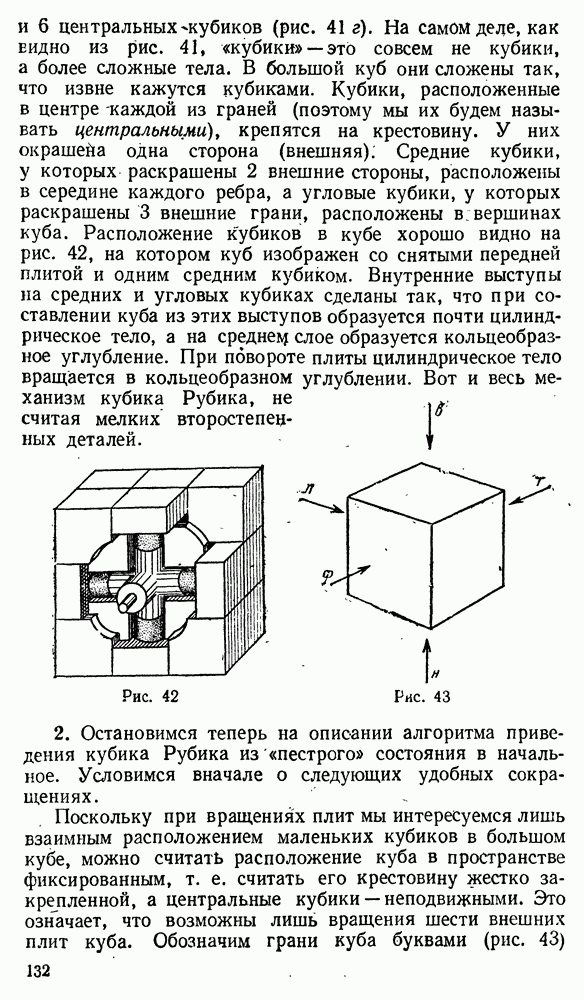
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 16. СИММЕТРИЧЕСКИЕ И ЧЕТНОСИММЕТРИЧЕСКИЕ МНОГОЧЛЕНЫ
Многочлен  называется симметрическим, если он является инвариантным относительно действия любой перестановки из
называется симметрическим, если он является инвариантным относительно действия любой перестановки из  т. е. группой инерции такого многочлена является вся симметрическая группа
т. е. группой инерции такого многочлена является вся симметрическая группа 
Например, симметрическими будут такие многочлены с  переменными:
переменными:

Действительно, орбитальный многочлен любого одночлена — симметрический, а

Многочлены  называются элементарными симметрическими многочленами. Запишем их полностью для
называются элементарными симметрическими многочленами. Запишем их полностью для  :
:

Непосредственно видно, что а) сумма симметрических многочленов — симметрический многочлен; б) произведение симметрических многочленов — симметрический многочлен. Поэтому если в произвольный многочлен  с
с  переменными подставить вместо
переменными подставить вместо  элементарные симметрические многочлены
элементарные симметрические многочлены  , то получим некоторый многочлен от
, то получим некоторый многочлен от  , который будет симметрическим. Например, если
, который будет симметрическим. Например, если

то

— симметрический многочлен.
Оказывается, что так можно получить каждый симметрический многочлен.
Теорема. Каждый симметрический многочлен является многочленом от элементарных симметрических многочленов.
Эта теорема называется основной теоремой о симметрических многочленах. Мы докажем эту теорему лишь для многочленов с тремя неизвестными. Рассмотрение этого случая даст нам возможность обозреть все этапы полного доказательства.
Понятно, что каждый симметрический многочлен с произвольным числом переменных является суммой орбитальных многочленов. А потому для доказательства теоремы в случае  достаточно убедиться, что многочлены вида
достаточно убедиться, что многочлены вида  можно представить в виде многочленов от
можно представить в виде многочленов от 
1) Убедимся методом математической индукции по числу к, что каждая степенная сумма  выражается через элементарные симметрические многочлены.
выражается через элементарные симметрические многочлены.
Действительно,  совпадает с
совпадает с  . Выразим теперь
. Выразим теперь  для произвольного k через многочлены
для произвольного k через многочлены  . Имеем
. Имеем

Отсюда

Аналогично,

Определяя из двух последних равенств многочлен  и подставляя его в предыдущее, будем иметь
и подставляя его в предыдущее, будем иметь

В соответствии с предположением индукции степенные суммы  можно записать в виде многочленов от элементарных симметрических многочленов, следовательно, через них можно выразить и сумму
можно записать в виде многочленов от элементарных симметрических многочленов, следовательно, через них можно выразить и сумму 
2) В § 13 было установлено, что любой орбитальный многочлен вида  выражается через степенные суммы. По только что доказанному,
выражается через степенные суммы. По только что доказанному,  можно представить в виде многочлена от элементарных симметрических многочленов.
можно представить в виде многочлена от элементарных симметрических многочленов.
3) Пусть  — некоторый орбитальный многочлен, и пусть, например, число
— некоторый орбитальный многочлен, и пусть, например, число  — наименьшее из чисел
— наименьшее из чисел  . Тогда имеем
. Тогда имеем

 — орбита одночлена с меньшим числом переменных, т. е. этот случай сводится к предыдущим.
— орбита одночлена с меньшим числом переменных, т. е. этот случай сводится к предыдущим.
Основная теорема о симметрических многочленах для  доказана. Для
доказана. Для  доказательство будет вполне аналогично, но значительно проще. Предлагаем читателю провести его самостоятельно.
доказательство будет вполне аналогично, но значительно проще. Предлагаем читателю провести его самостоятельно.
Рассмотрим несколько примеров применения основной теоремы о симметрических многочленах.
1. Решить систему

Выразим симметрические многочлены в левых частях обоих уравнений через  и введем новые неизвестные
и введем новые неизвестные 
Получим вспомогательную систему

Она имеет два решения:

Значит, множество решений исходной системы (1) равно объединению множества решений следующих двух систем:

Множество решений первой из них пусто, а множество решений второй  . Следовательно, множество решений исходной системы (1) есть
. Следовательно, множество решений исходной системы (1) есть

2. Доказать, что при  справедливо тождество
справедливо тождество

Выразим симметрический многочлен  через элементарные симметрические многочлены
через элементарные симметрические многочлены  Как было уже установлено при доказательстве теоремы о симметрических многочленах, многочленом от
Как было уже установлено при доказательстве теоремы о симметрических многочленах, многочленом от  который совпадает с суммой
который совпадает с суммой  является
является  Поэтому получим
Поэтому получим

Поскольку по условию  , то
, то  также равняется 0, откуда и вытекает правильность доказываемого тождества.
также равняется 0, откуда и вытекает правильность доказываемого тождества.
3. Составить квадратное уравнение с корнями  если
если

Такое уравнение можно составить, использовав теорему Виета. Для этого нужно найти, чему равняется произведение корней. Выражая  через элементарные симметрические многочлены, получим
через элементарные симметрические многочлены, получим  . Если в это равенство подставить вместо
. Если в это равенство подставить вместо  их значения, то будем иметь квадратное уравнение для
их значения, то будем иметь квадратное уравнение для 

Отсюда  . Следовательно, искомыми уравнениями будут
. Следовательно, искомыми уравнениями будут

Наряду с симметрическими многочленами часто приходится иметь дело с четносимметрическими многочленами. Четносимметрическими называются многочлены, инвариантные относительно всех четных перестановок. Следовательно, группа инерции четносимметрического многочлена будет содержать знакопеременную группу. Поскольку в симметрической группе  четной будет лишь тождественная перестановка, то каждый многочлен с двумя неизвестными четносимметрический, т. е. в этом случае понятие четносимметричности излишне. Однако уже среди многочленов с тремя неизвестными есть нечетносимметрические, например
четной будет лишь тождественная перестановка, то каждый многочлен с двумя неизвестными четносимметрический, т. е. в этом случае понятие четносимметричности излишне. Однако уже среди многочленов с тремя неизвестными есть нечетносимметрические, например  (группа инерции этого многочлена единичная).
(группа инерции этого многочлена единичная).
Понятно, что каждый симметрический многочлен четносимметрический, но не наоборот. Например, знакопеременный многочлен  четносимметрический для любого
четносимметрический для любого  , но не симметрический. Четносимметрическим будет, в частности, каждый многочлен, который под действием произвольной транспозиции меняет знак. Многочлены с таким свойством называются антисимметрическими. Как было установлено в § 13, многочлен
, но не симметрический. Четносимметрическим будет, в частности, каждый многочлен, который под действием произвольной транспозиции меняет знак. Многочлены с таким свойством называются антисимметрическими. Как было установлено в § 13, многочлен  антисимметрический. Вполне понятно также, что произведение симметрического многочлена на произвольный антисимметрический многочлен снова антисимметрический многочлен. В частности, антисимметрическими будут многочлены вида
антисимметрический. Вполне понятно также, что произведение симметрического многочлена на произвольный антисимметрический многочлен снова антисимметрический многочлен. В частности, антисимметрическими будут многочлены вида

где  — любой симметрический многочлен. Можно доказать, что каждый антисимметрический многочлен записывается в виде такого произведения (см. упражнение 7). Ясно, что произведение двух антисимметрических многочленов — многочлен симметрический.
— любой симметрический многочлен. Можно доказать, что каждый антисимметрический многочлен записывается в виде такого произведения (см. упражнение 7). Ясно, что произведение двух антисимметрических многочленов — многочлен симметрический.
Лемма. Действуя на произвольный четносимметрический многочлен  нечетными перестановками, будем получать один и тот же многочлен, т. е.
нечетными перестановками, будем получать один и тот же многочлен, т. е.

для любых нечетных перестановок  .
.
Действительно, в этом случае  — четные перестановки и, следовательно,
— четные перестановки и, следовательно,

Действуя на обе части этого равенства перестановкой  , получим
, получим

Поскольку  для любых перестановок
для любых перестановок  , то
, то

Используя ассоциативность умножения перестановок, получим

В силу определения обратной перестановки имеем  .
.
Теорема. Каждый четносимметрический многочлен может быть представлен,  притом единственным образом, в виде суммы симметрического и антисимметрического многочленов.
притом единственным образом, в виде суммы симметрического и антисимметрического многочленов.
Доказательство. Единственность. Пусть заданный четносимметрический многочлен  представлен в виде
представлен в виде

где g — некоторый симметрический,  — антисимметрический многочлены. Подействуем на обе части этого равенства какой-нибудь нечетной перестановкой а:
— антисимметрический многочлены. Подействуем на обе части этого равенства какой-нибудь нечетной перестановкой а:

Однако, в силу предположений о g и 

Складывали вычитая почленно равенства (I) и (2), получим

Отметим, что в силу ранее доказанной леммы правые части равенств (3) не изменятся, если вместо а взять какую-нибудь другую нечетную перестановку  .
.
Проведенные рассуждения доказывают, что если разложение (1) возможно, то обязательно для g и  справедливы формулы (3), т. е. g и
справедливы формулы (3), т. е. g и  если существуют, то определены однозначно.
если существуют, то определены однозначно.
Существование. Для доказательства существования разложения (1) необходимо проверить, что:
1)  где а — некоторая (безразлично какая) нечетная перестановка;
где а — некоторая (безразлично какая) нечетная перестановка;
2)  - симметрический многочлен;
- симметрический многочлен;
3)  - антисимметрический многочлен.
- антисимметрический многочлен.
Но 1) очевидно, а для доказательства 2) и 3) достаточно заметить следующее. Если Р — четная перестановка, то  в силу леммы, так как — нечетная перестановка. Поэтому
в силу леммы, так как — нечетная перестановка. Поэтому  . Если же Р — нечетная перестановка,
. Если же Р — нечетная перестановка,  в силу леммы, а
в силу леммы, а  так как будет четной перестановкой. Поэтому
так как будет четной перестановкой. Поэтому

Теорема доказана. В частности, любой многочлен с двумя неизвестными является суммой симметрического и антисимметрического многочленов.
Упражнения
1. Выразить через элементарные симметрические многочлены:

2. Решить системы уравнений:

3. Найти площадь треугольника, зная его периметр, сумму квадратов длин его сторон и сумму кубов длин его сторон.
4. Если некоторый многочлен  обращается в нуль при подстановке
обращается в нуль при подстановке  вместо
вместо  вместо
вместо  то он тождественно равен нулю. Доказать это.
то он тождественно равен нулю. Доказать это.
5. Теорема единственности: для произвольного симметрического многочлена  существует только один многочлен
существует только один многочлен  такой, что
такой, что  Доказать это утверждение, используя упражнение 4.
Доказать это утверждение, используя упражнение 4.
6. Если  — антисимметрический многочлен, то
— антисимметрический многочлен, то  Доказать это. Сформулировать и доказать аналогичное утверждение для многочленов с тремя переменными.
Доказать это. Сформулировать и доказать аналогичное утверждение для многочленов с тремя переменными.
7. Используя предыдущее упражнение доказать, что произвольный антисимметрический многочлен  с двумя переменными имеет вид
с двумя переменными имеет вид  где
где  - симметрический многочлен.
- симметрический многочлен.
8. Функция  от
от  переменных называется симметрической, если она не изменяет значений при произвольной перестановке аргументов, т. е. для любой перестановки
переменных называется симметрической, если она не изменяет значений при произвольной перестановке аргументов, т. е. для любой перестановки  имеем
имеем  Докажите, что функция
Докажите, что функция  симметрическая.
симметрическая.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- § 1. СУПЕРПОЗИЦИЯ ФУНКЦИЙ
- § 2. ПРЕОБРАЗОВАНИЯ
- 1. Отображение на все множество.
- 2. Взаимно однозначное отображение.
- 3. Взаимно однозначное отображение на все множество.
- § 3. УМНОЖЕНИЕ ПРЕОБРАЗОВАНИЙ
- Упражнения
- § 4. ГРУППА ПЕРЕСТАНОВОК И ПОЛУГРУППА ПРЕОБРАЗОВАНИЙ
- § 5. ГРАФЫ ПРЕОБРАЗОВАНИЙ. ОРБИТЫ. ЦИКЛИЧЕСКАЯ ФОРМА ЗАПИСИ ПЕРЕСТАНОВОК
- § 6. ПОРЯДОК ПЕРЕСТАНОВКИ
- § 7. ОБРАЗУЮЩИЕ СИММЕТРИЧЕСКОЙ ГРУППЫ
- Упражнения
- § 8. ПОДГРУППЫ СИММЕТРИЧЕСКИХ ГРУПП. ГРУППЫ ПЕРЕСТАНОВОК
- § 9. ГРУППЫ СИММЕТРИЙ
- 1. Группа симметрий правильного треугольника.
- 2. Группа симметрий квадрата.
- 3. Группа симметрий правильного n-угольника
- 4. Группа симметрий многоугольника, изображенного на рис. 26
- 5. Группа симметрий тетраэдра.
- 6. Группа симметрий куба.
- 7. Группа симметрий октаэдра.
- Упражнения
- § 10. ТЕОРЕМА КЭЛИ
- § 11. ТЕОРЕМА ЛАГРАНЖА
- § 12. ОРБИТЫ ГРУППЫ ПЕРЕСТАНОВОК. ЛЕММА БЕРНСАЙДА
- § 13. КОМБИНАТОРНЫЕ ЗАДАЧИ
- § 14. ДЕЙСТВИЕ ПЕРЕСТАНОВКИ НА МНОГОЧЛЕН
- § 15. ЧЕТНЫЕ И НЕЧЕТНЫЕ ПЕРЕСТАНОВКИ. ЗНАКОПЕРЕМЕННАЯ ГРУППА
- § 16. СИММЕТРИЧЕСКИЕ И ЧЕТНОСИММЕТРИЧЕСКИЕ МНОГОЧЛЕНЫ
- § 17. О РЕШЕНИИ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
- § 18. ИГРА «В ПЯТНАДЦАТЬ»
- § 19 ПЕРЕСТАНОВОЧНЫЕ КОНСТРУКЦИИ
- § 20. ВЕНГЕРСКИЙ ШАРНИРНЫЙ КУБИК
- § 21. ДРУГИЕ ИГРЫ
- ОТВЕТЫ, УКАЗАНИЯ, РЕШЕНИЯ
- СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ