| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
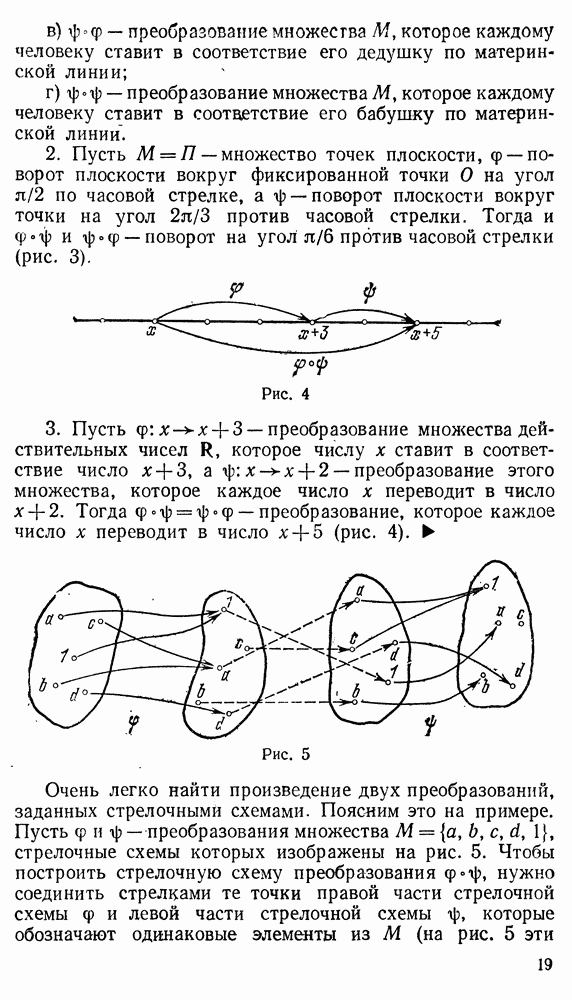
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 19 ПЕРЕСТАНОВОЧНЫЕ КОНСТРУКЦИИ
Нам понадобится в этом параграфе операция прямого произведения множеств. Прямым произведением множеств  называется множество всевозможных упорядоченных пар вида
называется множество всевозможных упорядоченных пар вида  первая компонента которых является элементом множества
первая компонента которых является элементом множества  , а вторая — элементом множества
, а вторая — элементом множества  Прямое произведение множеств
Прямое произведение множеств  обозначается символом
обозначается символом  Например, имеем
Например, имеем

Понятно, что для конечных множеств  имеет место равенство
имеет место равенство

Наглядно прямое произведение множеств удобно изображать в виде прямоугольной решетки: элементам множеств  ставятся в соответствие точки на «координатных осях»
ставятся в соответствие точки на «координатных осях»  (рис. 39), через эти точки проводят соответственно горизонтальные и вертикальные прямые, образующие прямоугольную решетку, и узлам этой решетки соответствуют элементы прямого произведения.
(рис. 39), через эти точки проводят соответственно горизонтальные и вертикальные прямые, образующие прямоугольную решетку, и узлам этой решетки соответствуют элементы прямого произведения.
Мы уже использовали такой способ изображения, например, в § 12 (рис - 32). Будем рассматривать только прямые произведения множеств натуральных чисел. Условимся располагать элементы прямого произведения  в следующем порядке:
в следующем порядке:

т. е. упорядочим по возрастанию вначале первые компоненты, а при равных первых компонентах — вторые, и тоже по возрастанию. (Такой порядок называется лексикографическим.)
Рассмотрим теперь конструкции, которые позволяют по перестановкам на множествах  строить перестановки на множествах
строить перестановки на множествах  . Самая простая среди них — это так называемая сумма перестановок.
. Самая простая среди них — это так называемая сумма перестановок.

Рис. 39
Пусть множества  не имеют общих элементов, т. е.
не имеют общих элементов, т. е.  — некоторая перестановка на множестве
— некоторая перестановка на множестве  — перестановка на множестве
— перестановка на множестве  . Суммой (прямой) перестановок
. Суммой (прямой) перестановок  называется перестановка на множестве
называется перестановка на множестве  которая на элементы
которая на элементы  действует так, как. а, а на элементы
действует так, как. а, а на элементы  — так, как
— так, как  . Мы будем обозначать эту перестановку символом
. Мы будем обозначать эту перестановку символом  Согласно определению имеем, что осфр действует на произвольный элемент
Согласно определению имеем, что осфр действует на произвольный элемент 

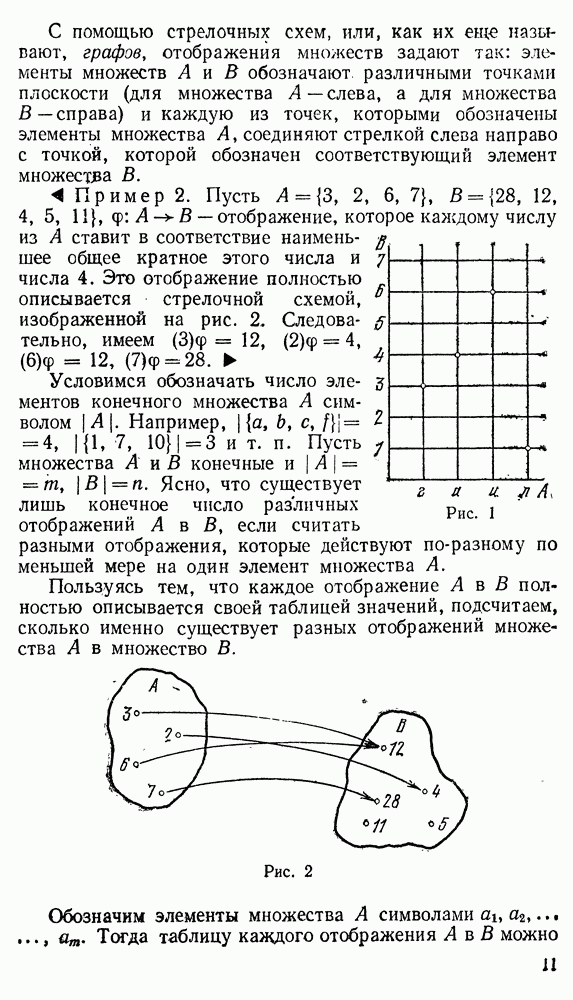
Примеры. 1. Пусть  и на множествах
и на множествах  заданы соответственно перестановки
заданы соответственно перестановки

Тогда

2. Согласно доказанной в § 5 теореме, любую перестановку можно разложить в произведение взаимно простых циклов. Понятие циклической перестановки мы рассматривали в двух различных смыслах — это собственно циклические перестановки и их расширения на большие множества. В формулировке теоремы понятие цикла употребляется во втором смысле, т. е. все циклические перестановки в разложении

перестановки  в произведение взаимно простых циклов — это перестановки на множестве М, являющиеся расширениями циклов
в произведение взаимно простых циклов — это перестановки на множестве М, являющиеся расширениями циклов  , которые действуют на непересекающихся подмножествах
, которые действуют на непересекающихся подмножествах  множества М. Применяя
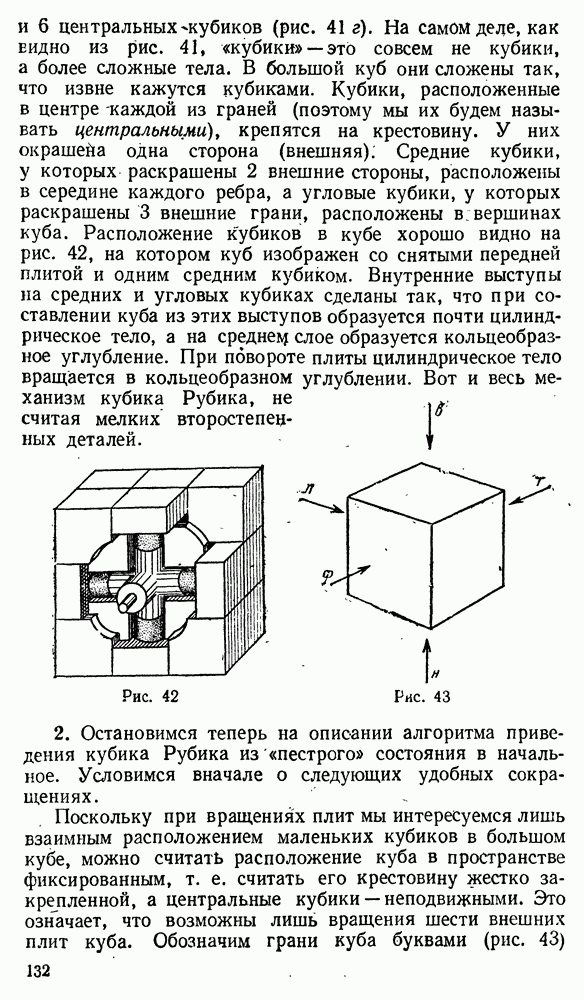
множества М. Применяя  раз конструкцию прямой суммы к циклам
раз конструкцию прямой суммы к циклам  получим равенство
получим равенство

Из этого примера понятно, что сумму перестановок  можно получить также следующим образом: рассмотреть расширения
можно получить также следующим образом: рассмотреть расширения  этих перестановок на множество
этих перестановок на множество  и перемножить их. Итак,
и перемножить их. Итак, 
Рассмотрим теперь несколько более сложную конструкцию, которая называется прямым произведением перестановок.
С помощью этой конструкции по перестановкам а и Р на множествах  соответственно строится перестановка на прямом произведении
соответственно строится перестановка на прямом произведении  . Эта перестановка действует на произвольный элемент
. Эта перестановка действует на произвольный элемент  из прямого произведения
из прямого произведения  так, что перестановка
так, что перестановка  изменяет первую компоненту пары, а перестановка
изменяет первую компоненту пары, а перестановка  — ее вторую компоненту. Мы будем обозначать так построенную перестановку символом
— ее вторую компоненту. Мы будем обозначать так построенную перестановку символом  Таким образом, для произвольной пары
Таким образом, для произвольной пары 

Примеры. 3. Пусть

Тогда  — перестановка на множестве
— перестановка на множестве  . Согласно определению, имеем
. Согласно определению, имеем

Таким образом, перестановка  имеет следующую таблицу значений:
имеет следующую таблицу значений:

Легко понять, как построить эту таблицу непосредственно по таблицам перестановок  Ранее мы оговорили, что все перестановки будут рассматриваться над начальными отрезками натуральных чисел. Перестановке
Ранее мы оговорили, что все перестановки будут рассматриваться над начальными отрезками натуральных чисел. Перестановке  можно поставить в соответствие перестановку на множестве
можно поставить в соответствие перестановку на множестве  занумеровав элементы прямого произведения следующим образом;
занумеровав элементы прямого произведения следующим образом;

Получим следующую перестановку:

Эту перестановку можно сконструировать в два этапа.
А именно: разбиваем множество  на две одинаковые части {1, 2, 3} {4, 5, 6} и на каждой из этих частей производим такую же перестановку, как
на две одинаковые части {1, 2, 3} {4, 5, 6} и на каждой из этих частей производим такую же перестановку, как  . Получим перестановку
. Получим перестановку

Затем переставляем эти части во второй строке таблицы, не изменяя порядок элементов в них.
Конечно, переход от записи  в виде (2) к записи (3) зависит от выбора нумерации. Но если нумерацию считать фиксированной, то любая из этих таблиц однозначно восстанавливается подругой. Поскольку приходится использовать как одну из них, так и другую, условимся элементы множества
в виде (2) к записи (3) зависит от выбора нумерации. Но если нумерацию считать фиксированной, то любая из этих таблиц однозначно восстанавливается подругой. Поскольку приходится использовать как одну из них, так и другую, условимся элементы множества  нумеровать согласно порядку (1). 4. Перестановку
нумеровать согласно порядку (1). 4. Перестановку

естественно сопоставлять произведению перестановок

В самом деле, перестановка  задается таблицей
задается таблицей

которой при задании нумерации элементов прямого произведения {1, 2, 3}х{1, 2, 3} соответственно упорядочению (1) отвечает как раз таблица 7.
С помощью второй конструкции можно строить перестановки на прямом произведении  множеств
множеств  применяя ее не к двум перестановкам, а к
применяя ее не к двум перестановкам, а к  , где
, где  . Пусть а — некоторая перестановка на множестве
. Пусть а — некоторая перестановка на множестве  — перестановки на множестве
— перестановки на множестве  . Множество
. Множество  разбивается на k непересекающихся частей следующим образом:
разбивается на k непересекающихся частей следующим образом:

 Преобразование, определяемое элементами
Преобразование, определяемое элементами  , действует на произвольную пару
, действует на произвольную пару  на
на  так, что на первую компоненту пары действует перестановка а, а на вторую — перестановка
так, что на первую компоненту пары действует перестановка а, а на вторую — перестановка  . Иными словами, на первые координаты всех пар из
. Иными словами, на первые координаты всех пар из  действует. перестановка а, на вторые координаты пар из множества
действует. перестановка а, на вторые координаты пар из множества  — перестановка
— перестановка  на вторые координаты пар из множества
на вторые координаты пар из множества  — перестановка
— перестановка  и т. д.
и т. д.
Будем называть так построенную перестановку сплетением перестановок  с помощью перестановки а и обозначать символом
с помощью перестановки а и обозначать символом

Итак, согласно определению, действие сплетения перестановок  с помощью перестановки а на произвольный элемент
с помощью перестановки а на произвольный элемент  определяется равенством
определяется равенством

То, что прямая сумма и прямое произведение перестановок — снова перестановка, вполне понятно и не требует дополнительных проверок. Для сплетения это совсем не очевидно. Поэтому покажем, что для произвольных перестановок  сплетение
сплетение  является перестановкой на множестве
является перестановкой на множестве 
Поскольку  — конечные множества, то достаточно проверить, что преобразование
— конечные множества, то достаточно проверить, что преобразование  инъективно. Пусть
инъективно. Пусть  — различные пары из прямого произведения
— различные пары из прямого произведения  . Это означает, что выполнено по крайней мере одно из неравенств
. Это означает, что выполнено по крайней мере одно из неравенств  или
или  . Если
. Если  , то
, то  и, независимо от того равны между собой числа
и, независимо от того равны между собой числа  или нет, пары
или нет, пары  между собой различны. Пусть теперь
между собой различны. Пусть теперь  Тогда
Тогда  и пары
и пары  между собой различны, поскольку
между собой различны, поскольку  . Итак, для произвольных различных пар
. Итак, для произвольных различных пар  из
из  имеем
имеем

т. е. сплетение перестановок  снова будет перестановкой.
снова будет перестановкой.
Примеры. 5. Пусть 

— перестановка на множестве 

— перестановки на множестве 
Сплетение  перестановок
перестановок  с помощью а действует на множестве так:
с помощью а действует на множестве так:

Таким образом, перестановка  имеет таблицу значений
имеет таблицу значений

При принятой нами нумерации множества  ей сопоставляется следующая таблица:
ей сопоставляется следующая таблица:

6. Пусть  . Сплетение
. Сплетение  перестановок
перестановок  с помощью перестановки а действует на произвольный элемент
с помощью перестановки а действует на произвольный элемент  согласно равенству
согласно равенству

Это действие совпадает с действием прямого произведения перестановок  , т. е. имеет место равенство
, т. е. имеет место равенство

Пусть теперь G и Н — произвольные множества перестановок на множествах  соответственно.
соответственно.
Определения. 1. Суммой множеств перестановок G и  (в предположении, что
(в предположении, что  ) называется множество всевозможных перестановок вида
) называется множество всевозможных перестановок вида  где а
где а 
2. Прямым произведением множеств перестановок G и  называется множество всевозможных перестановок вида
называется множество всевозможных перестановок вида  где
где 
3. Сплетением множеств перестановок G и Н называется множество всевозможных перестановок вида  , где
, где  .
.
Прямую сумму множеств перестановок G и М обозначим символом  их прямое произведение — символом
их прямое произведение — символом  а сплетение —
а сплетение —  . Понятно, что имеют место следующие равенства:
. Понятно, что имеют место следующие равенства:
а) 
б) 
в) 
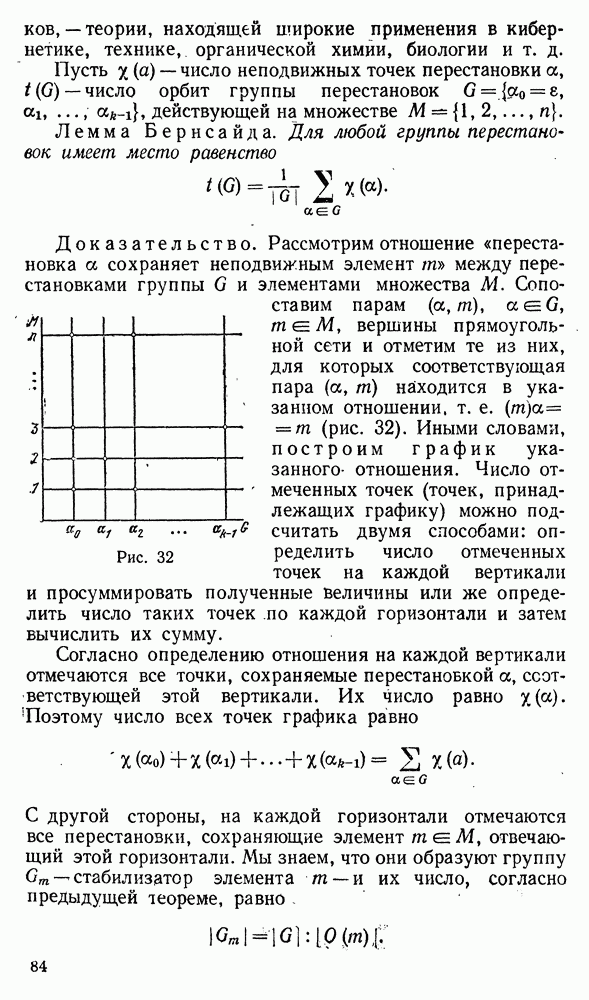
Теорема. Если  — группы перестановок, то
— группы перестановок, то  также являются группами перестановок на соответствующих множествах.
также являются группами перестановок на соответствующих множествах.
Доказательство. Достаточно убедиться, что произведение перестановок из одного из сконструированных множеств снова в нем содержится (см. упражнение 1 к § 8). Рассмотрим отдельно каждую из конструкций.
Пусть  — две перестановки из
— две перестановки из  Произведение
Произведение  этих перестановок действует на произвольный элемент
этих перестановок действует на произвольный элемент 

Но  совпадает либо с
совпадает либо с  (при
(при  ), либо с
), либо с  (при
(при  ). Если
). Если  то
то  тоже содержится в
тоже содержится в  Поэтому
Поэтому  Аналогично, если
Аналогично, если  то
то  тоже содержится в этом множестве и
тоже содержится в этом множестве и  Итак, произведение
Итак, произведение  перестановок
перестановок  множества
множества  действует на произвольный элемент
действует на произвольный элемент  таким же образом, как и перестановка
таким же образом, как и перестановка  Следовательно, имеет место равенство
Следовательно, имеет место равенство  Поскольку G и Н — группы, то
Поскольку G и Н — группы, то  замкнуто относительно умножения перестановок.
замкнуто относительно умножения перестановок.
Пусть теперь  — две перестановки из
— две перестановки из  Произведение
Произведение  действует на произвольную пару
действует на произвольную пару  согласно равенствам
согласно равенствам

т. е. на первую компоненту пары действует перестановка  а на вторую
а на вторую  . Поскольку пара
. Поскольку пара  произвольная, то это означает, что имеет место равенство
произвольная, то это означает, что имеет место равенство

Снова  замкнуто относительно умножения перестановок.
замкнуто относительно умножения перестановок.
И наконец, пусть  — две перестановки из
— две перестановки из  причем
причем

Рассмотрим действие произведения АВ этих перестановок на произвольную пару 
Имеем равенства

Таким образом, произведение АВ на первую компоненту пары  действует, как перестановка
действует, как перестановка  а на вторую компоненту — как перестановка
а на вторую компоненту — как перестановка  т. е. АВ является сплетением перестановок
т. е. АВ является сплетением перестановок  с помощью перестановки
с помощью перестановки  а следовательно, содержится в
а следовательно, содержится в  . Итак,
. Итак,  замкнуто относительно умножения перестановок. Теорема доказана.
замкнуто относительно умножения перестановок. Теорема доказана.
Конструкции прямой суммы, прямого произведения и сплетения групп перестановок позволяют по данным группам конструировать новые группы, т. е. существенно обогащают теорию новыми примерами. Оказывается, что многие из естественно возникающих групп перестановок можно построить из более простых с помощью рассмотренных в этом параграфе конструкций, а это оказывает существенную помощь при изучении таких групп перестановок.
Упражнения
1. Доказать, что прямая сумма перестановок — ассоциативная операция, т. е. для произвольных трех перестановок  соответственно над множествами
соответственно над множествами  которые попарно не пересекаются, имеет место равенство
которые попарно не пересекаются, имеет место равенство

2. Пусть  - тип перестановки а на множестве
- тип перестановки а на множестве  - тип перестановки
- тип перестановки  на множестве
на множестве  Каков тип перестановки
Каков тип перестановки  на множестве
на множестве 
3. Установите, что для порядков перестановок  выполняется соотношение
выполняется соотношение

4. Постройте таблицу перестановки  , где
, где

и таблицу, соответствующую  при принятой нумерации множества {1, 2, 3}х{1, 2, 3}.
при принятой нумерации множества {1, 2, 3}х{1, 2, 3}.
5. Как, зная порядок - перестановок  , определить порядок перестановки
, определить порядок перестановки 
6. Проверить, что группа перестановок

есть прямая сумма циклических групп второго порядка на множествах {1, 2} и {3, 4}, а группа перестановок

является прямым произведением циклической группы второго порядка над множеством М = {1, 2} на себя, причем подстановки из этого прямого произведения записаны с учетом принятой нами нумерации элементов множества 
7. Указать обратные к перестановкам  , где
, где  перестановки на некоторых множествах,
перестановки на некоторых множествах,
8. Пусть

Построить перестановки  Совпадают ли они? Построить таблицы этих перестановок, записанные с учетом принятой нумерации элементов множества
Совпадают ли они? Построить таблицы этих перестановок, записанные с учетом принятой нумерации элементов множества 
Как определить обратную к перестановке вида 
10. Доказать, что сплетение двух циклических групп второго порядка совпадает с группой симметрий квадрата, при соответствующих обозначениях его вершин.
11. Пусть  Укажите конструкцию, с помощью которой группа симметрий этого многочлена строится из симметрических групп
Укажите конструкцию, с помощью которой группа симметрий этого многочлена строится из симметрических групп  действующих на подходящих множествах,
действующих на подходящих множествах,
12. Перестановка а над множеством М имеет следующее разложение в произведение взаимно простых циклов;

Докажите, что множество всех перестановок, которые коммутируют с а, совпадает с прямой суммой циклических групп  действующих на множествах
действующих на множествах

соответственно,
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- § 1. СУПЕРПОЗИЦИЯ ФУНКЦИЙ
- § 2. ПРЕОБРАЗОВАНИЯ
- 1. Отображение на все множество.
- 2. Взаимно однозначное отображение.
- 3. Взаимно однозначное отображение на все множество.
- § 3. УМНОЖЕНИЕ ПРЕОБРАЗОВАНИЙ
- Упражнения
- § 4. ГРУППА ПЕРЕСТАНОВОК И ПОЛУГРУППА ПРЕОБРАЗОВАНИЙ
- § 5. ГРАФЫ ПРЕОБРАЗОВАНИЙ. ОРБИТЫ. ЦИКЛИЧЕСКАЯ ФОРМА ЗАПИСИ ПЕРЕСТАНОВОК
- § 6. ПОРЯДОК ПЕРЕСТАНОВКИ
- § 7. ОБРАЗУЮЩИЕ СИММЕТРИЧЕСКОЙ ГРУППЫ
- Упражнения
- § 8. ПОДГРУППЫ СИММЕТРИЧЕСКИХ ГРУПП. ГРУППЫ ПЕРЕСТАНОВОК
- § 9. ГРУППЫ СИММЕТРИЙ
- 1. Группа симметрий правильного треугольника.
- 2. Группа симметрий квадрата.
- 3. Группа симметрий правильного n-угольника
- 4. Группа симметрий многоугольника, изображенного на рис. 26
- 5. Группа симметрий тетраэдра.
- 6. Группа симметрий куба.
- 7. Группа симметрий октаэдра.
- Упражнения
- § 10. ТЕОРЕМА КЭЛИ
- § 11. ТЕОРЕМА ЛАГРАНЖА
- § 12. ОРБИТЫ ГРУППЫ ПЕРЕСТАНОВОК. ЛЕММА БЕРНСАЙДА
- § 13. КОМБИНАТОРНЫЕ ЗАДАЧИ
- § 14. ДЕЙСТВИЕ ПЕРЕСТАНОВКИ НА МНОГОЧЛЕН
- § 15. ЧЕТНЫЕ И НЕЧЕТНЫЕ ПЕРЕСТАНОВКИ. ЗНАКОПЕРЕМЕННАЯ ГРУППА
- § 16. СИММЕТРИЧЕСКИЕ И ЧЕТНОСИММЕТРИЧЕСКИЕ МНОГОЧЛЕНЫ
- § 17. О РЕШЕНИИ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
- § 18. ИГРА «В ПЯТНАДЦАТЬ»
- § 19 ПЕРЕСТАНОВОЧНЫЕ КОНСТРУКЦИИ
- § 20. ВЕНГЕРСКИЙ ШАРНИРНЫЙ КУБИК
- § 21. ДРУГИЕ ИГРЫ
- ОТВЕТЫ, УКАЗАНИЯ, РЕШЕНИЯ
- СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ