§ 2. ПРЕОБРАЗОВАНИЯ

Как известно, отображением множества А в множество В называется соответствие, по которому каждому элементу множества А сопоставляется однозначно определенный элемент множества В; этот элемент b называется образом элемента а; элемент а, в свою очередь, называется прообразом элемента b.

Отображения одного множества в другое будем обозначать строчными буквами греческого алфавита.

Если задано отображение множества А в множество В, то это обозначается одним из двух способов:

Образ элемента при отображении будем обозначать так: (знак отображения будем записывать справа от символа элемента).

Отображение одного множества в другое можно задавать описательно, указывая правило, по которому каждому элементу какого-то множества А ставится в соответствие его образ из множества В, а также с помощью таблиц, графиков, стрелочных схем.

Остановимся на указанных способах задания отображений произвольных множеств (как числовых, так и нечисловых). Строя таблицу отображения в нее записывают все возможные пары вида

Такая таблица полностью задает отображение лишь тогда, когда множество А конечно и исчерпывается элементами

Построение графиков отображений нечисловых множеств А, В несколько отличается от построения графиков числовых функций, с которым читатель хорошо знаком. Оно осуществляется так. Проводят два взаимно перпендикулярных луча, которые выходят из одной точки, — «оси координат». На горизонтальном луче произвольным способом (например, через одинаковые промежутки) отмечают точки, которые отвечают элементам множества А, а на вертикальном — точки, которые отвечают элементам множества В. Через эти точки проводят соответственно вертикальные и горизонтальные прямые, которые образуют прямоугольную сетку. Чтобы построить график отображения нужно поставить точки в тех вершинах сетки, «координатами» которых являются всевозможные пары вида , где а — произвольный элемент множества А.

Пример 1. Пусть есть отображение, по которому каждой букве из множества А ставится в соответствие ее порядковый номер в слове «логарифм». График этого отображения дан на рис. 1.

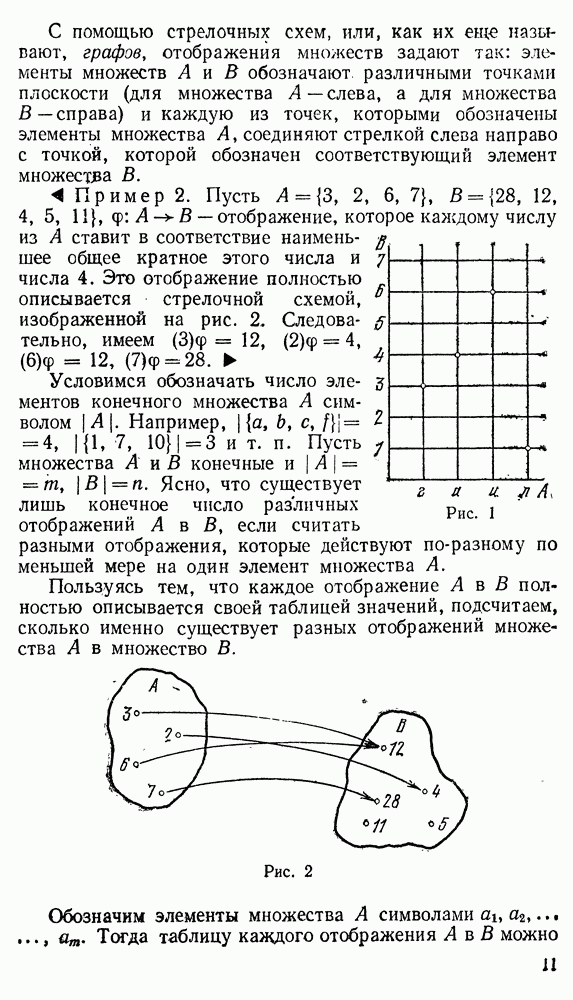
С помощью стрелочных схем, или, как их еще называют, графов, отображения множеств задают так: элементы множеств А и В обозначают, различными точками плоскости (для множества А — слева, а для множества В — справа) и каждую из точек, которыми обозначены элементы множества А, соединяют стрелкой слева направо с точкой, которой обозначен соответствующий элемент множества В.

Пример 2. Пусть — отображение, которое каждому числу из А ставит в соответствие наименьшее общее кратное этого числа и числа 4. Это отображение полностью описывается стрелочной схемой, изображенной на рис. 2, Следовательно, имеем ,

Условимся обозначать число элементов конечного множества А символом . Например, и т. п. Пусть множества А и В конечные и

Ясно, что существует лишь конечное число различных отображений А в В, если считать разными отображения, которые действуют по-разному по меньшей мере на один элемент множества А.

Пользуясь тем, что каждое отображение А в В полностью описывается своей таблицей значений, подсчитаем, сколько именно существует разных отображений множества Л в множество В.

Рис. 1

Рис. 2

Обозначим элементы множества А символами .

Тогда таблицу каждого отображения А в В можно будет, записать так:

где — обозначения некоторых, не обязательно разных элементов множества В. Верхний ряд таблицы одинаков для всех отображений А в В, а нижний меняется, потому что разным отображениям отвечают разные таблицы. При этом разных отображений А в В будет столько, сколькими разными способами можно заполнить второй ряд рассмотренной таблицы. В каждую клетку второго ряда таблицы можно записать обозначения любого элемента множества В. Таким образом, каждую из клеток нижнего ряда таблицы отображения можно заполнить разными способами независимо от способа заполнения других клеток. А это означает, что в таблице отображения можно образовать всего

разных нижних рядов. Следовательно, существует разных отображений А в В.

Выделяется и отдельно изучается несколько важных классов отображений одного множества в другое.