| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 12. ЧАСТИЦЫ И ФИЗИЧЕСКИЕ СИСТЕМЫ. СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ ЧАСТИЦ ПО СОСТОЯНИЯМ. ПОНЯТИЕ ТЕМПЕРАТУРЫ
ЧАСТИЦА
Частицей обычно называется физический объект, свойства которого сосредоточены В пределах относительно малых объемов (по сравнению с объемом всей системы). Линейные размеры этого объема должна быть настолько малы, чтобы весьма важные в физике понятия «координаты частицы» и «расстояние между частицами» имели определенный смысл.
Однако указание на относительную малость размеров объекта не является существенной частью определения понятия «частица»; необходим перечень
физических требований, которым дол жен удовлетворять объект для того, чтобы его можно было назвать частицей. Ни в классической, ни в квантовой физике полный перечень таких требований не приводится, поэтому частицей называют и электрон или протон, и атом или атомное ядро. В период господства классической механики (конец XIX в.), основными объектами которой являлись «материальная точка» и «абсолютно твердое тело», простейшими физическими телами могли считаться частицы, не имеющие никакой внутренней структуры, абсолютно твердые, абсолютно упругие и т. п. Современная физика придает понятию «частица» более свободное определение, вследствие чего элементарными называются частицы с весьма различными свойствами (фотоны, электроны, нейтроны и т. д.).
Перечень требований, которым должны удовлетворять частицы, очевидно, не может быть исчерпывающим и будет отражать определенный уровень физических знаний; наиболее же важным является следующее условие:
физический объект можно назвать частицей (входящей в состав некоторой системы), если во всех физических явлениях, в которых он участвует, изменения в его внутреннем состоянии не обнаруживаются, или если влиянием его внутреннего состояния на общий ход физических процессов в системе можно пренебречь.
При этом условии понятие «частица» приобретает относительный смысл.. Если в некоторой области физических явлений, изучаемой при помощи определенной аппаратуры, данное тело не обнаруживает своей внутренней структуры и обладает постоянными физическими свойствами, то в этой области и по отношению к этой аппаратуре рассматриваемое тело можно назвать частицей. В других физических условиях и по отношению к другой (более чувствительной) аппаратуре это тело может вести себя как сложное, т. е. может обнаружиться состав и внутренняя структура частицы, влияние внутренних изменений на ее отношение к действию внешних сил и т. п. Как правило, при относительно малых энергиях и слабых воздействиях поведение многих Тел определяется в основном только внешними воздействиями, т. е. тела не обнаруживают (точнее, почти не обнаруживают) своего внутреннего состояния; при этих условиях все свойства частиц можно полагать неизменными. В области же высоких энергий и сильных внешних воздействий тела показывают свойства, свидетельствующие о наличии у них состава, структуры и спектра внутренних состояний. Так, например, ядро какого-нибудь тяжелого элемента при столкновении с протоном, имеющим малую энергию, ведет себя как одна частица с определенным зарядом и массой; если же протон имеет достаточно большую энергию, то при взаимодействии с ним ядро обнаруживает свой сложный состав, структуру и внутреннее состояние. Мы называем молекулу частицей газа, несмотря на наличие у нее состава и структуры, а также нормального и возбужденных состояний. При этом мы исходим из предположения, что изменения во внутреннем состоянии одной молекулы не влияют на ход процессов, происходящих в газе. Однако возможно, что это влияние исчезающе мало в каждом отдельном акте взаимодействия данной молекулы с остальными, о если число таких актов чрезвычайно велико, то после суммирования оно может Сказаться заметным,
ФИЗИЧЕСКАЯ СИСТЕМА
Понятие «физическая система», как и любое другое понятие, также должно быть по возможности точно определено. Это определение может быть лаконичным или подробным, но оно должно охватывать существенные особенности физических объектов, называемых системами, отличающие их от объектов, названных частицами. Возможно, что нахождение достаточно четких и однозначных определений для физической системы будет трудной задачей, однако независимо от их качества, они необходимы.
Физической системой называют локализованную в некотором ограниченном объеме устойчивую совокупность взаимодействующих частиц, которая в физических процессах ведет себя как один объект, обладающий определенными свойствами.
Свойства физической системы (так же как и одной частицы) могут быть выражены числовыми значениями определенных величин (массы, электрического заряда, спина и т. д.), а также характеристическими функциями, т. е. формулами для расчета различных функций состояния: энергии, энтропии, спектра излучения и т. п.
Основные отличительные особенности физических систем, которые должны быть подчеркнуты в определениях этого понятия, заключаются в следующем:
1) устойчивость по отношению к различным внешним воздействиям;
2) наличие качественно новых свойств по сравнению с составными частями;
3) существование спектра возможных состояний, среди которых одно или несколько состояний выделяются как наиболее устойчивые (стационарные, равновесные);
4) существование тенденции к переходу в равновесное состояние;
5) наличие хаотического (теплового) движения частиц внутри системы, оцениваемое температурой.
Свойства физических систем формируются из свойств составных частиц и определяются характером их взаимодействия между собой. Прежде всего следует заметить одно интересное обстоятельство: система обладает устойчивостью и обнаруживает качественно новые свойства лишь в том случае, когда Она укомплектована из частиц, обладающих различными (полярными) свойствами. Наиболее простым и наглядным примером является атом водорода; каждый протон или электрон в свободном (изолированном) состоянии может иметь любые значения энергии, но составленный из них атом может существовать только в состояниях с определенными значениями энергии; одни только протоны или одни только электроны устойчивой (прочной) системы не образуют. Ниже мы перечислим все важнейшие свойства физических систем атомного масштаба:
1. Масса (инертная) физической системы  всегда меньше суммы масс составных частей этой системы (измеренных в их свободном состоянии). Разность
всегда меньше суммы масс составных частей этой системы (измеренных в их свободном состоянии). Разность

называемая дефектом массы этой системы, будучи умноженной на квадрат скорости света, показывает ту энергию, которая выделилась при образовании данной системы из свободных частиц. Такой же величины энергию  необходимо затратить, чтобы разрушить систему, т. е. удалить ее составные части на столь большие расстояния, при которых их взаимодействием можно было бы пренебречь.
необходимо затратить, чтобы разрушить систему, т. е. удалить ее составные части на столь большие расстояния, при которых их взаимодействием можно было бы пренебречь.  называется энергией связи данной системы и характеризует его устойчивость (прочность по отношению к различным внешним воздействиям). Для некоторых систем трудно измерить
называется энергией связи данной системы и характеризует его устойчивость (прочность по отношению к различным внешним воздействиям). Для некоторых систем трудно измерить  (ввиду относительной малости), но легко измерить
(ввиду относительной малости), но легко измерить 
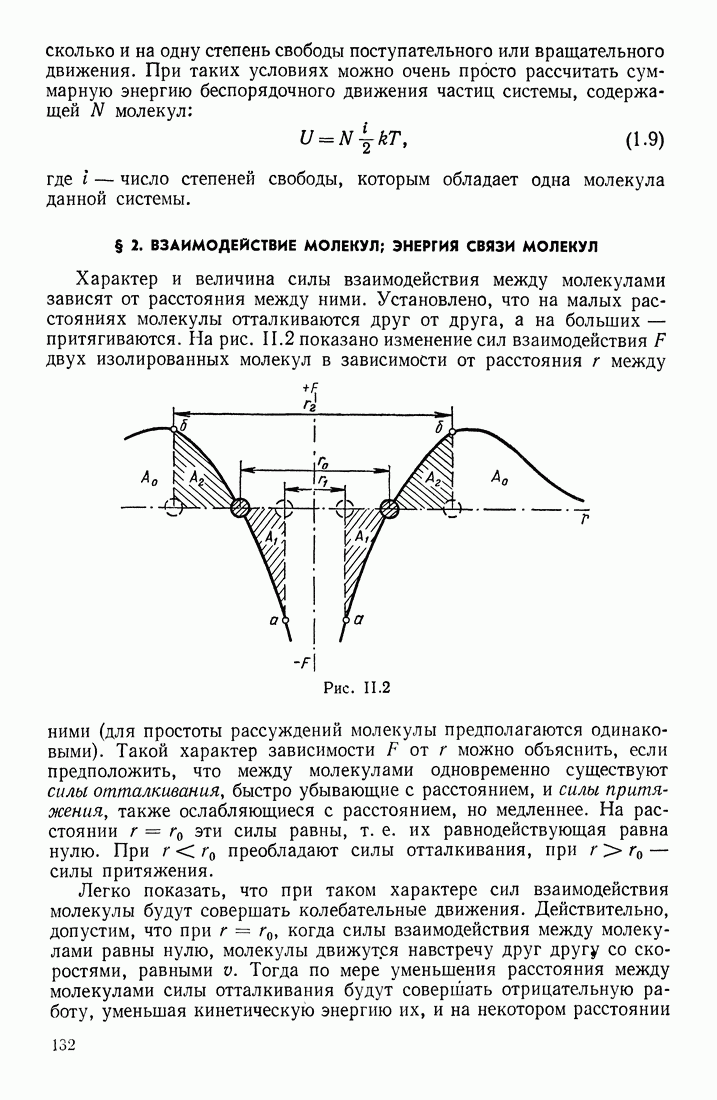
Физические системы образуются и существуют благодаря силам взаимодействия между ее составными частями. На относительно больших расстояниях всегда должны действовать силы притяжения (без них система не могла бы образоваться), но на малых расстояниях либо эти силы должны уравновешиваться, вызывая, например, центростремительные ускорения (как в солнечной системе или боровской модели атома), либо же должны появиться силы отталкивания. Можно указать на физические системы, которые существуют весьма малое время только вследствие того, что между ее составными частицами при их сближении не возникают силы отталкивания (например, позитроний). Силы отталкивания, если они существуют, определяют форму образовавшихся систем (например, молекул из атомов, атомных ядер из нуклонов). Энергия связи системы определяется интенсивностью сил притяжения (см. рис. II.2 и соответствующий текст).
Характерными примерами возникновения физических систем с выделением энергии связи являются: конденсация паров в жидкость, кристаллизация, соединение атомов в молекулы, образование атомов водорода из протонов и электронов, образование атомных ядер из протонов и нейтронов.
Обычно выделяющуюся при образовании (или затрачиваемую при разрушении) энергию  делят на число частиц и находят среднюю энергию, необходимую для удаления одной частицы из состава системы. Однако, ввиду того что энергия связи пропорциональна массе всей системы, более подходящей характеристикой системы следует считать удельную энергию связи, приходящуюся на единицу массы. Приведем
делят на число частиц и находят среднюю энергию, необходимую для удаления одной частицы из состава системы. Однако, ввиду того что энергия связи пропорциональна массе всей системы, более подходящей характеристикой системы следует считать удельную энергию связи, приходящуюся на единицу массы. Приведем
таблицу измеренных значений удельной энергии,  для перечисленных выше процессов образования систем:
для перечисленных выше процессов образования систем:

2. В физических системах обнаруживаются волновые свойства составляющих ее частиц. Выше упоминалось о появлении квантовых свойств у атома водорода; то же самое имеет место и у атомных ядер, сложных атомов, молекул и т. п. В этих системах волновые свойства частиц имеют важное значение в формировании поведения всей системы в целом. Вследствие этого процессы, в которых участвуют так называемые «микросистемы» (ядра, атомы, молекулы), описываются понятиями и законами квантовой физики, тогда как для «макросистем» могут быть использованы с удовлетворительной точностью понятия и законы классической физики.
3. Физическая система характеризуется набором (спектром) возможных для нее состояний. У некоторых систем спектр возможных состояний совпадает с «энергетическим спектром», т. е. одному уровню энергии соответствует одно-единственное состояние. У других систем каждому уровню в энергетическом спектре может соответствовать несколько (иногда очень много) различных состояний. Например, у атома водорода (см. § 10—11) одному значению главного квантового числа  , определяющего энергию атома
, определяющего энергию атома  соответствует
соответствует  различных состояний, отличающихся значениями остальных квантовых чисел. Уровень энергии, который охватывает некоторое множество различных состояний, называется вырожденным, степенью вырождения называется число различных состояний, имеющих данное значение энергии.
различных состояний, отличающихся значениями остальных квантовых чисел. Уровень энергии, который охватывает некоторое множество различных состояний, называется вырожденным, степенью вырождения называется число различных состояний, имеющих данное значение энергии.

Рис. IV.67
При помощи внешнего воздействия можно устранить вырождение, т. е. изменить величину энергии для тех различных состояний, которые ранее (при отсутствии внешнего воздействия) имели одинаковые энергии. Рассмотрим пример — идеализированный атом водорода по первичной теории Бора. Внесем небольшое уточнение; учтем, что протон имеет (см. ч. III, §20) собственный механический (и магнитный) момент  и примем направление вектора
и примем направление вектора  за ось всего атома (рис. IV. 67). Проведем плоскость
за ось всего атома (рис. IV. 67). Проведем плоскость  перпендикулярную этой оси. Допустим, что атом находится в возбужденном состоянии, соответствующем
перпендикулярную этой оси. Допустим, что атом находится в возбужденном состоянии, соответствующем  и энергии
и энергии  При этой энергии атом может находиться в
При этой энергии атом может находиться в  различных состояниях. Эти состояния отличаются: 1) размерами орбит (определяемыми числами
различных состояниях. Эти состояния отличаются: 1) размерами орбит (определяемыми числами  разрешаемыми ориентациями плоскостей каждой орбиты относительно плоскости
разрешаемыми ориентациями плоскостей каждой орбиты относительно плоскости  (числа
(числа  наконец, 3) двумя возможными ориентациями вектора собственного механического (и магнитного) момента электрона — спина — относительно плоскости орбиты (число
наконец, 3) двумя возможными ориентациями вектора собственного механического (и магнитного) момента электрона — спина — относительно плоскости орбиты (число 
Если ввести такой атом в электрическое поле, то на протон и электрон будут действовать различно направленные силы, вследствие чего атом будет несколько деформирован. Эта деформация будет различной для каждого из 18 состояний, охватываемых  так как она будет зависеть от размеров орбит, ориентаций их плоскостей и направления спина электрона относительно внешнего поля. Ввиду этого вместо одного уровня
так как она будет зависеть от размеров орбит, ориентаций их плоскостей и направления спина электрона относительно внешнего поля. Ввиду этого вместо одного уровня  образуются 18 близко расположенных подуровней, которые можно обозначить через
образуются 18 близко расположенных подуровней, которые можно обозначить через  Различие между энергиями этих подуровней будет зависеть от напряженности внешнего поля, .но оно оказывается значительно меньше, чем различие между соседними уровнями энергии атома. Существование такого расщепления, очевидно, можно обнаружить, если исследовать излучение атома, помещенного в достаточно сильное поле. При переходе электрона из одного подуровня,
Различие между энергиями этих подуровней будет зависеть от напряженности внешнего поля, .но оно оказывается значительно меньше, чем различие между соседними уровнями энергии атома. Существование такого расщепления, очевидно, можно обнаружить, если исследовать излучение атома, помещенного в достаточно сильное поле. При переходе электрона из одного подуровня,
принадлежащего уровню  на какой-нибудь подуровень, входящий в состав уровня
на какой-нибудь подуровень, входящий в состав уровня  будет излучаться фотон с частотой
будет излучаться фотон с частотой

Следовательно, вместо одной спектральной линии с частотой  которая излучалась бы изолированным атомом, в этом случае будет наблюдаться некоторое множество близких друг к другу спектральных линий.
которая излучалась бы изолированным атомом, в этом случае будет наблюдаться некоторое множество близких друг к другу спектральных линий.
Расщепление спектральных линий (т. е. энергетических уровней) атомов, помещенных в магнитном поле, было обнаружено Зееманом (1896), а в электрическом поле — Штарком (1913).
Заметим, что существование «вырождения» энергетических уровней у атома водорода следует только из первоначальной модели Бора. В этой модели предполагалось, что энергия атома состоит только из кинетической энергии электрона и потенциальной энергии взаимодействия протона с электроном, рассматриваемых как точечные заряды (или равномерно заряженные сферы). Существование других видов взаимодействия между протоном и электроном, например взаимодействие, обусловленное наличием у них магнитных моментов, не предполагалось. Однако если учесть, что в атоме имеется определенное направление, выделенное моментом протона, то в общем случае следует полагать, что энергия взаимодействия должна определяться не только размерами орбиты, но и ориентацией плоскостей орбит и спина электрона относительно этого направления. Эта дополнительная энергия взаимодействия ничтожно мала по сравнению с кулоновской потенциальной энергией, однако если эту энергию учесть, то вырождение будет отсутствовать. В частности, для каждого из состояний с  (см.
(см.  когда, по квантовой теории, представление об орбите теряет смысл, уровень энергии оказывается расщепленным на два подуровня: один из них соответствует энергии атома при одинаковых направлениях собственных магнитных моментов протона и электрона, другой
когда, по квантовой теории, представление об орбите теряет смысл, уровень энергии оказывается расщепленным на два подуровня: один из них соответствует энергии атома при одинаковых направлениях собственных магнитных моментов протона и электрона, другой  при противоположных направлениях.
при противоположных направлениях.
У физических систем следует различать:
1) спектр состояний самой системы в целом. Обозначим уровни энергии, соответствующие устойчивым (стационарным) состояниям системы, через  Например, у идеального газа этот спектр непрерывный, у атома водорода имеет дискретную структуру, приведенную в § 9;
Например, у идеального газа этот спектр непрерывный, у атома водорода имеет дискретную структуру, приведенную в § 9;
2) спектр состояний, в которых могут находиться отдельные составные части этой системы. Например, у атома кислорода ядро имеет свой спектр устойчивых состояний, электроны же, окружающие ядро, имеют другой, существенно отличный от первого спектр значений кинетической энергии. Заметим также, что и потенциальная энергия взаимодействия электрона с ядром также имеет дискретный набор «дозволенных» значений. Уровни энергии какой-нибудь составной частицы системы будем обозначать через  (большим значениям индекса соответствуют большие энергии).
(большим значениям индекса соответствуют большие энергии).
В некоторых физических системах имеется ограниченное количество «мест», которые могут быть заняты частицами с определенной энергией  допустим, что в системе имеется:
допустим, что в системе имеется:

и т. д. Число  равно произведению числа
равно произведению числа  различных состояний частицы, соответствующих данному уровню
различных состояний частицы, соответствующих данному уровню  на число мест в структуре системы (в его объеме), где находятся эти уровни:
на число мест в структуре системы (в его объеме), где находятся эти уровни:  Оба числа
Оба числа  могут быть различными для различных 8. Следовательно, если система содержит
могут быть различными для различных 8. Следовательно, если система содержит  одинаковых частиц, то для их распределения внутри системы имеется
одинаковых частиц, то для их распределения внутри системы имеется  мест Это число может быть конечным, если конечна каждая из составляющих
мест Это число может быть конечным, если конечна каждая из составляющих  и еслиспектр частиц внутри системы ограничен какими-то (минимальным и максимальным) значениями энергии уровней
и еслиспектр частиц внутри системы ограничен какими-то (минимальным и максимальным) значениями энергии уровней  Если же верхнего предела для энергии уровней нет, то общее число мест в системе для пребывания в них рассматриваемых частиц может быть неограниченным. Возникает вопрос: каким образом распределяются частицы по этим местам, или, как принято выражаться, в каком порядке «заполняются» частицами возможные для них энергетические уровни. Ответ на этот вопрос связан с весьма важной тенденцией, которая имеется у всех физических систем,
Если же верхнего предела для энергии уровней нет, то общее число мест в системе для пребывания в них рассматриваемых частиц может быть неограниченным. Возникает вопрос: каким образом распределяются частицы по этим местам, или, как принято выражаться, в каком порядке «заполняются» частицами возможные для них энергетические уровни. Ответ на этот вопрос связан с весьма важной тенденцией, которая имеется у всех физических систем,
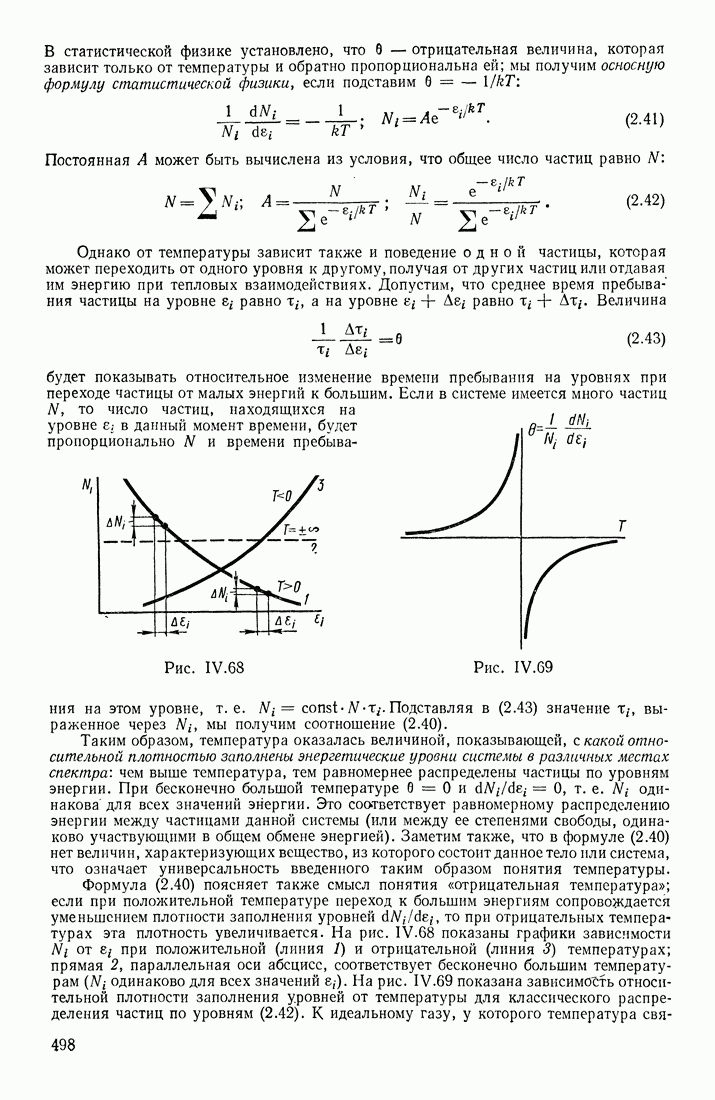
4. В физических системах существует тенденция к преимущественному заполнению уровней с малыми значениями энергии. Под действием этой «упорядочивающей тенденции» частицы в первую очередь занимают места с малыми значениями энергии («низшие уровни») и лишь после того, как все места в них будут заняты, начинается заполнение состояний с большими значениями энергии («высшие», или «верхние», уровни). Если число частиц данного сорта в системе  меньше полного числа возможных (устойчивых для них) состояний, то незаполненными («вакантными») должны оставаться состояния, принадлежащие высшим уровням.
меньше полного числа возможных (устойчивых для них) состояний, то незаполненными («вакантными») должны оставаться состояния, принадлежащие высшим уровням.
Коэффициентом заполнения уровня  в системе будем называть отношение числа
в системе будем называть отношение числа  частиц, занимающих такие уровни, к соответствующему числу мест в системе с энергией 8,:
частиц, занимающих такие уровни, к соответствующему числу мест в системе с энергией 8,:

Для заполненных уровней 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Часть I. МЕХАНИКА
- § 1. СИСТЕМЫ ОТСЧЕТА; ЛИНЕЙНЫЕ И УГЛОВЫЕ СКОРОСТИ И УСКОРЕНИЯ
- ДВИЖЕНИЕ ПО КРИВОЛИНЕЙНОЙ ТРАЕКТОРИИ
- § 2. ЗАКОНЫ МЕХАНИКИ НЬЮТОНА. СИСТЕМЫ ЕДИНИЦ
- СИЛА. ДЕФОРМАЦИЯ. МАССА
- ОСНОВНЫЕ ЗАКОНЫ МЕХАНИКИ
- ИМПУЛЬС. РАБОТА. МОЩНОСТЬ
- ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН
- § 3. ДВИЖЕНИЕ ТЕЛА В ПОЛЕ ТЯГОТЕНИЯ ЗЕМЛИ
- ГРАВИТАЦИОННОЕ ПОЛЕ. ВЕС ТЕЛА
- ДВИЖЕНИЕ КОСМИЧЕСКИХ ОБЪЕКТОВ
- § 4. ДВИЖЕНИЕ ТЕЛ С ПЕРЕМЕННОЙ МАССОЙ
- § 5. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ В МЕХАНИКЕ
- ПРЕОБРАЗОВАНИЯ КООРДИНАТ, СКОРОСТЕЙ И УСКОРЕНИЙ
- Глава 2. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА
- § 6. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ВРАЩАЮЩЕГОСЯ ТЕЛА; МОМЕНТ ИНЕРЦИИ ТЕЛ
- § 7. ЗАКОНЫ МЕХАНИКИ ДЛЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
- § 8. СВОБОДНЫЕ ОСИ. БАЛАНСИРОВКА РОТОРОВ. ГИРОСКОПЫ
- Глава 3. ЗАКОНЫ СОХРАНЕНИЯ В СИСТЕМЕ ВЗАИМОДЕЙСТВУЮЩИХ ТЕЛ
- § 9. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА (КОЛИЧЕСТВА ДВИЖЕНИЯ)
- § 10. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА (МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ)
- § 11. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
- § 12. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ НЕКОТОРЫХ СИСТЕМ
- § 13. СТОЛКНОВЕНИЕ ШАРОВ
- § 14. О ЦЕНТРЕ МАСС СИСТЕМЫ
- Глава 4. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ
- § 15. ПЕРИОДИЧЕСКОЕ ДВИЖЕНИЕ; ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
- § 16. СКОРОСТЬ И УСКОРЕНИЕ КОЛЕБЛЮЩЕГОСЯ ТЕЛА. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- § 17. СИЛА И ЭНЕРГИЯ ПРИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЯХ. ПРОСТЕЙШИЕ МЕХАНИЧЕСКИЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
- § 18. СОБСТВЕННЫЕ, СВОБОДНЫЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ПАРАМЕТРИЧЕСКОЕ ВОЗБУЖДЕНИЕ КОЛЕБАНИЙ
- § 19. ПОНЯТИЕ О НЕЛИНЕЙНЫХ КОЛЕБАНИЯХ
- § 20. СЛОЖЕНИЕ И РАЗЛОЖЕНИЕ КОЛЕБАНИЙ
- § 21. АВТОКОЛЕБАНИЯ
- Глава 5. ВОЛНОВЫЕ ПРОЦЕССЫ; ОСНОВЫ АКУСТИКИ
- § 22. ОБРАЗОВАНИЕ И РАСПРОСТРАНЕНИЕ ВОЛН В УПРУГОЙ СРЕДЕ
- § 23. ФОРМУЛА ГАРМОНИЧЕСКОЙ ВОЛНЫ
- ВОЛНА В УПРУГОЙ СРЕДЕ
- § 24. ПОТОК ЭНЕРГИИ В ВОЛНОВЫХ ПРОЦЕССАХ
- § 25. ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ ВОЛН. РАСПРОСТРАНЕНИЕ ВОЛН В СРЕДАХ С ДИСПЕРСИЕЙ
- § 26. СТОЯЧИЕ ВОЛНЫ
- § 27. ЗВУКОВЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- ЭФФЕКТ ДОПЛЕРА
- ХАРАКТЕРИСТИКИ ЗВУКОВОГО ОЩУЩЕНИЯ
- § 28. УЛЬТРАЗВУКИ И ИХ ПРИМЕНЕНИЯ
- Глава 6. МЕХАНИКА ЖИДКОСТЕЙ И ГАЗОВ
- § 29. ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ. БАРОМЕТРИЧЕСКАЯ ФОРМУЛА
- § 30. ЛАМИНАРНОЕ И ТУРБУЛЕНТНОЕ ТЕЧЕНИЯ. ФОРМУЛА БЕРНУЛЛИ
- СЖИМАЕМОСТЬ И ВЯЗКОСТЬ В ПОТОКЕ
- РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ В ЛАМИНАРНОМ ПОТОКЕ
- Часть II. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
- § 1. ТЕПЛОВОЕ ДВИЖЕНИЕ
- § 2. ВЗАИМОДЕЙСТВИЕ МОЛЕКУЛ; ЭНЕРГИЯ СВЯЗИ МОЛЕКУЛ
- § 3. АГРЕГАТНЫЕ СОСТОЯНИЯ И ФАЗОВЫЕ ПЕРЕХОДЫ. РАВНОВЕСНЫЕ И НЕРАВНОВЕСНЫЕ СОСТОЯНИЯ И ПРОЦЕССЫ
- СВОЙСТВА ТЕРМОДИНАМИЧЕСКИХ СИСТЕМ
- ВИДЫ ТЕРМОДИНАМИЧЕСКИХ ПРОЦЕССОВ
- § 4. ВНУТРЕННЯЯ ЭНЕРГИЯ ТЕРМОДИНАМИЧЕСКОЙ СИСТЕМЫ. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- § 5. ВНЕШНЯЯ РАБОТА СИСТЕМЫ И ТЕПЛООБМЕН С ОКРУЖАЮЩЕЙ СРЕДОЙ. ТЕПЛОЕМКОСТЬ ТЕЛ
- § 6. ИЗОПРОЦЕССЫ; АДИАБАТИЧЕСКИЙ ПРОЦЕСС. ЭНТРОПИЯ СИСТЕМЫ. ЗАМКНУТЫЕ (КРУГОВЫЕ) ПРОЦЕССЫ
- ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ ИЗОПРОЦЕССОВ
- КРУГОВЫЕ ПРОЦЕССЫ
- § 7. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ. ЗАКОН ВОЗРАСТАНИЯ ЭНТРОПИИ
- ТЕПЛОВЫЕ И ХОЛОДИЛЬНЫЕ МАШИНЫ
- ЭНТРОПИЯ И ВЕРОЯТНОСТЬ
- Глава 2. ИДЕАЛЬНЫЙ ГАЗ
- § 8. ОСНОВНОЕ УРАВНЕНИЕ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ. СРЕДНИЕ СКОРОСТИ МОЛЕКУЛ
- § 9. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
- § 10. ИЗОПРОЦЕССЫ В ИДЕАЛЬНОМ ГАЗЕ; ТЕПЛОЕМКОСТИ ГАЗОВ
- § 11. КРУГОВЫЕ ПРОЦЕССЫ, СОВЕРШАЕМЫЕ ИДЕАЛЬНЫМ ГАЗОМ; ЦИКЛ КАРНО. ЭНТРОПИЯ ИДЕАЛЬНОГО ГАЗА
- ЦИКЛ КАРНО
- ПРОЦЕССЫ, ВЫЗЫВАЮЩИЕ ИЗМЕНЕНИЕ ЭНТРОПИИ
- ПАРАДОКС ГИББСА
- § 12. ДИФФУЗИЯ, ТЕПЛОПРОВОДНОСТЬ И ВНУТРЕННЕЕ ТРЕНИЕ В ГАЗАХ; ЧИСЛО СТОЛКНОВЕНИЙ И ДЛИНА СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ
- Глава 3. РЕАЛЬНЫЕ ГАЗЫ, ЖИДКОСТИ И ТВЕРДЫЕ ТЕЛА
- § 13. ОТСТУПЛЕНИЯ ОТ ЗАКОНОВ ИДЕАЛЬНЫХ ГАЗОВ. НАСЫЩЕННЫЕ ПАРЫ. КРИТИЧЕСКОЕ СОСТОЯНИЕ
- ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ГАЗОВ
- ПАР
- ПЕРЕХОДЫ в СИСТЕМЕ ЖИДКОСТЬ — ПАР — ГАЗ
- § 14. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА. ВНУТРЕННЯЯ ЭНЕРГИЯ РЕАЛЬНОГО ГАЗА
- ПАРАМЕТРЫ КРИТИЧЕСКОГО СОСТОЯНИЯ
- ПРИМЕНЕНИЯ УРАВНЕНИЯ ВАН-ДЕР-ВААЛЬСА
- § 15. ЖИДКОСТИ; ИХ ОСНОВНЫЕ СВОЙСТВА. МОЛЕКУЛЯРНОЕ ДАВЛЕНИЕ И ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ
- СВОЙСТВА ЖИДКОСТЕЙ
- МОЛЕКУЛЯРНЫЕ СИЛЫ В ПОВЕРХНОСТНОМ СЛОЕ
- § 16. КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- § 17. ИСПАРЕНИЕ И КИПЕНИЕ ЖИДКОСТЕЙ; КОНДЕНСАЦИЯ ПАРОВ
- ИСПАРЕНИЕ И КОНДЕНСАЦИЯ
- КИПЕНИЕ
- УДЕЛЬНАЯ ТЕПЛОТА ПАРООБРАЗОВАНИЯ
- § 18. КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТЕЛА. КРИСТАЛЛИЗАЦИЯ, ПЛАВЛЕНИЕ И ИСПАРЕНИЕ ТВЕРДЫХ ТЕЛ
- КРИСТАЛЛИЗАЦИЯ
- ТЕМПЕРАТУРА ПЛАВЛЕНИЯ
- ТРОЙНАЯ ТОЧКА
- § 19. ТИПЫ КРИСТАЛЛИЧЕСКИХ РЕШЕТОК. ТЕПЛОВЫЕ И УПРУГИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ
- ТЕПЛОЕМКОСТЬ КРИСТАЛЛА
- ТЕПЛОВОЕ РАСШИРЕНИЕ КРИСТАЛЛОВ
- УПРУГОСТЬ И ПЛАСТИЧНОСТЬ
- ЖИДКИЕ КРИСТАЛЛЫ
- Часть III. ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
- § 1. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ. ПРОВОДНИКИ И ДИЭЛЕКТРИКИ
- § 2. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ; ИНДУКЦИЯ И НАПРЯЖЕННОСТЬ ПОЛЯ. ЗАКОН КУЛОНА
- § 3. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ СИСТЕМЫ ЗАРЯДОВ; ТЕОРЕМА ОСТРОГРАДСКОГО—ГАУССА
- ПРИМЕНЕНИЕ ТЕОРЕМЫ ОСТРОГРАДСКОГО—ГАУССА
- ФОРМУЛЫ ДЛЯ НАПРЯЖЕННОСТИ ПОЛЯ
- § 4. РАБОТА ПЕРЕМЕЩЕНИЯ ЗАРЯДА В ЭЛЕКТРИЧЕСКОМ ПОЛЕ; РАЗНОСТЬ ПОТЕНЦИАЛОВ. ЭНЕРГИЯ ВЗАИМОДЕЙСТВИЯ ЗАРЯДОВ
- § 5. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 6. ДИЭЛЕКТРИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКОВ
- ЭЛЕКТРОСТРИКЦИЯ
- ПЬЕЗОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ
- СЕГНЕТОЭЛЕКТРИКИ
- ЭЛЕКТРЕТЫ
- § 7. ЭЛЕКТРОЕМКОСТЬ. ЭНЕРГИЯ ЗАРЯЖЕННОГО ПРОВОДНИКА. ПЛОТНОСТЬ ЭНЕРГИИ ПОЛЯ
- Глава 2. ЭЛЕКТРИЧЕСКИЙ ТОК
- § 8. ЭЛЕКТРИЧЕСКИЙ ТОК ПРОВОДИМОСТИ; ПЛОТНОСТЬ ТОКА
- § 9. ЭЛЕКТРОННАЯ ТЕОРИЯ ПРОВОДИМОСТИ МЕТАЛЛОВ. ЗАКОНЫ ОМА И ДЖОУЛЯ—ЛЕНЦА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ. СВЯЗЬ МЕЖДУ ЭЛЕКТРОПРОВОДНОСТЬЮ И ТЕПЛОПРОВОДНОСТЬЮ
- § 10. РАБОТА ЭЛЕКТРИЧЕСКОГО ТОКА. СОПРОТИВЛЕНИЕ ПРОВОДНИКОВ. СВЕРХПРОВОДИМОСТЬ
- § 11. ЭЛЕКТРОДВИЖУЩАЯ СИЛА; ЗАКОН ОМА И ПРАВИЛА КИРХГОФА
- ЗАКОН ОМА ДЛЯ ЗАМКНУТОГО КОНТУРА
- ПРАВИЛА КИРХГОФА
- ЭЛЕКТРОСТАТИЧЕСКИЙ ГЕНЕРАТОР ТОКА
- § 12. РАБОТА ВЫХОДА ЭЛЕКТРОНОВ ИЗ МЕТАЛЛА. КОНТАКТНАЯ РАЗНОСТЬ ПОТЕНЦИАЛОВ. ТЕРМОЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ
- ЭМИССИЯ ЭЛЕКТРОНОВ ИЗ МЕТАЛЛА
- КОНТАКТНАЯ РАЗНОСТЬ ПОТЕНЦИАЛОВ
- ЗАКОН ВОЛЬТА. ТЕРМОЭЛЕМЕНТЫ
- ЭФФЕКТ ПЕЛЬТЬЕ
- § 13. ТЕРМОЭЛЕКТРОННАЯ ЭМИССИЯ. ЭЛЕКТРИЧЕСКИИ ТОК В ВАКУУМЕ. ЭЛЕКТРОННАЯ ЛАМПА
- § 14. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ. ПОНЯТИЕ О ПЛАЗМЕ
- ДВИЖЕНИЕ ИОНОВ В ГАЗЕ
- ВИДЫ РАЗРЯДОВ В ГАЗАХ
- ПЛАЗМА
- § 15. ЭЛЕКТРИЧЕСКИЙ ТОК В ЖИДКОСТЯХ. ЗАКОНЫ ФАРАДЕЯ
- § 16. ПОЛУПРОВОДНИКИ И ИХ ПРИМЕНЕНИЯ
- ЭЛЕКТРОПРОВОДНОСТЬ ПОЛУПРОВОДНИКОВ
- ЯВЛЕНИЯ НА ГРАНИЦЕ ДВУХ ПОЛУПРОВОДНИКОВ
- ПРИМЕНЕНИЯ ПОЛУПРОВОДНИКОВ
- Глава 3. ЭЛЕКТРОМАГНЕТИЗМ
- § 17. МАГНИТНОЕ ПОЛЕ
- § 18. НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ ВОКРУГ ДВИЖУЩЕГОСЯ ЗАРЯДА И ПРОВОДНИКОВ С ТОКАМИ
- § 19. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ЗАРЯДЫ И ПРОВОДНИКИ С ТОКОМ; СИЛА ЛОРЕНЦА И ЗАКОН АМПЕРА. ИНДУКЦИЯ МАГНИТНОГО ПОЛЯ
- § 20. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА КОНТУР С ТОКОМ. ДВИЖЕНИЕ ЗАРЯДА В МАГНИТНОМ ПОЛЕ
- МАГНИТНЫЙ МОМЕНТ ЭЛЕКТРОНА
- ДВИЖЕНИЕ ЗАРЯДА В МАГНИТНОМ ПОЛЕ
- ЭФФЕКТ ХОЛЛА
- § 21. РАБОТА ПЕРЕМЕЩЕНИЯ ПРОВОДНИКА С ТОКОМ В МАГНИТНОМ ПОЛЕ
- § 22. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ; ЗАКОНЫ ФАРАДЕЯ И ЛЕНЦА. ВРАЩАЮЩИИСЯ ВИТОК В МАГНИТНОМ ПОЛЕ
- РАМКА В МАГНИТНОМ ПОЛЕ
- ЗАКОНЫ ФАРАДЕЯ И ЛЕНЦА
- § 23. ЯВЛЕНИЯ САМОИНДУКЦИИ И ВЗАИМОИНДУКЦИИ. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ. ВИХРЕВЫЕ ТОКИ
- ИНДУКТИВНОСТЬ СОЛЕНОИДА
- РАСЧЕТ ИНДУКЦИОННЫХ ТОКОВ
- ВЗАИМНАЯ ИНДУКЦИЯ
- ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ
- ТОКИ ФУКО
- § 24. ТОК СМЕЩЕНИЯ И ЕГО МАГНИТНОЕ ПОЛЕ; ТЕОРИЯ МАКСВЕЛЛА
- § 25. МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ. ДИАМАГНЕТИЗМ; ПАРАМАГНИТНЫЕ И ФЕРРОМАГНИТНЫЕ ВЕЩЕСТВА
- НАМАГНИЧЕННОСТЬ
- МАГНИТНЫЕ СВОЙСТВА АТОМОВ И МОЛЕКУЛ
- ДИАМАГНЕТИЗМ И ПАРАМАГНЕТИЗМ
- ФЕРРОМАГНЕТИКИ
- ПАРАМАГНИТНЫЙ РЕЗОНАНС
- § 26. МАГНИТНОЕ ПОЛЕ В ФЕРРОМАГНИТНЫХ ТЕЛАХ РАЗЛИЧНОЙ ФОРМЫ; МАГНИТОДВИЖУЩАЯ СИЛА И МАГНИТНОЕ СОПРОТИВЛЕНИЕ
- Глава 4. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- § 27. КОЛЕБАТЕЛЬНЫЙ КОНТУР. НЕЗАТУХАЮЩИЕ И ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
- § 28. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ; ЭЛЕКТРИЧЕСКИЙ РЕЗОНАНС
- § 29. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- УРАВНЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ
- ЭНЕРГИЯ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ
- ИЗЛУЧЕНИЕ ВОЛНЫ ЭЛЕКТРОНОМ
- ЧЕРЕНКОВСКОЕ ИЗЛУЧЕНИЕ
- Часть IV. ОПТИКА И ФИЗИКА АТОМА
- § 1. ВОЛНОВАЯ (ЭЛЕКТРОМАГНИТНАЯ) И КОРПУСКУЛЯРНАЯ (ФОТОННАЯ) ТЕОРИИ СВЕТА
- СПЕКТРАЛЬНЫЙ СОСТАВ ИЗЛУЧЕНИЯ
- ХАРАКТЕРИСТИКИ ИЗЛУЧЕНИЯ
- ИДЕАЛИЗАЦИЯ СВЕТОВОЙ ВОЛНЫ
- § 2. ФОТОМЕТРИЧЕСКИЕ ПОНЯТИЯ И ВЕЛИЧИНЫ. ДАВЛЕНИЕ СВЕТА
- § 3. РАСПРОСТРАНЕНИЕ, ОТРАЖЕНИЕ, ПРЕЛОМЛЕНИЕ И ПОГЛОЩЕНИЕ СВЕТА. ДИСПЕРСИЯ. РАССЕЯНИЕ СВЕТА
- СБЕТ НА ГРАНИЦЕ ДВУХ СРЕД
- СВЕТ И ЦВЕТ
- ДИСПЕРСИЯ СВЕТА
- РАССЕЯНИЕ СВЕТА
- § 4. ИНТЕРФЕРЕНЦИЯ СВЕТА; КОГЕРЕНТНОСТЬ СВЕТОВЫХ ЛУЧЕЙ. ИНТЕРФЕРОМЕТРЫ
- § 5. ДИФРАКЦИЯ СВЕТА; ДИФРАКЦИОННЫЙ СПЕКТР
- ДИФРАКЦИЯ ПЛОСКОЙ ВОЛНЫ ОТ ПРЯМОЛИНЕЙНОЙ ТОНКОЙ ЩЕЛИ
- ДИФРАКЦИЯ ПЛОСКОЙ ВОЛНЫ ОТ НЕСКОЛЬКИХ ЩЕЛЕЙ
- ДИФРАКЦИОННАЯ РЕШЕТКА
- § 6. РАСПРОСТРАНЕНИЕ СВЕТА В АНИЗОТРОПНОЙ СРЕДЕ, ПОЛУЧЕНИЕ И ПРИМЕНЕНИЕ ПОЛЯРИЗОВАННОГО СВЕТА
- ПОЛЯРИЗОВАННЫЙ СВЕТ
- СПОСОБЫ ПОЛУЧЕНИЯ ПОЛЯРИЗОВАННОГО СВЕТА
- ИНТЕРФЕРЕНЦИЯ ПОЛЯРИЗОВАННОГО СВЕТА
- ОПТИЧЕСКАЯ АНИЗОТРОПИЯ
- § 7. ЛИНЗЫ; ИХ ОПТИЧЕСКАЯ СИЛА. АБЕРРАЦИИ. ДИАФРАГМЫ В ОПТИЧЕСКИХ ПРИБОРАХ
- ТОЛСТЫЕ ЛИНЗЫ. АБЕРРАЦИИ
- § 8. ПОНЯТИЕ О ГОЛОГРАФИИ
- Глава 2. ФИЗИКА АТОМОВ И МОЛЕКУЛ. ОСНОВЫ КВАНТОВОЙ ТЕОРИИ
- § 9. СТРОЕНИЕ АТОМА. ОПЫТЫ РЕЗЕРФОРДА, ФРАНКА И ГЕРЦА. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ АТОМА ВОДОРОДА
- ОПЫТ ФРАНКА И ГЕРЦА
- СПЕКТРЫ ИЗЛУЧЕНИЯ АТОМОВ
- ТЕОРИЯ АТОМА ВОДОРОДА
- § 10. КОРПУСКУЛЯРНО-ВОЛНОВЫЕ СВОЙСТВА ЧАСТИЦ. ФОТОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ. ФОРМУЛА ДЕ БРОЙЛЯ. ДИФРАКЦИЯ ЭЛЕКТРОНОВ
- ЭФФЕКТ КОМПТОНА
- ФОТОН И ЭЛЕКТРОМАГНИТНАЯ ВОЛНА
- ФОРМУЛА ДЕ БРОЙЛЯ
- ДИФРАКЦИЯ ЭЛЕКТРОНОВ
- § 11. ОСНОВНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ ТЕОРИИ. УРАВНЕНИЕ ШРЕДИНГЕРА. СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ ГЕЙЗЕНБЕРГА
- УРАВНЕНИЕ ШРЕДИНГЕРА
- РЕШЕНИЯ УРАВНЕНИЯ ШРЕДИНГЕРА
- СВОБОДНЫЙ ЭЛЕКТРОН
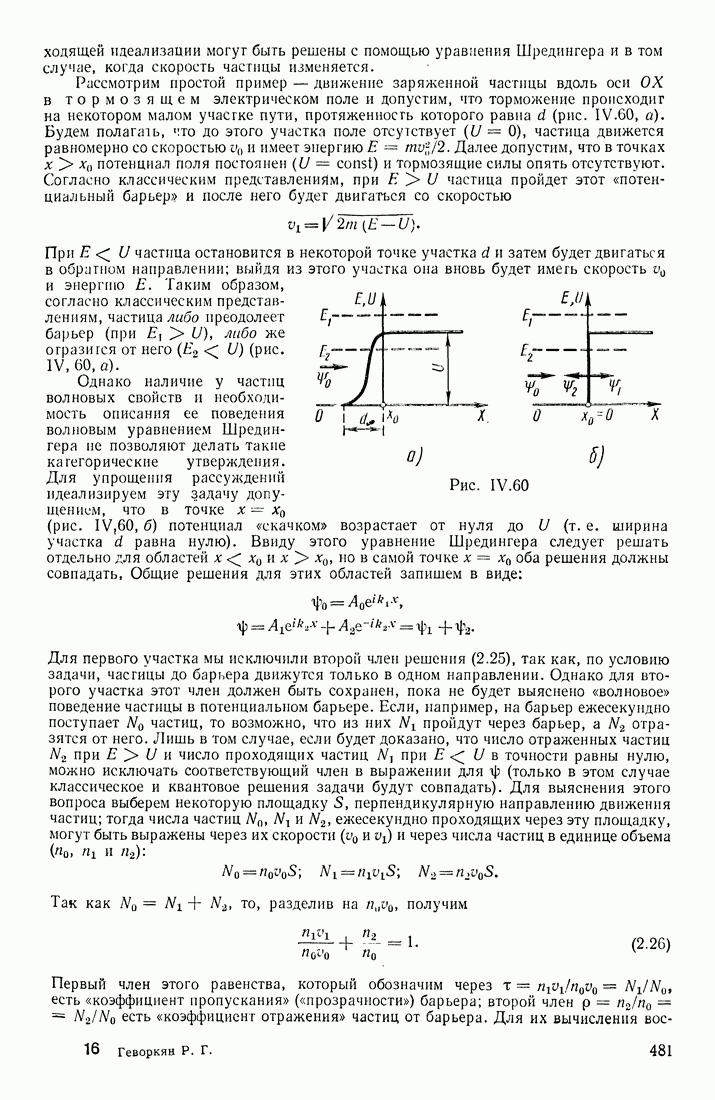
- ПОТЕНЦИАЛЬНЫЙ БАРЬЕР
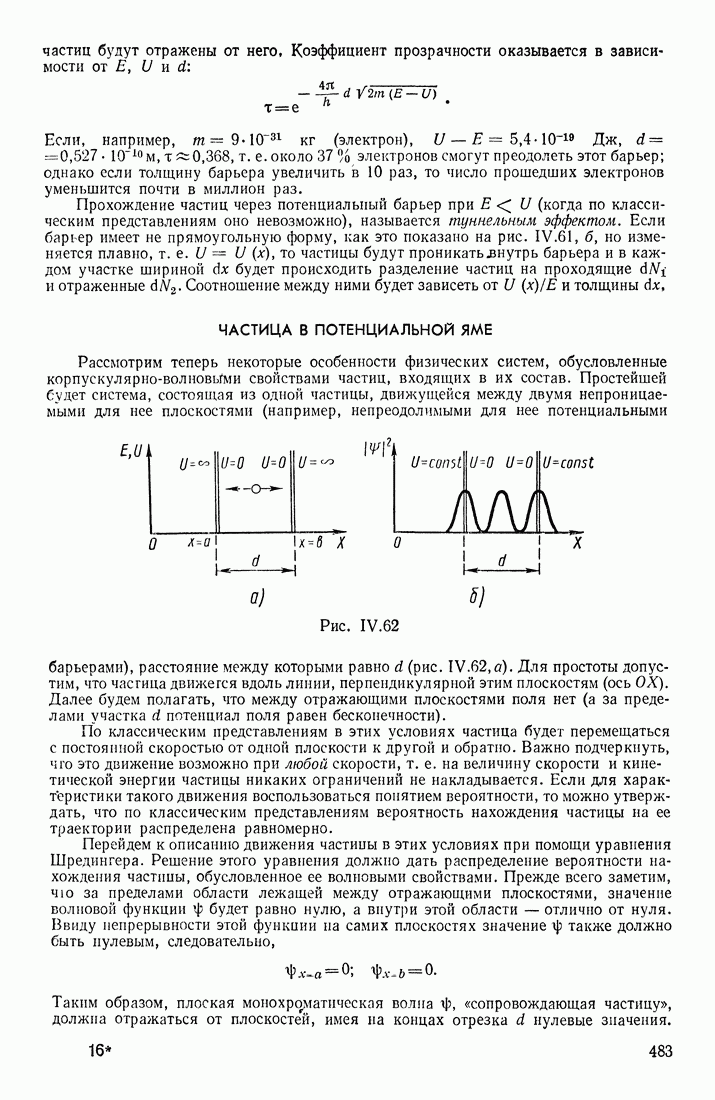
- ЧАСТИЦА В ПОТЕНЦИАЛЬНОЙ ЯМЕ
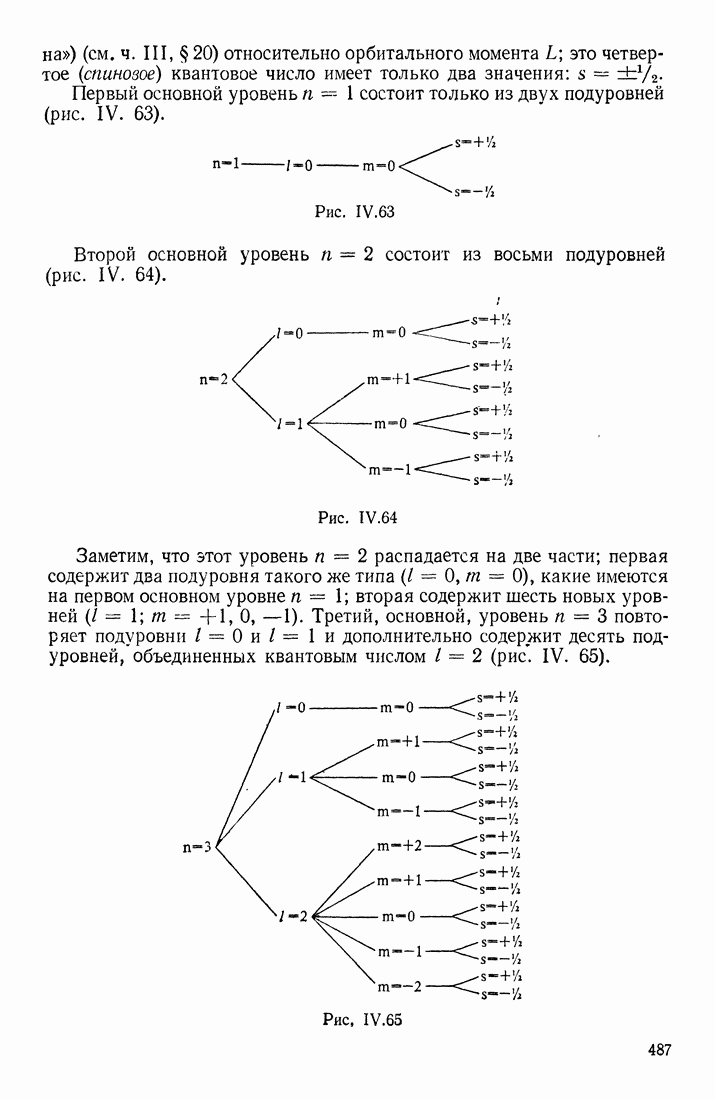
- АТОМ ВОДОРОДА. КВАНТОВЫЕ ЧИСЛА
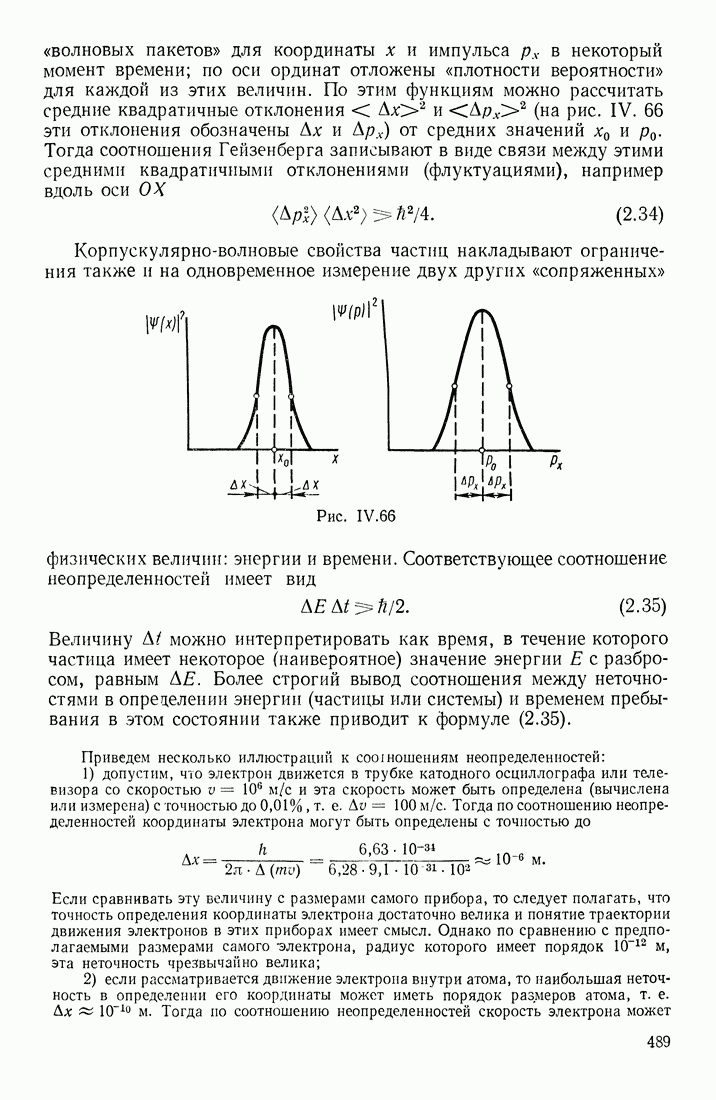
- СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ
- § 12. ЧАСТИЦЫ И ФИЗИЧЕСКИЕ СИСТЕМЫ. СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ ЧАСТИЦ ПО СОСТОЯНИЯМ. ПОНЯТИЕ ТЕМПЕРАТУРЫ
- РОЛЬ ТЕПЛОВОГО ДВИЖЕНИЯ ЧАСТИЦ
- ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ПО СОСТОЯНИЯМ
- ТЕМПЕРАТУРА
- ЭНЕРГЕТИЧЕСКИЙ СПЕКТР СИСТЕМЫ
- РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ПО СКОРОСТЯМ
- § 13. ВЗАИМОДЕЙСТВИЕ АТОМОВ И МОЛЕКУЛ. ЭНЕРГИЯ СВЯЗИ АТОМОВ
- ВЗАИМОДЕЙСТВИЕ МОЛЕКУЛ
- ИОННАЯ СВЯЗЬ
- РОЛЬ ЭЛЕКТРОННОГО ГАЗА В МЕТАЛЛАХ
- Глава 3. ИЗЛУЧЕНИЕ И ПОГЛОЩЕНИЕ ЭНЕРГИИ АТОМАМИ И МОЛЕКУЛАМИ
- § 14. АТОМНЫЕ И МОЛЕКУЛЯРНЫЕ СПЕКТРЫ ИЗЛУЧЕНИЯ; СПОСОБЫ ВОЗБУЖДЕНИЯ
- СТРУКТУРА ЭЛЕКТРОННОЙ ОБОЛОЧКИ
- СПЕКТРЫ ИЗЛУЧЕНИЯ АТОМОВ
- СПЕКТРЫ ИЗЛУЧЕНИЯ МОЛЕКУЛ
- КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА
- § 15. ТЕПЛОВОЕ ИЗЛУЧЕНИЕ
- ФОРМУЛА ПЛАНКА
- ЗАКОНЫ ИЗЛУЧЕНИЯ ЧЕРНОГО ТЕЛА
- ПРИМЕНЕНИЕ ЗАКОНОВ ТЕПЛОВОГО ИЗЛУЧЕНИЯ
- § 16. РЕНТГЕНОВСКИЕ ЛУЧИ. ХАРАКТЕРИСТИЧЕСКИЙ РЕНТГЕНОВСКИЙ СПЕКТР ЭЛЕМЕНТОВ
- ХАРАКТЕРИСТИЧЕСКИЙ РЕНТГЕНОВСКИЙ СПЕКТР
- ДИФРАКЦИЯ И ИНТЕРФЕРЕНЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ
- ДОЗИМЕТРИЯ
- § 17. ЛЮМИНЕСЦЕНТНОЕ ИЗЛУЧЕНИЕ
- ПРИРОДА ЛЮМИНЕСЦЕНЦИИ
- ХАРАКТЕРИСТИКИ ЛЮМИНЕСЦИРУЮЩИХ ВЕЩЕСТВ
- ГАШЕНИЕ ЛЮМИНЕСЦЕНЦИИ
- ПРИМЕНЕНИЯ ЛЮМИНЕСЦЕНЦИИ
- § 18. ИНДУЦИРОВАННОЕ ИЗЛУЧЕНИЕ. ЛАЗЕРЫ
- ЛАЗЕРЫ
- ПРЕИМУЩЕСТВА ЛАЗЕРОВ
- ПРИМЕНЕНИЕ ЛАЗЕРОВ
- Глава 4. АТОМНЫЕ ЯДРА И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- § 19. ОСНОВНЫЕ СВОЙСТВА АТОМНЫХ ЯДЕР
- РАДИОАКТИВНОСТЬ
- ВНУТРИЯДЕРНЫЕ СИЛЫ
- ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЯДЕР
- МЕХАНИЧЕСКИЙ МОМЕНТ ЯДРА
- МАГНИТНЫЕ МОМЕНТЫ ЯДЕР
- ЭЛЕКТРИЧЕСКИЕ МОМЕНТЫ ЯДЕР
- СПЕКТР ВОЗБУЖДЕННЫХ СОСТОЯНИЙ
- § 20. МОДЕЛЬНЫЕ ПРЕДСТАВЛЕНИЯ О СТРУКТУРЕ ЯДЕР
- КАПЕЛЬНАЯ МОДЕЛЬ ЯДРА
- ОБОЛОЧЕЧНАЯ МОДЕЛЬ
- ОБОБЩЕННАЯ МОДЕЛЬ
- ОПТИЧЕСКАЯ МОДЕЛЬ
- УСЛОВИЕ СТАБИЛЬНОСТИ
- § 21. РАДИОАКТИВНЫЕ ЯДРА И ИХ ИЗЛУЧЕНИЯ
- СЕМЕЙСТВА РАДИОАКТИВНЫХ ЭЛЕМЕНТОВ
- ВЗАИМОДЕЙСТВИЯ ЯДЕРНЫХ ИЗЛУЧЕНИЙ С ВЕЩЕСТВОМ
- БЕТА-РАСПАД ЯДЕР
- ЭНЕРГИЯ СВЯЗИ ЯДЕР
- ИЗОМЕРЫ
- § 22. ЯДЕРНЫЕ РЕАКЦИИ ДЕЛЕНИЯ И СИНТЕЗА. ТЕРМОЯДЕРНЫЕ РЕАКЦИИ
- БОМБАРДИРОВКА ЯДЕР ЧАСТИЦАМИ
- ЭФФЕКТИВНЫЕ СЕЧЕНИЯ РЕАКЦИЙ
- ЯДЕРНЫЕ РЕАКТОРЫ
- ЯДЕРНЫЙ СИНТЕЗ
- § 23. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- РАСПАДЫ ЧАСТИЦ
- ВИДЫ ВЗАИМОДЕЙСТВИЯ
- ЗАКЛЮЧЕНИЕ
- § 1. ФИЗИЧЕСКИЕ ИЗМЕРЕНИЯ. СВЯЗЬ МЕЖДУ СПОСОБАМИ ИЗМЕРЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН И ФОРМУЛИРОВКАМИ ЗАКОНОВ ФИЗИКИ
- § 2. О ТЕОРИИ ОТНОСИТЕЛЬНОСТИ ЭЙНШТЕЙНА
- § 3. ЗАКОНЫ СОХРАНЕНИЯ, ПРЕВРАЩЕНИЯ И ПЕРЕРАСПРЕДЕЛЕНИЯ ЭНЕРГИИ В ФИЗИЧЕСКИХ СИСТЕМАХ
- § 4. О ВАРИАЦИОННЫХ ПРИНЦИПАХ ФИЗИКИ
- § 5. СТАТИСТИЧЕСКИЕ ЗАКОНЫ И ФЛУКТУАЦИИ
- § 6. О ДУАЛИЗМЕ В ФИЗИКЕ