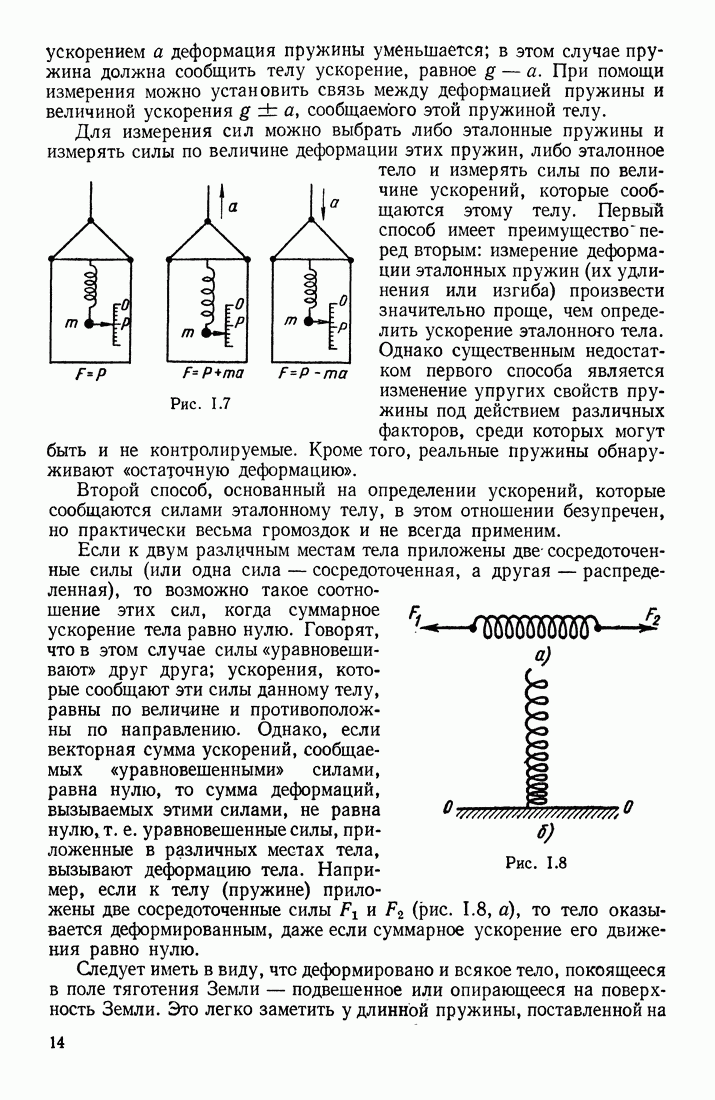
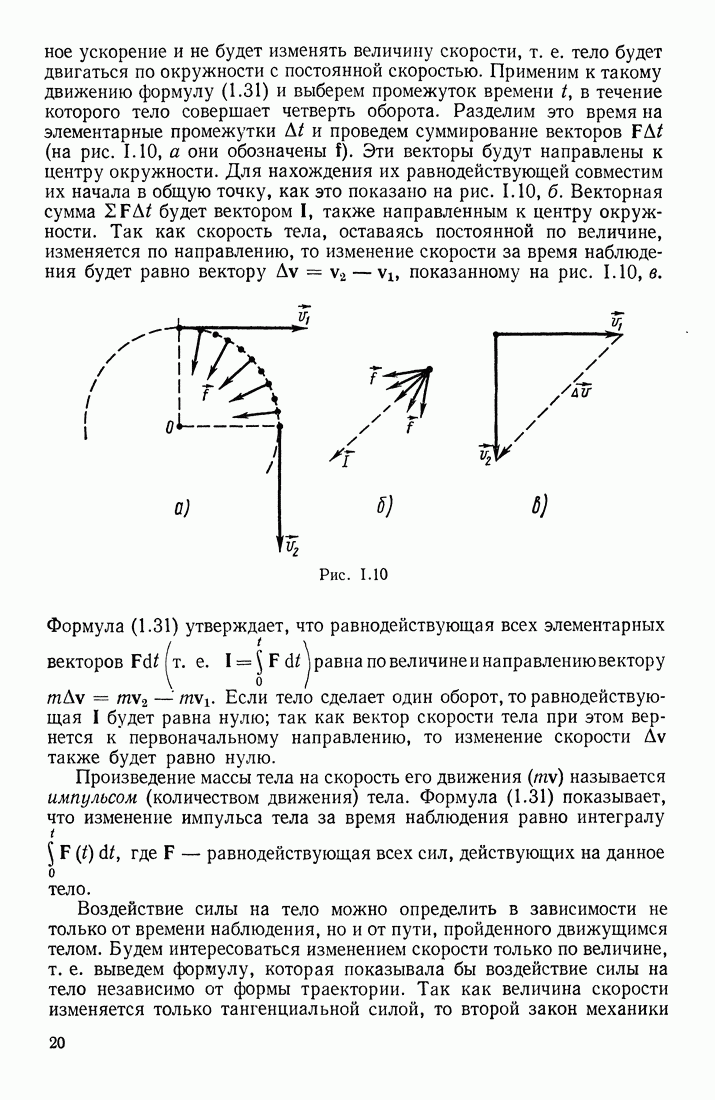
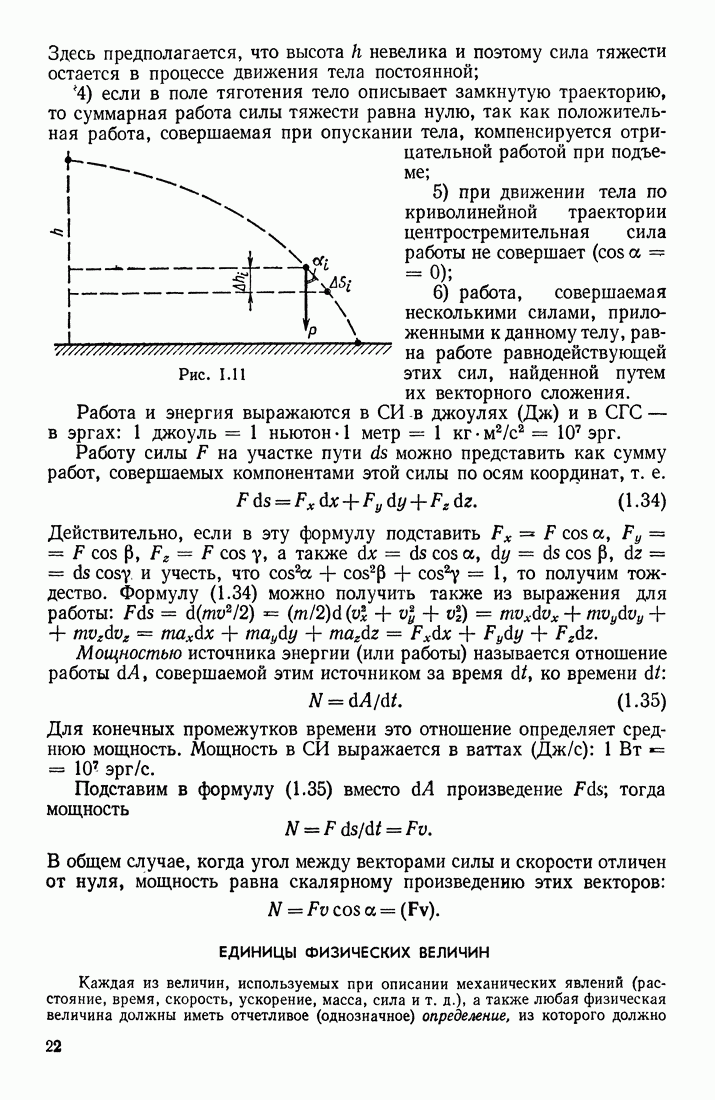
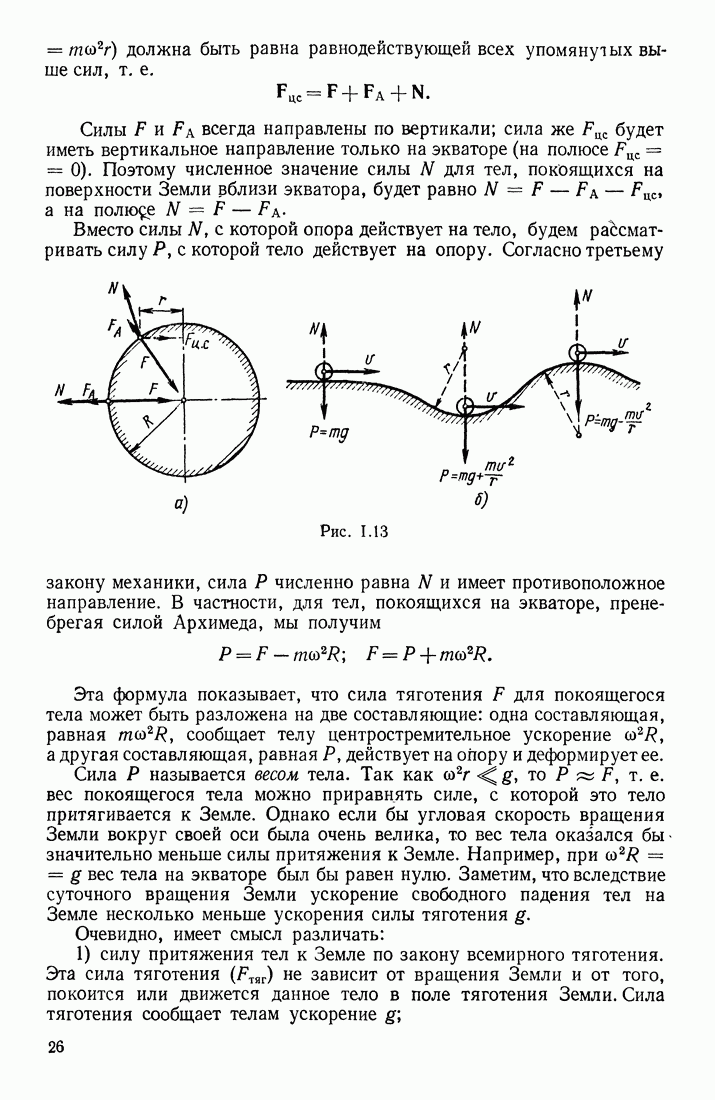
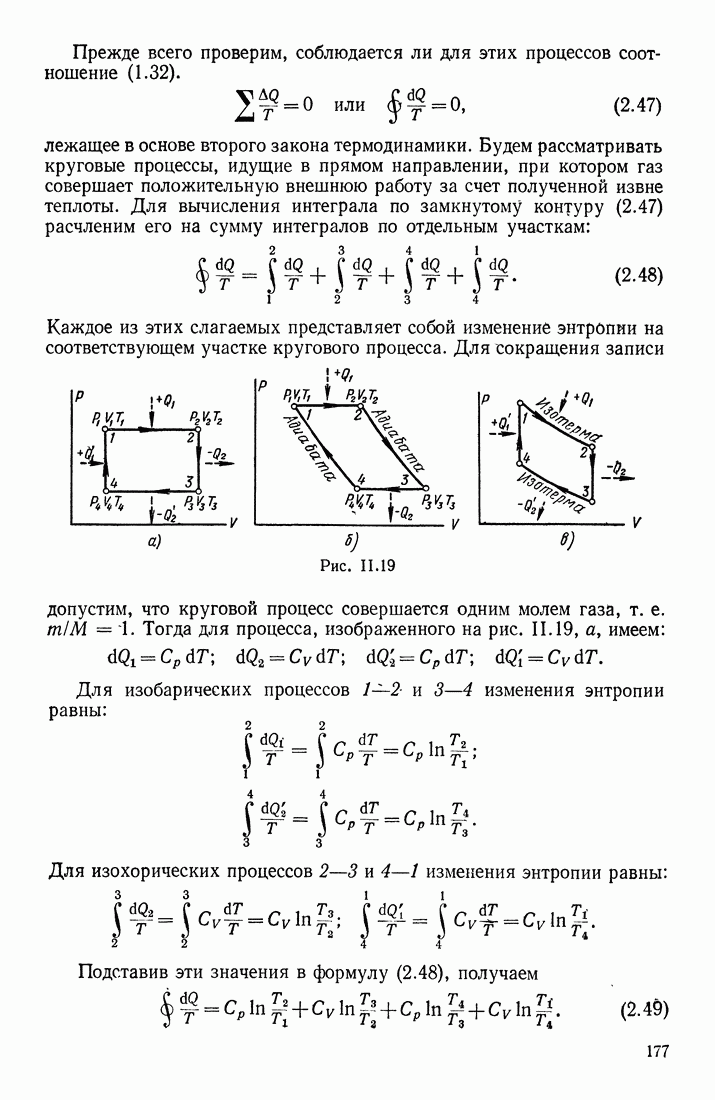
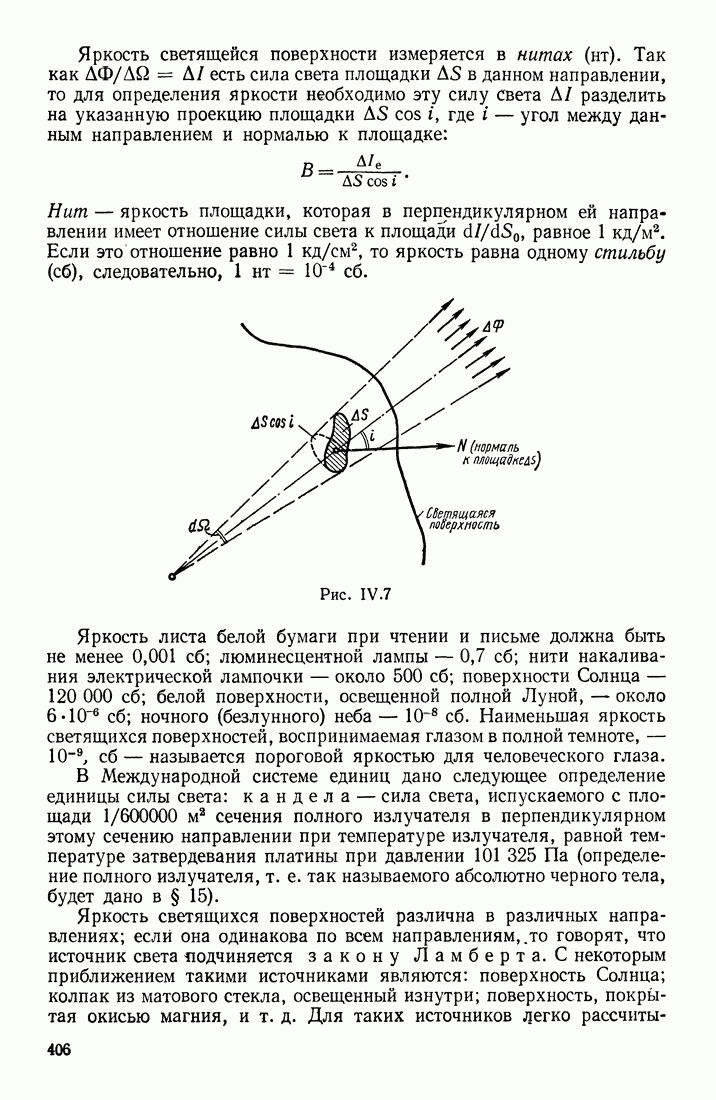
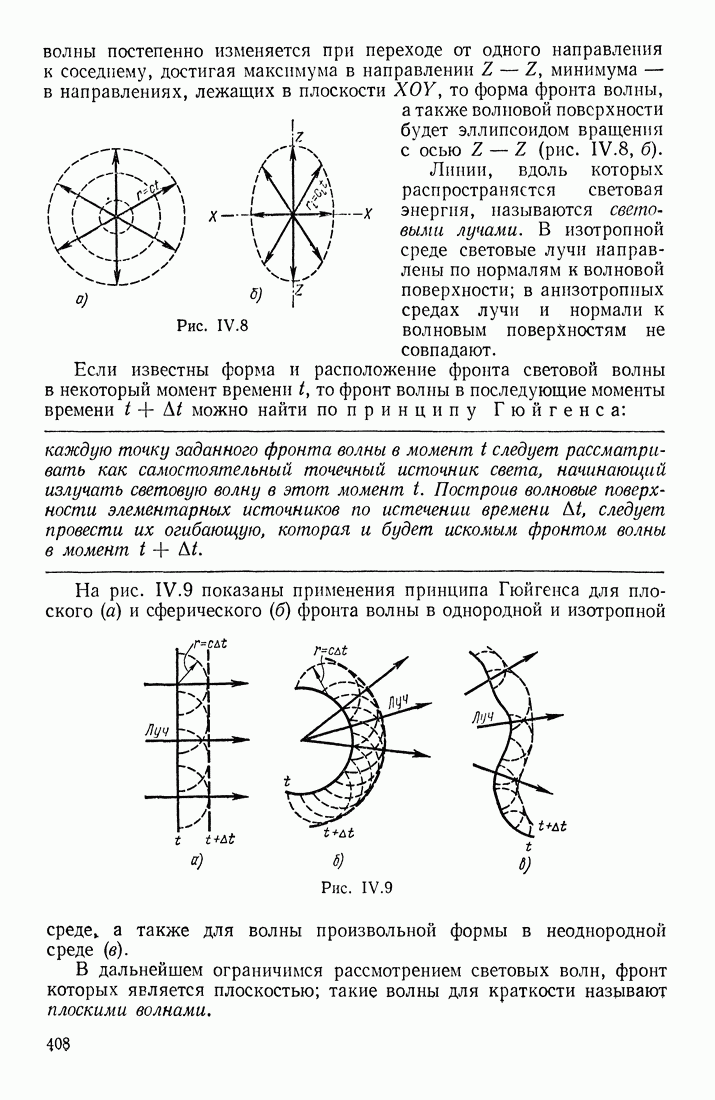
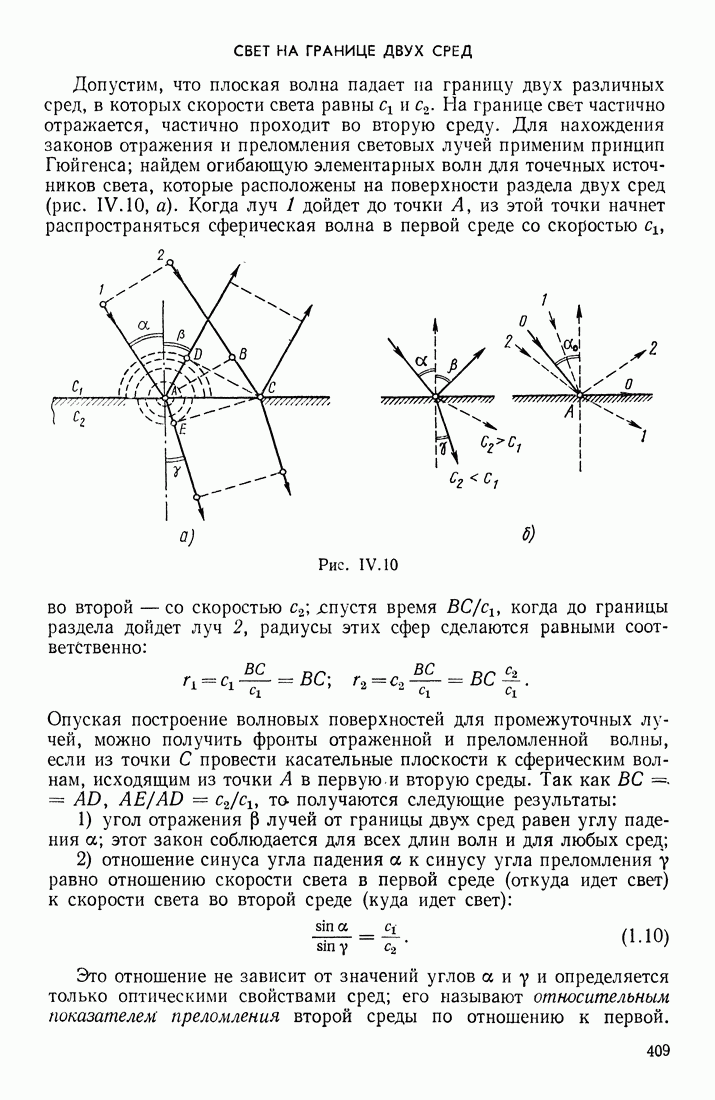
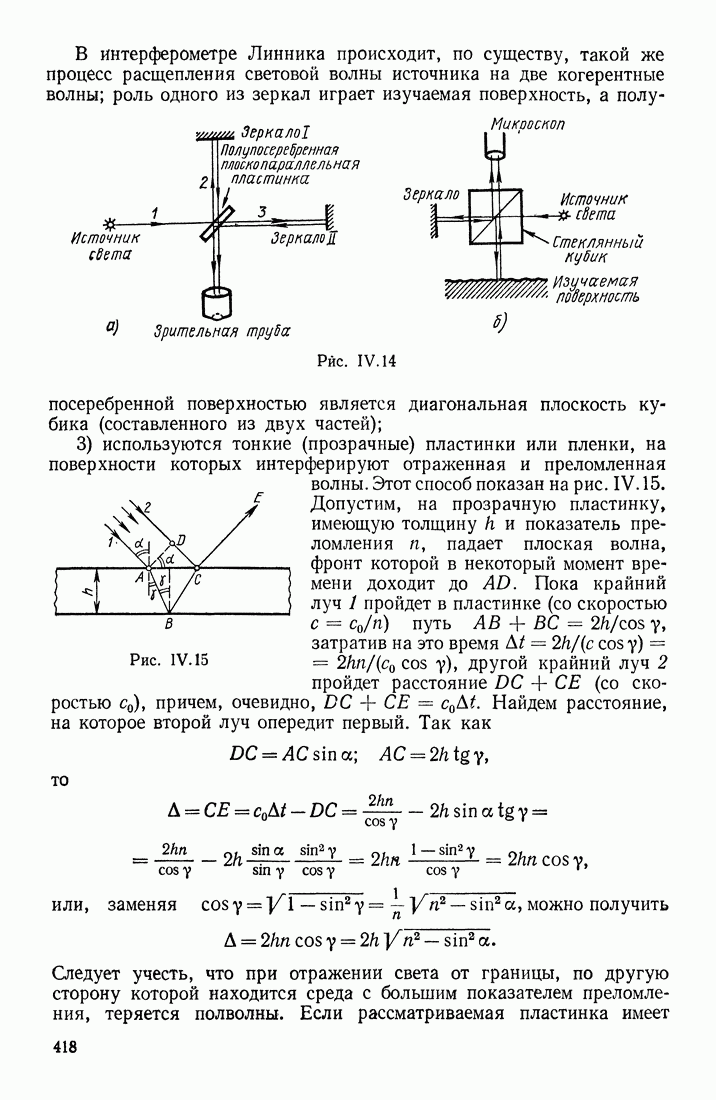
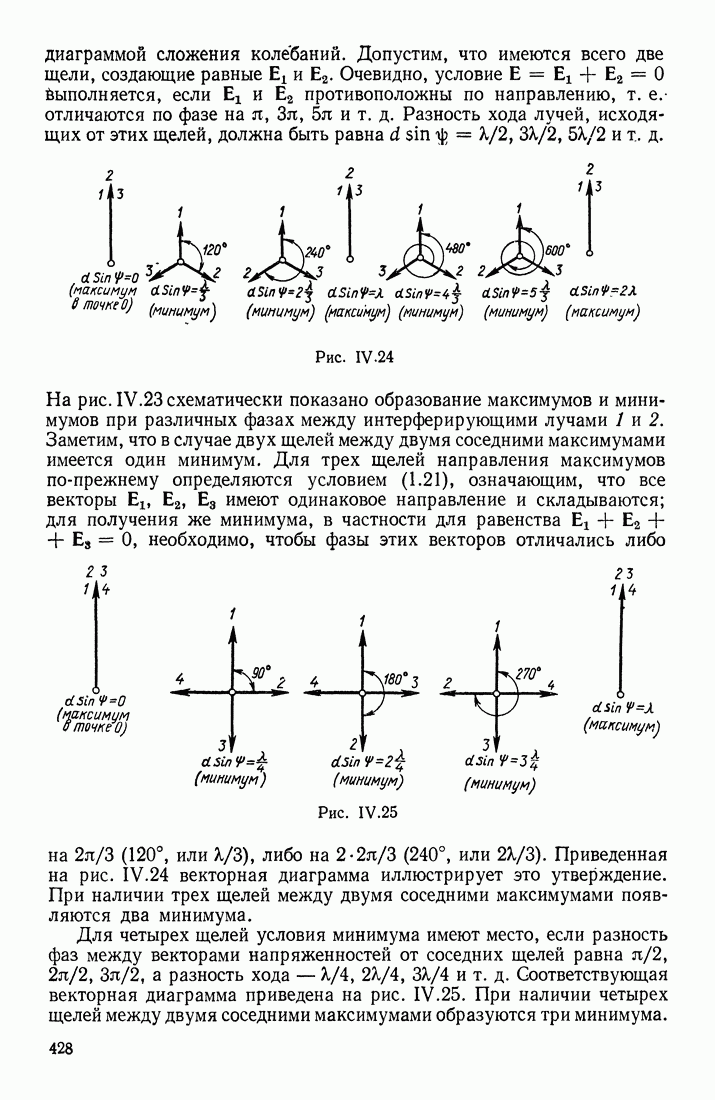
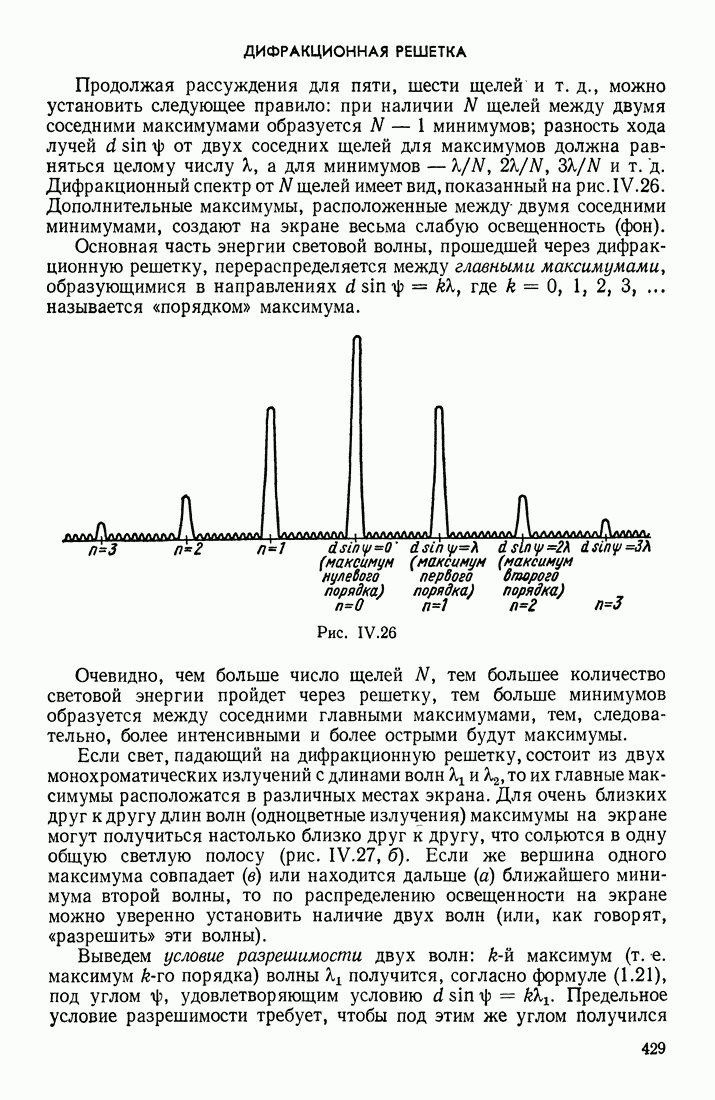
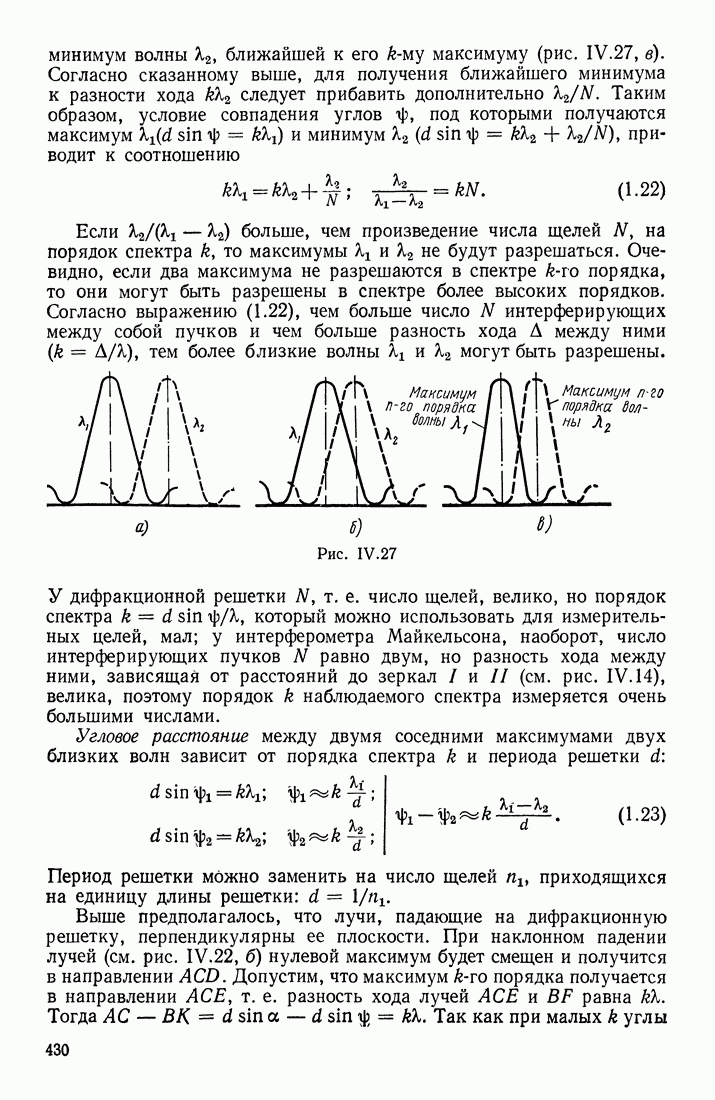
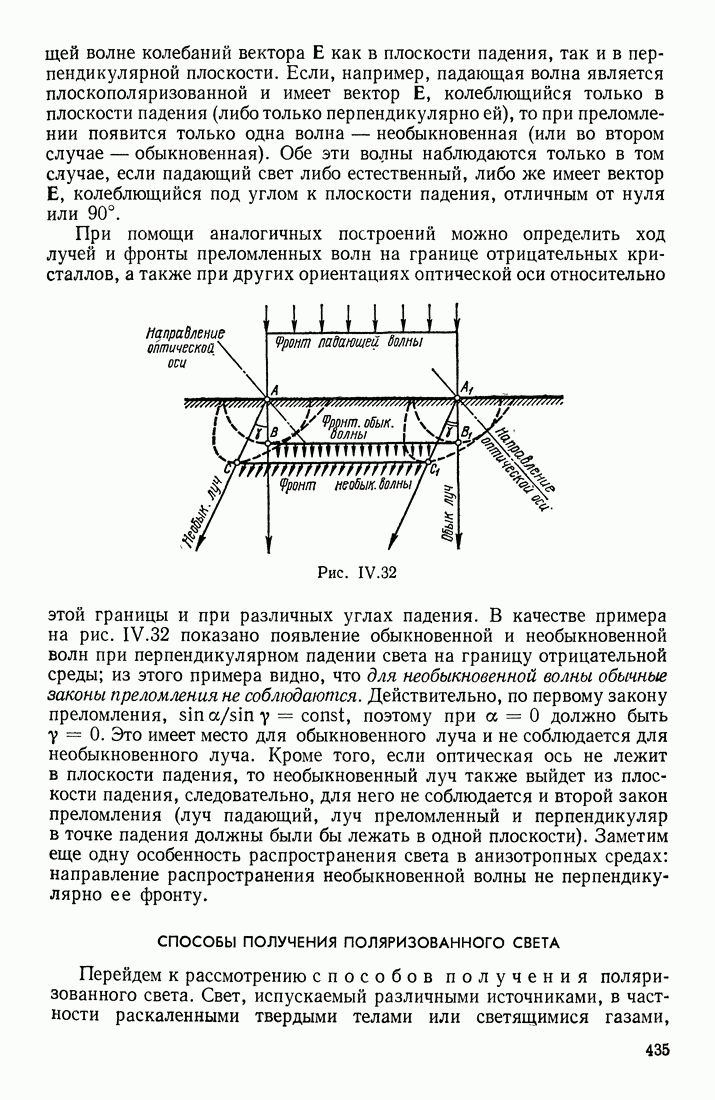
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 23. ФОРМУЛА ГАРМОНИЧЕСКОЙ ВОЛНЫ
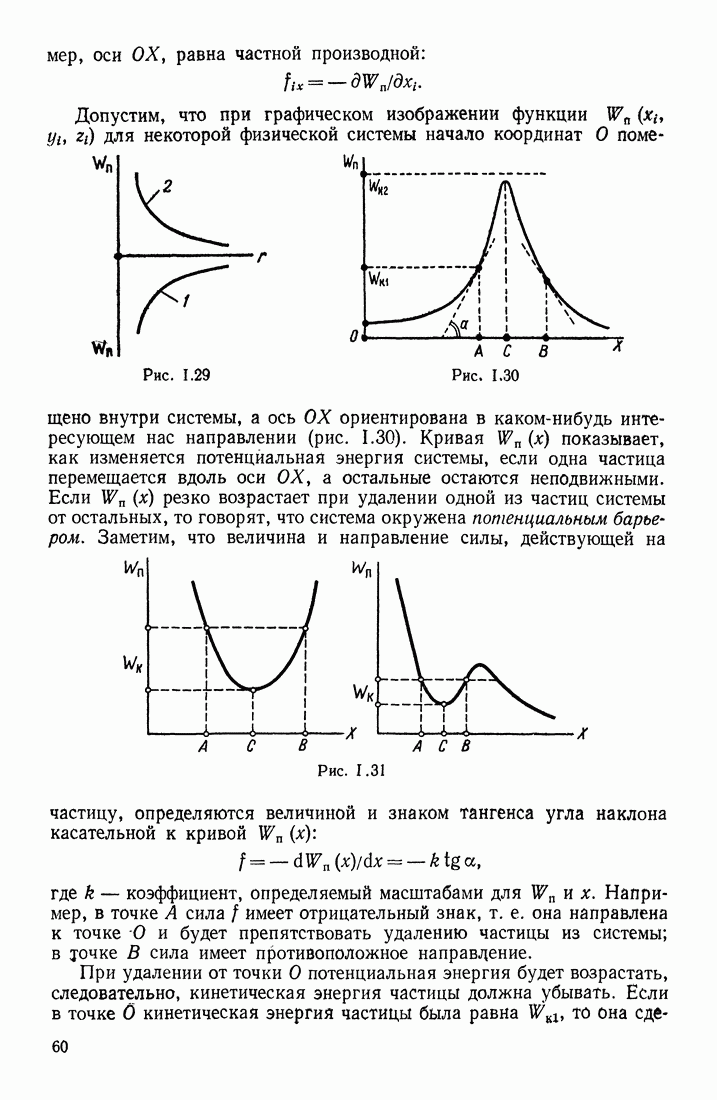
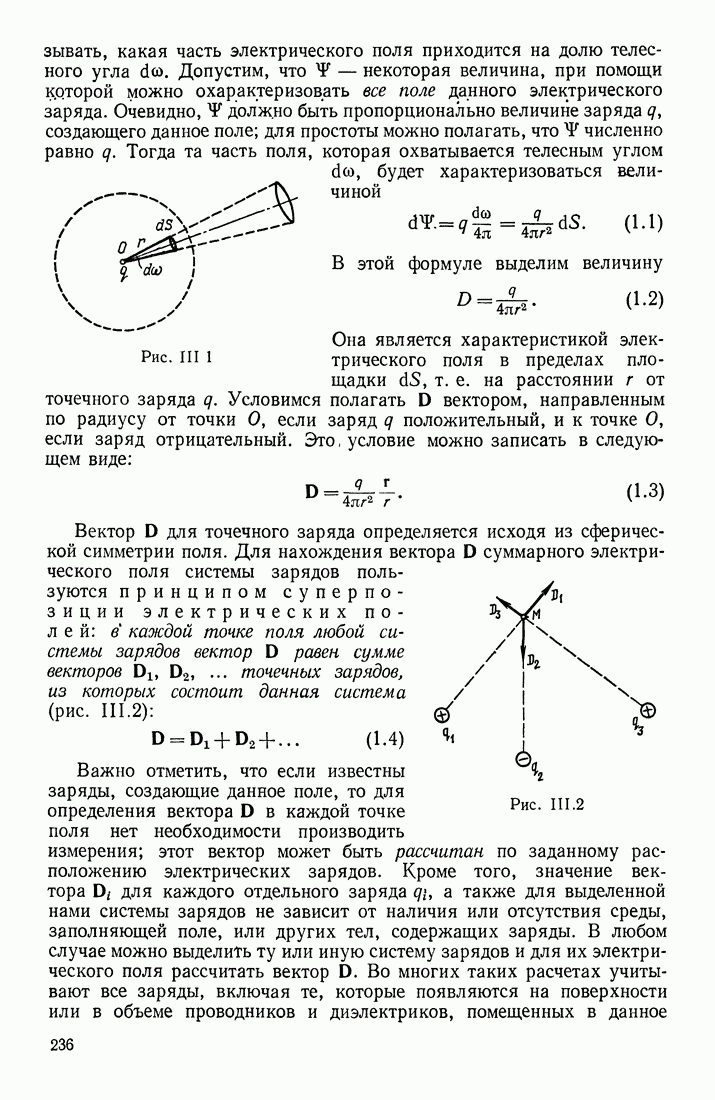
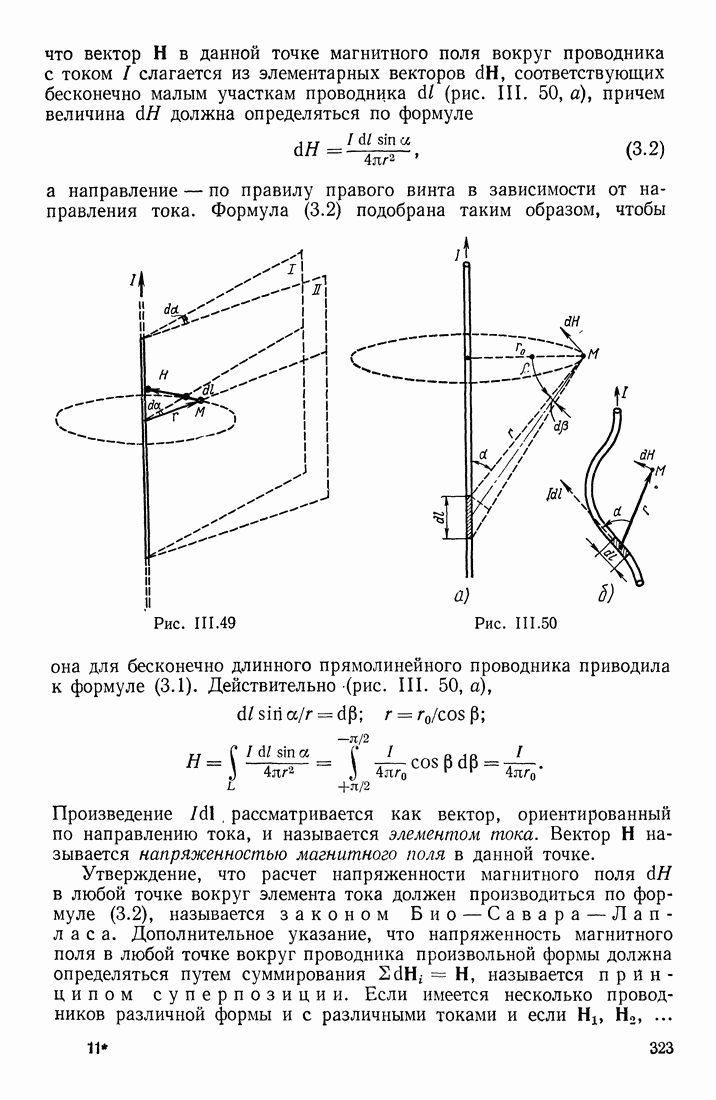
При описании волнового процесса требуется найти амплитуды и фазы колебательного движения в различных, точках среды и изменение этих величин с течением времени. Эта задача может быть решена, если известно, по какому закону колеблется и как взаимодействует со средой тело, вызвавшее волновой процесс. Однако во многих случаях не существенно, каким телом возбуждена данная волна; решается более простая задача: дано состояние колебательного движения в одних точках среды в определенный момент времени, например известно расположение фронта волны или волновой поверхности; требуется определить состояние колебательного движения в других точках среды. Эта задача будет рассматриваться в § 25. Здесь же мы найдем связь между состояниями колебательного движения в различных точках среды в простейшем случае, когда в этой среде распространяется плоская или сферическая синусоидальная волна.
ВЫВОД ФОРМУЛЫ ВОЛНЫ
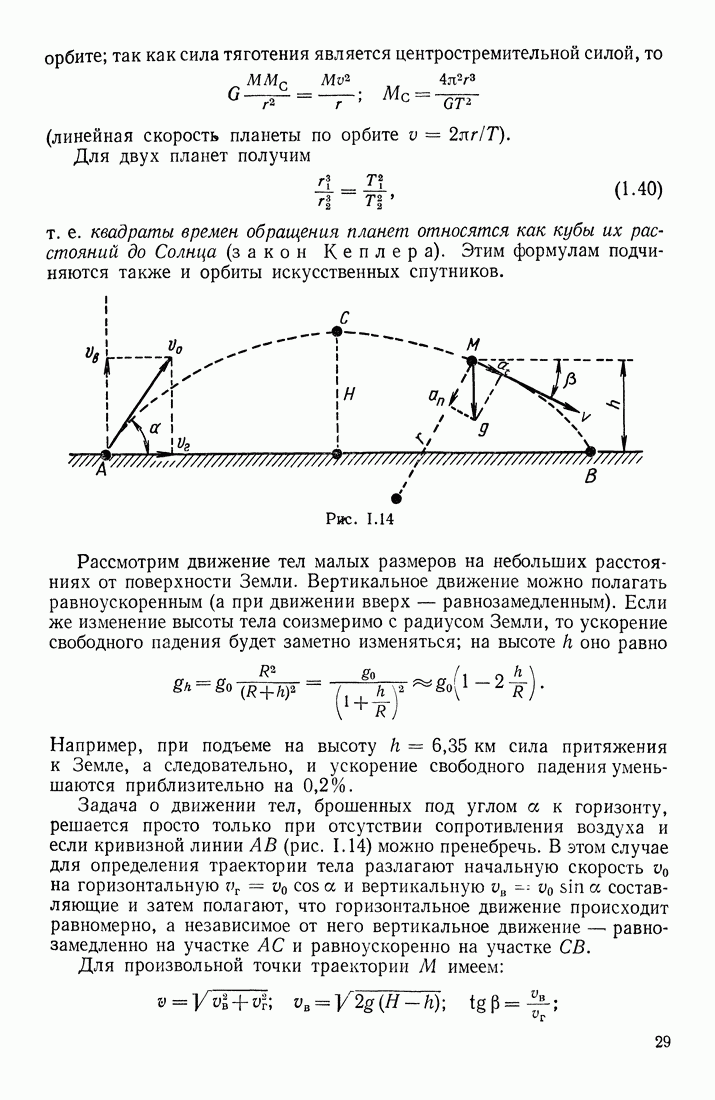
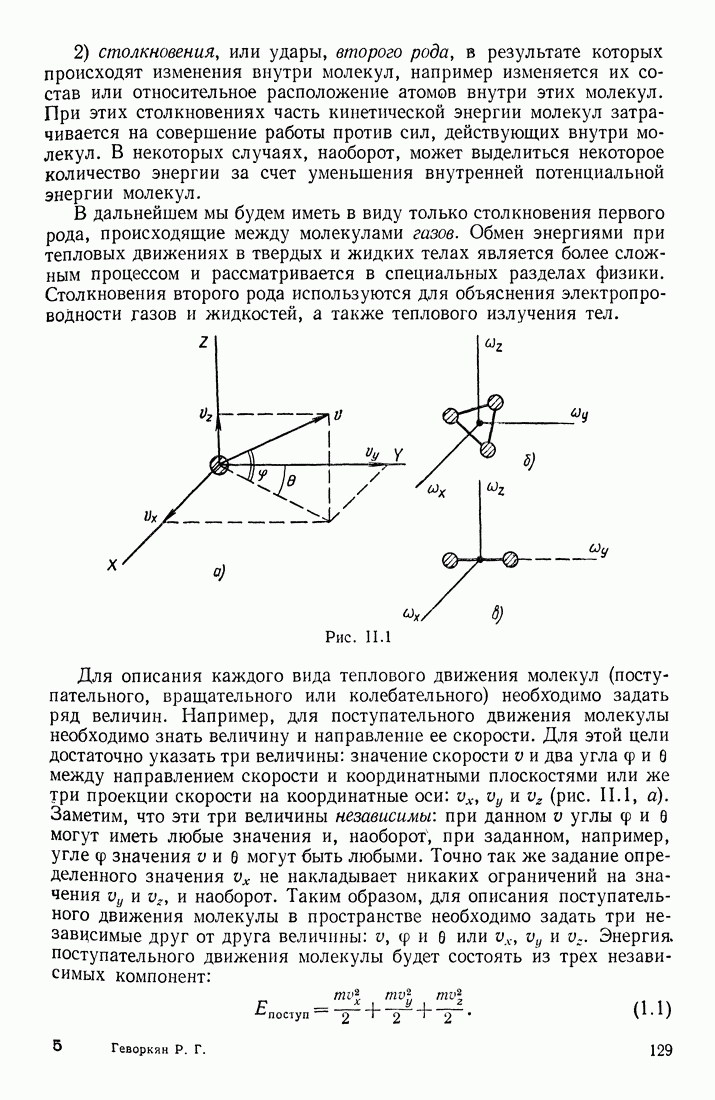
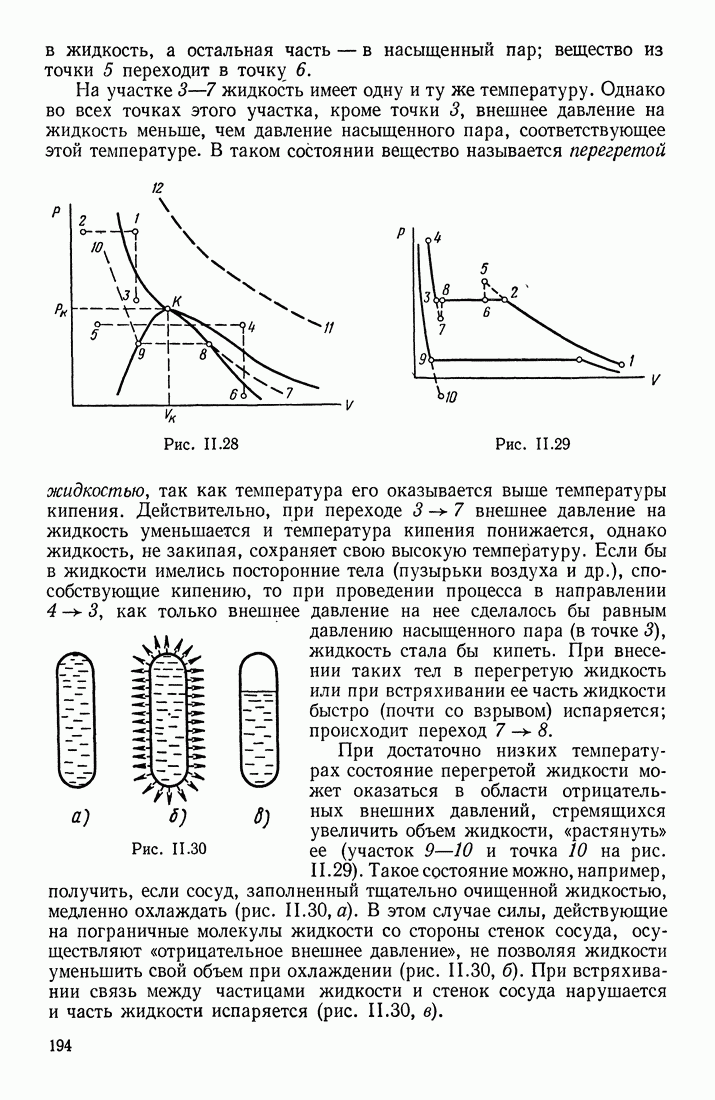
Допустим, что волновой процесс распространяется в положительном направлении оси  т. е. в сторону возрастания координаты х (рис. 1.55). Обозначим через у колеблющуюся величину; этой величиной могут быть: смещение частиц среды относительно их положения равновесия; отклонение давления или плотности в данном месте среды от равновесного значения и т. д.
т. е. в сторону возрастания координаты х (рис. 1.55). Обозначим через у колеблющуюся величину; этой величиной могут быть: смещение частиц среды относительно их положения равновесия; отклонение давления или плотности в данном месте среды от равновесного значения и т. д.

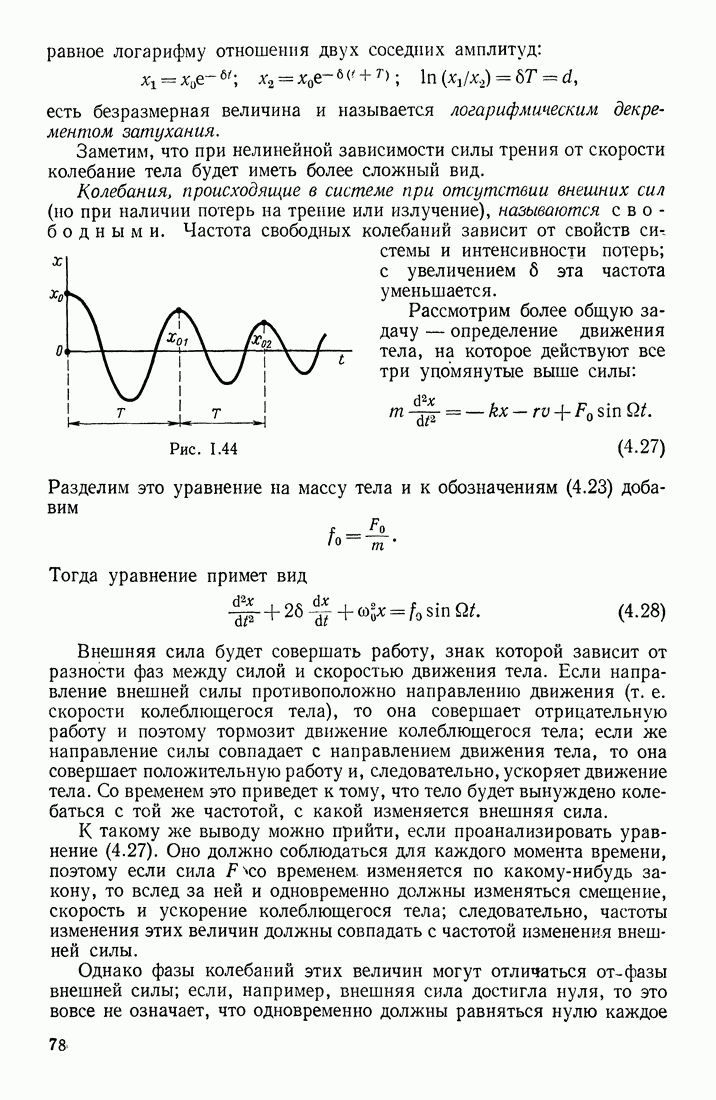
Рис. 1.55
Для простоты рассуждений предположим, что распространяющаяся волна — синусоидальная, т. е. в каждой точке среды величина у изменяется со временем по гармоническому закону. Допустим, что начало отсчета времени выбрано так, что в точке О при  т. е.
т. е.  тогда
тогда

где со  угловая частота;
угловая частота;  период;
период;  амплитуда колебаний;
амплитуда колебаний;  аргумент синуса (определяющий значение колеблющейся величины в каждый заданный момент времени) — фаза
аргумент синуса (определяющий значение колеблющейся величины в каждый заданный момент времени) — фаза
колебаний в точке О. Требуется найти фазу колебаний в любой другой точке А, отстоящей от О на расстоянии х.
Так как точка А расположена относительно О в направлении распространения волны, то в данный момент времени  в этой точке будет такое состояние колебательного движения, какое было в точке О на
в этой точке будет такое состояние колебательного движения, какое было в точке О на  секунд раньше; здесь
секунд раньше; здесь  есть скорость распространения фазы колебаний в направлении
есть скорость распространения фазы колебаний в направлении  Таким образом, фаза колебаний в точке А в момент
Таким образом, фаза колебаний в точке А в момент  равна фазе колебаний в точке О в более ранний момент
равна фазе колебаний в точке О в более ранний момент  т. е. равна со
т. е. равна со 
Следовательно, значение колеблющейся величины в точке А в момент времени 

Мы получили формулу (уравнение) синусоидальной волны, величина  называется фазовой скоростью волны.
называется фазовой скоростью волны.
Допустим теперь, что волна распространяется в обратном направлении, т. е. от  , в сторону убывания координаты х. Тогда определенное состояние колебания, т. е. определенная фаза волны, достигает точки А на
, в сторону убывания координаты х. Тогда определенное состояние колебания, т. е. определенная фаза волны, достигает точки А на  секунд раньше, чем точки О, следовательно, фаза в точке А в данный момент времени больше фазы в точке О на сот
секунд раньше, чем точки О, следовательно, фаза в точке А в данный момент времени больше фазы в точке О на сот  Если по-прежнему принять фазу в точке О в момент
Если по-прежнему принять фазу в точке О в момент  равной
равной  то в точке А в этот же момент времени фаза будет равна
то в точке А в этот же момент времени фаза будет равна  сот
сот  Таким образом, фюрмулу Синусоидальной волны можно написать в общем виде:
Таким образом, фюрмулу Синусоидальной волны можно написать в общем виде:

где знак минус берется для волны, распространяющейся в направлении возрастания х, а плюс — в обратном направлении.
При выводе формулы (5.3) предполагалось, что амплитуда колебаний  по мере распространения волны не изменяется и среда однородна (т. е. скорость распространения фазы колебаний везде одинаковая). Эти два предположения означают, что мы рассматривали плоскую волну. У сферической волны амплитуда колебаний уменьшается обратно пропорционально расстоянию и формула волны имеет вид
по мере распространения волны не изменяется и среда однородна (т. е. скорость распространения фазы колебаний везде одинаковая). Эти два предположения означают, что мы рассматривали плоскую волну. У сферической волны амплитуда колебаний уменьшается обратно пропорционально расстоянию и формула волны имеет вид

Расстояние  пройденное волной (т. е. определенной фазой колебаний) за один период колебаний, называется длиной волны; очевидно,
пройденное волной (т. е. определенной фазой колебаний) за один период колебаний, называется длиной волны; очевидно,

В формуле волны (5.3) колеблющаяся величина зависит от двух переменных:  Если найти производную от у по времени, пблагая х постоянной, то эта частная производная
Если найти производную от у по времени, пблагая х постоянной, то эта частная производная

показывает скорость изменения колеблющейся величины в данной точке среды. Производная же от у по х при постоянном 

есть разность значений колеблющейся величины, рассчитанная на единицу расстояния между точками среды  т. е. показывает, как увеличивается или уменьшается у вдоль оси
т. е. показывает, как увеличивается или уменьшается у вдоль оси  (в данный момент времени t).
(в данный момент времени t).
Найдем частные производные от колеблющейся величины у по времени при постоянном 

Если у есть смещение частиц среды при колебаниях, то  и а будут скоростью и ускорением этих частиц при их колебательном движении в точке с координатой х. Амплитудные значения этих величин связаны между собой:
и а будут скоростью и ускорением этих частиц при их колебательном движении в точке с координатой х. Амплитудные значения этих величин связаны между собой:

Частные производные от у по х при постоянном  будут равны:
будут равны:

Следовательно,

Это есть дифференциальное уравнение плоской гармонической волны, распространяющейся по оси  Оно получено нами из формулы волны (5.3). Однако можно сделать и обратное заключение: если какая-нибудь физическая величина
Оно получено нами из формулы волны (5.3). Однако можно сделать и обратное заключение: если какая-нибудь физическая величина  зависит от времени и координат так, что ее частные производные удовлетворяют уравнению (5.6), то величина у распространяется в среде в виде плоской волны (см. уравнение (5.3)) со скоростью
зависит от времени и координат так, что ее частные производные удовлетворяют уравнению (5.6), то величина у распространяется в среде в виде плоской волны (см. уравнение (5.3)) со скоростью

и частотой колебаний

Дифференциальное уравнение плоской гармонической волны, распространяющейся вдоль оси  можно записать не только в виде (5.6), содержащем вторые производные по координате и времени, но и в виде
можно записать не только в виде (5.6), содержащем вторые производные по координате и времени, но и в виде
связи между этими производными и самой колеблющейся величиной:

Второе уравнение явно не содержит времени; если произвести замену  (длина волны), то
(длина волны), то

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Часть I. МЕХАНИКА
- § 1. СИСТЕМЫ ОТСЧЕТА; ЛИНЕЙНЫЕ И УГЛОВЫЕ СКОРОСТИ И УСКОРЕНИЯ
- ДВИЖЕНИЕ ПО КРИВОЛИНЕЙНОЙ ТРАЕКТОРИИ
- § 2. ЗАКОНЫ МЕХАНИКИ НЬЮТОНА. СИСТЕМЫ ЕДИНИЦ
- СИЛА. ДЕФОРМАЦИЯ. МАССА
- ОСНОВНЫЕ ЗАКОНЫ МЕХАНИКИ
- ИМПУЛЬС. РАБОТА. МОЩНОСТЬ
- ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН
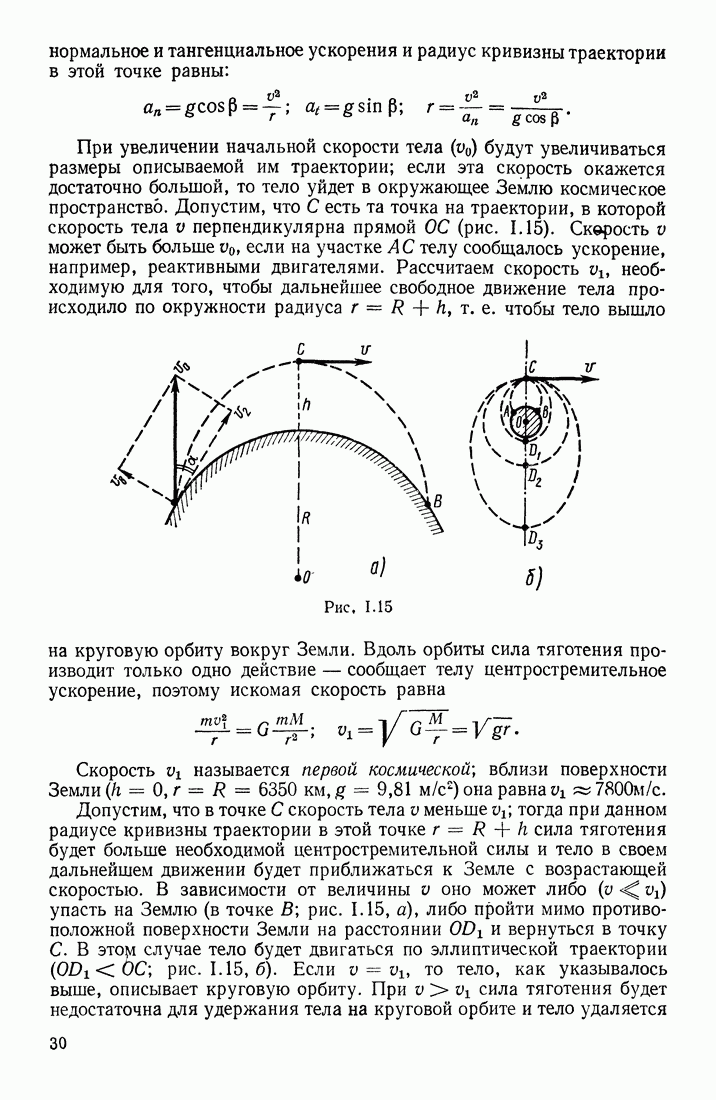
- § 3. ДВИЖЕНИЕ ТЕЛА В ПОЛЕ ТЯГОТЕНИЯ ЗЕМЛИ
- ГРАВИТАЦИОННОЕ ПОЛЕ. ВЕС ТЕЛА
- ДВИЖЕНИЕ КОСМИЧЕСКИХ ОБЪЕКТОВ
- § 4. ДВИЖЕНИЕ ТЕЛ С ПЕРЕМЕННОЙ МАССОЙ
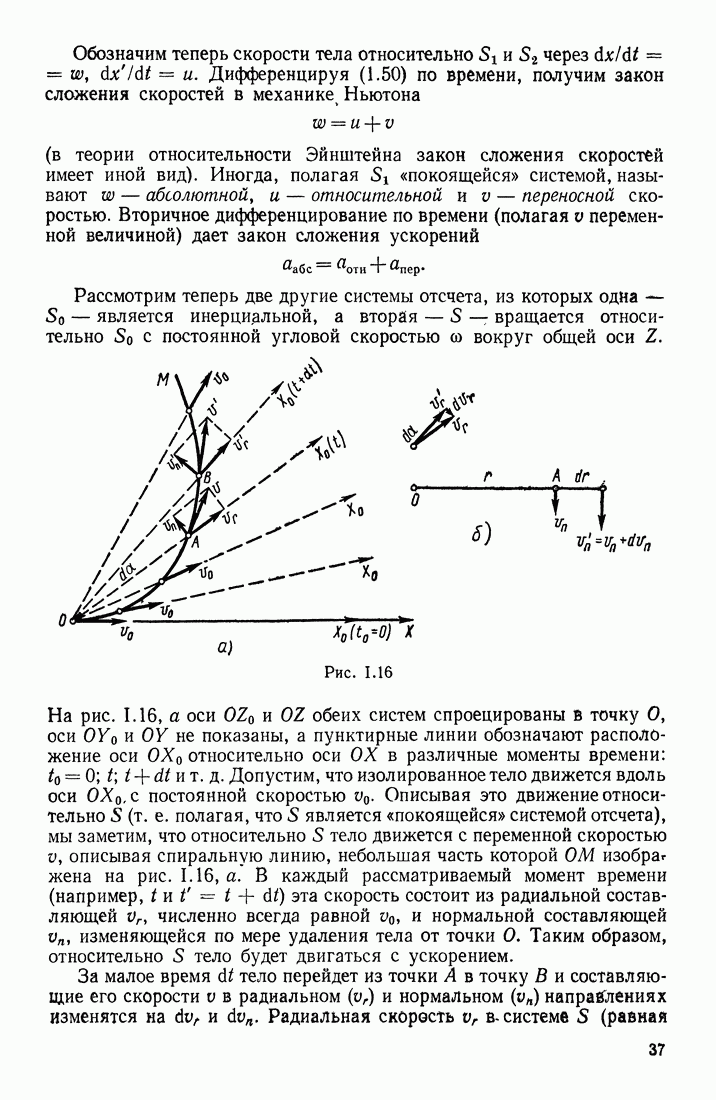
- § 5. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ В МЕХАНИКЕ
- ПРЕОБРАЗОВАНИЯ КООРДИНАТ, СКОРОСТЕЙ И УСКОРЕНИЙ
- Глава 2. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА
- § 6. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ВРАЩАЮЩЕГОСЯ ТЕЛА; МОМЕНТ ИНЕРЦИИ ТЕЛ
- § 7. ЗАКОНЫ МЕХАНИКИ ДЛЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
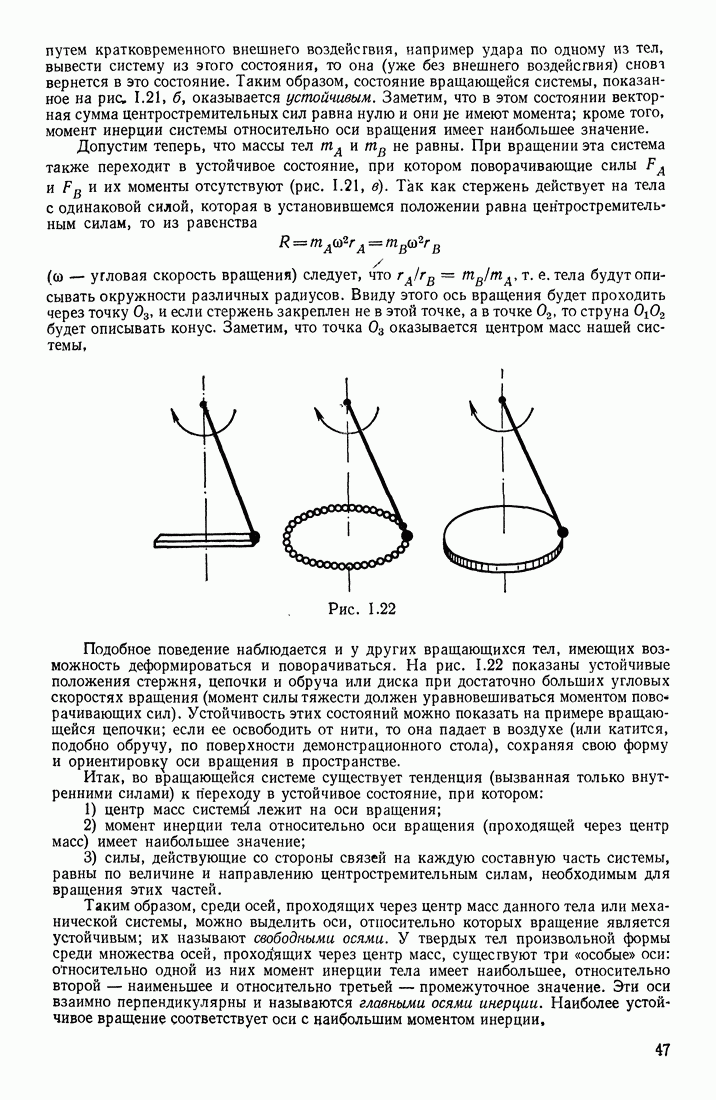
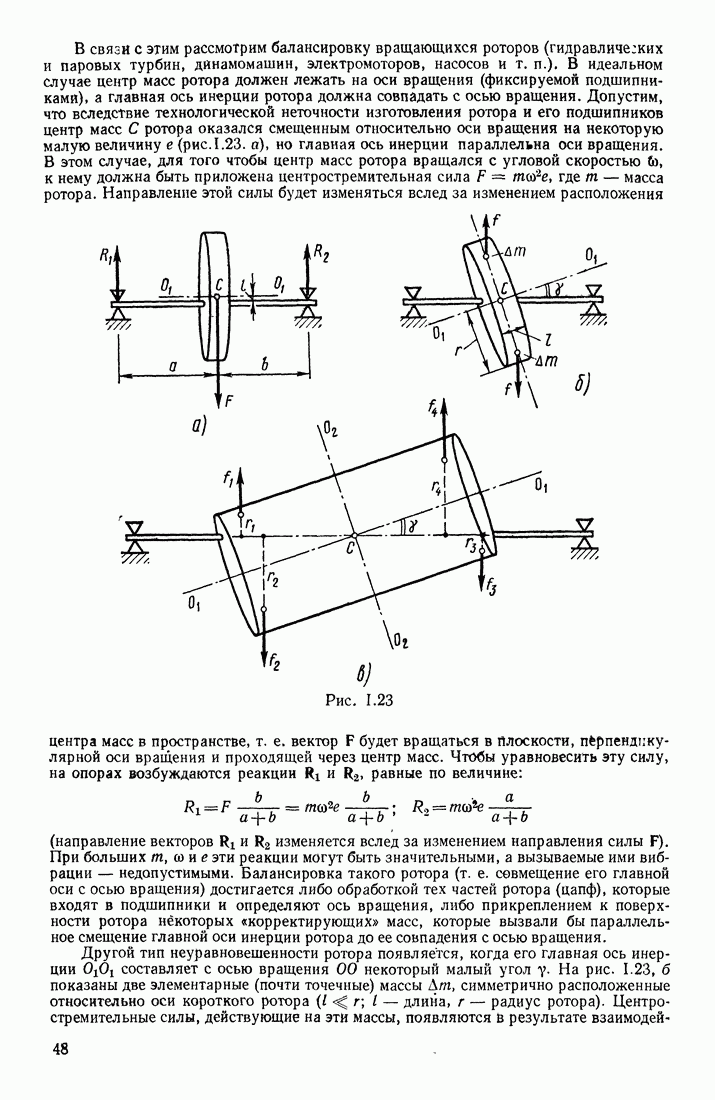
- § 8. СВОБОДНЫЕ ОСИ. БАЛАНСИРОВКА РОТОРОВ. ГИРОСКОПЫ
- Глава 3. ЗАКОНЫ СОХРАНЕНИЯ В СИСТЕМЕ ВЗАИМОДЕЙСТВУЮЩИХ ТЕЛ
- § 9. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА (КОЛИЧЕСТВА ДВИЖЕНИЯ)
- § 10. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА (МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ)
- § 11. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
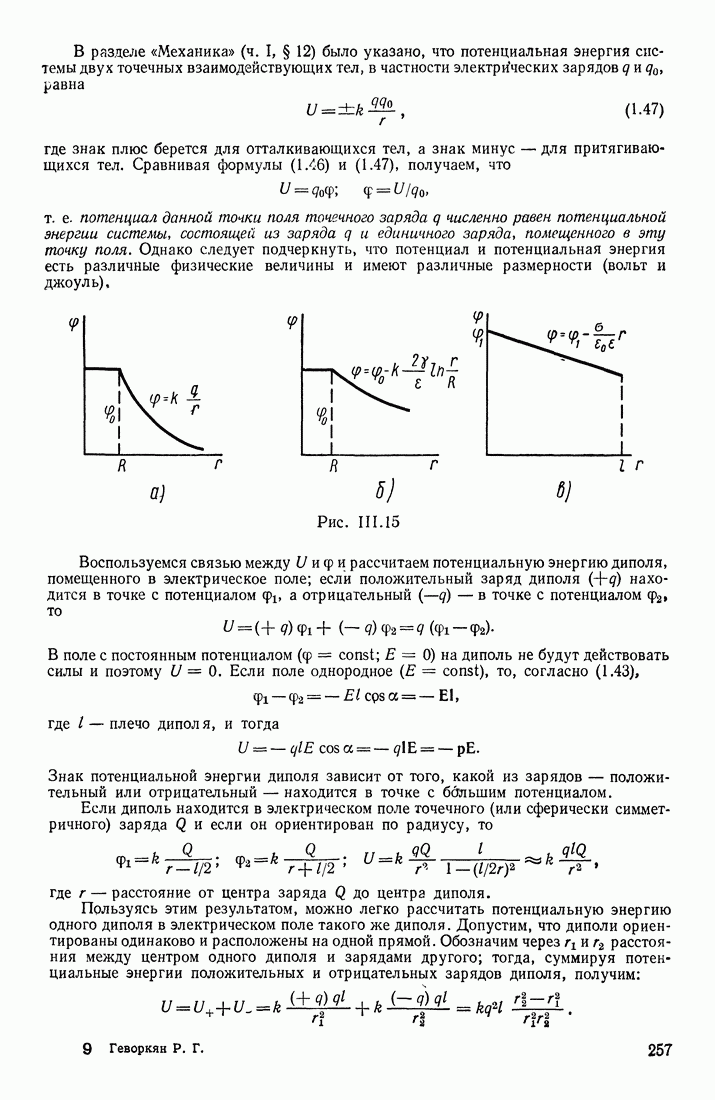
- § 12. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ НЕКОТОРЫХ СИСТЕМ
- § 13. СТОЛКНОВЕНИЕ ШАРОВ
- § 14. О ЦЕНТРЕ МАСС СИСТЕМЫ
- Глава 4. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ
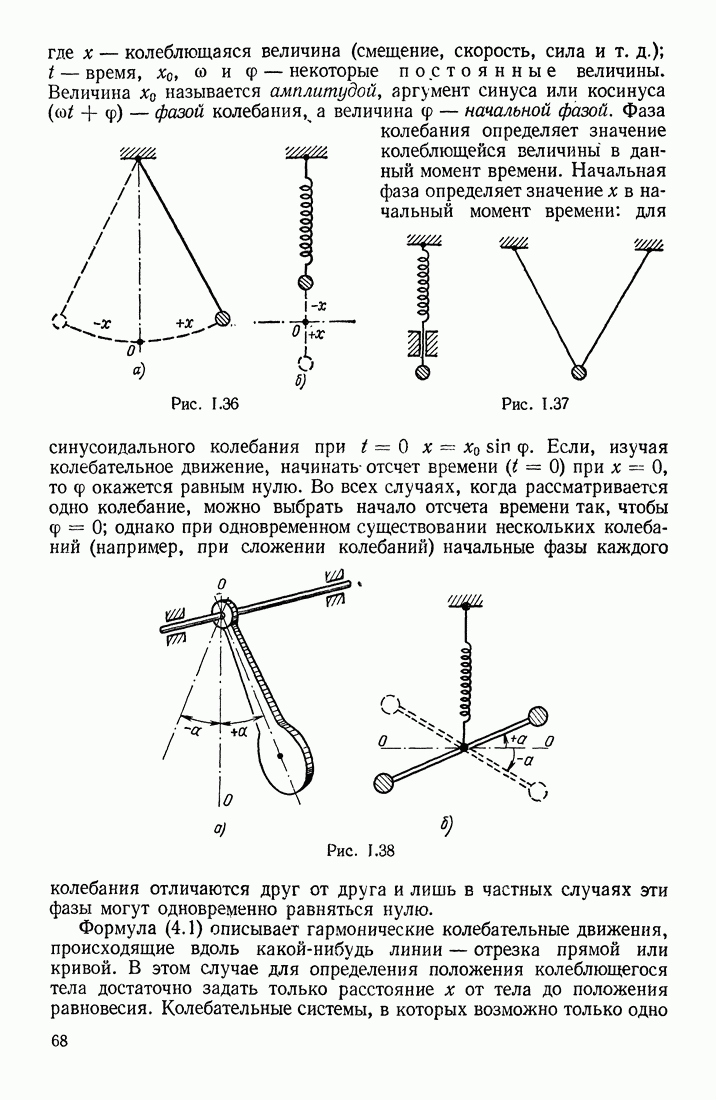
- § 15. ПЕРИОДИЧЕСКОЕ ДВИЖЕНИЕ; ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
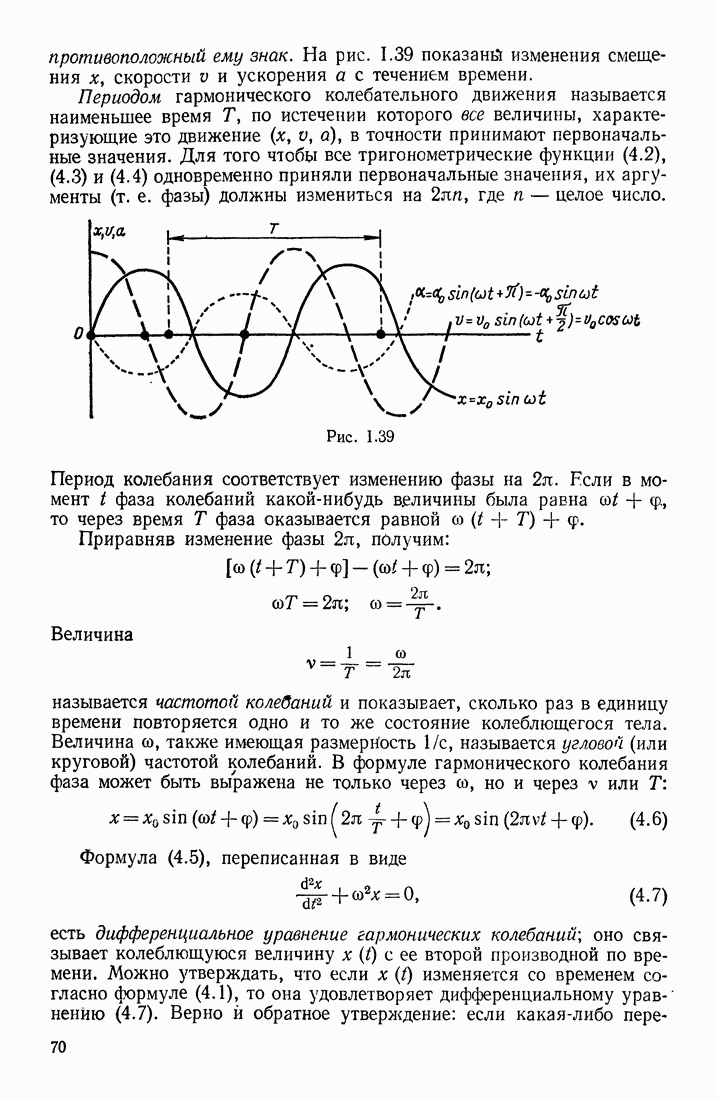
- § 16. СКОРОСТЬ И УСКОРЕНИЕ КОЛЕБЛЮЩЕГОСЯ ТЕЛА. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- § 17. СИЛА И ЭНЕРГИЯ ПРИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЯХ. ПРОСТЕЙШИЕ МЕХАНИЧЕСКИЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
- § 18. СОБСТВЕННЫЕ, СВОБОДНЫЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ПАРАМЕТРИЧЕСКОЕ ВОЗБУЖДЕНИЕ КОЛЕБАНИЙ
- § 19. ПОНЯТИЕ О НЕЛИНЕЙНЫХ КОЛЕБАНИЯХ
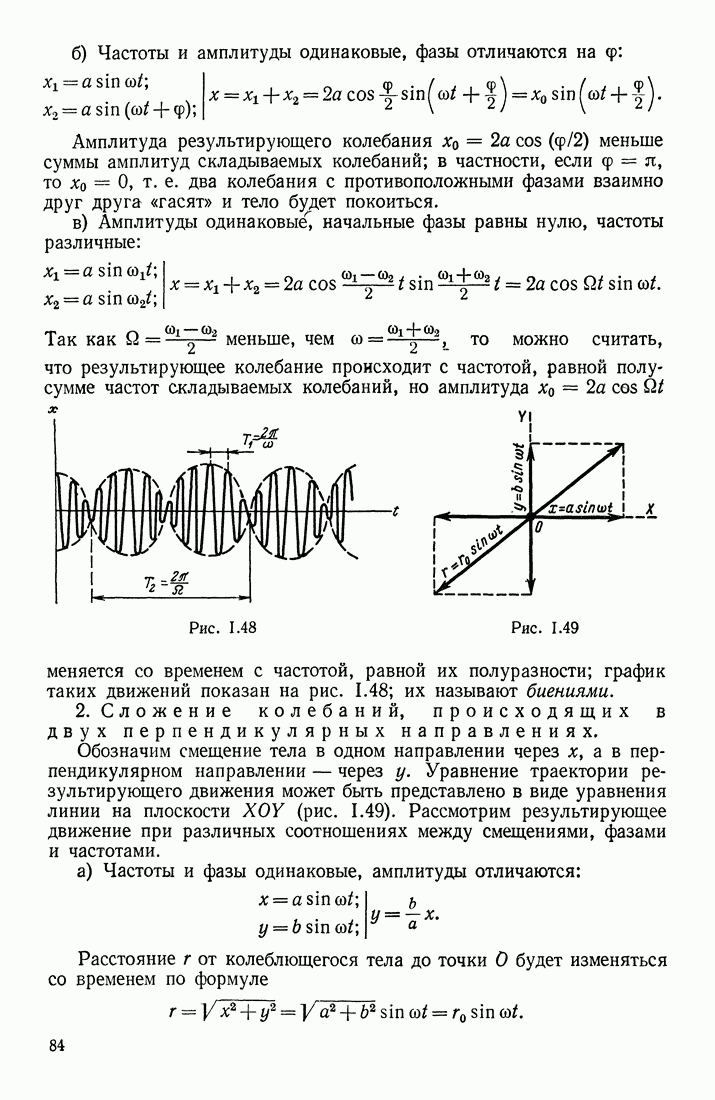
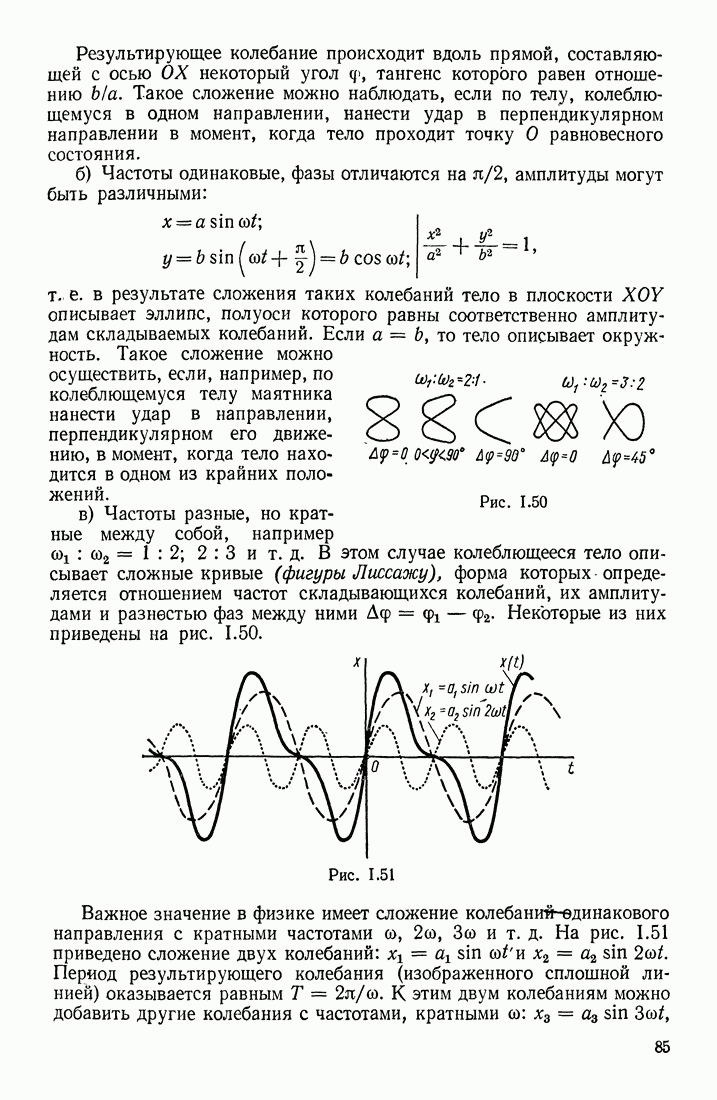
- § 20. СЛОЖЕНИЕ И РАЗЛОЖЕНИЕ КОЛЕБАНИЙ
- § 21. АВТОКОЛЕБАНИЯ
- Глава 5. ВОЛНОВЫЕ ПРОЦЕССЫ; ОСНОВЫ АКУСТИКИ
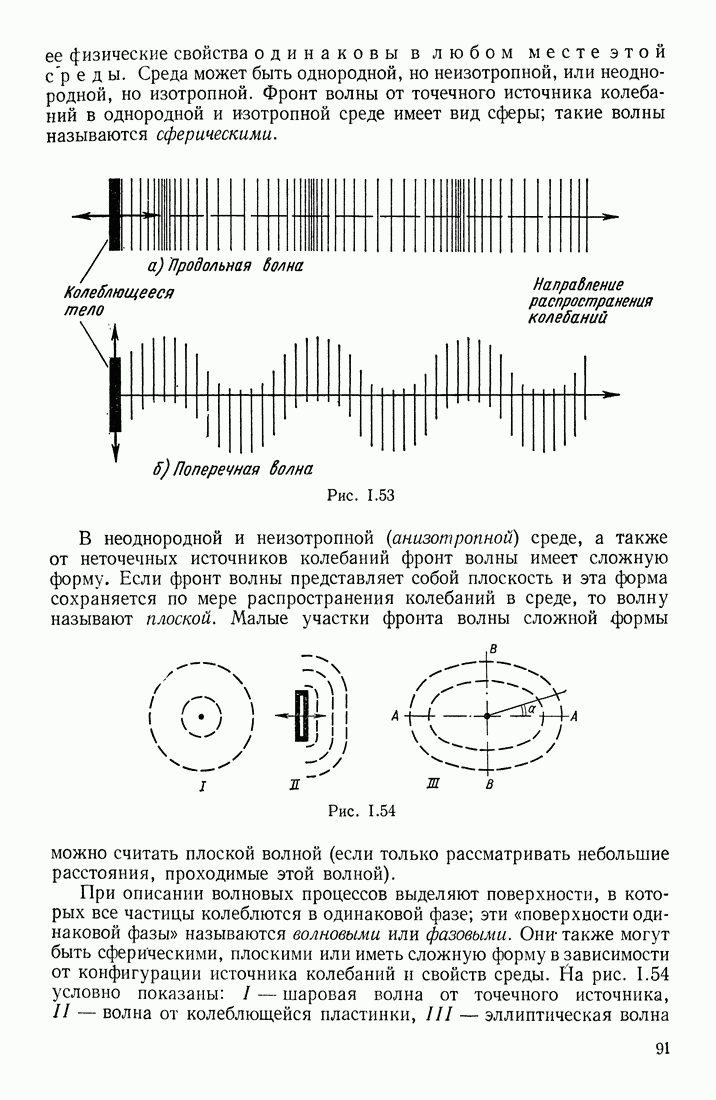
- § 22. ОБРАЗОВАНИЕ И РАСПРОСТРАНЕНИЕ ВОЛН В УПРУГОЙ СРЕДЕ
- § 23. ФОРМУЛА ГАРМОНИЧЕСКОЙ ВОЛНЫ
- ВОЛНА В УПРУГОЙ СРЕДЕ
- § 24. ПОТОК ЭНЕРГИИ В ВОЛНОВЫХ ПРОЦЕССАХ
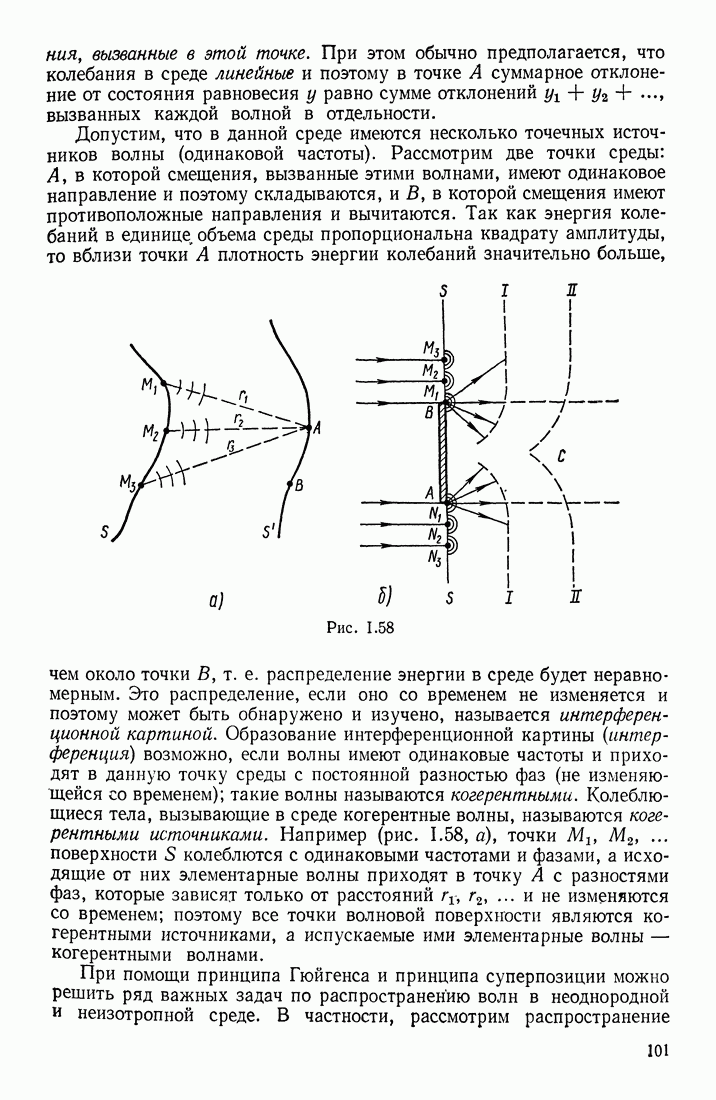
- § 25. ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ ВОЛН. РАСПРОСТРАНЕНИЕ ВОЛН В СРЕДАХ С ДИСПЕРСИЕЙ
- § 26. СТОЯЧИЕ ВОЛНЫ
- § 27. ЗВУКОВЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- ЭФФЕКТ ДОПЛЕРА
- ХАРАКТЕРИСТИКИ ЗВУКОВОГО ОЩУЩЕНИЯ
- § 28. УЛЬТРАЗВУКИ И ИХ ПРИМЕНЕНИЯ
- Глава 6. МЕХАНИКА ЖИДКОСТЕЙ И ГАЗОВ
- § 29. ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ. БАРОМЕТРИЧЕСКАЯ ФОРМУЛА
- § 30. ЛАМИНАРНОЕ И ТУРБУЛЕНТНОЕ ТЕЧЕНИЯ. ФОРМУЛА БЕРНУЛЛИ
- СЖИМАЕМОСТЬ И ВЯЗКОСТЬ В ПОТОКЕ
- РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ В ЛАМИНАРНОМ ПОТОКЕ
- Часть II. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
- § 1. ТЕПЛОВОЕ ДВИЖЕНИЕ
- § 2. ВЗАИМОДЕЙСТВИЕ МОЛЕКУЛ; ЭНЕРГИЯ СВЯЗИ МОЛЕКУЛ
- § 3. АГРЕГАТНЫЕ СОСТОЯНИЯ И ФАЗОВЫЕ ПЕРЕХОДЫ. РАВНОВЕСНЫЕ И НЕРАВНОВЕСНЫЕ СОСТОЯНИЯ И ПРОЦЕССЫ
- СВОЙСТВА ТЕРМОДИНАМИЧЕСКИХ СИСТЕМ
- ВИДЫ ТЕРМОДИНАМИЧЕСКИХ ПРОЦЕССОВ
- § 4. ВНУТРЕННЯЯ ЭНЕРГИЯ ТЕРМОДИНАМИЧЕСКОЙ СИСТЕМЫ. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- § 5. ВНЕШНЯЯ РАБОТА СИСТЕМЫ И ТЕПЛООБМЕН С ОКРУЖАЮЩЕЙ СРЕДОЙ. ТЕПЛОЕМКОСТЬ ТЕЛ
- § 6. ИЗОПРОЦЕССЫ; АДИАБАТИЧЕСКИЙ ПРОЦЕСС. ЭНТРОПИЯ СИСТЕМЫ. ЗАМКНУТЫЕ (КРУГОВЫЕ) ПРОЦЕССЫ
- ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ ИЗОПРОЦЕССОВ
- КРУГОВЫЕ ПРОЦЕССЫ
- § 7. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ. ЗАКОН ВОЗРАСТАНИЯ ЭНТРОПИИ
- ТЕПЛОВЫЕ И ХОЛОДИЛЬНЫЕ МАШИНЫ
- ЭНТРОПИЯ И ВЕРОЯТНОСТЬ
- Глава 2. ИДЕАЛЬНЫЙ ГАЗ
- § 8. ОСНОВНОЕ УРАВНЕНИЕ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ. СРЕДНИЕ СКОРОСТИ МОЛЕКУЛ
- § 9. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
- § 10. ИЗОПРОЦЕССЫ В ИДЕАЛЬНОМ ГАЗЕ; ТЕПЛОЕМКОСТИ ГАЗОВ
- § 11. КРУГОВЫЕ ПРОЦЕССЫ, СОВЕРШАЕМЫЕ ИДЕАЛЬНЫМ ГАЗОМ; ЦИКЛ КАРНО. ЭНТРОПИЯ ИДЕАЛЬНОГО ГАЗА
- ЦИКЛ КАРНО
- ПРОЦЕССЫ, ВЫЗЫВАЮЩИЕ ИЗМЕНЕНИЕ ЭНТРОПИИ
- ПАРАДОКС ГИББСА
- § 12. ДИФФУЗИЯ, ТЕПЛОПРОВОДНОСТЬ И ВНУТРЕННЕЕ ТРЕНИЕ В ГАЗАХ; ЧИСЛО СТОЛКНОВЕНИЙ И ДЛИНА СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ
- Глава 3. РЕАЛЬНЫЕ ГАЗЫ, ЖИДКОСТИ И ТВЕРДЫЕ ТЕЛА
- § 13. ОТСТУПЛЕНИЯ ОТ ЗАКОНОВ ИДЕАЛЬНЫХ ГАЗОВ. НАСЫЩЕННЫЕ ПАРЫ. КРИТИЧЕСКОЕ СОСТОЯНИЕ
- ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ГАЗОВ
- ПАР
- ПЕРЕХОДЫ в СИСТЕМЕ ЖИДКОСТЬ — ПАР — ГАЗ
- § 14. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА. ВНУТРЕННЯЯ ЭНЕРГИЯ РЕАЛЬНОГО ГАЗА
- ПАРАМЕТРЫ КРИТИЧЕСКОГО СОСТОЯНИЯ
- ПРИМЕНЕНИЯ УРАВНЕНИЯ ВАН-ДЕР-ВААЛЬСА
- § 15. ЖИДКОСТИ; ИХ ОСНОВНЫЕ СВОЙСТВА. МОЛЕКУЛЯРНОЕ ДАВЛЕНИЕ И ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ
- СВОЙСТВА ЖИДКОСТЕЙ
- МОЛЕКУЛЯРНЫЕ СИЛЫ В ПОВЕРХНОСТНОМ СЛОЕ
- § 16. КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- § 17. ИСПАРЕНИЕ И КИПЕНИЕ ЖИДКОСТЕЙ; КОНДЕНСАЦИЯ ПАРОВ
- ИСПАРЕНИЕ И КОНДЕНСАЦИЯ
- КИПЕНИЕ
- УДЕЛЬНАЯ ТЕПЛОТА ПАРООБРАЗОВАНИЯ
- § 18. КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТЕЛА. КРИСТАЛЛИЗАЦИЯ, ПЛАВЛЕНИЕ И ИСПАРЕНИЕ ТВЕРДЫХ ТЕЛ
- КРИСТАЛЛИЗАЦИЯ
- ТЕМПЕРАТУРА ПЛАВЛЕНИЯ
- ТРОЙНАЯ ТОЧКА
- § 19. ТИПЫ КРИСТАЛЛИЧЕСКИХ РЕШЕТОК. ТЕПЛОВЫЕ И УПРУГИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ
- ТЕПЛОЕМКОСТЬ КРИСТАЛЛА
- ТЕПЛОВОЕ РАСШИРЕНИЕ КРИСТАЛЛОВ
- УПРУГОСТЬ И ПЛАСТИЧНОСТЬ
- ЖИДКИЕ КРИСТАЛЛЫ
- Часть III. ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
- § 1. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ. ПРОВОДНИКИ И ДИЭЛЕКТРИКИ
- § 2. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ; ИНДУКЦИЯ И НАПРЯЖЕННОСТЬ ПОЛЯ. ЗАКОН КУЛОНА
- § 3. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ СИСТЕМЫ ЗАРЯДОВ; ТЕОРЕМА ОСТРОГРАДСКОГО—ГАУССА
- ПРИМЕНЕНИЕ ТЕОРЕМЫ ОСТРОГРАДСКОГО—ГАУССА
- ФОРМУЛЫ ДЛЯ НАПРЯЖЕННОСТИ ПОЛЯ
- § 4. РАБОТА ПЕРЕМЕЩЕНИЯ ЗАРЯДА В ЭЛЕКТРИЧЕСКОМ ПОЛЕ; РАЗНОСТЬ ПОТЕНЦИАЛОВ. ЭНЕРГИЯ ВЗАИМОДЕЙСТВИЯ ЗАРЯДОВ
- § 5. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 6. ДИЭЛЕКТРИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
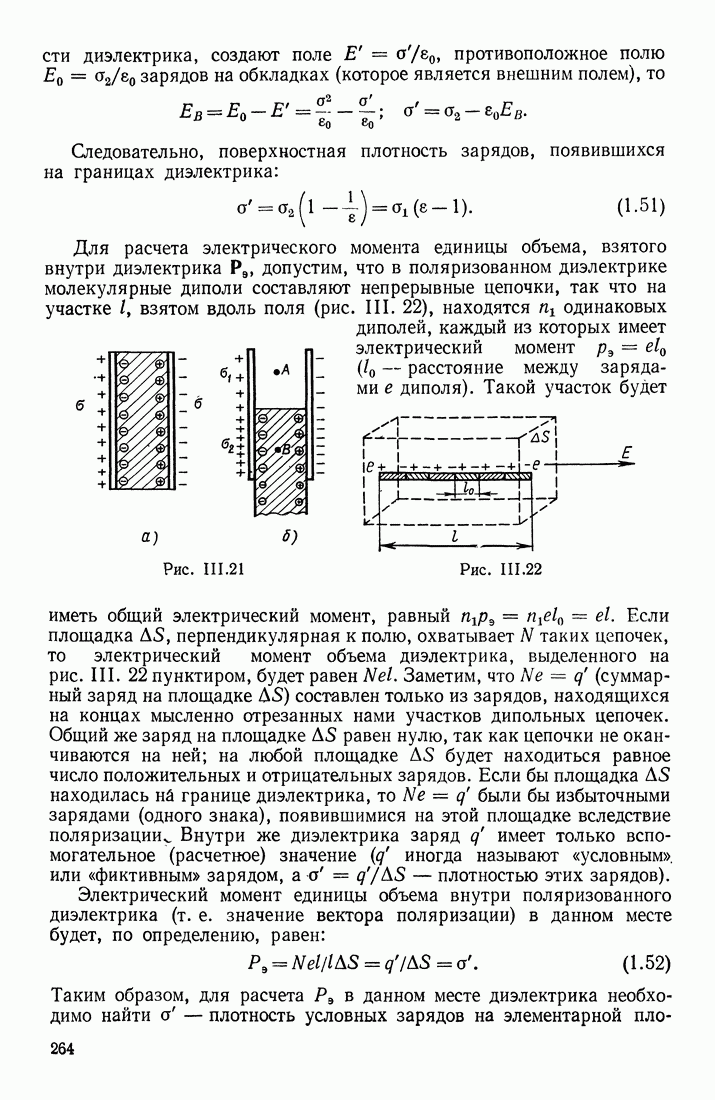
- ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКОВ
- ЭЛЕКТРОСТРИКЦИЯ
- ПЬЕЗОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ
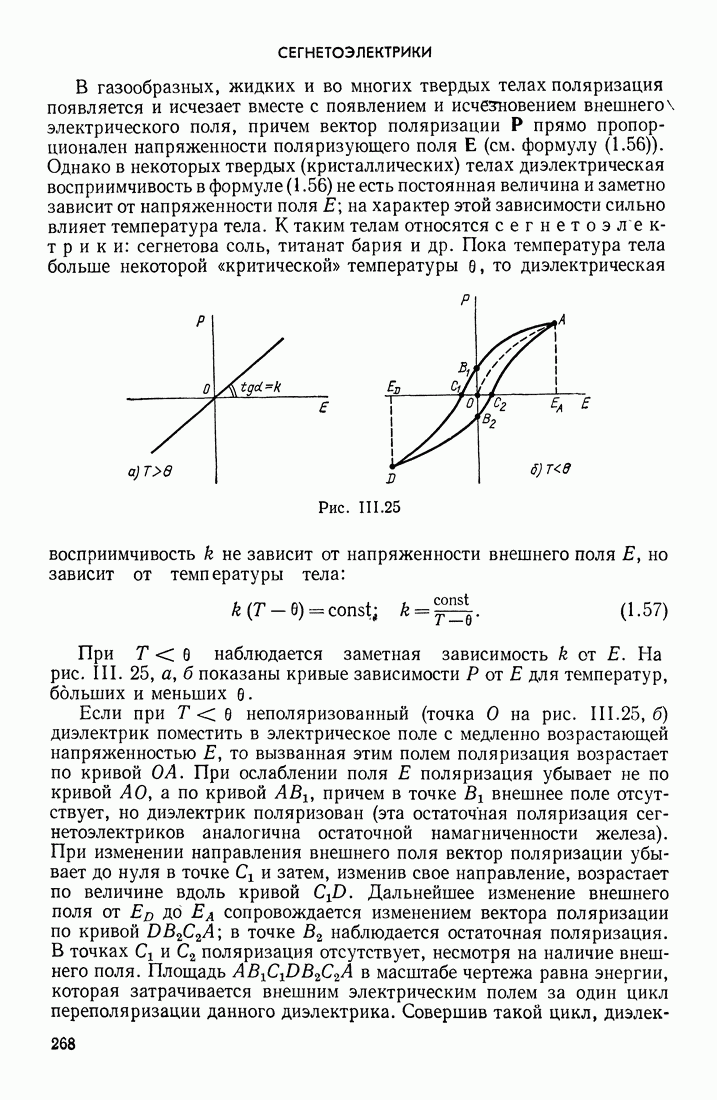
- СЕГНЕТОЭЛЕКТРИКИ
- ЭЛЕКТРЕТЫ
- § 7. ЭЛЕКТРОЕМКОСТЬ. ЭНЕРГИЯ ЗАРЯЖЕННОГО ПРОВОДНИКА. ПЛОТНОСТЬ ЭНЕРГИИ ПОЛЯ
- Глава 2. ЭЛЕКТРИЧЕСКИЙ ТОК
- § 8. ЭЛЕКТРИЧЕСКИЙ ТОК ПРОВОДИМОСТИ; ПЛОТНОСТЬ ТОКА
- § 9. ЭЛЕКТРОННАЯ ТЕОРИЯ ПРОВОДИМОСТИ МЕТАЛЛОВ. ЗАКОНЫ ОМА И ДЖОУЛЯ—ЛЕНЦА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ. СВЯЗЬ МЕЖДУ ЭЛЕКТРОПРОВОДНОСТЬЮ И ТЕПЛОПРОВОДНОСТЬЮ
- § 10. РАБОТА ЭЛЕКТРИЧЕСКОГО ТОКА. СОПРОТИВЛЕНИЕ ПРОВОДНИКОВ. СВЕРХПРОВОДИМОСТЬ
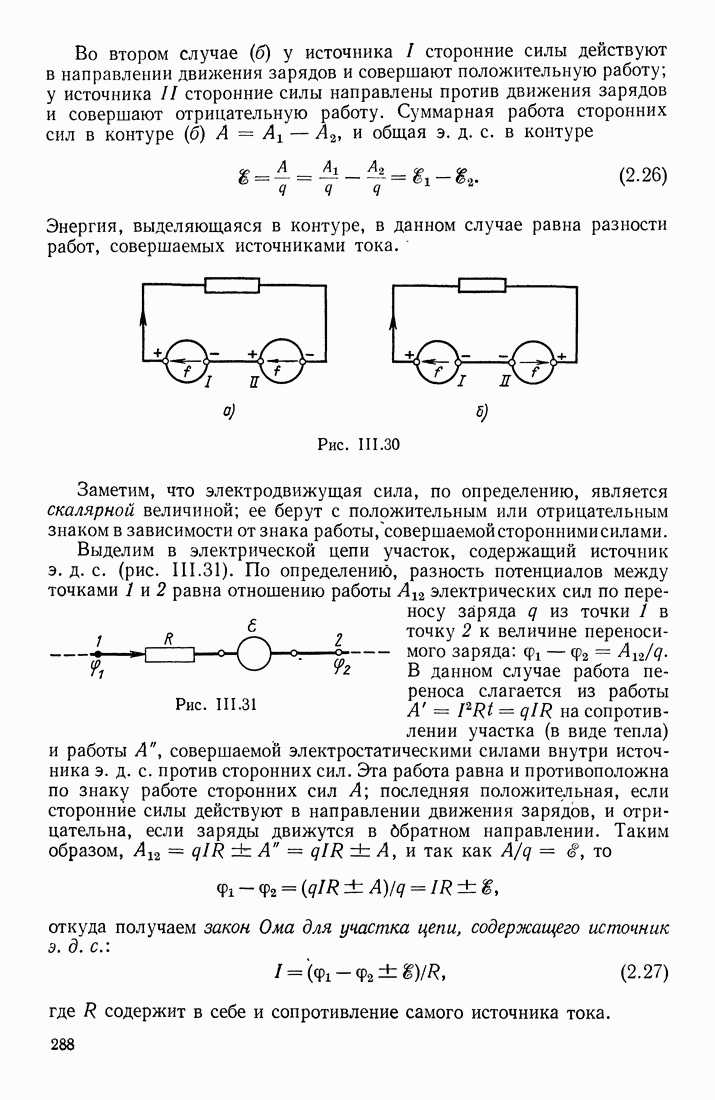
- § 11. ЭЛЕКТРОДВИЖУЩАЯ СИЛА; ЗАКОН ОМА И ПРАВИЛА КИРХГОФА
- ЗАКОН ОМА ДЛЯ ЗАМКНУТОГО КОНТУРА
- ПРАВИЛА КИРХГОФА
- ЭЛЕКТРОСТАТИЧЕСКИЙ ГЕНЕРАТОР ТОКА
- § 12. РАБОТА ВЫХОДА ЭЛЕКТРОНОВ ИЗ МЕТАЛЛА. КОНТАКТНАЯ РАЗНОСТЬ ПОТЕНЦИАЛОВ. ТЕРМОЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ
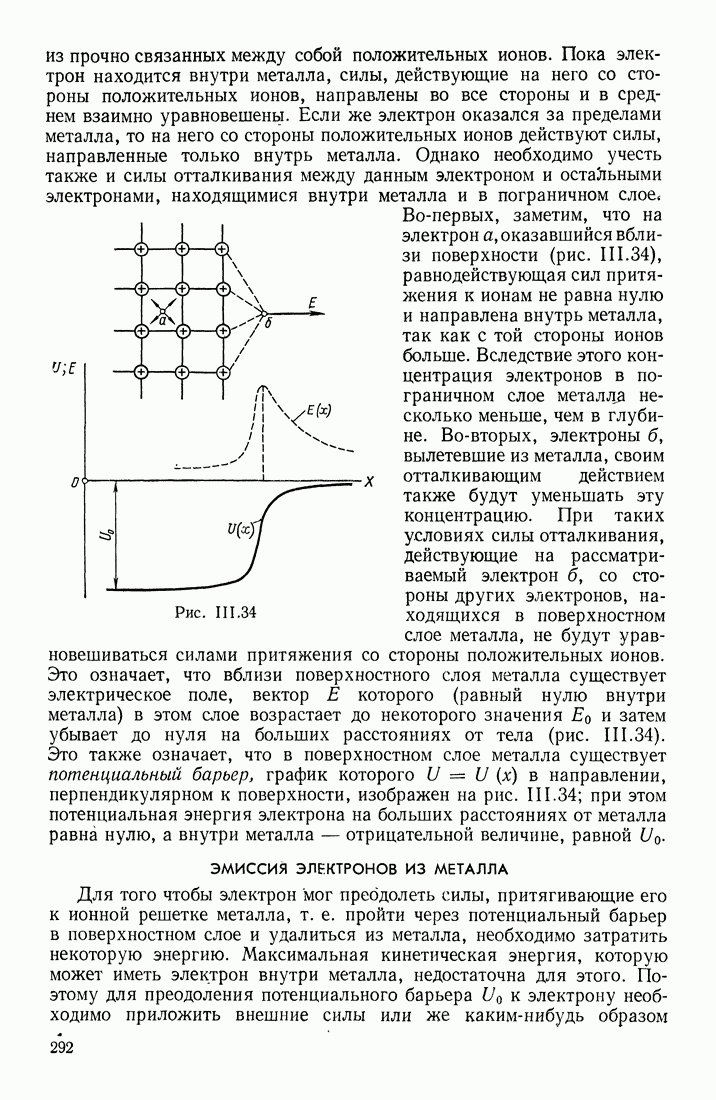
- ЭМИССИЯ ЭЛЕКТРОНОВ ИЗ МЕТАЛЛА
- КОНТАКТНАЯ РАЗНОСТЬ ПОТЕНЦИАЛОВ
- ЗАКОН ВОЛЬТА. ТЕРМОЭЛЕМЕНТЫ
- ЭФФЕКТ ПЕЛЬТЬЕ
- § 13. ТЕРМОЭЛЕКТРОННАЯ ЭМИССИЯ. ЭЛЕКТРИЧЕСКИИ ТОК В ВАКУУМЕ. ЭЛЕКТРОННАЯ ЛАМПА
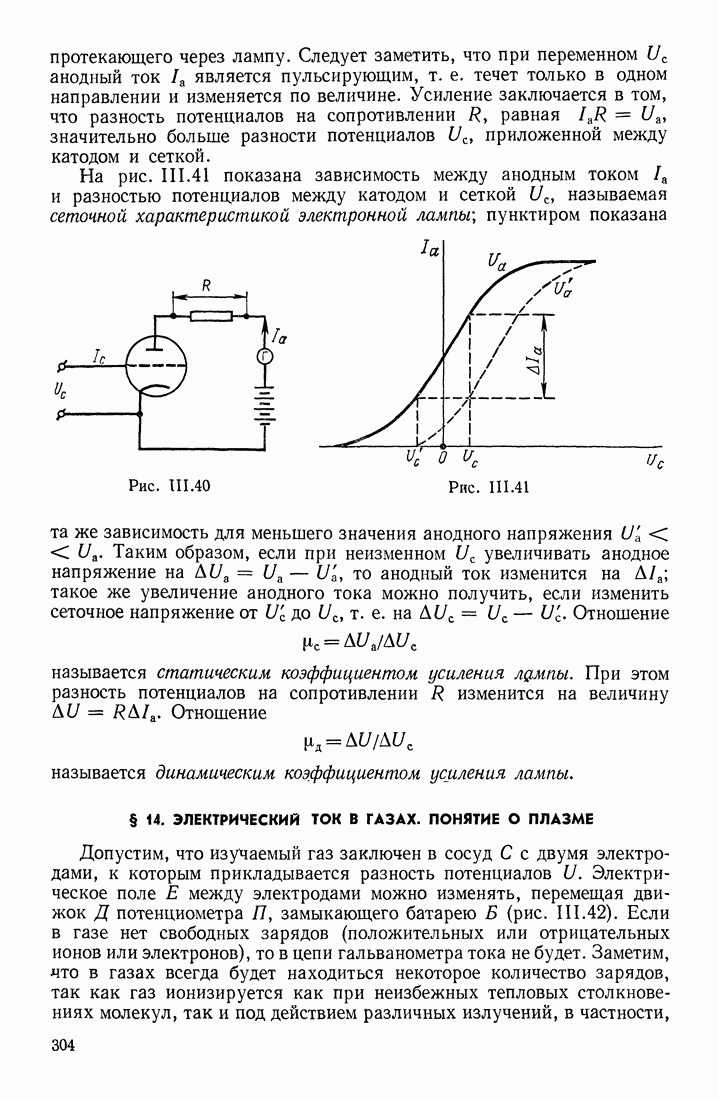
- § 14. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ. ПОНЯТИЕ О ПЛАЗМЕ
- ДВИЖЕНИЕ ИОНОВ В ГАЗЕ
- ВИДЫ РАЗРЯДОВ В ГАЗАХ
- ПЛАЗМА
- § 15. ЭЛЕКТРИЧЕСКИЙ ТОК В ЖИДКОСТЯХ. ЗАКОНЫ ФАРАДЕЯ
- § 16. ПОЛУПРОВОДНИКИ И ИХ ПРИМЕНЕНИЯ
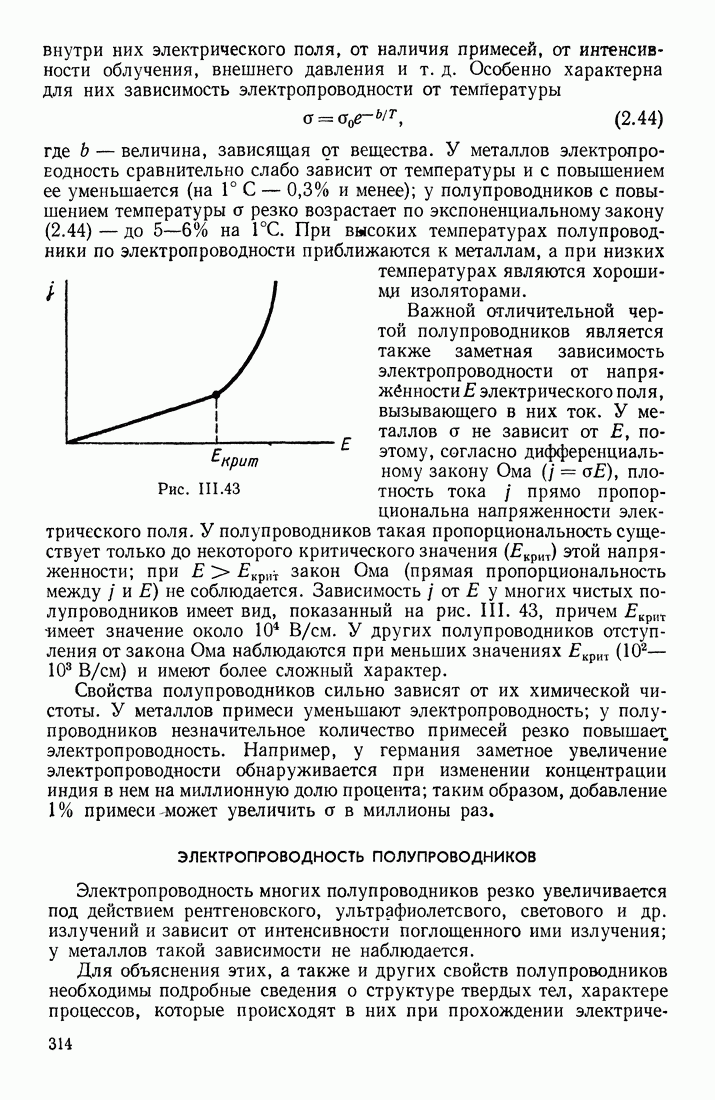
- ЭЛЕКТРОПРОВОДНОСТЬ ПОЛУПРОВОДНИКОВ
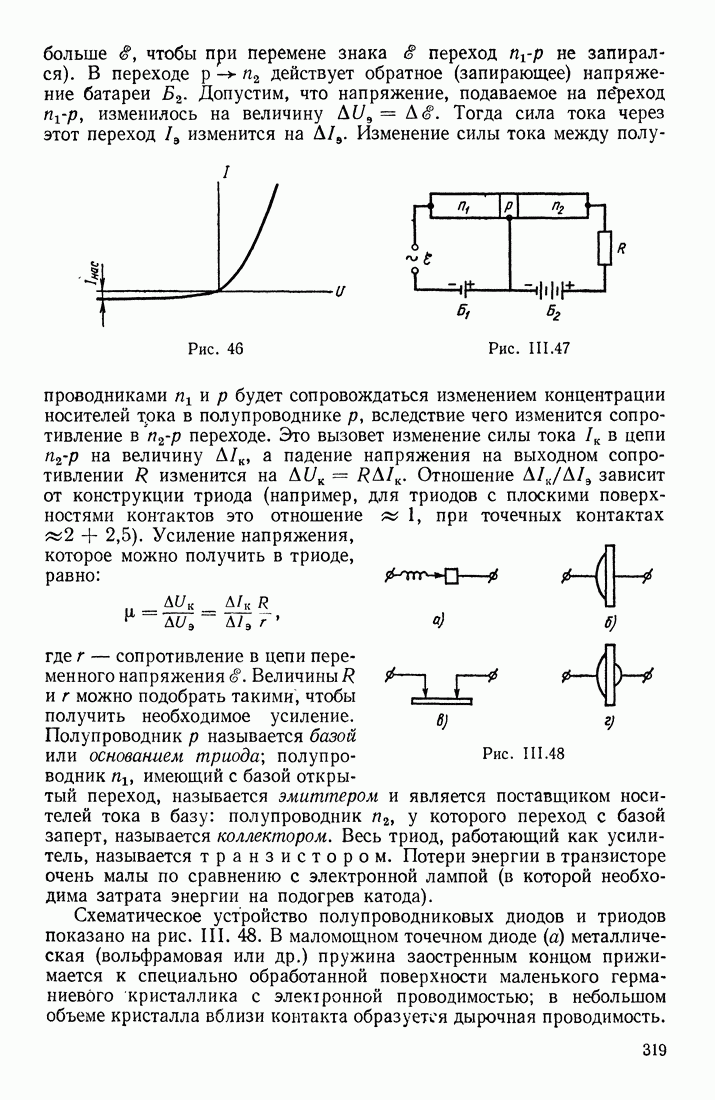
- ЯВЛЕНИЯ НА ГРАНИЦЕ ДВУХ ПОЛУПРОВОДНИКОВ
- ПРИМЕНЕНИЯ ПОЛУПРОВОДНИКОВ
- Глава 3. ЭЛЕКТРОМАГНЕТИЗМ
- § 17. МАГНИТНОЕ ПОЛЕ
- § 18. НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ ВОКРУГ ДВИЖУЩЕГОСЯ ЗАРЯДА И ПРОВОДНИКОВ С ТОКАМИ
- § 19. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ЗАРЯДЫ И ПРОВОДНИКИ С ТОКОМ; СИЛА ЛОРЕНЦА И ЗАКОН АМПЕРА. ИНДУКЦИЯ МАГНИТНОГО ПОЛЯ
- § 20. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА КОНТУР С ТОКОМ. ДВИЖЕНИЕ ЗАРЯДА В МАГНИТНОМ ПОЛЕ
- МАГНИТНЫЙ МОМЕНТ ЭЛЕКТРОНА
- ДВИЖЕНИЕ ЗАРЯДА В МАГНИТНОМ ПОЛЕ
- ЭФФЕКТ ХОЛЛА
- § 21. РАБОТА ПЕРЕМЕЩЕНИЯ ПРОВОДНИКА С ТОКОМ В МАГНИТНОМ ПОЛЕ
- § 22. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ; ЗАКОНЫ ФАРАДЕЯ И ЛЕНЦА. ВРАЩАЮЩИИСЯ ВИТОК В МАГНИТНОМ ПОЛЕ
- РАМКА В МАГНИТНОМ ПОЛЕ
- ЗАКОНЫ ФАРАДЕЯ И ЛЕНЦА
- § 23. ЯВЛЕНИЯ САМОИНДУКЦИИ И ВЗАИМОИНДУКЦИИ. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ. ВИХРЕВЫЕ ТОКИ
- ИНДУКТИВНОСТЬ СОЛЕНОИДА
- РАСЧЕТ ИНДУКЦИОННЫХ ТОКОВ
- ВЗАИМНАЯ ИНДУКЦИЯ
- ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ
- ТОКИ ФУКО
- § 24. ТОК СМЕЩЕНИЯ И ЕГО МАГНИТНОЕ ПОЛЕ; ТЕОРИЯ МАКСВЕЛЛА
- § 25. МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ. ДИАМАГНЕТИЗМ; ПАРАМАГНИТНЫЕ И ФЕРРОМАГНИТНЫЕ ВЕЩЕСТВА
- НАМАГНИЧЕННОСТЬ
- МАГНИТНЫЕ СВОЙСТВА АТОМОВ И МОЛЕКУЛ
- ДИАМАГНЕТИЗМ И ПАРАМАГНЕТИЗМ
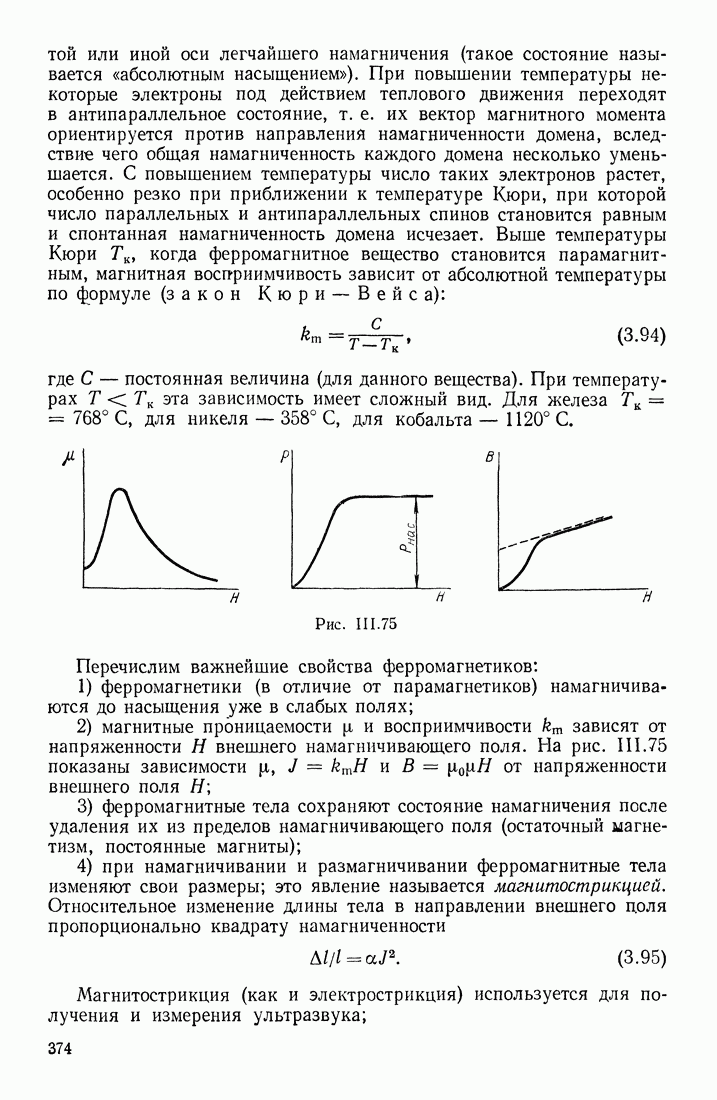
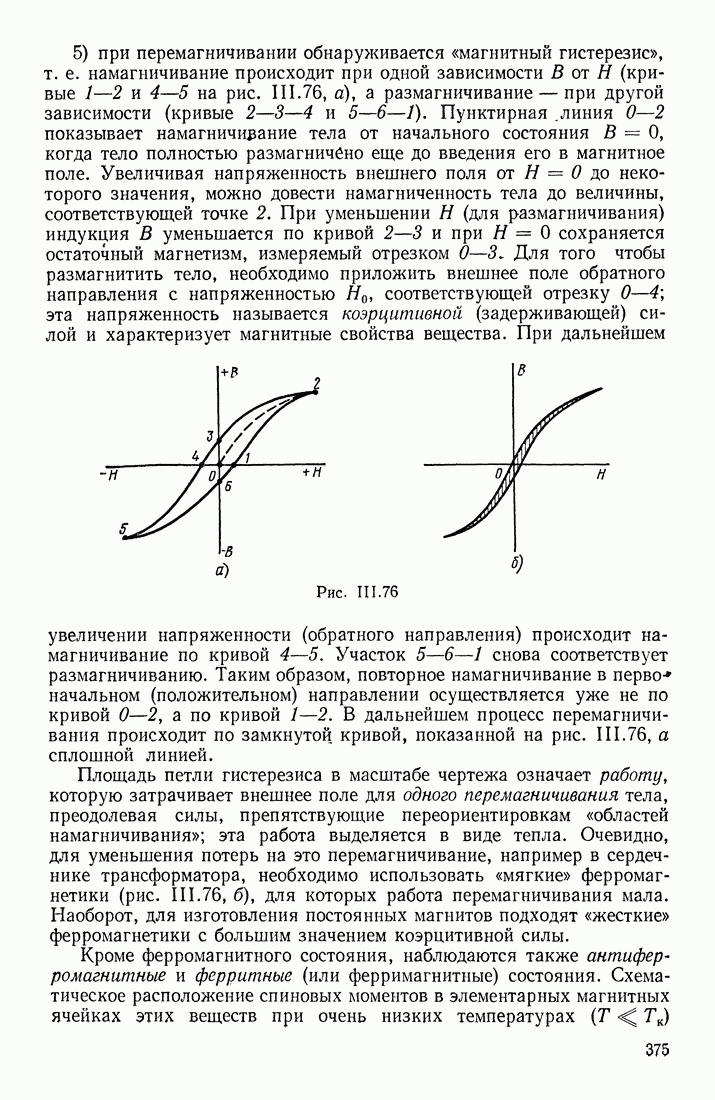
- ФЕРРОМАГНЕТИКИ
- ПАРАМАГНИТНЫЙ РЕЗОНАНС
- § 26. МАГНИТНОЕ ПОЛЕ В ФЕРРОМАГНИТНЫХ ТЕЛАХ РАЗЛИЧНОЙ ФОРМЫ; МАГНИТОДВИЖУЩАЯ СИЛА И МАГНИТНОЕ СОПРОТИВЛЕНИЕ
- Глава 4. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- § 27. КОЛЕБАТЕЛЬНЫЙ КОНТУР. НЕЗАТУХАЮЩИЕ И ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
- § 28. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ; ЭЛЕКТРИЧЕСКИЙ РЕЗОНАНС
- § 29. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- УРАВНЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ
- ЭНЕРГИЯ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ
- ИЗЛУЧЕНИЕ ВОЛНЫ ЭЛЕКТРОНОМ
- ЧЕРЕНКОВСКОЕ ИЗЛУЧЕНИЕ
- Часть IV. ОПТИКА И ФИЗИКА АТОМА
- § 1. ВОЛНОВАЯ (ЭЛЕКТРОМАГНИТНАЯ) И КОРПУСКУЛЯРНАЯ (ФОТОННАЯ) ТЕОРИИ СВЕТА
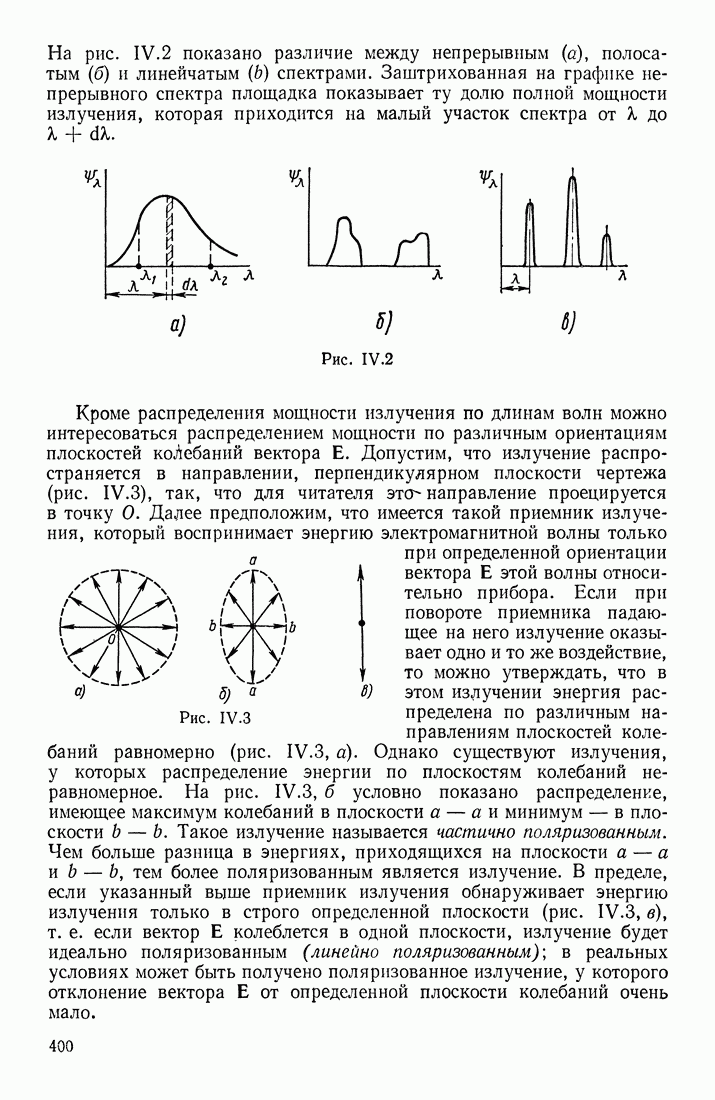
- СПЕКТРАЛЬНЫЙ СОСТАВ ИЗЛУЧЕНИЯ
- ХАРАКТЕРИСТИКИ ИЗЛУЧЕНИЯ
- ИДЕАЛИЗАЦИЯ СВЕТОВОЙ ВОЛНЫ
- § 2. ФОТОМЕТРИЧЕСКИЕ ПОНЯТИЯ И ВЕЛИЧИНЫ. ДАВЛЕНИЕ СВЕТА
- § 3. РАСПРОСТРАНЕНИЕ, ОТРАЖЕНИЕ, ПРЕЛОМЛЕНИЕ И ПОГЛОЩЕНИЕ СВЕТА. ДИСПЕРСИЯ. РАССЕЯНИЕ СВЕТА
- СБЕТ НА ГРАНИЦЕ ДВУХ СРЕД
- СВЕТ И ЦВЕТ
- ДИСПЕРСИЯ СВЕТА
- РАССЕЯНИЕ СВЕТА
- § 4. ИНТЕРФЕРЕНЦИЯ СВЕТА; КОГЕРЕНТНОСТЬ СВЕТОВЫХ ЛУЧЕЙ. ИНТЕРФЕРОМЕТРЫ
- § 5. ДИФРАКЦИЯ СВЕТА; ДИФРАКЦИОННЫЙ СПЕКТР
- ДИФРАКЦИЯ ПЛОСКОЙ ВОЛНЫ ОТ ПРЯМОЛИНЕЙНОЙ ТОНКОЙ ЩЕЛИ
- ДИФРАКЦИЯ ПЛОСКОЙ ВОЛНЫ ОТ НЕСКОЛЬКИХ ЩЕЛЕЙ
- ДИФРАКЦИОННАЯ РЕШЕТКА
- § 6. РАСПРОСТРАНЕНИЕ СВЕТА В АНИЗОТРОПНОЙ СРЕДЕ, ПОЛУЧЕНИЕ И ПРИМЕНЕНИЕ ПОЛЯРИЗОВАННОГО СВЕТА
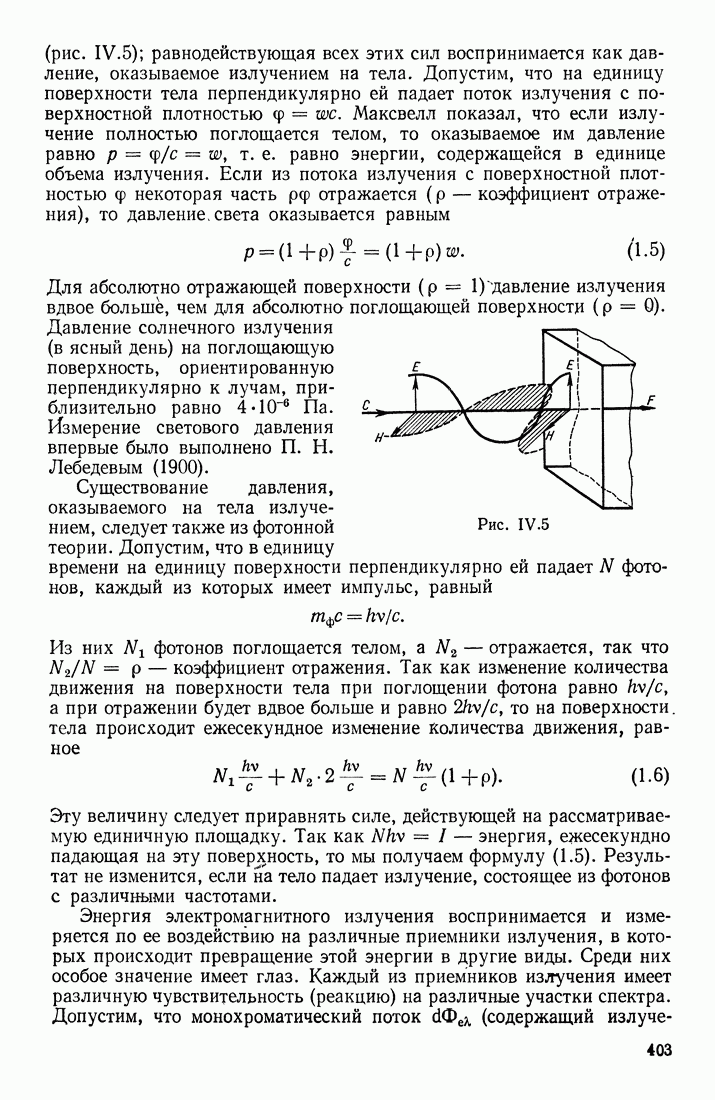
- ПОЛЯРИЗОВАННЫЙ СВЕТ
- СПОСОБЫ ПОЛУЧЕНИЯ ПОЛЯРИЗОВАННОГО СВЕТА
- ИНТЕРФЕРЕНЦИЯ ПОЛЯРИЗОВАННОГО СВЕТА
- ОПТИЧЕСКАЯ АНИЗОТРОПИЯ
- § 7. ЛИНЗЫ; ИХ ОПТИЧЕСКАЯ СИЛА. АБЕРРАЦИИ. ДИАФРАГМЫ В ОПТИЧЕСКИХ ПРИБОРАХ
- ТОЛСТЫЕ ЛИНЗЫ. АБЕРРАЦИИ
- § 8. ПОНЯТИЕ О ГОЛОГРАФИИ
- Глава 2. ФИЗИКА АТОМОВ И МОЛЕКУЛ. ОСНОВЫ КВАНТОВОЙ ТЕОРИИ
- § 9. СТРОЕНИЕ АТОМА. ОПЫТЫ РЕЗЕРФОРДА, ФРАНКА И ГЕРЦА. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ АТОМА ВОДОРОДА
- ОПЫТ ФРАНКА И ГЕРЦА
- СПЕКТРЫ ИЗЛУЧЕНИЯ АТОМОВ
- ТЕОРИЯ АТОМА ВОДОРОДА
- § 10. КОРПУСКУЛЯРНО-ВОЛНОВЫЕ СВОЙСТВА ЧАСТИЦ. ФОТОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ. ФОРМУЛА ДЕ БРОЙЛЯ. ДИФРАКЦИЯ ЭЛЕКТРОНОВ
- ЭФФЕКТ КОМПТОНА
- ФОТОН И ЭЛЕКТРОМАГНИТНАЯ ВОЛНА
- ФОРМУЛА ДЕ БРОЙЛЯ
- ДИФРАКЦИЯ ЭЛЕКТРОНОВ
- § 11. ОСНОВНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ ТЕОРИИ. УРАВНЕНИЕ ШРЕДИНГЕРА. СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ ГЕЙЗЕНБЕРГА
- УРАВНЕНИЕ ШРЕДИНГЕРА
- РЕШЕНИЯ УРАВНЕНИЯ ШРЕДИНГЕРА
- СВОБОДНЫЙ ЭЛЕКТРОН
- ПОТЕНЦИАЛЬНЫЙ БАРЬЕР
- ЧАСТИЦА В ПОТЕНЦИАЛЬНОЙ ЯМЕ
- АТОМ ВОДОРОДА. КВАНТОВЫЕ ЧИСЛА
- СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ
- § 12. ЧАСТИЦЫ И ФИЗИЧЕСКИЕ СИСТЕМЫ. СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ ЧАСТИЦ ПО СОСТОЯНИЯМ. ПОНЯТИЕ ТЕМПЕРАТУРЫ
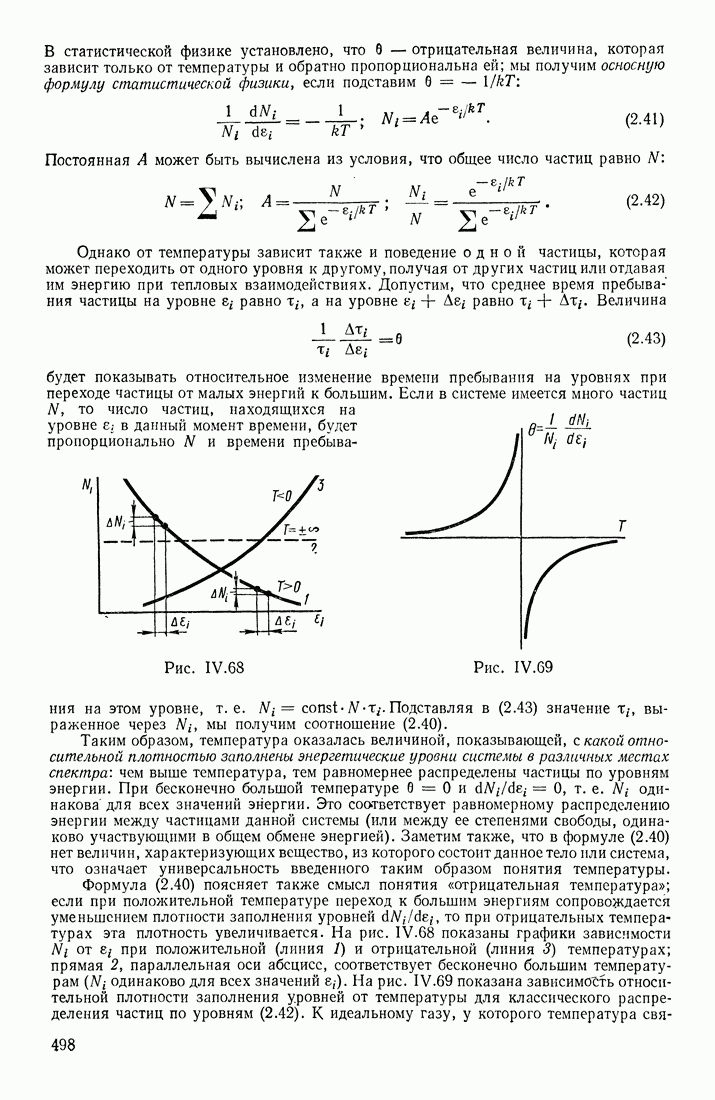
- РОЛЬ ТЕПЛОВОГО ДВИЖЕНИЯ ЧАСТИЦ
- ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ПО СОСТОЯНИЯМ
- ТЕМПЕРАТУРА
- ЭНЕРГЕТИЧЕСКИЙ СПЕКТР СИСТЕМЫ
- РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ПО СКОРОСТЯМ
- § 13. ВЗАИМОДЕЙСТВИЕ АТОМОВ И МОЛЕКУЛ. ЭНЕРГИЯ СВЯЗИ АТОМОВ
- ВЗАИМОДЕЙСТВИЕ МОЛЕКУЛ
- ИОННАЯ СВЯЗЬ
- РОЛЬ ЭЛЕКТРОННОГО ГАЗА В МЕТАЛЛАХ
- Глава 3. ИЗЛУЧЕНИЕ И ПОГЛОЩЕНИЕ ЭНЕРГИИ АТОМАМИ И МОЛЕКУЛАМИ
- § 14. АТОМНЫЕ И МОЛЕКУЛЯРНЫЕ СПЕКТРЫ ИЗЛУЧЕНИЯ; СПОСОБЫ ВОЗБУЖДЕНИЯ
- СТРУКТУРА ЭЛЕКТРОННОЙ ОБОЛОЧКИ
- СПЕКТРЫ ИЗЛУЧЕНИЯ АТОМОВ
- СПЕКТРЫ ИЗЛУЧЕНИЯ МОЛЕКУЛ
- КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА
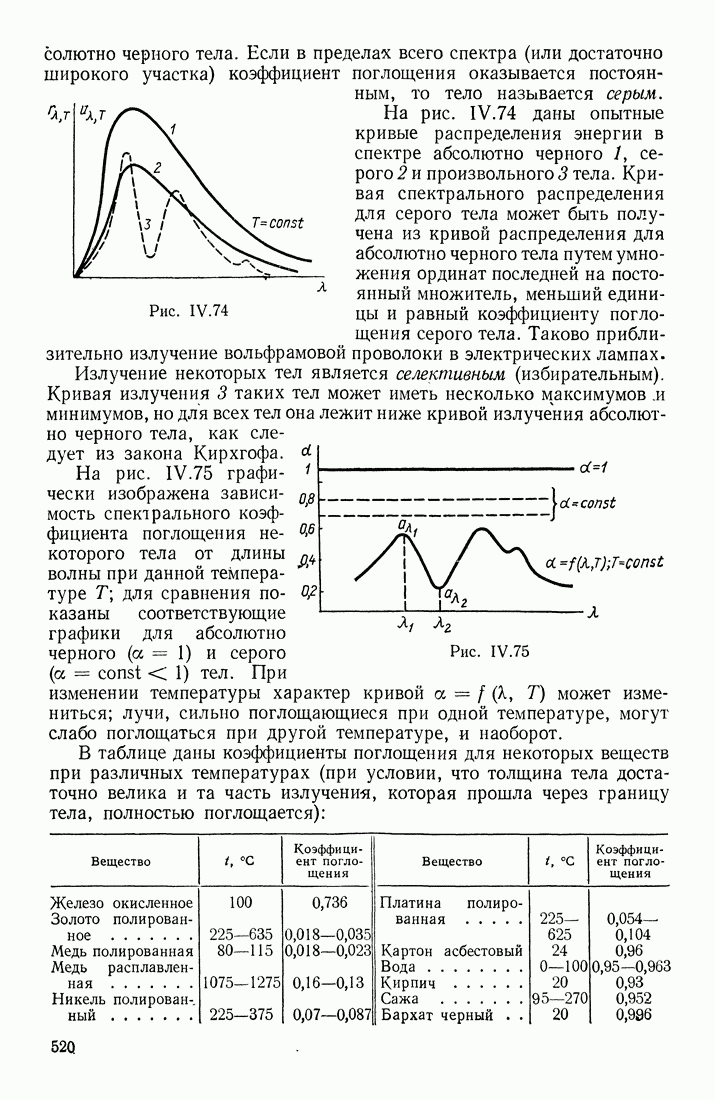
- § 15. ТЕПЛОВОЕ ИЗЛУЧЕНИЕ
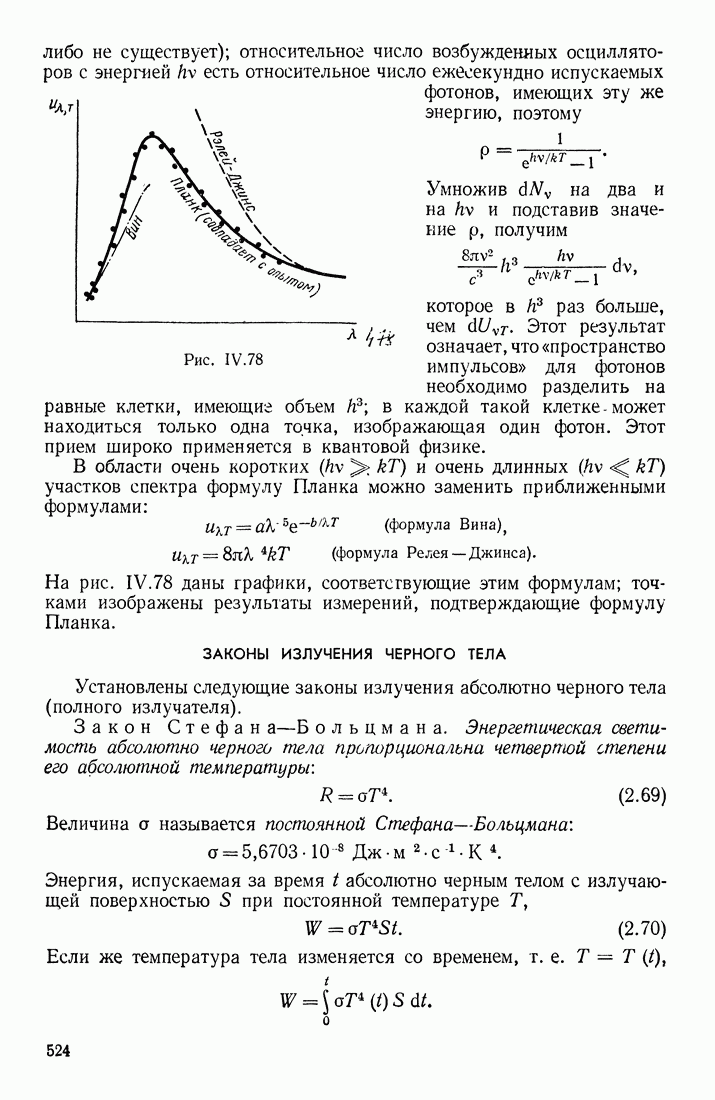
- ФОРМУЛА ПЛАНКА
- ЗАКОНЫ ИЗЛУЧЕНИЯ ЧЕРНОГО ТЕЛА
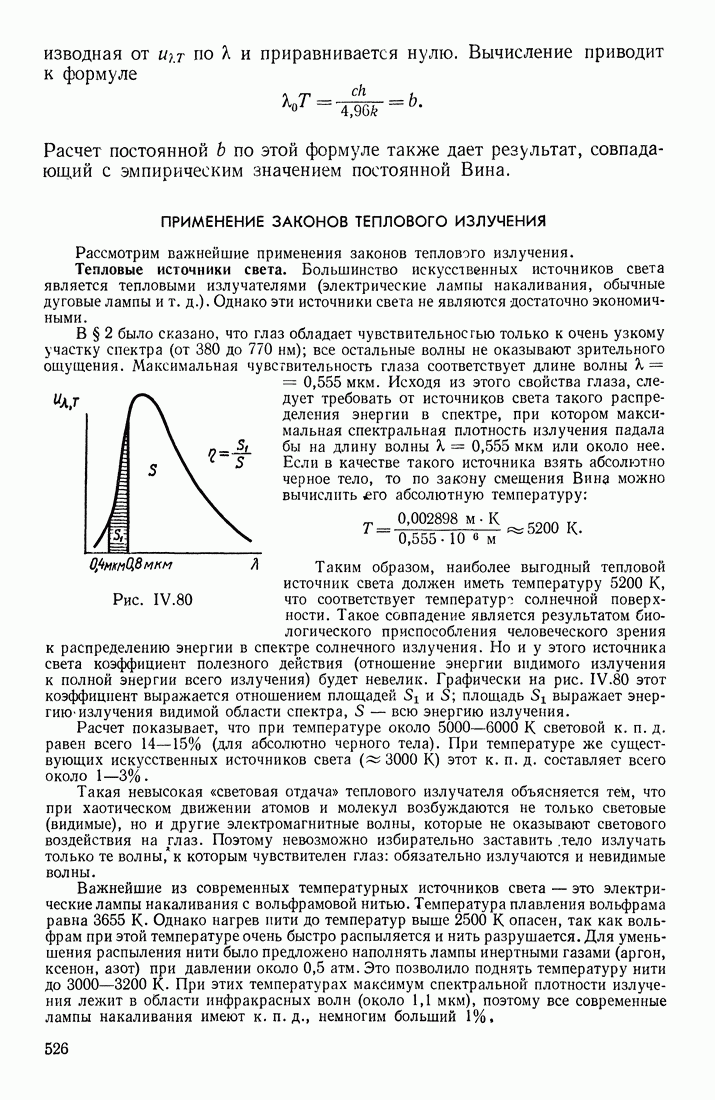
- ПРИМЕНЕНИЕ ЗАКОНОВ ТЕПЛОВОГО ИЗЛУЧЕНИЯ
- § 16. РЕНТГЕНОВСКИЕ ЛУЧИ. ХАРАКТЕРИСТИЧЕСКИЙ РЕНТГЕНОВСКИЙ СПЕКТР ЭЛЕМЕНТОВ
- ХАРАКТЕРИСТИЧЕСКИЙ РЕНТГЕНОВСКИЙ СПЕКТР
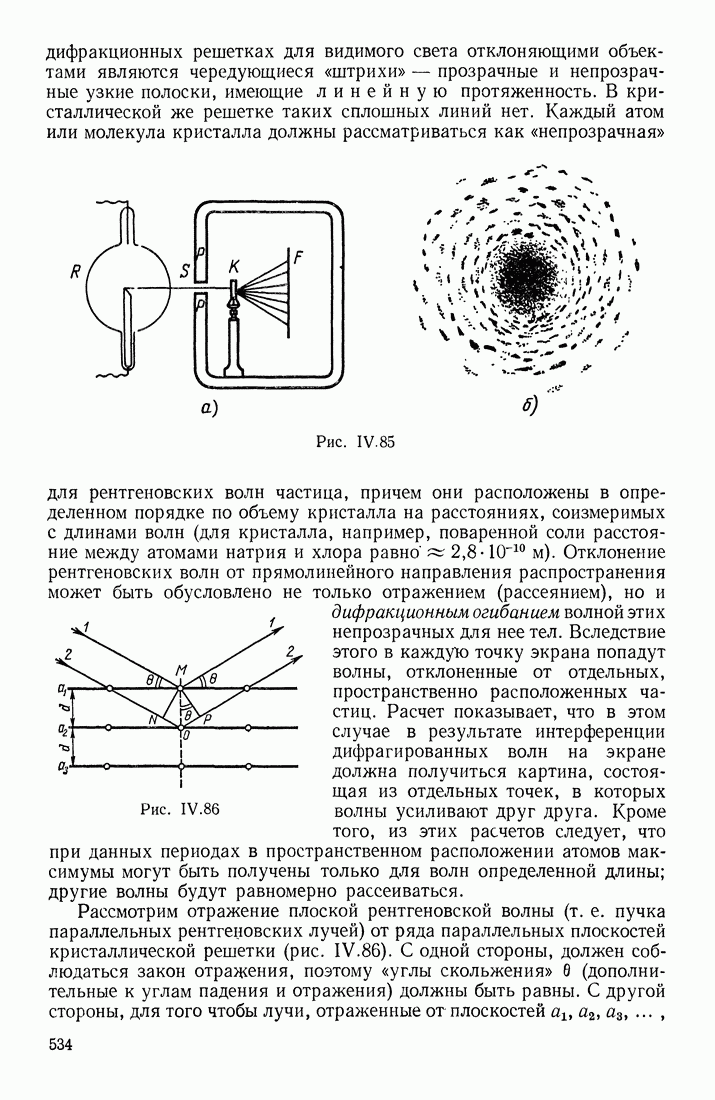
- ДИФРАКЦИЯ И ИНТЕРФЕРЕНЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ
- ДОЗИМЕТРИЯ
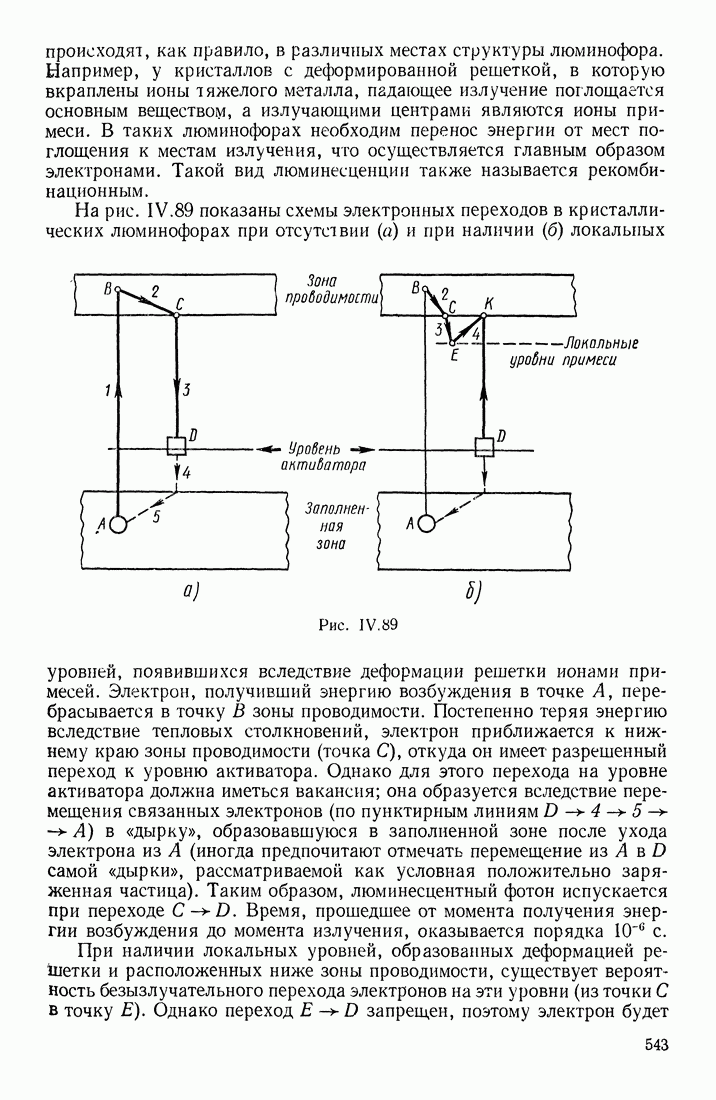
- § 17. ЛЮМИНЕСЦЕНТНОЕ ИЗЛУЧЕНИЕ
- ПРИРОДА ЛЮМИНЕСЦЕНЦИИ
- ХАРАКТЕРИСТИКИ ЛЮМИНЕСЦИРУЮЩИХ ВЕЩЕСТВ
- ГАШЕНИЕ ЛЮМИНЕСЦЕНЦИИ
- ПРИМЕНЕНИЯ ЛЮМИНЕСЦЕНЦИИ
- § 18. ИНДУЦИРОВАННОЕ ИЗЛУЧЕНИЕ. ЛАЗЕРЫ
- ЛАЗЕРЫ
- ПРЕИМУЩЕСТВА ЛАЗЕРОВ
- ПРИМЕНЕНИЕ ЛАЗЕРОВ
- Глава 4. АТОМНЫЕ ЯДРА И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- § 19. ОСНОВНЫЕ СВОЙСТВА АТОМНЫХ ЯДЕР
- РАДИОАКТИВНОСТЬ
- ВНУТРИЯДЕРНЫЕ СИЛЫ
- ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЯДЕР
- МЕХАНИЧЕСКИЙ МОМЕНТ ЯДРА
- МАГНИТНЫЕ МОМЕНТЫ ЯДЕР
- ЭЛЕКТРИЧЕСКИЕ МОМЕНТЫ ЯДЕР
- СПЕКТР ВОЗБУЖДЕННЫХ СОСТОЯНИЙ
- § 20. МОДЕЛЬНЫЕ ПРЕДСТАВЛЕНИЯ О СТРУКТУРЕ ЯДЕР
- КАПЕЛЬНАЯ МОДЕЛЬ ЯДРА
- ОБОЛОЧЕЧНАЯ МОДЕЛЬ
- ОБОБЩЕННАЯ МОДЕЛЬ
- ОПТИЧЕСКАЯ МОДЕЛЬ
- УСЛОВИЕ СТАБИЛЬНОСТИ
- § 21. РАДИОАКТИВНЫЕ ЯДРА И ИХ ИЗЛУЧЕНИЯ
- СЕМЕЙСТВА РАДИОАКТИВНЫХ ЭЛЕМЕНТОВ
- ВЗАИМОДЕЙСТВИЯ ЯДЕРНЫХ ИЗЛУЧЕНИЙ С ВЕЩЕСТВОМ
- БЕТА-РАСПАД ЯДЕР
- ЭНЕРГИЯ СВЯЗИ ЯДЕР
- ИЗОМЕРЫ
- § 22. ЯДЕРНЫЕ РЕАКЦИИ ДЕЛЕНИЯ И СИНТЕЗА. ТЕРМОЯДЕРНЫЕ РЕАКЦИИ
- БОМБАРДИРОВКА ЯДЕР ЧАСТИЦАМИ
- ЭФФЕКТИВНЫЕ СЕЧЕНИЯ РЕАКЦИЙ
- ЯДЕРНЫЕ РЕАКТОРЫ
- ЯДЕРНЫЙ СИНТЕЗ
- § 23. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- РАСПАДЫ ЧАСТИЦ
- ВИДЫ ВЗАИМОДЕЙСТВИЯ
- ЗАКЛЮЧЕНИЕ
- § 1. ФИЗИЧЕСКИЕ ИЗМЕРЕНИЯ. СВЯЗЬ МЕЖДУ СПОСОБАМИ ИЗМЕРЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН И ФОРМУЛИРОВКАМИ ЗАКОНОВ ФИЗИКИ
- § 2. О ТЕОРИИ ОТНОСИТЕЛЬНОСТИ ЭЙНШТЕЙНА
- § 3. ЗАКОНЫ СОХРАНЕНИЯ, ПРЕВРАЩЕНИЯ И ПЕРЕРАСПРЕДЕЛЕНИЯ ЭНЕРГИИ В ФИЗИЧЕСКИХ СИСТЕМАХ
- § 4. О ВАРИАЦИОННЫХ ПРИНЦИПАХ ФИЗИКИ
- § 5. СТАТИСТИЧЕСКИЕ ЗАКОНЫ И ФЛУКТУАЦИИ
- § 6. О ДУАЛИЗМЕ В ФИЗИКЕ