| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 31. Непосредственное доказательство известных формул изгиба призм, вызванного только их продольными удлинениями
Весьма желательно (§ 3) получить подобное доказательство этих формул (1), которые могут быть записаны в следующем виде:

когда мы прибавляем к переменному удлинению у общее удлинение  Отсюда для случая, когда линия
Отсюда для случая, когда линия  проходит через центр тяжести, выводим выражения (2) для полного растягивающего усилия
проходит через центр тяжести, выводим выражения (2) для полного растягивающего усилия  и для изгибающего момента М:
и для изгибающего момента М:

(§ 3). Это дает возможность ввести их в учебные курсы, которые не содержат предварительного обоснования дифференциальных и интегральных формул теории упругости, и отказаться от необоснованных и часто ошибочных гипотез.
Чтобы достичь этого, мы представим умозрительно, в каких условиях растянутые волокна призмы не оказывают друг на друга в боковом направлении никакого действия перпендикулярно к их длине или к ребрам призмы, что обязательно приведет к рассмотрению поперечных сжатий, сопровождающих в таком случае их продольные удлинения. Затем покажем, что очень малые основания этих волокон, сохраняя свою смежность, могут всегда быть одновременно изменены так, чтобы было выполнено условие равенства нулю нормального воздействия, когда продольные удлинения изменяются линейно или равномерно при переходе от одного волокна к другому в двух поперечных направлениях. Далее мы найдем, что если только оба крайних основания призмы испытывают продольные растяжения,
изменяющиеся в соответствии с этим линейным законом, при наличии или при отсутствии поперечных касательных сил, распределенных некоторым образом, то такое же воздействие непременно испытывают все другие сечения призмы, боковые грани которой не испытывают никакого внешнего воздействия. Следовательно, мы получаем (даже когда имеются постоянные боковые давления, подобные давлению жидкости) именно известные формулы изгиба, поддающиеся с приближением распространению на случай, когда силы, действующие на концах призмы, приложены и распределены несколько иначе. Эти формулы должны к тому же всегда дополняться менее простыми формулами, дающими сдвиг в тех случаях, когда влиянием его нельзя пренебрегать.
Итак, предположим, что упругое однородное тело мысленно разделено на элементы в виде совершенно одинаковых прямоугольных параллелепипедов, заменяя в случае необходимости обычно искривленные поверхности рядом малых плоскостей. Стороны этих элементов после воздействия внешних сил немного удлиняются или укорачиваются и даже обычно наклоняются по отношению друг к другу, образуя слегка косоугольные параллелепипеды.
Приближение или удаление всяких внутренних молекул по отношению к молекулам близлежащих элементов производит новые молекулярные действия, равнодействующие которых через различные грани контакта этих элементов представляют собой взаимные давления или растягивающие усилия. Величина и направление этих давлений или растягивающих усилий зависят от относительной величины малых удлинений или сжатий сторон, так же как от малых наклонов их друг к другу.
Если, например, стороны остаются прямоугольными и одна из них  (рис. 9) становится
(рис. 9) становится  или удлиняется так, что стороны
или удлиняется так, что стороны  не изменяются, когда молекулы
не изменяются, когда молекулы  смежных элементов, которые участвовали в этом движении, примут новое положение
смежных элементов, которые участвовали в этом движении, примут новое положение  то все молекулы
то все молекулы  внутренней части будут удаляться, но в большей мере от молекул
внутренней части будут удаляться, но в большей мере от молекул  расположенных за гранями
расположенных за гранями  перпендикулярными к увеличенному измерению
перпендикулярными к увеличенному измерению  чем от молекул
чем от молекул  расположенных за гранями, параллельными
расположенных за гранями, параллельными  Если измерение
Если измерение  сжимается, а не растягивается,
сжимается, а не растягивается,
то все расстояния между внутренними молекулами рассматриваемого элемента и молекулами вне его, наоборот, уменьшаются, но всегда в большей степени по граням  чем по четырем другим граням.
чем по четырем другим граням.
Всякое удлинение элемента в направлении одного из его трех измерений вызывает, таким образом, силы притяжения и производит растяжения или напряжения по его шести граням, а всякое сжатие вызывает на тех же гранях силы отталкивания или, собственно говоря, давления.

Рис. 9
Но растяжения или сжатия, вызванные этими причинами и отнесенные к единице площади граней, более значительны на гранях, перпендикулярных к растянутым или сжатым измерениям элемента, чем на гранях, параллельных им. Изменяя растяжения или сжатия, мы можем дать им желаемую величину в пределах сцепления материала.
Кроме того, структура материала (зернистая, волокнистая, пластинчатая и т. д.) в соответствии с особенностями его молекулярного строения, хотя и предполагаемая одинаковой во всех точках однородного тела, может быть весьма неравномерной в различных направлениях, и растяжения или сжатия могут иметь более или менее косые направления на гранях, где они действуют, даже в том случае, когда элементы останутся прямоугольными; тем более эти направления становятся косыми, как мы только что заметили, если элементы превращаются в слегка косоугольные. Таким образом, эти составляющие воздействий могут даже иногда быть чисто касательными или сводиться к некоторым видам трения или сходного с ним прилипания на тех же гранях.
Это строение материала может быть между прочим таким, что всякое очень малое изменение малых призм 
меняющее или не меняющее угол  между боковыми гранями, но не изменяющее перпендикулярности ребер
между боковыми гранями, но не изменяющее перпендикулярности ребер  к обоим основаниям
к обоим основаниям  действительно производит на эти основания только воздействия, продольные или параллельные
действительно производит на эти основания только воздействия, продольные или параллельные  а на четыре боковые грани только воздействия поперечные, т. е. перпендикулярные к тем же ребрам. И всякий очень малый наклон ребер к основаниям вызывает только касательные действия, продольные на боковых гранях и поперечные на основаниях. Как нетрудно видеть, для этого достаточно, чтобы молекулы размещались с некоторой симметрией по отношению ко всем сечениям, поперечным или параллельным граням
а на четыре боковые грани только воздействия поперечные, т. е. перпендикулярные к тем же ребрам. И всякий очень малый наклон ребер к основаниям вызывает только касательные действия, продольные на боковых гранях и поперечные на основаниях. Как нетрудно видеть, для этого достаточно, чтобы молекулы размещались с некоторой симметрией по отношению ко всем сечениям, поперечным или параллельным граням  взятым за основания. Мы всегда будем предполагать этот вид молекулярного строения.
взятым за основания. Мы всегда будем предполагать этот вид молекулярного строения.

Рис. 10.
Если одновременно имеется растяжение элементов в одном или в двух направлениях и сжатие в другом или в двух других, то из теоремы сложения результатов действия сил и малых перемещений (теорема, доказательство которой мы здесь не приводим, дана в § 6) следует, что давления на различных гранях будут равнодействующими того, что было бы вызвано этими двумя последовательно произведенными видоизменениями. Из той же теоремы также следует, что два, три и т. д. малых равных изменения вызовут двойные, тройные и т. д. силы, т. е. что силы пропорциональны малым изменениям как линейных размеров, так и углов.
Итак, эти изменения могут находиться между собой в таких соотношениях, чтобы в направлении сквозь какие-либо грани, например боковые, имелось бы взаимное уничтожение сил или компенсация сил притяжения и отталкивания, так что эти четыре грани  элемента не испытывают ни давления, ни растягивающих усилий со стороны смежных элементов, тогда как другие грани, т. е. основания
элемента не испытывают ни давления, ни растягивающих усилий со стороны смежных элементов, тогда как другие грани, т. е. основания  подвергаются каким угодно воздействиям. Пусть все углы элемента остаются прямыми, и мы получили на единицу длины удлинение 9 в продольном направлении
подвергаются каким угодно воздействиям. Пусть все углы элемента остаются прямыми, и мы получили на единицу длины удлинение 9 в продольном направлении  (рис. 10), удлинения —9 (или сжатия 9) в поперечных
(рис. 10), удлинения —9 (или сжатия 9) в поперечных
направлениях  и что в соответствии со строением материала всякое удлинение в одном направлении вызывает соответственно на единице площади перпендикулярных граней и на единице площади параллельных граней растягивающие усилия, равные этому удлинению, умноженному на два числа
и что в соответствии со строением материала всякое удлинение в одном направлении вызывает соответственно на единице площади перпендикулярных граней и на единице площади параллельных граней растягивающие усилия, равные этому удлинению, умноженному на два числа  для первых и только на
для первых и только на  для вторых граней.
для вторых граней.
Получим: 1) на гранях  перпендикулярных к
перпендикулярных к  растягивающие усилия
растягивающие усилия  на других гранях
на других гранях  растягивающие усилия
растягивающие усилия 
Если  то последние будут равны нулю, а первые, т. е. растягивающие усилия на основаниях, будут тогда иметь значение
то последние будут равны нулю, а первые, т. е. растягивающие усилия на основаниях, будут тогда иметь значение 
Таким образом, если  то боковые волокна не будут испытывать никакого действия, когда поперечные сжатия
то боковые волокна не будут испытывать никакого действия, когда поперечные сжатия
9 составят  часть продольного удлинения 9. И растягивающие усилия на основаниях будут в таком случае равны продольному удлинению 9, умноженному на число
часть продольного удлинения 9. И растягивающие усилия на основаниях будут в таком случае равны продольному удлинению 9, умноженному на число  Это то число, каким бы оно ни было в различных случаях, на которое нужно умножить относительное продольное растяжение призматического элемента, чтобы получить способную вызвать это растяжение силу, отнесенную к единице поверхности основания элемента, когда боковые грани не испытывают никакого воздействия перпендикулярно к ребрам; это число обычно называется коэффициентом упругости при растяжении материала в направлении ребер малой призмы.
Это то число, каким бы оно ни было в различных случаях, на которое нужно умножить относительное продольное растяжение призматического элемента, чтобы получить способную вызвать это растяжение силу, отнесенную к единице поверхности основания элемента, когда боковые грани не испытывают никакого воздействия перпендикулярно к ребрам; это число обычно называется коэффициентом упругости при растяжении материала в направлении ребер малой призмы.
Установив это, получаем призму, из продольных призматических волокон с каким-либо основанием, разделенным двумя системами прямоугольных плоскостей, параллельных ее ребрам. Допустим, что эти волокна сами разделены на элементарные прямоугольные параллелепипеды плоскостями, перпендикулярными к тем же ребрам. По отношению к этим плоскостям молекулярное строение считается симметричным, что мы определили, анализируя воздействия, и что очень часто имеет место.
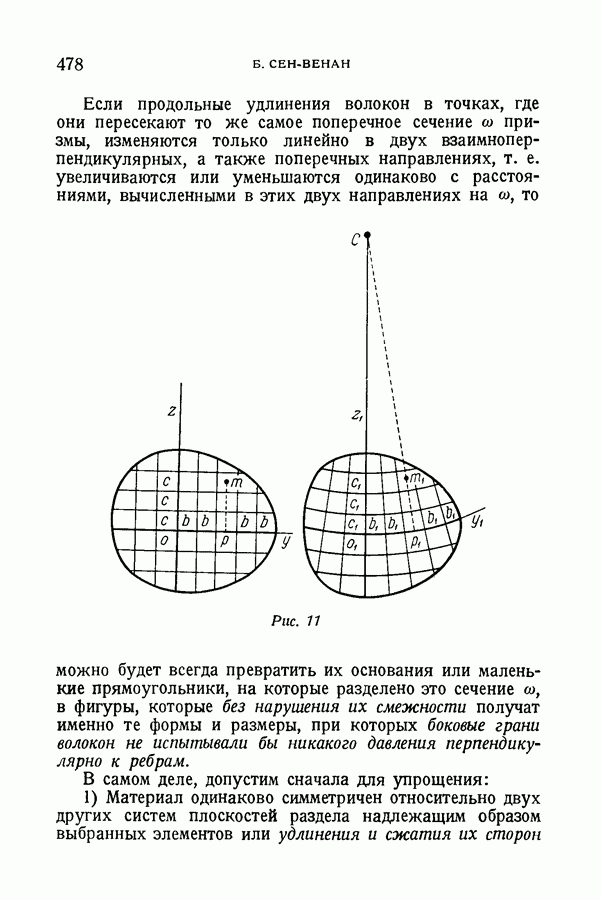
Если продольные удлинения волокон в точках, где они пересекают то же самое поперечное сечение со призмы, изменяются только линейно в двух взаимноперпендикулярных, а также поперечных направлениях, т. е. увеличиваются или уменьшаются одинаково с расстояниями, вычисленными в этих двух направлениях на  то можно будет всегда превратить их основания или маленькие прямоугольники, на которые разделено это сечение
то можно будет всегда превратить их основания или маленькие прямоугольники, на которые разделено это сечение  в фигуры, которые без нарушения их смежности получат именно те формы и размеры, при которых боковые грани волокон не испытывали бы никакого давления перпендикулярно к ребрам.
в фигуры, которые без нарушения их смежности получат именно те формы и размеры, при которых боковые грани волокон не испытывали бы никакого давления перпендикулярно к ребрам.

Рис. 77
В самом деле, допустим сначала для упрощения: 1) Материал одинаково симметричен относительно двух других систем плоскостей раздела надлежащим образом выбранных элементов или удлинения и сжатия их сторон
вызывают, как мы заметили, только давления, перпендикулярные к их граням.
2) Продольное удлинение изменяется только в одном из двух направлений  линий, делящих сечение
линий, делящих сечение  и для какого-либо волокна, основание которого имеет центр в точке
и для какого-либо волокна, основание которого имеет центр в точке  оно может быть представлено посредством отношения где
оно может быть представлено посредством отношения где  постоянная, обязательно весьма большая по сравнению с z, в которую превращается координата
постоянная, обязательно весьма большая по сравнению с z, в которую превращается координата  т. е. положительное или отрицательное расстояние от
т. е. положительное или отрицательное расстояние от  до линии
до линии  делящей сечение в другом направлении. Представим в виде
делящей сечение в другом направлении. Представим в виде  постоянные отношения (в только что приведенном примере то и другое равны
постоянные отношения (в только что приведенном примере то и другое равны  которые следует иметь между поперечными сжатиями в направлениях осей
которые следует иметь между поперечными сжатиями в направлениях осей  и продольным удлинением волокна, чтобы боковые грани не испытывали ни нормальных растягивающих усилий, ни нормального давления. Затем опишем на плоскости дугу окружности огуг радиуса
и продольным удлинением волокна, чтобы боковые грани не испытывали ни нормальных растягивающих усилий, ни нормального давления. Затем опишем на плоскости дугу окружности огуг радиуса  (рис. 11) и концентрические дуги
(рис. 11) и концентрические дуги  малые расстояния между которыми
малые расстояния между которыми  равны первоначальным сторонам
равны первоначальным сторонам  элементов, уменьшенным в отношении
элементов, уменьшенным в отношении  вследствие продольных удлинений элементов, т. е. умноженным на
вследствие продольных удлинений элементов, т. е. умноженным на  Если мы проведем из центра С радиусы к точкам, делящим дугу
Если мы проведем из центра С радиусы к точкам, делящим дугу  на части
на части  равные сторонам
равные сторонам  оснований тех же элементов в другом направлении, то разобьем плоскость на четырехсторонники, которые можно рассматривать как прямолинейные ввиду их малости; какой-либо один из них с центром
оснований тех же элементов в другом направлении, то разобьем плоскость на четырехсторонники, которые можно рассматривать как прямолинейные ввиду их малости; какой-либо один из них с центром  на расстоянии тхрг от дуги охух получит в направлении дуг ширину, которая будет первоначальной шириной
на расстоянии тхрг от дуги охух получит в направлении дуг ширину, которая будет первоначальной шириной  соответствующего элемента, поскольку — — тгрх равно — или поскольку равно 1.
соответствующего элемента, поскольку — — тгрх равно — или поскольку равно 1.
Отсюда следует, что при  малые четырехсторонники, соответствующие тому же числу прямоугольников, которые служили основаниями в элементах или волокнах, действительно имеют вследствие перемещений такие размеры, при которых боковые грани не испытывают нормальных давлений. Эти четырехсторонники должны иметь
малые четырехсторонники, соответствующие тому же числу прямоугольников, которые служили основаниями в элементах или волокнах, действительно имеют вследствие перемещений такие размеры, при которых боковые грани не испытывают нормальных давлений. Эти четырехсторонники должны иметь
такую форму, чтобы боковые грани не испытывали поперечных касательных воздействий, так как их углы остаются прямыми. Следствием сказанного является возможность взаимного превращения прямоугольников в четырехсторонники без нарушения смежности.
Построение, благодаря которому видна эта возможность, производится легко, если растяжения будут представлены посредством  вместо или если волокна, разрезающие
вместо или если волокна, разрезающие  не будут неизменяемой длины. Тогда мы должны только взять центр с дуг на расстоянии
не будут неизменяемой длины. Тогда мы должны только взять центр с дуг на расстоянии  вместо у и точки деления
вместо у и точки деления  первой дуги на расстояниях, равных первоначальным расстояниям
первой дуги на расстояниях, равных первоначальным расстояниям  умноженным на
умноженным на  или же, изобразив фигуру, как если бы она имела постоянную
или же, изобразив фигуру, как если бы она имела постоянную  мы сжали бы все малые четырехсторонники в отношении
мы сжали бы все малые четырехсторонники в отношении  по дугам и в отношении
по дугам и в отношении  по радиусам, что не помешало бы им оставаться смежными.
по радиусам, что не помешало бы им оставаться смежными.
Если удлинение изменяется линейно одновременно в двух направлениях  или если оно представлено посредством выражения
или если оно представлено посредством выражения  причем
причем  представляет собой расстояние
представляет собой расстояние  вдоль у, то можно сделать построение сначала так, как если бы оно сводилось к
вдоль у, то можно сделать построение сначала так, как если бы оно сводилось к  а затем так, как если бы оно сводилось к
а затем так, как если бы оно сводилось к  и окончательно составить геометрически совокупность поперечных перемещений, найденных в соответствии с этими предположениями, что дает, как это легко видеть, сетку криволинейных четырехсторонников в двух направлениях, всегда ортогональных и удовлетворяющих таким образом желаемым условиям.
и окончательно составить геометрически совокупность поперечных перемещений, найденных в соответствии с этими предположениями, что дает, как это легко видеть, сетку криволинейных четырехсторонников в двух направлениях, всегда ортогональных и удовлетворяющих таким образом желаемым условиям.
Но можно, пренебрегая разницей между  и между и
и между и  а также другими очень малыми величинами второго порядка, построить сетку другим способом, который имеет
а также другими очень малыми величинами второго порядка, построить сетку другим способом, который имеет
преимущество, что он одинаково применим в обычном случае, когда материал призмы имеет плоскости симметрии только в виде поперечных сечений и когда, следовательно, равенство нулю взаимных поперечных действий волокон требует, чтобы стороны их прямоугольных оснований не только сжимались, но и обычно слегка наклонялись друг к другу на величину, пропорциональную продольным удлинениям.
Так как тогда  представляют собой относительную величину сжатий сторон, а
представляют собой относительную величину сжатий сторон, а  малый наклон, который они принимают друг к другу, или уменьшение двух противоположных углов элементов поверхности, мы, очевидно, получим, если
малый наклон, который они принимают друг к другу, или уменьшение двух противоположных углов элементов поверхности, мы, очевидно, получим, если  продольное удлинение, а
продольное удлинение, а  новая постоянная, выражения:
новая постоянная, выражения:

Если проинтегрировать первые два из этих уравнений, то к их интегралам нужно соответственно добавить
произвольные функции  при подстановке решений в третье уравнение оно принимает вид
при подстановке решений в третье уравнение оно принимает вид

Соотношение удовлетворяется, если положить обе его части равньши той же произвольной постоянной. Эта постоянная равна  если мы считаем, чтобы абстрагироваться от общего поворота и поступательного смещения, что первый элемент линии
если мы считаем, чтобы абстрагироваться от общего поворота и поступательного смещения, что первый элемент линии  остается неподвижным, так же как начало координат о, т. е.
остается неподвижным, так же как начало координат о, т. е.  при
при  Из этого следует: чтобы удовлетворить трем дифференциальным уравнениям (114), выражающим необходимые условия, при которых волокна не подвергались бы воздействиям в поперечных направлениях, необходимо иметь:
Из этого следует: чтобы удовлетворить трем дифференциальным уравнениям (114), выражающим необходимые условия, при которых волокна не подвергались бы воздействиям в поперечных направлениях, необходимо иметь:

так как эти условия вполне согласуются между собой; это дает положения точек новой сетки, образованной основаниями элементов, или две системы линий, которые их ограничивают. Следовательно, второе из выражений (115), если придавать z различные постоянные значения, дает уравнения слегка искривленных линий, в которые превращаются прямые, первоначально проведенные на сечении  параллельно оси у. Это параболы, радиус кривизны которых почти постоянен и равен обратной величине производной
параллельно оси у. Это параболы, радиус кривизны которых почти постоянен и равен обратной величине производной  и которые, таким образом, почти сливаются при
и которые, таким образом, почти сливаются при  с найденными выше дугами окружности, радиусы которых могли рассматриваться как равные, имея в виду, что величина
с найденными выше дугами окружности, радиусы которых могли рассматриваться как равные, имея в виду, что величина  считается значительно большей, чем z или
считается значительно большей, чем z или  Первое выражение (115) дает то же для линий раздела, которые были первоначально параллельны оси z, т. е. для парабол или дуг окружности, радиус которых является
Первое выражение (115) дает то же для линий раздела, которые были первоначально параллельны оси z, т. е. для парабол или дуг окружности, радиус которых является
обратной величиной суммы  и которые, как сказано выше, сводятся к прямым линиям при
и которые, как сказано выше, сводятся к прямым линиям при  углы малых прямоугольников должны оставаться прямыми, если одновременно имеем
углы малых прямоугольников должны оставаться прямыми, если одновременно имеем  или при зависимости продольного удлинения только от координаты
или при зависимости продольного удлинения только от координаты 
Итак, каждый раз (в соответствии с вышеизложенным), когда мы получим призму, строение которой представляет собой по отношению к поперечным сечениям такую симметрию, что изменение размеров ее волокон или продольных элементов и изменение углов ее оснований могли бы создавать на последних только продольные воздействия, а на боковых гранях только воздействия, параллельные тем же основаниям, если продольные удлинения этих волокон изменяются только линейно в двух поперечных направлениях в точках, где они пересекают какое-либо сечение, то основания продольных элементов могут всегда принимать без нарушения смежности такие формы, что волокна не оказывают друг на друга в боковом направлении никакого воздействия перпендикулярно к их длине.
Эта лемма легко приводит нас к искомому доказательству известных формул изгиба для случая, когда они являются точными.
Действительно, начнем с самого простого случая равномерного, или кругового, изгиба, когда продольные перемещения считаются такими, что все поперечные сечения
остаются плоскими и нормальными к волокнам, равномерно растянутым или сжатым от одного конца до другого и превратившимся в дуги окружности, центры которых находятся на одной прямой, являющейся общим пересечением новых плоскостей сечений. Таким образом, если  удлинение волокна, которое проходит через центры тяжести сечений,
удлинение волокна, которое проходит через центры тяжести сечений,  радиус волокна или расстояние до линии пересечения новых плоскостей, о которой мы говорили, а
радиус волокна или расстояние до линии пересечения новых плоскостей, о которой мы говорили, а  радиус какого-либо другого волокна, то получаем для новой длины части этого волокна, равной первоначально единице, выражение
радиус какого-либо другого волокна, то получаем для новой длины части этого волокна, равной первоначально единице, выражение  следовательно, формулу
следовательно, формулу

для продольного удлинения (так как 80 и считаются очень малыми и их произведением можно пренебречь). Предположим также, что относительные поперечные перемещения на всех сечениях со таковы, что волокна не оказывают друг на друга в боковом направлении никакого поперечного действия, возможность чего нами только что доказана для случая, когда продольные удлинения выражаются подобной формулой.
Если мы обозначим через  число, только что названное коэффициентом упругости растяжения, то продольные усилия на элементах
число, только что названное коэффициентом упругости растяжения, то продольные усилия на элементах  сечений будут
сечений будут

Действия на обоих крайних основаниях получат одинаковое выражение, а действия на боковых гранях призмы будут равны нулю.
Так как задача об определении малых относительных перемещений точек упругого тела полностью решается, когда даны внешние силы, которые на него действуют, то взаимно, призма, боковые грани которой не испытывают никакого воздействия и к крайним основаниям которой приложены продольные усилия  т. е. усилия (положительные или отрицательные), одинаковые на обоих основаниях в соответственных точках, нормальные к элементам
т. е. усилия (положительные или отрицательные), одинаковые на обоих основаниях в соответственных точках, нормальные к элементам
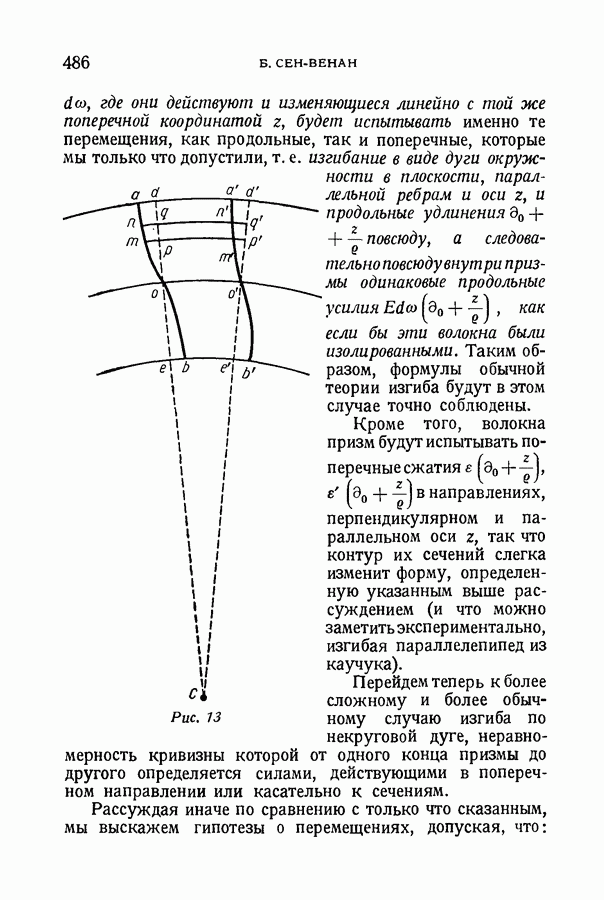
 где они действуют и изменяющиеся линейно с той же поперечной координатой z, будет испытывать именно те перемещения, как продольные, так и поперечные, которые мы только что допустили, т. е. изгибание в виде дуги окружности в плоскости, параллельной ребрам и оси z, и продольные удлинения
где они действуют и изменяющиеся линейно с той же поперечной координатой z, будет испытывать именно те перемещения, как продольные, так и поперечные, которые мы только что допустили, т. е. изгибание в виде дуги окружности в плоскости, параллельной ребрам и оси z, и продольные удлинения  повсюду, а следовательно повсюду внут
повсюду, а следовательно повсюду внут  призмы одинаковые продольные усилия
призмы одинаковые продольные усилия  как если бы эти волокна были изолированными. Таким образом, формулы обычной теории изгиба будут в этом случае точно соблюдены.
как если бы эти волокна были изолированными. Таким образом, формулы обычной теории изгиба будут в этом случае точно соблюдены.

Рис. 13
Кроме того, волокна призм будут испытывать поперечные сжатия  направлениях, перпендикулярном и параллельном оси z, так что контур их сечений слегка изменит форму, определенную указанным выше рассуждением (и что можно заметить экспериментально, изгибая параллелепипед из каучука).
направлениях, перпендикулярном и параллельном оси z, так что контур их сечений слегка изменит форму, определенную указанным выше рассуждением (и что можно заметить экспериментально, изгибая параллелепипед из каучука).
Перейдем теперь к более сложному и более обычному случаю изгиба по некруговой дуге, неравномерность кривизны которой от одного конца призмы до другого определяется силами, действующими в поперечном направлении или касательно к сечениям.
Рассуждая иначе по сравнению с только что сказанным, мы выскажем гипотезы о перемещениях, допуская, что:
1) Различные сечения со изгибаются и наклоняются к волокнам одинаково, так что части ттпп волокон, находящиеся между двумя очень близкими сечениями  имеют после изгиба такую же длину, как и части
имеют после изгиба такую же длину, как и части  находящиеся между двумя плоскостями
находящиеся между двумя плоскостями  проведенными нормально к центральному волокну
проведенными нормально к центральному волокну  проходящему через центры тяжести о, о сечений, и следовательно, продольные удлинения могут быть всегда представлены посредством выражения
проходящему через центры тяжести о, о сечений, и следовательно, продольные удлинения могут быть всегда представлены посредством выражения  где
где  удлинение волокна
удлинение волокна  его радиус кривизны
его радиус кривизны  расстояние от какого-либо волокна до прямой о, проведенной через центр сечения параллельно линии пересечения с двух нормальных плоскостей.
расстояние от какого-либо волокна до прямой о, проведенной через центр сечения параллельно линии пересечения с двух нормальных плоскостей.
2) Волокна сжимаются в боковом направлении (так как это оказывается возможным во всех случаях, когда удлинение имеет линейное выражение) так, что они не давят друг на друга перпендикулярно к их длине и, следовательно, продольное усилие на элементе  равно
равно  это не препятствует тем же волокнам иметь возможность оказывать друг на друга продольные воздействия, аналогичные трению, на их различных боковых гранях, таких, как
это не препятствует тем же волокнам иметь возможность оказывать друг на друга продольные воздействия, аналогичные трению, на их различных боковых гранях, таких, как  пп и т. д., в силу их малых сдвигов друг по отношению к другу или наклонов, которые принимают их ребра к основаниям
пп и т. д., в силу их малых сдвигов друг по отношению к другу или наклонов, которые принимают их ребра к основаниям  или
или  .
.
3)  постоянно, так что различные сечения
постоянно, так что различные сечения  уже подвергшиеся действию в касательном направлении со стороны тех поперечных сил, которые зависят от этих наклонов и которые мы называем постоянной равнодействующей
уже подвергшиеся действию в касательном направлении со стороны тех поперечных сил, которые зависят от этих наклонов и которые мы называем постоянной равнодействующей  полагаемой параллельной
полагаемой параллельной  или
или  подвергаются действию продольных сил, имеющих то же значение
подвергаются действию продольных сил, имеющих то же значение  но мы получаем кривизну у, равномерно изменяющуюся от одного конца призмы до другого и равную
но мы получаем кривизну у, равномерно изменяющуюся от одного конца призмы до другого и равную  где
где  момент инерции
момент инерции  сечения со относительно линии о, а
сечения со относительно линии о, а  переменный момент вокруг той же линии о внешних сил, которые действуют на конец призмы; таким образом, эти силы находятся в равновесии по отношению к повороту ввиду наличия в том же сечении усилий
переменный момент вокруг той же линии о внешних сил, которые действуют на конец призмы; таким образом, эти силы находятся в равновесии по отношению к повороту ввиду наличия в том же сечении усилий
 так как полный момент этих усилий равен
так как полный момент этих усилий равен 
4) Наконец, в соответствии с криволинейной формой  принятой всеми сечениями, продольные касательные действия на боковых внешних гранях призмы равняются нулю и на гранях
принятой всеми сечениями, продольные касательные действия на боковых внешних гранях призмы равняются нулю и на гранях  пп и т. д. какого-либо элемента волокна разности, которые дают эти касательные действия в силу того, что наклоны ребер к основаниям в
пп и т. д. какого-либо элемента волокна разности, которые дают эти касательные действия в силу того, что наклоны ребер к основаниям в  не такие же, как в
не такие же, как в  не такие, как в
не такие, как в  уравновешиваются именно разностью (возникшей вследствие изменения
уравновешиваются именно разностью (возникшей вследствие изменения  продольных усилий
продольных усилий  которые действуют в противоположных направлениях на двух основаниях
которые действуют в противоположных направлениях на двух основаниях  того же элемента.
того же элемента.
Совместность первых трех этих допущений относительно перемещений сама по себе очевидна; и так как они обеспечивают либо равновесие относительно поступательного смещения, либо относительно общего поворота всякой пластинки, заключенной между двумя сечениями  то они согласуются также с четвертым допущением, выполнение которого сводится к тому, чтобы выбрать среди бесконечно большого числаформ, приписываемых искривленной поверхности изогнутых сечений, такую, которая создает равновесие части или каждого элемента пластинки в отдельности; эта форма должна всегда существовать, хотя бы мы могли ее определить для каждого случая только в результате более или менее сложного анализа, различные примеры которого мы указали выше.
то они согласуются также с четвертым допущением, выполнение которого сводится к тому, чтобы выбрать среди бесконечно большого числаформ, приписываемых искривленной поверхности изогнутых сечений, такую, которая создает равновесие части или каждого элемента пластинки в отдельности; эта форма должна всегда существовать, хотя бы мы могли ее определить для каждого случая только в результате более или менее сложного анализа, различные примеры которого мы указали выше.
Если перемещения точек призмы таковы, как мы только что допустили, то ее боковые грани не будут испытывать никакого воздействия, а ее два крайных основания будут подвержены воздействию продольных сил  и сил касательных или поперечных, которые зависят от новой формы поверхностей первоначально плоских сечений.
и сил касательных или поперечных, которые зависят от новой формы поверхностей первоначально плоских сечений.
Так как относительные перемещения производятся единственным способом заданными внешними силами, то взаимно: призма, боковые грани которой не подвергаются никакому воздействию и два крайних основания которой подвергаются одновременно: I) в продольном направлении растяжениям (положительным или отрицательным), которые изменяются линейно или могут выражаться посредством  где
где  постоянная, имеющая одинаковое значение на обоих основаниях, но
постоянная, имеющая одинаковое значение на обоих основаниях, но  имеют обычно различные значения, одно из которых может равняться нулю, а поперечная координата z вычисляется и направляется одинаковым образом на том и на другом основании
имеют обычно различные значения, одно из которых может равняться нулю, а поперечная координата z вычисляется и направляется одинаковым образом на том и на другом основании  в поперечном или касательном направлении действиям, которые имеют одинаковые величины и направления в соответственных точках этих двух оснований, расстояние между которыми мы обозначили через а, и равнодействующую
в поперечном или касательном направлении действиям, которые имеют одинаковые величины и направления в соответственных точках этих двух оснований, расстояние между которыми мы обозначили через а, и равнодействующую  составляющую с величиной
составляющую с величиной  определенное отношение, которое зависит от формы и величины сечений
определенное отношение, которое зависит от формы и величины сечений
и от способа распределения действий; я утверждаю, что эта призма получит во всех ее частях продольные удлинения  причем величины
причем величины  изменяются равномерно по длине оси между ее крайними значениями
изменяются равномерно по длине оси между ее крайними значениями  элементы
элементы  каждого внутреннего сечения будут подвергаться нормальным или продольным усилиям и точно таким же касательным действиям, как каждое из двух крайных оснований; равнодействующая этих сил должна давать момент (с плечом рычага, равным расстоянию от каждого основания до какого-либо сечения), способный уравновесить именно момент продольных воздействий относительно той же оси, проведенной на этом сечении через его центр.
каждого внутреннего сечения будут подвергаться нормальным или продольным усилиям и точно таким же касательным действиям, как каждое из двух крайных оснований; равнодействующая этих сил должна давать момент (с плечом рычага, равным расстоянию от каждого основания до какого-либо сечения), способный уравновесить именно момент продольных воздействий относительно той же оси, проведенной на этом сечении через его центр.
Таким образом, для подобного способа воздействия мы точно получим известные формулы обычной теории изгиба призм, сопровождаемого растяжением центрального волокна; эти формулы дают, между прочим, как мы сказали, только часть перемещений, вызванных продольными удлинениями волокон, к которым нужно добавить, чтобы получить другие части и тем самым полные условия сопротивления, несколько более сложные формулы, которые могут быть получены только путем анализа и которые дают перемещения, вызванные малыми сдвигами пластинок или волокон друг по отношению к другу; этими перемещениями чаще всего ввиду их малости можно пренебречь, но в некоторых случаях они заметно увеличирают стрелу прогиба, так же как максимальное удлинение в косом направлении, которое следует ограничить, чтобы предотвратить разрушение.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ЖИЗНЬ И НАУЧНАЯ ДЕЯТЕЛЬНОСТЬ Б. СЕН-ВЕНАНА
- МЕМУАР О КРУЧЕНИИ ПРИЗМ
- § 1. Прямые и обратные решения задач о твердых упругих телах
- § 2. Смешанный, или полуобратный, метод
- ГЛАВА II. ФОРМУЛЫ ВНУТРЕННЕГО РАВНОВЕСИЯ УПРУГИХ ТВЕРДЫХ ТЕЛ. КРАТКОЕ НАПОМИНАНИЕ ОБ ИХ ОБОСНОВАНИИ ДЛЯ ПЕРЕМЕЩЕНИЙ ПРОИЗВОЛЬНОЙ ВЕЛИЧИНЫ
- § 3. Средние перемещения малых молекулярных групп
- § 4. Удлинения. Сдвиги
- § 5. Условия, при которых даже значительные перемещения точек упругих тел не изменяют их связности. Очень малые сдвиги
- § 6. Зависимости между сдвигами и удлинениями в различных направлениях. Изменение осей
- § 7. Различные сдвиги относительно прямой или в различных направлениях относительно той же прямой. Главный сдвиг и т. д.
- § 8. Зависимости удлинений и сдвигов от весьма малых перемещений
- § 9. Давления. Их равнодействующая на различных гранях элемента. Их непрерывное изменение
- § 10. Соотношения между давлениями на различные грани, имеющие центр в одной точке
- § 11. Следствия. Изменение плоскостей давления. Плоскостл, слегка наклоненные друг к другу
- § 12. Зависимость составляющих давления от удлинений и сдвигов
- § 13. Соображения о числе отличных друг от друга коэффициентов
- § 14. Однородные тела
- § 15. Тело с тремя плоскостями симметрии или главными плоскостями упругости
- § 16. Выбор осей координат с целью приведения к одной двух касательных составляющих давления. Коэффициент упругости при сдвиге
- § 17. Тело с одинаковой упругостью сдвига во всех направлениях, перпендикулярных к одной прямой или относительно этой прямой и во всех проходящих через нее плоскостях
- § 18. Тело, в котором имеется ось упругости
- § 19. Изотропное тело
- § 20. Соотношения между давлениями и внешними или объемными силами
- § 21. Неопределенные дифференциальные уравнения, справедливые во всех точках тела
- § 22. Определенные уравнения, справедливые только в некоторых точках
- § 23. Применение этих уравнений. Прямые, обратные и смешанные задачи
- § 24. Условия сопротивления последующему разрушению или прогрессирующему и опасному изменению строения тела
- § 25. Установление условий прочности. Опасные точки
- § 26. Условия прочности, когда сдвиги равны нулю или пренебрежимо малы в трех направлениях х, у, z
- § 27. Условия прочности, когда рассматриваются только сдвиги
- § 28. Различные виды разрушений
- ГЛАВА III. ПРИМЕНЕНИЕ ТЕОРИИ В ПРОСТОМ СЛУЧАЕ РАСТЯЖЕНИЯ ИЛИ СЖАТИЯ ПРИЗМЫ С ПРОИЗВОЛЬНЫМ СНОВАНИЕМ
- § 30. Полное решение поставленной задачи
- § 31. Перемещения, не являющиеся очень малыми
- § 32. Более общая задача. Однородная призма без плоскости упругости
- § 33. Применение этих выводов на практике
- ГЛАВА IV. ПРИМЕНЕНИЕ ТЕОРИИ К ИЗГИБУ ПРИЗМЫ
- § 34. Изгиб по дуге окружности. Смешанный, или полуобратный, метод, которым мы воспользуемся
- § 35. Исследование выражений для перемещений
- § 36. Давления. Изгибающий момент
- § 37. Обобщение для случая, когда имеются продольные растяжения, равнодействующая которых не равна нулю и является постоянной
- § 38. Решение предложенной задачи определения перемещений по силам (обратная или отчасти обратная задача по отношению к только что решенной)
- § 39. Распространение этого решения на сколь угодно большой изгиб
- § 40. Неравномерный, или некруговой, изгиб
- § 41. Практические применения. Случай, когда сила или пара сил, изгибающая призму, действует в плоскости, параллельной одной из двух главных осей ее сечений
- § 42. Случай, когда плоскость действия изгибающих сил расположена косо по отношению к главным осям сечений. Определение плоскости действительного изгиба и кривизны. Условие сопротивления
- § 43. Новая форма контура сечения изогнутой призмы
- § 44. Криволинейная форма и наклон к оси первоначально плоских и нормальных сечений при неравномерном, или некруговом, изгибе
- ГЛАВА V. О КРУЧЕНИИ ПРИЗМ. ОБЩИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- § 45. Постановка задачи. Условия, относящиеся как к перемещениям, так и к силам. Геометрическое определение движения при кручении
- § 46. Обозначения, используемые в дальнейшем (вместе с обозначениями, приведенными в §§ 4, 6, 8, 11, 15, 18, 21, 22, 24, 27, 30, 36, 40)
- § 47. Характеристические уравнения кручения или выражения для условий относительно перемещений
- § 48. Выражения, относящиеся к силам, т. е. к внешним боковым давлениям
- § 49. Предполагаемая неподвижность одной из точек оси и т. д. Приведение к случаю очень малых перемещений
- § 50. Сдвиги. Крутящие моменты. Неопределенные и определенные уравнения
- § 51. Упрощения для первых решений. Одинаковая упругость при сдвиге. Равенство нулю изгибов, а также продольных и поперечных удлинений
- ГЛАВА VI. КРУЧЕНИЕ ПРИЗМЫ ИЛИ ЦИЛИНДРА С ЭЛЛИПТИЧЕСКИМ ОСНОВАНИЕМ
- § 53. Сдвиги и крутящий момент
- § 54. Поперечные перемещения
- § 55. Давления, которые при этом возникают
- § 56. Решение задачи определения перемещений по данным силам
- § 57. Искривление сечения. Его влияние. Случай кругового сечения, когда искривление отсутствует
- § 58. Практический случай
- § 59. Кручение может иметь место только относительно оси призмы
- § 60. Значительные перемещения, вызванные кручением
- § 61. Наибольший сдвиг. Опасные точки
- § 62. Сравнение с прежней теорией. Объяснение
- § 63. Условие отсутствия разрушения или прочности сцепления
- ГЛАВА VII. ОБЩИЕ ВЫРАЖЕНИЯ ДЛЯ ИНТЕГРАЛОВ НЕОПРЕДЕЛЕННОГО УРАВНЕНИЯ И ВЫТЕКАЮЩИЕ ОТСЮДА ВЫРАЖЕНИЯ СДВИГОВ И КРУТЯЩЕГО МОМЕНТА
- § 65. Случай, когда сечение симметрично, а силы распределены симметрично по отношению к одной из двух осей у или z или по отношению к обеим осям
- § 66. Целое многочленное выражение. Его запись в полярных координатах и распространение на произвольные показатели степени
- § 67. Члены ряда, исчезающие при симметричном сечении. Члены, исчезающие при сечении, одинаковом в обоих направлениях у и z
- ГЛАВА VIII. КРУЧЕНИЕ ПРИЗМЫ С ПРЯМОУГОЛЬНЫМ ОСНОВАНИЕМ
- § 69. Неопределенные и определенные уравнения
- § 70. Решение этих уравнений
- § 71. Сдвиги. Проверка
- § 72. Касательные давления. Крутящий момент. Нормальные давления
- § 73. Задача о перемещениях при заданных силах. Случай из практики
- § 74. Первый пример. Случай, когда одна из сторон прямоугольника очень велика по сравнению с другой
- § 75. Второй пример. Призма с основанием в виде квадрата (рис. 37)
- § 76. Искривленная поверхность сечений после кручения. Разрезы. Рельеф. Экспериментальное подтверждение
- § 77. Крутящий момент для квадратной призмы
- § 78. Экспериментальное подтверждение
- § 79. Другой способ определения численного соотношения между сопротивлением квадратных призм и сопротивлением круговых цилиндров при одинаковом моменте инерции их оснований
- § 80. Продолжение. Общее целое выражение крутящего момента для прямоугольной призмы
- § 81. Относительные сдвиги волокон призмы с квадратным сечением
- § 82. Опасные точки. Наибольший сдвиг
- § 83. Условие прочности квадратной призмы. Экспериментальное подтверждение
- § 84. Случай любого соотношения между двумя измерениями основания. Вычисление u при b/c=2. Границы случаев, когда искривленное сечение делится на четыре или на восемь частей
- § 85. Крутящий момент для прямоугольных призм
- § 86. Сравнение с опытными данными
- § 87. Относительные сдвиги волокон для прямоугольных сечений. Наибольшие сдвиги для точек каждой из их сторон
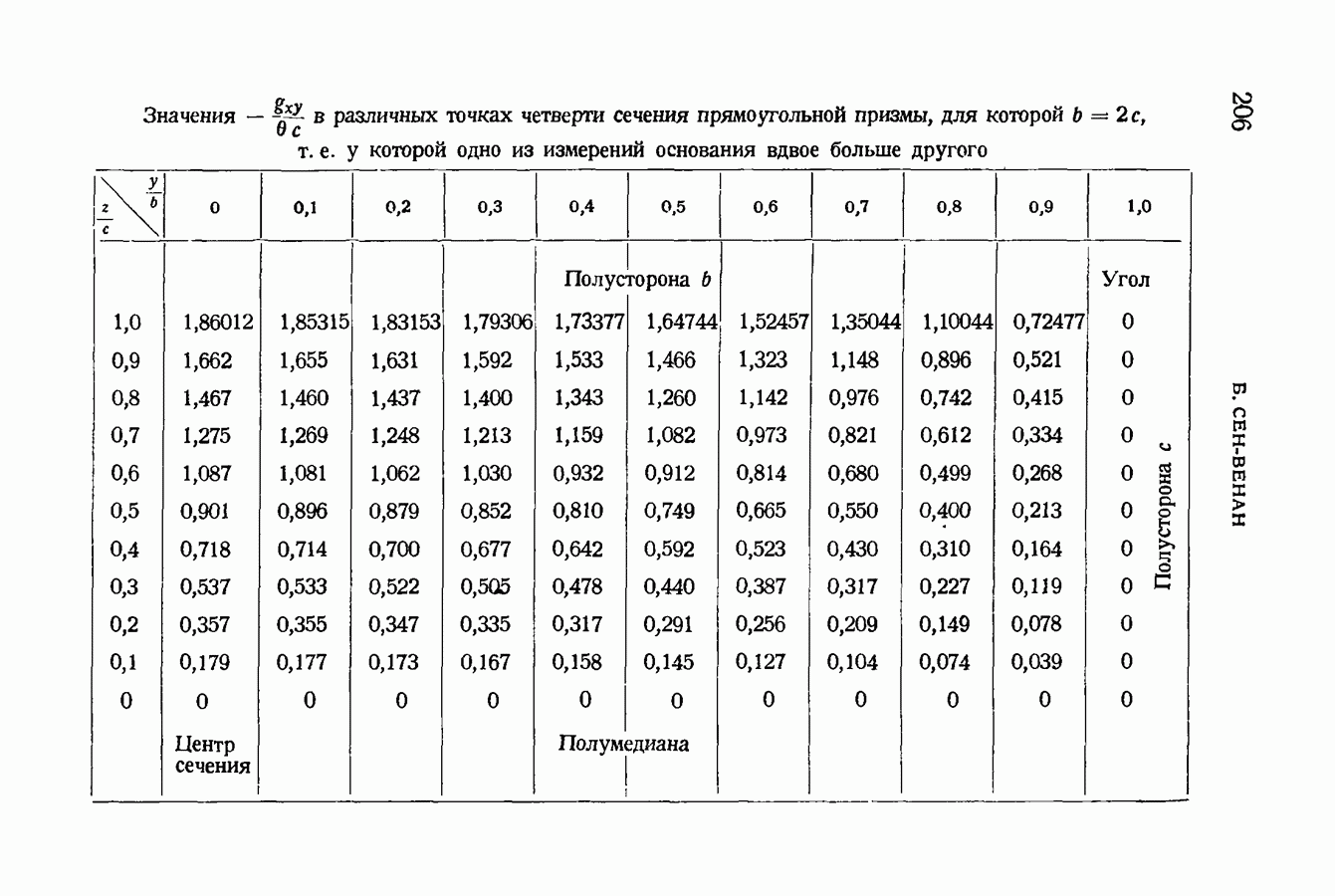
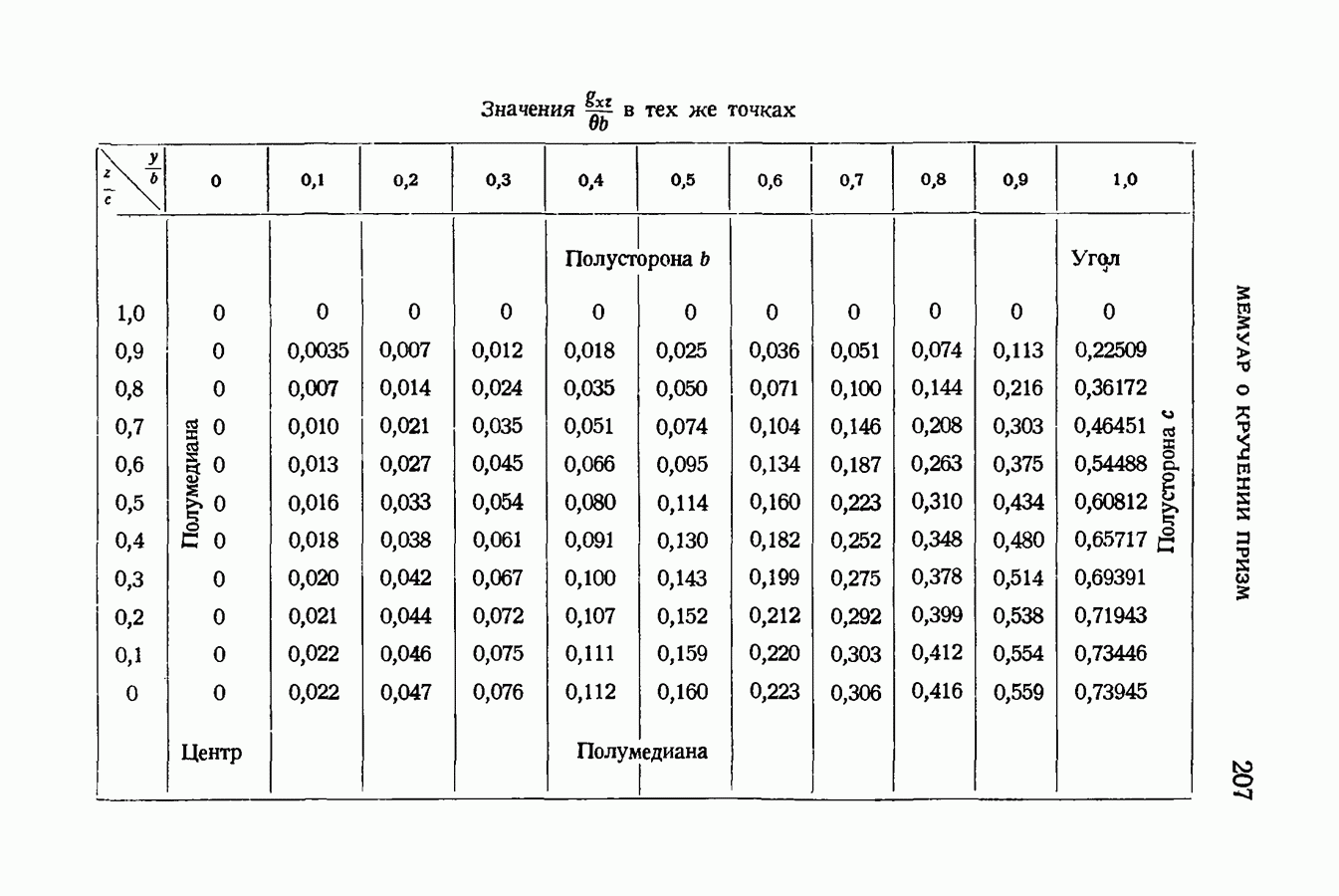
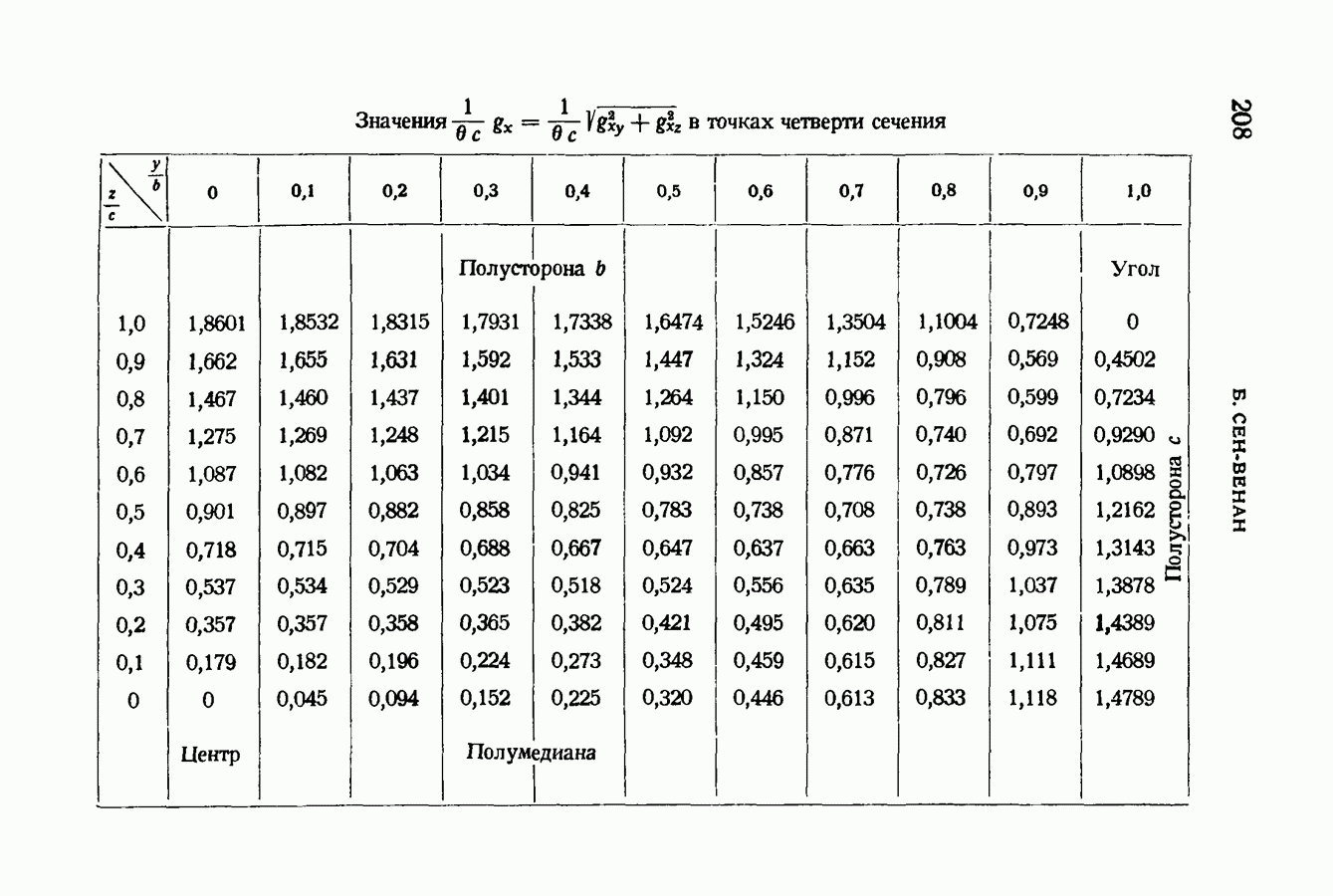
- § 88. Опасная точка, в которой имеет место наибольший сдвиг. Опыты
- § 89. Уравнение отсутствия разрушения или прочности сцепления скрученной призмы. Наибольшие сдвиги
- ГЛАВА IX. КРУЧЕНИЕ ПРИЗМ С ДРУГИМИ ОСНОВАНИЯМИ, НЕ В ВИДЕ ЭЛЛИПСА ИЛИ ПРЯМОУГОЛЬНИКА
- § 90. Бесконечность числа видов уравнения контура сечения и выражений для продольного перемещения u
- § 91. Трансцендентные и алгебраические виды выражения u
- § 92. Симметричные алгебраические кривые. Кривые, одинаковые в двух направлениях
- § 93. Способы, с помощью которых уравнениям придают определенную форму и делают их однородными
- § 94. Симметричные и равные замкнутые кривые четвертой степени
- § 95. Нахождение этих кривых
- § 96. Кривые восьмой степени, симметричные и одинаковые в двух направлениях
- § 97. Условия, при которых эти кривые замкнуты
- § 98. Кривые восьмой степени, у которых наименьший диаметр равен половине наибольшего
- § 99. Кривые, представленные уравнениями, в которых радиус-вектор имеет отрицательные показатели степени. Кривые двенадцатой и шестнадцатой степеней и т. д.
- § 100. Сдвиги и крутящий момент в призмах, имеющих основания в виде кривых четвертой и восьмой степеней
- § 101. Вычисление крутящих моментов. Ничтожность влияния выступов сечения или ребер призм
- § 102. Топографические разрезы и рельеф искривленных поверхностей, в которые превращаются сечения
- § 103. Сдвиги, опасные точки и условия прочности для криволинейных квадратов четвертой степени
- § 104. Те же сдвиги и т. д. для криволинейного основания восьмой степени с выступающими ребрами
- § 105. Контуры, неодинаковые относительно осей у и z. Несимметричные контуры. Призма с основанием в виде равностороннего треугольника. Заключение к главе
- ГЛАВА X. СЛУЧАЙ, КОГДА УПРУГОСТЬ ПРИ СДВИГЕ НЕОДИНАКОВА В НАПРАВЛЕНИЯХ ДВУХ ПОПЕРЕЧНЫХ ОСЕЙ
- § 107. Применение формул в случае эллиптического цилиндра или призмы. Частный случай, когда длина осей пропорциональна корням квадратным из упругостей при сдвиге в направлениях этих осей
- § 108. Продолжение. Условие прочности для такой же эллиптической призмы с неодинаковой упругостью
- § 109. Изменения в общих выражениях интегралов неопределенного уравнения главы VII, когда упругость при сдвиге неодинакова
- § 110. Прямоугольная призма с неодинаковой упругостью. Перемещения. Сдвиги. Крутящий момент
- § 111. Случай, когда … очень мало сравнительно с …
- § 112. Случай, когда …
- § 113. Общий случай, когда стороны 2b, 2c прямоугольника с неодинаковой упругостью находятся между собой в любом соотношении
- § 114. Призмы с другими основаниями (кроме эллипса и прямоугольника), аналогичными рассмотренным в главе IX
- § 115. Нормальность сечений, ставших искривленными, к ребрам, превратившимся в спирали
- ГЛАВА XI. О КРУЧЕНИИ ПОЛЫХ ПРИЗМ
- § 116. Полая эллиптическая призма
- § 117. Полая прямоугольная призма
- § 118. Полые призмы с другими основаниями
- ГЛАВА XII. СЛУЧАЙ ОДНОВРЕМЕННОГО КРУЧЕНИЯ, ИЗГИБА, УДЛИНЕНИЙ И ПОПЕРЕЧНЫХ СДВИГОВ. УСЛОВИЯ ПРОЧНОСТИ ПРИ ИХ ОДНОВРЕМЕННОМ ВОЗДЕЙСТВИИ
- § 119. Определение перемещений. Самое простое геометрическое сложение перемещений, вызванных различного рода усилиями
- § 120. Наложение перемещений, вызванных силами, производящими одновременно растяжение, изгиб и кручение призмы
- § 121. Общие условия прочности при различных воздействиях
- § 122. Более частные и более простые условия
- § 123. Простой и непосредственный вывод этих формул
- § 124. Формулы сопротивления в случае замены удлинений и сдвигов их выражениями через внешние силы, действующие на тело
- § 125. Видоизменения, касающиеся сдвигов, для некоторых особых сечений
- § 126. Первое применение. Призма, испытывающая одновременно изгиб и поперечный сдвиг. Случай, когда наиболее подверженное опасности сечение может изгибаться
- § 127. Та же призма. Случай, когда наиболее подверженное опасности сечение вынуждено оставаться плоским. Сомнительный случай
- § 128. Цилиндр с круговым основанием, одновременно изгибаемый, скручиваемый и растягиваемый
- § 129. Вращающийся вал, изгибаемый и скручиваемый посредством двух шестерен или двух приводных ремней. Консоль переменного диаметра, удовлетворяющая условию равного сопротивления
- § 130. Прямоугольная призма, одновременно изогнутая и скрученная. Общие формулы
- § 131. Та же прямоугольная призма. Случай ее изгибания в плоскости наиболее легкого изгиба, т.е. в плоскости, параллельной наименьшим сторонам 2c (см. § 133)
- § 132. Призма с квадратным основанием, изогнутая в любой плоскости и одновременно скрученная
- § 133. Призма с прямоугольным основанием, одна из сторон которого вдвое больше другой, изогнутая в любой плоскости, параллельной или наклоненной к ее граням, и одновременно скрученная
- § 134. Одновременный изгиб и кручение призм с другими основаниями (кроме круга и прямоугольника). Эллиптический цилиндр
- ГЛАВА XIII. РЕЗЮМЕ ЭТОГО МЕМУАРА, КРАТКОЕ ПОВТОРЕНИЕ ФОРМУЛ И ПРАКТИЧЕСКИЕ ПРАВИЛА, ЧИСЛЕННЫЕ ПРИМЕРЫ
- § 136. Краткое повторение формул и практические правила
- § 137. Числовые примеры
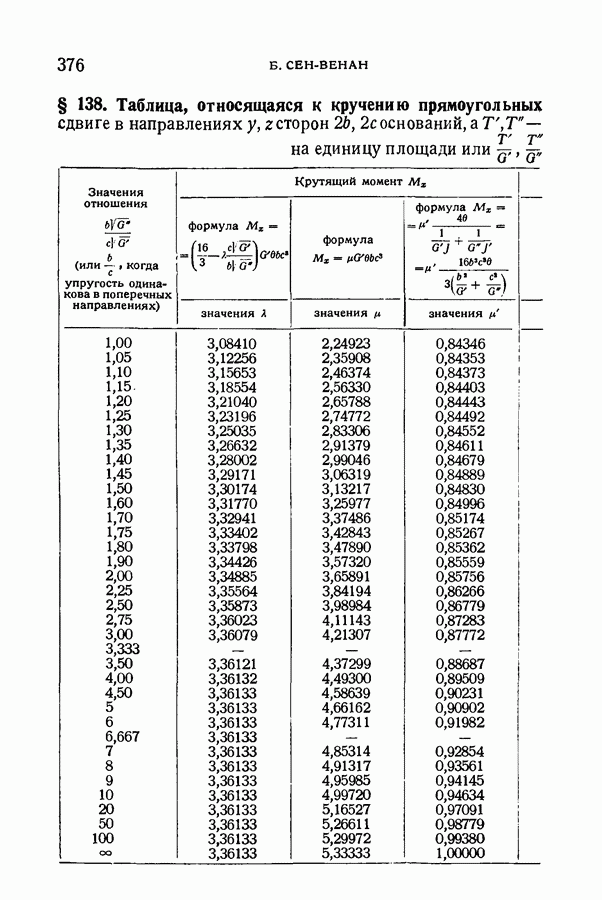
- § 138. Таблица, относящаяся к кручению прямоугольных призм
- МЕМУАР ОБ ИЗГИБЕ ПРИЗМ
- § 1. Прежние исследования по теории изгиба
- § 2. Принятая в настоящее время теория изгиба, вызванного неравномерным продольным растяжением волокон. Гипотезы, на которых она обычно основывается. Ненужность этих гипотез ввиду их неточности для вывода формул
- § 3. Предмет и краткое содержание этого мемуара
- § 4. Краткое разъяснение формул давлений внутри твердых упругих тел. Зависимости между давлениями в различных направлениях в одной точке
- § 5. Продолжение. Удлинения, сдвиги. Линейные выражения для составляющих давления
- § 6. Продолжение. Притяжения и отталкивания, функции молекулярных расстояний. Теорема геометрического сложения сил и малых перемещений
- § 7. Продолжение. Число существенно различных коэффициентов. Его сокращение с тридцати шести до пятнадцати
- § 8. Продолжение. Изменения осей и плоскостей, относительно которых рассматривают давления, удлинения и сдвиги
- § 9. Упрощение формул для составляющих давления в случае тел с различным строением
- § 10. Неопределенные дифференциальные уравнения равновесия упругих твердых тел. Выражения удлинений и сдвигов через очень малые перемещения
- § 11. Определенные уравнения, удовлетворяющиеся только в точках поверхности
- § 12. Применение этих формул к растяжению призмы. Сопровождающие его поперечные сжатия. Коэффициент упругости
- § 13. Применение общих формул Пуассоном и Коши для приближенного решения задачи изгиба
- § 14. Принятые условия и уравнения нашей задачи о неравномерном изгибе призм
- § 15. Первые следствия заданных условий и соотношений
- § 16. Первое интегрирование
- § 17. Распределение сил. Обстоятельства, сопровождающие неравномерный изгиб. Наклон и кривизна сечений. Взаимный наклон волокон. Полная стрела прогиба
- § 18. Кривые контуров сечений, для которых произвольная функция F полностью определяется через у и z. Эллиптический контур и т. д.
- § 19. Способ приложения и распределения внешних сил, уточняющий для различных контуров обычные формулы изгиба, вызванного продольными удлинениями. Значения величины центрального наклона. Сечения эллиптические, круговые, в виде ложного эллипса и т. д.
- § 20. Те же контуры. Полная стрела прогиба при изгибе
- § 21. Те же контуры. Искривленные поверхности, образованные первоначально плоскими сечениями. Их обычная топография
- § 22. Продолжение. Случай, когда каждая искривленная поверхность сечений является общей для бесконечного числа контуров
- § 23. Подробное изложение вопроса для различных сечений. Окружность. Ложный эллипс (овал). Сечения с контуром девятой степени, которые искривляются точно по цилиндрической поверхности с основанием в виде кривой третьей степени, имеющей форму гуська
- § 24. Прямоугольная призма. Преобразование неопределенных и определенных условий
- § 25. Интегрирование с помощью трансцендентного ряда
- § 26. Выражения для перемещений точек прямоугольной призмы
- § 27. Давления … Проверка полученных результатов
- § 28. Центральный сдвиг. Изогнутая ось. Стрела прогиба при изгибе
- § 29. Искривленная поверхность, образованная первоначально плоскими прямоугольными поперечными сечениями
- § 30. Сечения произвольной формы
- § 31. Непосредственное доказательство известных формул изгиба призм, вызванного только их продольными удлинениями
- § 32. Заключение. Общий обзор для случая, когда способ приложения и распределения внешних сил на концах призмы отличен от способа, дающего совершенно точные формулы в соответствии со смешанным методом