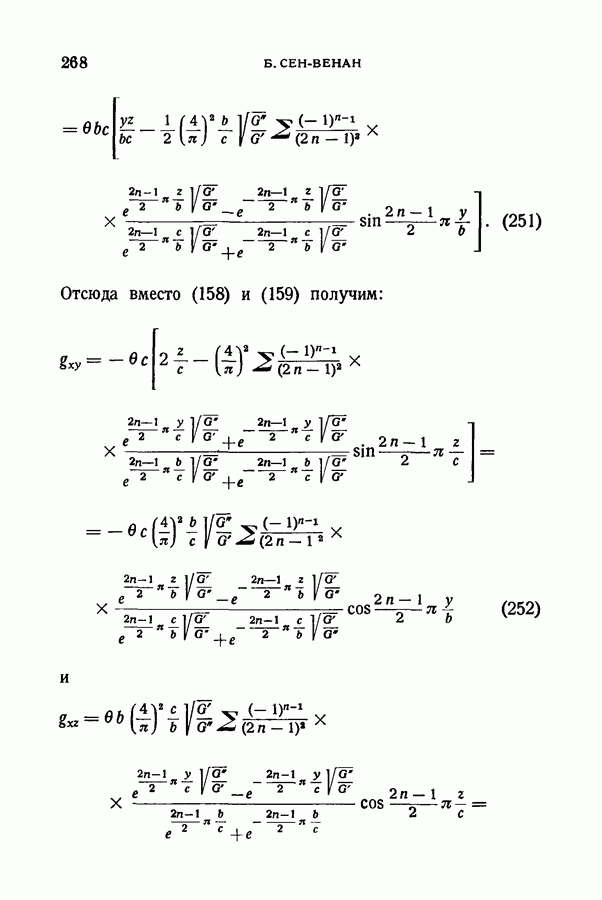| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 72. Касательные давления. Крутящий момент. Нормальные давления
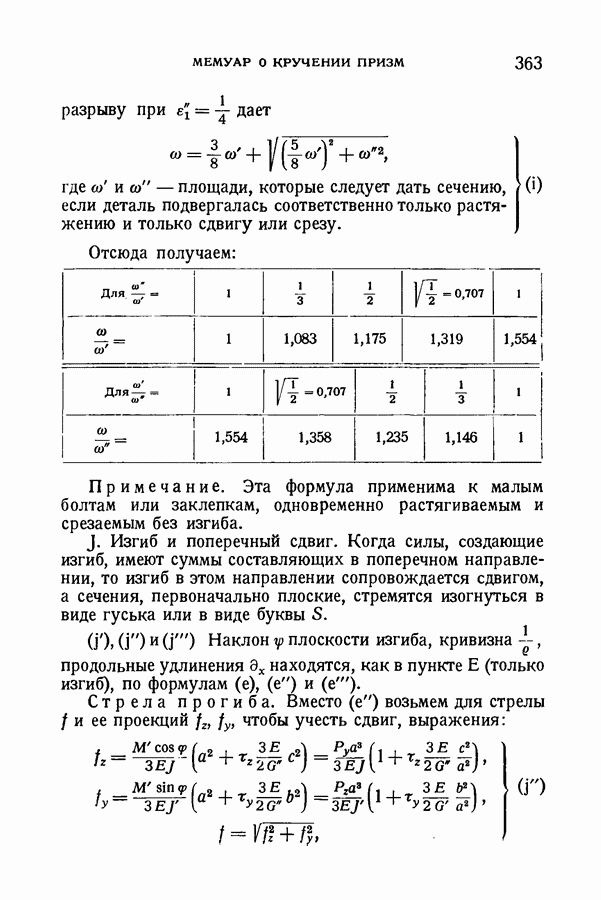
Отсюда следует:

Отсюда для крутящего момента  пользуясь сначала первым выражением (158), а также первым выражением (159) и принимая во внимание, что
пользуясь сначала первым выражением (158), а также первым выражением (159) и принимая во внимание, что

получаем следующее выражение:

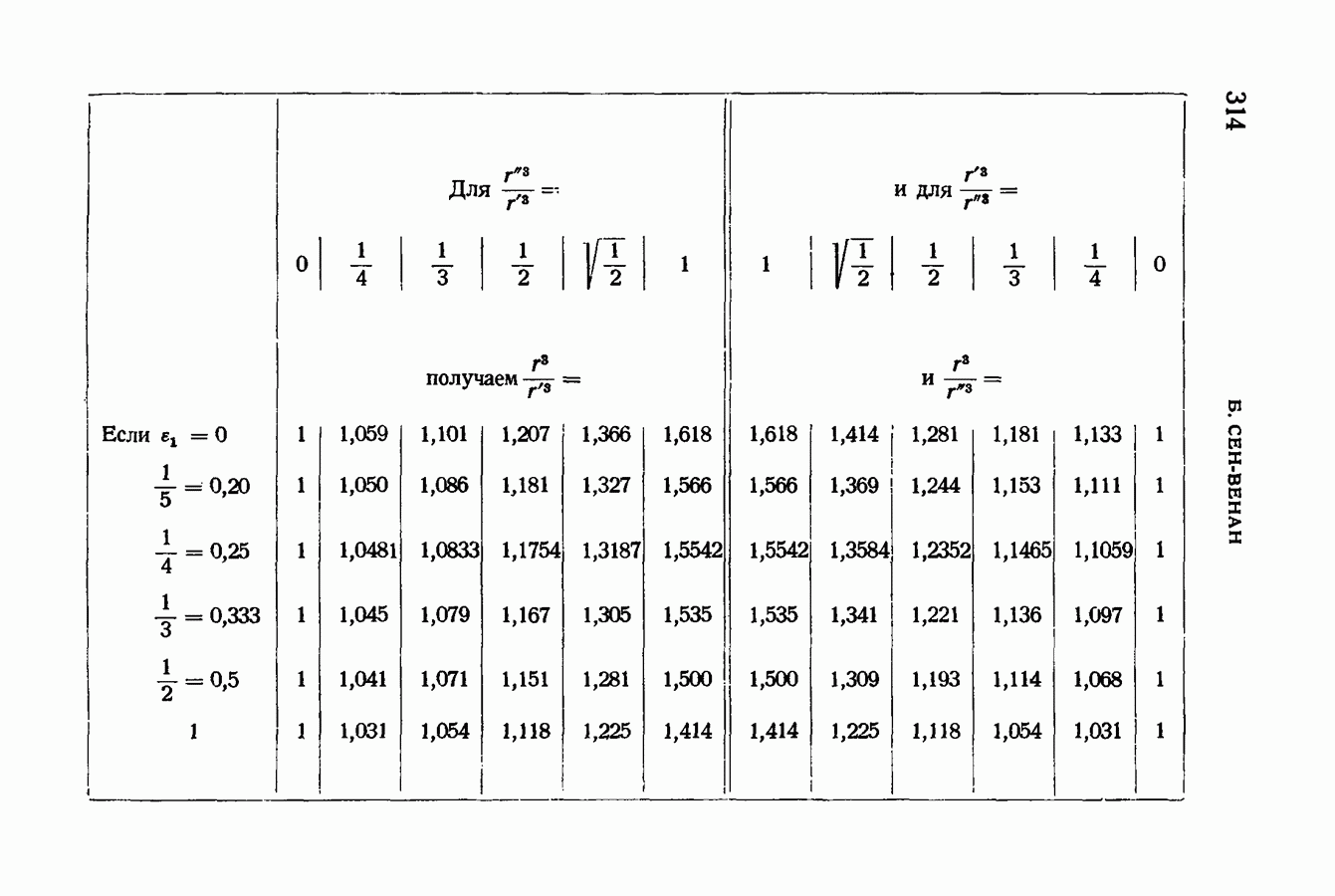
Но мы имеем, как известно (это можно проверить численно):

Второй член в квадратных скобках равен, следовательно, первому члену и может быть объединен с ним, так что получаем первое из двух следующих выражений; второе,
очевидно, получили бы, приняв для  их вторые выражения (158), (159):
их вторые выражения (158), (159):

Эти два выражения должны быть тождественными. Это просто доказывает, что вообще два следующих аналитических выражения не изменяют своей величины, когда в них подставляют у вместо  (первое получено при замене - на
(первое получено при замене - на  в фигурных скобках первого выражения
в фигурных скобках первого выражения  умноженного на
умноженного на  а второе — при подстановке
а второе — при подстановке  вместо
вместо  и
и  вместо
вместо 

и

Последнее выражение меняет только знак.
Если к условиям относительно перемещений, поставленным в § 69 в начале этой главы, мы добавляем условия § 51, относящиеся к общим упрощениям первых решений, то не только

но также (162)

Тогда все другие составляющие давления равны нулю, или

т. е. давления полностью равны нулю на боковых гранях, а на основаниях равны нулю только давления в продольном или нормальном направлении.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ЖИЗНЬ И НАУЧНАЯ ДЕЯТЕЛЬНОСТЬ Б. СЕН-ВЕНАНА
- МЕМУАР О КРУЧЕНИИ ПРИЗМ
- § 1. Прямые и обратные решения задач о твердых упругих телах
- § 2. Смешанный, или полуобратный, метод
- ГЛАВА II. ФОРМУЛЫ ВНУТРЕННЕГО РАВНОВЕСИЯ УПРУГИХ ТВЕРДЫХ ТЕЛ. КРАТКОЕ НАПОМИНАНИЕ ОБ ИХ ОБОСНОВАНИИ ДЛЯ ПЕРЕМЕЩЕНИЙ ПРОИЗВОЛЬНОЙ ВЕЛИЧИНЫ
- § 3. Средние перемещения малых молекулярных групп
- § 4. Удлинения. Сдвиги
- § 5. Условия, при которых даже значительные перемещения точек упругих тел не изменяют их связности. Очень малые сдвиги
- § 6. Зависимости между сдвигами и удлинениями в различных направлениях. Изменение осей
- § 7. Различные сдвиги относительно прямой или в различных направлениях относительно той же прямой. Главный сдвиг и т. д.
- § 8. Зависимости удлинений и сдвигов от весьма малых перемещений
- § 9. Давления. Их равнодействующая на различных гранях элемента. Их непрерывное изменение
- § 10. Соотношения между давлениями на различные грани, имеющие центр в одной точке
- § 11. Следствия. Изменение плоскостей давления. Плоскостл, слегка наклоненные друг к другу
- § 12. Зависимость составляющих давления от удлинений и сдвигов
- § 13. Соображения о числе отличных друг от друга коэффициентов
- § 14. Однородные тела
- § 15. Тело с тремя плоскостями симметрии или главными плоскостями упругости
- § 16. Выбор осей координат с целью приведения к одной двух касательных составляющих давления. Коэффициент упругости при сдвиге
- § 17. Тело с одинаковой упругостью сдвига во всех направлениях, перпендикулярных к одной прямой или относительно этой прямой и во всех проходящих через нее плоскостях
- § 18. Тело, в котором имеется ось упругости
- § 19. Изотропное тело
- § 20. Соотношения между давлениями и внешними или объемными силами
- § 21. Неопределенные дифференциальные уравнения, справедливые во всех точках тела
- § 22. Определенные уравнения, справедливые только в некоторых точках
- § 23. Применение этих уравнений. Прямые, обратные и смешанные задачи
- § 24. Условия сопротивления последующему разрушению или прогрессирующему и опасному изменению строения тела
- § 25. Установление условий прочности. Опасные точки
- § 26. Условия прочности, когда сдвиги равны нулю или пренебрежимо малы в трех направлениях х, у, z
- § 27. Условия прочности, когда рассматриваются только сдвиги
- § 28. Различные виды разрушений
- ГЛАВА III. ПРИМЕНЕНИЕ ТЕОРИИ В ПРОСТОМ СЛУЧАЕ РАСТЯЖЕНИЯ ИЛИ СЖАТИЯ ПРИЗМЫ С ПРОИЗВОЛЬНЫМ СНОВАНИЕМ
- § 30. Полное решение поставленной задачи
- § 31. Перемещения, не являющиеся очень малыми
- § 32. Более общая задача. Однородная призма без плоскости упругости
- § 33. Применение этих выводов на практике
- ГЛАВА IV. ПРИМЕНЕНИЕ ТЕОРИИ К ИЗГИБУ ПРИЗМЫ
- § 34. Изгиб по дуге окружности. Смешанный, или полуобратный, метод, которым мы воспользуемся
- § 35. Исследование выражений для перемещений
- § 36. Давления. Изгибающий момент
- § 37. Обобщение для случая, когда имеются продольные растяжения, равнодействующая которых не равна нулю и является постоянной
- § 38. Решение предложенной задачи определения перемещений по силам (обратная или отчасти обратная задача по отношению к только что решенной)
- § 39. Распространение этого решения на сколь угодно большой изгиб
- § 40. Неравномерный, или некруговой, изгиб
- § 41. Практические применения. Случай, когда сила или пара сил, изгибающая призму, действует в плоскости, параллельной одной из двух главных осей ее сечений
- § 42. Случай, когда плоскость действия изгибающих сил расположена косо по отношению к главным осям сечений. Определение плоскости действительного изгиба и кривизны. Условие сопротивления
- § 43. Новая форма контура сечения изогнутой призмы
- § 44. Криволинейная форма и наклон к оси первоначально плоских и нормальных сечений при неравномерном, или некруговом, изгибе
- ГЛАВА V. О КРУЧЕНИИ ПРИЗМ. ОБЩИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- § 45. Постановка задачи. Условия, относящиеся как к перемещениям, так и к силам. Геометрическое определение движения при кручении
- § 46. Обозначения, используемые в дальнейшем (вместе с обозначениями, приведенными в §§ 4, 6, 8, 11, 15, 18, 21, 22, 24, 27, 30, 36, 40)
- § 47. Характеристические уравнения кручения или выражения для условий относительно перемещений
- § 48. Выражения, относящиеся к силам, т. е. к внешним боковым давлениям
- § 49. Предполагаемая неподвижность одной из точек оси и т. д. Приведение к случаю очень малых перемещений
- § 50. Сдвиги. Крутящие моменты. Неопределенные и определенные уравнения
- § 51. Упрощения для первых решений. Одинаковая упругость при сдвиге. Равенство нулю изгибов, а также продольных и поперечных удлинений
- ГЛАВА VI. КРУЧЕНИЕ ПРИЗМЫ ИЛИ ЦИЛИНДРА С ЭЛЛИПТИЧЕСКИМ ОСНОВАНИЕМ
- § 53. Сдвиги и крутящий момент
- § 54. Поперечные перемещения
- § 55. Давления, которые при этом возникают
- § 56. Решение задачи определения перемещений по данным силам
- § 57. Искривление сечения. Его влияние. Случай кругового сечения, когда искривление отсутствует
- § 58. Практический случай
- § 59. Кручение может иметь место только относительно оси призмы
- § 60. Значительные перемещения, вызванные кручением
- § 61. Наибольший сдвиг. Опасные точки
- § 62. Сравнение с прежней теорией. Объяснение
- § 63. Условие отсутствия разрушения или прочности сцепления
- ГЛАВА VII. ОБЩИЕ ВЫРАЖЕНИЯ ДЛЯ ИНТЕГРАЛОВ НЕОПРЕДЕЛЕННОГО УРАВНЕНИЯ И ВЫТЕКАЮЩИЕ ОТСЮДА ВЫРАЖЕНИЯ СДВИГОВ И КРУТЯЩЕГО МОМЕНТА
- § 65. Случай, когда сечение симметрично, а силы распределены симметрично по отношению к одной из двух осей у или z или по отношению к обеим осям
- § 66. Целое многочленное выражение. Его запись в полярных координатах и распространение на произвольные показатели степени
- § 67. Члены ряда, исчезающие при симметричном сечении. Члены, исчезающие при сечении, одинаковом в обоих направлениях у и z
- ГЛАВА VIII. КРУЧЕНИЕ ПРИЗМЫ С ПРЯМОУГОЛЬНЫМ ОСНОВАНИЕМ
- § 69. Неопределенные и определенные уравнения
- § 70. Решение этих уравнений
- § 71. Сдвиги. Проверка
- § 72. Касательные давления. Крутящий момент. Нормальные давления
- § 73. Задача о перемещениях при заданных силах. Случай из практики
- § 74. Первый пример. Случай, когда одна из сторон прямоугольника очень велика по сравнению с другой
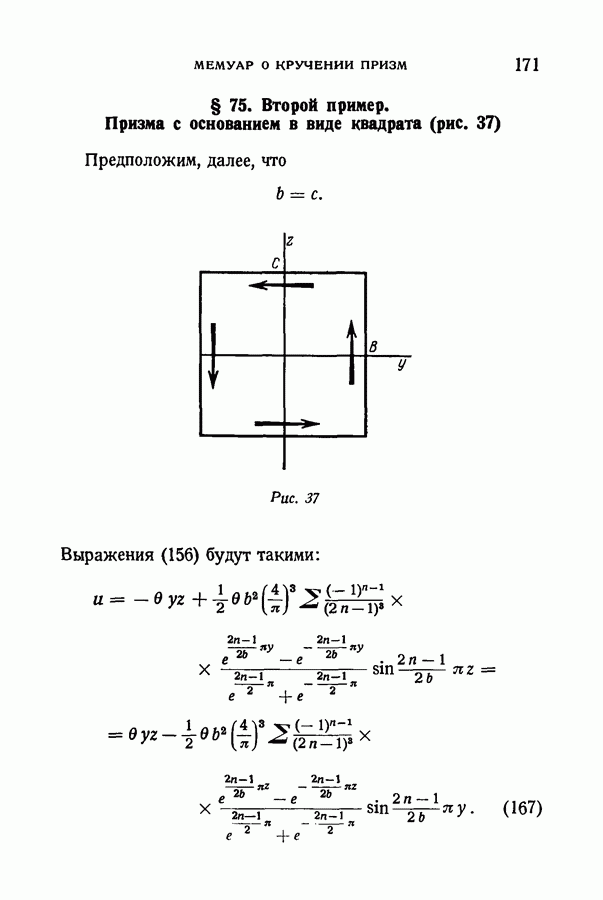
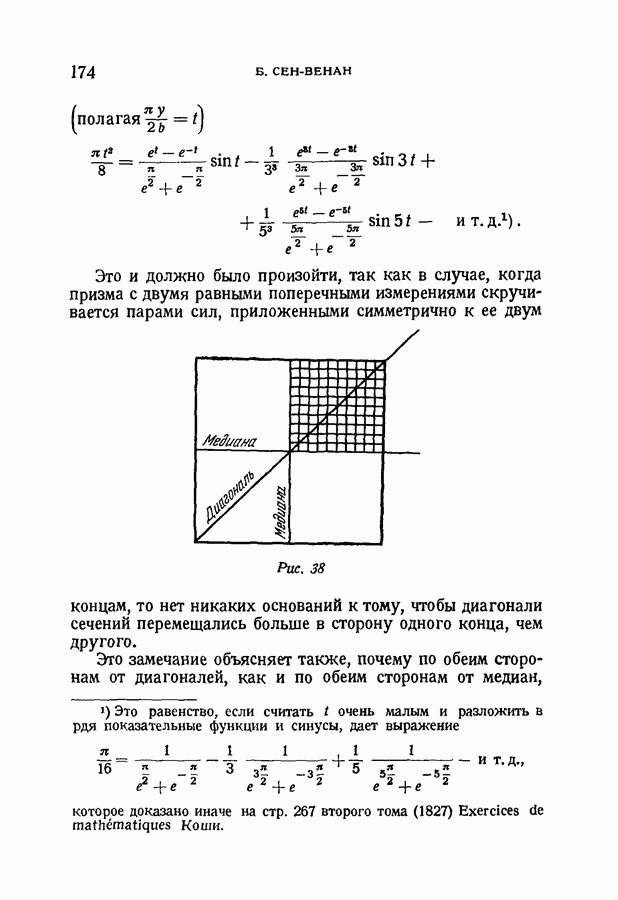
- § 75. Второй пример. Призма с основанием в виде квадрата (рис. 37)
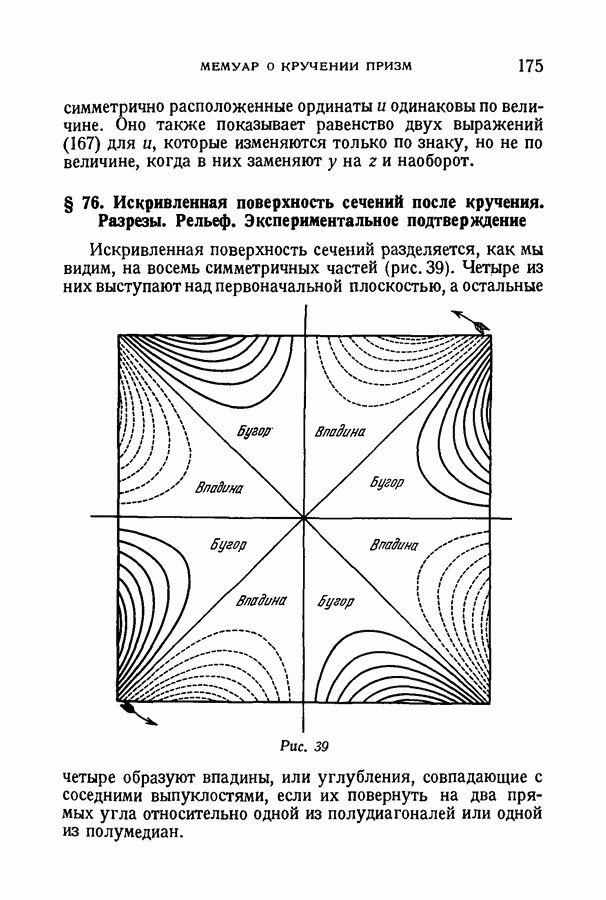
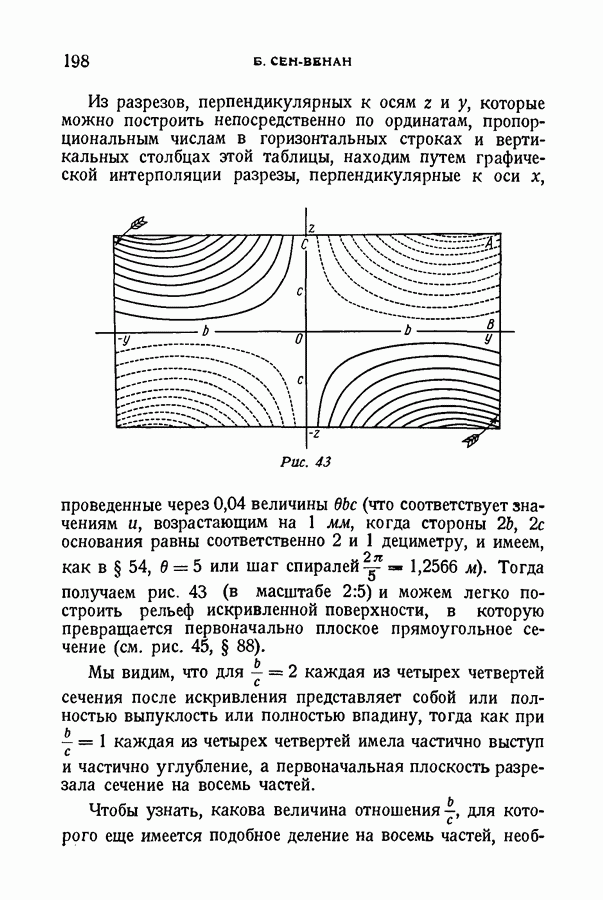
- § 76. Искривленная поверхность сечений после кручения. Разрезы. Рельеф. Экспериментальное подтверждение
- § 77. Крутящий момент для квадратной призмы
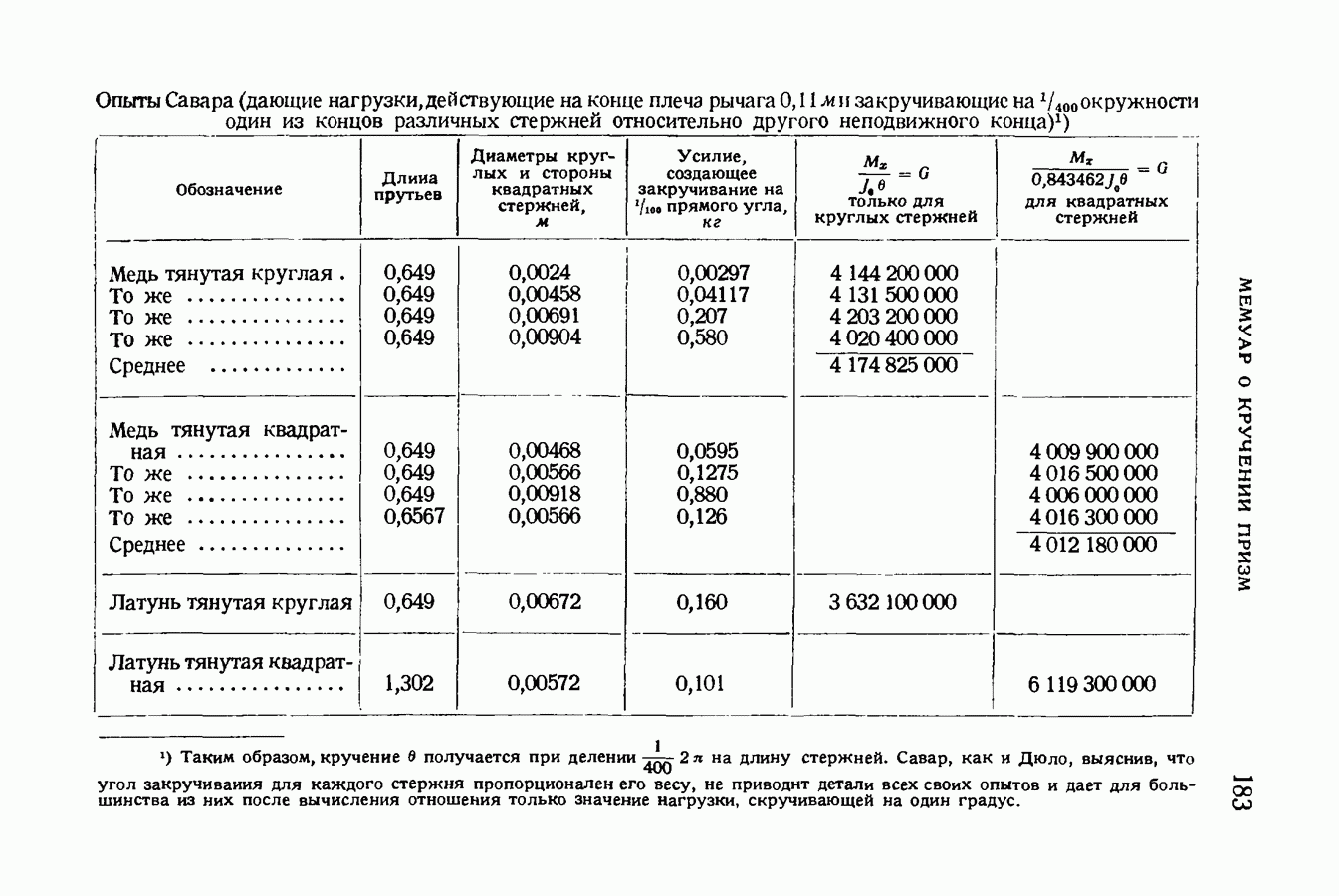
- § 78. Экспериментальное подтверждение
- § 79. Другой способ определения численного соотношения между сопротивлением квадратных призм и сопротивлением круговых цилиндров при одинаковом моменте инерции их оснований
- § 80. Продолжение. Общее целое выражение крутящего момента для прямоугольной призмы
- § 81. Относительные сдвиги волокон призмы с квадратным сечением
- § 82. Опасные точки. Наибольший сдвиг
- § 83. Условие прочности квадратной призмы. Экспериментальное подтверждение
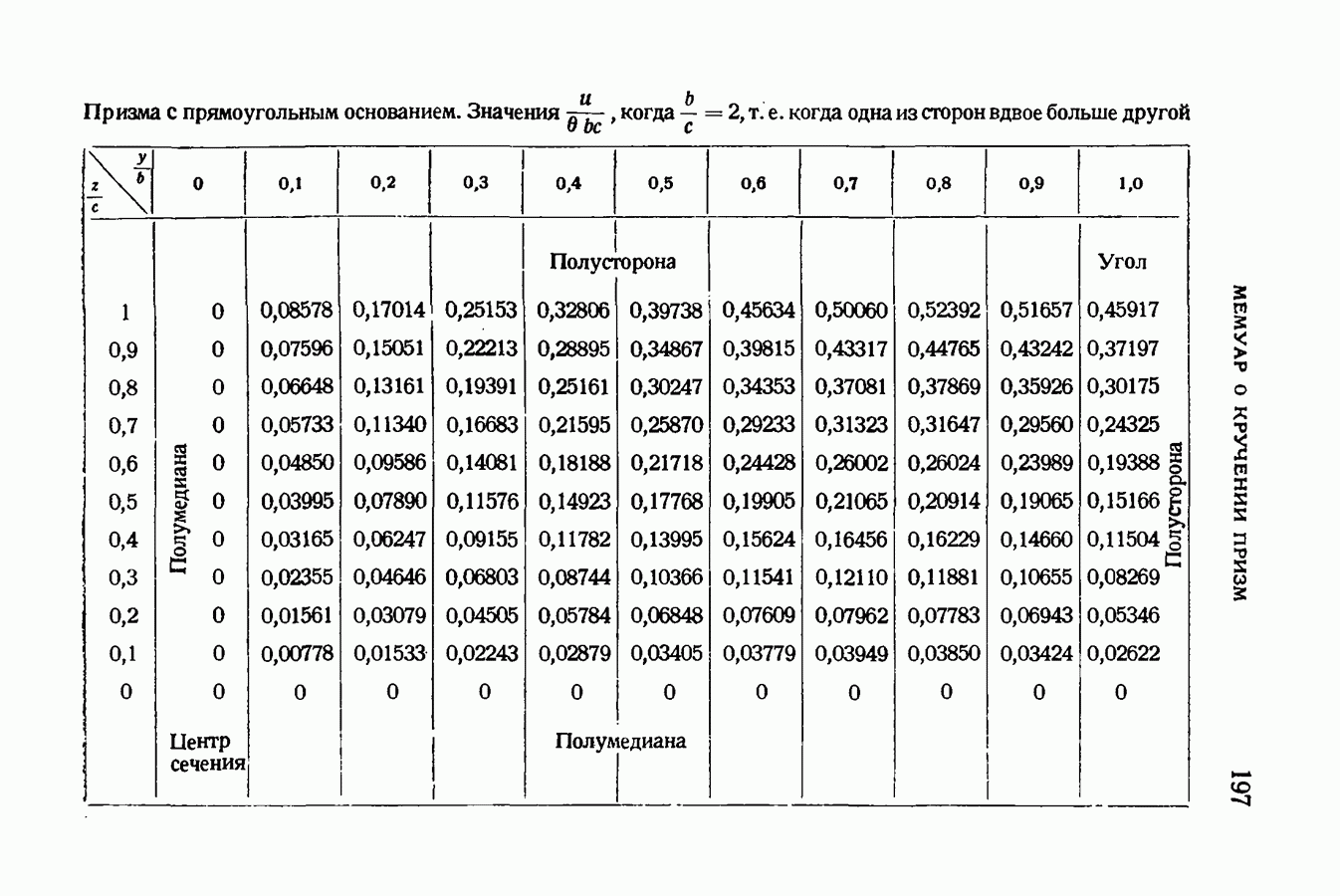
- § 84. Случай любого соотношения между двумя измерениями основания. Вычисление u при b/c=2. Границы случаев, когда искривленное сечение делится на четыре или на восемь частей
- § 85. Крутящий момент для прямоугольных призм
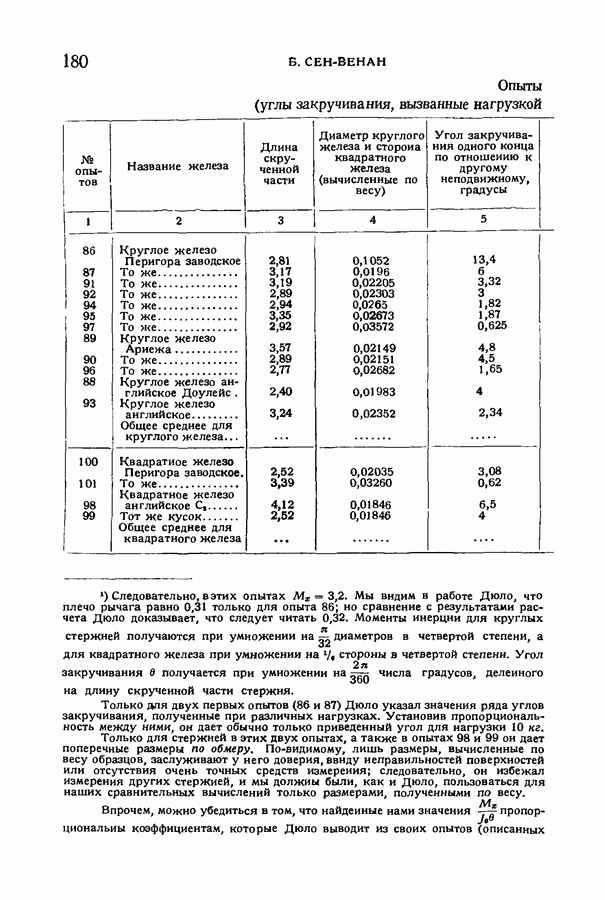
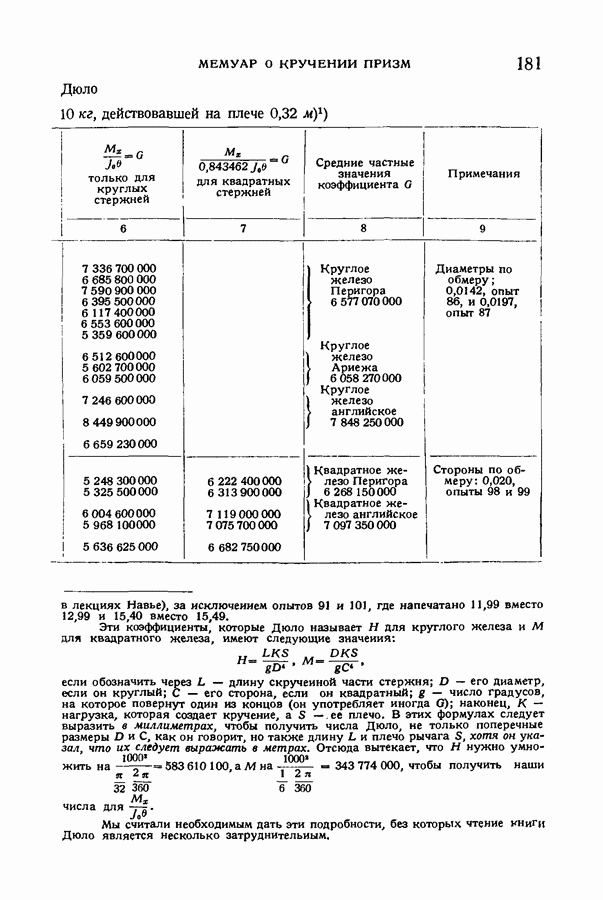
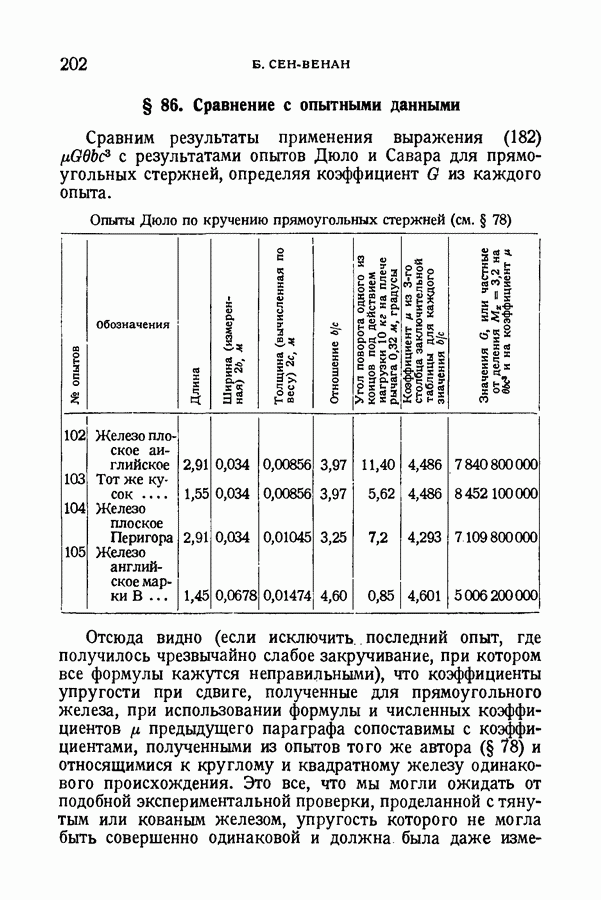
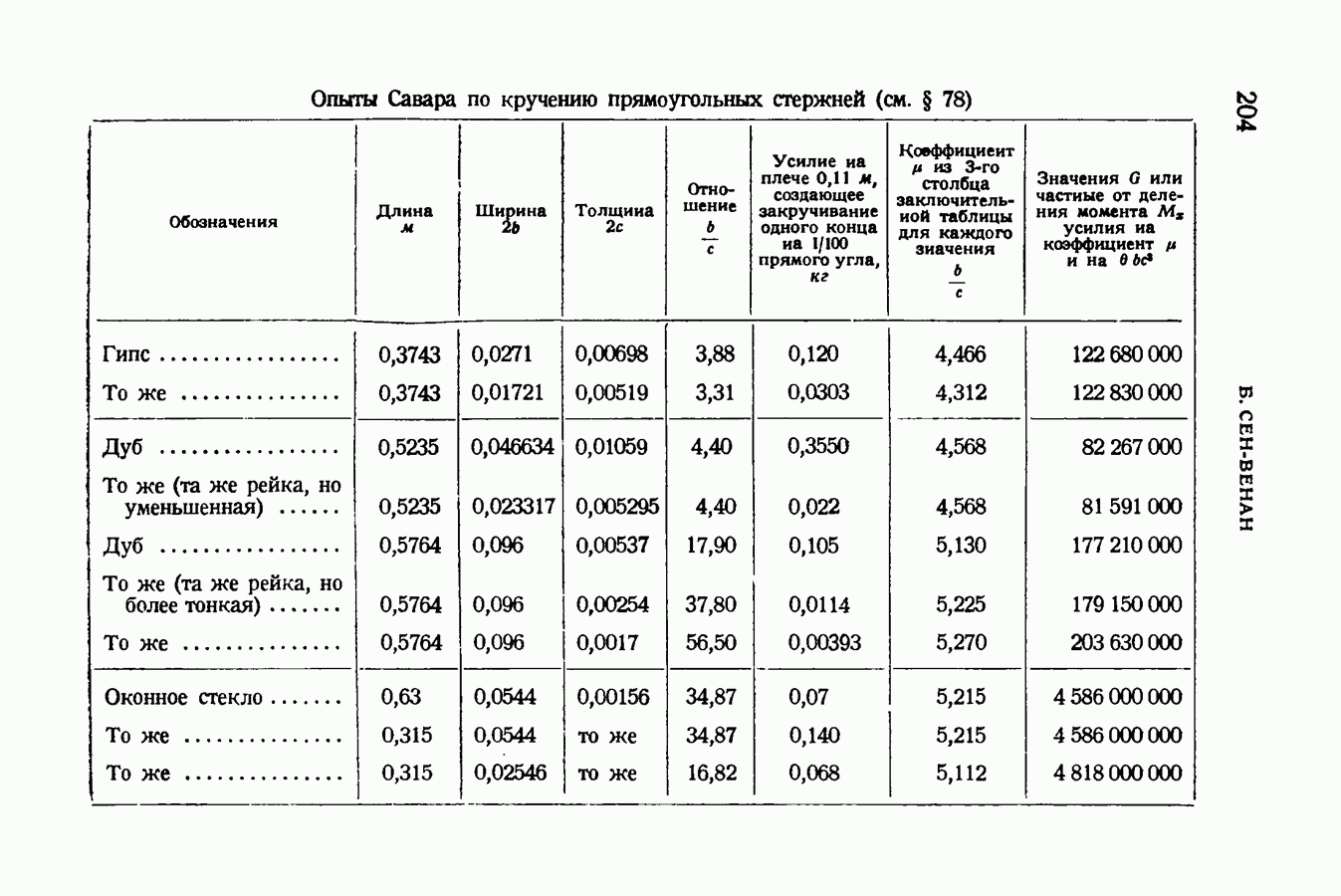
- § 86. Сравнение с опытными данными
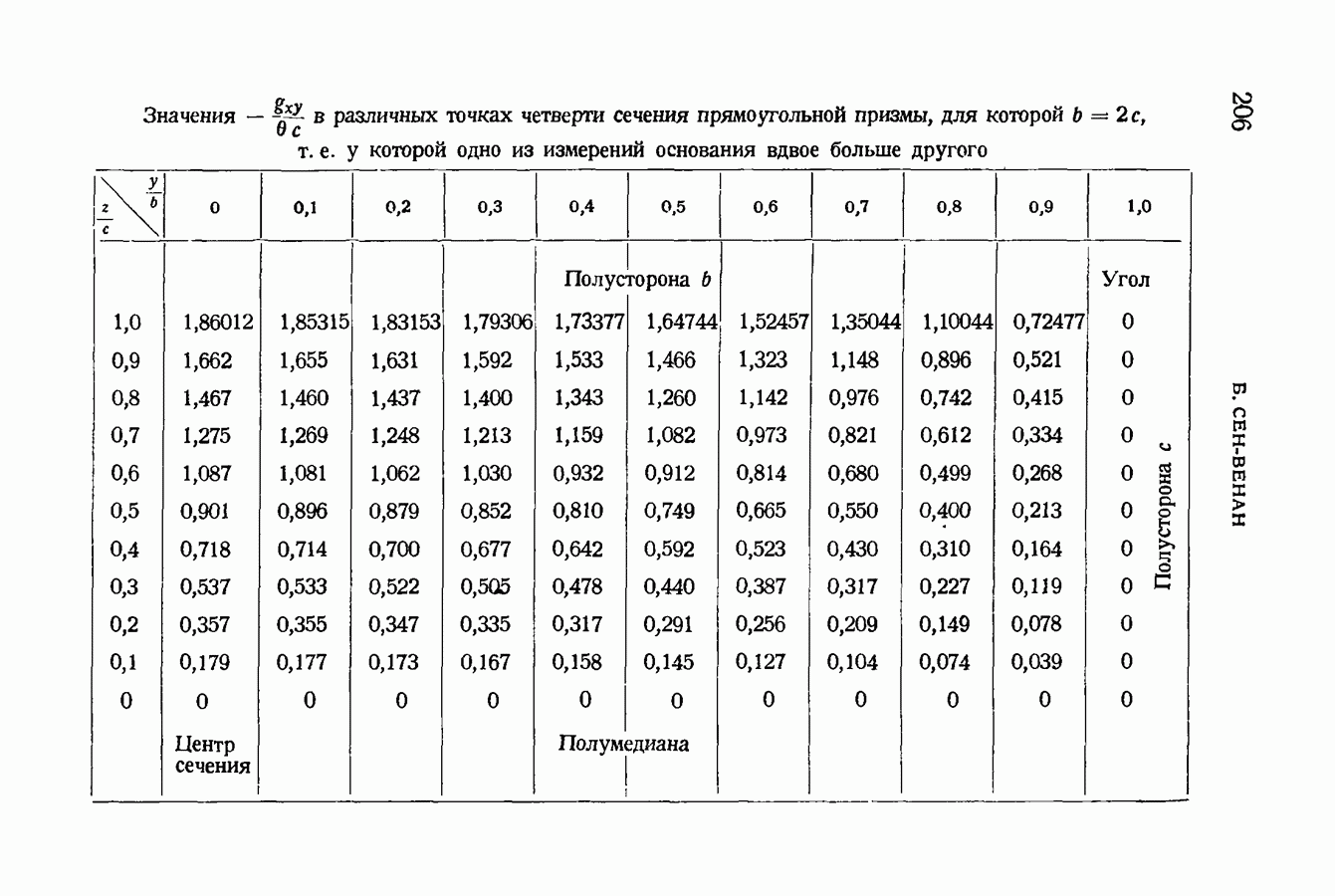
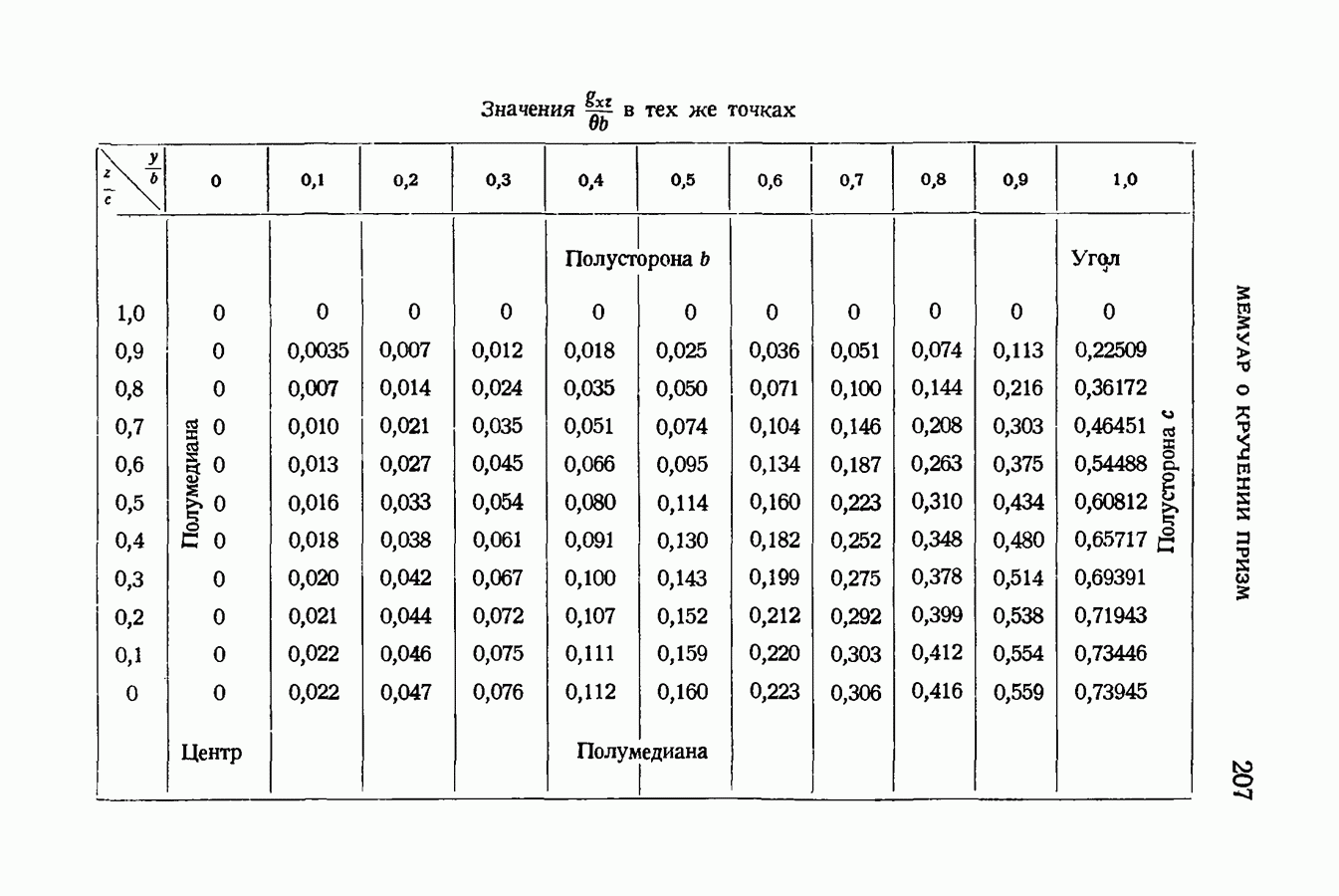
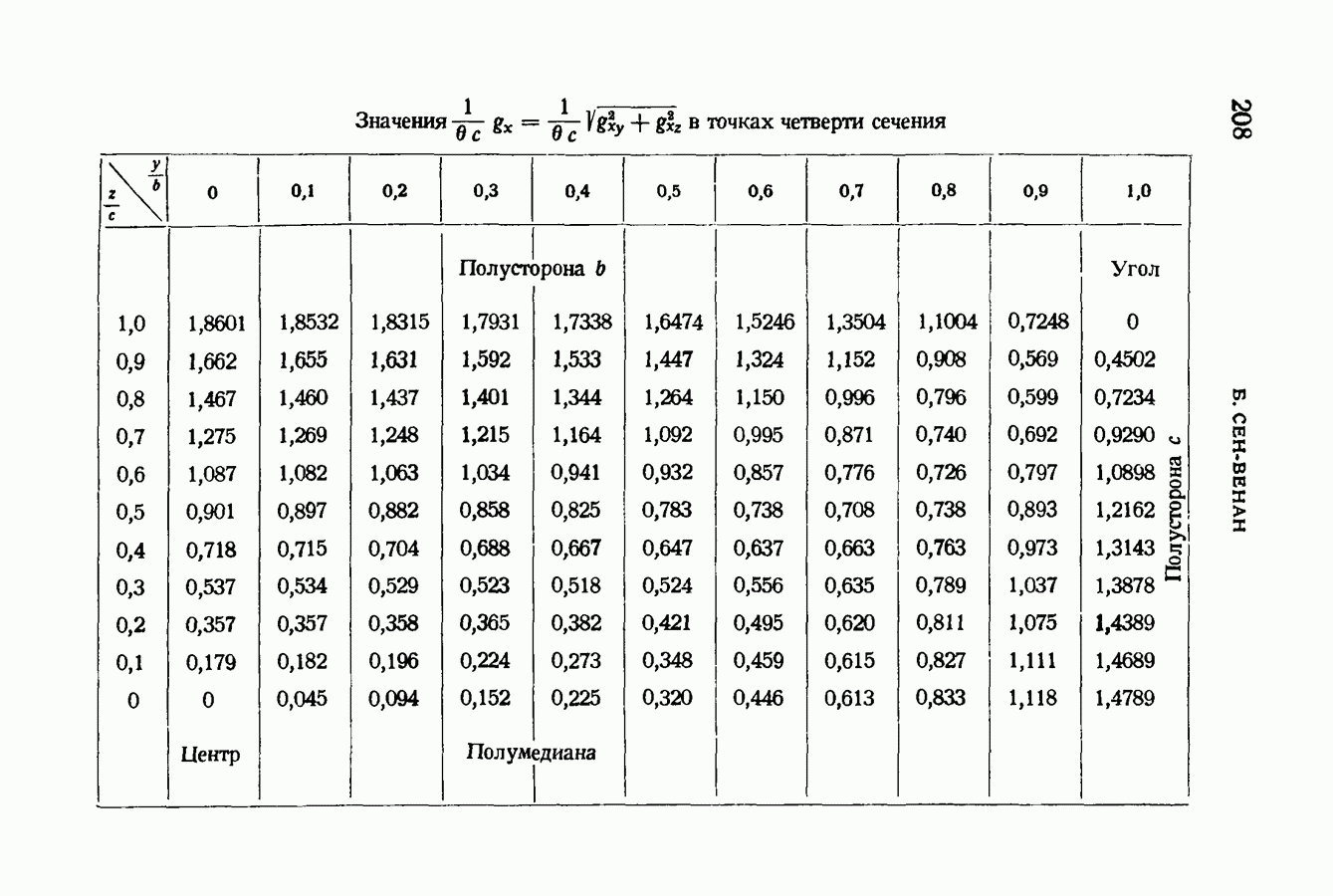
- § 87. Относительные сдвиги волокон для прямоугольных сечений. Наибольшие сдвиги для точек каждой из их сторон
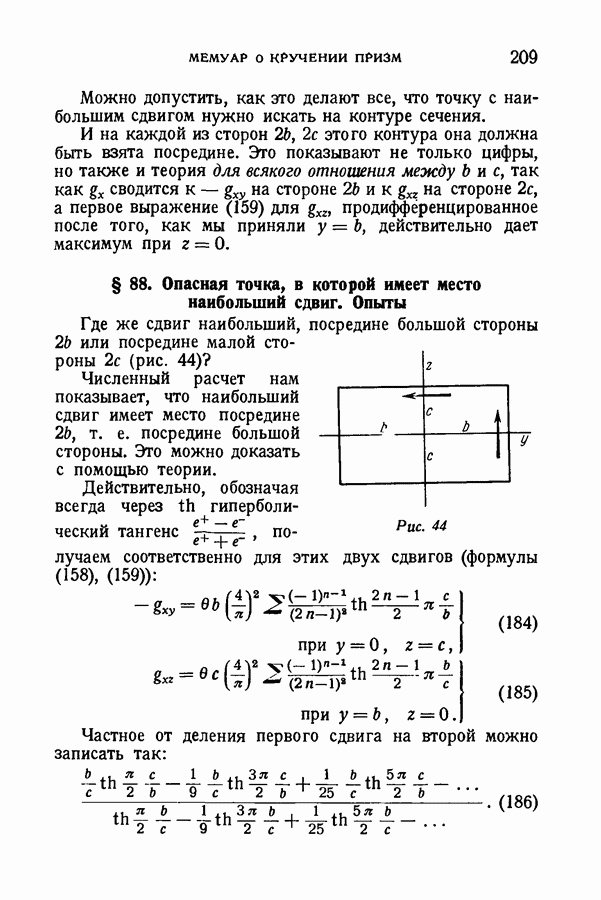
- § 88. Опасная точка, в которой имеет место наибольший сдвиг. Опыты
- § 89. Уравнение отсутствия разрушения или прочности сцепления скрученной призмы. Наибольшие сдвиги
- ГЛАВА IX. КРУЧЕНИЕ ПРИЗМ С ДРУГИМИ ОСНОВАНИЯМИ, НЕ В ВИДЕ ЭЛЛИПСА ИЛИ ПРЯМОУГОЛЬНИКА
- § 90. Бесконечность числа видов уравнения контура сечения и выражений для продольного перемещения u
- § 91. Трансцендентные и алгебраические виды выражения u
- § 92. Симметричные алгебраические кривые. Кривые, одинаковые в двух направлениях
- § 93. Способы, с помощью которых уравнениям придают определенную форму и делают их однородными
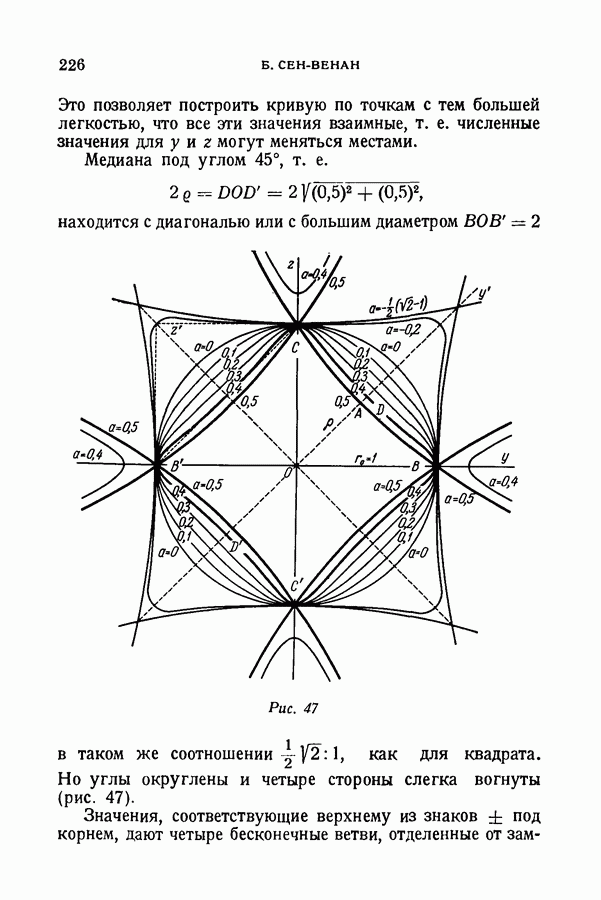
- § 94. Симметричные и равные замкнутые кривые четвертой степени
- § 95. Нахождение этих кривых
- § 96. Кривые восьмой степени, симметричные и одинаковые в двух направлениях
- § 97. Условия, при которых эти кривые замкнуты
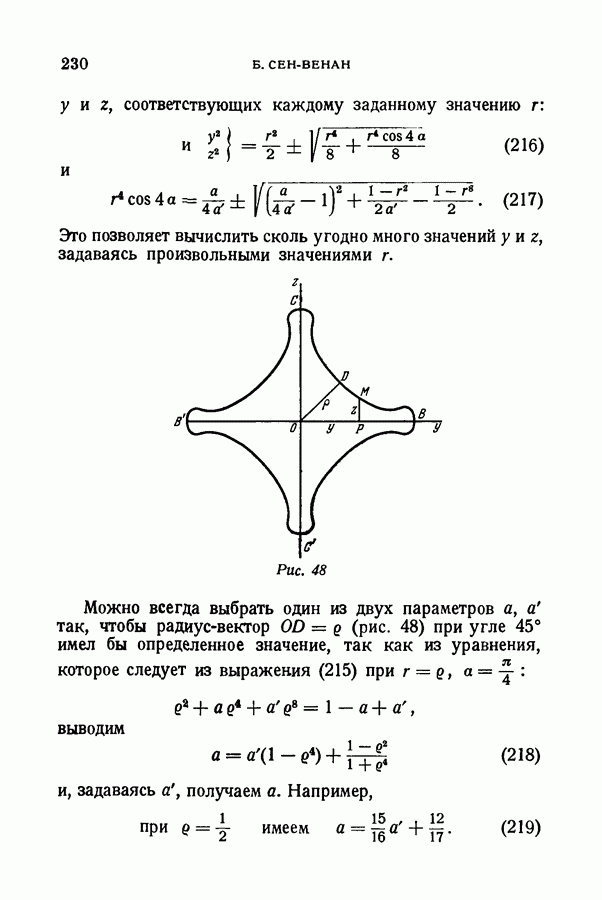
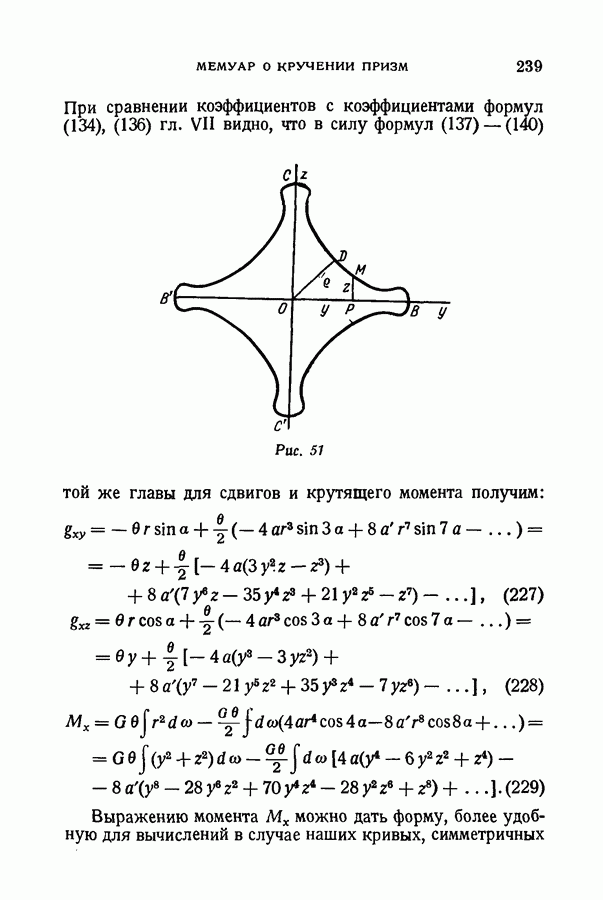
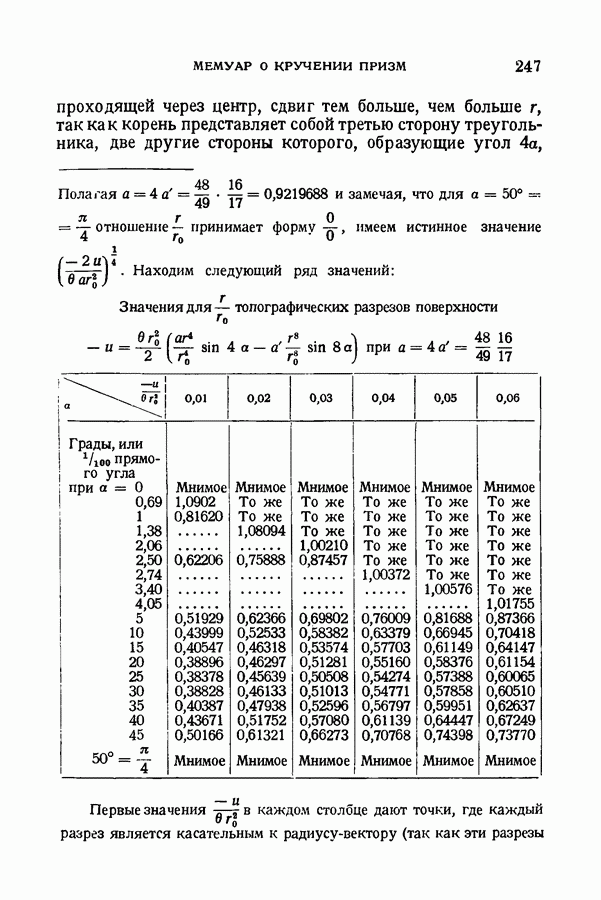
- § 98. Кривые восьмой степени, у которых наименьший диаметр равен половине наибольшего
- § 99. Кривые, представленные уравнениями, в которых радиус-вектор имеет отрицательные показатели степени. Кривые двенадцатой и шестнадцатой степеней и т. д.
- § 100. Сдвиги и крутящий момент в призмах, имеющих основания в виде кривых четвертой и восьмой степеней
- § 101. Вычисление крутящих моментов. Ничтожность влияния выступов сечения или ребер призм
- § 102. Топографические разрезы и рельеф искривленных поверхностей, в которые превращаются сечения
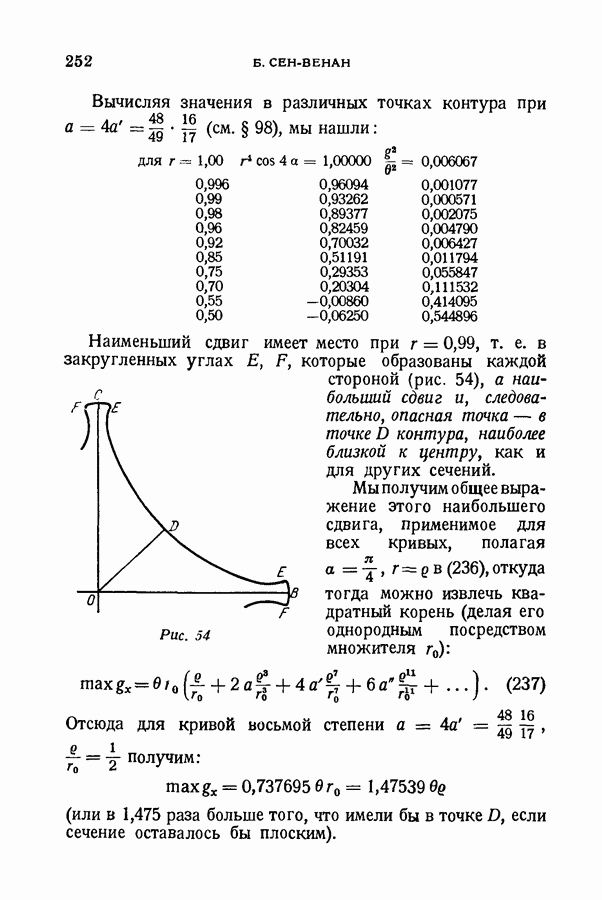
- § 103. Сдвиги, опасные точки и условия прочности для криволинейных квадратов четвертой степени
- § 104. Те же сдвиги и т. д. для криволинейного основания восьмой степени с выступающими ребрами
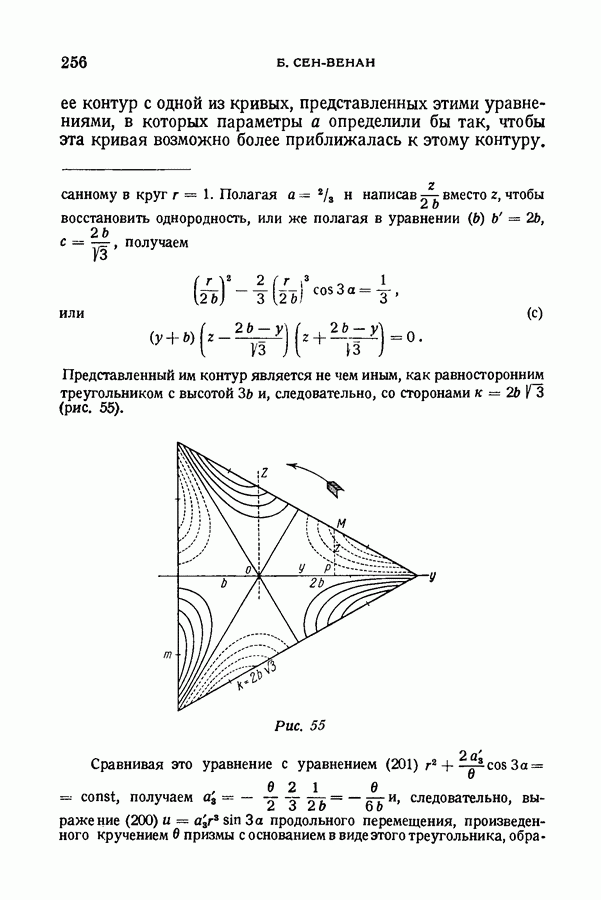
- § 105. Контуры, неодинаковые относительно осей у и z. Несимметричные контуры. Призма с основанием в виде равностороннего треугольника. Заключение к главе
- ГЛАВА X. СЛУЧАЙ, КОГДА УПРУГОСТЬ ПРИ СДВИГЕ НЕОДИНАКОВА В НАПРАВЛЕНИЯХ ДВУХ ПОПЕРЕЧНЫХ ОСЕЙ
- § 107. Применение формул в случае эллиптического цилиндра или призмы. Частный случай, когда длина осей пропорциональна корням квадратным из упругостей при сдвиге в направлениях этих осей
- § 108. Продолжение. Условие прочности для такой же эллиптической призмы с неодинаковой упругостью
- § 109. Изменения в общих выражениях интегралов неопределенного уравнения главы VII, когда упругость при сдвиге неодинакова
- § 110. Прямоугольная призма с неодинаковой упругостью. Перемещения. Сдвиги. Крутящий момент
- § 111. Случай, когда … очень мало сравнительно с …
- § 112. Случай, когда …
- § 113. Общий случай, когда стороны 2b, 2c прямоугольника с неодинаковой упругостью находятся между собой в любом соотношении
- § 114. Призмы с другими основаниями (кроме эллипса и прямоугольника), аналогичными рассмотренным в главе IX
- § 115. Нормальность сечений, ставших искривленными, к ребрам, превратившимся в спирали
- ГЛАВА XI. О КРУЧЕНИИ ПОЛЫХ ПРИЗМ
- § 116. Полая эллиптическая призма
- § 117. Полая прямоугольная призма
- § 118. Полые призмы с другими основаниями
- ГЛАВА XII. СЛУЧАЙ ОДНОВРЕМЕННОГО КРУЧЕНИЯ, ИЗГИБА, УДЛИНЕНИЙ И ПОПЕРЕЧНЫХ СДВИГОВ. УСЛОВИЯ ПРОЧНОСТИ ПРИ ИХ ОДНОВРЕМЕННОМ ВОЗДЕЙСТВИИ
- § 119. Определение перемещений. Самое простое геометрическое сложение перемещений, вызванных различного рода усилиями
- § 120. Наложение перемещений, вызванных силами, производящими одновременно растяжение, изгиб и кручение призмы
- § 121. Общие условия прочности при различных воздействиях
- § 122. Более частные и более простые условия
- § 123. Простой и непосредственный вывод этих формул
- § 124. Формулы сопротивления в случае замены удлинений и сдвигов их выражениями через внешние силы, действующие на тело
- § 125. Видоизменения, касающиеся сдвигов, для некоторых особых сечений
- § 126. Первое применение. Призма, испытывающая одновременно изгиб и поперечный сдвиг. Случай, когда наиболее подверженное опасности сечение может изгибаться
- § 127. Та же призма. Случай, когда наиболее подверженное опасности сечение вынуждено оставаться плоским. Сомнительный случай
- § 128. Цилиндр с круговым основанием, одновременно изгибаемый, скручиваемый и растягиваемый
- § 129. Вращающийся вал, изгибаемый и скручиваемый посредством двух шестерен или двух приводных ремней. Консоль переменного диаметра, удовлетворяющая условию равного сопротивления
- § 130. Прямоугольная призма, одновременно изогнутая и скрученная. Общие формулы
- § 131. Та же прямоугольная призма. Случай ее изгибания в плоскости наиболее легкого изгиба, т.е. в плоскости, параллельной наименьшим сторонам 2c (см. § 133)
- § 132. Призма с квадратным основанием, изогнутая в любой плоскости и одновременно скрученная
- § 133. Призма с прямоугольным основанием, одна из сторон которого вдвое больше другой, изогнутая в любой плоскости, параллельной или наклоненной к ее граням, и одновременно скрученная
- § 134. Одновременный изгиб и кручение призм с другими основаниями (кроме круга и прямоугольника). Эллиптический цилиндр
- ГЛАВА XIII. РЕЗЮМЕ ЭТОГО МЕМУАРА, КРАТКОЕ ПОВТОРЕНИЕ ФОРМУЛ И ПРАКТИЧЕСКИЕ ПРАВИЛА, ЧИСЛЕННЫЕ ПРИМЕРЫ
- § 136. Краткое повторение формул и практические правила
- § 137. Числовые примеры
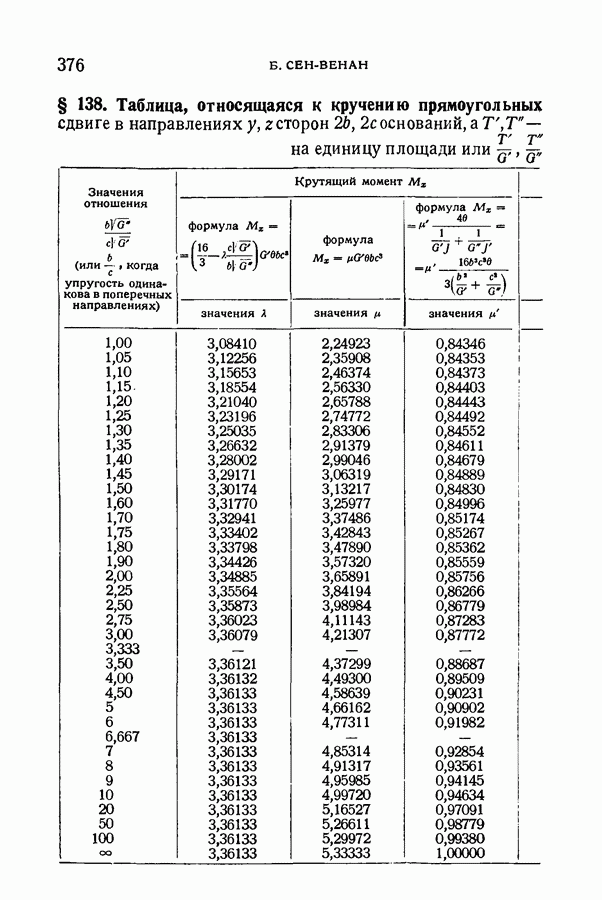
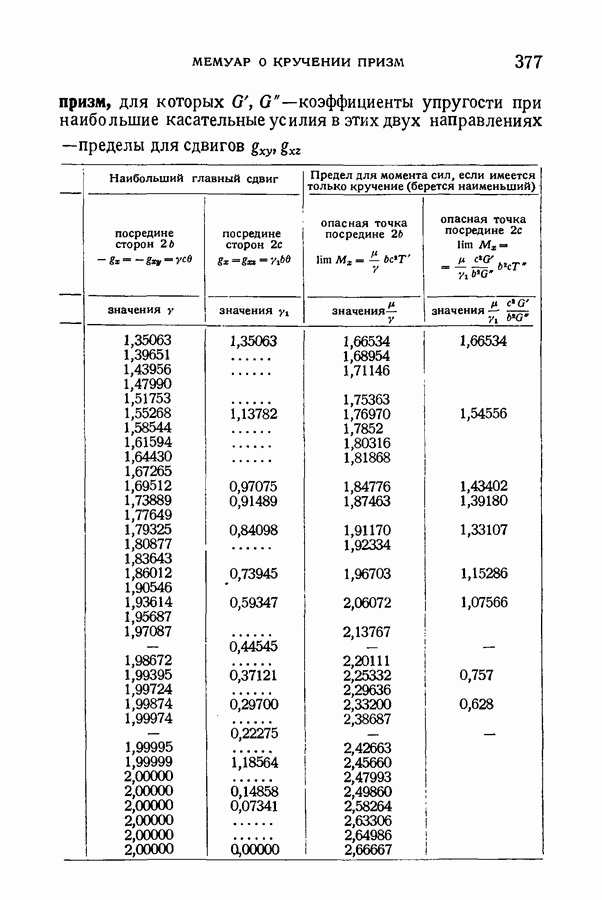
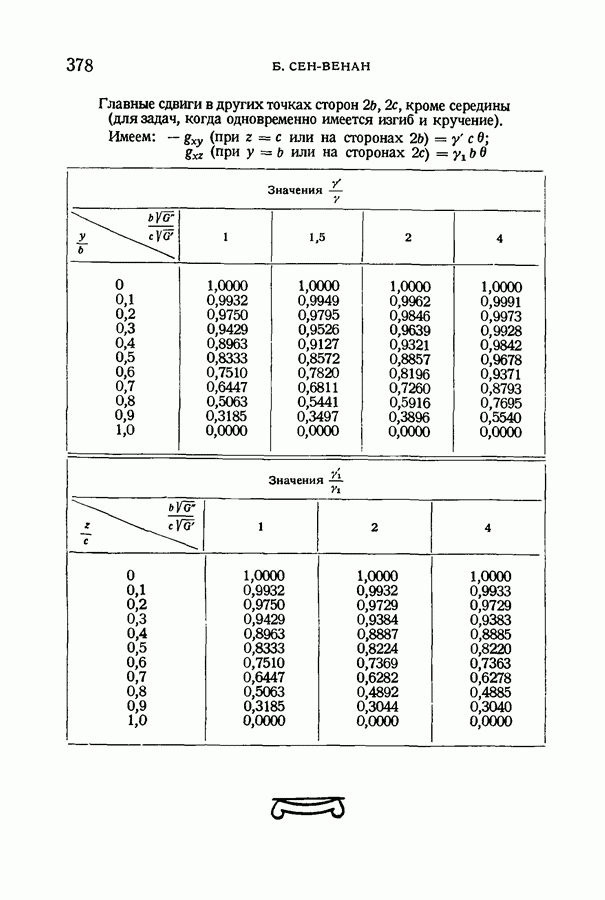
- § 138. Таблица, относящаяся к кручению прямоугольных призм
- МЕМУАР ОБ ИЗГИБЕ ПРИЗМ
- § 1. Прежние исследования по теории изгиба
- § 2. Принятая в настоящее время теория изгиба, вызванного неравномерным продольным растяжением волокон. Гипотезы, на которых она обычно основывается. Ненужность этих гипотез ввиду их неточности для вывода формул
- § 3. Предмет и краткое содержание этого мемуара
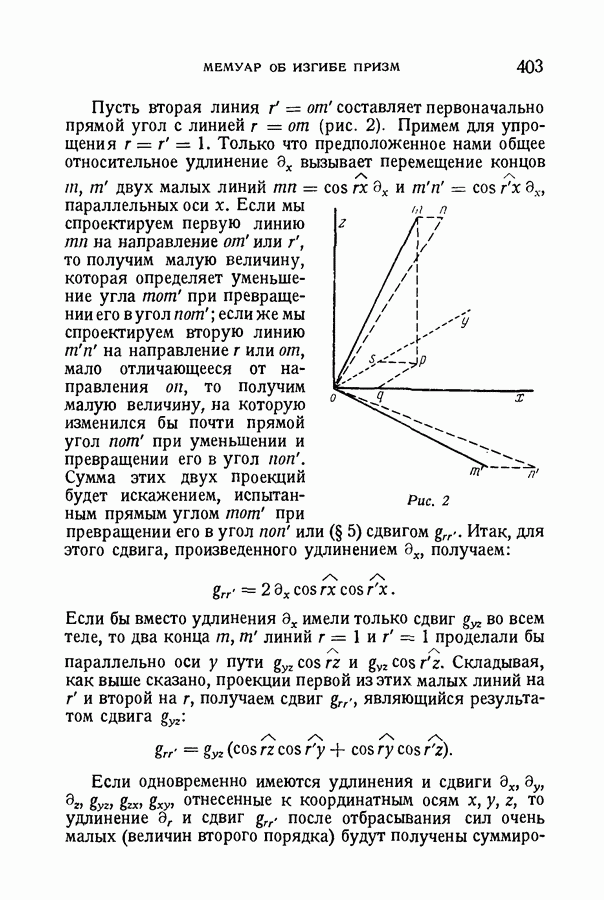
- § 4. Краткое разъяснение формул давлений внутри твердых упругих тел. Зависимости между давлениями в различных направлениях в одной точке
- § 5. Продолжение. Удлинения, сдвиги. Линейные выражения для составляющих давления
- § 6. Продолжение. Притяжения и отталкивания, функции молекулярных расстояний. Теорема геометрического сложения сил и малых перемещений
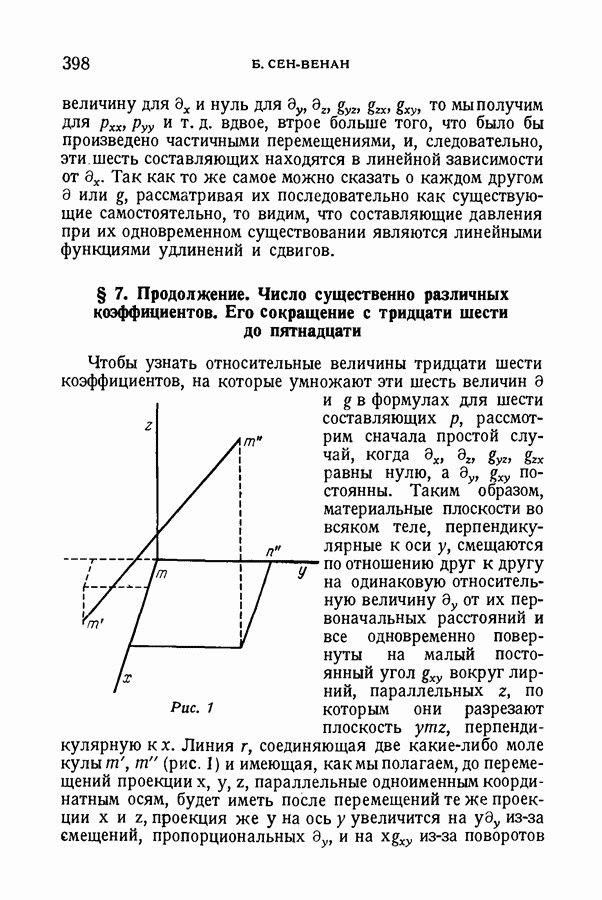
- § 7. Продолжение. Число существенно различных коэффициентов. Его сокращение с тридцати шести до пятнадцати
- § 8. Продолжение. Изменения осей и плоскостей, относительно которых рассматривают давления, удлинения и сдвиги
- § 9. Упрощение формул для составляющих давления в случае тел с различным строением
- § 10. Неопределенные дифференциальные уравнения равновесия упругих твердых тел. Выражения удлинений и сдвигов через очень малые перемещения
- § 11. Определенные уравнения, удовлетворяющиеся только в точках поверхности
- § 12. Применение этих формул к растяжению призмы. Сопровождающие его поперечные сжатия. Коэффициент упругости
- § 13. Применение общих формул Пуассоном и Коши для приближенного решения задачи изгиба
- § 14. Принятые условия и уравнения нашей задачи о неравномерном изгибе призм
- § 15. Первые следствия заданных условий и соотношений
- § 16. Первое интегрирование
- § 17. Распределение сил. Обстоятельства, сопровождающие неравномерный изгиб. Наклон и кривизна сечений. Взаимный наклон волокон. Полная стрела прогиба
- § 18. Кривые контуров сечений, для которых произвольная функция F полностью определяется через у и z. Эллиптический контур и т. д.
- § 19. Способ приложения и распределения внешних сил, уточняющий для различных контуров обычные формулы изгиба, вызванного продольными удлинениями. Значения величины центрального наклона. Сечения эллиптические, круговые, в виде ложного эллипса и т. д.
- § 20. Те же контуры. Полная стрела прогиба при изгибе
- § 21. Те же контуры. Искривленные поверхности, образованные первоначально плоскими сечениями. Их обычная топография
- § 22. Продолжение. Случай, когда каждая искривленная поверхность сечений является общей для бесконечного числа контуров
- § 23. Подробное изложение вопроса для различных сечений. Окружность. Ложный эллипс (овал). Сечения с контуром девятой степени, которые искривляются точно по цилиндрической поверхности с основанием в виде кривой третьей степени, имеющей форму гуська
- § 24. Прямоугольная призма. Преобразование неопределенных и определенных условий
- § 25. Интегрирование с помощью трансцендентного ряда
- § 26. Выражения для перемещений точек прямоугольной призмы
- § 27. Давления … Проверка полученных результатов
- § 28. Центральный сдвиг. Изогнутая ось. Стрела прогиба при изгибе
- § 29. Искривленная поверхность, образованная первоначально плоскими прямоугольными поперечными сечениями
- § 30. Сечения произвольной формы
- § 31. Непосредственное доказательство известных формул изгиба призм, вызванного только их продольными удлинениями
- § 32. Заключение. Общий обзор для случая, когда способ приложения и распределения внешних сил на концах призмы отличен от способа, дающего совершенно точные формулы в соответствии со смешанным методом