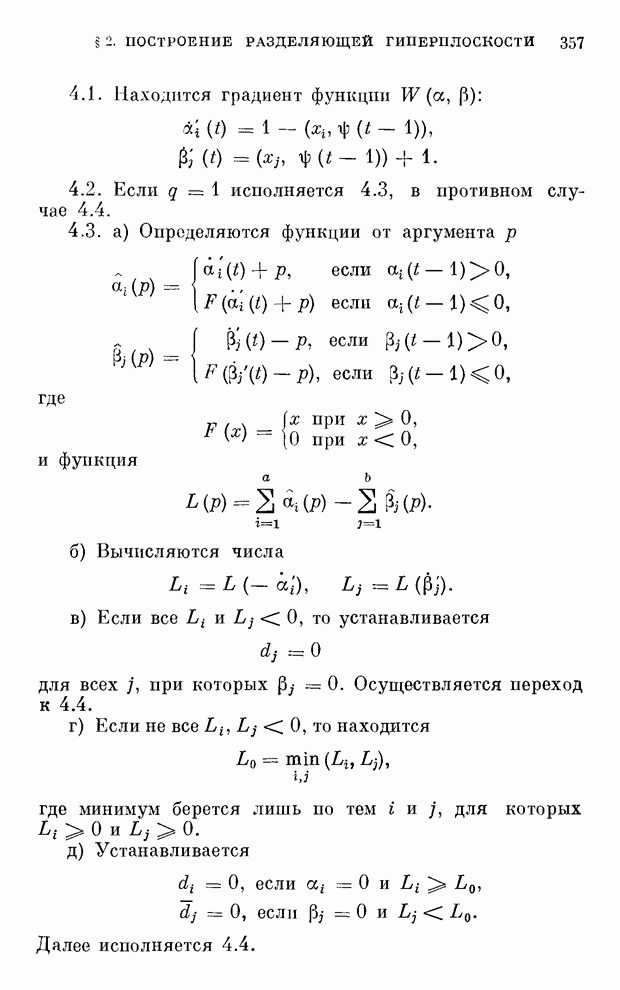| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 6. Градиентные методы построения разделяющей гиперплоскости (вычисление обобщенного портрета)
В предыдущем параграфе мы рассмотрели различные модификации метода Гаусса – Зайделя. Известно, что, вообще говоря, метод Гаусса – Зайделя является малоэффективным средством поиска максимума квадратичной формы. Поэтому хотелось бы использовать для построения разделяющей гиперплоскости более эффективные модификации методов поиска максимума квадратичной формы.
В настоящее время наиболее
эффективным методом максимизации квадратичной формы считается метод сопряженных
направлений. Особенность метода состоит в том, что с его помощью гарантируется
достижение точного максимума за ![]() шагов (
шагов (![]() – размерность квадратичной формы).
Подробно остановимся на методе сопряженных градиентов в главе XVI, а в этом
параграфе рассмотрим модификации этого метода для поиска максимума квадратичной
формы в положительном квадранте.
– размерность квадратичной формы).
Подробно остановимся на методе сопряженных градиентов в главе XVI, а в этом
параграфе рассмотрим модификации этого метода для поиска максимума квадратичной
формы в положительном квадранте.
Рассмотрим метод сопряженных градиентов
для поиска максимума квадратичной функции ![]() ; здесь
; здесь ![]() – положительно определенная матрица.
Согласно этому методу поиск максимума функции начинается в произвольной точке
– положительно определенная матрица.
Согласно этому методу поиск максимума функции начинается в произвольной точке ![]() . Первый шаг делается
в направлении градиента функции в этой точке. Обозначим градиент функции в
точке
. Первый шаг делается
в направлении градиента функции в этой точке. Обозначим градиент функции в
точке ![]() через
через
![]() ,
направление движения из точки
,
направление движения из точки ![]() через
через ![]() . Таким образом,
. Таким образом,
![]() .
.
Шаг делается в направлении ![]() до достижения максимума
по этому направлению. Согласно формуле (16.26) главы XVI точка
до достижения максимума
по этому направлению. Согласно формуле (16.26) главы XVI точка ![]() , доставляющая этот
максимум, задается выражением
, доставляющая этот
максимум, задается выражением
 ,
,
где
![]() – матрица
квадратичной формы функции
– матрица
квадратичной формы функции ![]() . Затем последовательно находятся точки
. Затем последовательно находятся точки ![]() . В общем случае
направление движения из точки
. В общем случае
направление движения из точки ![]() определяется (16.25) вектором
определяется (16.25) вектором
 , (14.17)
, (14.17)
где
![]() и
и ![]() – соответственно
градиенты функции
– соответственно
градиенты функции ![]() в
точках
в
точках ![]() и
и ![]() , a
, a ![]() – направление движения из точки
– направление движения из точки ![]() .
.
Движение по направлению ![]() ведется до
достижения условного максимума. Точка
ведется до
достижения условного максимума. Точка ![]() , доставляющая этот максимум, находится
(16.26) из выражения
, доставляющая этот максимум, находится
(16.26) из выражения
 . (14.18)
. (14.18)
Формулы
(14.17) и (14.18) задают, таким образом, алгоритм поиска максимума квадратичной
функции ![]() .
Как уже указывалось, этот метод гарантирует отыскание максимума за
.
Как уже указывалось, этот метод гарантирует отыскание максимума за ![]() шагов.
шагов.
Для вычисления максимума функции ![]() в положительном
квадранте можно использовать модификации метода сопряженных градиентов.
Модификации направлены на то, чтобы ограничить область поиска максимума
положительным квадрантом. При этом число шагов, необходимых для достижения
максимума, может быть большим
в положительном
квадранте можно использовать модификации метода сопряженных градиентов.
Модификации направлены на то, чтобы ограничить область поиска максимума
положительным квадрантом. При этом число шагов, необходимых для достижения
максимума, может быть большим ![]() , однако оно остается конечным.
, однако оно остается конечным.
Рассмотрим следующую модификацию метода сопряженных градиентов:
1) Поиск максимума функции ![]() в области
в области ![]() начинается с точки
начинается с точки ![]() . При этом движение
в соответствии с формулами (14.17) и (14.18) происходит лишь до тех пор, пока
точка
. При этом движение
в соответствии с формулами (14.17) и (14.18) происходит лишь до тех пор, пока
точка ![]() находится
внутри области
находится
внутри области ![]() .
Если траектория движения не выводит за ограничения, то не более чем за
.
Если траектория движения не выводит за ограничения, то не более чем за ![]() шагов максимум будет
найден.
шагов максимум будет
найден.
2) Если же на некотором шаге ![]() оказывается, что
точка, в которой достигается условный максимум по направлению, лежит за
пределами ограничений, то величина шага должна быть сокращена. Нетрудно
убедиться, что при этом максимально допустимая величина шага определяется
формулой
оказывается, что
точка, в которой достигается условный максимум по направлению, лежит за
пределами ограничений, то величина шага должна быть сокращена. Нетрудно
убедиться, что при этом максимально допустимая величина шага определяется
формулой
 , (14.19)
, (14.19)
где
минимум берется лишь по тем координатам ![]() , для которых
, для которых ![]() . При этом для всех
. При этом для всех ![]() оказывается
оказывается
![]() ,
,
но
по крайней мере для одной координаты ![]() окажется, что
окажется, что ![]() , т. е. движение происходит до
выхода на ограничение.
, т. е. движение происходит до
выхода на ограничение.
Итак, в этом случае
![]() .
.
3) Если на некотором шаге ![]() траектория выводит
на ограничение, т. е. величину шага приходится уменьшать по формуле (14.19), то
некоторые координаты
траектория выводит
на ограничение, т. е. величину шага приходится уменьшать по формуле (14.19), то
некоторые координаты ![]() обратятся в нуль. Дальнейший
поиск максимума ведется в положительном квадранте координатного подпространства
обратятся в нуль. Дальнейший
поиск максимума ведется в положительном квадранте координатного подпространства
![]() размерности
размерности
![]() ,
задаваемого уравнениями
,
задаваемого уравнениями
![]() .
.
Для этого действуем снова в
соответствии с пп. 1) и 2), но уже в подпространстве ![]() . При этом либо условный
максимум функции в этом подпространстве будет найден не более чем за
. При этом либо условный
максимум функции в этом подпространстве будет найден не более чем за ![]() шагов, либо при
поиске еще раз будут нарушены ограничения. В последнем случае вновь сокращается
размерность пространства и ищется условный максимум функции в положительном
квадранте нового подпространства.
шагов, либо при
поиске еще раз будут нарушены ограничения. В последнем случае вновь сокращается
размерность пространства и ищется условный максимум функции в положительном
квадранте нового подпространства.
4) Так продолжается до тех пор,
пока в положительном квадранте некоторого координатного подпространства ![]() не будет найден
условный максимум функции. Пусть он достигается в точке
не будет найден
условный максимум функции. Пусть он достигается в точке ![]() . Если при этом выполняются
условия:
. Если при этом выполняются
условия:
 ,
если
,
если ![]() ,
,
 ,
если
,
если ![]()
![]() ,
,
то
в действительности точка ![]() доставляет условный максимум функции и
в положительном квадранте исходного пространства
доставляет условный максимум функции и
в положительном квадранте исходного пространства ![]() . В противном случае точка
. В противном случае точка ![]() берется за начальную
и поиск максимума продолжается по той же схеме, начиная с п. 1).
берется за начальную
и поиск максимума продолжается по той же схеме, начиная с п. 1).
Легко убедиться в том, что при
подобной модификации метода сопряженных градиентов максимум функции ![]() будет найден за
конечное число шагов. В самом деле, в силу алгоритма каждый раз за конечное
число шагов будет достигаться условный максимум на соответствующем
подпространстве
будет найден за
конечное число шагов. В самом деле, в силу алгоритма каждый раз за конечное
число шагов будет достигаться условный максимум на соответствующем
подпространстве ![]() ,
причем каждый раз условный максимум будет достигаться на разных координатных
подпространствах. Конечность числа шагов следует из того, что число различных
координатных подпространств конечно.
,
причем каждый раз условный максимум будет достигаться на разных координатных
подпространствах. Конечность числа шагов следует из того, что число различных
координатных подпространств конечно.
Рассмотрим еще одну модификацию метода сопряженных градиентов.
Определим следующую функцию ![]() :
:
 .
.
Вектор
![]() есть
условный градиент функции
есть
условный градиент функции ![]() на множестве
на множестве ![]() (см. формулу (П. 8)
приложения). Будем теперь совершать восхождение к максимуму, используя (14.17),
(14.18), (14.19), где
(см. формулу (П. 8)
приложения). Будем теперь совершать восхождение к максимуму, используя (14.17),
(14.18), (14.19), где ![]() заменено на условный градиент
заменено на условный градиент ![]() . Движение начинается
из произвольной точки положительного квадранта и происходит до момента
нарушения ограничения в точке
. Движение начинается
из произвольной точки положительного квадранта и происходит до момента
нарушения ограничения в точке ![]() . Тогда снова начинается восхождение по
методу сопряженных градиентов из точки
. Тогда снова начинается восхождение по
методу сопряженных градиентов из точки ![]() и т. д. Поиск максимума заканчивается,
когда выполнятся неравенства
и т. д. Поиск максимума заканчивается,
когда выполнятся неравенства
![]() .
.
Важной особенностью
модифицированного метода поиска максимума функции ![]() в положительном квадранте является то
обстоятельство, что он допускает последовательную процедуру поиска. Пусть
пространство
в положительном квадранте является то
обстоятельство, что он допускает последовательную процедуру поиска. Пусть
пространство ![]() имеет
координаты
имеет
координаты ![]() .
Можно сначала найти условный максимум функции при ограничениях
.
Можно сначала найти условный максимум функции при ограничениях ![]() и
и ![]() . Затем, используя
найденную точку максимума как начальную точку, найти максимум
. Затем, используя
найденную точку максимума как начальную точку, найти максимум ![]() в области
в области ![]() .
.
Применим вторую модификацию
метода сопряженных градиентов к задаче нахождения обобщенного портрета. Максимизируемая
функция ![]() имеет
вид
имеет
вид
 .
.
Квадратичная часть этой функции есть
 .
.
Обозначим составляющие условного градиента через


где
положено  .
Обозначим составляющие вектора
.
Обозначим составляющие вектора ![]() , задающего направление движения на
, задающего направление движения на ![]() -м шаге, через
-м шаге, через ![]() ,
, ![]() .
.
При вычислении величины шага по
формуле (14.18) необходимо вычислять величину ![]() , т. е. значение квадратичной функции
, т. е. значение квадратичной функции ![]() при подстановке в
нее вектора
при подстановке в
нее вектора ![]() .
В нашем случае
.
В нашем случае
 ,
,
где обозначено
![]() .
.
Таким образом, заменяя формулы (14.17), (14.18) и (14.19) в соответствии с введенными обозначениями, приходим к следующему алгоритму.
Находится условный градиент в
точке ![]() :
:

 ,
,
Определяется направление движения:
![]() ,
,
![]() ,
,
где
 .
.
Далее вычисляется
 .
.
Новое значение ![]() и
и ![]() находится по
формулам
находится по
формулам
![]() ,
,
![]() .
.
Здесь
![]() – величина
шага, определяемая из условия достижения максимума по направлению или выхода на
ограничение:
– величина
шага, определяемая из условия достижения максимума по направлению или выхода на
ограничение:
![]() ,
,
где
 ,
,


Наконец,
![]() .
.
Первый шаг ![]() отличается от общего лишь
тем, что значения
отличается от общего лишь
тем, что значения ![]() ,
,
![]() задаются
следующим образом
задаются
следующим образом
![]() ,
,
![]() .
.
Критерий останова:  и
и  или
или ![]() .
.
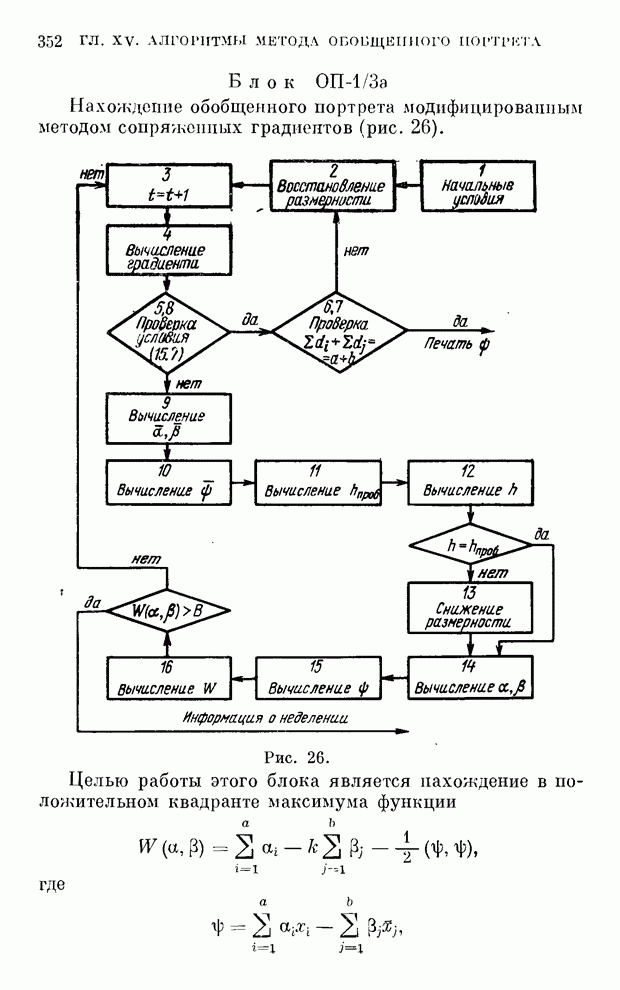
В главе XV будет подробно рассмотрена структура алгоритма построения обобщенного портрета на основе метода сопряженных градиентов в первой модификации.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ЧАСТЬ ПЕРВАЯ ЭЛЕМЕНТАРНАЯ ТЕОРИЯ
- Глава I. Персептрон Розенблатта
- § 1. Феномен восприятия
- § 2. Физиологическая модель восприятия
- § 3. Техническая модель. Персептрон
- § 4. Математическая модель
- § 5. Обобщенная математическая модель
- § 6. Теорема Новикова
- § 7. Доказательство теоремы Новикова
- § 8. Двухуровневая схема распознавания
- Глава II. Задача обучения машин распознаванию образов
- § 1. Задача имитации
- § 2. Качество обучения
- § 3. Надежность обучения
- § 4. Обучение – задача выбора
- § 5. Две задачи конструирования обучающихся устройств
- § 6. Математическая постановка задачи обучения
- § 7. Три пути решения задачи о минимизации среднего риска
- § 8. Задача обучения распознаванию образов и методы минимизации среднего риска
- Глава III. Методы обучения, основанные на восстановлении распределения вероятностей
- § 1. О восстановлении распределения вероятностей
- § 2. Классификация оценок
- § 3. Метод максимума правдоподобия
- § 4. Байесов принцип восстановления
- § 5. Сравнение байесова метода оценивания и оценивания методом максимума правдоподобия
- § 6. Оценка параметров распределения дискретных независимых признаков
- § 7. Байесовы оценки параметров распределения дискретных независимых признаков
- § 8. Восстановление параметров нормального распределения методом максимума правдоподобия
- § 9. Байесов метод восстановления нормального распределения
- Глава IV. Рекуррентные алгоритмы обучения распознаванию образов
- § 1. Метод стохастической аппроксимации
- § 2. Детерминистская и стохастическая постановки задачи обучения распознаванию образов
- § 3. Конечно-сходящиеся рекуррентные процедуры
- § 4. Теоремы об останове
- § 5. Метод циклического повторения обучающей последовательности
- § 6. Метод потенциальных функций
- Глава V. Алгоритмы, минимизирующие эмпирический риск
- § 1. Метод минимизации эмпирического риска
- § 2. Равномерная сходимость частот появления событий к их вероятностям
- § 3. Теорема Гливенко
- § 4. Частный случай
- § 5. Оценка числа различных линейных разделений векторов
- § 6. Условия равномерной сходимости частот появления событий к их вероятностям
- § 7. Свойства функции роста
- § 8. Оценка уклонения эмпирически оптимального решающего правила
- § 9. Метод минимизации эмпирического риска в детерминистской постановке задачи обучения распознаванию образов
- § 10. Замечание об оценке скорости равномерной сходимости частот появления событий к их вероятностям
- § 11. Замечания об особенностях метода минимизации эмпирического риска
- § 12. Алгоритмы метода обобщенного портрета
- § 13. Алгоритм Кора
- Глава VI. Метод упорядоченной минимизации риска
- § 1. О критериях оценки качества алгоритмов
- § 2. Минимаксный критерий
- § 3. Критерий минимакса потерь
- § 4. Критерий Байеса
- § 5. Упорядочение классов решающих правил
- § 6. О критериях выбора
- § 7. Несмещенность оценки скользящего контроля
- § 8. Упорядочение по размерностям
- § 9. Упорядочение по относительным расстояниям
- § 10. Упорядочение по эмпирическим оценкам относительного расстояния и задача минимизации суммарного риска
- § 11. О выборе оптимальной совокупности признаков
- § 12. Алгоритмы упорядоченной минимизации суммарного риска
- § 13. Алгоритмы построения экстремальных кусочно-линейных решающих правил
- § 14. Приложение к главе VI
- Глава VII. Примеры применения методов обучения распознаванию образов
- § 1. Задача о различении нефтеносных и водоносных пластов в скважине
- § 2. Задача о различении сходных почерков
- § 3. Задача о контроле качества продукции
- § 4. Задача о прогнозе погоды
- § 5. Применение метода обучения распознаванию образов в медицине
- § 6. Замечания о применениях методов обучения распознаванию образов
- Глава VIII. Несколько общих замечаний
- § 1. Еще раз о постановке задачи
- § 2. Физики об интуиции
- § 3. Машинная интуиция
- § 4. О мире, в котором возможна интуиция
- Часть вторая. СТАТИСТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ
- Глава IX. О сходимости рекуррентных алгоритмов обучения распознаванию образов
- § 1. Определение понятия сходимости
- § 2. Выпуклые функции
- § 3. Обобщенный градиент
- § 4. Условия сходимости рекуррентных алгоритмов
- § 5. Еще одно условие сходимости рекуррентных алгоритмов
- Глава X. Достаточные условия равномерной сходимости частот к вероятностям по классу событий
- § 1. О близости минимума эмпирического риска к минимуму среднего риска
- § 2. Определение равномерной сходимости частот к вероятностям
- § 3. Определение функции роста
- § 4. Свойства функции роста
- § 5. Основная лемма
- § 6. Вывод достаточных условий равномерной сходимости частот к вероятностям по классу событий
- § 7. О равномерной сходимости с вероятностью единица
- § 8. Примеры и дополнительные замечания
- § 9. Приложение к главе X
- Глава XI. Необходимые и достаточные условия равномерной сходимости частот к веронтностям по классу событий
- § 1. Энтропия системы событий
- § 2. Асимптотические свойства энтропии
- § 3. Необходимые и достаточные условия равномерной сходимости (доказательство достаточности)
- § 4. Доказательство необходимости условий равномерной сходимости
- § 5. Примеры и дополнительные критерии
- Глава XII. Оценки равномерного относительного уклонения частот от вероятностей в классе событий
- § 1. О равномерном относительном уклонении
- § 2. Оценка равномерного относительного уклонения частот в двух полувыборках
- § 3. Оценка равномерного относительного уклонения частот от вероятностей
- Глава XIII. Применение теории равномерной сходимости к методам минимизации эмпирического риска
- § 1. Оценка достаточной длины обучающей последовательности в задачах обучения распознаванию
- § 2. Равномерная сходимость средних к математическим ожиданиям
- Часть третья. МЕТОДЫ ПОСТРОЕНИЯ РАЗДЕЛЯЮЩИХ ПОВЕРХНОСТЕЙ
- Глава XIV. Построение разделяющей гиперплоскости (метод обобщенного портрета)
- § 1. Оптимальная разделяющая гиперплоскость
- § 2. Однопараметрическое семейство разделяющих гиперплоскостей
- § 3. Некоторые свойства обобщенного портрета
- § 4. Двойственная задача
- § 5. Алгоритмы персептронного типа
- § 6. Градиентные методы построения разделяющей гиперплоскости (вычисление обобщенного портрета)
- § 7. Теория оптимальной разделяющей гиперплоскости
- § 8. Двойственная задача
- § 9. Методы вычисления оптимальной разделяющей гиперплоскости
- § 10. Построение оптимальной разделяющей гиперплоскости модифицированным методом Гаусса–Зайделя
- § 11. Применение метода обобщенного портрета для нахождения оптимальной разделяющей гиперплоскости
- § 12. Некоторые статистические особенности метода обобщенного портрета
- § 13. Приложение к главе XIV
- Глава XV. АЛГОРИТМЫ ОБУЧЕНИЯ РАСПОЗНАВАНИЮ ОБРАЗОВ, РЕАЛИЗУЮЩИЕ МЕТОД ОБОБЩЕННОГО ПОРТРЕТА
- § 1. Способы представления информации
- § 2. Алгоритм построения разделяющей гиперплоскости
- § 3. Алгоритм построения разделяющей гиперплоскости, минимизирующей число ошибочно классифицируемых векторов
- § 4. Алгоритм построения кусочно-линейной разделяющей поверхности
- § 5. Алгоритмы построения разделяющей гиперплоскости в пространстве минимального числа признаков
- § 6. Алгоритм построения экстремальной линейной разделяющей поверхности
- § 7. Алгоритм построения экстремальной кусочно-линейной разделяющей поверхности
- § 8. Алгоритм построения разделяющей гиперплоскости с оценкой ее качества методом скользящего контроля
- § 9. Алгоритмы построения экстремальных разделяющих гиперповерхностей с помощью процедуры скользящий контроль
- § 10. О работе с алгоритмами
- Глава XVI. МЕТОД СОПРЯЖЕННЫХ НАПРАВЛЕНИЙ
- § 1. Идея метода
- § 2. Метод сопряженных градиентов
- § 3. Метод параллельных касательных (партан)
- § 4. Анализ погрешностей метода
- КОММЕНТАРИИ
- ЛИТЕРАТУРА