КОММЕНТАРИИ

К главе I

Считается, что первой работой, положившей начало исследованию в области обучения распознаванию образов, была работа Ф. Розенблатта [90]. Американский физиолог Ф. Розенблатт рассмотрел модель восприятия, которая, вообще говоря, не являлась новой в физиологии. Однако в отличие от других физиологов Ф. Розенблатт построил эту модель не умозрительно, а в виде технического устройства, которое он назвал персептроном. Первоначально алгоритм построения весов -элементов персептрона (алгоритм поощрения в терминологии Ф. Розенблатта) отличался от того алгоритма построения разделяющей гиперплоскости, который был описан в главе I. Сразу же после публикации сообщения о персептроне появилось множество различных исследований законов поощрения. Все они, как правило, обосновывались ссылками на физиологические феномены. И только с появлением теоремы американского математика А. Новикова [87] алгоритм построения весов -элементов получил геометрическую интерпретацию. В свое время теорема А. Новикова произвела чрезвычайно сильное впечатление на исследователей. Достаточно сказать, что она была передоказана не менее чем десятью авторами.

Теорема Новикова явилась поворотным пунктом в исследовании феномена восприятия. Она продемонстрировала, что исследования можно вести на языке математики, и это во многом определило стиль и уровень последующих работ.

Что касается дальнейших построений моделей восприятия, то они пошли по пути усложнения конструкции персептрона. Ф. Розенблатт строил и многослойные персептроны, и персептроны с перекрестными связями [54]. Однако эти модели, как правило, не оправдывали возложенных на них надежд – на них не удалось продемонстрировать ни новых свойств восприятия, ни получить новых теоретических результатов. Подробно исследование возможных и невозможных путей обобщения с помощью персептрона рассмотрено в книге М. Минского, С. Пейперта «Персептроны» [46].

В дальнейшем исследование феномена восприятия пошло по пути моделирования на ЭВМ. Однако после появления персептрона в технике возник интерес к адаптирующимся элементам. Так были построены на фотохимическом принципе обучающаяся матрица К. Штейнбуха [92], адалины Б. Уидроу [94, 95]. Эти элементы находят применение в различных технических конструкциях.

Что касается закона поощрения -элементов персептрона, то, как теперь выясняется, он фактически реализует релаксационные методы решения линейных неравенств, рассмотренные еще в 1954 г. Т. Моцкиным и И. Шенбергом [86].

К главе II

Сейчас, вероятно, трудно определить, кто первый предложил рассматривать задачу обучения распознаванию образов как задачу минимизации среднего риска. Такие работы постановочного характера появились в начале 60-х годов почти одновременно. При этом уже с самого начала обнаруживалась «специализация» в постановке. Одни авторы [53, 72, 73, 74] примыкали к классическим работам дискриминантного анализа и рассматривали задачу обучения распознаванию образов как задачу параметрической статистики, другие [1, 67, 68, 70, 71] предпочитали видеть проблему обучения в создании алгоритмов постепенного улучшения качества решающего правила (рекуррентных алгоритмов), третьи связывали алгоритмы обучения распознаванию образов с методом минимизации эмпирического риска [9–19, 24, 41, 81].

Иначе говоря, при постановке задачи методы обучения распознаванию образов оказались связанными со всеми тремя путями минимизации риска.

Интересно отметить, что содержательная постановка задачи обучения распознаванию образов появилась в 1957–1958 годах, а формальная постановка – только в 1962–1966 годах. Эти пять – восемь лет от содержательной до формальной постановки были чрезвычайно яркими годами – годами «распознавательной романтики». В те времена казалось, что задача обучения распознаванию образов несет в себе начало какой-то новой, никак не основанной на системе старых понятий, идеи, хотелось найти новые постановки, а не сводить задачу к уже известным математическим схемам. В этом смысле сведение задачи обучения распознаванию образов к схеме минимизации среднего риска вызывает некоторое разочарование. Правда, существуют попытки понять задачу в более сложной постановке [32]. Однако таких работ пока чрезвычайно мало.

Сейчас, через много лет после периода «распознавательной романтики», трудно оценить, что принесла формализация задачи. Не оказалось ли так, что из стремления найти строгую постановку пришлось сузить ту содержательную задачу, которую пытались решать в начале 60-х годов.

К главе III

Вероятно, трудно различить, где кончаются классические методы дискриминантного анализа и начинается задача обучения распознаванию образов, решаемая методами параметрической статистики. По определению задача дискриминантного анализа состоит в отнесении объекта к одному из  классов, заданных функциями распределения. На практике почти все исследования проводятся для случая, когда плотности распределения вероятностей векторов каждого класса заданы нормальным законом. Проблемы, которые подымались дискриминантным анализом, в основном концентрировались вокруг построения линейной дискриминантной функции. Постановка такой задачи впервые была дана Р. Фишером [77], который для решения ее предложил минимизировать некоторую функцию (функцию Фишера). В 1962 году задача построении линейной дискриминантной функции для нормальных распределений была решена Т. В. Андерсоном и Р. Р. Бахадуром [74, 2].

Другие исследования связаны с попыткой сформулировать функционал, минимизация которого приводила бы к построению линейной дискриминантной функции (не только для нормальных распределений). Сначала в качестве такого функционала использовали функцию Фишера, а затем рассматривались и другие функции [62]. Подробный обзор литературы по дискриминантному анализу приведен в [63].

Случай независимо распределенных дискретных признаков также известен в дискриминантном анализе. В 1952 году А. М. Аттли [93] построил на этом принципе вероятностный дискриминантный автомат, алгоритм которого, по существу, мало чем отличается от совместных алгоритмов, использующих гипотезу о независимости дискретных признаков.

В общем, различая работы по классическому дискриминантному анализу и параметрическим методам обучения распознаванию образов, вероятно, можно указать на то, что в последних как-то больше акцентируется внимание на восстановлении параметров распределения с учетом ограниченности объема выборки.

К главе IV

Идея метода стохастической аппроксимации возникла, по-видимому, давно, но в четкой форме была сформулирована в 1951 году Г. Роббинсом и С. Монро [89]. Они указали итеративную процедуру, позволяющую определять корень уравнения регрессии. В 1952 году Е. Кифер и Дж. Вольфовиц применили этот метод для поиска минимума функционала [82]. Начиная с этого времени ведутся работы по определению условий сходимости метода. Подробно с библиографией метода стохастической аппроксимации можно ознакомиться в обзоре [42]. В 1965 году Я. З. Цыпкин указал на связь метода стохастической аппроксимации с рекуррентными алгоритмами обучения распознаванию образов [67, 68]. Эти работы стимулировали исследования по теории метода стохастической аппроксимации.

С 1964 года М. А. Айзерман, Э. М. Браверман, JI. И. Розоноэр разрабатывали теорию метода потенциальных функции, которая оказалась чрезвычайно близкой теории стохастической аппроксимации. Этими учеными получены достаточно тонкие условия сходимости процедур стохастической аппроксимации [1]. Дальнейшие обобщения были получены недавно Б. Т. Поляком и Я. З. Цыпкиным [52].

Конечно-сходящиеся рекуррентные алгоритмы исследовал В. А. Якубович [70, 71]. Ему же принадлежит и сам термин.

К главе V

Построение алгоритмов обучения распознаванию образов на основе методов минимизации эмпирического риска началось сразу же с появлением первых работ Ф. Розенблатта. За границей – это работы О. Селфриджа [91], система программ Г. С. Себастиана [58], в СССР работы [9–19]. Однако наиболее четко идеология минимизации эмпирического риска проявились у В. Хайлимена [81]. Хайлимен предлагал различные алгоритмы построения линейного решающего правила, минимизирующего число ошибок. Он оценивал вероятность ошибок на экзамене по частоте ошибок на обучении и применял сглаживание функции штрафа для построения эффективного алгоритма минимизации. Обобщение этой постановки на произвольные классы решающих правил было дано в работе [41].

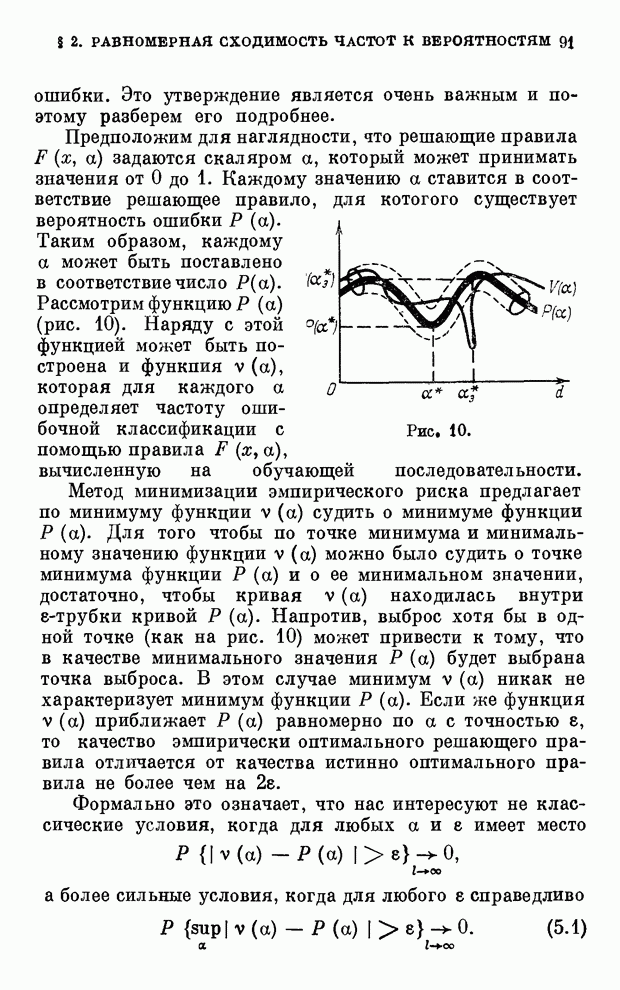
Впервые идея о связи равномерной близости частот к вероятностям по классу событий с оценкой качества алгоритма, минимизирующего эмпирический риск, была высказана в работе [16]. Однако в этой работе был исследован лишь случай конечного числа событий. Затем удалось получить условие равномерной сходимости для случая, когда частоты равны нулю [17]. И, наконец, были получены исчерпывающие необходимые и достаточные условия равномерной сходимости частот появления событий к их вероятностям [18].

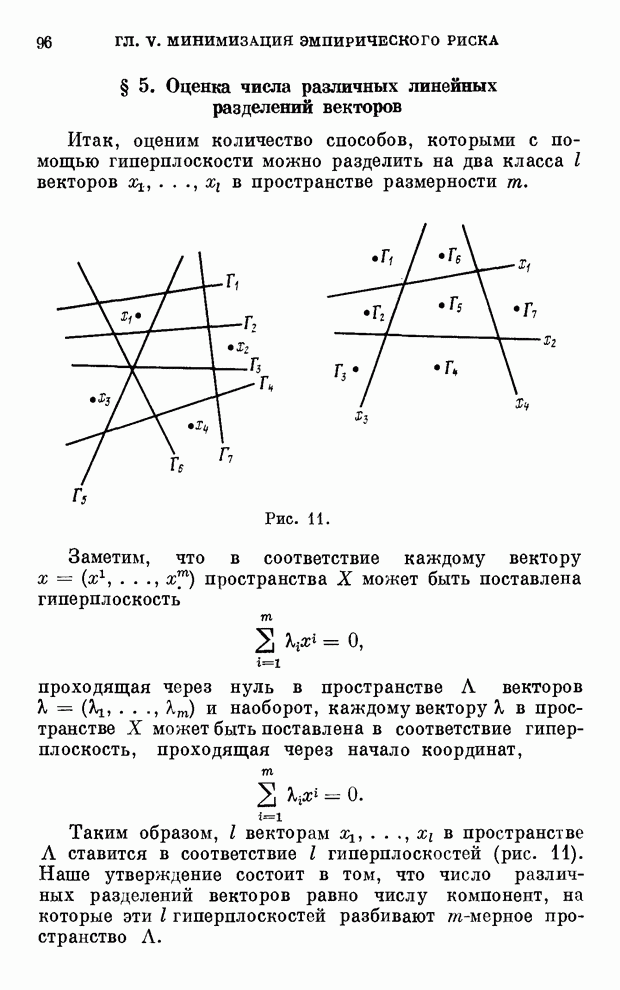
Несмотря на то, что условия равномерной сходимости частот к вероятностям не были известны, многие авторы понимали, что емкость класса решающих правил влияет на экстраполяционную способность алгоритма. Такие идеи можно проследить у М. М. Бонгарда [4]. Н. Нельсон в своей монографии [49] приводит оценку числа линейных решающих правил, разделяющих в -мерном пространстве  векторов.

Что же касается конструктивных идей построения алгоритмов обучения распознаванию образов, реализующих метод минимизации эмпирического риска, то они много разнообразней идей, основанных на реализации других методов минимизации среднего риска. Во всяком случае методы минимизации эмпирического риска позволяют эффективно искать решающие правила не только в классе линейных или кусочно-линейных правил, но и в иных классах решающих правил, например в классе логических функций определенного вида [4, 9, 10].

К главе VI

Одной из наиболее важных особенностей в исследованиях обучения распознаванию образов является стремление строить конструктивные методы обучения более эффективные, чем те, которые вытекают из стандартных приемов минимизации риска, принятых в математической статистике. Здесь существует два возможных направления исследования, идя по которым можно надеяться достигнуть успеха.

Первое направление связано с определением класса решающих правил, внутри которого ищется нужное. Классическая статистика игнорирует такую проблему, отмечая, что априори нет никаких формальных способов определить, какой класс решающих правил окажется предпочтительнее, и поэтому определение класса решающих правил считается внешним моментом в постановке задачи. В теории же обучения распознаванию образов допускаются неформальные методологические соображения.

Второе направление связано с созданием конструктивных квазибайесовых процедур, использующих некоторые априорные гипотезы о характере тех задач, которые предстоит решать.

Первые работы по теории обучения распознаванию образов во многом были посвящены исследованию этих двух особенностей задачи. Именно поэтому период «распознавательной романтики» так богат гипотезами о структуре «разумных» задач. В этом отношении, вероятно, наиболее интересной работой остается монография М. М. Бонгарда [4]. Гипотеза о структуре «разумных» задач, по существу, содержится и в алгоритмах Браиловского – Лунца [5], [6], и в идеях раздвигающей метрики Себастиана – Неймарка [48], [58], и во многих других алгоритмах. Наконец, следует отметить работу Н. В. Загоруйко [30], который явно высказал гипотезу о структуре «разумных» задач в терминах сложности. Во всех этих работах гипотеза о структуре «разумных» задач нужна была для того, чтобы ввести априорное упорядочение возможных задач и искать решение не в классе всех возможных задач, а в некотором подклассе, т. е., по существу, для того, чтобы провести идею упорядочения минимизации риска.

Следует отметить, что идея упорядоченной минимизации риска не является новой в математике. Она появлялась каждый раз, когда метод минимизации эмпирического риска приводил к абсурдным результатам. Впервые, вероятно, эта идея возникла при исследовании задачи об определении степени полиномиальной регрессии. Известно, что если априори задана степень полиномиальной регрессии, то метод наименьших квадратов является, вообще говоря, эффективным средством построения регрессии [43]. Другое дело, если заранее степень регрессии неизвестна и предлагается, используя выборку фиксированной длины, определить и степень регрессии и значение ее параметров. В этом случае заранее известно, что минимум эмпирического риска будет достигнут, если степень полинома равна длине выборки. Однако такое решение является абсурдным. Поэтому в свое время К. Ф. Гаусс предложил минимизировать не величину эмпирического риска , а величину , где  – объем выборки, a  – степень полинома. По существу, эта процедура поиска полиномиальной регрессии является двухуровневой процедурой. На первом уровне методом наименьших квадратов строится  оценка регрессии различной степени, а на втором уровне выбирается то решение, которое минимизирует приведенную оценку.

С тех пор предлагалось много идей поиска полиномиальной регрессии, однако все они касались лишь критерия выбора второго уровня, оставляя неизменной двухуровневую схему упорядоченной минимизации риска.

Идея упорядоченной минимизации появилась и в связи с решением некорректных задач математической физики. Согласно А. Н. Тихонову [60], решение уравнения

называется корректным, если оно существует, единственно и если малой вариации  соответствует малое изменение . Однако уже для простейших задач (таких как решение некоторых типов линейных интегральных уравнений) последнее условие не имеет места: достаточно малому изменению  может соответствовать большое изменение . Такая неустойчивость решения делает организацию поиска решения невозможной. Поэтому А. Н. Тихонов предложил искать решение не путем минимизации

,             (*)

а минимизируя функционал

,                      (**)

где  – есть некоторая константа.

Последний метод носит название метода регуляризации Тихонова [61]. Заметим, что регуляризация по Тихонову есть тоже проявление метода упорядоченной минимизации. В самом деле, введем сначала априорный порядок в классе возможных решений

     ,

на первом уровне в каждом классе найдем решение , доставляющее условный минимум , а затем из найденных решений отберем то, которое удовлетворит критерию выбора второго уровня. Такая процедура поиска решения эквивалентна минимизации функционала , причем значение  определяет правило выбора второго уровня. В самом деле, минимизация (*) при условии  эквивалентна минимизации (**), где  – множитель Лагранжа.

Таким образом, оказывается, что идея упорядоченной минимизации риска уже встречалась в математике. Однако ни для одной из проблем, к решению которой она привлекалась, так и не удалось до конца ответить на вопросы: как вводить априорное упорядочение и каков должен быть критерий выбора второго уровня.

В задаче обучения распознаванию образов были рассмотрены две процедуры выбора второго уровня: процедура метода скользящего контроля [45] и процедуры выбора правила с наилучшим гарантированным качеством. Что же касается способов введения порядка, то, как оказалось, в задаче обучения распознаванию образов они далеко не безразличны даже с формальной точки зрения.

К главе VII

Применение методов обучения распознаванию образов началось одновременно с появлением первых работ по теории обучения. В настоящее время установилась хорошая традиция, согласно которой каждый вновь предложенный алгоритм обучения немедленно опробывается на решении тех или иных задач практики. Установились и свои традиционные сферы приложения методов обучения к решению задач практики.

Это прежде всего – геология, метеорология, контроль качества, медицина, криминалистика. Большие работы ведутся по созданию буквочитающих автоматов, автоматов воспринимающих речь.

В главе VII приведены результаты практического применения алгоритмов метода обобщенного портрета. Эти результаты могли быть получены только благодаря работам больших коллективов ученых. Так, задача о различении водоносных и нефтеносных пластов в скважине была поставлена в Московском институте нефтехимической и газовой промышленности под руководством Ш. А. Губермана [25] и была успешно решена также группой М. М. Бонгарда, работы по криминалистике поставлены в Институте судебных экспертиз под руководством JI. Г. Эджубова [28], работы по контролю качества электронных приборов были поставлены В. С. Морозовым [47], работы по применению методов обучения распознаванию образов в метеорологии ведутся в Гидрометцентре СССР под руководством А. И. Снитковского [3] и в ВЦСО АН СССР под руководством Л. Н. Романова [56]; наконец, работы но применению методов обучения в медицине ведутся в Институте экспериментальной и клинической онкологии под руководством Т. Г. Глазковой и К. Н. Гурария [23] и в I Московском медицинском институте под руководством Л. Д. Линденбратена. Благодаря этим коллективам была отработана стандартная методика использования алгоритмов метода обобщенного портрета, найдены оптимальные параметры алгоритмов, словом, сделано все, что необходимо для того, чтобы алгоритмы превратить в рабочий инструмент для решения практических задач.

Кроме названных, существует большое количество других коллективов, которые успешно применяют современные методы обучения распознавания образов для решения задач практики. В Москве это – группы С. Н. Браинеса, П. Е. Кунина, которые применяют методы распознавания в медицине [7, 38]; коллектив, возглавляемый Ю. И. Журавлевым, который ведет большие работы по применению распознавания в геологии [29]. В Ленинграде коллектив сотрудников, возглавляемый В. А. Якубовичем, провел значительные исследования в криминалистике [35]. В Горьком большая группа сотрудников под руководством Ю. И. Неймарка весьма успешно применяет методы обучения распознаванию образов в медицине [48]. В Новосибирске коллектив, возглавляемый И. Г. Загоруйко [30], применяет методы распознавания в социологии и другие. В настоящее время идея применения методов обучения распознаванию образов весьма популярна и эти методы привлекаются для решения самых различных задач практики.

Особое место в практическом применении методов обучения распознаванию образов занимают работы по созданию читающих автоматов и автоматов, воспринимающих речь. Эти задачи явились первыми объектами приложения методов обучения распознаванию образов.

Однако, несмотря на это, проблема создания читающих автоматов и автоматов, воспринимающих речь, до сих пор далека от завершения. Эти две задачи сейчас составляют самостоятельные направления исследований [30, 31].

К главе VIII

Применение методов обучения распознаванию образов для решения задач практики принесло свои неожиданности: прежде всего, оказалось, что результаты, полученные при использовании различных алгоритмов обучения распознаванию образов для решения одной и той же задачи, не слишком сильно различаются между собой (конечно, речь идет об алгоритмах обучения, имеющих разумное статистическое обоснование). Неожиданным оказался тот факт, что метод минимизации эмпирического риска в, казалось бы, разных классах решающих правил позволяет отыскивать решающие правила, обладающие примерно одинаковыми качествами.

Такое утверждение с формальной точки зрения не выдерживает никакой критики: нетрудно представить себе два различных класса решающих правил таких, что для одних задач в первом классе есть удовлетворительные решающие правила и нет удовлетворительных правил во втором классе, а для других задач, напротив, предпочтительней второй класс.

Создатели алгоритмов обучения распознаванию образов рассчитывали именно на такую ситуацию. Однако оказалось, что классы задач, которые приходится решать, и классы конструктивных решающих правил, которыми пользуются, таковы, что если некоторую задачу решает один алгоритм, то близкое качество решения может быть получено и с помощью другого.

Этому факту не может быть дано объяснения, если не привлечь гипотезу о семиотической структуре мира, который мы пытаемся познать. Такая гипотеза пока не сформулирована, хотя на необходимость ее указывали представители самых разных отраслей знаний, цель исследования которых состоит в познании законов природы.

Так, свое понимание семиотической структуры мира И. Ньютон высказал в «Правилах умозаключения в физике», изложенных в третьей части знаменитой книги «Математические начала натуральной философии». И первое правило таково: «Не должно принимать в природе иных причин, сверх тех, которые истинны и достаточны для объяснения явлений. Но этому поводу философы утверждают, что природа ничего не делает напрасно, а было бы напрасным совершать многим то, что может быть сделано меньшим. Природа проста и не роскошествует излишними причинами вещей». Этот принцип был сформулирован около трехсот лет назад. С тех пор было предложено много различных гипотез о структуре мира. И все они как-то оказывались связанными с понятием «сложность».

В последнее время (особенно в связи с появлением вычислительной техники) понятие сложность стало предметом исследования математиков: по разным причинам хотелось бы иметь возможность оценить меру сложности различных математических объектов и в частности функций. Оказалось, что понятие простоты или сложности функции вовсе не так просто, как могло показаться с первого взгляда. Во всяком случае, до сих пор не удалось построить критерий сложности функции, который удовлетворил бы всех исследователей. Для тех же объектов, для которых удается ввести естественный критерий сложности, неожиданно обнаруживаются любопытные факты. 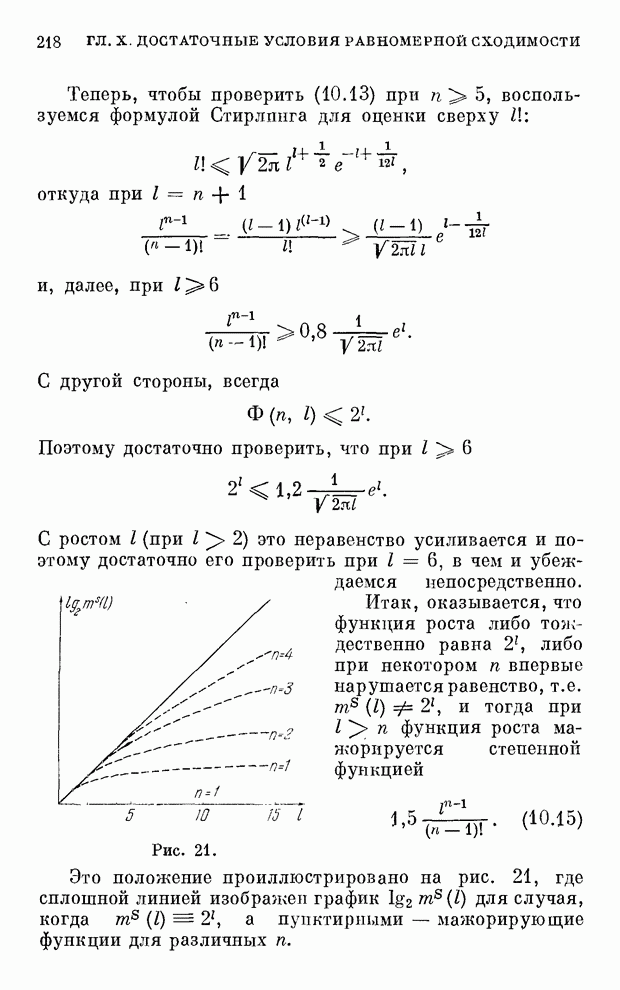Так, если ввести понятие сложности для классификации логических функций  переменных в зависимости от того, с помощью какого числа базисных (например, пороговых) элементов эти функции могут быть реализованы, то окажется, что из всех  возможных функций подавляющее большинство составляют наиболее сложные, т. е. те, которые могут быть реализованы лишь с помощью  элементов, и лишь ничтожная часть функций имеет малую сложность (число функций, реализуемых одним пороговым элементом, меньше ). Но самое интересное заключается в том, что, хотя почти все функции сложные, построить (просто выписать в виде таблицы значения во всех  точках) сложную функцию чрезвычайно трудно. Во всяком случае, уже для  нет примеров сложной функции.

Еще пример. Можно ввести естественное определение сложности числа такое, что алгебраические числа будут проще трансцендентных. И опять здесь оказывается, что трансцендентных чисел на числовой оси подавляющее большинство, и, несмотря на это, нам известно чрезвычайно мало трансцендентных чисел, а известные способы конструирования трансцендентных чисел позволяют получить лишь ничтожное меньшинство всех имеющихся трансцендентных чисел.

Если при любом «разумном» определении сложности окажется, что сложные функции составляют подавляющее большинство всех функций, то гипотеза «мир прост» становится чрезвычайно содержательной. Вопросы исследования сложности математических объектов в настоящее время являются чрезвычайно актуальными [20,37].

К главе IX

В настоящее время существуют достаточно тонкие критерии, позволяющие судить о сходимости процессов, полученных с помощью процедуры стохастической аппроксимации. В этой главе изложены условия, при которых процедура стохастической аппроксимации применена для минимизации функционала

с выпуклыми по  при любом фиксированном  функциями потерь . Результаты для этого частного случая могут быть получены из общих теорем о сходимости процессов процедуры стохастической аппроксимации. Однако здесь приведены доказательства сходимости для этого частного процесса процедуры стохастической аппроксимации непосредственно в том виде, в каком они были получены Б. М. Литваковым [44]. Аналогичные результаты получены и Ю. М. Ермольевым [27]. Вообще же для рассмотренного случая известно [26], что если  – одноэкстремальная функция, то при определенных условиях процедура стохастической аппроксимации приведет к глобальному минимуму, если же  – многоэкстремальная функция, то процедура стохастической аппроксимации гарантирует достижение лишь локального минимума.

К главам X, XI, XII

Задача восстановления вероятностной меры по эмпирическим данным является одной из основных задач статистики. Известные методы решения этой задачи распадаются на два типа: параметрические и непараметрические методы.

Параметрические методы основаны на том, что предполагается вид распределения, зависящий от конечного числа параметров. В этом случае восстановление распределения эквивалентно оценке этих параметров по эмпирическим данным.

Непараметрические методы не связаны с предположением о виде функции распределения. Они основаны на реализации одной из двух идей:

1) восстановление плотности распределения вероятностей (в этом случае достаточна гипотеза о гладкости функции плотности распределения вероятностей);

2) восстановление вероятностей определенного множества событий.

Методы восстановления функции плотности распределения вероятностей предлагались Е. Парзеном [88], Н. Н. Ченцовым [69], М. А. Айзерманом, Э. М. Браверманом, Л. И. Розоноэром [1]. Последние авторы рассматривали эту задачу в связи с проблемой обучения распознаванию образов в вероятностной постановке. Однако восстановление плотности распределения вероятностей требует значительного объема выборки. Это особенно существенно в многомерном случае, когда для восстановления плотности распределения часто необходима длина выборки во много раз большая, чем , где  – размерность пространства.

Вторая идея связана с восстановлением вероятностей класса событий. Вероятностная мера будет восстановлена, если восстановить сразу вероятности всех событий полной -алгебры. Однако, как показано в книге, вообще говоря, это сделать невозможно. Этот метод применим в том случае, когда требуется определить вероятности определенного, сравнительно узкого класса событий.

Если класс состоит всего из одного события, то вопрос стоит о сходимости частоты к вероятности для одного фиксированного события. Ответ на этот вопрос был получен еще в XVIII веке Яковом Бернулли (сходимость почти наверное установлена Э. Борелем одновременно с введением этого понятия).

Случай конечного числа событий принципиального интереса не представляет, так как равномерная сходимость частот к вероятностям здесь легко следует из закона Бернулли.

В 30-е годы особое внимание уделялось равномерной сходимости эмпирических кривых распределения к функциям распределения. В 1933 году В. И. Гливенко доказал [79], что имеет место равномерная сходимость эмпирических кривых к функциям распределения для произвольной функции распределения. В том же году А. Н. Колмогоров для непрерывной функции распределения установил следующую асимптотическую оценку [83]:

,

где  – эмпирическая кривая распределения,

.

Дальнейшие уточнения были получены Н. В. Смирновым [59]. Он исследовал также уклонение эмпирических кривых, построенных по двум независимым выборкам, при неизменном распределении [59]. Как сказано в основном тексте, исследование близости эмпирических кривых к функциям распределения равносильно исследованию равномерной близости частот к вероятностям по классу событий вида

.

Разумеется, из равномерной близости эмпирических кривых к функциям распределения следует равномерная близость частот к вероятностям и в более широких классах событий (но не для всех событий!).

Таким образом, интерес исследований 30–40-х годов к равномерной сходимости ограничивался одномерным случаем, что, видимо, связано с ограниченностью вычислительных возможностей того времени. После появления быстродействующих вычислительных машин стали возможными новые методы обработки статистических данных, например, такие, которые применяются в задачах обучения распознаванию. В связи с этим возникла необходимость предельно обобщить теорему Гливенко и выяснить, насколько широк может быть класс событий, чтобы еще имела место равномерная сходимость частот к вероятностям, и как изменяется скорость такой сходимости с расширением класса. Ответы на эти вопросы получены нами в работах [18, 19] и составляют предмет изложения глав X, XI и XII. Полученные оценки не так точны, как оценки Колмогорова – Смирнова для близости эмпирических кривых к функциям распределения. Вопрос получения асимптотически точных оценок остается пока открытым.

Отметим, что необходимые и достаточные условия равномерной сходимости частот к вероятностям оказались связанными с определенным образом введенной энтропией класса событий относительно выборок конечной длины. Эта энтропия во многом аналогична шенноновской энтропии, рассматриваемой в теории информации.

К главе XIII

Начиная с первых работ по распознаванию указывалось, что эффективное обучение возможно только в том случае, когда на класс задач наложено заранее достаточно жесткое ограничение (априорная гипотеза). Однако оценки достаточной длины обучающей последовательности в зависимости от той или иной гипотезы были получены не сразу. К числу первых, безусловно, относится оценка Новикова для персептрона, хотя в первоначальном варианте она оценивала число исправлений, а не длину обучения. Длину обучения легко оценить, если теорему Новикова дополнить условием останова.

В ряде работ оценивается достаточная длина выборки в случае гипотезы о нормальном распределении классов [55].

В работе [16] мы исходим из предположения, что классы заведомо безошибочно разделимы одним из  заданных решающих правил. При этом оказалось, что достаточная длина обучающей выборки оценивается сверху:

,

где  – точность,  – надежность выбора решающего правила. Этот результат немедленно прилагается к задаче нахождения линейного решающего правила для дискретных ограниченных множеств.

Случай, когда разделяемые множества могут быть заключены в параллелепипед с гранями, параллельными осям координат, рассматривал Б. М. Курилов [39].

У. Хаилимен [81] предлагал для оценки достаточной длины обучения в классе линейных решающих правил воспользоваться обычным биномиальным распределением. Этот путь является ложным, так как при этом не учитывается требование равномерной близости оценок риска к их истинному значению по всему классу решающих правил. Этим путем можно вывести конечные оценки длины обучения для сколь угодно емких классов решающих правил, что неверно.

В работе [17] мы ввели в рассмотрение функцию роста и получили оценки достаточной длины в детерминированной постановке задачи обучения распознаванию, а в статье [18], уже опираясь на общие результаты по равномерной сходимости частот событий к их вероятностям, получили оценки и в общем случае. В этой книге оценки несколько уточнены.

Отметим, что приводимые оценки достаточной длины обучения завышены, во-первых, потому, что они рассчитаны на наихудший случай, и, во-вторых, поскольку при их выводе был сделан ряд огрублений. Но существенно, что они позволяют увидеть качественную зависимость требуемой длины обучения от параметров класса решающих правил и устанавливают, что существуют не слишком «страшные» оценки, не зависящие от распределения.

Вопрос о равномерной по параметру сходимости средних к математическим ожиданиям возник в связи с исследованием эффективности оценок максимального правдоподобия. Упомянутый результат Л. Лe-Кама [85] получен им на основе идей А. Вальда [96]. Результат, основанный на сведении к равномерной сходимости частот к вероятностям, получен в [19]. Оба условия являются лишь достаточными и не перекрывают друг друга. Необходимых и достаточных условий равномерной сходимости средних к математическим ожиданиям пока нет.

К главе XIV

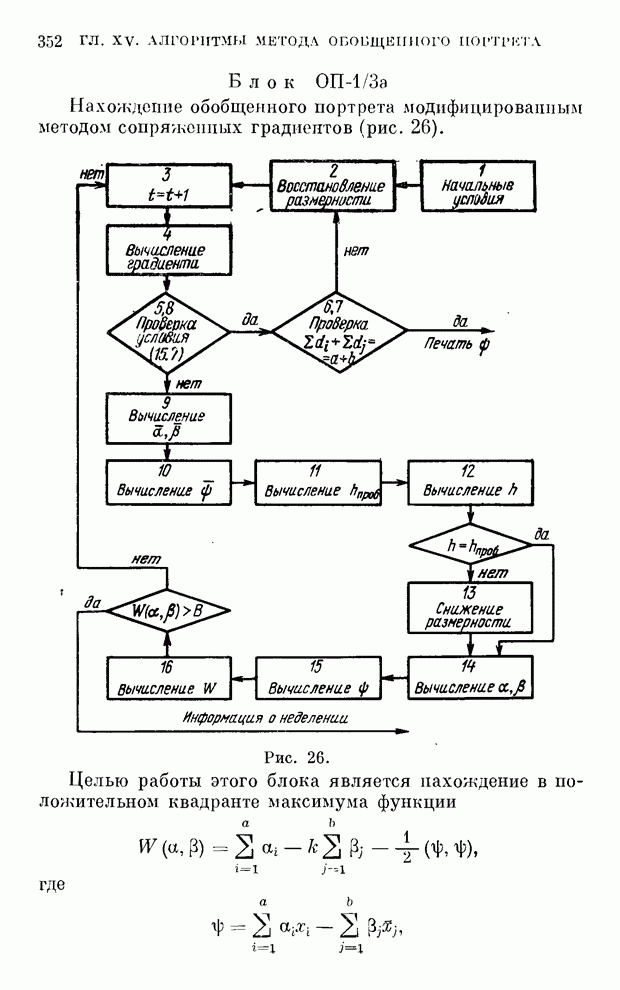
Метод обобщенного портрета был предложен в 1963 году в работах [13, 15]. Позже [17] было показано, что построение обобщенного портрета эквивалентно отысканию максимума неположительно определенной квадратичной формы в положительном квадранте, а известные алгоритмы построения разделяющей гиперплоскости различаются так, как различаются методы минимизации квадратичной формы в положительном квадранте. В этой же работе и было предложено использовать метод сопряженных направлений.

К главе XV

Библиотека программ метода обобщенного портрета была создана А. А. Журавель и Т. Г. Глазковой. Подробное описание библиотеки дано в статьях [12, 11].

Предлагаемые здесь программы несколько отличаются от тех, которые были изложены в этих работах.

К главе XVI

Метод сопряженных направлений был предложен в 1952 году для решения системы линейных алгебраических уравнений [80]. Этот метод позволяет находить решение алгебраических уравнений (или, что то же самое, точку минимума квадратичного функционала в конечномерном пространстве) за конечное число шагов. Позже метод был обобщен для случая неквадратичных функционалов [75]. В 1969 году Б. Т. Поляк предложил обобщение метода сопряженных градиентов для решения задач с ограничениями [51]. На многочисленных примерах неоднократно демонстрировалась эффективность этого метода для решения различных задач.