| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 12. Некоторые статистические особенности метода обобщенного портрета
В главе VI были получены оценки качества алгоритмов, строящих разделяющие гиперплоскости методом минимизации эмпирического риска.
В частности, было показано, что
для детерминистского случая математическое ожидание вероятности ошибочной
классификации с помощью решающего правила, построенного по выборке длины ![]() , не может быть меньше
, не может быть меньше
![]() ,
,
где
![]() –
константа,
–
константа, ![]() –
емкость класса.
–
емкость класса.
Были получены и верхние оценки качества. Верхние оценки были двух типов – зависящие от размерности пространства (эти оценки следует из общей теории равномерной сходимости) и оценки, зависящие от относительного расстояния (эти оценки следуют из обобщенной теоремы Новикова 6.2).
В этом параграфе будут
исследованы оценки качества алгоритмов, реализующих метод обобщенного портрета.
Будет показано, что для этих алгоритмов справедливы одновременно оценки обоих
типов (тем самым выполняется лучшая из них). При этом существенно то, что
верхняя оценка, зависящая от размерности, значительно ближе к нижней ![]() , чем оценки для
произвольных алгоритмов, строящих разделяющую гиперплоскость на основе минимума
эмпирического риска. Тем самым будут показаны особые статистические свойства
метода обобщенного портрета.
, чем оценки для
произвольных алгоритмов, строящих разделяющую гиперплоскость на основе минимума
эмпирического риска. Тем самым будут показаны особые статистические свойства
метода обобщенного портрета.
Итак, пусть задача такова, что
для любой выборки длины ![]() при заданном параметре
при заданном параметре ![]() существует
обобщенный портрет множества
существует
обобщенный портрет множества ![]() относительно
относительно ![]() .
.
Оказывается, что при этом
качество ![]() алгоритма,
использующего метод обобщенного портрета, может быть оценено:
алгоритма,
использующего метод обобщенного портрета, может быть оценено:
![]() , (14.36)
, (14.36)
где
![]() –
размерность пространства.
–
размерность пространства.
Эта оценка может быть еще
усилена. В § 3 было показано, что обобщенный портрет ![]() всегда может быть разложен по
своим крайним векторам в виде
всегда может быть разложен по
своим крайним векторам в виде
 .
.
Это
разложение, вообще говоря, не единственно. Назовем крайний вектор информативным,
если он входит с ненулевым весом во все разложения вектора ![]() . Обозначим через
. Обозначим через ![]() – математическое
ожидание числа информативных векторов в выборке длины
– математическое
ожидание числа информативных векторов в выборке длины ![]() . Ниже будет показано, что
справедлива оценка
. Ниже будет показано, что
справедлива оценка
![]() . (14.37)
. (14.37)
Будет показано также, что всегда имеет место неравенство
![]() .
.
В практических задачах часто
оказывается, что ![]() много
меньше
много
меньше ![]() , и
тогда методом обобщенного портрета удается по выборке, соизмеримой с
размерностью пространства, построить разделяющую гиперплоскость, гарантирующую
малую вероятность ошибочной классификации.
, и
тогда методом обобщенного портрета удается по выборке, соизмеримой с
размерностью пространства, построить разделяющую гиперплоскость, гарантирующую
малую вероятность ошибочной классификации.
Для вывода оценок (14.36) и
(14.37) воспользуемся свойством несмещенности оценки скользящего контроля (см.
§ 7 главы VI). Несмещенность означает, что математическое ожидание частоты ошибок
на экзамене после обучения на последовательности длины ![]() равно математическому
ожиданию частоты ошибок при скользящем контроле на последовательности длины
равно математическому
ожиданию частоты ошибок при скользящем контроле на последовательности длины ![]() . Применительно к
методу обобщенного портрета скользящий контроль проводится так: из обучающей
выборки последовательно (каждый раз по одному) удаляются векторы
. Применительно к
методу обобщенного портрета скользящий контроль проводится так: из обучающей
выборки последовательно (каждый раз по одному) удаляются векторы ![]() ; по оставшейся части
выборки строится обобщенный портрет
; по оставшейся части
выборки строится обобщенный портрет ![]() и проверяется правильность опознания
удаленного вектора; после этого подсчитывается частота ошибок.
и проверяется правильность опознания
удаленного вектора; после этого подсчитывается частота ошибок.
Справедлива теорема
Теорема 14.11. Число ошибок при скользящем
контроле не превосходит числа информативных векторов обобщенного портрета ![]() , построенного по
всей выборке.
, построенного по
всей выборке.
Доказательство. Достаточно показать, что при удалении неинформативного вектора из обучающей выборки в ходе скользящего контроля ошибки на этом векторе не произойдет.
В самом деле, если вектор ![]() не является
информативным, то существует разложение обобщенного портрета
не является
информативным, то существует разложение обобщенного портрета
 ,
,
![]() ;
;
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,
![]() , (14.38)
, (14.38)
в
которое вектор ![]() входит
с нулевым весом. Но это значит, что вектор
входит
с нулевым весом. Но это значит, что вектор ![]() является одновременно обобщенным
портретом и для выборки, из которой вектор
является одновременно обобщенным
портретом и для выборки, из которой вектор ![]() удален, так как для него выполняются
все условия теоремы 14.6 применительно к укороченной выборке, т. е.
удален, так как для него выполняются
все условия теоремы 14.6 применительно к укороченной выборке, т. е. ![]() . Следовательно,
. Следовательно,
![]()
или
![]() ,
,
а значит, удаленный вектор опознается правильно. Теорема доказана.
Из теоремы, с учетом несмещенности оценки скользящего контроля, немедленно вытекает неравенство (14.37).
Покажем еще, что число
информативных векторов никогда не превосходит размерность пространства ![]() . Для этого
достаточно построить разложение вида (14.38), в которое с ненулевым весом
входит не более
. Для этого
достаточно построить разложение вида (14.38), в которое с ненулевым весом
входит не более ![]() векторов.
векторов.
Действительно, если в разложении
(14.38) входит более ![]() векторов, то всегда можно построить разложение
того же вида, в которое входит меньшее число векторов. Всякая система из
векторов, то всегда можно построить разложение
того же вида, в которое входит меньшее число векторов. Всякая система из ![]() векторов линейно
зависима. Поэтому существуют числа
векторов линейно
зависима. Поэтому существуют числа ![]() такие, что
такие, что
 ,
,
причем
в это разложение входят только те векторы, которые входят в (14.38) с ненулевым
весом, и по крайней мере одно ![]() положительно.
положительно.
Тогда выражение
 (14.39)
(14.39)
задает
семейство разложений обобщенного портрета по своим крайним векторам. Поскольку
все ![]() и
и ![]() положительны, то при
достаточно малых по модулю
положительны, то при
достаточно малых по модулю ![]() все коэффициенты остаются
положительными. В то же время, поскольку среди чисел
все коэффициенты остаются
положительными. В то же время, поскольку среди чисел ![]() есть положительные, при
достаточно большом
есть положительные, при
достаточно большом ![]() некоторые
коэффициенты станут отрицательными. Значит, найдется
некоторые
коэффициенты станут отрицательными. Значит, найдется ![]() , при котором впервые один или
несколько коэффициентов разложения (14.39) обратятся в нуль, в то время как
остальные сохранят положительное значение. Применяя это построение, если нужно,
несколько раз получим искомое разложение.
, при котором впервые один или
несколько коэффициентов разложения (14.39) обратятся в нуль, в то время как
остальные сохранят положительное значение. Применяя это построение, если нужно,
несколько раз получим искомое разложение.
Для метода обобщенного портрета
при ![]() удается
получить также оценку качества, зависящую от относительного расстояния между
классами. При
удается
получить также оценку качества, зависящую от относительного расстояния между
классами. При ![]() оценка
совпадает с выведенной в главе VI (теорема 6.2) оценкой качества для
персептронного алгоритма с многократным повторением обучающей
последовательности, а именно:
оценка
совпадает с выведенной в главе VI (теорема 6.2) оценкой качества для
персептронного алгоритма с многократным повторением обучающей
последовательности, а именно:
 , (14.40)
, (14.40)
где
![]() ,
,
![]() –
расстояние от начала координат до выпуклой оболочки множества векторов
–
расстояние от начала координат до выпуклой оболочки множества векторов ![]() ,
, ![]() . Математическое ожидание
берется по всем выборкам фиксированной длины.
. Математическое ожидание
берется по всем выборкам фиксированной длины.
Нетрудно убедиться, что число ![]() и модуль обобщенного
портрета, полученного при
и модуль обобщенного
портрета, полученного при ![]() , связаны соотношением
, связаны соотношением
![]() .
.
Если, как и раньше, воспользоваться несмещенностью оценки скользящего контроля, то для вывода (14.40) достаточно доказать следующую теорему.
Теорема 14.12. Число ошибок при скользящем
контроле для метода обобщенного портрета при ![]() не превосходит
не превосходит ![]() .
.
Доказательство. Пусть дана
обучающая последовательность ![]() ,
, ![]() и максимум соответствующей функции
и максимум соответствующей функции ![]() при
при ![]() ;
; ![]() достигается в точке
достигается в точке ![]() ,
, ![]() .
.
Соответственно ![]() – обобщенный
портрет. Обозначим через
– обобщенный
портрет. Обозначим через ![]() точку, доставляющую максимум функции
точку, доставляющую максимум функции ![]() на множестве
на множестве ![]() ,
, ![]() . Очевидно, что ей
соответствует обобщенный портрет, построенный по выборке без вектора
. Очевидно, что ей
соответствует обобщенный портрет, построенный по выборке без вектора ![]() :
:
 .
.
Обозначим
через ![]() значение
функции
значение
функции ![]() в
точке
в
точке ![]()
![]() ,
, ![]() ,
, ![]() . Очевидно, что
. Очевидно, что
![]()
и одновременно
![]() .
.
Поэтому
![]() . (14.41)
. (14.41)
Далее,
![]() .
.
Для
крайнего вектора ![]()
![]() . (14.42)
. (14.42)
Будем
считать далее, что обобщенный портрет ![]() неправильно опознает вектор
неправильно опознает вектор ![]() . Это значит, что
. Это значит, что
![]() . (14.43)
. (14.43)
Кроме
того, как было показано при доказательстве предыдущей теоремы, это возможно
только в том случае, когда ![]() является крайним вектором обобщенного
портрета
является крайним вектором обобщенного
портрета ![]() .
.
Исследуем теперь левую часть
неравенства (14.41). Для этого рассмотрим один шаг максимизации функции ![]() из точки
из точки ![]() вдоль оси
вдоль оси ![]() и выберем
оптимальное значение
и выберем
оптимальное значение ![]() . Имеем
. Имеем
![]() .
.
Отсюда
получаем оптимальное значение ![]() :
:
 .
.
Увеличение
![]() на этом
шаге составит
на этом
шаге составит
 .
.
Так
как ![]() не
больше, чем приращение функции при полной максимизации, то
не
больше, чем приращение функции при полной максимизации, то
 . (14.44)
. (14.44)
Объединяя (14.41), (14.42), (14.44), получим
 ,
,
откуда, учитывая (14.43)
 .
.
Аналогично оценивается ![]() :
:
 .
.
Учитывая,
что ![]() ,
, ![]() , имеем
, имеем
![]() ,
,
![]() .
.
Пусть теперь при скользящем
контроле число неправильно опознаваемых векторов первого и второго классов
равно соответственно ![]() и
и ![]() . Тогда в силу теоремы 14.10 при
отрицательном
. Тогда в силу теоремы 14.10 при
отрицательном ![]()
 ,
,
где
![]() и
и ![]() берутся только по
тем векторам, которые неправильно опознаются при скользящем контроле.
берутся только по
тем векторам, которые неправильно опознаются при скользящем контроле.
Далее,
![]() .
.
Окончательно
при ![]()
 .
.
При
![]()
 .
.
В
случае ![]()
![]() .
.
Теорема доказана.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ЧАСТЬ ПЕРВАЯ ЭЛЕМЕНТАРНАЯ ТЕОРИЯ
- Глава I. Персептрон Розенблатта
- § 1. Феномен восприятия
- § 2. Физиологическая модель восприятия
- § 3. Техническая модель. Персептрон
- § 4. Математическая модель
- § 5. Обобщенная математическая модель
- § 6. Теорема Новикова
- § 7. Доказательство теоремы Новикова
- § 8. Двухуровневая схема распознавания
- Глава II. Задача обучения машин распознаванию образов
- § 1. Задача имитации
- § 2. Качество обучения
- § 3. Надежность обучения
- § 4. Обучение – задача выбора
- § 5. Две задачи конструирования обучающихся устройств
- § 6. Математическая постановка задачи обучения
- § 7. Три пути решения задачи о минимизации среднего риска
- § 8. Задача обучения распознаванию образов и методы минимизации среднего риска
- Глава III. Методы обучения, основанные на восстановлении распределения вероятностей
- § 1. О восстановлении распределения вероятностей
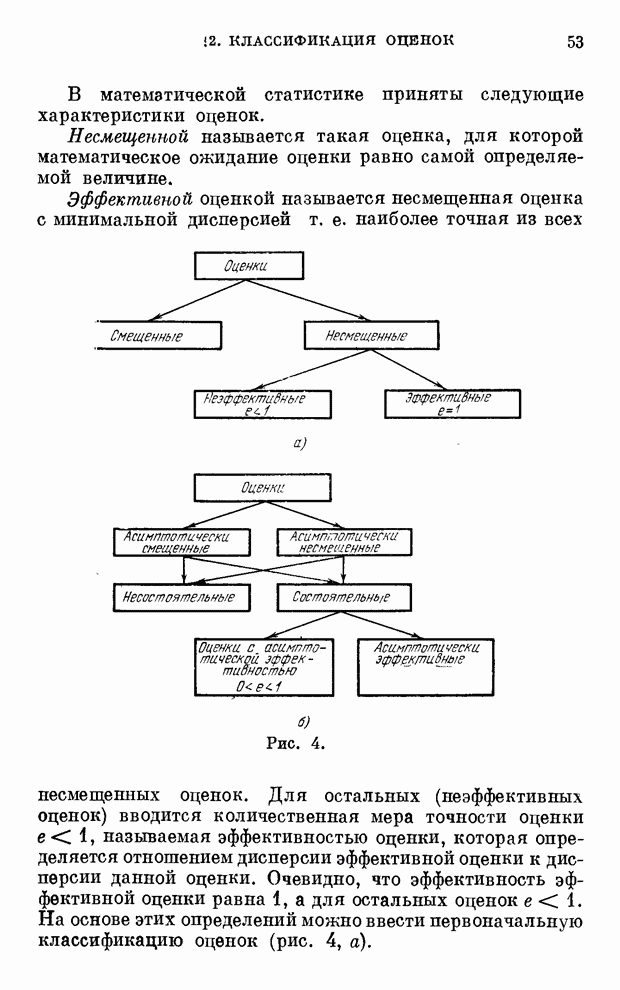
- § 2. Классификация оценок
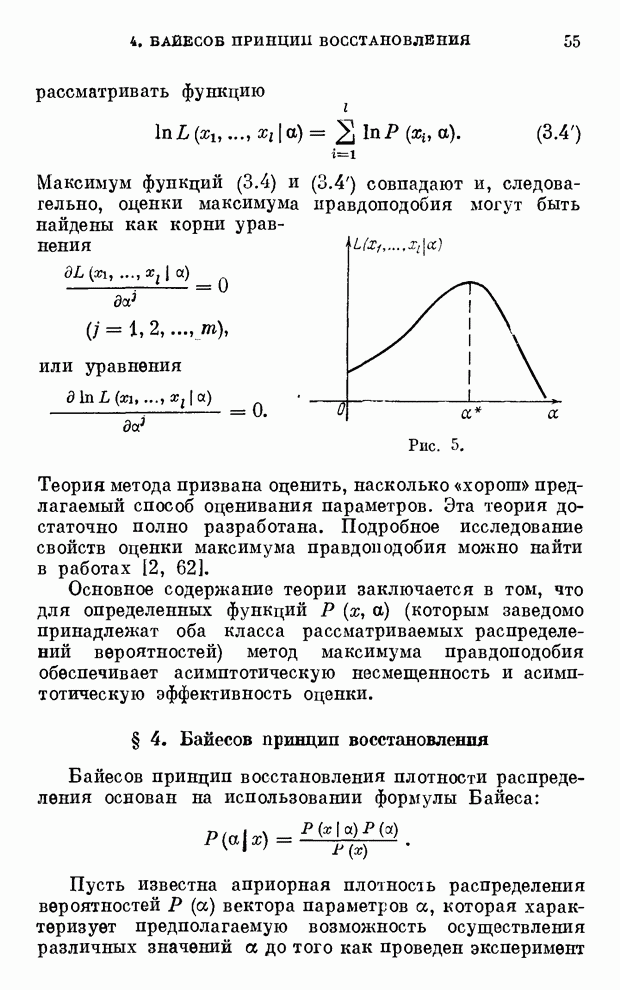
- § 3. Метод максимума правдоподобия
- § 4. Байесов принцип восстановления
- § 5. Сравнение байесова метода оценивания и оценивания методом максимума правдоподобия
- § 6. Оценка параметров распределения дискретных независимых признаков
- § 7. Байесовы оценки параметров распределения дискретных независимых признаков
- § 8. Восстановление параметров нормального распределения методом максимума правдоподобия
- § 9. Байесов метод восстановления нормального распределения
- Глава IV. Рекуррентные алгоритмы обучения распознаванию образов
- § 1. Метод стохастической аппроксимации
- § 2. Детерминистская и стохастическая постановки задачи обучения распознаванию образов
- § 3. Конечно-сходящиеся рекуррентные процедуры
- § 4. Теоремы об останове
- § 5. Метод циклического повторения обучающей последовательности
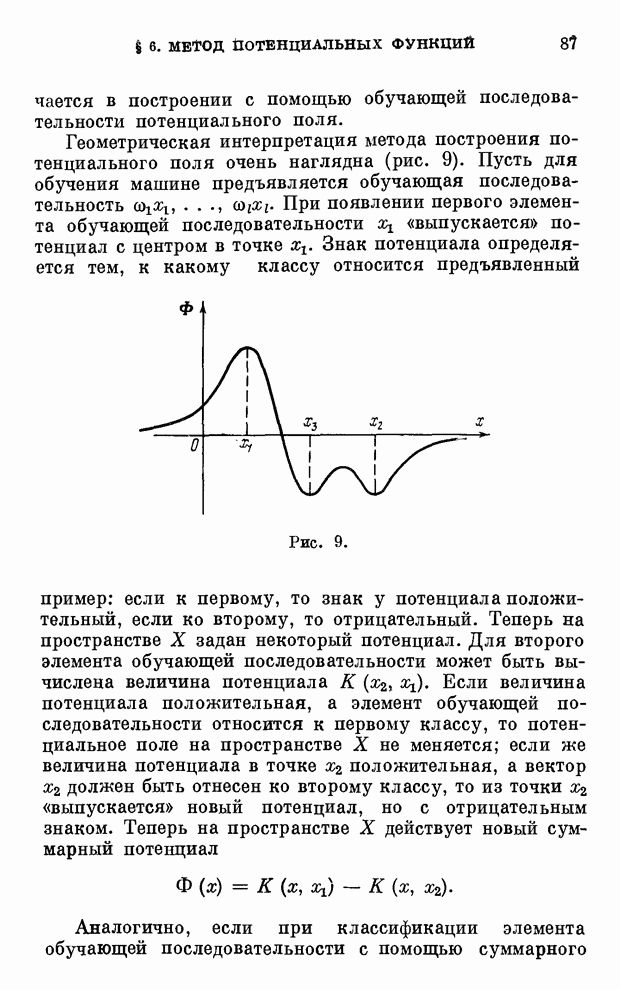
- § 6. Метод потенциальных функций
- Глава V. Алгоритмы, минимизирующие эмпирический риск
- § 1. Метод минимизации эмпирического риска
- § 2. Равномерная сходимость частот появления событий к их вероятностям
- § 3. Теорема Гливенко
- § 4. Частный случай
- § 5. Оценка числа различных линейных разделений векторов
- § 6. Условия равномерной сходимости частот появления событий к их вероятностям
- § 7. Свойства функции роста
- § 8. Оценка уклонения эмпирически оптимального решающего правила
- § 9. Метод минимизации эмпирического риска в детерминистской постановке задачи обучения распознаванию образов
- § 10. Замечание об оценке скорости равномерной сходимости частот появления событий к их вероятностям
- § 11. Замечания об особенностях метода минимизации эмпирического риска
- § 12. Алгоритмы метода обобщенного портрета
- § 13. Алгоритм Кора
- Глава VI. Метод упорядоченной минимизации риска
- § 1. О критериях оценки качества алгоритмов
- § 2. Минимаксный критерий
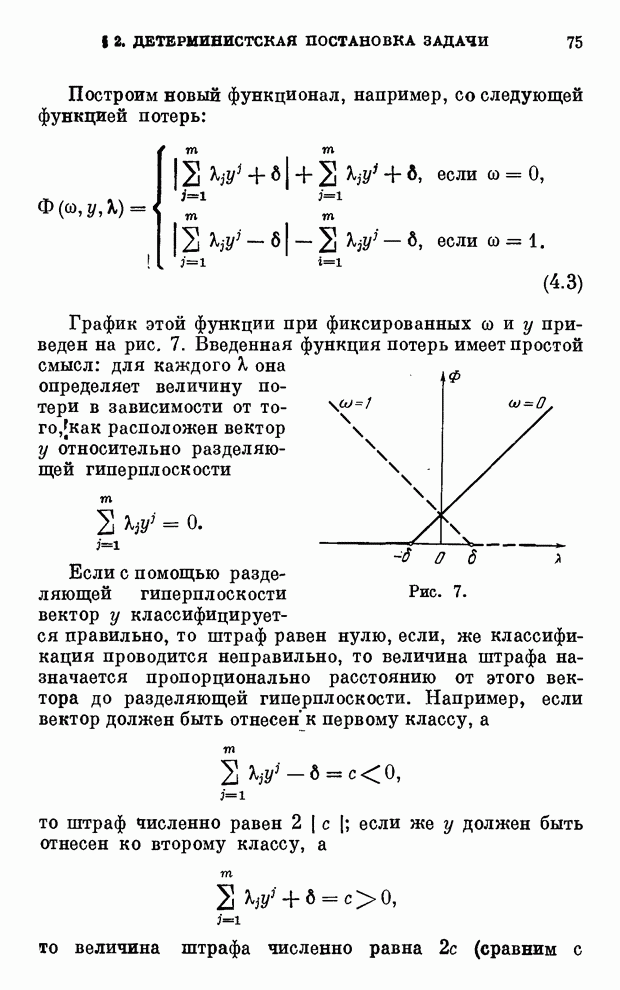
- § 3. Критерий минимакса потерь
- § 4. Критерий Байеса
- § 5. Упорядочение классов решающих правил
- § 6. О критериях выбора
- § 7. Несмещенность оценки скользящего контроля
- § 8. Упорядочение по размерностям
- § 9. Упорядочение по относительным расстояниям
- § 10. Упорядочение по эмпирическим оценкам относительного расстояния и задача минимизации суммарного риска
- § 11. О выборе оптимальной совокупности признаков
- § 12. Алгоритмы упорядоченной минимизации суммарного риска
- § 13. Алгоритмы построения экстремальных кусочно-линейных решающих правил
- § 14. Приложение к главе VI
- Глава VII. Примеры применения методов обучения распознаванию образов
- § 1. Задача о различении нефтеносных и водоносных пластов в скважине
- § 2. Задача о различении сходных почерков
- § 3. Задача о контроле качества продукции
- § 4. Задача о прогнозе погоды
- § 5. Применение метода обучения распознаванию образов в медицине
- § 6. Замечания о применениях методов обучения распознаванию образов
- Глава VIII. Несколько общих замечаний
- § 1. Еще раз о постановке задачи
- § 2. Физики об интуиции
- § 3. Машинная интуиция
- § 4. О мире, в котором возможна интуиция
- Часть вторая. СТАТИСТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ
- Глава IX. О сходимости рекуррентных алгоритмов обучения распознаванию образов
- § 1. Определение понятия сходимости
- § 2. Выпуклые функции
- § 3. Обобщенный градиент
- § 4. Условия сходимости рекуррентных алгоритмов
- § 5. Еще одно условие сходимости рекуррентных алгоритмов
- Глава X. Достаточные условия равномерной сходимости частот к вероятностям по классу событий
- § 1. О близости минимума эмпирического риска к минимуму среднего риска
- § 2. Определение равномерной сходимости частот к вероятностям
- § 3. Определение функции роста
- § 4. Свойства функции роста
- § 5. Основная лемма
- § 6. Вывод достаточных условий равномерной сходимости частот к вероятностям по классу событий
- § 7. О равномерной сходимости с вероятностью единица
- § 8. Примеры и дополнительные замечания
- § 9. Приложение к главе X
- Глава XI. Необходимые и достаточные условия равномерной сходимости частот к веронтностям по классу событий
- § 1. Энтропия системы событий
- § 2. Асимптотические свойства энтропии
- § 3. Необходимые и достаточные условия равномерной сходимости (доказательство достаточности)
- § 4. Доказательство необходимости условий равномерной сходимости
- § 5. Примеры и дополнительные критерии
- Глава XII. Оценки равномерного относительного уклонения частот от вероятностей в классе событий
- § 1. О равномерном относительном уклонении
- § 2. Оценка равномерного относительного уклонения частот в двух полувыборках
- § 3. Оценка равномерного относительного уклонения частот от вероятностей
- Глава XIII. Применение теории равномерной сходимости к методам минимизации эмпирического риска
- § 1. Оценка достаточной длины обучающей последовательности в задачах обучения распознаванию
- § 2. Равномерная сходимость средних к математическим ожиданиям
- Часть третья. МЕТОДЫ ПОСТРОЕНИЯ РАЗДЕЛЯЮЩИХ ПОВЕРХНОСТЕЙ
- Глава XIV. Построение разделяющей гиперплоскости (метод обобщенного портрета)
- § 1. Оптимальная разделяющая гиперплоскость
- § 2. Однопараметрическое семейство разделяющих гиперплоскостей
- § 3. Некоторые свойства обобщенного портрета
- § 4. Двойственная задача
- § 5. Алгоритмы персептронного типа
- § 6. Градиентные методы построения разделяющей гиперплоскости (вычисление обобщенного портрета)
- § 7. Теория оптимальной разделяющей гиперплоскости
- § 8. Двойственная задача
- § 9. Методы вычисления оптимальной разделяющей гиперплоскости
- § 10. Построение оптимальной разделяющей гиперплоскости модифицированным методом Гаусса–Зайделя
- § 11. Применение метода обобщенного портрета для нахождения оптимальной разделяющей гиперплоскости
- § 12. Некоторые статистические особенности метода обобщенного портрета
- § 13. Приложение к главе XIV
- Глава XV. АЛГОРИТМЫ ОБУЧЕНИЯ РАСПОЗНАВАНИЮ ОБРАЗОВ, РЕАЛИЗУЮЩИЕ МЕТОД ОБОБЩЕННОГО ПОРТРЕТА
- § 1. Способы представления информации
- § 2. Алгоритм построения разделяющей гиперплоскости
- § 3. Алгоритм построения разделяющей гиперплоскости, минимизирующей число ошибочно классифицируемых векторов
- § 4. Алгоритм построения кусочно-линейной разделяющей поверхности
- § 5. Алгоритмы построения разделяющей гиперплоскости в пространстве минимального числа признаков
- § 6. Алгоритм построения экстремальной линейной разделяющей поверхности
- § 7. Алгоритм построения экстремальной кусочно-линейной разделяющей поверхности
- § 8. Алгоритм построения разделяющей гиперплоскости с оценкой ее качества методом скользящего контроля
- § 9. Алгоритмы построения экстремальных разделяющих гиперповерхностей с помощью процедуры скользящий контроль
- § 10. О работе с алгоритмами
- Глава XVI. МЕТОД СОПРЯЖЕННЫХ НАПРАВЛЕНИЙ
- § 1. Идея метода
- § 2. Метод сопряженных градиентов
- § 3. Метод параллельных касательных (партан)
- § 4. Анализ погрешностей метода
- КОММЕНТАРИИ
- ЛИТЕРАТУРА