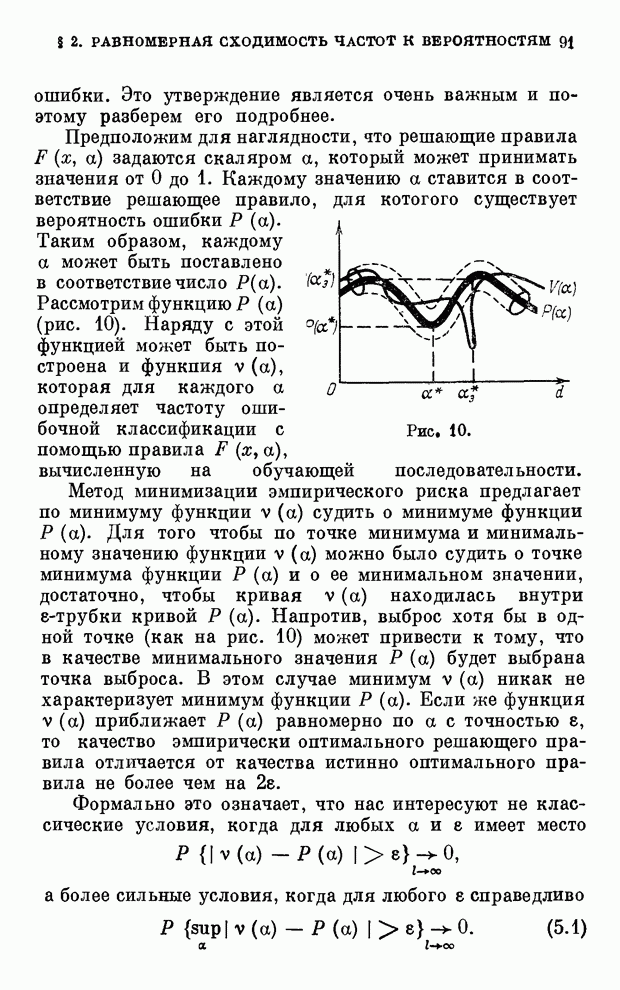
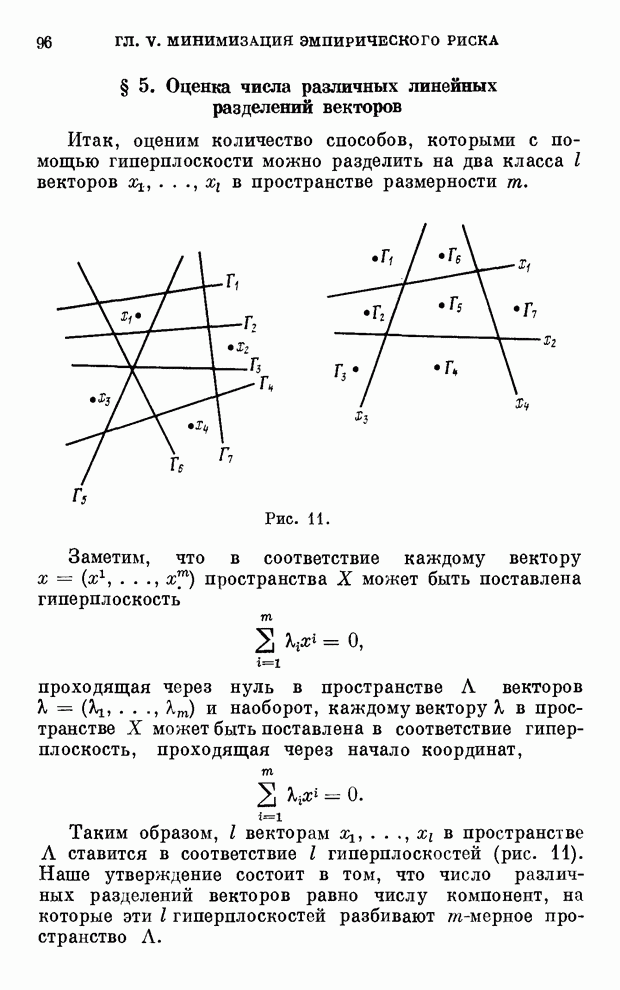
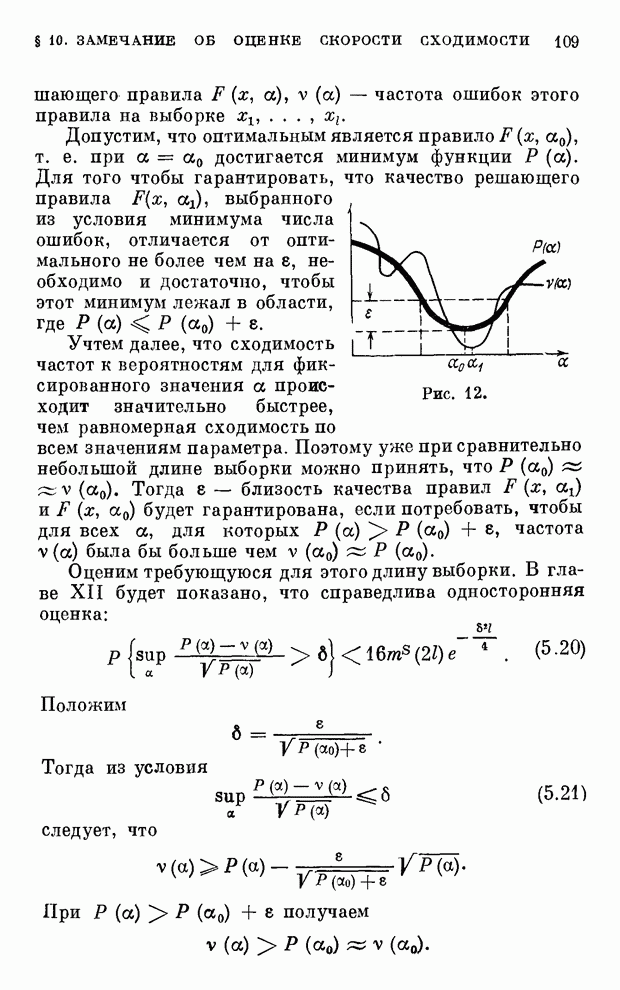
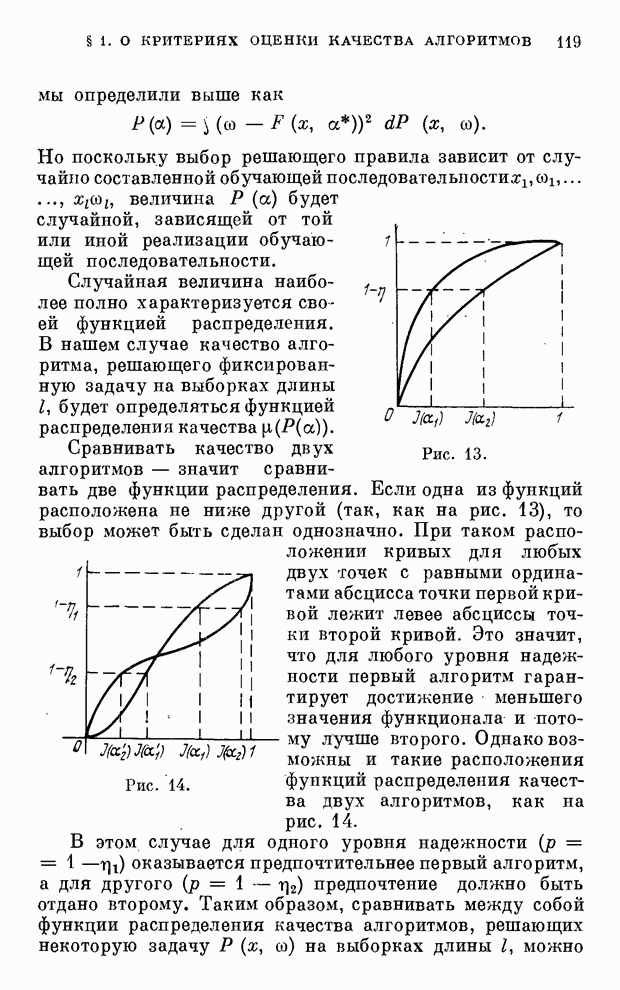
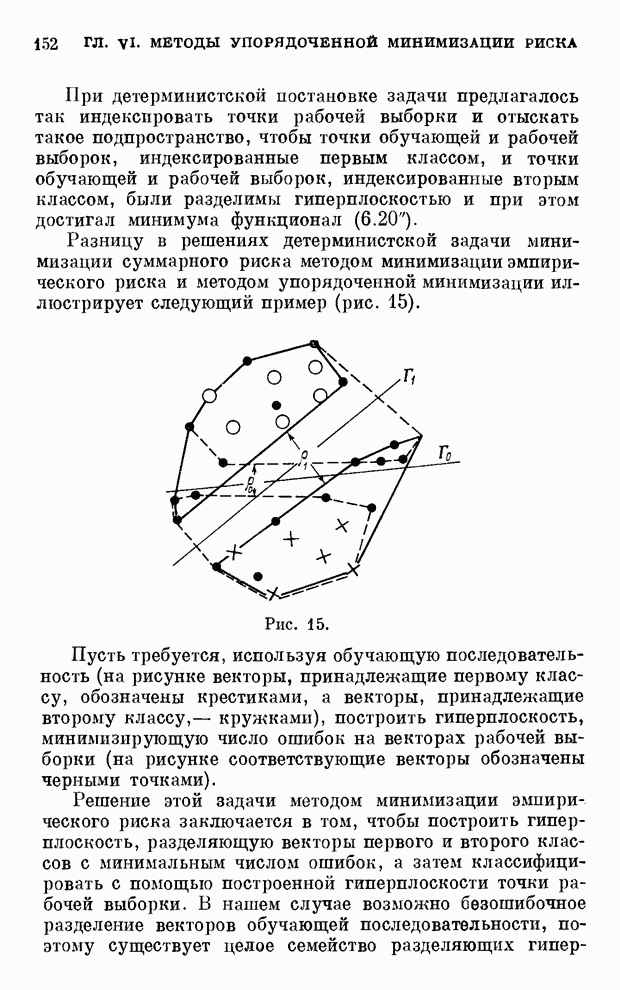
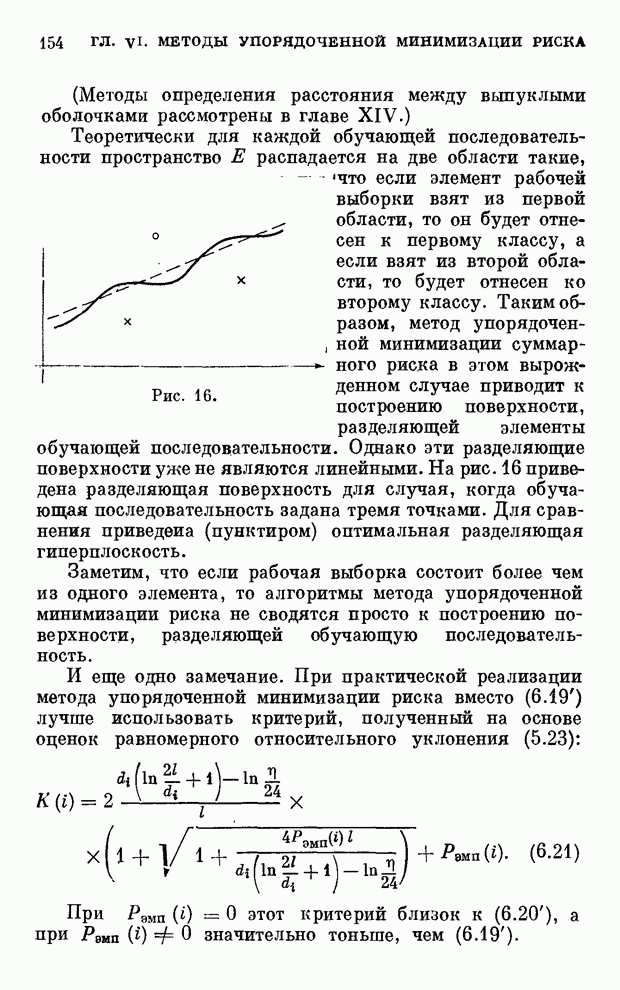
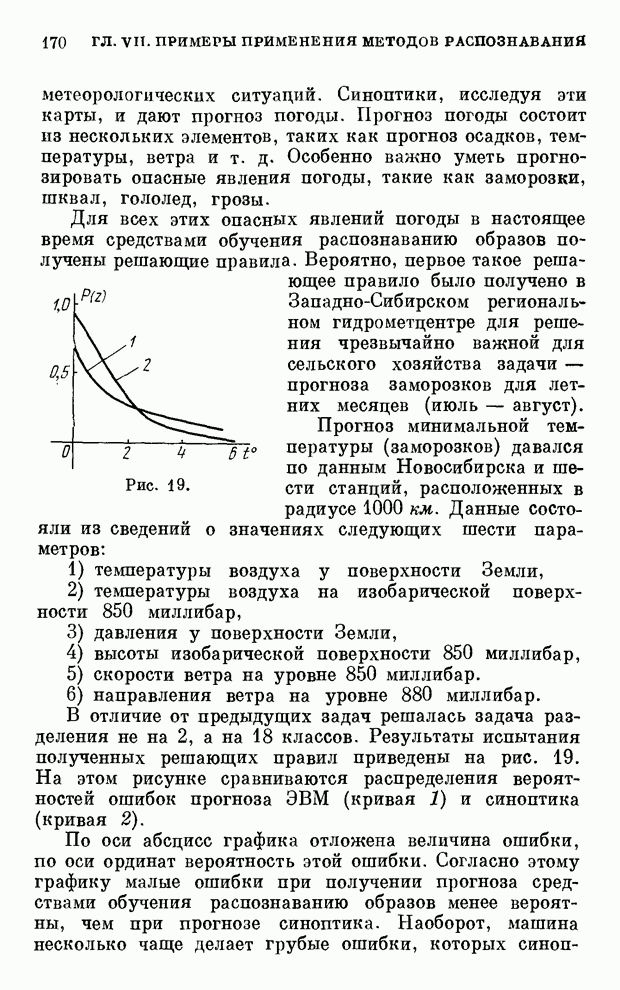
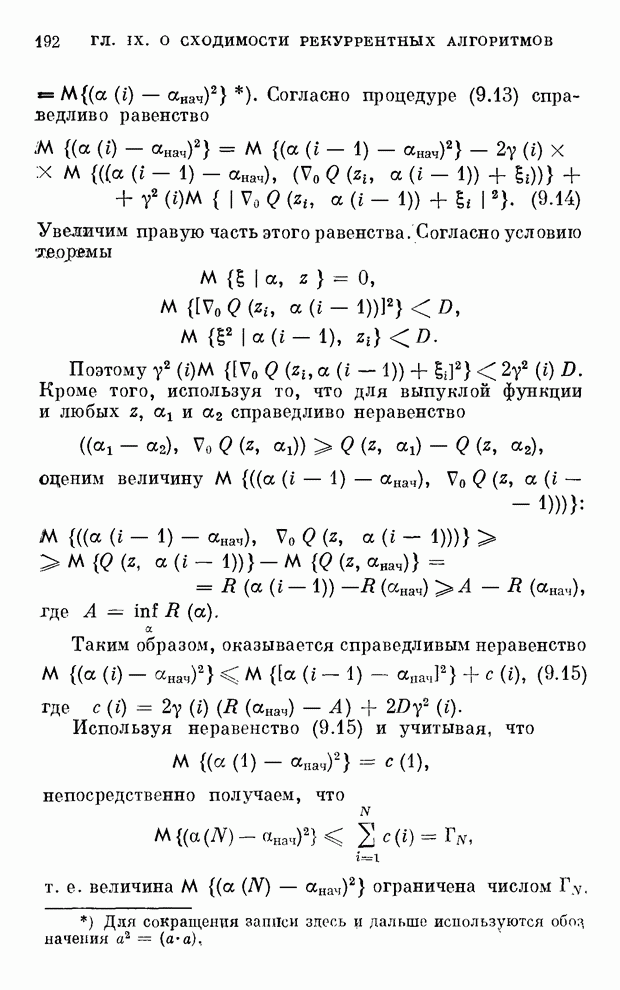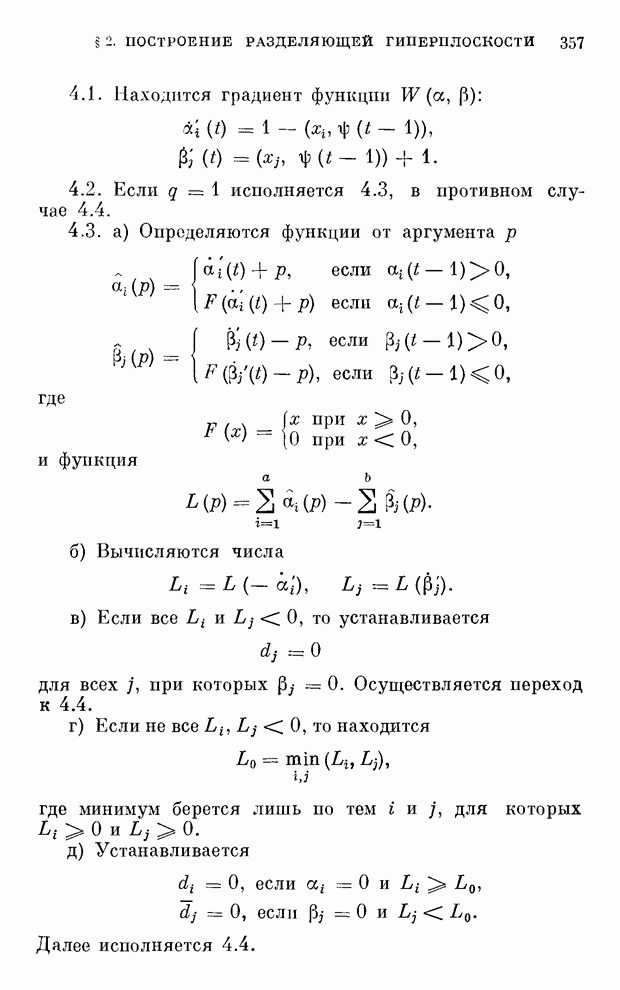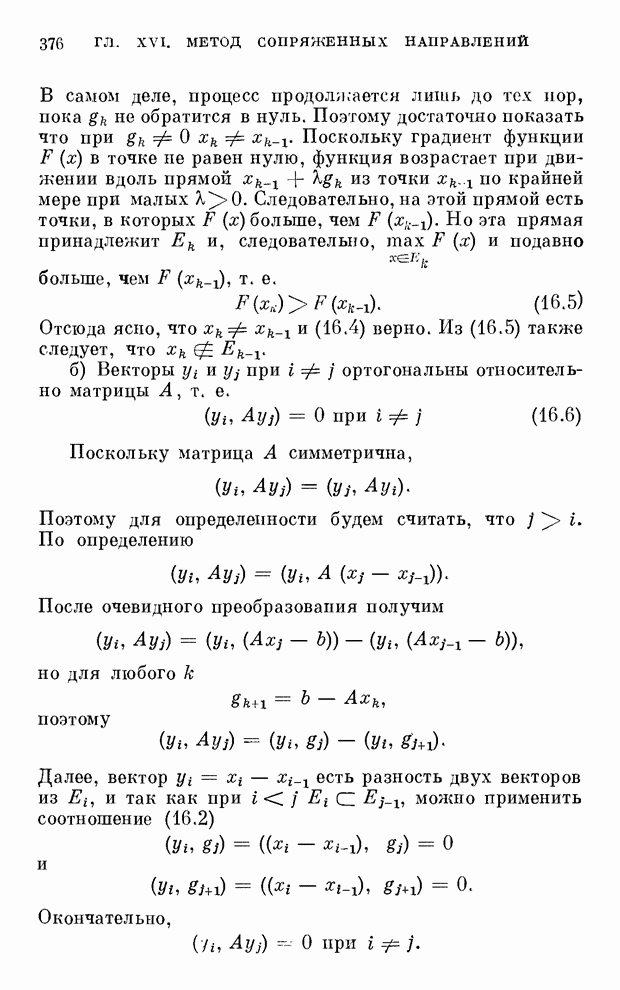| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 1. Способы представления информации
В задачах обучения распознаванию
образов принято два способа представления информации – непрерывный и
дискретный. При непрерывном способе представления все координаты вектора ![]() могут принимать
любые значения числовой оси. При дискретном способе каждая координата вектора
могут принимать
любые значения числовой оси. При дискретном способе каждая координата вектора ![]() может принимать лишь
фиксированное число значений.
может принимать лишь
фиксированное число значений.
Оба способа представления информации имеют как свои сильные, так и слабые стороны.
Сильной стороной непрерывного
способа является точность задания значений координат. Каждая координата вектора
здесь равна тому значению параметра, которое было замерено. Однако при таком
способе представления информации для хранения значения каждого параметра
требуется одна ячейка памяти вычислительной машины. А так как в задачах
распознавания ситуация описывается большим числом параметров (вектор ![]() имеет размерность
порядка десятков и сотен), то хранение одной ситуации в памяти машины требует
слишком большого объема памяти. Кроме того, часто, например в задачах
медицинской диагностики, ситуации описываются признаками, которые не имеют
точного количественного выражения (например, надо отразить, что у данного
больного повышена «бледность кожных покровов»). В этом случае принят следующий
способ записи такой информации. Договариваются, что единица означает наличие
данного признака, нуль – его отсутствие.
имеет размерность
порядка десятков и сотен), то хранение одной ситуации в памяти машины требует
слишком большого объема памяти. Кроме того, часто, например в задачах
медицинской диагностики, ситуации описываются признаками, которые не имеют
точного количественного выражения (например, надо отразить, что у данного
больного повышена «бледность кожных покровов»). В этом случае принят следующий
способ записи такой информации. Договариваются, что единица означает наличие
данного признака, нуль – его отсутствие.
Возможен способ записи информации, при котором кодируется не только наличие или отсутствие некоторого признака, но и степень проявления признака. Например, следующие характеристики: «бледность кожного покрова не выражена», «бледность кожного покрова выражена слабо», «бледность кожного покрова сильно выражена» – могут иметь соответствующие коды 100, 010, 001.
Таким образом, наличие качественных признаков описания объекта предопределяет дискретный способ представления информации.
В задачах обучения распознаванию образов принято дискретно кодировать не только признаки, отражающие качественную характеристику объекта, но и параметры, которые принимают непрерывные значения. При этом пользуются следующим способом представления дискретной информации.
Весь диапазон значений параметра
разбивается на ряд градаций. Единицей кодируется ![]() -й разряд кода признака, если значение
параметра принадлежит
-й разряд кода признака, если значение
параметра принадлежит ![]() -й градации; если же значение параметра
не принадлежит
-й градации; если же значение параметра
не принадлежит ![]() -й
градации, то в
-й
градации, то в ![]() -м
разряде проставляется нуль.
-м
разряде проставляется нуль.
Пример. Пусть значение параметра ![]() принадлежит отрезку
принадлежит отрезку ![]() и этот отрезок
разбивается на пять градаций:
и этот отрезок
разбивается на пять градаций:
![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Кодом
10000 обозначаются величины ![]() , 01000 – величины
, 01000 – величины ![]() , 00100 – величины
, 00100 – величины ![]() , 00010 – величины
, 00010 – величины ![]() , 00001 – величины
, 00001 – величины ![]() .
.
Рассмотренный дискретный способ
представления информации замечателен не только тем, что позволяет компактно
записывать информацию. Дискретизация величины ![]() есть нелинейная операция, с помощью
которой вектор
есть нелинейная операция, с помощью
которой вектор ![]() переводится
в бинарный вектор
переводится
в бинарный вектор ![]() .
.
Поэтому увеличение числа градаций
при кодировке значения параметра эквивалентно использованию более
разнообразного класса разделяющих поверхностей в пространстве ![]() . Однако, как было
установлено в первой части книги, чрезмерная емкость класса решающих правил при
ограниченном объеме обучающей последовательности недопустима и поэтому
возникает проблема экстремальной разбивки на градации непрерывных признаков.
. Однако, как было
установлено в первой части книги, чрезмерная емкость класса решающих правил при
ограниченном объеме обучающей последовательности недопустима и поэтому
возникает проблема экстремальной разбивки на градации непрерывных признаков.
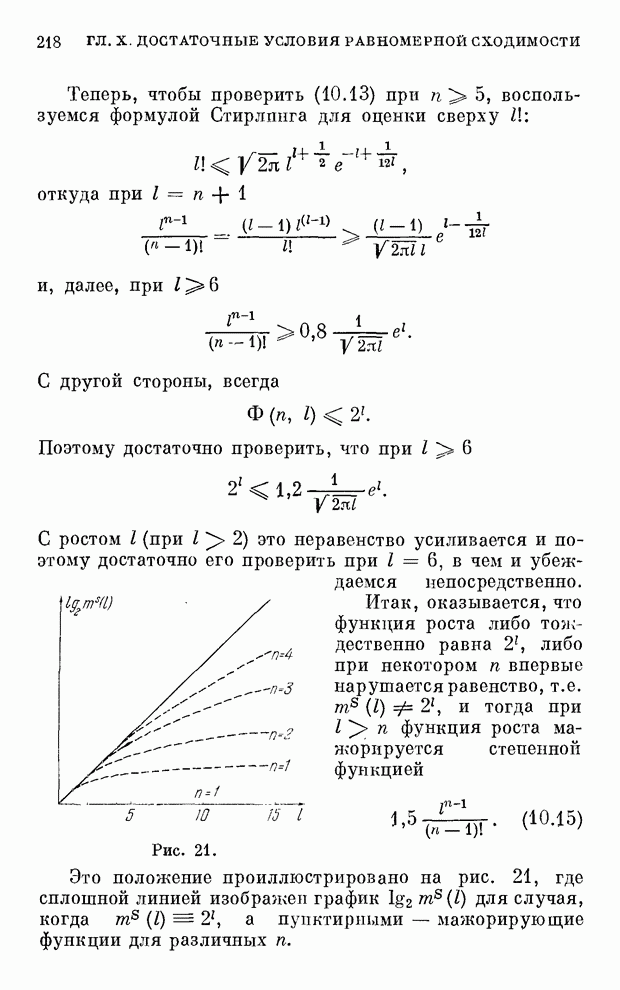
В этом параграфе будет приведен алгоритм определения экстремальной разбивки значения признаков на градации. Принцип, который реализует алгоритм, заключается в следующем: необходимо так разбить значения параметра, чтобы оценка неопределенности (энтропии) при классификации с помощью этого признака была минимальной или близка к минимальной (оценка энтропии производится с помощью элементов обучающей последовательности).
Итак, пусть признак ![]() может принимать
значения из интервала
может принимать
значения из интервала ![]() и пусть вектор, обладающий этим
признаком, принадлежит одному из
и пусть вектор, обладающий этим
признаком, принадлежит одному из ![]() классов. Будем считать, что существуют
условные вероятности принадлежности к каждому классу
классов. Будем считать, что существуют
условные вероятности принадлежности к каждому классу
![]() .
.
Для
каждого фиксированного значения признака ![]() может быть определена мера
неопределенности (энтропия) принадлежности к тому или иному классу. Она равна
может быть определена мера
неопределенности (энтропия) принадлежности к тому или иному классу. Она равна
 .
.
Среднее значение по мере ![]() энтропии вычисляется
так:
энтропии вычисляется
так:
 .
.
Пусть
теперь параметр ![]() разбит
на
разбит
на ![]() градаций.
Тогда средняя энтропия может быть записана в виде
градаций.
Тогда средняя энтропия может быть записана в виде
 . (15.1)
. (15.1)
Воспользуемся теперь формулой Байеса
 . (15.2)
. (15.2)
Подставляя (15.2) в (15.1), получим
 .
.
Подставляя
теперь байесовы оценки ![]() ,
, ![]() ,
, ![]() , найденные по обучающей
последовательности (см. главу III), получим
, найденные по обучающей
последовательности (см. главу III), получим

 , (15.3)
, (15.3)
где
![]() – число
векторов
– число
векторов ![]() -гo класса в обучающей выборке,
-гo класса в обучающей выборке, ![]() – число векторов
– число векторов ![]() -гo класса, у которых
-гo класса, у которых ![]() ;
;  – длина выборки.
– длина выборки.
Формула (15.3) получена в
предположении, что априорные значения ![]() ,
, ![]() равновероятно распределены на
симплексах:
равновероятно распределены на
симплексах:
 ,
, ![]() ;
;
 ,
, ![]() . (15.4)
. (15.4)
В более общем случае целесообразно рассмотреть формулу
 , (15.5)
, (15.5)
где
параметр ![]() определяется
характером априорной информации.
определяется
характером априорной информации.
Реализация сформулированного принципа состоит в таком подборе разбивки на градации, чтобы обеспечить минимум (15.5).
Алгоритм удобно реализовать в
следующей форме: сначала разбить параметр на большое число градации, а затем,
«склеивая» соседние градации, добиваться минимизации значения ![]() .
.
Можно оценить и количество
информации ![]() о
принадлежности объекта к тому или иному классу, которое несет сведение о
значении параметра
о
принадлежности объекта к тому или иному классу, которое несет сведение о
значении параметра
![]() ,
,
где
 .
.
Часто разумно продолжать
«склеивать» градации и после достижения минимума по ![]() функции
функции ![]() , но лишь до тех пор, пока
величина
, но лишь до тех пор, пока
величина ![]() не
уменьшится в
не
уменьшится в ![]() раз
(
раз
(![]() , так же
как и
, так же
как и ![]() , –
параметры алгоритма).
, –
параметры алгоритма).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ЧАСТЬ ПЕРВАЯ ЭЛЕМЕНТАРНАЯ ТЕОРИЯ
- Глава I. Персептрон Розенблатта
- § 1. Феномен восприятия
- § 2. Физиологическая модель восприятия
- § 3. Техническая модель. Персептрон
- § 4. Математическая модель
- § 5. Обобщенная математическая модель
- § 6. Теорема Новикова
- § 7. Доказательство теоремы Новикова
- § 8. Двухуровневая схема распознавания
- Глава II. Задача обучения машин распознаванию образов
- § 1. Задача имитации
- § 2. Качество обучения
- § 3. Надежность обучения
- § 4. Обучение – задача выбора
- § 5. Две задачи конструирования обучающихся устройств
- § 6. Математическая постановка задачи обучения
- § 7. Три пути решения задачи о минимизации среднего риска
- § 8. Задача обучения распознаванию образов и методы минимизации среднего риска
- Глава III. Методы обучения, основанные на восстановлении распределения вероятностей
- § 1. О восстановлении распределения вероятностей
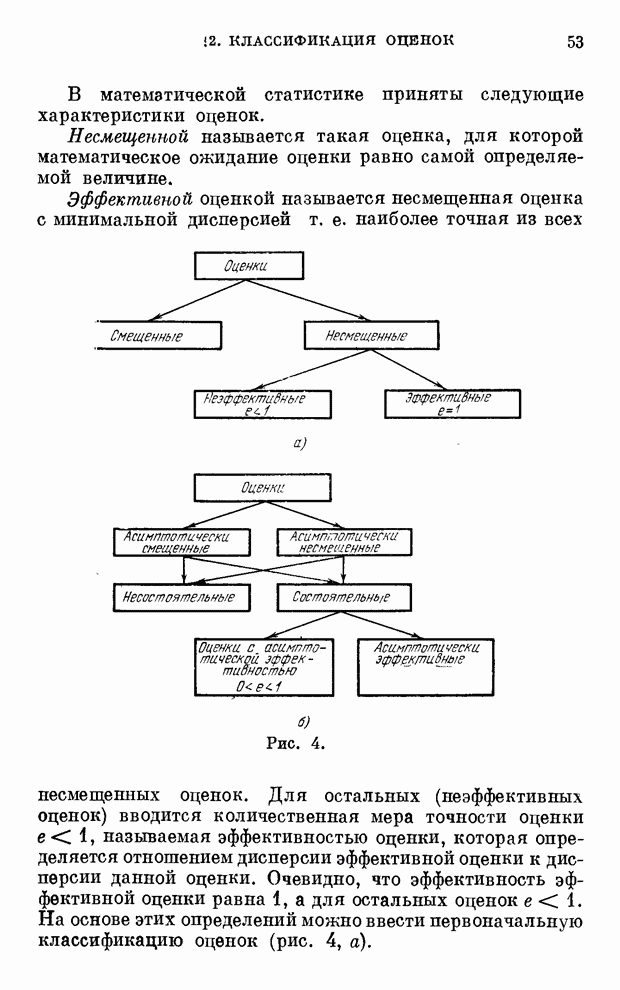
- § 2. Классификация оценок
- § 3. Метод максимума правдоподобия
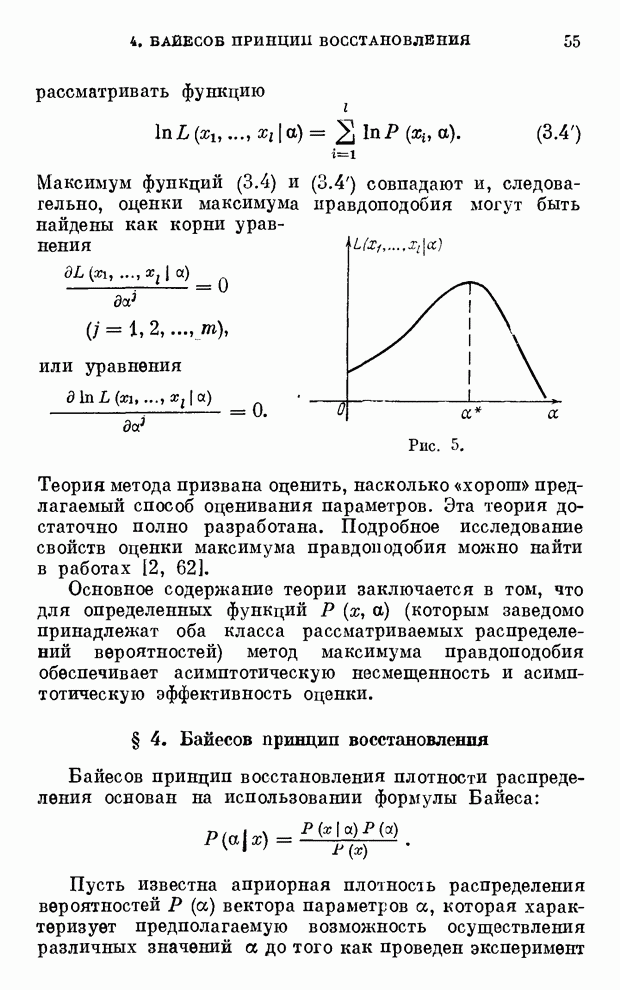
- § 4. Байесов принцип восстановления
- § 5. Сравнение байесова метода оценивания и оценивания методом максимума правдоподобия
- § 6. Оценка параметров распределения дискретных независимых признаков
- § 7. Байесовы оценки параметров распределения дискретных независимых признаков
- § 8. Восстановление параметров нормального распределения методом максимума правдоподобия
- § 9. Байесов метод восстановления нормального распределения
- Глава IV. Рекуррентные алгоритмы обучения распознаванию образов
- § 1. Метод стохастической аппроксимации
- § 2. Детерминистская и стохастическая постановки задачи обучения распознаванию образов
- § 3. Конечно-сходящиеся рекуррентные процедуры
- § 4. Теоремы об останове
- § 5. Метод циклического повторения обучающей последовательности
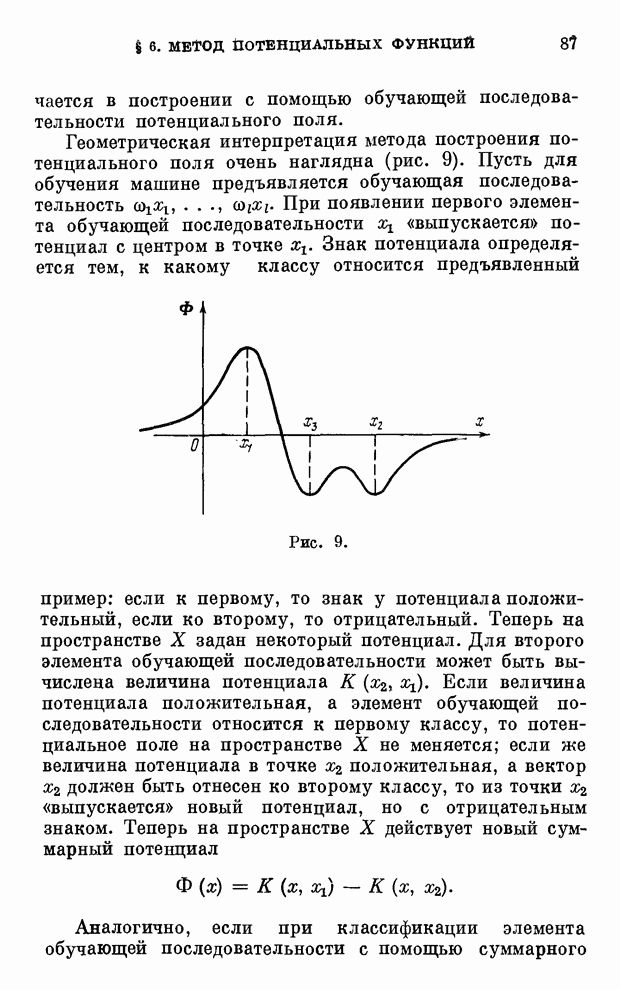
- § 6. Метод потенциальных функций
- Глава V. Алгоритмы, минимизирующие эмпирический риск
- § 1. Метод минимизации эмпирического риска
- § 2. Равномерная сходимость частот появления событий к их вероятностям
- § 3. Теорема Гливенко
- § 4. Частный случай
- § 5. Оценка числа различных линейных разделений векторов
- § 6. Условия равномерной сходимости частот появления событий к их вероятностям
- § 7. Свойства функции роста
- § 8. Оценка уклонения эмпирически оптимального решающего правила
- § 9. Метод минимизации эмпирического риска в детерминистской постановке задачи обучения распознаванию образов
- § 10. Замечание об оценке скорости равномерной сходимости частот появления событий к их вероятностям
- § 11. Замечания об особенностях метода минимизации эмпирического риска
- § 12. Алгоритмы метода обобщенного портрета
- § 13. Алгоритм Кора
- Глава VI. Метод упорядоченной минимизации риска
- § 1. О критериях оценки качества алгоритмов
- § 2. Минимаксный критерий
- § 3. Критерий минимакса потерь
- § 4. Критерий Байеса
- § 5. Упорядочение классов решающих правил
- § 6. О критериях выбора
- § 7. Несмещенность оценки скользящего контроля
- § 8. Упорядочение по размерностям
- § 9. Упорядочение по относительным расстояниям
- § 10. Упорядочение по эмпирическим оценкам относительного расстояния и задача минимизации суммарного риска
- § 11. О выборе оптимальной совокупности признаков
- § 12. Алгоритмы упорядоченной минимизации суммарного риска
- § 13. Алгоритмы построения экстремальных кусочно-линейных решающих правил
- § 14. Приложение к главе VI
- Глава VII. Примеры применения методов обучения распознаванию образов
- § 1. Задача о различении нефтеносных и водоносных пластов в скважине
- § 2. Задача о различении сходных почерков
- § 3. Задача о контроле качества продукции
- § 4. Задача о прогнозе погоды
- § 5. Применение метода обучения распознаванию образов в медицине
- § 6. Замечания о применениях методов обучения распознаванию образов
- Глава VIII. Несколько общих замечаний
- § 1. Еще раз о постановке задачи
- § 2. Физики об интуиции
- § 3. Машинная интуиция
- § 4. О мире, в котором возможна интуиция
- Часть вторая. СТАТИСТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ
- Глава IX. О сходимости рекуррентных алгоритмов обучения распознаванию образов
- § 1. Определение понятия сходимости
- § 2. Выпуклые функции
- § 3. Обобщенный градиент
- § 4. Условия сходимости рекуррентных алгоритмов
- § 5. Еще одно условие сходимости рекуррентных алгоритмов
- Глава X. Достаточные условия равномерной сходимости частот к вероятностям по классу событий
- § 1. О близости минимума эмпирического риска к минимуму среднего риска
- § 2. Определение равномерной сходимости частот к вероятностям
- § 3. Определение функции роста
- § 4. Свойства функции роста
- § 5. Основная лемма
- § 6. Вывод достаточных условий равномерной сходимости частот к вероятностям по классу событий
- § 7. О равномерной сходимости с вероятностью единица
- § 8. Примеры и дополнительные замечания
- § 9. Приложение к главе X
- Глава XI. Необходимые и достаточные условия равномерной сходимости частот к веронтностям по классу событий
- § 1. Энтропия системы событий
- § 2. Асимптотические свойства энтропии
- § 3. Необходимые и достаточные условия равномерной сходимости (доказательство достаточности)
- § 4. Доказательство необходимости условий равномерной сходимости
- § 5. Примеры и дополнительные критерии
- Глава XII. Оценки равномерного относительного уклонения частот от вероятностей в классе событий
- § 1. О равномерном относительном уклонении
- § 2. Оценка равномерного относительного уклонения частот в двух полувыборках
- § 3. Оценка равномерного относительного уклонения частот от вероятностей
- Глава XIII. Применение теории равномерной сходимости к методам минимизации эмпирического риска
- § 1. Оценка достаточной длины обучающей последовательности в задачах обучения распознаванию
- § 2. Равномерная сходимость средних к математическим ожиданиям
- Часть третья. МЕТОДЫ ПОСТРОЕНИЯ РАЗДЕЛЯЮЩИХ ПОВЕРХНОСТЕЙ
- Глава XIV. Построение разделяющей гиперплоскости (метод обобщенного портрета)
- § 1. Оптимальная разделяющая гиперплоскость
- § 2. Однопараметрическое семейство разделяющих гиперплоскостей
- § 3. Некоторые свойства обобщенного портрета
- § 4. Двойственная задача
- § 5. Алгоритмы персептронного типа
- § 6. Градиентные методы построения разделяющей гиперплоскости (вычисление обобщенного портрета)
- § 7. Теория оптимальной разделяющей гиперплоскости
- § 8. Двойственная задача
- § 9. Методы вычисления оптимальной разделяющей гиперплоскости
- § 10. Построение оптимальной разделяющей гиперплоскости модифицированным методом Гаусса–Зайделя
- § 11. Применение метода обобщенного портрета для нахождения оптимальной разделяющей гиперплоскости
- § 12. Некоторые статистические особенности метода обобщенного портрета
- § 13. Приложение к главе XIV
- Глава XV. АЛГОРИТМЫ ОБУЧЕНИЯ РАСПОЗНАВАНИЮ ОБРАЗОВ, РЕАЛИЗУЮЩИЕ МЕТОД ОБОБЩЕННОГО ПОРТРЕТА
- § 1. Способы представления информации
- § 2. Алгоритм построения разделяющей гиперплоскости
- § 3. Алгоритм построения разделяющей гиперплоскости, минимизирующей число ошибочно классифицируемых векторов
- § 4. Алгоритм построения кусочно-линейной разделяющей поверхности
- § 5. Алгоритмы построения разделяющей гиперплоскости в пространстве минимального числа признаков
- § 6. Алгоритм построения экстремальной линейной разделяющей поверхности
- § 7. Алгоритм построения экстремальной кусочно-линейной разделяющей поверхности
- § 8. Алгоритм построения разделяющей гиперплоскости с оценкой ее качества методом скользящего контроля
- § 9. Алгоритмы построения экстремальных разделяющих гиперповерхностей с помощью процедуры скользящий контроль
- § 10. О работе с алгоритмами
- Глава XVI. МЕТОД СОПРЯЖЕННЫХ НАПРАВЛЕНИЙ
- § 1. Идея метода
- § 2. Метод сопряженных градиентов
- § 3. Метод параллельных касательных (партан)
- § 4. Анализ погрешностей метода
- КОММЕНТАРИИ
- ЛИТЕРАТУРА