| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 13. Приложение к главе XIV
1.
Рассмотрим в евклидовом пространстве ![]() конечную систему векторов
конечную систему векторов ![]() .
.
Множество ![]() векторов
векторов ![]() , представимых в виде
, представимых в виде
 ,
,
![]() ,
,
 ,
,
образует
минимальный выпуклый конус, содержащий систему векторов ![]() , или, иначе, выпуклый конус,
порожденный системой векторов
, или, иначе, выпуклый конус,
порожденный системой векторов ![]() .
.
Определение 1. Система векторов ![]() не развернута, если
порожденный ею выпуклый конус не содержит нуля.
не развернута, если
порожденный ею выпуклый конус не содержит нуля.
Определение
2. Система
векторов ![]() сильно
развернута, если порожденный ею выпуклый конус
сильно
развернута, если порожденный ею выпуклый конус ![]() содержит все пространство
содержит все пространство ![]() .
.
Определения 1 и 2 эквивалентны следующим двум определениям.
Определение 1'. Система векторов ![]() не развернута, если
существует такой вектор
не развернута, если
существует такой вектор ![]() , что для всех
, что для всех ![]()
![]() .
.
Определение 2'. Система векторов ![]() сильно развернута,
если для всякого
сильно развернута,
если для всякого ![]() найдется
такой вектор
найдется
такой вектор ![]() ,
что
,
что
![]() .
.
Докажем, что определения 1 и 2 эквивалентны 1' и 2'.
Теорема П.1. Определение 1' эквивалентно 1.
Доказательство. Пусть система
векторов не развернута в смысле 1'. Значит, существует такое ![]() , что
, что
![]()
для
всех ![]() .
.
Рассмотрим произвольный элемент ![]() выпуклого конуса,
порожденного системой
выпуклого конуса,
порожденного системой ![]() :
:
 ,
,
![]() ,
,
![]() . (П.1)
. (П.1)
Умножим
скалярно (П. 1) слева и справа на ![]() :
:
![]() .
.
Так
как ![]() и по
крайней мере одно
и по
крайней мере одно ![]() ,
то
,
то
![]() ,
,
т.е. ![]() .
.
Таким образом, из 1' следует 1.
Пусть теперь система векторов ![]() выпукла в смысле
определения 1. Рассмотрим выпуклую оболочку
выпукла в смысле
определения 1. Рассмотрим выпуклую оболочку ![]() системы
системы ![]() , т. е. множество векторов
, т. е. множество векторов ![]() , представимых в виде
, представимых в виде

![]() ,
,
![]() ,
,
![]() .
.
Согласно
определению 1, это множество не содержит нуля. Кроме того, оно замкнуто и
ограничено. Поэтому вектор ![]() , на котором достигается
, на котором достигается ![]() , не равен нулю и
принадлежит множеству
, не равен нулю и
принадлежит множеству ![]() .
.
Покажем теперь, что для любого ![]()
![]() .
.
Рассмотрим отрезок
![]()
![]() .
.
Легко
видеть, что этот отрезок принадлежит ![]() . Найдем модуль произвольного вектора
. Найдем модуль произвольного вектора ![]() , конец которого
лежит на отрезке
, конец которого
лежит на отрезке ![]() :
:
![]()
![]() ,
,
где
![]() – величина
второго порядка малости по
– величина
второго порядка малости по ![]() .
.
Так как ![]() , то коэффициент при линейном
члене должен быть неположительным, т. е.
, то коэффициент при линейном
члене должен быть неположительным, т. е.
![]() ,
,
откуда следует
![]() .
.
Последнее
неравенство справедливо для любого ![]() , а следовательно, и для
, а следовательно, и для ![]() . Значит, условие
определения 1 выполнено.
. Значит, условие
определения 1 выполнено.
Таким образом, эквивалентность 1 и 1' показана.
Теорема П.2. Определения 2' и 2 эквивалентны.
Доказательство. Пусть справедливо
2. Это значит, что произвольный вектор ![]() может быть представлен в виде
может быть представлен в виде
![]() ,
,
где
![]() ,
,
![]() ,
,  .
.
Умножим
скалярно последнее равенство на ![]() :
:
![]() . (П.2)
. (П.2)
Учитывая,
что ![]() , из
равенства (П.2) имеем, что по крайней мере для одного
, из
равенства (П.2) имеем, что по крайней мере для одного ![]()
![]() ,
,
т. е. система строго невыпукла в определении 2'.
Покажем теперь, что из 2' следует
2. Допустим, что не существует вектора ![]() такого, что для всех
такого, что для всех ![]()
![]() .
.
Отсюда
следует, что нуль принадлежит выпуклому конусу, порожденному ![]() , так как в противном
случае в силу эквивалентности 1 и 1' найдется вектор
, так как в противном
случае в силу эквивалентности 1 и 1' найдется вектор ![]() такой, что для всех
такой, что для всех ![]()
![]() ,
,
в противоречии с 2' .
Назовем вектор ![]() базовым, если
существует представление нуля вида
базовым, если
существует представление нуля вида

![]() ,
,
в
которое вектор ![]() входит
с ненулевым весом (т. е.
входит
с ненулевым весом (т. е. ![]() ).
).
Выпуклый конус, порожденный всеми
базовыми векторами из ![]() , совпадает с гиперпространством
, совпадает с гиперпространством ![]() , порожденным этими
векторами. Действительно, если вектор
, порожденным этими
векторами. Действительно, если вектор ![]() базовый, то вектор
базовый, то вектор ![]() принадлежит конусу,
порожденному базовыми векторами из
принадлежит конусу,
порожденному базовыми векторами из ![]() , так как из соотношения
, так как из соотношения
![]()
![]()
следует, что
 . (П.3)
. (П.3)
Произвольный вектор ![]() пространства
пространства ![]() , порожденного
базовыми векторами из
, порожденного
базовыми векторами из ![]() , представим в виде
, представим в виде
![]() ,
,
где
![]() – базовые
векторы; здесь некоторые
– базовые
векторы; здесь некоторые ![]() могут быть отрицательными.
могут быть отрицательными.
Представим все члены суммы с
отрицательными коэффициентами ![]() в виде
в виде ![]() , a
, a ![]() в соответствии с (П.3) разложим по
базовым векторам с неотрицательными коэффициентами.
в соответствии с (П.3) разложим по
базовым векторам с неотрицательными коэффициентами.
Таким образом, получим представление
![]() ,
,
![]() ,
, ![]()
для
произвольного ![]() .
.
Далее рассмотрим следующие возможности.
А. Пространство ![]() , порожденное
базовыми векторами, совпадает со всем пространством
, порожденное
базовыми векторами, совпадает со всем пространством ![]() . В этом случае, как только
что показано, выпуклый конус, порожденный
. В этом случае, как только
что показано, выпуклый конус, порожденный ![]() , совпадает с
, совпадает с ![]() , т. е. выполняются условия
определения 2.
, т. е. выполняются условия
определения 2.
Б. Пространство ![]() имеет размерность
меньшую, чем
имеет размерность
меньшую, чем ![]() ,
и при этом все векторы из
,
и при этом все векторы из ![]() базовые. В этом случае рассмотрим
произвольный вектор
базовые. В этом случае рассмотрим
произвольный вектор ![]() из
из ![]() , ортогональный
, ортогональный ![]() . Очевидно, что при этом для
всех
. Очевидно, что при этом для
всех ![]() выполняется
равенство
выполняется
равенство
![]()
в противоречии с определением 2'.
В. Пространство ![]() имеет размерность
меньшую, чем
имеет размерность
меньшую, чем ![]() ,
и не все векторы
,
и не все векторы ![]() базовые.
базовые.
Тогда пространство ![]() представим в виде
произведения двух ортогональных подпространств
представим в виде
произведения двух ортогональных подпространств
![]() .
.
Рассмотрим множество проекций ![]() небазовых векторов в
пространстве
небазовых векторов в
пространстве ![]() .
.
Утверждается, что множество ![]() образует неразвернутую
систему векторов. Действительно, если это не так, то, как уже было показано,
выпуклый конус, порожденный
образует неразвернутую
систему векторов. Действительно, если это не так, то, как уже было показано,
выпуклый конус, порожденный ![]() , содержит 0, т. е. существуют такие
, содержит 0, т. е. существуют такие ![]() ,
, ![]() , что
, что
![]() ,
,
где
![]() – проекции
небазовых векторов в
– проекции
небазовых векторов в ![]() .
.
Рассмотрим вектор
![]() , (П.4)
, (П.4)
где
![]() – небазовые
векторы, проекции которых равны соответственно
– небазовые
векторы, проекции которых равны соответственно ![]() .
.
Тогда
![]() .
.
Следовательно, вектор ![]() принадлежит
пространству
принадлежит
пространству ![]() .
Поэтому вектор
.
Поэтому вектор ![]() может
быть представлен как линейная комбинация базовых векторов
может
быть представлен как линейная комбинация базовых векторов ![]() с неотрицательными
коэффициентами
с неотрицательными
коэффициентами
![]() . (П.5)
. (П.5)
Суммируя (П.4) и (П.5), имеем
![]() . (П.6)
. (П.6)
Легко видеть, что в разложении
нуля (П.6) хотя бы один небазовый вектор ![]() участвует с ненулевым весом.
участвует с ненулевым весом.
Полученное противоречие
доказывает, что множество проекций ![]() не развернуто.
не развернуто.
Покажем теперь, что это
утверждение находится в противоречии с тем, что множество векторов ![]() сильно развернуто в
смысле определения 2'.
сильно развернуто в
смысле определения 2'.
Поскольку множество ![]() не пусто и не
развернуто, то, согласно определению 1', в
не пусто и не
развернуто, то, согласно определению 1', в ![]() существует такой вектор
существует такой вектор ![]() , что
, что
![]() , (П.7)
, (П.7)
а следовательно,
![]() , (П.8)
, (П.8)
для базовых векторов и
![]()
для небазовых векторов, в противоречии с определением 2'. Эквивалентность определений 2 и 2' доказана.
Фактически попутно доказана следующая теорема.
Теорема П.3. Если минимальный выпуклый
конус, порожденный конечной системой векторов ![]() , не совпадает со всем пространством
, не совпадает со всем пространством ![]() , то существует
вектор
, то существует
вектор ![]() такой,
что для всех
такой,
что для всех ![]()
![]() , (П.9)
, (П.9)
причем
для небазовых векторов неравенство переходит в строгое ![]() . Если же система векторов
. Если же система векторов ![]() сильно развернута,
то всякий ее вектор является базовым.
сильно развернута,
то всякий ее вектор является базовым.
Замечание. Если ![]() – произвольный вектор такой,
что для всех
– произвольный вектор такой,
что для всех ![]() выполняется
(П.9), то для всякого базового вектора
выполняется
(П.9), то для всякого базового вектора ![]() неравенство переходит в равенство, т.
е.
неравенство переходит в равенство, т.
е.
![]() .
.
Действительно,
пусть ![]() –
базовый вектор. В силу (П.9)
–
базовый вектор. В силу (П.9)
![]() . (П.10)
. (П.10)
В
то же время, как показано выше ((П.3)), вектор ![]() разложим по базовым векторам с
неотрицательными коэффициентами
разложим по базовым векторам с
неотрицательными коэффициентами
![]()
![]() .
.
Следовательно,
![]() . (П.11)
. (П.11)
Из (П.10) и (П.11) получаем
![]() .
.
2. Из теоремы П.3 легко следует известная теорема Куна – Таккера.
Теорема П.4. (Куна – Таккера). Пусть заданы дифференцируемая
функция ![]() и
линейные функции
и
линейные функции ![]() при
при
![]() . Пусть
. Пусть ![]() доставляет условный
минимум
доставляет условный
минимум ![]() при
ограничениях
при
ограничениях
![]() .
.
Тогда
существуют такие числа ![]() , что выполняются условия
, что выполняются условия
 (П.12)
(П.12)
Доказательство. Если ![]() равен нулю, то
утверждение леммы тривиально, так как можно положить все
равен нулю, то
утверждение леммы тривиально, так как можно положить все ![]() равными нулю.
равными нулю.
Занумеруем от 1 до ![]() те ограничения, для
которых
те ограничения, для
которых
![]() .
.
Допустим, что ![]() и утверждение теоремы
неверно. Это значит, что система векторов
и утверждение теоремы
неверно. Это значит, что система векторов
![]()
такова,
что ![]() не
является базовым вектором системы.
не
является базовым вектором системы.
Действительно, если бы вектор ![]() был базовым, то
существовало бы представление
был базовым, то
существовало бы представление
 ,
,
а значит, и представление (П. 12).
Следовательно, в соответствии с
теоремой П.3, существует вектор ![]() такой, что
такой, что
![]()
для
всех ![]()
![]() и
и
![]() . (П.13)
. (П.13)
Рассмотрим точку ![]() . При достаточно
малом
. При достаточно
малом ![]() ограничения
не нарушатся, так как при
ограничения
не нарушатся, так как при ![]()
![]() ,
,
а
при ![]()
![]()
и, следовательно, по непрерывности
![]()
при
достаточно малых ![]() .
.
В то же время
![]()
и,
следовательно, в силу (П. 13) при достаточно малых положительных ![]()
![]()
в противоречии с условиями теоремы. Теорема доказана.
Замечание. Теорема обобщается и на случай, когда среди ограничений есть ограничения вида равенств
![]() . (П.
14)
. (П.
14)
Действительно, ограничение (П.14) равносильно двум ограничениям:
![]() и
и
![]() .
.
Поэтому условия (П. 12)
сохраняются, но ![]() ,
соответствующие ограничениям вида равенств, могут быть отрицательными.
,
соответствующие ограничениям вида равенств, могут быть отрицательными.
В случае, когда функция ![]() дифференцируема и
выпукла, условия (П. 12) становятся не только необходимыми, но и достаточными
условиями минимума.
дифференцируема и
выпукла, условия (П. 12) становятся не только необходимыми, но и достаточными
условиями минимума.
Теорема П.5. Пусть функция ![]() дифференцируема и
выпукла. Если в точке
дифференцируема и
выпукла. Если в точке ![]() , удовлетворяющей неравенствам
, удовлетворяющей неравенствам
![]()
![]() ,
,
выполняются
условия (П. 12),
т. е. существуют такие ![]() , что
, что
![]() ,
,
![]() ,
,
то
точка ![]() доставляет
условный минимум функции
доставляет
условный минимум функции ![]() при ограничениях
при ограничениях
![]() . (П.
15)
. (П.
15)
Доказательство. Пусть ![]() – точка, о которой
говорится в условии теоремы. Если теорема неверна, то найдется точка
– точка, о которой
говорится в условии теоремы. Если теорема неверна, то найдется точка ![]() , удовлетворяющая (П.
15), такая, что
, удовлетворяющая (П.
15), такая, что
![]() . (П.
16)
. (П.
16)
Рассмотрим отрезок
![]() при
при
![]() .
.
В
силу выпуклости допустимой области этот отрезок целиком лежит в пределах
ограничений. Кроме того, из выпуклости ![]() следует (см. § 2 главы IX), что
следует (см. § 2 главы IX), что
![]()
и, следовательно,
![]() . (П.17)
. (П.17)
Как и раньше, будем считать, что
от 1 до ![]() занумерованы
те ограничения, которые достигаются в точке
занумерованы
те ограничения, которые достигаются в точке ![]() , т. е.
, т. е.
![]()
![]() ,
,
![]()
![]() .
.
Тогда,
поскольку отрезок ![]() целиком
лежит в пределах ограничений, имеем
целиком
лежит в пределах ограничений, имеем
![]()
![]() . (П.18)
. (П.18)
Из
(П.17) и (П.18), учитывая замечание к теореме П.3, получаем, что вектор ![]() не является базовым
в системе
не является базовым
в системе
![]()
и,
следовательно, не существует представления  в противоречии с условием теоремы.
Теорема доказана.
в противоречии с условием теоремы.
Теорема доказана.
3. Пусть точка ![]() удовлетворяет
системе ограничений
удовлетворяет
системе ограничений ![]() :
:
![]()
![]() ,
,
![]()
![]() ,
,
т.
е. первые ![]() ограничений
достигаются в точке
ограничений
достигаются в точке ![]() .
.
Назовем единичный вектор ![]() допустимым
направлением в точке
допустимым
направлением в точке ![]() , если существует
, если существует ![]() такое, что
такое, что ![]() при
при ![]() . Нетрудно убедиться,
что допустимыми в
. Нетрудно убедиться,
что допустимыми в ![]() являются
те и только те направления
являются
те и только те направления ![]() , для которых выполняются неравенства
, для которых выполняются неравенства
![]()
![]() .
.
Условный градиент в точке ![]() определяется так.
Прежде всего, находится направление
определяется так.
Прежде всего, находится направление ![]() наибольшего возрастания функции среди
допустимых, т. е.
наибольшего возрастания функции среди
допустимых, т. е.
![]() ,
,
где максимум берется по допустимым направлениям. При этом может оказаться, что
![]() .
.
Это означает, что по всякому допустимому направлению функция не возрастает. В этом случае условный градиент считается равным нулю.
Если же
![]() ,
,
то
в качестве условного градиента берется вектор, по направлению совпадающий с ![]() , а по модулю равный
, а по модулю равный ![]() .
.
Таким образом,
 .
.
Справедлива теорема.
Теорема П.6 Условный градиент, в точке ![]() представим в виде
представим в виде
 , (П.19)
, (П.19)
причем

![]() , (П.20)
, (П.20)
и обратно, всякий вектор, удовлетворяющий (П.19), (П.20), является условным градиентом.
Доказательство. Допустим, что ![]() ; тогда по теореме
Куна – Таккера существует представление
; тогда по теореме
Куна – Таккера существует представление

и, следовательно,
 , (П.21)
, (П.21)
что и требуется.
Обратно, пусть справедливо (П. 21); в этом случае разложение (П. 19) может задавать только нулевой вектор. Действительно, пусть
 ,
,
![]() ,
,
![]()
![]() ,
,
![]() .
.
Тогда
![]() .
.
Если при этом
![]() ,
,
то
![]() есть
допустимое направление, по которому функция
есть
допустимое направление, по которому функция ![]() возрастает в противоречии с допущением.
Таким образом,
возрастает в противоречии с допущением.
Таким образом, ![]() .
.
Допустим теперь, что ![]() . Тогда, как нетрудно
убедиться, направление
. Тогда, как нетрудно
убедиться, направление ![]() совпадает с направлением обобщенного
портрета класса
совпадает с направлением обобщенного
портрета класса ![]() ,
состоящего из одного вектора
,
состоящего из одного вектора ![]() , относительно класса
, относительно класса ![]() , состоящего из
векторов
, состоящего из
векторов ![]() для
для
![]() .
.
Действительно, при этом ![]() есть единичный
вектор, на котором достигается максимум
есть единичный
вектор, на котором достигается максимум
![]()
при ограничениях
![]() ,
,
причем
заведомо известно, что ![]() .
.
Поэтому в силу теорем, доказанных
выше, вектор ![]() однозначно
задается разложением
однозначно
задается разложением
 , (П.22)
, (П.22)
![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Умножим
равенство скалярно на ![]() :
:
![]() ,
,
откуда
![]() .
.
Поэтому
![]() .
.
Полагая ![]() , получим разложение (П. 19).
Теорема доказана.
, получим разложение (П. 19).
Теорема доказана.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ЧАСТЬ ПЕРВАЯ ЭЛЕМЕНТАРНАЯ ТЕОРИЯ
- Глава I. Персептрон Розенблатта
- § 1. Феномен восприятия
- § 2. Физиологическая модель восприятия
- § 3. Техническая модель. Персептрон
- § 4. Математическая модель
- § 5. Обобщенная математическая модель
- § 6. Теорема Новикова
- § 7. Доказательство теоремы Новикова
- § 8. Двухуровневая схема распознавания
- Глава II. Задача обучения машин распознаванию образов
- § 1. Задача имитации
- § 2. Качество обучения
- § 3. Надежность обучения
- § 4. Обучение – задача выбора
- § 5. Две задачи конструирования обучающихся устройств
- § 6. Математическая постановка задачи обучения
- § 7. Три пути решения задачи о минимизации среднего риска
- § 8. Задача обучения распознаванию образов и методы минимизации среднего риска
- Глава III. Методы обучения, основанные на восстановлении распределения вероятностей
- § 1. О восстановлении распределения вероятностей
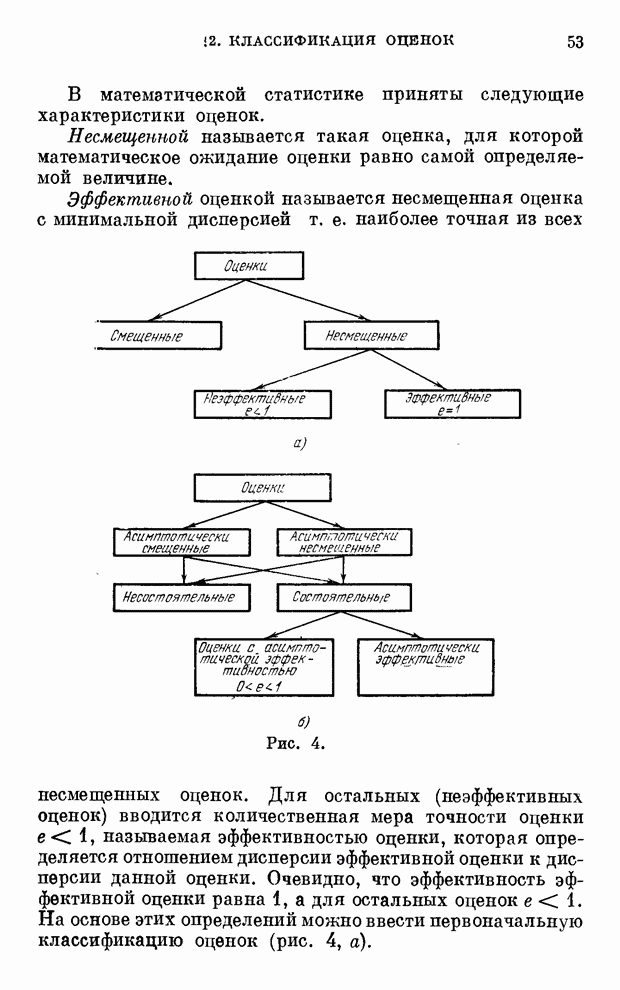
- § 2. Классификация оценок
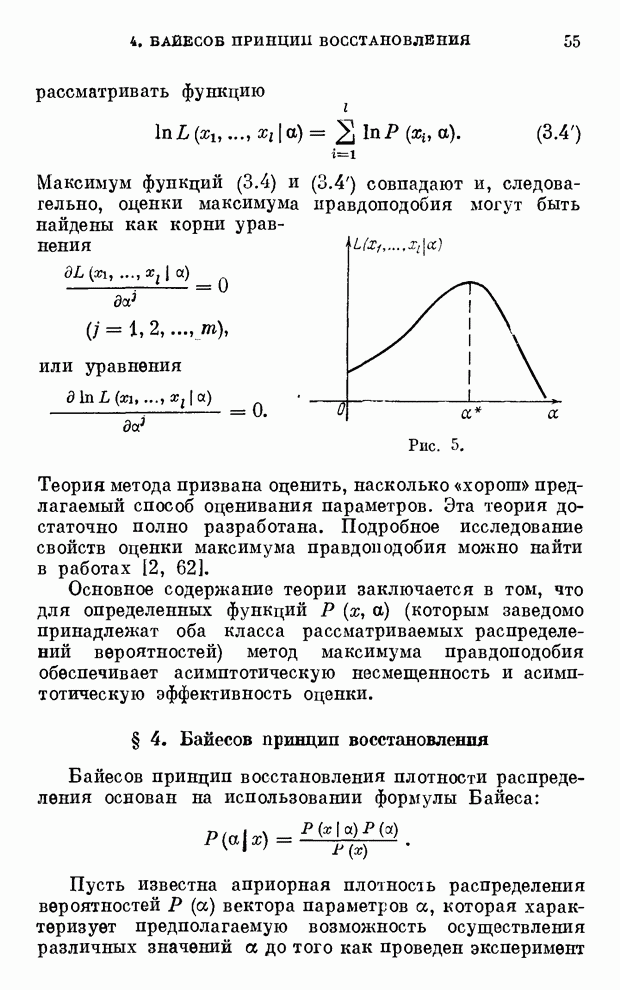
- § 3. Метод максимума правдоподобия
- § 4. Байесов принцип восстановления
- § 5. Сравнение байесова метода оценивания и оценивания методом максимума правдоподобия
- § 6. Оценка параметров распределения дискретных независимых признаков
- § 7. Байесовы оценки параметров распределения дискретных независимых признаков
- § 8. Восстановление параметров нормального распределения методом максимума правдоподобия
- § 9. Байесов метод восстановления нормального распределения
- Глава IV. Рекуррентные алгоритмы обучения распознаванию образов
- § 1. Метод стохастической аппроксимации
- § 2. Детерминистская и стохастическая постановки задачи обучения распознаванию образов
- § 3. Конечно-сходящиеся рекуррентные процедуры
- § 4. Теоремы об останове
- § 5. Метод циклического повторения обучающей последовательности
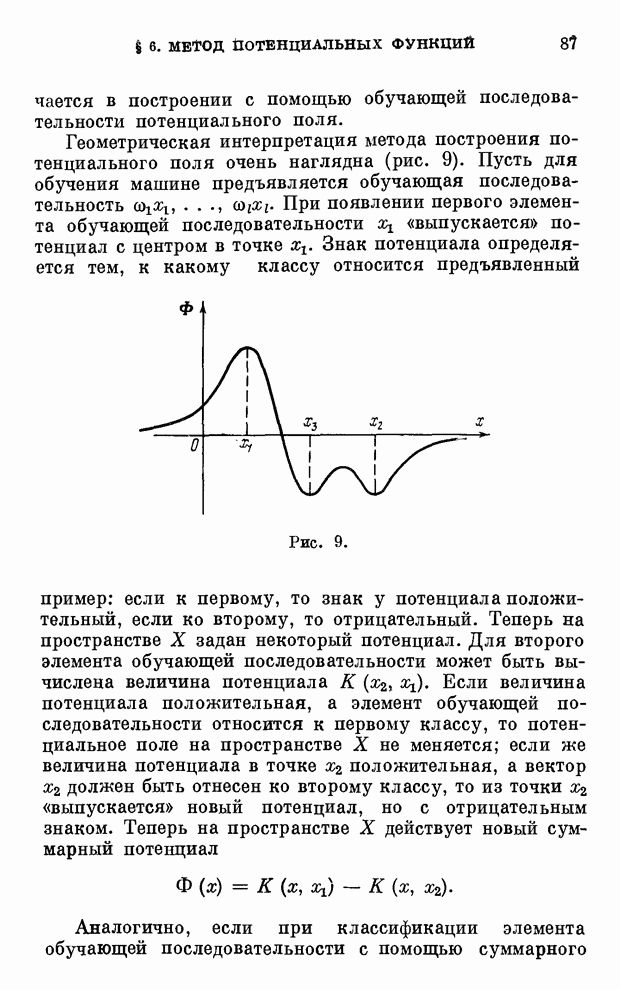
- § 6. Метод потенциальных функций
- Глава V. Алгоритмы, минимизирующие эмпирический риск
- § 1. Метод минимизации эмпирического риска
- § 2. Равномерная сходимость частот появления событий к их вероятностям
- § 3. Теорема Гливенко
- § 4. Частный случай
- § 5. Оценка числа различных линейных разделений векторов
- § 6. Условия равномерной сходимости частот появления событий к их вероятностям
- § 7. Свойства функции роста
- § 8. Оценка уклонения эмпирически оптимального решающего правила
- § 9. Метод минимизации эмпирического риска в детерминистской постановке задачи обучения распознаванию образов
- § 10. Замечание об оценке скорости равномерной сходимости частот появления событий к их вероятностям
- § 11. Замечания об особенностях метода минимизации эмпирического риска
- § 12. Алгоритмы метода обобщенного портрета
- § 13. Алгоритм Кора
- Глава VI. Метод упорядоченной минимизации риска
- § 1. О критериях оценки качества алгоритмов
- § 2. Минимаксный критерий
- § 3. Критерий минимакса потерь
- § 4. Критерий Байеса
- § 5. Упорядочение классов решающих правил
- § 6. О критериях выбора
- § 7. Несмещенность оценки скользящего контроля
- § 8. Упорядочение по размерностям
- § 9. Упорядочение по относительным расстояниям
- § 10. Упорядочение по эмпирическим оценкам относительного расстояния и задача минимизации суммарного риска
- § 11. О выборе оптимальной совокупности признаков
- § 12. Алгоритмы упорядоченной минимизации суммарного риска
- § 13. Алгоритмы построения экстремальных кусочно-линейных решающих правил
- § 14. Приложение к главе VI
- Глава VII. Примеры применения методов обучения распознаванию образов
- § 1. Задача о различении нефтеносных и водоносных пластов в скважине
- § 2. Задача о различении сходных почерков
- § 3. Задача о контроле качества продукции
- § 4. Задача о прогнозе погоды
- § 5. Применение метода обучения распознаванию образов в медицине
- § 6. Замечания о применениях методов обучения распознаванию образов
- Глава VIII. Несколько общих замечаний
- § 1. Еще раз о постановке задачи
- § 2. Физики об интуиции
- § 3. Машинная интуиция
- § 4. О мире, в котором возможна интуиция
- Часть вторая. СТАТИСТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ
- Глава IX. О сходимости рекуррентных алгоритмов обучения распознаванию образов
- § 1. Определение понятия сходимости
- § 2. Выпуклые функции
- § 3. Обобщенный градиент
- § 4. Условия сходимости рекуррентных алгоритмов
- § 5. Еще одно условие сходимости рекуррентных алгоритмов
- Глава X. Достаточные условия равномерной сходимости частот к вероятностям по классу событий
- § 1. О близости минимума эмпирического риска к минимуму среднего риска
- § 2. Определение равномерной сходимости частот к вероятностям
- § 3. Определение функции роста
- § 4. Свойства функции роста
- § 5. Основная лемма
- § 6. Вывод достаточных условий равномерной сходимости частот к вероятностям по классу событий
- § 7. О равномерной сходимости с вероятностью единица
- § 8. Примеры и дополнительные замечания
- § 9. Приложение к главе X
- Глава XI. Необходимые и достаточные условия равномерной сходимости частот к веронтностям по классу событий
- § 1. Энтропия системы событий
- § 2. Асимптотические свойства энтропии
- § 3. Необходимые и достаточные условия равномерной сходимости (доказательство достаточности)
- § 4. Доказательство необходимости условий равномерной сходимости
- § 5. Примеры и дополнительные критерии
- Глава XII. Оценки равномерного относительного уклонения частот от вероятностей в классе событий
- § 1. О равномерном относительном уклонении
- § 2. Оценка равномерного относительного уклонения частот в двух полувыборках
- § 3. Оценка равномерного относительного уклонения частот от вероятностей
- Глава XIII. Применение теории равномерной сходимости к методам минимизации эмпирического риска
- § 1. Оценка достаточной длины обучающей последовательности в задачах обучения распознаванию
- § 2. Равномерная сходимость средних к математическим ожиданиям
- Часть третья. МЕТОДЫ ПОСТРОЕНИЯ РАЗДЕЛЯЮЩИХ ПОВЕРХНОСТЕЙ
- Глава XIV. Построение разделяющей гиперплоскости (метод обобщенного портрета)
- § 1. Оптимальная разделяющая гиперплоскость
- § 2. Однопараметрическое семейство разделяющих гиперплоскостей
- § 3. Некоторые свойства обобщенного портрета
- § 4. Двойственная задача
- § 5. Алгоритмы персептронного типа
- § 6. Градиентные методы построения разделяющей гиперплоскости (вычисление обобщенного портрета)
- § 7. Теория оптимальной разделяющей гиперплоскости
- § 8. Двойственная задача
- § 9. Методы вычисления оптимальной разделяющей гиперплоскости
- § 10. Построение оптимальной разделяющей гиперплоскости модифицированным методом Гаусса–Зайделя
- § 11. Применение метода обобщенного портрета для нахождения оптимальной разделяющей гиперплоскости
- § 12. Некоторые статистические особенности метода обобщенного портрета
- § 13. Приложение к главе XIV
- Глава XV. АЛГОРИТМЫ ОБУЧЕНИЯ РАСПОЗНАВАНИЮ ОБРАЗОВ, РЕАЛИЗУЮЩИЕ МЕТОД ОБОБЩЕННОГО ПОРТРЕТА
- § 1. Способы представления информации
- § 2. Алгоритм построения разделяющей гиперплоскости
- § 3. Алгоритм построения разделяющей гиперплоскости, минимизирующей число ошибочно классифицируемых векторов
- § 4. Алгоритм построения кусочно-линейной разделяющей поверхности
- § 5. Алгоритмы построения разделяющей гиперплоскости в пространстве минимального числа признаков
- § 6. Алгоритм построения экстремальной линейной разделяющей поверхности
- § 7. Алгоритм построения экстремальной кусочно-линейной разделяющей поверхности
- § 8. Алгоритм построения разделяющей гиперплоскости с оценкой ее качества методом скользящего контроля
- § 9. Алгоритмы построения экстремальных разделяющих гиперповерхностей с помощью процедуры скользящий контроль
- § 10. О работе с алгоритмами
- Глава XVI. МЕТОД СОПРЯЖЕННЫХ НАПРАВЛЕНИЙ
- § 1. Идея метода
- § 2. Метод сопряженных градиентов
- § 3. Метод параллельных касательных (партан)
- § 4. Анализ погрешностей метода
- КОММЕНТАРИИ
- ЛИТЕРАТУРА