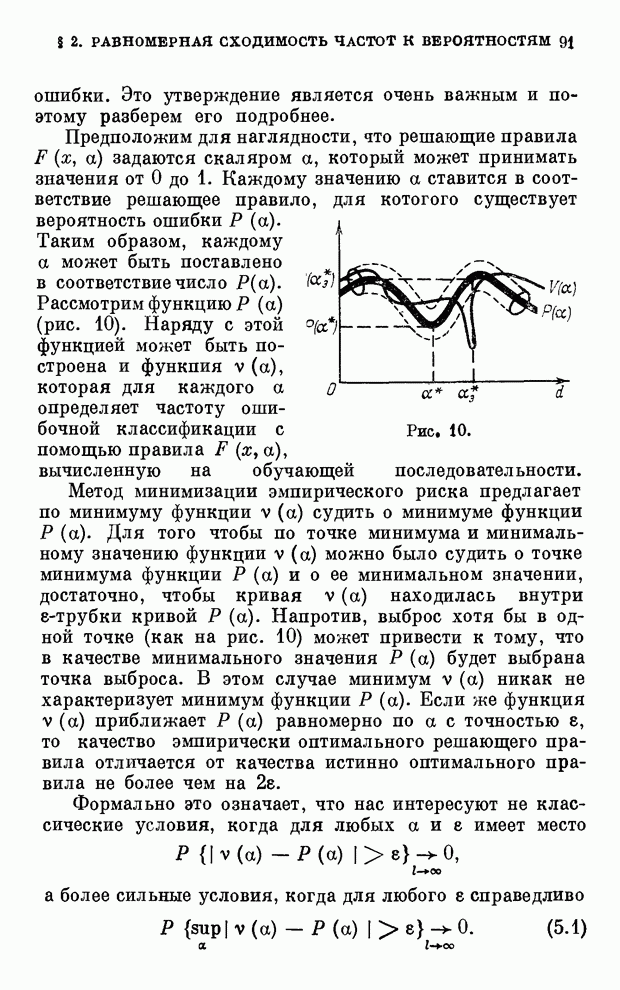
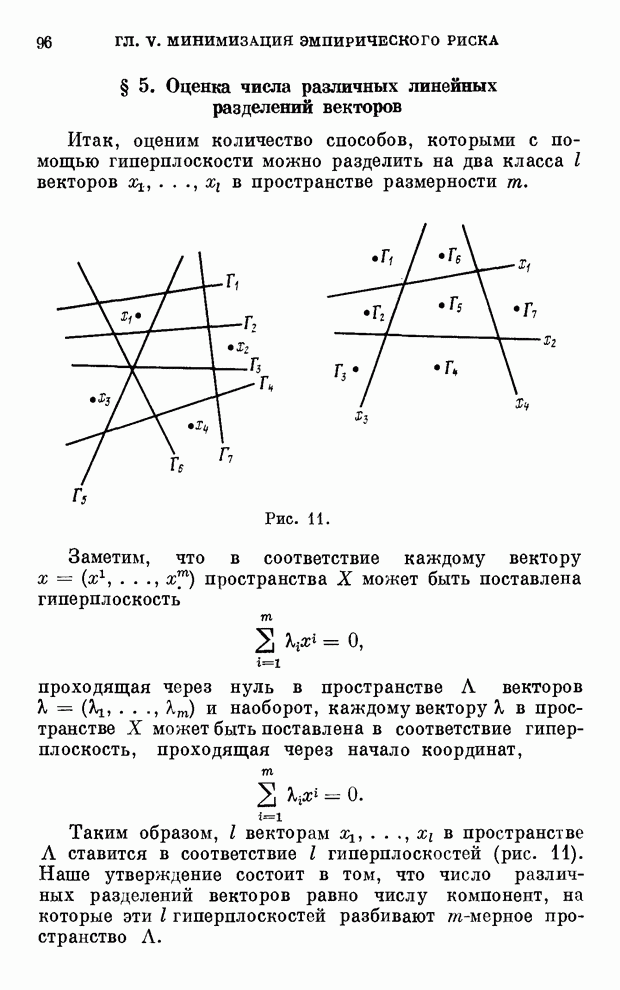
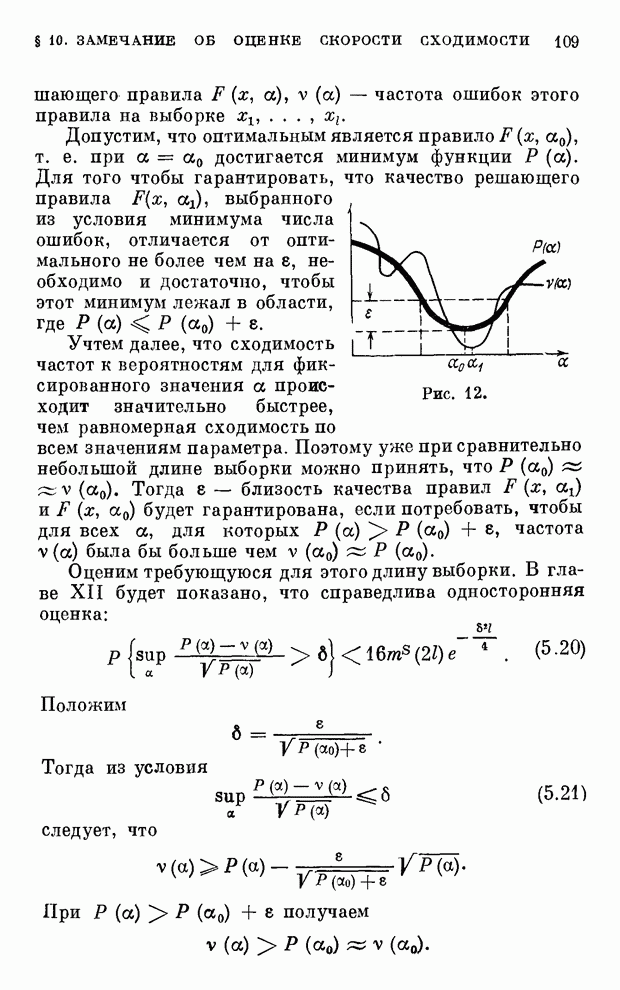
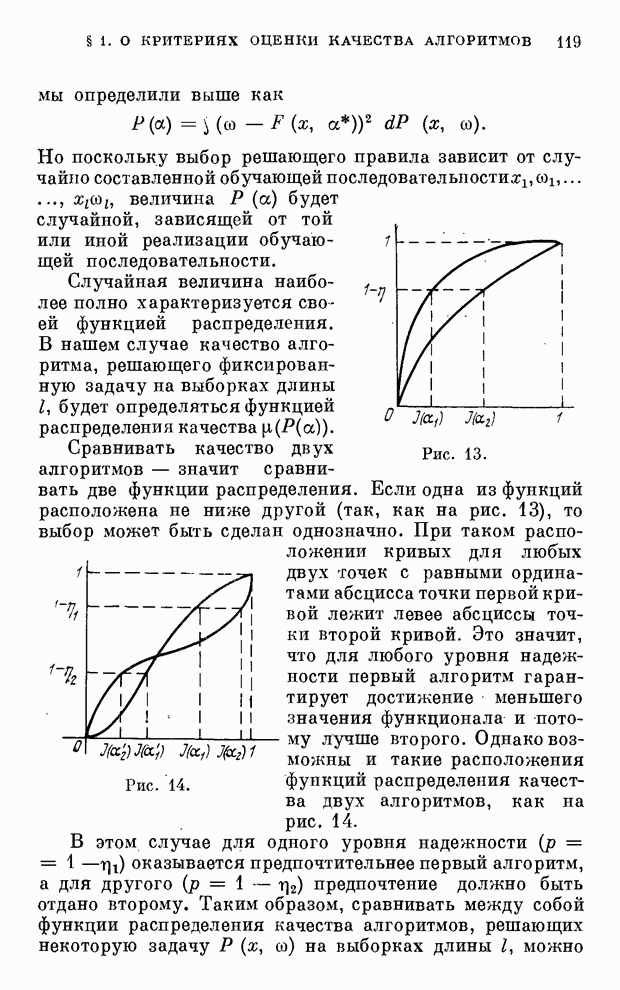
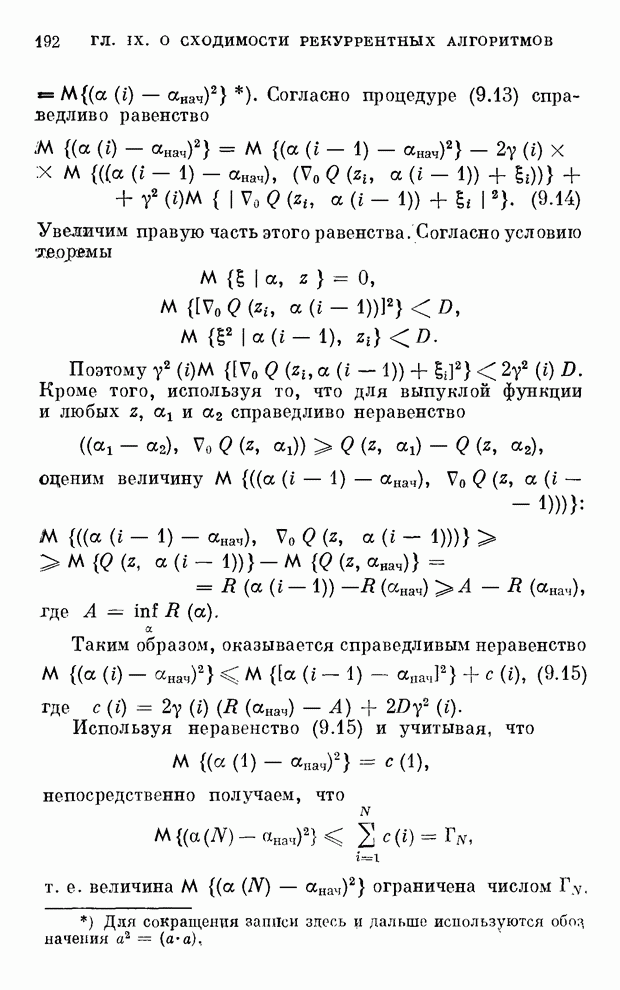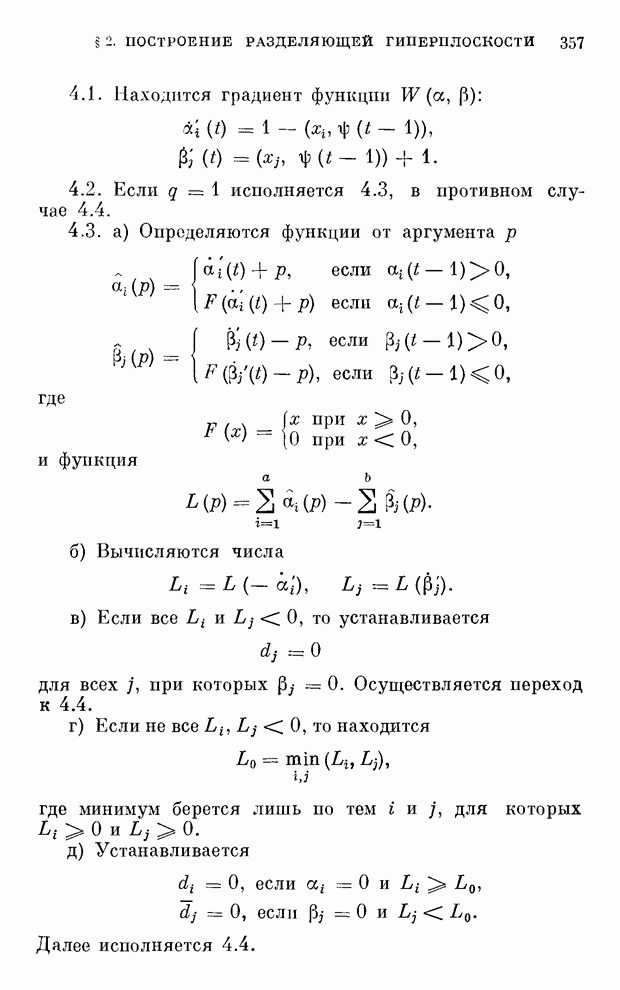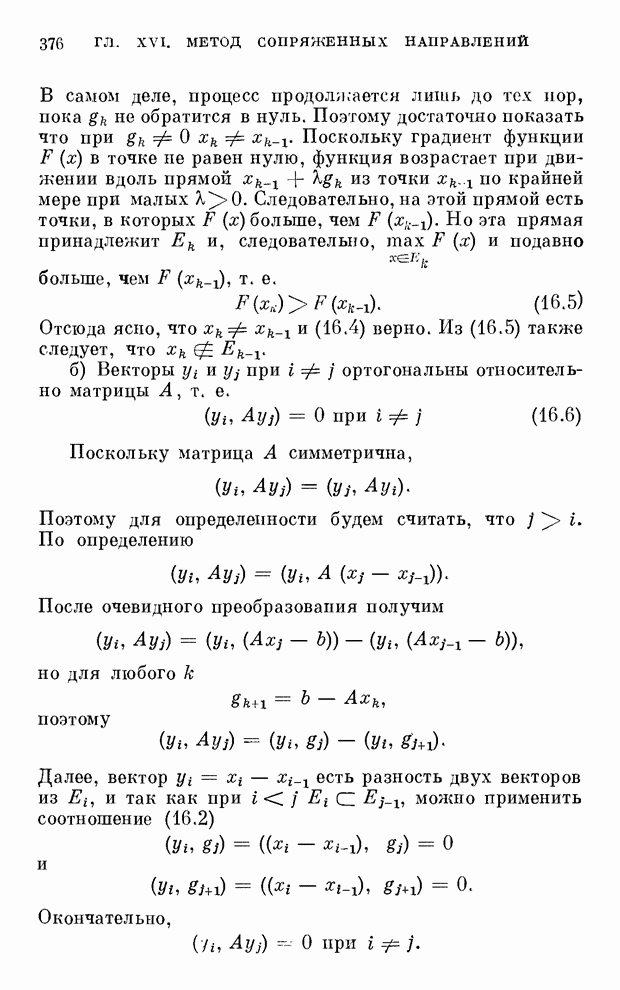| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 8. Двухуровневая схема распознавания
Итак, исследование персептрона
приводит к рассмотрению двухуровневой модели. На первом уровне осуществляется
отображение исходного пространства описаний ![]() в новое пространство
в новое пространство ![]() . На втором уровне реализуется
алгоритм обучения – построение разделяющей гиперплоскости в этом новом
пространстве на основании обучающей последовательности.
. На втором уровне реализуется
алгоритм обучения – построение разделяющей гиперплоскости в этом новом
пространстве на основании обучающей последовательности.
Для того чтобы вторая часть могла
решать свою задачу, необходимо, чтобы после отображения ![]() множества векторов,
соответствующие разным классам, были разделимы гиперплоскостью.
множества векторов,
соответствующие разным классам, были разделимы гиперплоскостью.
Возникает естественный вопрос, насколько универсальна идея персептрона, т. е. существует ли такое отображение, при котором любые два непересекающихся в исходном пространстве множества были бы разделимы в новом пространстве гиперплоскостью.
Оказывается, да – универсальна. При не слишком стеснительных ограничениях, например, считая исходное пространство бинарным, такое отображение действительно можно построить. В. А. Якубович показал даже, что преобразование
![]()
может быть осуществлено с помощью пороговых функций, т. е. буквально можно построить универсальный персептрон.
Беда лишь в том, что у универсального персептрона:
а) размерность спрямляющего пространства оказывается огромной,
б)
почти для всех пар непересекающихся в исходном пространстве множеств отношение ![]() в спрямляющем
пространстве чрезмерно велико.
в спрямляющем
пространстве чрезмерно велико.
Как будет показано ниже, это приводит к катастрофически большой оценке необходимой длины обучающей последовательности.
Поэтому всякая реальная машина
должна использовать специализированное отображение ![]() , при котором лишь относительно
немногие пары непересекающихся в исходном пространстве множеств переходят в
разделимые гиперплоскостью.
, при котором лишь относительно
немногие пары непересекающихся в исходном пространстве множеств переходят в
разделимые гиперплоскостью.
Выбор такого отображения тесно связан со спецификой данной задачи обучения и должен делаться в нашей схеме до начала обучения, т. е. опираться на априорные сведения о природе распознаваемых образов.
Например, при распознавании
изображений в качестве функций ![]() берутся такие функции, которые по набору чисел
берутся такие функции, которые по набору чисел
![]() ,
характеризующих яркость точек рецепторного поля, строят новые описания в
терминах кривых, пересечений, кривизны и т. п.
,
характеризующих яркость точек рецепторного поля, строят новые описания в
терминах кривых, пересечений, кривизны и т. п.
Совсем иные преобразования могут понадобиться при применении распознавания, скажем, в медицине или геологии. В каждой конкретной области приложений выбор отображения чрезвычайно сильно связан с конкретными особенностями этой области знаний.
В пределе наилучшее отображение будет таким, когда все точки, относящиеся к одному классу в исходном пространстве, перейдут в одну точку (а разные классы, естественно, в разные точки). При таком отображении задача обучения совсем вырождается, так как для обучения достаточно показать по одному представителю каждого класса. Построение такого пространства является недосягаемой мечтой всякого, кто строит отображения по априорным данным.
На практике же оказывается, что построение даже «хорошего» спрямляющего пространства представляет собой чрезвычайно сложную задачу. Поэтому часто в построенном пространстве целесообразно искать разделение не с помощью гиперплоскостей, а с помощью более сложных разделяющих поверхностей. Строго говоря, такая схема уже не является персептронной. Однако это обстоятельство никак не меняет основного принципа построения машины, обучающейся распознаванию образов: машина реализует двухэтапную систему обучения, где на первом этапе по априорным данным задается класс возможных решающих правил, а на втором этапе из заданного множества решающих правил выбирается нужное. С этой точки зрения персептрон Розенблатта реализует некоторые кусочно-линейные решающие правила: задание отображения определяет возможные для данного персептрона кусочно-линейные решающие правила, а алгоритм настройки весов позволяет выбрать в заданном множестве решающих правил нужное.
Итак, задача обучения машин распознаванию образов приводит к двухэтапной схеме распознавания. В эту схему укладываются отнюдь не только персептроноподобные распознающие машины – во всякой программе распознавания априори заложен некоторый запас решающих правил, выбранный из тех или иных соображений (например, решающие правила, реализуемые булевыми функциями определенного вида, пороговыми функциями, функциями, инвариантными относительно определенных преобразований, и т. д.). И только из этого запаса с помощью обучающей последовательности выбирается нужное правило.
В дальнейших главах книги мы ограничимся исследованием второго этапа решения задачи. Именно эта часть задачи была предметом исследования большинства (если не всех) теоретических работ по распознаванию, не привязанных к конкретным приложениям.
Проблемы, возникающие здесь, тесно переплетаются с задачами математической статистики. С точки зрения математической статистики не очень существенно, какова природа решающих правил. Как будет показано, основную роль здесь играют некоторые общие статистические характеристики класса решающих правил в целом.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ЧАСТЬ ПЕРВАЯ ЭЛЕМЕНТАРНАЯ ТЕОРИЯ
- Глава I. Персептрон Розенблатта
- § 1. Феномен восприятия
- § 2. Физиологическая модель восприятия
- § 3. Техническая модель. Персептрон
- § 4. Математическая модель
- § 5. Обобщенная математическая модель
- § 6. Теорема Новикова
- § 7. Доказательство теоремы Новикова
- § 8. Двухуровневая схема распознавания
- Глава II. Задача обучения машин распознаванию образов
- § 1. Задача имитации
- § 2. Качество обучения
- § 3. Надежность обучения
- § 4. Обучение – задача выбора
- § 5. Две задачи конструирования обучающихся устройств
- § 6. Математическая постановка задачи обучения
- § 7. Три пути решения задачи о минимизации среднего риска
- § 8. Задача обучения распознаванию образов и методы минимизации среднего риска
- Глава III. Методы обучения, основанные на восстановлении распределения вероятностей
- § 1. О восстановлении распределения вероятностей
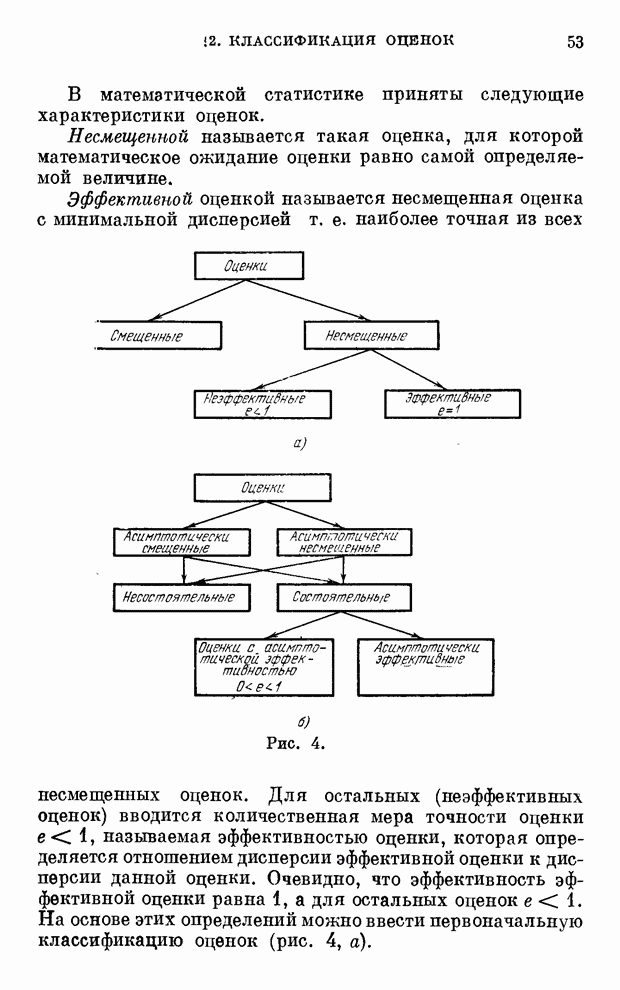
- § 2. Классификация оценок
- § 3. Метод максимума правдоподобия
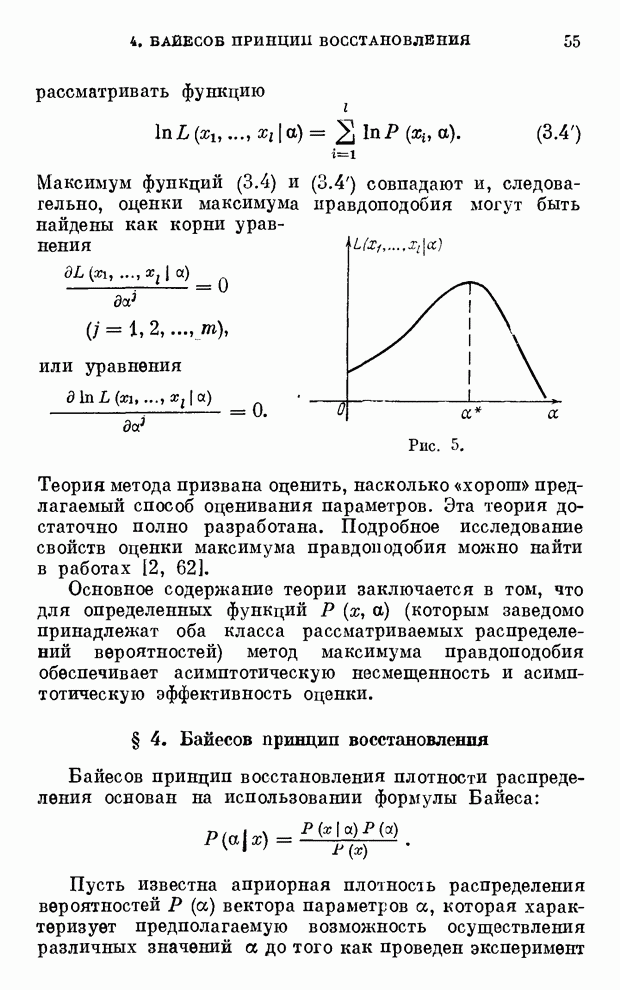
- § 4. Байесов принцип восстановления
- § 5. Сравнение байесова метода оценивания и оценивания методом максимума правдоподобия
- § 6. Оценка параметров распределения дискретных независимых признаков
- § 7. Байесовы оценки параметров распределения дискретных независимых признаков
- § 8. Восстановление параметров нормального распределения методом максимума правдоподобия
- § 9. Байесов метод восстановления нормального распределения
- Глава IV. Рекуррентные алгоритмы обучения распознаванию образов
- § 1. Метод стохастической аппроксимации
- § 2. Детерминистская и стохастическая постановки задачи обучения распознаванию образов
- § 3. Конечно-сходящиеся рекуррентные процедуры
- § 4. Теоремы об останове
- § 5. Метод циклического повторения обучающей последовательности
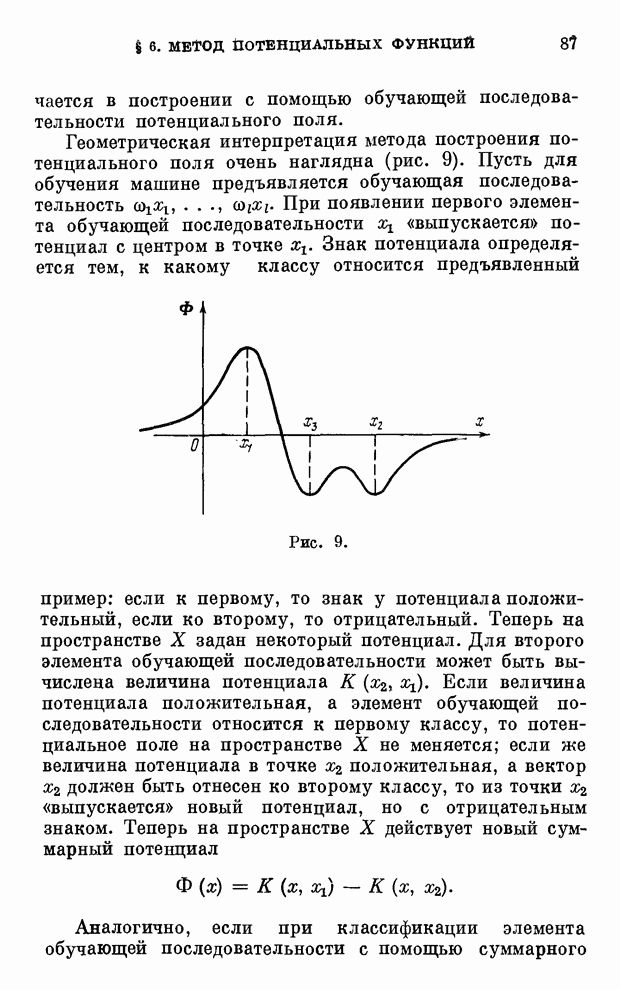
- § 6. Метод потенциальных функций
- Глава V. Алгоритмы, минимизирующие эмпирический риск
- § 1. Метод минимизации эмпирического риска
- § 2. Равномерная сходимость частот появления событий к их вероятностям
- § 3. Теорема Гливенко
- § 4. Частный случай
- § 5. Оценка числа различных линейных разделений векторов
- § 6. Условия равномерной сходимости частот появления событий к их вероятностям
- § 7. Свойства функции роста
- § 8. Оценка уклонения эмпирически оптимального решающего правила
- § 9. Метод минимизации эмпирического риска в детерминистской постановке задачи обучения распознаванию образов
- § 10. Замечание об оценке скорости равномерной сходимости частот появления событий к их вероятностям
- § 11. Замечания об особенностях метода минимизации эмпирического риска
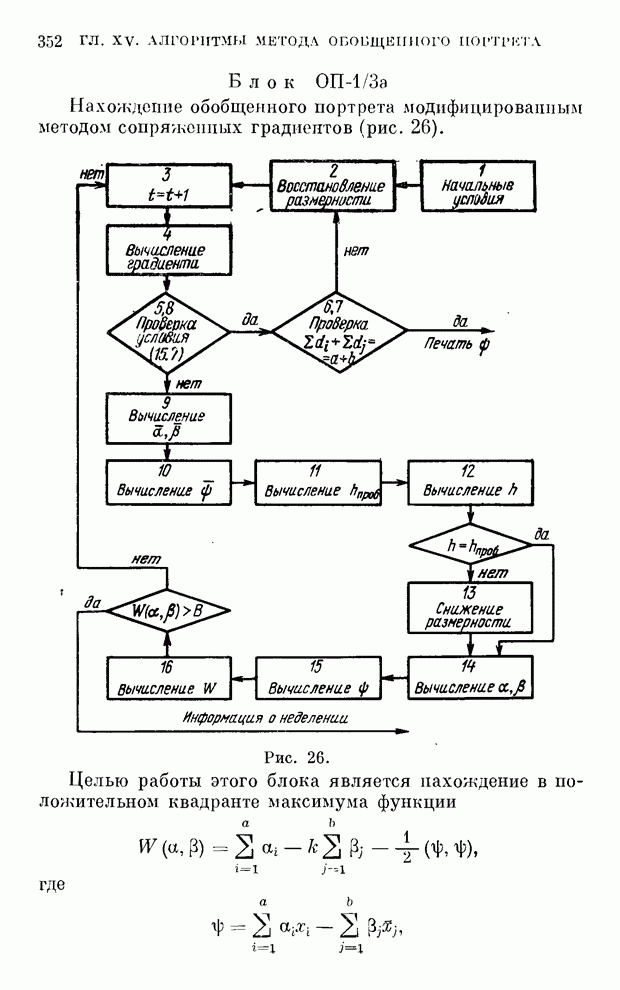
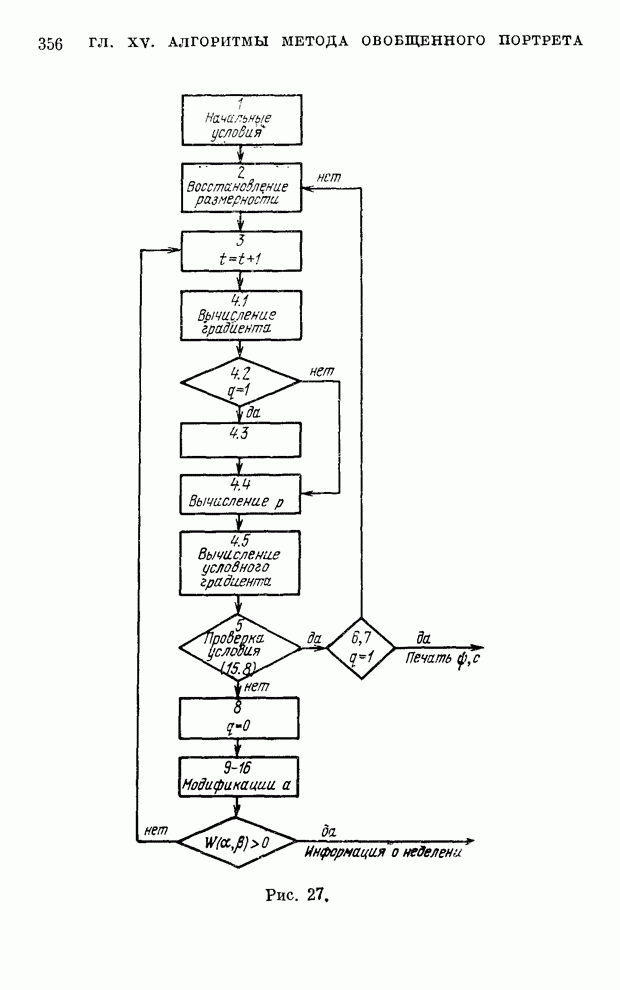
- § 12. Алгоритмы метода обобщенного портрета
- § 13. Алгоритм Кора
- Глава VI. Метод упорядоченной минимизации риска
- § 1. О критериях оценки качества алгоритмов
- § 2. Минимаксный критерий
- § 3. Критерий минимакса потерь
- § 4. Критерий Байеса
- § 5. Упорядочение классов решающих правил
- § 6. О критериях выбора
- § 7. Несмещенность оценки скользящего контроля
- § 8. Упорядочение по размерностям
- § 9. Упорядочение по относительным расстояниям
- § 10. Упорядочение по эмпирическим оценкам относительного расстояния и задача минимизации суммарного риска
- § 11. О выборе оптимальной совокупности признаков
- § 12. Алгоритмы упорядоченной минимизации суммарного риска
- § 13. Алгоритмы построения экстремальных кусочно-линейных решающих правил
- § 14. Приложение к главе VI
- Глава VII. Примеры применения методов обучения распознаванию образов
- § 1. Задача о различении нефтеносных и водоносных пластов в скважине
- § 2. Задача о различении сходных почерков
- § 3. Задача о контроле качества продукции
- § 4. Задача о прогнозе погоды
- § 5. Применение метода обучения распознаванию образов в медицине
- § 6. Замечания о применениях методов обучения распознаванию образов
- Глава VIII. Несколько общих замечаний
- § 1. Еще раз о постановке задачи
- § 2. Физики об интуиции
- § 3. Машинная интуиция
- § 4. О мире, в котором возможна интуиция
- Часть вторая. СТАТИСТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ
- Глава IX. О сходимости рекуррентных алгоритмов обучения распознаванию образов
- § 1. Определение понятия сходимости
- § 2. Выпуклые функции
- § 3. Обобщенный градиент
- § 4. Условия сходимости рекуррентных алгоритмов
- § 5. Еще одно условие сходимости рекуррентных алгоритмов
- Глава X. Достаточные условия равномерной сходимости частот к вероятностям по классу событий
- § 1. О близости минимума эмпирического риска к минимуму среднего риска
- § 2. Определение равномерной сходимости частот к вероятностям
- § 3. Определение функции роста
- § 4. Свойства функции роста
- § 5. Основная лемма
- § 6. Вывод достаточных условий равномерной сходимости частот к вероятностям по классу событий
- § 7. О равномерной сходимости с вероятностью единица
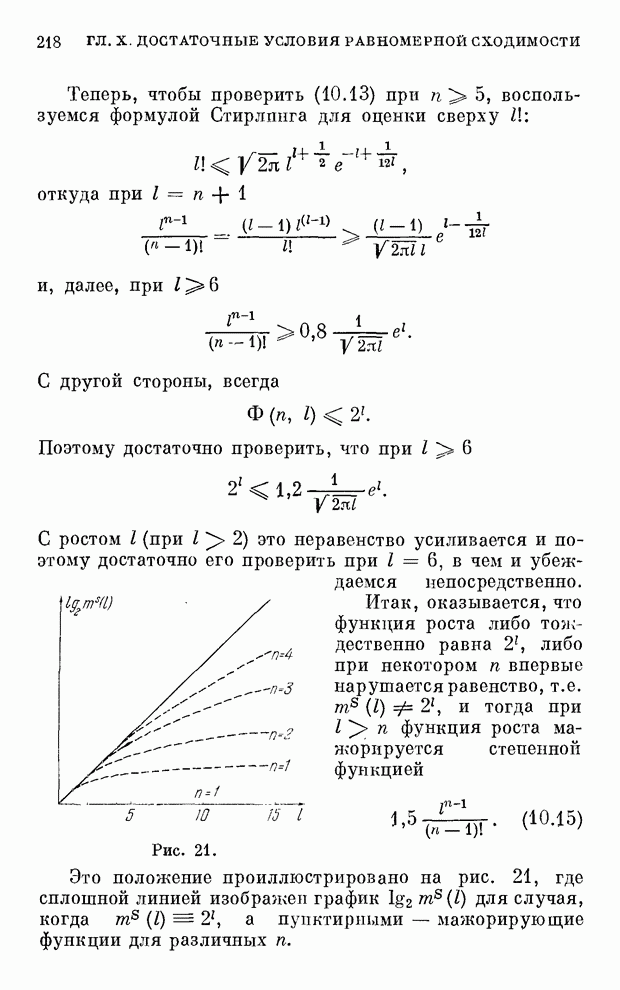
- § 8. Примеры и дополнительные замечания
- § 9. Приложение к главе X
- Глава XI. Необходимые и достаточные условия равномерной сходимости частот к веронтностям по классу событий
- § 1. Энтропия системы событий
- § 2. Асимптотические свойства энтропии
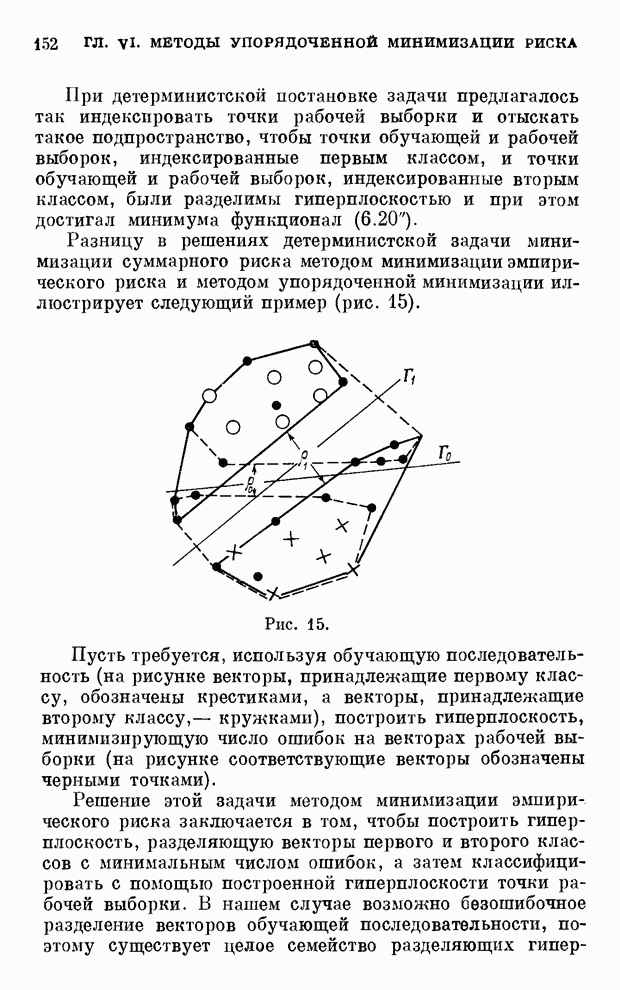
- § 3. Необходимые и достаточные условия равномерной сходимости (доказательство достаточности)
- § 4. Доказательство необходимости условий равномерной сходимости
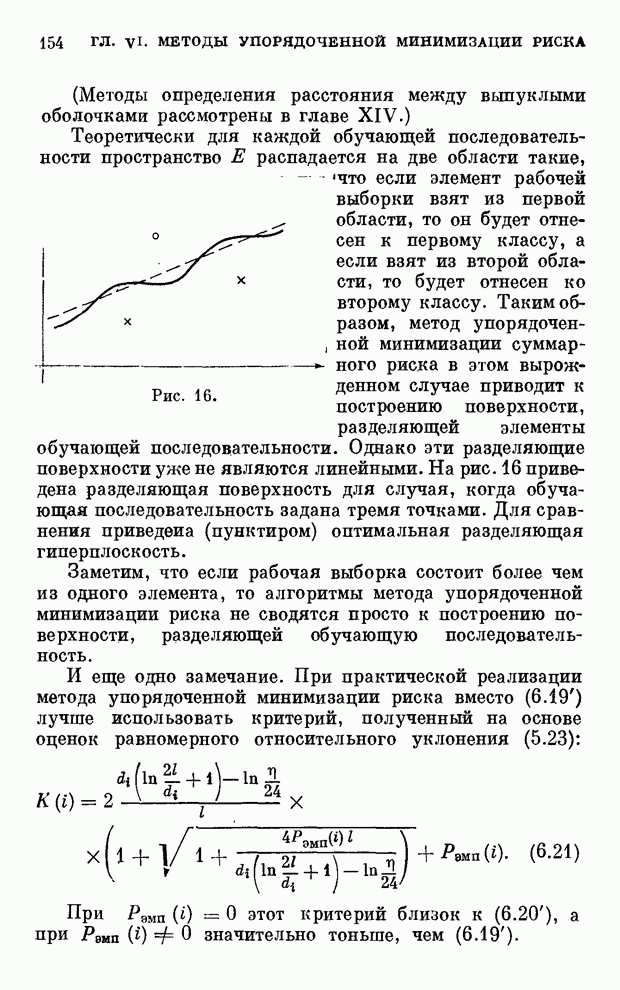
- § 5. Примеры и дополнительные критерии
- Глава XII. Оценки равномерного относительного уклонения частот от вероятностей в классе событий
- § 1. О равномерном относительном уклонении
- § 2. Оценка равномерного относительного уклонения частот в двух полувыборках
- § 3. Оценка равномерного относительного уклонения частот от вероятностей
- Глава XIII. Применение теории равномерной сходимости к методам минимизации эмпирического риска
- § 1. Оценка достаточной длины обучающей последовательности в задачах обучения распознаванию
- § 2. Равномерная сходимость средних к математическим ожиданиям
- Часть третья. МЕТОДЫ ПОСТРОЕНИЯ РАЗДЕЛЯЮЩИХ ПОВЕРХНОСТЕЙ
- Глава XIV. Построение разделяющей гиперплоскости (метод обобщенного портрета)
- § 1. Оптимальная разделяющая гиперплоскость
- § 2. Однопараметрическое семейство разделяющих гиперплоскостей
- § 3. Некоторые свойства обобщенного портрета
- § 4. Двойственная задача
- § 5. Алгоритмы персептронного типа
- § 6. Градиентные методы построения разделяющей гиперплоскости (вычисление обобщенного портрета)
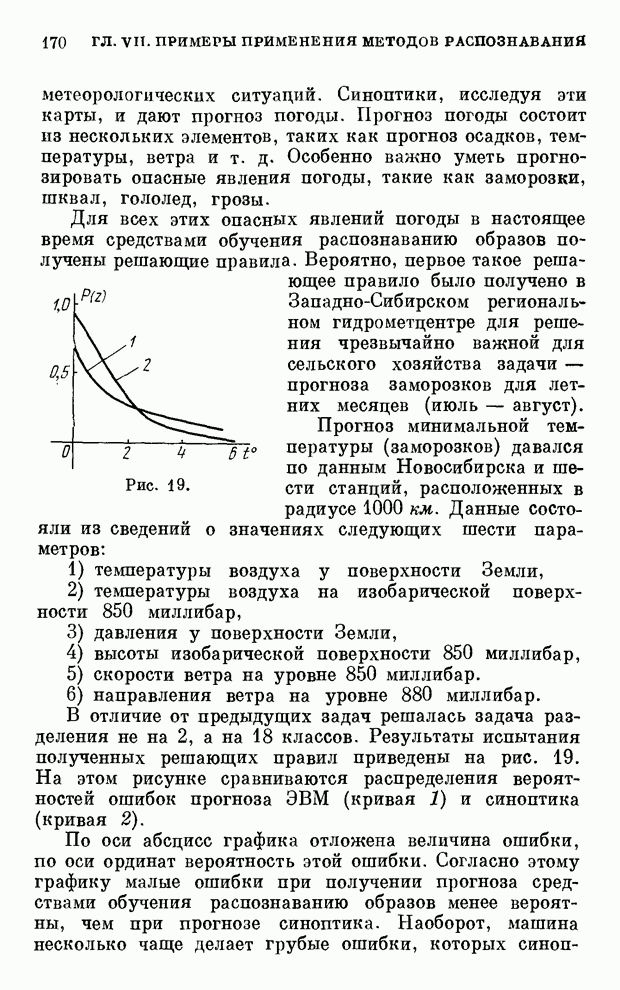
- § 7. Теория оптимальной разделяющей гиперплоскости
- § 8. Двойственная задача
- § 9. Методы вычисления оптимальной разделяющей гиперплоскости
- § 10. Построение оптимальной разделяющей гиперплоскости модифицированным методом Гаусса–Зайделя
- § 11. Применение метода обобщенного портрета для нахождения оптимальной разделяющей гиперплоскости
- § 12. Некоторые статистические особенности метода обобщенного портрета
- § 13. Приложение к главе XIV
- Глава XV. АЛГОРИТМЫ ОБУЧЕНИЯ РАСПОЗНАВАНИЮ ОБРАЗОВ, РЕАЛИЗУЮЩИЕ МЕТОД ОБОБЩЕННОГО ПОРТРЕТА
- § 1. Способы представления информации
- § 2. Алгоритм построения разделяющей гиперплоскости
- § 3. Алгоритм построения разделяющей гиперплоскости, минимизирующей число ошибочно классифицируемых векторов
- § 4. Алгоритм построения кусочно-линейной разделяющей поверхности
- § 5. Алгоритмы построения разделяющей гиперплоскости в пространстве минимального числа признаков
- § 6. Алгоритм построения экстремальной линейной разделяющей поверхности
- § 7. Алгоритм построения экстремальной кусочно-линейной разделяющей поверхности
- § 8. Алгоритм построения разделяющей гиперплоскости с оценкой ее качества методом скользящего контроля
- § 9. Алгоритмы построения экстремальных разделяющих гиперповерхностей с помощью процедуры скользящий контроль
- § 10. О работе с алгоритмами
- Глава XVI. МЕТОД СОПРЯЖЕННЫХ НАПРАВЛЕНИЙ
- § 1. Идея метода
- § 2. Метод сопряженных градиентов
- § 3. Метод параллельных касательных (партан)
- § 4. Анализ погрешностей метода
- КОММЕНТАРИИ
- ЛИТЕРАТУРА