| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 10. Оптические системы
Все сказанное в предыдущем параграфе о линзах относилось к малым линзам, поперечник которых значительно меньше их фокусного расстояния. Кроме того, все сделанные выводы справедливы лишь для лучей, образующих весьма малый угол с оптической осью. Для обычного применения линз — получения изображения каких-либо предметов—линзы малого размера так же мало годятся, как и малые зеркала в соответствующих случаях. Так же как и в случае зеркал, малая линза сконцентрирует в изображении слишком малое количество света.
При увеличении размера линзы преломленные ею лучи уже не собираются в одну точку, так как угол с осью становится большим. Возникает, так же как и в зеркалах, сферическая аберрация. Если мы имеем предмет, состоящий из ряда светящихся точек, то изображение этого предмета получится расплывчатым, ибо пучки лучей, исходящие из каждой точки предмета, уже не соберутся линзой в соответствующие точки изображения.
С другой стороны, если наш предмет имеет большие размеры в направлении, перпендикулярном к оси, то даже при малой линзе лучи предмета, проходящие сквозь линзу, будут образовывать
большие углы с оптической осью. Следовательно, изображение краев предмета также будет плохим.
Чтобы ослабить влияние этих недостатков, свойственных отдельным линзам, составляют по нескольку линз вместе, располагая их одну за другой. Комбинация нескольких линз (в которую могут входить также и зеркала) называется оптической системой.
В состав оптической системы могут входить элементы (линзы или зеркала) с большими аберрациями, но противоположных знаков. Эти аберрации как бы компенсируют друг друга, и в системе достигается своеобразное равновесие, соответствующее малым результирующим аберрациям. Достаточно вынуть из сложного первоклассного фотообъектива одну из линз, чтобы равновесие нарушилось и возникла большая аберрация.
Если оптические оси всех линз совпадают, то оптическая система носит название центрированной.
Самым простым примером оптической системы является пара тонких линз, сложенных вплотную. В этом случае фокусное расстояние системы очень просто связано с фокусными расстояниями отдельных линз:

где  фокусное расстояние системы,
фокусное расстояние системы,  фокусное расстояние первой линзы,
фокусное расстояние первой линзы,  фокусное расстояние второй линзы.
фокусное расстояние второй линзы.
Формулу (8) можно словами выразить следующим образом: оптическая сила двух тонких линз, сложенных вместе, равна сумме оптических сил этих линз.
Сложнее обстоит дело в случае двух линз, расположенных на некотором расстоянии. Для них уже формула (8) несправедлива, и, поскольку в этом случае система приобретает определенную толщину, возникает вопрос, откуда отсчитывать все расстояния по оптической оси. Если в случае тонкой линзы мы за опорную брали точку С (рис. 17), то теперь надо выбрать какие-то новые точки за опорные в нашей оптической системе.
Собственно говоря, переход от одной линзы к двум или нескольким принципиально чрезвычайно прост.. Мы рассматриваем последовательное действие линз. При этом изображение, даваемое первой линзой, очевидно, служит предметом для второй, следующей за ней линзой; изображение, даваемое второй линзой уже от этого «предмета», служит предметом для третьей и т. д. Зная расположение линз и их фокусные расстояния, применяя к каждой линзе формулу (7), легко найти место окончательного изображения, даваемого системой.
Однако оказывается, что для полной характеристики системы достаточно задать лишь расположение нескольких основных точек, тесно связанных с ее структурой. Расположение этих точек, конечно, приходится рассчитывать, исходя из отдельных элементов системы

Рис. 21. Основные элементы оптической системы.
(линз, зеркал и расстояний между ними), но если эти точки известны, то можно забыть о всей детальной структуре системы и для построения изображения пользоваться только ими.
К числу таких точек, во-первых, относятся главные фокусы системы, т. е. точки, в которых сходятся параллельные лучи, падающие на систему. Если система не собирающая, а рассеивающая, то это будут соответственно мнимые точки, из которых как бы исходят рассеянные системой параллельные лучи.
Наоборот, если мы поместим какой-либо точечный источник в главный фокус системы, то система делает пучок лучей параллельным.
Если же построить плоскости,  роходящие перпендикулярно к оптической оси через главные фокусы, то все сказанное относится к любой точке этих плоскостей. На рис. 21 прямые, проходящие через
роходящие перпендикулярно к оптической оси через главные фокусы, то все сказанное относится к любой точке этих плоскостей. На рис. 21 прямые, проходящие через  изображают следы этих плоскостей,
изображают следы этих плоскостей,  главные фокусы системы.
главные фокусы системы.
Кроме главных фокусов на оптической оси системы существуют еще две сопряженные точки, называемые просто главными точками. Если мы поместим в одну из главных точек предмет, то система дает его изображение в другой главной точке, причем изображение будет прямое и равное предмету по величине.
На рис. 21 точки  главные точки системы. Плоскости, проходящие через эти точки оптической системы перпендикулярно к ее оси, называются главными плоскостями. Нетрудно сообразить, что у одной тонкой линзы обе главные плоскости сливаются в одну и совпадают с самой линзой. У линзы, имеющей конечную толщину (толстой линзы), главные плоскости раздвинуты на некоторое расстояние. Чем сильнее раздвинуты эти плоскости, тем сильнее система отличается от тонкой линзы.
главные точки системы. Плоскости, проходящие через эти точки оптической системы перпендикулярно к ее оси, называются главными плоскостями. Нетрудно сообразить, что у одной тонкой линзы обе главные плоскости сливаются в одну и совпадают с самой линзой. У линзы, имеющей конечную толщину (толстой линзы), главные плоскости раздвинуты на некоторое расстояние. Чем сильнее раздвинуты эти плоскости, тем сильнее система отличается от тонкой линзы.
Фокусными расстояниями системы называют отрезки  т. е. фокусные расстояния у системы измеряются от главных плоскостей, а не от поверхностей, ограничивающих систему линз.
т. е. фокусные расстояния у системы измеряются от главных плоскостей, а не от поверхностей, ограничивающих систему линз.
В случае, если система с обеих сторон граничит с одной и той же средой, 
Пусть перпендикулярно к оси системы расположен предмет, представленный стрелкой. Найдем его изображение, пользуясь известными нам свойствами точек  и проходящих через них плоскостей.
и проходящих через них плоскостей.
Для этой цели проследим ход лучей, исходящих из конца стрелки  Один луч, проходящий через главный фокус должен, очевидно, по выходе из системы пойти параллельно ее оси, причем он выйдет из плоскости
Один луч, проходящий через главный фокус должен, очевидно, по выходе из системы пойти параллельно ее оси, причем он выйдет из плоскости  на расстоянии, равном расстоянию отточки пересечения его с главкой плоскостью
на расстоянии, равном расстоянию отточки пересечения его с главкой плоскостью  до оптической оси. Другой луч,
до оптической оси. Другой луч,
идущий параллельно оси системы, пройдет по выходе из нее через  При этом расстояние, на котором он выйдет из плоскости
При этом расстояние, на котором он выйдет из плоскости  определяется, как и для первого луча, на основании свойств главных плоскостей. Пересечение этих двух лучей по выходе из системы дает точку
определяется, как и для первого луча, на основании свойств главных плоскостей. Пересечение этих двух лучей по выходе из системы дает точку  положение которой таким образом вполне определено и которая является изображением точки
положение которой таким образом вполне определено и которая является изображением точки  так как через нее пройдут все остальные лучи, выходящие из
так как через нее пройдут все остальные лучи, выходящие из 
Из соображений симметрии ясно, что перпендикуляр  является изображением
является изображением  причем изображением перевернутым.
причем изображением перевернутым.
Из рис. 21 легко получить формулу, связывающую расстояние предмета  с расстоянием изображения
с расстоянием изображения 
Из равенства  тангенс угла
тангенс угла  равен
равен  В Угол
В Угол  равен углу
равен углу  тангенс которого откуда получаем:
тангенс которого откуда получаем:

С другой стороны, при помощи точно таких же рассуждений получим:

Исключая из обеих формул  получаем:
получаем:

или, сокращая на  и преобразовывая, находим:
и преобразовывая, находим:

В случае одинаковых сред  Тогда предыдущая формула окончательно приобретает вид:
Тогда предыдущая формула окончательно приобретает вид:

Эта формула носит название формулы Ньютона. При помощи нее можно сказать, как будет двигаться изображение при движении предмета, т. е. как меняется  в зависимости от
в зависимости от 
Из формулы (9) видно, как связано увеличение, даваемое системой, с расположением предмета. Увеличение измеряется отношением

Мы видим, что чем ближе к фокусу предмет, тем больше его изображение. Наоборот, чем дальше от второго фокуса изображение,
тем оно больше. Это нетрудно показать, заменив в формуле  через
через  из (9):
из (9):

До сих пор речь шла лишь о предметах, не имеющих протяжения вдоль оси системы. Для того чтобы получить продольное увеличение, даваемое системой, найдем, как будет изображаться бесконечно малый отрезок  расположенный вдоль оси.
расположенный вдоль оси.
Увеличением в данном случае будет отношение  т. е. производная от
т. е. производная от  по
по  Согласно формуле (9) эта производная имеет следующий вид:
Согласно формуле (9) эта производная имеет следующий вид:

Мы видим, что с убыванием  возрастает
возрастает  так как
так как  Это означает, что при приближении предмета изображение удаляется.
Это означает, что при приближении предмета изображение удаляется.
Кроме того, продольное увеличение равно квадрату поперечного увеличения  и (12)]. Если предмет будет иметь вид маленького шара, то изображение получится в виде эллипсоида. При поперечном увеличении, равном трем, продольное равно девяти, т. е. отношение осей такого эллипсоида равно трем. Чем больше увеличение, тем сильнее эллипсоид будет отличаться от сферы.
и (12)]. Если предмет будет иметь вид маленького шара, то изображение получится в виде эллипсоида. При поперечном увеличении, равном трем, продольное равно девяти, т. е. отношение осей такого эллипсоида равно трем. Чем больше увеличение, тем сильнее эллипсоид будет отличаться от сферы.
Все сказанное свидетельствует о том, что идеального изображения, по форме подобного предмету, не может быть. Оптические системы разрешают эту задачу лишь приближенно.
Все полученные нами выводы относятся и к отдельной линзе. Как мы уже указывали, для нее главные плоскости сливаются. Формулы (10), (11) и (12) справедливы и для нее и легко могут быть получены из формулы (9).
| << Предыдущий параграф | Следующий параграф >> |
- ЧАСТЬ ЧЕТВЕРТАЯ. ОПТИКА
- § 2. Электромагнитная теория света
- § 3. Скорость света
- § 4. Опыт Майкельсона
- § 5. Отрицательный результат опыта Майкельсона и теория относительности
- § 6. Некоторые замечания о теории относительности
- § 7. Явление Доплера для световых волн
- ГЛАВА II. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- § 8. Законы отражения и преломления света
- § 9. Линза
- § 10. Оптические системы
- § 11. Глаз как оптическая система
- § 12. Приборы, вооружающие глаз
- § 13. Фотоаппарат и проекционный аппарат
- § 14. Принцип Ферма
- § 15. Электронная оптика
- ГЛАВА III. ИНТЕРФЕРЕНЦИЯ СВЕТА
- § 16. Принцип суперпозиции. Когерентность
- § 17. Зеркала Френеля
- § 18. Цвета тонких пленок. Полосы равной толщины
- § 19. Полосы равного наклона. Просветленная оптика
- § 20. Интерферометры
- § 21. Интерференционное измерение технических мер длины
- § 22. Интерференция многих колебаний
- § 23. Интерференционная спектроскопия
- ГЛАВА IV. ДИФРАКЦИЯ СВЕТА
- § 24. Явление дифракции. Опыт Френеля
- § 25. Принцип Гюйгенса-Френеля
- § 26. Метод зон Френеля
- § 27. Дифракция от узкой щели
- § 28. Дифракционная решетка
- § 29. Дифракционный спектр. Решетки Роуланда и эшелон Майкельсона
- § 30. Плоскостные решетки. Пространственная решетка
- § 31. Структурный рентгеновский анализ
- § 32. Дифракция света на ультразвуковых волнах
- § 33. Дифракция от мелких частиц
- § 34. Разрешающая способность оптических инструментов. Звездный интерферометр
- ГЛАВА V. ПОЛЯРИЗАЦИЯ СВЕТА
- § 35. Поляризация света
- § 36. Двойное лучепреломление
- § 37. Интерференция поляризованного света
- § 38. Оптический метод исследования упругих натяжений. Эффект Керра
- § 39. Вращение плоскости поляризации. Эллиптическая поляризация
- ГЛАВА VI. ДИСПЕРСИЯ, ПОГЛОЩЕНИЕ И ИЗЛУЧЕНИЕ СВЕТА
- § 40. Отражение света
- § 41. Давление света. Опыты Лебедева
- § 42. Дисперсия. Опыты Ньютона
- § 43. Молекулярная теория дисперсии
- § 44. Хроматическая аберрация. Спектрограф
- § 45. Поглощение света
- § 46. Закон Бугера. Опыты Вавилова
- § 47. Атом как элементарный излучатель света
- § 48. Эффект Вавилова — Черенкова
- ГЛАВА VII. ТЕРМОДИНАМИКА ИЗЛУЧЕНИЯ И СВЕТОВОЙ ПОТОК
- § 49. Излучение черного тела. Формула Планка. Закон Вина
- § 50. Излучение нечерных тел. Законы Кирхгофа
- § 51. Приемники излучения
- § 52. Световые величины и их измерения
- § 53 Температурные излучатели как источники света
- ЧАСТЬ ПЯТАЯ. АТОМНАЯ ФИЗИКА
- ГЛАВА VIII. СТРОЕНИЕ АТОМА И ТЕОРИЯ БОРА
- § 55. Опыты, обнаружившие ядерное строение атомов
- § 56. Противоречие между фактическим строением атомов и выводами классической электродинамики. Строение линейчатых спектров
- § 57. Опытные основания теории квантов в первые годы ее развития
- § 58. Теория Бора. Происхождение спектра водорода
- § 59. Квантовые числа
- § 60. Принцип Паули. Строение электронных оболочек атомов
- § 61. Общая картина возникновения спектров
- ГЛАВА IX. ОСНОВЫ КВАНТОВОЙ (ВОЛНОВОЙ) МЕХАНИКИ
- § 62. Волновые свойства частиц. Формула де Бройля. Дифракция электронов
- § 63. Уравнение Шредингера. Просачивание через энергетический барьер. Нулевая энергия
- § 64. Волномеханическая теория атома водорода
- § 65. Соотношение неопределенностей и его разные трактовки
- ГЛАВА X. КВАНТОВАЯ ОПТИКА
- § 66. Развитие квантовой оптики
- § 67. Спектр щелочных металлов. Спин электрона
- § 68. Спектр гелия. Символика спектральных термов
- § 69. Сверхтонкая структура спектральных линий
- § 70. Атом в силовом поле
- § 71. Молекулярные спектры и строение молекул
- § 72. Комбинационное рассеяние света
- § 73. Квантовая картина испускания света атомами и молекулами
- § 74. Люминесценция
- § 75. Возбуждение люминесценции ударами частиц вещества
- § 76. Применения люминесценции
- § 77. Фотохимические реакции
- ГЛАВА XI. ЗАКОН ПРОПОРЦИОНАЛЬНОСТИ МАССЫ И ЭНЕРГИИ И РЕЛЯТИВИСТСКИЕ СООТНОШЕНИЯ
- § 78. Закон пропорциональности массы и энергии
- § 79. Предварительные замечания о релятивистских эффектах. Зависимость массы от скорости
- § 80. Корпускулярные свойства фотонов. Явление Комптона
- § 81. Вывод закона Эйнштейна сложения скоростей из закона пропорциональности массы и энергии и законов сохранения энергии или количества движения
- § 82. Две трактовки закона пропорциональности массы и энергии и уточнение закона тяготения
- § 83. Красное смещение спектральных линий. Поперечный эффект Доплера
- § 84. Влияние гравитационного поля на скорость света в вакууме и показатель преломления вакуума
- ЧАСТЬ ШЕСТАЯ. ЯДЕРНАЯ ФИЗИКА
- § 85. Заряд и масса ядра. Масс-спектральный анализ
- § 86. Состав ядер. Изотопы. Атомные единицы массы и энергии
- § 87. Радиоактивный распад ядер. Закон радиоактивного смещения. Изомеры
- § 88. Альфа-лучи. Потери энергии на ионизацию. Квантовомеханическое объяснение альфа-радиоактивности
- § 89. Бета- и гамма-лучи
- § 90. Искусственное расщепление ядер. Открытие нейтрона
- § 91. Открытие позитрона. Взаимопревращение фотонов определенной энергии и электронно-позитронных пар
- § 92. Индуцированная позитронная и электронная радиоактивность. Фоторасщепление ядер, K-захват
- § 93. Энергетические уровни ядер. Внутренняя конверсия. Нейтрино
- § 94. Капельная теория строения ядер
- § 95. Деление ядер и развитие капельной теории строения ядер
- ГЛАВА XIII. КОСМИЧЕСКИЕ ЛУЧИ
- § 96. Методы исследования и первые итоги изучения космических лучей
- § 97. Каскадное образование электронно-позитронных пар в космических лучах. Потери энергии электронами на тормозное излучение
- § 98. «мю»-мезоны. Зависимость времени жизни неустойчивых частиц от скорости движения
- § 99. «пи»-мезоны
- § 100. Взрывные ядерные ливни и их каскадное развитие в космических лучах
- § 101. Корпускулярный и энергетический спектр космических лучей. Происхождение космического излучения
- ГЛАВА XIV. ЭКСПЕРИМЕНТАЛЬНЫЕ СРЕДСТВА ЯДЕРНОЙ ФИЗИКИ
- § 102. Циклотроны
- § 103. Фазотроны
- § 104. Бетатроны
- § 105. Синхротроны и синхрофазотроны
- § 106. Линейные ускорители электронов и ионов
- § 107. Лабораторные источники нейтронов. Замедлители нейтронов в ядерных реакторах
- § 108. Усовершенствование методов наблюдения и счета частиц
- ГЛАВА XV. ЯДЕРНЫЕ РЕАКЦИИ И АТОМНАЯ ЭНЕРГИЯ
- § 109. Основные виды и обозначения ядерных реакций. Конкурирующие процессы в ядерных реакциях
- § 110. Энергетический эффект, энергия возбуждения и порог ядерных реакций
- § 111. Превращения элементарных частиц
- § 112. Ядерные силы
- § 113. Энергия связи ядер и средняя энергия связи нуклона
- § 114. Полуэмпирическая формула для энергии ядерной связи и для атомных энергий и масс
- § 115. Взаимосвязь энергии и строения ядер. Внутриядерное движение нуклонов и нуклонные оболочки. Спины и магнитные моменты ядер
- § 116. Энергия отделения частиц и анализ возможного хода ядерной реакции
- § 117. Выход продуктов ядерной реакции. Эффективные сечения. Резонансные явления
- § 118. Цепной процесс деления ядер. Активно делящиеся вещества. Ядерные реакторы
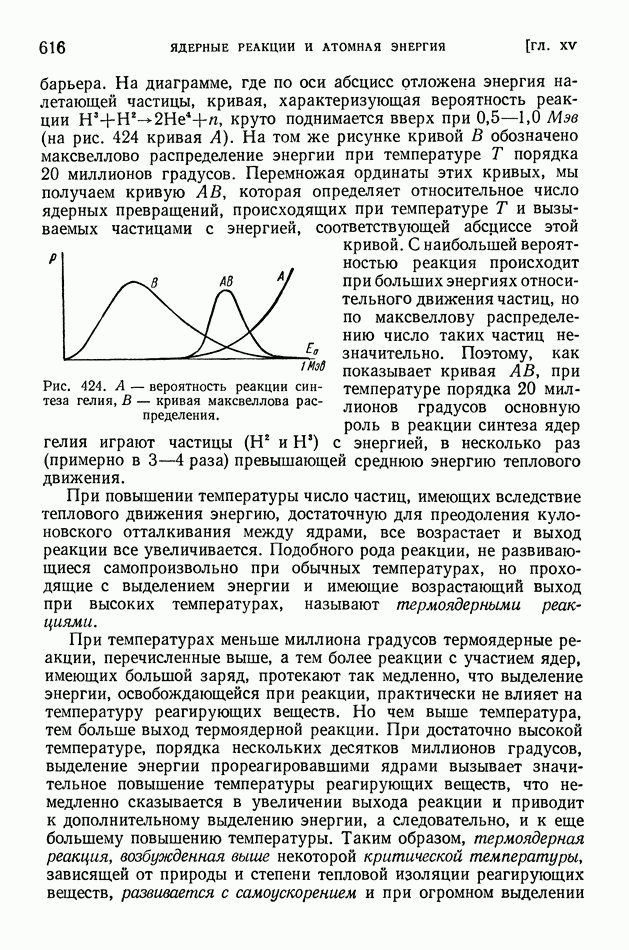
- § 119. Термоядерные реакции
- § 120. Применение ядерных реакций
- § 121. Ядерные реакции в звездах