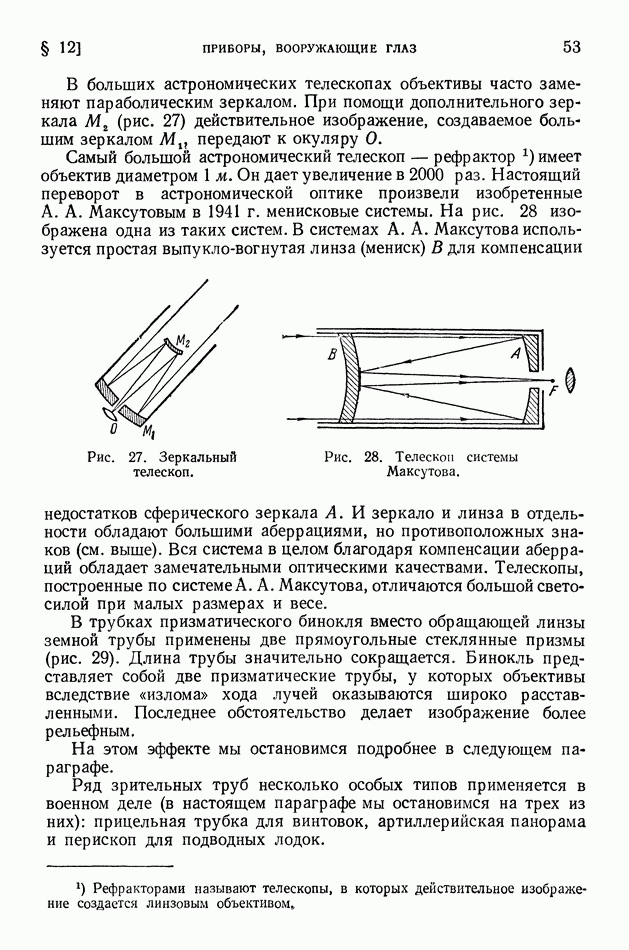
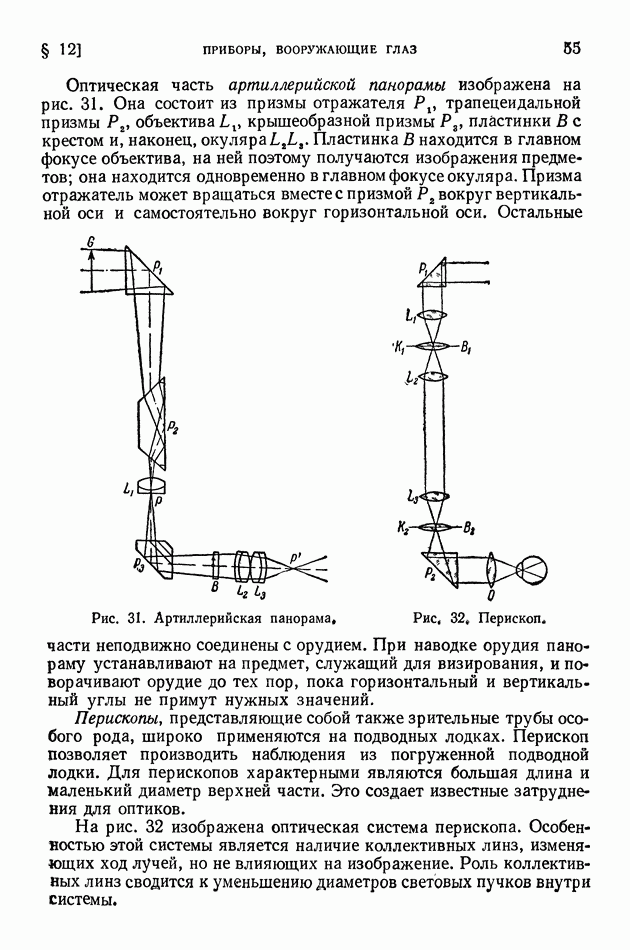
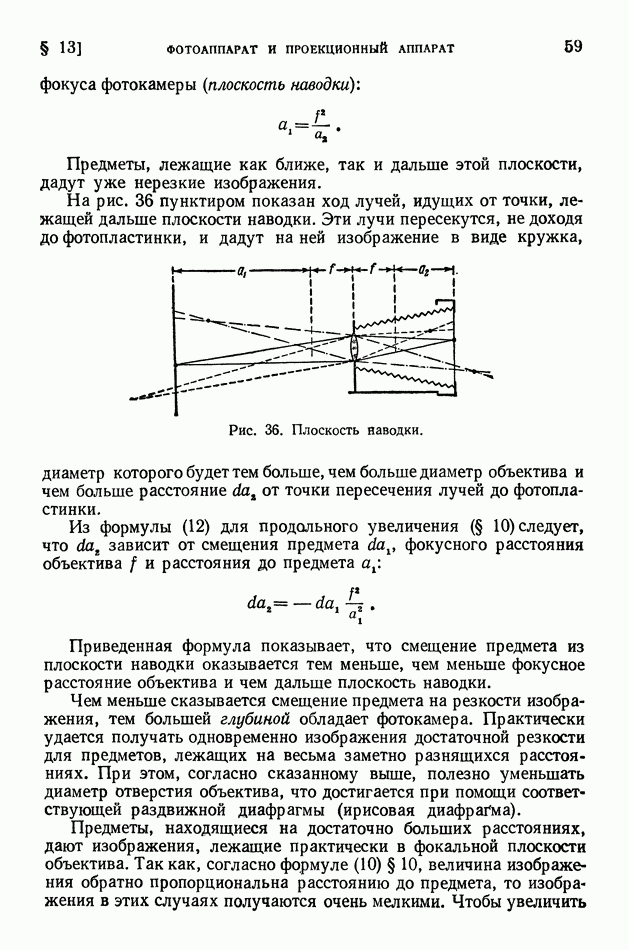
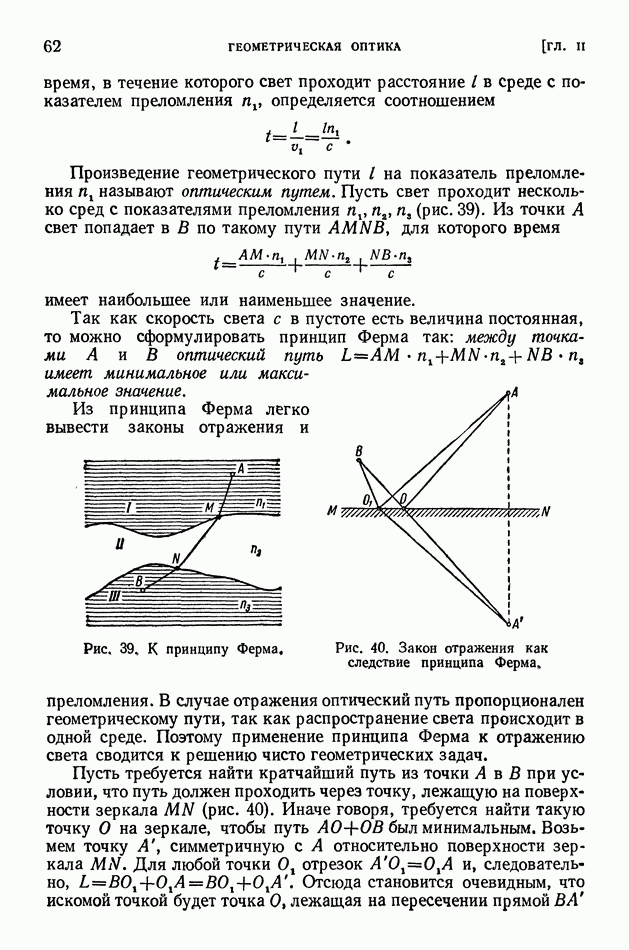
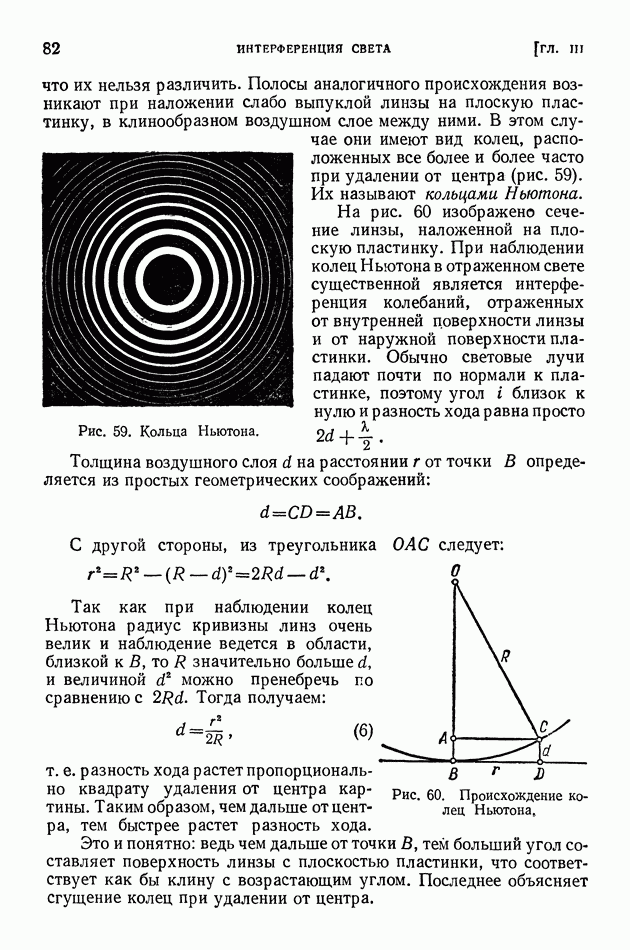
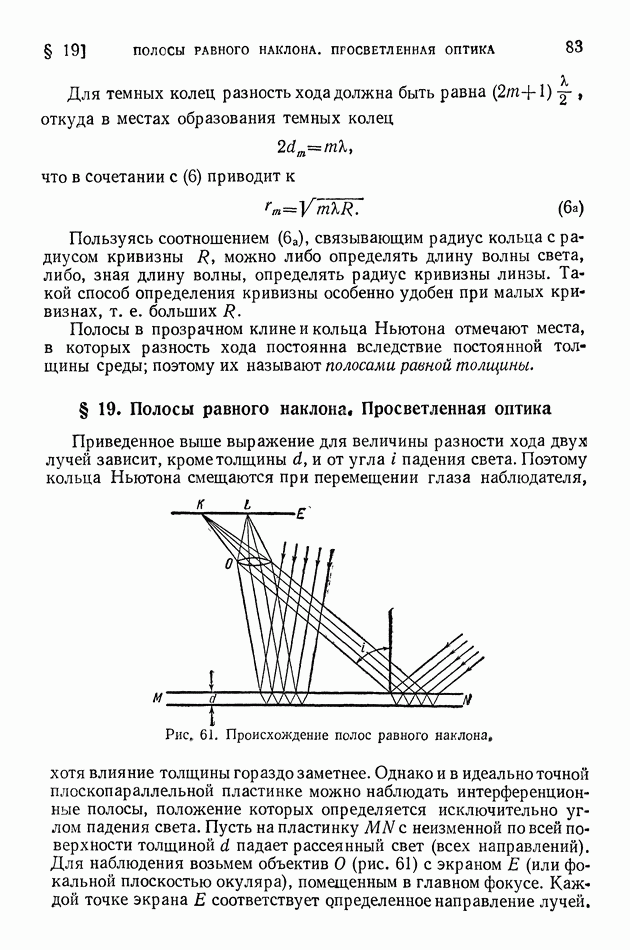
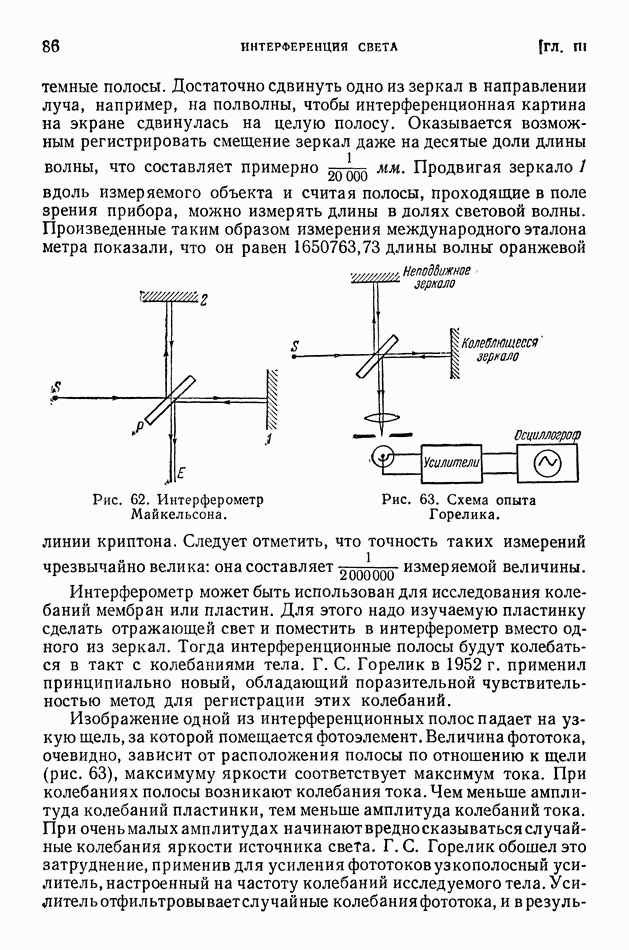
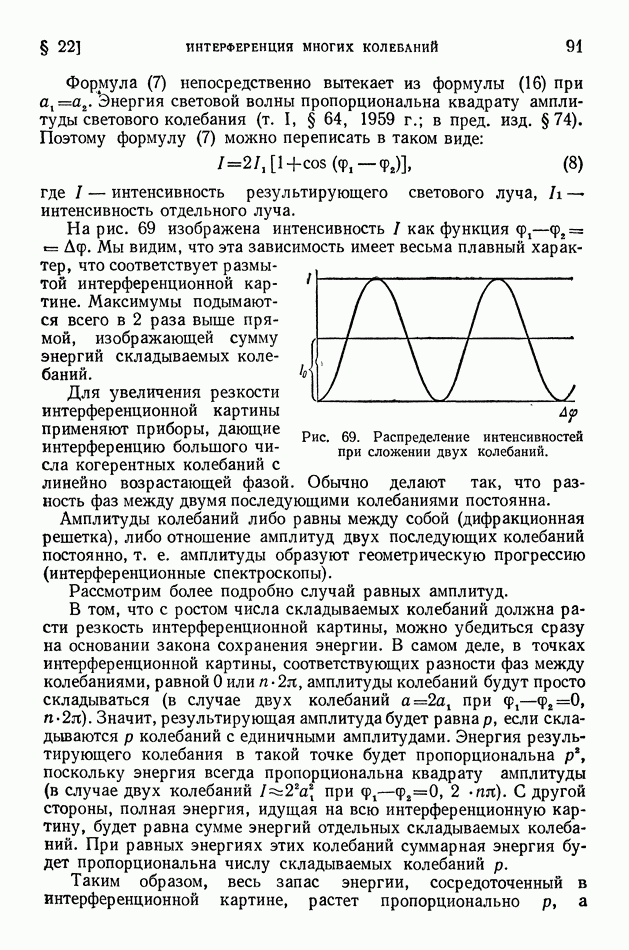
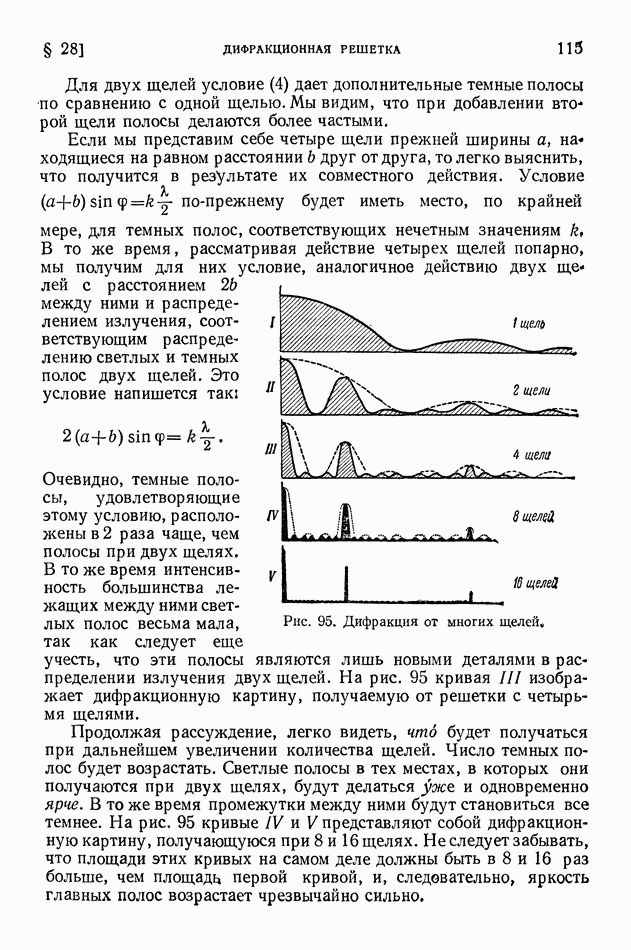
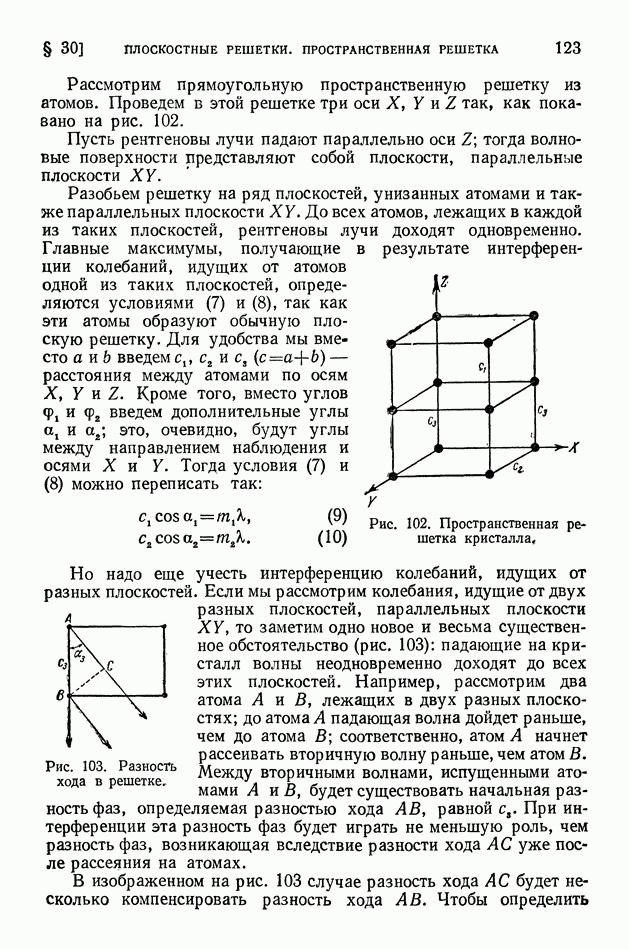
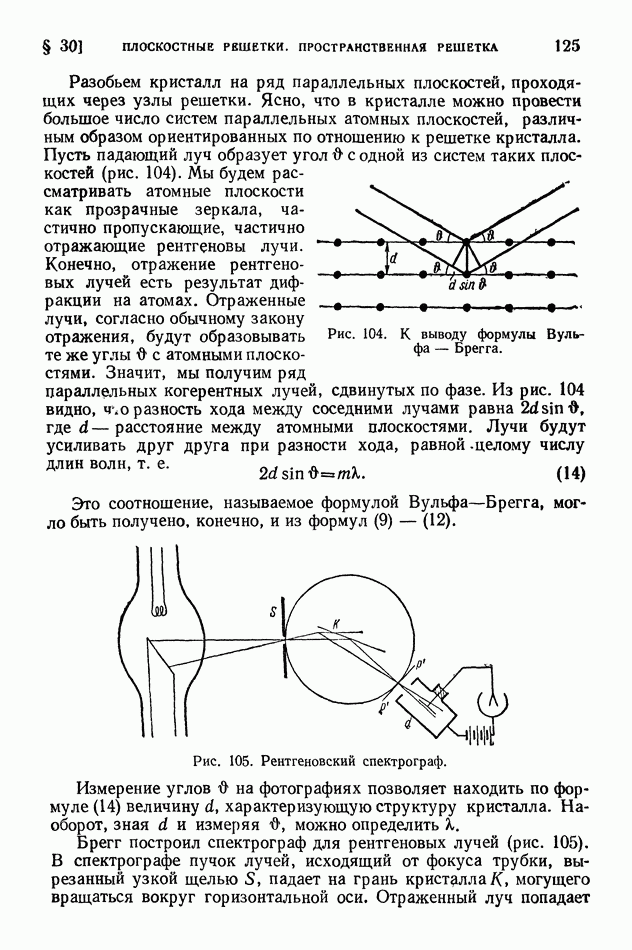
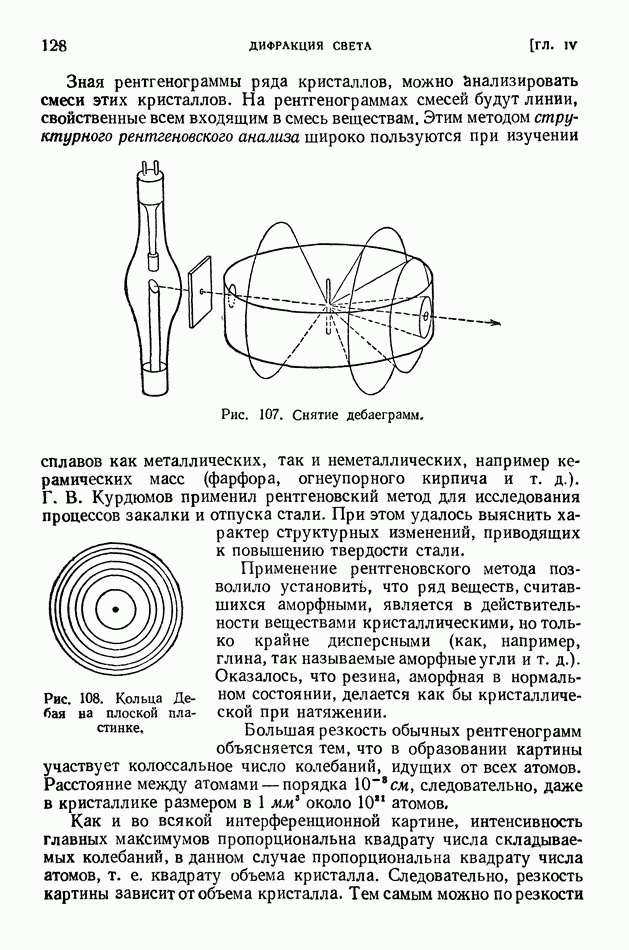
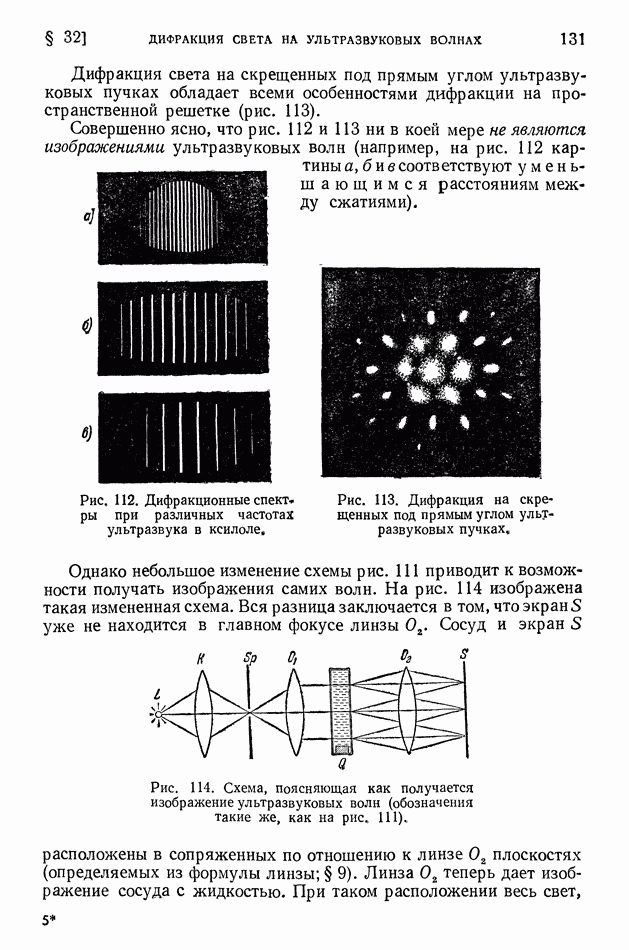
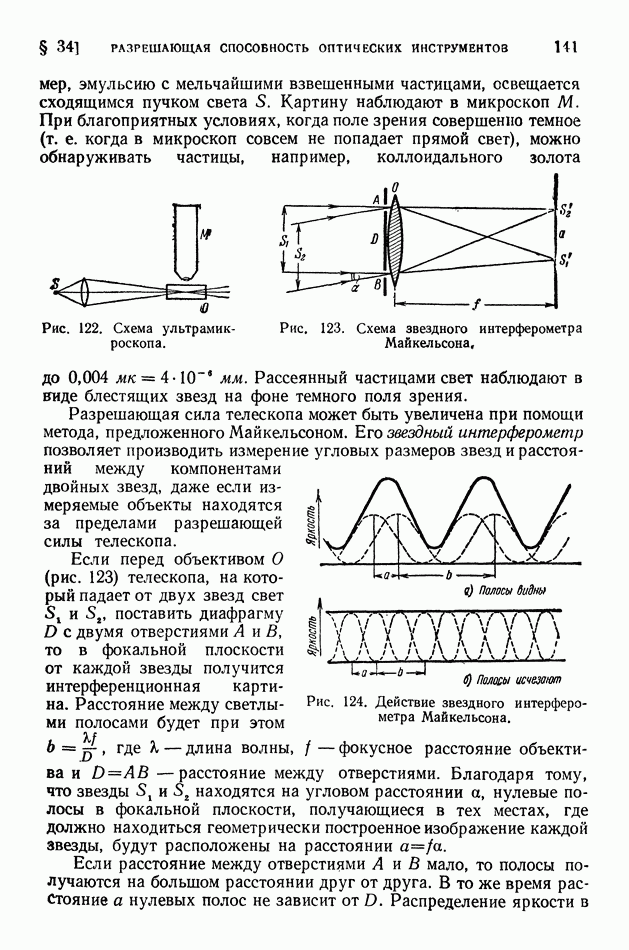
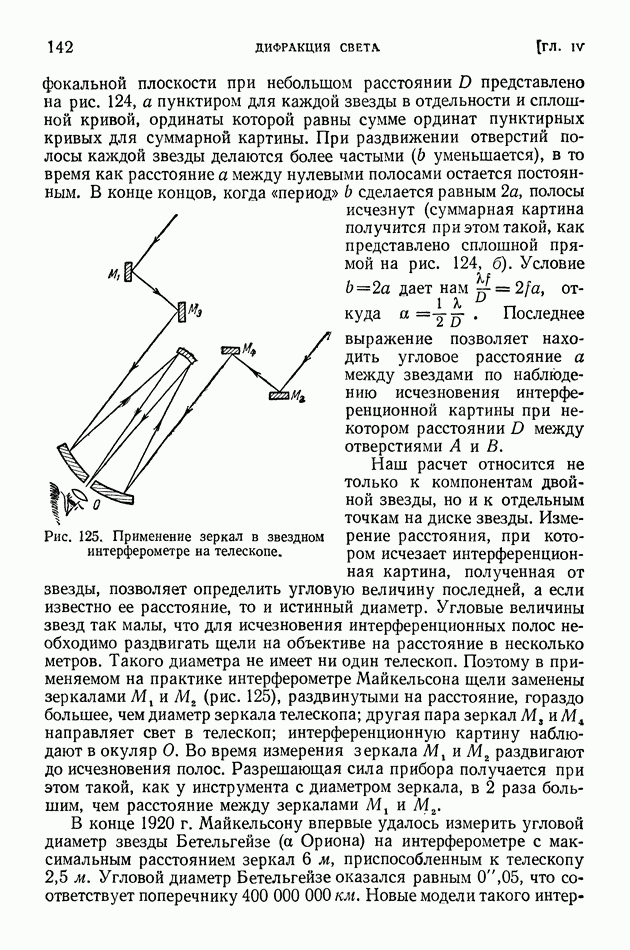
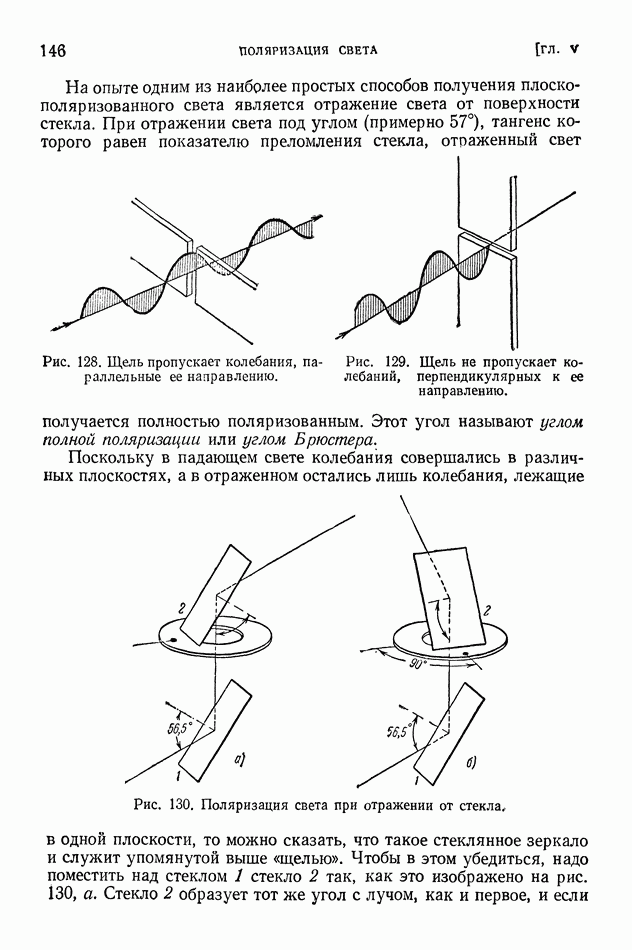
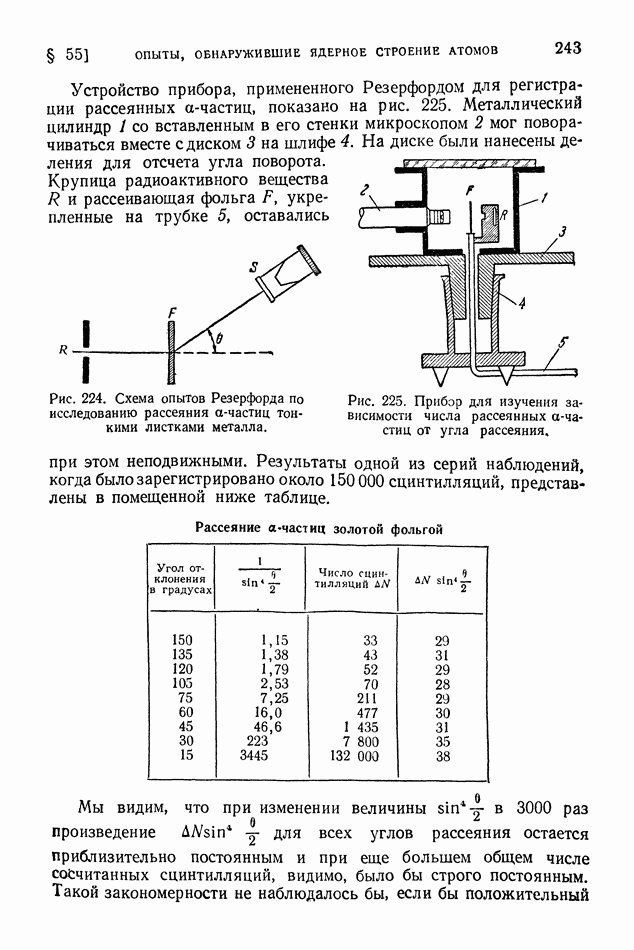
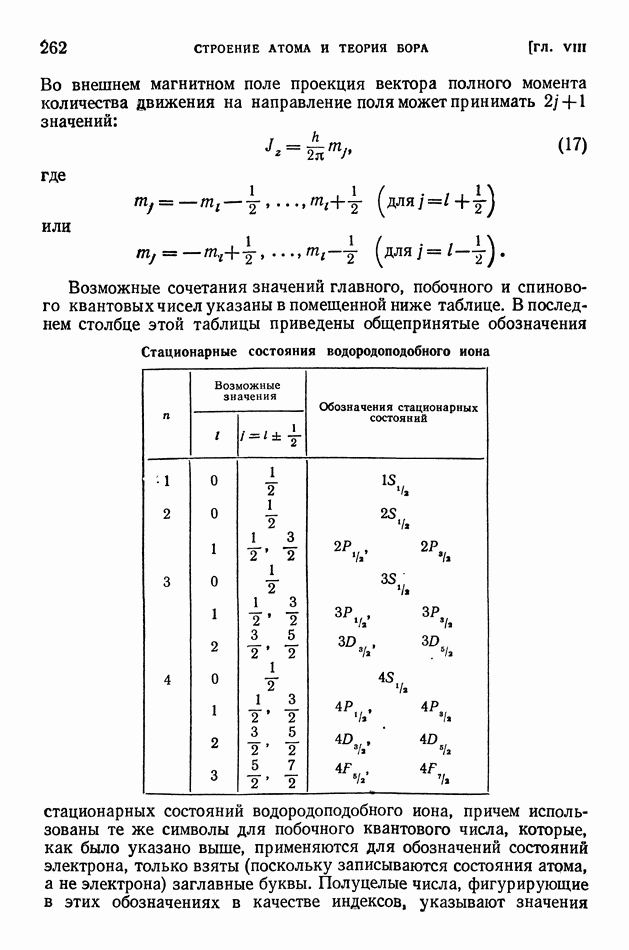
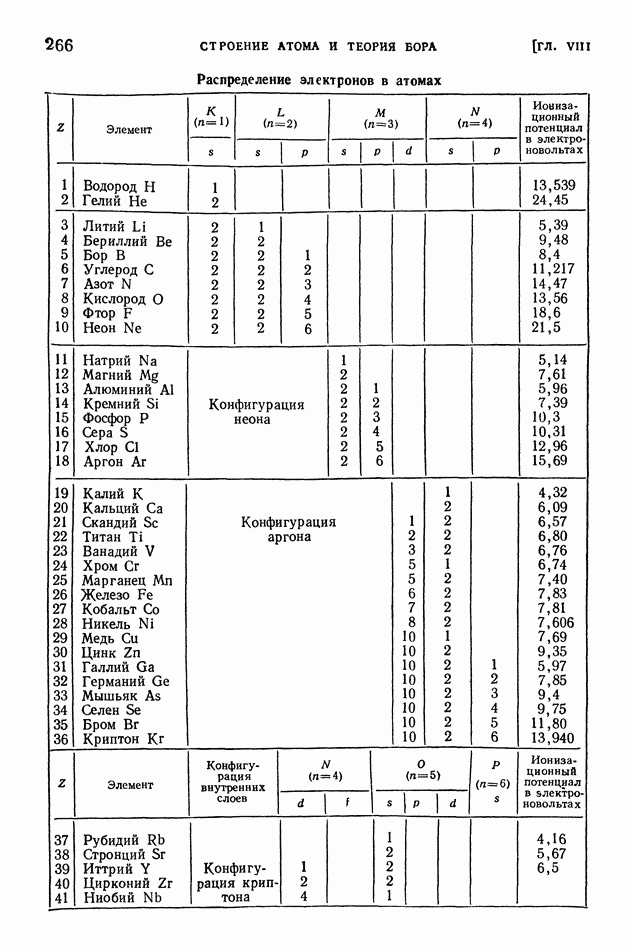
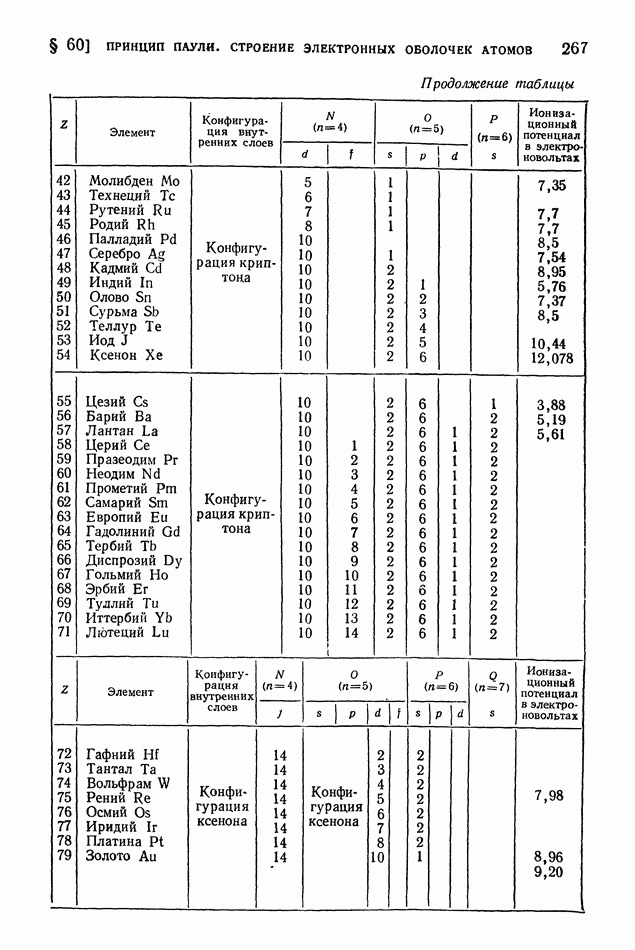
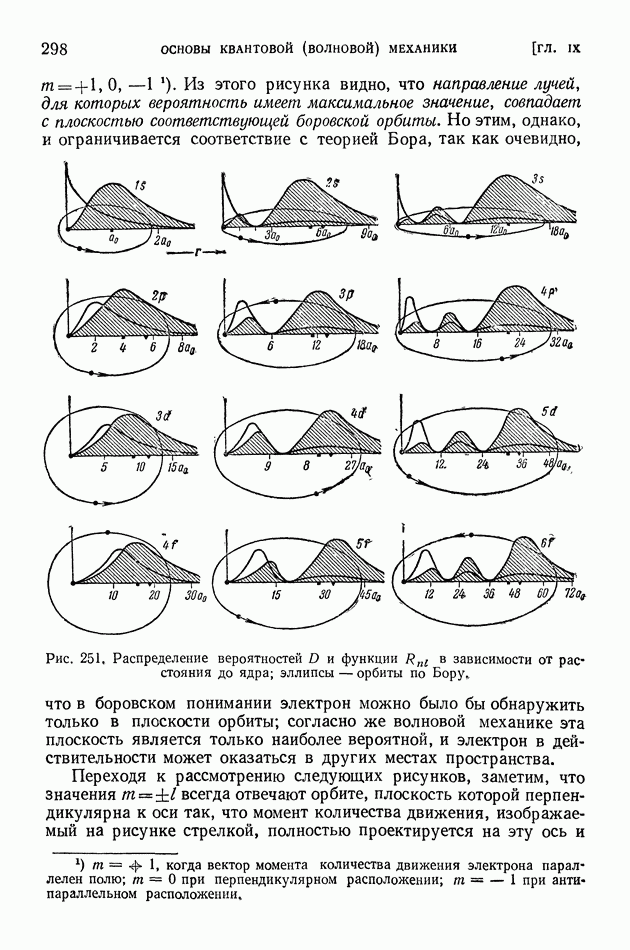
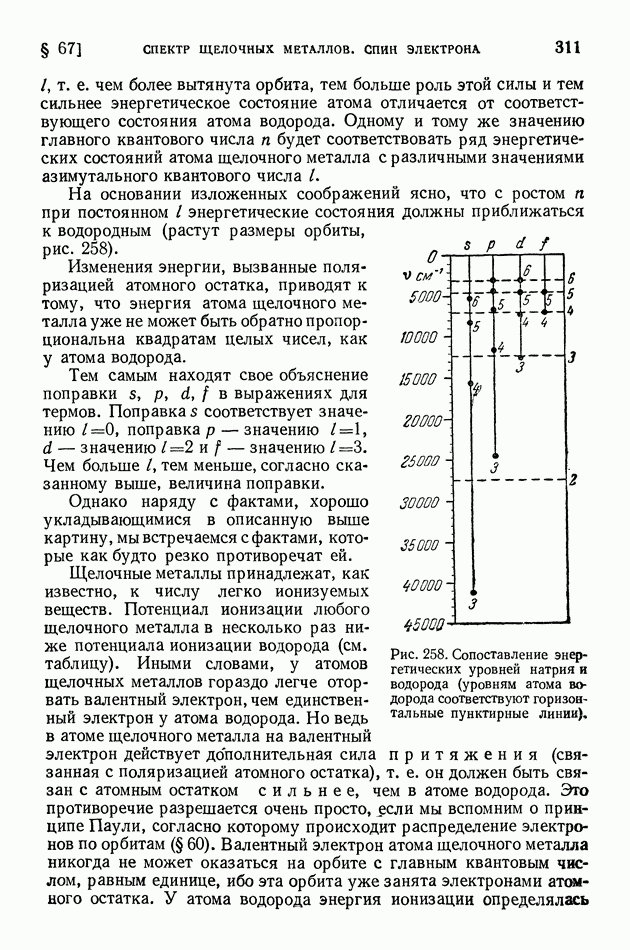
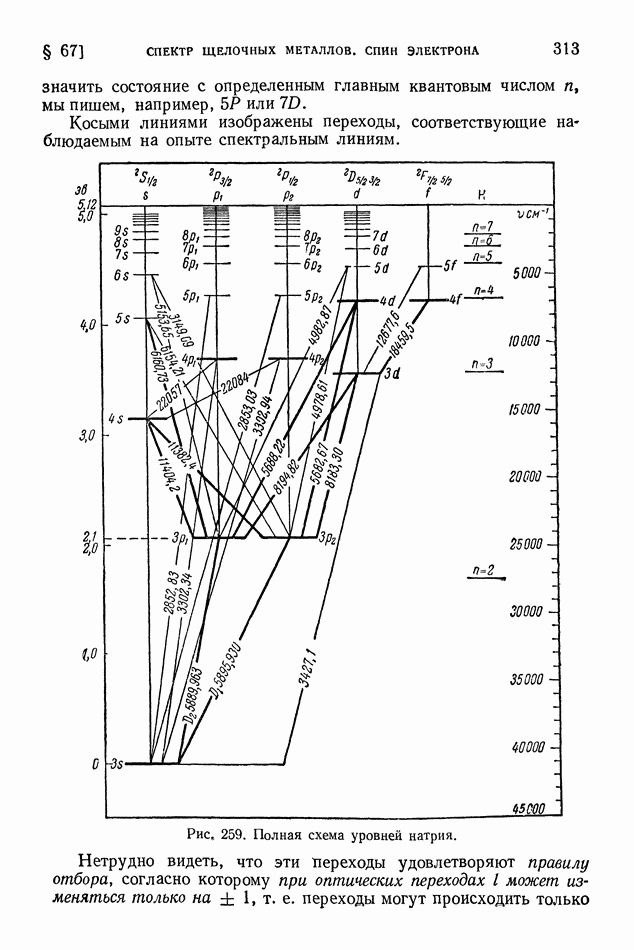
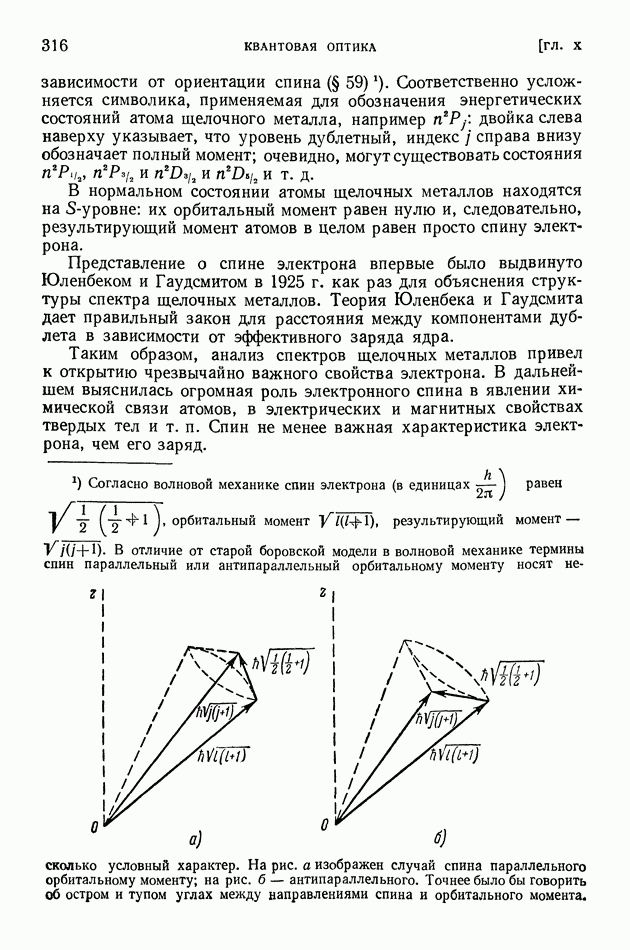
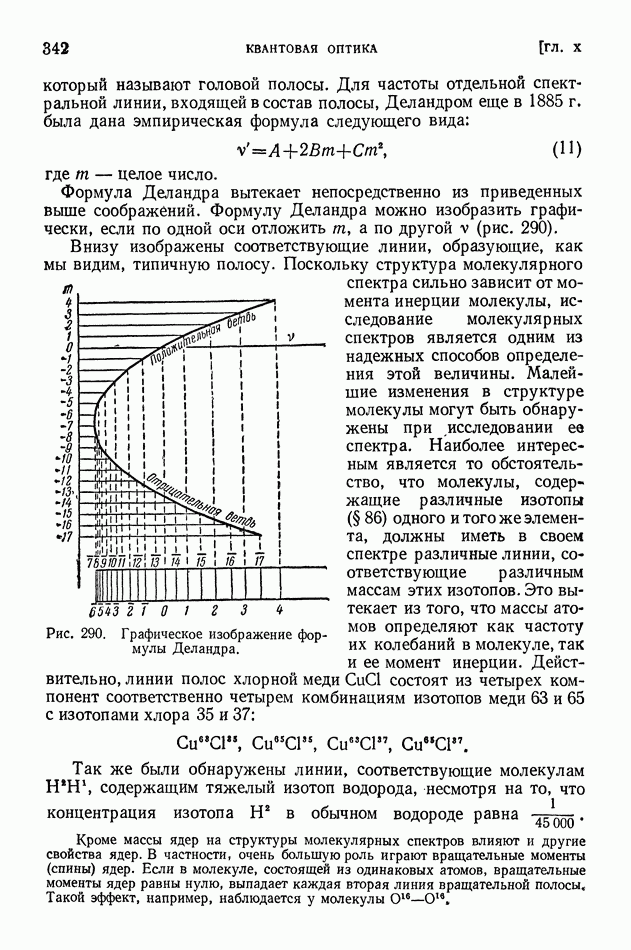
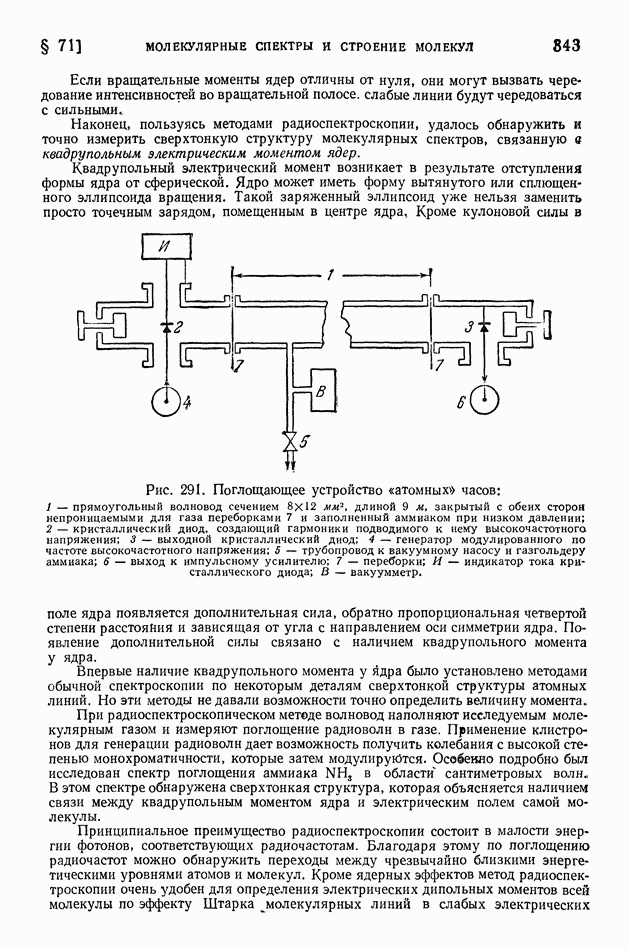
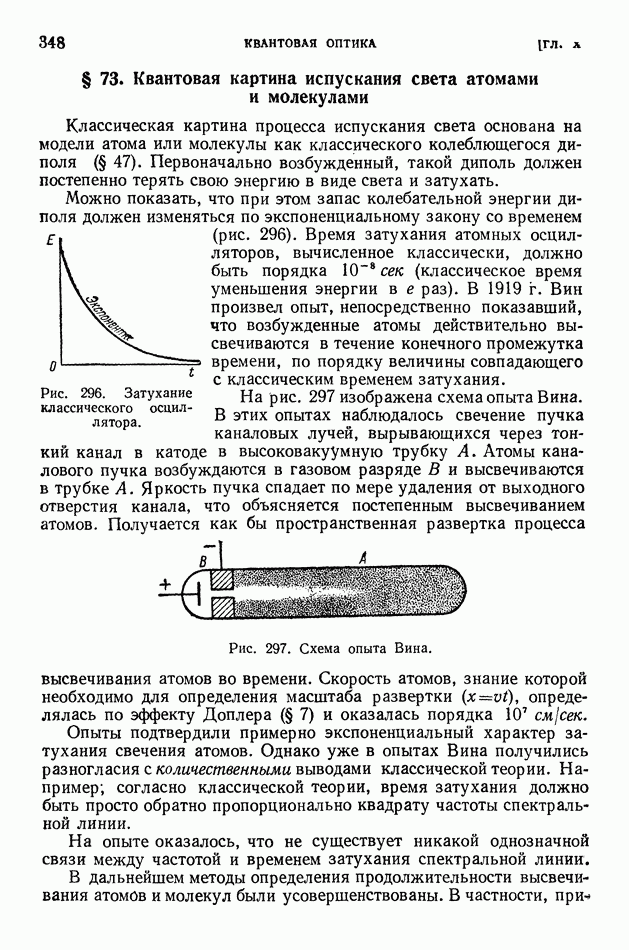
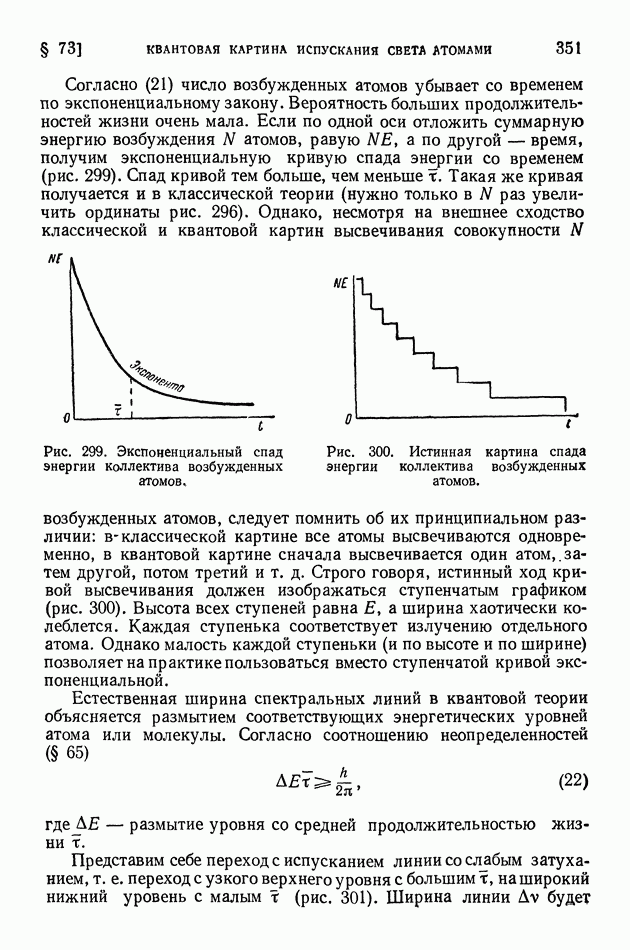
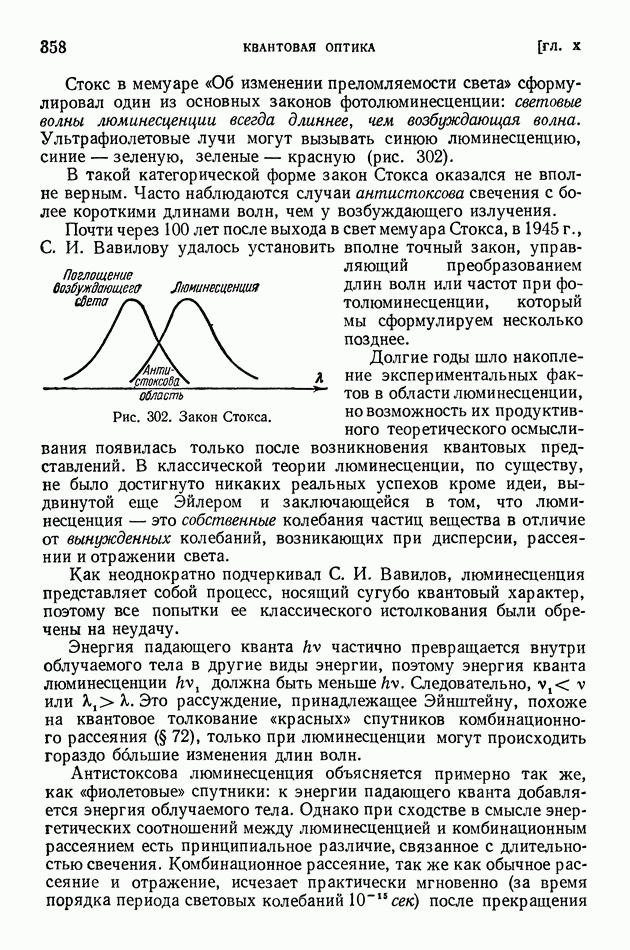
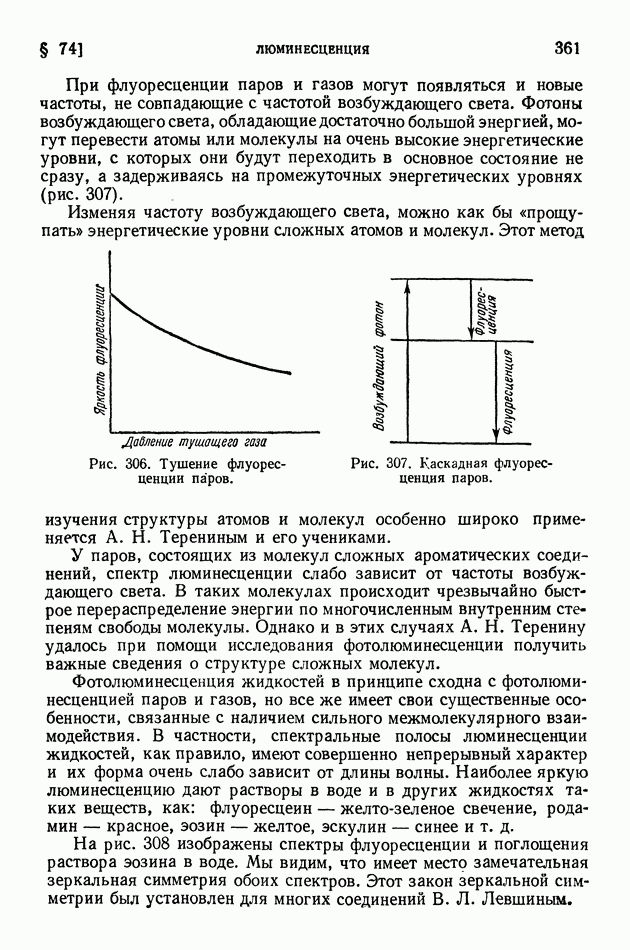
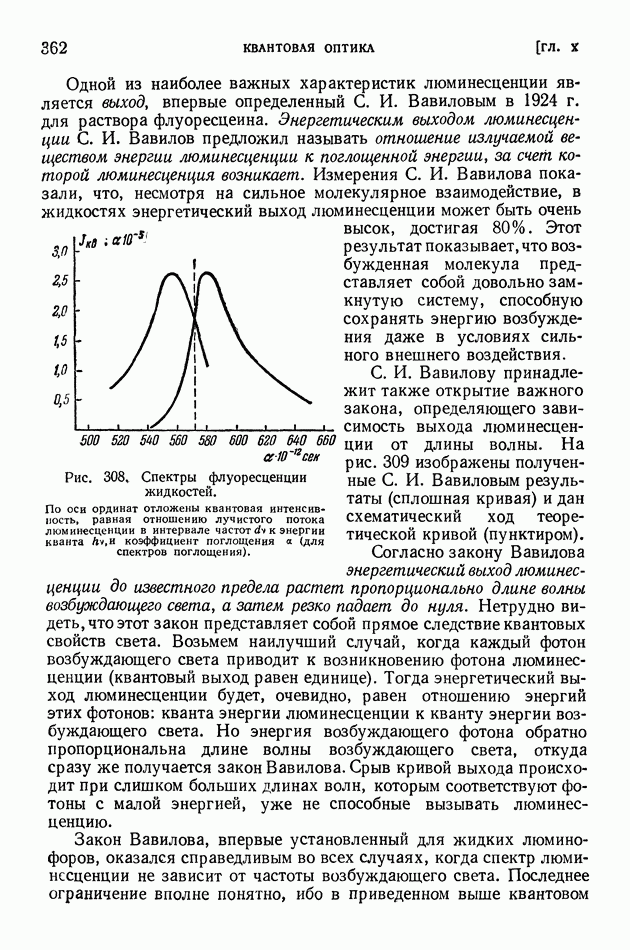
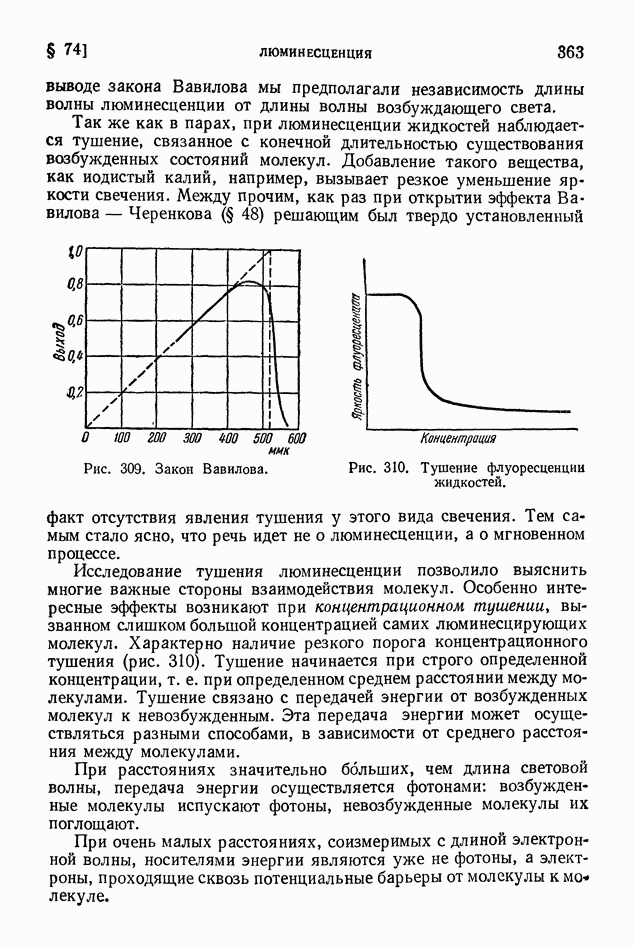
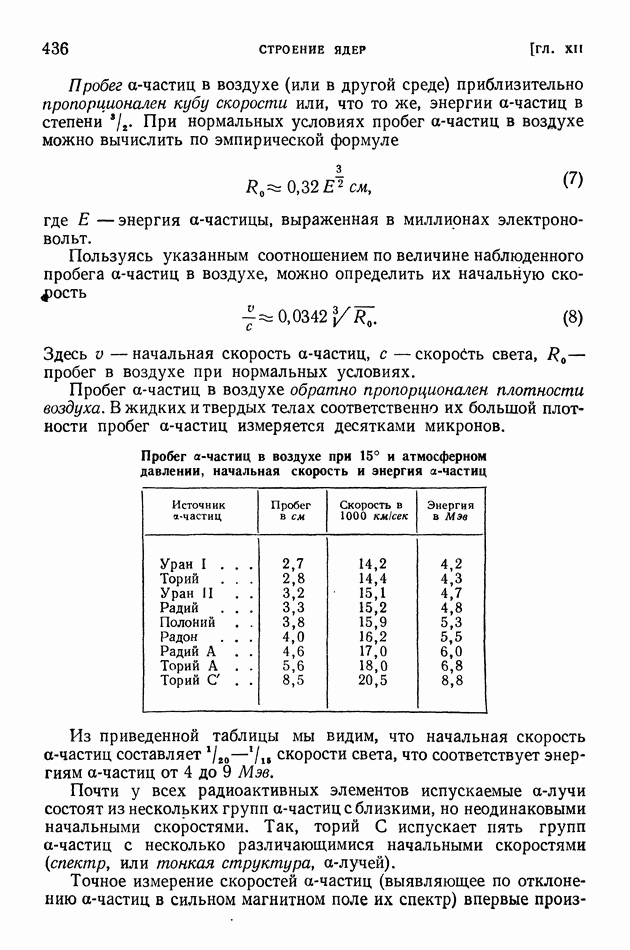
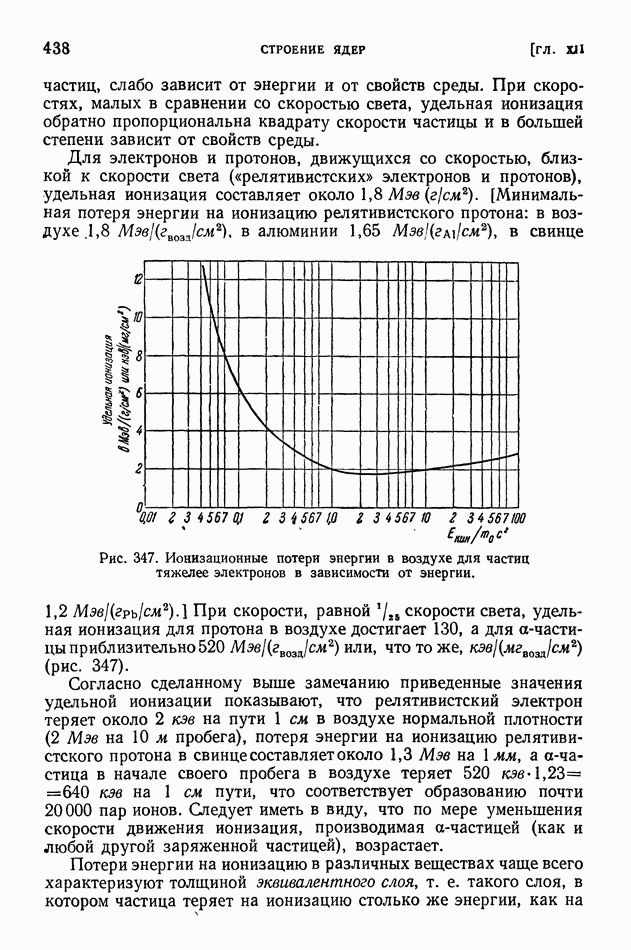
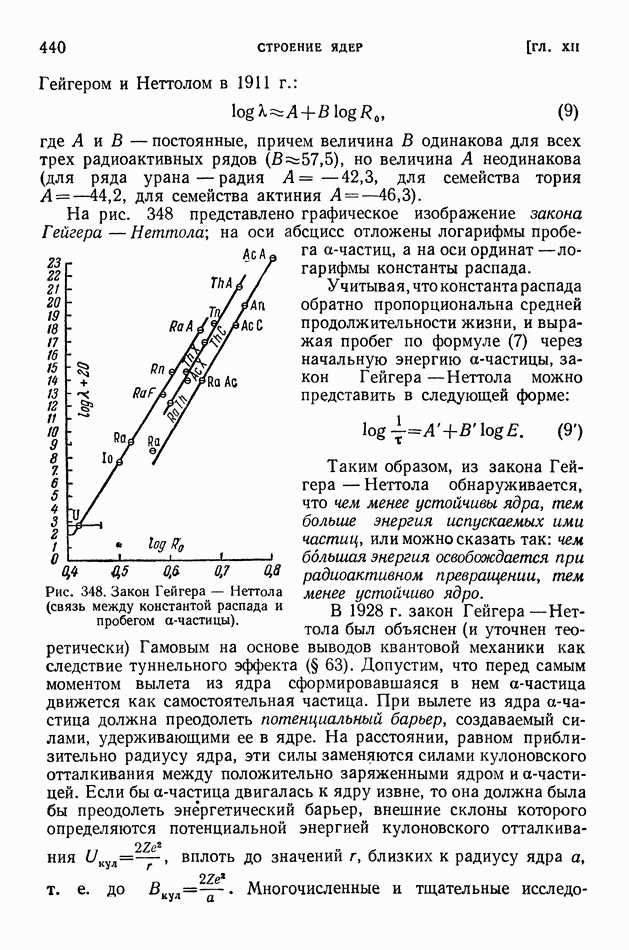
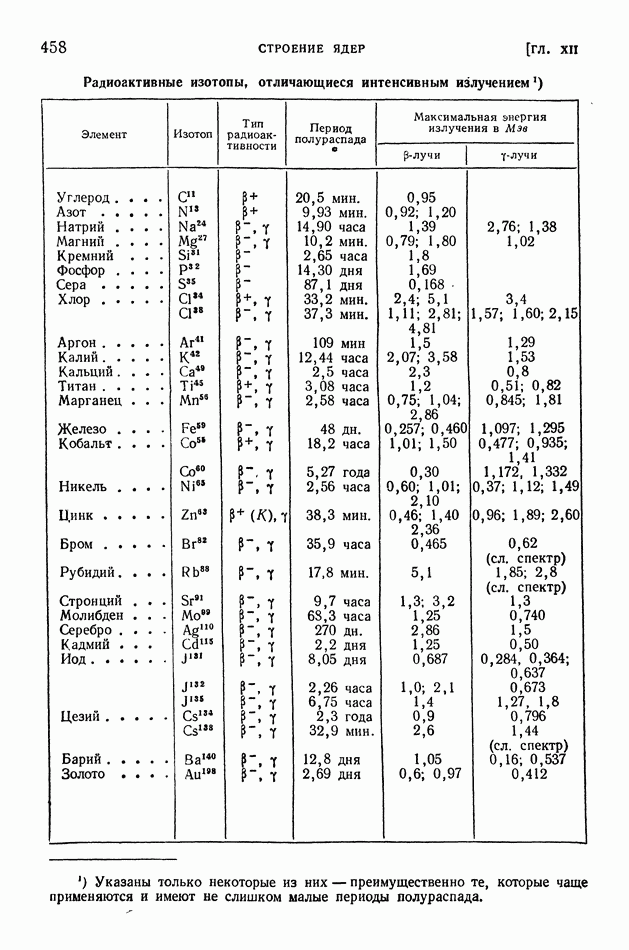
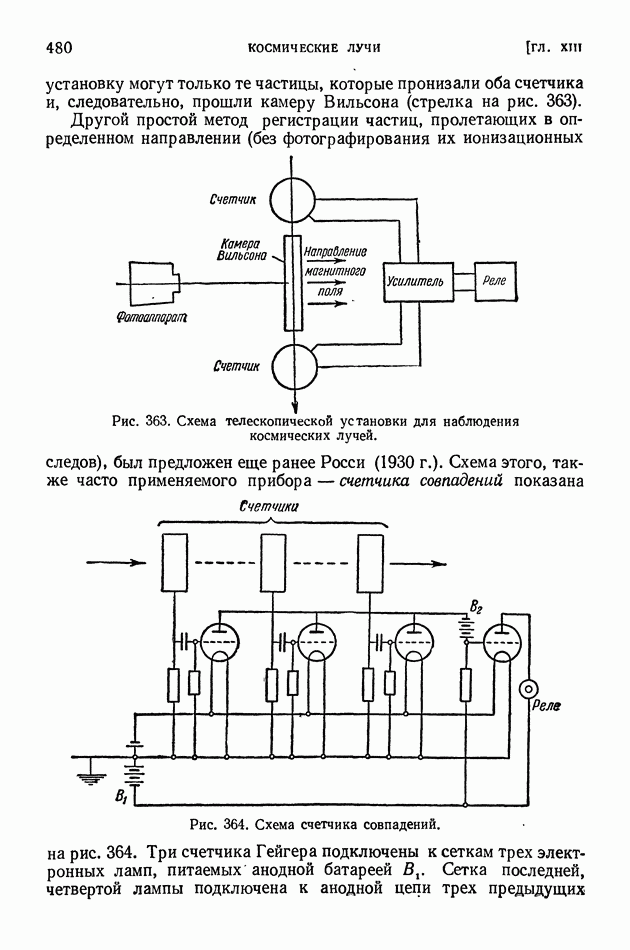
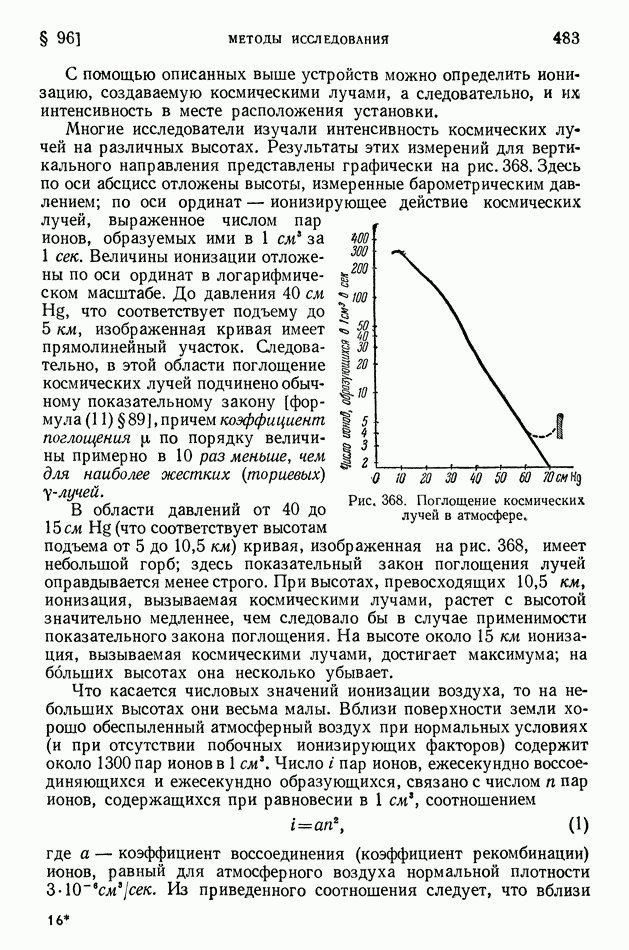
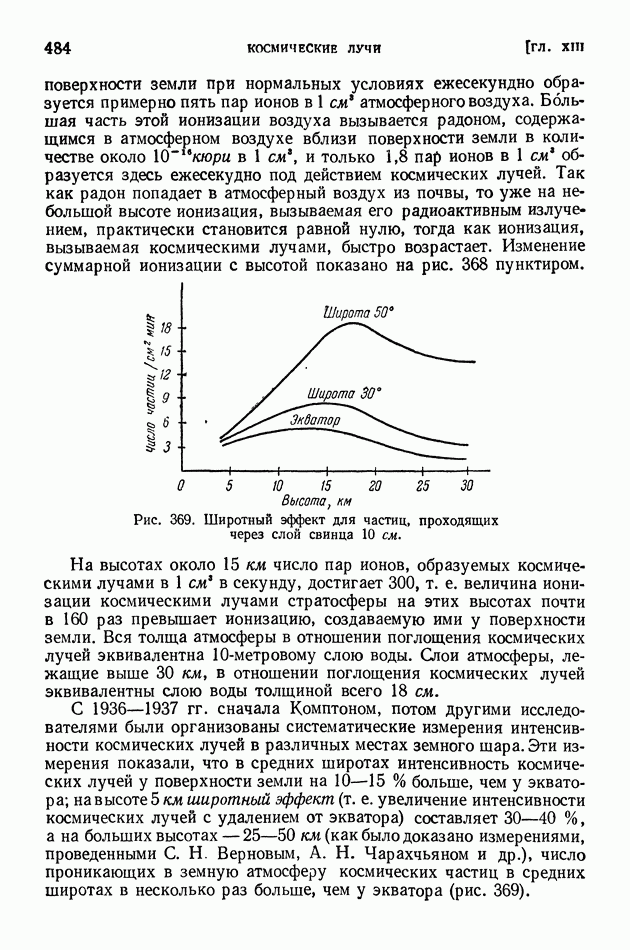
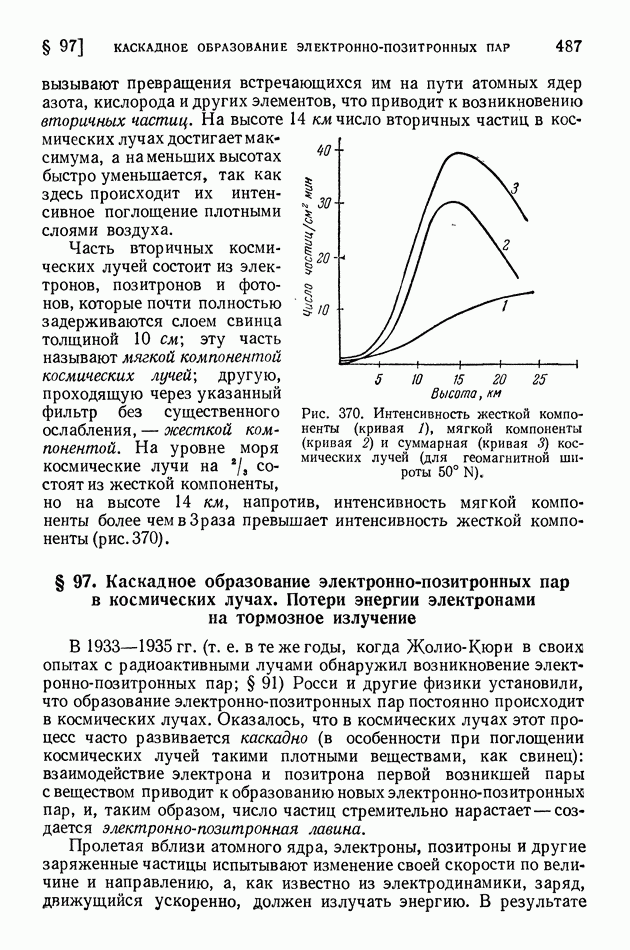
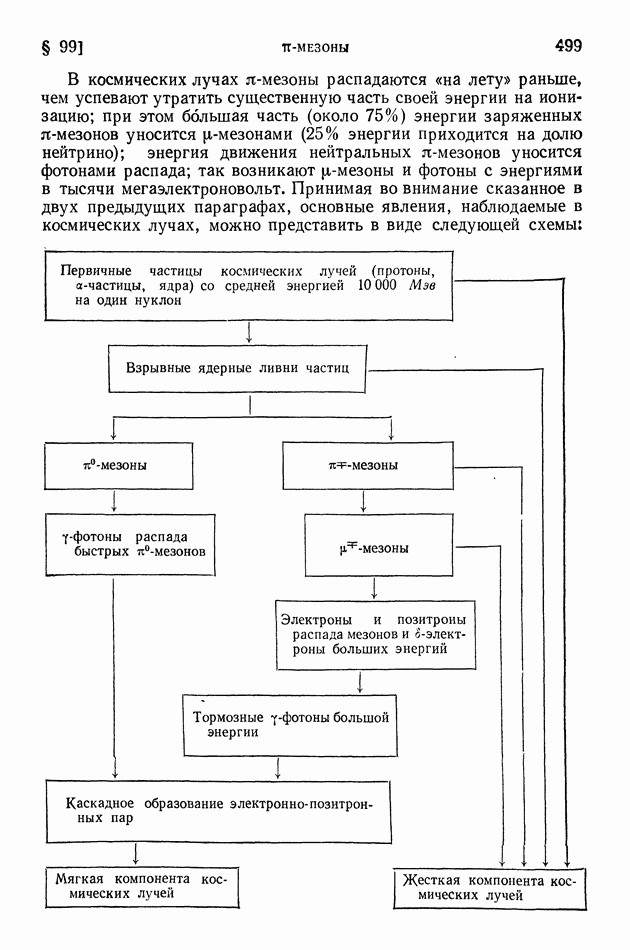
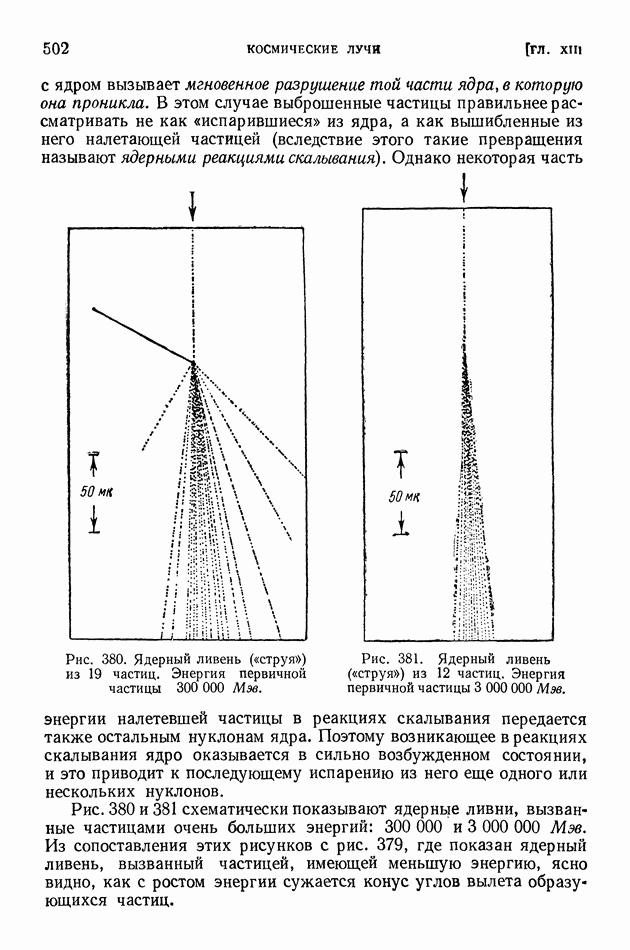
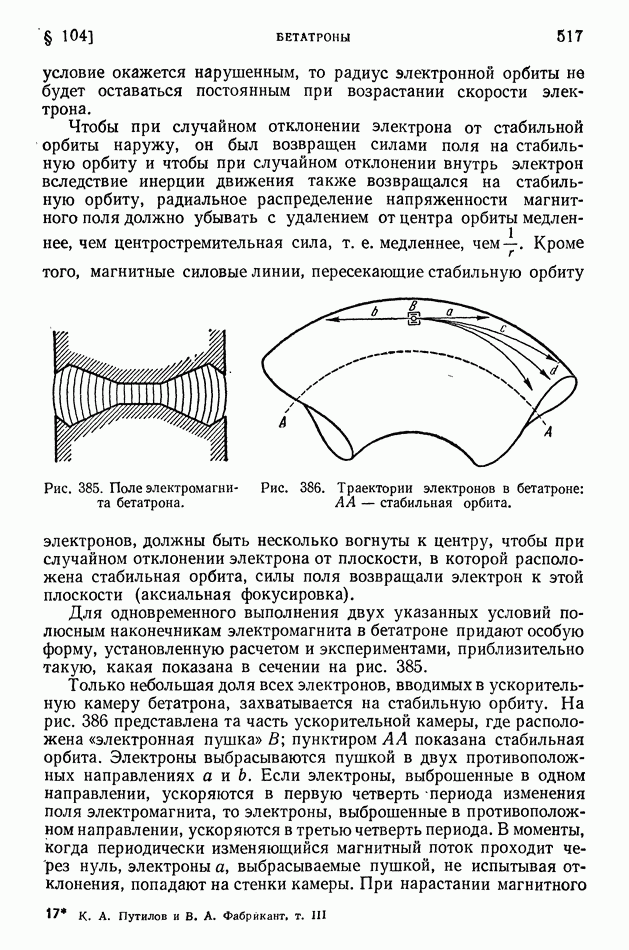
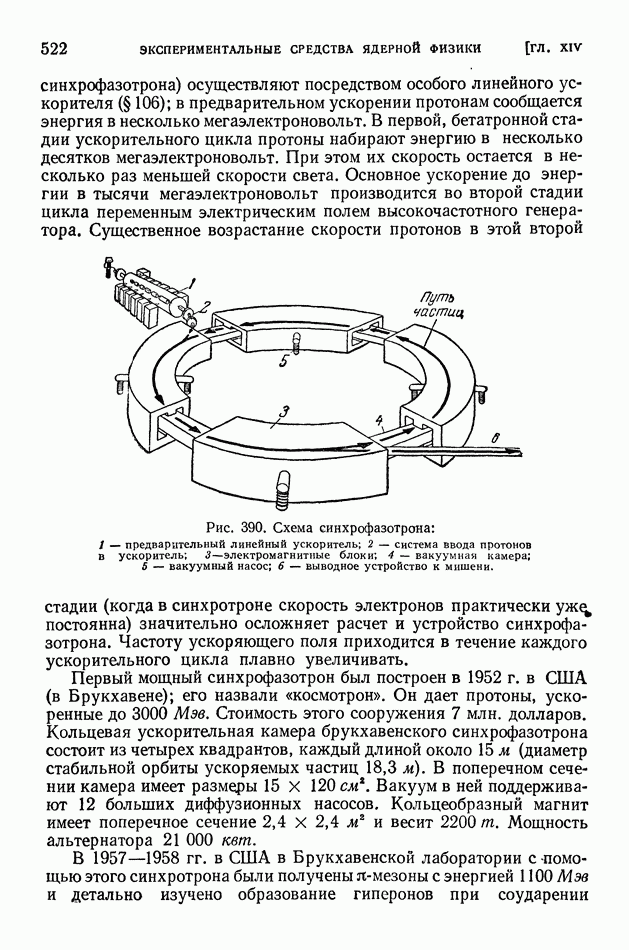
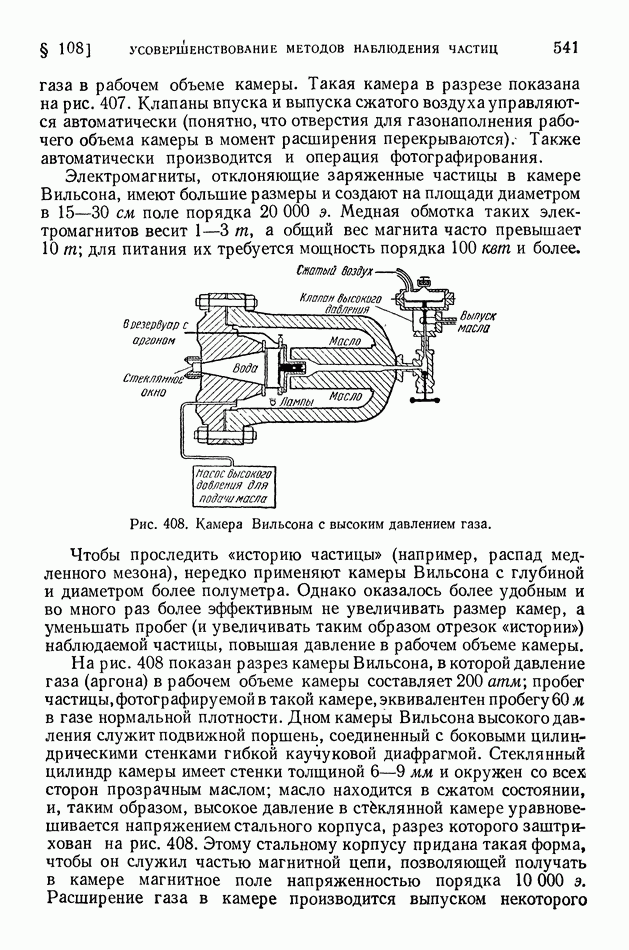
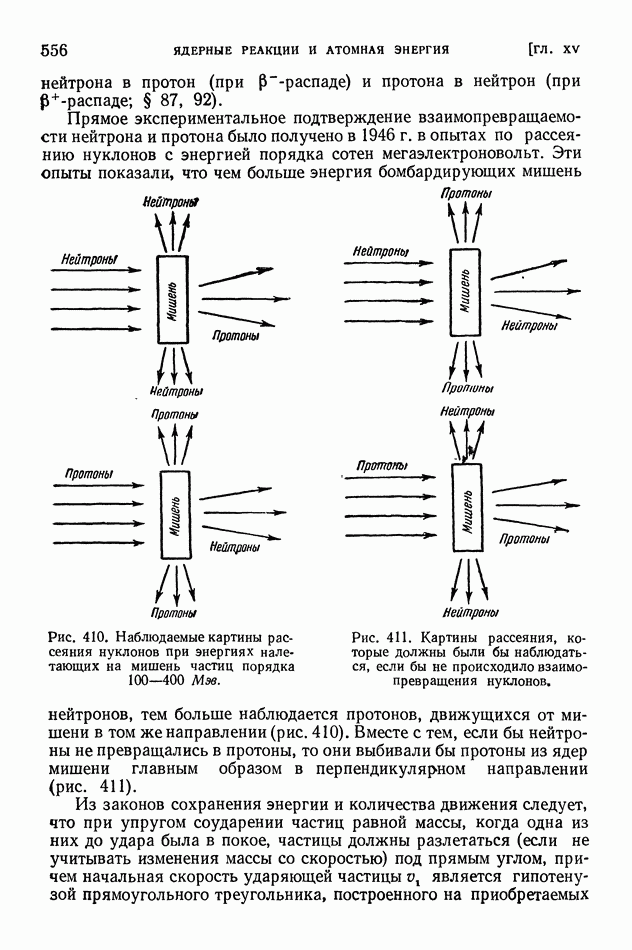
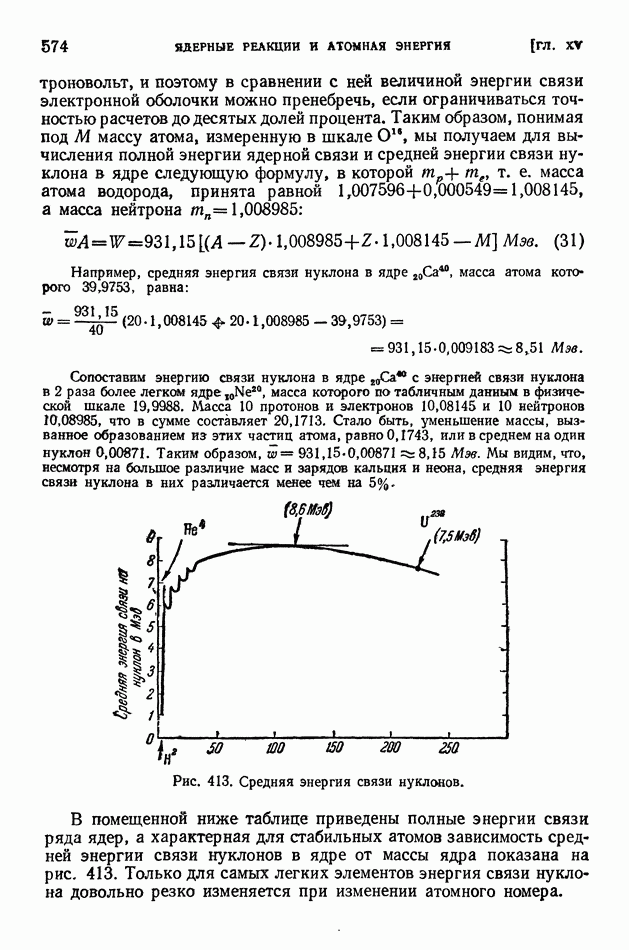
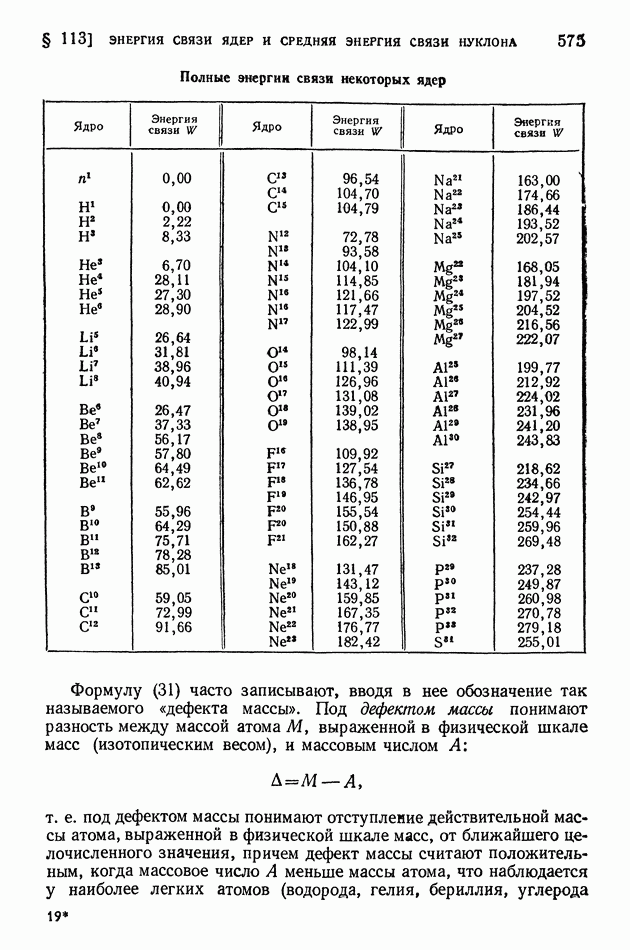
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 110. Энергетический эффект, энергия возбуждения и порог ядерных реакций
Уравнения ядерных реакций составляют по тому же принципу, как и уравнения обычных химических реакций. Но в отличие от термохимических уравнений (т. I, §80, 1959 г.; в пред. изд. § 132), которые принято писать для молей реагирующих веществ, т. е. для авогадрова числа молекул, уравнения ядерных реакций записывают для отдельных ядер (символы молекул в термохимических уравнениях означают величины внутренней энергии молей веществ; символы ядер в уравнениях ядерных реакций означают внутренние энергии отдельных ядер).
Под энергетическим эффектом  ядерной реакции понимают убыль внутренней энергии ядер и частиц, причем исходные и образовавшиеся ядра и частицы сопоставляют в их основных состояниях:
ядерной реакции понимают убыль внутренней энергии ядер и частиц, причем исходные и образовавшиеся ядра и частицы сопоставляют в их основных состояниях:

Пользуясь законом пропорциональности массы и энергии (§ 86)  внутреннюю энергию ядер и частиц выражают через их массу покоя. Так, для реакции
внутреннюю энергию ядер и частиц выражают через их массу покоя. Так, для реакции

энергетический эффект равен

Вместе с тем, если обозначить сумму кинетических энергий исходного ядра и частиц, выраженную в мегаэлектроновольт  через
через  и образовавшихся — через
и образовавшихся — через  то по закону сохранения энергии
то по закону сохранения энергии

где  энергия в мегаэлектроновольтах, излучаемая при реакции.
энергия в мегаэлектроновольтах, излучаемая при реакции.
Стало быть, согласно (1):

Прирост кинетической энергии частиц при ядерной реакции в сумме с энергией фотонов, излученных при этой реакции, часто называют освобожденной энергией. Уравнение (2) показывает, что энергетический эффект реакции как раз и представляет собой «освобождаему  энергию».
энергию».
Допустим, что исходное ядро находилось в покое и не подвергалось никакому воздействию. Ясно, что если происходит распад этого ядра, то энергия движения образовавшихся частиц  и излученная энергия [т. е. правая часть уравнения (2)] не могут быть величинами отрицательными. Стало быть, самопроизвольный распад невозбужденного ядра может произойти только в том случае, если энергетический эффект этого процесса положителен. Понятно, что это не ограничивает возможности других вынужденных ядерных превращений, так как каждому ядру всегда может быть сообщена достаточно большая энергия возбуждения, чтобы ядро распалось на составляющие его нуклоны.
и излученная энергия [т. е. правая часть уравнения (2)] не могут быть величинами отрицательными. Стало быть, самопроизвольный распад невозбужденного ядра может произойти только в том случае, если энергетический эффект этого процесса положителен. Понятно, что это не ограничивает возможности других вынужденных ядерных превращений, так как каждому ядру всегда может быть сообщена достаточно большая энергия возбуждения, чтобы ядро распалось на составляющие его нуклоны.
Но невозбужденное ядро может испытывать только такое превращение, которое ведет к уменьшению его внутренней энергии и к освобождению энергии. Поскольку внутренние энергии ядер пропорциональны массам покоя, то очевидно, что распад невозбужденного ядра может происходить только в том случае, когда масса покоя образующегося ядра и выброшенных частиц меньше массы исходного ядра.
Рассмотрим, например, возможен ли спонтанный распад  -частицы на два дейтона. Масса атома
-частицы на два дейтона. Масса атома  равна 4,0039, а масса двух атомов тяжелого водорода 4,0295. Следовательно, распад
равна 4,0039, а масса двух атомов тяжелого водорода 4,0295. Следовательно, распад  на два
на два  энергетически невозможен, так как он привел бы к возрастанию массы покоя. Для того чтобы этот процесс произошел, нужно сообщить
энергетически невозможен, так как он привел бы к возрастанию массы покоя. Для того чтобы этот процесс произошел, нужно сообщить  -частице энергию возбуждения не меньшую, чем
-частице энергию возбуждения не меньшую, чем 
Проверим, устойчиво ли ядро изотопа бериллия  в отношении распада на две
в отношении распада на две  -частицы:
-частицы:  Масса атома
Масса атома  равна 8,0079, а масса двух атомов гелия 8,0078. Следовательно, указанное превращение возможно (такой распад действительно происходит), но освобождающаяся энергия невелика:
равна 8,0079, а масса двух атомов гелия 8,0078. Следовательно, указанное превращение возможно (такой распад действительно происходит), но освобождающаяся энергия невелика: 
Обычно в лабораторной системе координат ядро-мишень А можно считать неподвижным, тогда  где
где  энергия налетающей частицы. В этом случае изуравнения (2) следует:
энергия налетающей частицы. В этом случае изуравнения (2) следует:

Но при расчетах обычно целесообразнее пользоваться системой координат, связанной с центром масс взаимодействующих частиц. Если ядерная реакция происходит с образованием промежуточного (составного) ядра, то в лабораторной системе координат составное ядро сохраняет движение  скоростью и) центра масс исходного ядра и налетающей частицы (скорость которой обозначим через
скоростью и) центра масс исходного ядра и налетающей частицы (скорость которой обозначим через  в системе же координат, связанной с центром масс, составное ядро неподвижно. По закону сохранения количества движения
в системе же координат, связанной с центром масс, составное ядро неподвижно. По закону сохранения количества движения

Стало быть, в лабораторной системе координат составное ядро имеет кинетическую энергию

Если мы вычтем эту величину из обеих частей энергетического баланса (3), то в левой части получим энергию движения образовавшихся частиц относительно составного ядра, т. е. в системе координат центра масс взаимодействующих частиц, плюс излученная энергия, а в правой:  Очевидно, что фигурирующая здесь разность кинетической энергии налетающей частицы
Очевидно, что фигурирующая здесь разность кинетической энергии налетающей частицы  и энергии движения
и энергии движения  сообщенного этой частицей составному ядру (и то и другое в лабораторной системе координат), представляет собой ту часть кинетической энергии налетающей частицы, которая при ее поглощении исходным ядром переходит в энергию внутриядерного движения нуклонов. Иначе говоря, это энергия движения исходных частиц в системе их центра масс. Поскольку, как была показано,
сообщенного этой частицей составному ядру (и то и другое в лабораторной системе координат), представляет собой ту часть кинетической энергии налетающей частицы, которая при ее поглощении исходным ядром переходит в энергию внутриядерного движения нуклонов. Иначе говоря, это энергия движения исходных частиц в системе их центра масс. Поскольку, как была показано,

Итак:

Здесь  кинетическая энергия движения частицы относительно исходного ядра.
кинетическая энергия движения частицы относительно исходного ядра.
Для реакций, проходящих с образованием промежуточного ядра,

по закону сохранения энергии наряду с уравнением (2) имеем:

Пусть точное значение массы составного ядра в его основном состоянии есть  тогда энергия возбуждения составного ядра
тогда энергия возбуждения составного ядра

Подставляя сюда  из предыдущего уравнения, получаем (при
из предыдущего уравнения, получаем (при  т. е. когда исходное ядро было неподвижно в лабораторной системе координат):
т. е. когда исходное ядро было неподвижно в лабораторной системе координат):

Что представляет собой первый член этой формулы? Он определяет, насколько сумма энергий ядра А (отличающегося от С только тем, что в нем нет частицы а) и частицы а превышает энергию ядра С, взятого в основном состоянии. Следовательно, это есть энергия, которую необходимо затратить, чтобы отделить частицу а от ядра С. Эта энергия отделения частицы а от ядра, или энергия связи частицы а в невозбужденном ядре С, вместе с тем определяет «сродство» ядра  к частице
к частице 

Из уравнения (6) следует, что энергия возбуждения превышает энергию связи частицы а в невозбужденном ядре С на величину, равную кинетической энергии сталкивающихся частиц в системе координат, связанной с их центром масс. Согласно (4) и (6)

где  кинетическая энергия налетающей частицы в лабораторной системе координат.
кинетическая энергия налетающей частицы в лабораторной системе координат.
Следует отметить (и при расчетах это важно иметь в виду), что в приведенных формулах вместо массы ядер можно поставить массы атомов, отличающиеся от массы ядер на массу связанных с ними электронов. Поскольку число электронов в реакции не изменяется, а связь с ядром тех электронов, которые могут оказаться отщепленными, ничтожно мала в сравнении со связью ядерных частиц, то
суммарная масса электронов при вычислении  или Евозб автоматически сокращается.
или Евозб автоматически сокращается.
Для примера приведем расчет энергетического эффекта и энергии возбуждения для реакции слияния ядер тяжелого и сверхтяжелого водорода в ядро гелия (т. е. слияния дейтона и тритона в  -частицу):
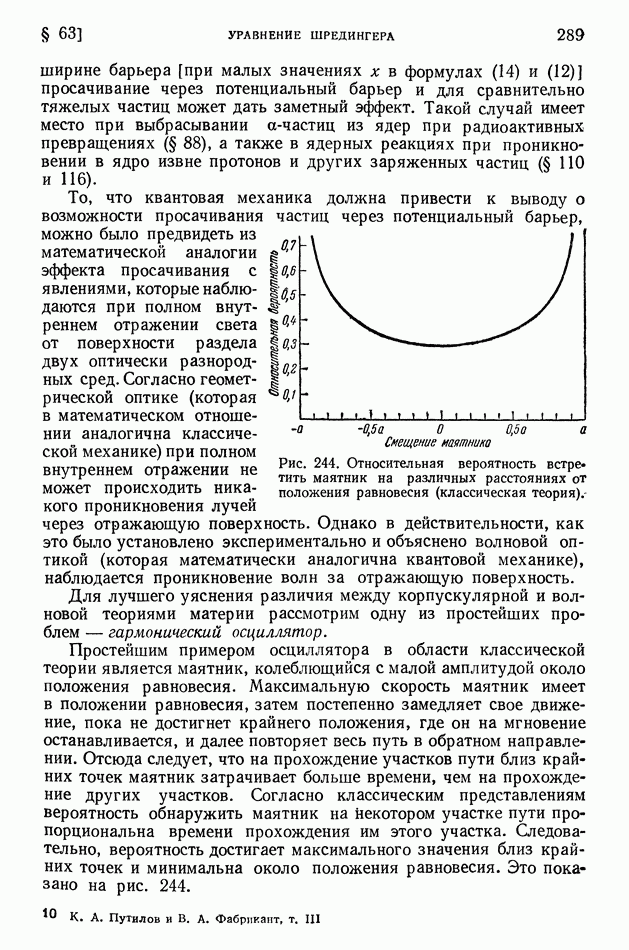
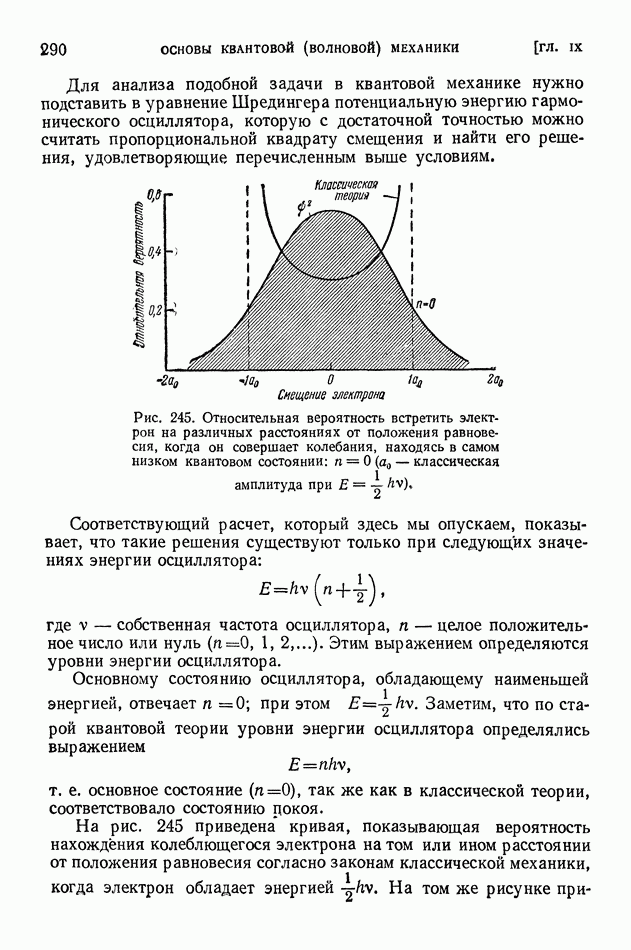
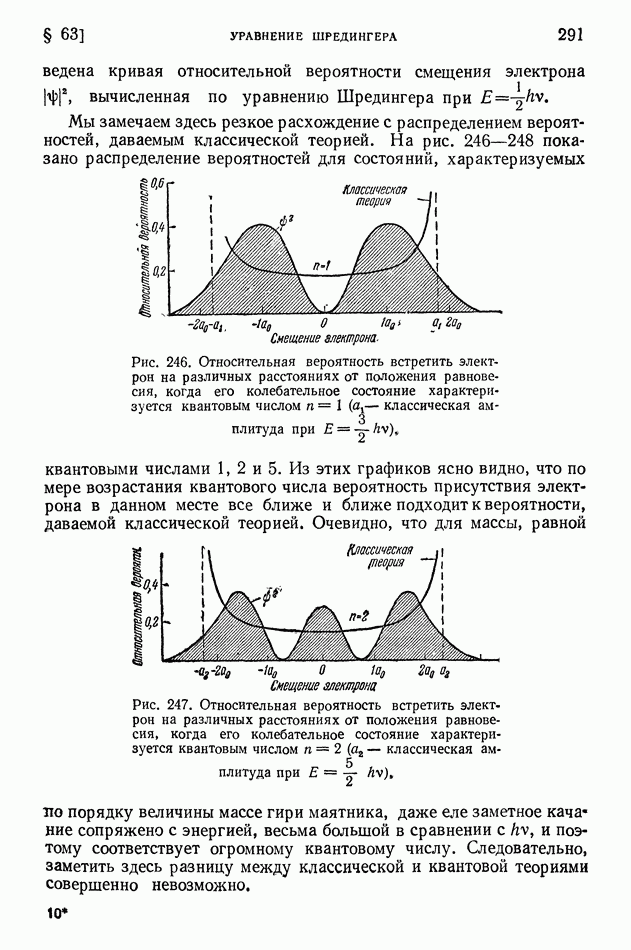
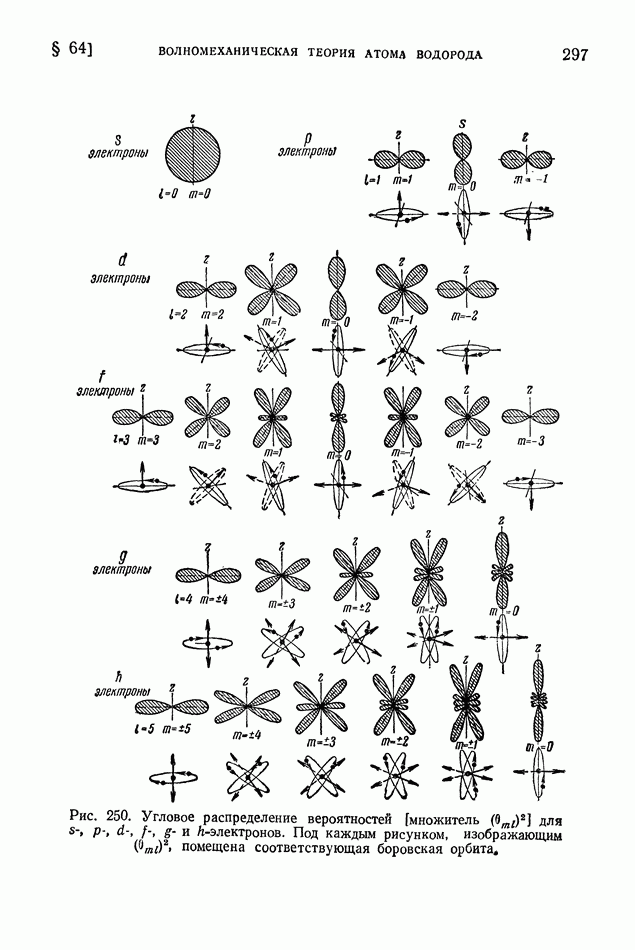
-частицу):

Масса  Масса
Масса  Масса
Масса  Их сумма 5,031708 Их сумма 5,012885
Их сумма 5,031708 Их сумма 5,012885
Следовательно, согласно (1) и (6)

Этот пример показывает, как велик энергетический эффект некоторых ядерных реакций. Действительно, для авогадрова числа прореагировавших ядер, т. е. для  смеси тяжелых изотопов водорода, выделение энергии должно составить (учитываем, что
смеси тяжелых изотопов водорода, выделение энергии должно составить (учитываем, что  ккал)
ккал)

Такое количество тепла выделяется при сгорании  нефти с теплотворной способностью
нефти с теплотворной способностью 
Выделение больших количеств энергии характерно для многих ядерных реакций. Рассмотренную здесь реакцию можно осуществлять при энергии дейтонов в сотые доли мегаэлектроновольта, так же как и ряд аналогичных реакций, например реакцию  энергетический эффект которой еще больше
энергетический эффект которой еще больше  и которая может идти при энергии дейтонов порядка
и которая может идти при энергии дейтонов порядка  В этих реакциях при каждом превращении исходного ядра освобождается энергия, которая в тысячи раз превосходит кинетическую энергию налетающего дейтона. Но при малой энергии дейтонов эффективным, т. е. приводящим к таким превращениям, оказывается только один дейтон из миллионов. Поэтому в конечном счете в таких реакциях затраченная энергия оказывается больше освобожденной.
В этих реакциях при каждом превращении исходного ядра освобождается энергия, которая в тысячи раз превосходит кинетическую энергию налетающего дейтона. Но при малой энергии дейтонов эффективным, т. е. приводящим к таким превращениям, оказывается только один дейтон из миллионов. Поэтому в конечном счете в таких реакциях затраченная энергия оказывается больше освобожденной.
Энергия возбуждения промежуточного ядра в реакции  составляющая
составляющая  значительно превышает работу, потребную для выброса нуклона из ядра
значительно превышает работу, потребную для выброса нуклона из ядра  Поэтому и происходит испускание нуклона из промежуточного ядра
Поэтому и происходит испускание нуклона из промежуточного ядра  причем понятно, что выбрасываемой частицей в данном случае должен оказаться нейтрон, а не протон, так как промежуточное ядро
причем понятно, что выбрасываемой частицей в данном случае должен оказаться нейтрон, а не протон, так как промежуточное ядро  в сравнении с наиболее устойчивыми легкими ядрами, у которых число нейтронов равно числу протонов, имеет избыточный нейтрон.
в сравнении с наиболее устойчивыми легкими ядрами, у которых число нейтронов равно числу протонов, имеет избыточный нейтрон.
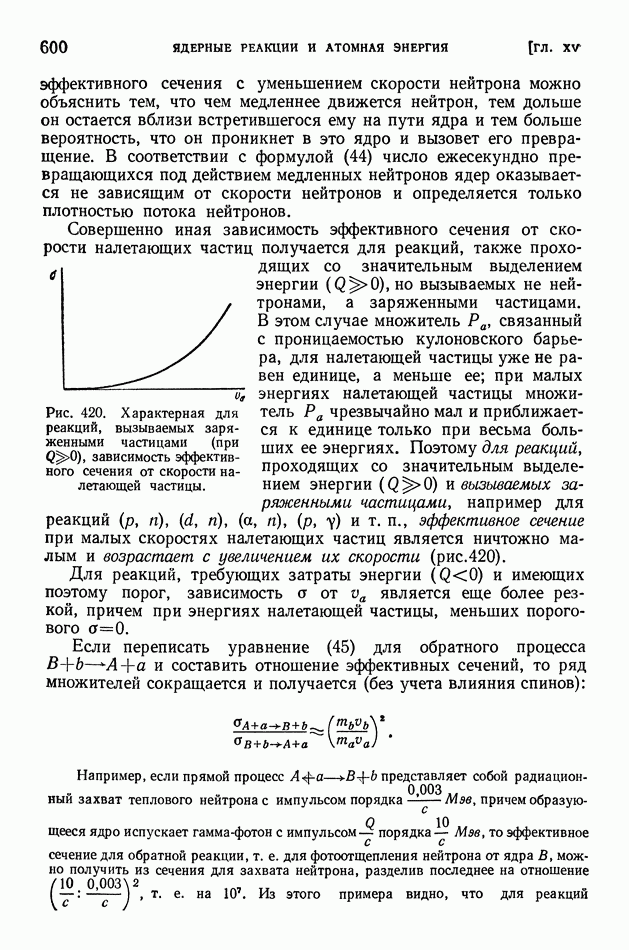
Руководствуясь уравнением (5), рассмотрим, какие ядерные реакции могут происходить при сколь угодно малых значениях кинетической энергии  налетающей частицы и какие реакции становятся возможными, когда энергия налетающей частицы достаточно велика.
налетающей частицы и какие реакции становятся возможными, когда энергия налетающей частицы достаточно велика.
Поскольку левая часть уравнения (5) не может быть отрицательной, то казалось бы, что все реакции, приводящие к выделению энергии  могут идти при
могут идти при  а для того чтобы произошла реакция, приводящая к поглощению энергии
а для того чтобы произошла реакция, приводящая к поглощению энергии  налетающая частица должна сообщить ядру энергию, не меньшую
налетающая частица должна сообщить ядру энергию, не меньшую  В действительности дело обстоит, как будет сейчас пояснено, несколько сложнее.
В действительности дело обстоит, как будет сейчас пояснено, несколько сложнее.
Минимальную энергию налетающей частицы, необходимую для возможности осуществления какой-либо ядерной реакции, называют порогом этой реакции. Когда гамма-излучение отсутствует и энергия образовавшихся частиц пренебрежимо мала, то из (5) получается:

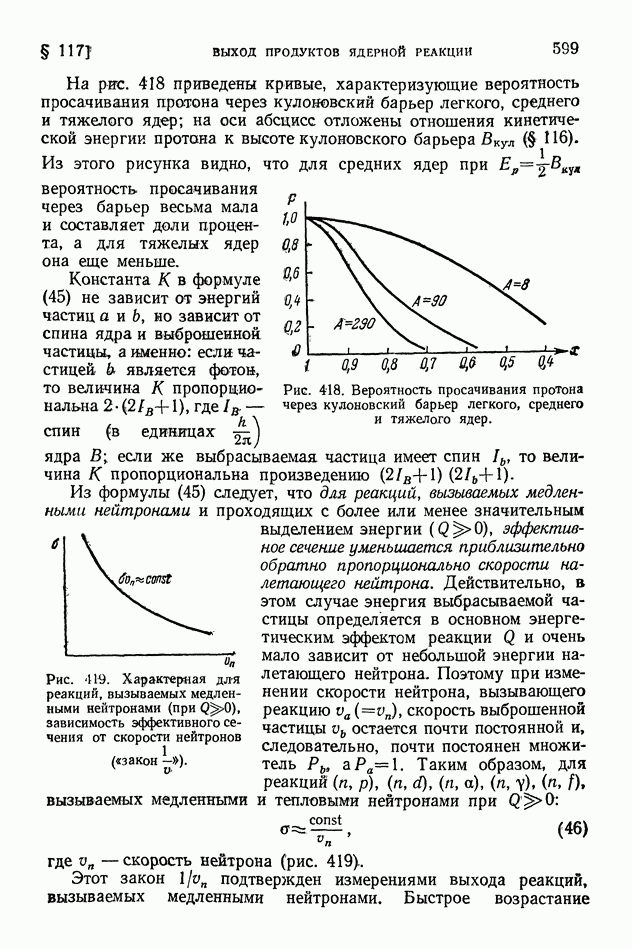
Но в реакциях, происходящих с выбросом заряженной частицы, левая часть энергетического баланса (5) не может быть меньше энергии, приобретаемой частицей вследствие кулоновского отталкивания между ней и ядром. Если выброс частицы  происходит не вследствие «просачивания» ее через барьер, когда выход реакции мал, а «с перевалом» через барьер, то минимальной кинетической энергией образовавшегося ядра и выброшенной частицы будет высота кулоновского барьера
происходит не вследствие «просачивания» ее через барьер, когда выход реакции мал, а «с перевалом» через барьер, то минимальной кинетической энергией образовавшегося ядра и выброшенной частицы будет высота кулоновского барьера  (§ 88, 115, рис. 359, таблица на стр. 594). Для этих реакций согласно (5)
(§ 88, 115, рис. 359, таблица на стр. 594). Для этих реакций согласно (5)

Если выбрасывается нейтрон, но реакция вызывается заряженной частицей, то и в этом случае порог может оказаться больше определяемого формулой (7). Заряженная налетающая частица а, чтобы проникнуть в ядро А у должна преодолеть кулоновский барьер Вкул (или «просочиться» через него; но в этом случае выход реакции мал). Поэтому вероятность таких реакций становится значительной только при 

Ядерные реакции термодинамически необратимы (т. I, § 103,1959; в предыдущих изданиях § 137), что не означает, однако, невозможности осуществления обратной реакции. Разрядка аккумулятора при значительной величине разрядного тока также представляет собой явление термодинамически необратимое (так как процесс неравновесен и сопровождается рассеянием работы в тепло), но это не исключает возможности осуществления обратного процесса, т. е. новой зарядки аккумулятора (т. II, § 42, 1959; в предыдущих изданиях § 48). Ядерные реакции, проходящие с выделением энергии  иногда называют прямыми:
иногда называют прямыми:

а реакции, требующие затраты энергии, обратными:

Энергия, необходимая для осуществления обратной ядерной реакции, определяется ее порогом, т. е. формулой (7) или (8).
Так, например, при поглощении ядрами бора  тепловых нейтронов образуются
тепловых нейтронов образуются  и
и  -частица В этой реакции выделяется энергия
-частица В этой реакции выделяется энергия 

Облучая  -частицами достаточной энергии, можно осуществить обратную ядерную реакцию, приводящую к образованию ядер бора:
-частицами достаточной энергии, можно осуществить обратную ядерную реакцию, приводящую к образованию ядер бора:

Порог этой реакции, вычисленный по формуле (7), будет

Кулоновский барьер ядер  для
для  -частиц имеет высоту
-частиц имеет высоту  и
и  Следовательно, в данном случае при энергии
Следовательно, в данном случае при энергии  вычисленной по формуле (7),
вычисленной по формуле (7),  -частицы смогут преодолеть кулоновский барьер ядра
-частицы смогут преодолеть кулоновский барьер ядра  и будет наблюдаться значительный выход продуктов реакции (ядер
и будет наблюдаться значительный выход продуктов реакции (ядер  и нейтронов).
и нейтронов).
Другой пример—фоторасщеп лен и  изотопа кислорода
изотопа кислорода 

В данном случае  и поэтому по. формуле (8)
и поэтому по. формуле (8)

Энергетический эффект некоторых ядерных реакций 
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ЧАСТЬ ЧЕТВЕРТАЯ. ОПТИКА
- § 2. Электромагнитная теория света
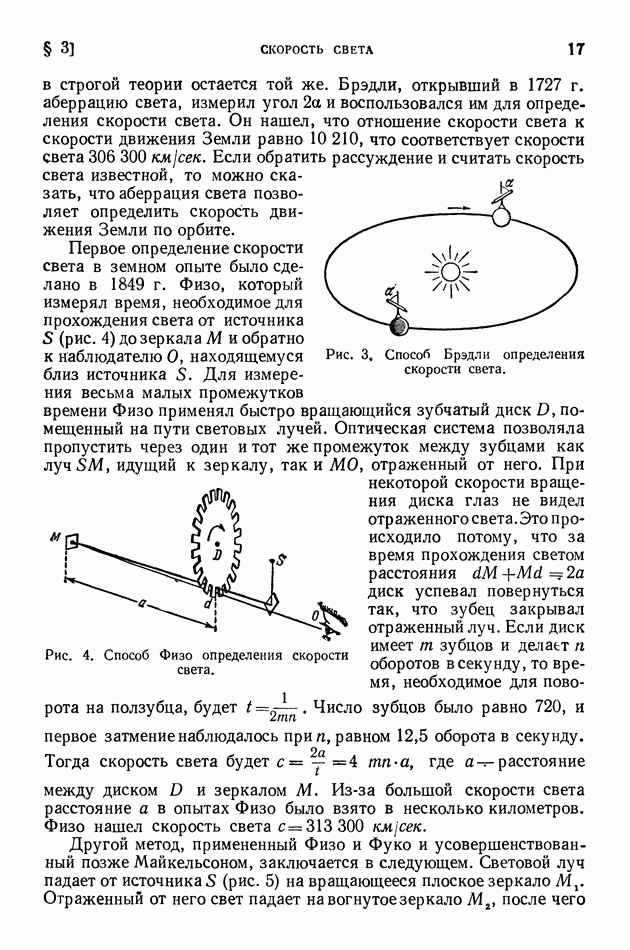
- § 3. Скорость света
- § 4. Опыт Майкельсона
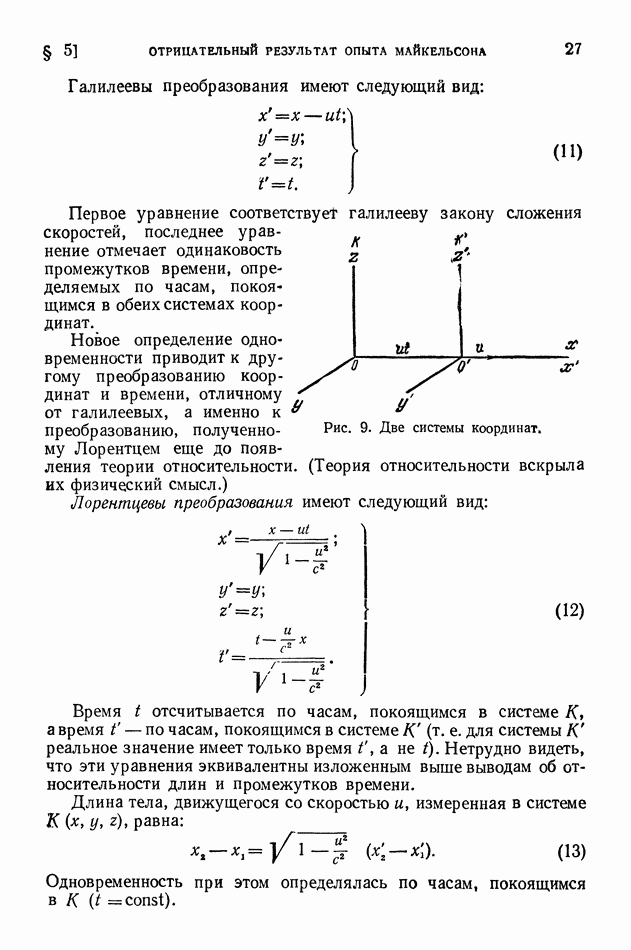
- § 5. Отрицательный результат опыта Майкельсона и теория относительности
- § 6. Некоторые замечания о теории относительности
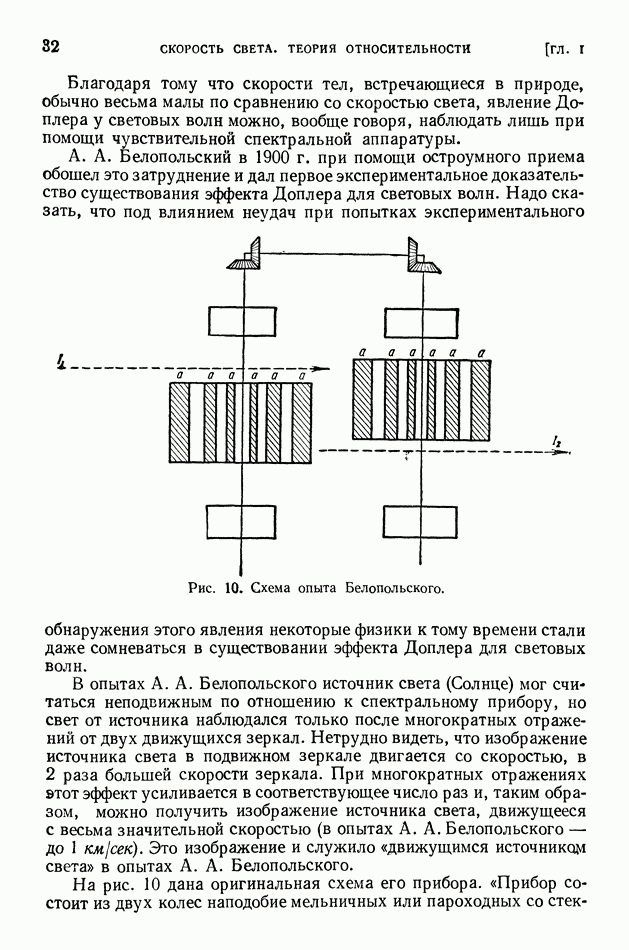
- § 7. Явление Доплера для световых волн
- ГЛАВА II. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
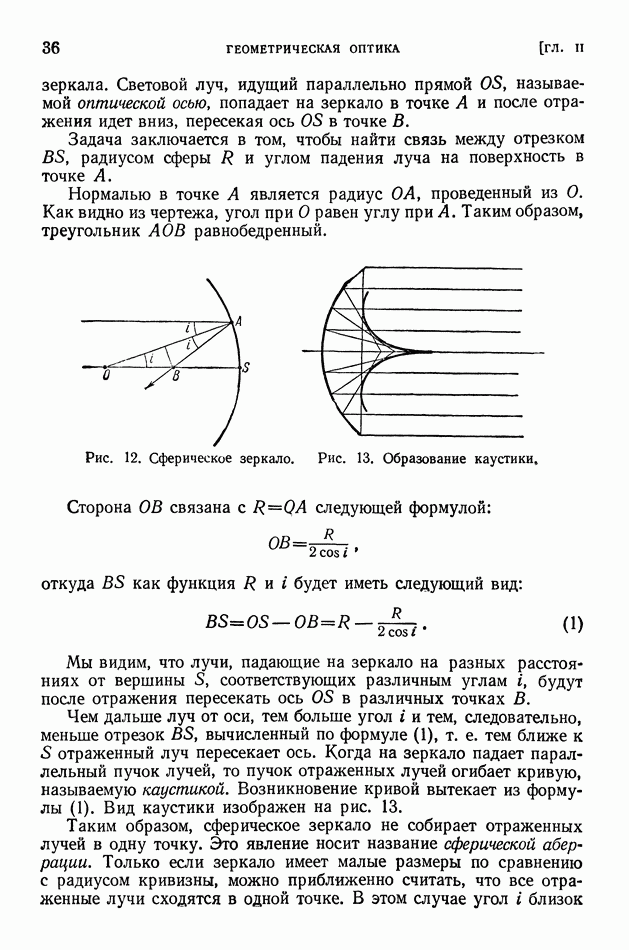
- § 8. Законы отражения и преломления света
- § 9. Линза
- § 10. Оптические системы
- § 11. Глаз как оптическая система
- § 12. Приборы, вооружающие глаз
- § 13. Фотоаппарат и проекционный аппарат
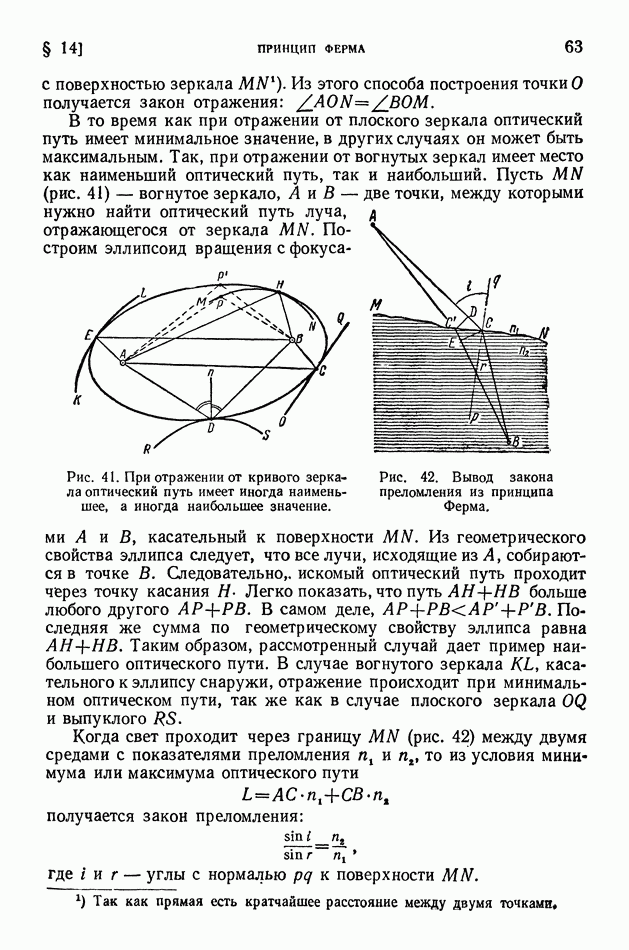
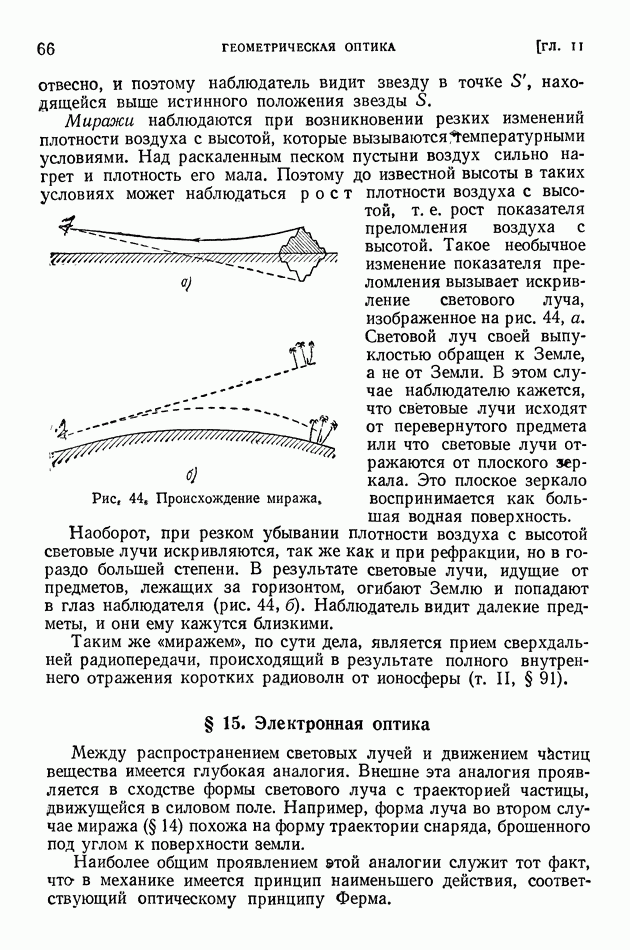
- § 14. Принцип Ферма
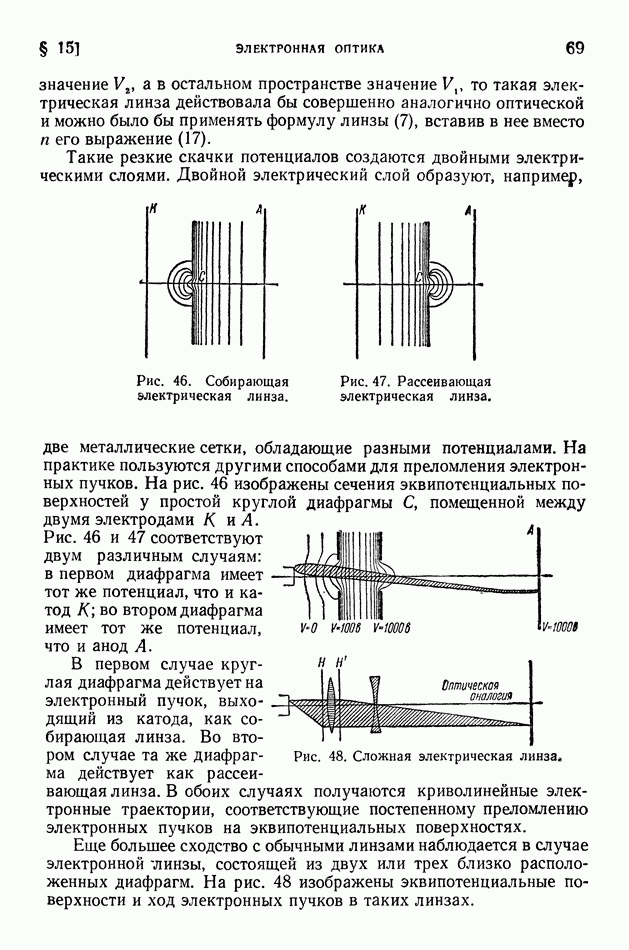
- § 15. Электронная оптика
- ГЛАВА III. ИНТЕРФЕРЕНЦИЯ СВЕТА
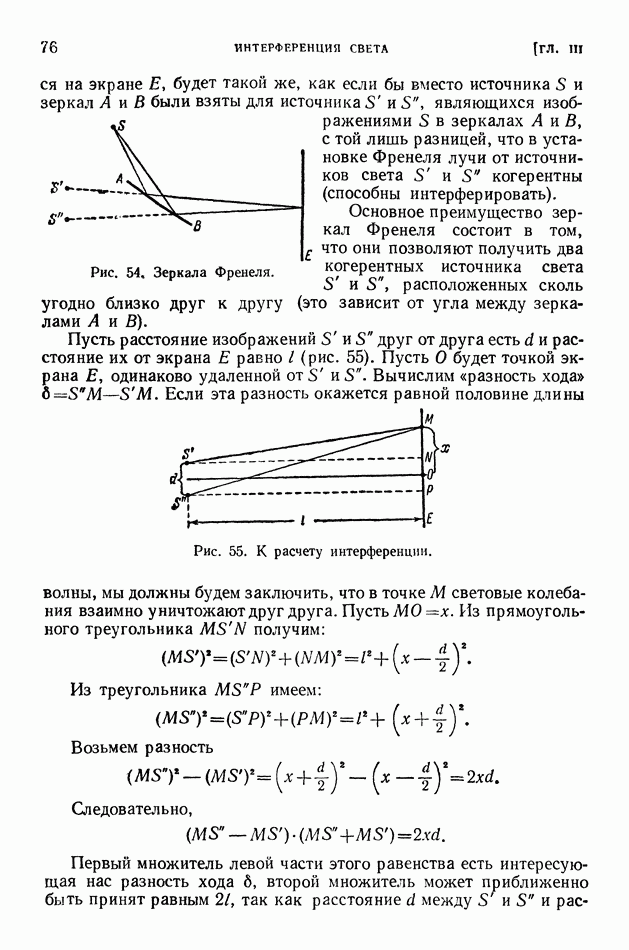
- § 16. Принцип суперпозиции. Когерентность
- § 17. Зеркала Френеля
- § 18. Цвета тонких пленок. Полосы равной толщины
- § 19. Полосы равного наклона. Просветленная оптика
- § 20. Интерферометры
- § 21. Интерференционное измерение технических мер длины
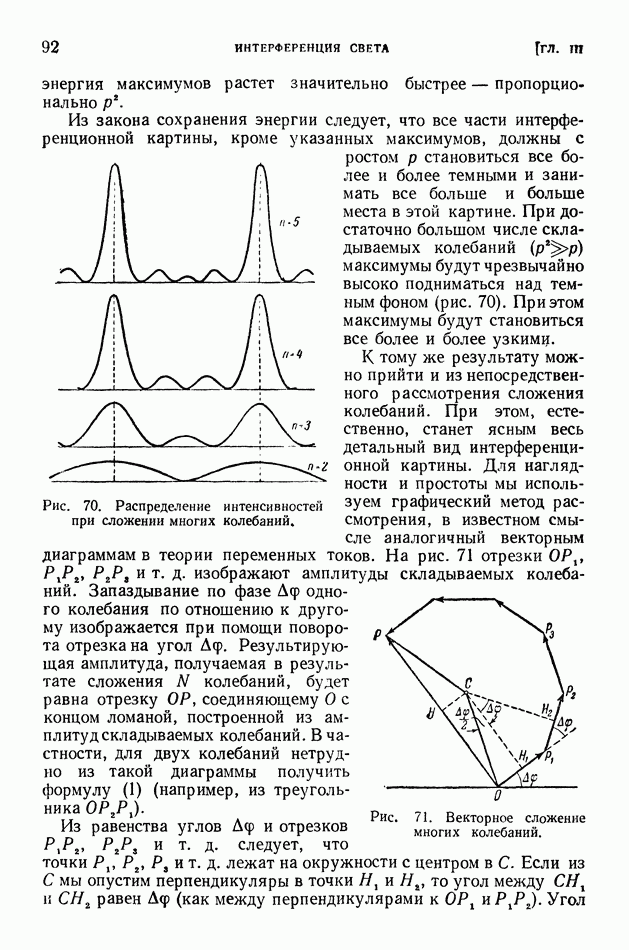
- § 22. Интерференция многих колебаний
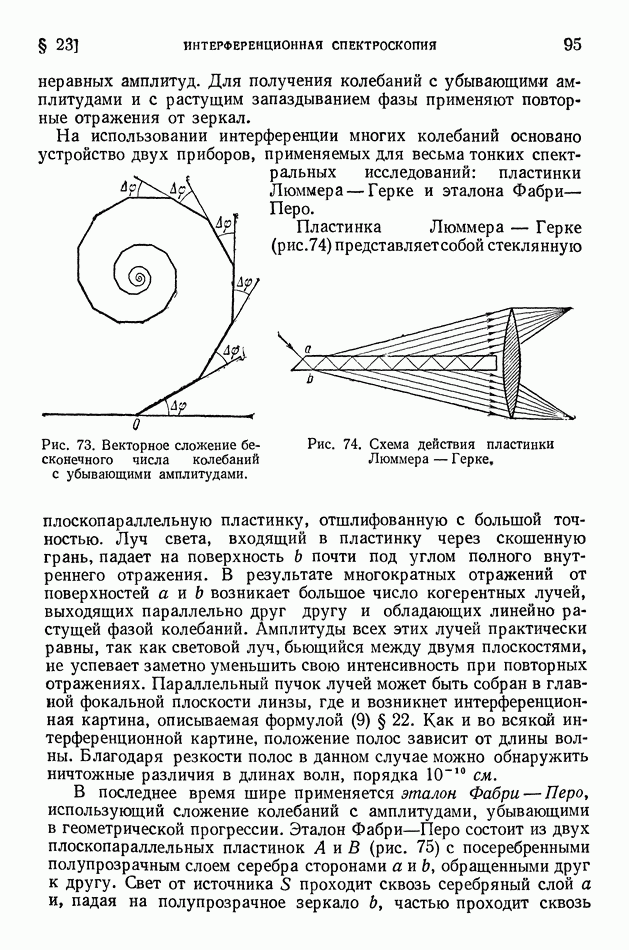
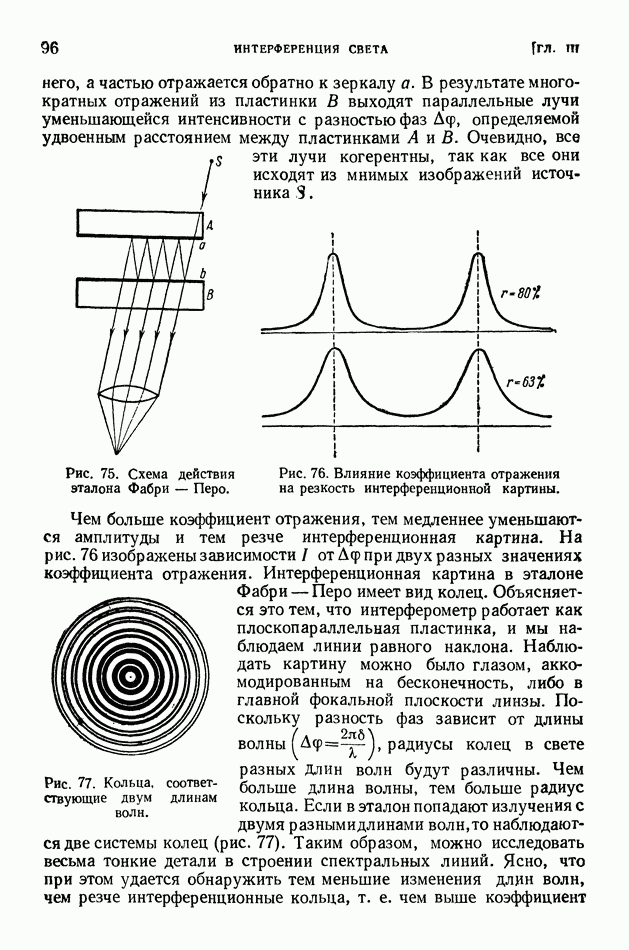
- § 23. Интерференционная спектроскопия
- ГЛАВА IV. ДИФРАКЦИЯ СВЕТА
- § 24. Явление дифракции. Опыт Френеля
- § 25. Принцип Гюйгенса-Френеля
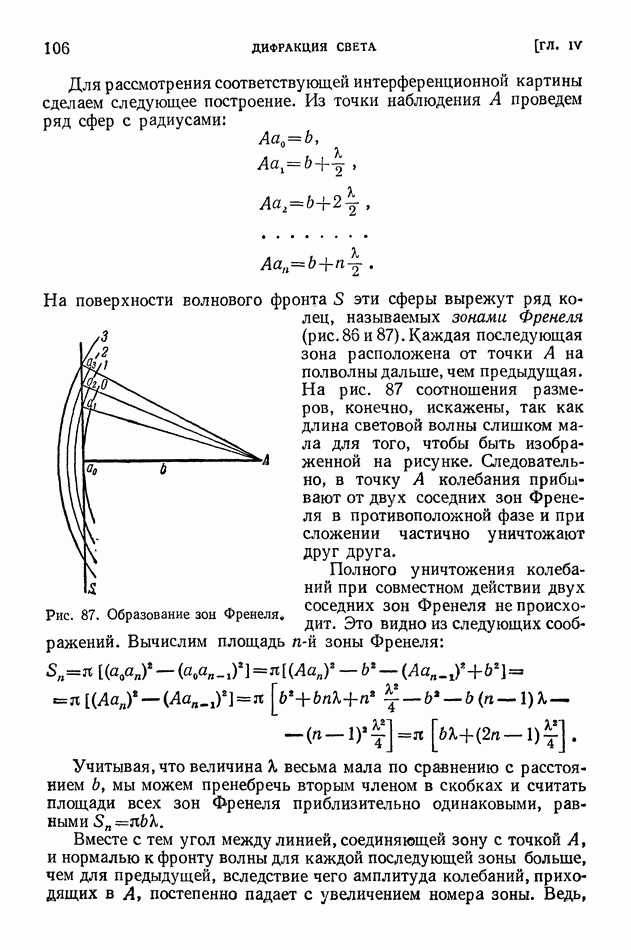
- § 26. Метод зон Френеля
- § 27. Дифракция от узкой щели
- § 28. Дифракционная решетка
- § 29. Дифракционный спектр. Решетки Роуланда и эшелон Майкельсона
- § 30. Плоскостные решетки. Пространственная решетка
- § 31. Структурный рентгеновский анализ
- § 32. Дифракция света на ультразвуковых волнах
- § 33. Дифракция от мелких частиц
- § 34. Разрешающая способность оптических инструментов. Звездный интерферометр
- ГЛАВА V. ПОЛЯРИЗАЦИЯ СВЕТА
- § 35. Поляризация света
- § 36. Двойное лучепреломление
- § 37. Интерференция поляризованного света
- § 38. Оптический метод исследования упругих натяжений. Эффект Керра
- § 39. Вращение плоскости поляризации. Эллиптическая поляризация
- ГЛАВА VI. ДИСПЕРСИЯ, ПОГЛОЩЕНИЕ И ИЗЛУЧЕНИЕ СВЕТА
- § 40. Отражение света
- § 41. Давление света. Опыты Лебедева
- § 42. Дисперсия. Опыты Ньютона
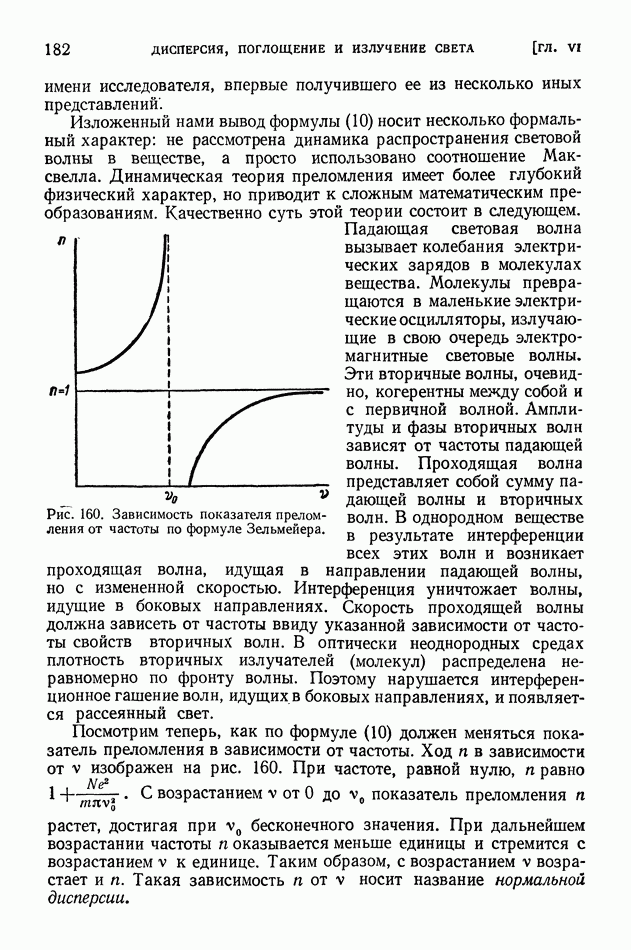
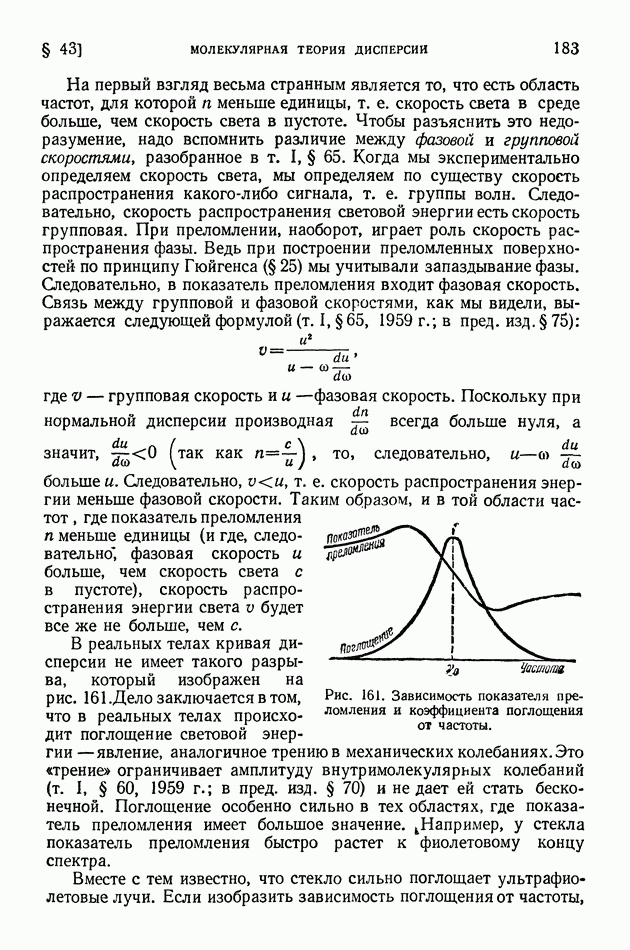
- § 43. Молекулярная теория дисперсии
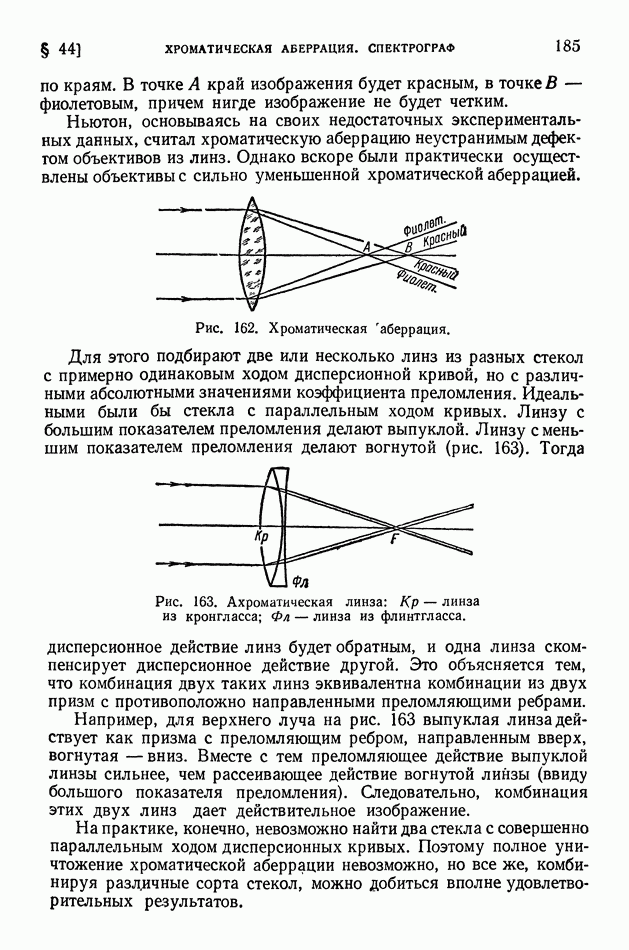
- § 44. Хроматическая аберрация. Спектрограф
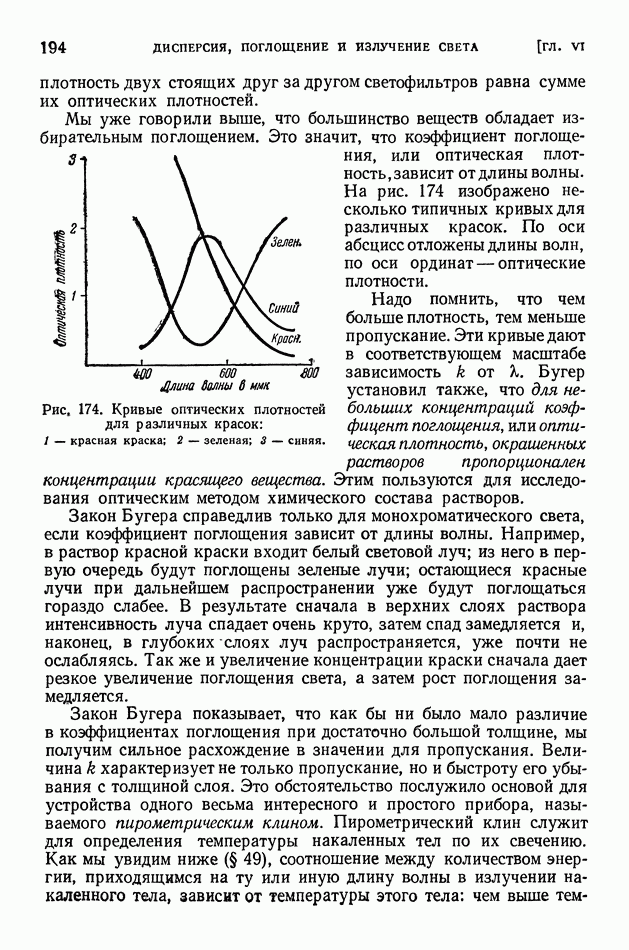
- § 45. Поглощение света
- § 46. Закон Бугера. Опыты Вавилова
- § 47. Атом как элементарный излучатель света
- § 48. Эффект Вавилова — Черенкова
- ГЛАВА VII. ТЕРМОДИНАМИКА ИЗЛУЧЕНИЯ И СВЕТОВОЙ ПОТОК
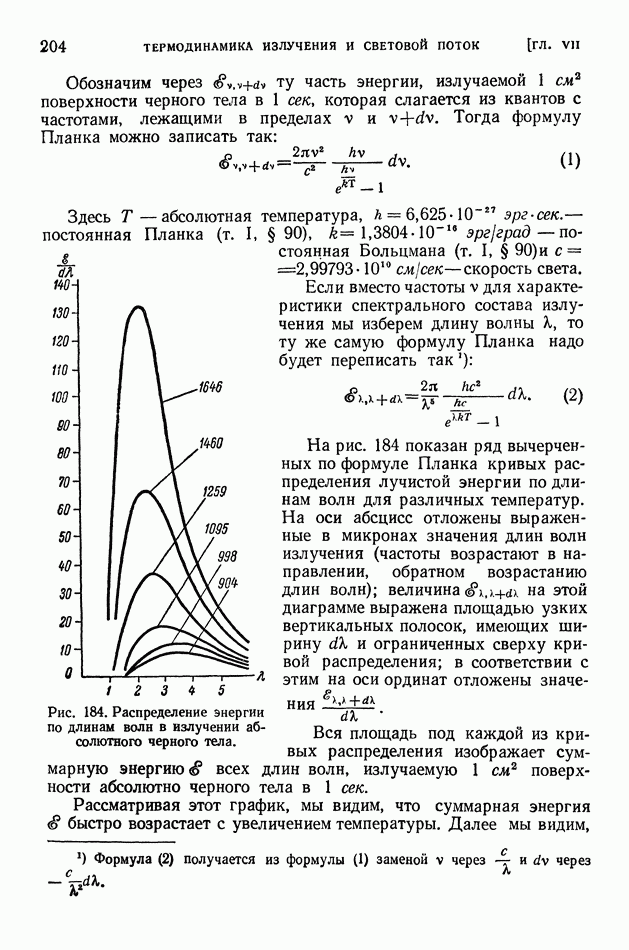
- § 49. Излучение черного тела. Формула Планка. Закон Вина
- § 50. Излучение нечерных тел. Законы Кирхгофа
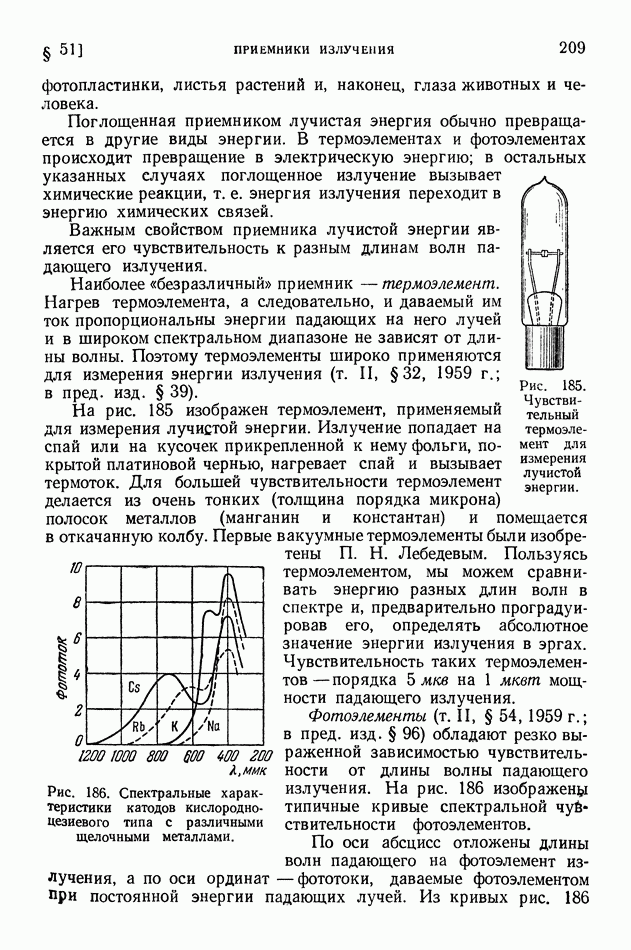
- § 51. Приемники излучения
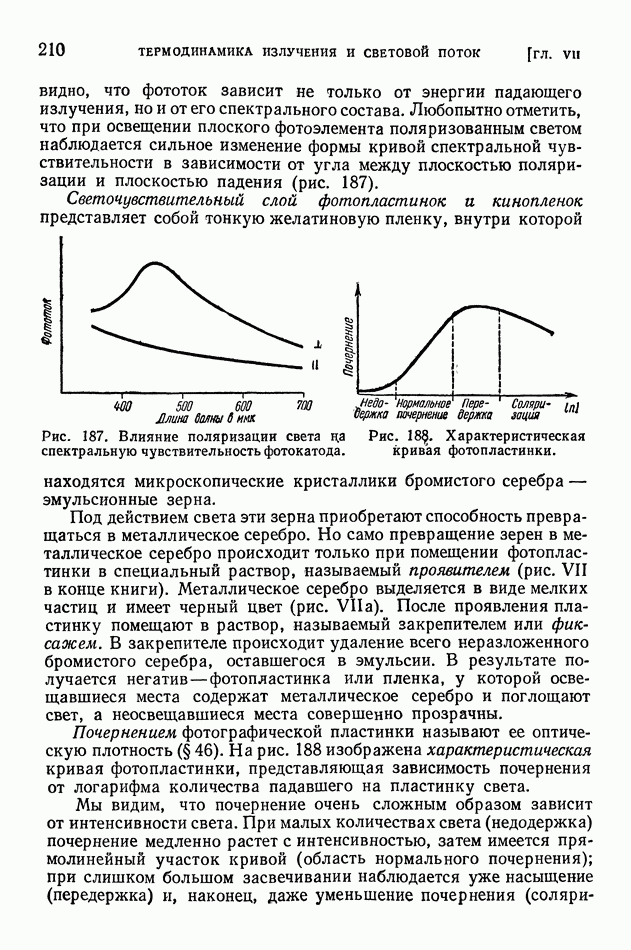
- § 52. Световые величины и их измерения
- § 53 Температурные излучатели как источники света
- ЧАСТЬ ПЯТАЯ. АТОМНАЯ ФИЗИКА
- ГЛАВА VIII. СТРОЕНИЕ АТОМА И ТЕОРИЯ БОРА
- § 55. Опыты, обнаружившие ядерное строение атомов
- § 56. Противоречие между фактическим строением атомов и выводами классической электродинамики. Строение линейчатых спектров
- § 57. Опытные основания теории квантов в первые годы ее развития
- § 58. Теория Бора. Происхождение спектра водорода
- § 59. Квантовые числа
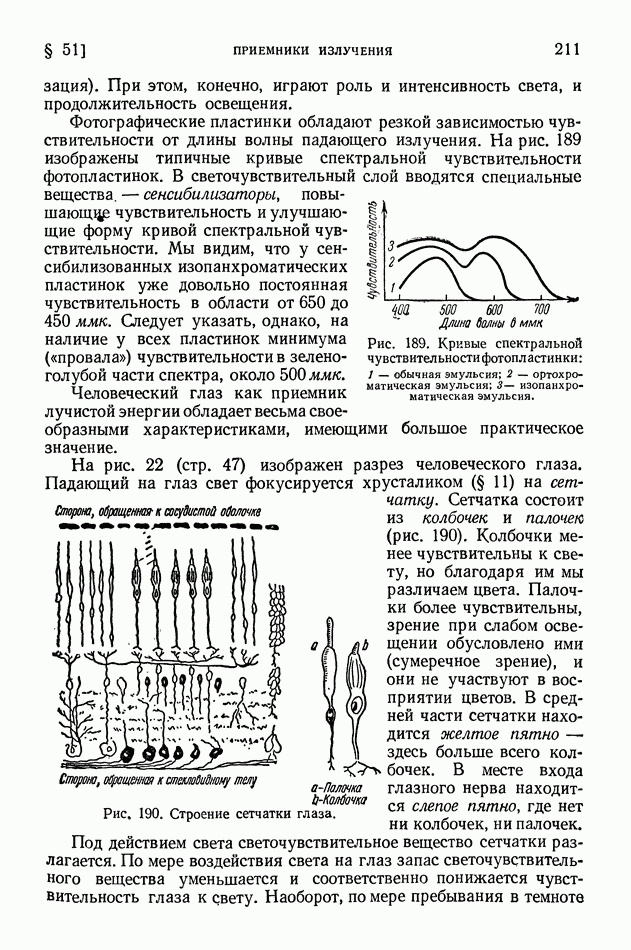
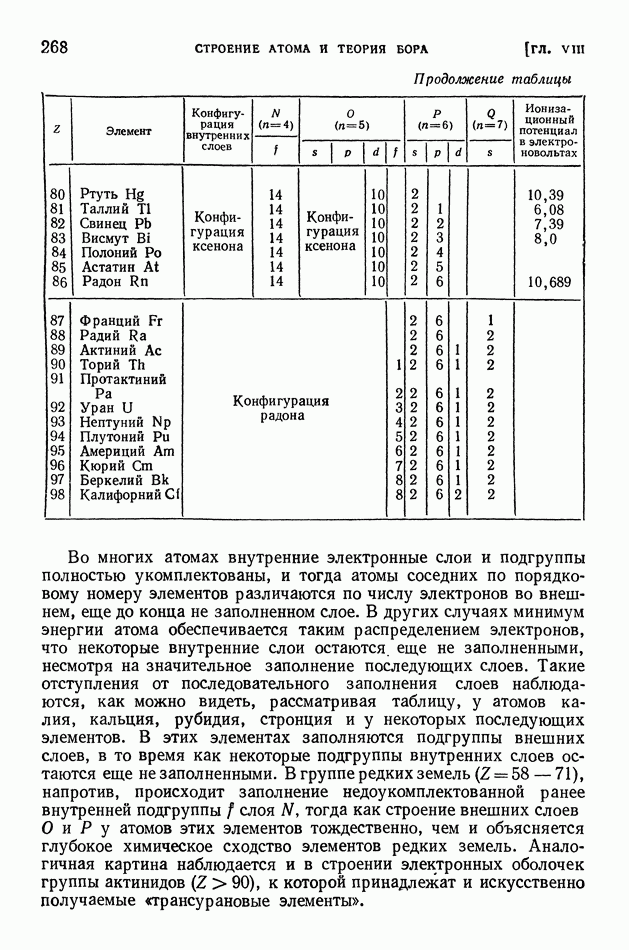
- § 60. Принцип Паули. Строение электронных оболочек атомов
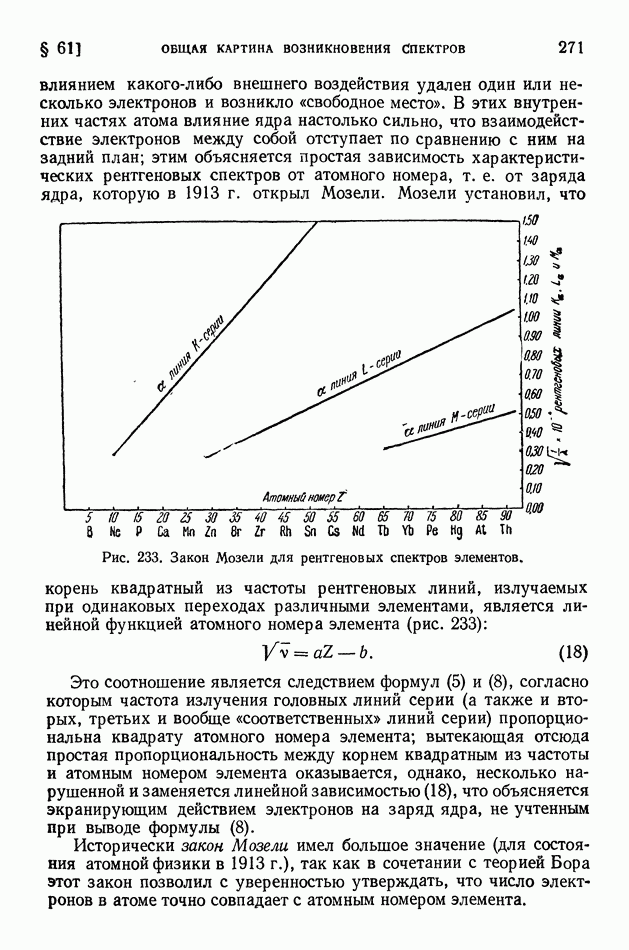
- § 61. Общая картина возникновения спектров
- ГЛАВА IX. ОСНОВЫ КВАНТОВОЙ (ВОЛНОВОЙ) МЕХАНИКИ
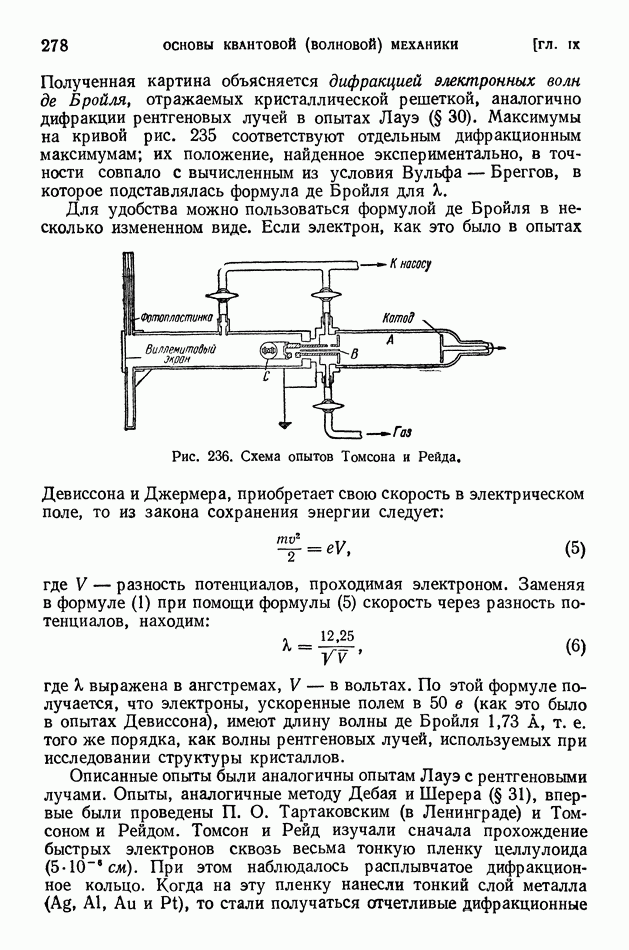
- § 62. Волновые свойства частиц. Формула де Бройля. Дифракция электронов
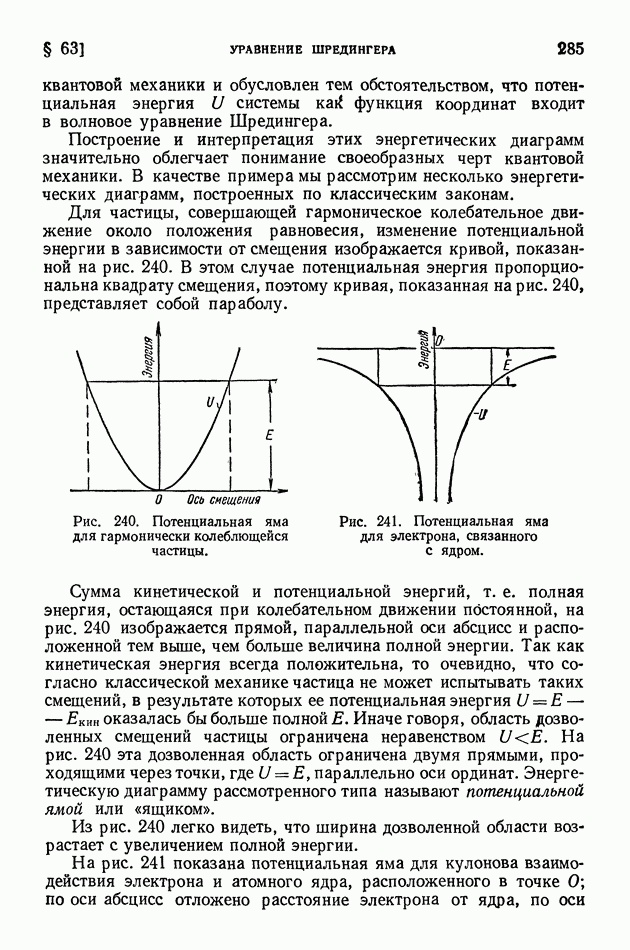
- § 63. Уравнение Шредингера. Просачивание через энергетический барьер. Нулевая энергия
- § 64. Волномеханическая теория атома водорода
- § 65. Соотношение неопределенностей и его разные трактовки
- ГЛАВА X. КВАНТОВАЯ ОПТИКА
- § 66. Развитие квантовой оптики
- § 67. Спектр щелочных металлов. Спин электрона
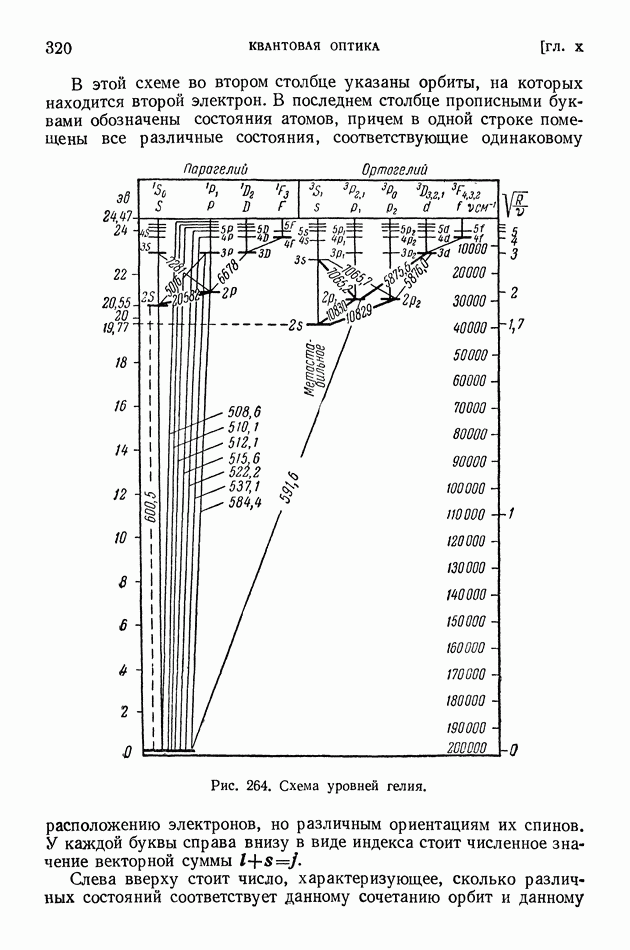
- § 68. Спектр гелия. Символика спектральных термов
- § 69. Сверхтонкая структура спектральных линий
- § 70. Атом в силовом поле
- § 71. Молекулярные спектры и строение молекул
- § 72. Комбинационное рассеяние света
- § 73. Квантовая картина испускания света атомами и молекулами
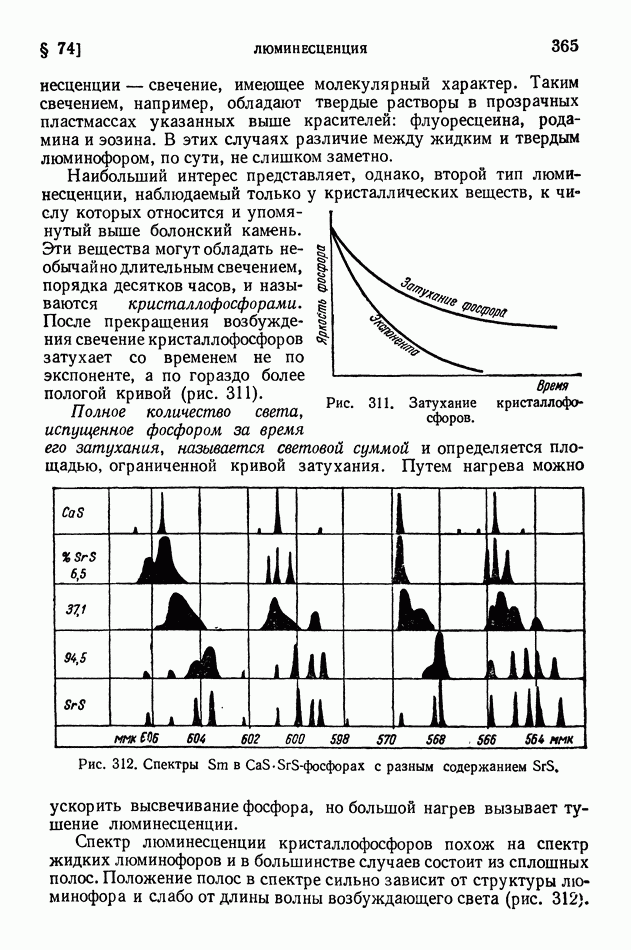
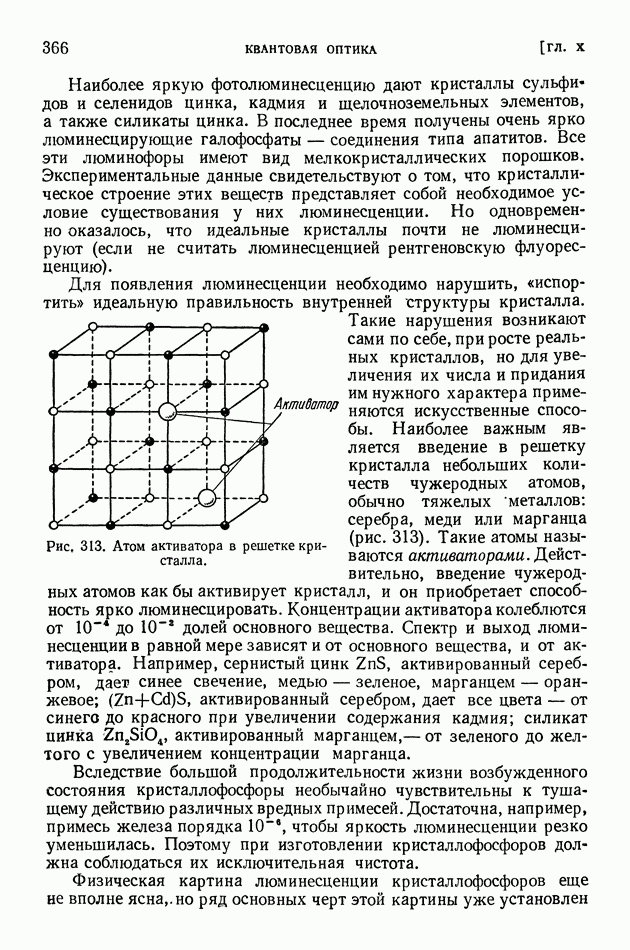
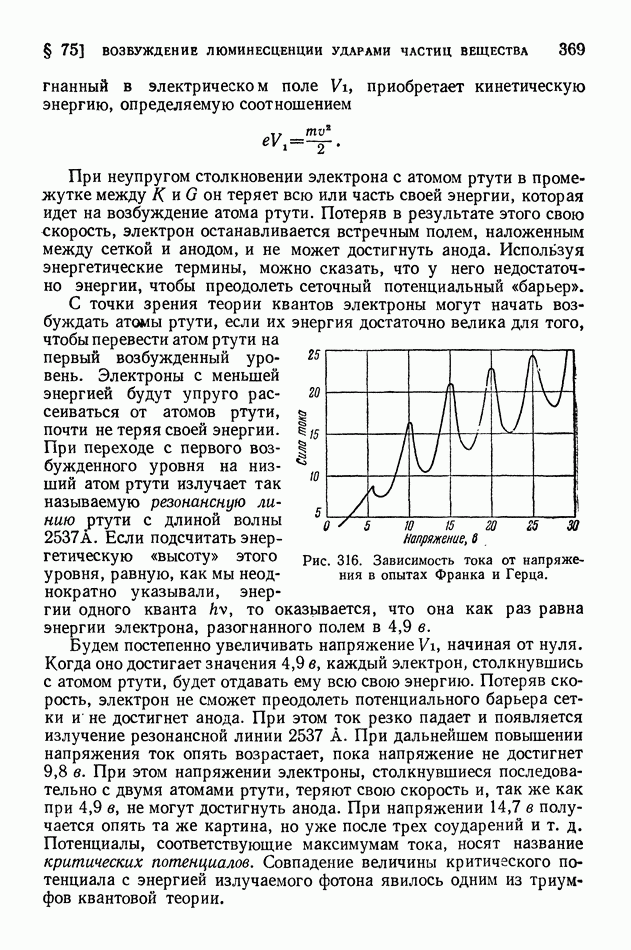
- § 74. Люминесценция
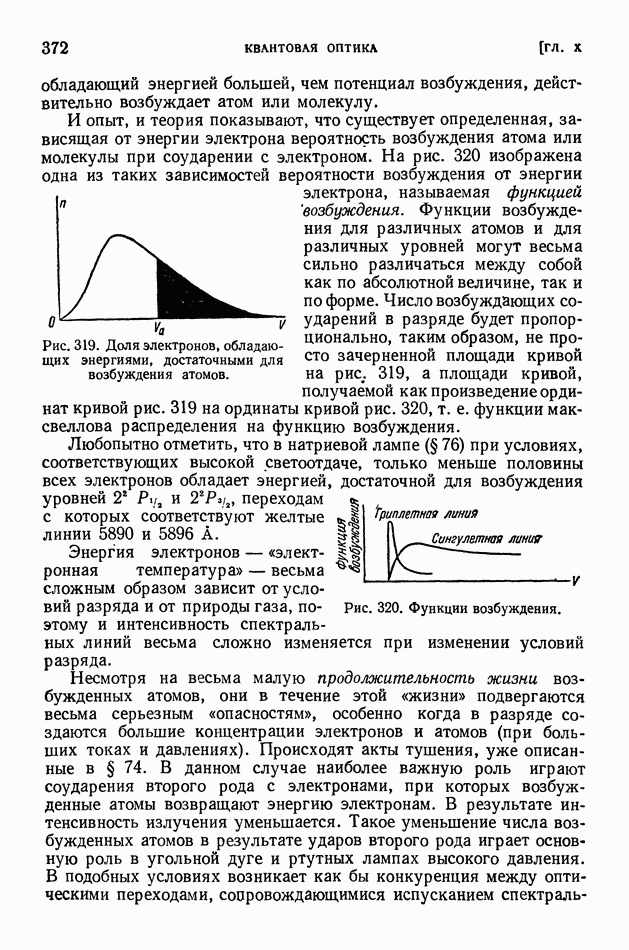
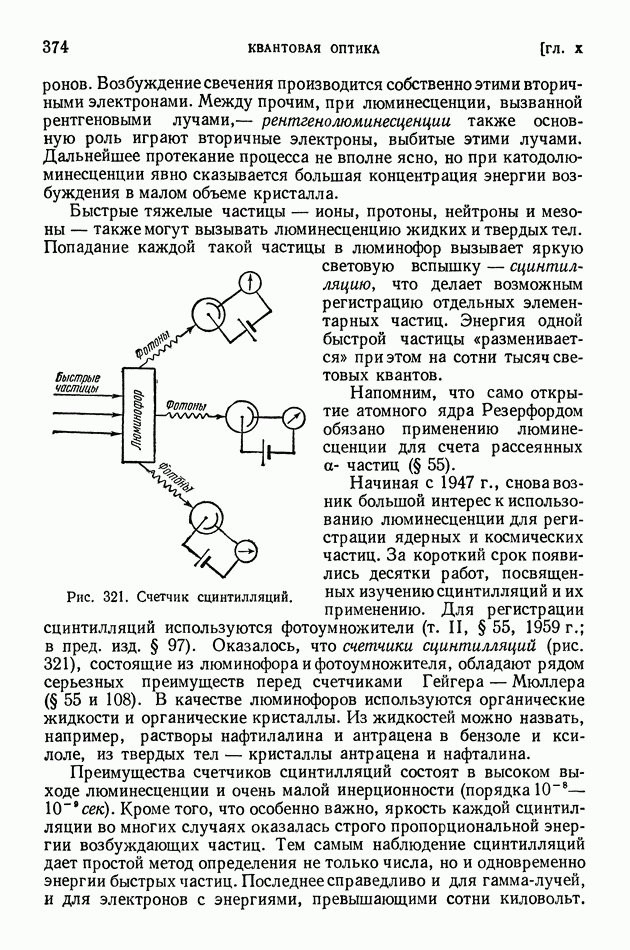
- § 75. Возбуждение люминесценции ударами частиц вещества
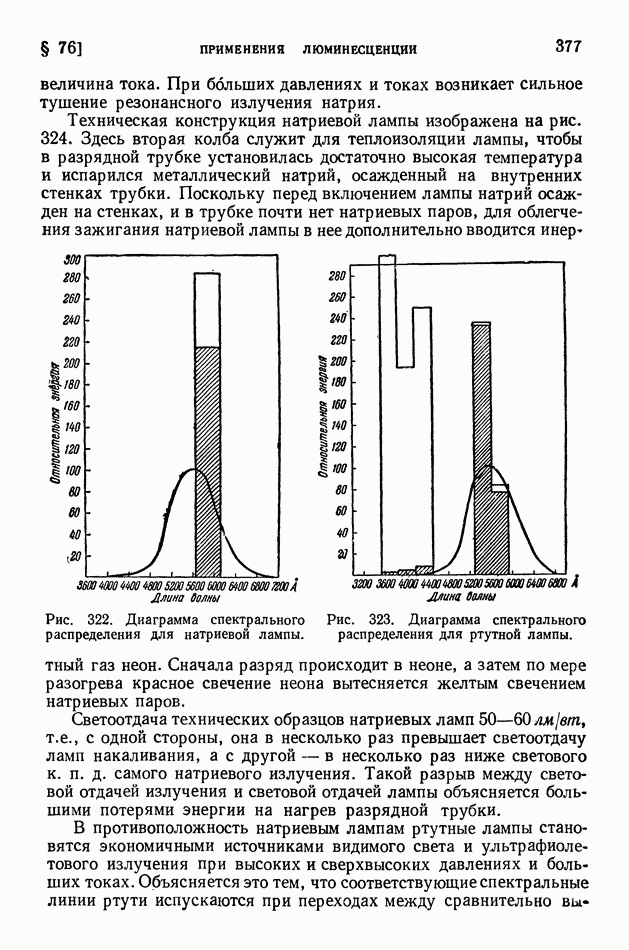
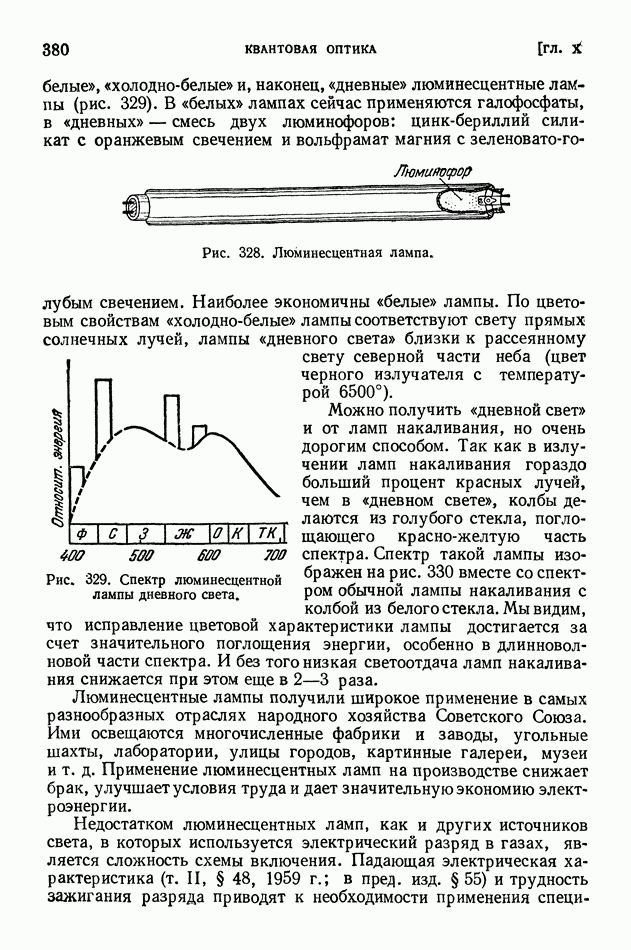
- § 76. Применения люминесценции
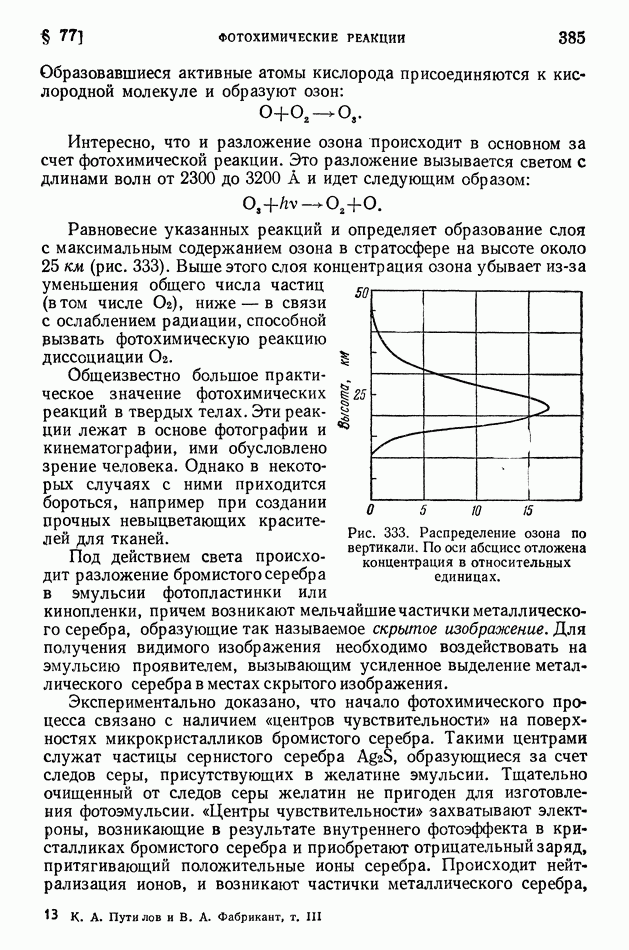
- § 77. Фотохимические реакции
- ГЛАВА XI. ЗАКОН ПРОПОРЦИОНАЛЬНОСТИ МАССЫ И ЭНЕРГИИ И РЕЛЯТИВИСТСКИЕ СООТНОШЕНИЯ
- § 78. Закон пропорциональности массы и энергии
- § 79. Предварительные замечания о релятивистских эффектах. Зависимость массы от скорости
- § 80. Корпускулярные свойства фотонов. Явление Комптона
- § 81. Вывод закона Эйнштейна сложения скоростей из закона пропорциональности массы и энергии и законов сохранения энергии или количества движения
- § 82. Две трактовки закона пропорциональности массы и энергии и уточнение закона тяготения
- § 83. Красное смещение спектральных линий. Поперечный эффект Доплера
- § 84. Влияние гравитационного поля на скорость света в вакууме и показатель преломления вакуума
- ЧАСТЬ ШЕСТАЯ. ЯДЕРНАЯ ФИЗИКА
- § 85. Заряд и масса ядра. Масс-спектральный анализ
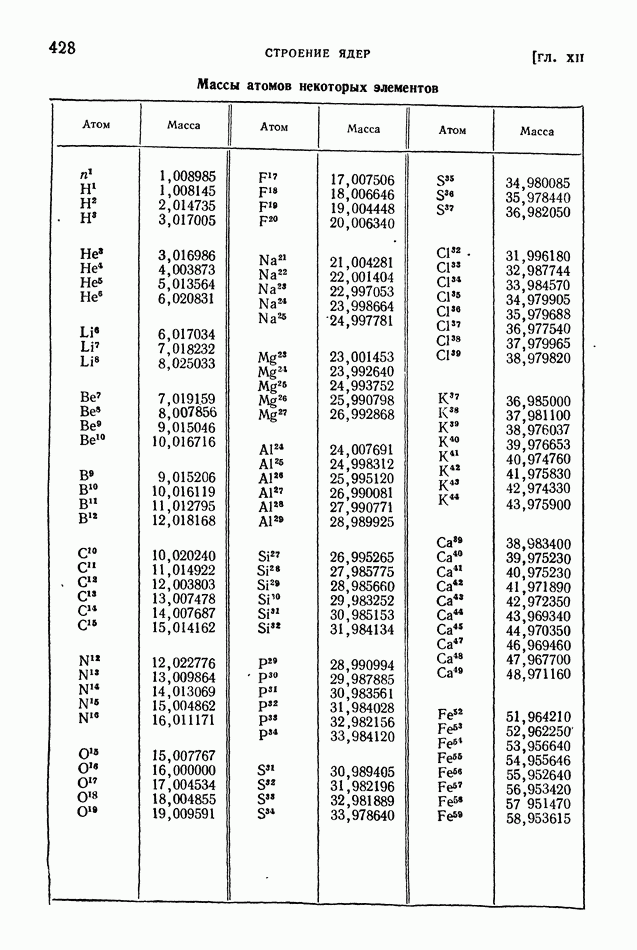
- § 86. Состав ядер. Изотопы. Атомные единицы массы и энергии
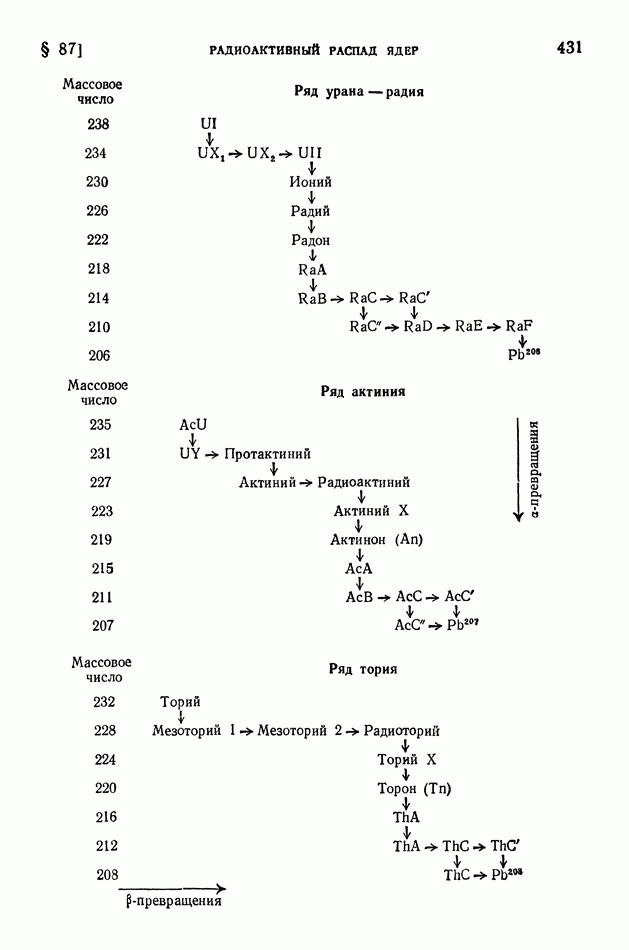
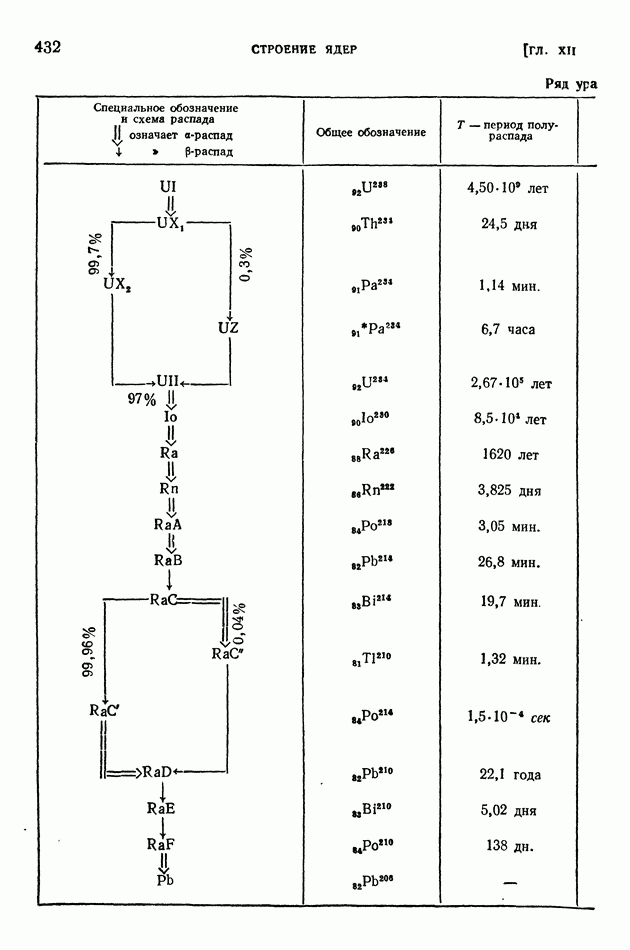
- § 87. Радиоактивный распад ядер. Закон радиоактивного смещения. Изомеры
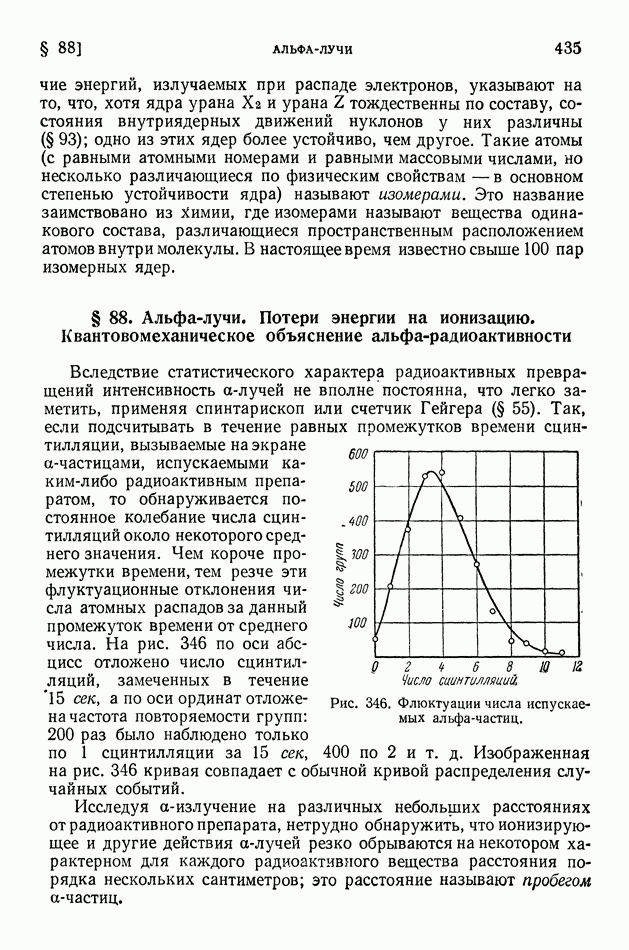
- § 88. Альфа-лучи. Потери энергии на ионизацию. Квантовомеханическое объяснение альфа-радиоактивности
- § 89. Бета- и гамма-лучи
- § 90. Искусственное расщепление ядер. Открытие нейтрона
- § 91. Открытие позитрона. Взаимопревращение фотонов определенной энергии и электронно-позитронных пар
- § 92. Индуцированная позитронная и электронная радиоактивность. Фоторасщепление ядер, K-захват
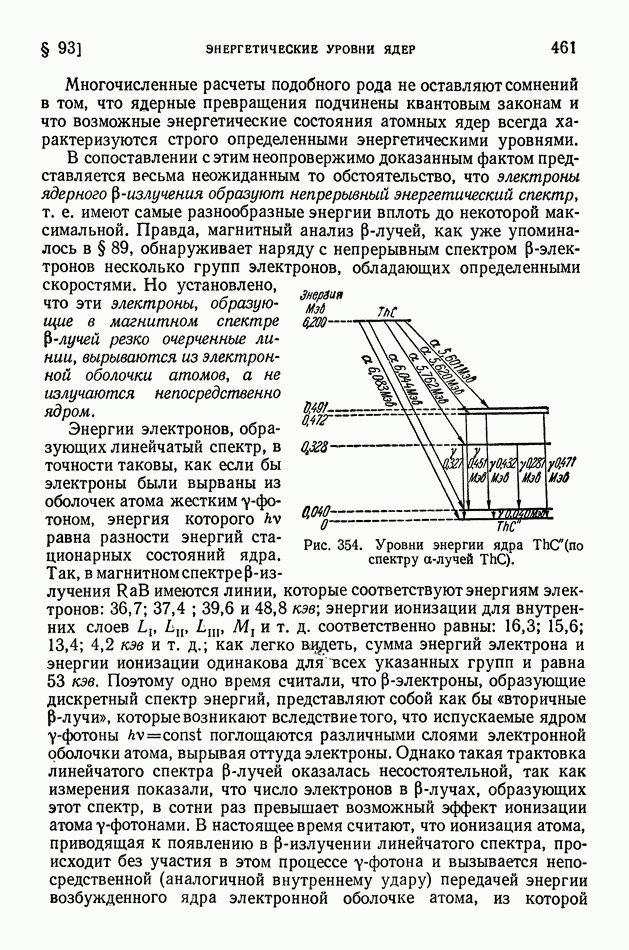
- § 93. Энергетические уровни ядер. Внутренняя конверсия. Нейтрино
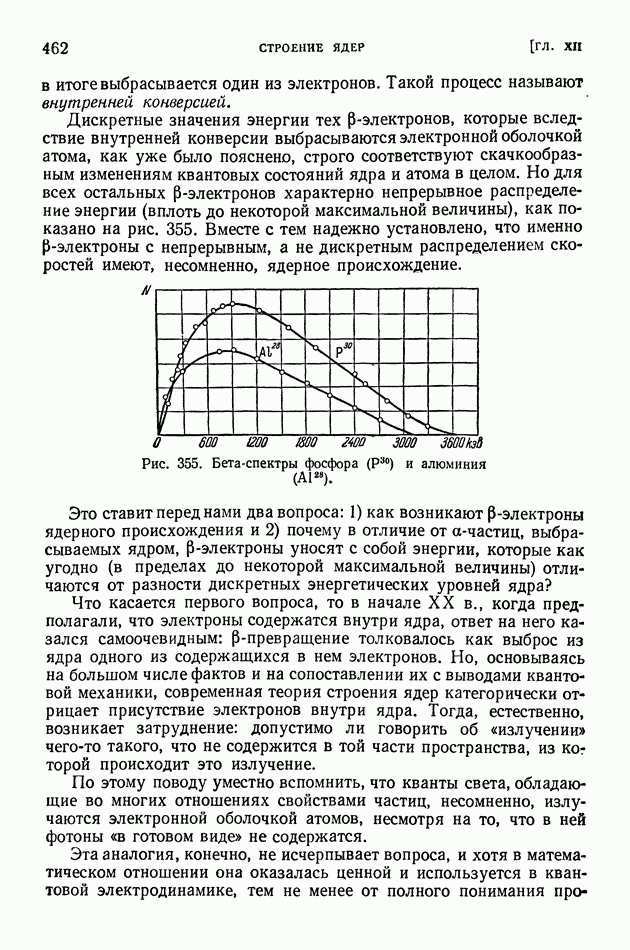
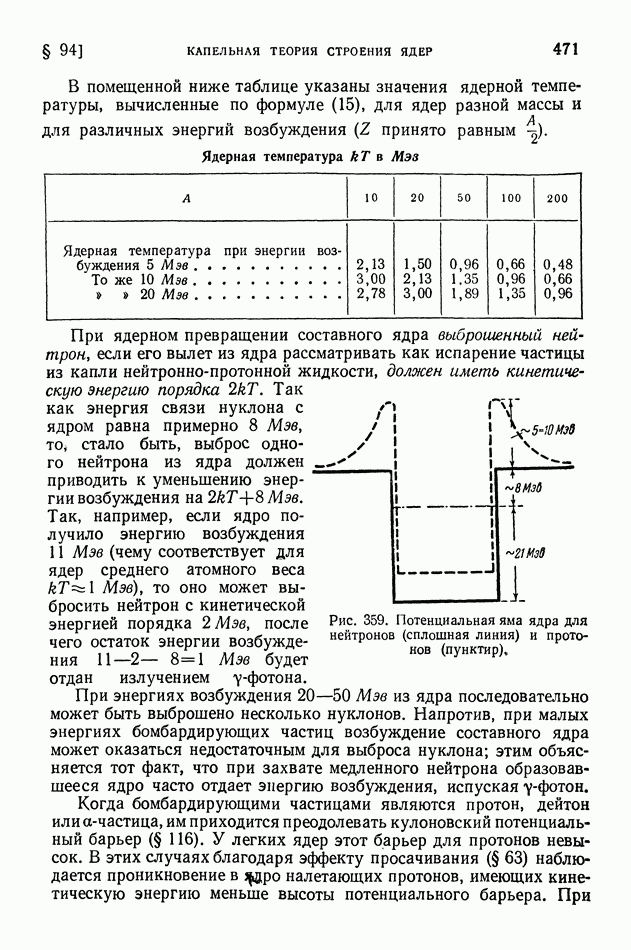
- § 94. Капельная теория строения ядер
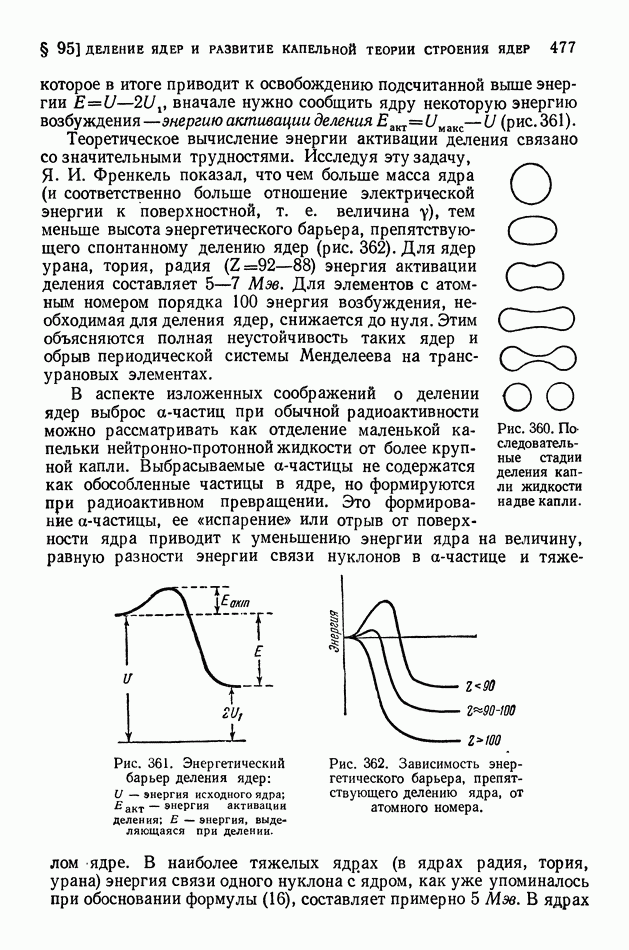
- § 95. Деление ядер и развитие капельной теории строения ядер
- ГЛАВА XIII. КОСМИЧЕСКИЕ ЛУЧИ
- § 96. Методы исследования и первые итоги изучения космических лучей
- § 97. Каскадное образование электронно-позитронных пар в космических лучах. Потери энергии электронами на тормозное излучение
- § 98. «мю»-мезоны. Зависимость времени жизни неустойчивых частиц от скорости движения
- § 99. «пи»-мезоны
- § 100. Взрывные ядерные ливни и их каскадное развитие в космических лучах
- § 101. Корпускулярный и энергетический спектр космических лучей. Происхождение космического излучения
- ГЛАВА XIV. ЭКСПЕРИМЕНТАЛЬНЫЕ СРЕДСТВА ЯДЕРНОЙ ФИЗИКИ
- § 102. Циклотроны
- § 103. Фазотроны
- § 104. Бетатроны
- § 105. Синхротроны и синхрофазотроны
- § 106. Линейные ускорители электронов и ионов
- § 107. Лабораторные источники нейтронов. Замедлители нейтронов в ядерных реакторах
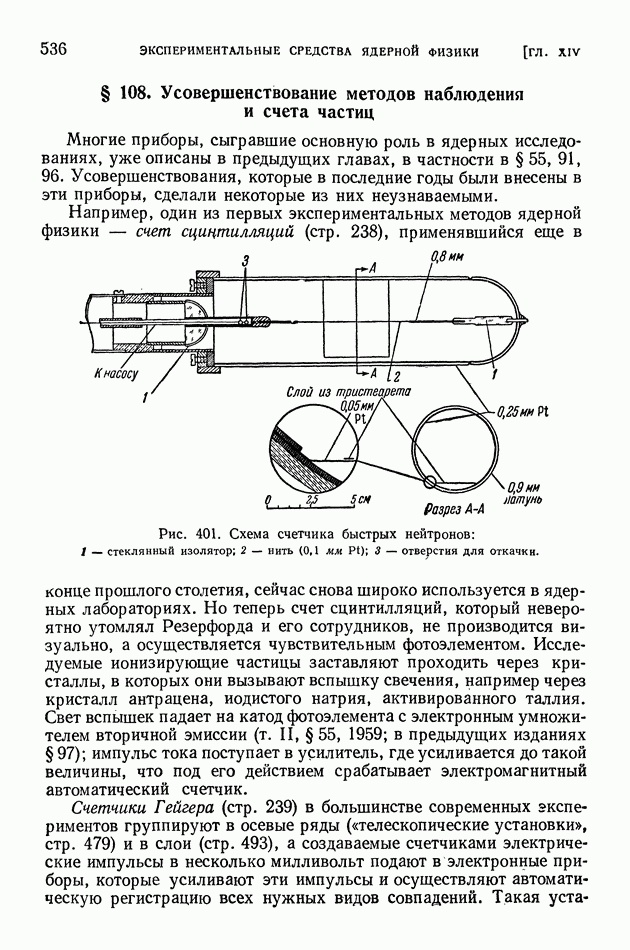
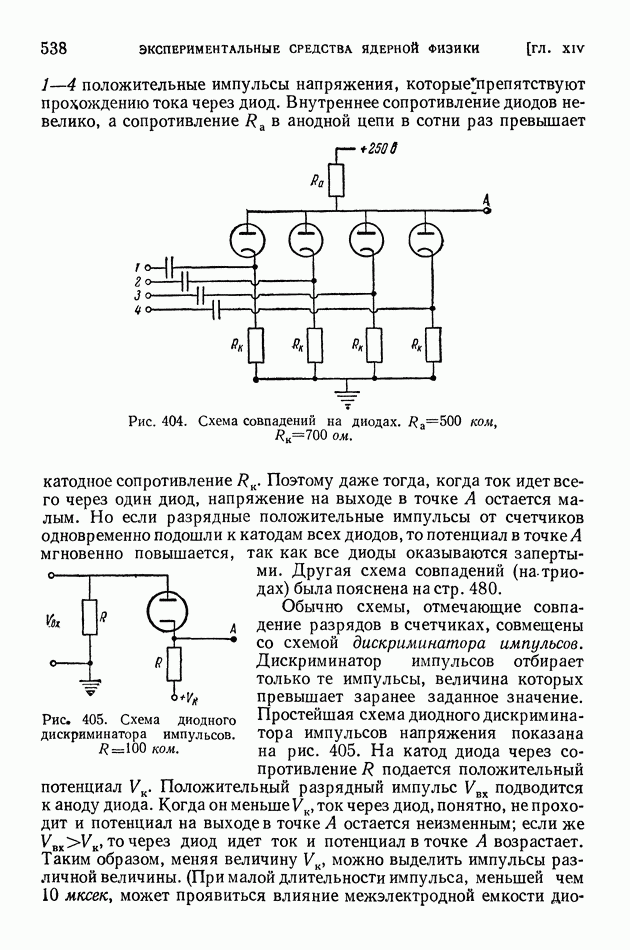
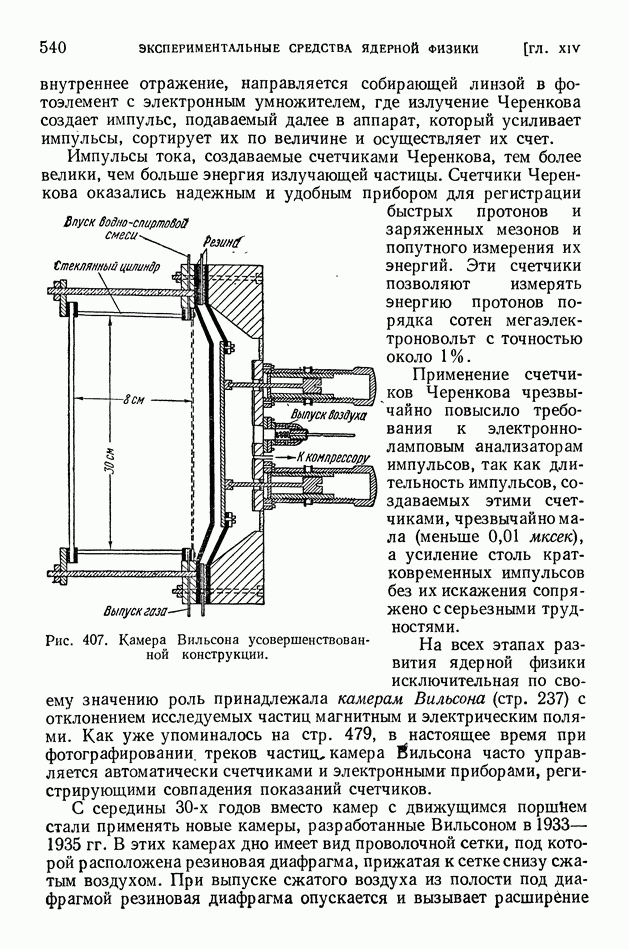
- § 108. Усовершенствование методов наблюдения и счета частиц
- ГЛАВА XV. ЯДЕРНЫЕ РЕАКЦИИ И АТОМНАЯ ЭНЕРГИЯ
- § 109. Основные виды и обозначения ядерных реакций. Конкурирующие процессы в ядерных реакциях
- § 110. Энергетический эффект, энергия возбуждения и порог ядерных реакций
- § 111. Превращения элементарных частиц
- § 112. Ядерные силы
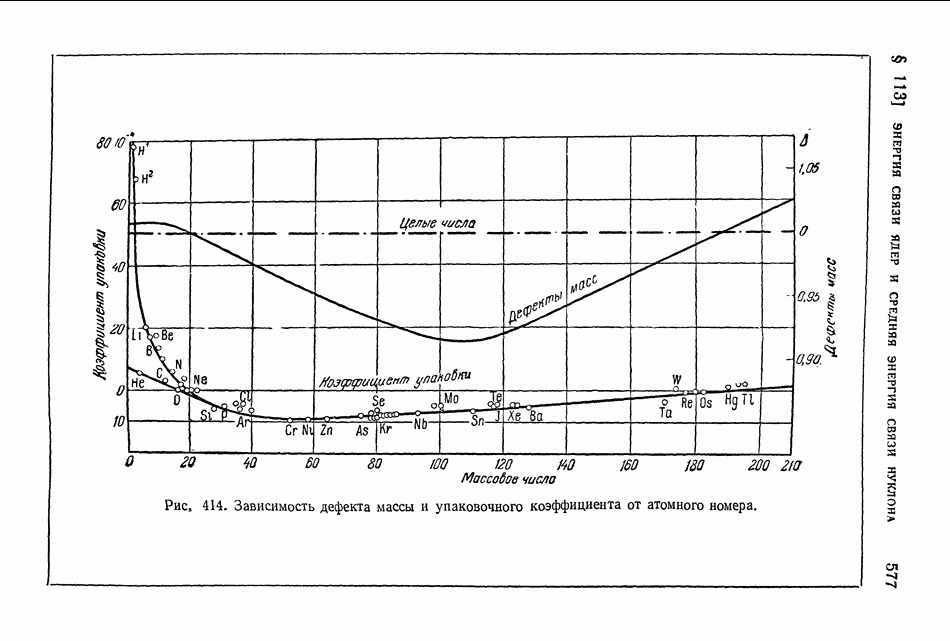
- § 113. Энергия связи ядер и средняя энергия связи нуклона
- § 114. Полуэмпирическая формула для энергии ядерной связи и для атомных энергий и масс
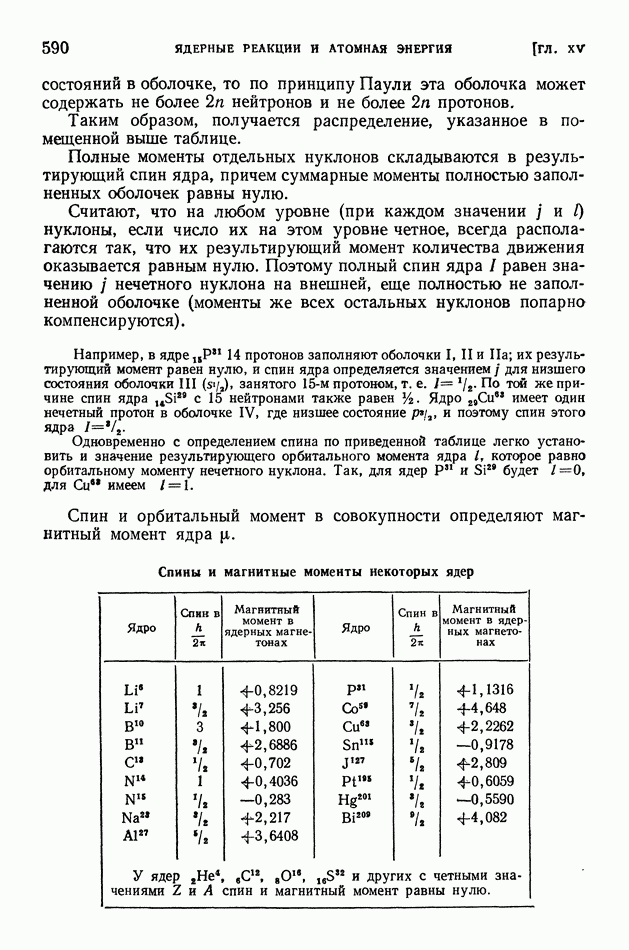
- § 115. Взаимосвязь энергии и строения ядер. Внутриядерное движение нуклонов и нуклонные оболочки. Спины и магнитные моменты ядер
- § 116. Энергия отделения частиц и анализ возможного хода ядерной реакции
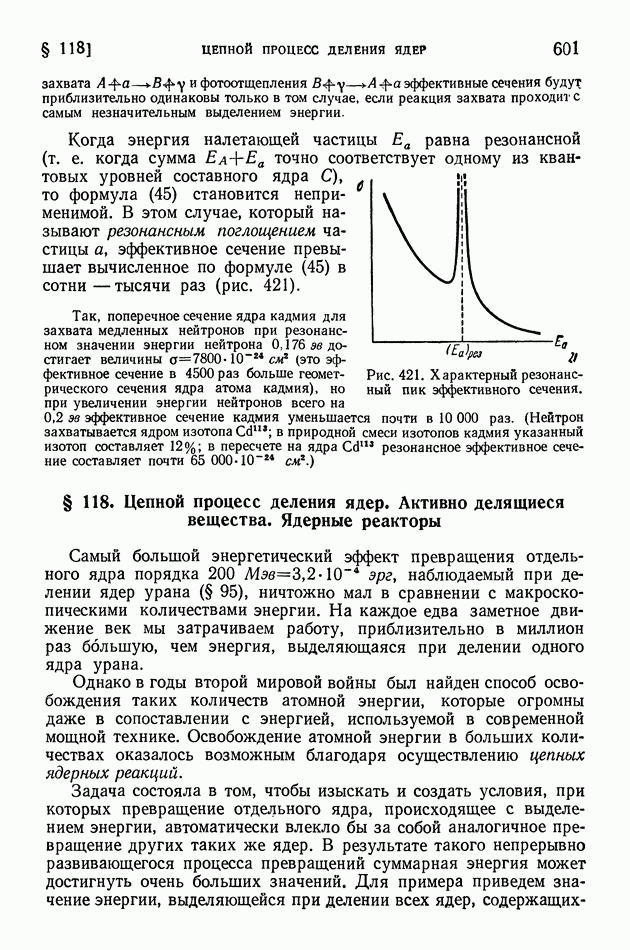
- § 117. Выход продуктов ядерной реакции. Эффективные сечения. Резонансные явления
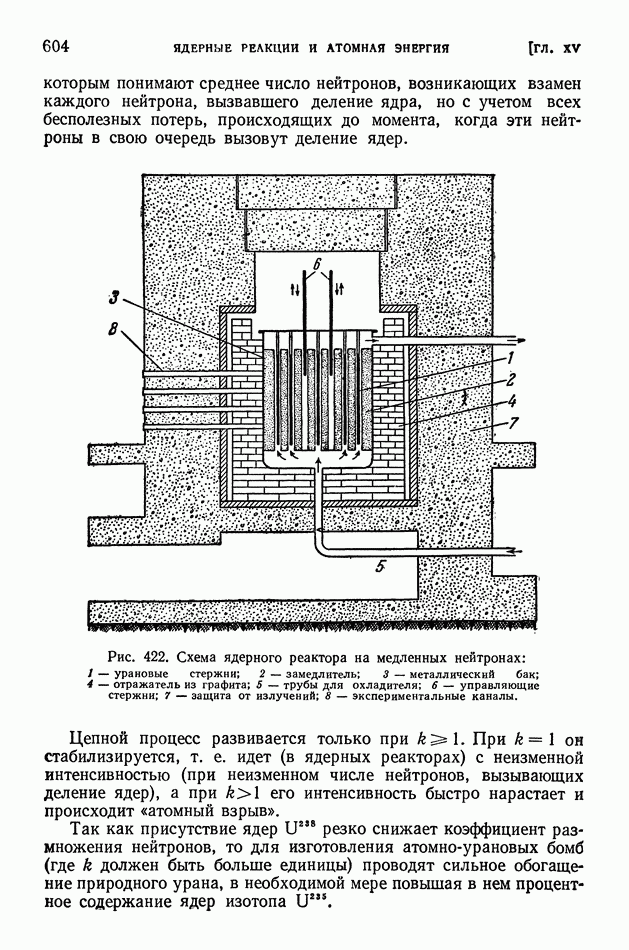
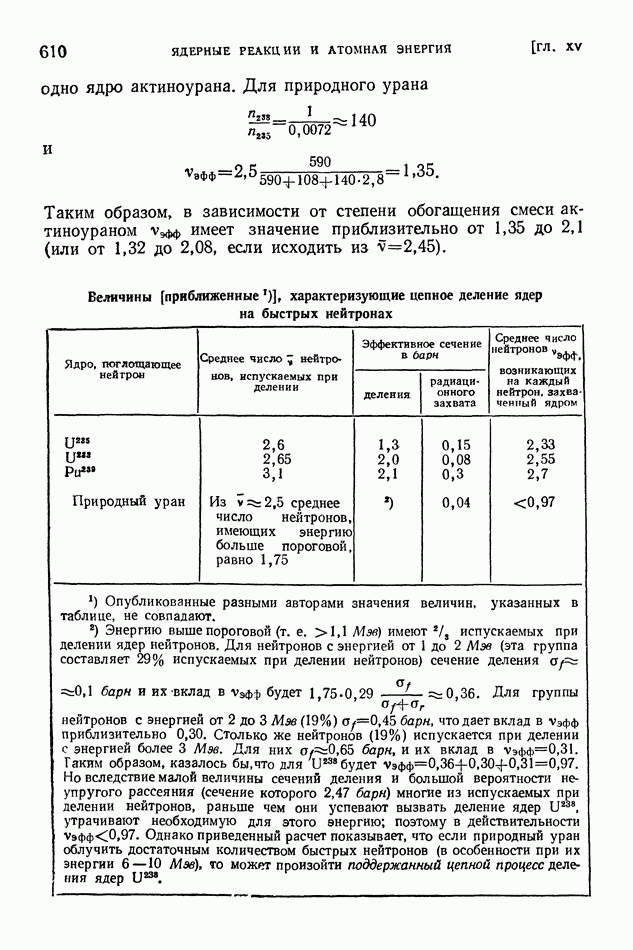
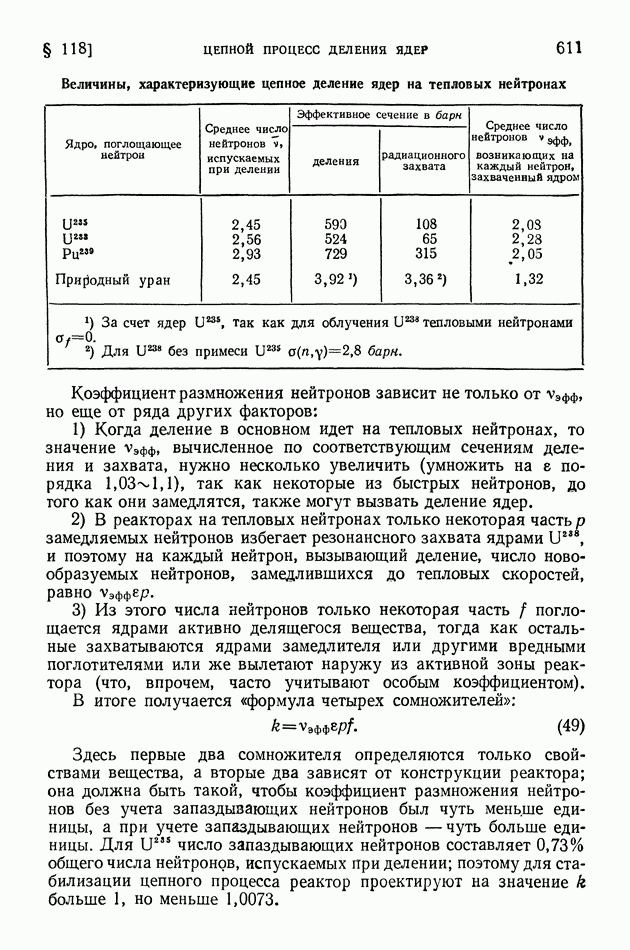
- § 118. Цепной процесс деления ядер. Активно делящиеся вещества. Ядерные реакторы
- § 119. Термоядерные реакции
- § 120. Применение ядерных реакций
- § 121. Ядерные реакции в звездах