| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 59. Квантовые числа
Найденные в предыдущем параграфе стационарные состояния атома водорода и водородоподобных ионов с учетом только круговых орбит определяются одним квантовым числом. Теория Бора была в дальнейшем развита Зоммерфельдом, который показал, что при полном вычислении стационарных состояний должны учитываться не только круговые, но и эллиптические орбиты, а также и та пространственная ориентация, которую орбиты могут принимать в магнитном поле. Все это привело к введению в теорию новых квантовых чисел. Те же квантовые числа, что и в теории Бора — Зоммерфельда, но в иной трактовке получаются при наиболее строгом вычислении стационарных состояний по методу, установленному (с 1926 г.) квантовой (волновой) механикой.
Для энергетических уровней водородоподобных ионов вычисления, проведенные с учетом эллиптичности орбит, а также и вычисления, основанные на волновой механике, дают ту же формулу, которая при простейших предположениях была выведена в предыдущем параграфе:

Квантовое число  определяющее дискретный ряд энергетических уровней, называют главным квантовым числом. В теории Бора — Зоммерфельда этим числом определяются также возможные значения больших полуосей эллиптических орбит [формула (10)]
определяющее дискретный ряд энергетических уровней, называют главным квантовым числом. В теории Бора — Зоммерфельда этим числом определяются также возможные значения больших полуосей эллиптических орбит [формула (10)]

Момент количества движения  (для круговых орбит
(для круговых орбит  в теории Бора — Зоммерфельда при учете эллиптических орбит определяется не главным квантовым числом, а другим квантовым числом
в теории Бора — Зоммерфельда при учете эллиптических орбит определяется не главным квантовым числом, а другим квантовым числом  которое называют квантовым числом орбитального момента, побочным или азимутальным квантовым числом. Согласно этой теории момент количества движения, который мы обозначим определяется формулой
которое называют квантовым числом орбитального момента, побочным или азимутальным квантовым числом. Согласно этой теории момент количества движения, который мы обозначим определяется формулой

здесь квантовое число I при данном  может принимать следующие значения:
может принимать следующие значения: 

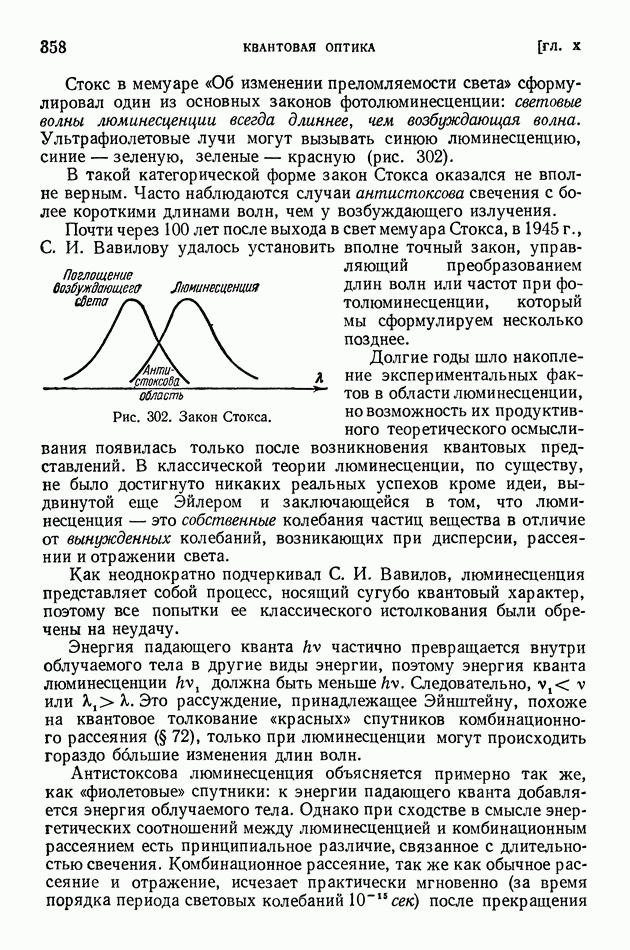
Рис. 230. Орбиты электрона при  радиус первой боровской орбиты.
радиус первой боровской орбиты.
Возможные значения малых полуосей  эллиптических орбит зависят от главного и побочного квантовых чисел
эллиптических орбит зависят от главного и побочного квантовых чисел

Таким образом, для электрона, находящегося в водородоподобном ионе на  энергетическом уровне, оказываются возможными: одна круговая орбита (при
энергетическом уровне, оказываются возможными: одна круговая орбита (при  эллиптических орбит с различным отношением полуосей. Например, при
эллиптических орбит с различным отношением полуосей. Например, при  возможны орбиты, показанные на рис. 230.
возможны орбиты, показанные на рис. 230.
Значения побочного квантового числа часто обозначают буквами:

Когда движение электрона характеризуется значением квантового числа  то электрон называют
то электрон называют  -электроном и т. д. (почему установилась такая традиция, пояснено в § 67).
-электроном и т. д. (почему установилась такая традиция, пояснено в § 67).
Следует отметить, что в настоящее время в связи с выводами, к которым приводит квантовая механика, геометрические заключения теории Бора-Зоммерфельда рассматривают только как приблизительную иллюстрацию к существенно иной трактовке движения электронов в атоме. По волновой механике орбитальный момент количества движения электрона определяется не соотношением (11), а соотношением

Это выражение существенно отличается от предыдущего, в особенности тем, что оно свидетельствует о возможности таких движений электрона, при которых (для  орбитальный момент количества движения электрона равен нулю. По первоначальным представлениям теории Бора такое движение электрона должно было бы соответствовать, очевидно, невозможному прохождению электрона через ядро (§ 67).
орбитальный момент количества движения электрона равен нулю. По первоначальным представлениям теории Бора такое движение электрона должно было бы соответствовать, очевидно, невозможному прохождению электрона через ядро (§ 67).
Третье квантовое число  (не путать с обозначением массы) определяет пространственное распределение траекторий движения электрона (в теории Бора — пространственную ориентацию орбит). Квантовое число
(не путать с обозначением массы) определяет пространственное распределение траекторий движения электрона (в теории Бора — пространственную ориентацию орбит). Квантовое число  называют магнитным квантовым числом, так как от этого числа зависит магнитный момент, создаваемый при движении электрона по, орбите (§ 70).
называют магнитным квантовым числом, так как от этого числа зависит магнитный момент, создаваемый при движении электрона по, орбите (§ 70).
При действии внешнего магнитного поля на атом могут осуществляться только такие ориентации орбит, при которых проекция вектора момента количества движения  на направление оси
на направление оси  совпадающее с направлением магнитного поля, кратна (принцип пространственного квантования):
совпадающее с направлением магнитного поля, кратна (принцип пространственного квантования):

где  положительное или отрицательное целое число, не превышающее по абсолютной величине I:
положительное или отрицательное целое число, не превышающее по абсолютной величине I:

Таким образом, при данных  электрон в атоме, находящемся в магнитном поле, может двигаться по
электрон в атоме, находящемся в магнитном поле, может двигаться по  орбитам, различающимся своей ориентацией по отношению к направлению магнитного поля.
орбитам, различающимся своей ориентацией по отношению к направлению магнитного поля.
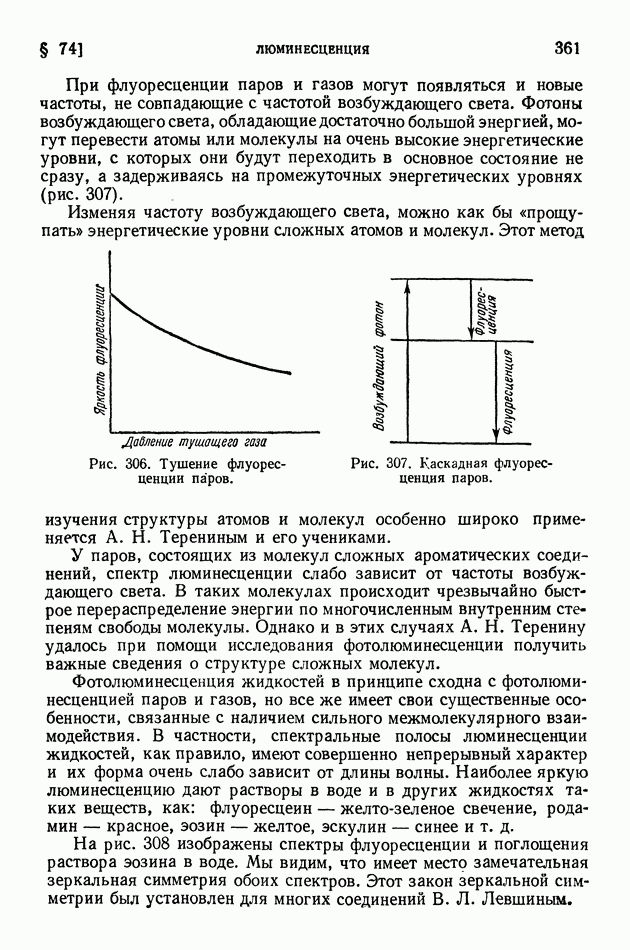
Выражение (14) для проекции момента количества движения, но при ином представлении о движении электрона в атоме, обобщено волновой механикой для любого произвольно выбираемого направления оси квантования (в случае, когда магнитное поле отсутствует). Рис. 231 иллюстрирует принцип пространственного квантования.
Итак, описание движения электрона может быть осуществлено с помощью трех квантовых чисел:  Однако такое описание является неполным. Для того чтобы сделать его полным, нужно ввести еще одно квантовое число: Опытные основания введения этого числа будут подробно рассмотрены ниже. Квантовое число
Однако такое описание является неполным. Для того чтобы сделать его полным, нужно ввести еще одно квантовое число: Опытные основания введения этого числа будут подробно рассмотрены ниже. Квантовое число  называемое спиновым числом, может принимать только два значения: Согласно наглядной, но грубой трактовке оно определяет направление вращения электрона вокруг собственной оси (т. II, стр. 327). С этим вращением электрона связаны его собственные механический (момент количества движения) и магнитный моменты, причем проекция собственного механического момента, называемого также спином электрона
называемое спиновым числом, может принимать только два значения: Согласно наглядной, но грубой трактовке оно определяет направление вращения электрона вокруг собственной оси (т. II, стр. 327). С этим вращением электрона связаны его собственные механический (момент количества движения) и магнитный моменты, причем проекция собственного механического момента, называемого также спином электрона  на ось
на ось  может принимать два значения:
может принимать два значения:


Рис. 231, Возможные значения проекций орбитального момента на направление магнитного поля для случаев 
Таким образом, электрон в атоме обладает орбитальным и собственным моментами количества движения. Можно произвести сложение этих двух векторов и получить вектор полного момента количества движения. Согласно квантовой механике полный момент количества движения электрона  определяется формулой (13), в которой целочисленные значения I должны быть заменены полуцелыми:
определяется формулой (13), в которой целочисленные значения I должны быть заменены полуцелыми:

(для обоих сомножителей под радикалом берутся одинаковые знаки, т. е.  или
или  . Отсюда следует, что при данном
. Отсюда следует, что при данном  величина
величина  может принимать два значения.
может принимать два значения.
Если ввести квантовое число называемое внутренним квантовым числом:

то полный момент количества движения, равный векторной сумме орбитального и собственного моментов, будет определяться формулой

Во внешнем магнитном поле проекция вектора полного момента количества движения на направление поля может принимать  значений:
значений:

где

или

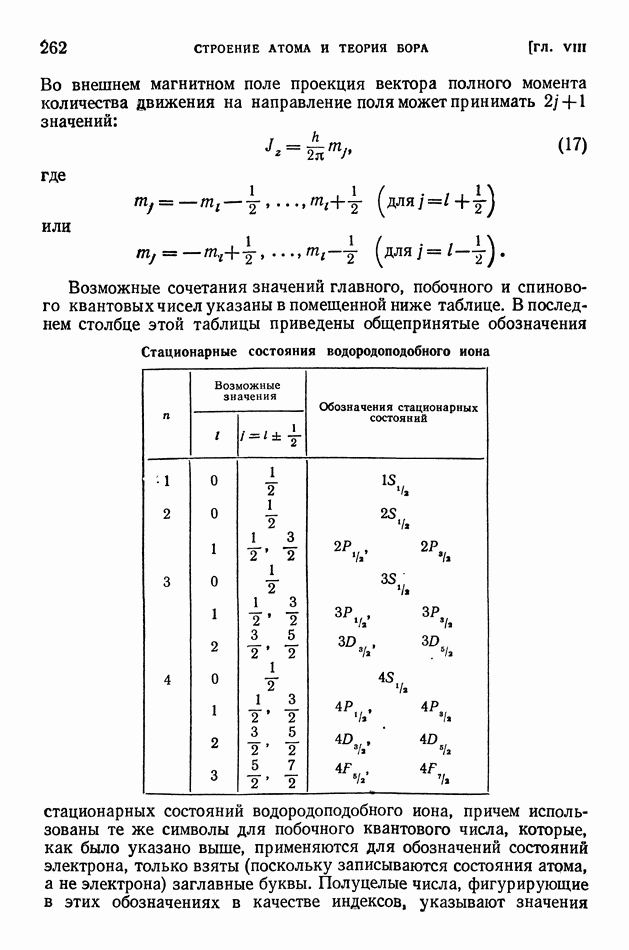
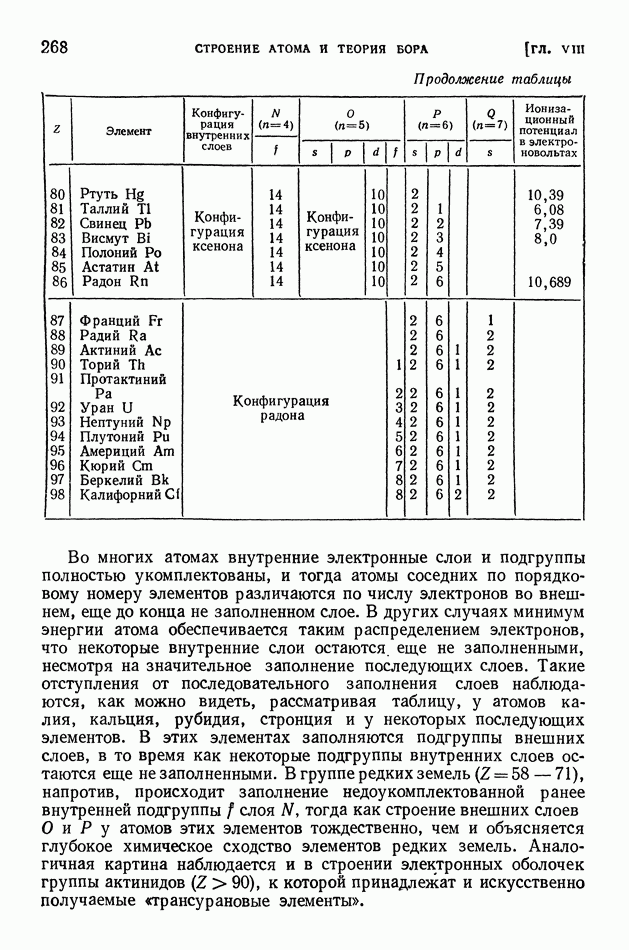
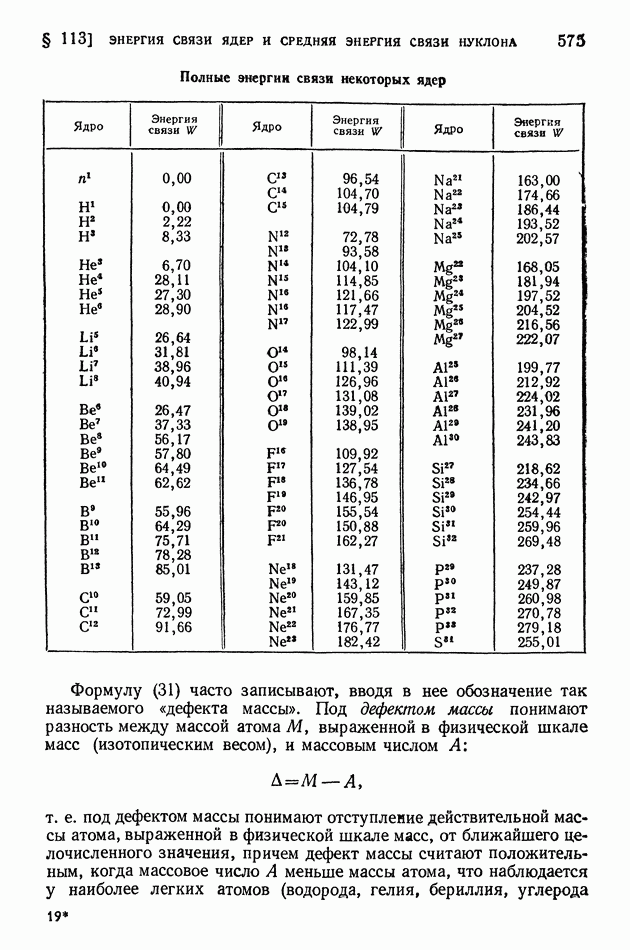
Возможные сочетания значений главного, побочного и спинового квантовых чисел указаны в помещенной ниже таблице.
Стационарные состояния водородоподобного иона
(см. скан)
В последнем столбце этой таблицы приведены общепринятые обозначения стационарных состояний водородоподобного иона, причем использованы те же символы для побочного квантового числа, которые, как было указано выше, применяются для обозначений состояний электрона, только взяты (поскольку записываются состояния атома, а не электрона) заглавные буквы. Полуцелые числа, фигурирующие в этих обозначениях в качестве индексов, указывают значения
числа  , определяющего по формуле (16) полный момент количества движения.
, определяющего по формуле (16) полный момент количества движения.
В формулу для уровней энергии атома водорода и водородоподобных ионов входит только главное квантовое число, т.е. энергия уровня не зависит от значений других квантовых чисел. Более строгое рассмотрение с учетом спина электрона и релятивистской зависимости его массы от скорости приводит к появлению в выражении для энергии уровня дополнительного члена, который зависит не только от  но и от квантового числа полного момента
но и от квантового числа полного момента 
Так как спин электрона может быть ориентирован только параллельно или антипараллельно вектору орбитального момента, то для всех состояний электрона с  полный момент принимает два значения:
полный момент принимает два значения:  в результате чего каждый уровень, соответствующий этим состояниям, расщепляется на два. Уровни с
в результате чего каждый уровень, соответствующий этим состояниям, расщепляется на два. Уровни с  -состояния) оказываются нерасщепленными, так как для них орбитальный момент равен нулю. Описанное расщепление уровней приводит к тому, что спектральные линии атома водорода оказываются двойными, т. е. состоят из двух близко расположенных линий. Это явление, которое наблюдается при достаточной разрешающей силе приборов, получило название тонкой структуры спектра
-состояния) оказываются нерасщепленными, так как для них орбитальный момент равен нулю. Описанное расщепление уровней приводит к тому, что спектральные линии атома водорода оказываются двойными, т. е. состоят из двух близко расположенных линий. Это явление, которое наблюдается при достаточной разрешающей силе приборов, получило название тонкой структуры спектра
В сложных атомах возможны только определенные сочетания состояний движения отдельных электронов. В этом случае орбитальные моменты отдельных электронов складываются в полный орбитальный момент атома, который будет характеризоваться побочным квантовым числом  принимающим ряд целочисленных значений, определяемых значениями побочных квантовых чисел отдельных электронов. Спины отдельных электронов, которые могут быть ориентированы параллельно или антипараллельно друг другу, также складываются в полный спиновый момент атома.
принимающим ряд целочисленных значений, определяемых значениями побочных квантовых чисел отдельных электронов. Спины отдельных электронов, которые могут быть ориентированы параллельно или антипараллельно друг другу, также складываются в полный спиновый момент атома.
Энергетические состояния сложного атома (спектральные термы) зависят от полного орбитального и полного спинового моментов, причем в зависимости от взаимной ориентации орбитального и спинового моментов каждое энергетическое состояние расщепляется на ряд близко расположенных уровней, что приводит к появлению в спектрах сложных атомов тонкой структуры. Тонкая структура сложных атомов значительно сложнее, чем у атома водорода. Здесь некоторые спектральные линии состоят уже не из двух, а из нескольких компонент.
Детальное изучение спектров привело к обнаружению сверхтонкой структуры спектральных линий, связанной с влиянием атомного ядра на энергетические уровни атомов (§ 69), а также показало, что не все переходы электрона между энергетическими уровнями равновозможны. Правила, определяющие переходы, которые осуществляются в действительности (правила отбора), пояснены в § 67 и 68
| << Предыдущий параграф | Следующий параграф >> |
- ЧАСТЬ ЧЕТВЕРТАЯ. ОПТИКА
- § 2. Электромагнитная теория света
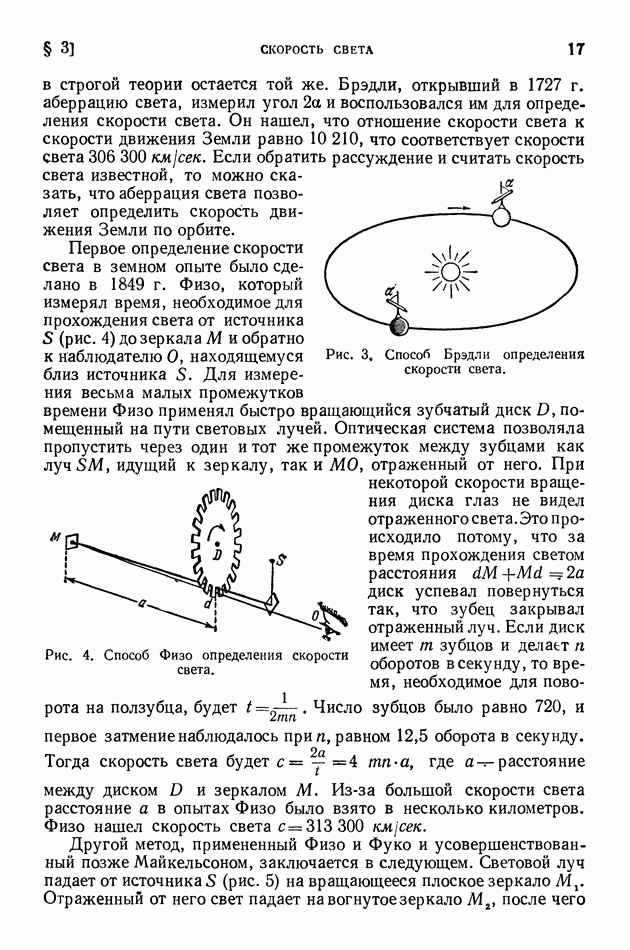
- § 3. Скорость света
- § 4. Опыт Майкельсона
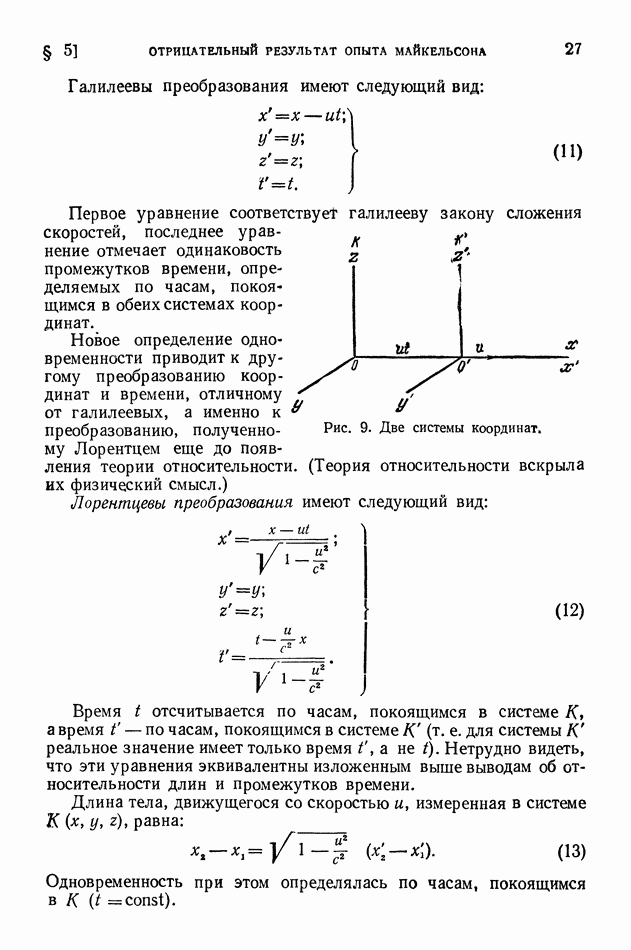
- § 5. Отрицательный результат опыта Майкельсона и теория относительности
- § 6. Некоторые замечания о теории относительности
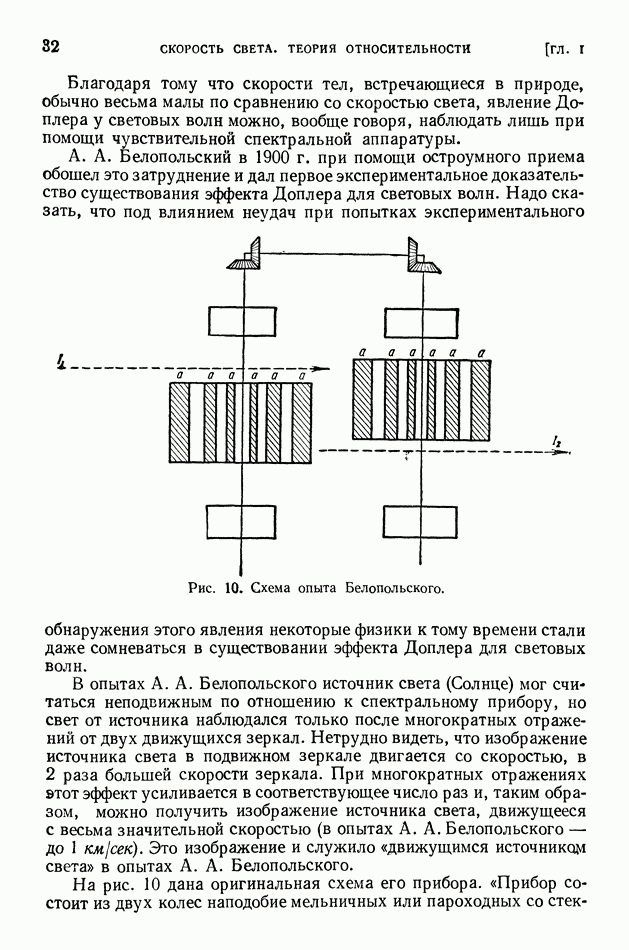
- § 7. Явление Доплера для световых волн
- ГЛАВА II. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
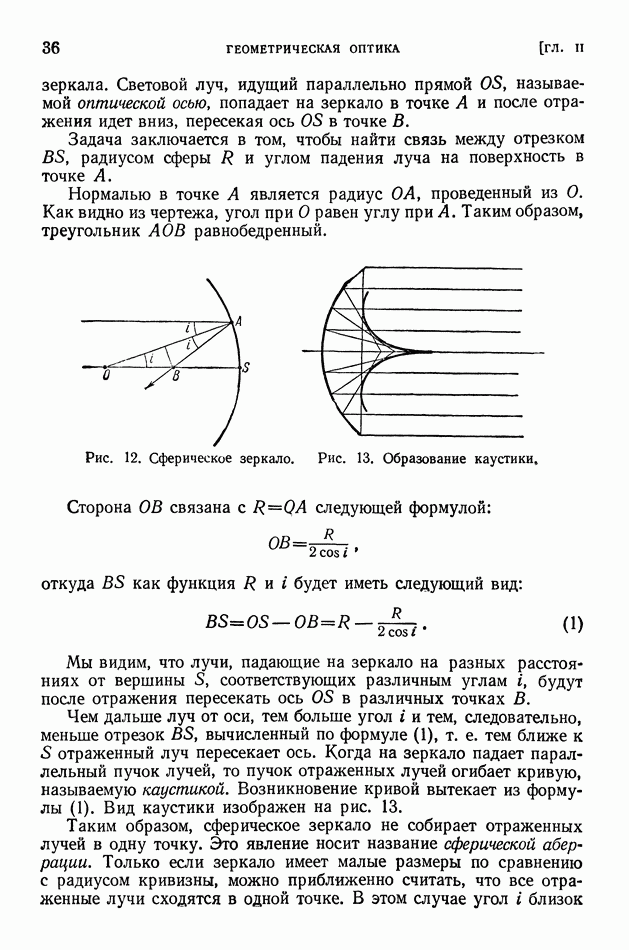
- § 8. Законы отражения и преломления света
- § 9. Линза
- § 10. Оптические системы
- § 11. Глаз как оптическая система
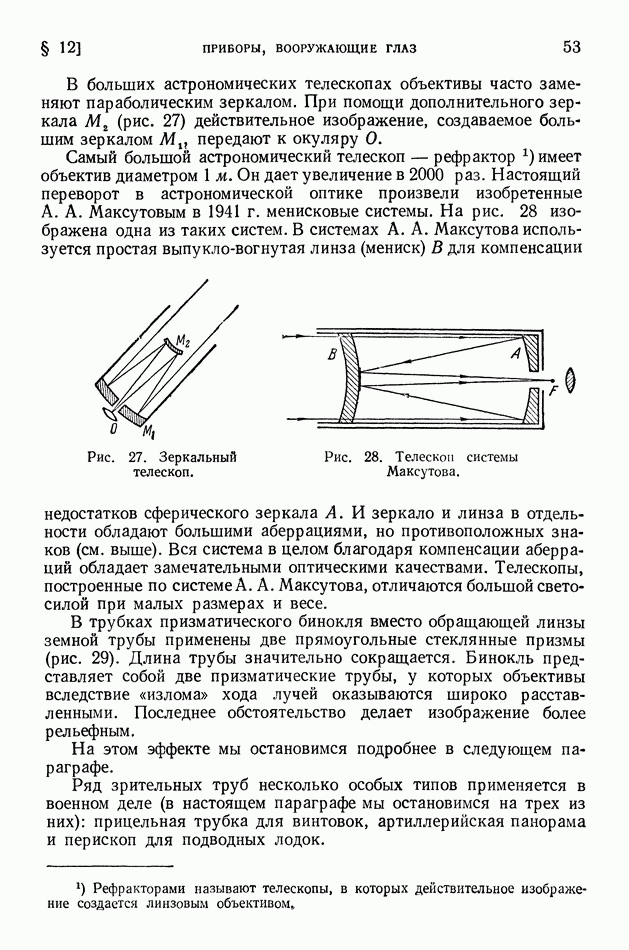
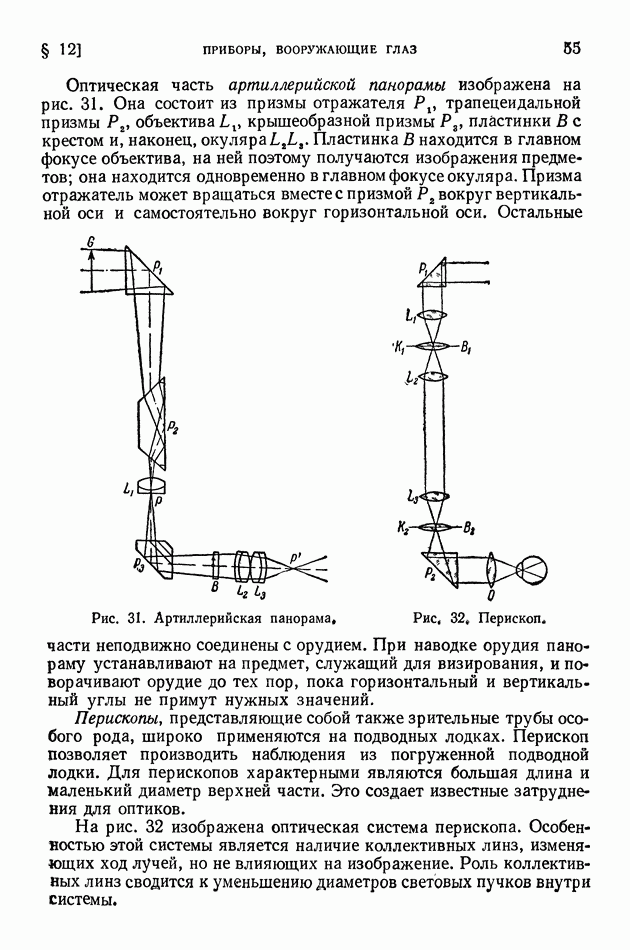
- § 12. Приборы, вооружающие глаз
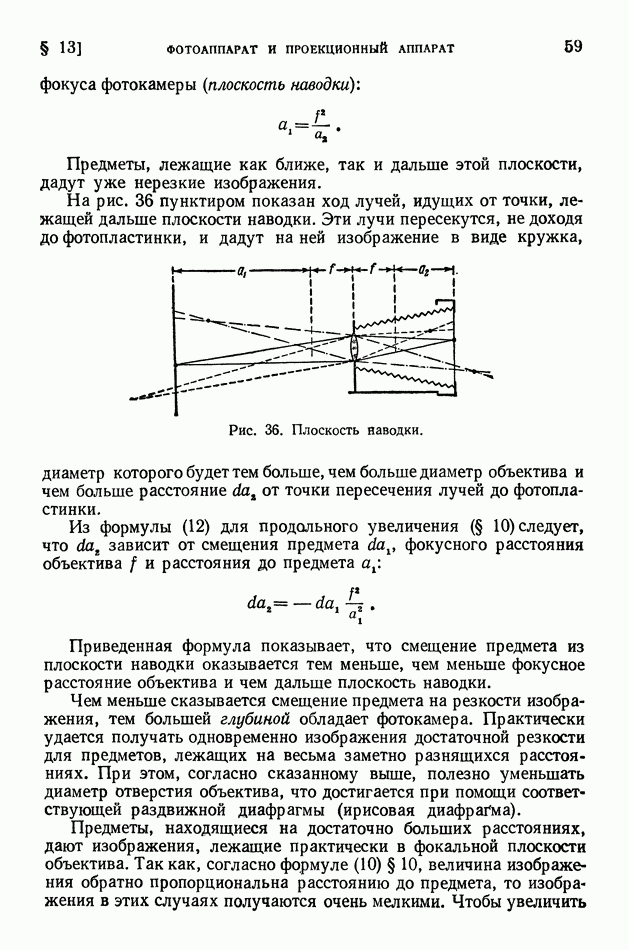
- § 13. Фотоаппарат и проекционный аппарат
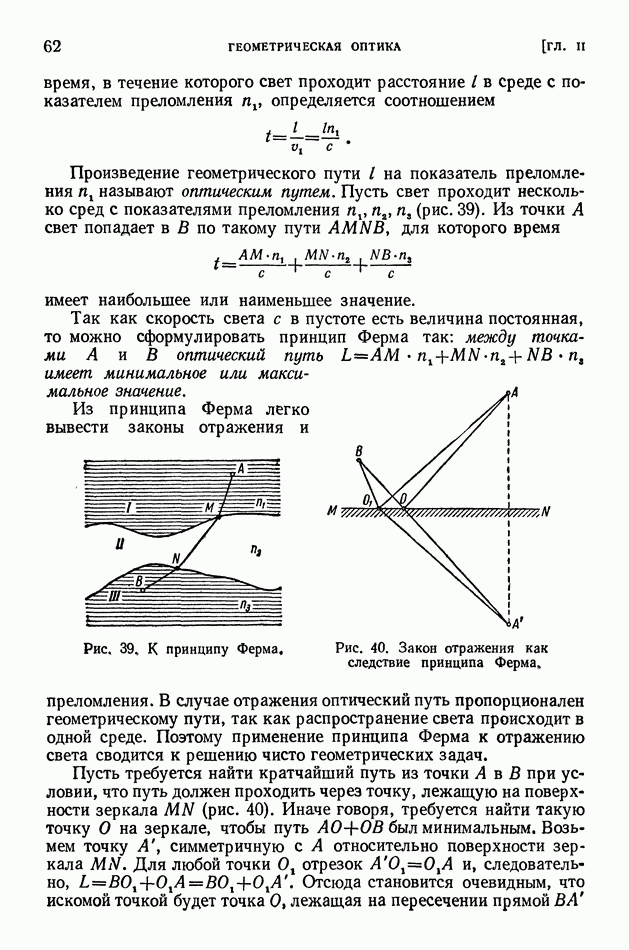
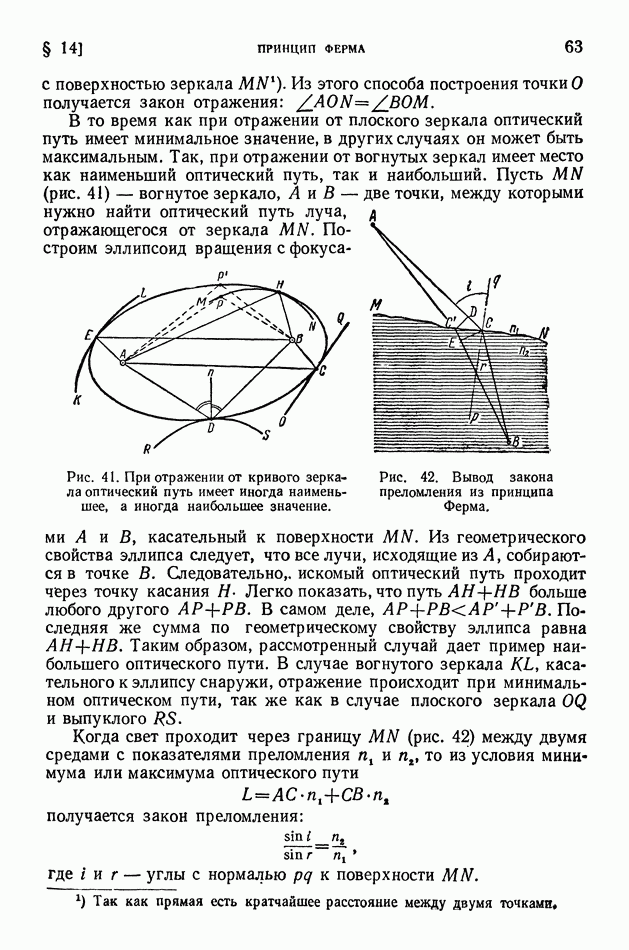
- § 14. Принцип Ферма
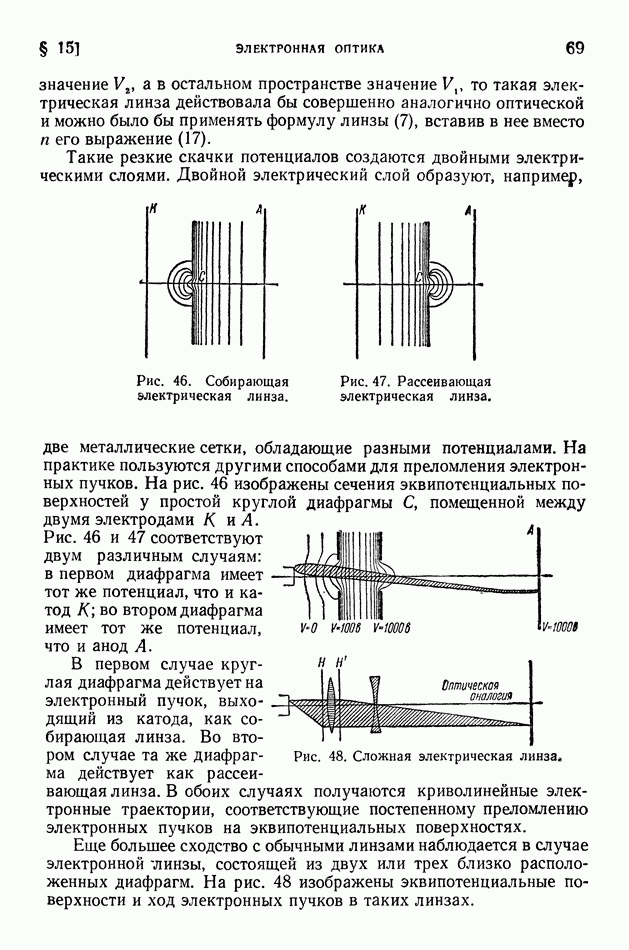
- § 15. Электронная оптика
- ГЛАВА III. ИНТЕРФЕРЕНЦИЯ СВЕТА
- § 16. Принцип суперпозиции. Когерентность
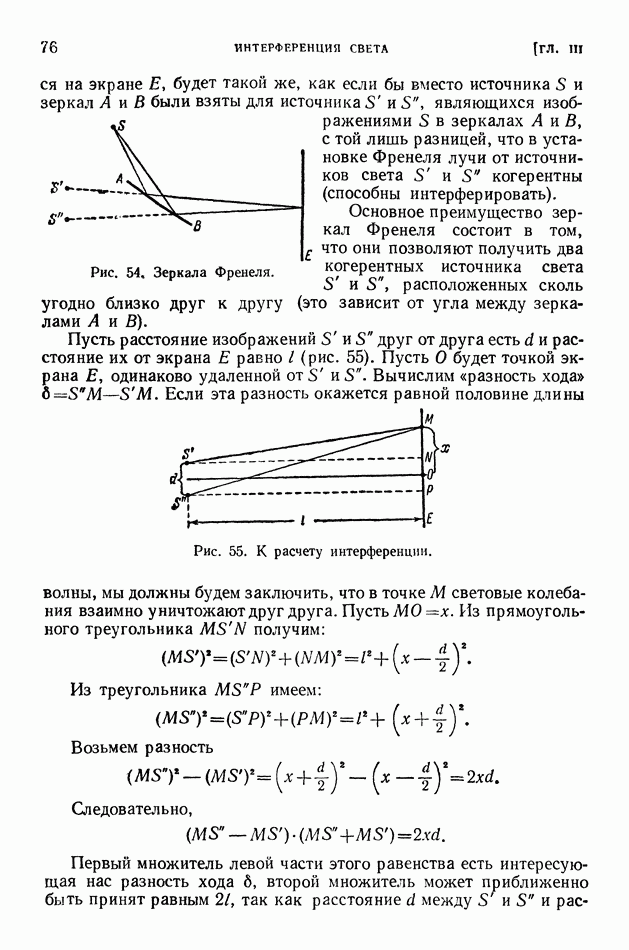
- § 17. Зеркала Френеля
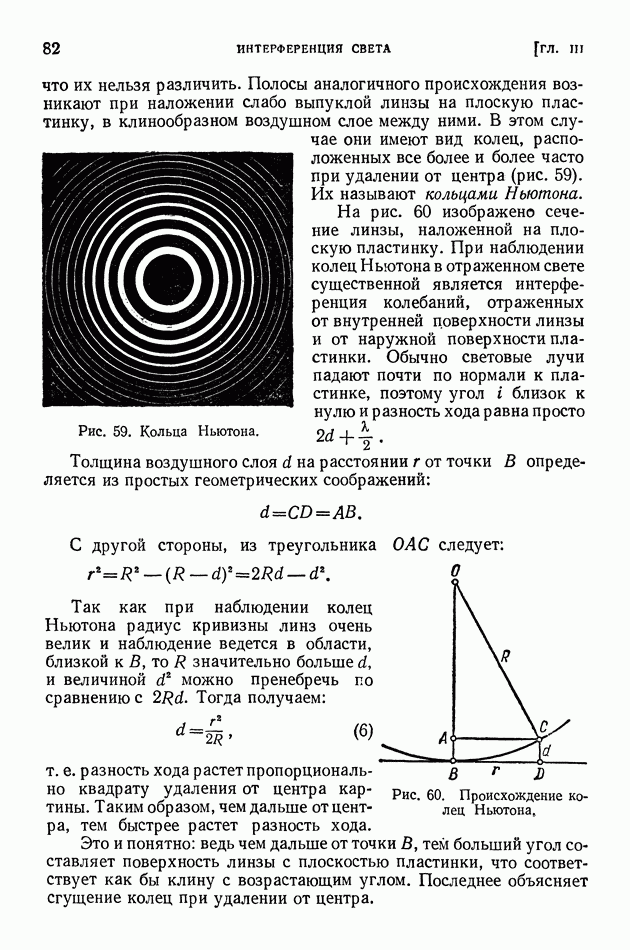
- § 18. Цвета тонких пленок. Полосы равной толщины
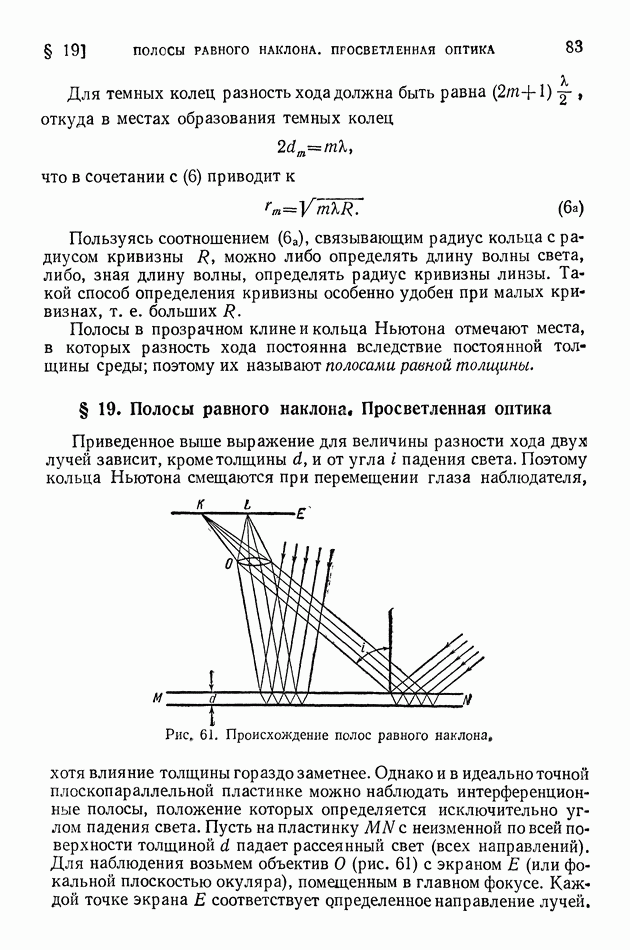
- § 19. Полосы равного наклона. Просветленная оптика
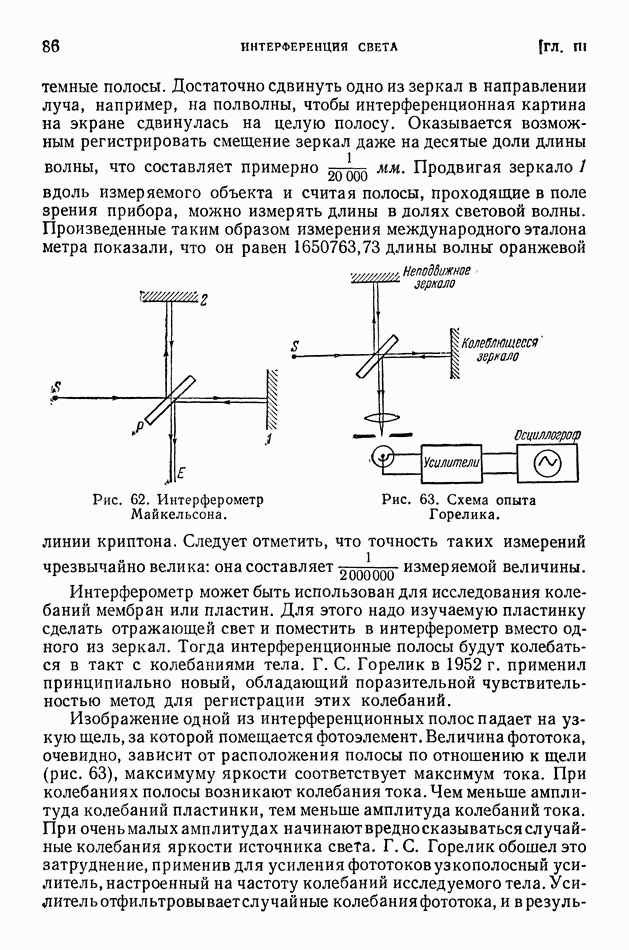
- § 20. Интерферометры
- § 21. Интерференционное измерение технических мер длины
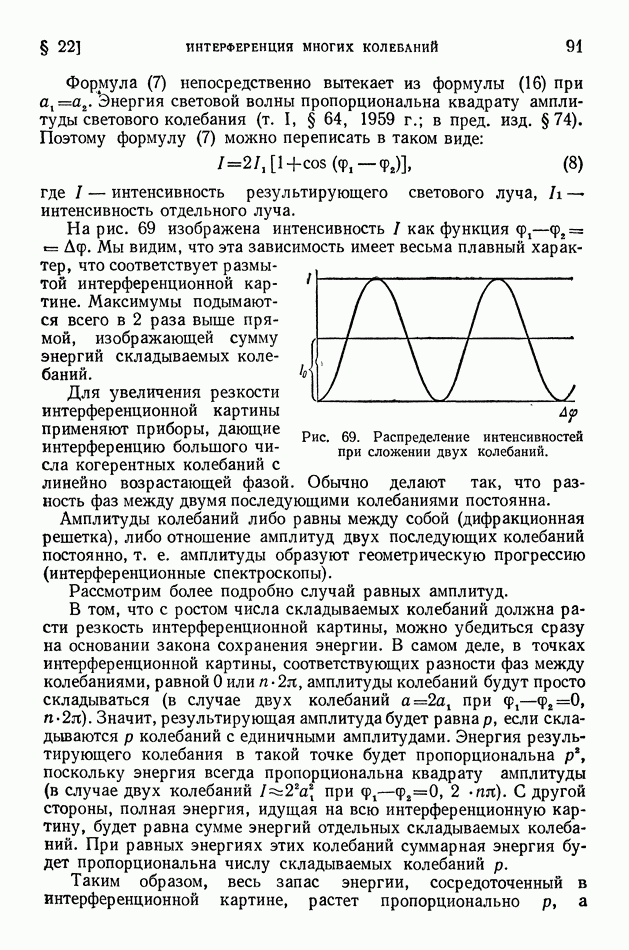
- § 22. Интерференция многих колебаний
- § 23. Интерференционная спектроскопия
- ГЛАВА IV. ДИФРАКЦИЯ СВЕТА
- § 24. Явление дифракции. Опыт Френеля
- § 25. Принцип Гюйгенса-Френеля
- § 26. Метод зон Френеля
- § 27. Дифракция от узкой щели
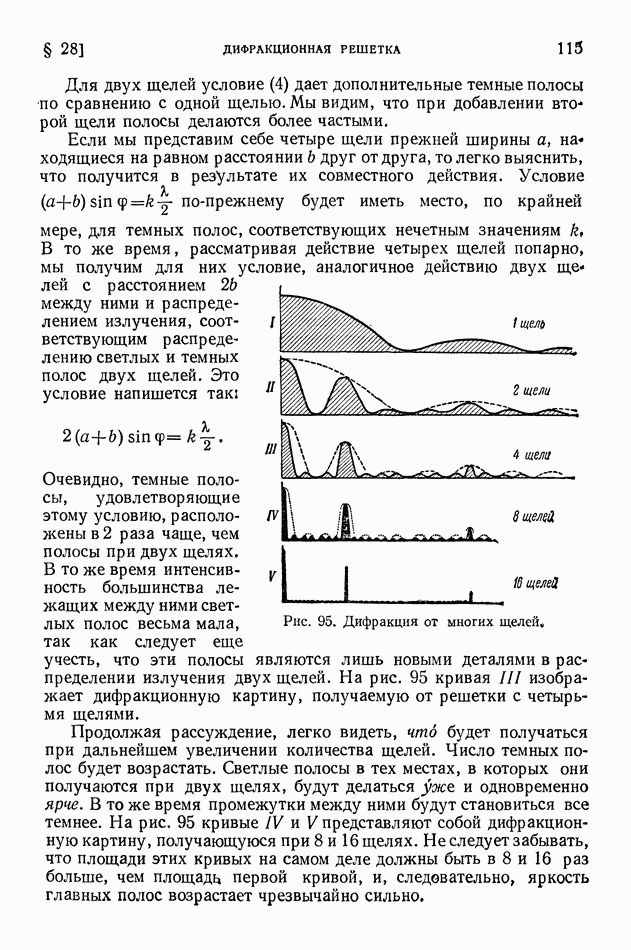
- § 28. Дифракционная решетка
- § 29. Дифракционный спектр. Решетки Роуланда и эшелон Майкельсона
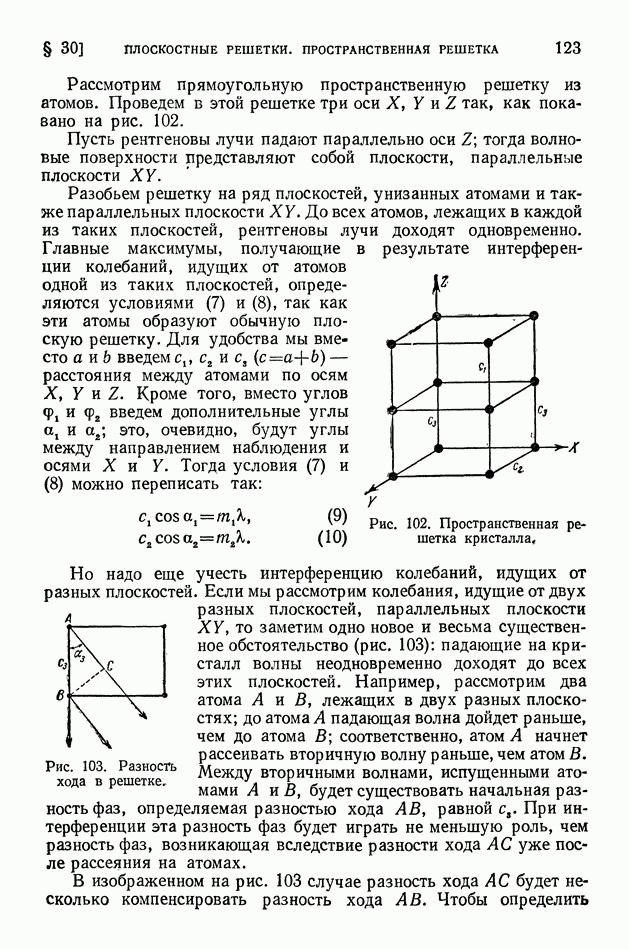
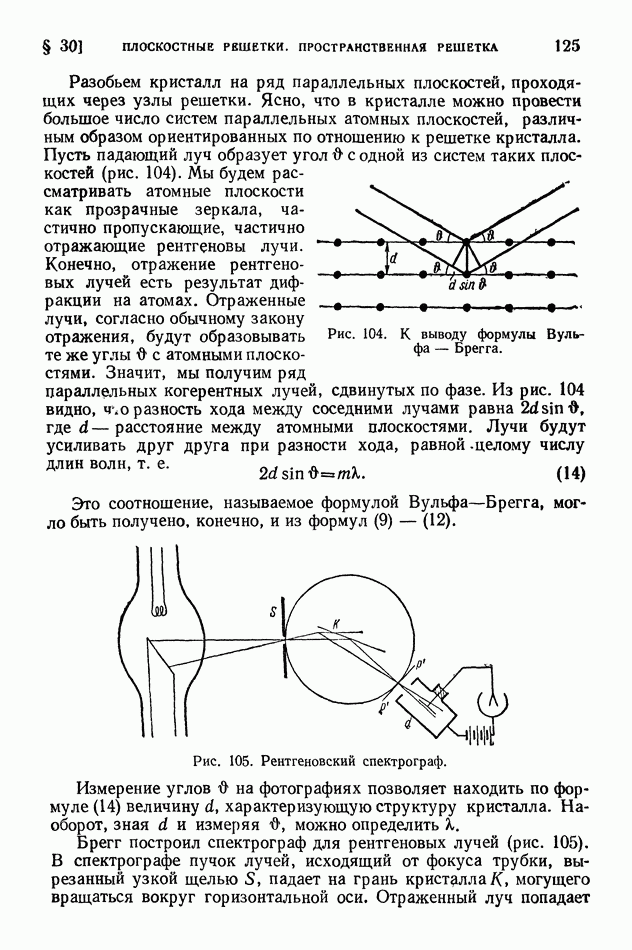
- § 30. Плоскостные решетки. Пространственная решетка
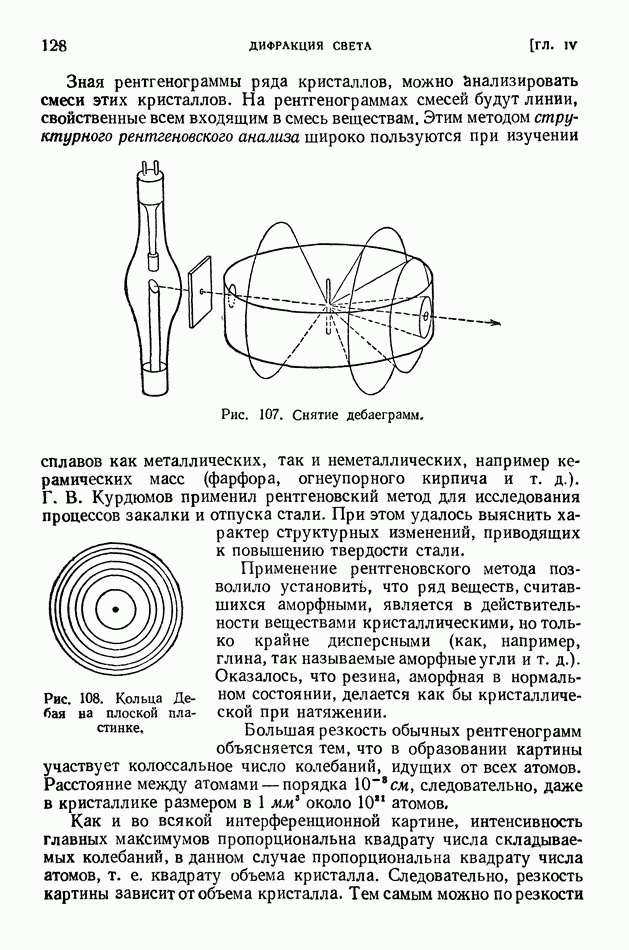
- § 31. Структурный рентгеновский анализ
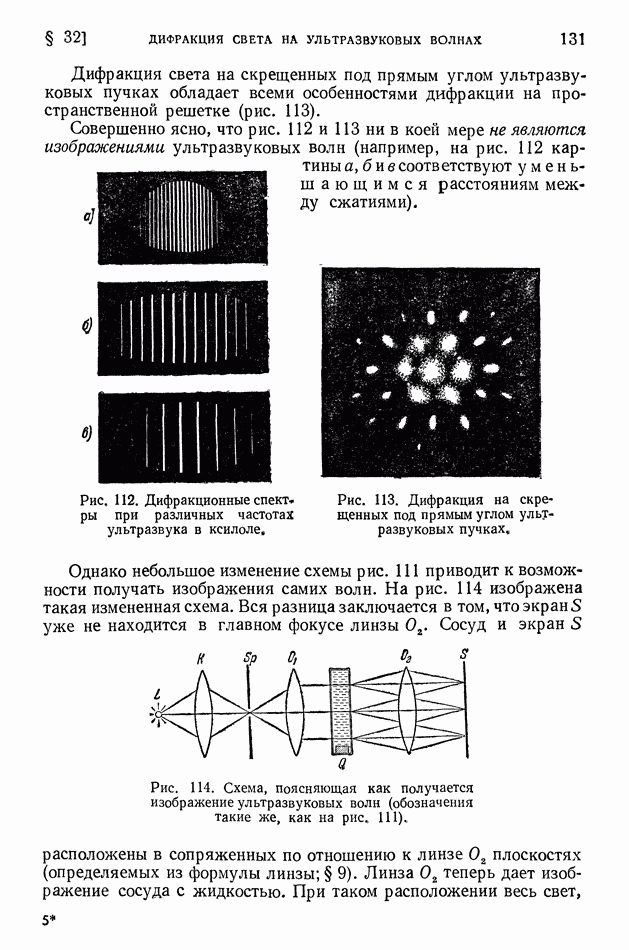
- § 32. Дифракция света на ультразвуковых волнах
- § 33. Дифракция от мелких частиц
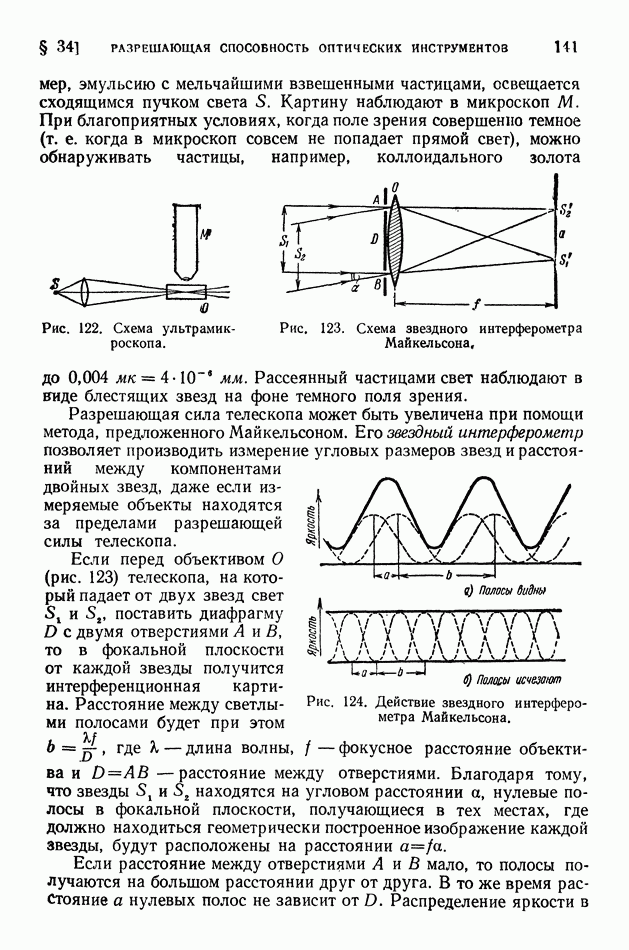
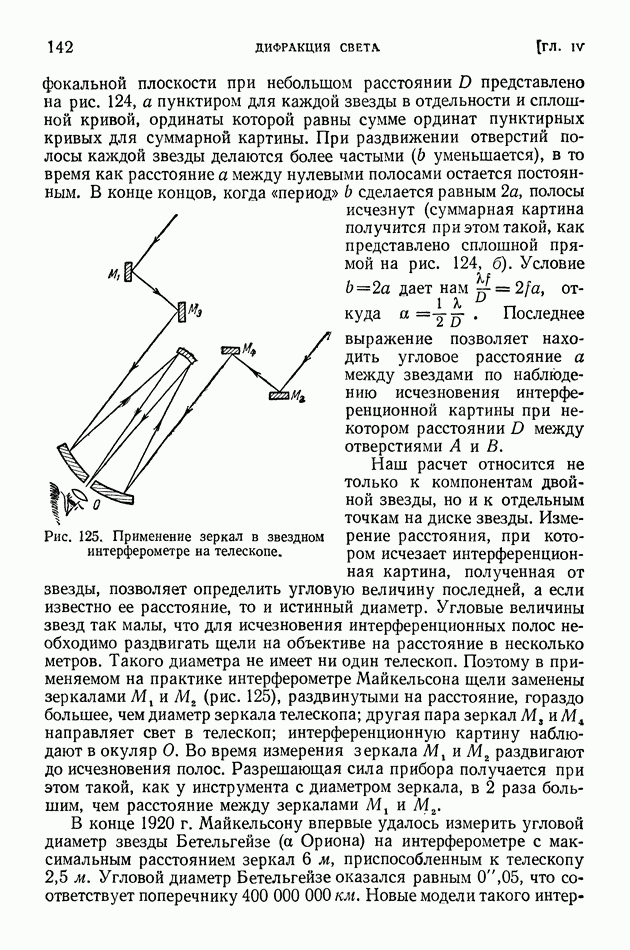
- § 34. Разрешающая способность оптических инструментов. Звездный интерферометр
- ГЛАВА V. ПОЛЯРИЗАЦИЯ СВЕТА
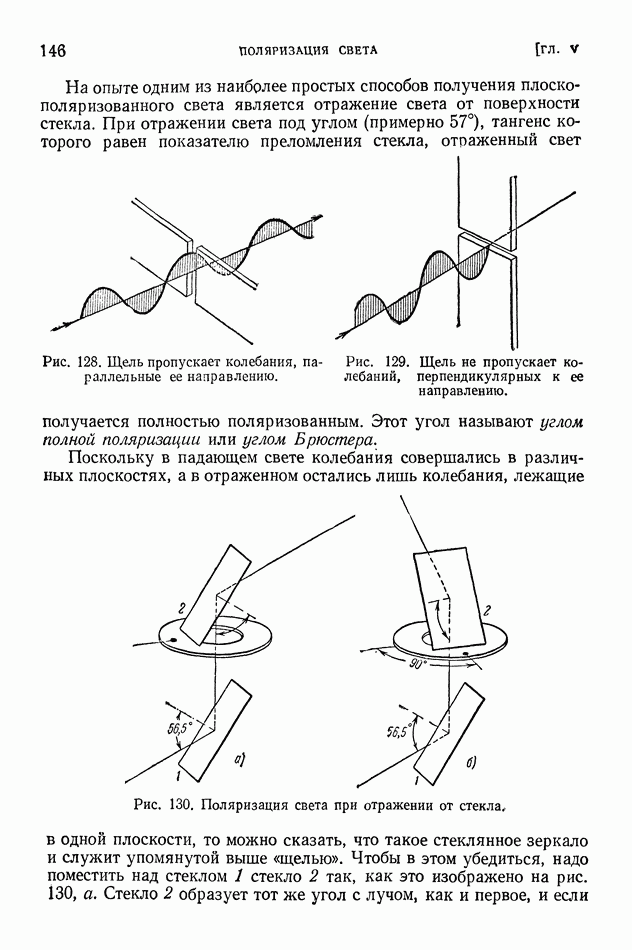
- § 35. Поляризация света
- § 36. Двойное лучепреломление
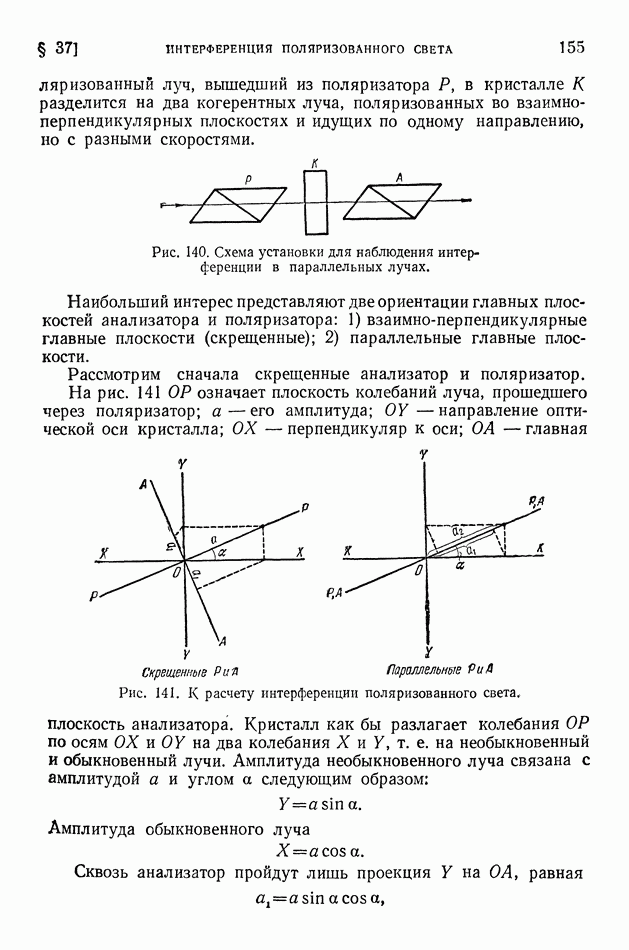
- § 37. Интерференция поляризованного света
- § 38. Оптический метод исследования упругих натяжений. Эффект Керра
- § 39. Вращение плоскости поляризации. Эллиптическая поляризация
- ГЛАВА VI. ДИСПЕРСИЯ, ПОГЛОЩЕНИЕ И ИЗЛУЧЕНИЕ СВЕТА
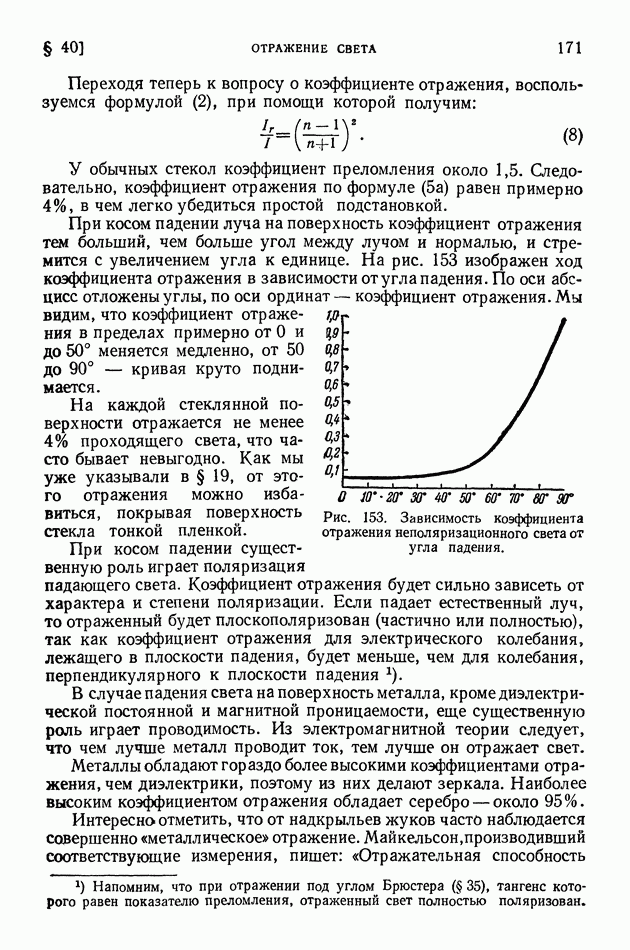
- § 40. Отражение света
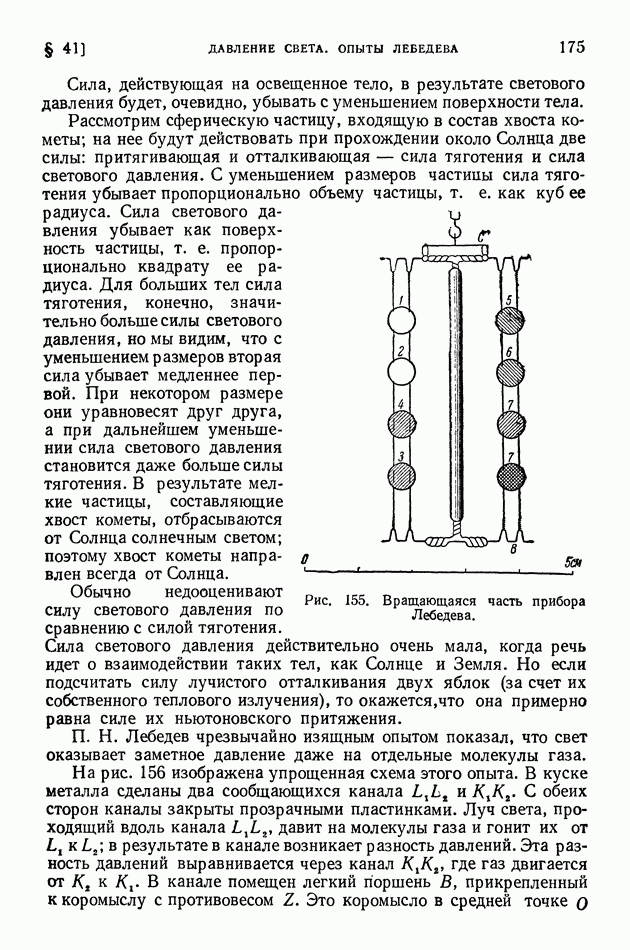
- § 41. Давление света. Опыты Лебедева
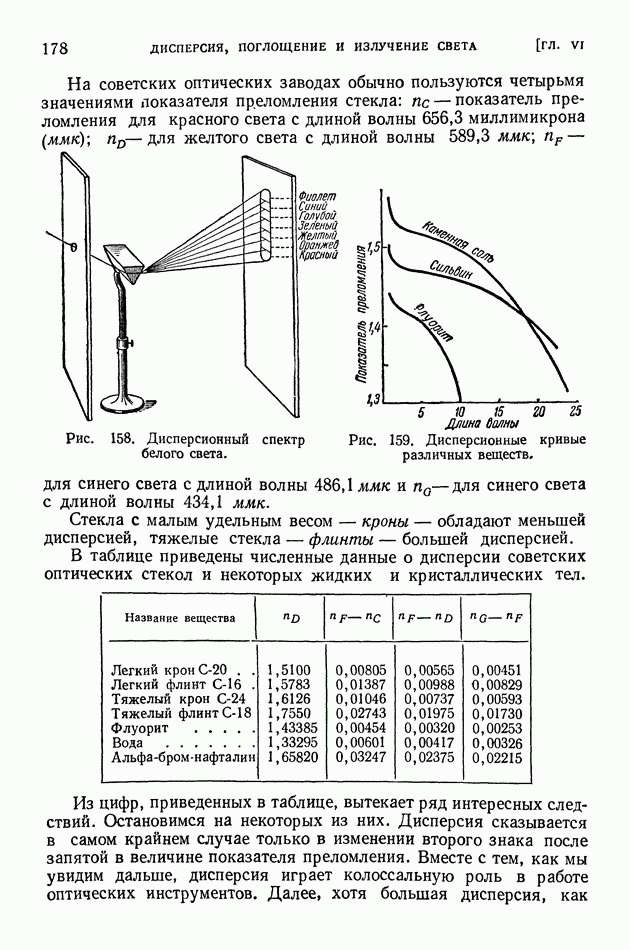
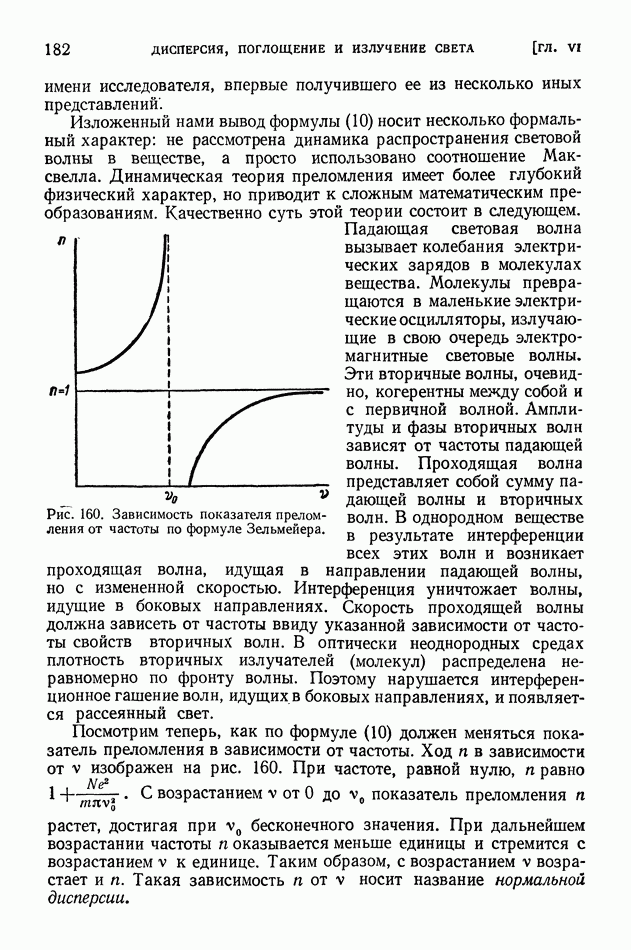
- § 42. Дисперсия. Опыты Ньютона
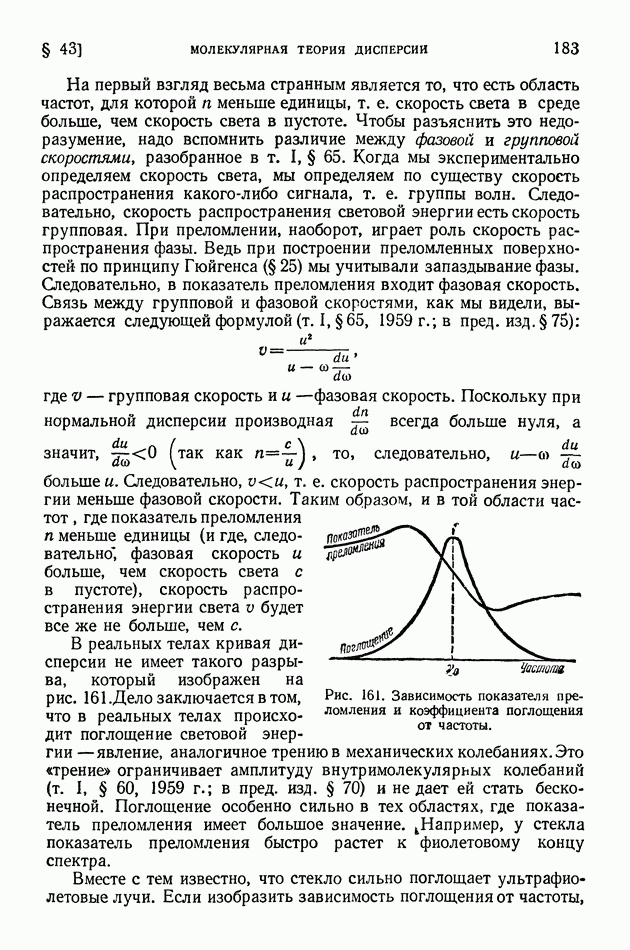
- § 43. Молекулярная теория дисперсии
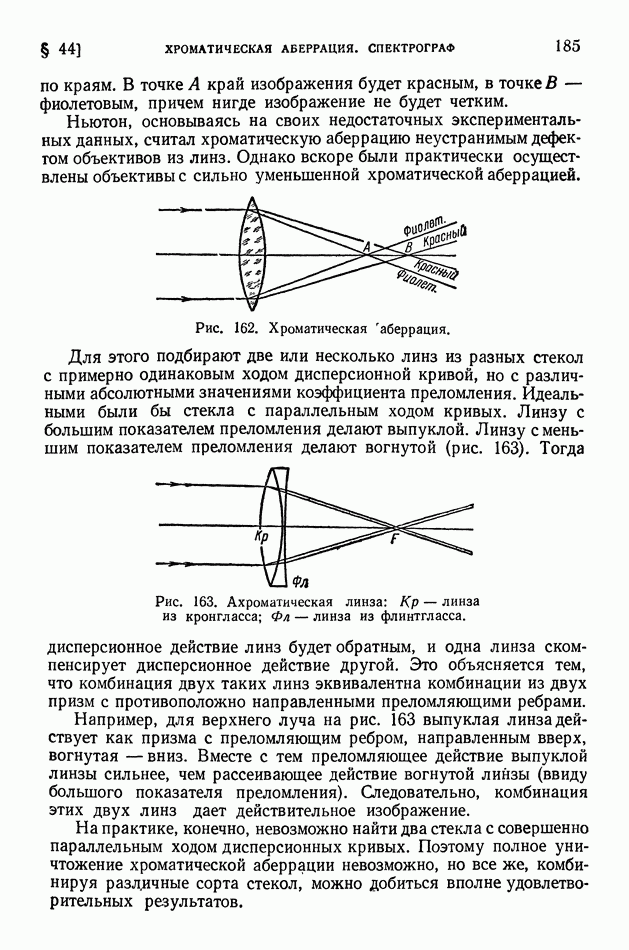
- § 44. Хроматическая аберрация. Спектрограф
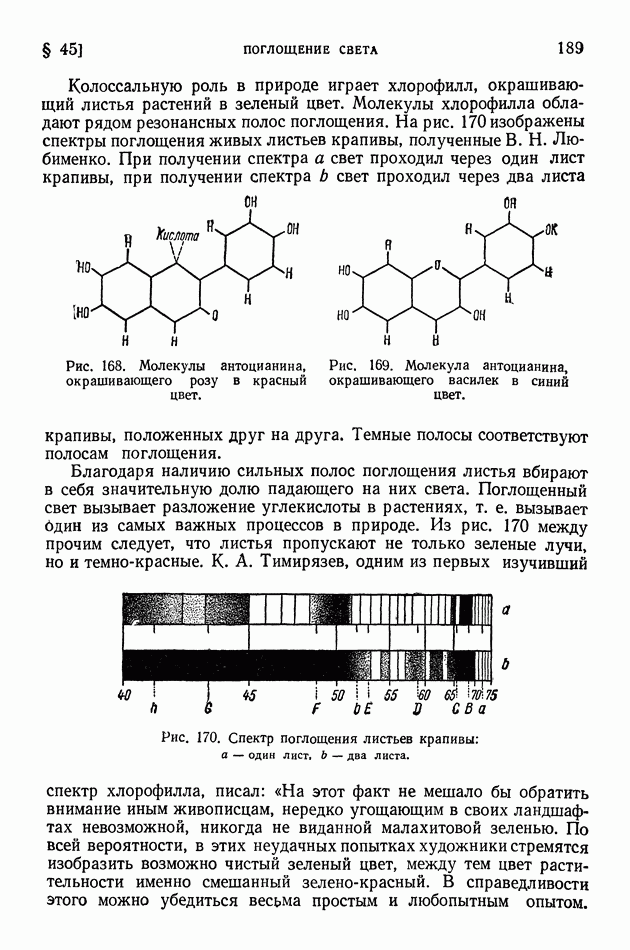
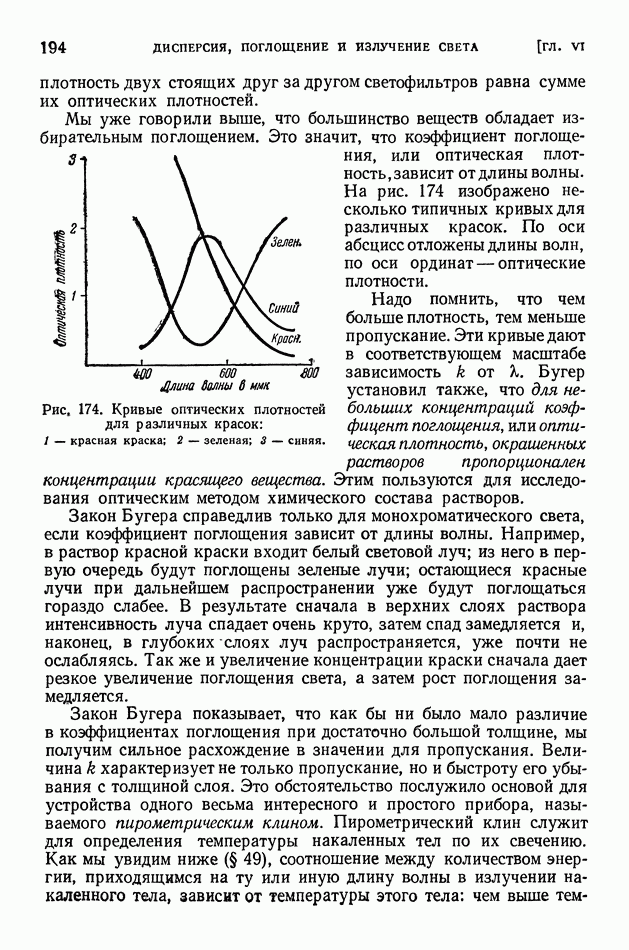
- § 45. Поглощение света
- § 46. Закон Бугера. Опыты Вавилова
- § 47. Атом как элементарный излучатель света
- § 48. Эффект Вавилова — Черенкова
- ГЛАВА VII. ТЕРМОДИНАМИКА ИЗЛУЧЕНИЯ И СВЕТОВОЙ ПОТОК
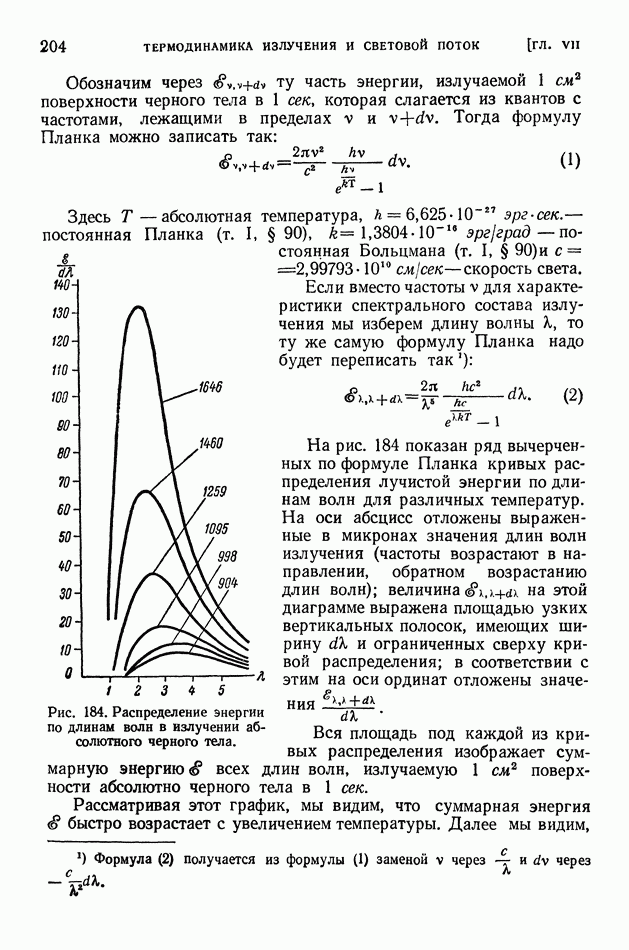
- § 49. Излучение черного тела. Формула Планка. Закон Вина
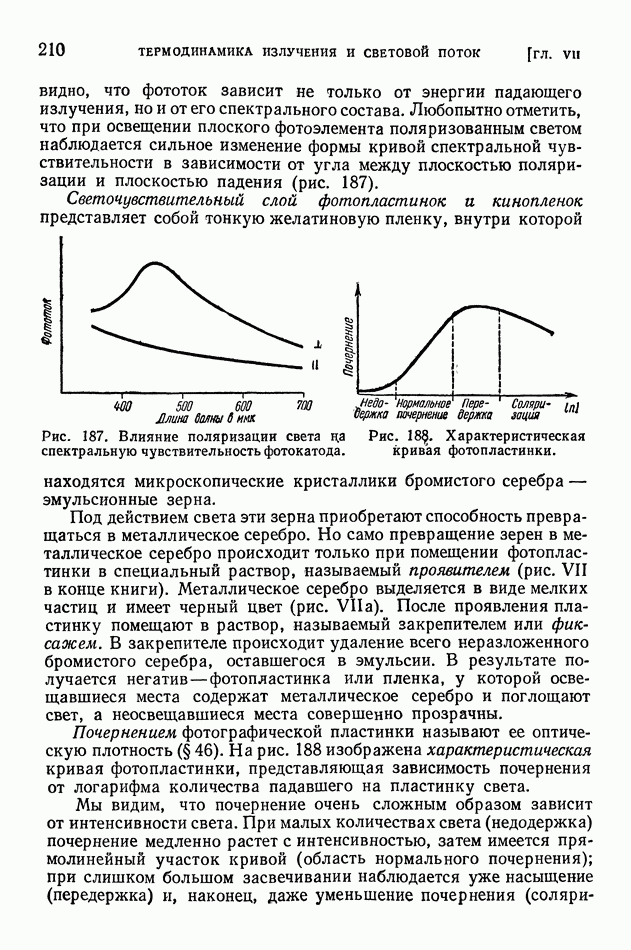
- § 50. Излучение нечерных тел. Законы Кирхгофа
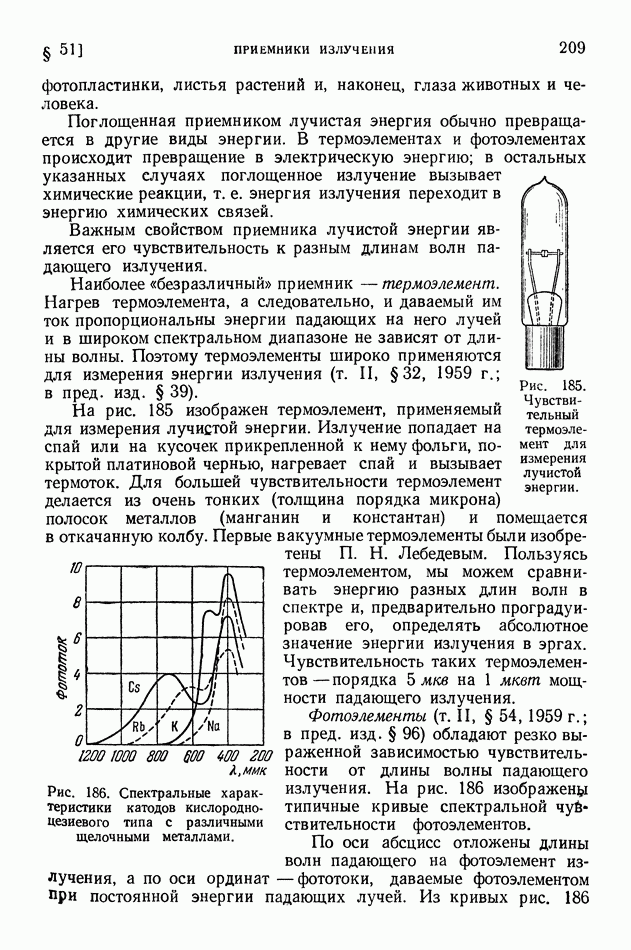
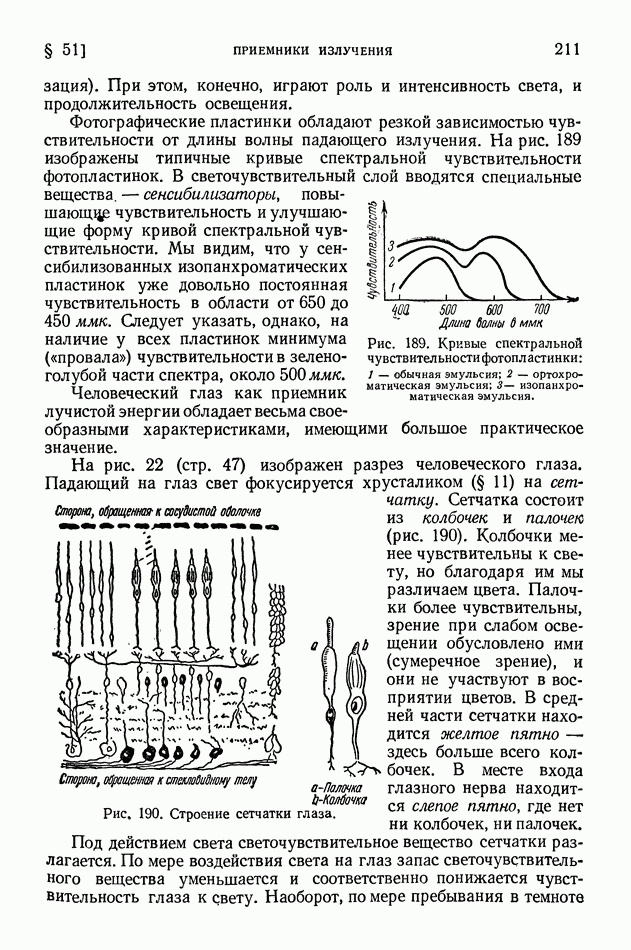
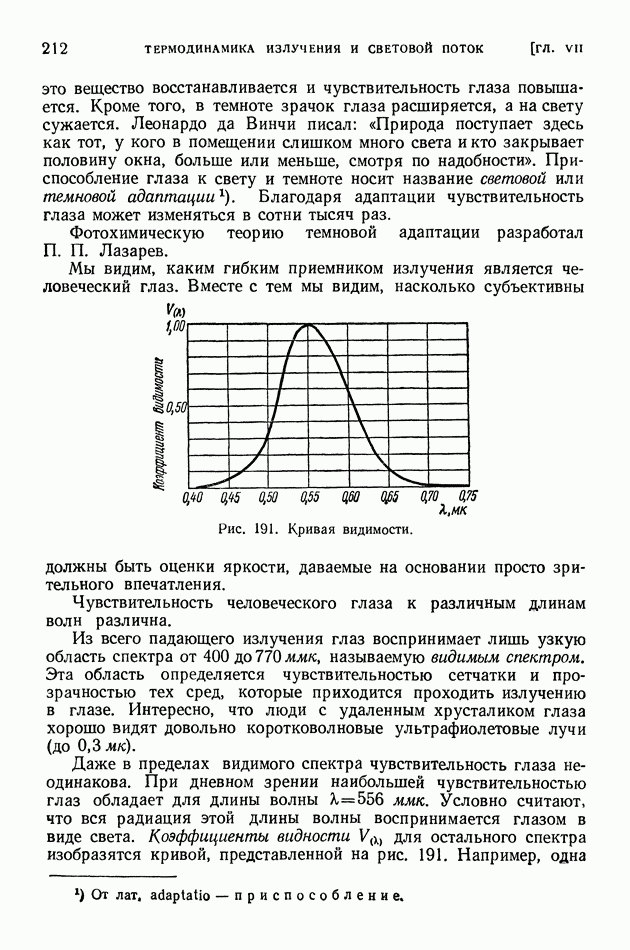
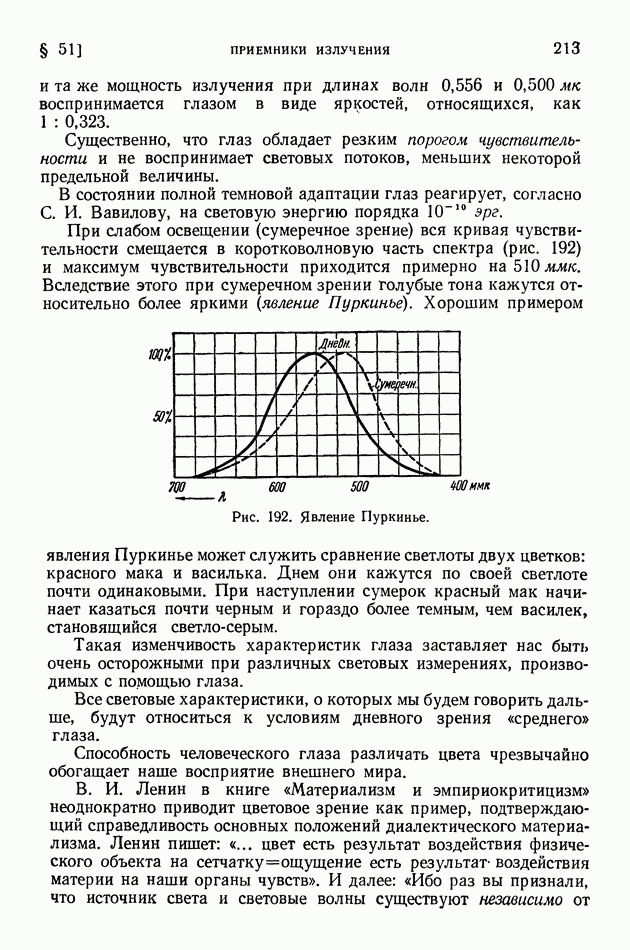
- § 51. Приемники излучения
- § 52. Световые величины и их измерения
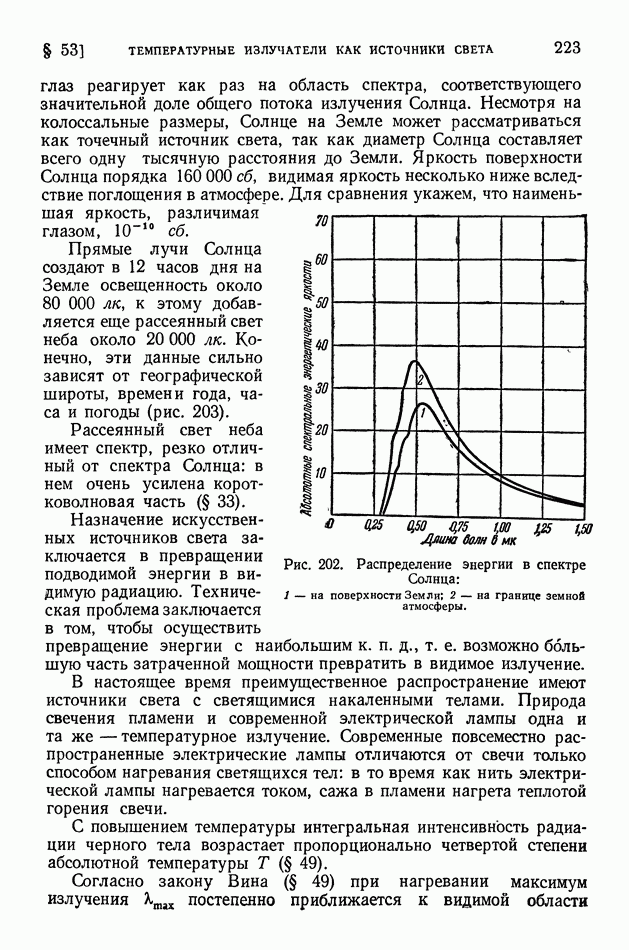
- § 53 Температурные излучатели как источники света
- ЧАСТЬ ПЯТАЯ. АТОМНАЯ ФИЗИКА
- ГЛАВА VIII. СТРОЕНИЕ АТОМА И ТЕОРИЯ БОРА
- § 55. Опыты, обнаружившие ядерное строение атомов
- § 56. Противоречие между фактическим строением атомов и выводами классической электродинамики. Строение линейчатых спектров
- § 57. Опытные основания теории квантов в первые годы ее развития
- § 58. Теория Бора. Происхождение спектра водорода
- § 59. Квантовые числа
- § 60. Принцип Паули. Строение электронных оболочек атомов
- § 61. Общая картина возникновения спектров
- ГЛАВА IX. ОСНОВЫ КВАНТОВОЙ (ВОЛНОВОЙ) МЕХАНИКИ
- § 62. Волновые свойства частиц. Формула де Бройля. Дифракция электронов
- § 63. Уравнение Шредингера. Просачивание через энергетический барьер. Нулевая энергия
- § 64. Волномеханическая теория атома водорода
- § 65. Соотношение неопределенностей и его разные трактовки
- ГЛАВА X. КВАНТОВАЯ ОПТИКА
- § 66. Развитие квантовой оптики
- § 67. Спектр щелочных металлов. Спин электрона
- § 68. Спектр гелия. Символика спектральных термов
- § 69. Сверхтонкая структура спектральных линий
- § 70. Атом в силовом поле
- § 71. Молекулярные спектры и строение молекул
- § 72. Комбинационное рассеяние света
- § 73. Квантовая картина испускания света атомами и молекулами
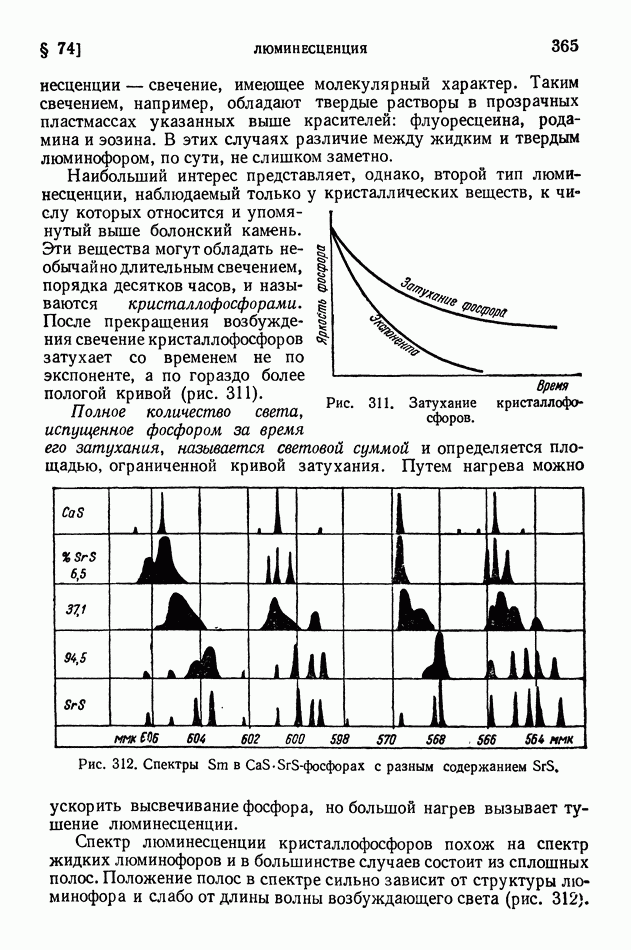
- § 74. Люминесценция
- § 75. Возбуждение люминесценции ударами частиц вещества
- § 76. Применения люминесценции
- § 77. Фотохимические реакции
- ГЛАВА XI. ЗАКОН ПРОПОРЦИОНАЛЬНОСТИ МАССЫ И ЭНЕРГИИ И РЕЛЯТИВИСТСКИЕ СООТНОШЕНИЯ
- § 78. Закон пропорциональности массы и энергии
- § 79. Предварительные замечания о релятивистских эффектах. Зависимость массы от скорости
- § 80. Корпускулярные свойства фотонов. Явление Комптона
- § 81. Вывод закона Эйнштейна сложения скоростей из закона пропорциональности массы и энергии и законов сохранения энергии или количества движения
- § 82. Две трактовки закона пропорциональности массы и энергии и уточнение закона тяготения
- § 83. Красное смещение спектральных линий. Поперечный эффект Доплера
- § 84. Влияние гравитационного поля на скорость света в вакууме и показатель преломления вакуума
- ЧАСТЬ ШЕСТАЯ. ЯДЕРНАЯ ФИЗИКА
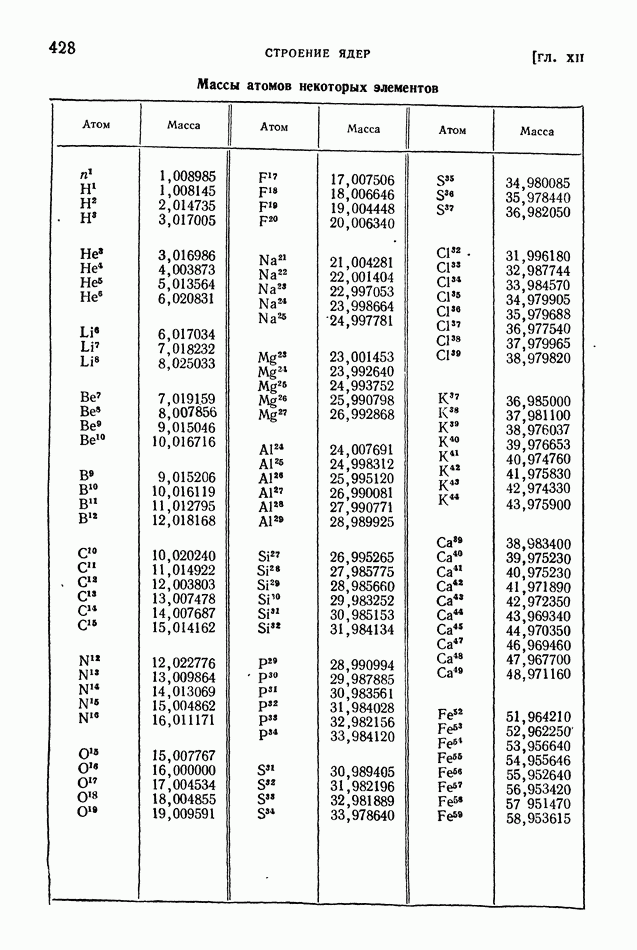
- § 85. Заряд и масса ядра. Масс-спектральный анализ
- § 86. Состав ядер. Изотопы. Атомные единицы массы и энергии
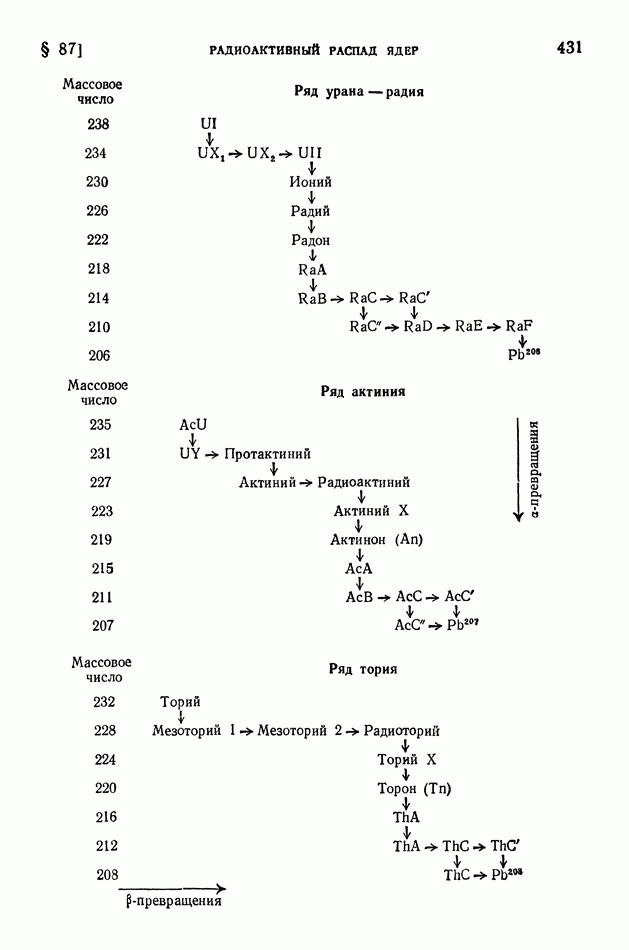
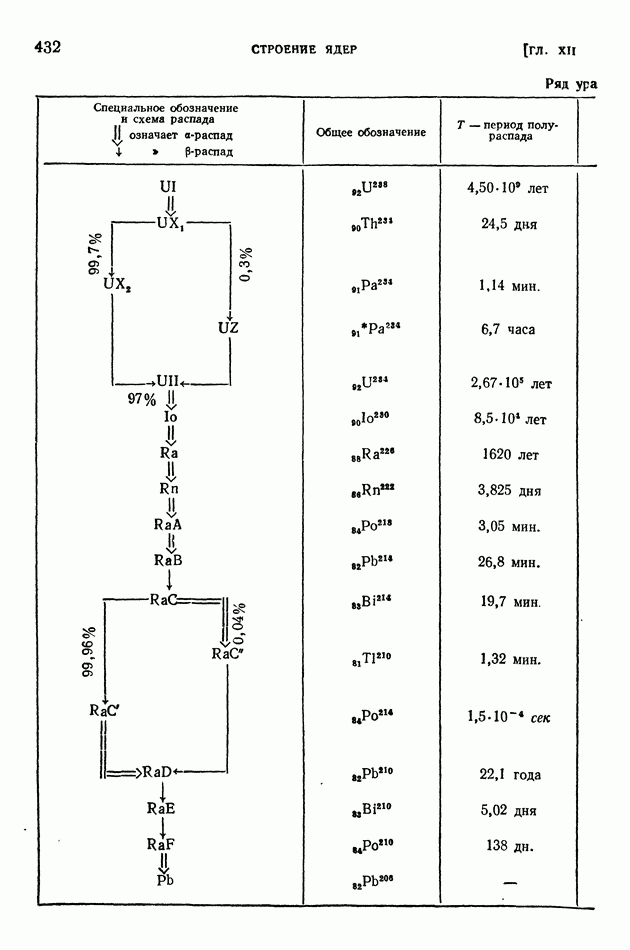
- § 87. Радиоактивный распад ядер. Закон радиоактивного смещения. Изомеры
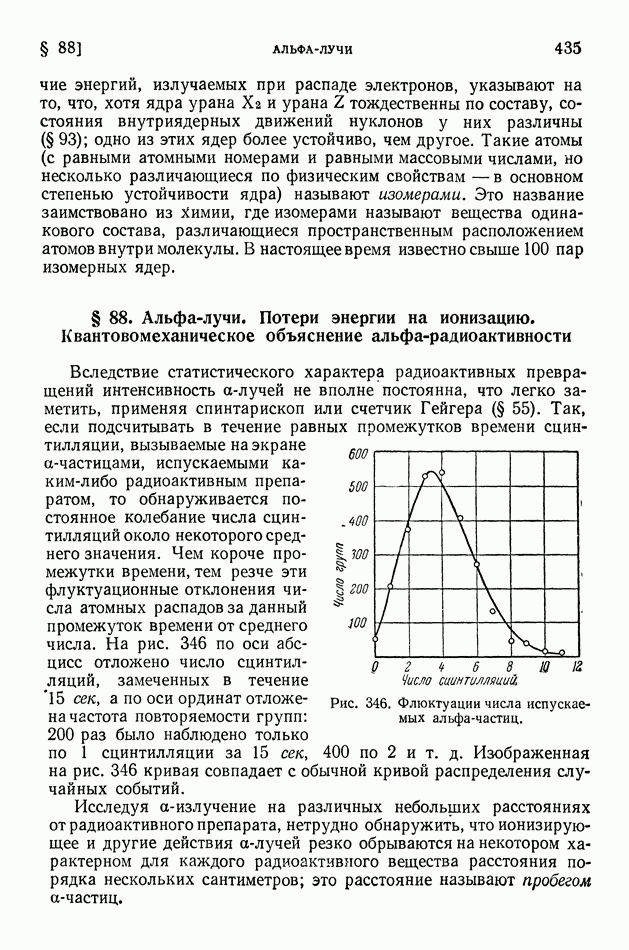
- § 88. Альфа-лучи. Потери энергии на ионизацию. Квантовомеханическое объяснение альфа-радиоактивности
- § 89. Бета- и гамма-лучи
- § 90. Искусственное расщепление ядер. Открытие нейтрона
- § 91. Открытие позитрона. Взаимопревращение фотонов определенной энергии и электронно-позитронных пар
- § 92. Индуцированная позитронная и электронная радиоактивность. Фоторасщепление ядер, K-захват
- § 93. Энергетические уровни ядер. Внутренняя конверсия. Нейтрино
- § 94. Капельная теория строения ядер
- § 95. Деление ядер и развитие капельной теории строения ядер
- ГЛАВА XIII. КОСМИЧЕСКИЕ ЛУЧИ
- § 96. Методы исследования и первые итоги изучения космических лучей
- § 97. Каскадное образование электронно-позитронных пар в космических лучах. Потери энергии электронами на тормозное излучение
- § 98. «мю»-мезоны. Зависимость времени жизни неустойчивых частиц от скорости движения
- § 99. «пи»-мезоны
- § 100. Взрывные ядерные ливни и их каскадное развитие в космических лучах
- § 101. Корпускулярный и энергетический спектр космических лучей. Происхождение космического излучения
- ГЛАВА XIV. ЭКСПЕРИМЕНТАЛЬНЫЕ СРЕДСТВА ЯДЕРНОЙ ФИЗИКИ
- § 102. Циклотроны
- § 103. Фазотроны
- § 104. Бетатроны
- § 105. Синхротроны и синхрофазотроны
- § 106. Линейные ускорители электронов и ионов
- § 107. Лабораторные источники нейтронов. Замедлители нейтронов в ядерных реакторах
- § 108. Усовершенствование методов наблюдения и счета частиц
- ГЛАВА XV. ЯДЕРНЫЕ РЕАКЦИИ И АТОМНАЯ ЭНЕРГИЯ
- § 109. Основные виды и обозначения ядерных реакций. Конкурирующие процессы в ядерных реакциях
- § 110. Энергетический эффект, энергия возбуждения и порог ядерных реакций
- § 111. Превращения элементарных частиц
- § 112. Ядерные силы
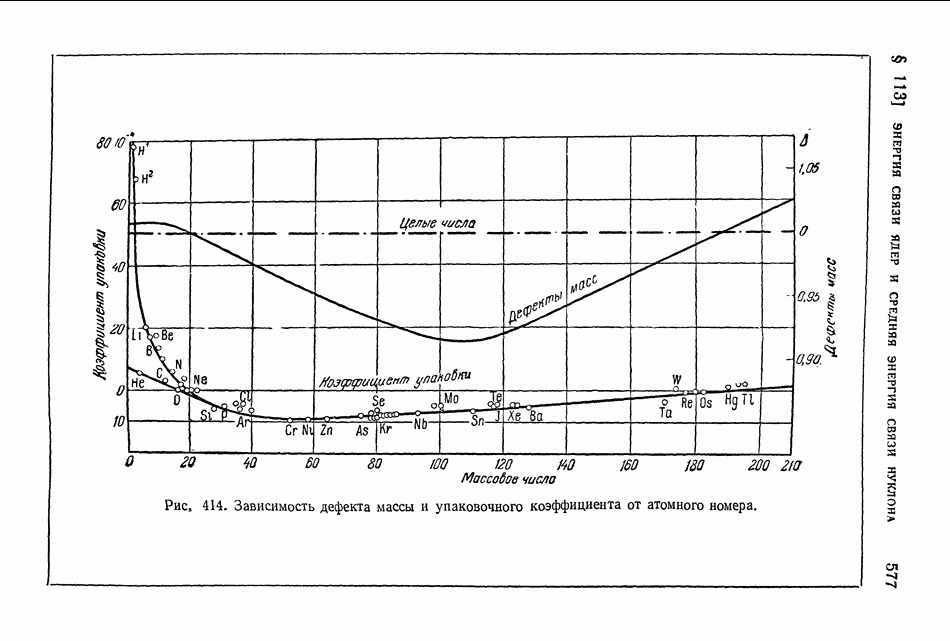
- § 113. Энергия связи ядер и средняя энергия связи нуклона
- § 114. Полуэмпирическая формула для энергии ядерной связи и для атомных энергий и масс
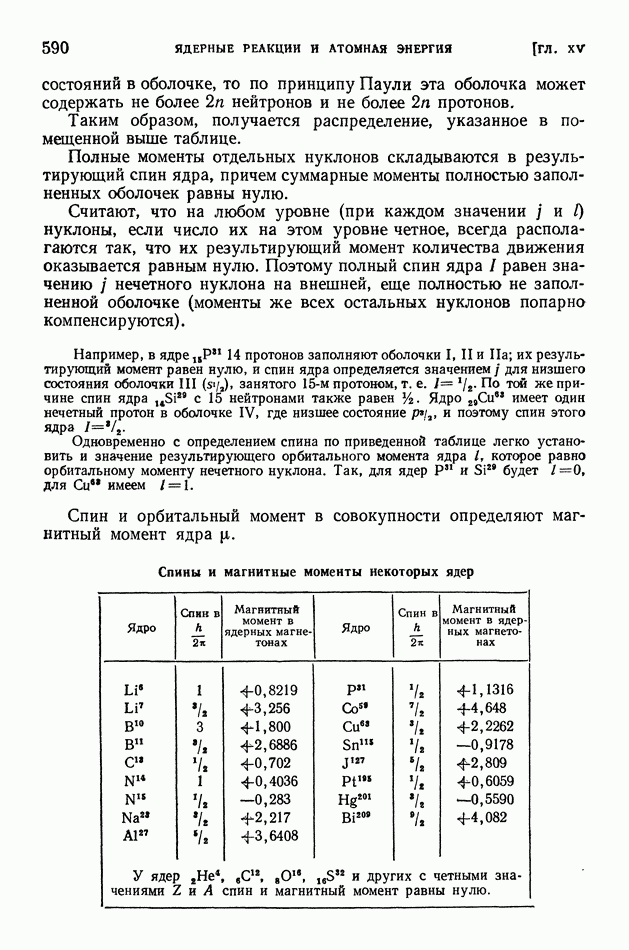
- § 115. Взаимосвязь энергии и строения ядер. Внутриядерное движение нуклонов и нуклонные оболочки. Спины и магнитные моменты ядер
- § 116. Энергия отделения частиц и анализ возможного хода ядерной реакции
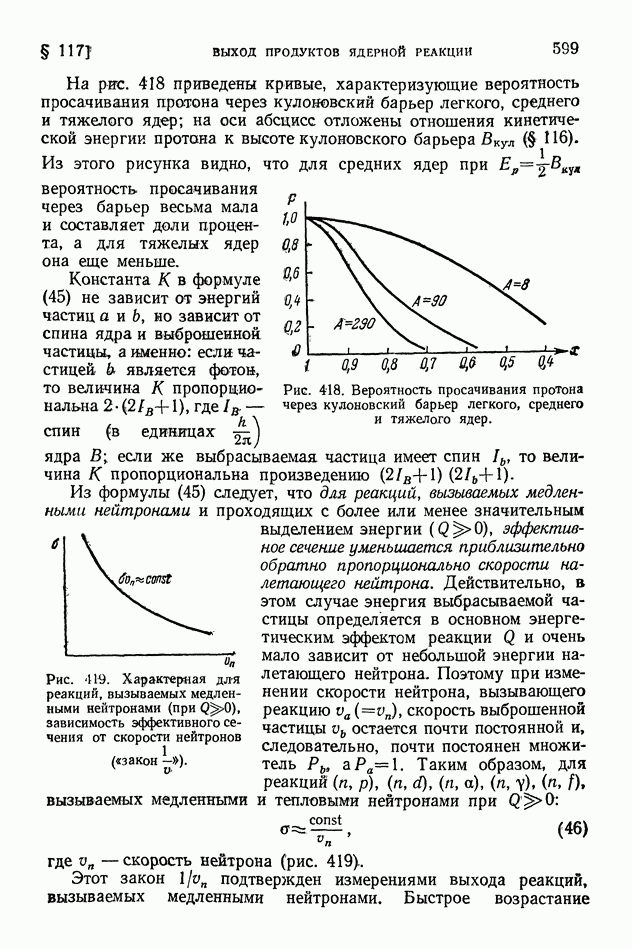
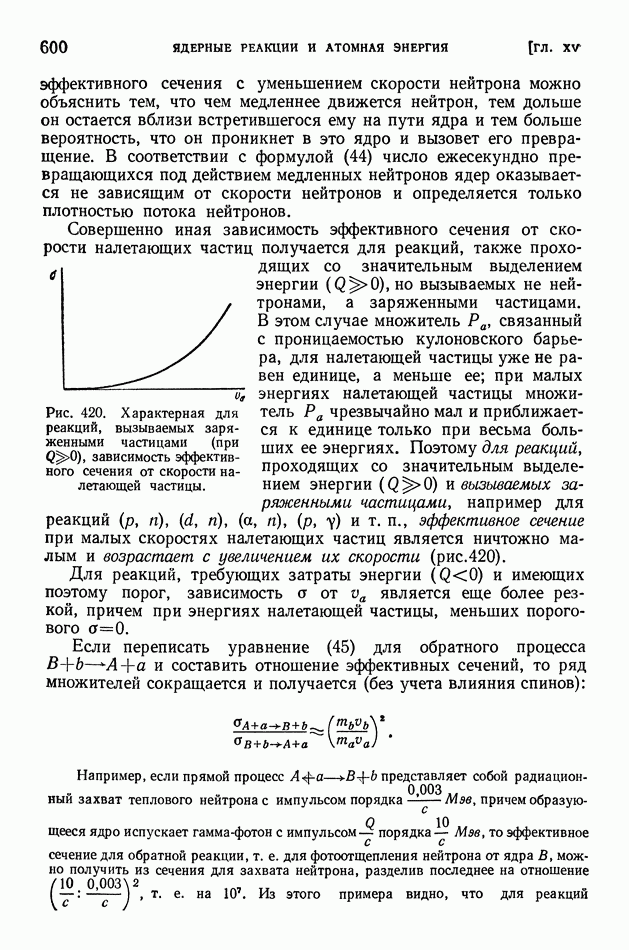
- § 117. Выход продуктов ядерной реакции. Эффективные сечения. Резонансные явления
- § 118. Цепной процесс деления ядер. Активно делящиеся вещества. Ядерные реакторы
- § 119. Термоядерные реакции
- § 120. Применение ядерных реакций
- § 121. Ядерные реакции в звездах