| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 22. Интерференция многих колебаний
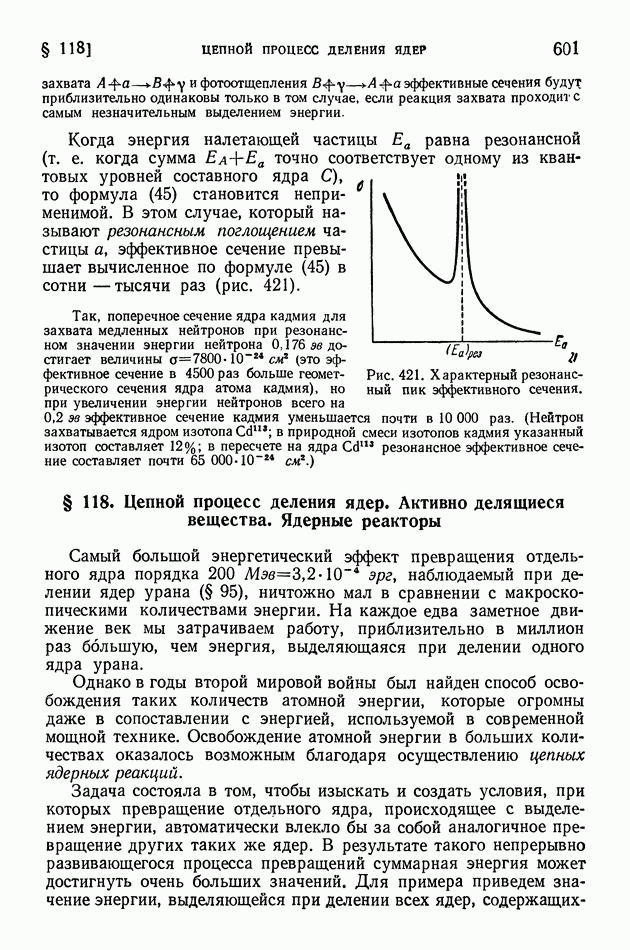
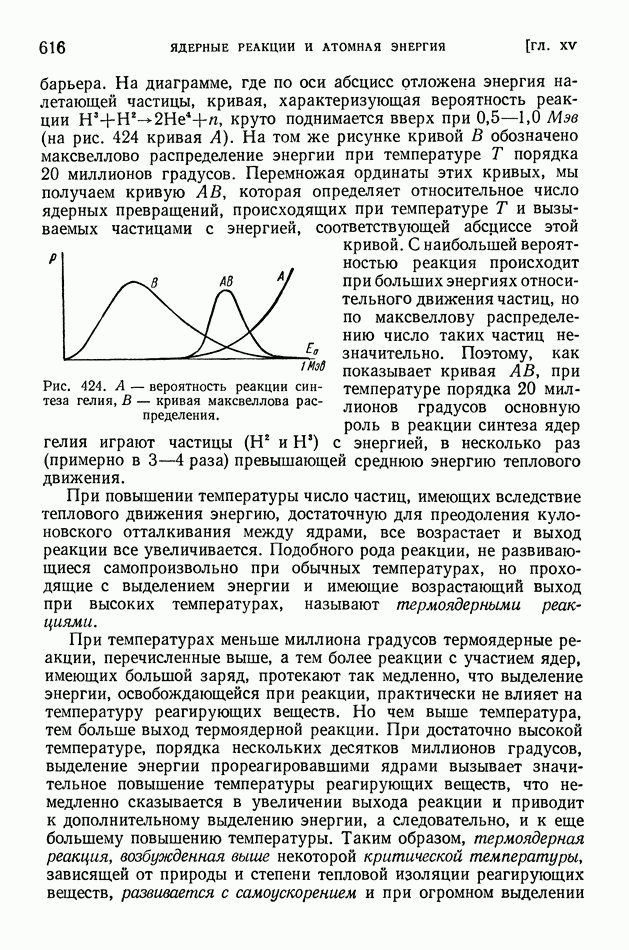
Выше мы показали, что расстояние между интерференционными полосами зависит от длины световой волны. Вследствие этого полосы, полученные в белом свете, имеют радужную окраску,
Таким образом, по интерференционной картине можно в известной степени судить о спектральном составе излучения. Однако для точных исследований малопригодны расплывчатые интерференционные картины, получающиеся в результате сложения двух колебаний, как это имеет место в зеркалах Френеля и интерферометрах Майкельсона, Жамена и Релея.
При сложении двух световых колебаний равной амплитуды получается колебание с амплитудой, определяемой следующей формулой:

Формула (7) непосредственно вытекает из формулы (16) при  Энергия световой волны пропорциональна квадрату амплитуды светового колебания (т. I, § 64, 1959 г.; в пред. изд. § 74). Поэтому формулу (7) можно переписать в таком виде:
Энергия световой волны пропорциональна квадрату амплитуды светового колебания (т. I, § 64, 1959 г.; в пред. изд. § 74). Поэтому формулу (7) можно переписать в таком виде:

где I — интенсивность результирующего светового луча,  интенсивность отдельного луча.
интенсивность отдельного луча.
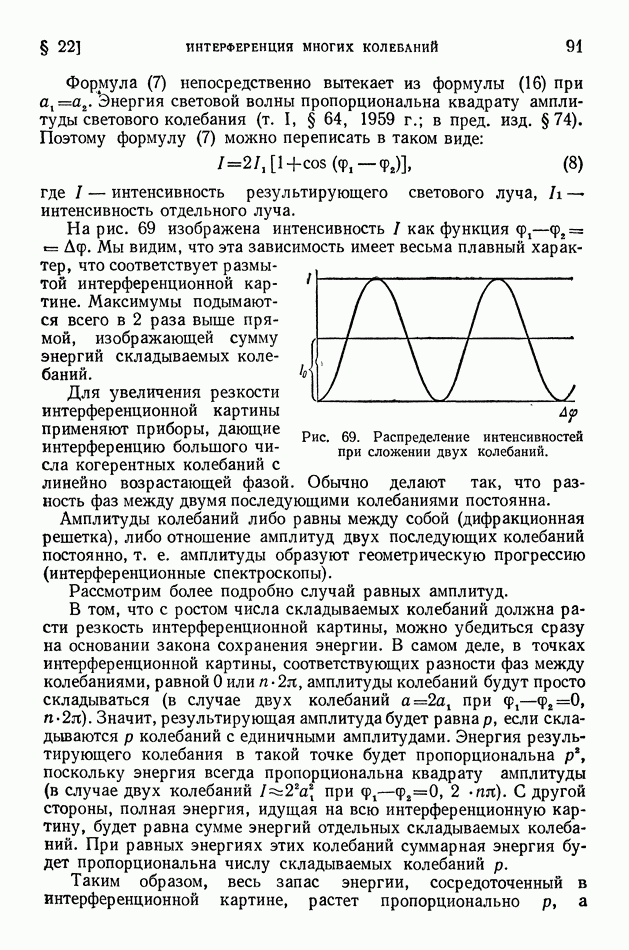
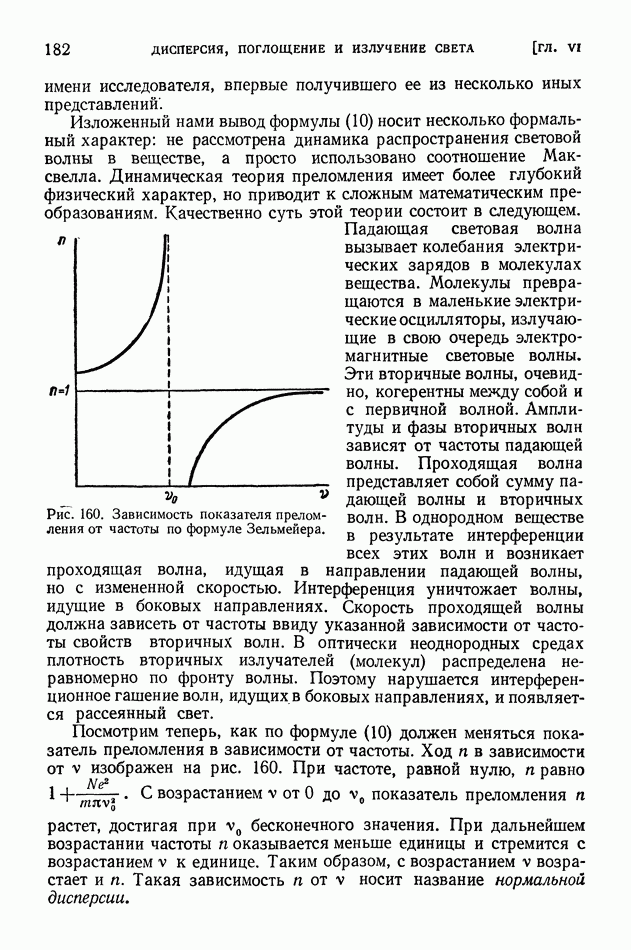
На рис. 69 изображена интенсивность  как функция
как функция  Мы видим, что эта зависимость имеет весьма плавный характер, что соответствует размытой интерференционной картине. Максимумы подымаются всего в 2 раза выше прямой, изображающей сумму энергий складываемых колебаний.
Мы видим, что эта зависимость имеет весьма плавный характер, что соответствует размытой интерференционной картине. Максимумы подымаются всего в 2 раза выше прямой, изображающей сумму энергий складываемых колебаний.

Рис. 69. Распределение интенсивностей при сложении двух колебаний.
Для увеличения резкости интерференционной картины применяют приборы, дающие интерференцию большого числа когерентных колебаний с линейно возрастающей фазой. Обычно делают так, что разность фаз между двумя последующими колебаниями постоянна.
Амплитуды колебаний либо равны между собой (дифракционная решетка), либо отношение амплитуд двух последующих колебаний постоянно, т. е. амплитуды образуют геометрическую прогрессию (интерференционные спектроскопы).
Рассмотрим более подробно случай равных амплитуд.
В том, что с ростом числа складываемых колебаний должна расти резкость интерференционной картины, можно убедиться сразу на основании закона сохранения энергии. В самом деле, в точках интерференционной картины, соответствующих разности фаз между колебаниями, равной  или
или  амплитуды колебаний будут просто складываться (в случае двух колебаний
амплитуды колебаний будут просто складываться (в случае двух колебаний  при
при  Значит, результирующая амплитуда будет равна
Значит, результирующая амплитуда будет равна  если складываются
если складываются  колебаний с единичными амплитудами. Энергия результирующего колебания в такой точке будет пропорциональна
колебаний с единичными амплитудами. Энергия результирующего колебания в такой точке будет пропорциональна  поскольку энергия всегда пропорциональна квадрату амплитуды (в случае двух колебаний
поскольку энергия всегда пропорциональна квадрату амплитуды (в случае двух колебаний  при
при  . С другой стороны, полная энергия, идущая на всю интерференционную картину, будет равна сумме энергий отдельных складываемых колебаний. При равных энергиях этих колебаний суммарная энергия будет пропорциональна числу складываемых колебаний
. С другой стороны, полная энергия, идущая на всю интерференционную картину, будет равна сумме энергий отдельных складываемых колебаний. При равных энергиях этих колебаний суммарная энергия будет пропорциональна числу складываемых колебаний 
Таким образом, весь запас энергии, сосредоточенный в интерференционной картине, растет пропорционально  а
а
энергия максимумов растет значительно быстрее — пропорционально 
Из закона сохранения энергии следует, что все части интерференционной картины, кроме указанных максимумов, должны с ростом  становиться все более и более темными и занимать все больше и больше места в этой картине. При достаточно большом числе складываемых колебаний
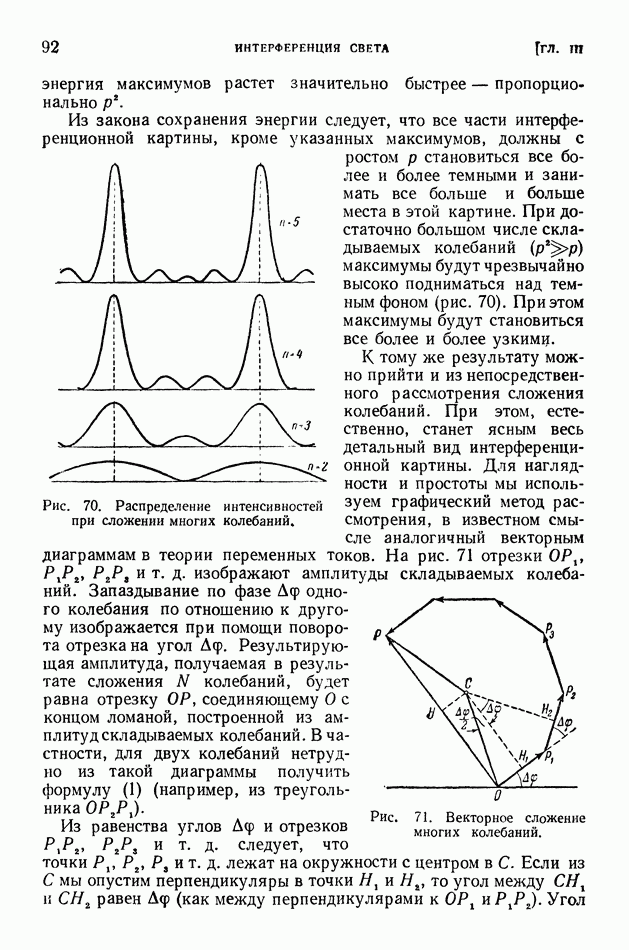
становиться все более и более темными и занимать все больше и больше места в этой картине. При достаточно большом числе складываемых колебаний  максимумы будут чрезвычайно высоко подниматься над темным фоном (рис. 70). При этом максимумы будут становиться все более и более узкими.
максимумы будут чрезвычайно высоко подниматься над темным фоном (рис. 70). При этом максимумы будут становиться все более и более узкими.

Рис. 70. Распределение интенсивностей при сложении многих колебаний
К тому же результату можно прийти и из непосредственного рассмотрения сложения колебаний. При этом, естественно, станет ясным весь детальный вид интерференционной картины. Для наглядности и простоты мы используем графический метод рассмотрения, в известном смысле аналогичный векторным диаграммам в теории переменных токов. На рис. 71 отрезки  изображают амплитуды складываемых колебаний. Запаздывание по фазе
изображают амплитуды складываемых колебаний. Запаздывание по фазе  одного колебания по отношению к другому изображается при помощи поворота отрезка на угол
одного колебания по отношению к другому изображается при помощи поворота отрезка на угол  Результирующая амплитуда, получаемая в результате сложения
Результирующая амплитуда, получаемая в результате сложения  колебаний, будет равна отрезку
колебаний, будет равна отрезку  соединяющему О с концом ломаной, построенной из амплитуд складываемых колебаний. В частности, для двух колебаний нетрудно из такой диаграммы получить формулу (1) (например, из треугольника
соединяющему О с концом ломаной, построенной из амплитуд складываемых колебаний. В частности, для двух колебаний нетрудно из такой диаграммы получить формулу (1) (например, из треугольника 

Рис. 71. Векторное сложение многих колебаний.
Из равенства углов  и отрезков
и отрезков  следует, что точки
следует, что точки  и т. д. лежат на окружности с центром в С. Если из С мы опустим перпендикуляры в точки
и т. д. лежат на окружности с центром в С. Если из С мы опустим перпендикуляры в точки  то угол между
то угол между  и
и  равен
равен  (как между перпендикулярами к
(как между перпендикулярами к  Угол
Угол
ОСН равен и радиус окружности  определится следующим соотношением:
определится следующим соотношением:

Переходим теперь к определению величины отрезка ОР — результирующей амплитуды.
Угол  равен
равен  так как при переходе от одной точки многоугольника к другой каждый раз радиус поворачивается на угол
так как при переходе от одной точки многоугольника к другой каждый раз радиус поворачивается на угол 
Опустим из С перпендикуляр на  Получим:
Получим:

откуда

или, воспользовавшись полученным выше соотношением для 

Энергия результирующего колебания будет пропорциональна  и если мы энергию отдельного колебания примем за единицу, то
и если мы энергию отдельного колебания примем за единицу, то

На рис. 70 изображена интенсивность  как функция
как функция  для этого случая.
для этого случая.
При  близком к нулю, можно синусы заменить аргументами, и тогда
близком к нулю, можно синусы заменить аргументами, и тогда

т. е. действительно интенсивность максимумов (главных) пропорциональна квадрату числа складываемых колебаний. В этом случае на рис. 71 один отрезок становится продолжением другого и многоугольник распрямляется в прямую линию.
Если  возрастает, то
возрастает, то  первый раз обратится в нуль, когда числитель в формуле (9) первый раз обратится в нуль. Это будет при
первый раз обратится в нуль, когда числитель в формуле (9) первый раз обратится в нуль. Это будет при

или при

На рис. 71 это соответствовало бы замкнутому многоугольнику: точка  совпадает с
совпадает с  . Условие (10) соответствует разности хода
. Условие (10) соответствует разности хода 
Формула (10) характеризует ширину главных максимумов. Мы видим, что ширина максимумов обратно пропорциональна числу складываемых колебаний, т. е. с ростом числа колебаний максимумы становятся уже. При большом числе колебаний существенны только эти главные максимумы.
В дальнейшем нам придется еще не раз иметь дело со сложением многих колебаний; всегда и всюду будут проявляться свойства интерференционных картин, вытекающие из формулы (9).
При этом, конечно, нас уже будет интересовать не зависимость I от  а зависимость
а зависимость  от угла наблюдения или координат на экране. Однако к этим зависимостям перейти нетрудно, зная, как связано
от угла наблюдения или координат на экране. Однако к этим зависимостям перейти нетрудно, зная, как связано  с соответствующими параметрами. При этом качественный характер картины будет тот же, что и на рис. 70, изменится только масштаб.
с соответствующими параметрами. При этом качественный характер картины будет тот же, что и на рис. 70, изменится только масштаб.
| << Предыдущий параграф | Следующий параграф >> |
- ЧАСТЬ ЧЕТВЕРТАЯ. ОПТИКА
- § 2. Электромагнитная теория света
- § 3. Скорость света
- § 4. Опыт Майкельсона
- § 5. Отрицательный результат опыта Майкельсона и теория относительности
- § 6. Некоторые замечания о теории относительности
- § 7. Явление Доплера для световых волн
- ГЛАВА II. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- § 8. Законы отражения и преломления света
- § 9. Линза
- § 10. Оптические системы
- § 11. Глаз как оптическая система
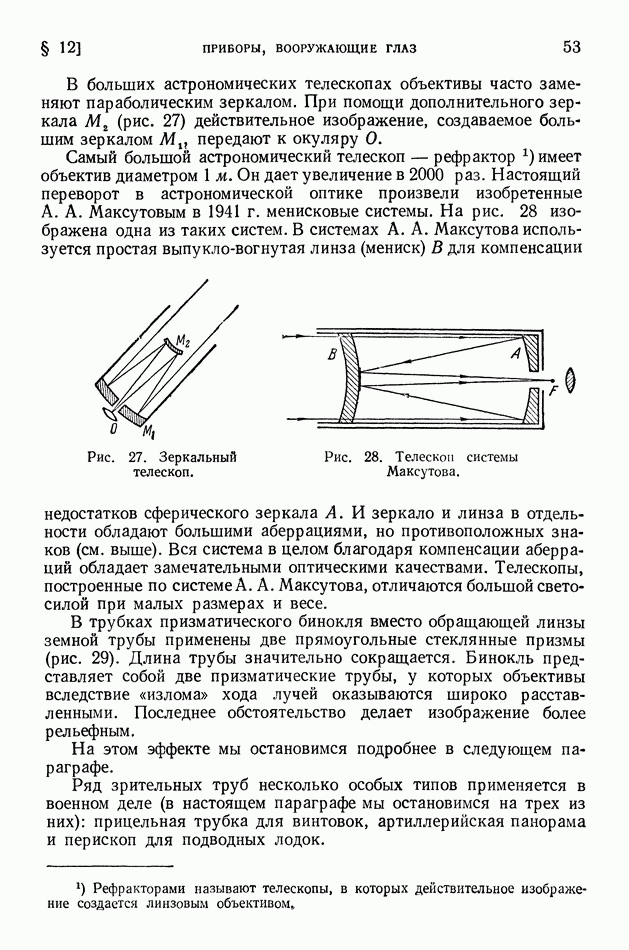
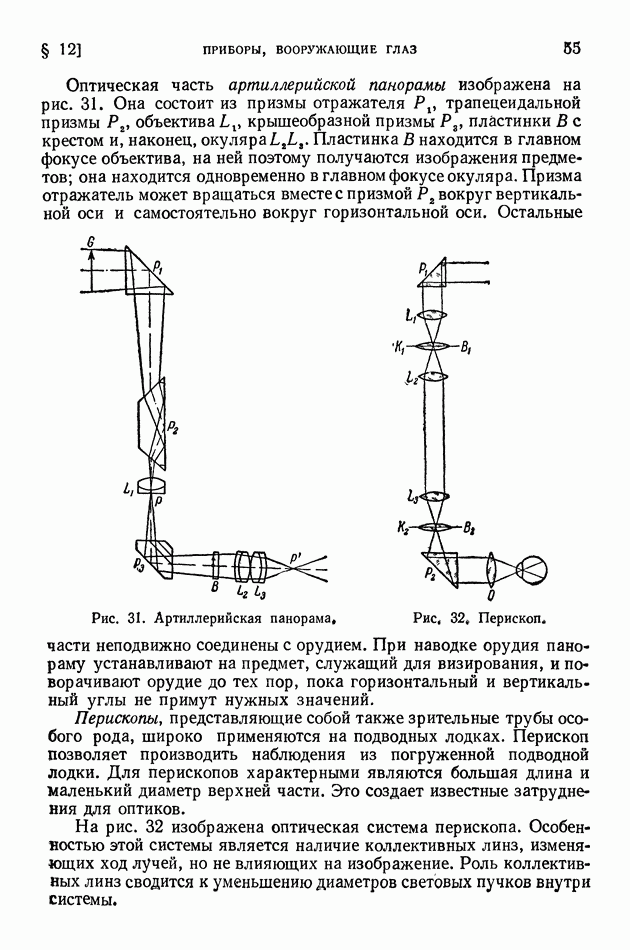
- § 12. Приборы, вооружающие глаз
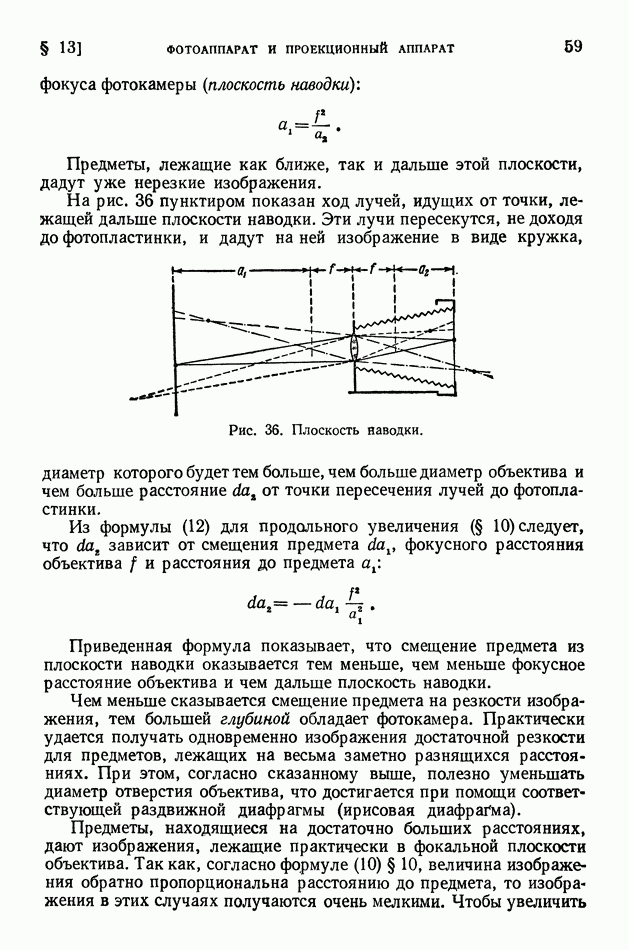
- § 13. Фотоаппарат и проекционный аппарат
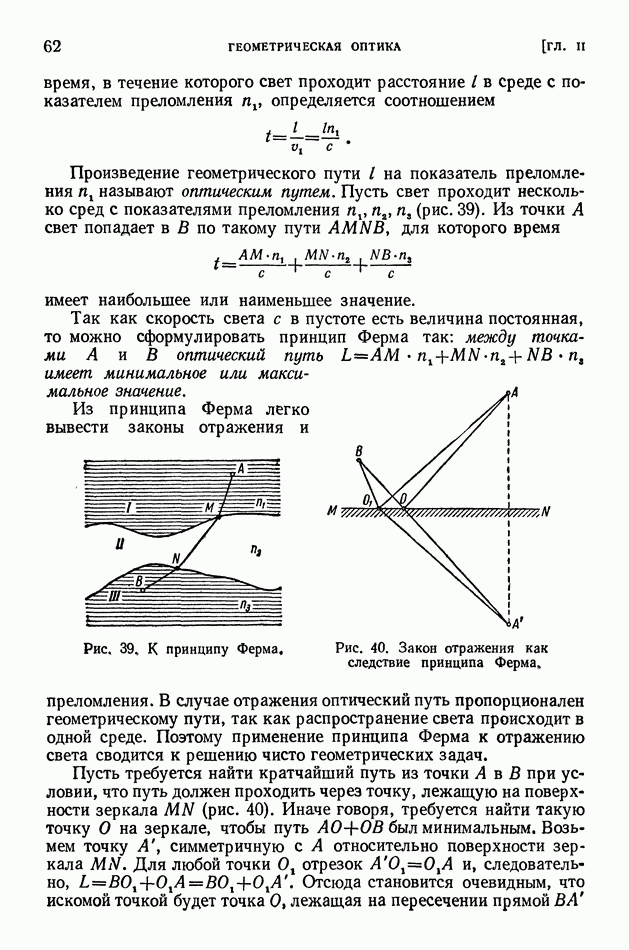
- § 14. Принцип Ферма
- § 15. Электронная оптика
- ГЛАВА III. ИНТЕРФЕРЕНЦИЯ СВЕТА
- § 16. Принцип суперпозиции. Когерентность
- § 17. Зеркала Френеля
- § 18. Цвета тонких пленок. Полосы равной толщины
- § 19. Полосы равного наклона. Просветленная оптика
- § 20. Интерферометры
- § 21. Интерференционное измерение технических мер длины
- § 22. Интерференция многих колебаний
- § 23. Интерференционная спектроскопия
- ГЛАВА IV. ДИФРАКЦИЯ СВЕТА
- § 24. Явление дифракции. Опыт Френеля
- § 25. Принцип Гюйгенса-Френеля
- § 26. Метод зон Френеля
- § 27. Дифракция от узкой щели
- § 28. Дифракционная решетка
- § 29. Дифракционный спектр. Решетки Роуланда и эшелон Майкельсона
- § 30. Плоскостные решетки. Пространственная решетка
- § 31. Структурный рентгеновский анализ
- § 32. Дифракция света на ультразвуковых волнах
- § 33. Дифракция от мелких частиц
- § 34. Разрешающая способность оптических инструментов. Звездный интерферометр
- ГЛАВА V. ПОЛЯРИЗАЦИЯ СВЕТА
- § 35. Поляризация света
- § 36. Двойное лучепреломление
- § 37. Интерференция поляризованного света
- § 38. Оптический метод исследования упругих натяжений. Эффект Керра
- § 39. Вращение плоскости поляризации. Эллиптическая поляризация
- ГЛАВА VI. ДИСПЕРСИЯ, ПОГЛОЩЕНИЕ И ИЗЛУЧЕНИЕ СВЕТА
- § 40. Отражение света
- § 41. Давление света. Опыты Лебедева
- § 42. Дисперсия. Опыты Ньютона
- § 43. Молекулярная теория дисперсии
- § 44. Хроматическая аберрация. Спектрограф
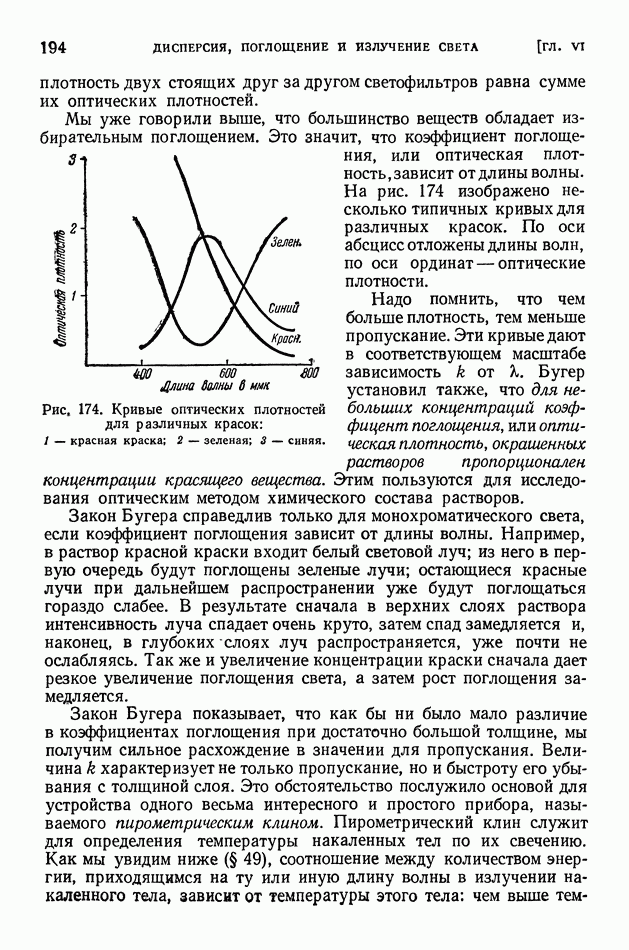
- § 45. Поглощение света
- § 46. Закон Бугера. Опыты Вавилова
- § 47. Атом как элементарный излучатель света
- § 48. Эффект Вавилова — Черенкова
- ГЛАВА VII. ТЕРМОДИНАМИКА ИЗЛУЧЕНИЯ И СВЕТОВОЙ ПОТОК
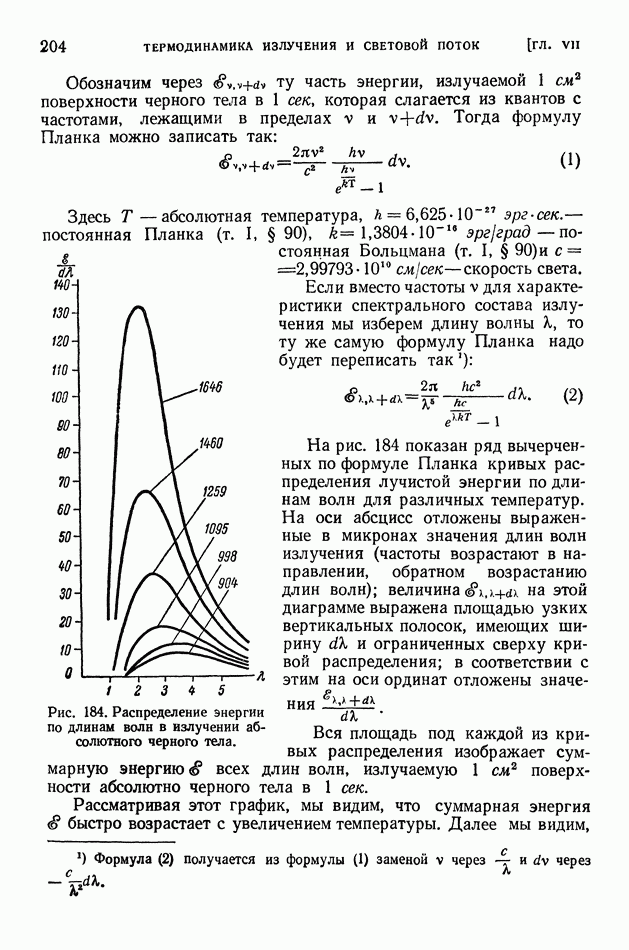
- § 49. Излучение черного тела. Формула Планка. Закон Вина
- § 50. Излучение нечерных тел. Законы Кирхгофа
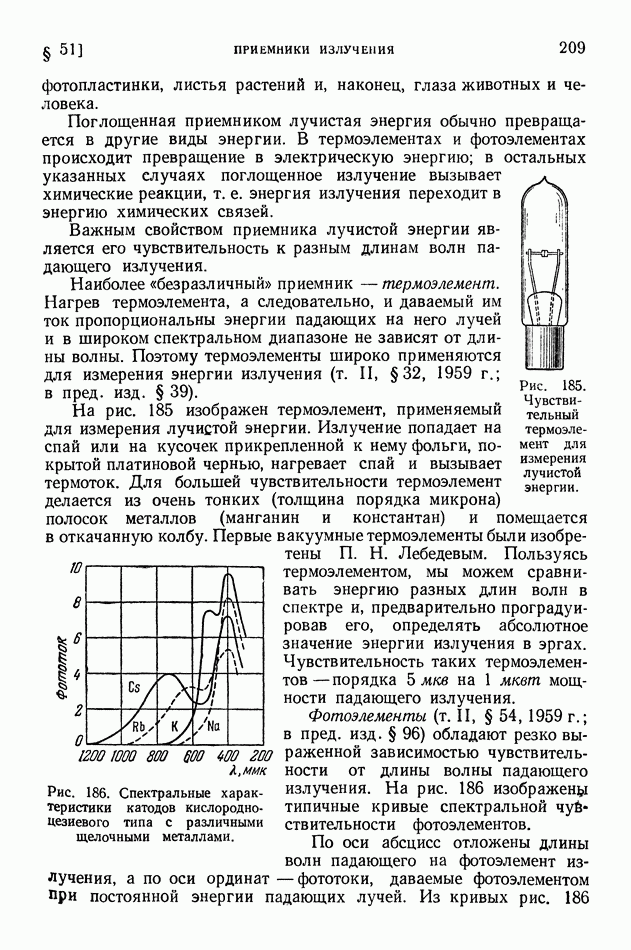
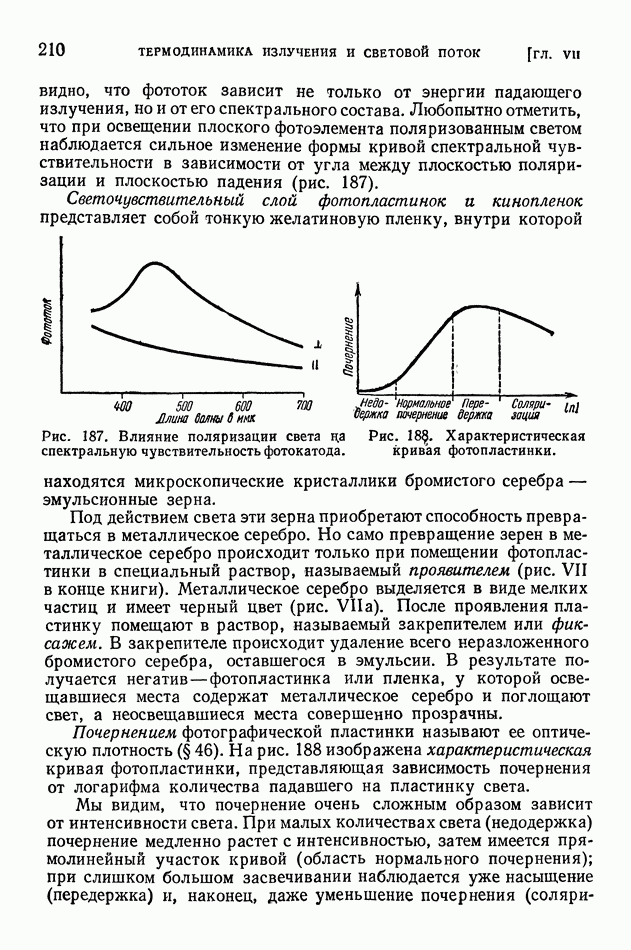
- § 51. Приемники излучения
- § 52. Световые величины и их измерения
- § 53 Температурные излучатели как источники света
- ЧАСТЬ ПЯТАЯ. АТОМНАЯ ФИЗИКА
- ГЛАВА VIII. СТРОЕНИЕ АТОМА И ТЕОРИЯ БОРА
- § 55. Опыты, обнаружившие ядерное строение атомов
- § 56. Противоречие между фактическим строением атомов и выводами классической электродинамики. Строение линейчатых спектров
- § 57. Опытные основания теории квантов в первые годы ее развития
- § 58. Теория Бора. Происхождение спектра водорода
- § 59. Квантовые числа
- § 60. Принцип Паули. Строение электронных оболочек атомов
- § 61. Общая картина возникновения спектров
- ГЛАВА IX. ОСНОВЫ КВАНТОВОЙ (ВОЛНОВОЙ) МЕХАНИКИ
- § 62. Волновые свойства частиц. Формула де Бройля. Дифракция электронов
- § 63. Уравнение Шредингера. Просачивание через энергетический барьер. Нулевая энергия
- § 64. Волномеханическая теория атома водорода
- § 65. Соотношение неопределенностей и его разные трактовки
- ГЛАВА X. КВАНТОВАЯ ОПТИКА
- § 66. Развитие квантовой оптики
- § 67. Спектр щелочных металлов. Спин электрона
- § 68. Спектр гелия. Символика спектральных термов
- § 69. Сверхтонкая структура спектральных линий
- § 70. Атом в силовом поле
- § 71. Молекулярные спектры и строение молекул
- § 72. Комбинационное рассеяние света
- § 73. Квантовая картина испускания света атомами и молекулами
- § 74. Люминесценция
- § 75. Возбуждение люминесценции ударами частиц вещества
- § 76. Применения люминесценции
- § 77. Фотохимические реакции
- ГЛАВА XI. ЗАКОН ПРОПОРЦИОНАЛЬНОСТИ МАССЫ И ЭНЕРГИИ И РЕЛЯТИВИСТСКИЕ СООТНОШЕНИЯ
- § 78. Закон пропорциональности массы и энергии
- § 79. Предварительные замечания о релятивистских эффектах. Зависимость массы от скорости
- § 80. Корпускулярные свойства фотонов. Явление Комптона
- § 81. Вывод закона Эйнштейна сложения скоростей из закона пропорциональности массы и энергии и законов сохранения энергии или количества движения
- § 82. Две трактовки закона пропорциональности массы и энергии и уточнение закона тяготения
- § 83. Красное смещение спектральных линий. Поперечный эффект Доплера
- § 84. Влияние гравитационного поля на скорость света в вакууме и показатель преломления вакуума
- ЧАСТЬ ШЕСТАЯ. ЯДЕРНАЯ ФИЗИКА
- § 85. Заряд и масса ядра. Масс-спектральный анализ
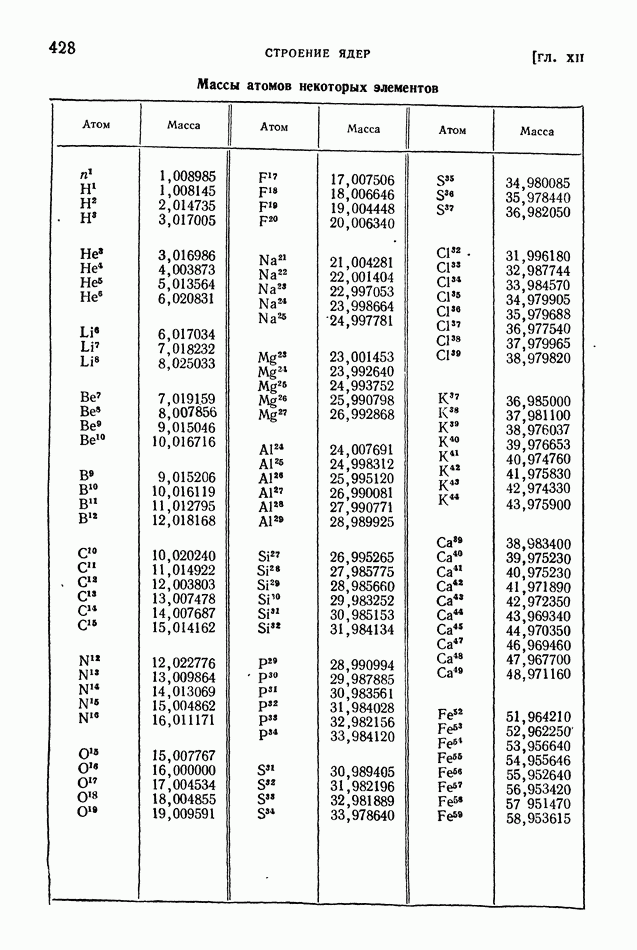
- § 86. Состав ядер. Изотопы. Атомные единицы массы и энергии
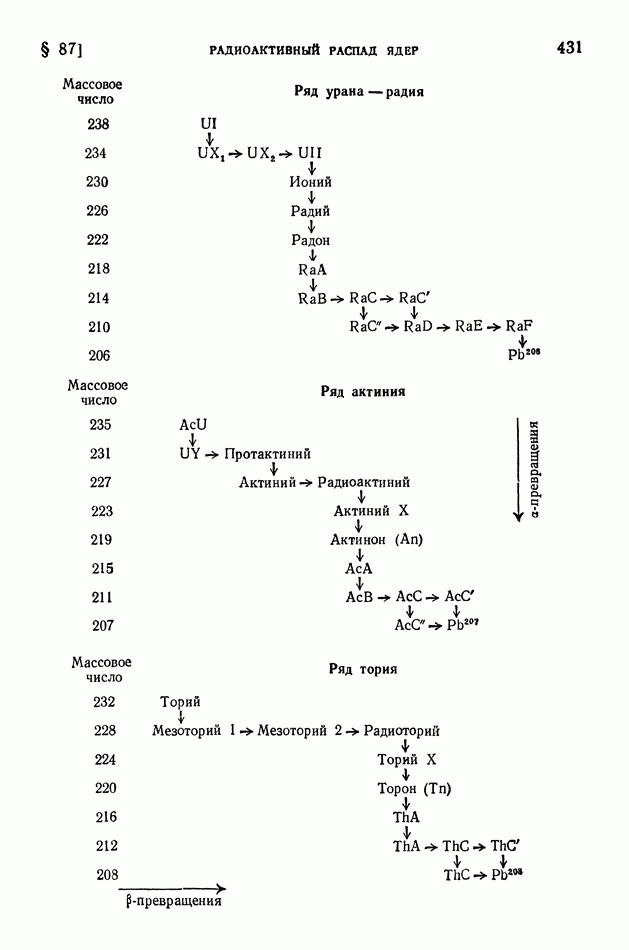
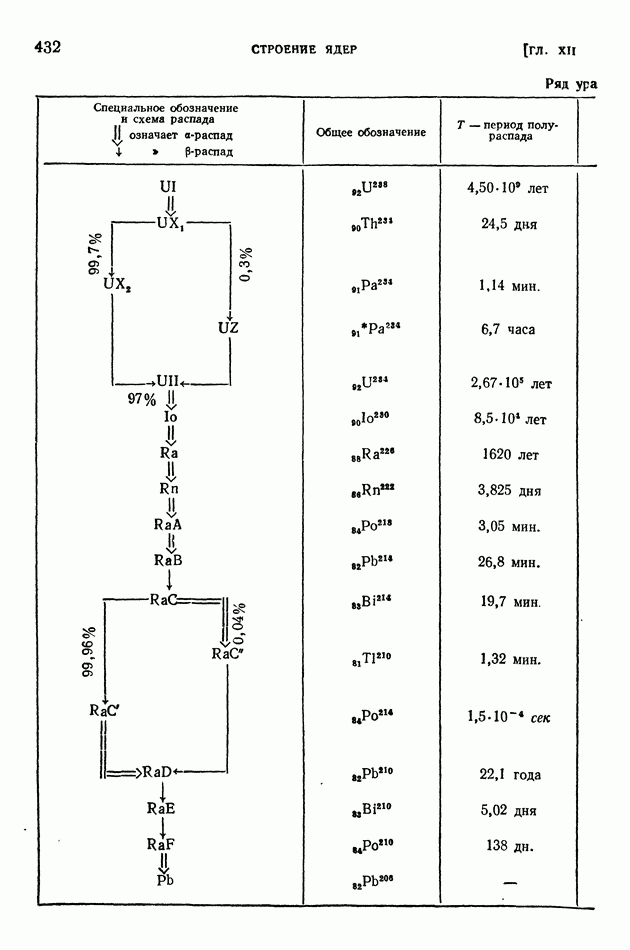
- § 87. Радиоактивный распад ядер. Закон радиоактивного смещения. Изомеры
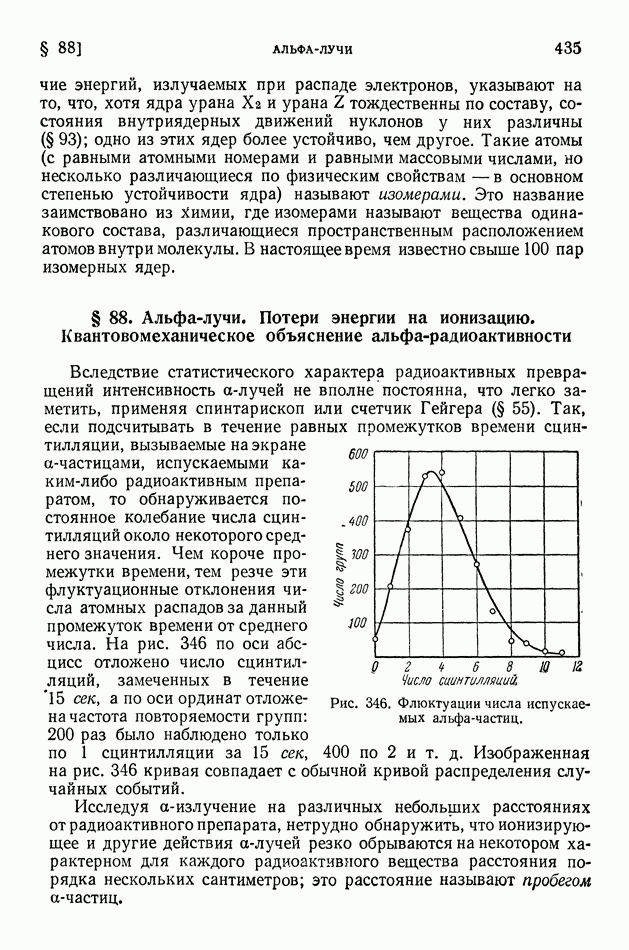
- § 88. Альфа-лучи. Потери энергии на ионизацию. Квантовомеханическое объяснение альфа-радиоактивности
- § 89. Бета- и гамма-лучи
- § 90. Искусственное расщепление ядер. Открытие нейтрона
- § 91. Открытие позитрона. Взаимопревращение фотонов определенной энергии и электронно-позитронных пар
- § 92. Индуцированная позитронная и электронная радиоактивность. Фоторасщепление ядер, K-захват
- § 93. Энергетические уровни ядер. Внутренняя конверсия. Нейтрино
- § 94. Капельная теория строения ядер
- § 95. Деление ядер и развитие капельной теории строения ядер
- ГЛАВА XIII. КОСМИЧЕСКИЕ ЛУЧИ
- § 96. Методы исследования и первые итоги изучения космических лучей
- § 97. Каскадное образование электронно-позитронных пар в космических лучах. Потери энергии электронами на тормозное излучение
- § 98. «мю»-мезоны. Зависимость времени жизни неустойчивых частиц от скорости движения
- § 99. «пи»-мезоны
- § 100. Взрывные ядерные ливни и их каскадное развитие в космических лучах
- § 101. Корпускулярный и энергетический спектр космических лучей. Происхождение космического излучения
- ГЛАВА XIV. ЭКСПЕРИМЕНТАЛЬНЫЕ СРЕДСТВА ЯДЕРНОЙ ФИЗИКИ
- § 102. Циклотроны
- § 103. Фазотроны
- § 104. Бетатроны
- § 105. Синхротроны и синхрофазотроны
- § 106. Линейные ускорители электронов и ионов
- § 107. Лабораторные источники нейтронов. Замедлители нейтронов в ядерных реакторах
- § 108. Усовершенствование методов наблюдения и счета частиц
- ГЛАВА XV. ЯДЕРНЫЕ РЕАКЦИИ И АТОМНАЯ ЭНЕРГИЯ
- § 109. Основные виды и обозначения ядерных реакций. Конкурирующие процессы в ядерных реакциях
- § 110. Энергетический эффект, энергия возбуждения и порог ядерных реакций
- § 111. Превращения элементарных частиц
- § 112. Ядерные силы
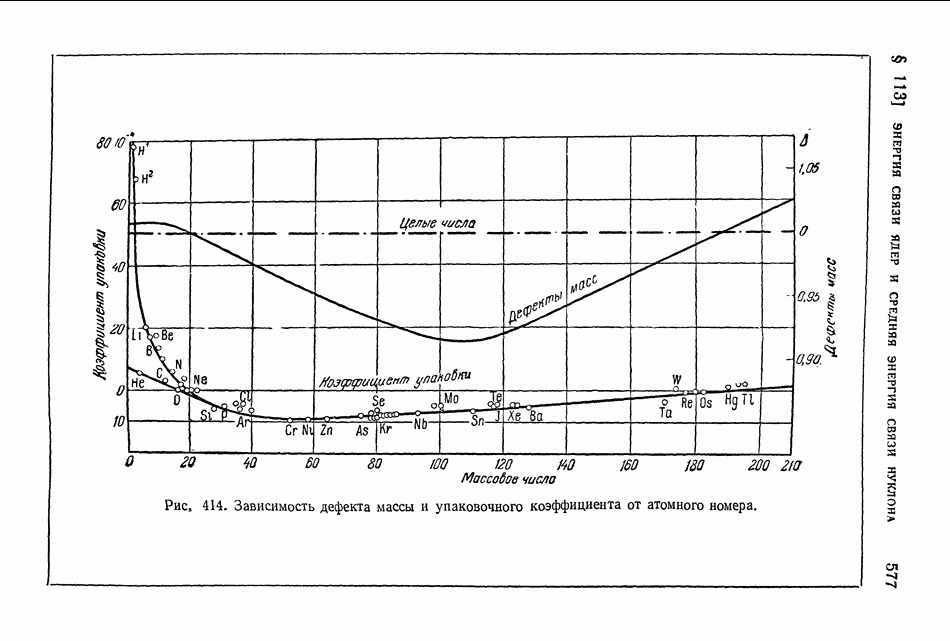
- § 113. Энергия связи ядер и средняя энергия связи нуклона
- § 114. Полуэмпирическая формула для энергии ядерной связи и для атомных энергий и масс
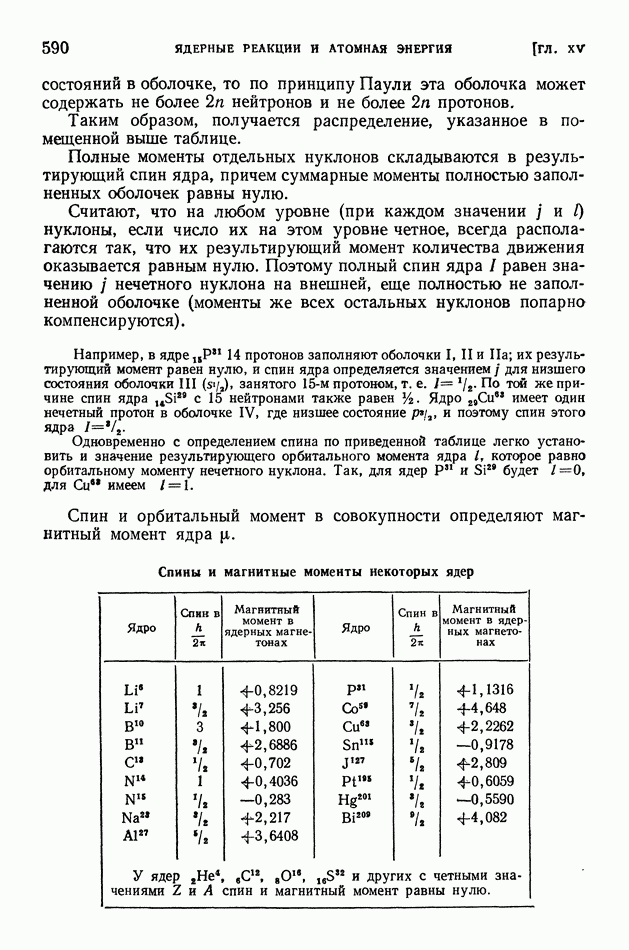
- § 115. Взаимосвязь энергии и строения ядер. Внутриядерное движение нуклонов и нуклонные оболочки. Спины и магнитные моменты ядер
- § 116. Энергия отделения частиц и анализ возможного хода ядерной реакции
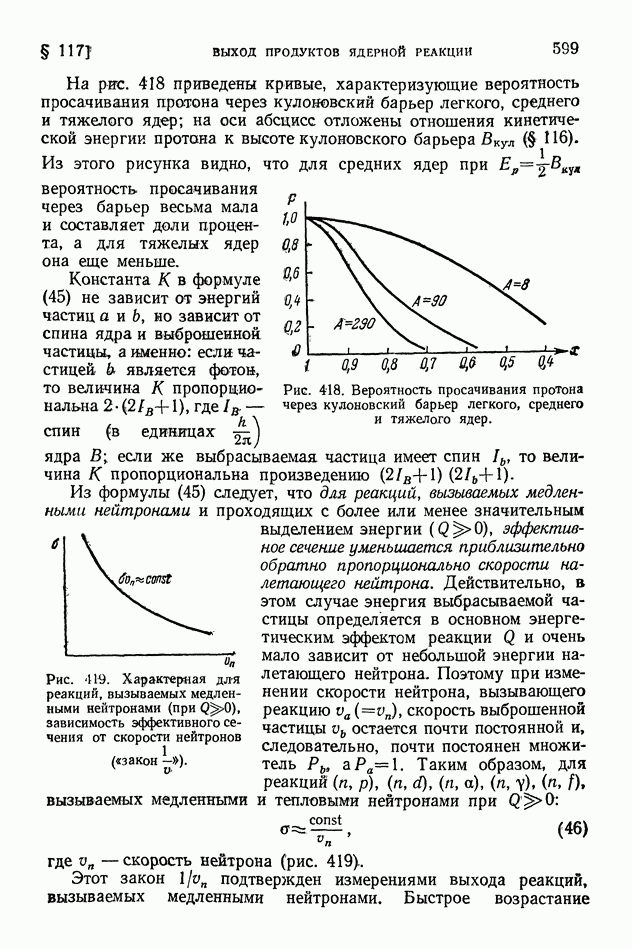
- § 117. Выход продуктов ядерной реакции. Эффективные сечения. Резонансные явления
- § 118. Цепной процесс деления ядер. Активно делящиеся вещества. Ядерные реакторы
- § 119. Термоядерные реакции
- § 120. Применение ядерных реакций
- § 121. Ядерные реакции в звездах