| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
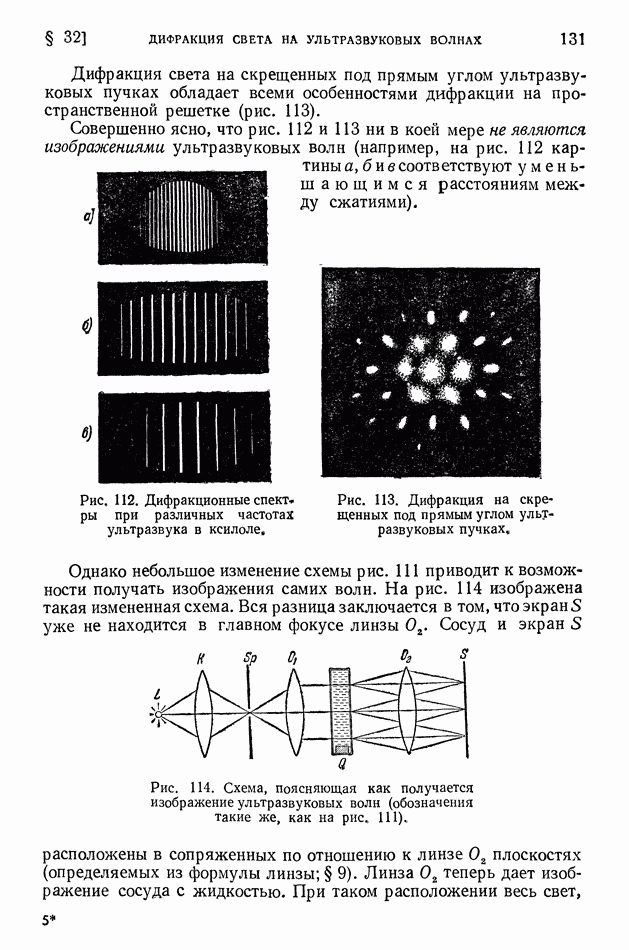
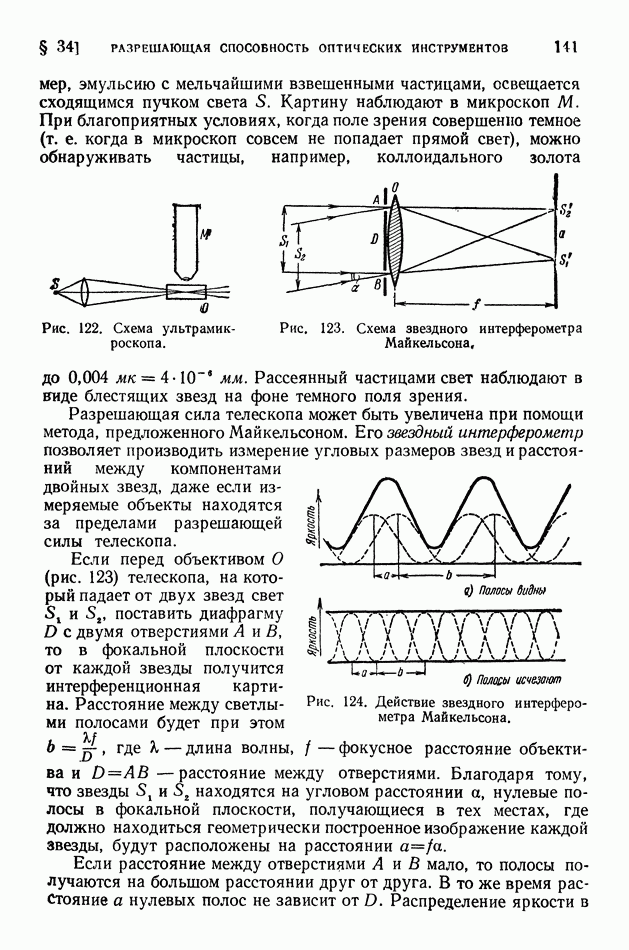
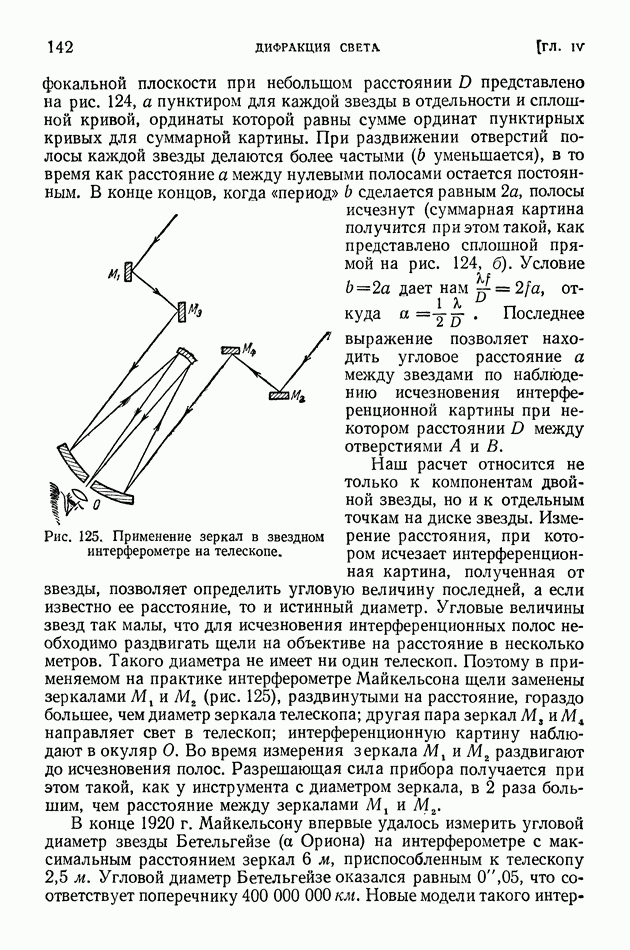
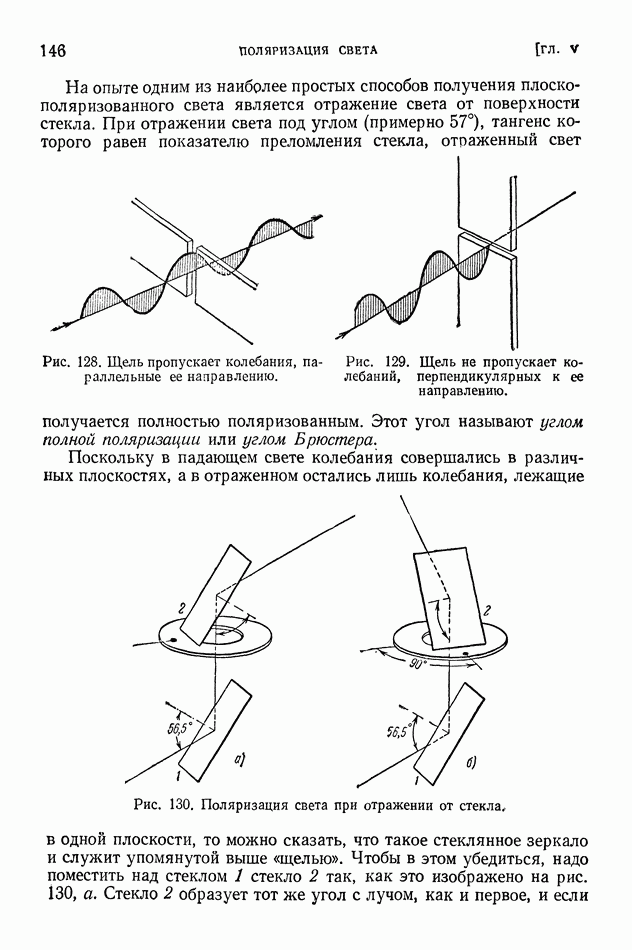
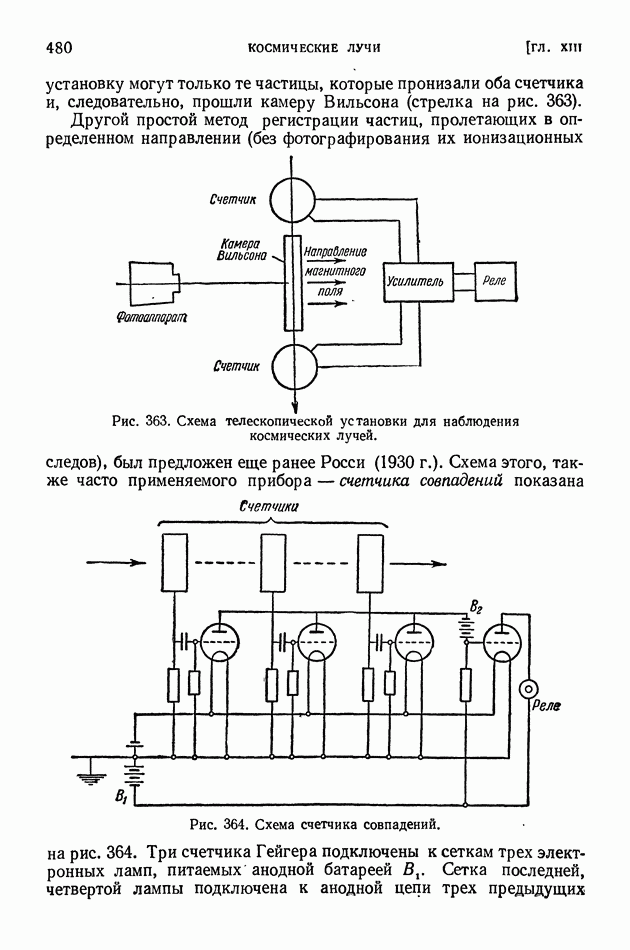
§ 27. Дифракция от узкой щели
Во многих оптических приборах используется дифракция света на узких щелях, применяемых в сочетании с линзами.
Рассчитаем действие щели в разных точках экрана, находящегося в фокусе линзы, когда на щель падает плоская волна (рис. 92). Ясно, что при таком расположении щели, линзы и экрана ни о каком резком изображении щели говорить нельзя. Согласно законам геометрической оптики линза должна дать на экране, помещенном в главной фокальной плоскости, не изображение щели, а четкое изображение бесконечно удаленного источника света, освещающего щель (например, точку или линию).
Однако дифракция на щели осложнит картину. Все точки волновой поверхности, совпадающей с плоскостью щели, колеблются с одинаковой фазой. Следовательно, интерференция при излучении вторичных колебаний в разных направлениях будет происходить только за счет разности хода отдельных колебаний, возникающей после прохождения щели.

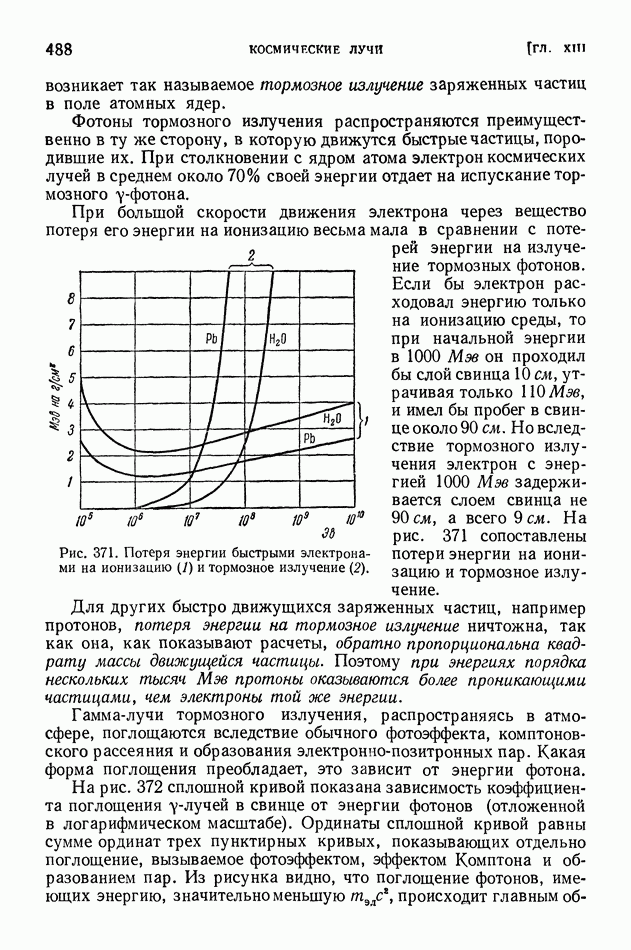
Рис. 92. Дифракция от щели.
Кроме того, так как линза не создает дополнительной разности хода (§ 14), то разность хода между отдельными колебаниями будет возникать только до линзы.
Для того чтобы определить разность хода между двумя колебаниями, достаточно из точки на поверхности щели, через которую проходит один луч, опустить перпендикуляр на другой луч (рис. 92). Тогда расстояние по этому второму лучу от плоскости щели до основания перпендикуляра и будет искомой разностью хода. В данном случае зоны Френеля, очевидно, будут иметь вид прямоугольных полосок, параллельных краям щели. Число зон Френеля будет зависеть от ширины щели а, угла наблюдения  и длины волны К. Поскольку разность хода между лучами, проходящими через края одной зоны Френеля, равна у, из геометрических соображений легко получить, что ширина зоны будет равна (разность хода — катет, ширина зоны — гипотенуза). Число зон Френеля
и длины волны К. Поскольку разность хода между лучами, проходящими через края одной зоны Френеля, равна у, из геометрических соображений легко получить, что ширина зоны будет равна (разность хода — катет, ширина зоны — гипотенуза). Число зон Френеля  укладывающихся в щели, будет равно:
укладывающихся в щели, будет равно:

Мы видим, что  при постоянных
при постоянных  зависит от угла наблюдения
зависит от угла наблюдения  Чем больше угол наблюдения, тем больше число зон Френеля укладывается в щели.
Чем больше угол наблюдения, тем больше число зон Френеля укладывается в щели.
Следует указать, что когда наблюдение ведется с помощью линзы (рис. 92), то при положении экрана в главном фокусе различным углам  соответствуют отдельные точки экрана. Поэтому мы можем говорить о наблюдении под различными углами, понимая под этим различные точки экрана. Когда
соответствуют отдельные точки экрана. Поэтому мы можем говорить о наблюдении под различными углами, понимая под этим различные точки экрана. Когда  равно целому четному числу
равно целому четному числу  где k — целое число), то все зоны можно разбить на у пар; в результате интерференции действие двух соседних зон Френеля равно нулю, а следовательно, равно нулю и действие всей щели. Таким образом, под углами
где k — целое число), то все зоны можно разбить на у пар; в результате интерференции действие двух соседних зон Френеля равно нулю, а следовательно, равно нулю и действие всей щели. Таким образом, под углами  соответствующими четным
соответствующими четным  мы будем наблюдать темноту. Формула, определяющая эти углы, имеет следующий вид:
мы будем наблюдать темноту. Формула, определяющая эти углы, имеет следующий вид:

где  целое число.
целое число.
Когда  равно целому нечетному числу
равно целому нечетному числу  то действие щели эквивалентно действию одной зоны Френеля, ибо действие остальных зон взаимно компенсируется. В этом случае мы наблюдаем максимум света.
то действие щели эквивалентно действию одной зоны Френеля, ибо действие остальных зон взаимно компенсируется. В этом случае мы наблюдаем максимум света.
Формула, определяющая направление максимумов света, имеет следующий вид:

Из рис. 92 видно, что смысл формул (1) и (2) заключается в следующем: если разность хода между крайними лучами, проходящими сквозь щель, равна четному числу полуволн, то мы наблюдаем темноту; если разность хода между этими лучами равна нечетному числу полуволн, то мы наблюдаем максимум света.
Мы видим, что в пространстве за щелью вместо геометрического силуэта щели получаются полосы, которые легко наблюдать на опыте. По мере удаления от центральной (нулевой) полосы, которой соответствует разность хода нуль, интенсивность отдельных полос быстро убывает (рис. 93). Чем уже щель, тем дальше отстоят друг от друга дифракционные полосы. Благодаря тому что они приходятся на разные углы в зависимости от длины волн  картина в белом свете имеет радужную окраску. Полученный результат справедлив и при наблюдении без линзы, когда точка наблюдения
картина в белом свете имеет радужную окраску. Полученный результат справедлив и при наблюдении без линзы, когда точка наблюдения  так далека от щели, что все лучи, идущие к ней, можно считать параллельными между собой.
так далека от щели, что все лучи, идущие к ней, можно считать параллельными между собой.
Если взять очень узкий, непрозрачный экран (нить), то получаемая дифракционная картина эквивалентна интерференционной от двух источников, помещенных на расстоянии диаметра нити. Роль этих источников света играют те зоны Френеля, которые
непосредственно прилегают к краям нити. Вместо геометрической тени при этом получается система полос, быстро убывающих по интенсивности, со светлой полосой в центре. Так как вся картина значительно превышает размеры геометрического силуэта нити, то дифракционной картиной пользуются для измерения диаметра очень тонких нитей, например для определения толщины волокон шерсти.

Рис. 93. Дифракционная картина от щели.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ЧАСТЬ ЧЕТВЕРТАЯ. ОПТИКА
- § 2. Электромагнитная теория света
- § 3. Скорость света
- § 4. Опыт Майкельсона
- § 5. Отрицательный результат опыта Майкельсона и теория относительности
- § 6. Некоторые замечания о теории относительности
- § 7. Явление Доплера для световых волн
- ГЛАВА II. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- § 8. Законы отражения и преломления света
- § 9. Линза
- § 10. Оптические системы
- § 11. Глаз как оптическая система
- § 12. Приборы, вооружающие глаз
- § 13. Фотоаппарат и проекционный аппарат
- § 14. Принцип Ферма
- § 15. Электронная оптика
- ГЛАВА III. ИНТЕРФЕРЕНЦИЯ СВЕТА
- § 16. Принцип суперпозиции. Когерентность
- § 17. Зеркала Френеля
- § 18. Цвета тонких пленок. Полосы равной толщины
- § 19. Полосы равного наклона. Просветленная оптика
- § 20. Интерферометры
- § 21. Интерференционное измерение технических мер длины
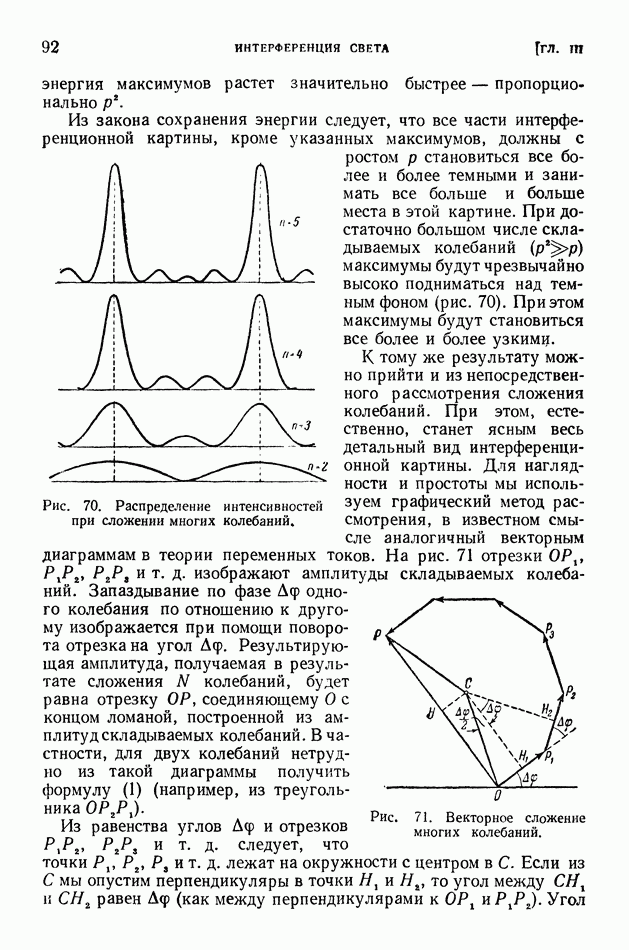
- § 22. Интерференция многих колебаний
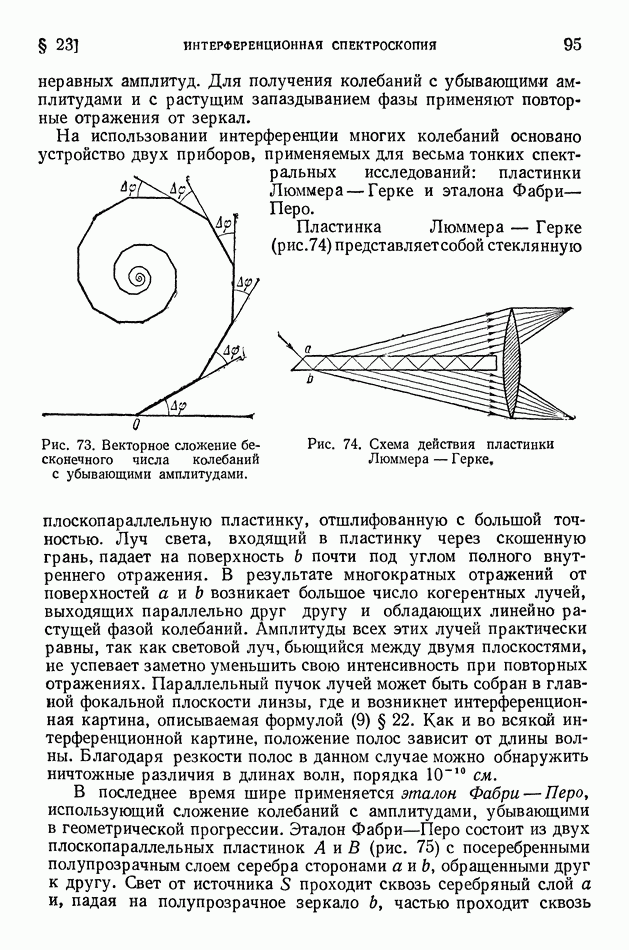
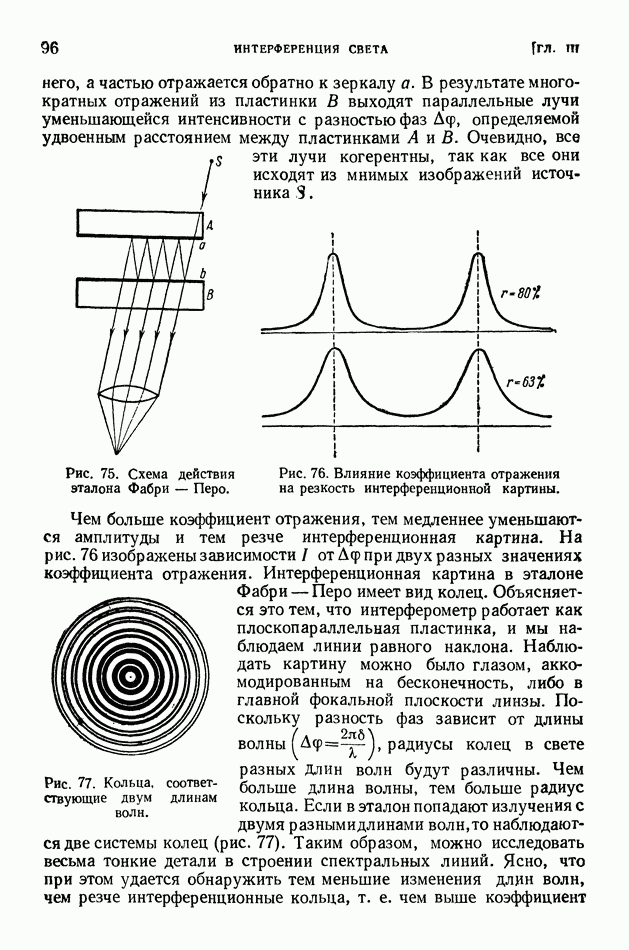
- § 23. Интерференционная спектроскопия
- ГЛАВА IV. ДИФРАКЦИЯ СВЕТА
- § 24. Явление дифракции. Опыт Френеля
- § 25. Принцип Гюйгенса-Френеля
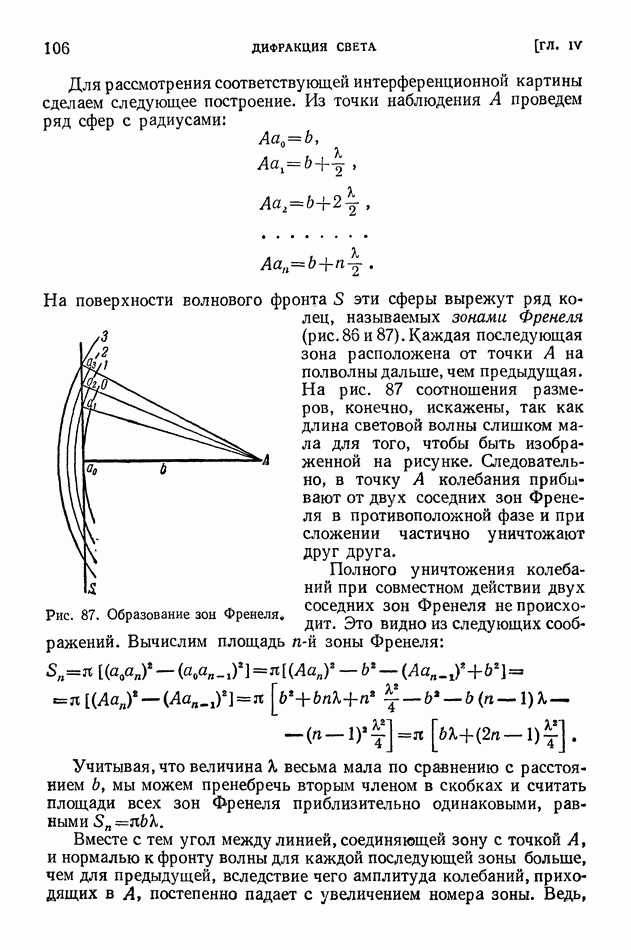
- § 26. Метод зон Френеля
- § 27. Дифракция от узкой щели
- § 28. Дифракционная решетка
- § 29. Дифракционный спектр. Решетки Роуланда и эшелон Майкельсона
- § 30. Плоскостные решетки. Пространственная решетка
- § 31. Структурный рентгеновский анализ
- § 32. Дифракция света на ультразвуковых волнах
- § 33. Дифракция от мелких частиц
- § 34. Разрешающая способность оптических инструментов. Звездный интерферометр
- ГЛАВА V. ПОЛЯРИЗАЦИЯ СВЕТА
- § 35. Поляризация света
- § 36. Двойное лучепреломление
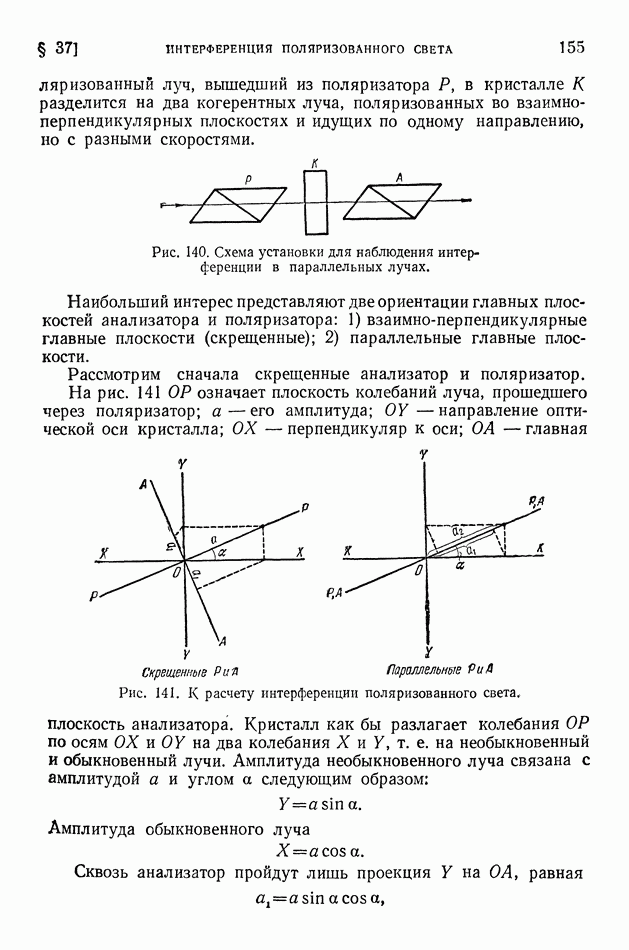
- § 37. Интерференция поляризованного света
- § 38. Оптический метод исследования упругих натяжений. Эффект Керра
- § 39. Вращение плоскости поляризации. Эллиптическая поляризация
- ГЛАВА VI. ДИСПЕРСИЯ, ПОГЛОЩЕНИЕ И ИЗЛУЧЕНИЕ СВЕТА
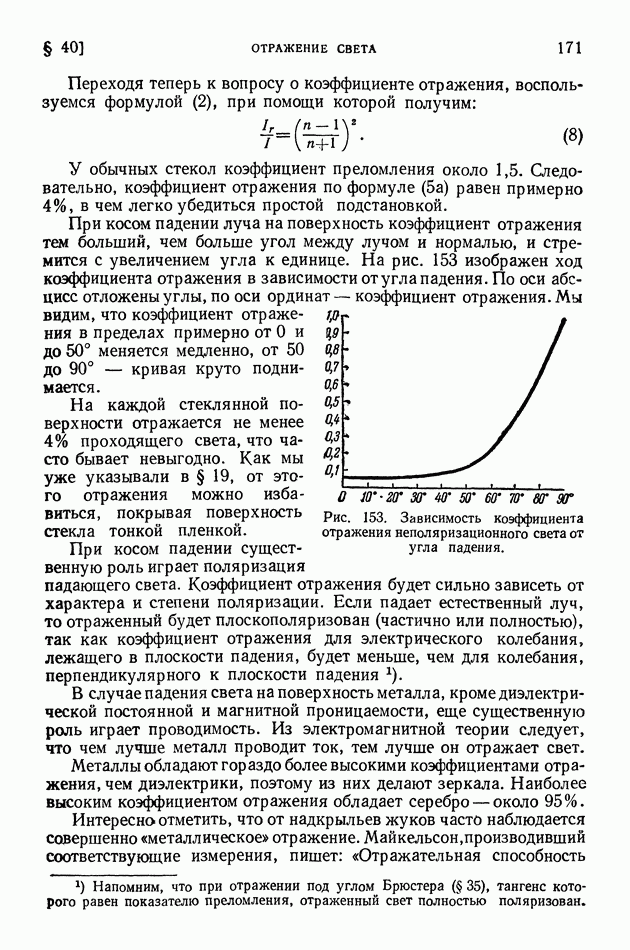
- § 40. Отражение света
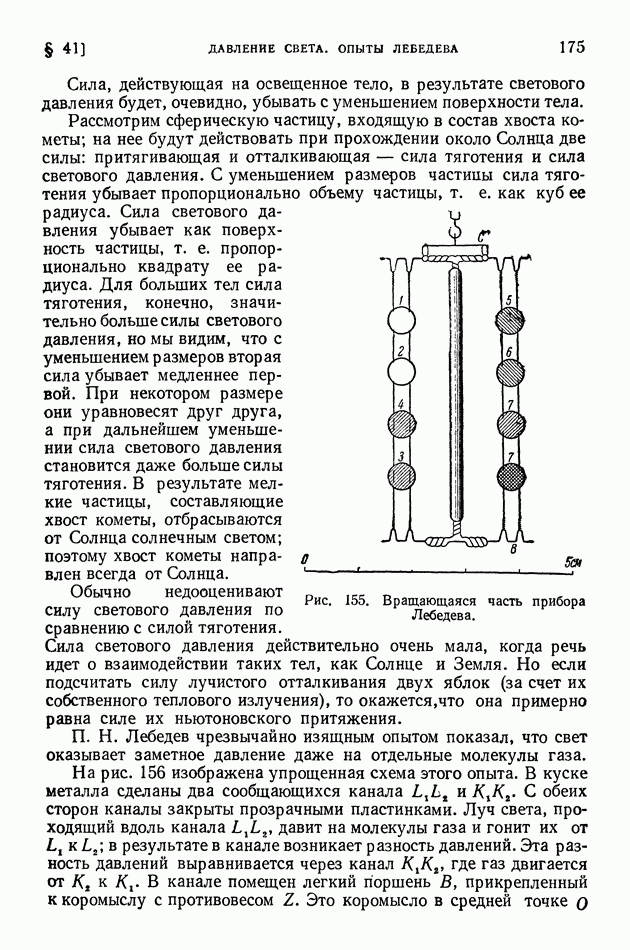
- § 41. Давление света. Опыты Лебедева
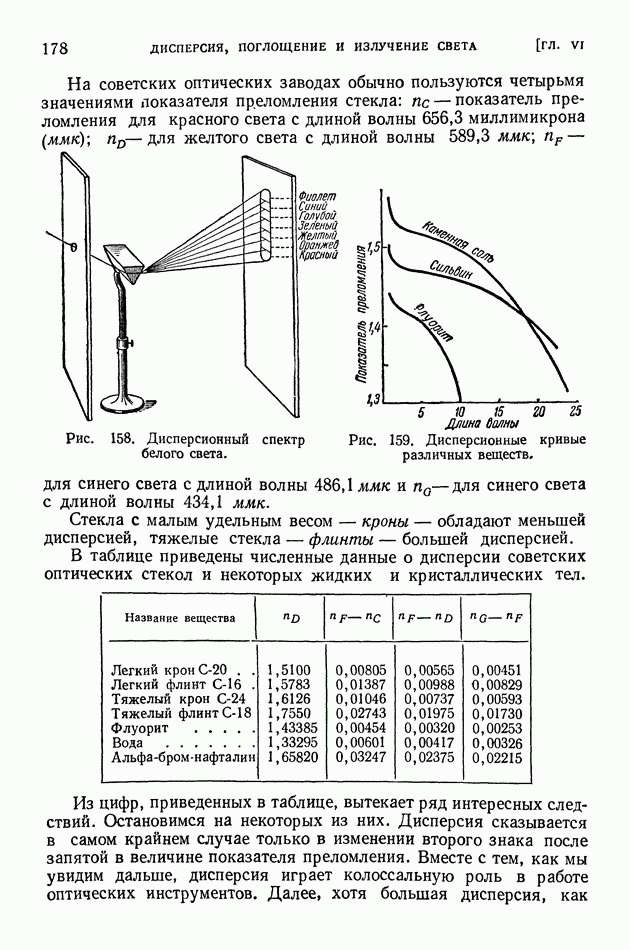
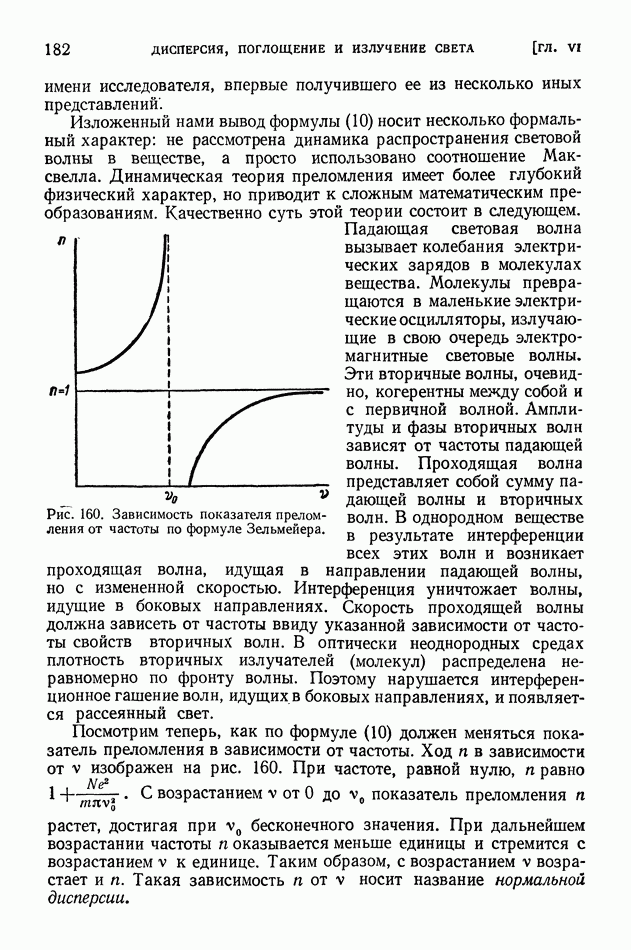
- § 42. Дисперсия. Опыты Ньютона
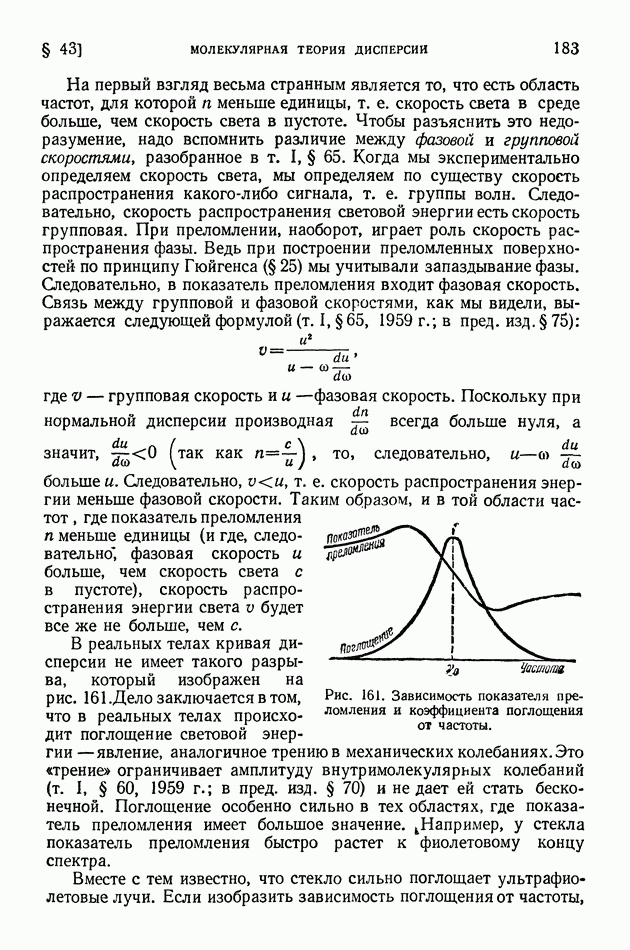
- § 43. Молекулярная теория дисперсии
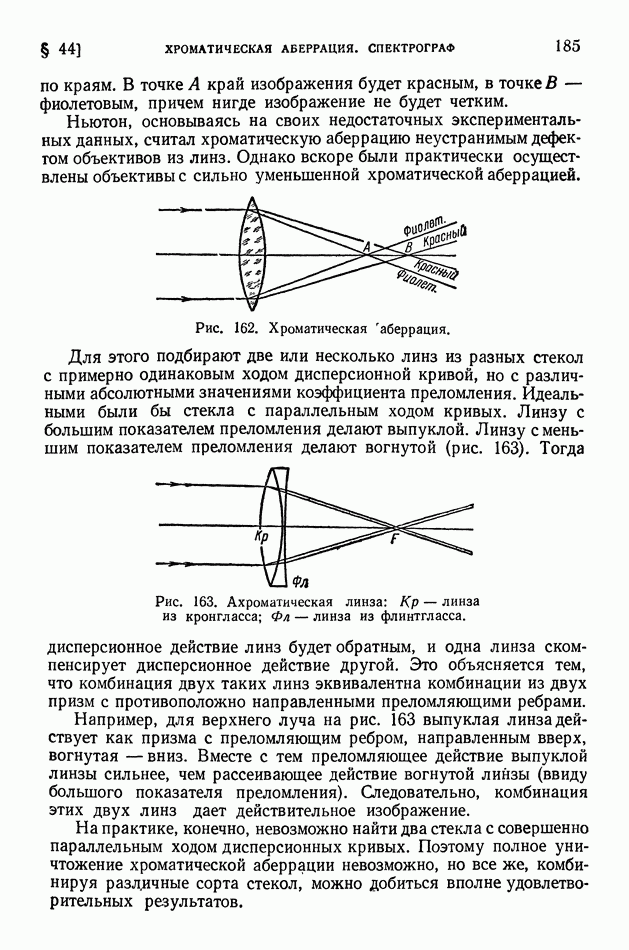
- § 44. Хроматическая аберрация. Спектрограф
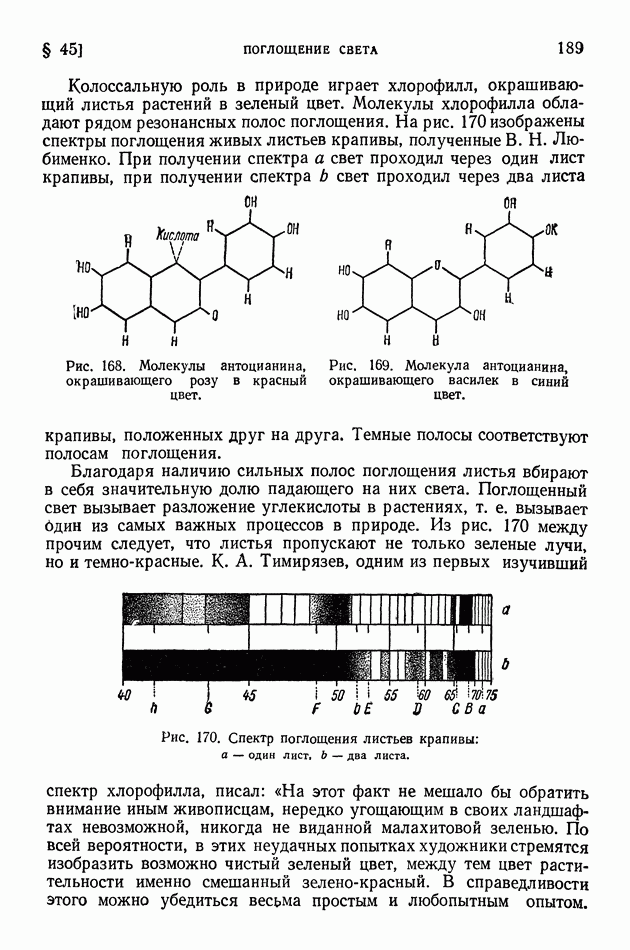
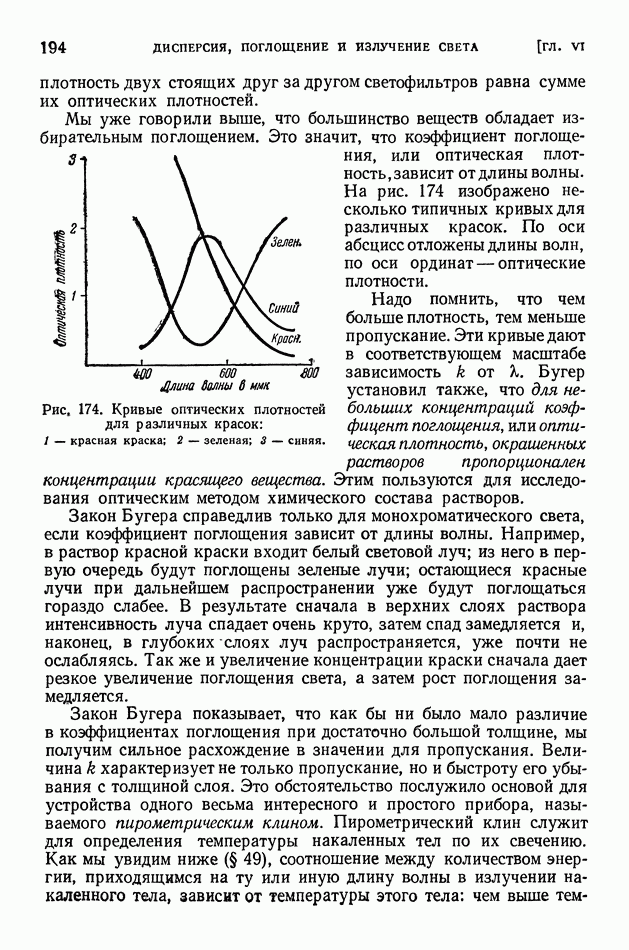
- § 45. Поглощение света
- § 46. Закон Бугера. Опыты Вавилова
- § 47. Атом как элементарный излучатель света
- § 48. Эффект Вавилова — Черенкова
- ГЛАВА VII. ТЕРМОДИНАМИКА ИЗЛУЧЕНИЯ И СВЕТОВОЙ ПОТОК
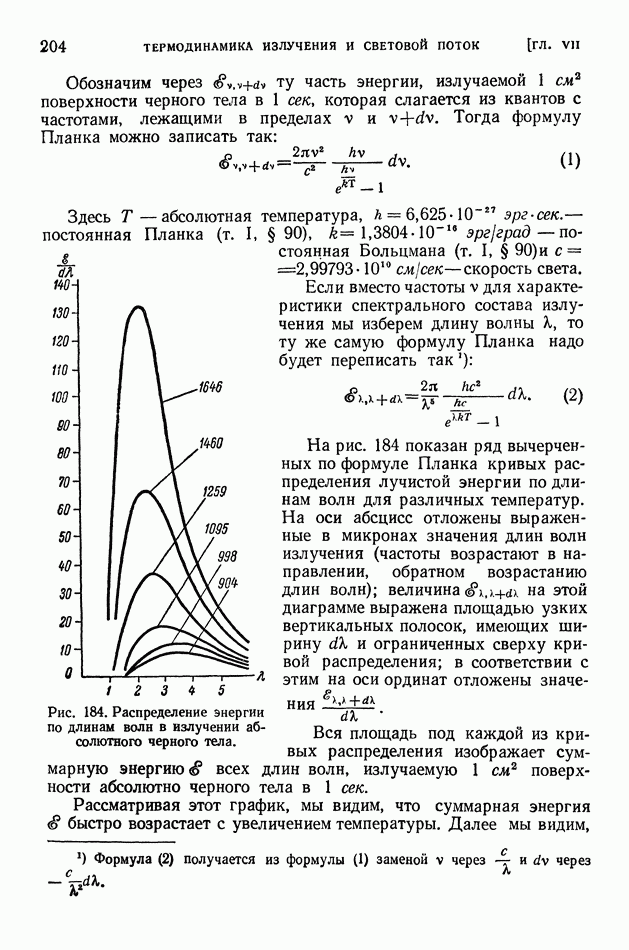
- § 49. Излучение черного тела. Формула Планка. Закон Вина
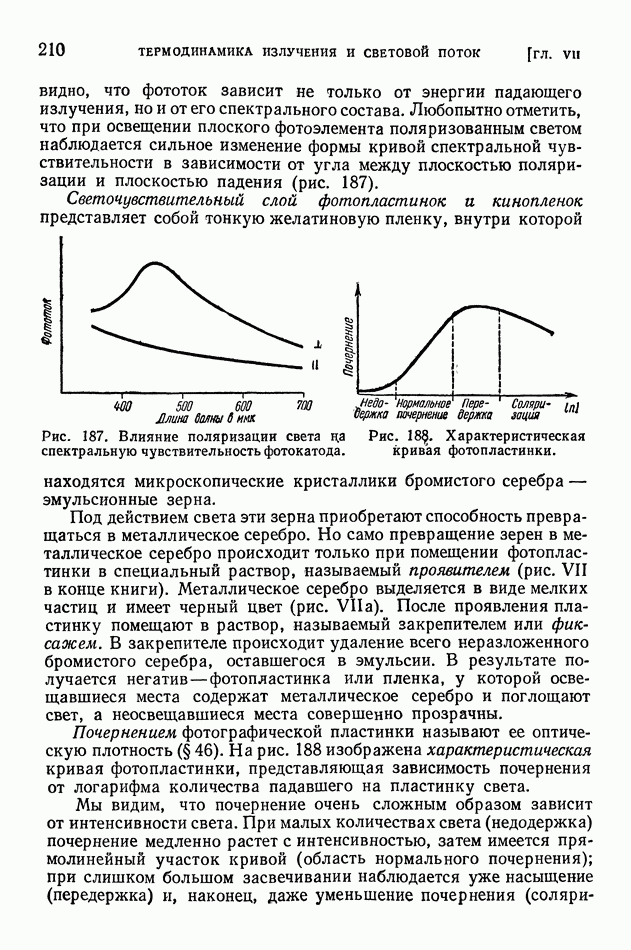
- § 50. Излучение нечерных тел. Законы Кирхгофа
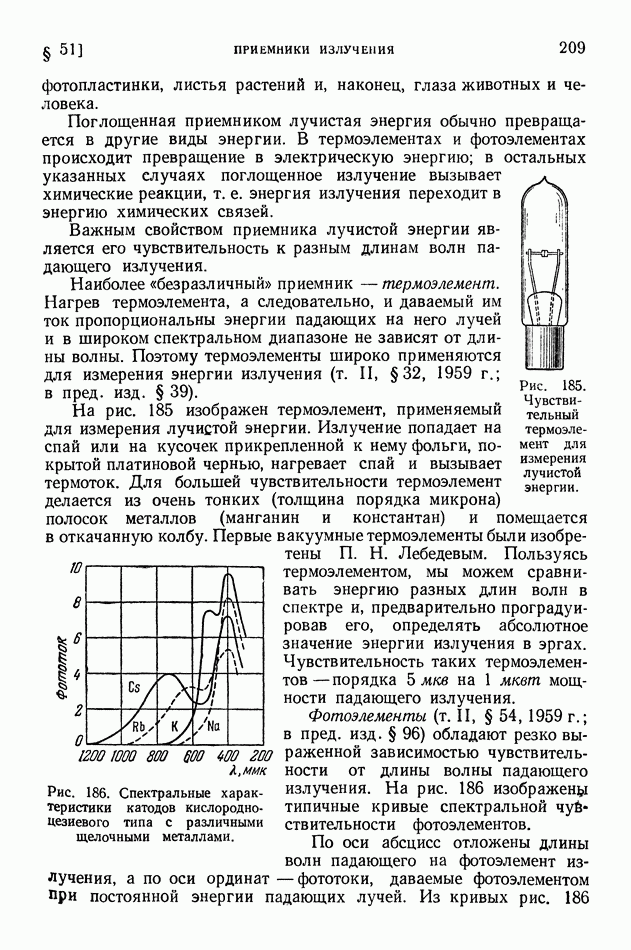
- § 51. Приемники излучения
- § 52. Световые величины и их измерения
- § 53 Температурные излучатели как источники света
- ЧАСТЬ ПЯТАЯ. АТОМНАЯ ФИЗИКА
- ГЛАВА VIII. СТРОЕНИЕ АТОМА И ТЕОРИЯ БОРА
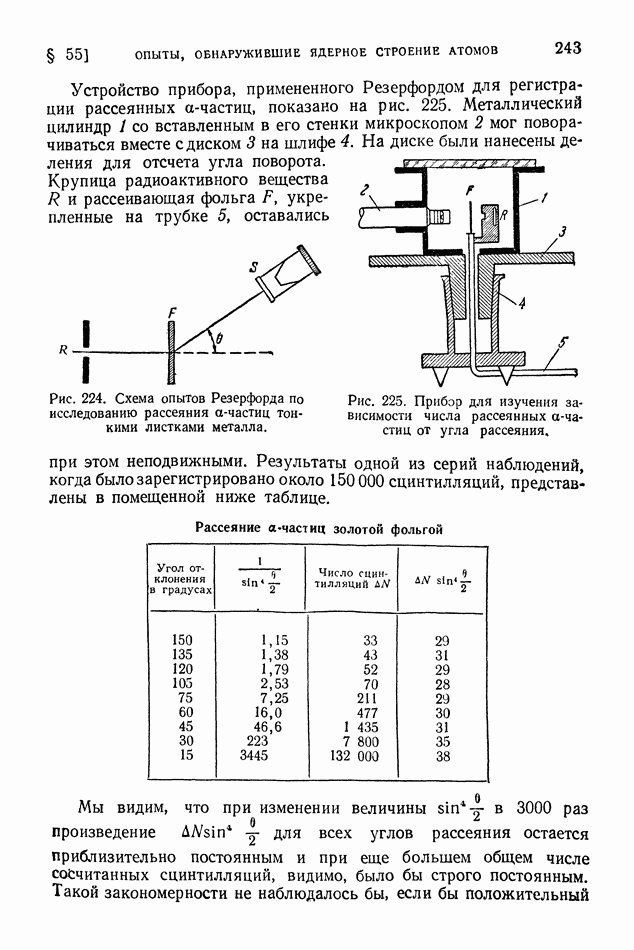
- § 55. Опыты, обнаружившие ядерное строение атомов
- § 56. Противоречие между фактическим строением атомов и выводами классической электродинамики. Строение линейчатых спектров
- § 57. Опытные основания теории квантов в первые годы ее развития
- § 58. Теория Бора. Происхождение спектра водорода
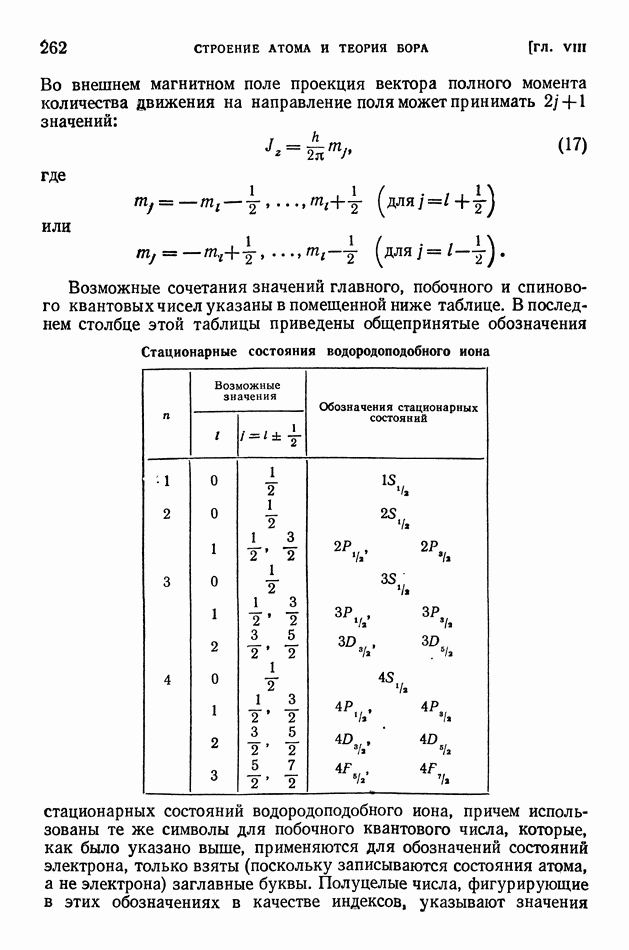
- § 59. Квантовые числа
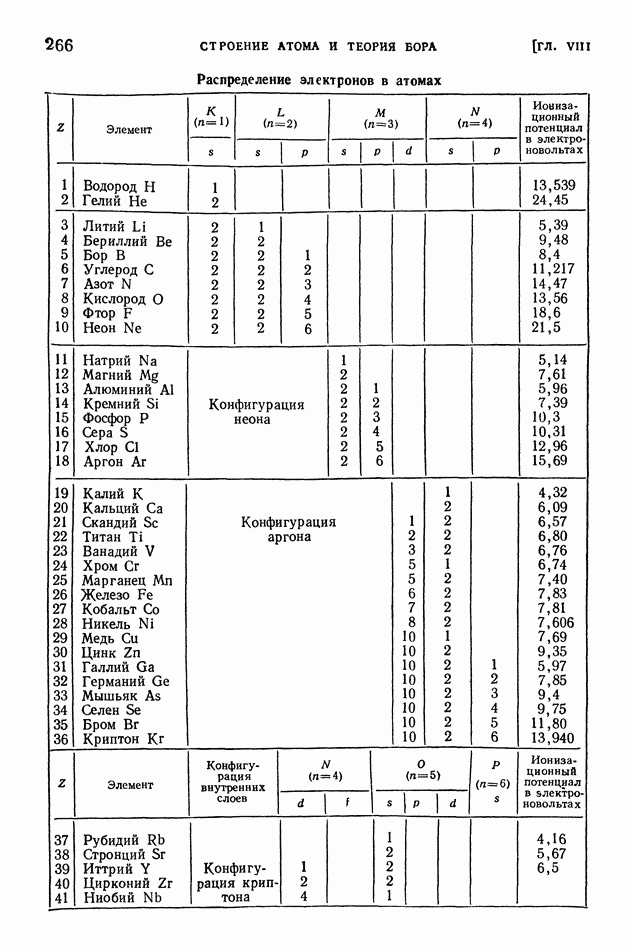
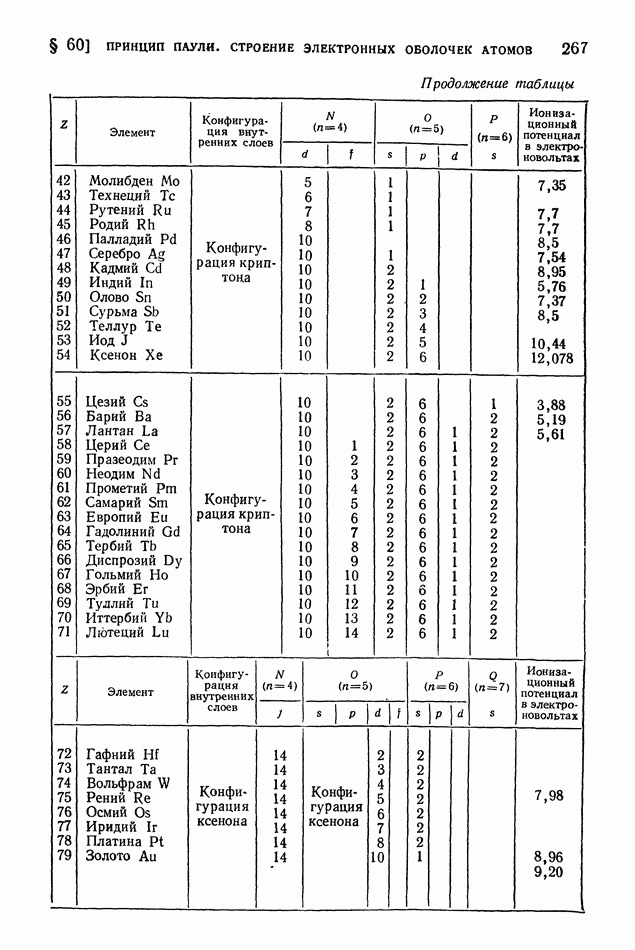
- § 60. Принцип Паули. Строение электронных оболочек атомов
- § 61. Общая картина возникновения спектров
- ГЛАВА IX. ОСНОВЫ КВАНТОВОЙ (ВОЛНОВОЙ) МЕХАНИКИ
- § 62. Волновые свойства частиц. Формула де Бройля. Дифракция электронов
- § 63. Уравнение Шредингера. Просачивание через энергетический барьер. Нулевая энергия
- § 64. Волномеханическая теория атома водорода
- § 65. Соотношение неопределенностей и его разные трактовки
- ГЛАВА X. КВАНТОВАЯ ОПТИКА
- § 66. Развитие квантовой оптики
- § 67. Спектр щелочных металлов. Спин электрона
- § 68. Спектр гелия. Символика спектральных термов
- § 69. Сверхтонкая структура спектральных линий
- § 70. Атом в силовом поле
- § 71. Молекулярные спектры и строение молекул
- § 72. Комбинационное рассеяние света
- § 73. Квантовая картина испускания света атомами и молекулами
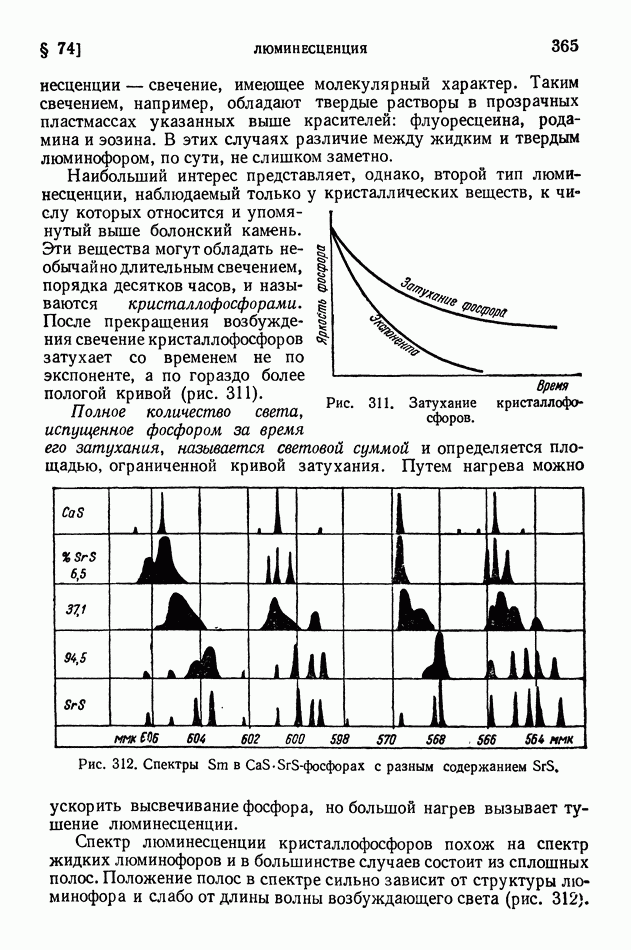
- § 74. Люминесценция
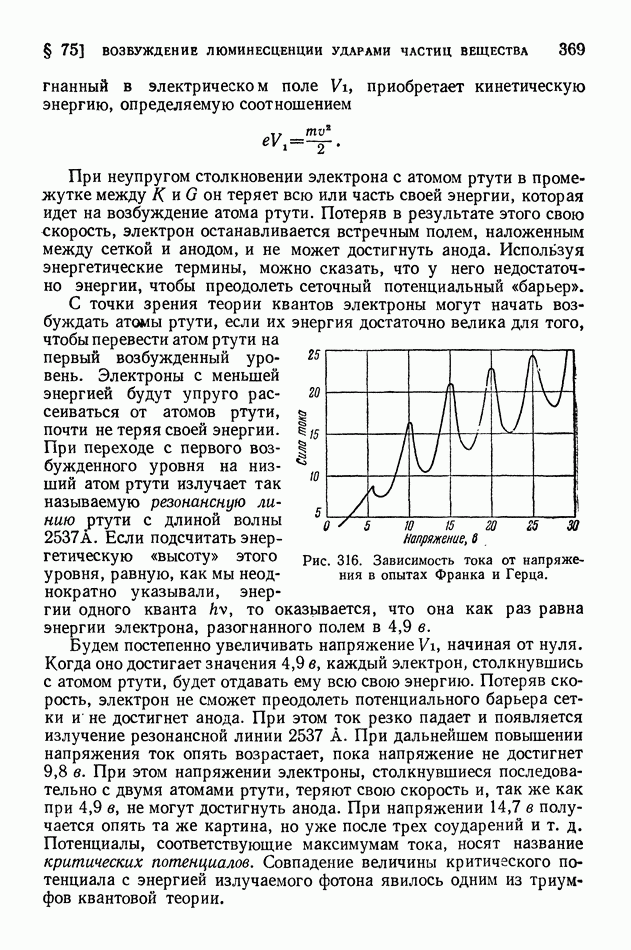
- § 75. Возбуждение люминесценции ударами частиц вещества
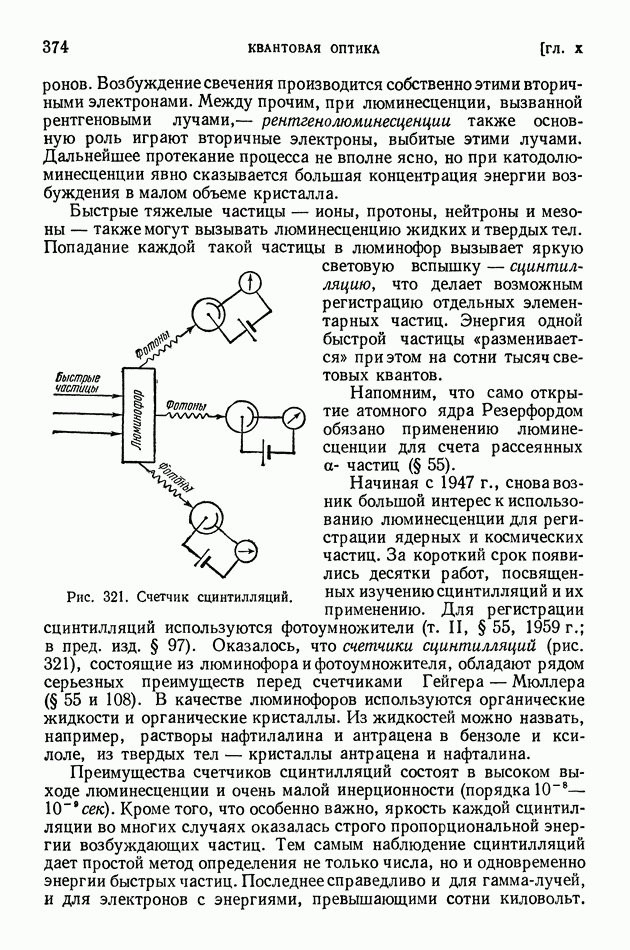
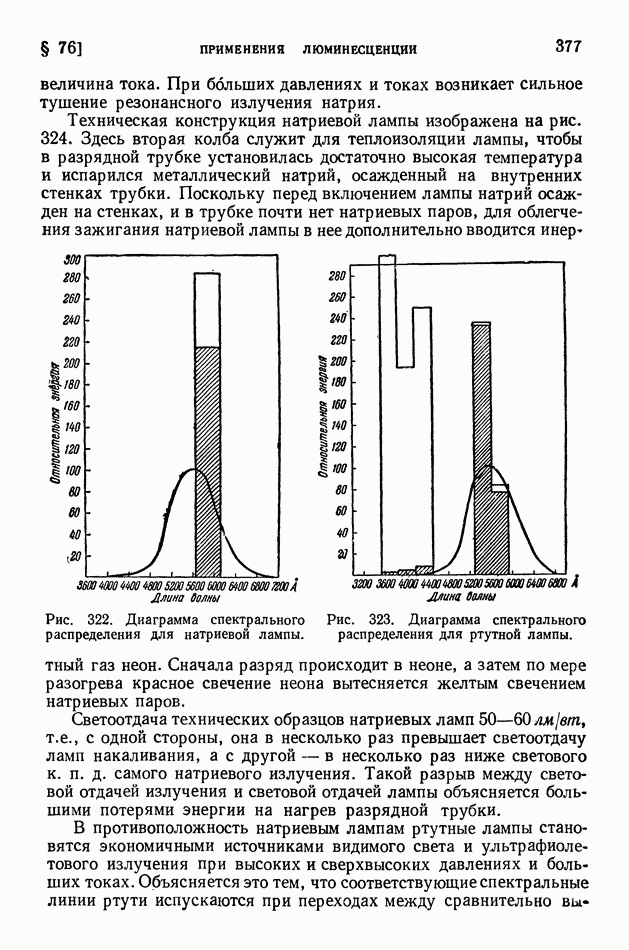
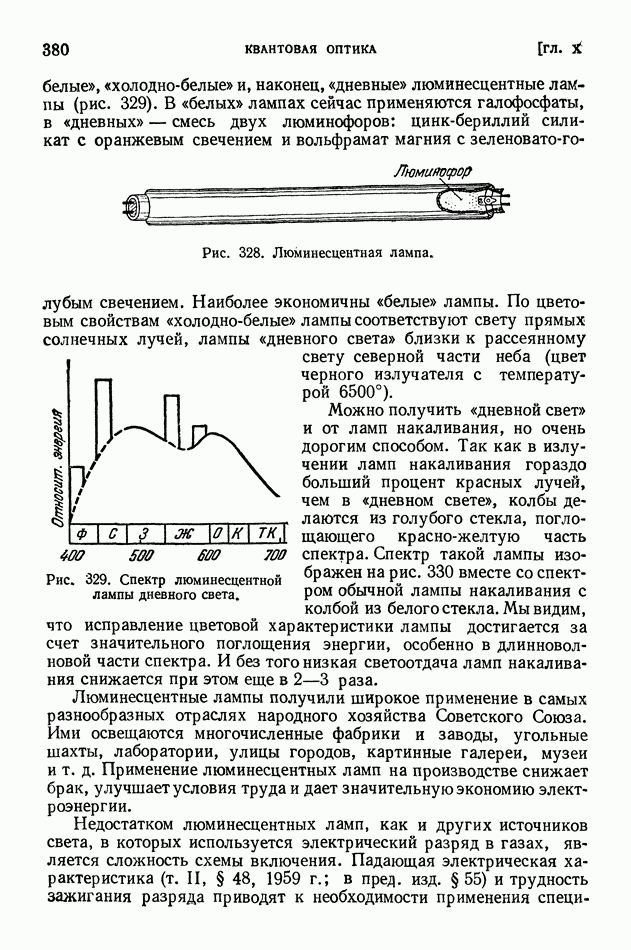
- § 76. Применения люминесценции
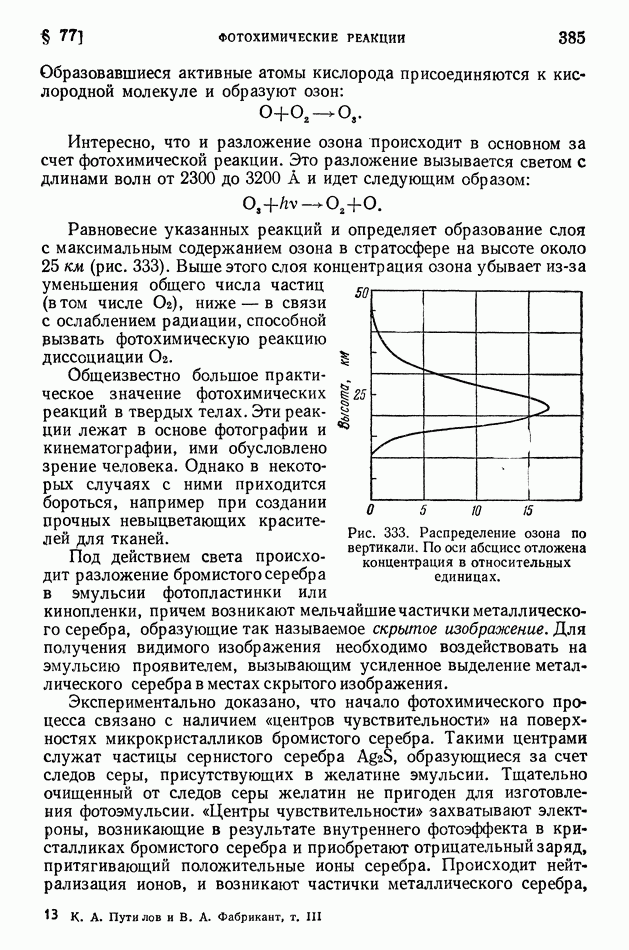
- § 77. Фотохимические реакции
- ГЛАВА XI. ЗАКОН ПРОПОРЦИОНАЛЬНОСТИ МАССЫ И ЭНЕРГИИ И РЕЛЯТИВИСТСКИЕ СООТНОШЕНИЯ
- § 78. Закон пропорциональности массы и энергии
- § 79. Предварительные замечания о релятивистских эффектах. Зависимость массы от скорости
- § 80. Корпускулярные свойства фотонов. Явление Комптона
- § 81. Вывод закона Эйнштейна сложения скоростей из закона пропорциональности массы и энергии и законов сохранения энергии или количества движения
- § 82. Две трактовки закона пропорциональности массы и энергии и уточнение закона тяготения
- § 83. Красное смещение спектральных линий. Поперечный эффект Доплера
- § 84. Влияние гравитационного поля на скорость света в вакууме и показатель преломления вакуума
- ЧАСТЬ ШЕСТАЯ. ЯДЕРНАЯ ФИЗИКА
- § 85. Заряд и масса ядра. Масс-спектральный анализ
- § 86. Состав ядер. Изотопы. Атомные единицы массы и энергии
- § 87. Радиоактивный распад ядер. Закон радиоактивного смещения. Изомеры
- § 88. Альфа-лучи. Потери энергии на ионизацию. Квантовомеханическое объяснение альфа-радиоактивности
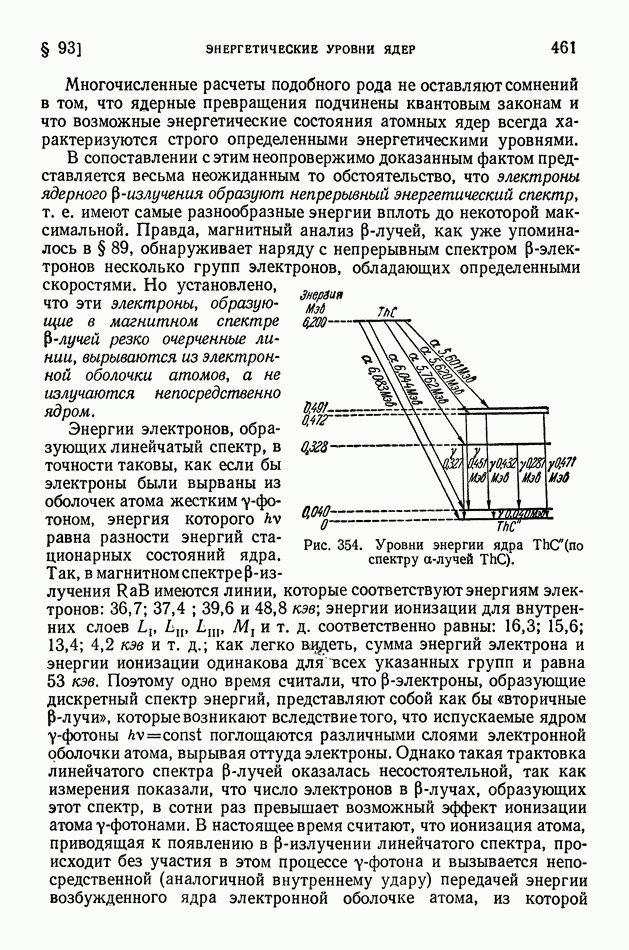
- § 89. Бета- и гамма-лучи
- § 90. Искусственное расщепление ядер. Открытие нейтрона
- § 91. Открытие позитрона. Взаимопревращение фотонов определенной энергии и электронно-позитронных пар
- § 92. Индуцированная позитронная и электронная радиоактивность. Фоторасщепление ядер, K-захват
- § 93. Энергетические уровни ядер. Внутренняя конверсия. Нейтрино
- § 94. Капельная теория строения ядер
- § 95. Деление ядер и развитие капельной теории строения ядер
- ГЛАВА XIII. КОСМИЧЕСКИЕ ЛУЧИ
- § 96. Методы исследования и первые итоги изучения космических лучей
- § 97. Каскадное образование электронно-позитронных пар в космических лучах. Потери энергии электронами на тормозное излучение
- § 98. «мю»-мезоны. Зависимость времени жизни неустойчивых частиц от скорости движения
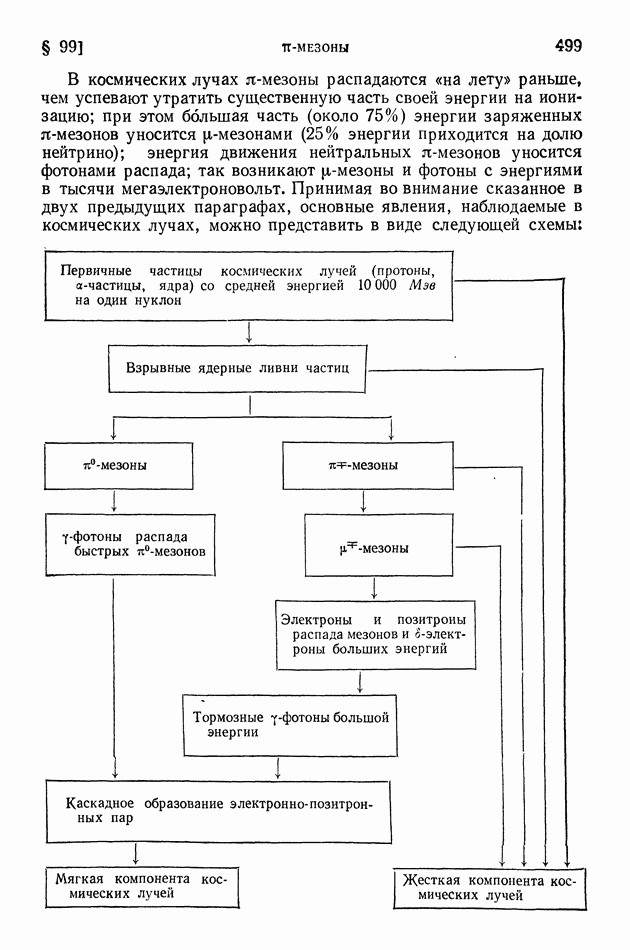
- § 99. «пи»-мезоны
- § 100. Взрывные ядерные ливни и их каскадное развитие в космических лучах
- § 101. Корпускулярный и энергетический спектр космических лучей. Происхождение космического излучения
- ГЛАВА XIV. ЭКСПЕРИМЕНТАЛЬНЫЕ СРЕДСТВА ЯДЕРНОЙ ФИЗИКИ
- § 102. Циклотроны
- § 103. Фазотроны
- § 104. Бетатроны
- § 105. Синхротроны и синхрофазотроны
- § 106. Линейные ускорители электронов и ионов
- § 107. Лабораторные источники нейтронов. Замедлители нейтронов в ядерных реакторах
- § 108. Усовершенствование методов наблюдения и счета частиц
- ГЛАВА XV. ЯДЕРНЫЕ РЕАКЦИИ И АТОМНАЯ ЭНЕРГИЯ
- § 109. Основные виды и обозначения ядерных реакций. Конкурирующие процессы в ядерных реакциях
- § 110. Энергетический эффект, энергия возбуждения и порог ядерных реакций
- § 111. Превращения элементарных частиц
- § 112. Ядерные силы
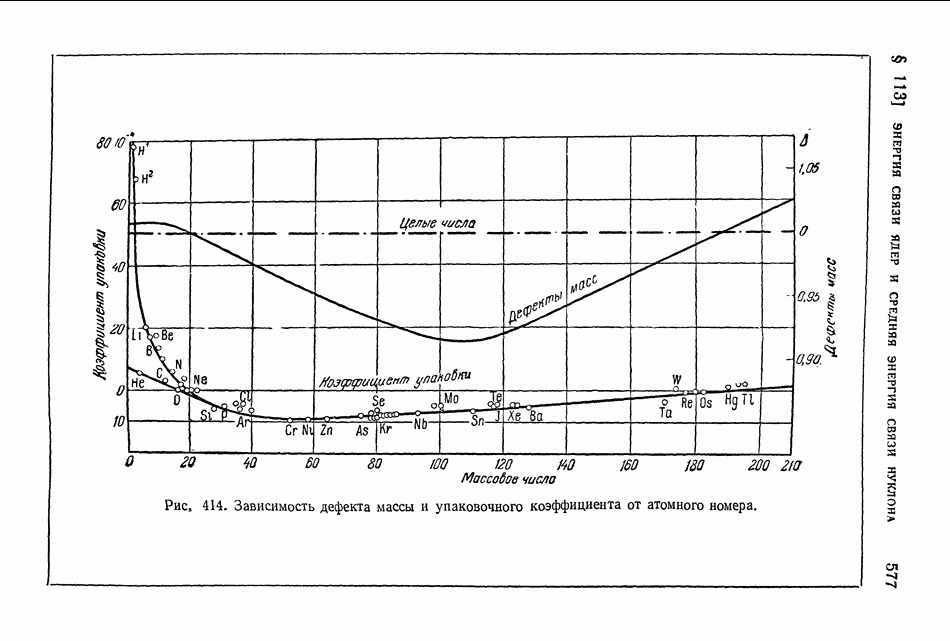
- § 113. Энергия связи ядер и средняя энергия связи нуклона
- § 114. Полуэмпирическая формула для энергии ядерной связи и для атомных энергий и масс
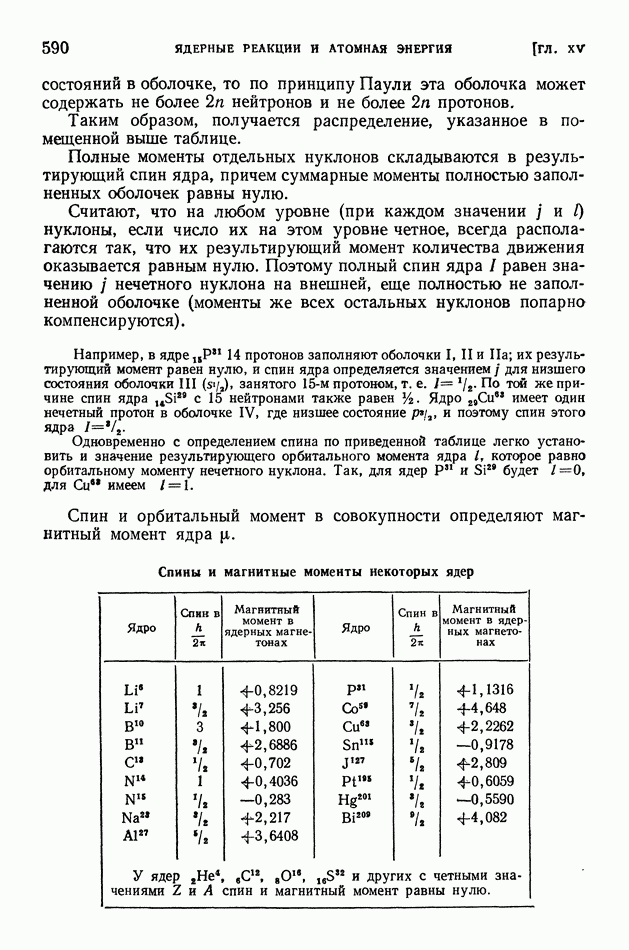
- § 115. Взаимосвязь энергии и строения ядер. Внутриядерное движение нуклонов и нуклонные оболочки. Спины и магнитные моменты ядер
- § 116. Энергия отделения частиц и анализ возможного хода ядерной реакции
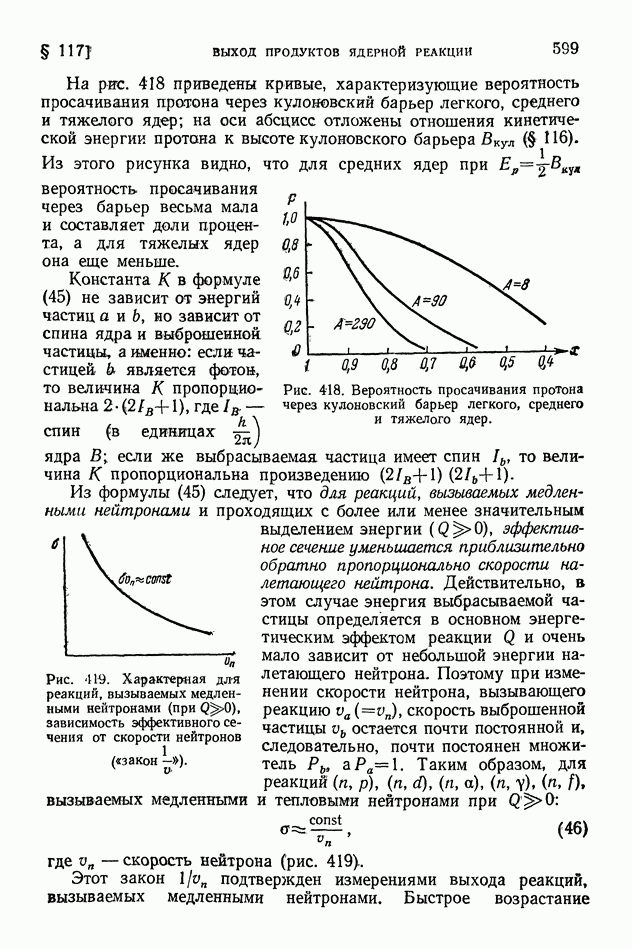
- § 117. Выход продуктов ядерной реакции. Эффективные сечения. Резонансные явления
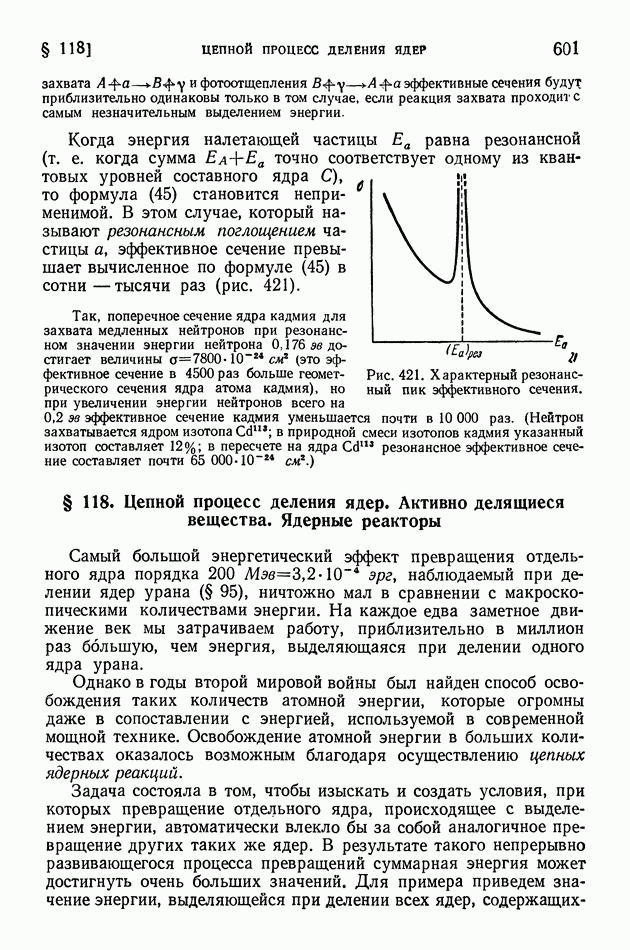
- § 118. Цепной процесс деления ядер. Активно делящиеся вещества. Ядерные реакторы
- § 119. Термоядерные реакции
- § 120. Применение ядерных реакций
- § 121. Ядерные реакции в звездах