| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА IX. ОСНОВЫ КВАНТОВОЙ (ВОЛНОВОЙ) МЕХАНИКИ
§ 62. Волновые свойства частиц. Формула де Бройля. Дифракция электронов
Теория Бора одержала ряд блестящих побед в истолковании атомной структуры и внутриатомных процессов; оба ее постулата выражают твердо установленные факты. Однако даже в тех проблемах, которые доставили успех теории Бора, с самого начала возникли существенные трудности.
В теории Бора квантовые условия совершенно внешним образом присоединялись к чуждой им классической механике; поэтому теория Бора не могла дать однозначного, годного для всех случаев метода квантования.
Далее, в теории Бора, с одной стороны, отвергалась классическая электродинамика в применении к движению электрона внутри атома, но, с другой, ее выводы использовались при решении вопроса об интенсивности и поляризации излучения. (С этой целью был введен принцип соответствия — эквивалентность классической и квантовой теорий в области больших квантовых чисел; однако обобщение результатов исследования на область малых квантовых чисел, где классические частоты движения уже не совпадают с квантовыми частотами излучения, приводило к неоднозначным и неопределенным заключениям об интенсивности линий и их поляризации.)
С еще большими трудностями теория Бора столкнулась при исследовании атомов с числом электронов более одного, даже простейшего из них — атома гелия. Попытка объяснить строение атома гелия методом теории Бора (Борн, Гейзенберг, Крамере) привела к противоречащим опыту результатам, в частности дала неправильную величину ионизационного потенциала. Аналогичные трудности возникли при исследовании взаимодействия двух атомов. Простейшая задача этого рода — образование молекулы водорода — оказалась также неразрешимой.
В результате постепенно было признано, что теория Бора: 1) лишена внутреннего единства, представляя искусственное соединение классической механики с квантовыми условиями, что ведет к
неоднозначности самого квантования; 2) приводит к неточным выводам за пределами расчета атома водорода; 3) не дает решения проблем об интенсивности спектральных линий и поляризации излучения.
Все эти недостатки были устранены в квантовой механике, основанной на коренном изменении наших представлений о природе материальных частиц.
Первым шагом к созданию новой квантовой теории была высказанная в 1924 г. французским физиком Луи де Бройлем гипотеза о существовании глубокой аналогии между свойствами света и свойствами материальных частиц. Если в одних условиях проявляются корпускулярные свойства света (как потока частиц — фотонов), а в других волновые, то и частицы вещества в известных условиях (в микроявлениях) могут также проявлять волновые свойства.
Еще в 20-х годах прошлого столетия Гамильтон показал, что обобщенные законы геометрической оптики и механики Ньютона могут быть представлены уравнениями, математическая форма которых тождественна: все законы геометрической оптики могут быть выведены из вариационного принципа Ферма, а законы механики — из вариационного принципа наименьшего действия. Это означает, что для определения траектории материальной точки в поле с потенциалом  можно воспользоваться решением математически сходной задачи по определению хода световых лучей в оптически неоднородной среде с соответственно подобранным показателем преломления
можно воспользоваться решением математически сходной задачи по определению хода световых лучей в оптически неоднородной среде с соответственно подобранным показателем преломления  (х, у, z).
(х, у, z).
Но применимость геометрической оптики ограничена случаями, когда величина отверстий, через которые проходят лучи, или размеры препятствий на пути лучей велики в сравнении с длиной их волны (точнее, в сравнении с зонами Френеля; § 26). Более общей и более точной является волновая оптика, объясняющая закономерное дифракционное отклонение световых лучей от прямолинейности при малых размерах экранов и отверстий, а также явления интерференции, поляризации и т. д. Открытие квантовой природы света показало, что особенности света не исчерпываются волновыми свойствами: оказалось, что волновая оптика должна быть дополнена анализом таких случаев, когда проявляются корпускулярные свойства своеобразных световых частиц — фотонов. В 1924 г. де Бройль писал: «В оптике в течение столетия слишком пренебрегали корпускулярным способом рассмотрения по сравнению с волновым; не делалась ли в теории вещества обратная ошибка? Не думали ли мы слишком много о картине частиц и не пренебрегали ли чрезмерно картиной волн?».
Наличие глубокой математической аналогии между ньютоновой механикой и геометрической оптикой подсказало, что законы механики, более общие, чем законы Ньютона, аналогичны законам, волновой оптики. В 1924-1926 гг. физики вслед за де Бройлем и Шредингером пришли к заключению, что для выявления законов
механики, применимых к мельчайшим частицам вещества, нужно формулировать задачи о движении этих частиц в виде уравнений, сходных с уравнениями волновой оптики. Вскоре подтвердилось, что эта мысль правильна и что движение мельчайших частиц вещества — электронов, атомов и т. д. — управляется законами, представляющими собой следствие волновых процессов. Так возникла волновая (квантовая) механика, точность которой оказалась изумительной. В сопоставлении с более общей и более точной волновой механикой обычную механику теперь считают упрощением, которое допустимо только для анализа движений макроскопических тел.
Физика еще не располагает объективными сведениями, которые позволили бы отчетливо определить природу волновых процессов, проявляющихся при движении мельчайших частиц вещества. Но какова бы ни была природа этих волновых процессов, они как всякие волновые процессы должны характеризоваться какой-то длиной волны и какой-то скоростью распространения. Де Бройль обосновал предположение, что движение каждой частицы сопровождается волновым процессом, для которого длина волны К связана с массой  и скоростью частицы
и скоростью частицы  весьма простым соотношением (формула де Бройля):
весьма простым соотношением (формула де Бройля):

где h - постоянная Планка.
Формула де Бройля обобщает формулу для длины световой волны, получаемую на основании закона пропорциональности массы и энергии, который будет пояснен в § 78; по закону пропорциональности массы и энергии всякой энергии  соответствует масса
соответствует масса  определяемая соотношением
определяемая соотношением

где с — скорость света. Энергия фотона равна  следовательно, масса фотона
следовательно, масса фотона

Из формулы (3) получается:

Формула (4) аналогична формуле (1), так как все фотоны имеют скорость с. Для частиц, движущихся со скоростями, малыми в сравнении со скоростью света, кинетическая энергия равна

и, стало быть, импульс будет 
Поэтому формулу де Бройля (1) часто записывают так:

где  полная энергия частицы,
полная энергия частицы,  потенциальная энергия и
потенциальная энергия и  кинетическая энергия.
кинетическая энергия.
В 1927 г. гипотеза де Бройля получила непосредственное экспериментальное подтверждение.
Американский физик Девиссон совместно со своими сотрудниками изучал в течение нескольких лет отражение пучка электронов от различных металлических поверхностей. На рис. 234 изображена схема этих опытов. Электроны, испускаемые накаленной вольфрамовой нитью, проходили через ряд диафрагм.

Рис. 234. Схема опытов Девиссона.

Рис. 235. Угловое распределение отраженных электронов в опытах Девиссона и Джермера.
Между первой диафрагмой и нитью была приложена разность потенциалов, ускорявшая движение электронов. Из этой электронной пушки А тонкий пучок электронов попадал на поверхность монокристалла В. Часть отраженных электронов улавливалась коллектором С, представлявшим собой двойной цилиндр Фарадея, между обкладками которого имелась хорошая изоляция. Количество электронов, попавших в коллектор, измерялось при помощи чувствительного гальванометра, соединенного с внутренним цилиндром коллектора.
В процессе измерений можно было вращать монокристалл В и перемещать коллектор С по дуге, изображенной на рис. 234. При различных положениях коллектора в него, очевидно, попадали электроны, отраженные под различными углами от поверхности монокристалла. На кривой углового распределения отраженных электронов обнаружилось наличие резких максимумов (рис. 235).
Полученная картина объясняется дифракцией электронных волн де Бройля, отражаемых кристаллической решеткой, аналогично дифракции рентгеновых лучей в опытах Лауэ (§ 30). Максимумы на кривой рис. 235 соответствуют отдельным дифракционным максимумам; их положение, найденное экспериментально, в точности совпало с вычисленным из условия Вульфа — Бреггов, в которое подставлялась формула де Бройля для 
Для удобства можно пользоваться формулой де Бройля в несколько измененном виде.

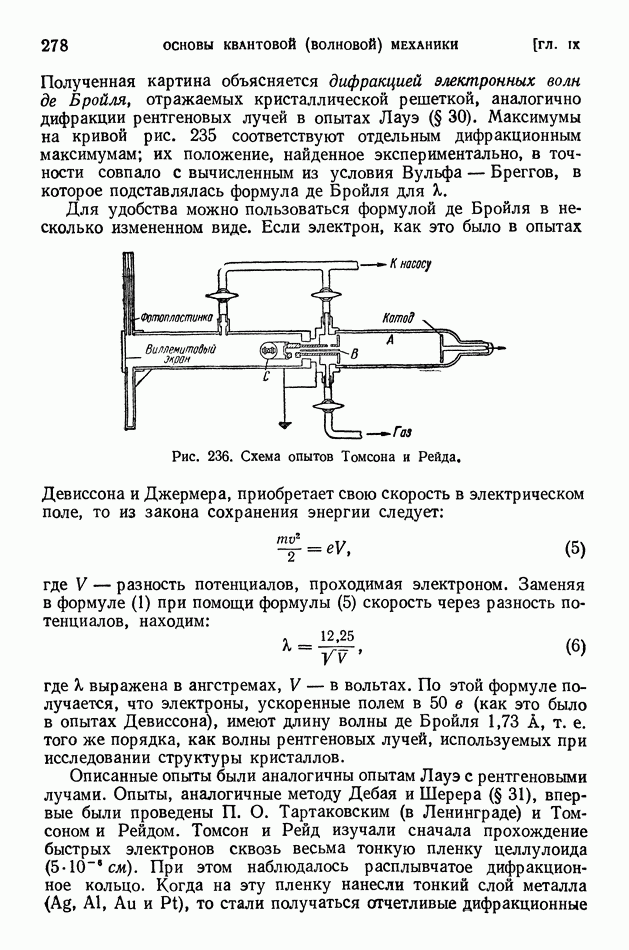
Рис. 236. Схема опытов Томсона и Рейда,
Если электрон, как это было в опытах Девиссона и Джермера, приобретает свою скорость в электрическом поле, то из закона сохранения энергии следует:

где  разность потенциалов, проходимая электроном. Заменяя в формуле (1) при помощи формулы (5) скорость через разность потенциалов, находим:
разность потенциалов, проходимая электроном. Заменяя в формуле (1) при помощи формулы (5) скорость через разность потенциалов, находим:

где  выражена в ангстремах,
выражена в ангстремах,  в вольтах. По этой формуле получается, что электроны, ускоренные полем в 50 в (как это было в опытах Девиссона), имеют длину волны де Бройля 1,73 А, т. е. того же порядка, как волны рентгеновых лучей, используемых при исследовании структуры кристаллов.
в вольтах. По этой формуле получается, что электроны, ускоренные полем в 50 в (как это было в опытах Девиссона), имеют длину волны де Бройля 1,73 А, т. е. того же порядка, как волны рентгеновых лучей, используемых при исследовании структуры кристаллов.
Описанные опыты были аналогичны опытам Лауэ с рентгеновыми лучами. Опыты, аналогичные методу Дебая и Шерера (§ 31), впервые были проведены П. О. Тартаковским (в Ленинграде) и Томсоном и Рейдом. Томсон и Рейд изучали сначала прохождение быстрых электронов сквозь весьма тонкую пленку целлулоида  При этом наблюдалось расплывчатое дифракционное кольцо. Когда на эту пленку нанесли тонкий слой металла
При этом наблюдалось расплывчатое дифракционное кольцо. Когда на эту пленку нанесли тонкий слой металла  то стали получаться оггчетливые дифракционные
то стали получаться оггчетливые дифракционные
картины, совершенно сходные с кольцами Дебая — Шерера, получавшимися при прохождении рентгеновых лучей сквозь металлическую фольгу или слой мелкокристаллического порошка. На рис. 236 изображена схема установки Томсона и Рейда. Источником электронов служил газовый разряд в трубке А. Электроны проходили сквозь узкий и длинный канал в аноде В. Исследуемая металлическая фольга помещалась в С. Прошедшие сквозь фольгу электроны попадали на светящийся под их ударами экран (покрытый виллемитом) или же на фотопластинку. В первом случае дифракционная картина была видна простым глазом, во втором — получался ее фотоснимок, так как электроны вызывают почернение фотопластинки (рис. 237). Когда к трубке подносили магнит, вся картина смещалась вследствие отклонения электронов. Это убедительно доказывает, что картина возникает в результате дифракции заряженных частиц, а не рентгеновых лучей.

Рис. 237. Электронограмма тонкого слоя золота.
Все результаты подобных опытов, а они немедленно были воспроизведены во многих лабораториях, оказались в полном согласии с формулой (1).
После того как волновая природа электронного пучка была установлена и справедливость формулы де Бройля подтверждена с большой точностью, дифракцию электронов стали широко применять для исследования структуры вещества. В ряде случаев применение электронных пучков дает значительные преимущества по сравнению с рентгеновыми лучами. Например, при исследовании тонких слоев газа, адсорбированного на поверхности металла, рентгеновы лучи малопригодны, а электронные лучи дают много интересных сведений. Объясняется это, во-первых, тем, что интенсивность рассеянных рентгеновых лучей вообще меньше, чем интенсивность электронных волн, и, во-вторых, тем, что интенсивность рассеянных рентгеновых лучей пропорциональна  атомный номер), а интенсивность рассеянных электронных волн пропорциональна
атомный номер), а интенсивность рассеянных электронных волн пропорциональна  Для слоя кислорода на вольфраме отношение интенсивности рентгеновых лучей равно
Для слоя кислорода на вольфраме отношение интенсивности рентгеновых лучей равно  а для электронов
а для электронов  . Ясно, что в первом случае дифракционная картина,
. Ясно, что в первом случае дифракционная картина,
даваемая кислородом, будет совершенно не заметна на фоне картины, даваемой вольфрамом. Во втором случае соотношение интенсивностей гораздо выгоднее.
Вирль с сотрудниками произвел большое количество опытов по дифракции электронов, проходящих сквозь струю пара. На рис. 238 изображена схема прибора Вирля. Пучок электронов и струя пара пересекаются под прямым углом. Так как здесь происходит дифракция на хаотически расположенных экранах-молекулах, то дифракционная картина тождественна картине, даваемой отдельным экраном-молекулой (§ 33).

Рис. 238. Схема прибора Вирля для получения дифракции электронов на молекулах паров.
Дифракция электронов на отдельной молекуле или атоме, естественно, зависит от структуры молекулы или атома. Тем самым дифракция электронов позволяет исследовать структуру молекул и атомов. Таким путем получено большое количество важных результатов.
Применимость формулы де Бройля не ограничивается только электронами: любой частице соответствует волна, определяемая этой формулой. Но длина волны обратно пропорциональна массе частицы, и, следовательно, весьма массивным частицам (и тем более макроскопическим телам) соответствуют такие короткие волны, что их невозможно обнаружить. (Например, теннисному мячу, летящему со скоростью  соответствует длина волны примерно
соответствует длина волны примерно  см, или
см, или  ) Для атомов при сравнительно небольшой скорости их движения длины волн де Бройля получаются такими же, как для более быстро движущихся электронов. Атомы водорода согласно формуле (1) при 0 °С обладают длиной волны
) Для атомов при сравнительно небольшой скорости их движения длины волн де Бройля получаются такими же, как для более быстро движущихся электронов. Атомы водорода согласно формуле (1) при 0 °С обладают длиной волны  т. е. около
т. е. около  Поэтому, как доказано опытами которые были проведены многими физиками, обнаруживаются отчетливые дифракционные максимумы при отражении пучка атомов
Поэтому, как доказано опытами которые были проведены многими физиками, обнаруживаются отчетливые дифракционные максимумы при отражении пучка атомов
гелия (а также и пучка молекул водорода) от поверхности монокристалла. Во всех этих опытах опять-таки блестяще подтвердилась формула де Бройля. Проявление волновых свойств при движении электронов и других мельчайших частиц вещества должно теперь считаться твердо установленным экспериментами.
В 1925-1926 гг., еще раньше, чем идеи де Бройля были подтверждены экспериментально, представление о волновых свойствах частиц вещества было положено Шредингером и Гейзенбергом в основу созданной ими квантовой механики (волновой механики). Можно сказать, что 1925-1930 гг. явились поворотными годами в развитии современной теоретической физики. В эти годы были опубликованы выдающиеся по своему значению физико-математические исследования Шредингера, Гейзенберга, Борна, Дирака, Фока, Паули и др. В короткий срок в обширной серии статей были развиты основные направления квантовой механики и достигнуты первые успехи в решении ряда квантовомеханических задач.
В последующие годы математический аппарат квантовой механики был усовершенствован и ее методами были рассмотрены оптические, магнитные, химические свойства различных атомов и молекул, силы связи между атомами и молекулами, термодинамические свойства газов и кристаллов, электропроводность металлов и множество других вопросов. При сопоставлении этих теоретических исследований с экспериментами обнаружилась исключительная, никогда не достигавшаяся раньше в физике точность квантовомеханических расчетов.
| << Предыдущий параграф | Следующий параграф >> |
- ЧАСТЬ ЧЕТВЕРТАЯ. ОПТИКА
- § 2. Электромагнитная теория света
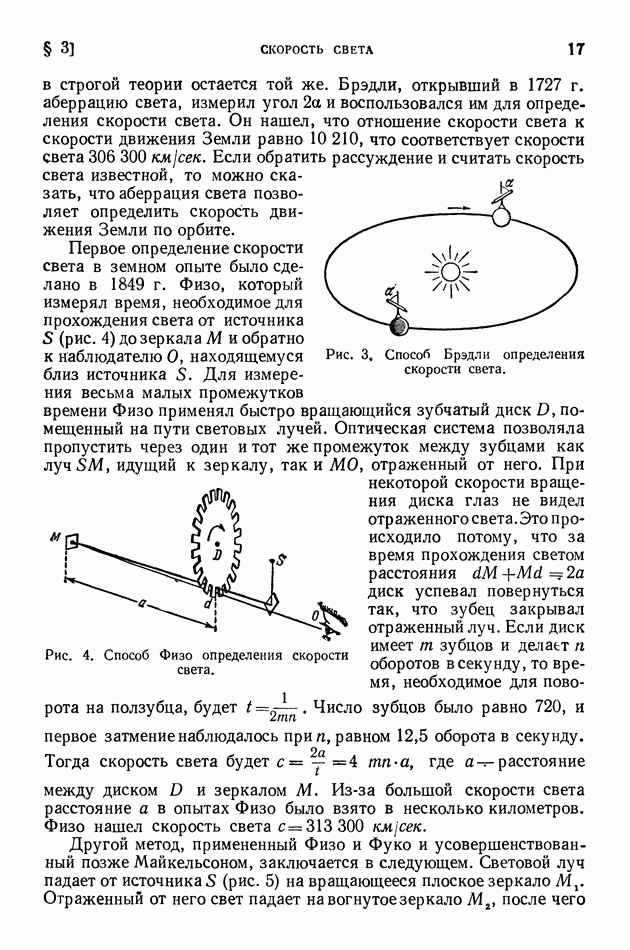
- § 3. Скорость света
- § 4. Опыт Майкельсона
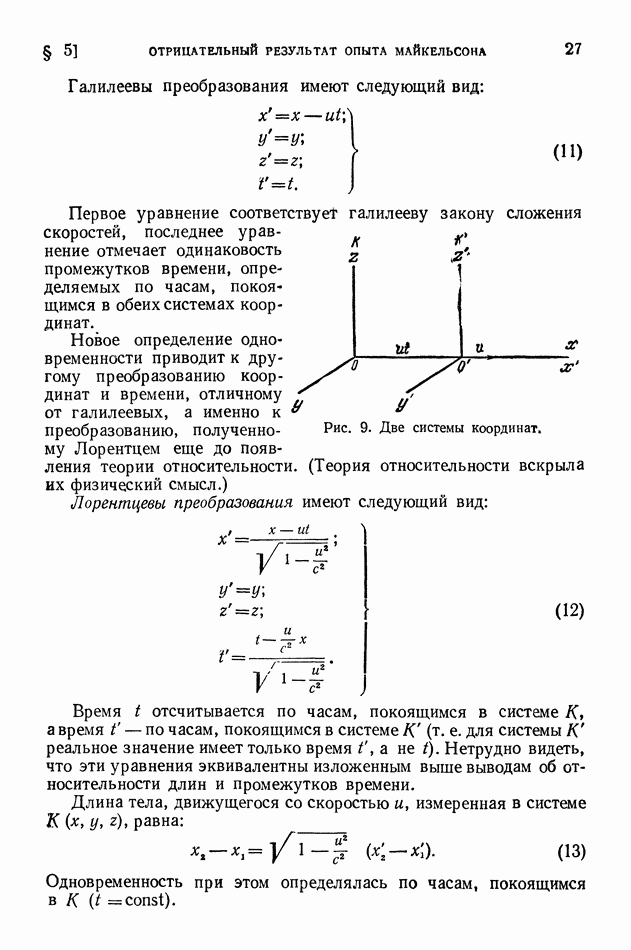
- § 5. Отрицательный результат опыта Майкельсона и теория относительности
- § 6. Некоторые замечания о теории относительности
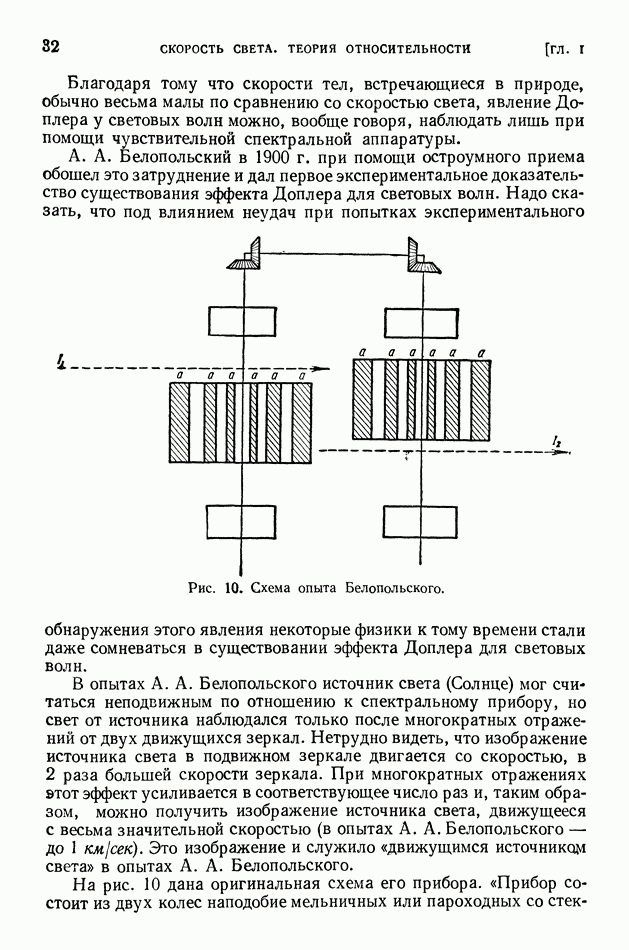
- § 7. Явление Доплера для световых волн
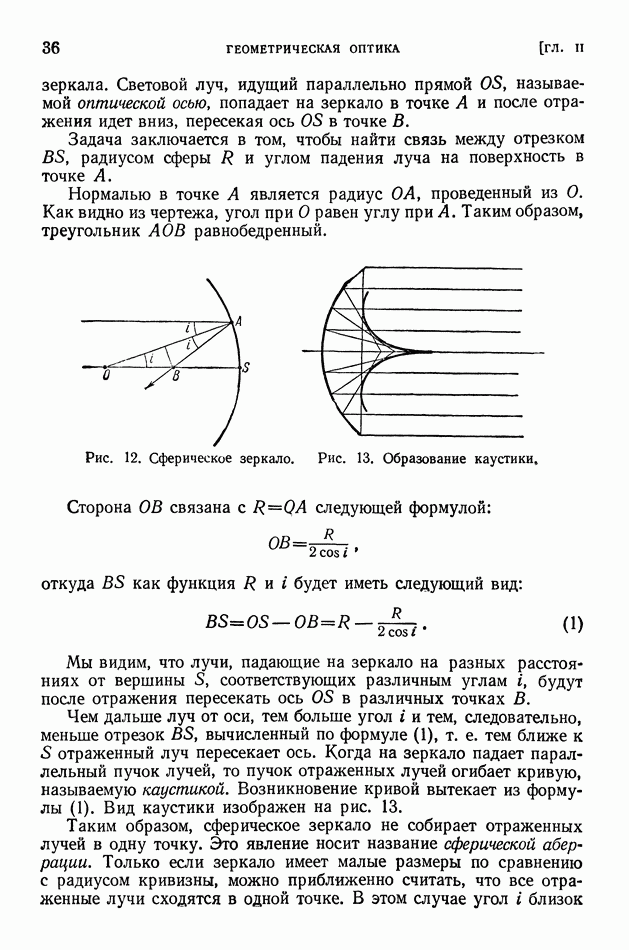
- ГЛАВА II. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- § 8. Законы отражения и преломления света
- § 9. Линза
- § 10. Оптические системы
- § 11. Глаз как оптическая система
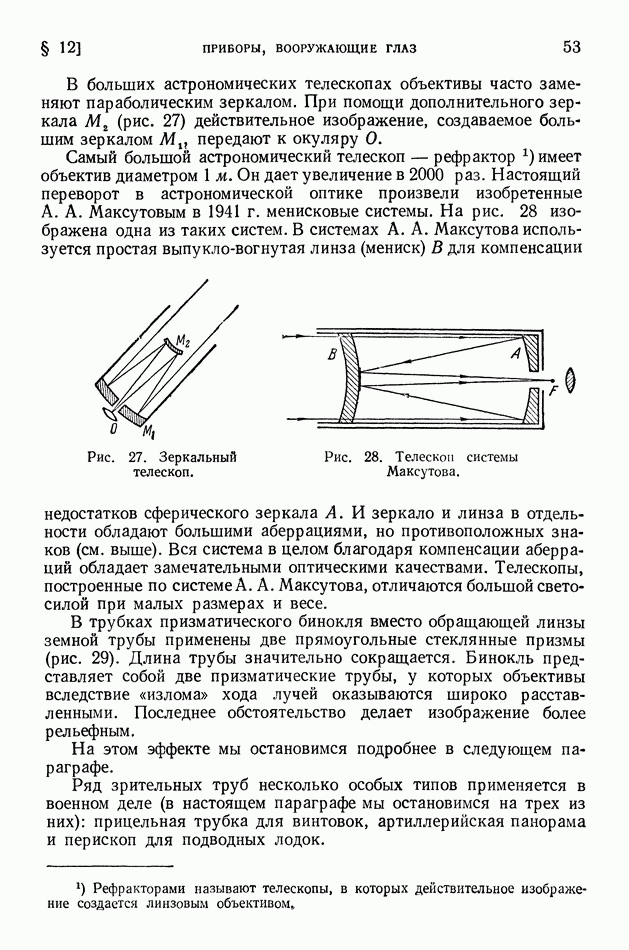
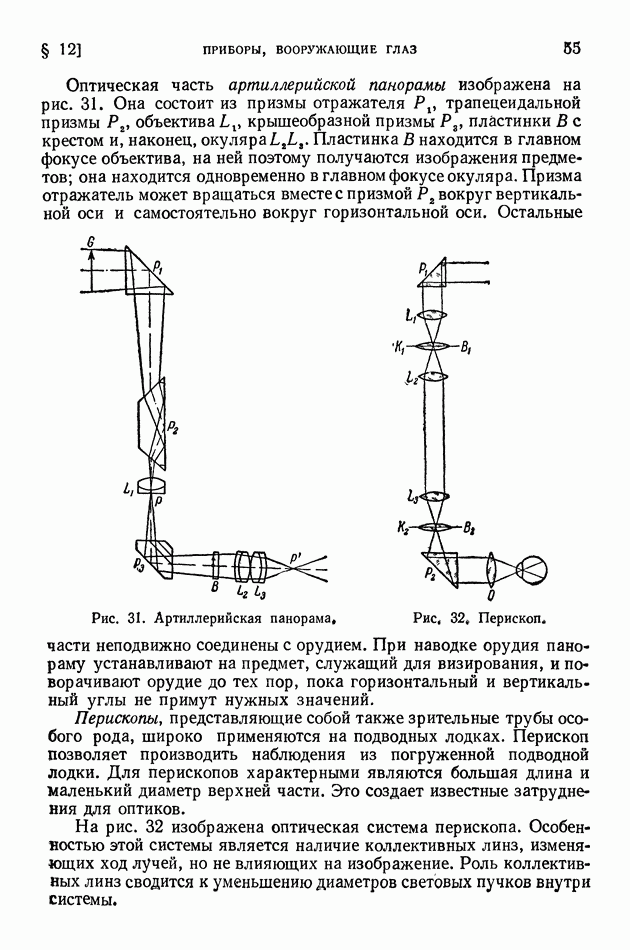
- § 12. Приборы, вооружающие глаз
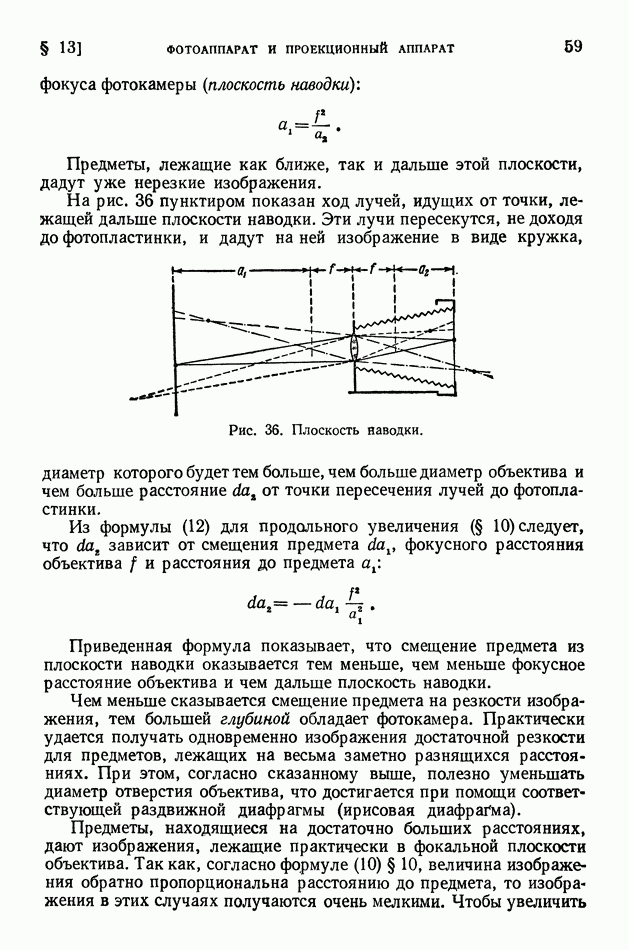
- § 13. Фотоаппарат и проекционный аппарат
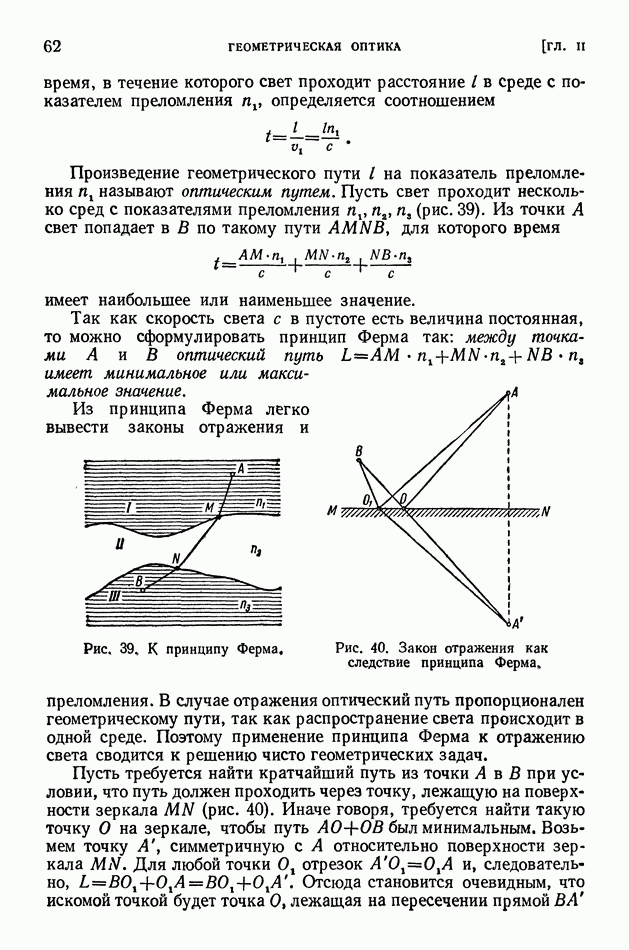
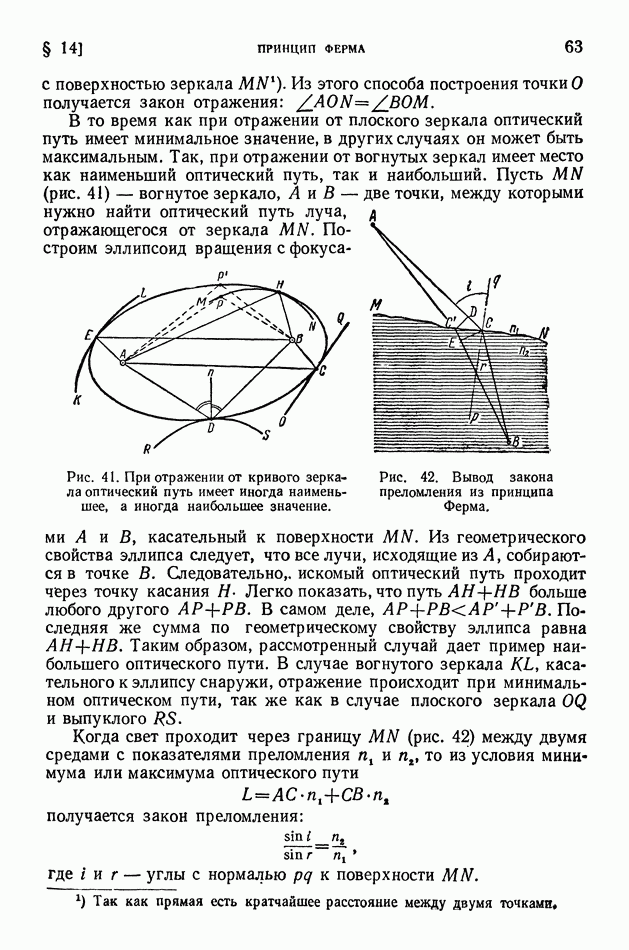
- § 14. Принцип Ферма
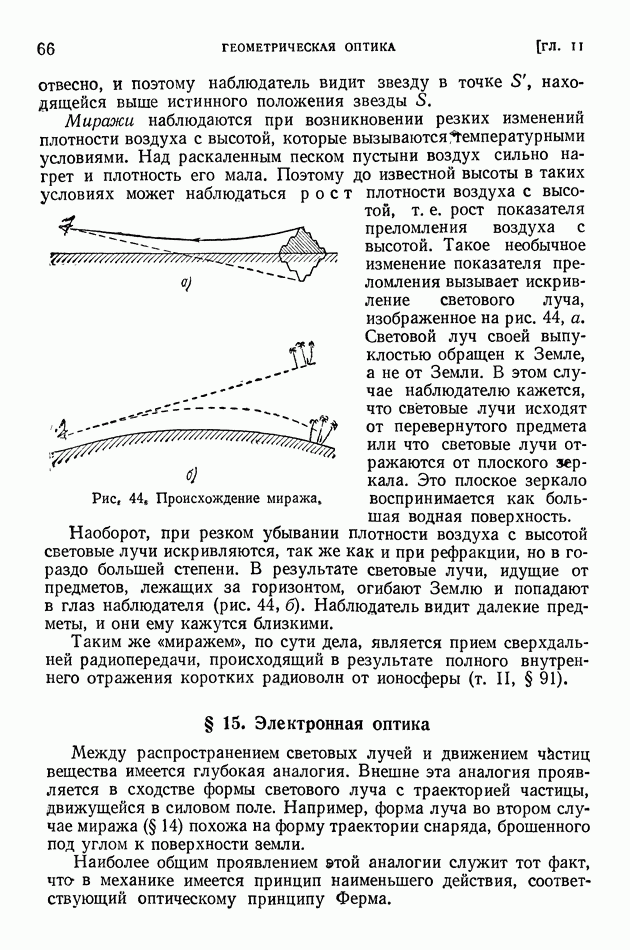
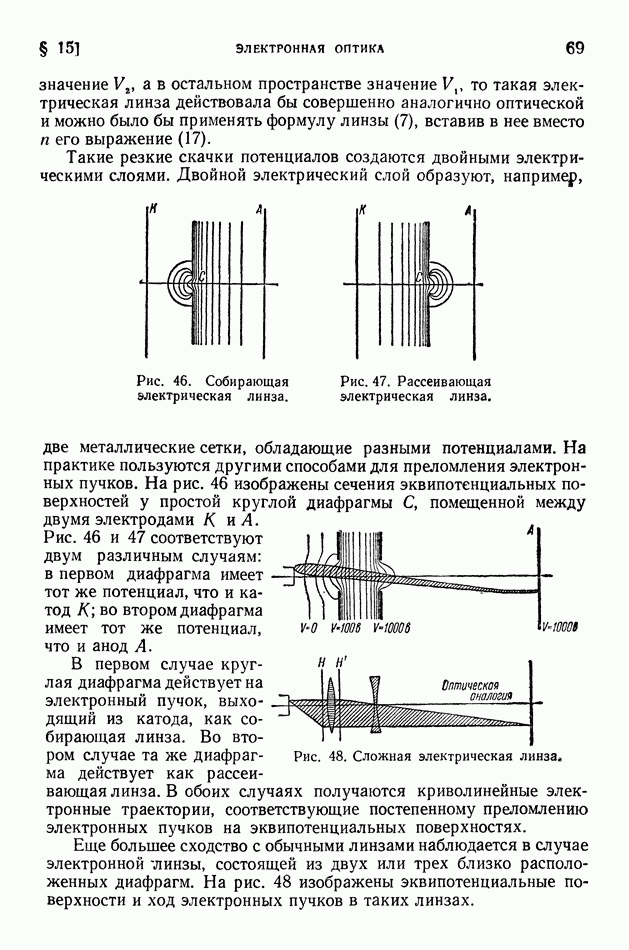
- § 15. Электронная оптика
- ГЛАВА III. ИНТЕРФЕРЕНЦИЯ СВЕТА
- § 16. Принцип суперпозиции. Когерентность
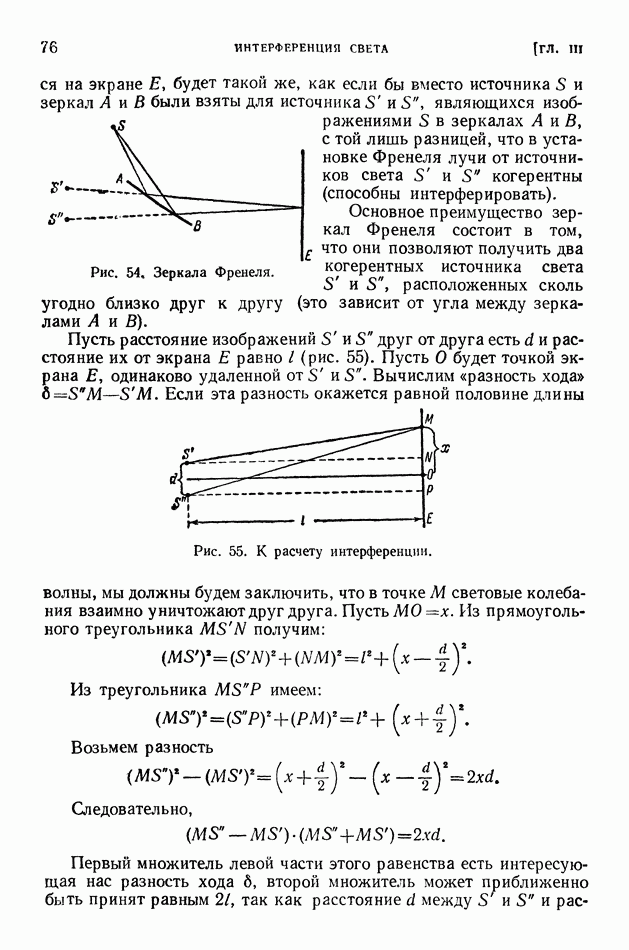
- § 17. Зеркала Френеля
- § 18. Цвета тонких пленок. Полосы равной толщины
- § 19. Полосы равного наклона. Просветленная оптика
- § 20. Интерферометры
- § 21. Интерференционное измерение технических мер длины
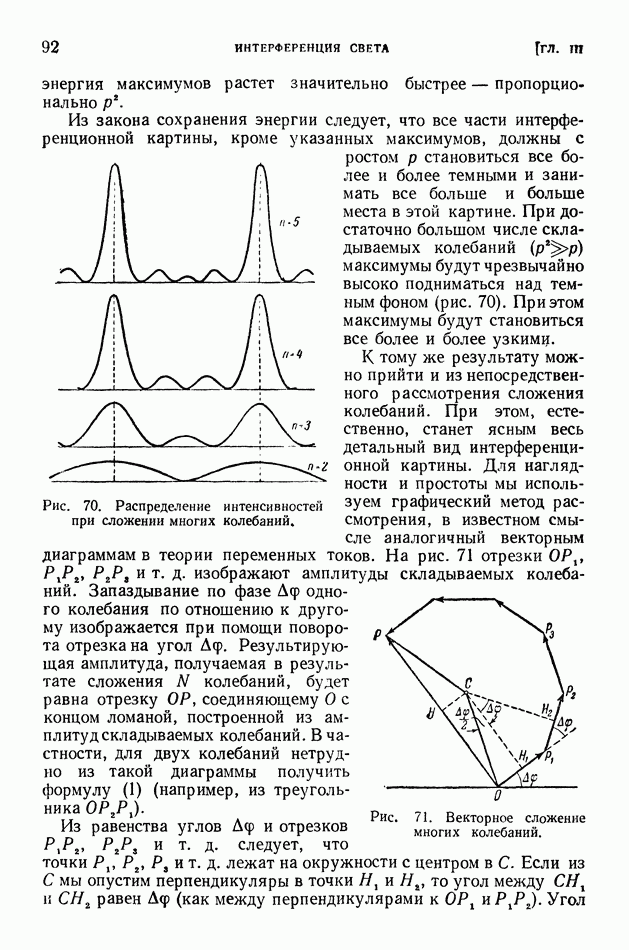
- § 22. Интерференция многих колебаний
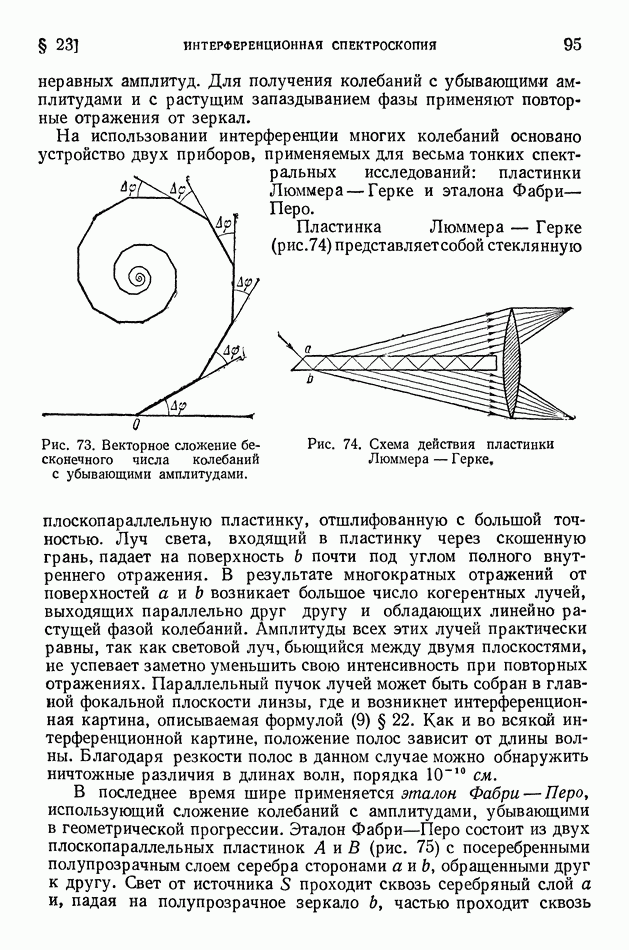
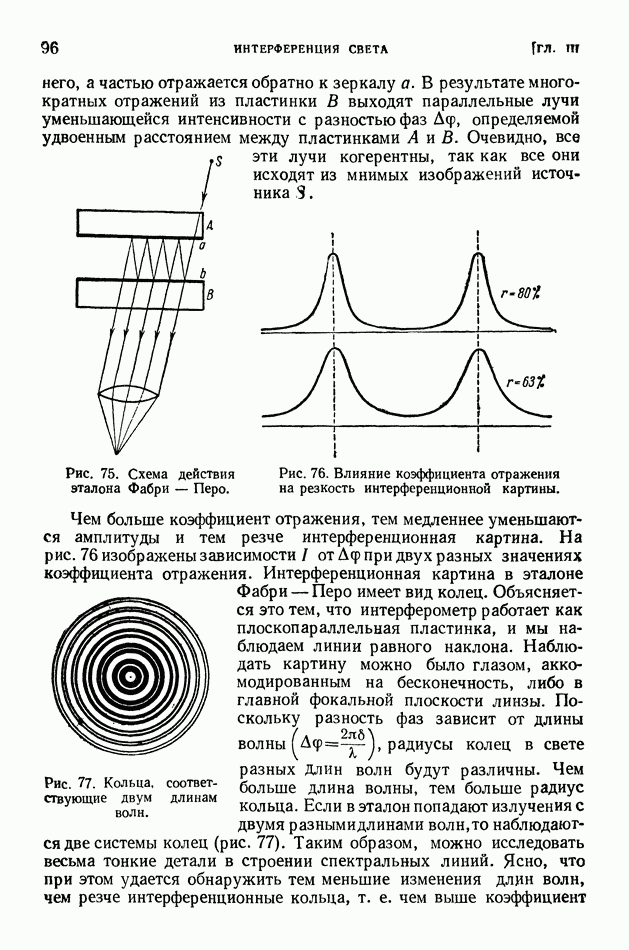
- § 23. Интерференционная спектроскопия
- ГЛАВА IV. ДИФРАКЦИЯ СВЕТА
- § 24. Явление дифракции. Опыт Френеля
- § 25. Принцип Гюйгенса-Френеля
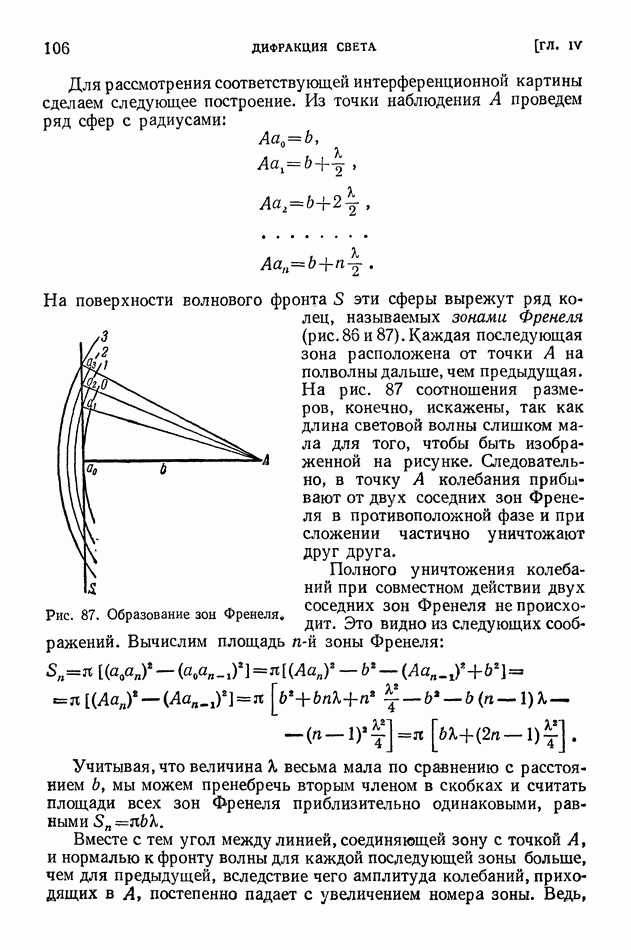
- § 26. Метод зон Френеля
- § 27. Дифракция от узкой щели
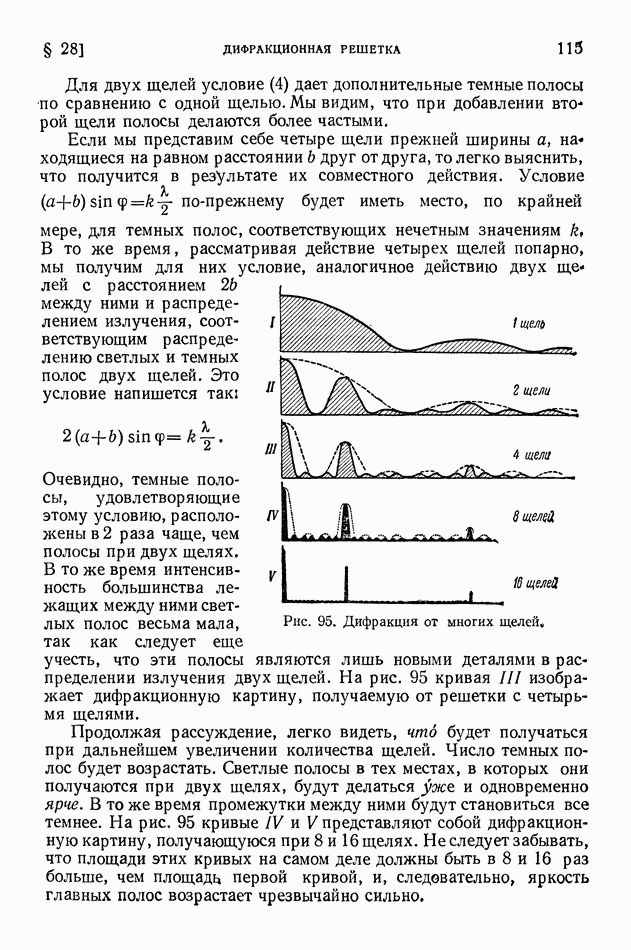
- § 28. Дифракционная решетка
- § 29. Дифракционный спектр. Решетки Роуланда и эшелон Майкельсона
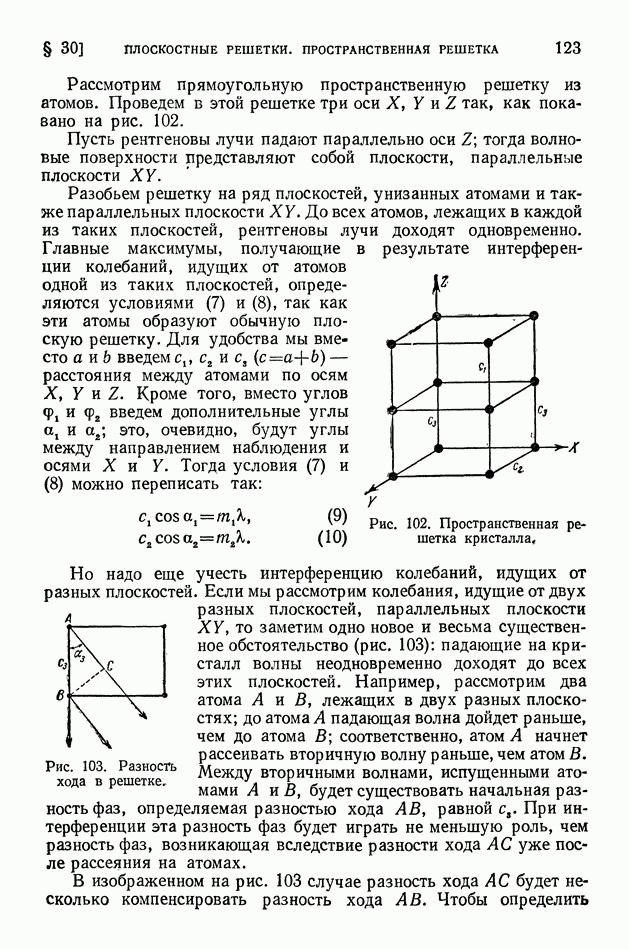
- § 30. Плоскостные решетки. Пространственная решетка
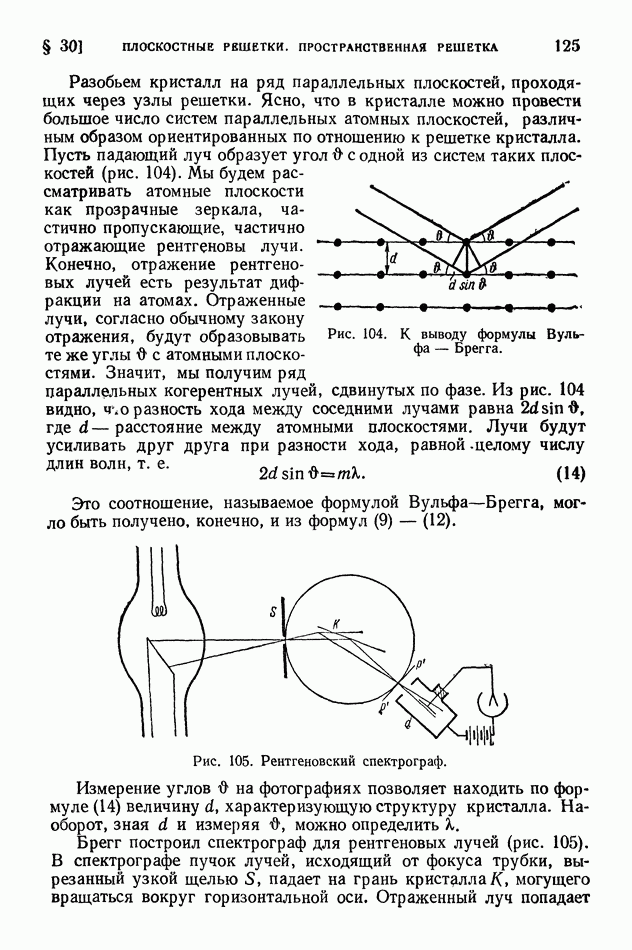
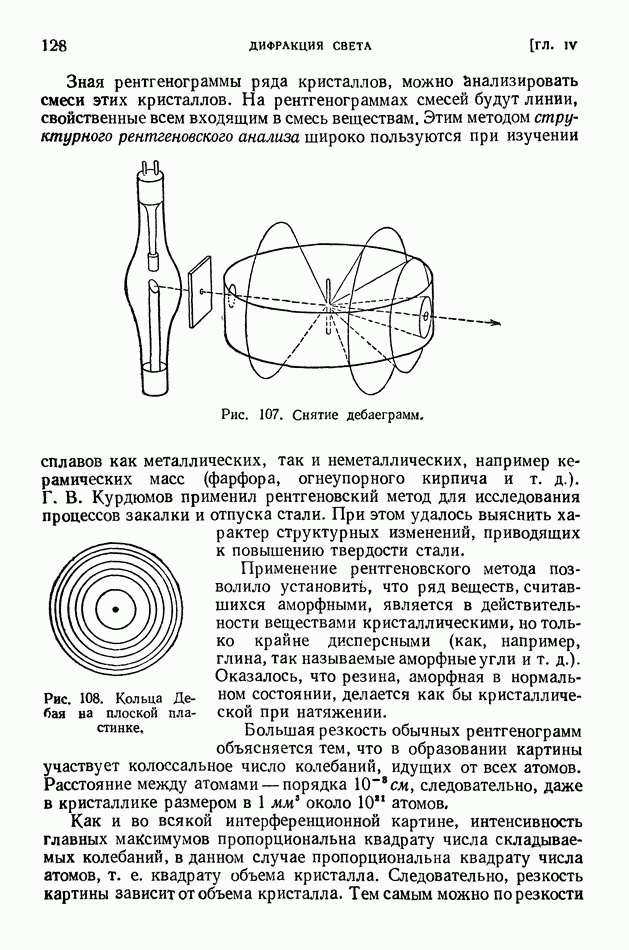
- § 31. Структурный рентгеновский анализ
- § 32. Дифракция света на ультразвуковых волнах
- § 33. Дифракция от мелких частиц
- § 34. Разрешающая способность оптических инструментов. Звездный интерферометр
- ГЛАВА V. ПОЛЯРИЗАЦИЯ СВЕТА
- § 35. Поляризация света
- § 36. Двойное лучепреломление
- § 37. Интерференция поляризованного света
- § 38. Оптический метод исследования упругих натяжений. Эффект Керра
- § 39. Вращение плоскости поляризации. Эллиптическая поляризация
- ГЛАВА VI. ДИСПЕРСИЯ, ПОГЛОЩЕНИЕ И ИЗЛУЧЕНИЕ СВЕТА
- § 40. Отражение света
- § 41. Давление света. Опыты Лебедева
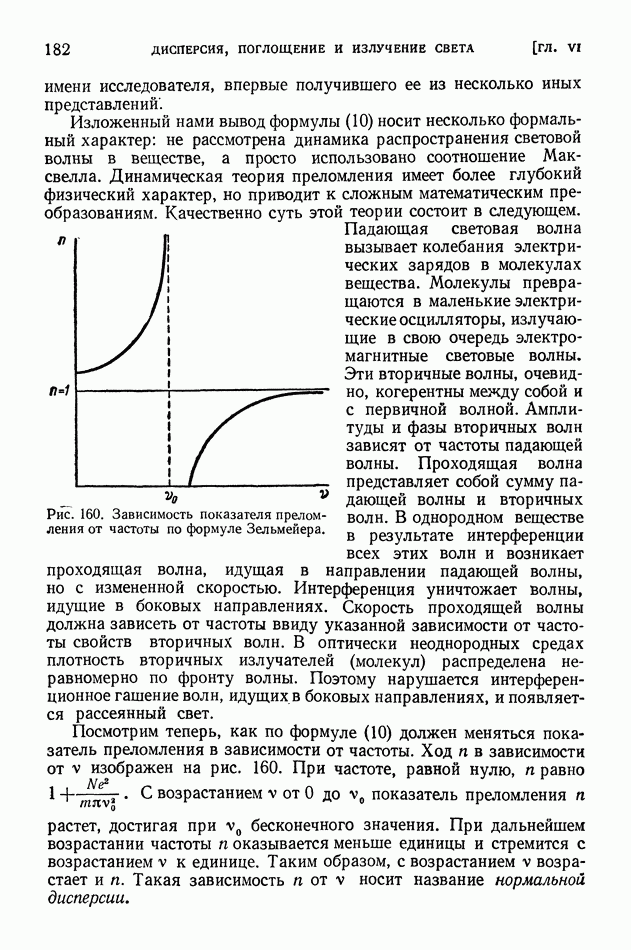
- § 42. Дисперсия. Опыты Ньютона
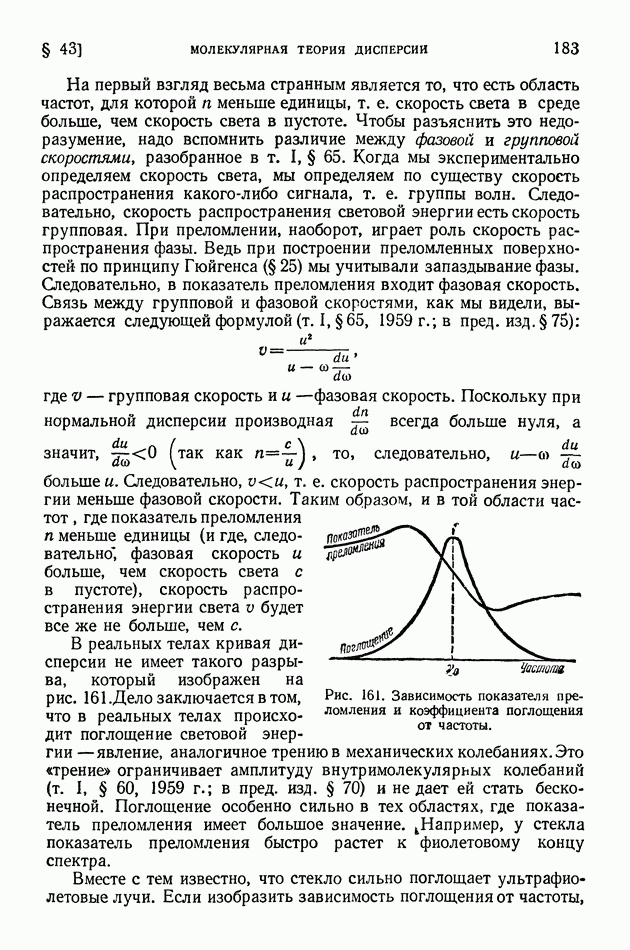
- § 43. Молекулярная теория дисперсии
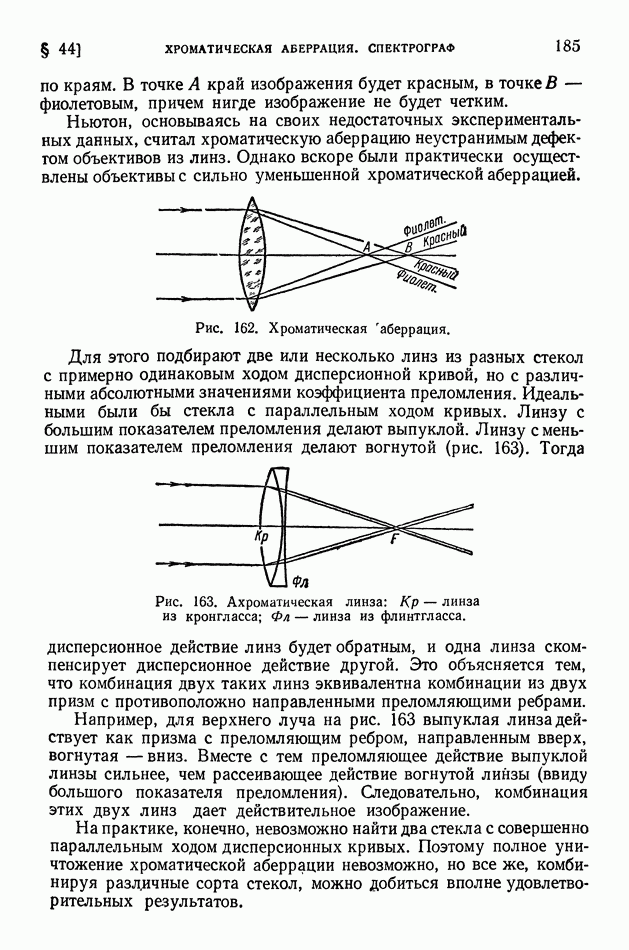
- § 44. Хроматическая аберрация. Спектрограф
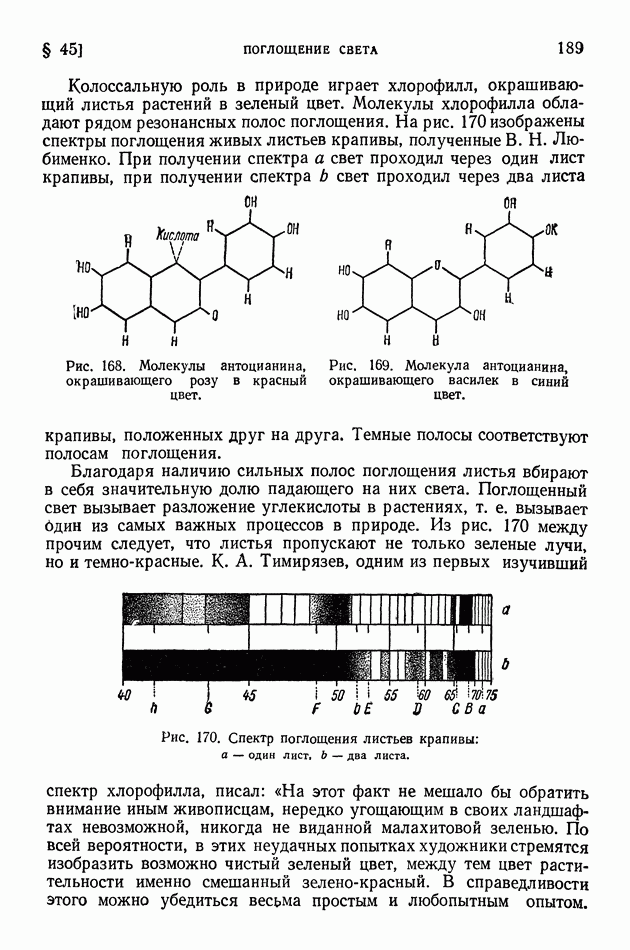
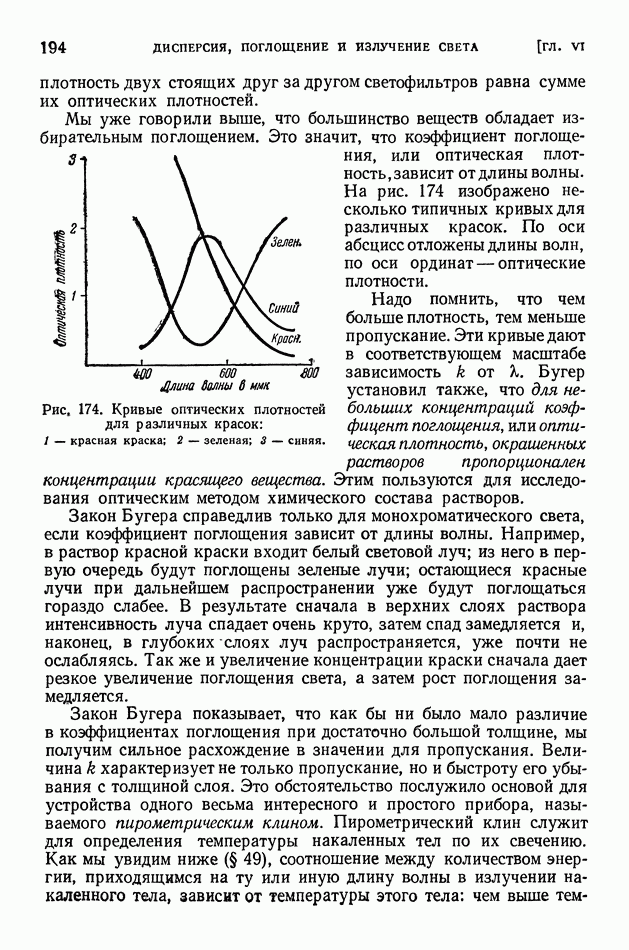
- § 45. Поглощение света
- § 46. Закон Бугера. Опыты Вавилова
- § 47. Атом как элементарный излучатель света
- § 48. Эффект Вавилова — Черенкова
- ГЛАВА VII. ТЕРМОДИНАМИКА ИЗЛУЧЕНИЯ И СВЕТОВОЙ ПОТОК
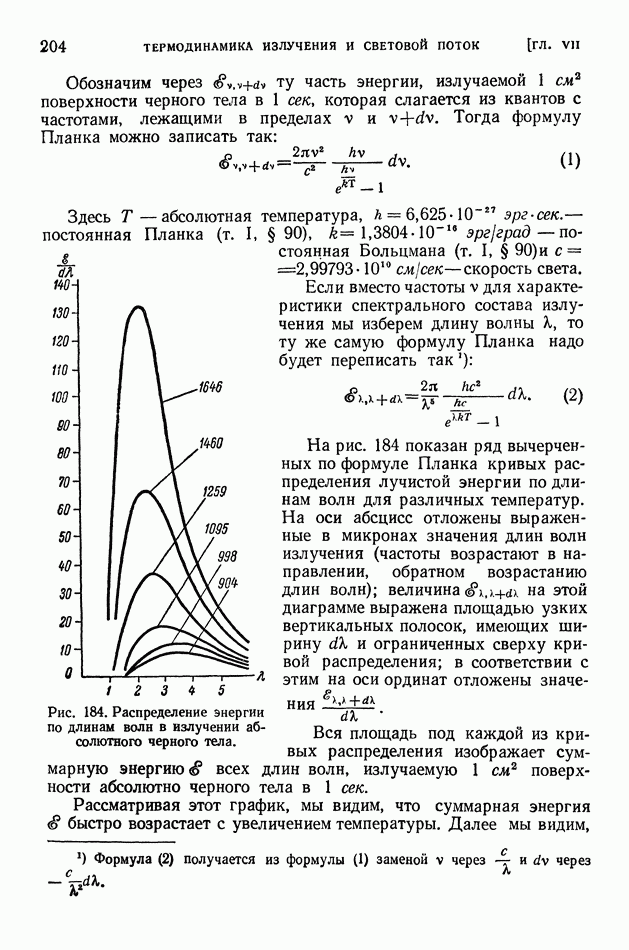
- § 49. Излучение черного тела. Формула Планка. Закон Вина
- § 50. Излучение нечерных тел. Законы Кирхгофа
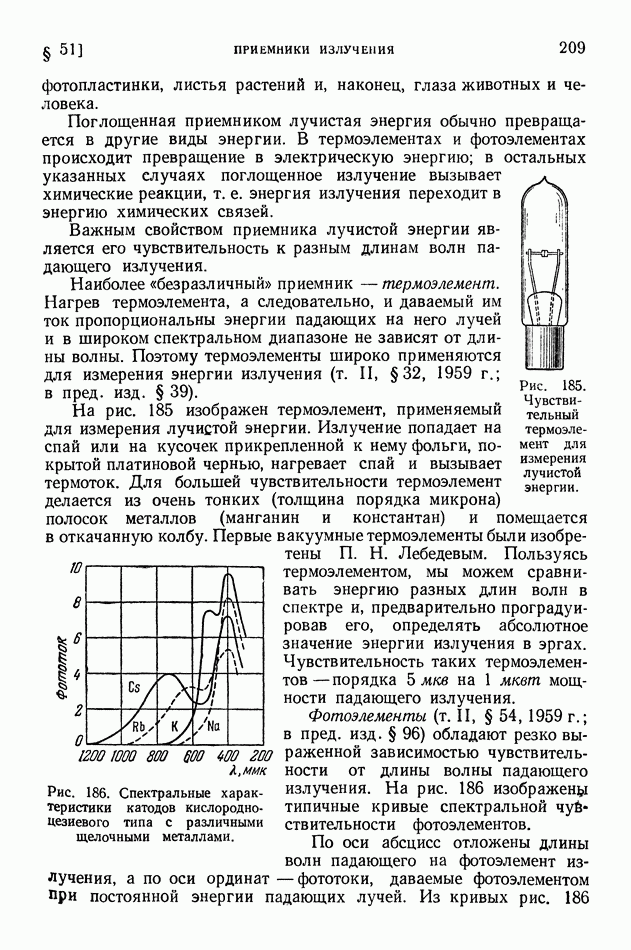
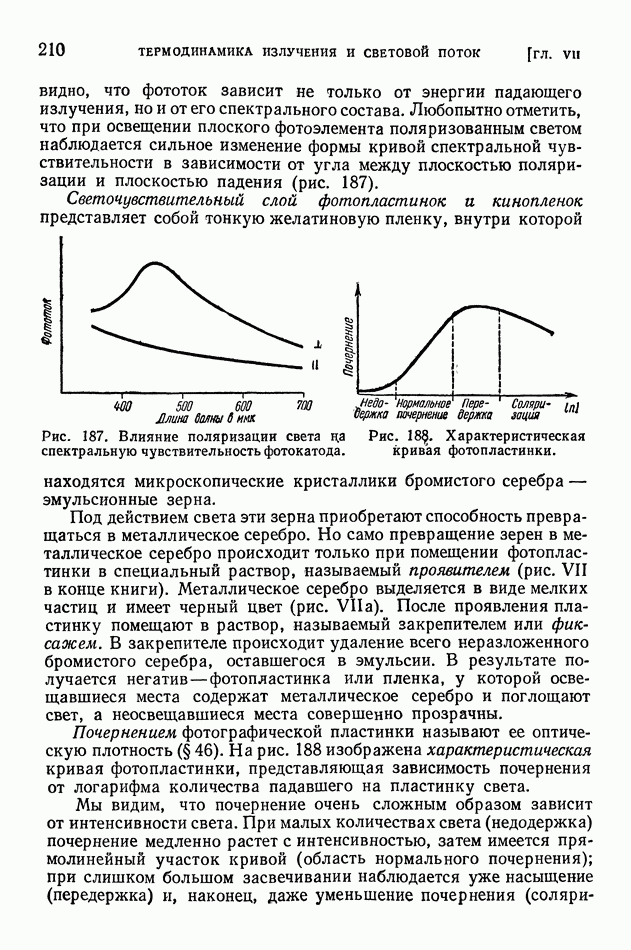
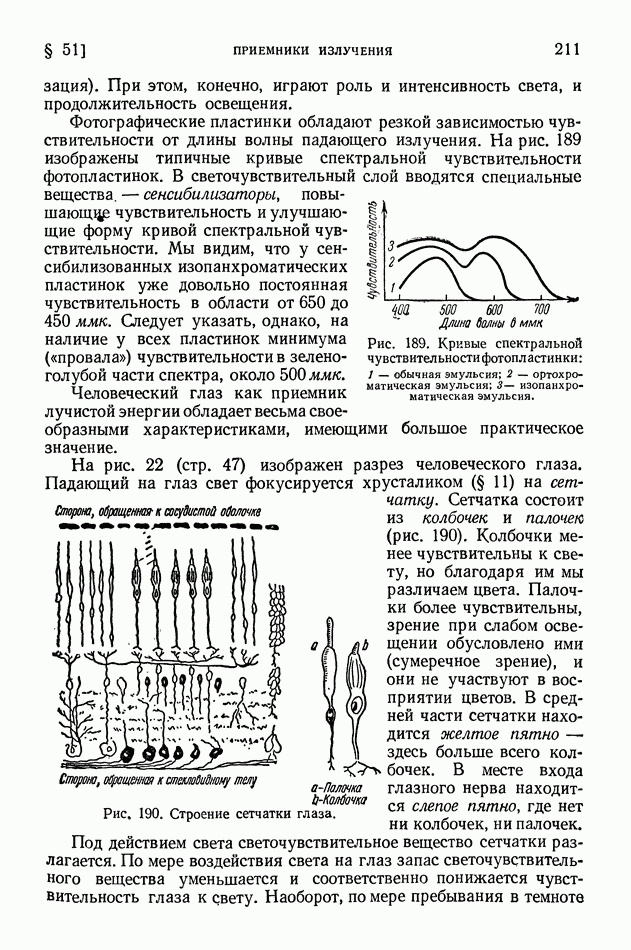
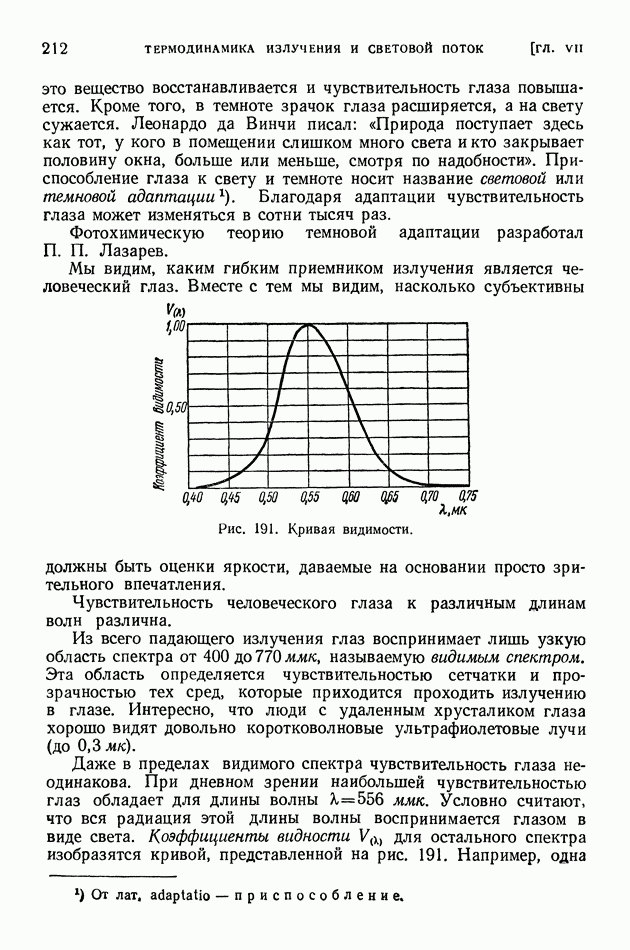
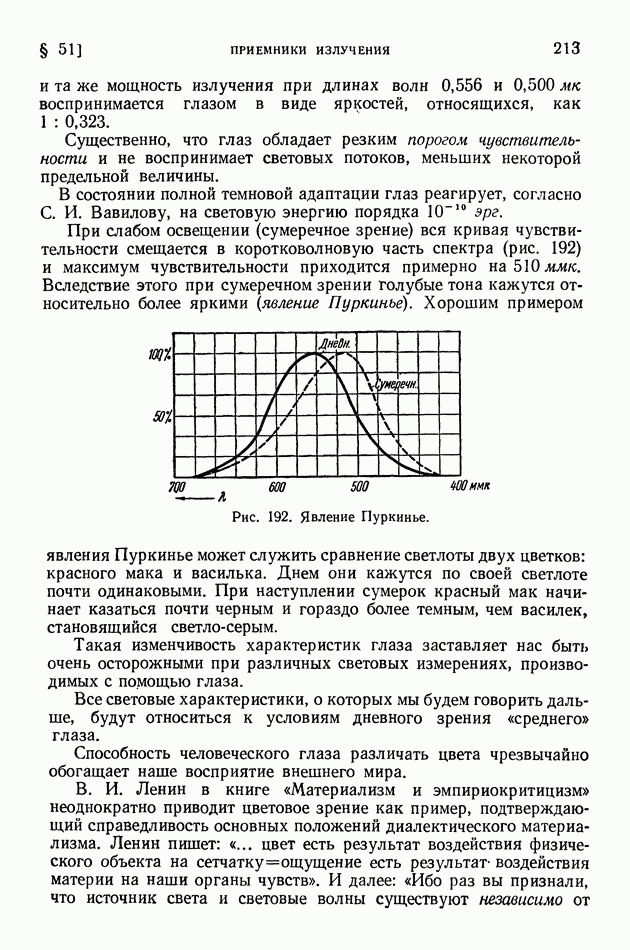
- § 51. Приемники излучения
- § 52. Световые величины и их измерения
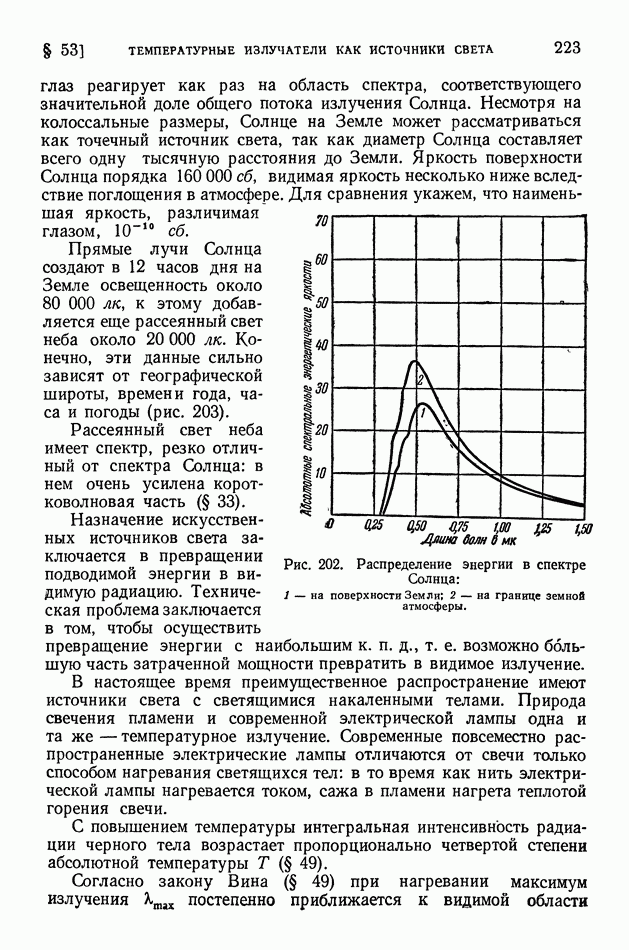
- § 53 Температурные излучатели как источники света
- ЧАСТЬ ПЯТАЯ. АТОМНАЯ ФИЗИКА
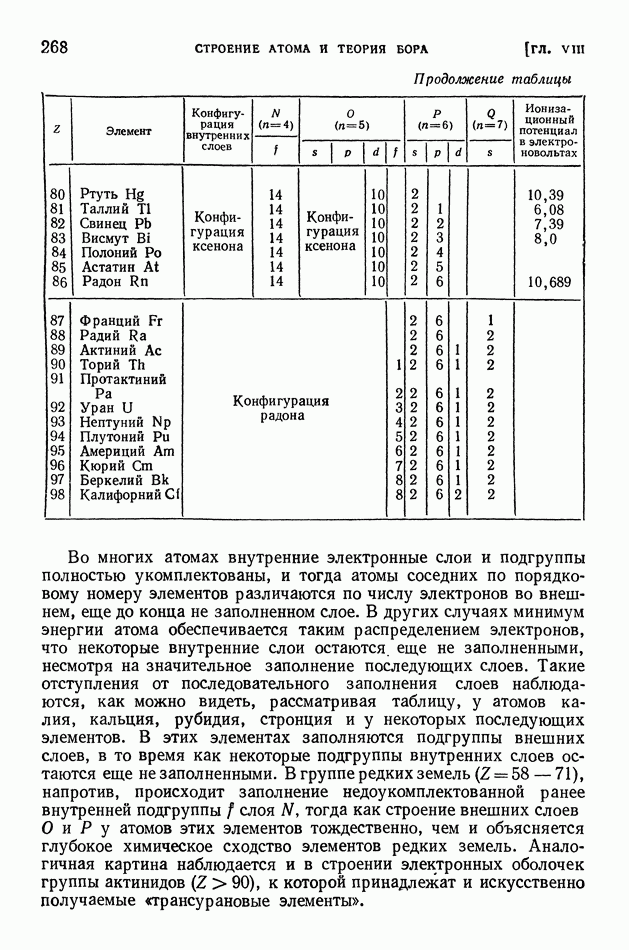
- ГЛАВА VIII. СТРОЕНИЕ АТОМА И ТЕОРИЯ БОРА
- § 55. Опыты, обнаружившие ядерное строение атомов
- § 56. Противоречие между фактическим строением атомов и выводами классической электродинамики. Строение линейчатых спектров
- § 57. Опытные основания теории квантов в первые годы ее развития
- § 58. Теория Бора. Происхождение спектра водорода
- § 59. Квантовые числа
- § 60. Принцип Паули. Строение электронных оболочек атомов
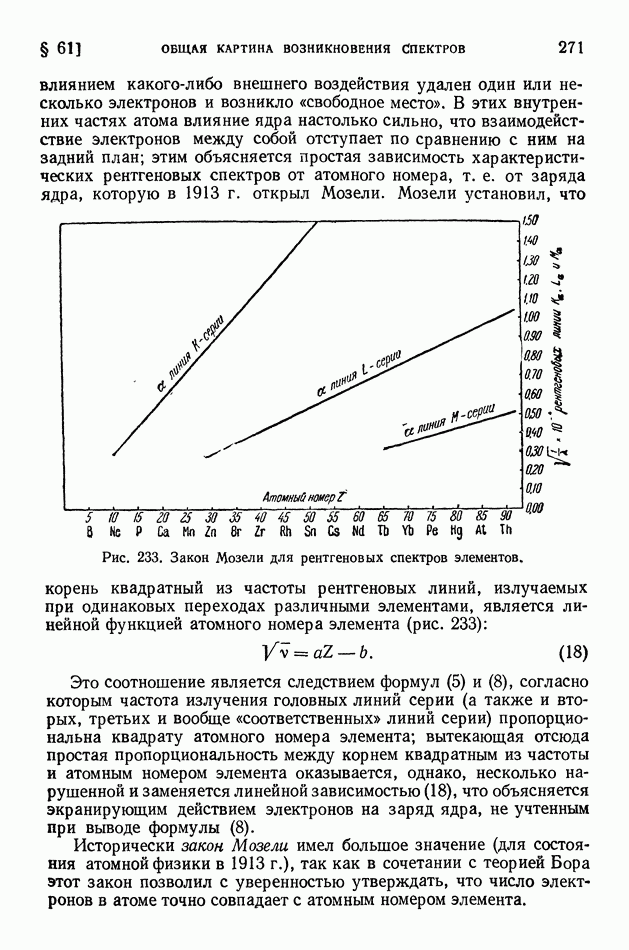
- § 61. Общая картина возникновения спектров
- ГЛАВА IX. ОСНОВЫ КВАНТОВОЙ (ВОЛНОВОЙ) МЕХАНИКИ
- § 62. Волновые свойства частиц. Формула де Бройля. Дифракция электронов
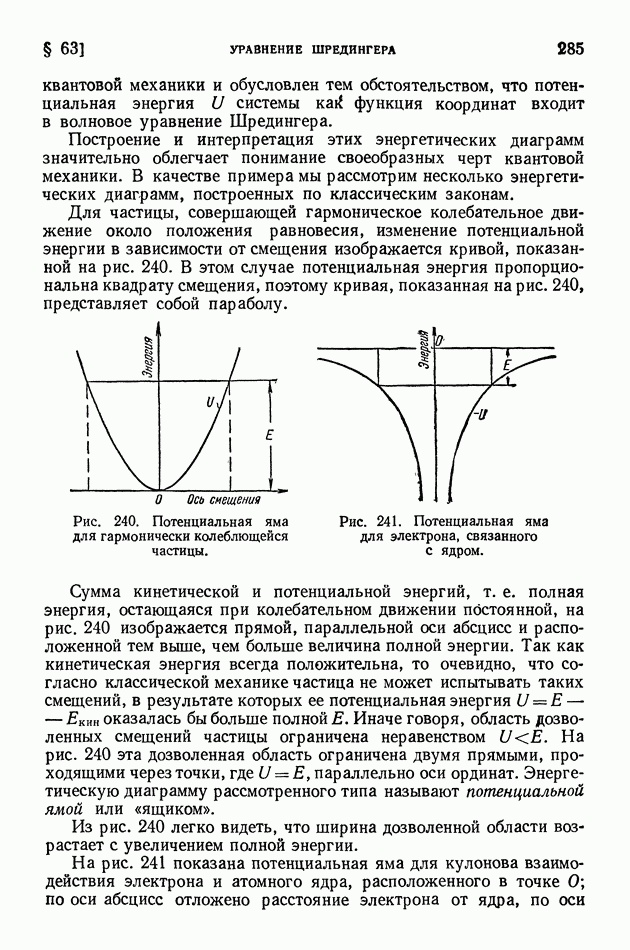
- § 63. Уравнение Шредингера. Просачивание через энергетический барьер. Нулевая энергия
- § 64. Волномеханическая теория атома водорода
- § 65. Соотношение неопределенностей и его разные трактовки
- ГЛАВА X. КВАНТОВАЯ ОПТИКА
- § 66. Развитие квантовой оптики
- § 67. Спектр щелочных металлов. Спин электрона
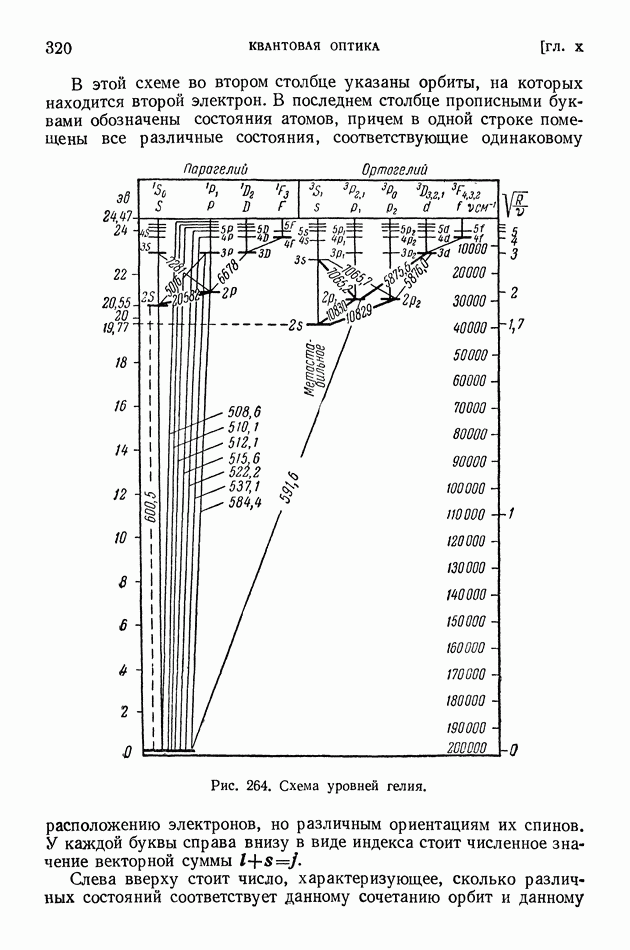
- § 68. Спектр гелия. Символика спектральных термов
- § 69. Сверхтонкая структура спектральных линий
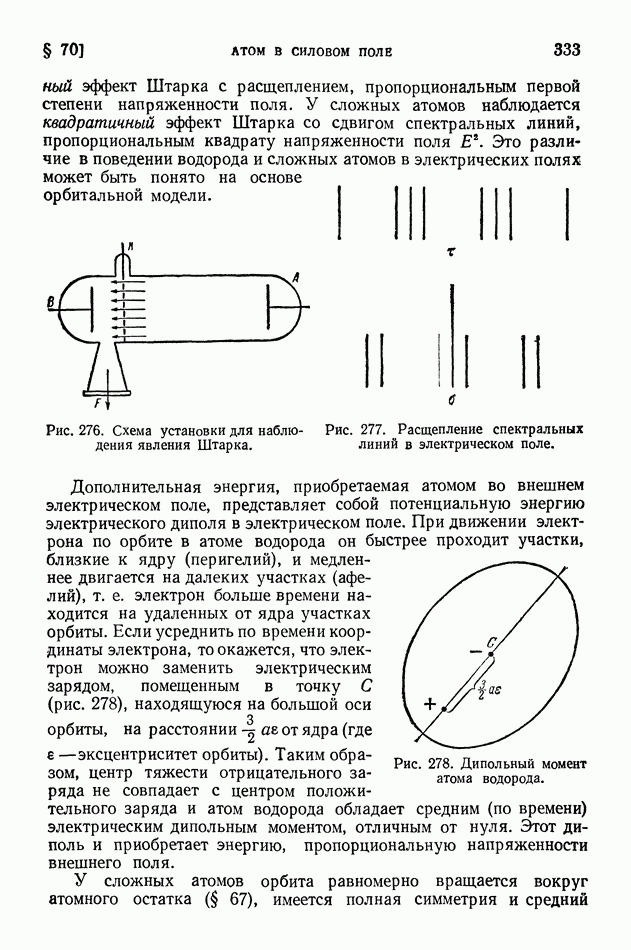
- § 70. Атом в силовом поле
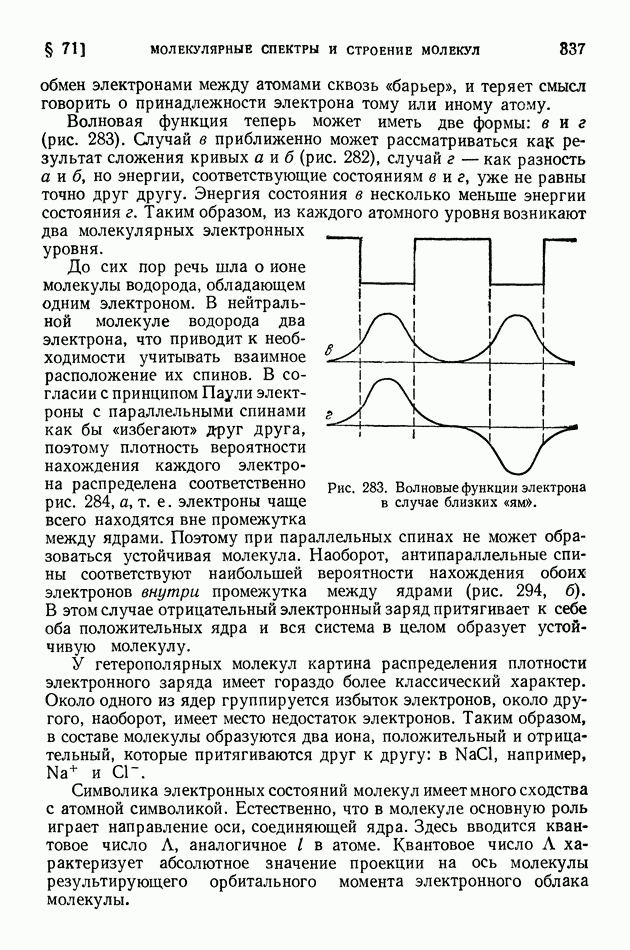
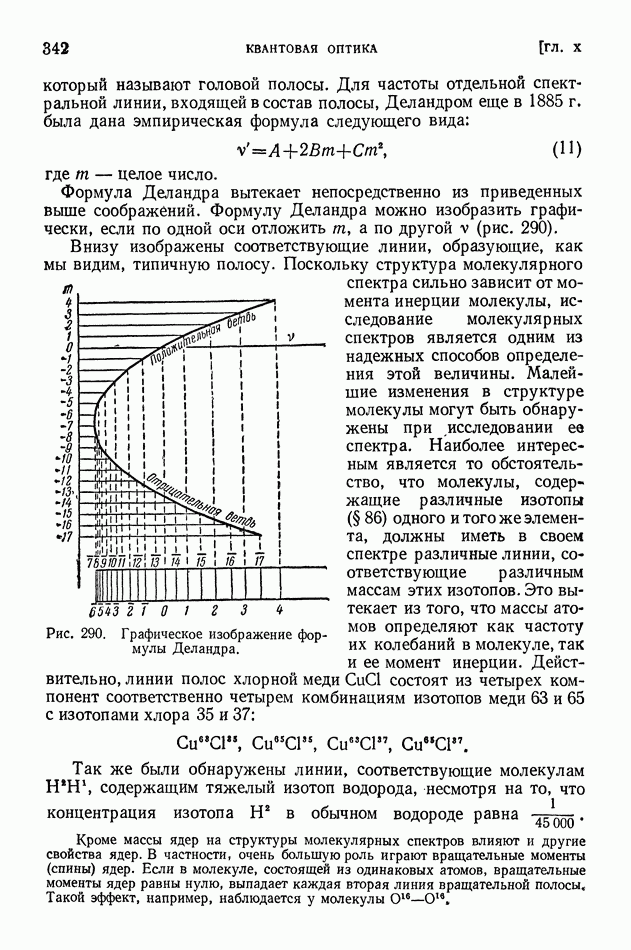
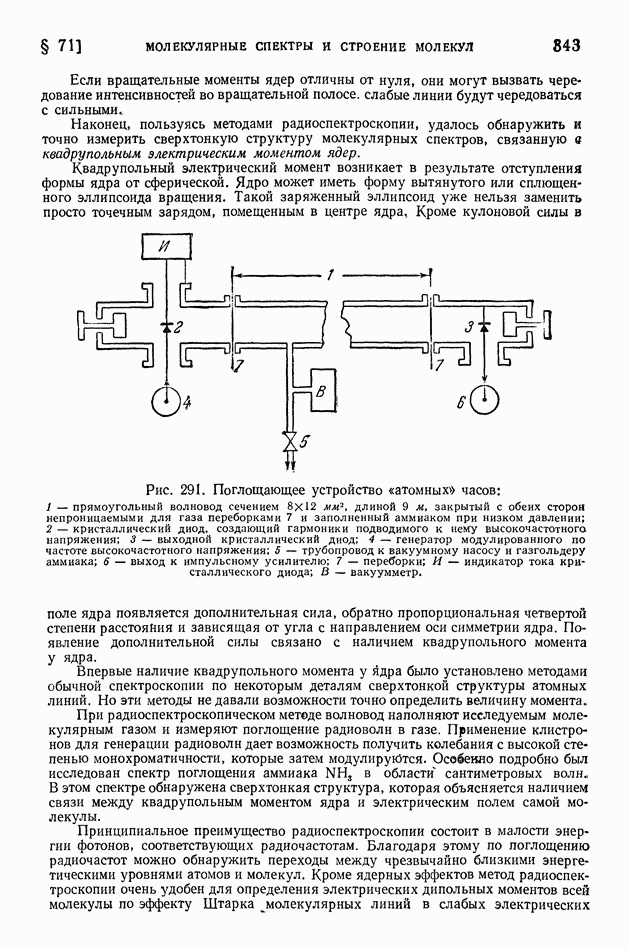
- § 71. Молекулярные спектры и строение молекул
- § 72. Комбинационное рассеяние света
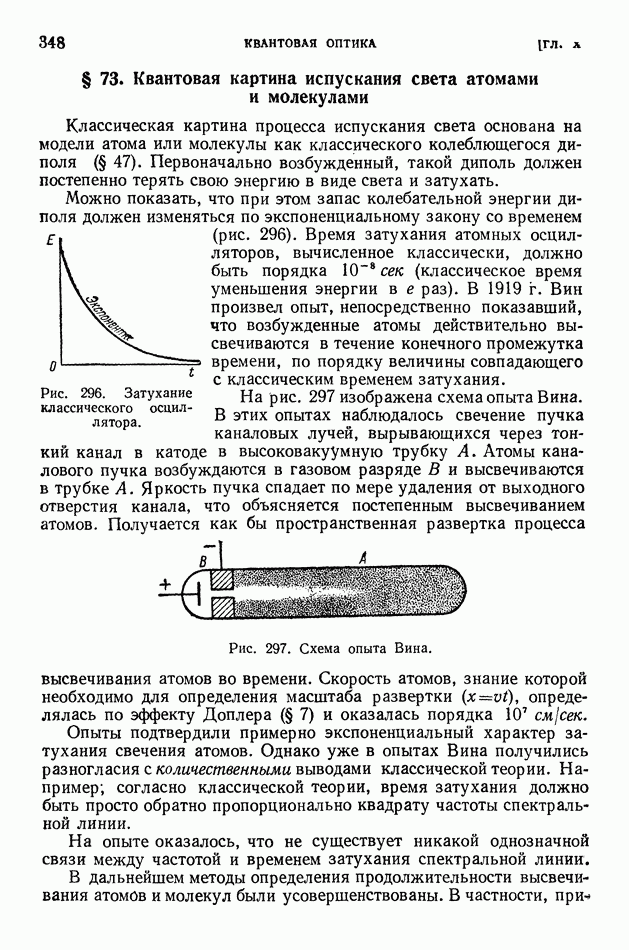
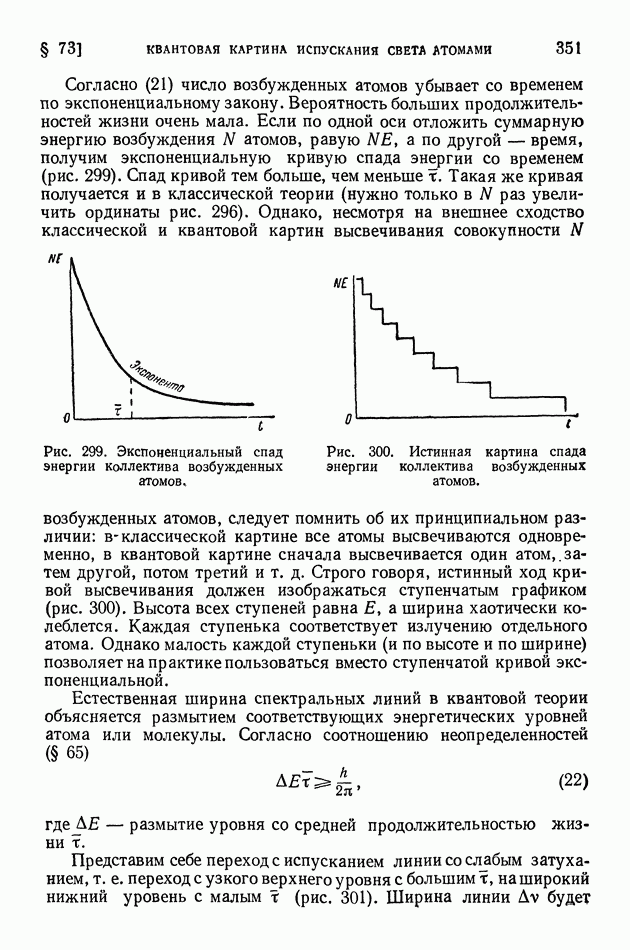
- § 73. Квантовая картина испускания света атомами и молекулами
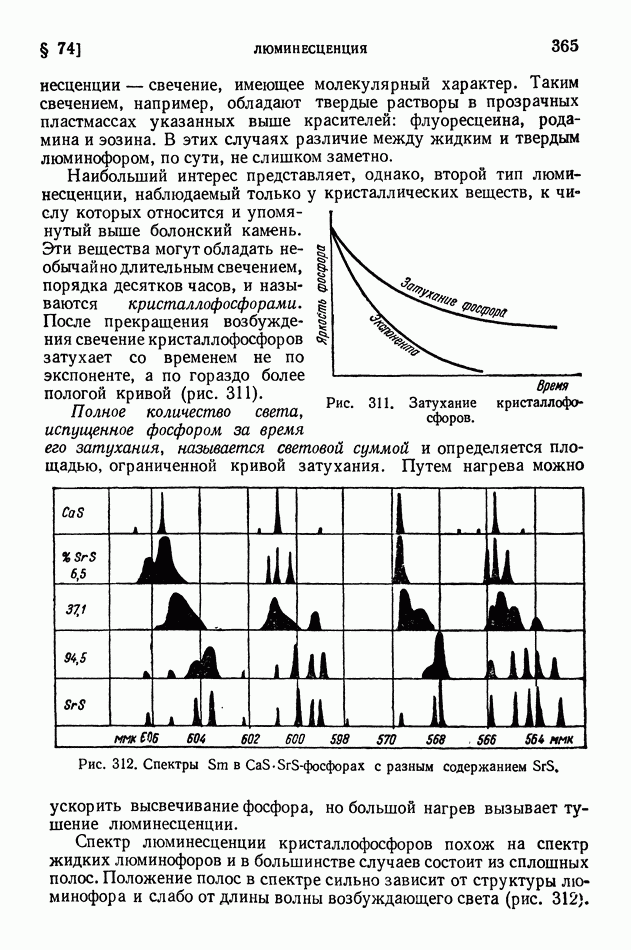
- § 74. Люминесценция
- § 75. Возбуждение люминесценции ударами частиц вещества
- § 76. Применения люминесценции
- § 77. Фотохимические реакции
- ГЛАВА XI. ЗАКОН ПРОПОРЦИОНАЛЬНОСТИ МАССЫ И ЭНЕРГИИ И РЕЛЯТИВИСТСКИЕ СООТНОШЕНИЯ
- § 78. Закон пропорциональности массы и энергии
- § 79. Предварительные замечания о релятивистских эффектах. Зависимость массы от скорости
- § 80. Корпускулярные свойства фотонов. Явление Комптона
- § 81. Вывод закона Эйнштейна сложения скоростей из закона пропорциональности массы и энергии и законов сохранения энергии или количества движения
- § 82. Две трактовки закона пропорциональности массы и энергии и уточнение закона тяготения
- § 83. Красное смещение спектральных линий. Поперечный эффект Доплера
- § 84. Влияние гравитационного поля на скорость света в вакууме и показатель преломления вакуума
- ЧАСТЬ ШЕСТАЯ. ЯДЕРНАЯ ФИЗИКА
- § 85. Заряд и масса ядра. Масс-спектральный анализ
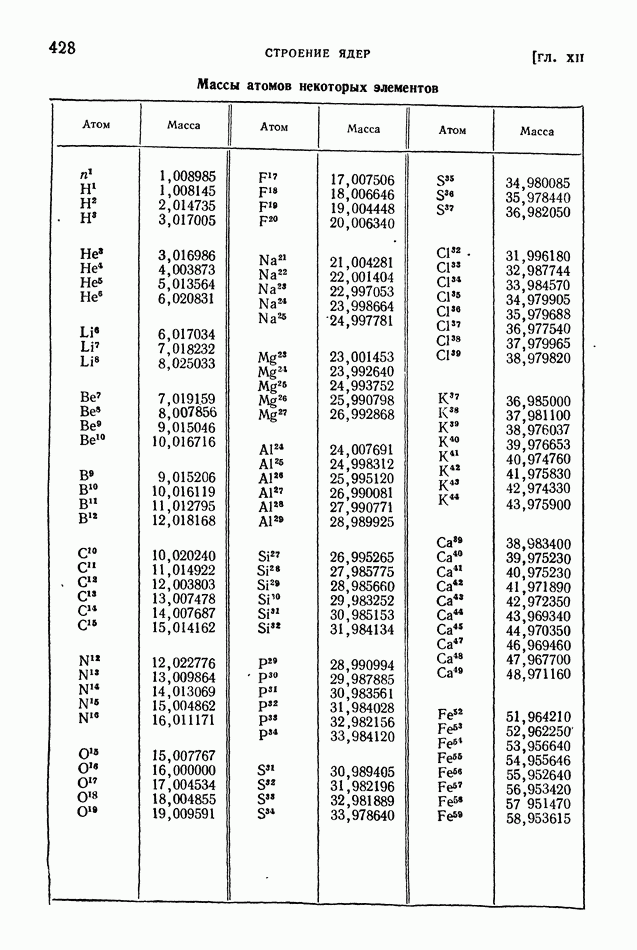
- § 86. Состав ядер. Изотопы. Атомные единицы массы и энергии
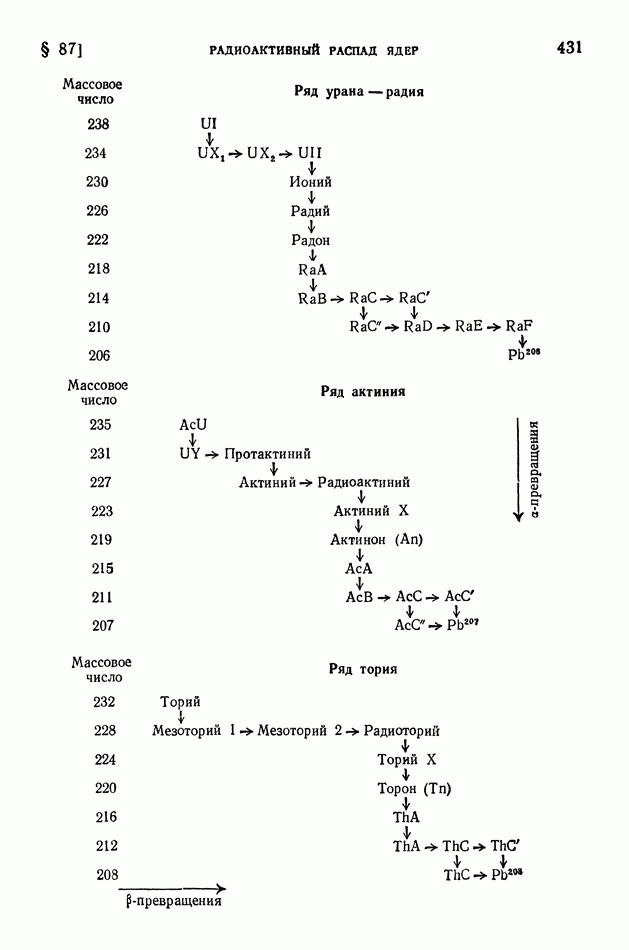
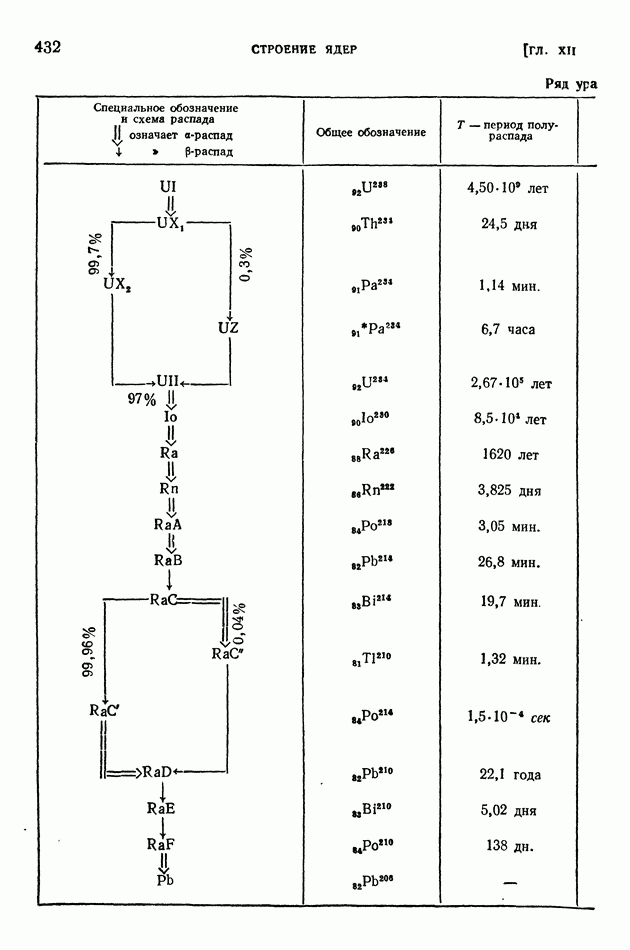
- § 87. Радиоактивный распад ядер. Закон радиоактивного смещения. Изомеры
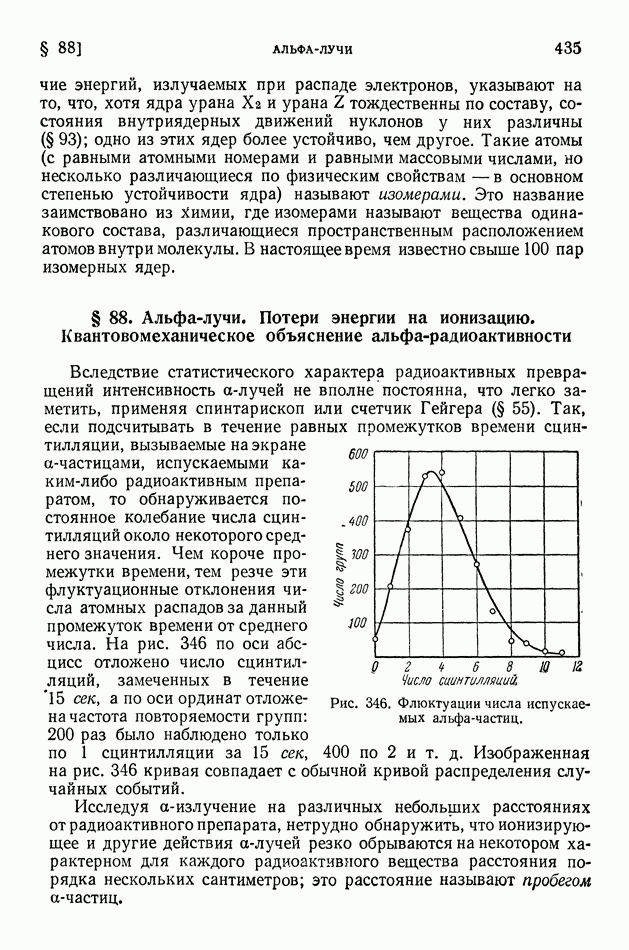
- § 88. Альфа-лучи. Потери энергии на ионизацию. Квантовомеханическое объяснение альфа-радиоактивности
- § 89. Бета- и гамма-лучи
- § 90. Искусственное расщепление ядер. Открытие нейтрона
- § 91. Открытие позитрона. Взаимопревращение фотонов определенной энергии и электронно-позитронных пар
- § 92. Индуцированная позитронная и электронная радиоактивность. Фоторасщепление ядер, K-захват
- § 93. Энергетические уровни ядер. Внутренняя конверсия. Нейтрино
- § 94. Капельная теория строения ядер
- § 95. Деление ядер и развитие капельной теории строения ядер
- ГЛАВА XIII. КОСМИЧЕСКИЕ ЛУЧИ
- § 96. Методы исследования и первые итоги изучения космических лучей
- § 97. Каскадное образование электронно-позитронных пар в космических лучах. Потери энергии электронами на тормозное излучение
- § 98. «мю»-мезоны. Зависимость времени жизни неустойчивых частиц от скорости движения
- § 99. «пи»-мезоны
- § 100. Взрывные ядерные ливни и их каскадное развитие в космических лучах
- § 101. Корпускулярный и энергетический спектр космических лучей. Происхождение космического излучения
- ГЛАВА XIV. ЭКСПЕРИМЕНТАЛЬНЫЕ СРЕДСТВА ЯДЕРНОЙ ФИЗИКИ
- § 102. Циклотроны
- § 103. Фазотроны
- § 104. Бетатроны
- § 105. Синхротроны и синхрофазотроны
- § 106. Линейные ускорители электронов и ионов
- § 107. Лабораторные источники нейтронов. Замедлители нейтронов в ядерных реакторах
- § 108. Усовершенствование методов наблюдения и счета частиц
- ГЛАВА XV. ЯДЕРНЫЕ РЕАКЦИИ И АТОМНАЯ ЭНЕРГИЯ
- § 109. Основные виды и обозначения ядерных реакций. Конкурирующие процессы в ядерных реакциях
- § 110. Энергетический эффект, энергия возбуждения и порог ядерных реакций
- § 111. Превращения элементарных частиц
- § 112. Ядерные силы
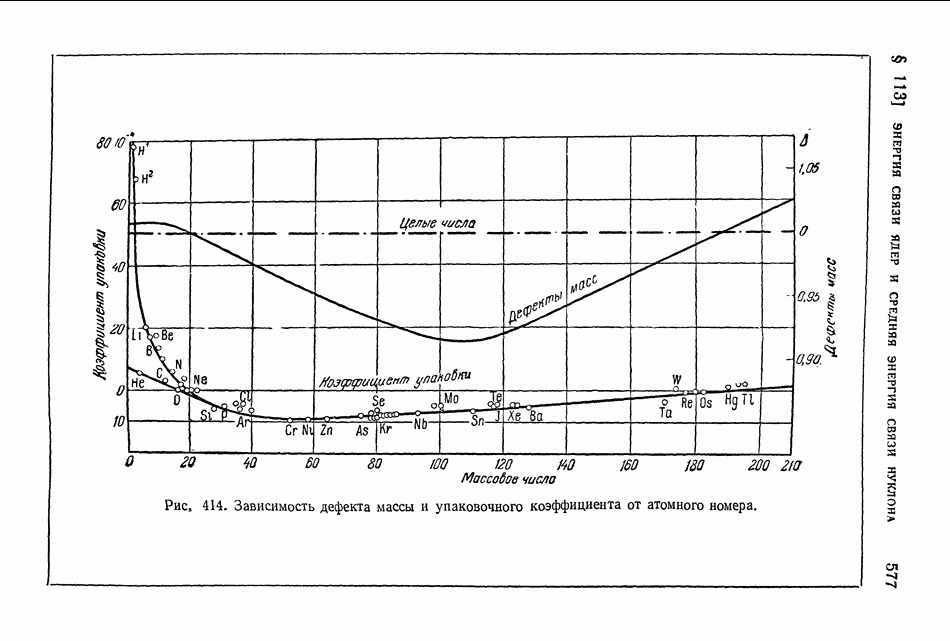
- § 113. Энергия связи ядер и средняя энергия связи нуклона
- § 114. Полуэмпирическая формула для энергии ядерной связи и для атомных энергий и масс
- § 115. Взаимосвязь энергии и строения ядер. Внутриядерное движение нуклонов и нуклонные оболочки. Спины и магнитные моменты ядер
- § 116. Энергия отделения частиц и анализ возможного хода ядерной реакции
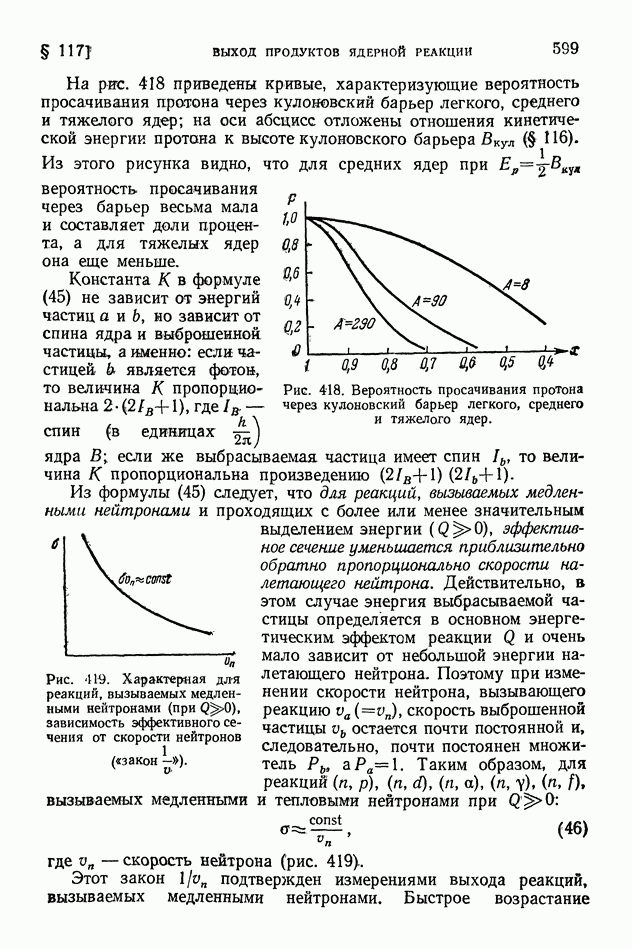
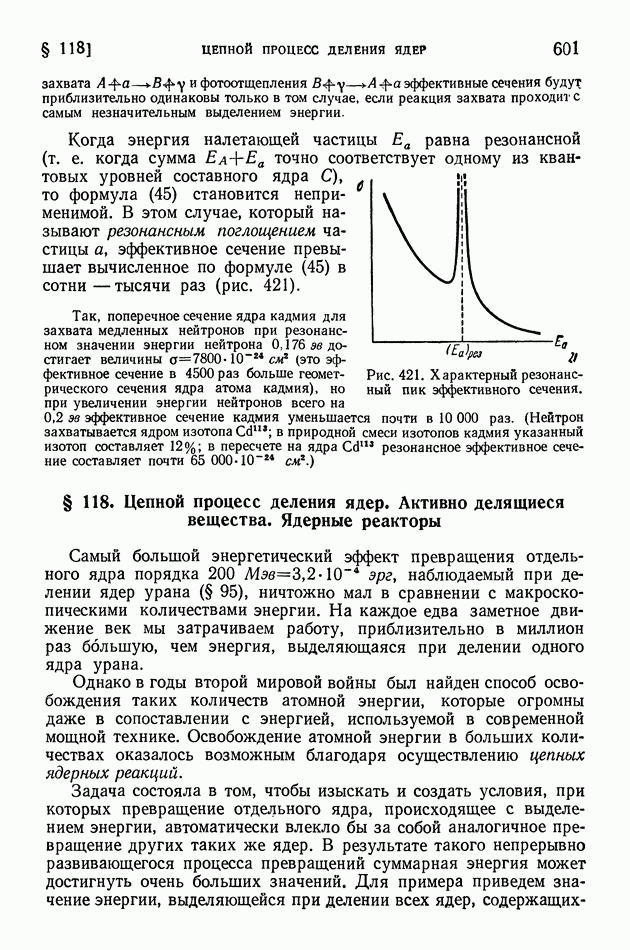
- § 117. Выход продуктов ядерной реакции. Эффективные сечения. Резонансные явления
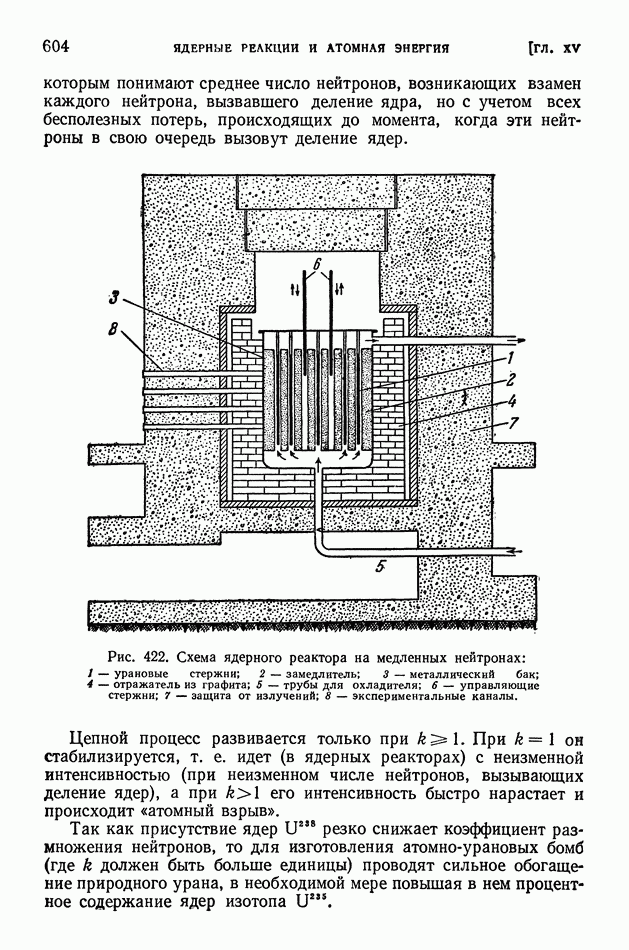
- § 118. Цепной процесс деления ядер. Активно делящиеся вещества. Ядерные реакторы
- § 119. Термоядерные реакции
- § 120. Применение ядерных реакций
- § 121. Ядерные реакции в звездах