§ 2. Электромагнитная теория света

Как было указано выше, Максвелл является создателем электромагнитной теории света. Правда, сам Максвелл уступал приоритет этого важнейшего открытия Фарадею. Он писал в «Динамической теории электромагнитного поля»: «Концепция распространения поперечных магнитных возмущений с исключением возможности продольных возмущений была отчетливо высказана профессором Фарадеем в его "Мыслях о лучевых колебаниях". Электромагнитная

теория света, предложенная им, является по существу той же самой, которую я начал развивать в этой статье, за исключением того, что в 1846 г. еще не было данных для вычисления скорости распространения». Однако А. Г. Столетов, много сделавший как раз для уточнения данных, необходимых для вычисления скорости распространения, справедливо указывал: «Мы далеко ушли вперед от смутной грезы Фарадея, который спрашивал себя, не есть ли радиация быстрое дрожание силовых линий, и вслед за тем как бы пугался своих мыслей, сознаваясь что это лишь "тень умозрения"».

Электромагнитная теория света, в сущности, является одним из следствий знаменитых уравнений Максвелла. Воспроизведем в возможно простой форме ход рассуждений Максвелла.

Рассмотрим плоское электромагнитное поле, в котором электрическое поле направлено параллельно оси и зависит только от одной координаты Тогда из уравнений Максвелла следует (см. т. II, § 76), что магнитное поле должно быть направлено параллельно оси у и тоже зависит только от Сами уравнения Максвелла в этом случае упрощаются; вместо векторных уравнений

останутся только два скалярных уравнения:

Из уравнений (1) и можно исключить либо либо и получить дифференциальные уравнения для каждой из этих величин в отдельности. Например, дифференцируя уравнение (1) по а уравнение по и умножая его на мы можем исключить и получим:

Такое же точно уравнение получится и для Нетрудно видеть, что уравнение (2) есть дифференциальное уравнение электрической волны, распространяющейся по направлению оси х со скоростью, определяемой соотношением

В самом деле, подстановкой можно проверить, что уравнению (2)

удовлетворяет зависящее от следующим образом:

где — произвольная функция, если только удовлетворяет уравнению (3).

Как было показано ранее (т. 1, § 63, 1959 г., в пред. изд. § 73), выражение (4) описывает распространяющуюся волну, причем вид аргумента функции соответствует эффекту запаздывания. Определенное значение бывшее в более ранний момент времени в точке будет в более поздний момент в точке причем ибо при соблюдении указанного условия аргумент функции в выражении (4) остается постоянным. Таким образом, есть скорость распространения фазы электромагнитной волны. Согласно формуле (3) в вакууме эта скорость должна быть равна с — отношению электромагнитной и электростатической единиц силы тока (т. II, § 60, 1959 г. и пред. изд.).

Пользуясь уравнением (3), можно уравнению (2) придать следующий вид:

В общем случае, когда зависит от всех трех координат волновое уравнение приобретает следующий вид:

где

Для монохроматической волны с частотой можно исключить время из уравнения Положим

где амплитуда Тогда

так как двойное дифференцирование по эквивалентно умножению на Подставив в формулу вместо выражение этой производной по после сокращения на получим:

Это уравнение также называют волновым. Иногда его записывают в несколько ином виде, а именно используют соотношение

Максвелл предположил, что свет представляет собой одну из разновидностей электромагнитных волн, и проверил свое предположение, сравнив скорость света, которая была определена Физо, с константой с, вычисленной из чисто электромагнитных измерений. Обе цифры совпали с точностью до тысячных долей процента! Нельзя не отметить, что такое прекрасное совпадение было в известной мере результатом случайности, так как обе величины были в то время измерены с ошибками порядка 3%. В проверке теории Максвелл оказался удачливее Ньютона, который по вине неточных астрономических данных на 20 лет отложил опубликование закона всемирного тяготения. Полученное Максвеллом совпадение послужило серьезным аргументом в пользу электромагнитной теории света, и новые измерения подтвердили это совпадение с большой точностью.

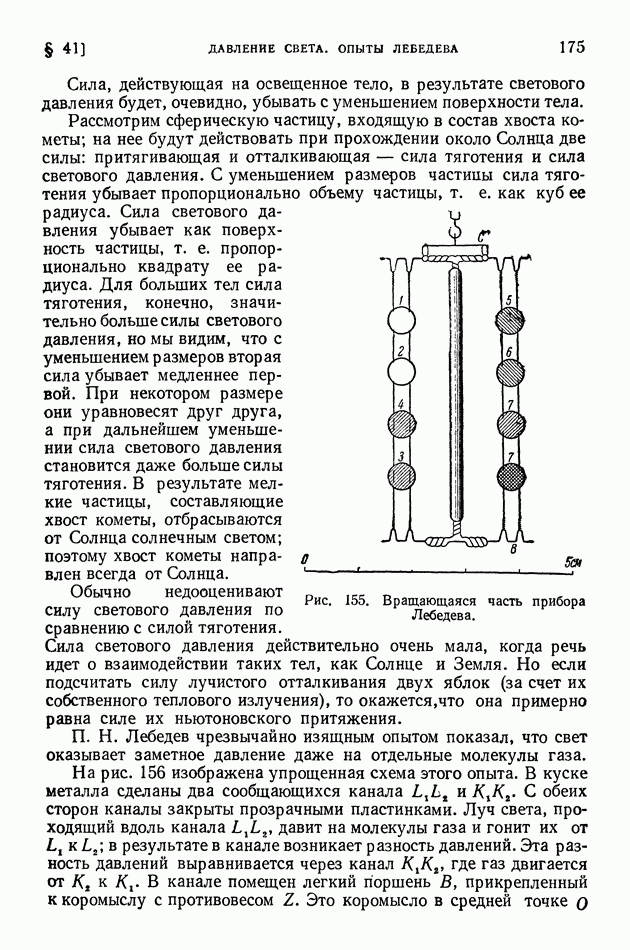
Вместе с тем электромагнитная теория света далеко не сразу получила общее признание. Только после известных опытов П. Н. Лебедева по световому давлению (§ 41) всякие сомнения в правильности этой теории исчезли. Кельвин сказал как-то К. А. Тимирязеву: «Вы, может быть, знаете, что я всю жизнь воевал с Максвеллом, и вот ваш Лебедев своими опытами заставил меня сдаться».

При распространении света в среде скорость изменяется согласно уравнению (3). Из этого уравнения следует, что показатель преломления я должен быть связан с электрическими и магнитными параметрами среды формулой Максвелла

Соотношение (6) хорошо согласуется с экспериментальными данными для ряда газов (азот, водород, углекислота) и жидкостей типа бензола и толуола. Но для многих других жидких и твердых тел наблюдаются серьезные расхождения, которые, однако, вызваны особыми причинами (§ 43).

В электромагнитной теории поперечность световых колебаний получила простое объяснение. Электрическое и магнитное поля волны направлены перпендикулярно к направлению распространения волны.

Геометрическое место точек с одинаковой фазой светового колебания называется волновой поверхностью. Реальные волновые поверхности имеют довольно сложную форму. Световая волна, испущенная отдельным атомом, с достаточной степенью точности может считаться сферической.

Очевидно, что чем дальше ушла сферическая волна от своего источника, тем меньше ее кривизна. В оптике часто оперируют с понятием плоская волна. Например, выше мы рассмотрели именно случай плоской волны. Следует, однако, помнить, что плоская волна представляет собой идеализацию, соответствующую бесконечно удаленному источнику света. Поскольку напряженности полей Е и Н

обратно пропорциональны расстоянию от источника (т. II, § 89, 1959 и пред. изд.), то в абсолютно плоской волне должны быть равны нулю. Практически плоской волной с конечными и считают часть волновой поверхности любой формы, кривизной которой можно в данной конкретной задаче пренебречь.

Поток энергии в световой волне определяется вектором Умова — Пойнтинга (т. II, § 89). Световые лучи совпадают с направлениями этого вектора. В изотропной среде световые лучи нормальны к волновым поверхностям. Согласно сказанному абсолютно плоская волна не может нести конечный поток энергии. Конечные потоки световой энергии всегда заключены в конечных телесных углах, образуемых световыми лучами. Если в выражении для численного значения вектора Умова — Пойнтинга заменить через [пользуясь соотношением (11), т. И, § 89], то мы получим, что поток энергии световой волны пропорционален Таким образом, энергия световых волн, так же как и волн любой другой природы, пропорциональна квадрату амплитуды.