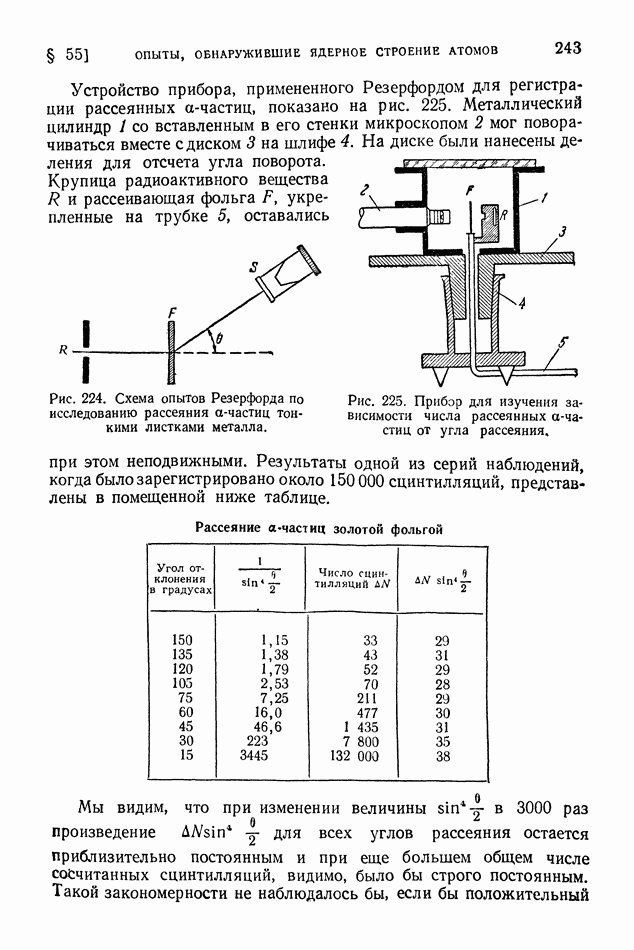
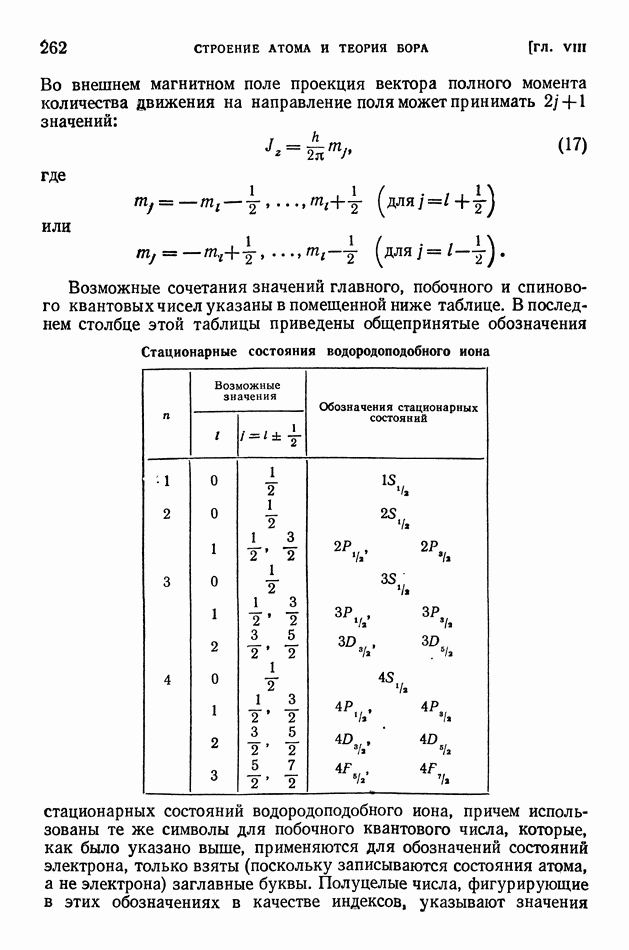
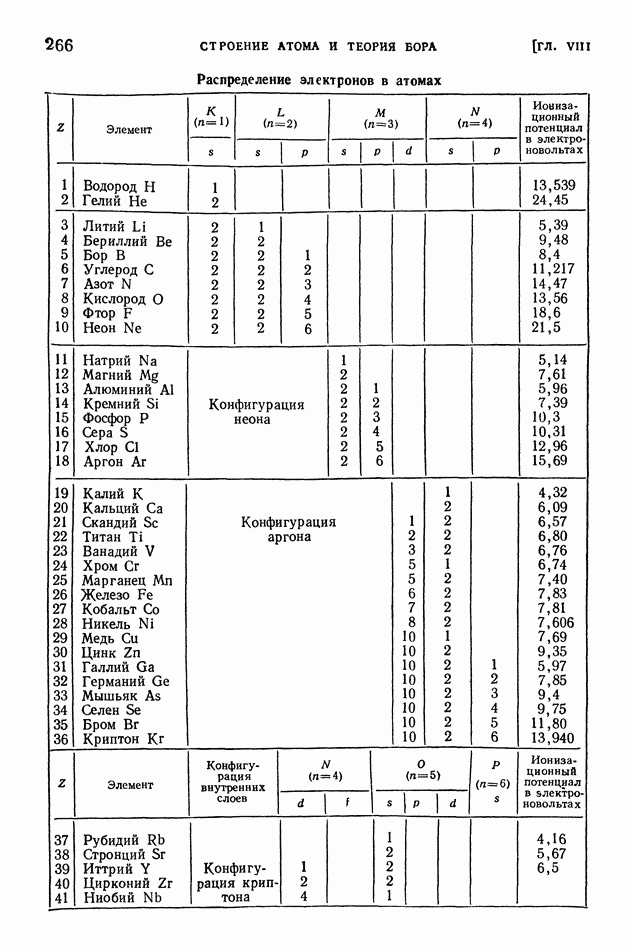
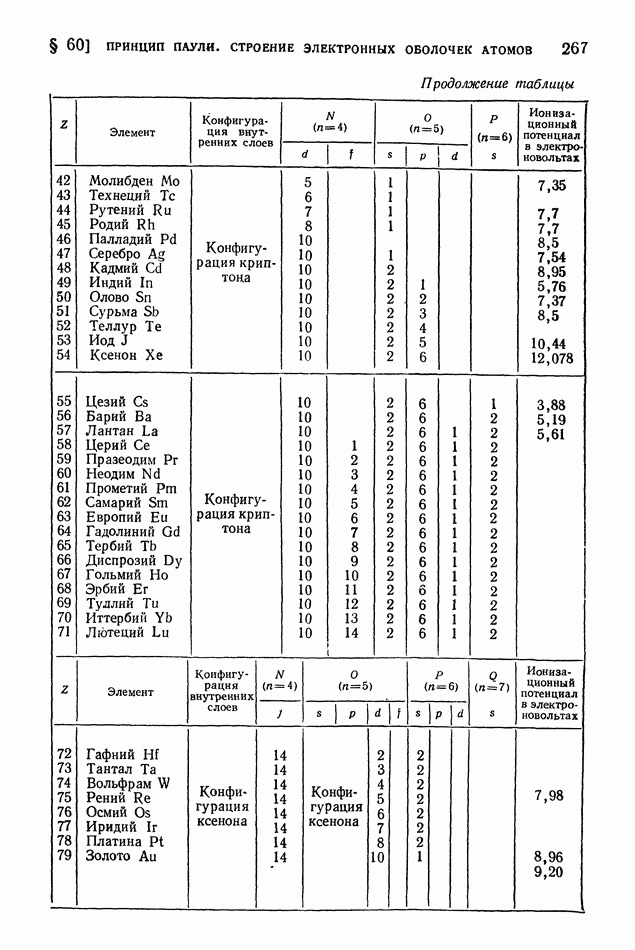
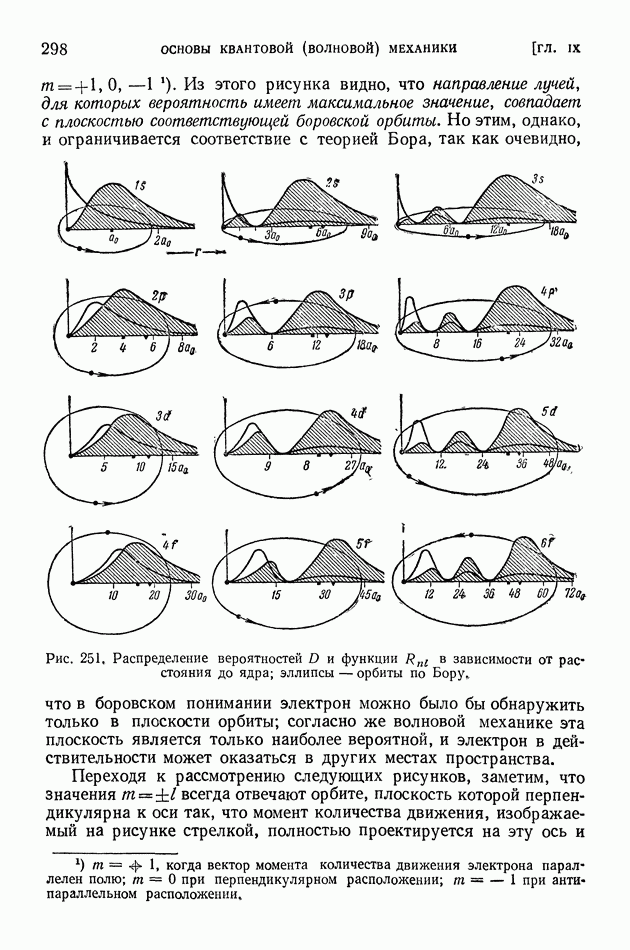
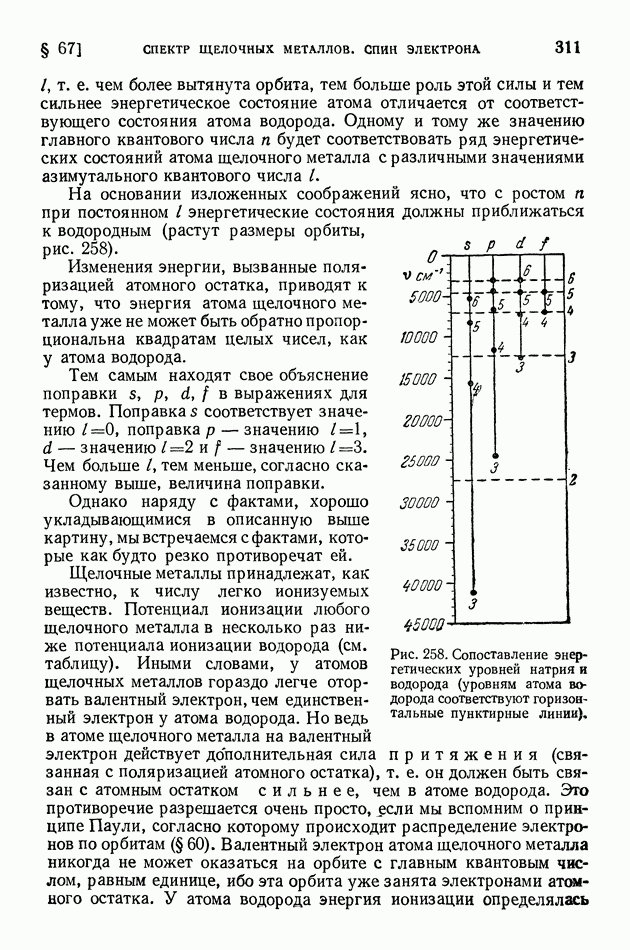
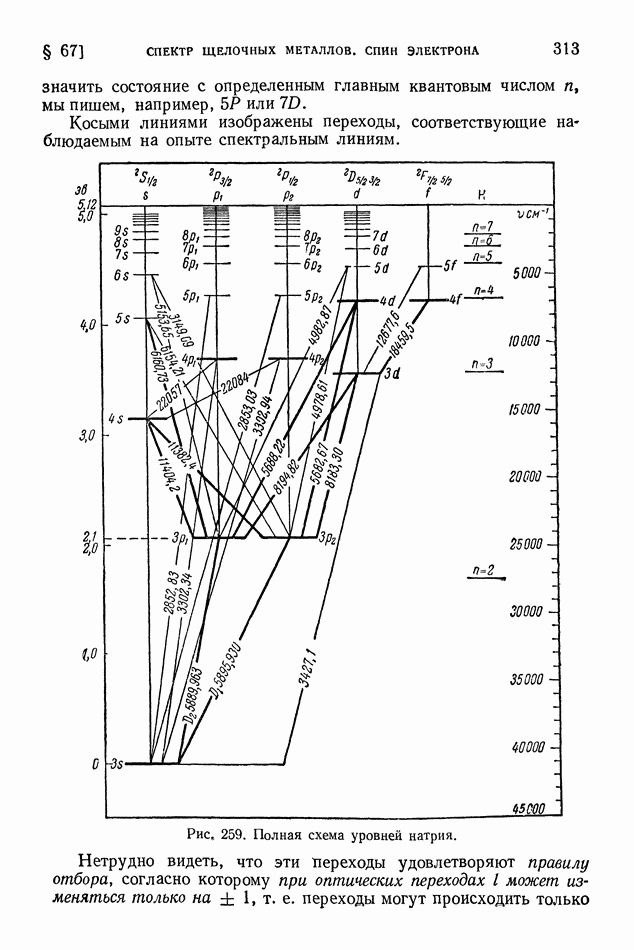
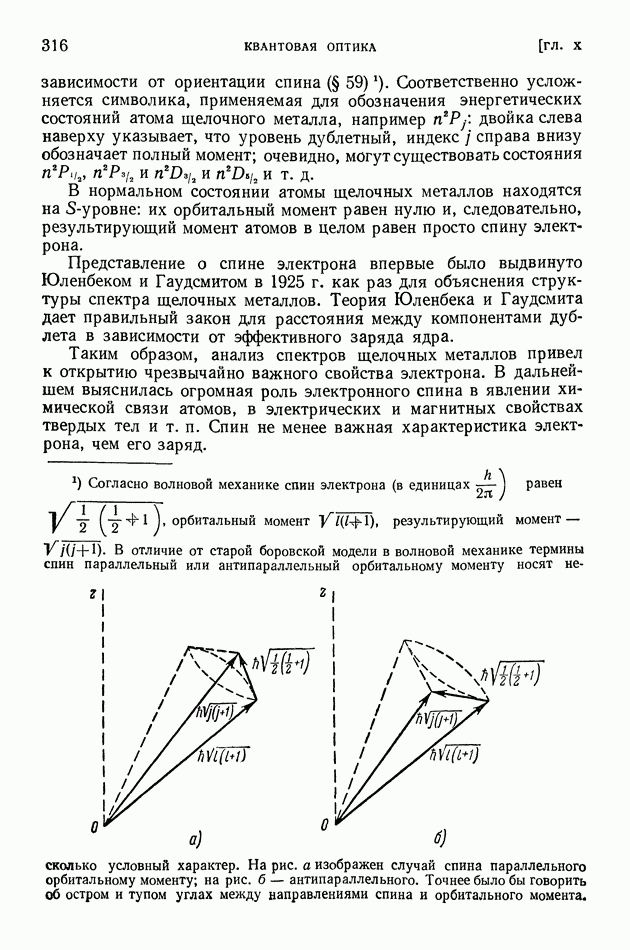
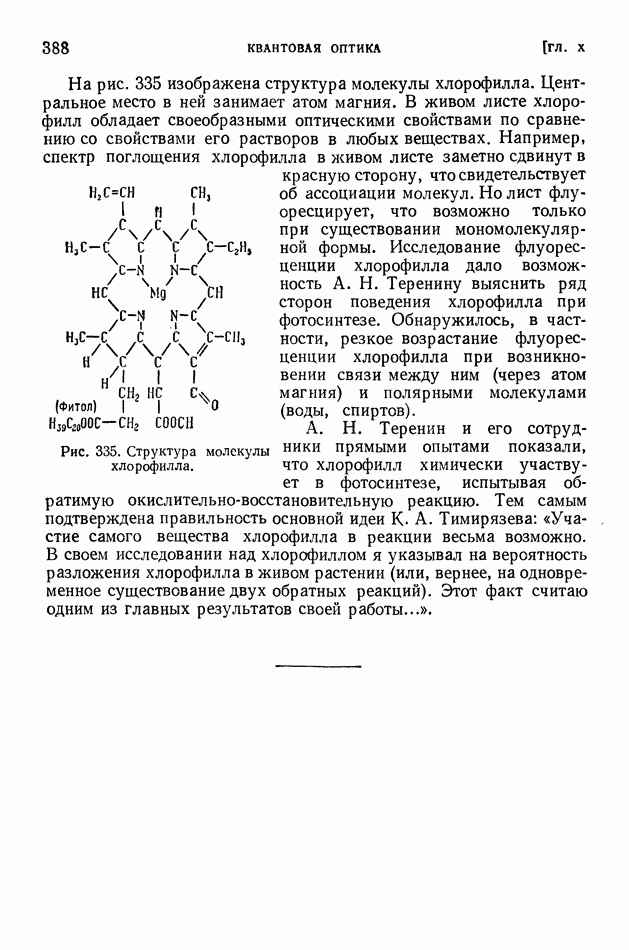
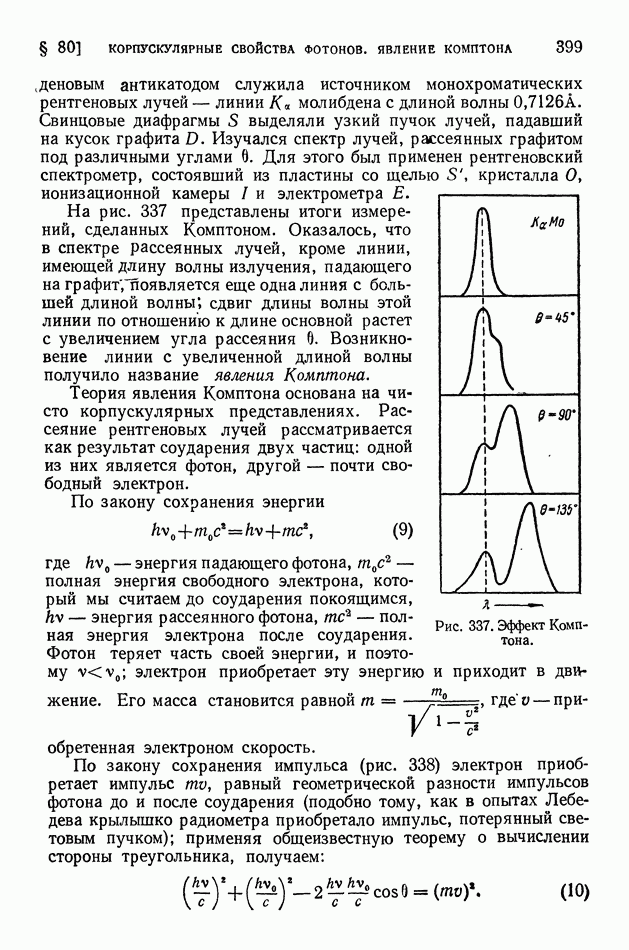
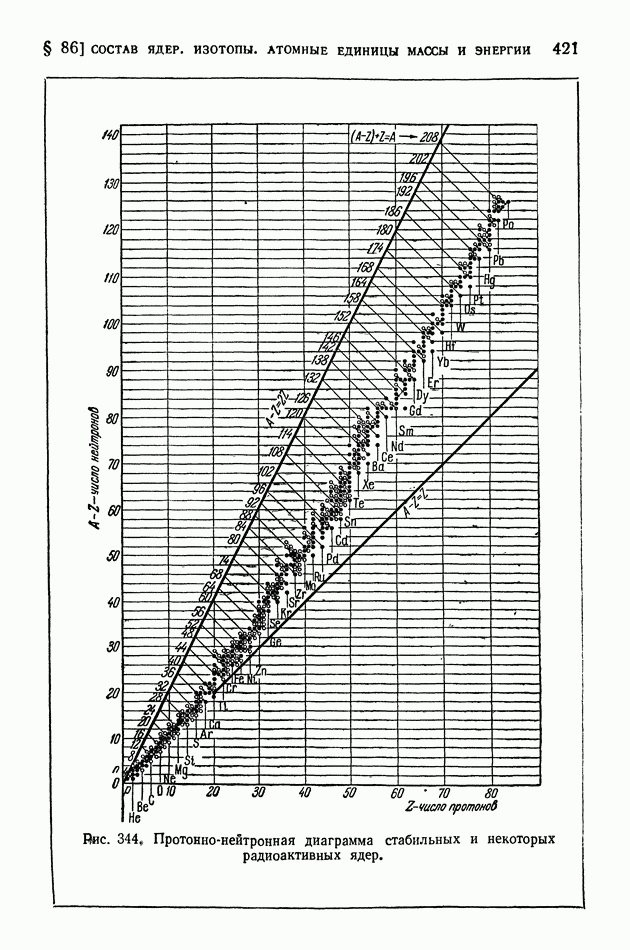
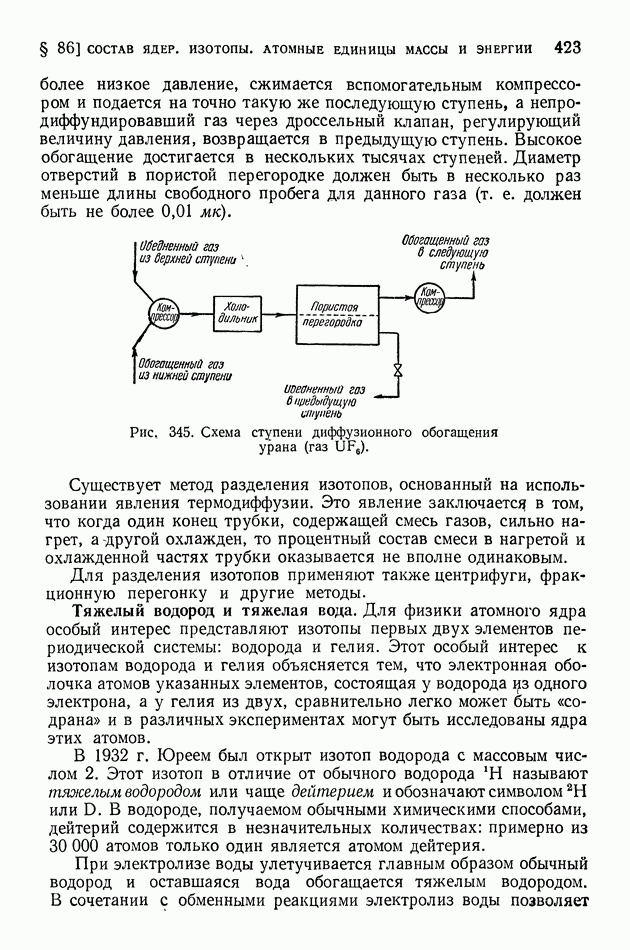
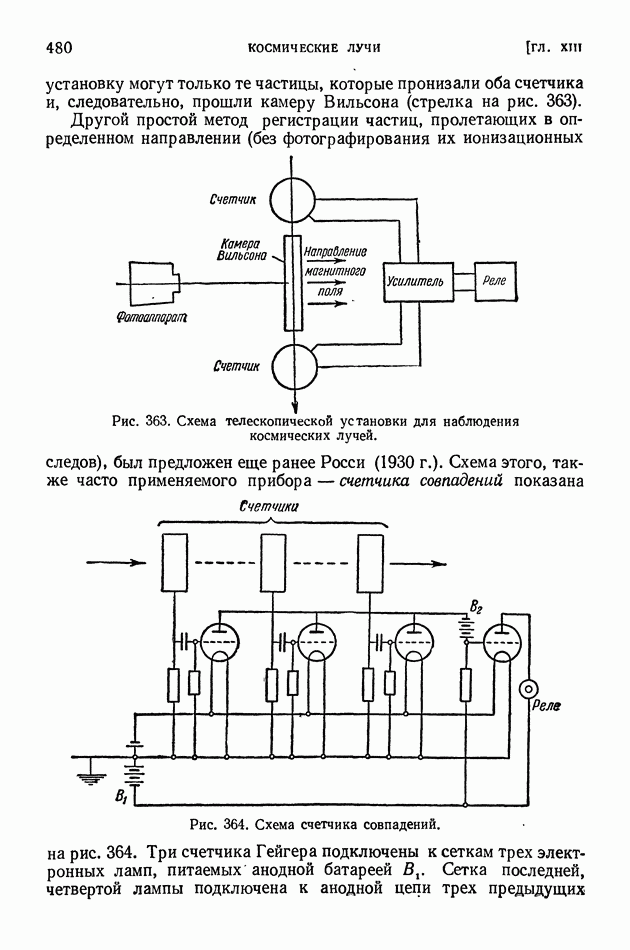
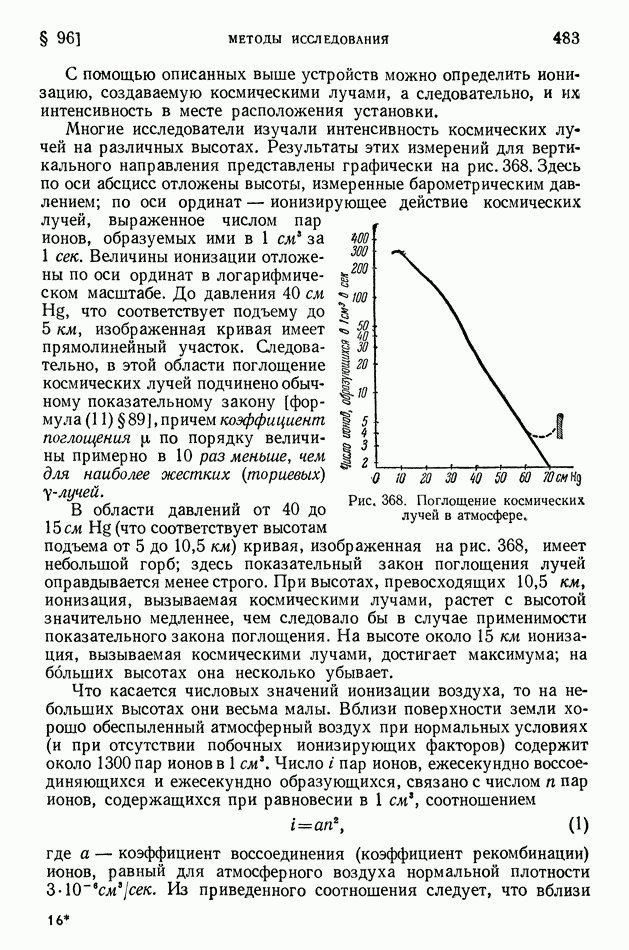
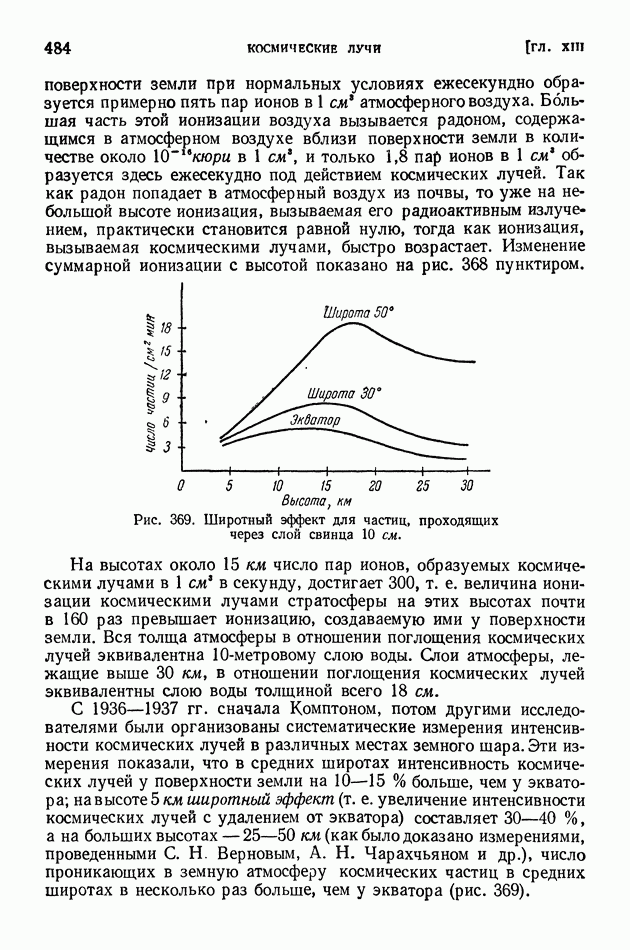
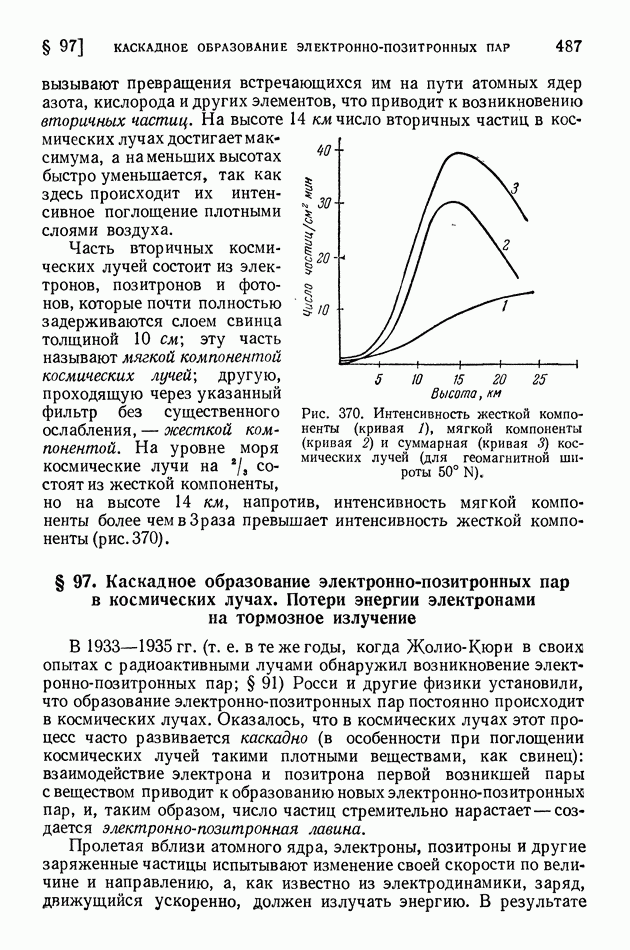
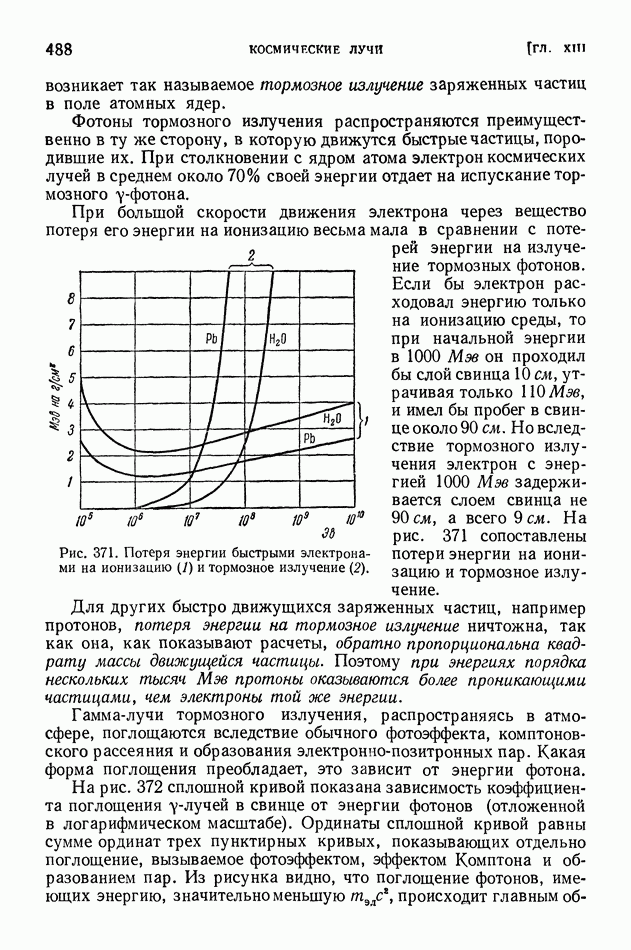
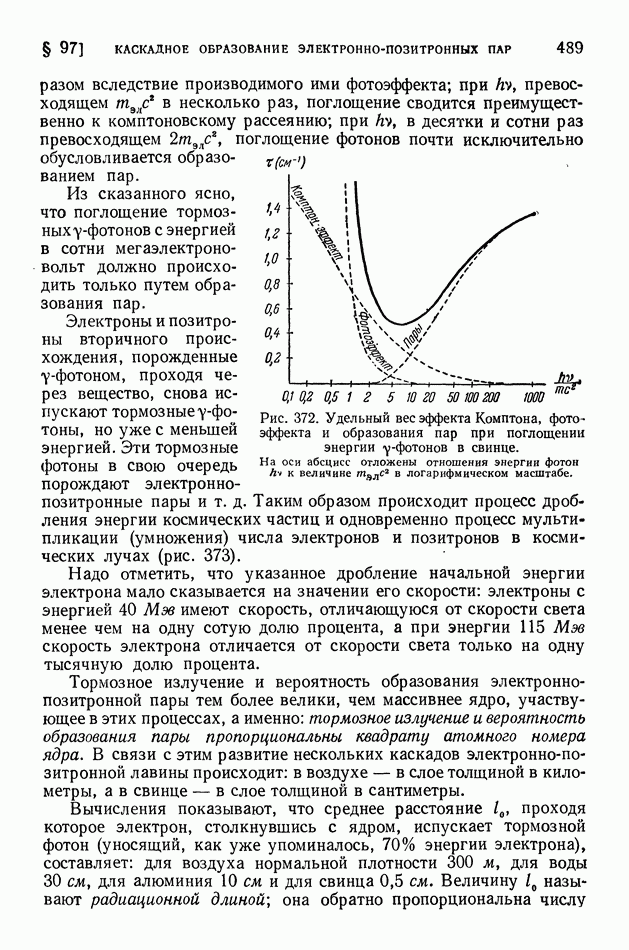
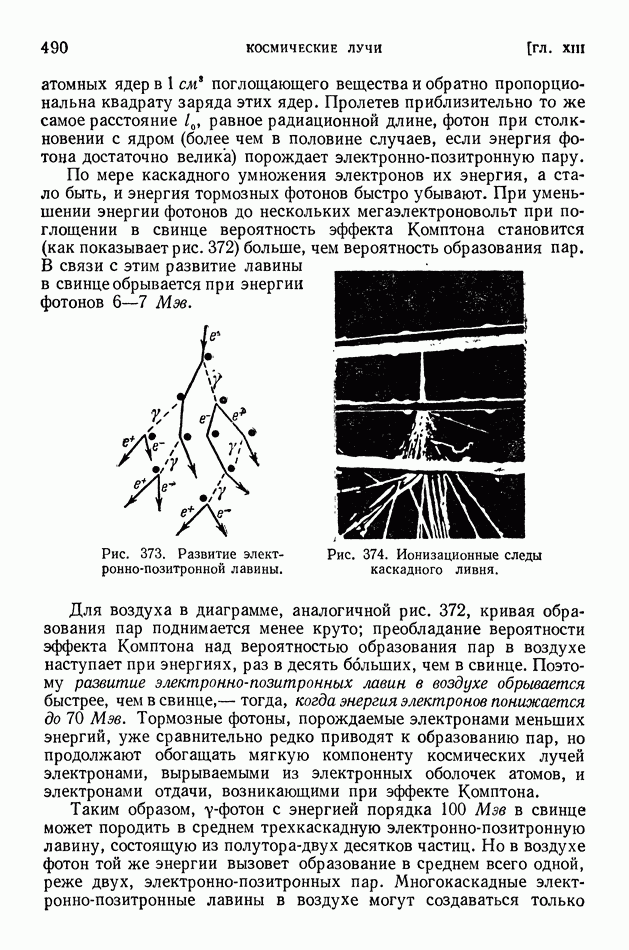
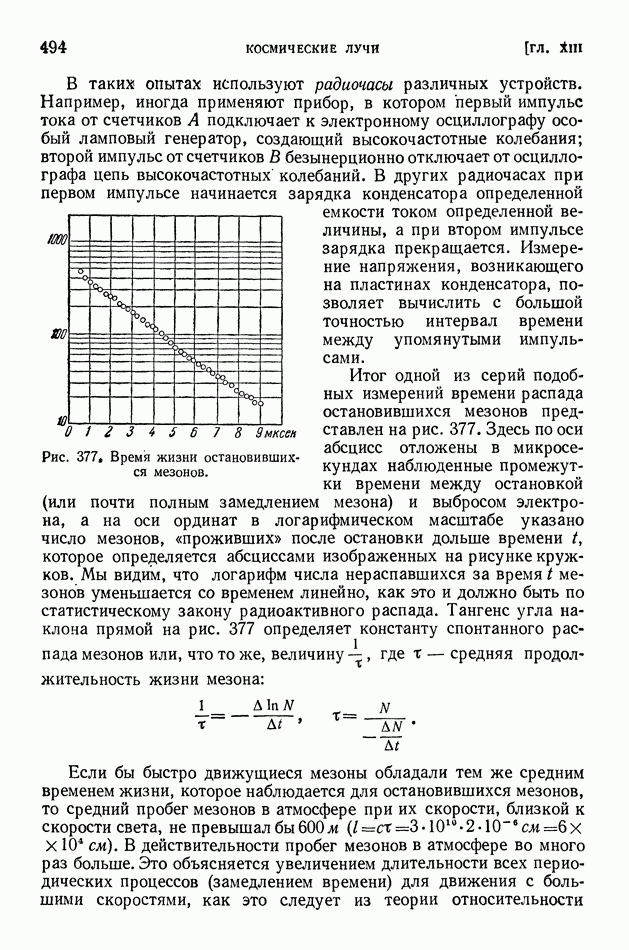
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. Опыт Майкельсона
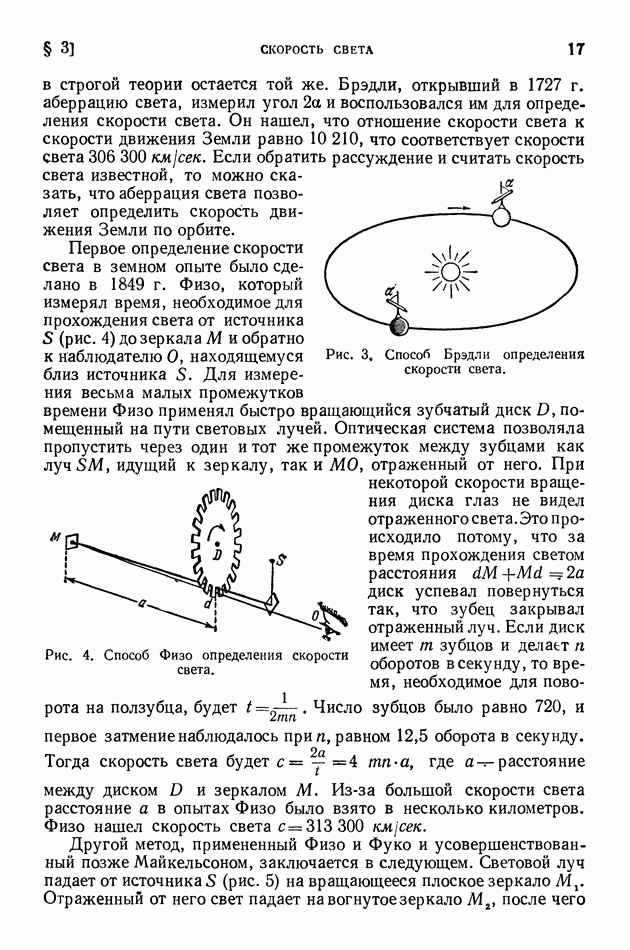
Описывая опыты по определению скорости света, мы как бы забыли о том, что все эти опыты производятся на Земле, несущейся в мировом пространстве с огромной скоростью, превышающей в десятки раз скорость артиллерийского снаряда. Правда, в этих опытах наблюдатель и источник света неподвижны относительно друг друга, но если считать, что Земля движется по отношению к неподвижному эфиру, в котором распространяются световые волны, то следует ожидать влияния этого движения на результаты наблюдений.
Разберем описанные выше методы определения скорости света, считая мировой эфир неподвижным, а Землю движущейся. В обоих методах — и Физо и Фуко — определялось время, необходимое световому лучу для того, чтобы пройти от какой-то точки А до точки В и вернуться обратно в точку А. Мы считали, что это время равно просто  где а — длина отрезка
где а — длина отрезка  с — скорость света.
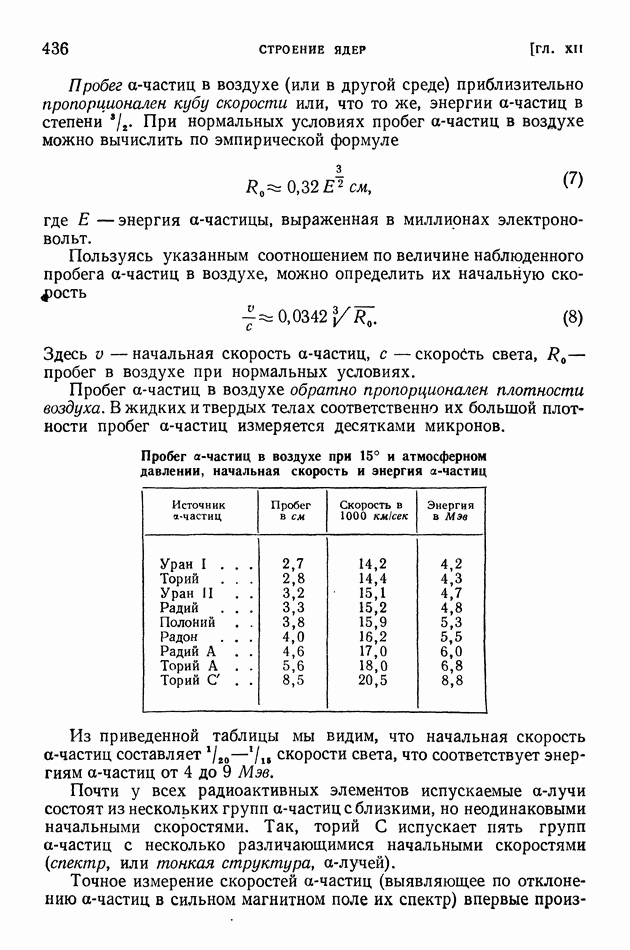
с — скорость света.
Теперь мы должны уточнить наше рассуждение. Прежде всего мы определим с как скорость света по отношению к неподвижному эфиру. Затем надо учесть, что в результате движения Земли, согласно законам механики Ньютона, скорость света по отношению к Земле уже не будет равна с. Если направление распространения светового луча совпадает с направлением движения Земли, то эта скорость должна быть равна  если свет и Земля движутся в противоположных направлениях, то
если свет и Земля движутся в противоположных направлениях, то  где
где  скорость Земли по отношению к эфиру. В первом случае свет должен «догонять» Землю, во втором, наоборот, свет и Земля движутся навстречу друг другу.
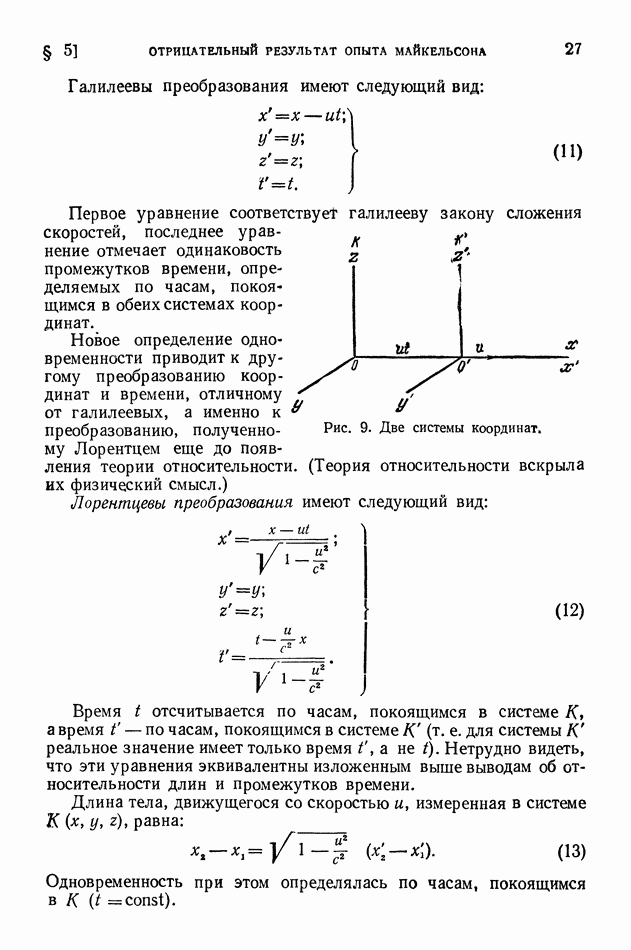
скорость Земли по отношению к эфиру. В первом случае свет должен «догонять» Землю, во втором, наоборот, свет и Земля движутся навстречу друг другу.
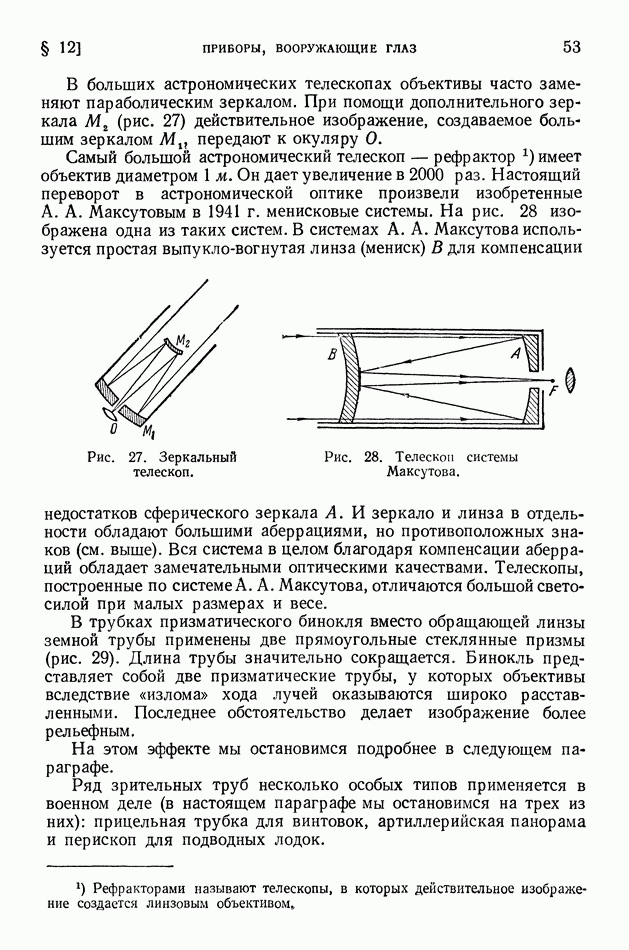
Рис. 6 изображает случай, когда отрезок  параллелен направлению движения Земли; тогда от А к В луч идет с относительной скоростью
параллелен направлению движения Земли; тогда от А к В луч идет с относительной скоростью  а в обратном — со скоростью
а в обратном — со скоростью 
Значит, от  до В он дойдет за время
до В он дойдет за время  а от В до А — за время полное же время
а от В до А — за время полное же время  определится следующим образом:
определится следующим образом:

или с точностью до величин четвертого порядка (относительно 


Рис. 6. Распространение света в движущейся системе.
Мы видим, что учет движения Земли привел к некоторой поправке, правда небольшой по величине:  следовательно,
следовательно, 
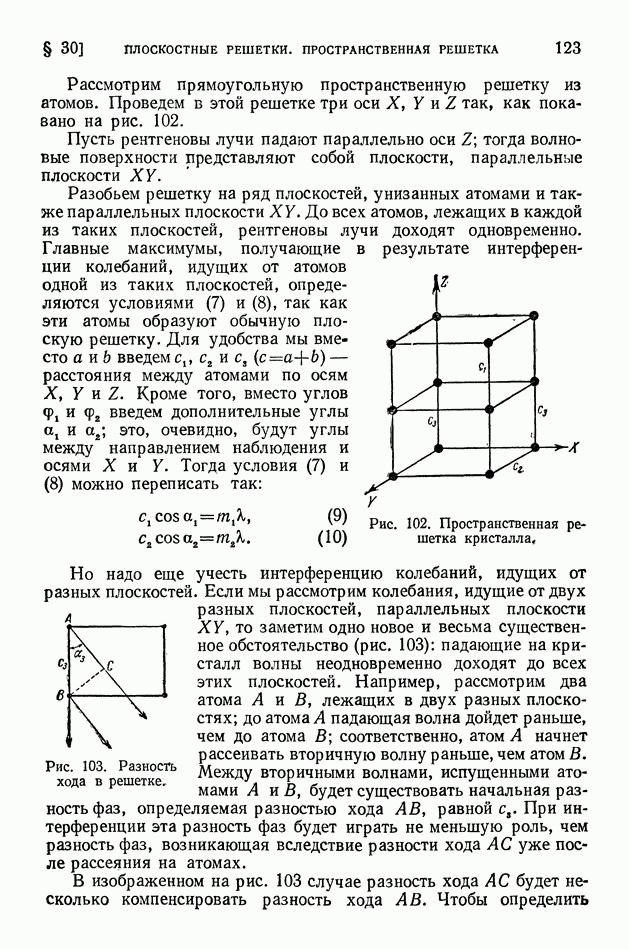
Рассмотрим теперь другой случай расположения отрезка А В (рис. 6, справа). Пусть отрезок  перпендикулярен к направлению движения Земли и в В помещено плоское зеркало. Скорость света по отношению к Земле в этом случае будет равна
перпендикулярен к направлению движения Земли и в В помещено плоское зеркало. Скорость света по отношению к Земле в этом случае будет равна  и в прямом (от А к В) и в обратном направлениях (от В к А).
и в прямом (от А к В) и в обратном направлениях (от В к А).
В этом случае косое направление скорости с по отношению к  определяется тем, что за время прохождения светового сигнала из
определяется тем, что за время прохождения светового сигнала из  сама точка В смещается вправо (аналогично будет при обратном пути от В к А).
сама точка В смещается вправо (аналогично будет при обратном пути от В к А).
Полное время распространения света определится как

Извлекая приближенно корень квадратный, получаем;

откуда с точностью до величин четвертого порядка

Сопоставляя  и мы видим, что
и мы видим, что

Таким образом, следует ожидать, что измерение разности времен  при двух взаимно-перпендикулярных расположениях А В позволит определить скорость движения Земли по отношению к эфиру.
при двух взаимно-перпендикулярных расположениях А В позволит определить скорость движения Земли по отношению к эфиру.
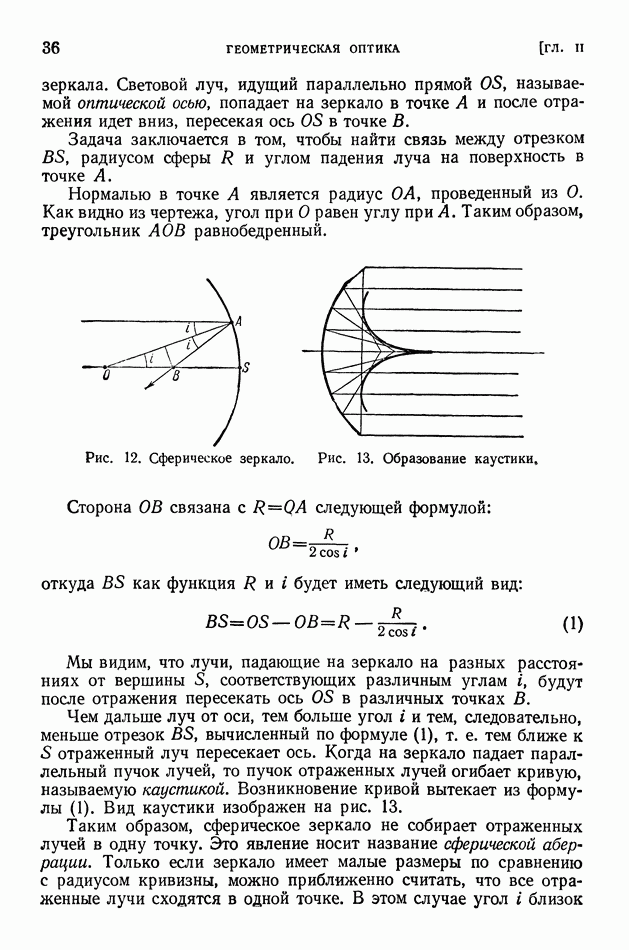
Неприятным в формуле (10) является то, что в нее входит квадрат отношения искомой скорости к скорости света. Тем самым речь идет об установлении «эффектов второго порядка малости».
Делалось много попыток обнаружить эффекты первого порядка, однако все они были неудачны. Часть из них, основанная на исследовании явлений преломления, интерференции, дифракции и др., покоилась на неверных принципиальных основаниях. Лоренц показал, что во всех этих случаях отсутствие эффектов первого порядка вытекает из теории неподвижного эфира с таким же успехом, как и из теории полностью увлекаемого эфира.
Другие попытки, носившие, правда, характер неосуществленных проектов, были основаны на схемах с часами, расположенными на расстоянии друг от друга. В таких схемах определяется время прохождения светом пути от одних часов до других. Зная расстояние между часами, мы можем вычислить скорость света. Так как в этом случае путь светового луча по отношению к Земле не замкнут (луч идет от  к В, но не возвращается опять в Л), можно было надеяться на обнаружение эффектов первого порядка, связанных с движением Земли.
к В, но не возвращается опять в Л), можно было надеяться на обнаружение эффектов первого порядка, связанных с движением Земли.
Однако очевидно, что для таких опытов нужно иметь совершенно одинаково (синхронно) идущие часы в точках  Майкельсон показал, что самые точные методы синхронизации часов, находящихся в разных точках, практически сводятся к посылке электромагнитных сигналов из одной точки в другую, т. е. ко всем теперь хорошо известной «поверке времени» по радио.
Майкельсон показал, что самые точные методы синхронизации часов, находящихся в разных точках, практически сводятся к посылке электромагнитных сигналов из одной точки в другую, т. е. ко всем теперь хорошо известной «поверке времени» по радио.
Но эти сигналы распространяются опять-таки со скоростью света. Таким образом, путь световой (электромагнитной) волны оказывается замкнутым, и мы опять приходим к эффектам второго порядка, соответствующим формулам (7), (9) и (10). Поэтому Майкельсон взялся за осуществление опыта, позволяющего непосредственно обнаружить эффекты второго порядка. Здесь сразу возникает законный вопрос: нельзя ли было воспользоваться для этих целей схемами опытов по определению скорости света, уже описанными выше? Ведь мы как раз показали, что во всех этих опытах должны были наблюдаться эффекты второго порядка. В принципе действительно это так: если бы Майкельсон при определении скорости света по методу Физо — Фуко проделал измерения для двух положений трубы (в которой распространялся свет), соответствующих рис. 6, он должен
был бы получить разность времен запаздывания, определяемую формулой (10).
Однако обнаружить существование этой разности он практически не смог бы, несмотря на использование больших расстояний. Ведь мы указывали, что Майкельсон определил скорость света с точностью до  т. е. примерное точностью до 0,000003 измеряемой величины. Как ни велика эта точность, она недостаточна для обнаружения эффектов второго порядка, соответствующих одной стомиллионной доле измеряемой величины (см. выше).
т. е. примерное точностью до 0,000003 измеряемой величины. Как ни велика эта точность, она недостаточна для обнаружения эффектов второго порядка, соответствующих одной стомиллионной доле измеряемой величины (см. выше).
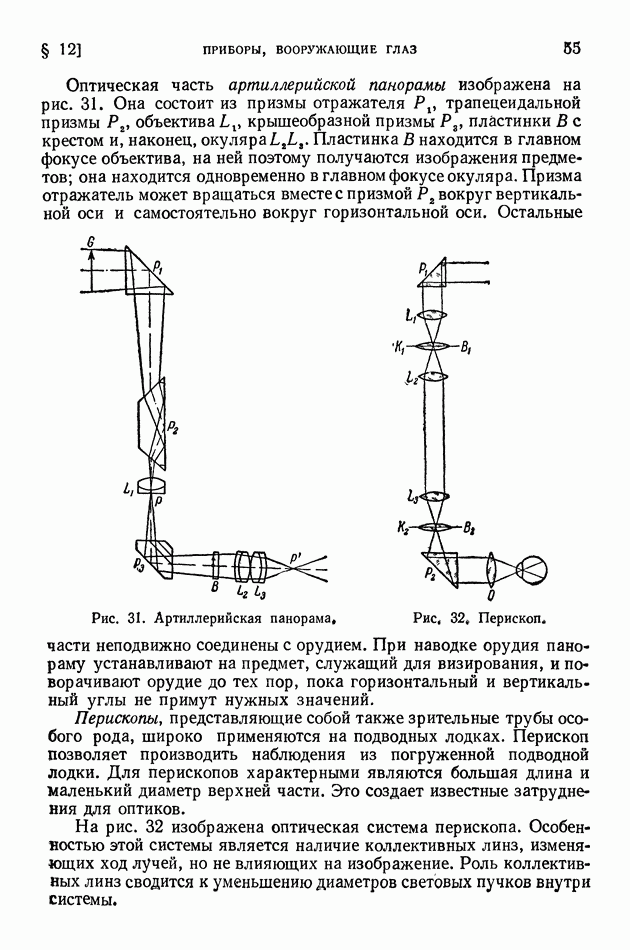
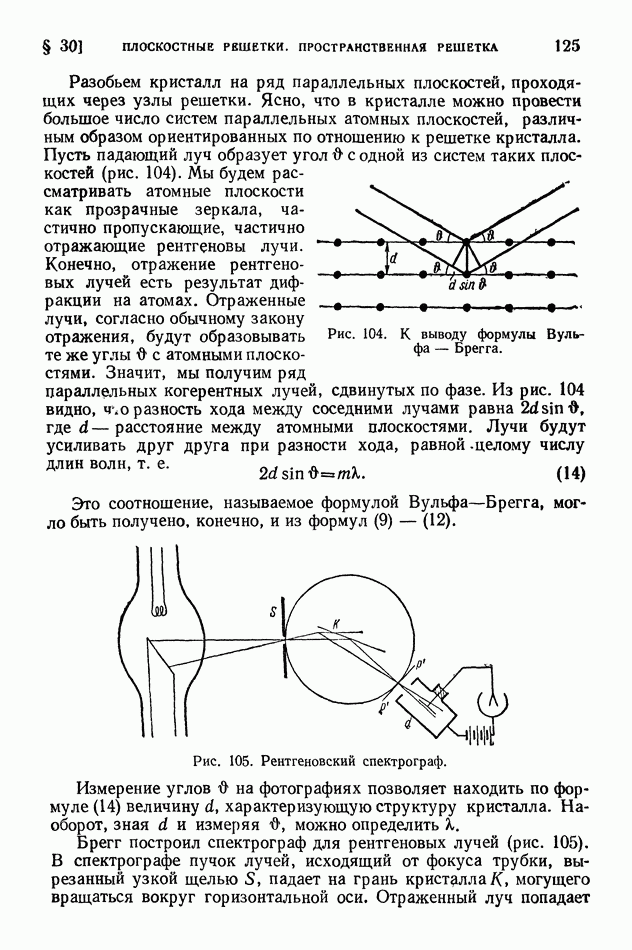
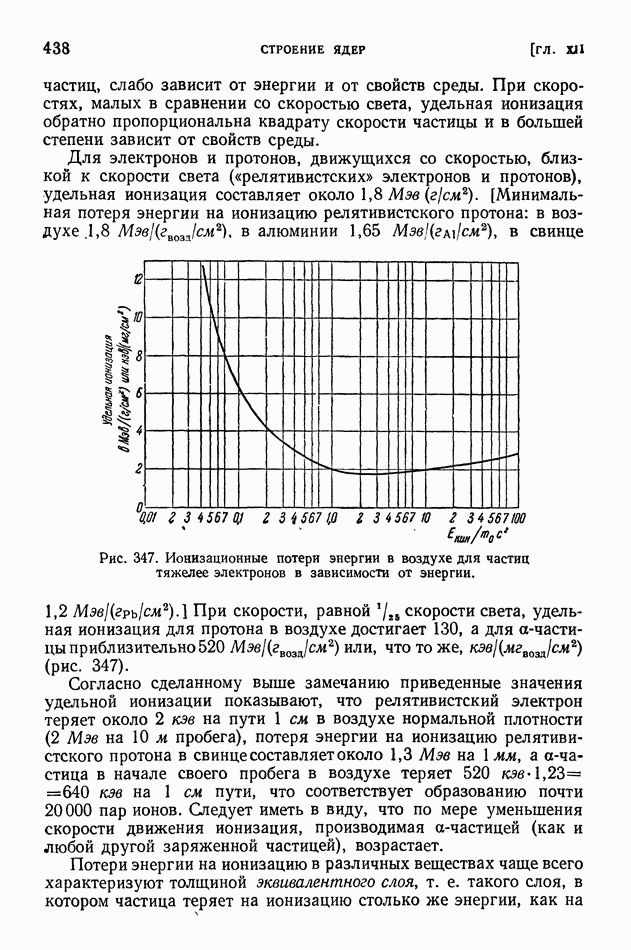
Майкельсон блестяще обошел это затруднение, использовав волновые свойства света. На рис. 7 изображена схема знаменитого опыта Майкельсона.
Луч света, выходящий из  падает на полупрозрачную пластинку
падает на полупрозрачную пластинку  расположенную под углом
расположенную под углом  половина света отражается по направлению к
половина света отражается по направлению к  , половина проходит сквозь пластинку к
, половина проходит сквозь пластинку к  помещены зеркала, отражающие световые лучи обратно; лучи, идущие обратно, опять попадают на пластинку
помещены зеркала, отражающие световые лучи обратно; лучи, идущие обратно, опять попадают на пластинку  причем половина света, отраженного от
причем половина света, отраженного от  пройдет сквозь пластинку и попадет в трубу
пройдет сквозь пластинку и попадет в трубу  точно так же половина света, отраженного от
точно так же половина света, отраженного от  отразится от пластинки
отразится от пластинки  и попадет в трубу (для наглядности мы несколько сместили на рисунке прямые и обратные лучи).
и попадет в трубу (для наглядности мы несколько сместили на рисунке прямые и обратные лучи).

Рис. 7. Схема опыта Майкельсона.
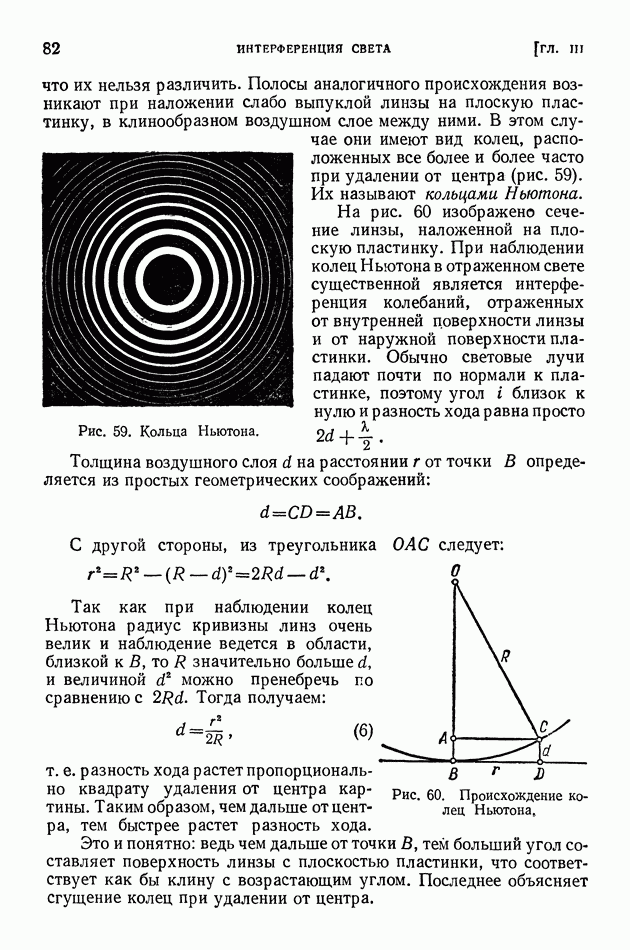
В результате в трубе сойдутся два световых луча, которые от  до
до  шли в равных условиях, а затем один из них прошел путь
шли в равных условиях, а затем один из них прошел путь  а другой
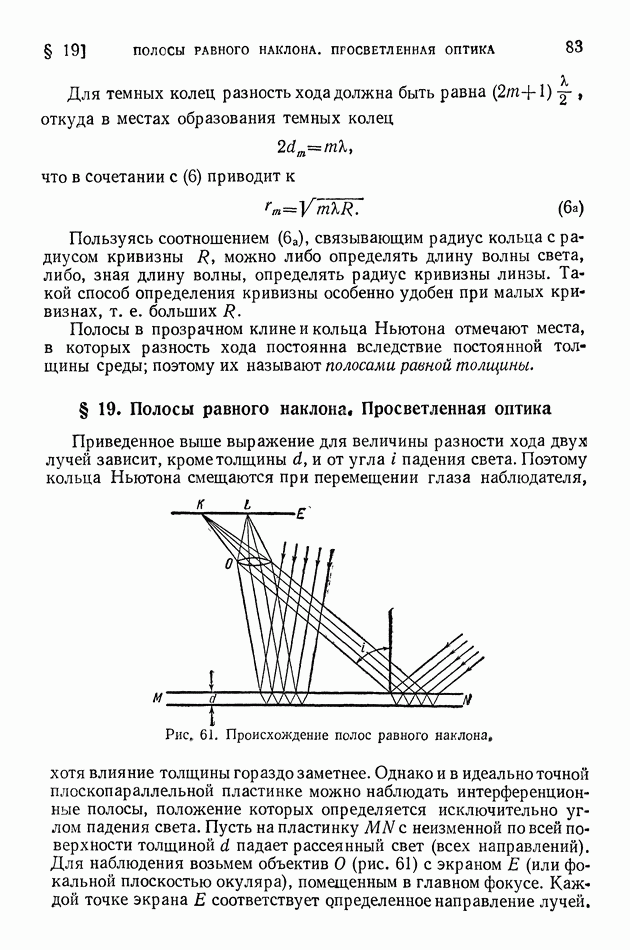
а другой  путь от
путь от  до
до  опять будет общим.
опять будет общим.
Если прибор движется вместе с Землей в направлении, указанном стрелкой, то, очевидно, условия распространения лучей соответствуют двум разобранным выше случаям ориентации отрезка А В (рис. 6). Если расстояния  равны друг другу, то второй луч запоздает по отношению к первому лучу на время, определяемое формулой (10), где а — расстояние от
равны друг другу, то второй луч запоздает по отношению к первому лучу на время, определяемое формулой (10), где а — расстояние от  до
до  или
или 
При повороте на 90° соотношение между лучами изменяется на обратное, и таким образом, если раньше запаздывание было равно —  то теперь это будет — —
то теперь это будет — —  полное изменение запаздывания при повороте будет равно
полное изменение запаздывания при повороте будет равно 
В приборе Майкельсона благодаря использованию многократных отражений а было порядка  (хотя весь прибор помещался на плите
(хотя весь прибор помещался на плите  следовательно, изменение запаздывания
следовательно, изменение запаздывания
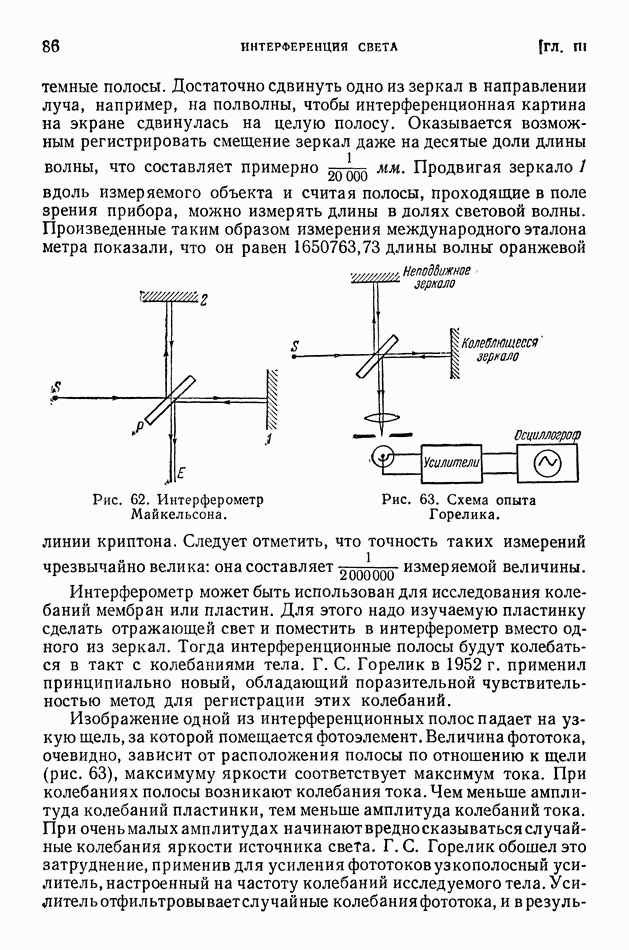
должно было быть примерно равным  сек. Чтобы обнаружить такую ничтожную величину, Майкельсону пришлось восполь зоваться волновыми свойствами света. Так как период светового колебания равен для видимых лучей
сек. Чтобы обнаружить такую ничтожную величину, Майкельсону пришлось восполь зоваться волновыми свойствами света. Так как период светового колебания равен для видимых лучей  то указанное выше изменение запаздывания соответствует 0,4 периода, т. е. составляет заметную долю периода. Майкельсон, наблюдая интерференцию колебаний первого и второго лучей, мог определить разность фаз этих колебаний с точностью до 0,01 периода (§ 20).
то указанное выше изменение запаздывания соответствует 0,4 периода, т. е. составляет заметную долю периода. Майкельсон, наблюдая интерференцию колебаний первого и второго лучей, мог определить разность фаз этих колебаний с точностью до 0,01 периода (§ 20).
Таким образом, наблюдения интерференции позволяли ему определять  долю искомого эффекта, несмотря на сравнительно малое расстояние
долю искомого эффекта, несмотря на сравнительно малое расстояние  вместо
вместо  Однако результат опыта оказался отрицательным. Никакого изменения запаздывания одного луча по отношению к другому при вращении прибора не было обнаружено. Так как ожидаемые эффекты пропорциональны квадрату скорости Земли, отсюда следовало, что скорость Земли по отношению к эфиру во всяком случае меньше
Однако результат опыта оказался отрицательным. Никакого изменения запаздывания одного луча по отношению к другому при вращении прибора не было обнаружено. Так как ожидаемые эффекты пропорциональны квадрату скорости Земли, отсюда следовало, что скорость Земли по отношению к эфиру во всяком случае меньше  т. е.
т. е.  от орбитальной скорости Земли.
от орбитальной скорости Земли.
Последующие опыты только уточнили этот результат, понизив верхний предел для скорости Земли по отношению к эфиру или, что то же, скорости «эфирного ветра» по отношению к Земле до величины, меньшей  орбитальной скорости Земли (Иллингворт, 1927).
орбитальной скорости Земли (Иллингворт, 1927).
| << Предыдущий параграф | Следующий параграф >> |
- ЧАСТЬ ЧЕТВЕРТАЯ. ОПТИКА
- § 2. Электромагнитная теория света
- § 3. Скорость света
- § 4. Опыт Майкельсона
- § 5. Отрицательный результат опыта Майкельсона и теория относительности
- § 6. Некоторые замечания о теории относительности
- § 7. Явление Доплера для световых волн
- ГЛАВА II. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- § 8. Законы отражения и преломления света
- § 9. Линза
- § 10. Оптические системы
- § 11. Глаз как оптическая система
- § 12. Приборы, вооружающие глаз
- § 13. Фотоаппарат и проекционный аппарат
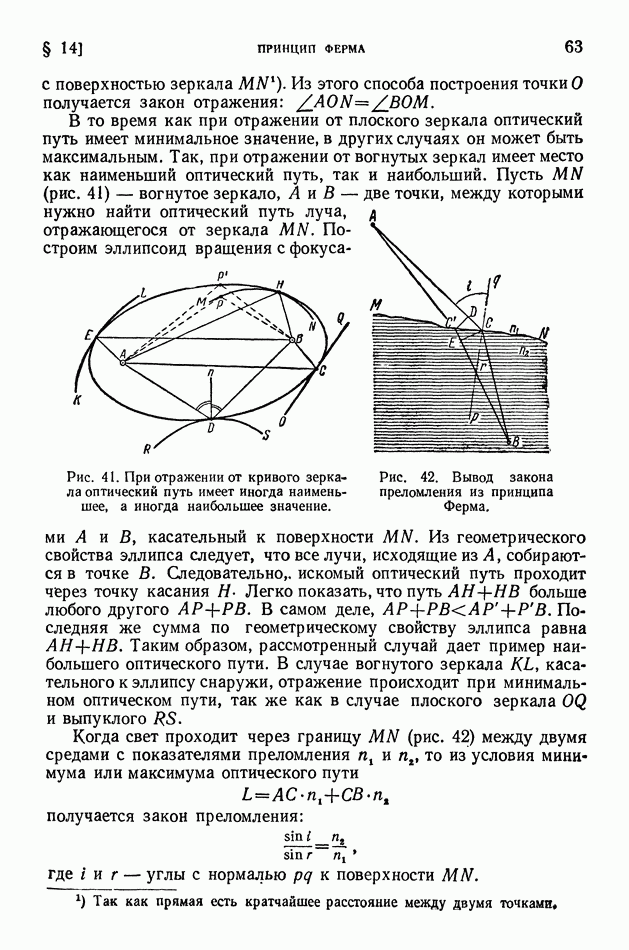
- § 14. Принцип Ферма
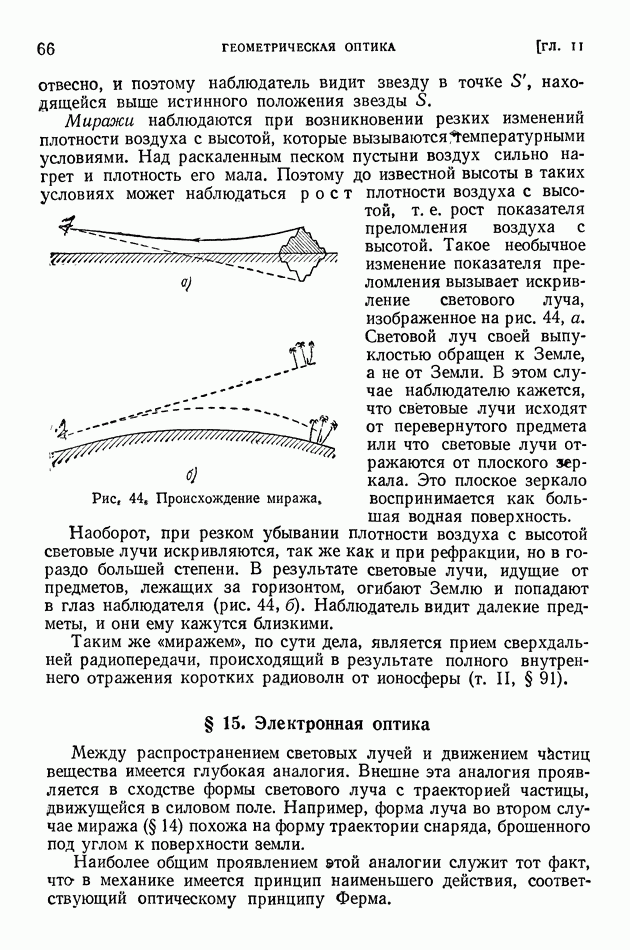
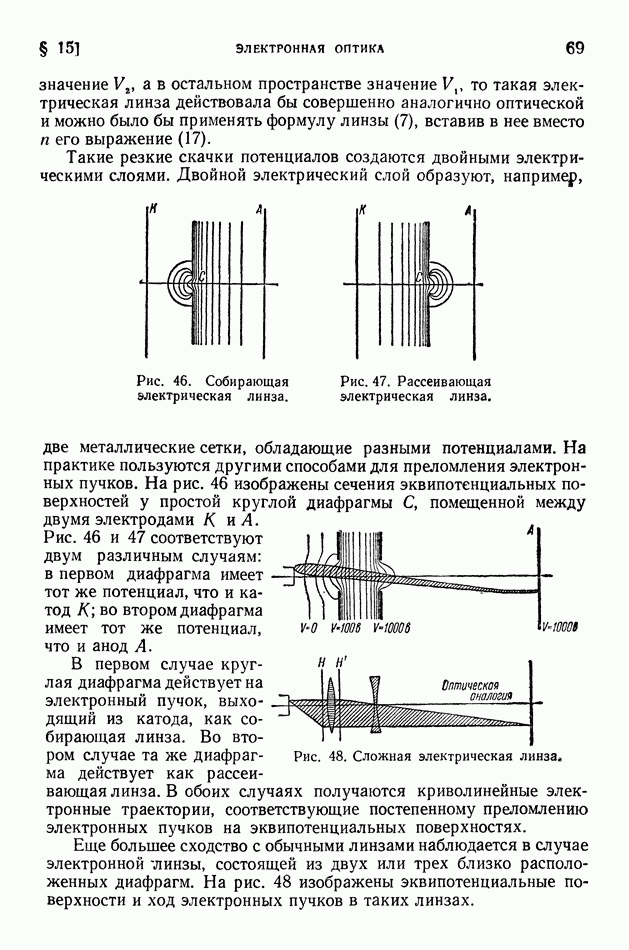
- § 15. Электронная оптика
- ГЛАВА III. ИНТЕРФЕРЕНЦИЯ СВЕТА
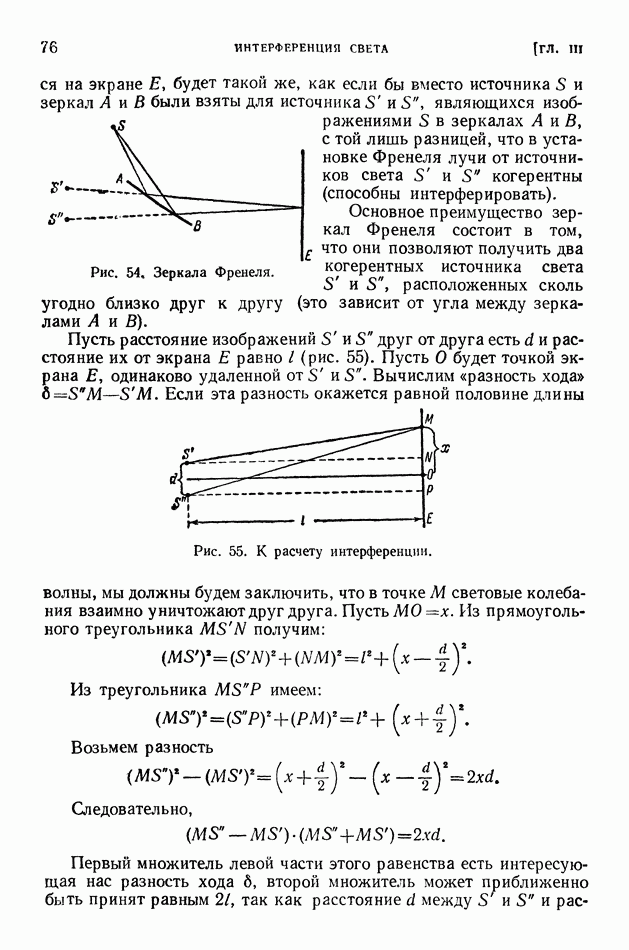
- § 16. Принцип суперпозиции. Когерентность
- § 17. Зеркала Френеля
- § 18. Цвета тонких пленок. Полосы равной толщины
- § 19. Полосы равного наклона. Просветленная оптика
- § 20. Интерферометры
- § 21. Интерференционное измерение технических мер длины
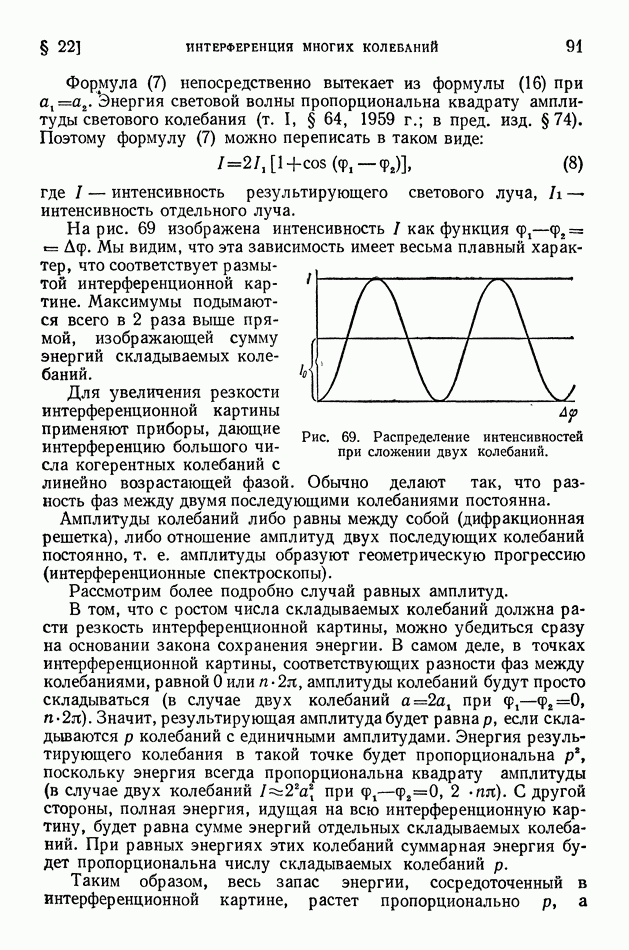
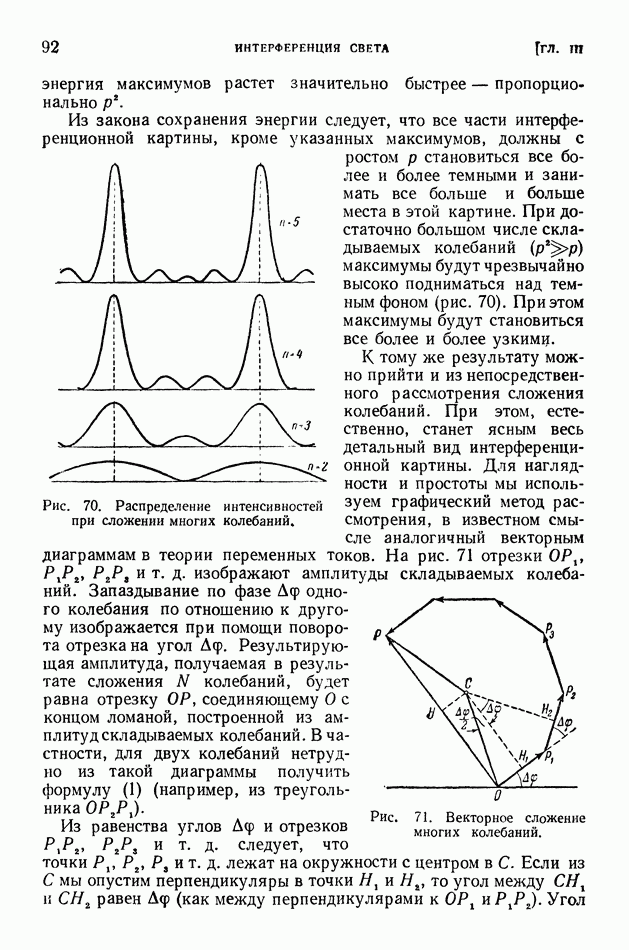
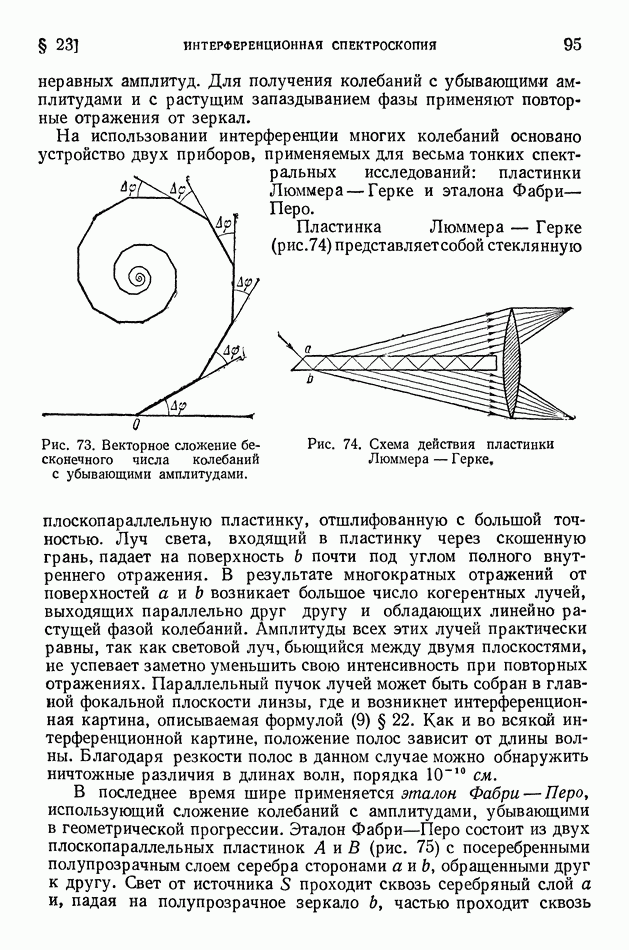
- § 22. Интерференция многих колебаний
- § 23. Интерференционная спектроскопия
- ГЛАВА IV. ДИФРАКЦИЯ СВЕТА
- § 24. Явление дифракции. Опыт Френеля
- § 25. Принцип Гюйгенса-Френеля
- § 26. Метод зон Френеля
- § 27. Дифракция от узкой щели
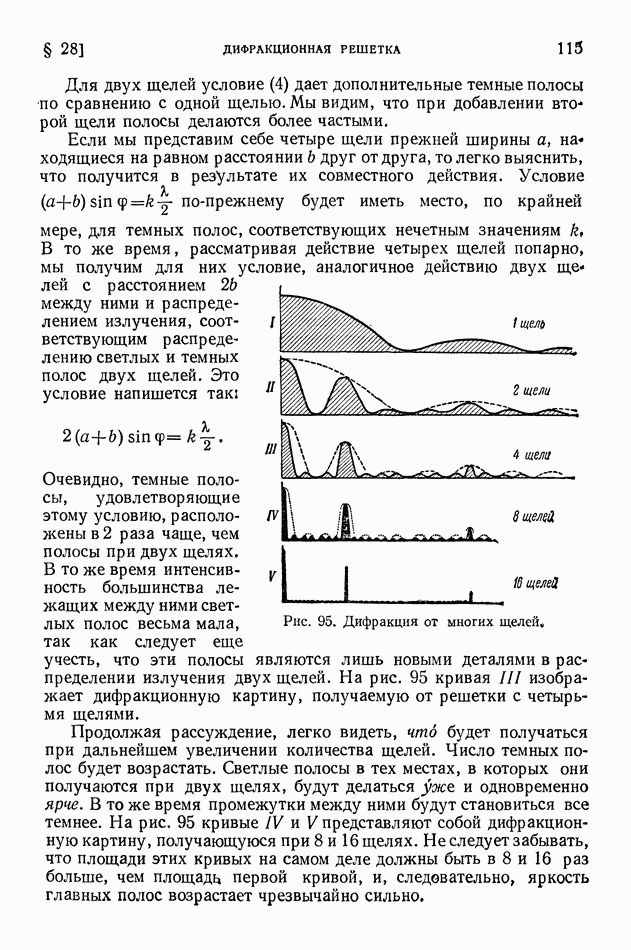
- § 28. Дифракционная решетка
- § 29. Дифракционный спектр. Решетки Роуланда и эшелон Майкельсона
- § 30. Плоскостные решетки. Пространственная решетка
- § 31. Структурный рентгеновский анализ
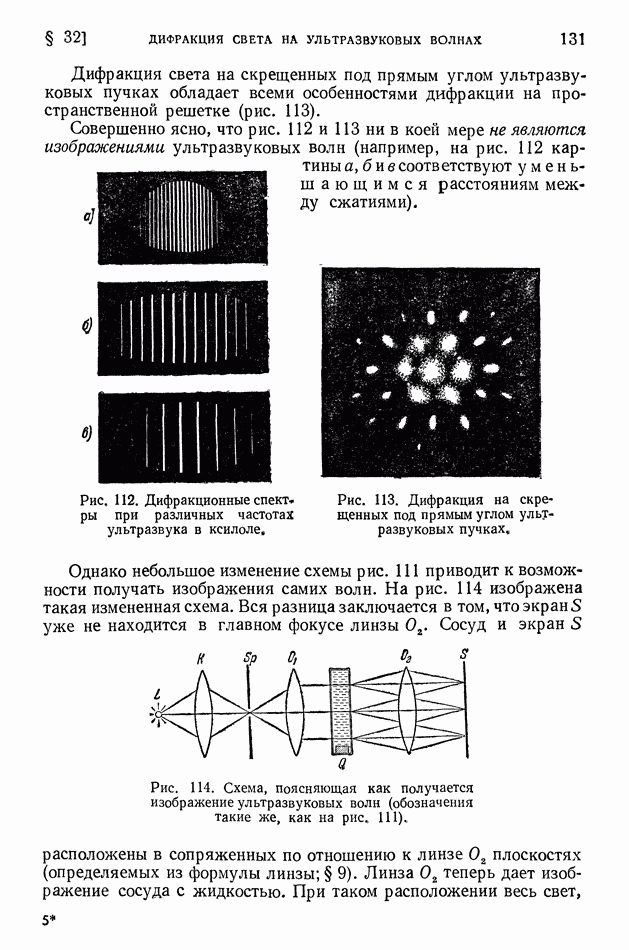
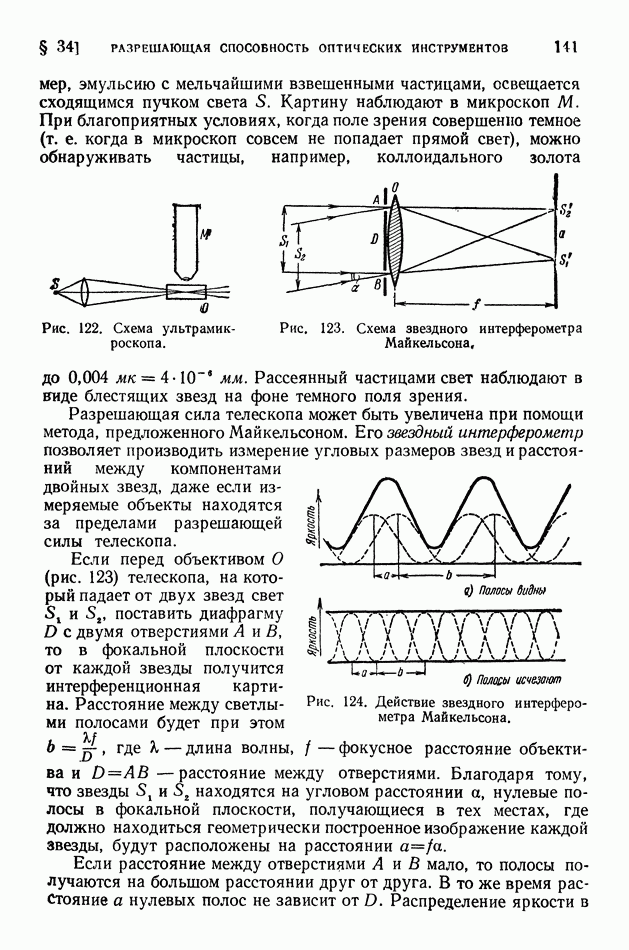
- § 32. Дифракция света на ультразвуковых волнах
- § 33. Дифракция от мелких частиц
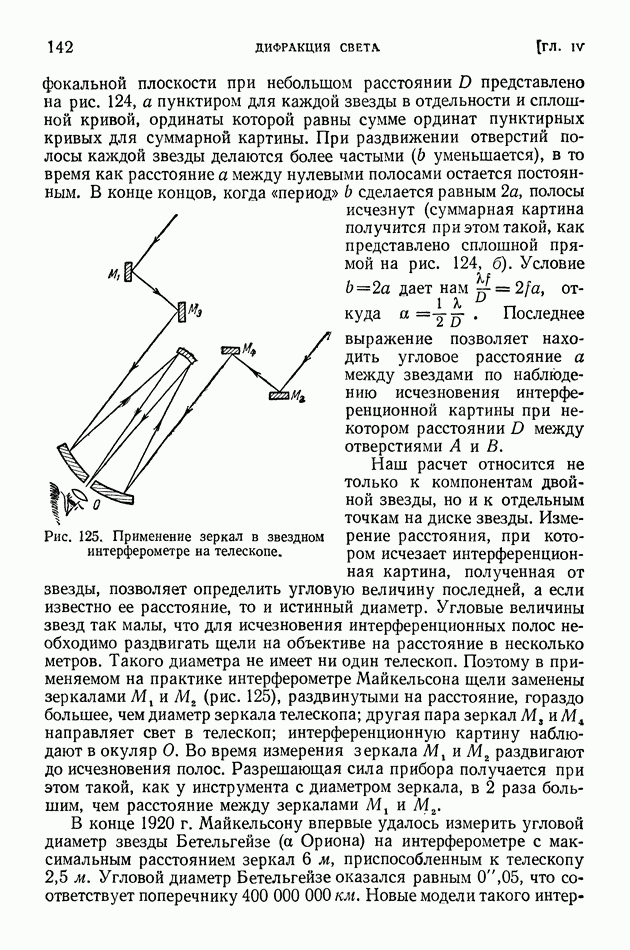
- § 34. Разрешающая способность оптических инструментов. Звездный интерферометр
- ГЛАВА V. ПОЛЯРИЗАЦИЯ СВЕТА
- § 35. Поляризация света
- § 36. Двойное лучепреломление
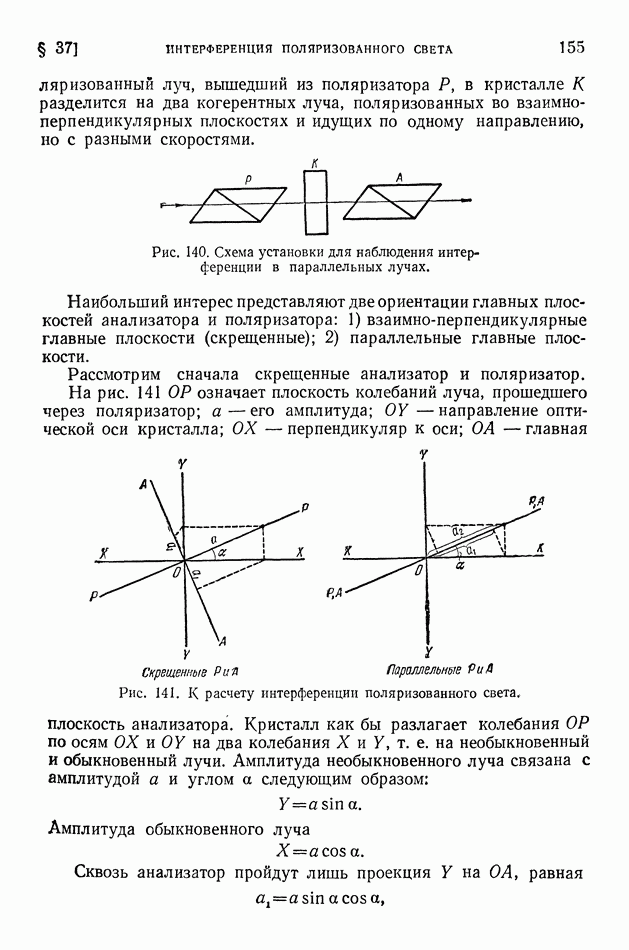
- § 37. Интерференция поляризованного света
- § 38. Оптический метод исследования упругих натяжений. Эффект Керра
- § 39. Вращение плоскости поляризации. Эллиптическая поляризация
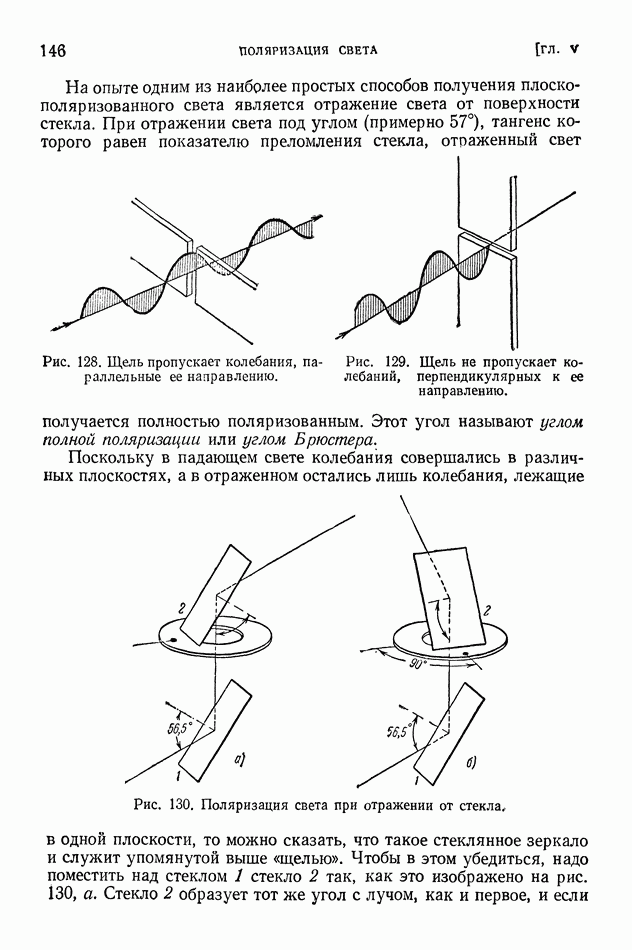
- ГЛАВА VI. ДИСПЕРСИЯ, ПОГЛОЩЕНИЕ И ИЗЛУЧЕНИЕ СВЕТА
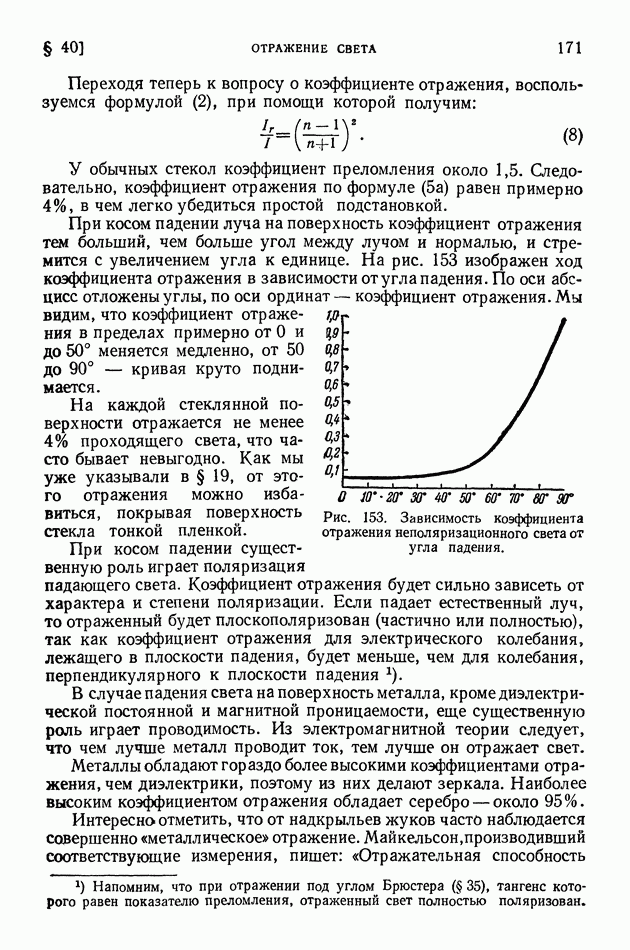
- § 40. Отражение света
- § 41. Давление света. Опыты Лебедева
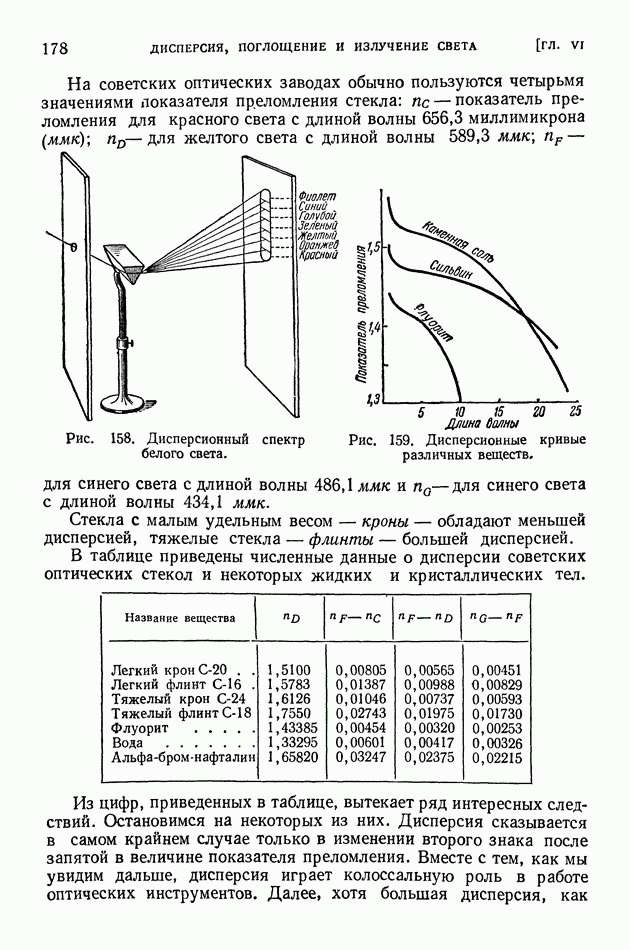
- § 42. Дисперсия. Опыты Ньютона
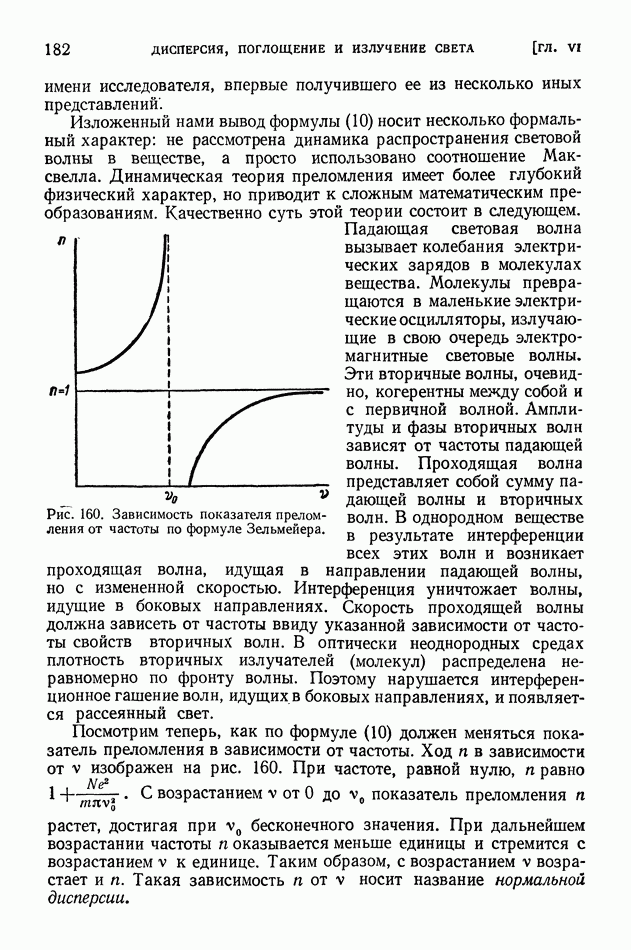
- § 43. Молекулярная теория дисперсии
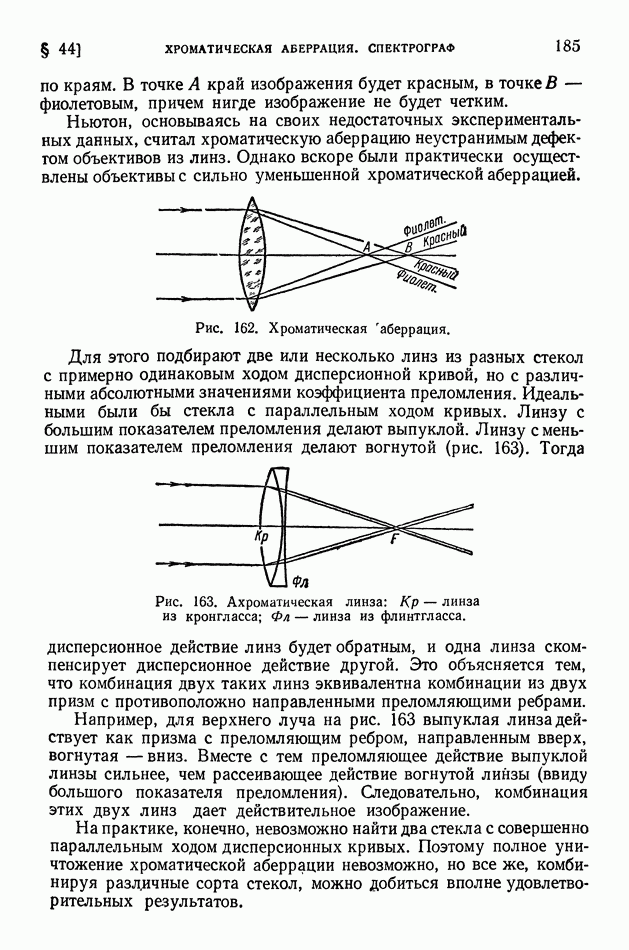
- § 44. Хроматическая аберрация. Спектрограф
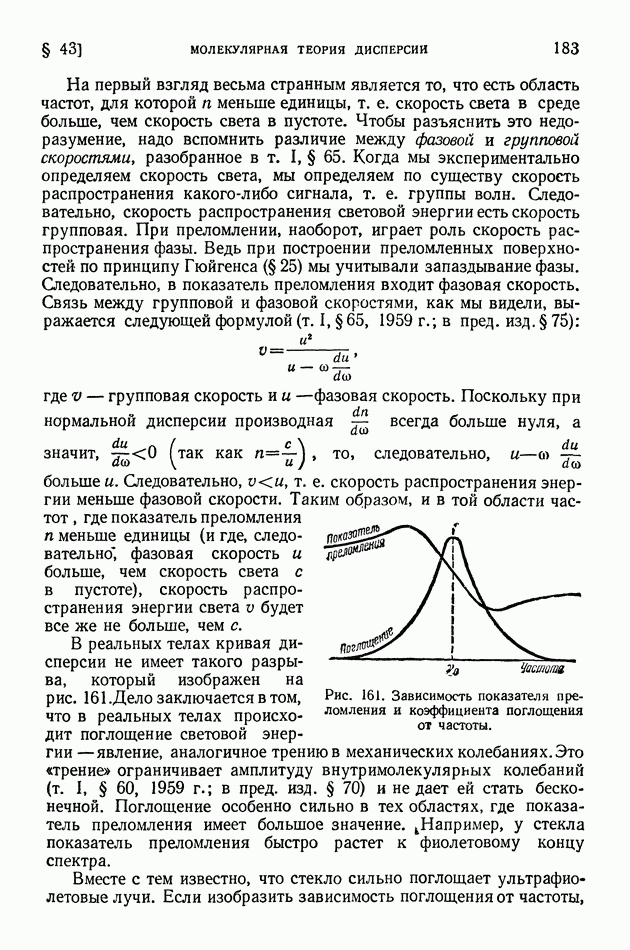
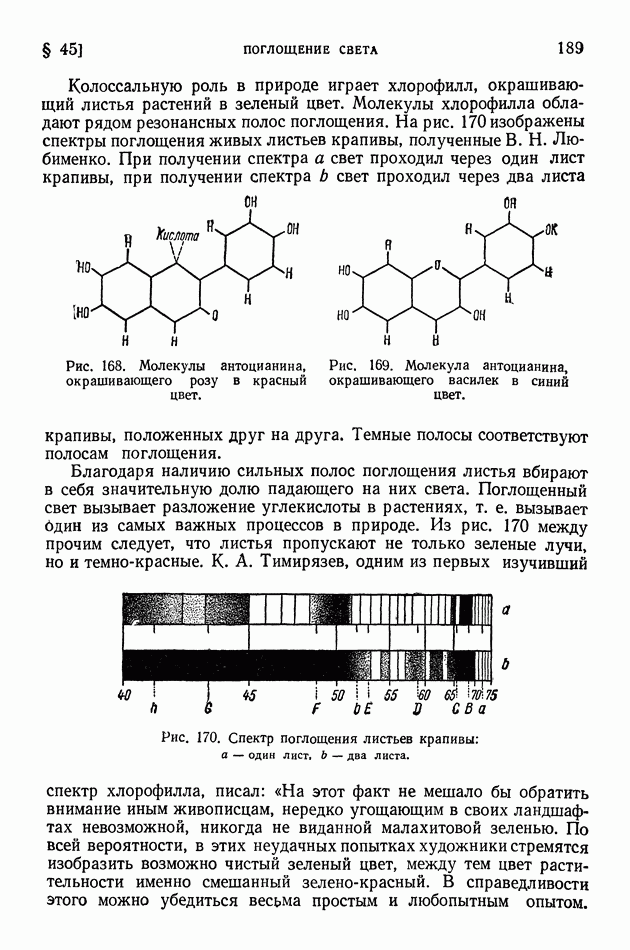
- § 45. Поглощение света
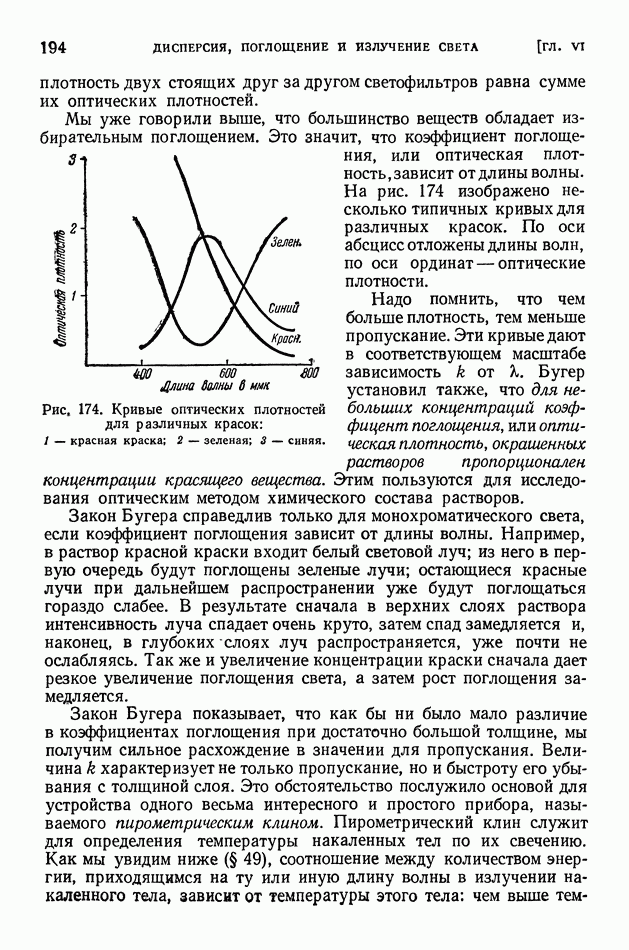
- § 46. Закон Бугера. Опыты Вавилова
- § 47. Атом как элементарный излучатель света
- § 48. Эффект Вавилова — Черенкова
- ГЛАВА VII. ТЕРМОДИНАМИКА ИЗЛУЧЕНИЯ И СВЕТОВОЙ ПОТОК
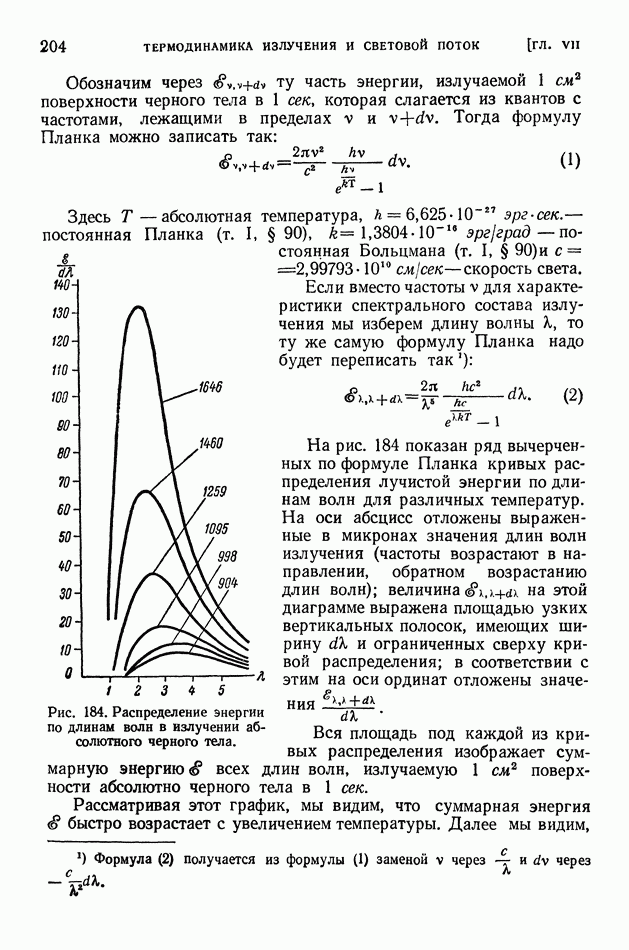
- § 49. Излучение черного тела. Формула Планка. Закон Вина
- § 50. Излучение нечерных тел. Законы Кирхгофа
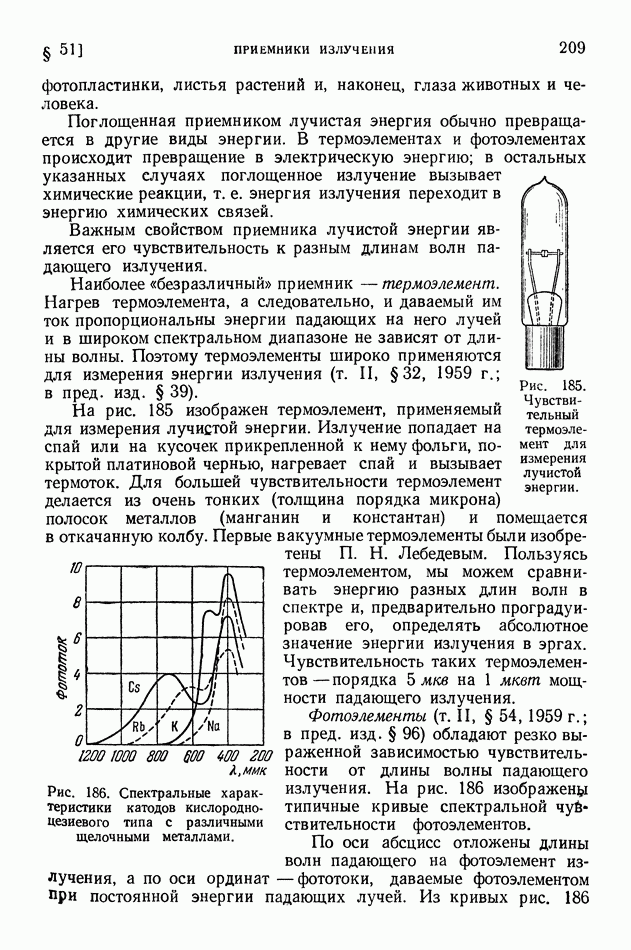
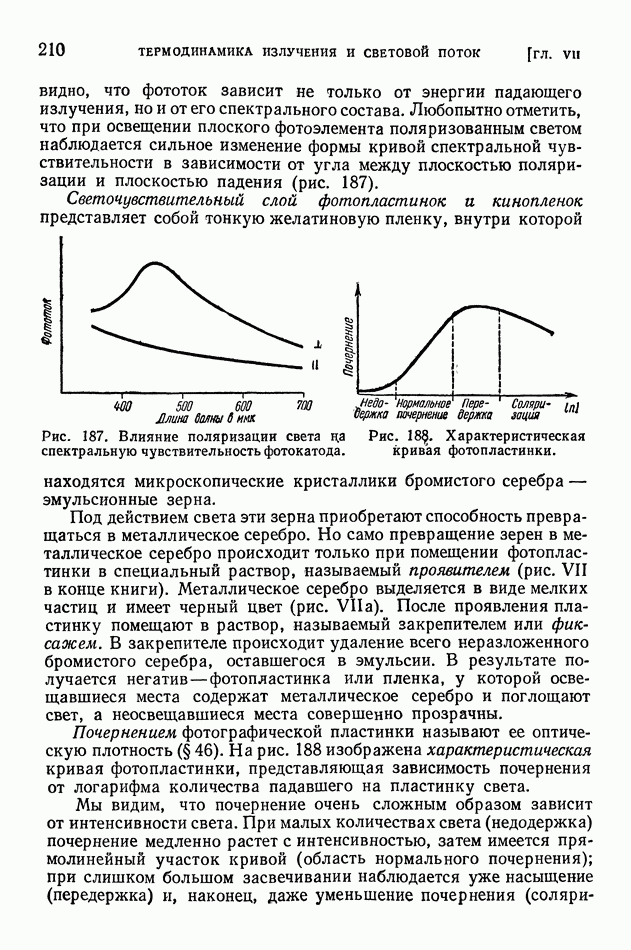
- § 51. Приемники излучения
- § 52. Световые величины и их измерения
- § 53 Температурные излучатели как источники света
- ЧАСТЬ ПЯТАЯ. АТОМНАЯ ФИЗИКА
- ГЛАВА VIII. СТРОЕНИЕ АТОМА И ТЕОРИЯ БОРА
- § 55. Опыты, обнаружившие ядерное строение атомов
- § 56. Противоречие между фактическим строением атомов и выводами классической электродинамики. Строение линейчатых спектров
- § 57. Опытные основания теории квантов в первые годы ее развития
- § 58. Теория Бора. Происхождение спектра водорода
- § 59. Квантовые числа
- § 60. Принцип Паули. Строение электронных оболочек атомов
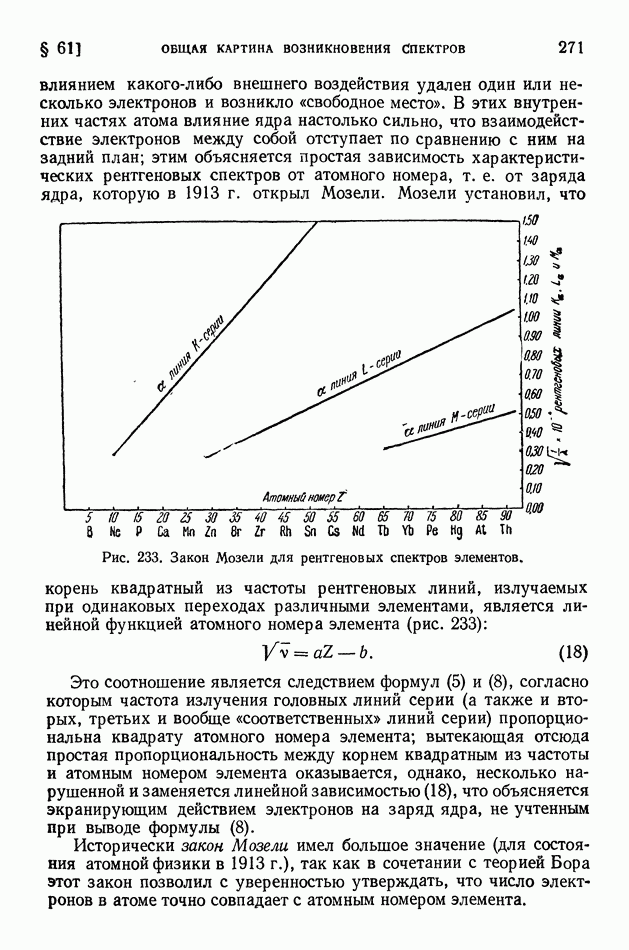
- § 61. Общая картина возникновения спектров
- ГЛАВА IX. ОСНОВЫ КВАНТОВОЙ (ВОЛНОВОЙ) МЕХАНИКИ
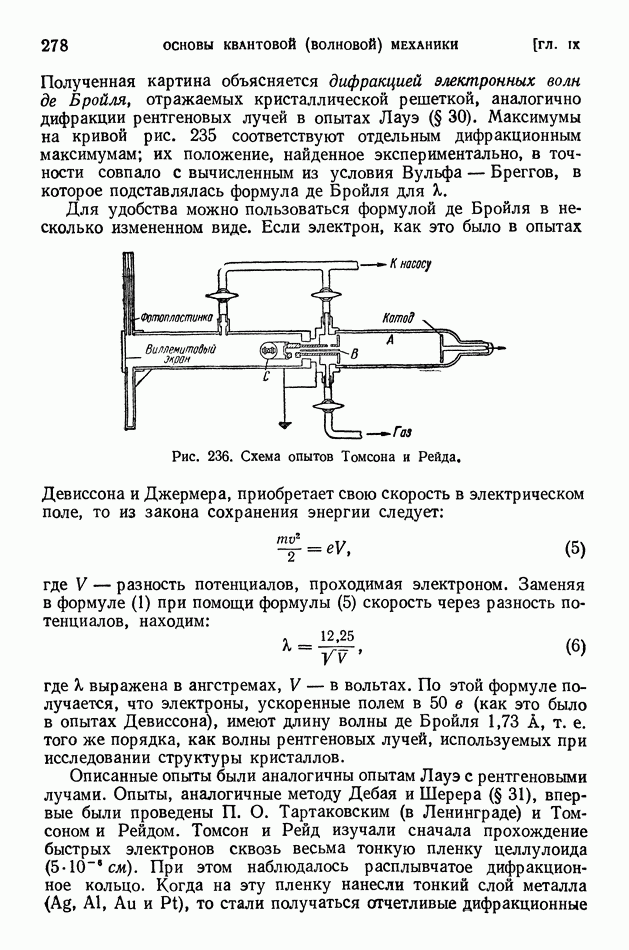
- § 62. Волновые свойства частиц. Формула де Бройля. Дифракция электронов
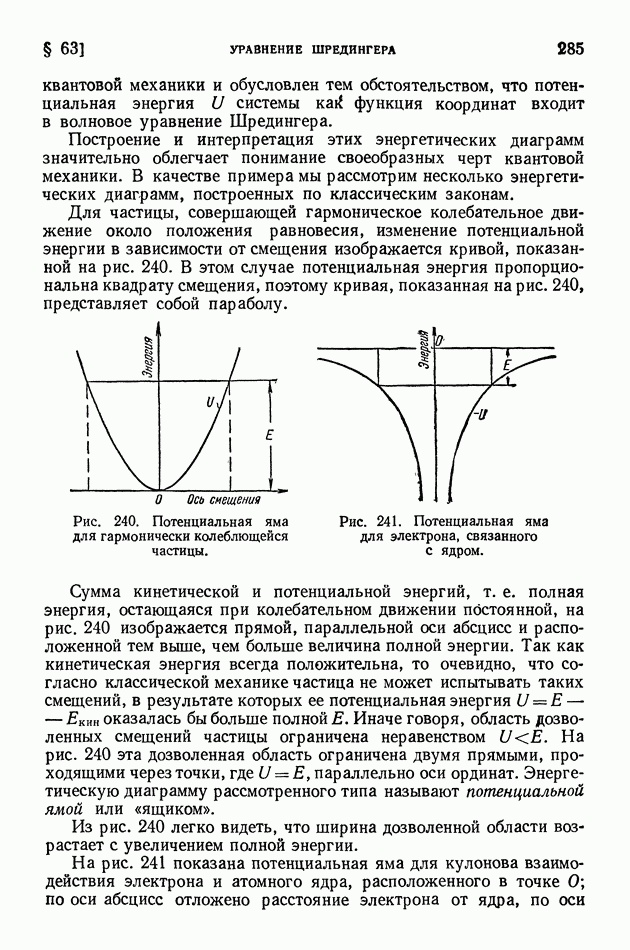
- § 63. Уравнение Шредингера. Просачивание через энергетический барьер. Нулевая энергия
- § 64. Волномеханическая теория атома водорода
- § 65. Соотношение неопределенностей и его разные трактовки
- ГЛАВА X. КВАНТОВАЯ ОПТИКА
- § 66. Развитие квантовой оптики
- § 67. Спектр щелочных металлов. Спин электрона
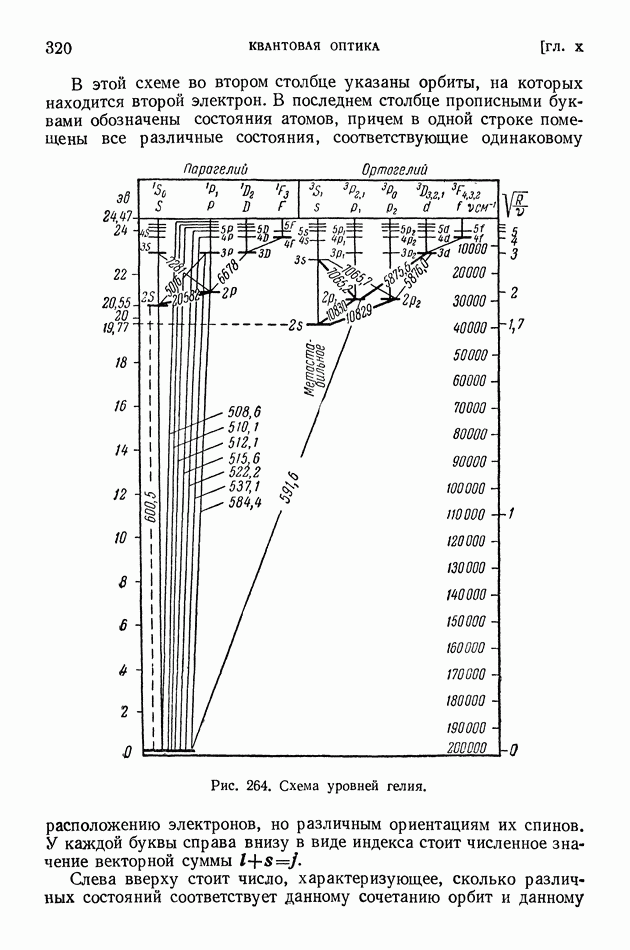
- § 68. Спектр гелия. Символика спектральных термов
- § 69. Сверхтонкая структура спектральных линий
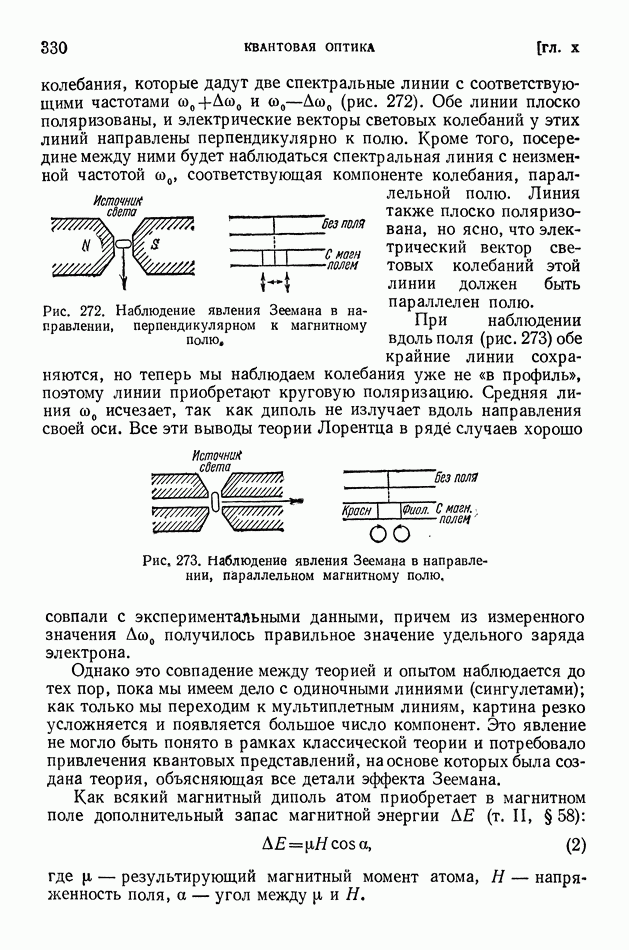
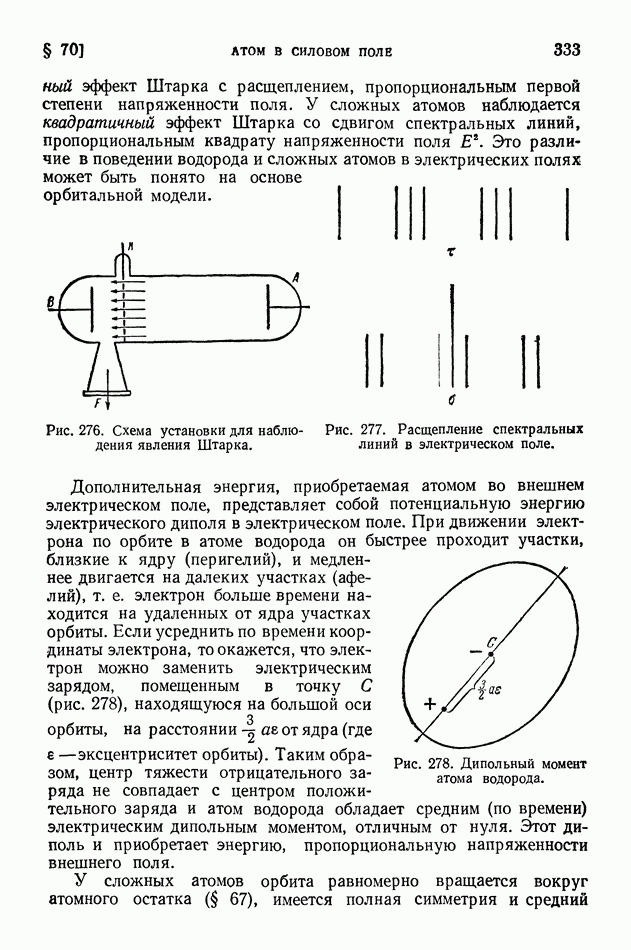
- § 70. Атом в силовом поле
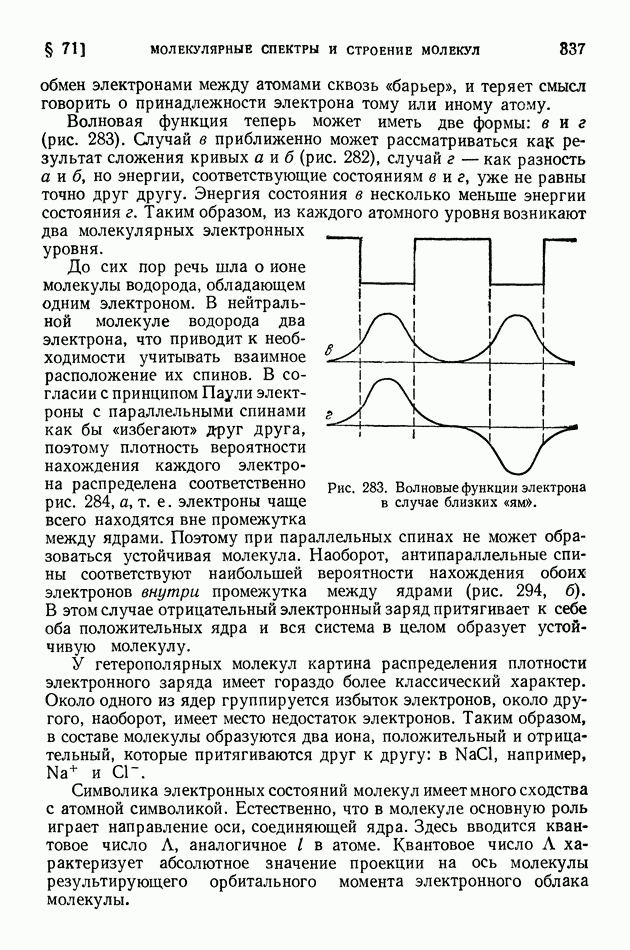
- § 71. Молекулярные спектры и строение молекул
- § 72. Комбинационное рассеяние света
- § 73. Квантовая картина испускания света атомами и молекулами
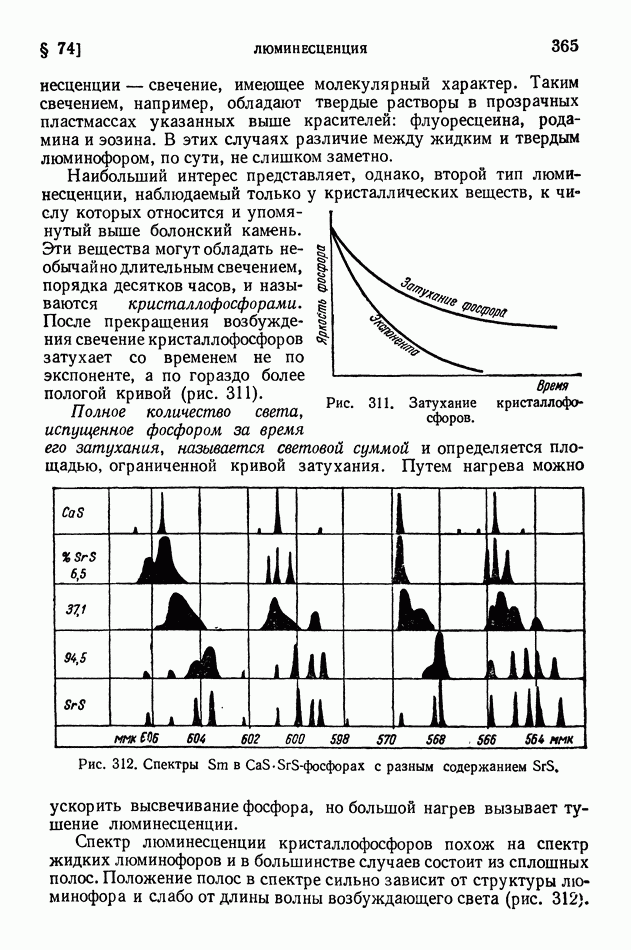
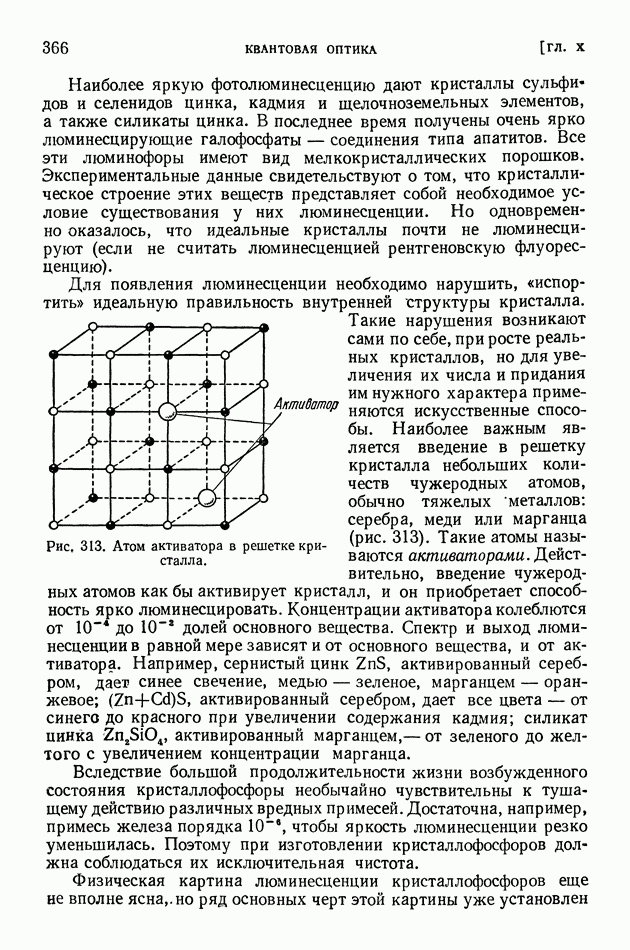
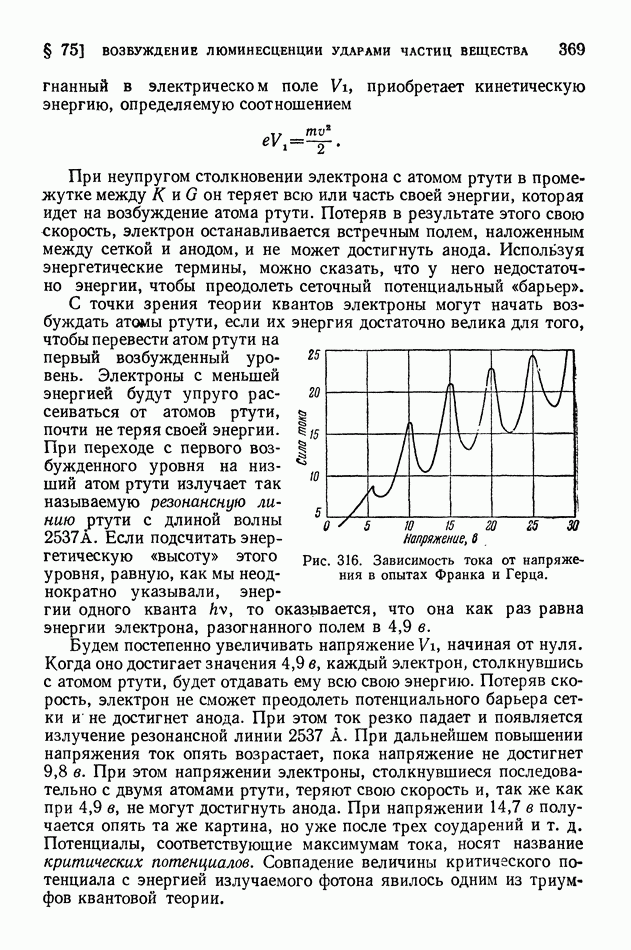
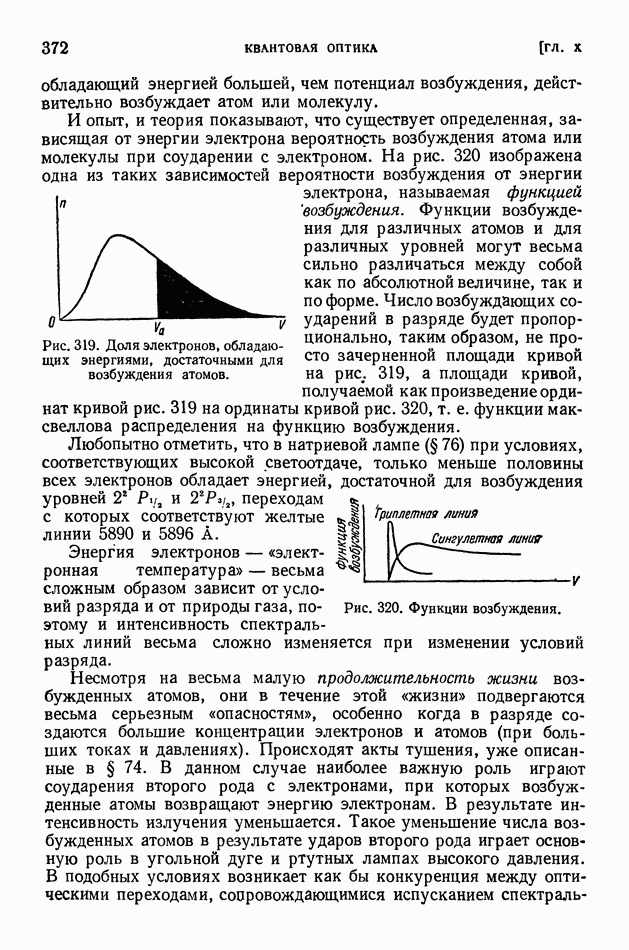
- § 74. Люминесценция
- § 75. Возбуждение люминесценции ударами частиц вещества
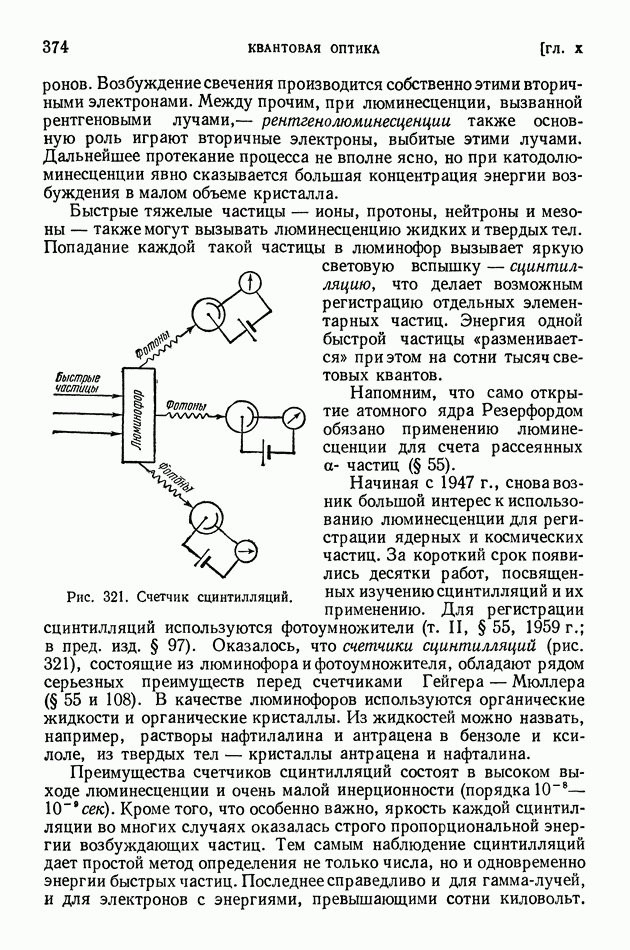
- § 76. Применения люминесценции
- § 77. Фотохимические реакции
- ГЛАВА XI. ЗАКОН ПРОПОРЦИОНАЛЬНОСТИ МАССЫ И ЭНЕРГИИ И РЕЛЯТИВИСТСКИЕ СООТНОШЕНИЯ
- § 78. Закон пропорциональности массы и энергии
- § 79. Предварительные замечания о релятивистских эффектах. Зависимость массы от скорости
- § 80. Корпускулярные свойства фотонов. Явление Комптона
- § 81. Вывод закона Эйнштейна сложения скоростей из закона пропорциональности массы и энергии и законов сохранения энергии или количества движения
- § 82. Две трактовки закона пропорциональности массы и энергии и уточнение закона тяготения
- § 83. Красное смещение спектральных линий. Поперечный эффект Доплера
- § 84. Влияние гравитационного поля на скорость света в вакууме и показатель преломления вакуума
- ЧАСТЬ ШЕСТАЯ. ЯДЕРНАЯ ФИЗИКА
- § 85. Заряд и масса ядра. Масс-спектральный анализ
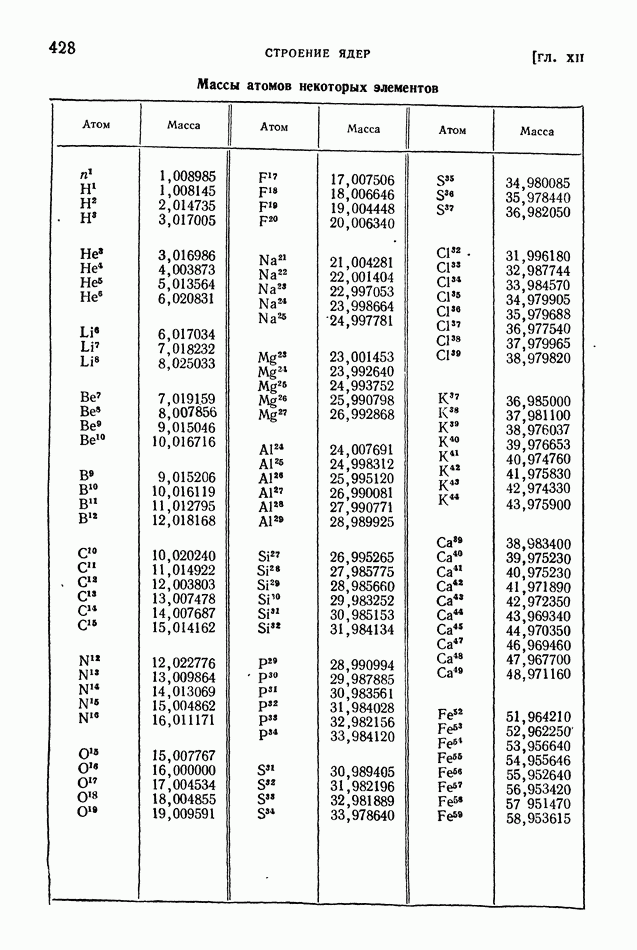
- § 86. Состав ядер. Изотопы. Атомные единицы массы и энергии
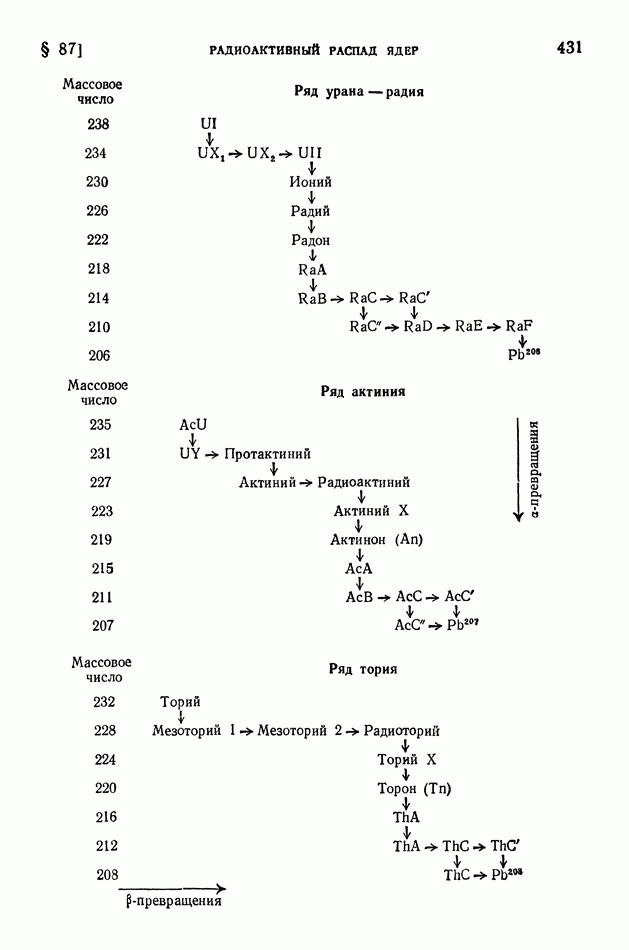
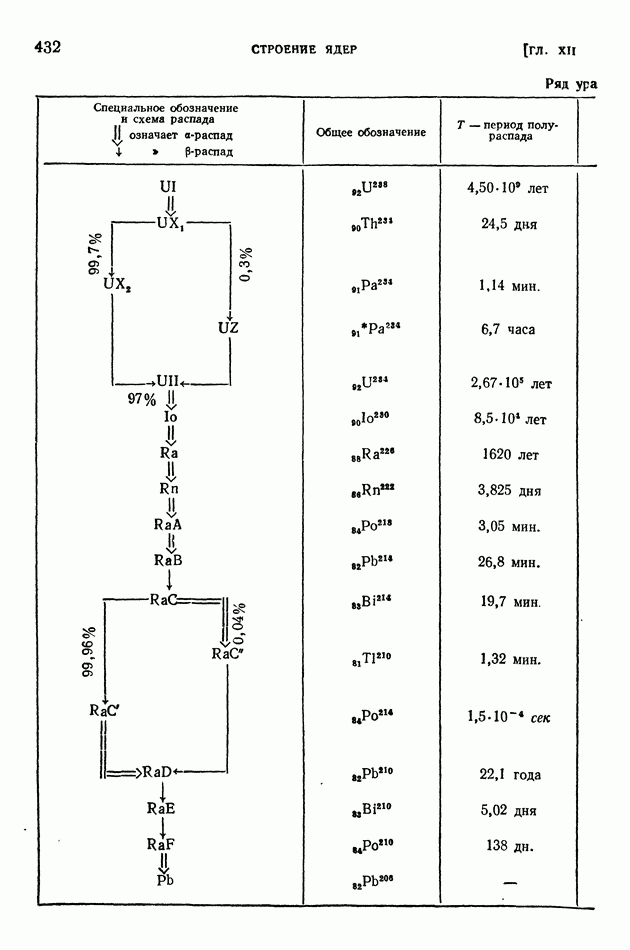
- § 87. Радиоактивный распад ядер. Закон радиоактивного смещения. Изомеры
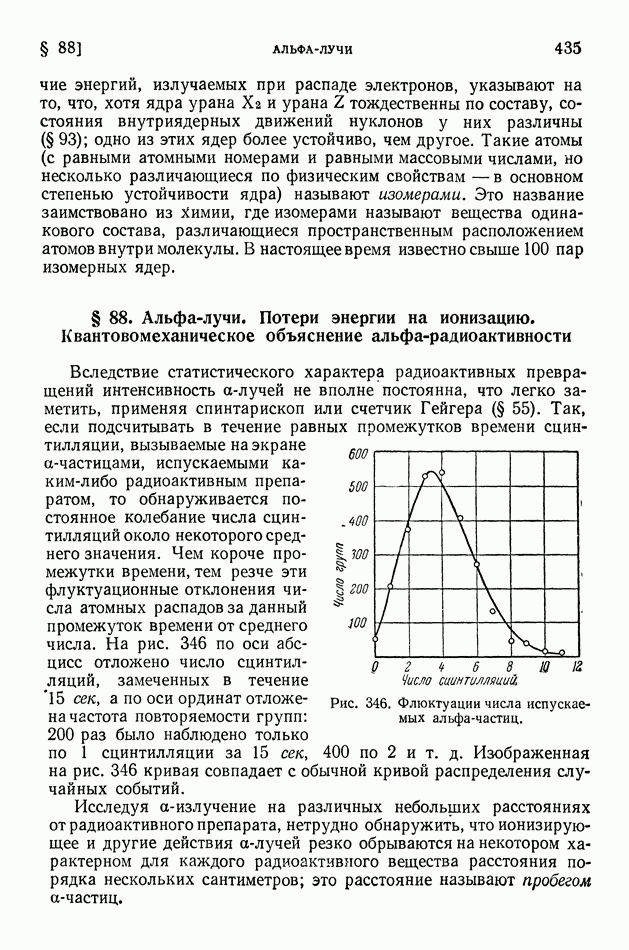
- § 88. Альфа-лучи. Потери энергии на ионизацию. Квантовомеханическое объяснение альфа-радиоактивности
- § 89. Бета- и гамма-лучи
- § 90. Искусственное расщепление ядер. Открытие нейтрона
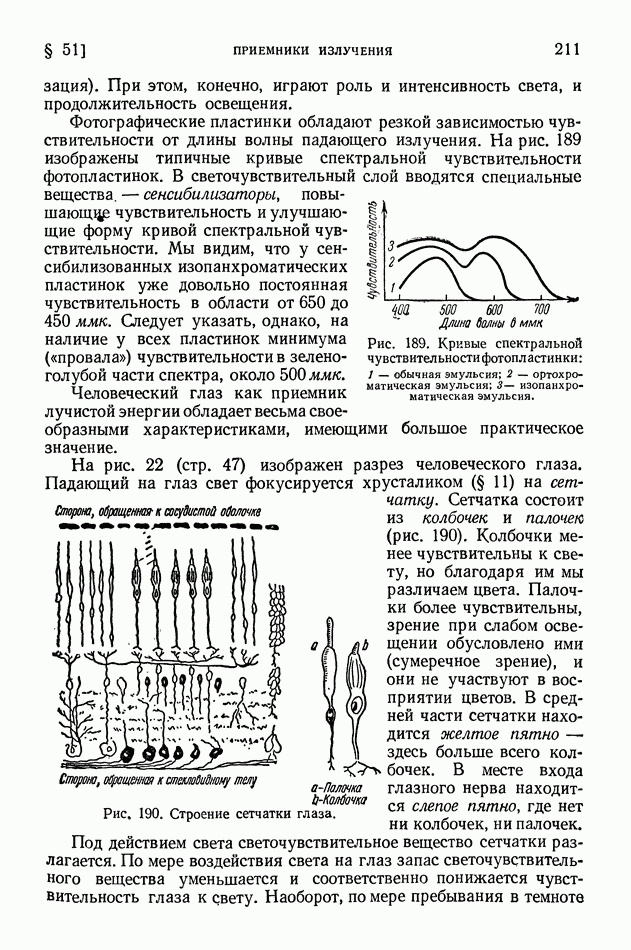
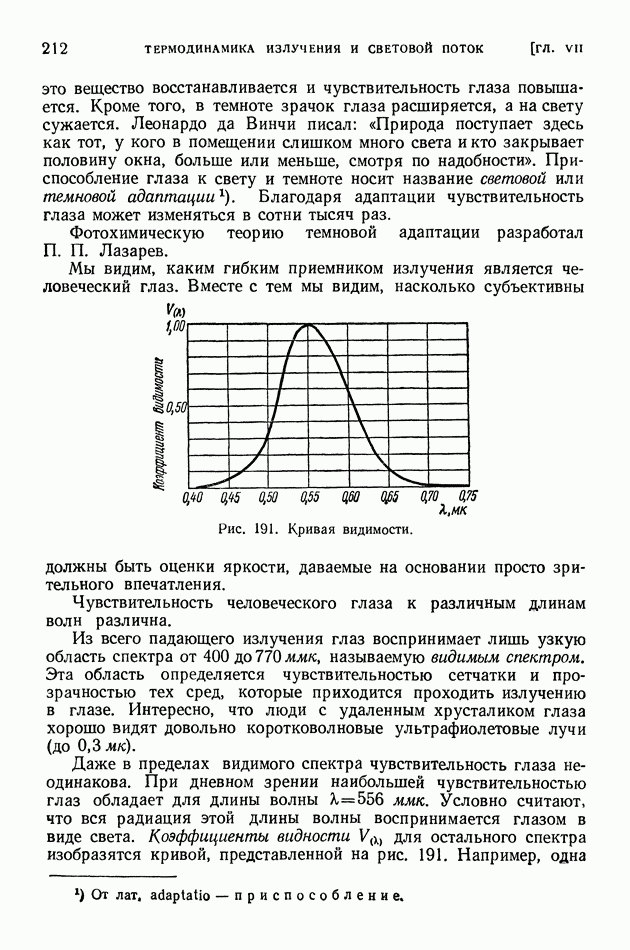
- § 91. Открытие позитрона. Взаимопревращение фотонов определенной энергии и электронно-позитронных пар
- § 92. Индуцированная позитронная и электронная радиоактивность. Фоторасщепление ядер, K-захват
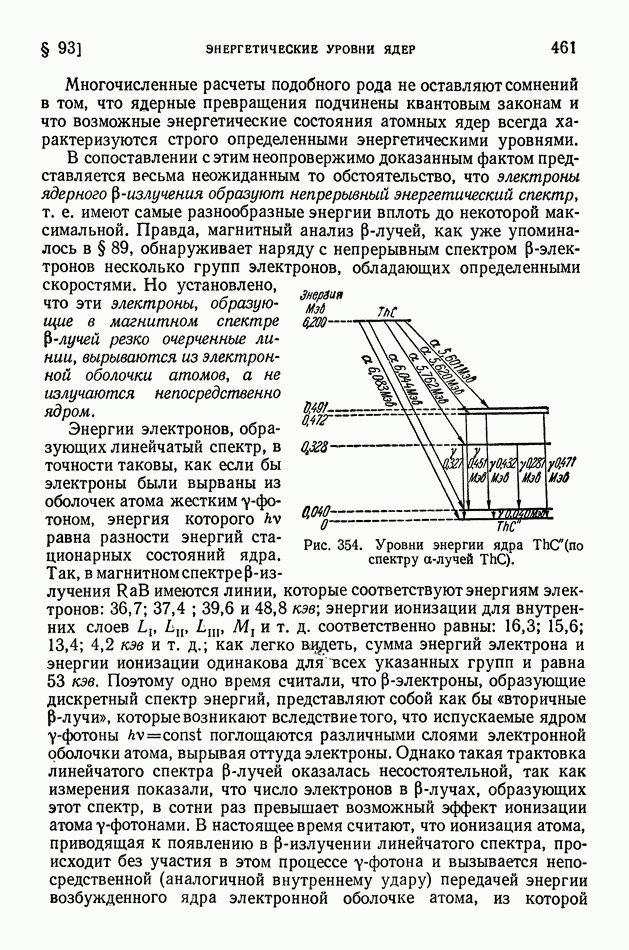
- § 93. Энергетические уровни ядер. Внутренняя конверсия. Нейтрино
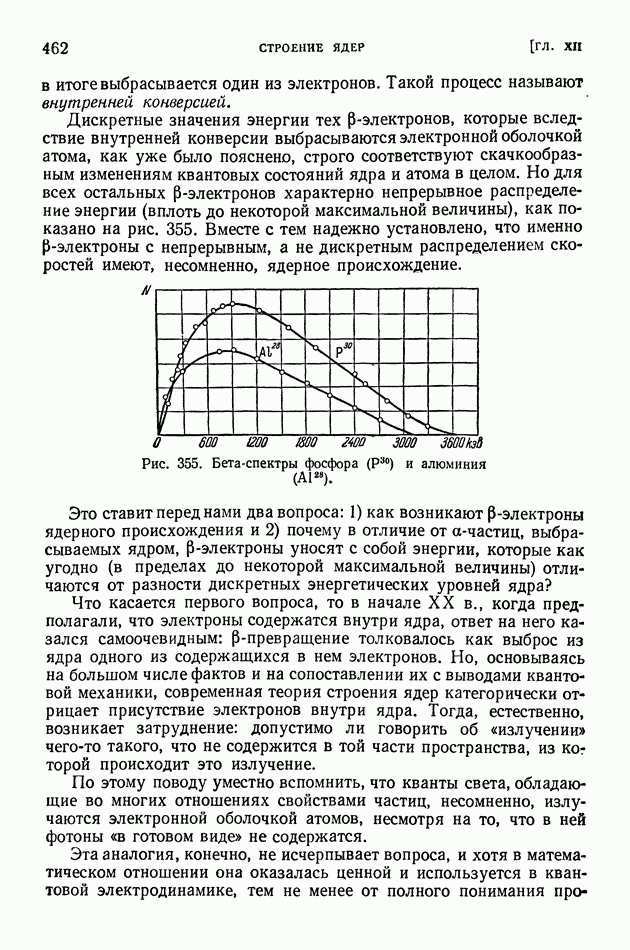
- § 94. Капельная теория строения ядер
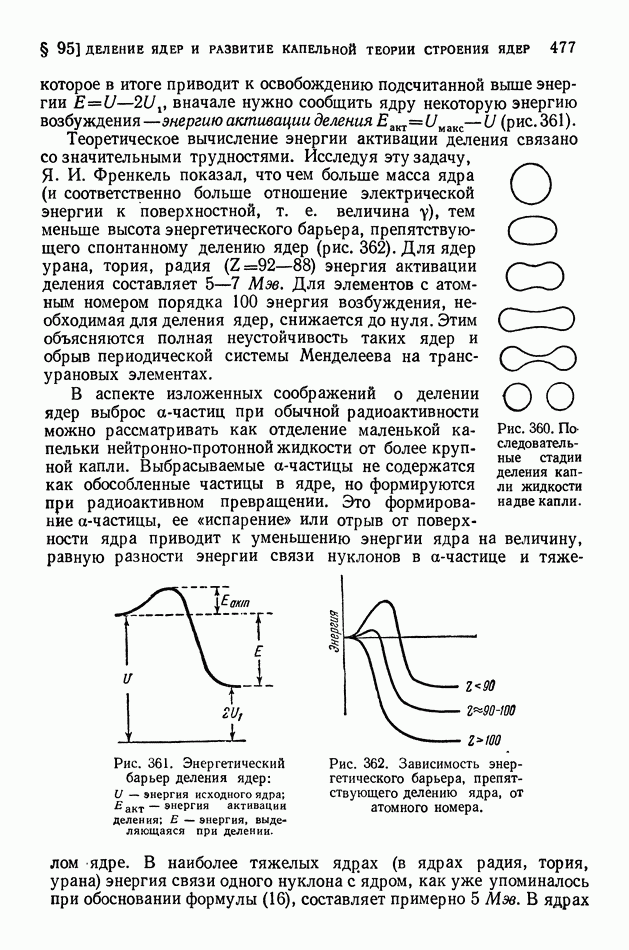
- § 95. Деление ядер и развитие капельной теории строения ядер
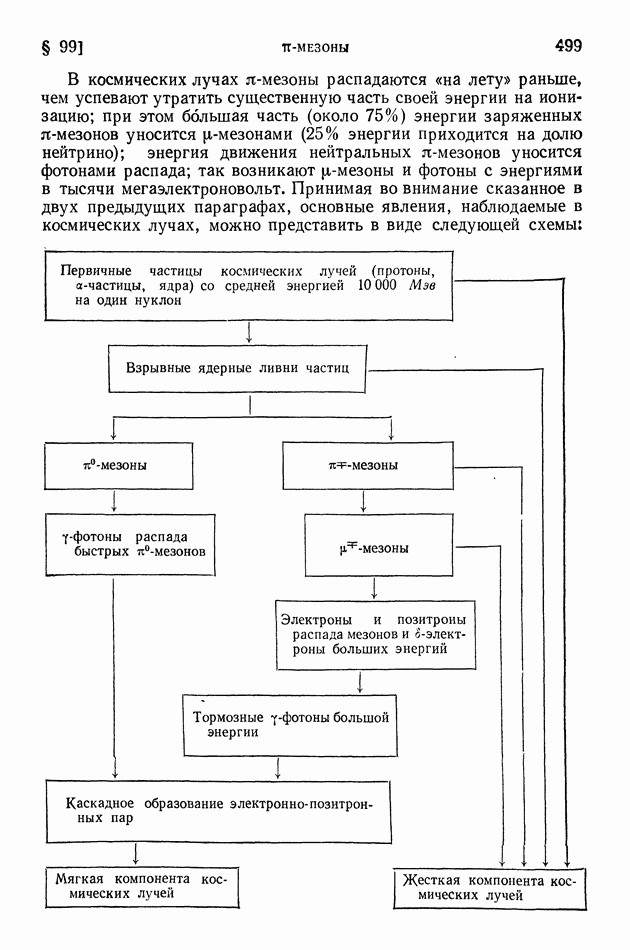
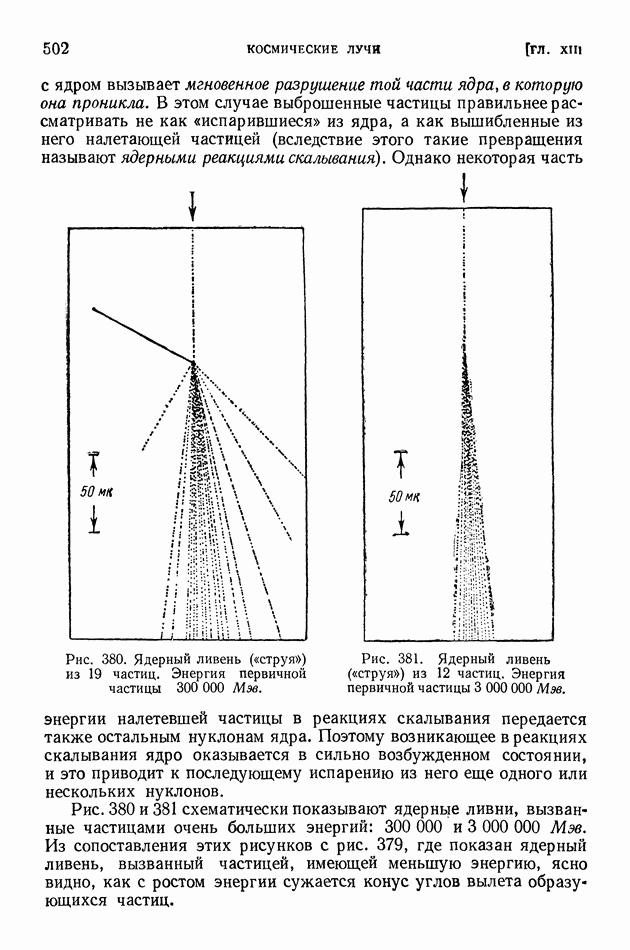
- ГЛАВА XIII. КОСМИЧЕСКИЕ ЛУЧИ
- § 96. Методы исследования и первые итоги изучения космических лучей
- § 97. Каскадное образование электронно-позитронных пар в космических лучах. Потери энергии электронами на тормозное излучение
- § 98. «мю»-мезоны. Зависимость времени жизни неустойчивых частиц от скорости движения
- § 99. «пи»-мезоны
- § 100. Взрывные ядерные ливни и их каскадное развитие в космических лучах
- § 101. Корпускулярный и энергетический спектр космических лучей. Происхождение космического излучения
- ГЛАВА XIV. ЭКСПЕРИМЕНТАЛЬНЫЕ СРЕДСТВА ЯДЕРНОЙ ФИЗИКИ
- § 102. Циклотроны
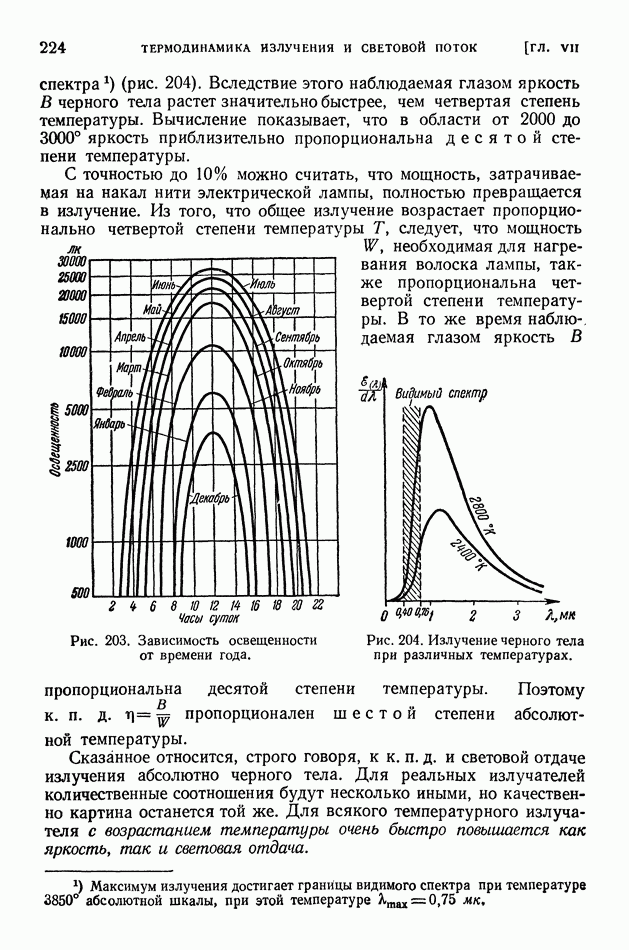
- § 103. Фазотроны
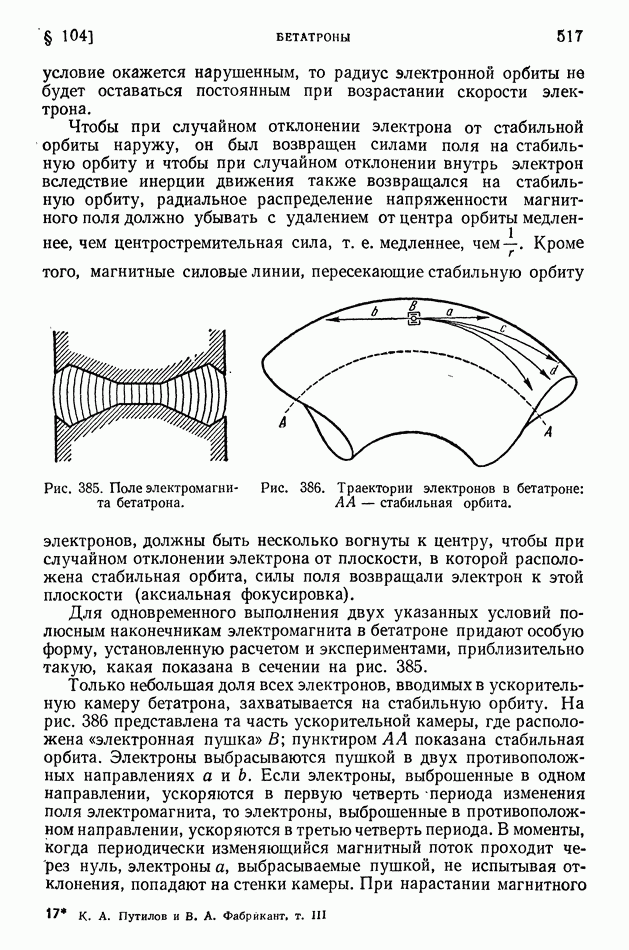
- § 104. Бетатроны
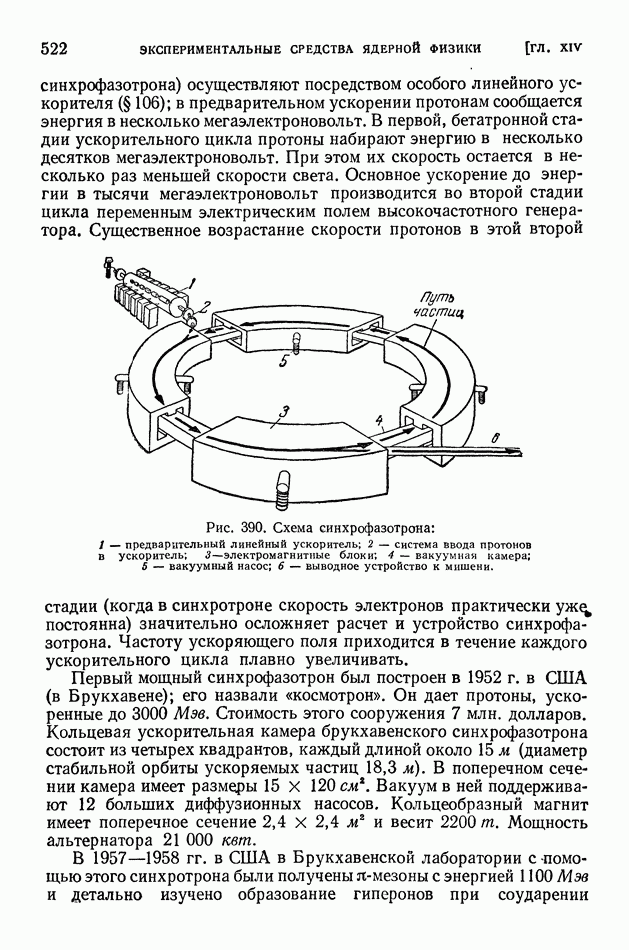
- § 105. Синхротроны и синхрофазотроны
- § 106. Линейные ускорители электронов и ионов
- § 107. Лабораторные источники нейтронов. Замедлители нейтронов в ядерных реакторах
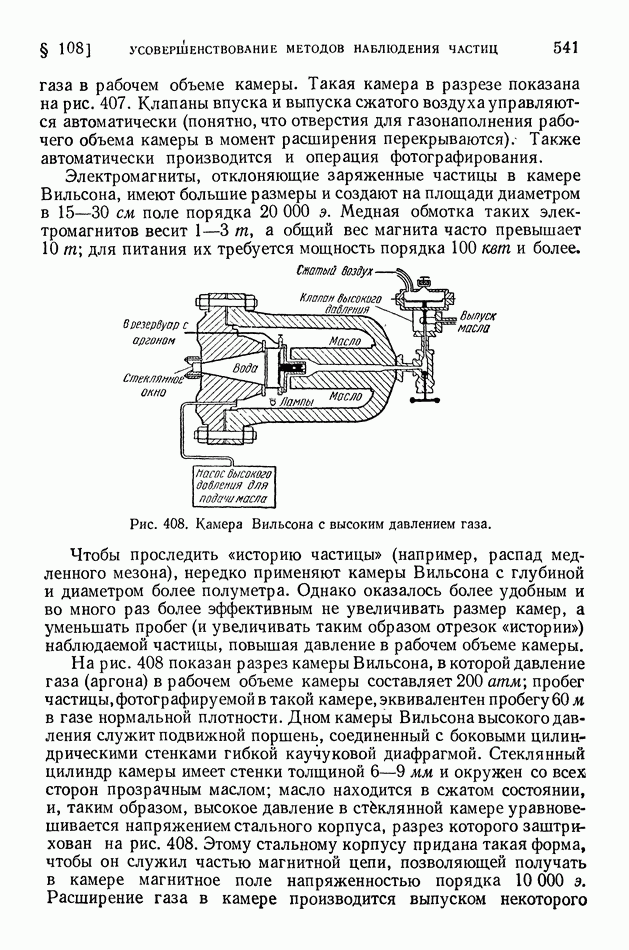
- § 108. Усовершенствование методов наблюдения и счета частиц
- ГЛАВА XV. ЯДЕРНЫЕ РЕАКЦИИ И АТОМНАЯ ЭНЕРГИЯ
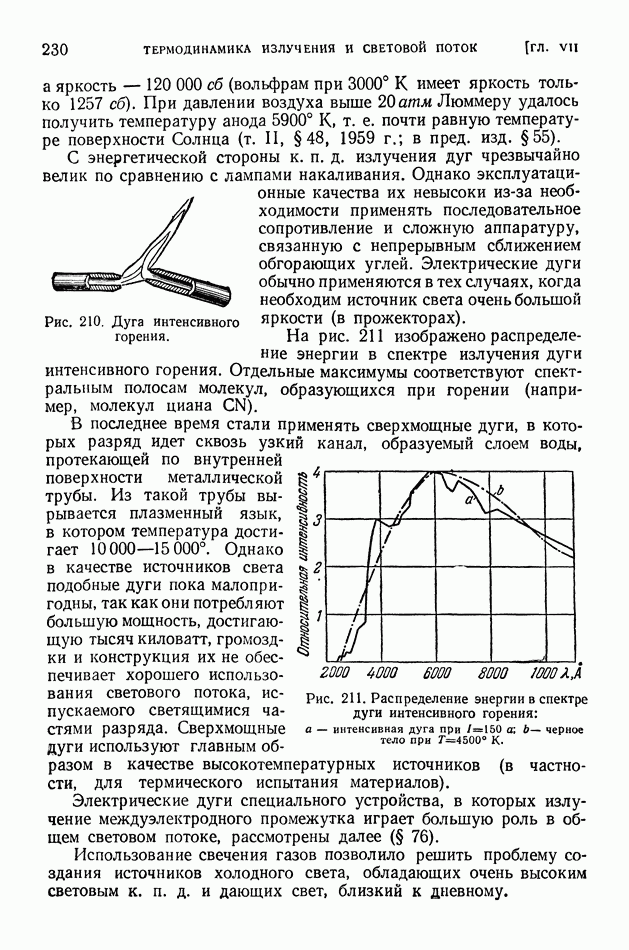
- § 109. Основные виды и обозначения ядерных реакций. Конкурирующие процессы в ядерных реакциях
- § 110. Энергетический эффект, энергия возбуждения и порог ядерных реакций
- § 111. Превращения элементарных частиц
- § 112. Ядерные силы
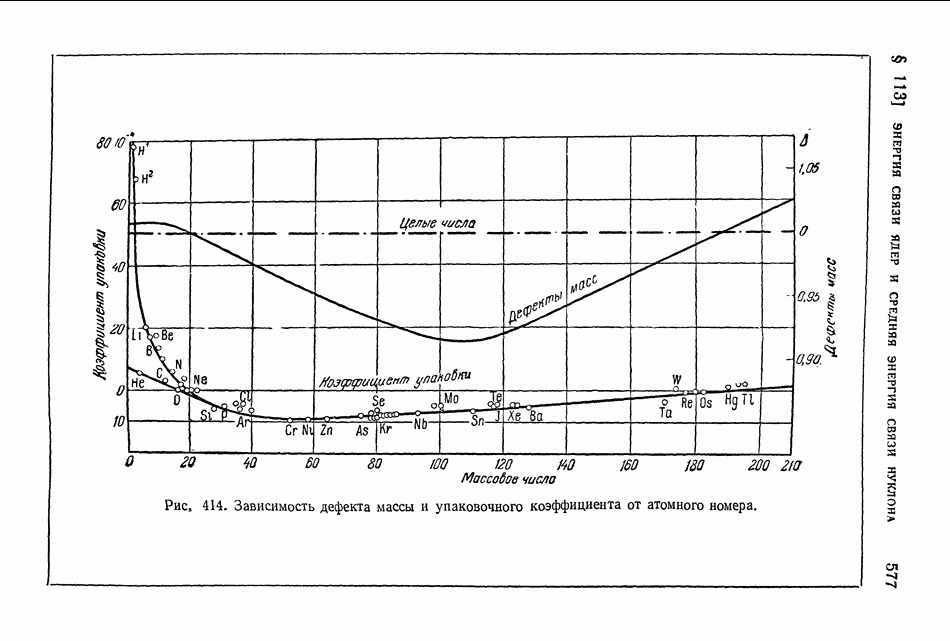
- § 113. Энергия связи ядер и средняя энергия связи нуклона
- § 114. Полуэмпирическая формула для энергии ядерной связи и для атомных энергий и масс
- § 115. Взаимосвязь энергии и строения ядер. Внутриядерное движение нуклонов и нуклонные оболочки. Спины и магнитные моменты ядер
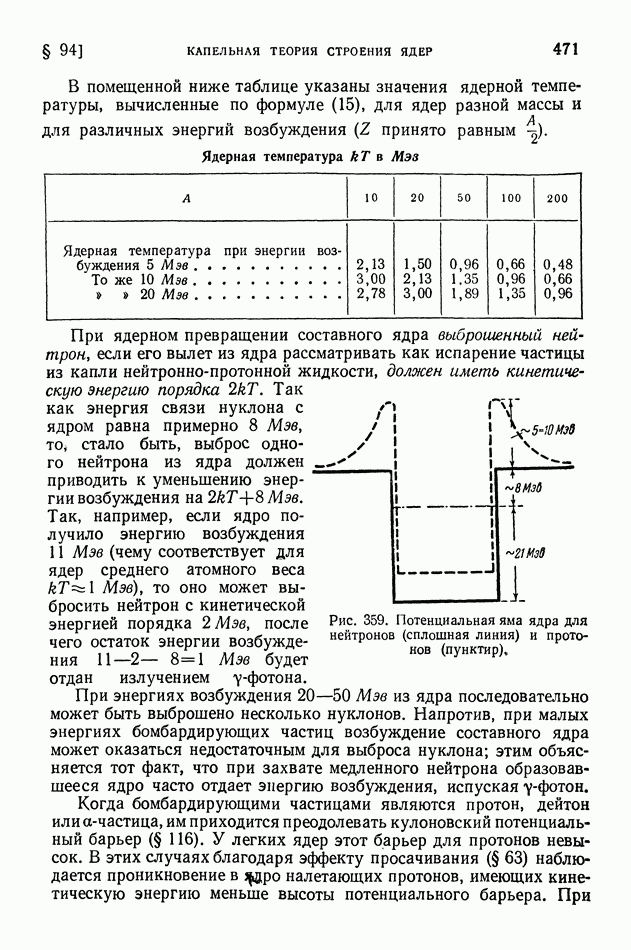
- § 116. Энергия отделения частиц и анализ возможного хода ядерной реакции
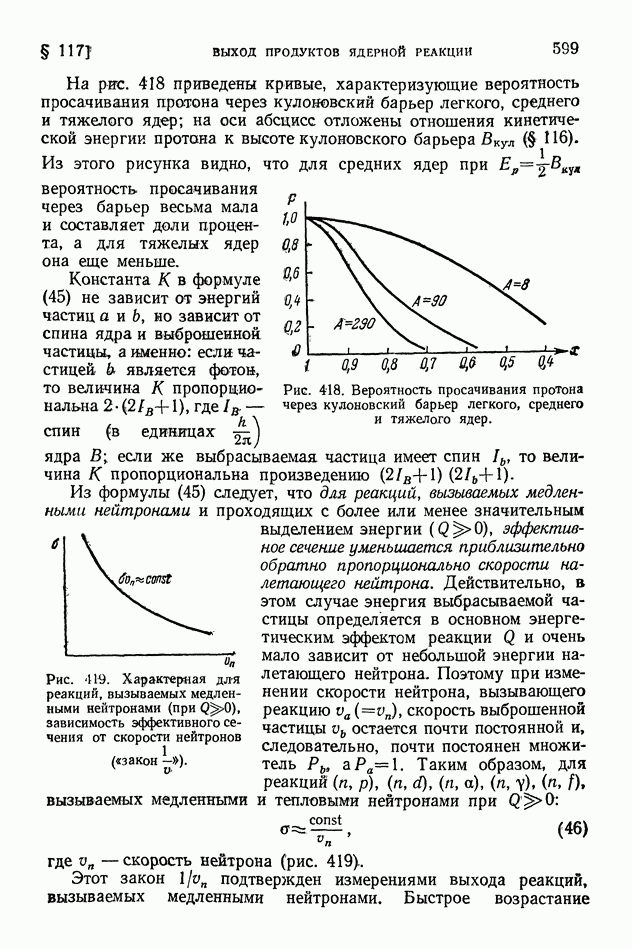
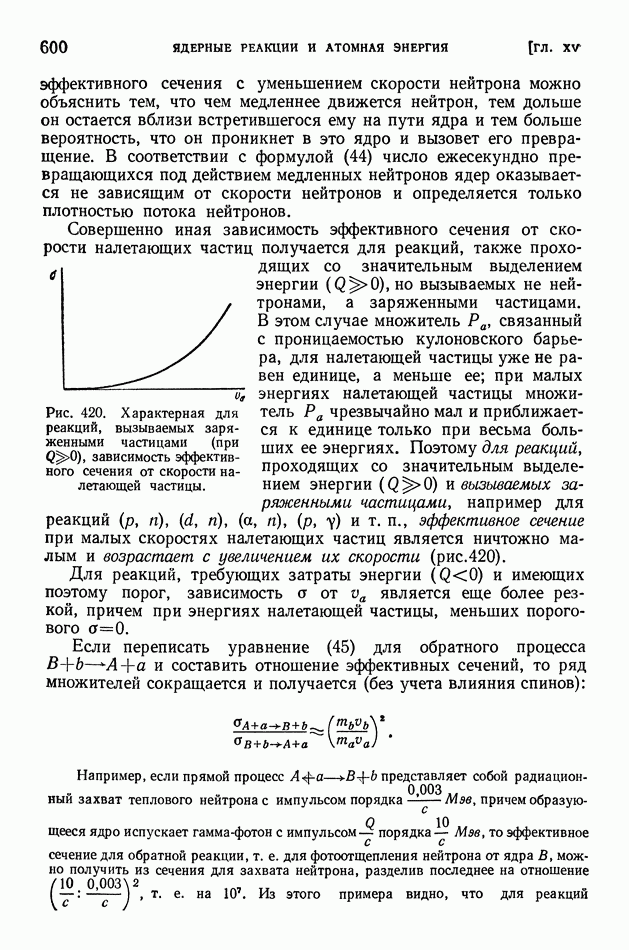
- § 117. Выход продуктов ядерной реакции. Эффективные сечения. Резонансные явления
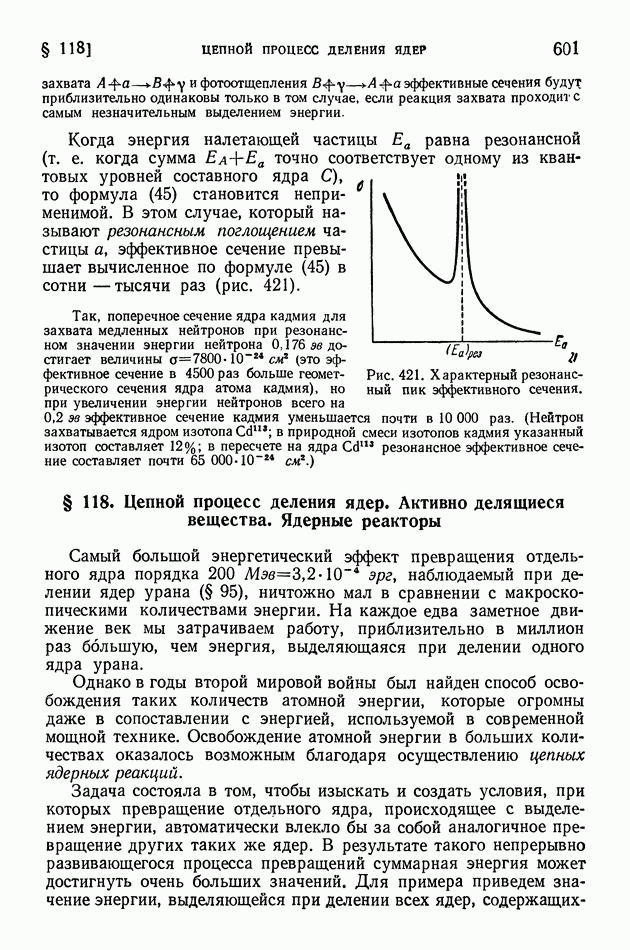
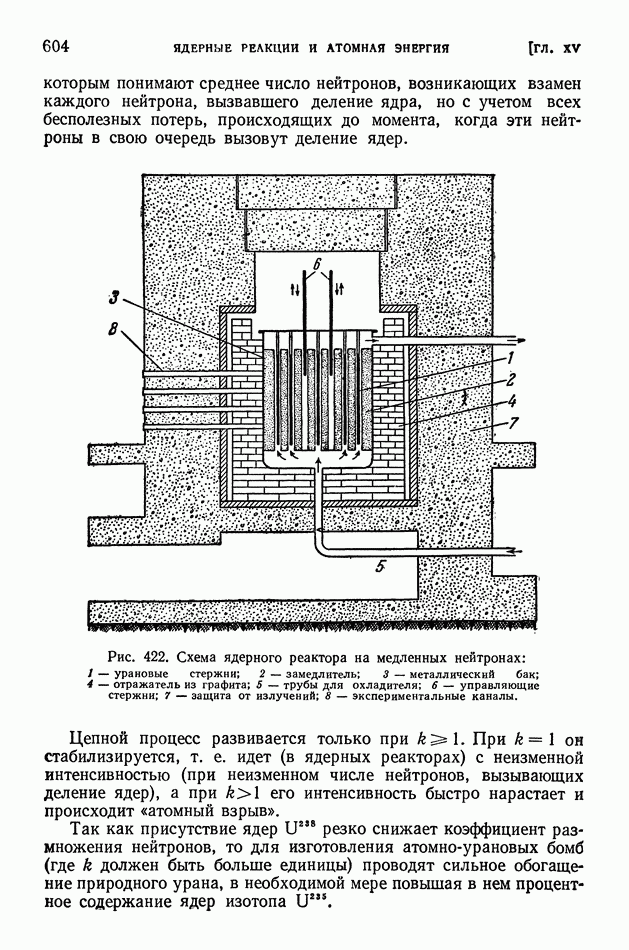
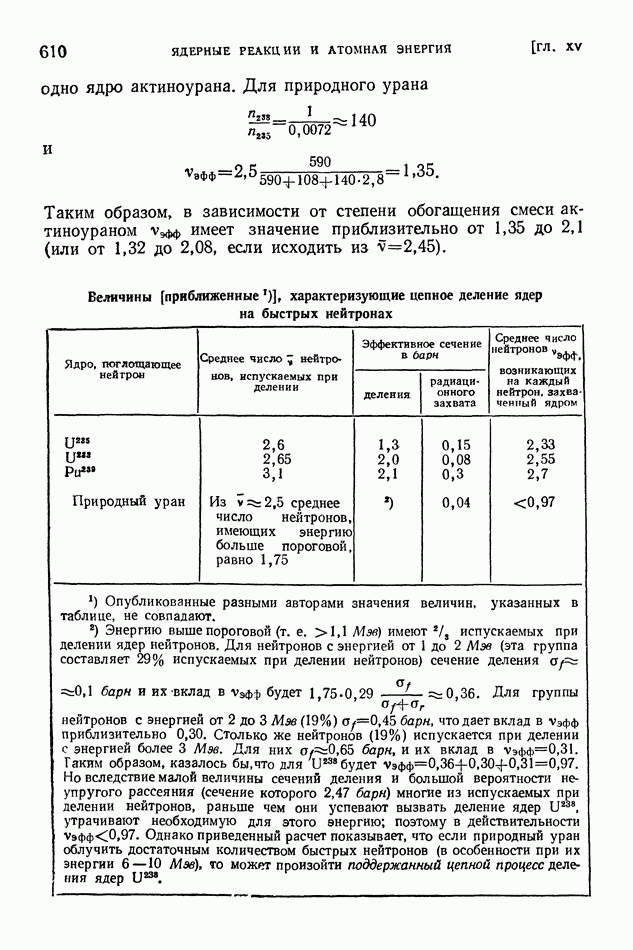
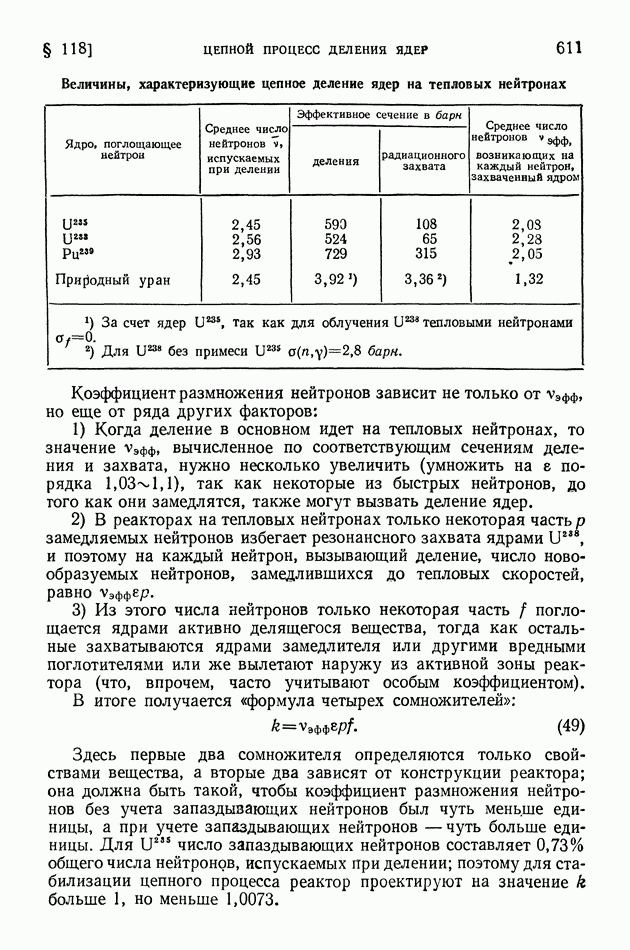
- § 118. Цепной процесс деления ядер. Активно делящиеся вещества. Ядерные реакторы
- § 119. Термоядерные реакции
- § 120. Применение ядерных реакций
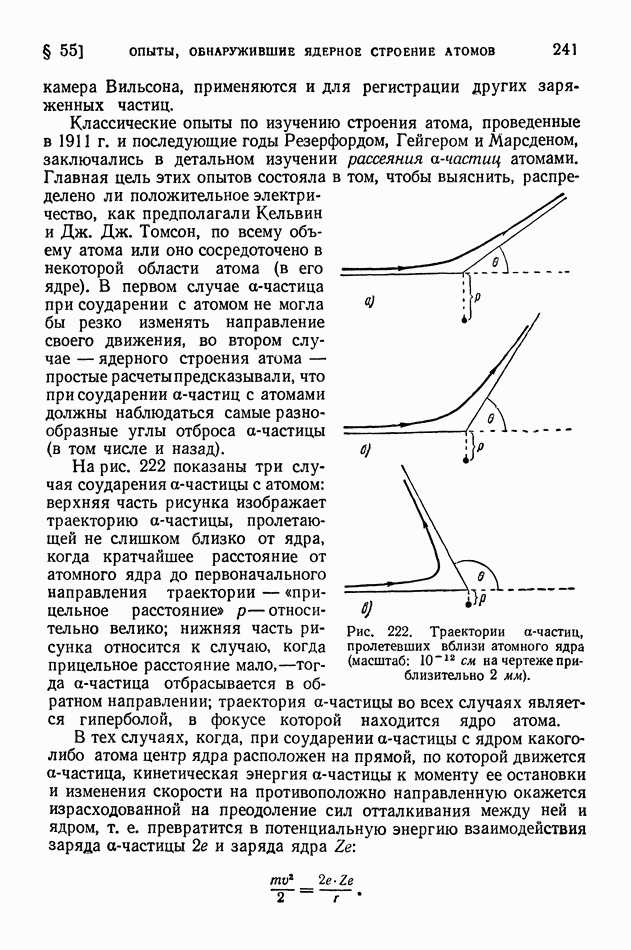
- § 121. Ядерные реакции в звездах