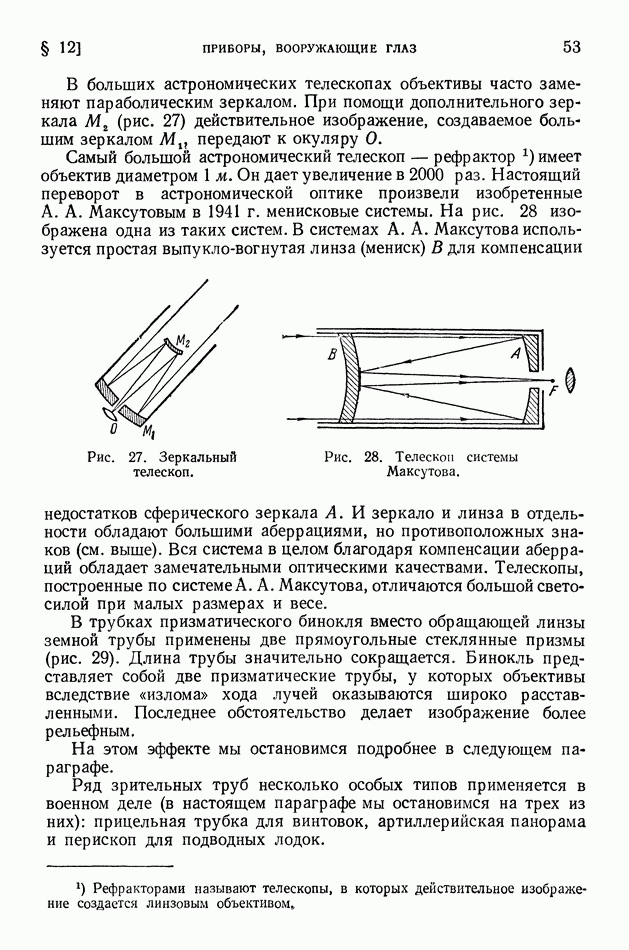
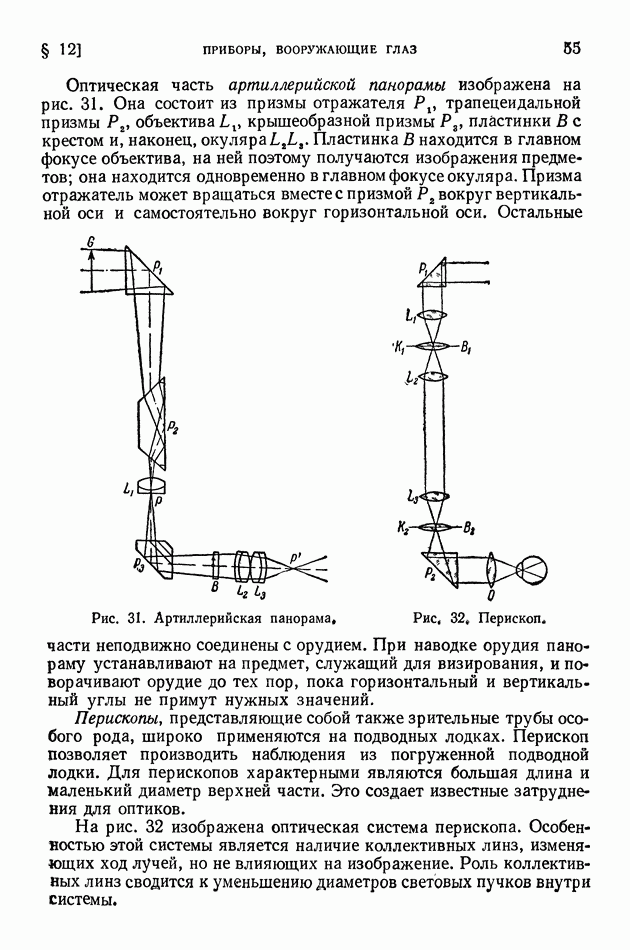
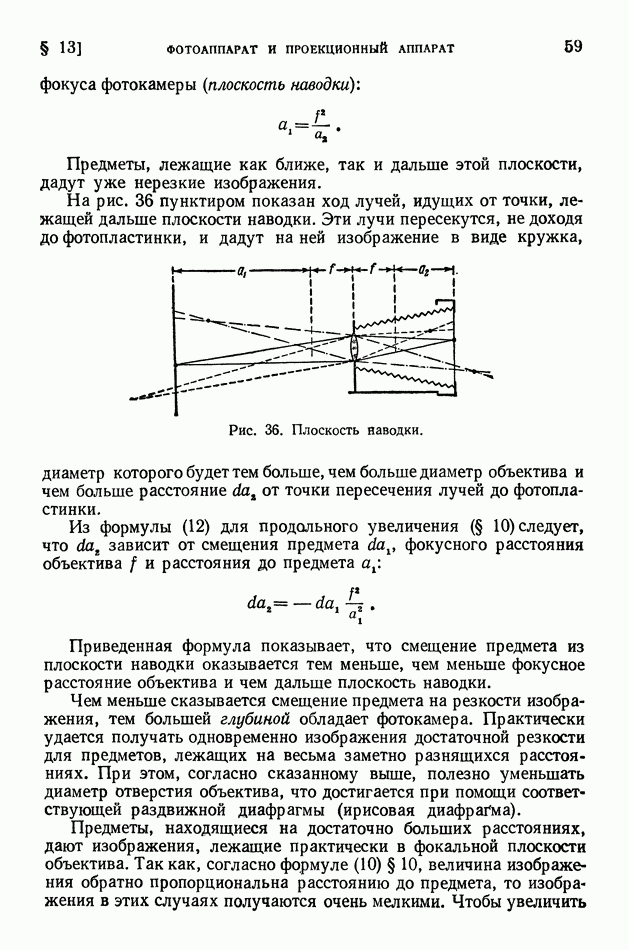
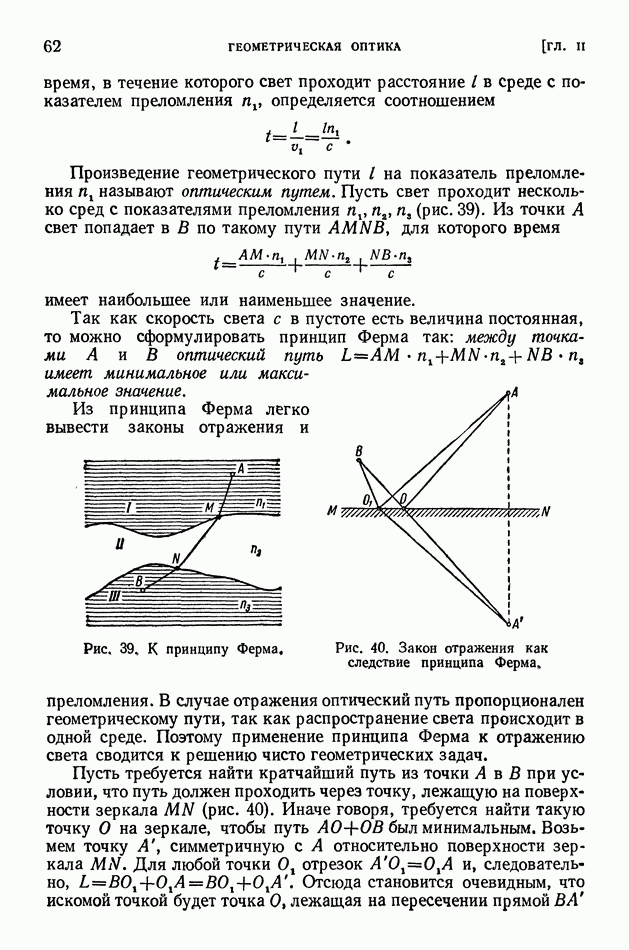
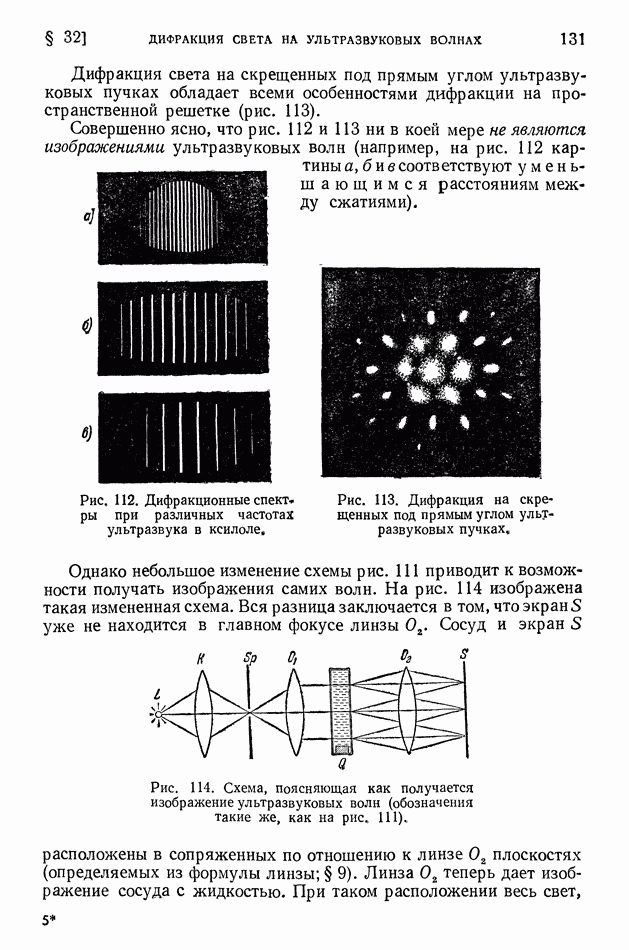
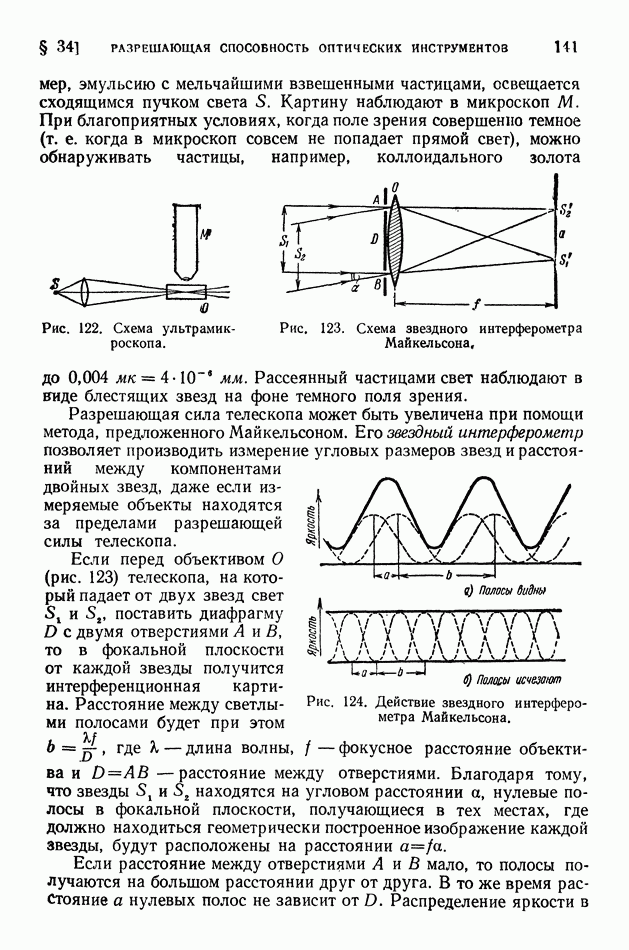
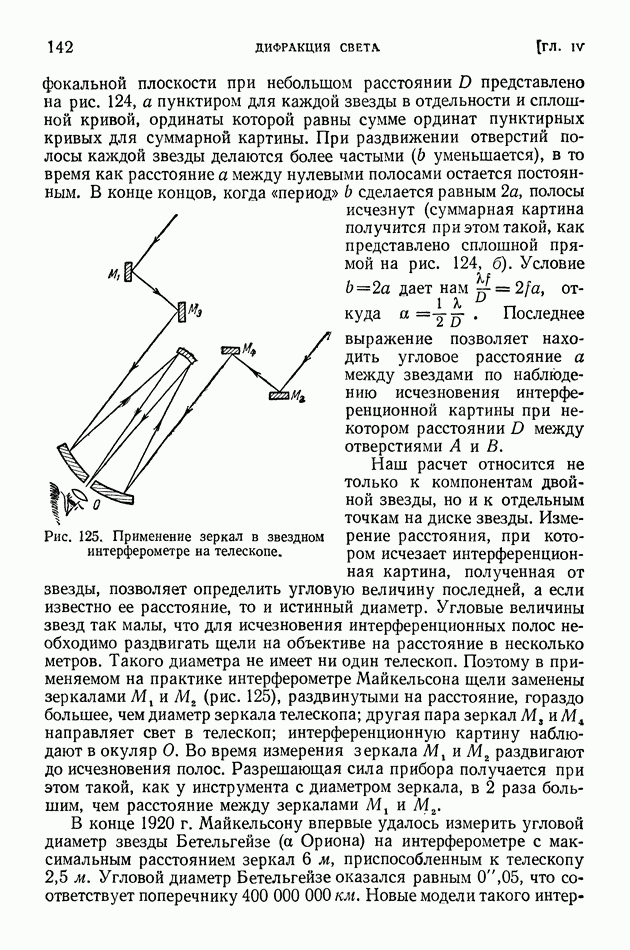
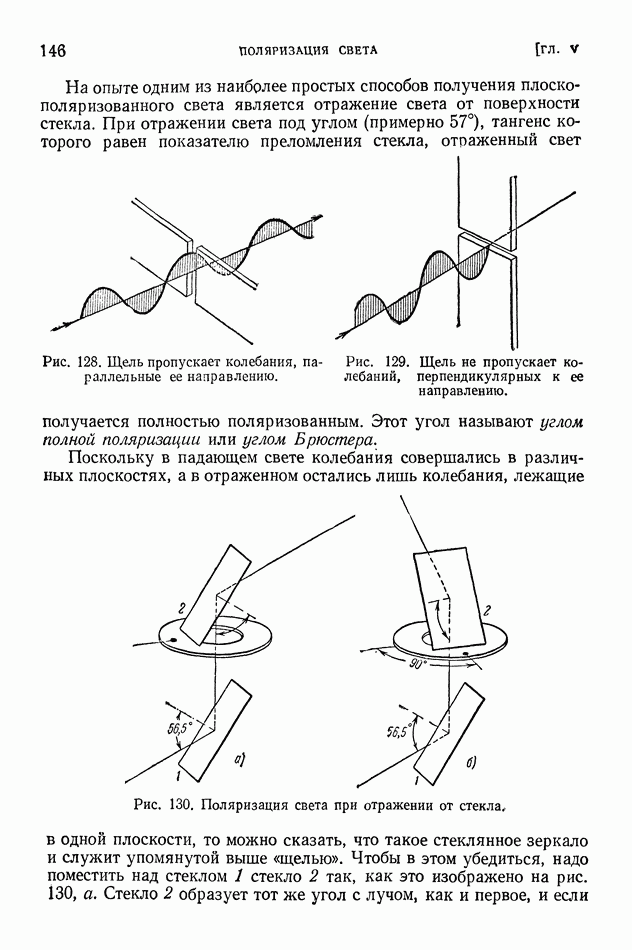
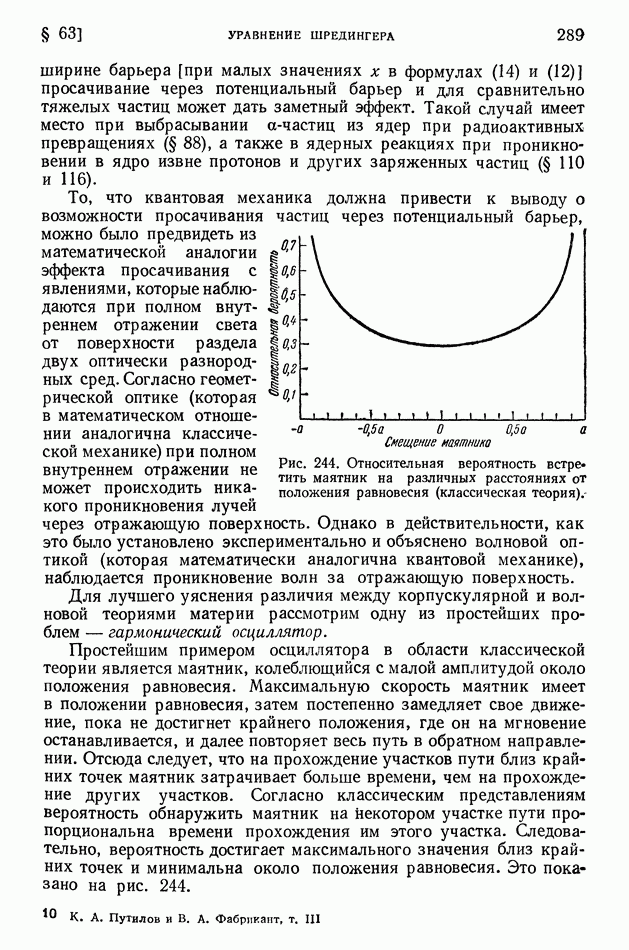
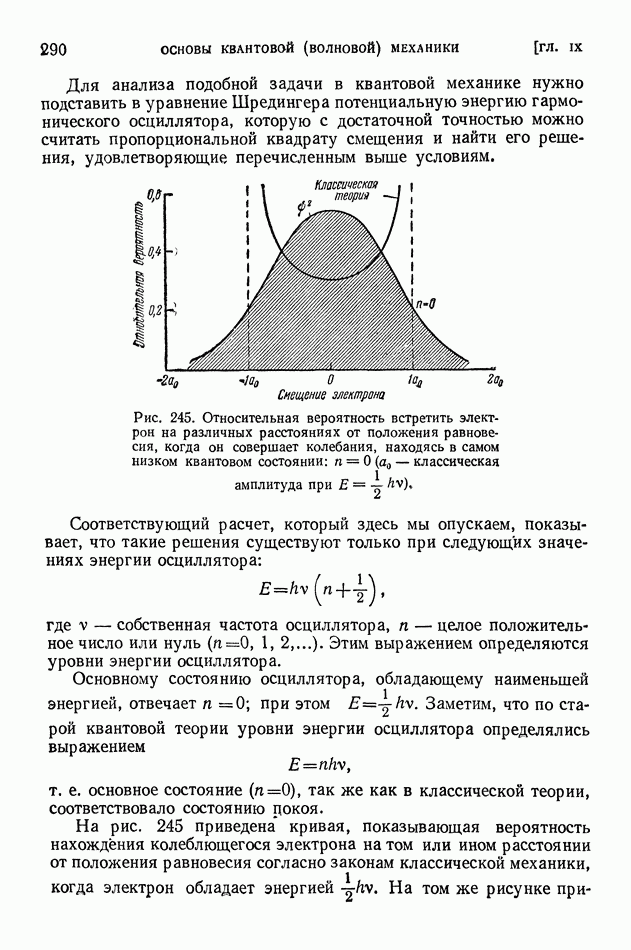
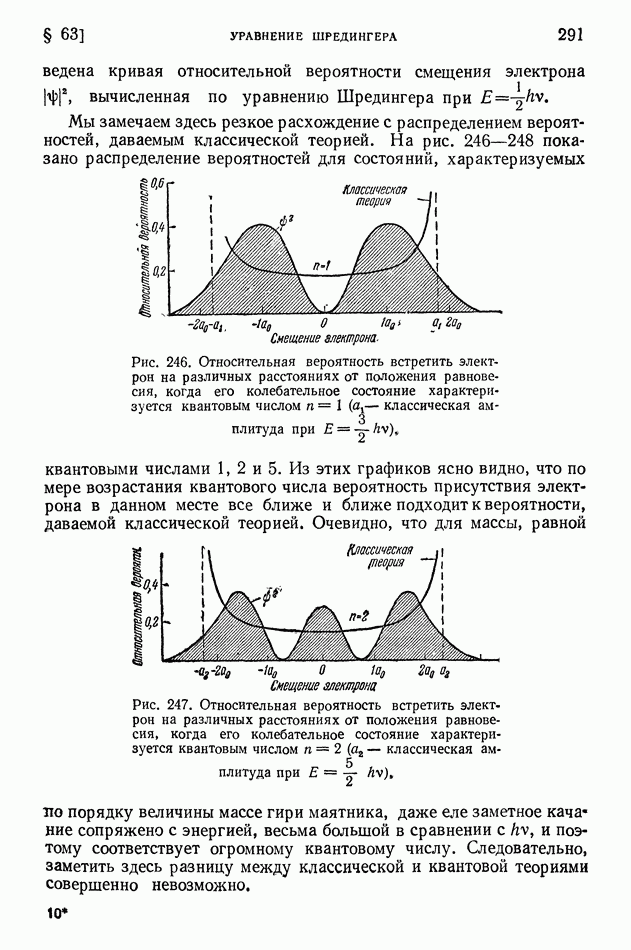
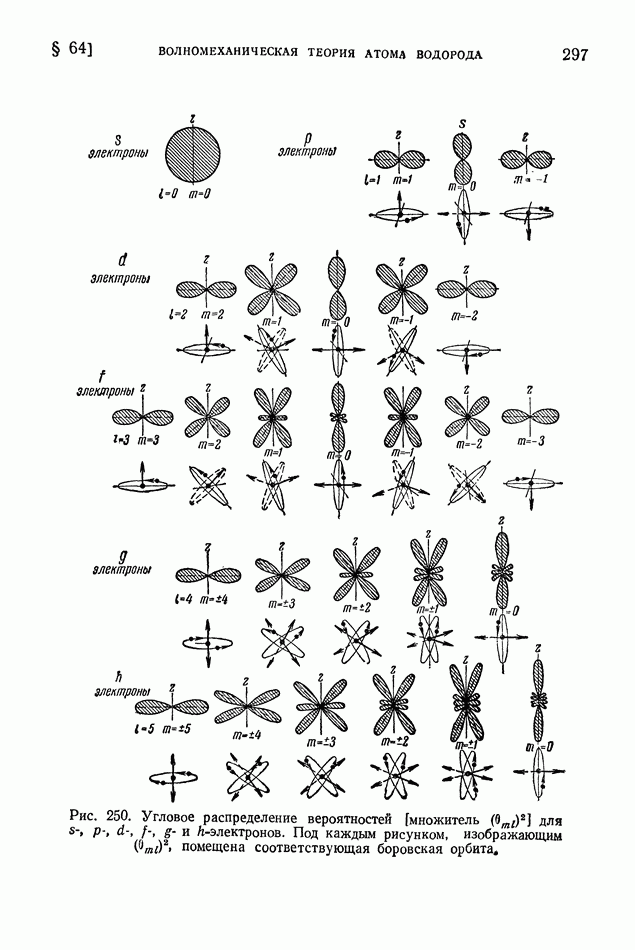
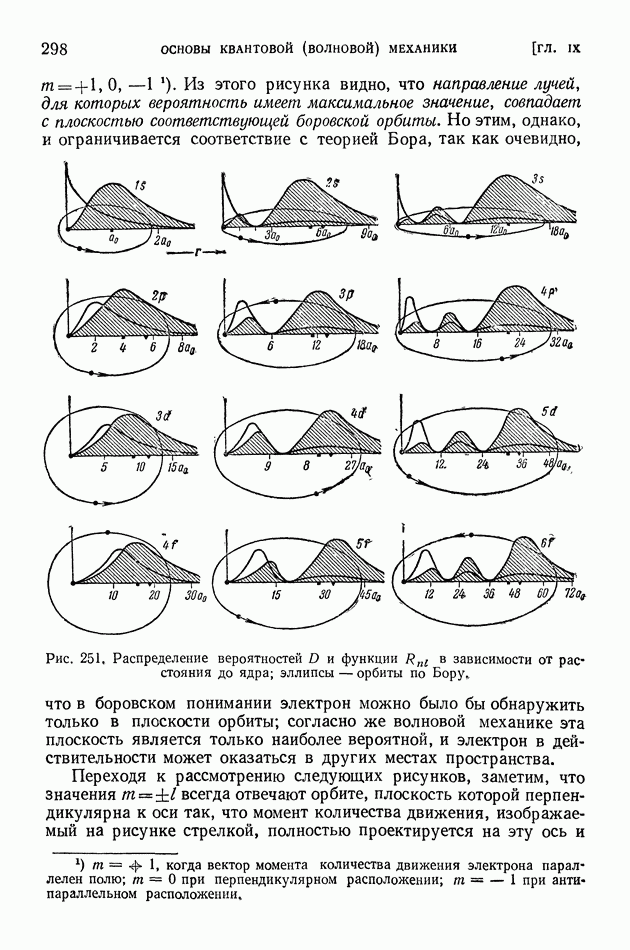
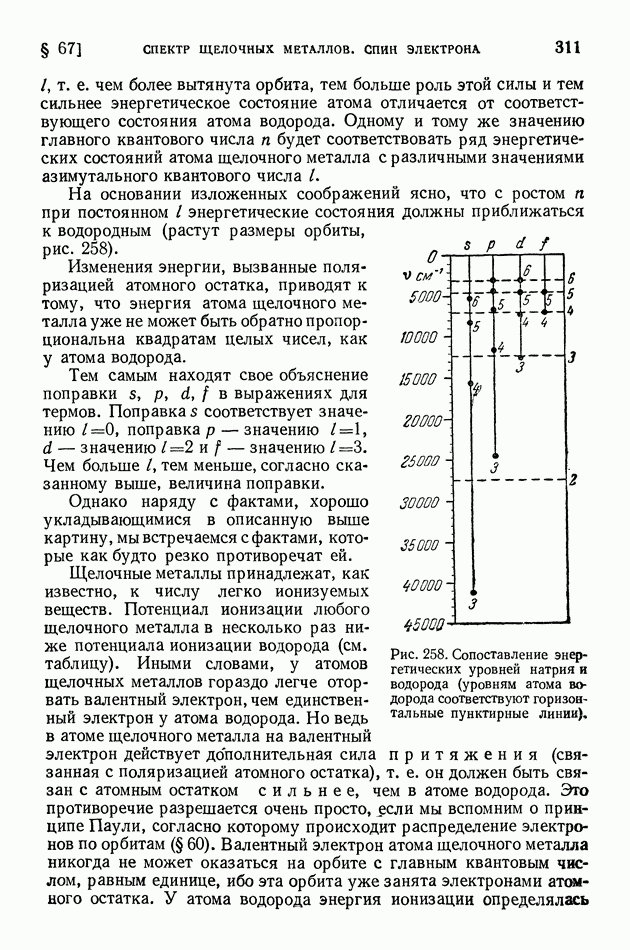
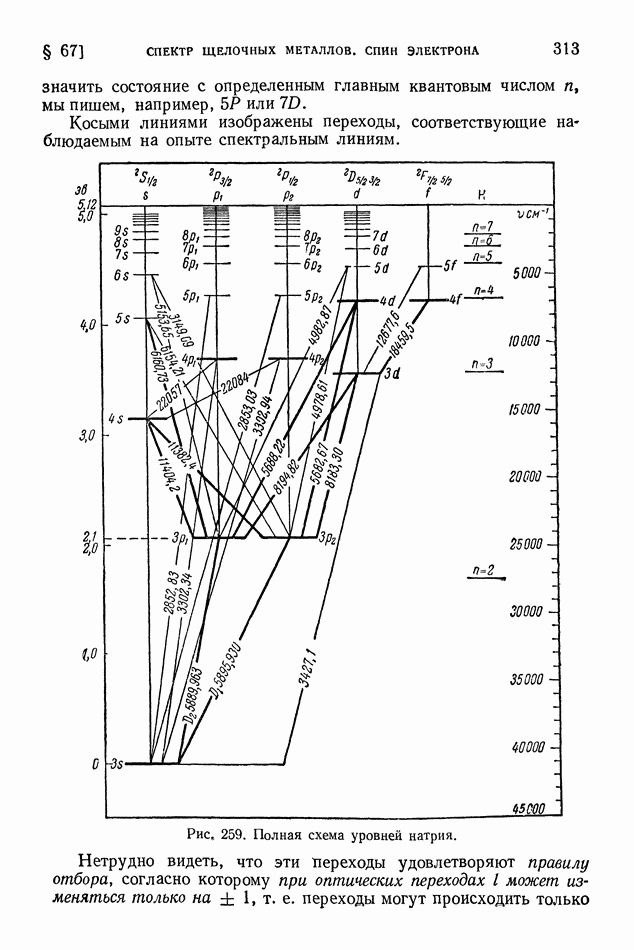
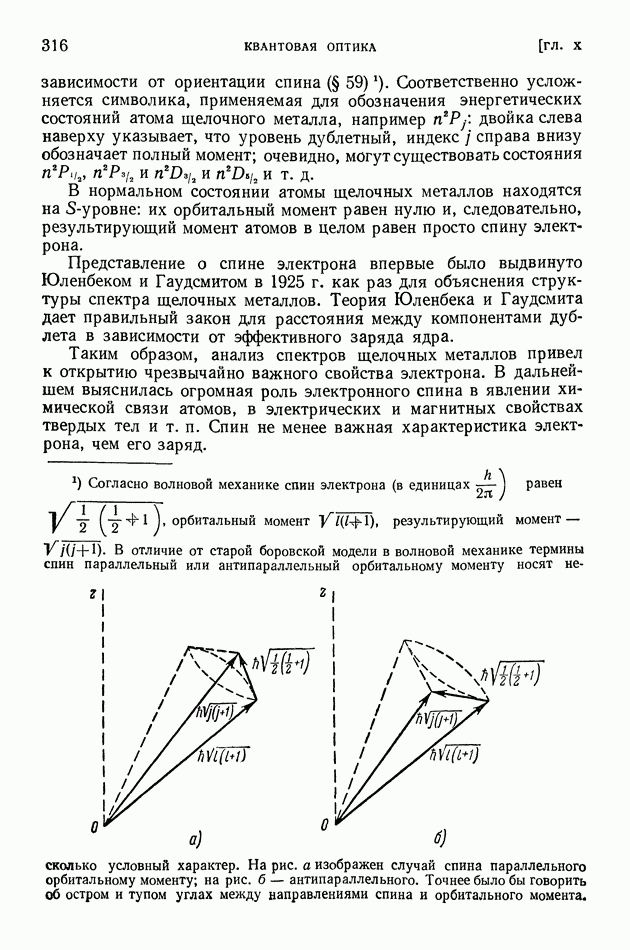
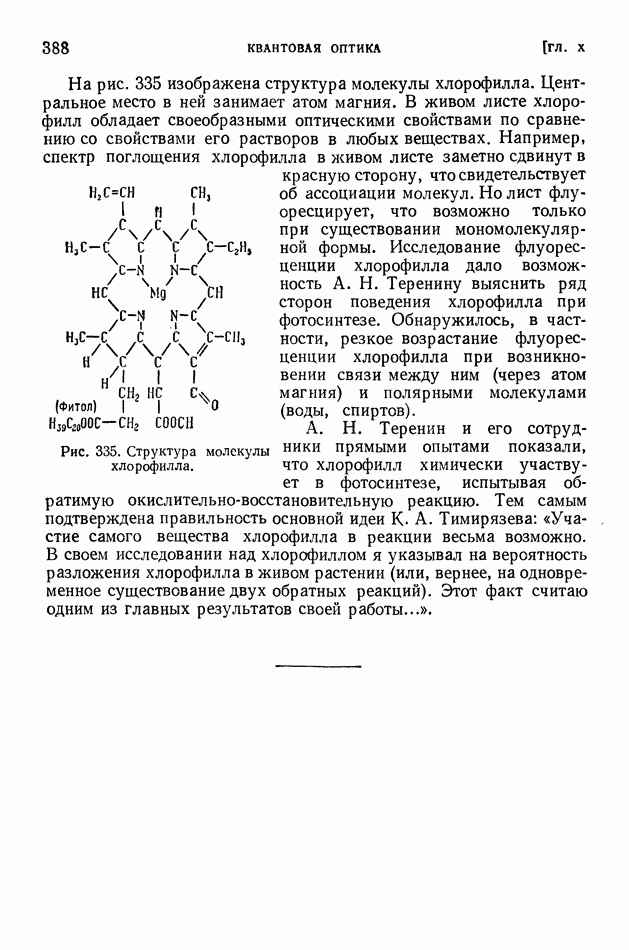
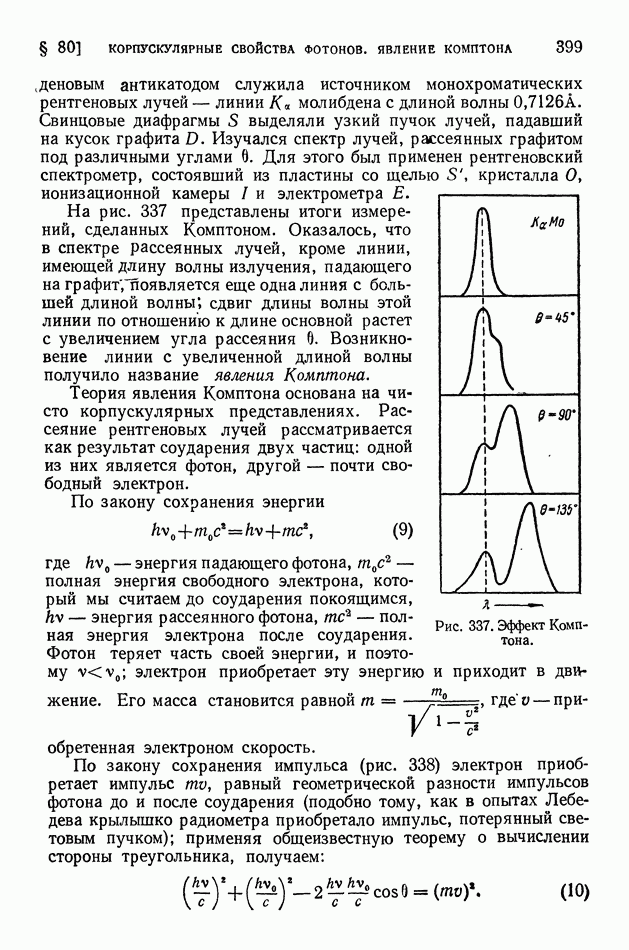
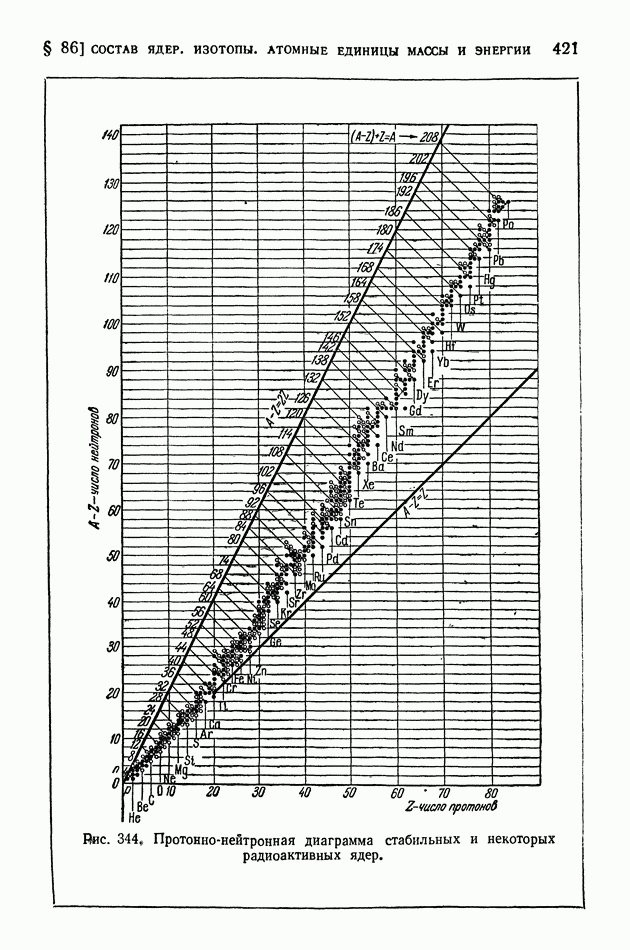
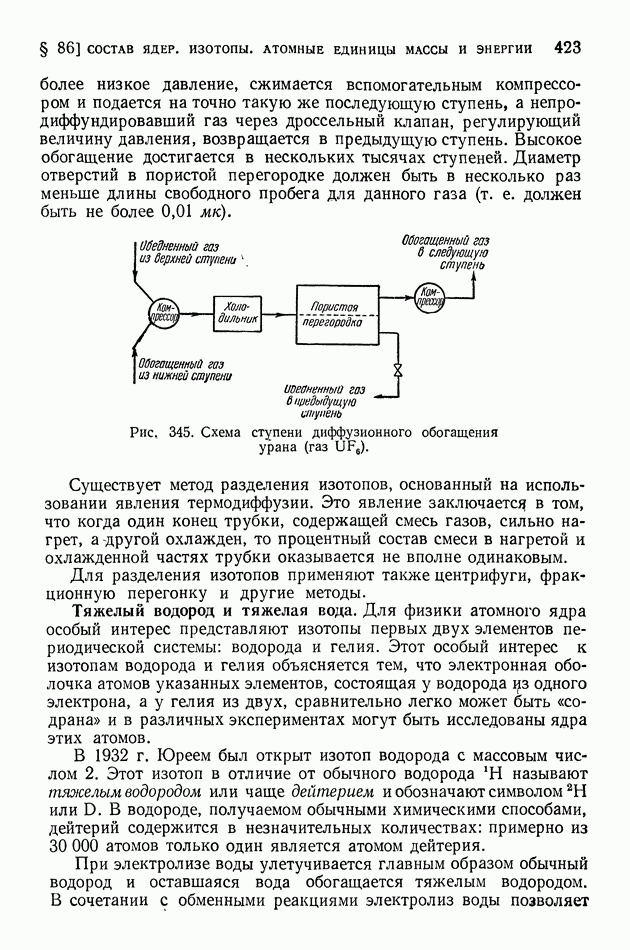
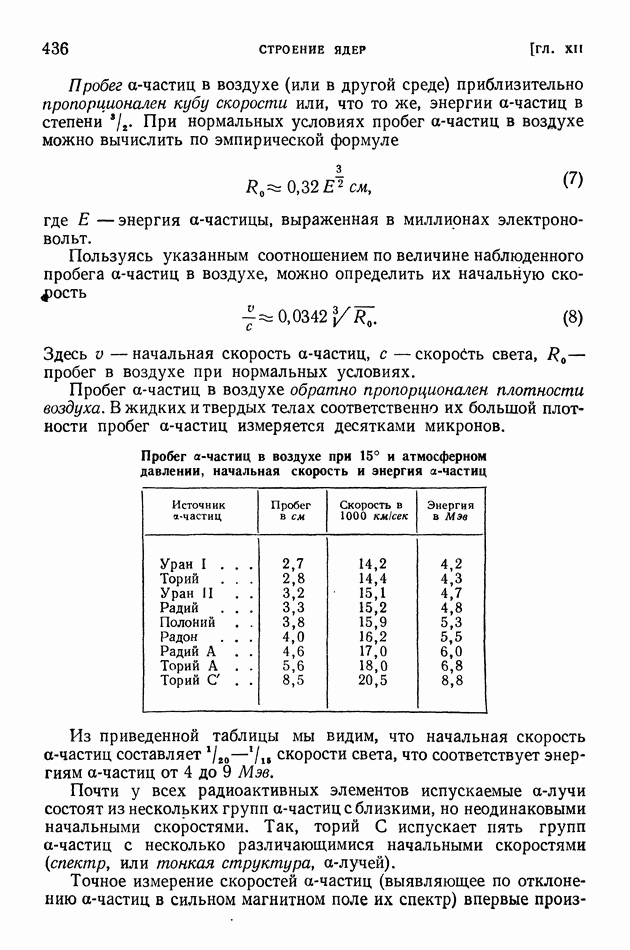
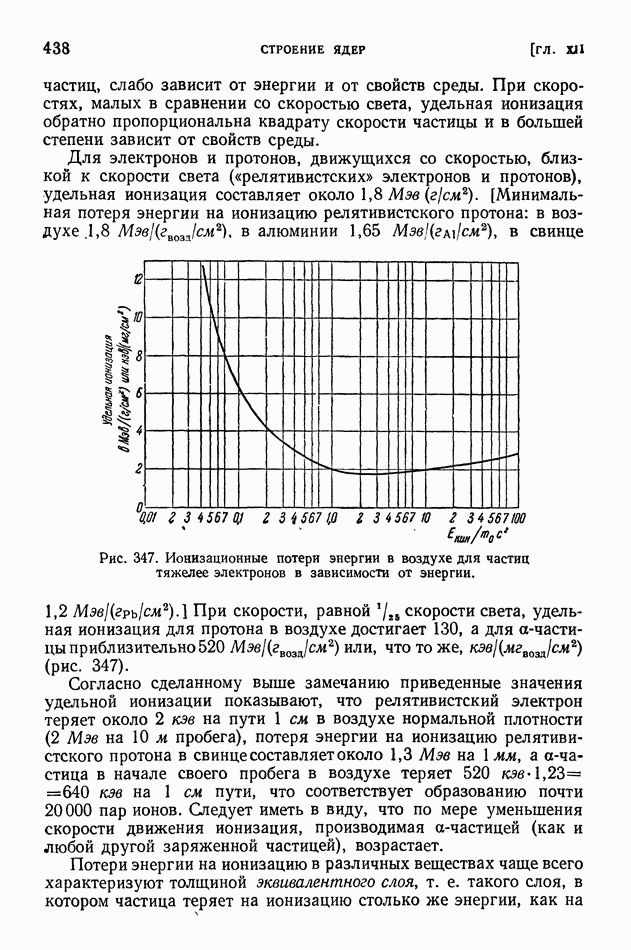
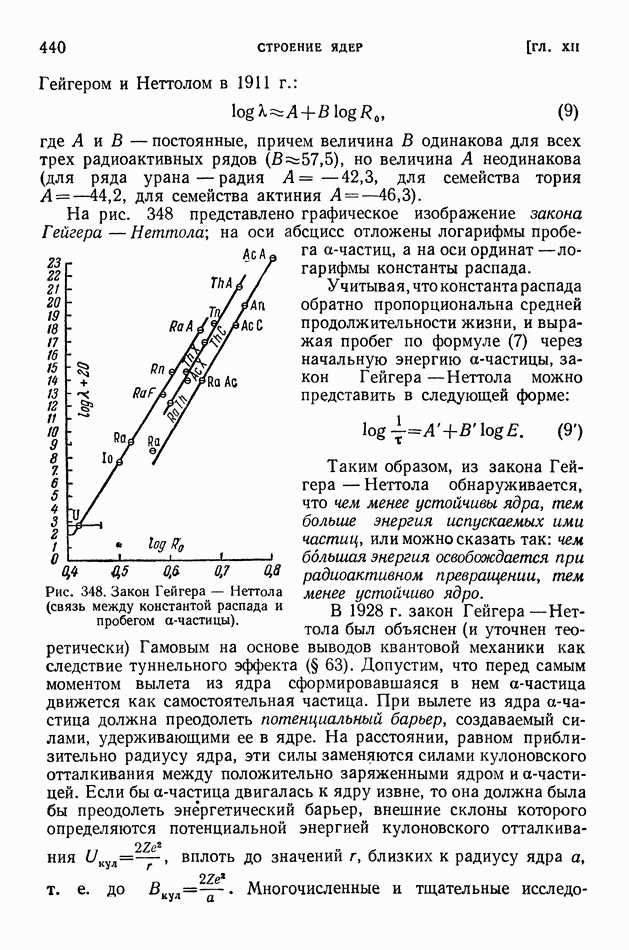
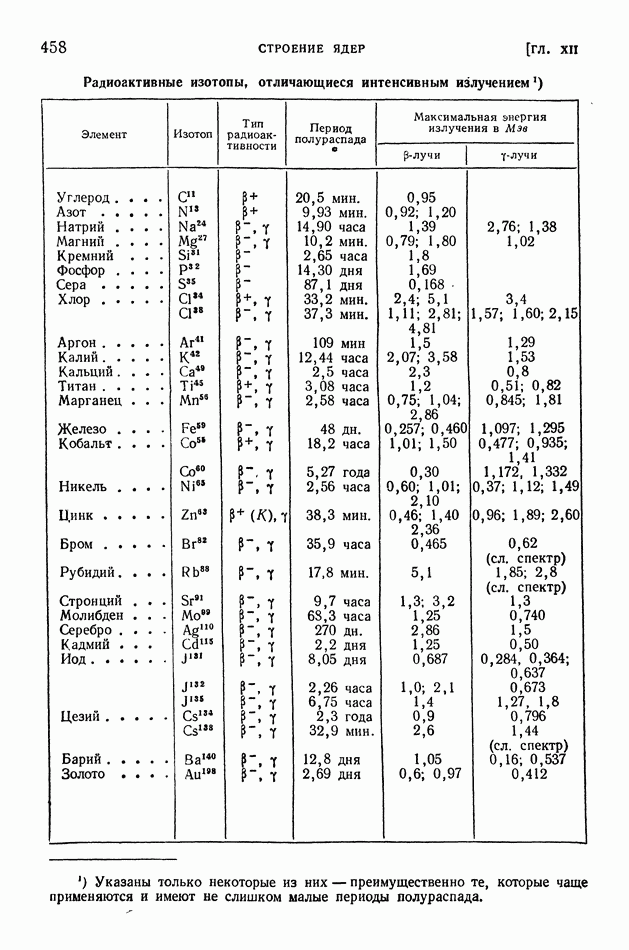
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 84. Влияние гравитационного поля на скорость света в вакууме и показатель преломления вакуума
Скорость света с, квадрат которой является коэффициентом пропорциональности в законе  (при обеих указанных выше трактовках этого закона) и которая входит во все предыдущие уравнения этой главы, представляет собой скорость распространения энергии электромагнитного излучения в вакууме, совпадающую с фазовой скоростью света в вакууме при исчезающе малой напряженности гравитационного поля. В отличие от этой универсальной константы фазовая скорость света в вакууме при наличии гравитационного поля не является строго постоянной величиной, но несколько уменьшается при возрастании гравитационного потенциала. Для вывода зависимости фазовой скорости света и показателя преломления вакуума от гравитационного потенциала рассмотрим парадокс равновесия лучистой энергии в поле тяжести.
(при обеих указанных выше трактовках этого закона) и которая входит во все предыдущие уравнения этой главы, представляет собой скорость распространения энергии электромагнитного излучения в вакууме, совпадающую с фазовой скоростью света в вакууме при исчезающе малой напряженности гравитационного поля. В отличие от этой универсальной константы фазовая скорость света в вакууме при наличии гравитационного поля не является строго постоянной величиной, но несколько уменьшается при возрастании гравитационного потенциала. Для вывода зависимости фазовой скорости света и показателя преломления вакуума от гравитационного потенциала рассмотрим парадокс равновесия лучистой энергии в поле тяжести.
Представим себе, что внутри высокого закрытого сверху и снизу цилиндра с непроницаемыми для тепла стенками, расположенного вертикально в гравитационном поле, содержится равновесное (черное) излучение при температуре  По закону пропорциональности энергии и массы излучение обладает массой, а
По закону пропорциональности энергии и массы излучение обладает массой, а
следовательно, весом; стало быть, верхние слои излучения давят на нижние и поэтому давление и плотность излучения внизу будут больше, чем наверху
Если  высота рассматриваемого столба излучения
высота рассматриваемого столба излучения  и — средняя по вертикали плотность излучения (которую приближенно мы примем равной среднеарифметическому значению плотностей излучения в верхнем и нижнем слоях), то давление, создаваемое весом столба излучения в равновесном гравитационном поле при ускорении тяжести
и — средняя по вертикали плотность излучения (которую приближенно мы примем равной среднеарифметическому значению плотностей излучения в верхнем и нижнем слоях), то давление, создаваемое весом столба излучения в равновесном гравитационном поле при ускорении тяжести  превышение давления внизу
превышение давления внизу  над давлением наверху
над давлением наверху  равно
равно  где
где  положительная разность гравитационных потенциалов:
положительная разность гравитационных потенциалов:  т. е.
т. е.

Из уравнений Максвелла строго вытекает, что давление равновесного излучения равно одной трети плотности излучения. Следовательно,

откуда

или

Итак, вследствие весомости излучения плотность равновесного излучения в гравитационном поле в нижних слоях, несомненно, превышает плотность излучения в верхних слоях и отношение  определяется формулой
определяется формулой  Но это заключение находится в обманчивом противоречии с законом Стефана — Больцмана
Но это заключение находится в обманчивом противоречии с законом Стефана — Больцмана  в пред. изд. § 94 и т. III, § 49), согласно которому плотность равновесного излучения пропорциональна четвертой степени абсолютной температуры, а температура при термодинамическом равновесии, понятно, одинакова для всех значений гравитационного потенциала и поэтому казалось бы, что и плотность должна быть одинаковой.
в пред. изд. § 94 и т. III, § 49), согласно которому плотность равновесного излучения пропорциональна четвертой степени абсолютной температуры, а температура при термодинамическом равновесии, понятно, одинакова для всех значений гравитационного потенциала и поэтому казалось бы, что и плотность должна быть одинаковой.
Дело в том, что при термодинамическом выводе закона Стефана — Больцмана приходится рассматривать работу расширения лучистой энергии, причем игнорируется факт весомости излучения и в связи с этим не принимается во внимание работа против силы тяжести. Поэтому упускается из виду, что коэффициент пропорциональности в законе Стефана — Больцмана  зависит от гравитационного потенциала. Закон Стефана — Больцмана можно вывести также, интегрируя уравнение Планка (§ 49) по всем длинам волн при
зависит от гравитационного потенциала. Закон Стефана — Больцмана можно вывести также, интегрируя уравнение Планка (§ 49) по всем длинам волн при  Тогда для константы закона Стефана — Больцмана получается нижеследующее выражение, содержащее фазовую скорость света с:
Тогда для константы закона Стефана — Больцмана получается нижеследующее выражение, содержащее фазовую скорость света с:

где  (здесь
(здесь  постоянная Больцмана и
постоянная Больцмана и  постоянная Планка).
постоянная Планка).
Из указанного выражения коэффициента пропорциональности а в законе Стефана — Больцмана следует, что при рассмотренном нами равновесии черного
излучения в фавитационном поле, вследствие несомненного равенства температур, плотности излучения в нижнем и верхнем слоях должны быть обратно пропорциональны кубу отношения фазовых скоростей света:

Это уравнение согласуется с уравнением  только в том случае, если признать, что фазовая скорость света
только в том случае, если признать, что фазовая скорость света  уменьшается под влиянием гравитационного поля Из
уменьшается под влиянием гравитационного поля Из  и
и  получаем:
получаем:

или

Вводя показатели преломления вакуума в гравитационном поле  , предыдущую формулу можно переписать так:
, предыдущую формулу можно переписать так:

Уравнение (25), если в нем положить  и соответственно 1, показывает, что превышение показателя преломления вакуума над единицей пропорционально гравитационному потенциалу:
и соответственно 1, показывает, что превышение показателя преломления вакуума над единицей пропорционально гравитационному потенциалу:  Вблизи поверхности Солнца показатель преломления вакуума имеет величину 1,00000424.
Вблизи поверхности Солнца показатель преломления вакуума имеет величину 1,00000424.
Вследствие весомости света световые лучи, посылаемые какой-либо звездой и проходящие вблизи Солнца, должны отклоняться от первоначального направления на некоторый угол, который нетрудно вычислить из условия, что момент количества движения световых частиц относительно Солнца остается постоянным. Этот угол равен  где
где  -радиус Солнца и
-радиус Солнца и  кратчайшее расстояние от центра Солнца до светового луча. Но вследствие возрастания показателя преломления вакуума при приближении к Солнцу, т. е. вследствие оптической неоднородности вакуума вблизи Солнца (напоминающей оптическую неоднородность земной атмосферы, § 14), угол отклонения лучей Солнцем оказывается, как показывают вычисления на основе формулы (25), в 2 раза большим и равным
кратчайшее расстояние от центра Солнца до светового луча. Но вследствие возрастания показателя преломления вакуума при приближении к Солнцу, т. е. вследствие оптической неоднородности вакуума вблизи Солнца (напоминающей оптическую неоднородность земной атмосферы, § 14), угол отклонения лучей Солнцем оказывается, как показывают вычисления на основе формулы (25), в 2 раза большим и равным 
Отклонение лучей в гравитационном поле, предсказанное теоретически Эйнштейном в 1915 г., было подтверждено наблюдениями, сделанными в  и последующих годах при полных солнечных затмениях.
и последующих годах при полных солнечных затмениях.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ЧАСТЬ ЧЕТВЕРТАЯ. ОПТИКА
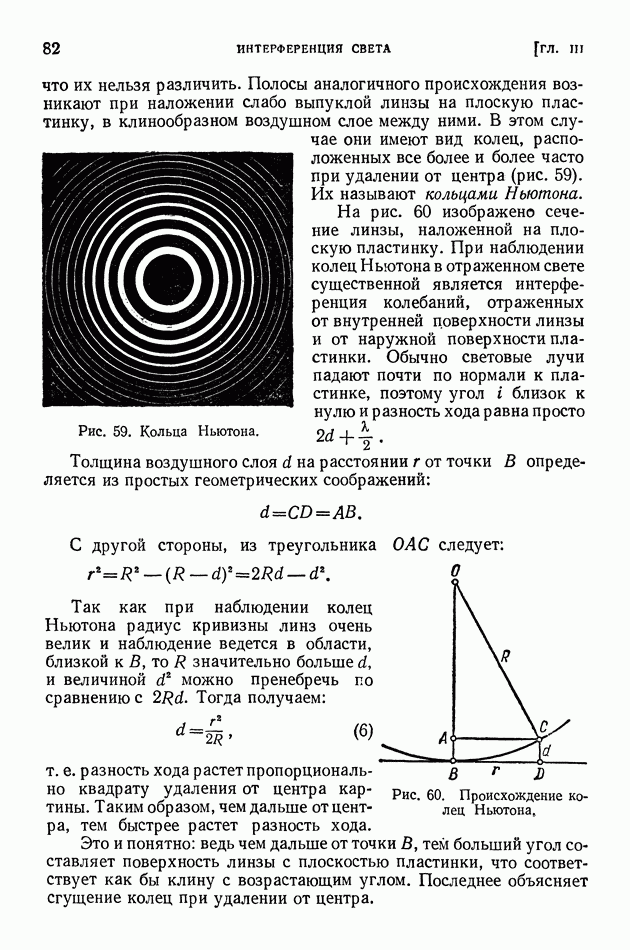
- § 2. Электромагнитная теория света
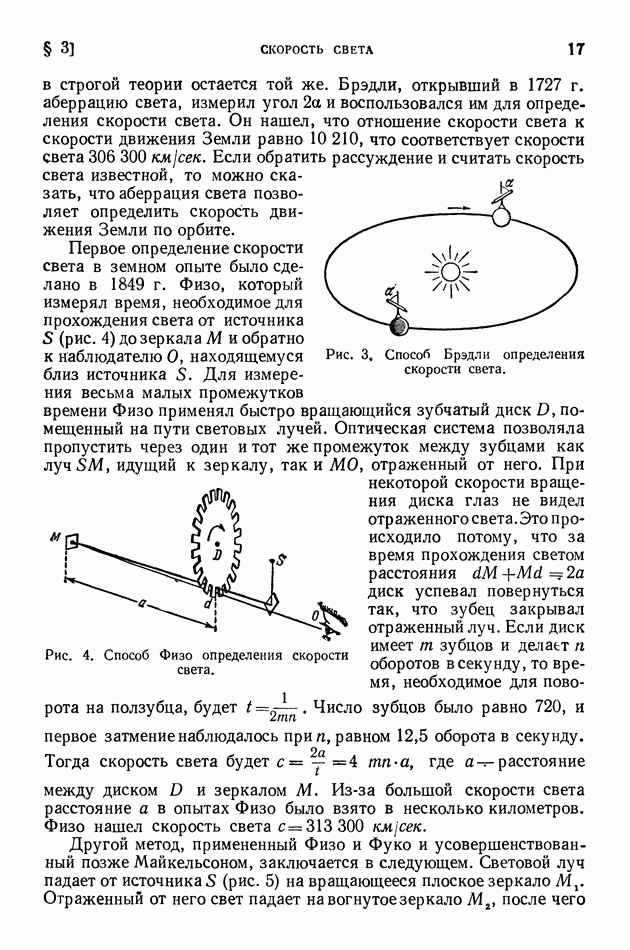
- § 3. Скорость света
- § 4. Опыт Майкельсона
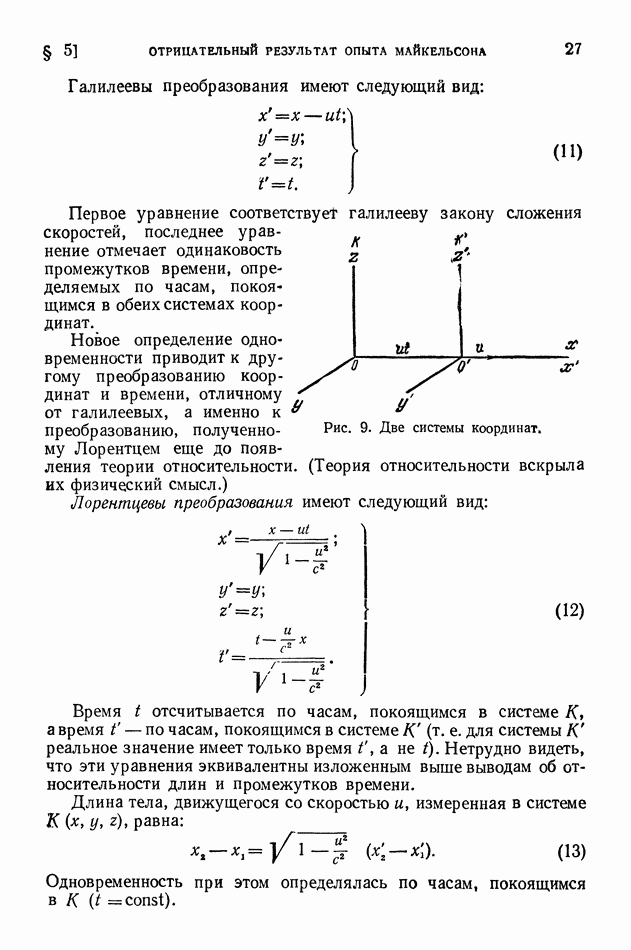
- § 5. Отрицательный результат опыта Майкельсона и теория относительности
- § 6. Некоторые замечания о теории относительности
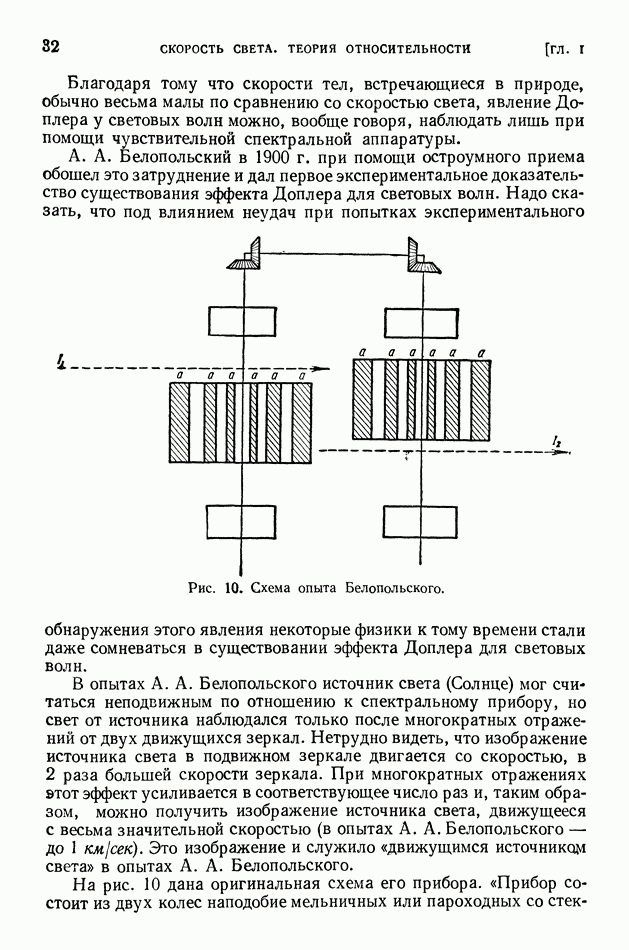
- § 7. Явление Доплера для световых волн
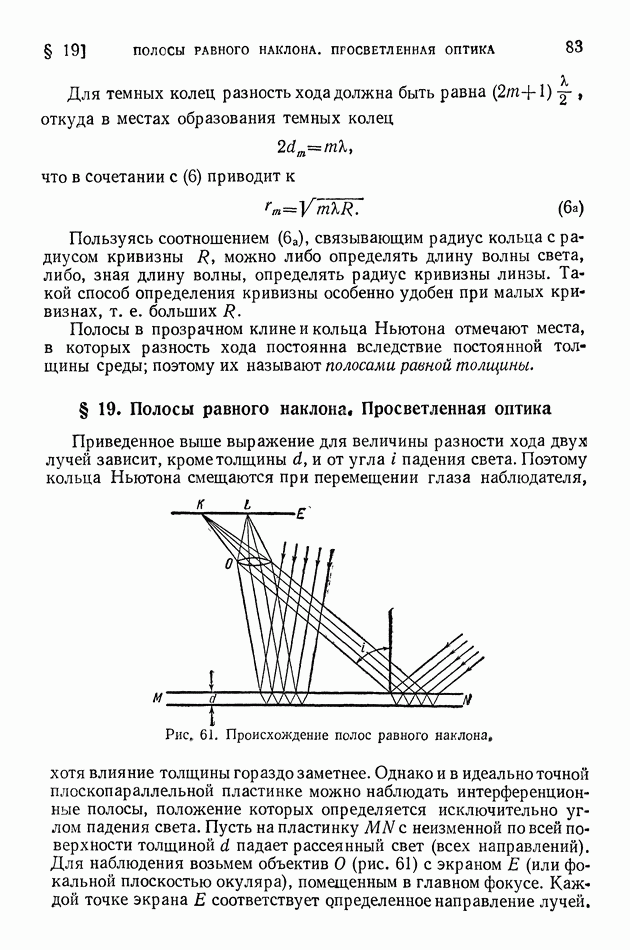
- ГЛАВА II. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
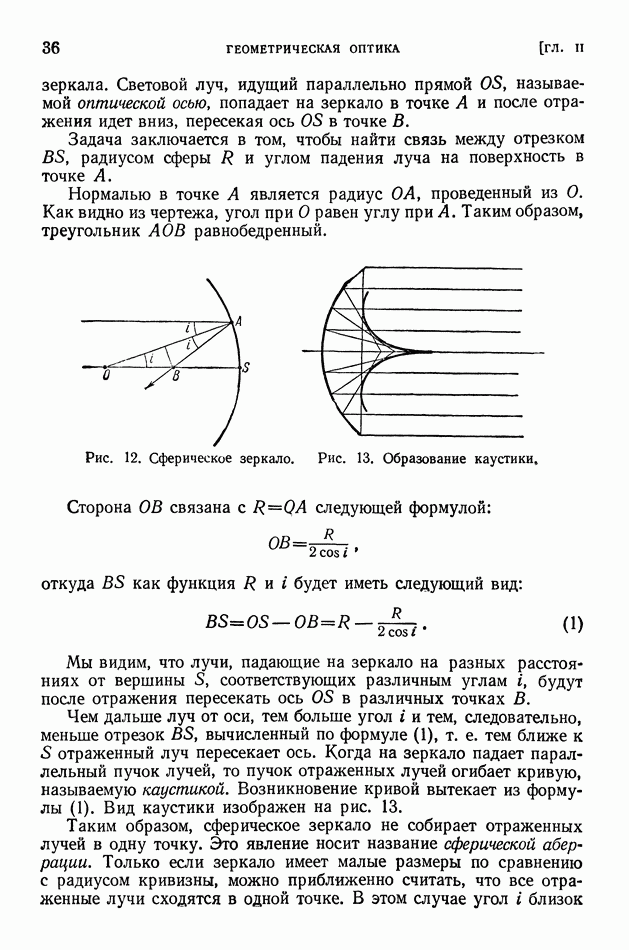
- § 8. Законы отражения и преломления света
- § 9. Линза
- § 10. Оптические системы
- § 11. Глаз как оптическая система
- § 12. Приборы, вооружающие глаз
- § 13. Фотоаппарат и проекционный аппарат
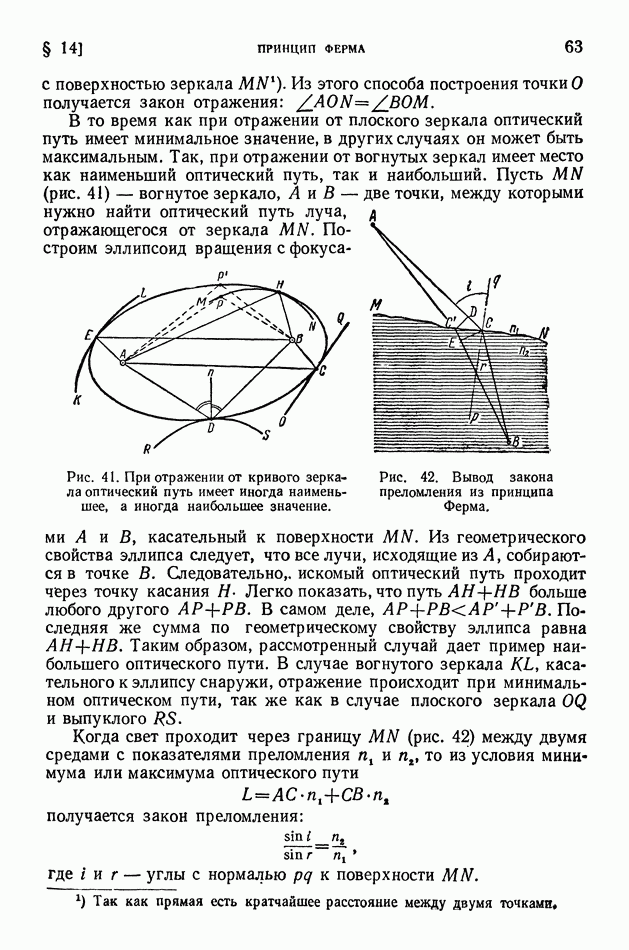
- § 14. Принцип Ферма
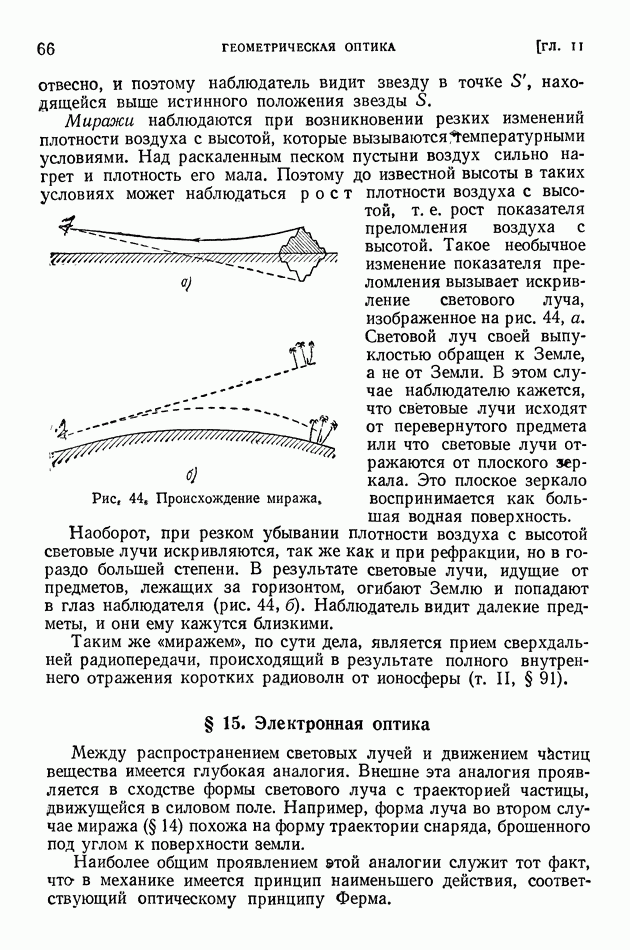
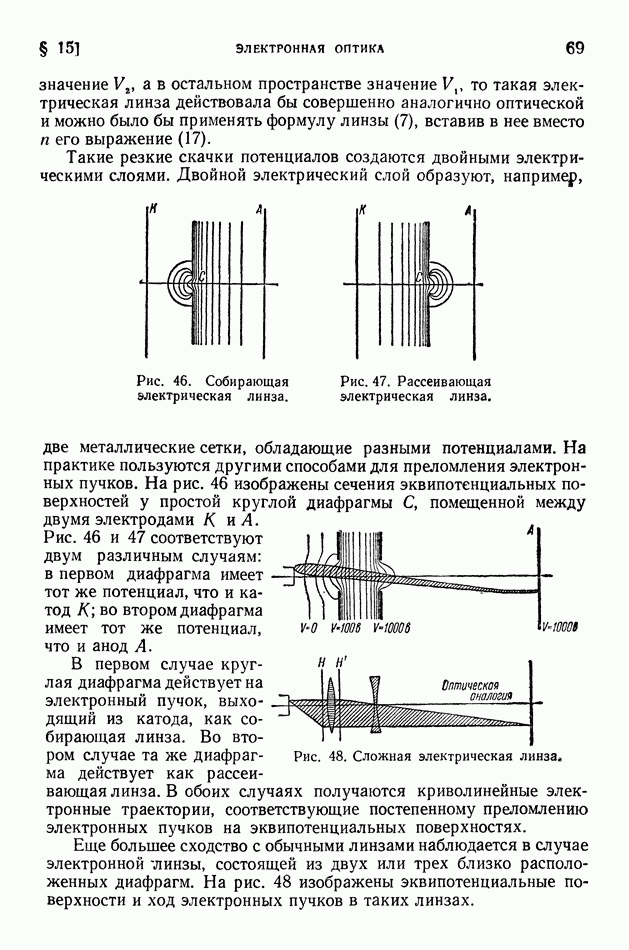
- § 15. Электронная оптика
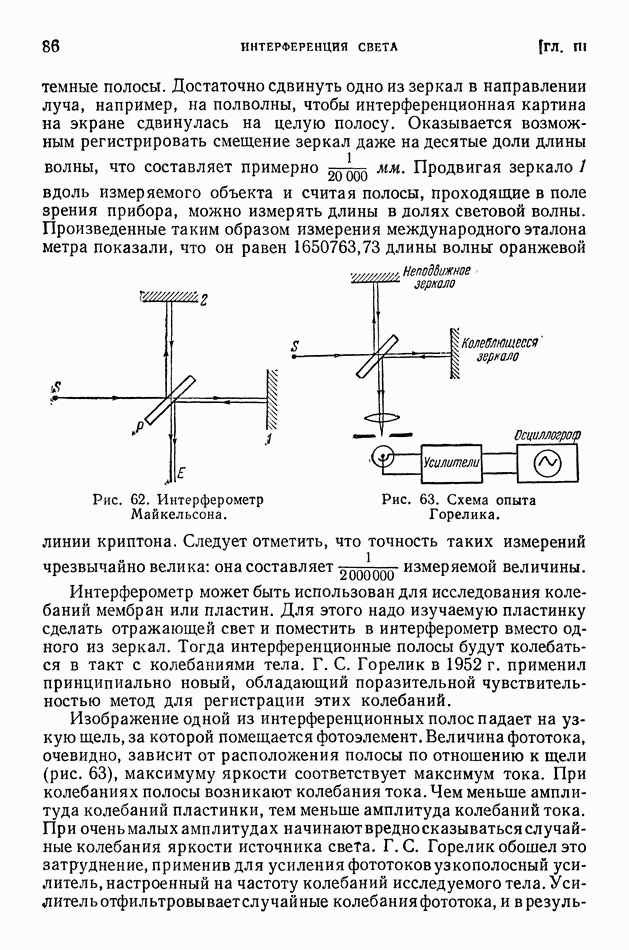
- ГЛАВА III. ИНТЕРФЕРЕНЦИЯ СВЕТА
- § 16. Принцип суперпозиции. Когерентность
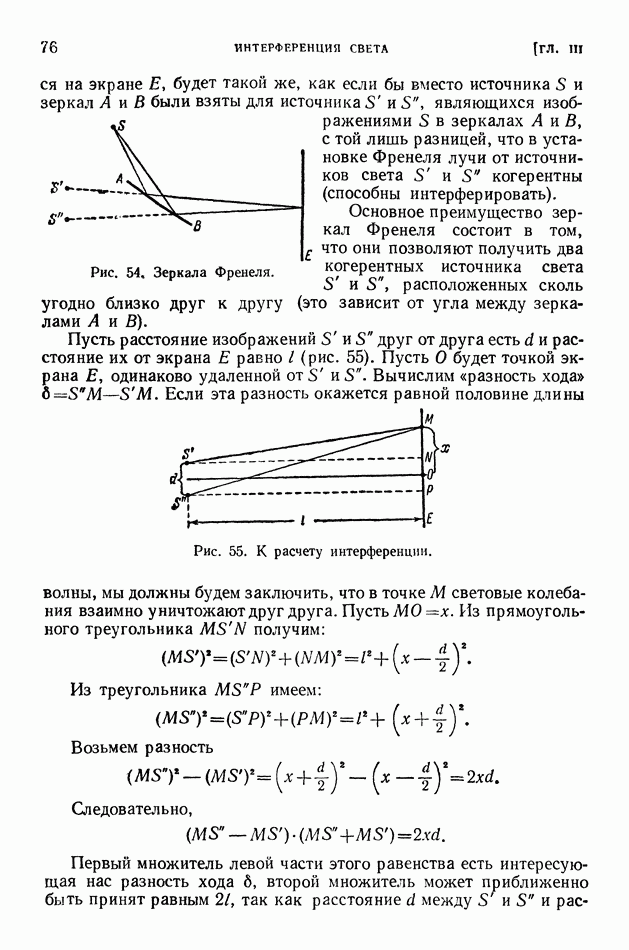
- § 17. Зеркала Френеля
- § 18. Цвета тонких пленок. Полосы равной толщины
- § 19. Полосы равного наклона. Просветленная оптика
- § 20. Интерферометры
- § 21. Интерференционное измерение технических мер длины
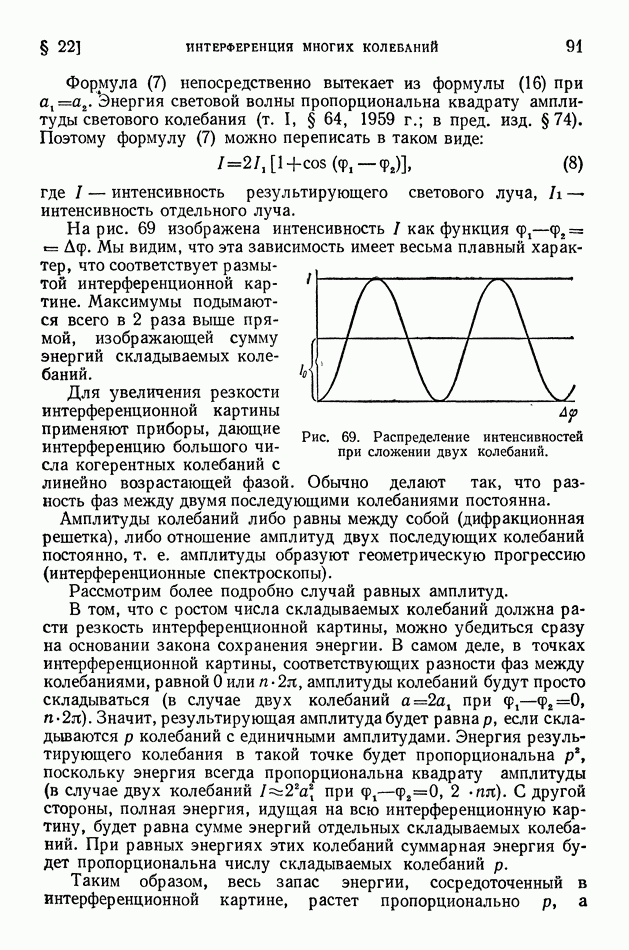
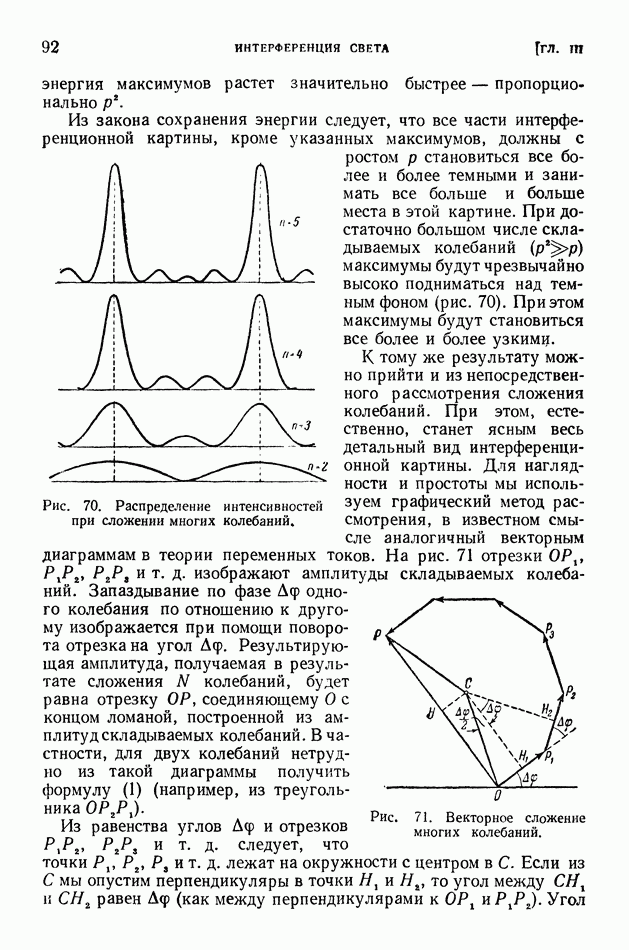
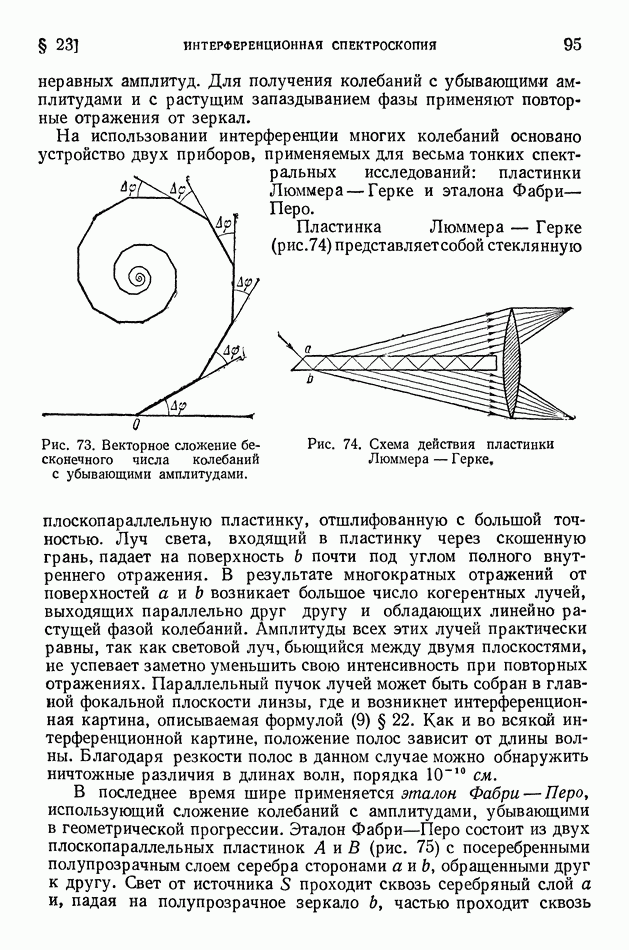
- § 22. Интерференция многих колебаний
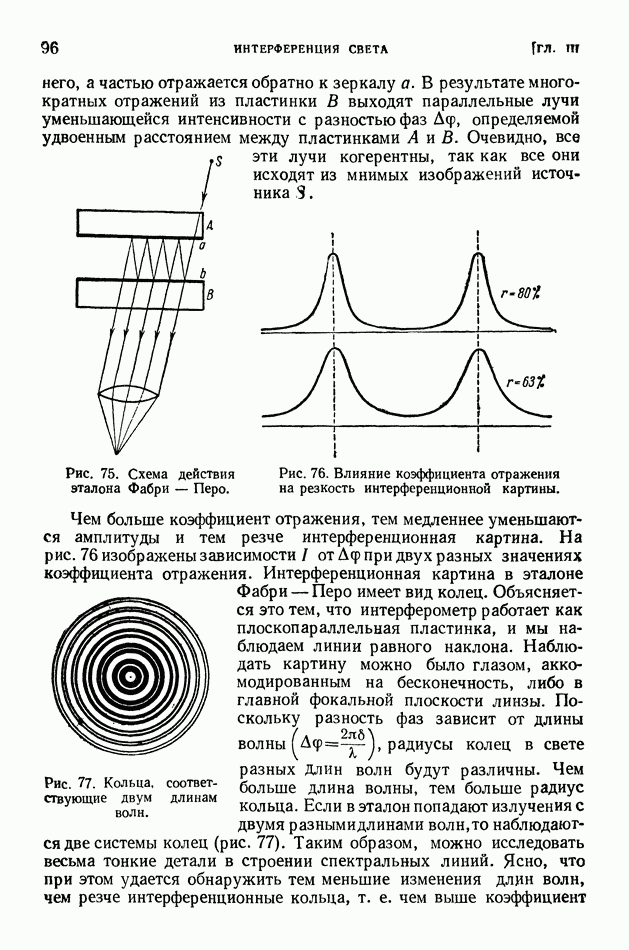
- § 23. Интерференционная спектроскопия
- ГЛАВА IV. ДИФРАКЦИЯ СВЕТА
- § 24. Явление дифракции. Опыт Френеля
- § 25. Принцип Гюйгенса-Френеля
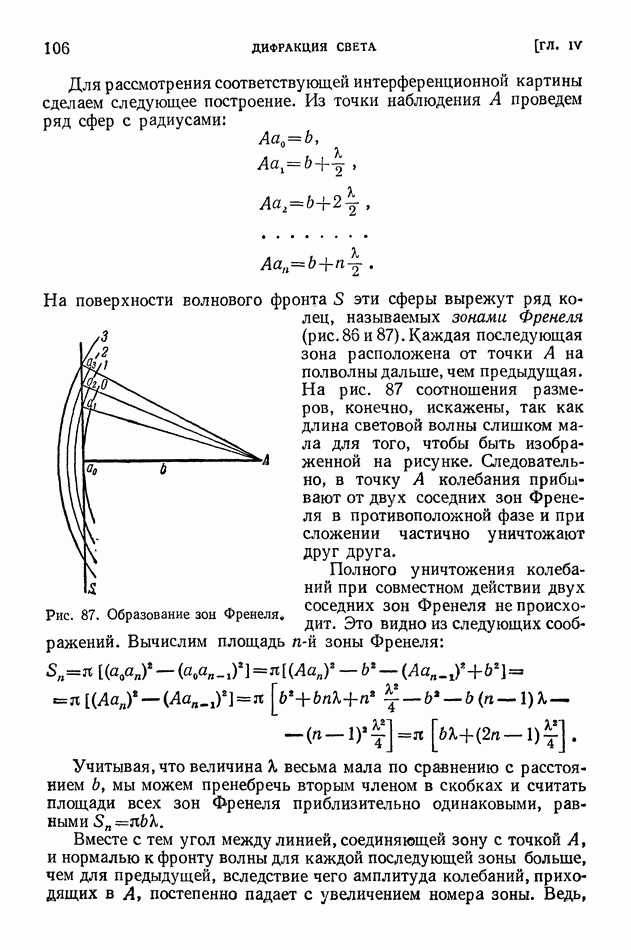
- § 26. Метод зон Френеля
- § 27. Дифракция от узкой щели
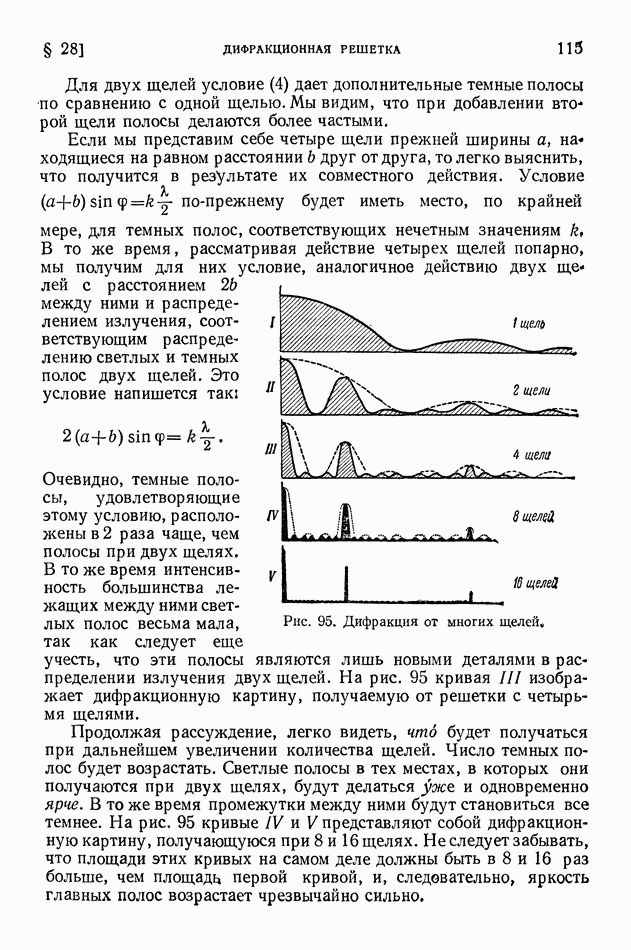
- § 28. Дифракционная решетка
- § 29. Дифракционный спектр. Решетки Роуланда и эшелон Майкельсона
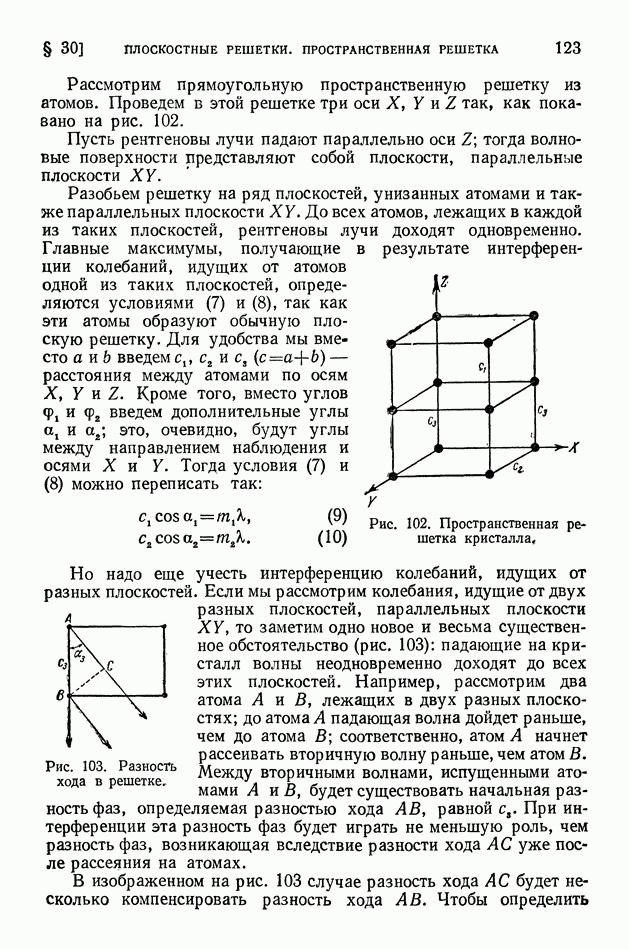
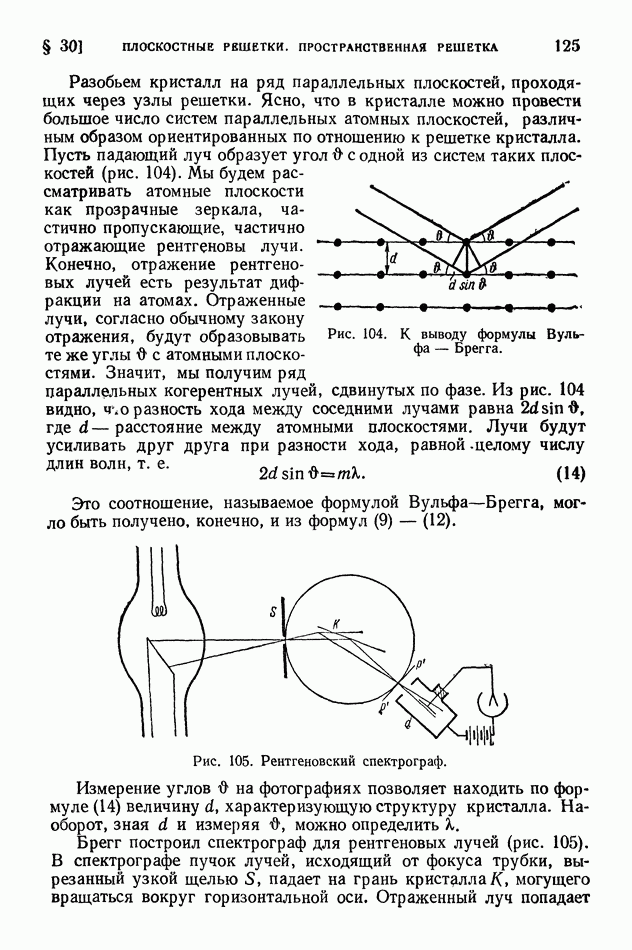
- § 30. Плоскостные решетки. Пространственная решетка
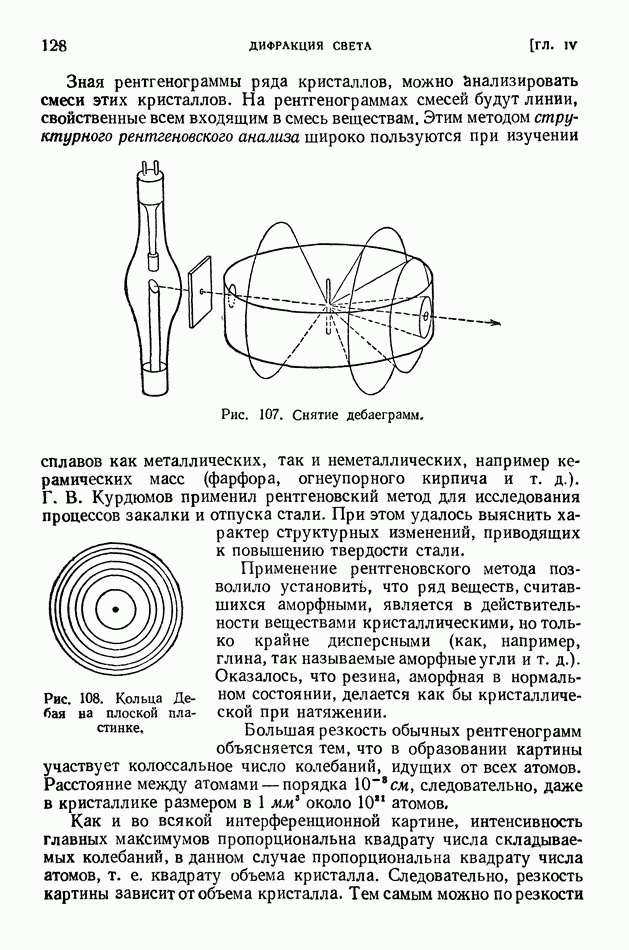
- § 31. Структурный рентгеновский анализ
- § 32. Дифракция света на ультразвуковых волнах
- § 33. Дифракция от мелких частиц
- § 34. Разрешающая способность оптических инструментов. Звездный интерферометр
- ГЛАВА V. ПОЛЯРИЗАЦИЯ СВЕТА
- § 35. Поляризация света
- § 36. Двойное лучепреломление
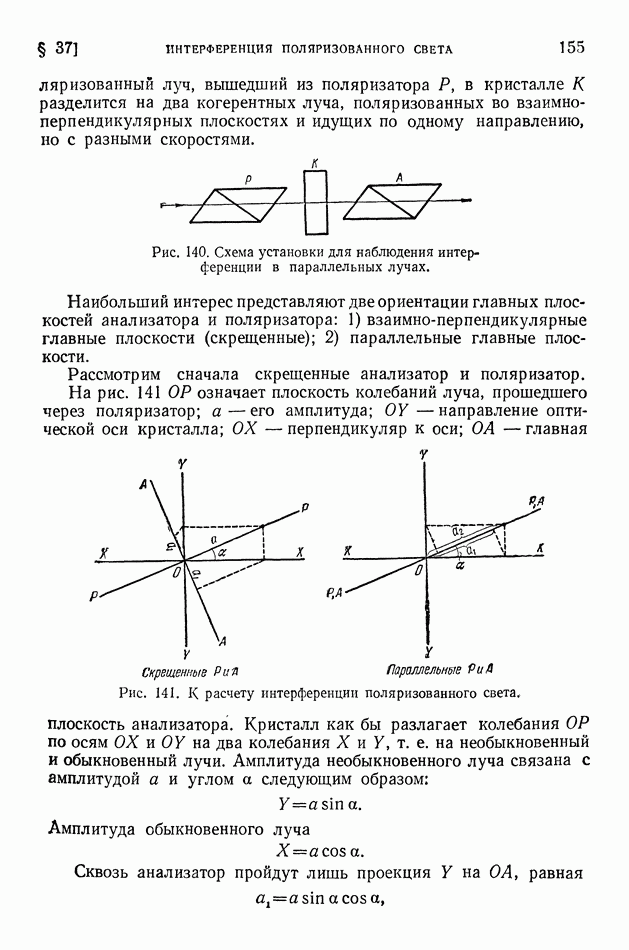
- § 37. Интерференция поляризованного света
- § 38. Оптический метод исследования упругих натяжений. Эффект Керра
- § 39. Вращение плоскости поляризации. Эллиптическая поляризация
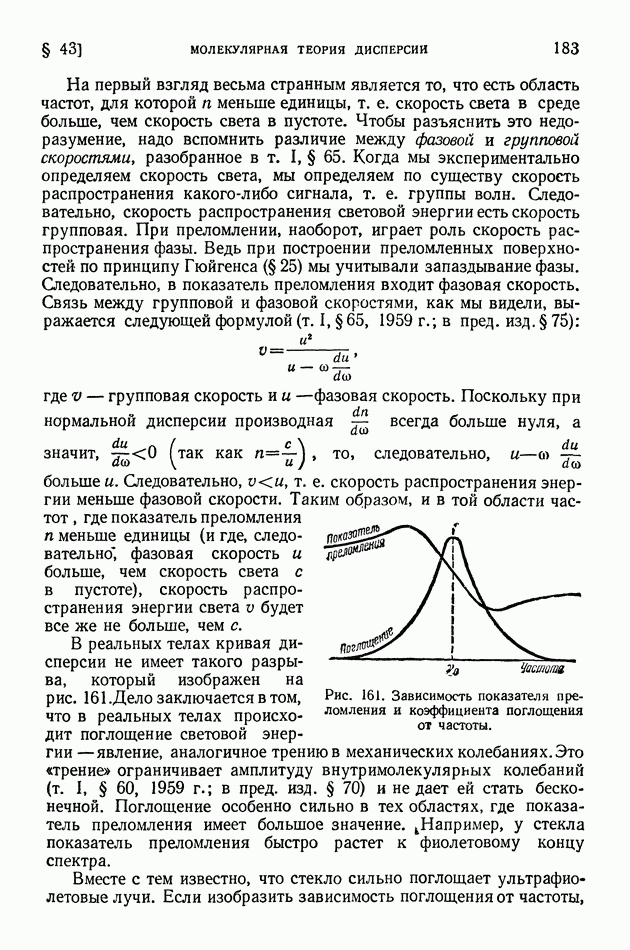
- ГЛАВА VI. ДИСПЕРСИЯ, ПОГЛОЩЕНИЕ И ИЗЛУЧЕНИЕ СВЕТА
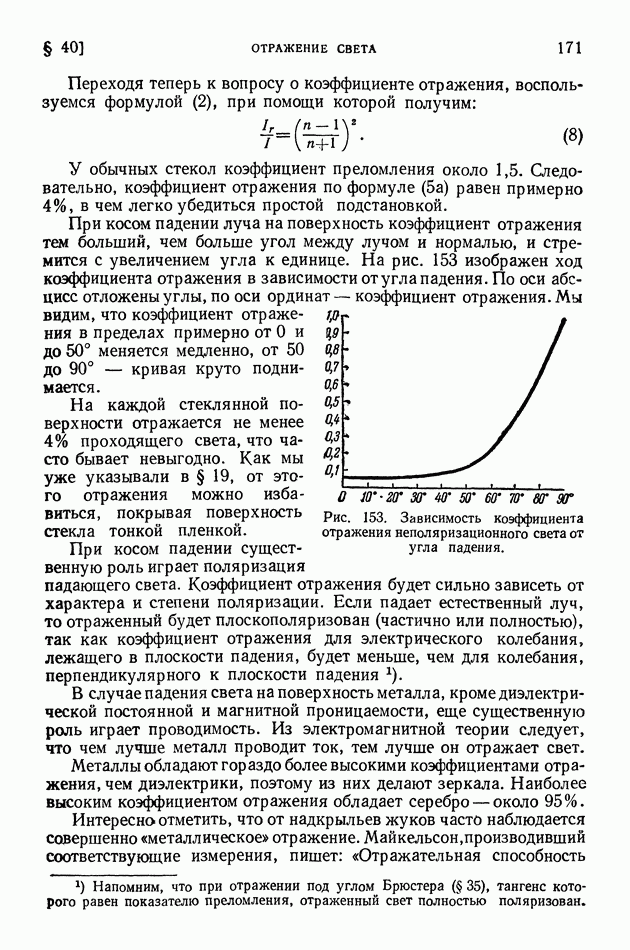
- § 40. Отражение света
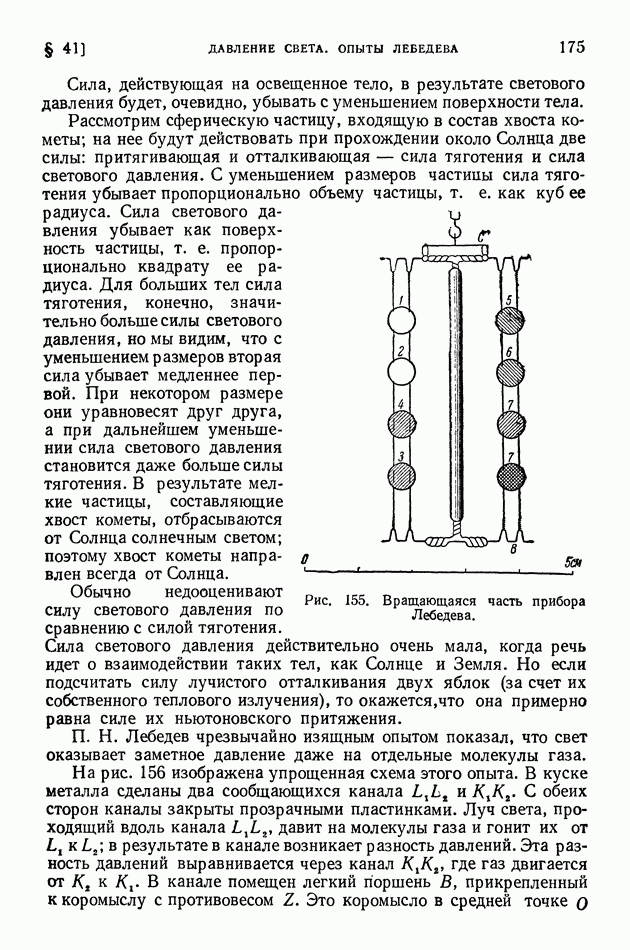
- § 41. Давление света. Опыты Лебедева
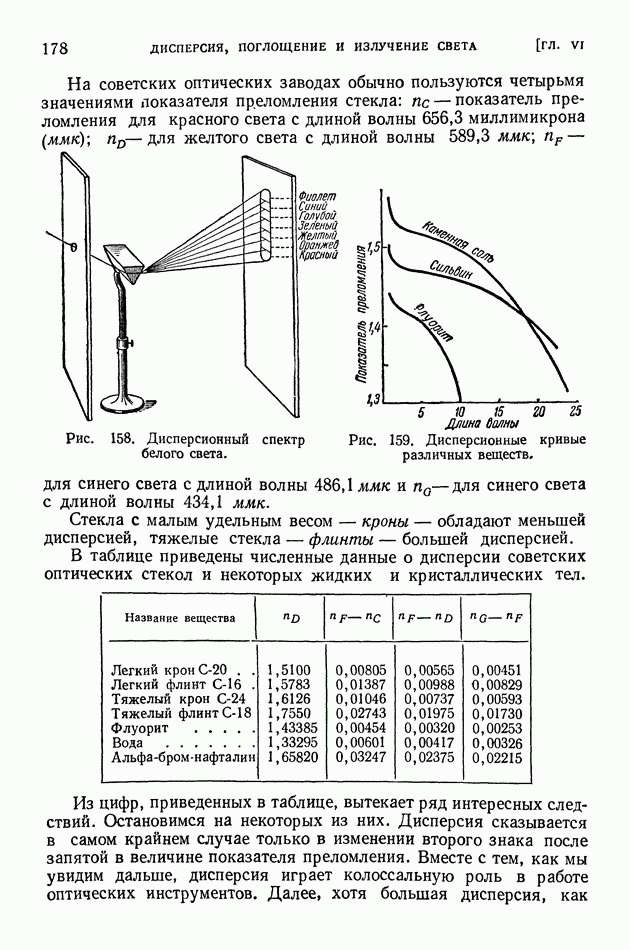
- § 42. Дисперсия. Опыты Ньютона
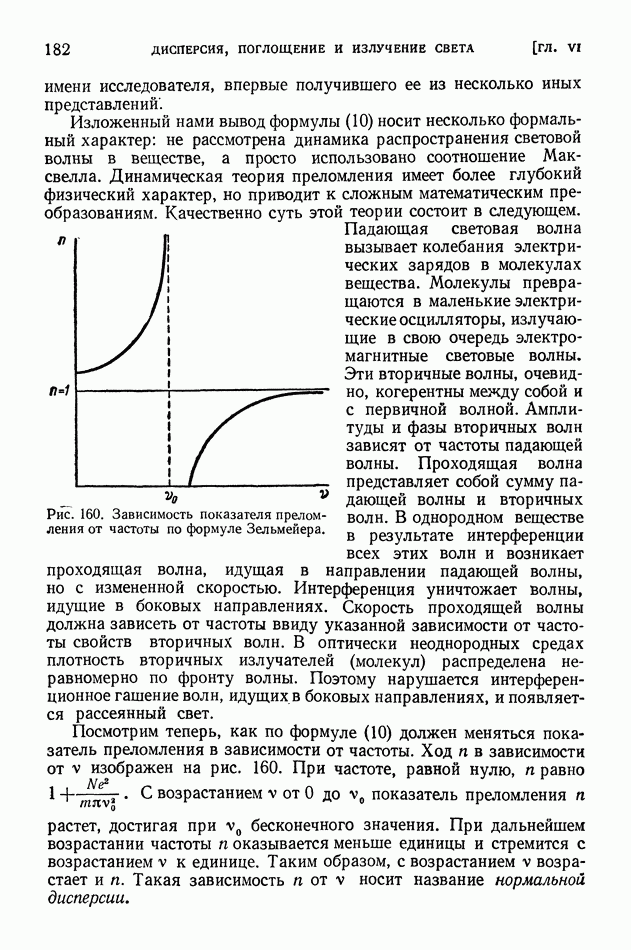
- § 43. Молекулярная теория дисперсии
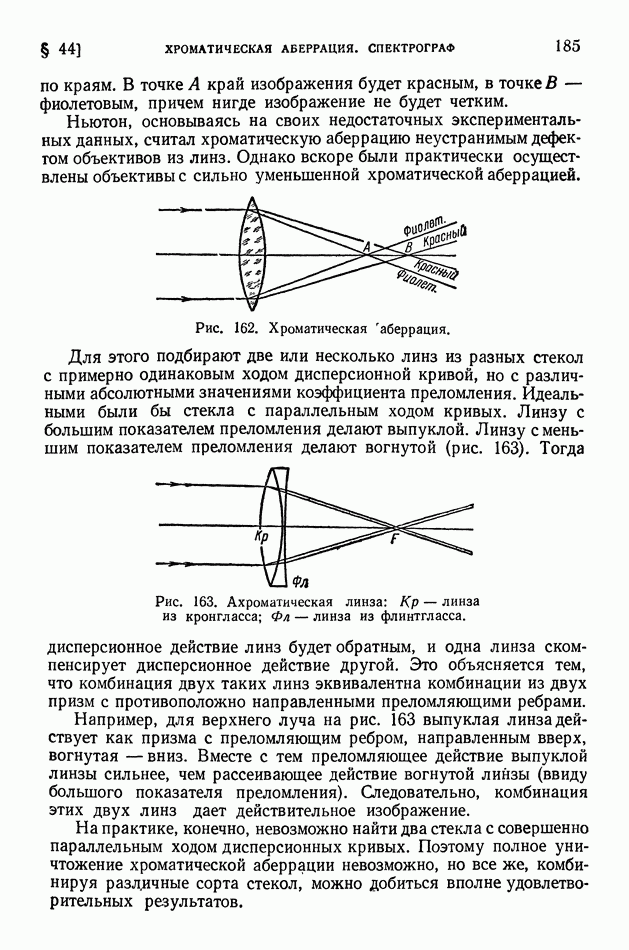
- § 44. Хроматическая аберрация. Спектрограф
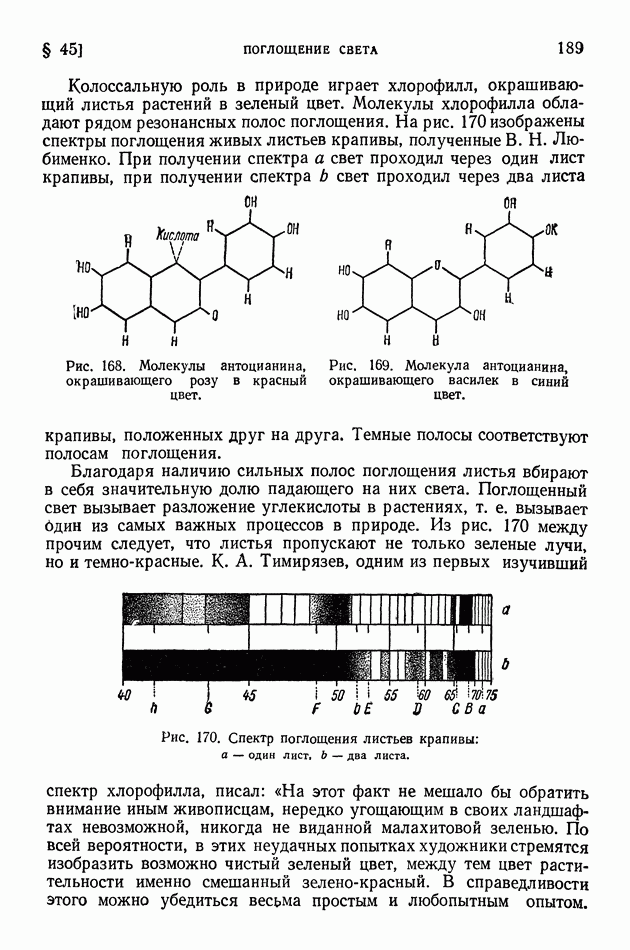
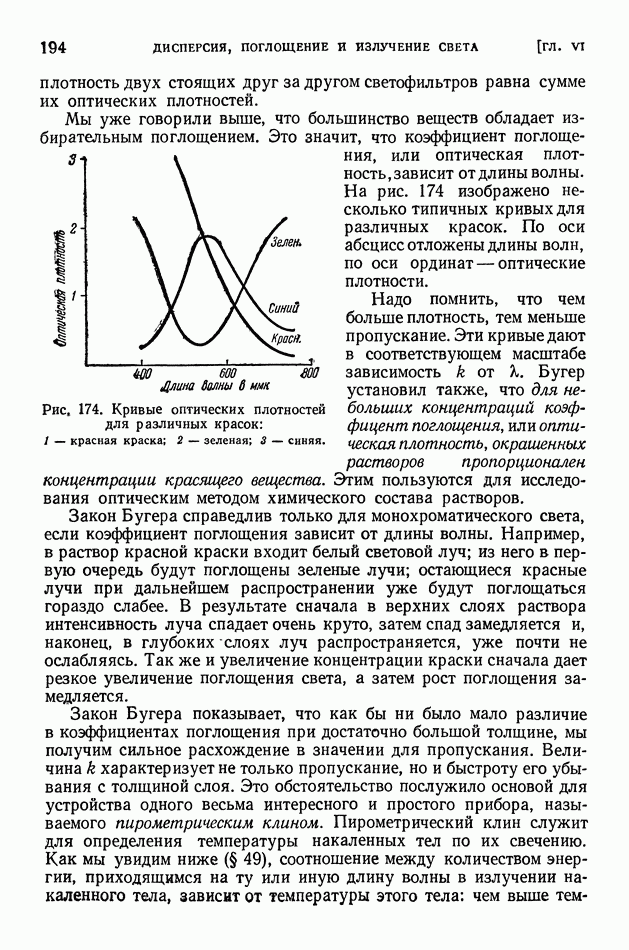
- § 45. Поглощение света
- § 46. Закон Бугера. Опыты Вавилова
- § 47. Атом как элементарный излучатель света
- § 48. Эффект Вавилова — Черенкова
- ГЛАВА VII. ТЕРМОДИНАМИКА ИЗЛУЧЕНИЯ И СВЕТОВОЙ ПОТОК
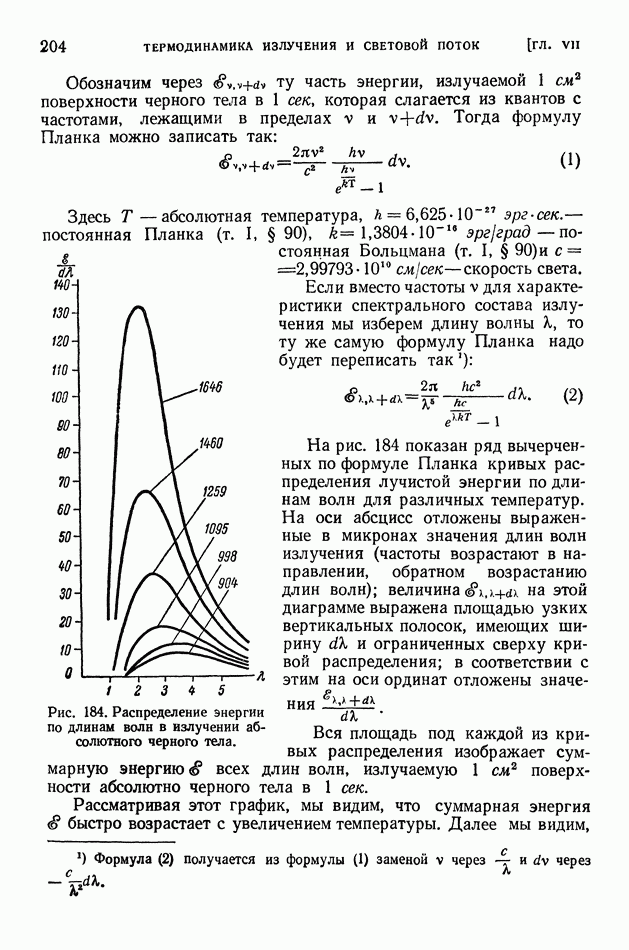
- § 49. Излучение черного тела. Формула Планка. Закон Вина
- § 50. Излучение нечерных тел. Законы Кирхгофа
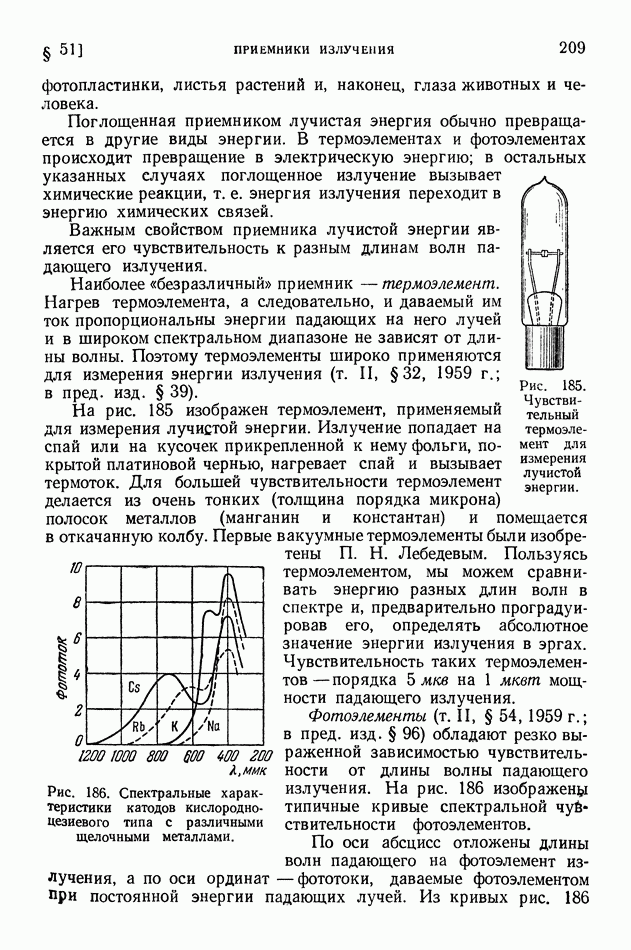
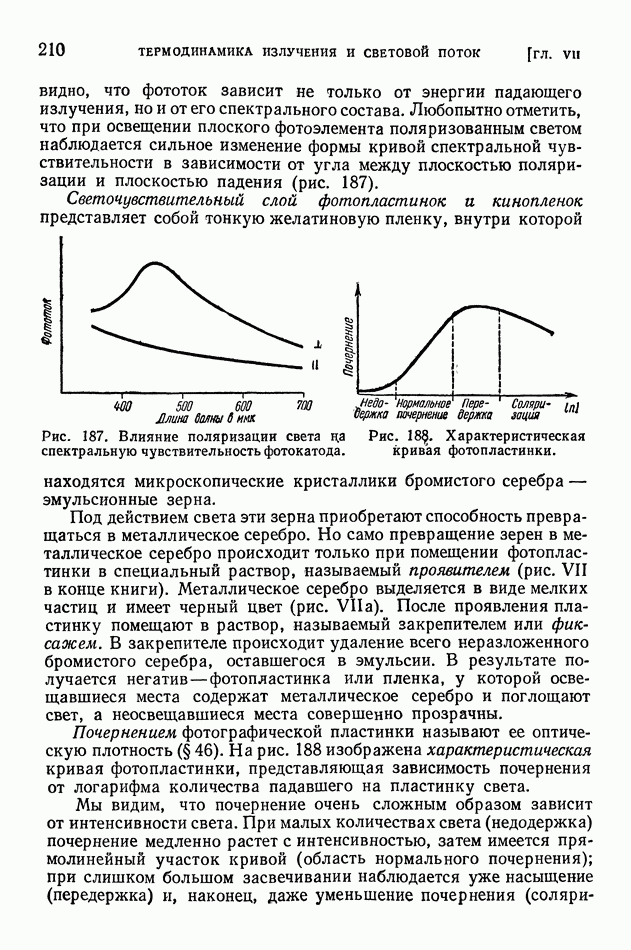
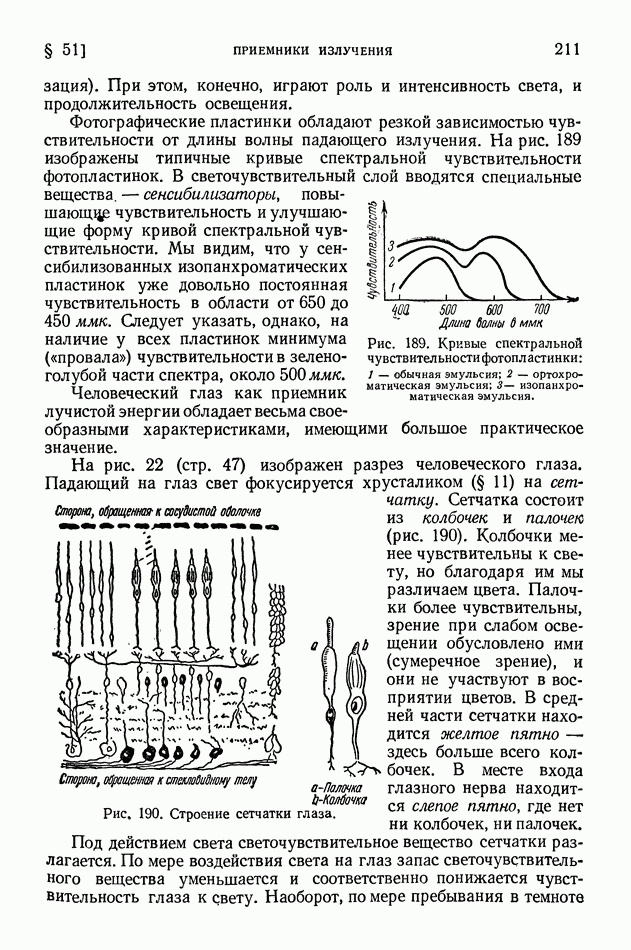
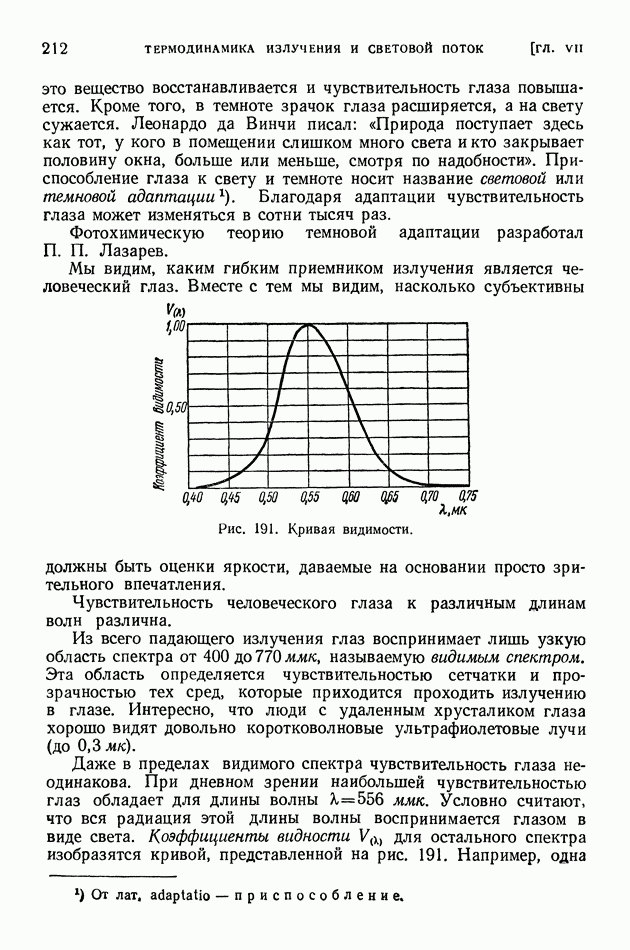
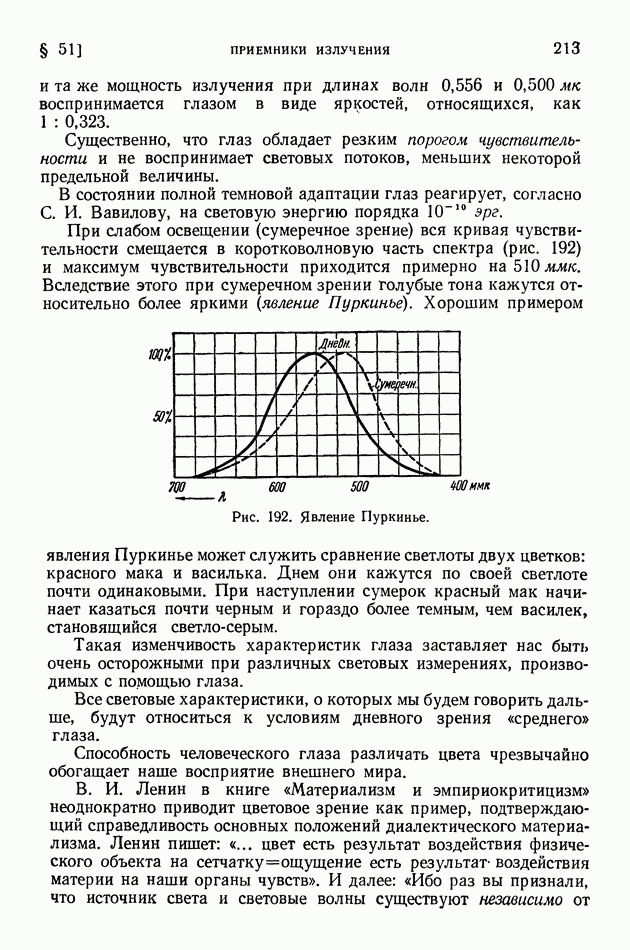
- § 51. Приемники излучения
- § 52. Световые величины и их измерения
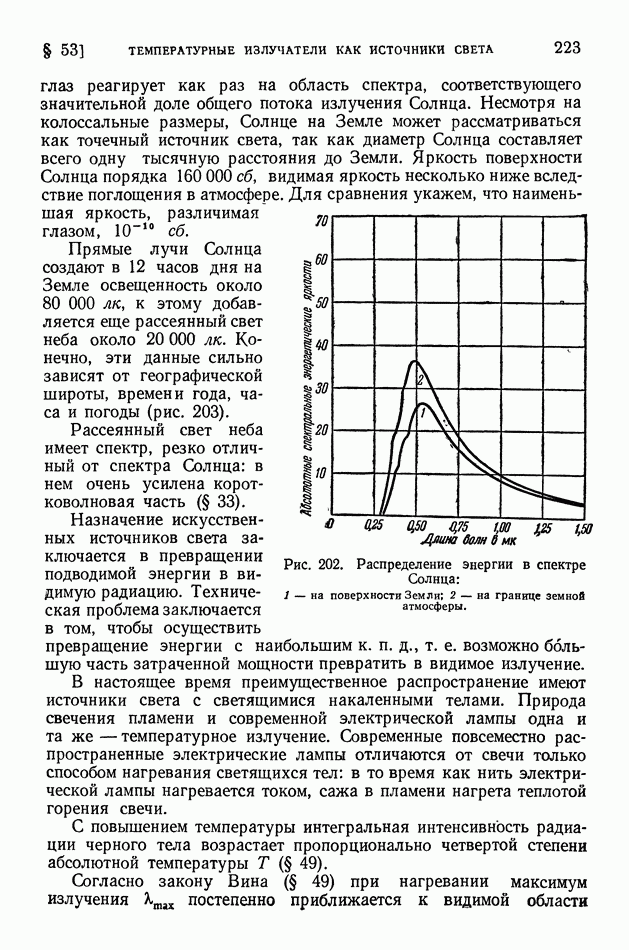
- § 53 Температурные излучатели как источники света
- ЧАСТЬ ПЯТАЯ. АТОМНАЯ ФИЗИКА
- ГЛАВА VIII. СТРОЕНИЕ АТОМА И ТЕОРИЯ БОРА
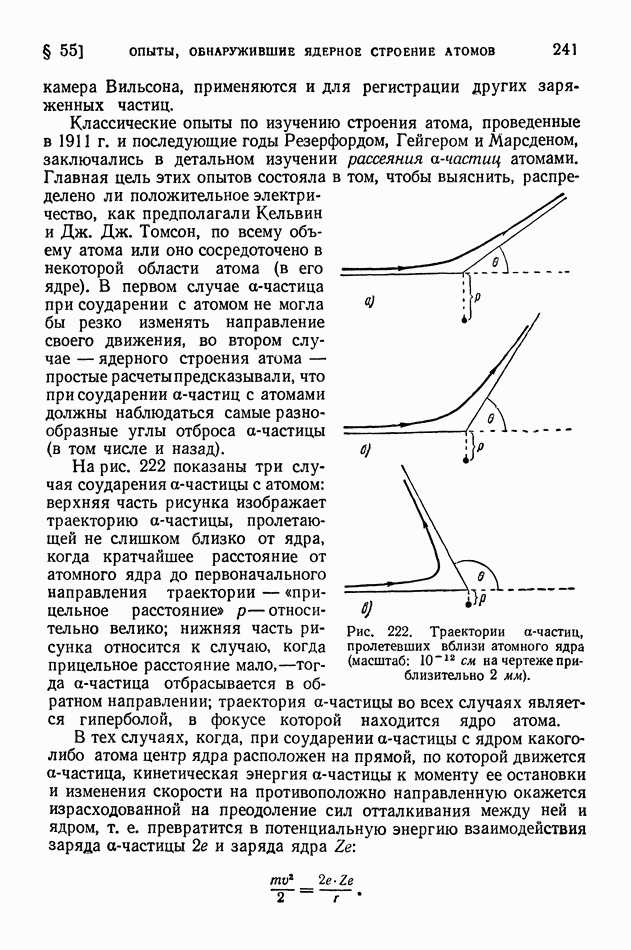
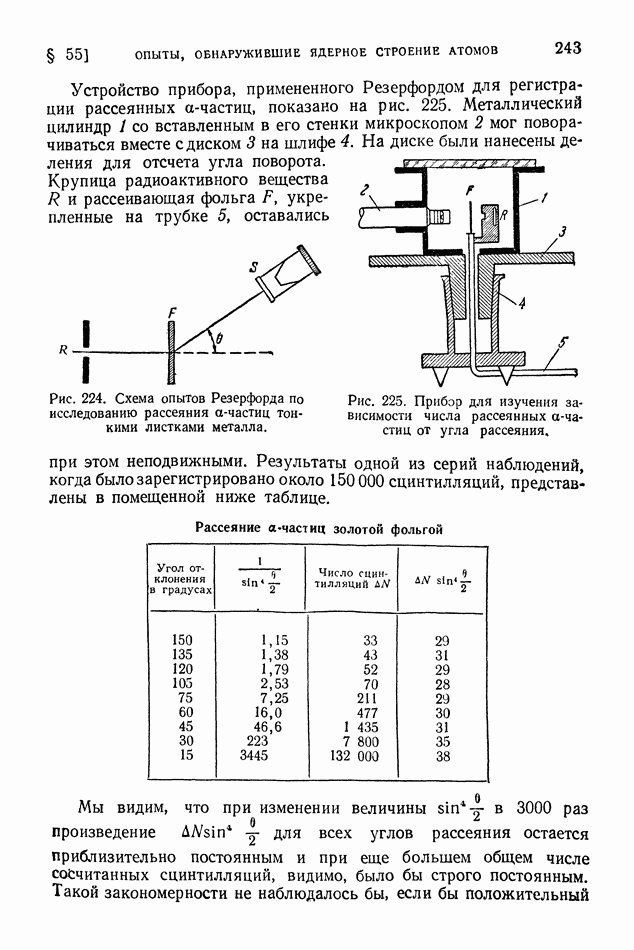
- § 55. Опыты, обнаружившие ядерное строение атомов
- § 56. Противоречие между фактическим строением атомов и выводами классической электродинамики. Строение линейчатых спектров
- § 57. Опытные основания теории квантов в первые годы ее развития
- § 58. Теория Бора. Происхождение спектра водорода
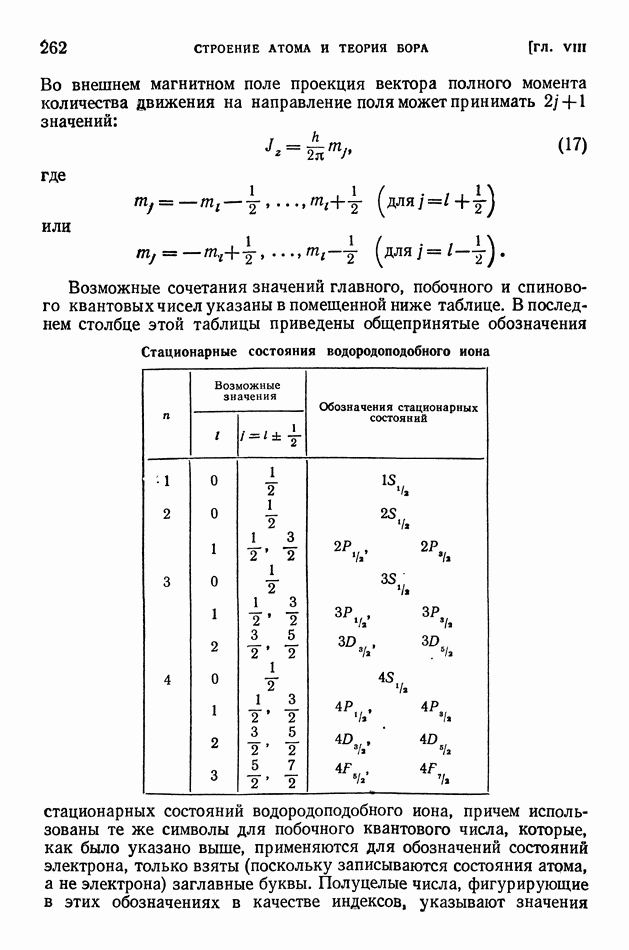
- § 59. Квантовые числа
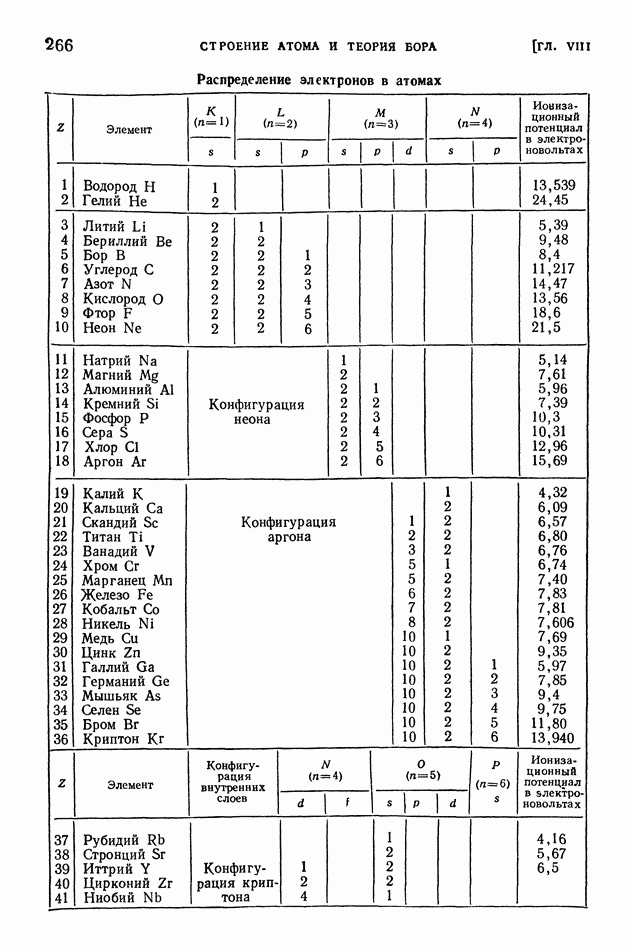
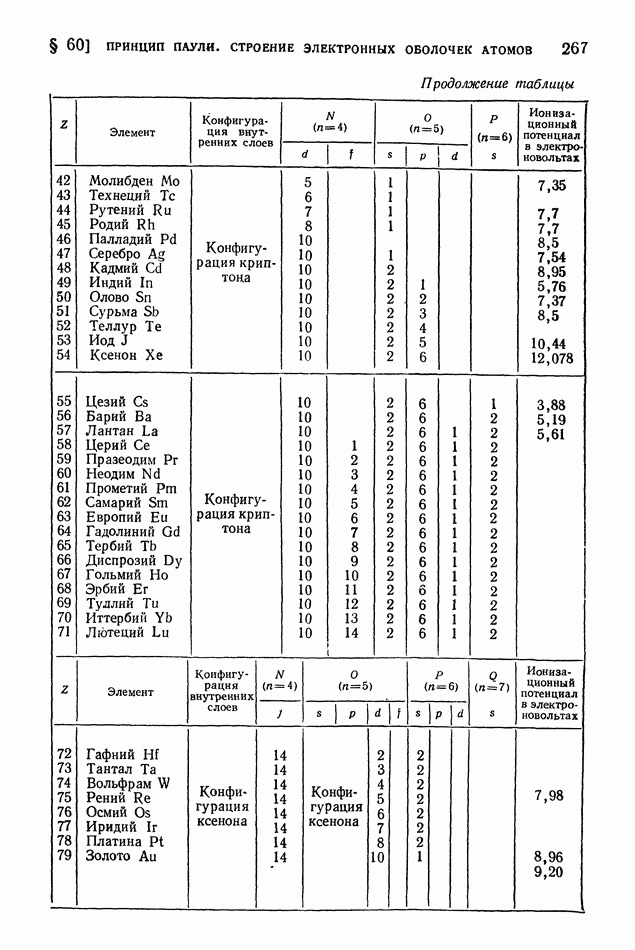
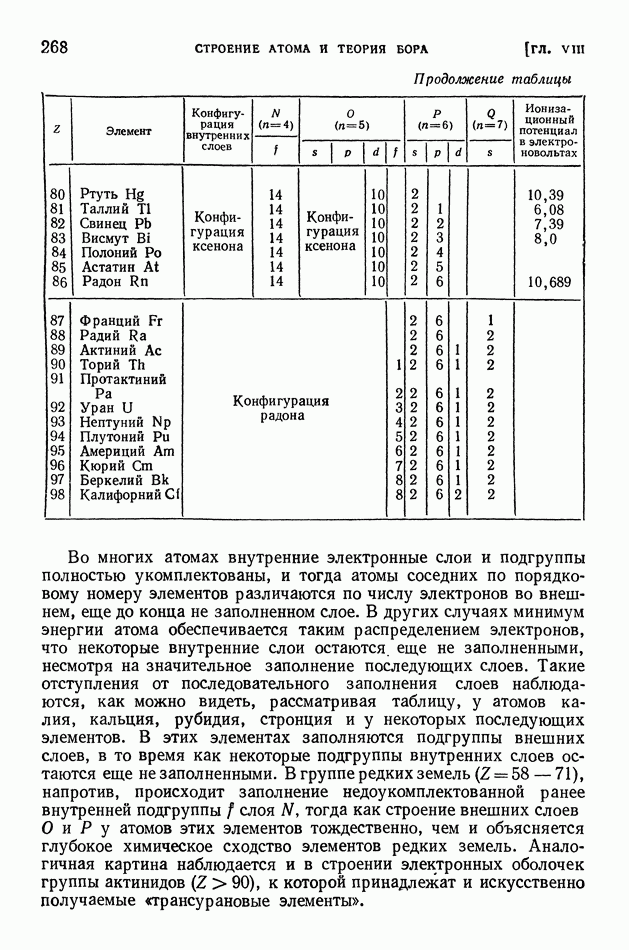
- § 60. Принцип Паули. Строение электронных оболочек атомов
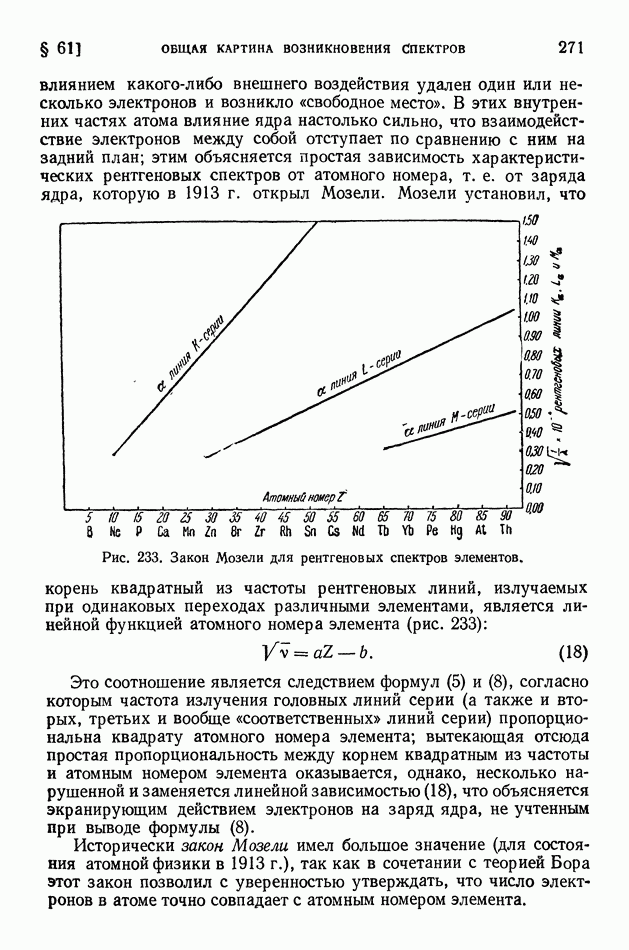
- § 61. Общая картина возникновения спектров
- ГЛАВА IX. ОСНОВЫ КВАНТОВОЙ (ВОЛНОВОЙ) МЕХАНИКИ
- § 62. Волновые свойства частиц. Формула де Бройля. Дифракция электронов
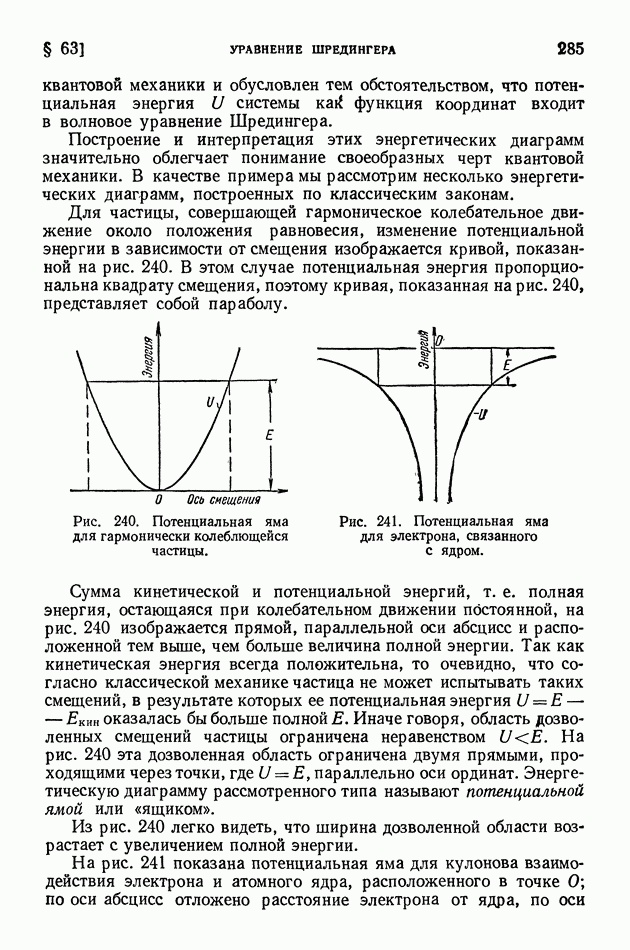
- § 63. Уравнение Шредингера. Просачивание через энергетический барьер. Нулевая энергия
- § 64. Волномеханическая теория атома водорода
- § 65. Соотношение неопределенностей и его разные трактовки
- ГЛАВА X. КВАНТОВАЯ ОПТИКА
- § 66. Развитие квантовой оптики
- § 67. Спектр щелочных металлов. Спин электрона
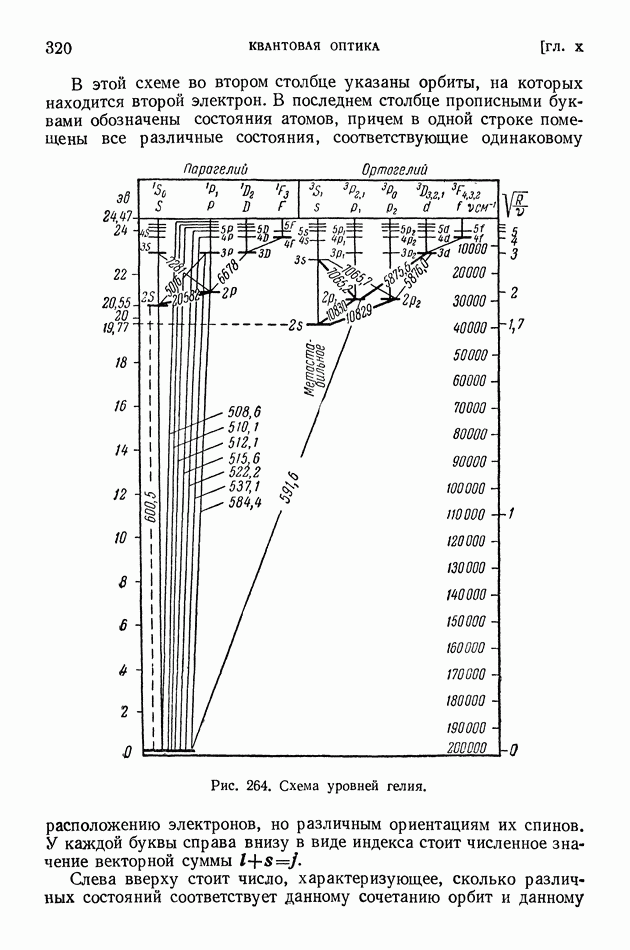
- § 68. Спектр гелия. Символика спектральных термов
- § 69. Сверхтонкая структура спектральных линий
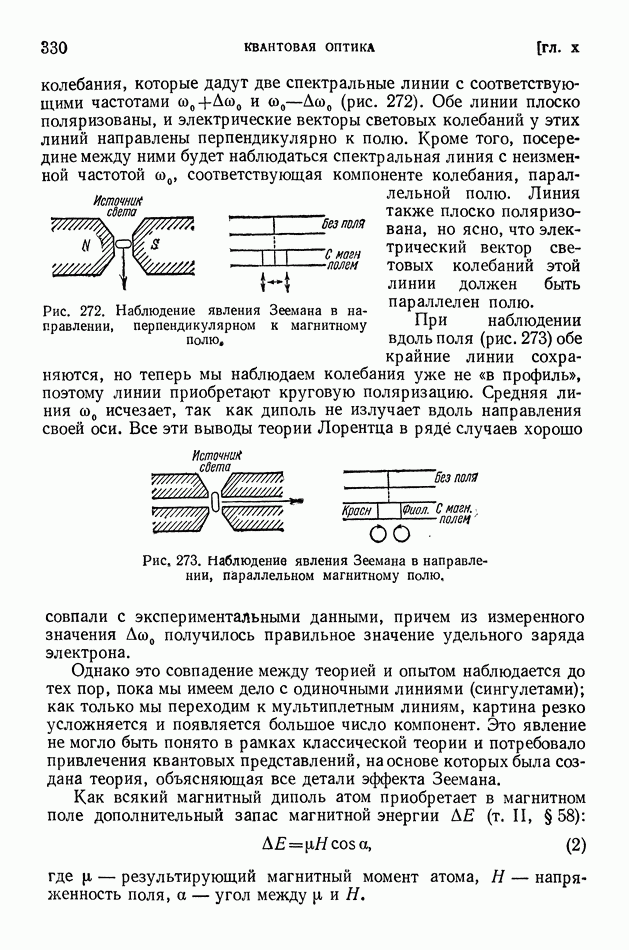
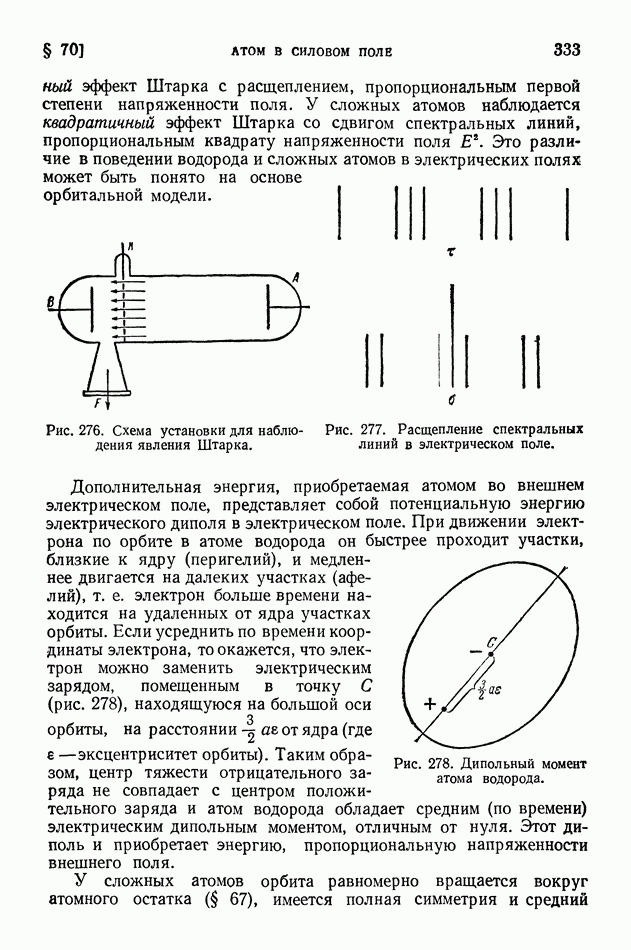
- § 70. Атом в силовом поле
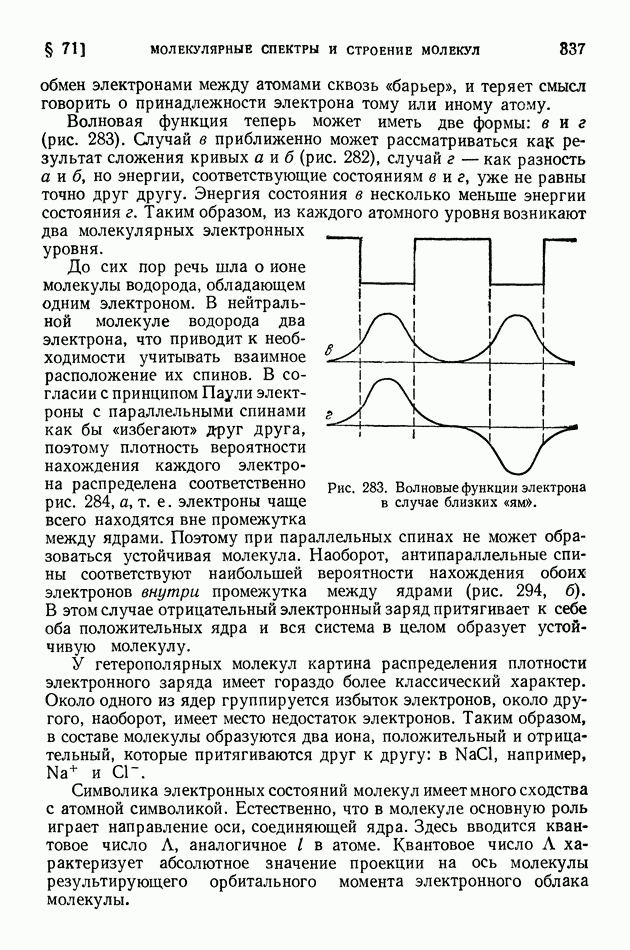
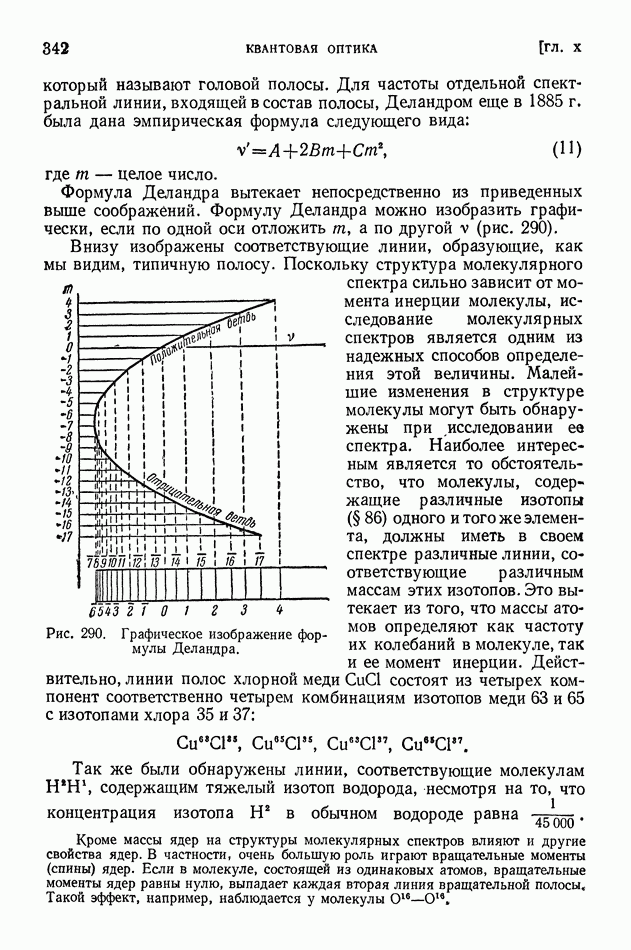
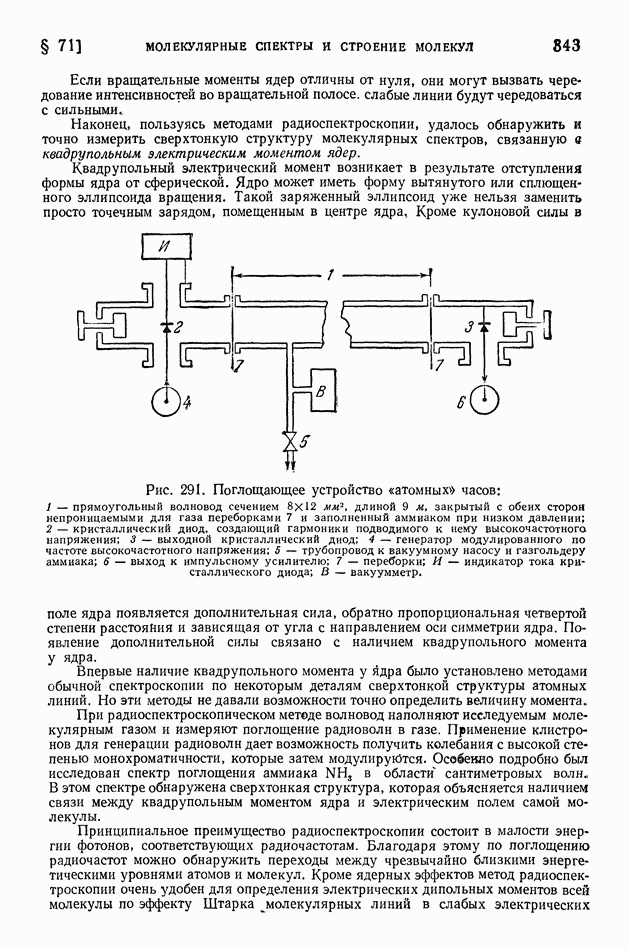
- § 71. Молекулярные спектры и строение молекул
- § 72. Комбинационное рассеяние света
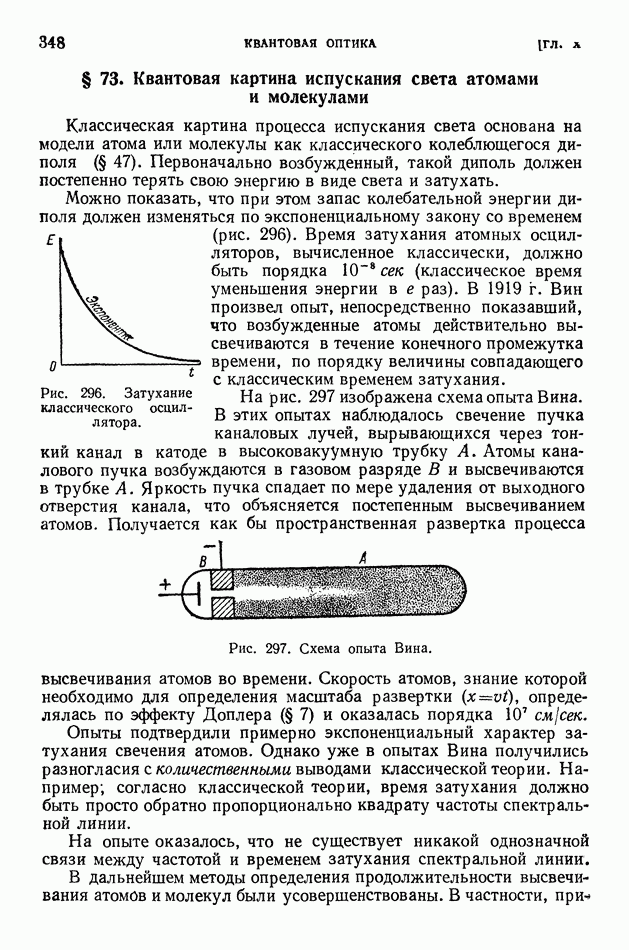
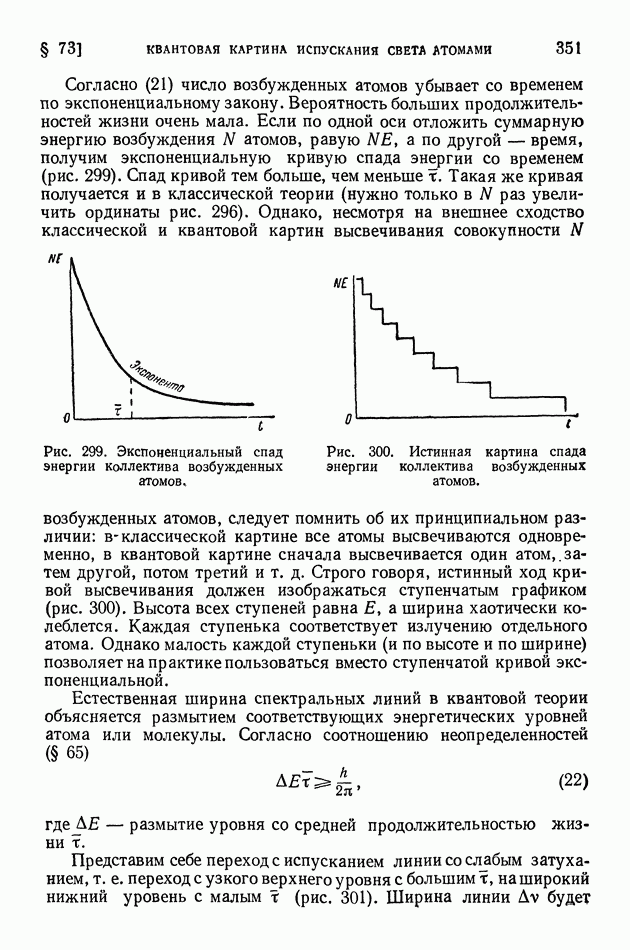
- § 73. Квантовая картина испускания света атомами и молекулами
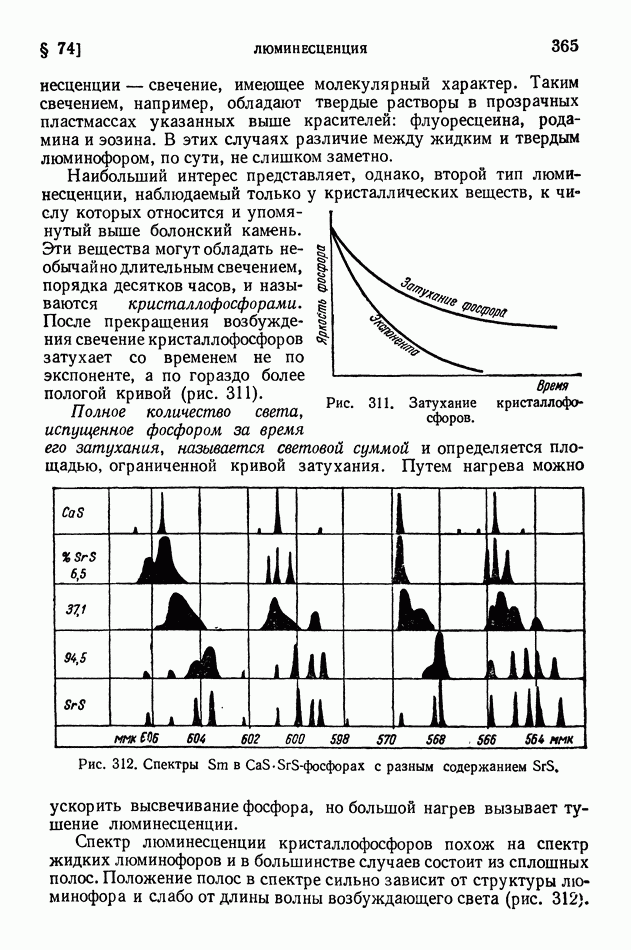
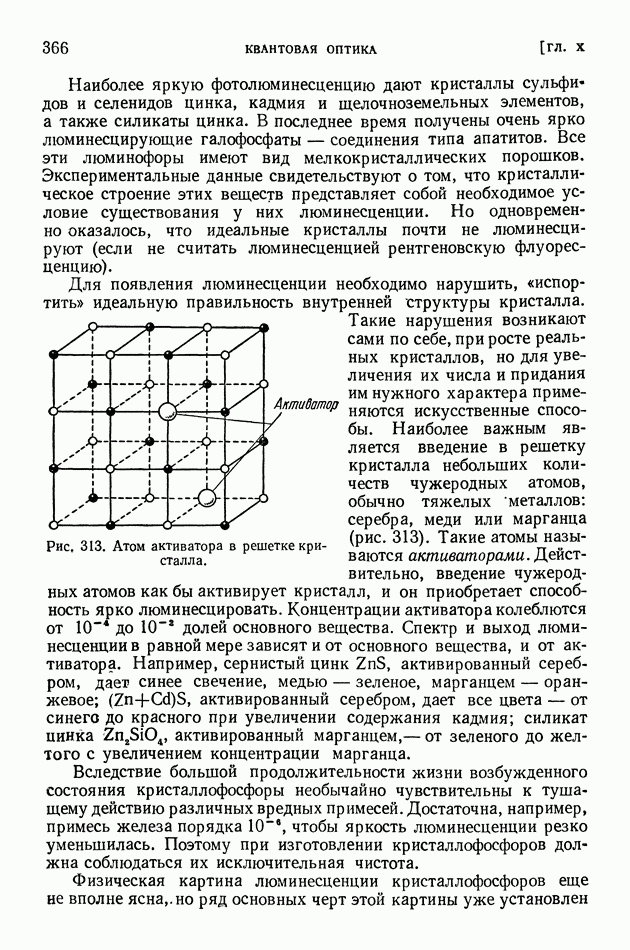
- § 74. Люминесценция
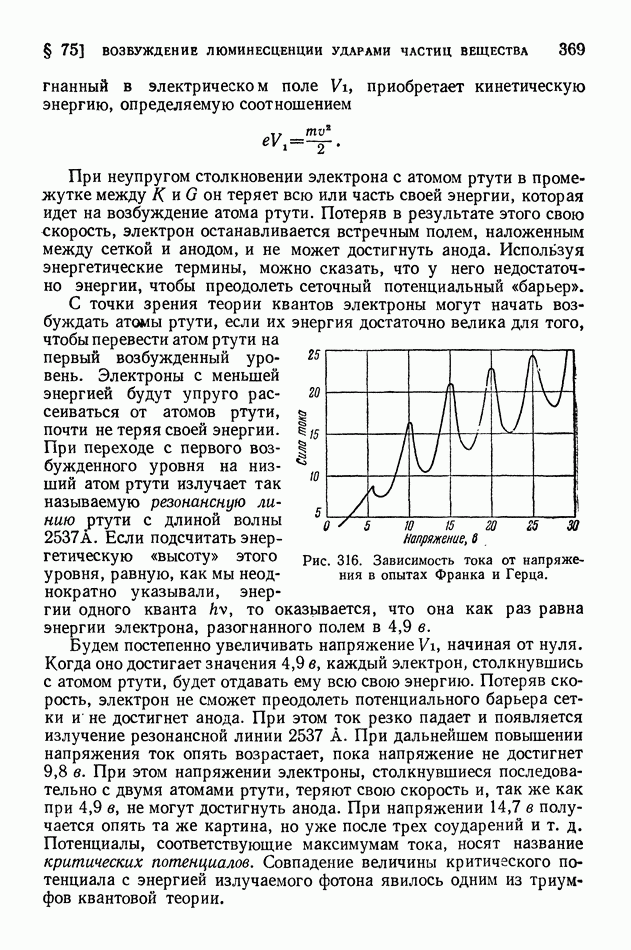
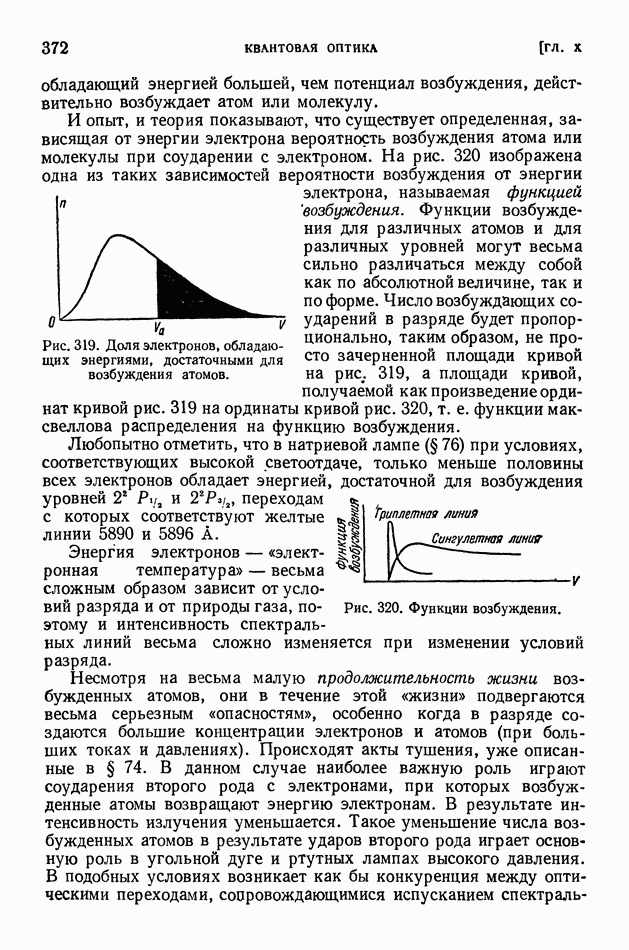
- § 75. Возбуждение люминесценции ударами частиц вещества
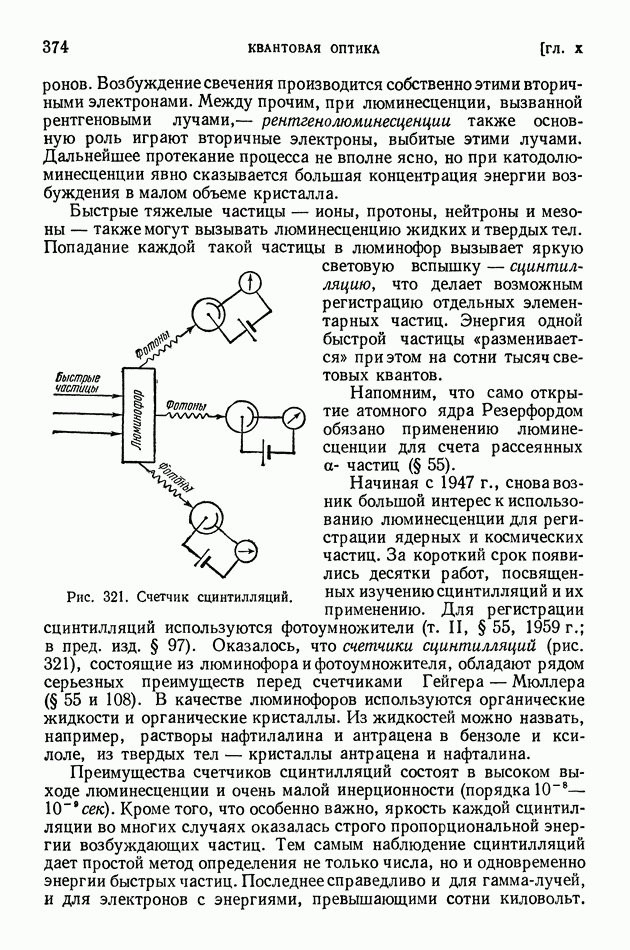
- § 76. Применения люминесценции
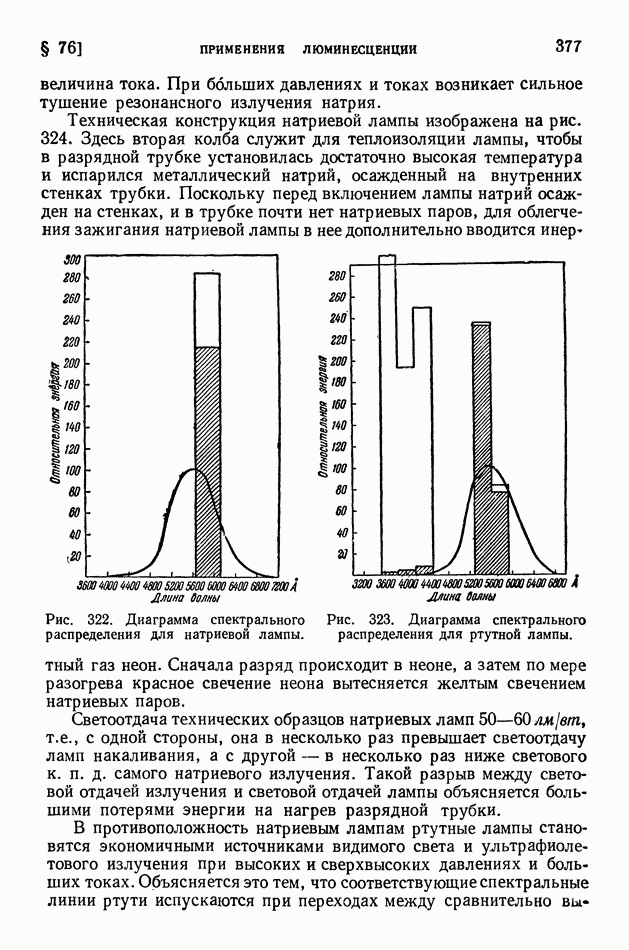
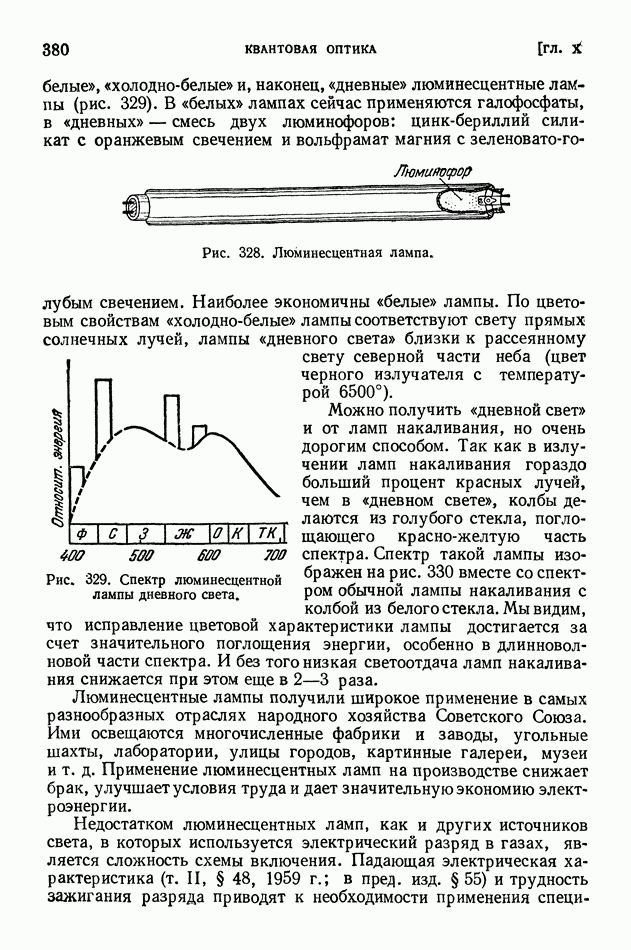
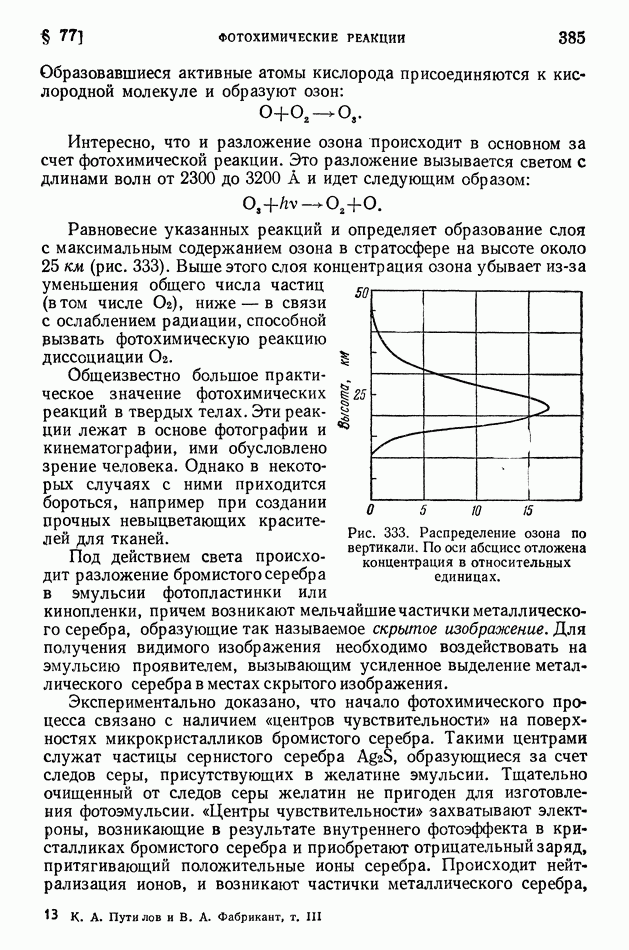
- § 77. Фотохимические реакции
- ГЛАВА XI. ЗАКОН ПРОПОРЦИОНАЛЬНОСТИ МАССЫ И ЭНЕРГИИ И РЕЛЯТИВИСТСКИЕ СООТНОШЕНИЯ
- § 78. Закон пропорциональности массы и энергии
- § 79. Предварительные замечания о релятивистских эффектах. Зависимость массы от скорости
- § 80. Корпускулярные свойства фотонов. Явление Комптона
- § 81. Вывод закона Эйнштейна сложения скоростей из закона пропорциональности массы и энергии и законов сохранения энергии или количества движения
- § 82. Две трактовки закона пропорциональности массы и энергии и уточнение закона тяготения
- § 83. Красное смещение спектральных линий. Поперечный эффект Доплера
- § 84. Влияние гравитационного поля на скорость света в вакууме и показатель преломления вакуума
- ЧАСТЬ ШЕСТАЯ. ЯДЕРНАЯ ФИЗИКА
- § 85. Заряд и масса ядра. Масс-спектральный анализ
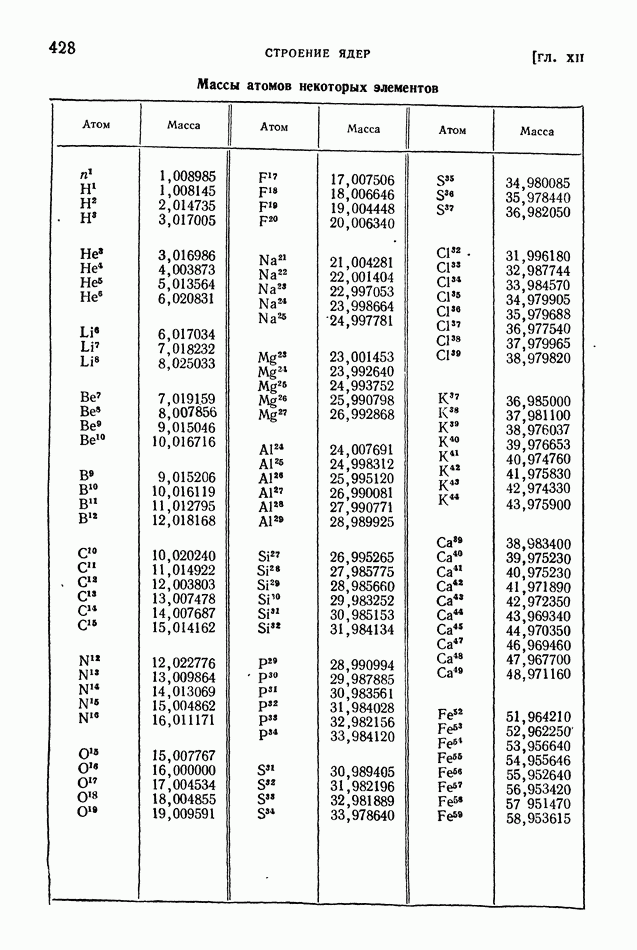
- § 86. Состав ядер. Изотопы. Атомные единицы массы и энергии
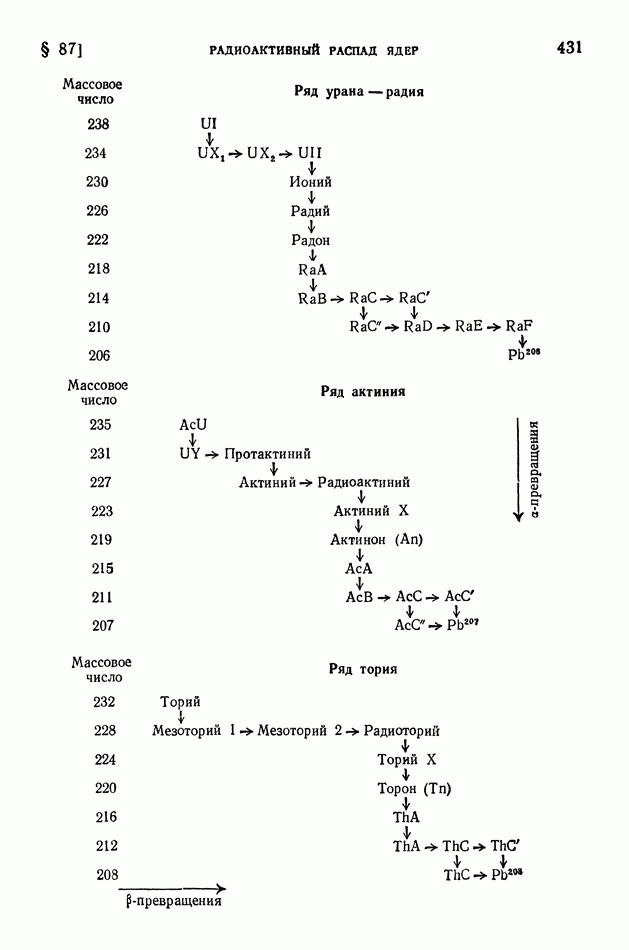
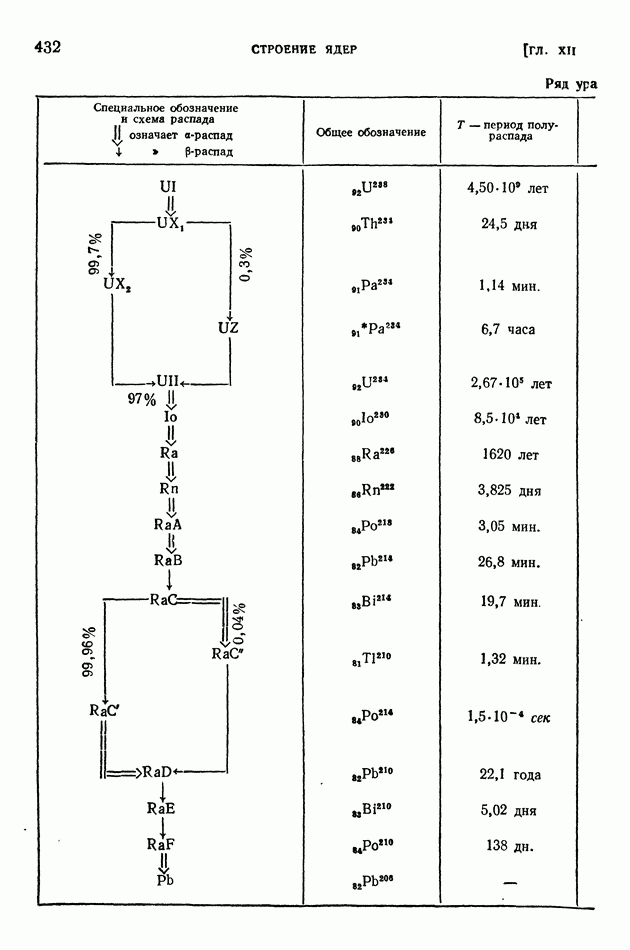
- § 87. Радиоактивный распад ядер. Закон радиоактивного смещения. Изомеры
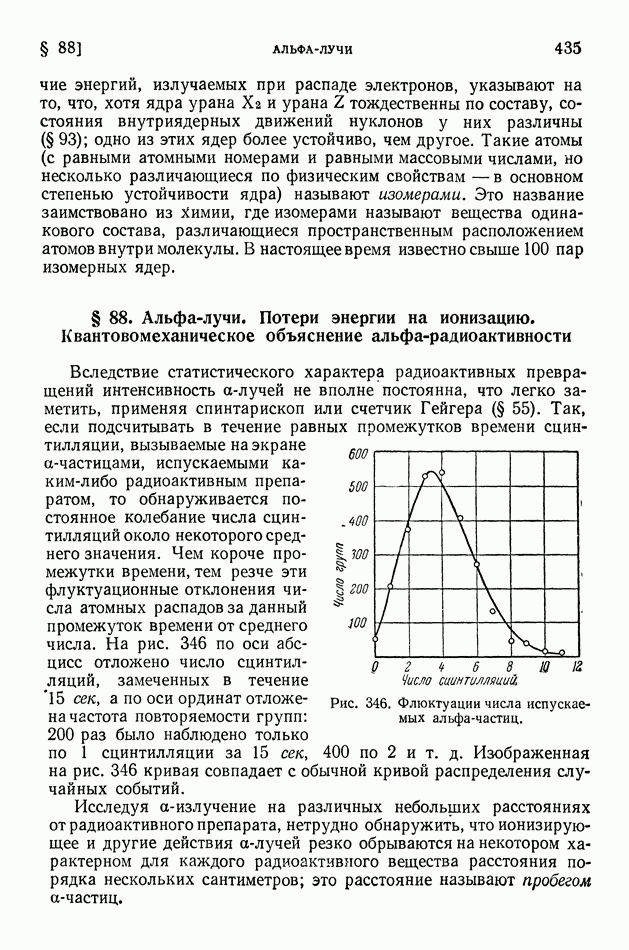
- § 88. Альфа-лучи. Потери энергии на ионизацию. Квантовомеханическое объяснение альфа-радиоактивности
- § 89. Бета- и гамма-лучи
- § 90. Искусственное расщепление ядер. Открытие нейтрона
- § 91. Открытие позитрона. Взаимопревращение фотонов определенной энергии и электронно-позитронных пар
- § 92. Индуцированная позитронная и электронная радиоактивность. Фоторасщепление ядер, K-захват
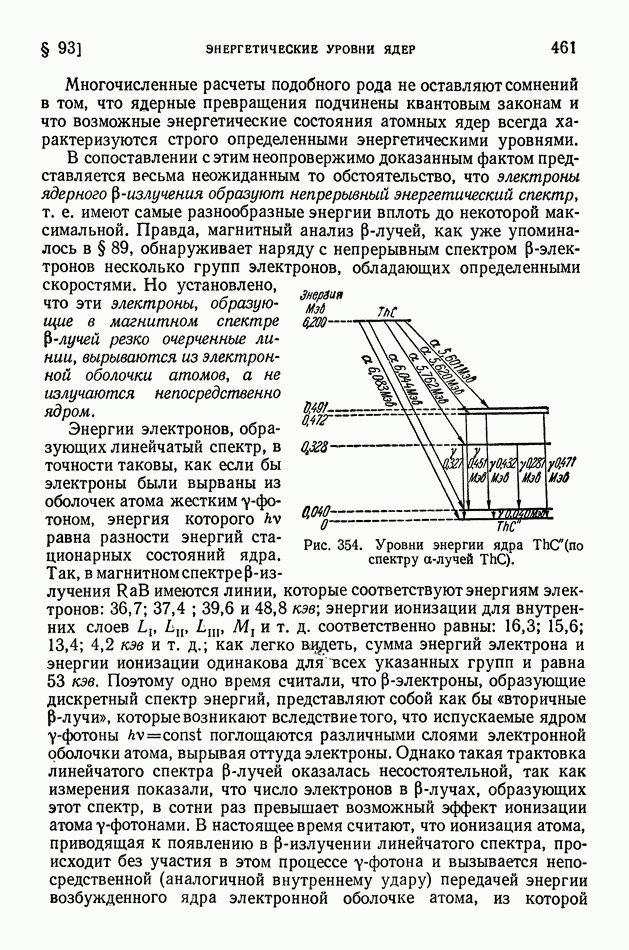
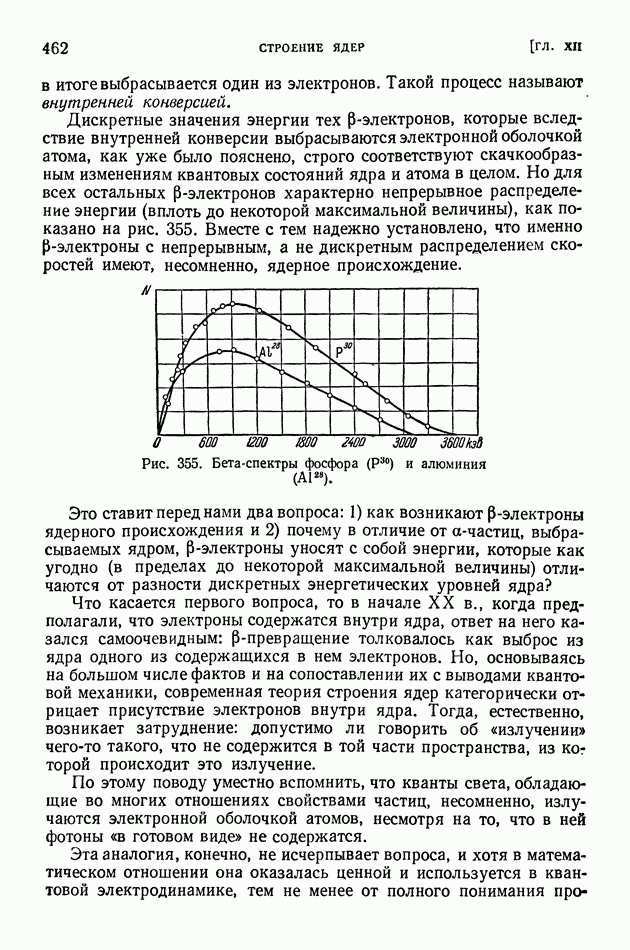
- § 93. Энергетические уровни ядер. Внутренняя конверсия. Нейтрино
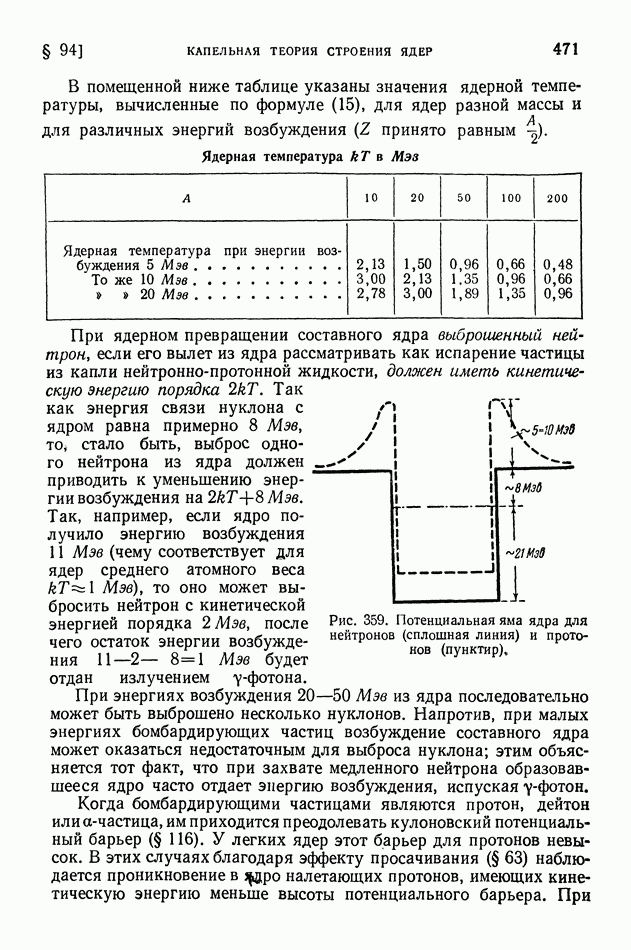
- § 94. Капельная теория строения ядер
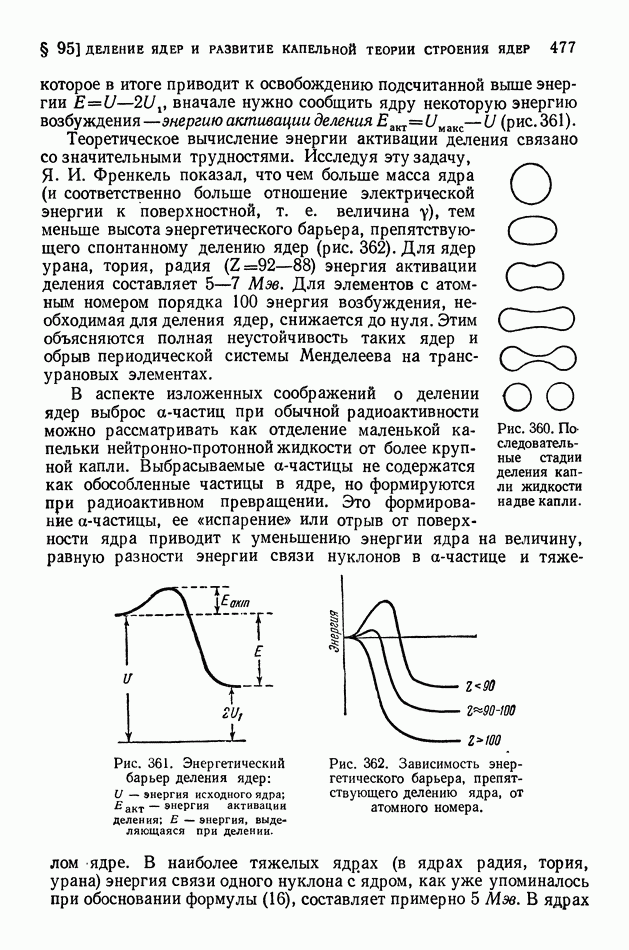
- § 95. Деление ядер и развитие капельной теории строения ядер
- ГЛАВА XIII. КОСМИЧЕСКИЕ ЛУЧИ
- § 96. Методы исследования и первые итоги изучения космических лучей
- § 97. Каскадное образование электронно-позитронных пар в космических лучах. Потери энергии электронами на тормозное излучение
- § 98. «мю»-мезоны. Зависимость времени жизни неустойчивых частиц от скорости движения
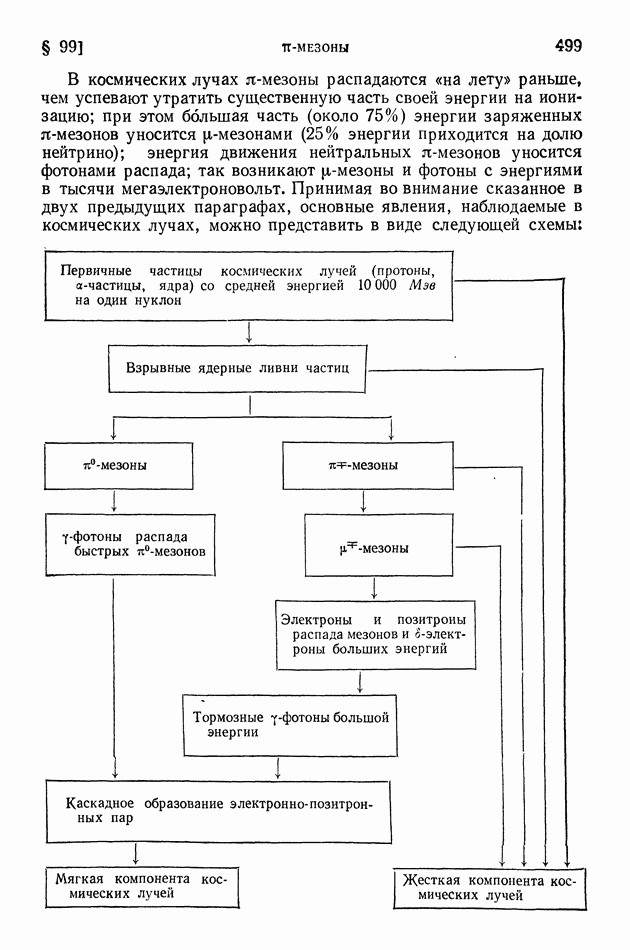
- § 99. «пи»-мезоны
- § 100. Взрывные ядерные ливни и их каскадное развитие в космических лучах
- § 101. Корпускулярный и энергетический спектр космических лучей. Происхождение космического излучения
- ГЛАВА XIV. ЭКСПЕРИМЕНТАЛЬНЫЕ СРЕДСТВА ЯДЕРНОЙ ФИЗИКИ
- § 102. Циклотроны
- § 103. Фазотроны
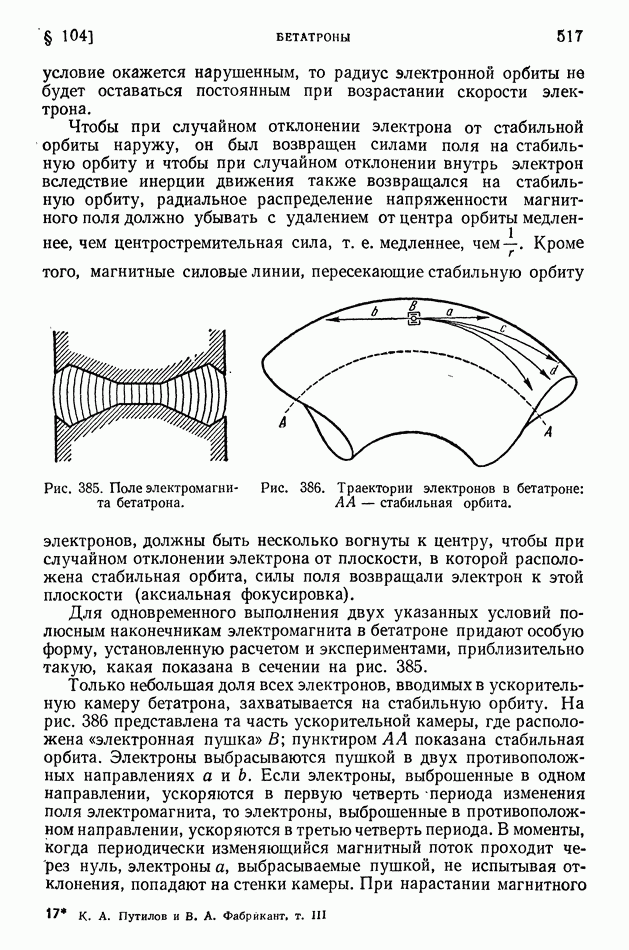
- § 104. Бетатроны
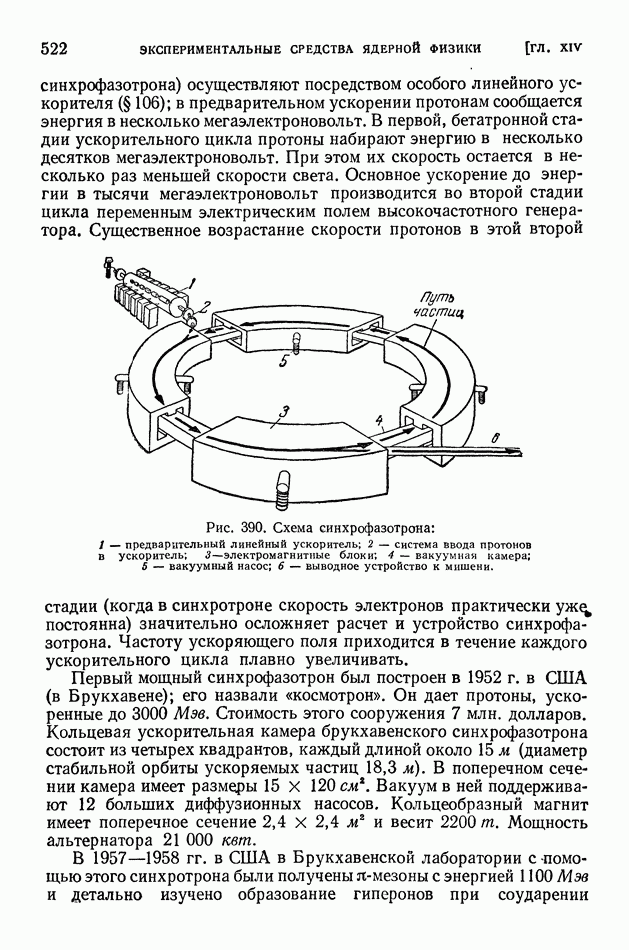
- § 105. Синхротроны и синхрофазотроны
- § 106. Линейные ускорители электронов и ионов
- § 107. Лабораторные источники нейтронов. Замедлители нейтронов в ядерных реакторах
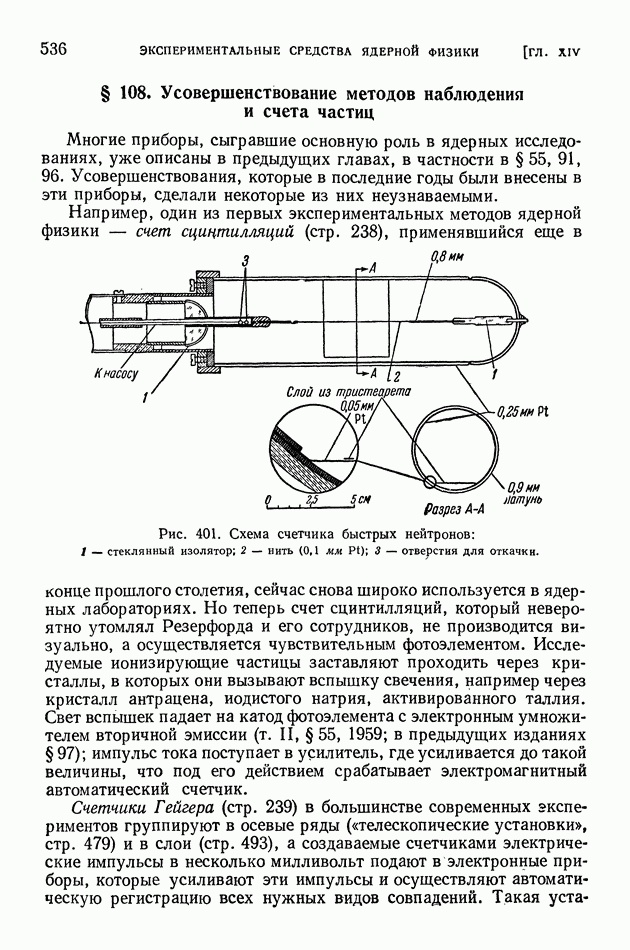
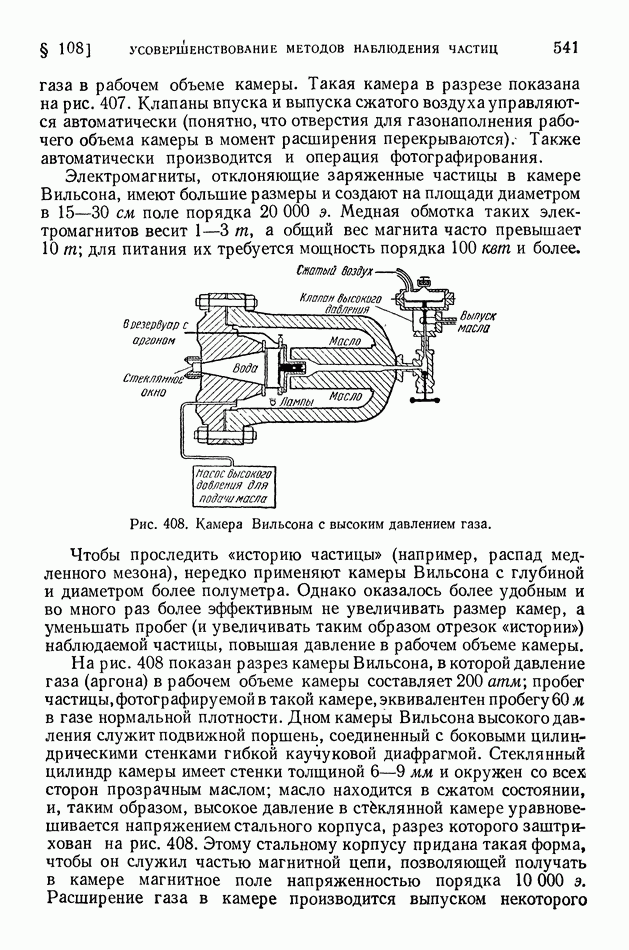
- § 108. Усовершенствование методов наблюдения и счета частиц
- ГЛАВА XV. ЯДЕРНЫЕ РЕАКЦИИ И АТОМНАЯ ЭНЕРГИЯ
- § 109. Основные виды и обозначения ядерных реакций. Конкурирующие процессы в ядерных реакциях
- § 110. Энергетический эффект, энергия возбуждения и порог ядерных реакций
- § 111. Превращения элементарных частиц
- § 112. Ядерные силы
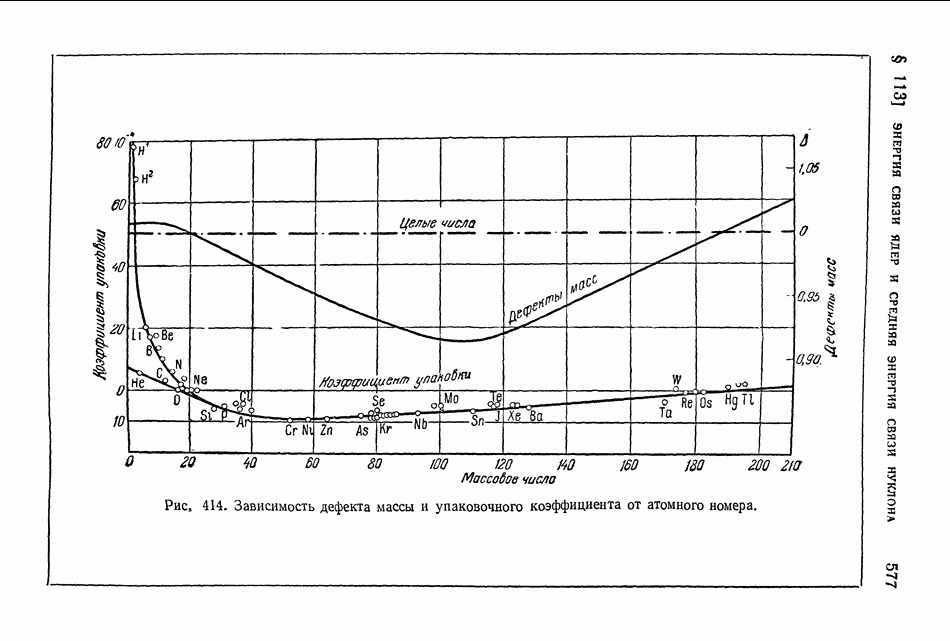
- § 113. Энергия связи ядер и средняя энергия связи нуклона
- § 114. Полуэмпирическая формула для энергии ядерной связи и для атомных энергий и масс
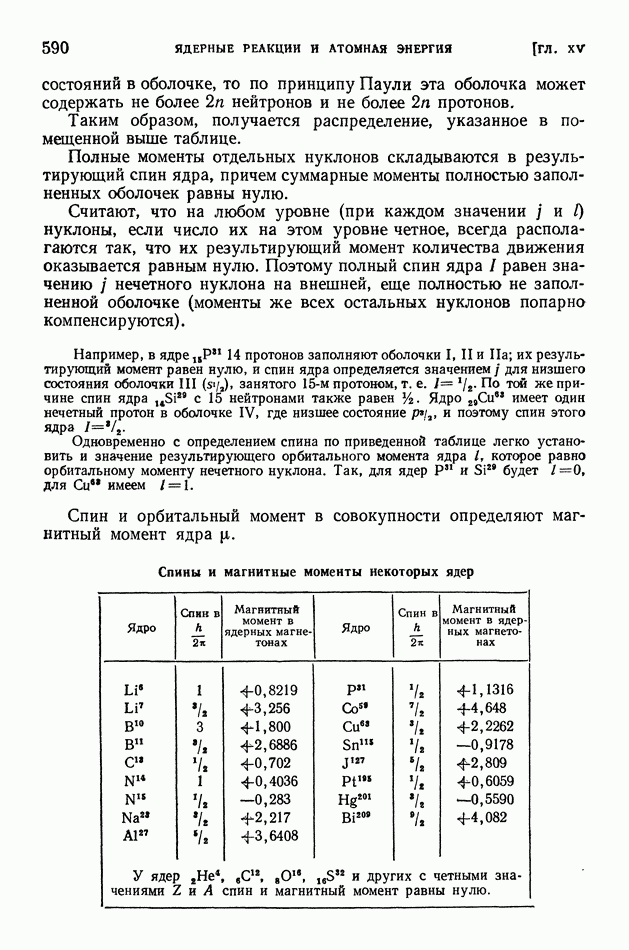
- § 115. Взаимосвязь энергии и строения ядер. Внутриядерное движение нуклонов и нуклонные оболочки. Спины и магнитные моменты ядер
- § 116. Энергия отделения частиц и анализ возможного хода ядерной реакции
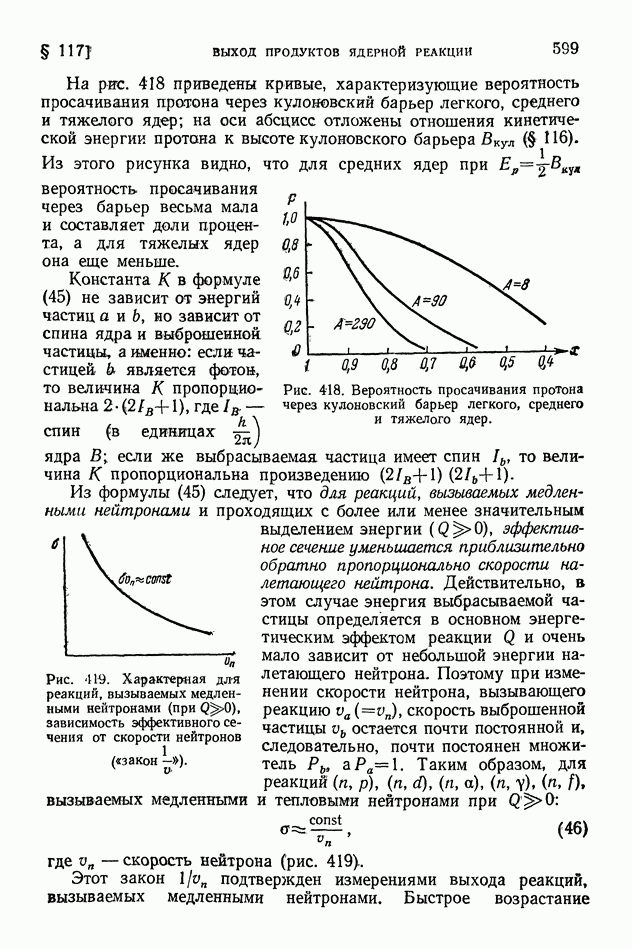
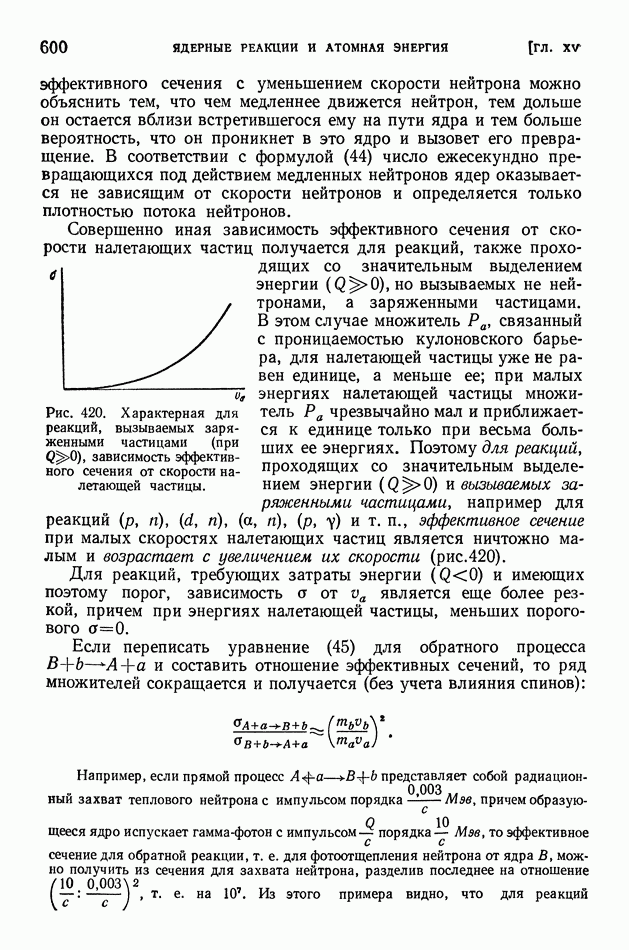
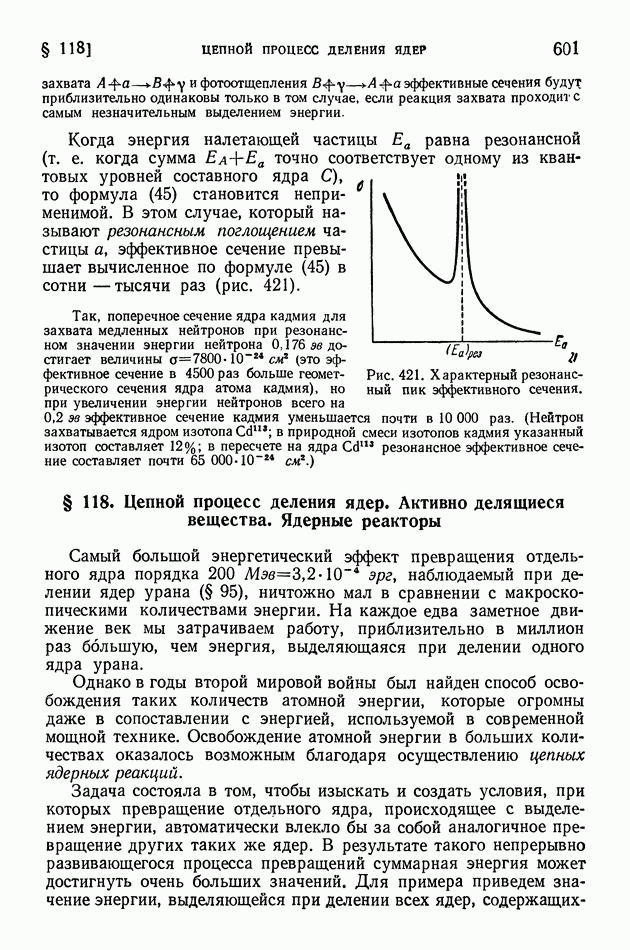
- § 117. Выход продуктов ядерной реакции. Эффективные сечения. Резонансные явления
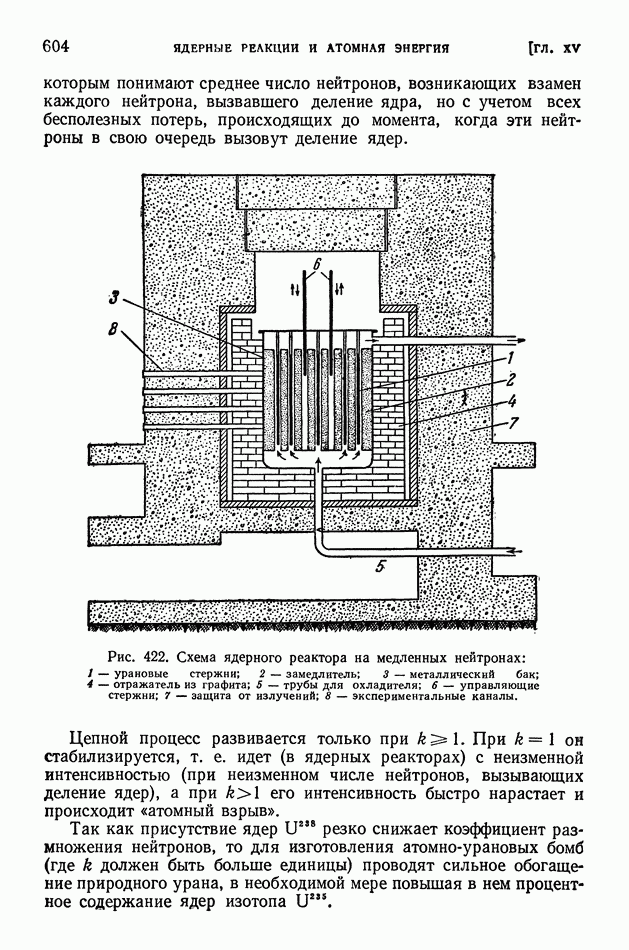
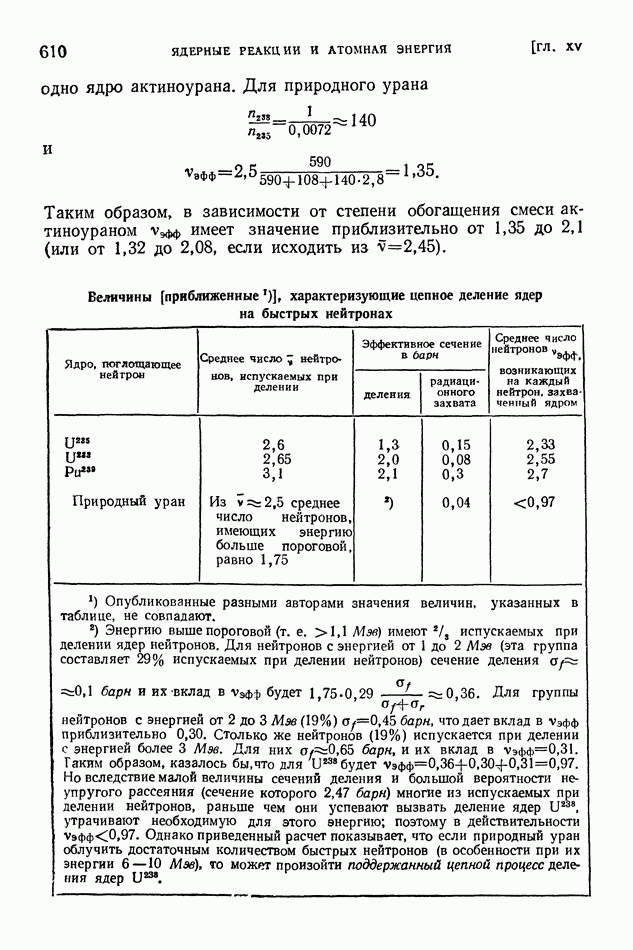
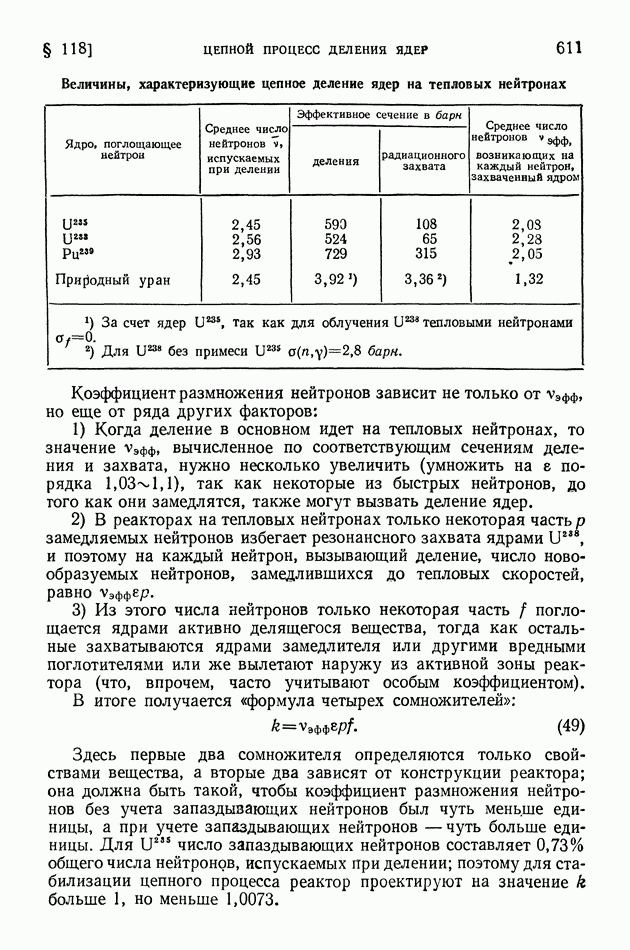
- § 118. Цепной процесс деления ядер. Активно делящиеся вещества. Ядерные реакторы
- § 119. Термоядерные реакции
- § 120. Применение ядерных реакций
- § 121. Ядерные реакции в звездах