| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 80. Корпускулярные свойства фотонов. Явление Комптона
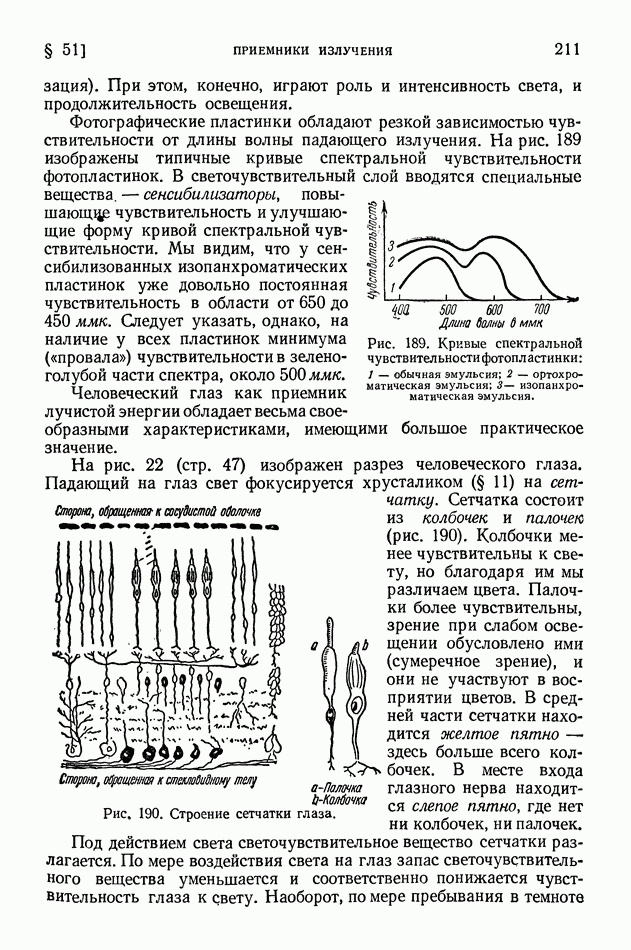
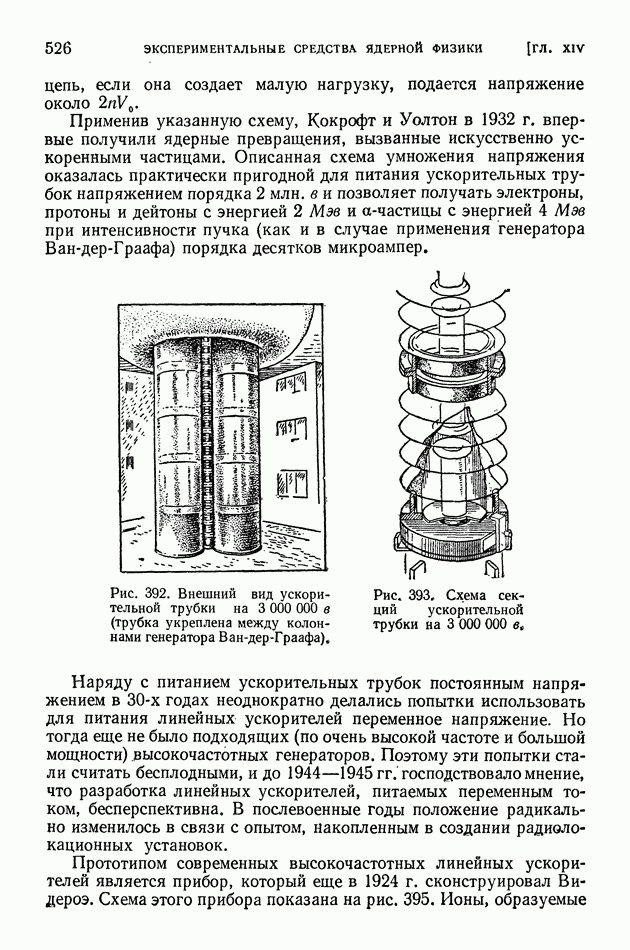
Начиная с 1905 г., когда Эйнштейн сформулировал квантовый закон фотоэффекта (т. II, § 54, 1959; в предыдущих изданиях § 96), постепенно были раскрыты корпускулярные свойства света. Важным этапом в развитии корпускулярных представлений о свете оказалось основанное на законе пропорциональности массы и энергии объяснение явления, открытого в 1923 г. Комптоном. Явление Комптона заключается, как подробно пояснено ниже, в особом характере рассеяния рентгеновых лучей и гамма-лучей на свободных электронах. Обнаружилось, что закон пропорциональности массы и энергии чрезвычайно облегчает понимание не только явления Комптона, но и ряда других явлений, в которых сказываются корпускулярные свойства излучения. Вместе с тем именно при анализе корпускулярных свойств фотонов видимого света, рентгеновых лучей и гамма-лучей в убедительной форме выявилась универсальная применимость закона пропорциональности массы и энергии.
Если исходить из закона пропорциональности массы и энергии и законов сохранения энергии и импульса, явление, открытое Комптоном, можно рассматривать как следствие давления света на отдельные электроны или, что физически равнозначно, как результат соударения фотонов с электронами.
Как уже было отмечено в § 41, волновая теория светового давление отличается некоторой сложностью. Наоборот, из корпускулярных представлений о свете сразу становится очевидным, что должно существовать световое давление как следствие ударов световых частиц. Однако старая ньютоновская теория истечения приводила к величине светового давления, в 2 раза превышающей истинное значение. На основании квантовой теории света нетрудно получить формулу (§ 41), правильно связывающую плотность излучения с величиной светового давления.
Действительно, если на единицу поверхности поглощающего тела падает в одну секунду  фотонов, то поток энергии равен
фотонов, то поток энергии равен  Но поток энергии излучения равен объемной плотности энергии и, умноженной на скорость света с, т. е.
Но поток энергии излучения равен объемной плотности энергии и, умноженной на скорость света с, т. е.  откуда
откуда

Величина  представляет собой импульс отдельного фотона; следовательно, полный импульс, передаваемый фотонами поглощающему телу в секунду (и проявляющийся как световое
представляет собой импульс отдельного фотона; следовательно, полный импульс, передаваемый фотонами поглощающему телу в секунду (и проявляющийся как световое
давление), равен  Таким образом, световое давление при полном поглощении света равно плотности световой энергии
Таким образом, световое давление при полном поглощении света равно плотности световой энергии  Это заключение, как было показано в § 41, согласуется с выводами волновой теории и с результатами опытов Лебедева.
Это заключение, как было показано в § 41, согласуется с выводами волновой теории и с результатами опытов Лебедева.
Мы видим, что волновая и квантовая теории в данном вопросе приводят к одному и тому же результату. Однако можно так видоизменить опыт Лебедева, чтобы и в явлении светового давления обнаружились специфические квантовые свойства света. Волновая теория дает правильную картину явления только для опытов с большим числом фотонов.

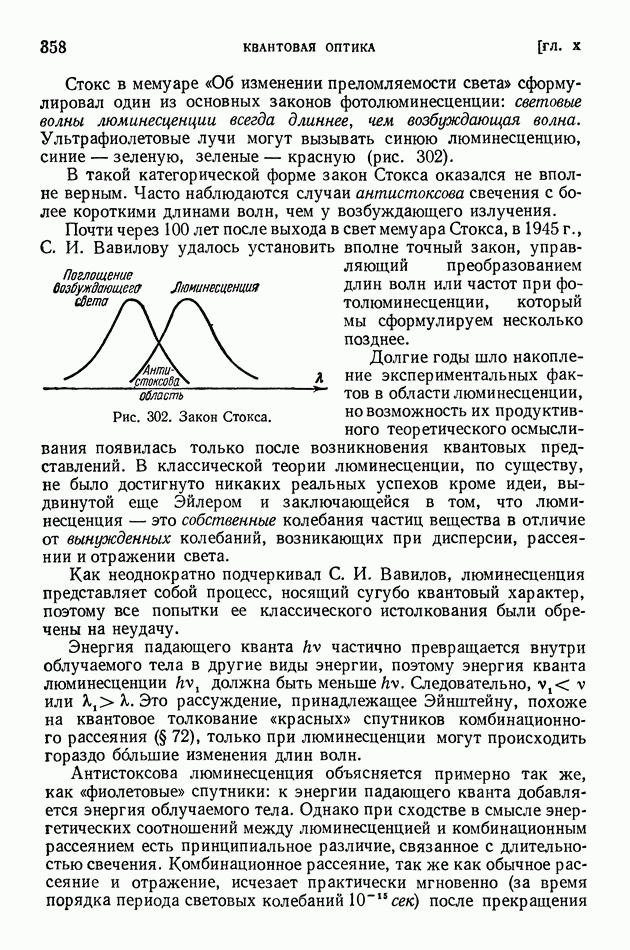
Рис. 336. Схема опытов Комптона
При достаточно слабом световом пучке должны наблюдаться толчки, возникающие при попадании отдельных фотонов на поверхность освещаемого тела. Но для обычных макроскопических тел (крылышко радиометра) и для фотонов видимого света, обладающих малой энергией, толчки от отдельных фотонов обнаружить практически невозможно, так как сталкивающиеся массы различаются в 1030—1035 раз. Положение становится существенно иным, если в качестве облучаемого тела фигурируют отдельные электроны, а свет состоит из фотонов жестких рентгеновых лучей или гамма-лучей. Масса фотона для жестких рентгеновых лучей, как уже упоминалось в § 78, сравнима с массой покоя электрона. Поэтому при взаимодействии жестких рентгеновых или гамма-лучей со свободными электронами должны проявиться, и действительно проявляются, корпускулярные свойства света.
Практически нет необходимости иметь совершенно свободные электроны; достаточно, чтобы энергия фотона во много раз превышала энергию связи электрона с атомом. Тогда эта связь при соударении фотона с электроном легко рвется и в целом явление мало отличается от случая соударения фотона со свободным электроном.
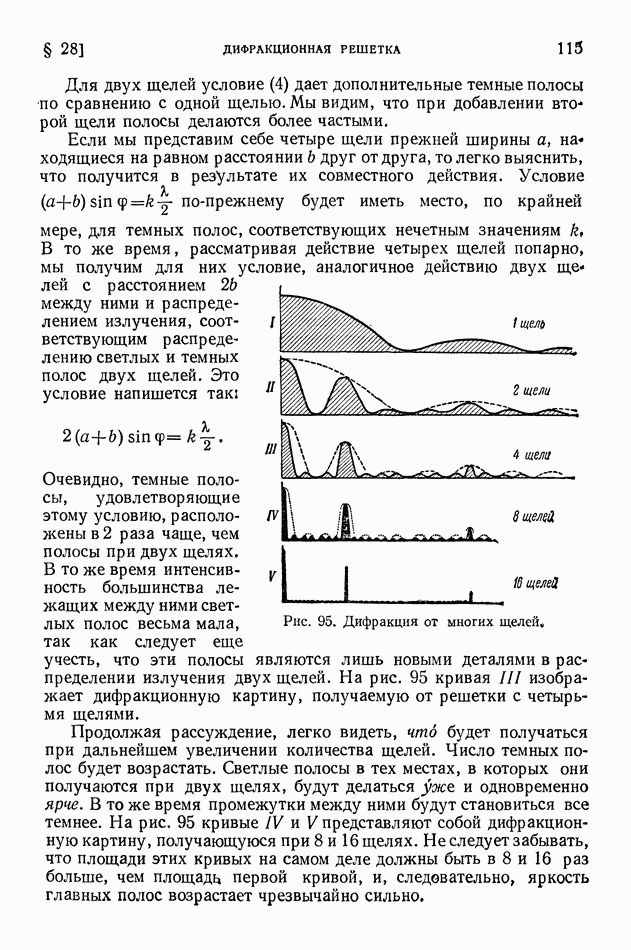
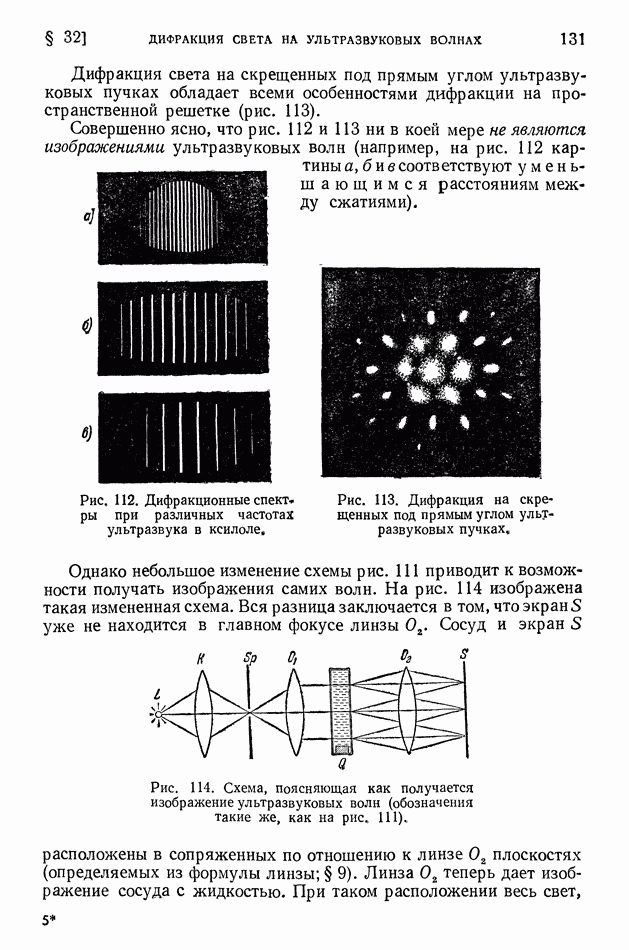
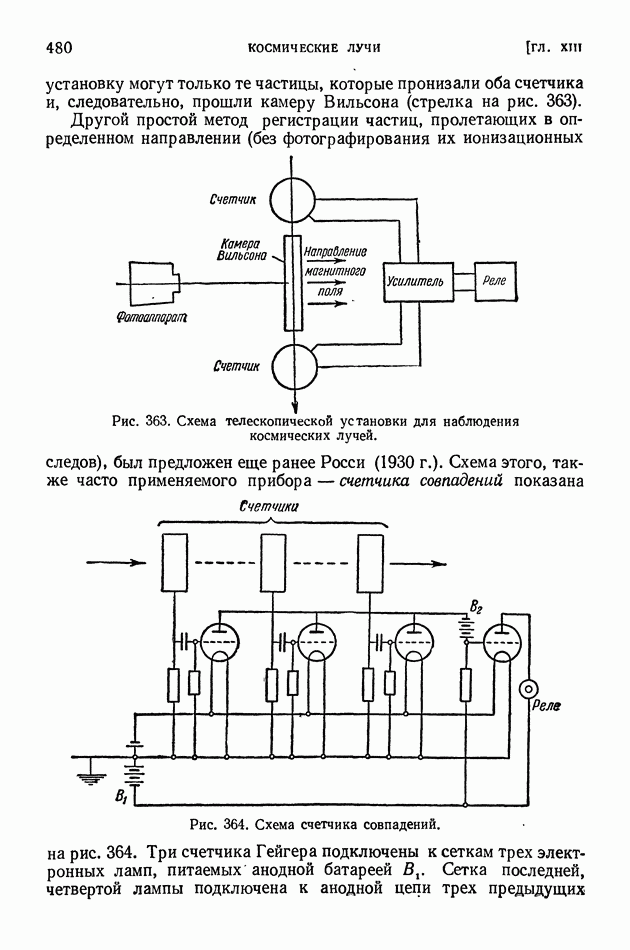
Впервые опыты по изучению соударений фотонов с электронами были проведены в 1922-1923 гг. А. Комптоном. Комптон исследовал рассеяние жестких рентгеновых лучей графитом. Схема опытов Комптона показана на рис. 336. Рентгеновская трубка с
молибденовым антикатодом служила источником монохроматических рентгеновых лучей — линии  молибдена с длиной волны
молибдена с длиной волны  Свинцовые диафрагмы
Свинцовые диафрагмы  выделяли узкий пучок лучей, падавший на кусок графита
выделяли узкий пучок лучей, падавший на кусок графита  Изучался спектр лучей, рассеянных графитом под различными углами 6. Для этого был применен рентгеновский спектрометр, состоявший из пластины со щелью
Изучался спектр лучей, рассеянных графитом под различными углами 6. Для этого был применен рентгеновский спектрометр, состоявший из пластины со щелью  кристалла О, ионизационной камеры
кристалла О, ионизационной камеры  и электрометра
и электрометра 
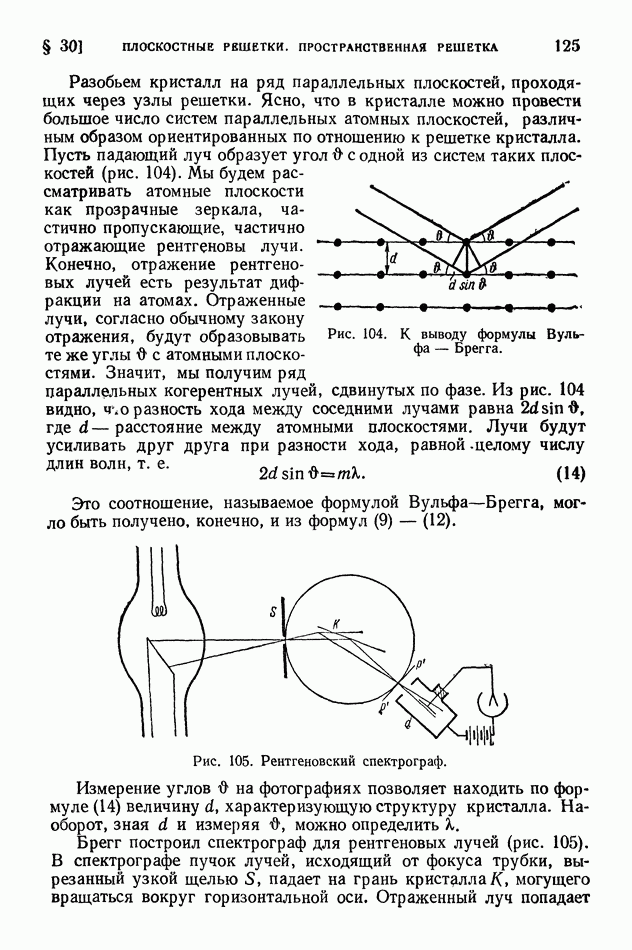
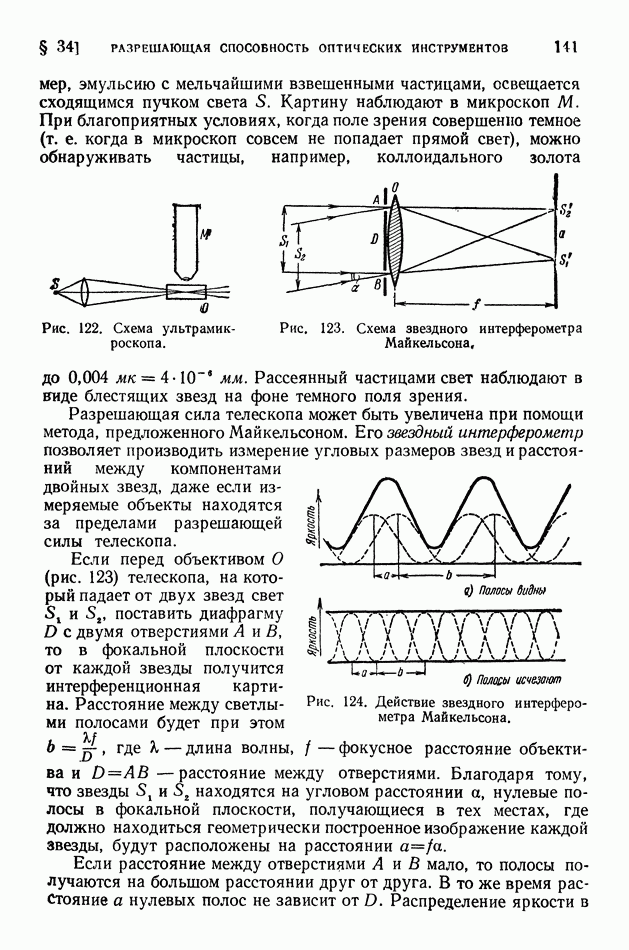
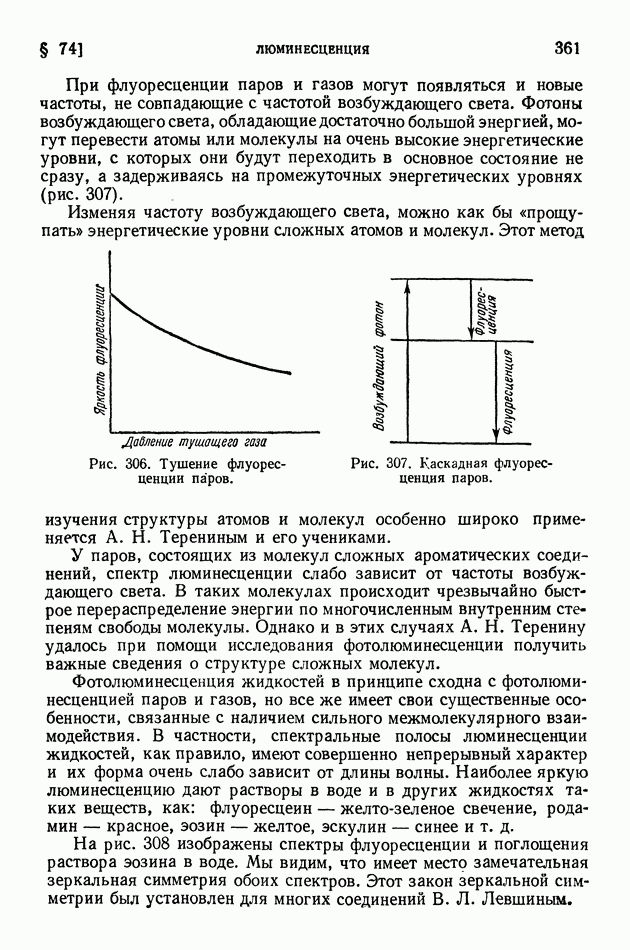
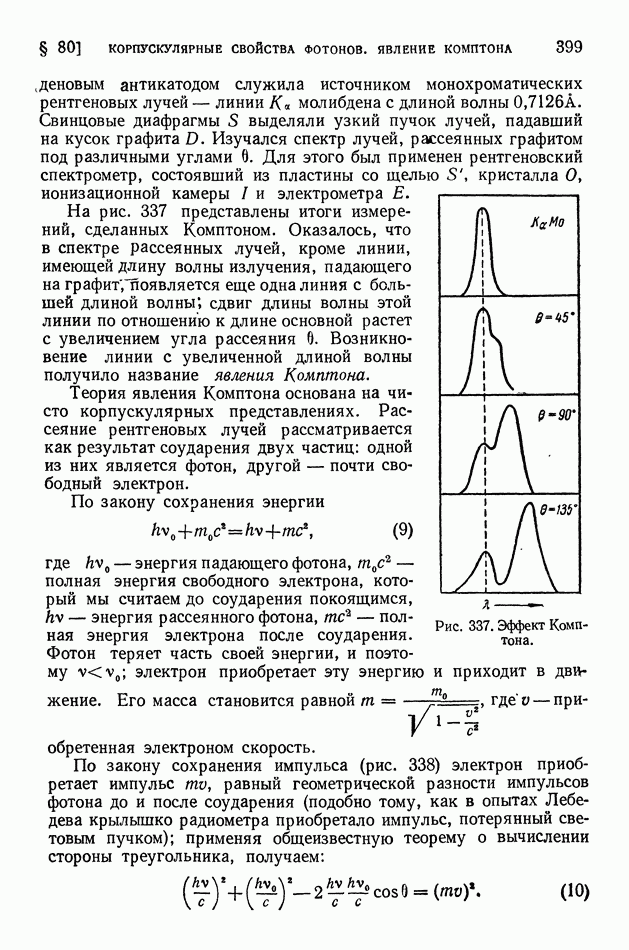
На рис. 337 представлены итоги измерений, сделанных Комптоном. Оказалось, что в спектре рассеянных лучей, кроме линии, имеющей длину волны излучения, падающего на графит появляется еще одна линия с большей длиной волны; сдвиг длины волны этой линии по отношению к длине основной растет с увеличением угла рассеяния 6. Возникновение линии с увеличенной длиной волны получило название явления Комптона.

Рис. 337. Эффект Комптона.
Теория явления Комптона основана на чисто корпускулярных представлениях. Рассеяние рентгеновых лучей рассматривается как результат соударения двух частиц: одной из них является фотон, другой — почти свободный электрон.
По закону сохранения энергии

где  энергия падающего фотона,
энергия падающего фотона,  полная энергия свободного электрона, который мы считаем до соударения покоящимся,
полная энергия свободного электрона, который мы считаем до соударения покоящимся,  энергия рассеянного фотона,
энергия рассеянного фотона,  полная энергия электрона после соударения. Фотон теряет часть своей энергии, и поэтому
полная энергия электрона после соударения. Фотон теряет часть своей энергии, и поэтому  электрон приобретает эту энергию и приходит в движение. Его масса становится равной
электрон приобретает эту энергию и приходит в движение. Его масса становится равной  где
где  приобретенная электроном скорость.
приобретенная электроном скорость.
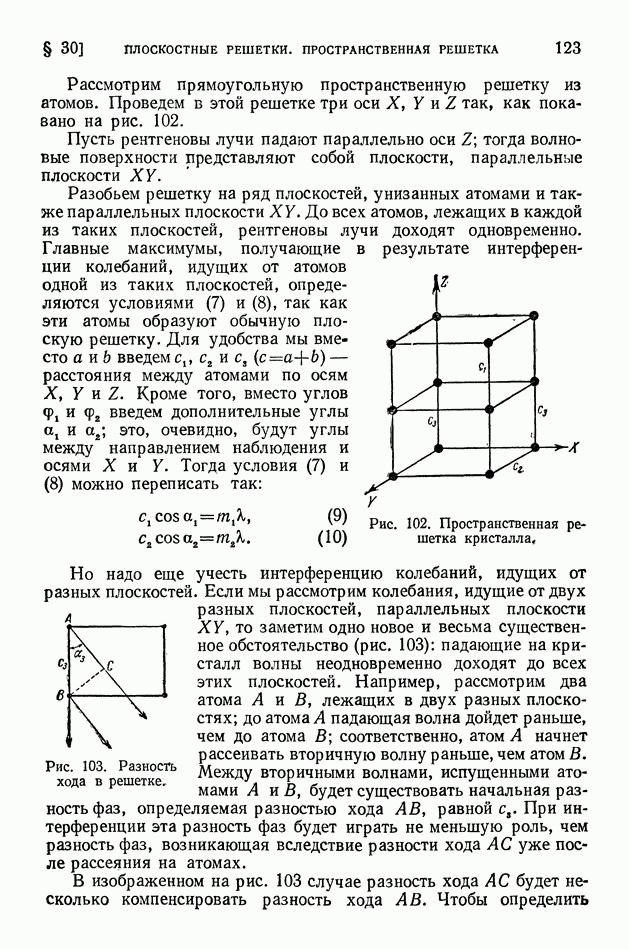
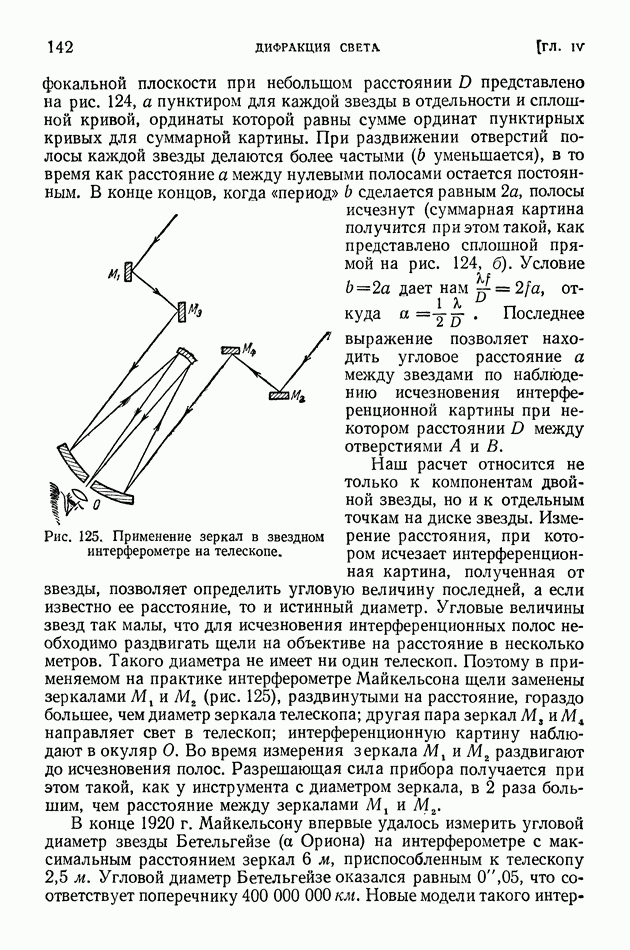
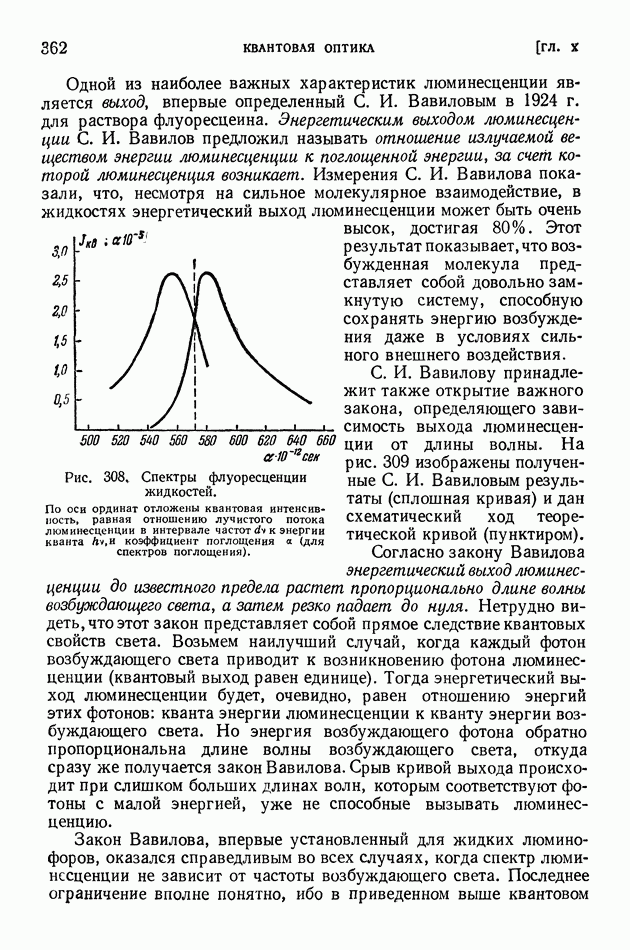
По закону сохранения импульса (рис. 338) электрон приобретает импульс  равный геометрической разности импульсов фотона до и после соударения (подобно тому, как в опытах Лебедева крылышко радиометра приобретало импульс, потерянный световым пучком); применяя общеизвестную теорему о вычислении стороны треугольника, получаем:
равный геометрической разности импульсов фотона до и после соударения (подобно тому, как в опытах Лебедева крылышко радиометра приобретало импульс, потерянный световым пучком); применяя общеизвестную теорему о вычислении стороны треугольника, получаем:

Совместное решение уравнений (9) и (10) дает (нужно помнить,

или

Подставив значение констант, получаем:

Величину  называют комптоновской длиной волны.
называют комптоновской длиной волны.
Формула (11) находится в прекрасном согласии с опытом. На рис. 337 вертикальные прямые соответствуют теоретическим значениям гизменения длины волны  Наиболее точные экспериментальные измерения комптоновской длины волны дали (0,02424 ±0,00004) А, тогда как теоретическое значение
Наиболее точные экспериментальные измерения комптоновской длины волны дали (0,02424 ±0,00004) А, тогда как теоретическое значение 

Рис. 338. Схема явления Комптона.
По формуле  величина комптоновского сдвига
величина комптоновского сдвига  не зависит от длины волны рассеиваемого излучения и измеряется даже для больших углов рассеяния всего сотыми долями ангстрема. Однако этот сдвиг длины волны по порядку величины близок к длине волны гамма-лучей, и поэтому явление Комптона легко наблюдать при рассеянии гамма-лучей и жестких рентгеновых лучей. Понятно, что в области видимого света, имеющего длину волны в тысячи ангстрем, практически почти невозможно обнаружить ее изменение на сотые доли ангстрема. Кроме того, и формула (11) для этого случая не пригодна, так как при взаимодействии с фотонами видимого света электроны вещества уже нельзя считать свободными даже приближенно.
не зависит от длины волны рассеиваемого излучения и измеряется даже для больших углов рассеяния всего сотыми долями ангстрема. Однако этот сдвиг длины волны по порядку величины близок к длине волны гамма-лучей, и поэтому явление Комптона легко наблюдать при рассеянии гамма-лучей и жестких рентгеновых лучей. Понятно, что в области видимого света, имеющего длину волны в тысячи ангстрем, практически почти невозможно обнаружить ее изменение на сотые доли ангстрема. Кроме того, и формула (11) для этого случая не пригодна, так как при взаимодействии с фотонами видимого света электроны вещества уже нельзя считать свободными даже приближенно.
Внутренние электроны атомного остатка так сильно связаны с атомом, что при их взаимодействии даже с жесткими рентгеновыми лучами сказывается масса всего атома в целом. Поэтому рассеяние на электронах атомного остатка происходит практически без изменения длины волны. В итоге при рассеянии периферическими и
внутренними электронами в рассеянном свете наряду с измененной длиной волны X имеется длина волны 
Опыты Комптона оставляли без внимания главный, прямой эффект давления света, т. е. в них не исследовалось движение электронов, вызванное соударением с фотоном (аналогичное движению крылышка радиометра в опытах Лебедева). Позже для изучения движения электронов отдачи в явлении Комптона были применены камеры Вильсона. Наиболее обстоятельное исследование электронов отдачи произвел Д. В. Скобельцын, применивший для этой цели магнитное поле. Из уравнений (9) и (10) нетрудно определить, как импульс и энергия электронов отдачи зависят от угла их вылета (рис. 338). В камере Вильсона трэки делают видимым каждый отдельный акт соударения фотона с электроном. Сравнения полученных таким способом результатов с теоретическими с еще большей наглядностью подтвердили справедливость корпускулярной картины явления. Придерживаясь только волновой теории света, было бы невозможно объяснить, почему электрон в одном акте отдачи получает такие большие порции энергии и импульса, которые наблюдаются на опыте.
В 1923 г. Бор, Крамере и Слэтер высказали сомнение в справедливости закона сохранения энергии для отдельных актов рассеяния. Они предположили, что рассеяние света происходит непрерывно, а электроны отдачи вылетают совершенно случайно, так что баланс энергии оправдывается только статистически для больших промежутков времени.
Однако уже в 1925 г. непосредственными опытами была доказана полная необоснованность сомнений в строгой выполнимости законов сохранения энергии и импульса при каждом акте рассеяния. В опытах Боте и Гейгера при помощи двух счетчиков (счетчика фотонов и счетчика электронов) была установлена полная одновременность возникновения рассеянного фотона и электрона отдачи. Кроме того, исследования углов вылета электронов и фотонов с одновременным определением по методу Скобельцына энергии электронов однозначно подтвердили справедливость уравнений (9) и (10).
В 1936 г. Шенкланд на основании опытов с гамма-лучами опять пытался возобновить точку зрения Бора, Крамерса и Слэтера, но тщательная проверка его опытов, проведенная многими физиками, в том числе и советскими, показала полную ошибочность полученных им результатов.
В настоящее время можно считать неопровержимо доказанным, что законы сохранения энергии и импульса совершенно строго соблюдаются при каждом акте рассеяния. Здесь, как и во всех других случаях, подтвердилось, что законы сохранения энергии, массы и импульса непосредственно связаны с самыми фундаментальными свойствами движущейся материи и никогда не нарушаются,
| << Предыдущий параграф | Следующий параграф >> |
- ЧАСТЬ ЧЕТВЕРТАЯ. ОПТИКА
- § 2. Электромагнитная теория света
- § 3. Скорость света
- § 4. Опыт Майкельсона
- § 5. Отрицательный результат опыта Майкельсона и теория относительности
- § 6. Некоторые замечания о теории относительности
- § 7. Явление Доплера для световых волн
- ГЛАВА II. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- § 8. Законы отражения и преломления света
- § 9. Линза
- § 10. Оптические системы
- § 11. Глаз как оптическая система
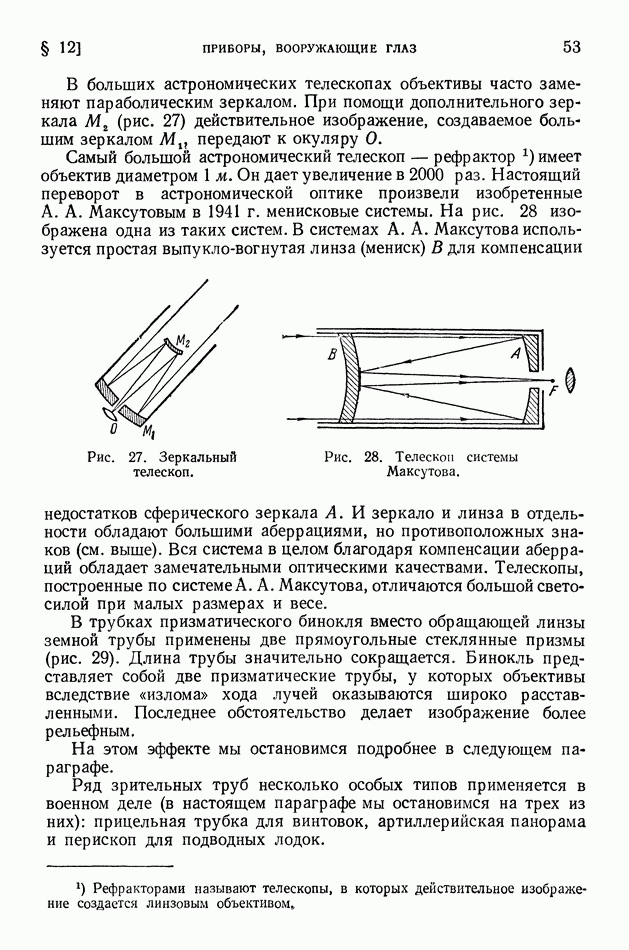
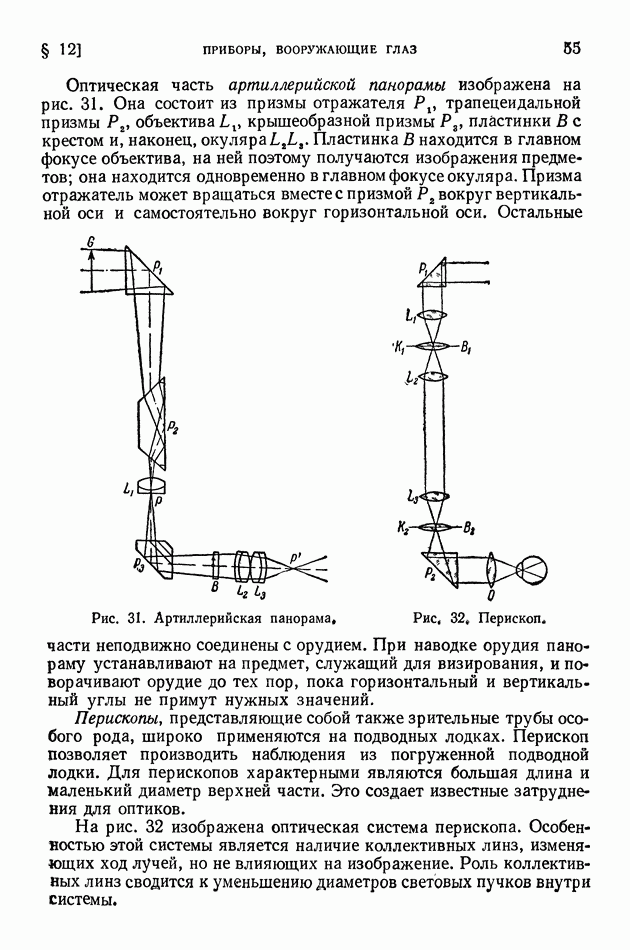
- § 12. Приборы, вооружающие глаз
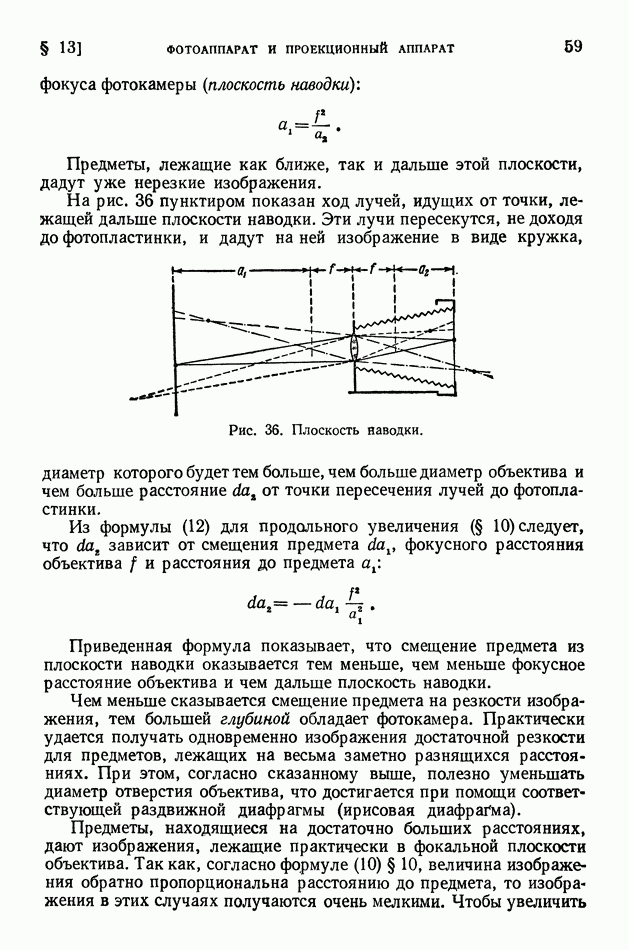
- § 13. Фотоаппарат и проекционный аппарат
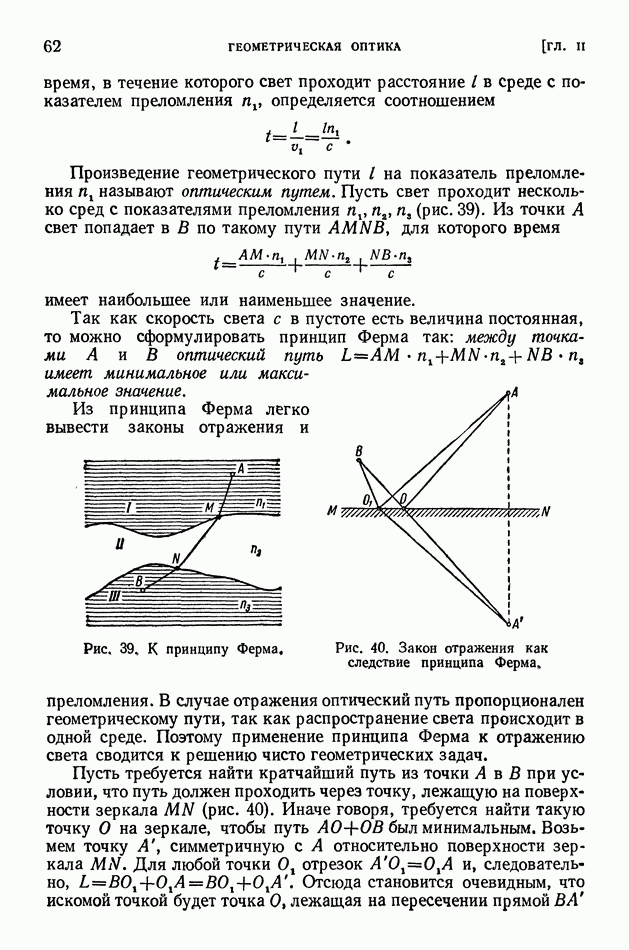
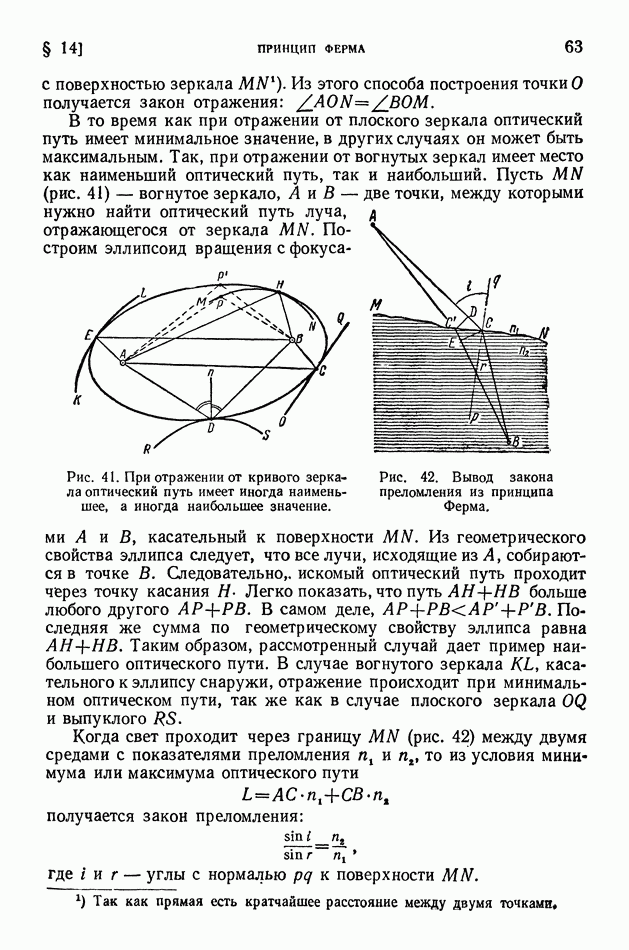
- § 14. Принцип Ферма
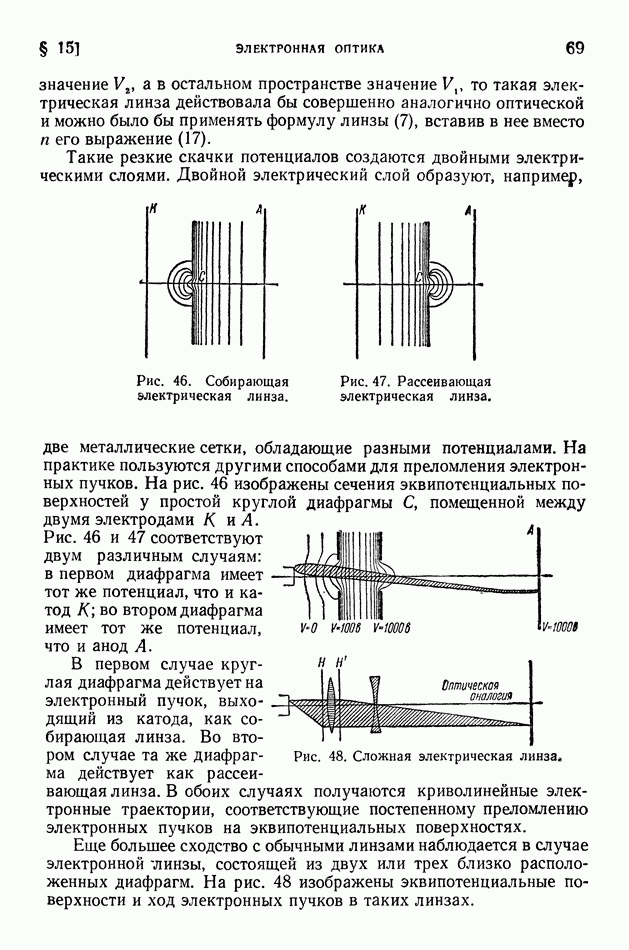
- § 15. Электронная оптика
- ГЛАВА III. ИНТЕРФЕРЕНЦИЯ СВЕТА
- § 16. Принцип суперпозиции. Когерентность
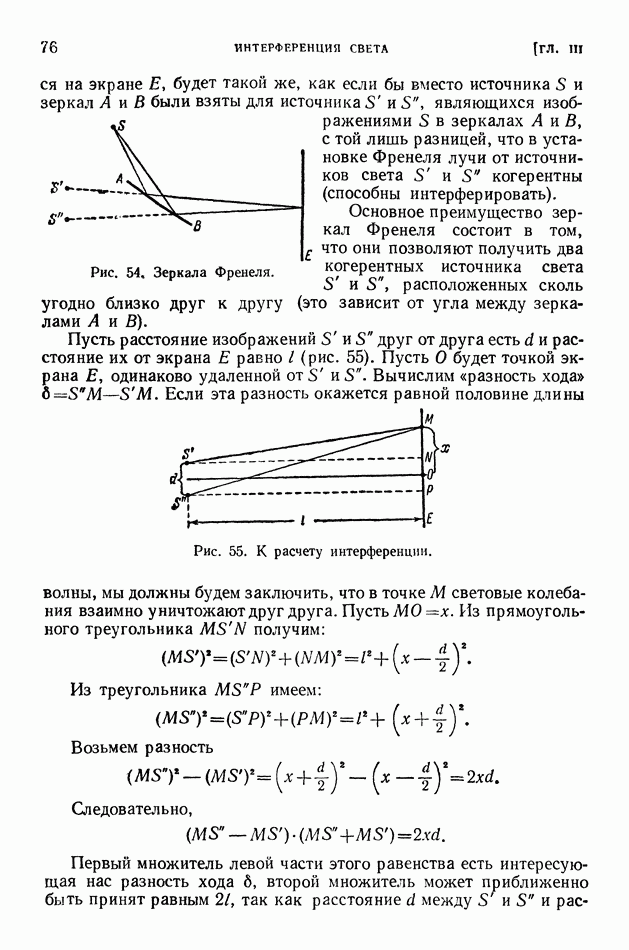
- § 17. Зеркала Френеля
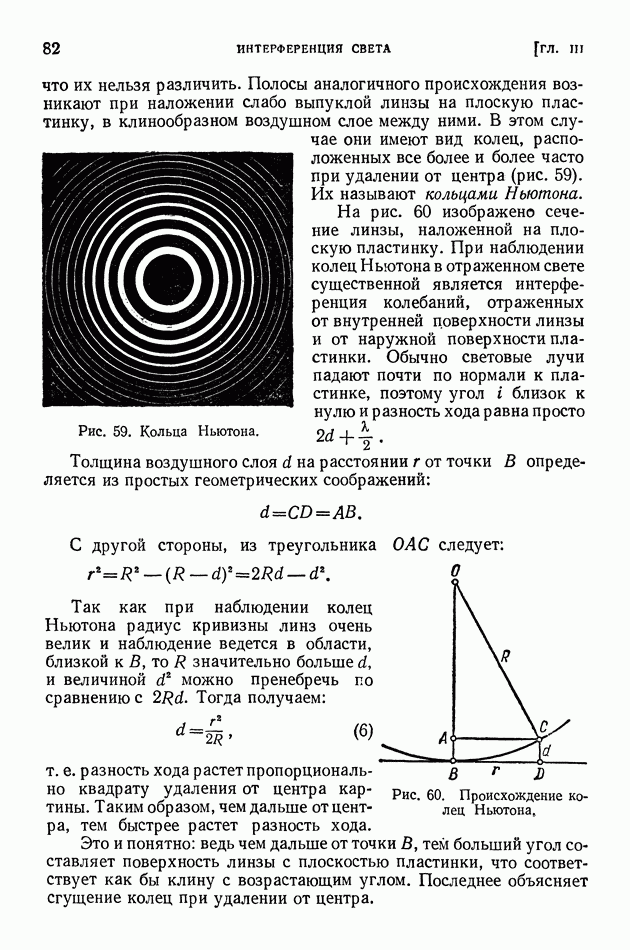
- § 18. Цвета тонких пленок. Полосы равной толщины
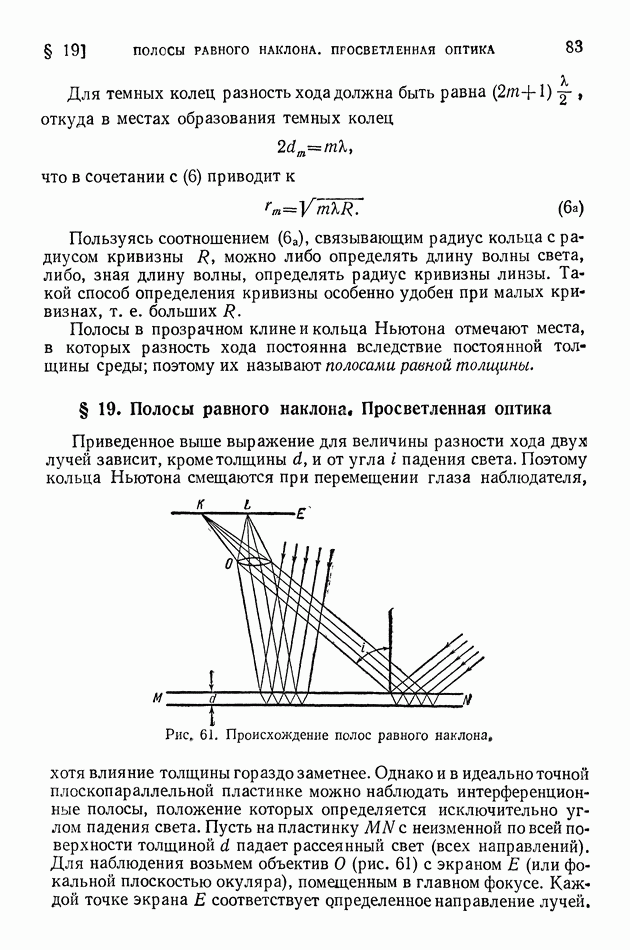
- § 19. Полосы равного наклона. Просветленная оптика
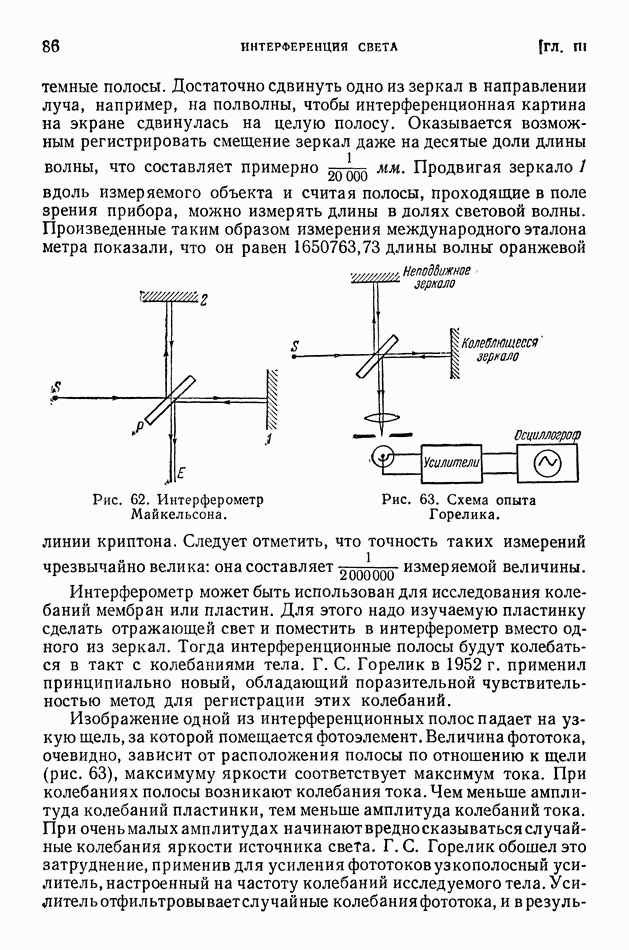
- § 20. Интерферометры
- § 21. Интерференционное измерение технических мер длины
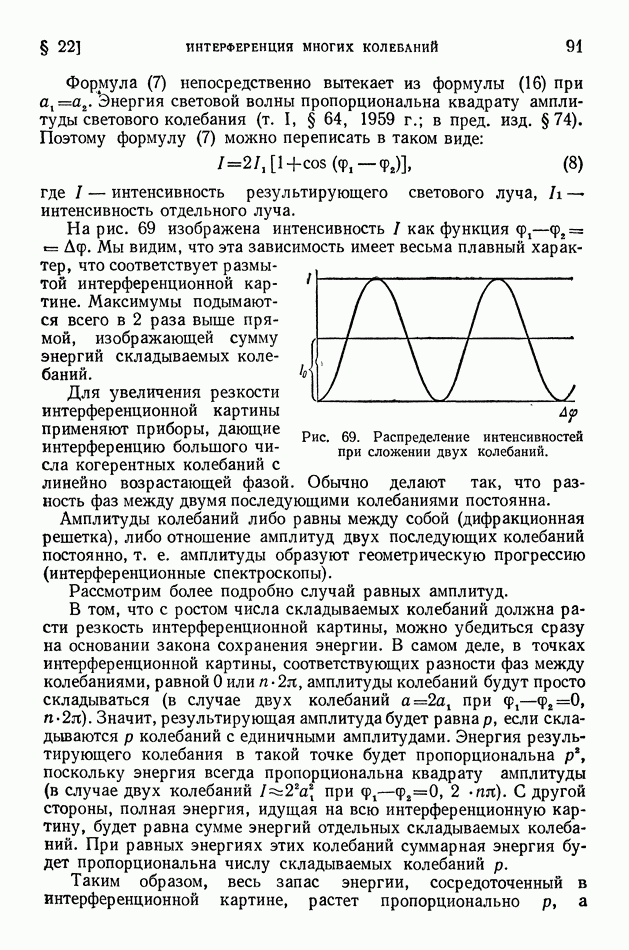
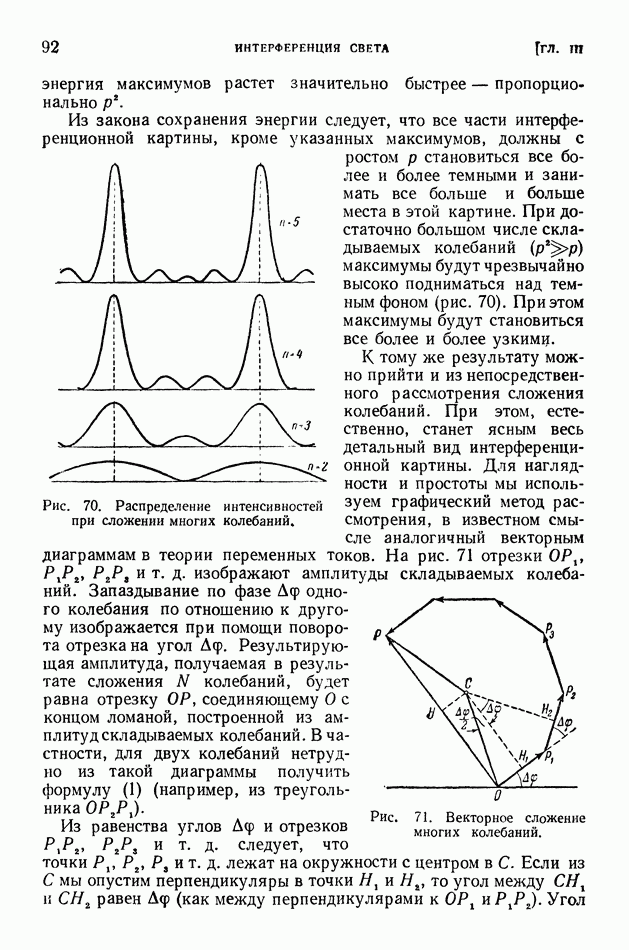
- § 22. Интерференция многих колебаний
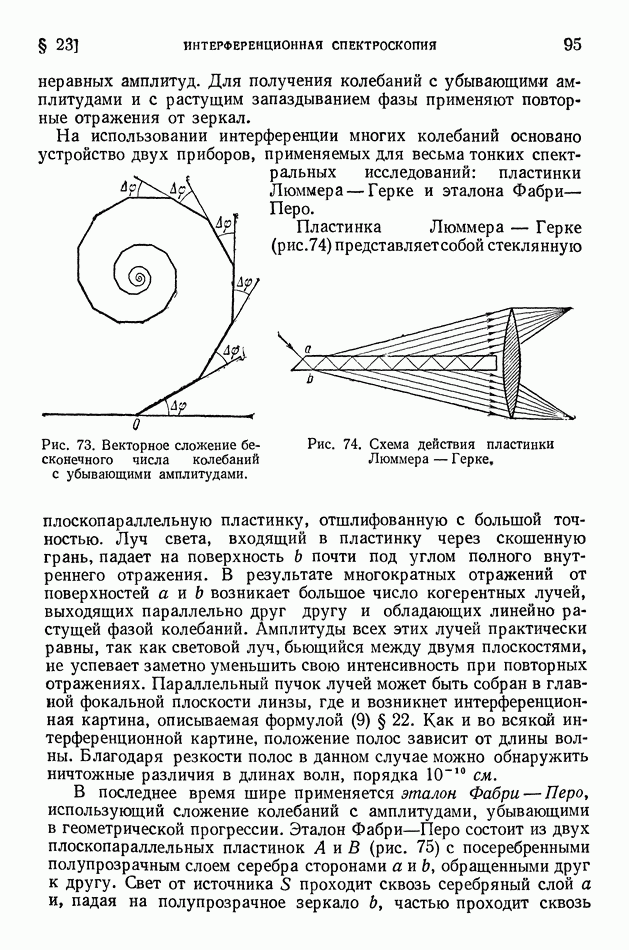
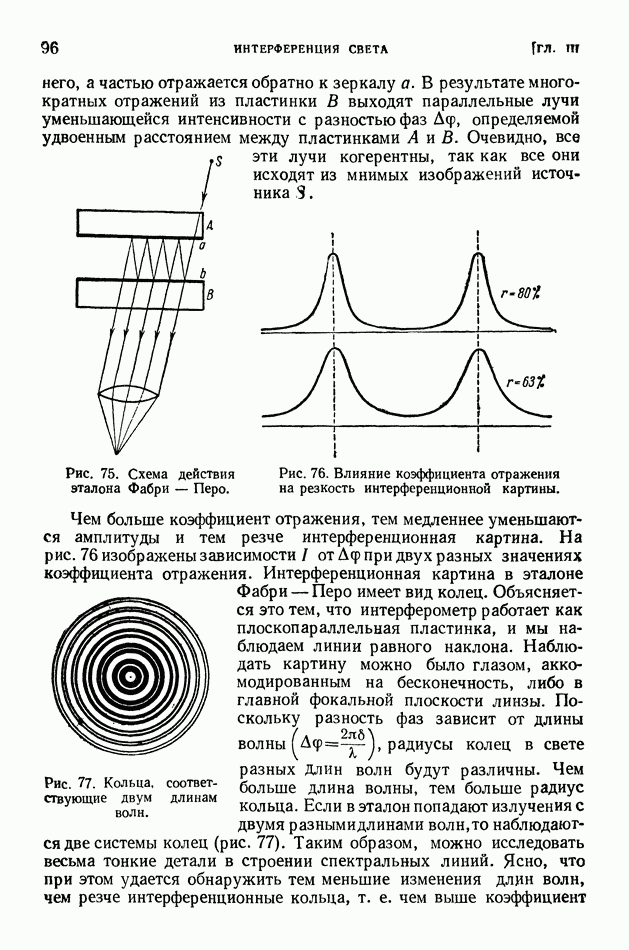
- § 23. Интерференционная спектроскопия
- ГЛАВА IV. ДИФРАКЦИЯ СВЕТА
- § 24. Явление дифракции. Опыт Френеля
- § 25. Принцип Гюйгенса-Френеля
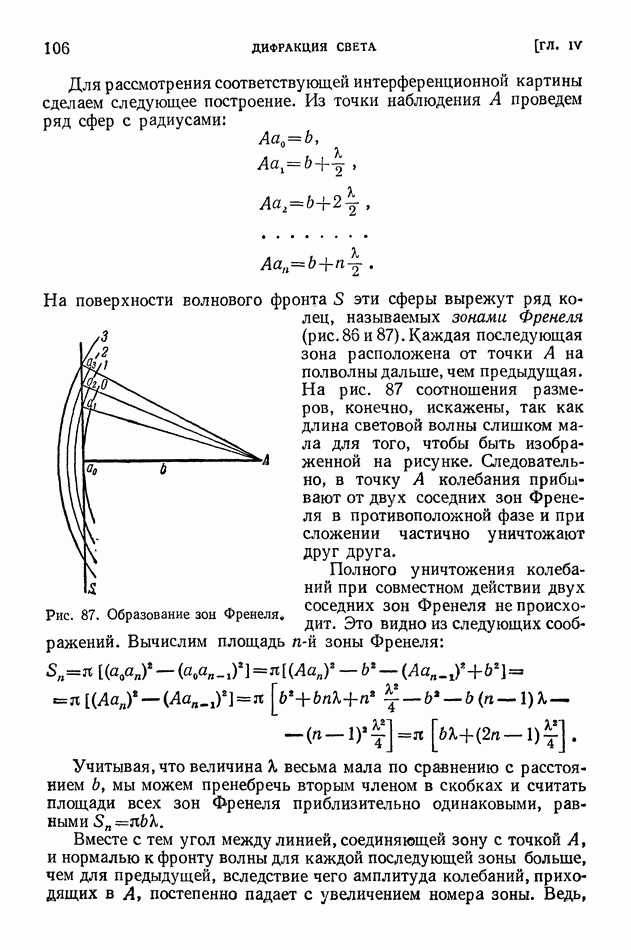
- § 26. Метод зон Френеля
- § 27. Дифракция от узкой щели
- § 28. Дифракционная решетка
- § 29. Дифракционный спектр. Решетки Роуланда и эшелон Майкельсона
- § 30. Плоскостные решетки. Пространственная решетка
- § 31. Структурный рентгеновский анализ
- § 32. Дифракция света на ультразвуковых волнах
- § 33. Дифракция от мелких частиц
- § 34. Разрешающая способность оптических инструментов. Звездный интерферометр
- ГЛАВА V. ПОЛЯРИЗАЦИЯ СВЕТА
- § 35. Поляризация света
- § 36. Двойное лучепреломление
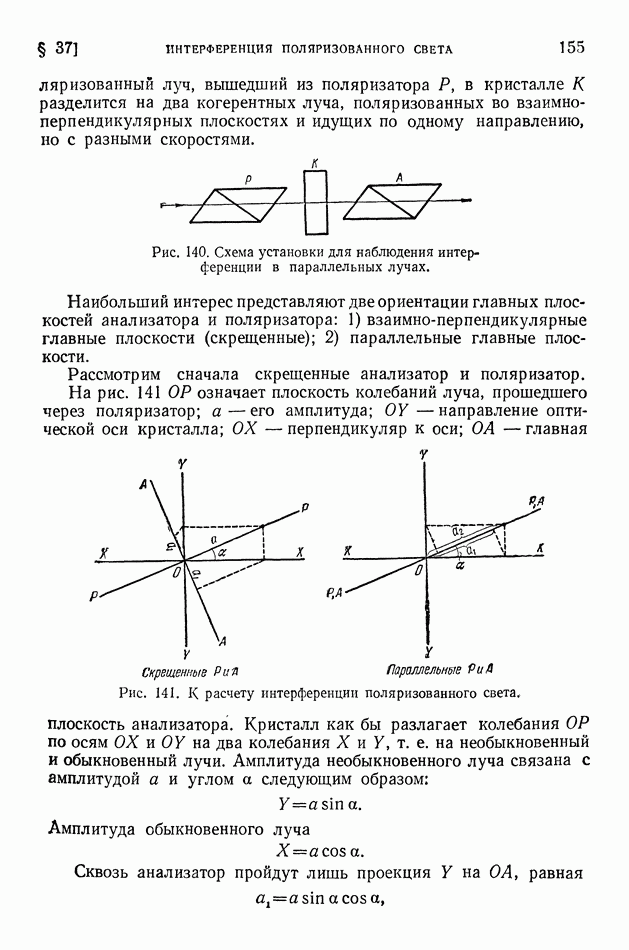
- § 37. Интерференция поляризованного света
- § 38. Оптический метод исследования упругих натяжений. Эффект Керра
- § 39. Вращение плоскости поляризации. Эллиптическая поляризация
- ГЛАВА VI. ДИСПЕРСИЯ, ПОГЛОЩЕНИЕ И ИЗЛУЧЕНИЕ СВЕТА
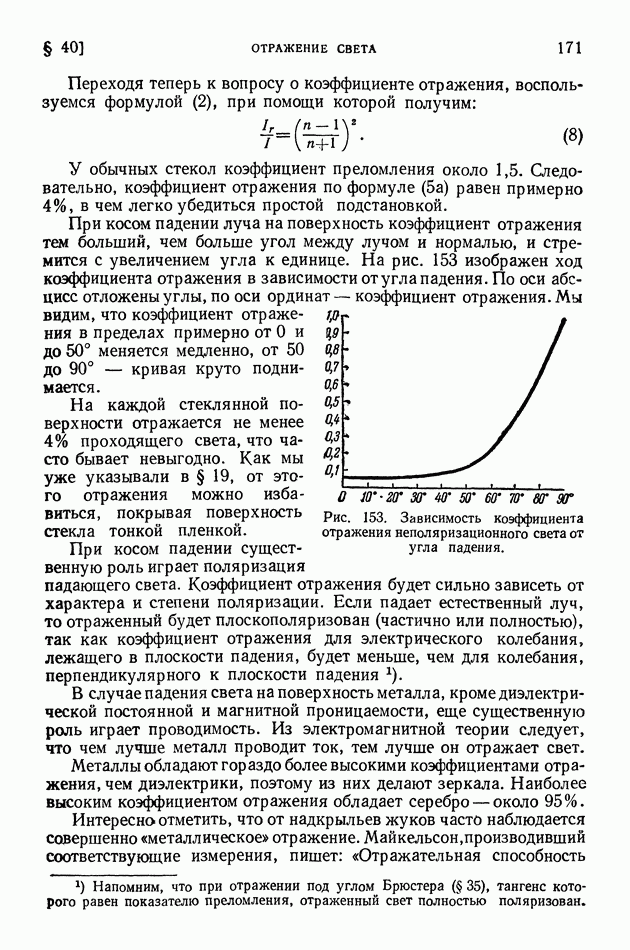
- § 40. Отражение света
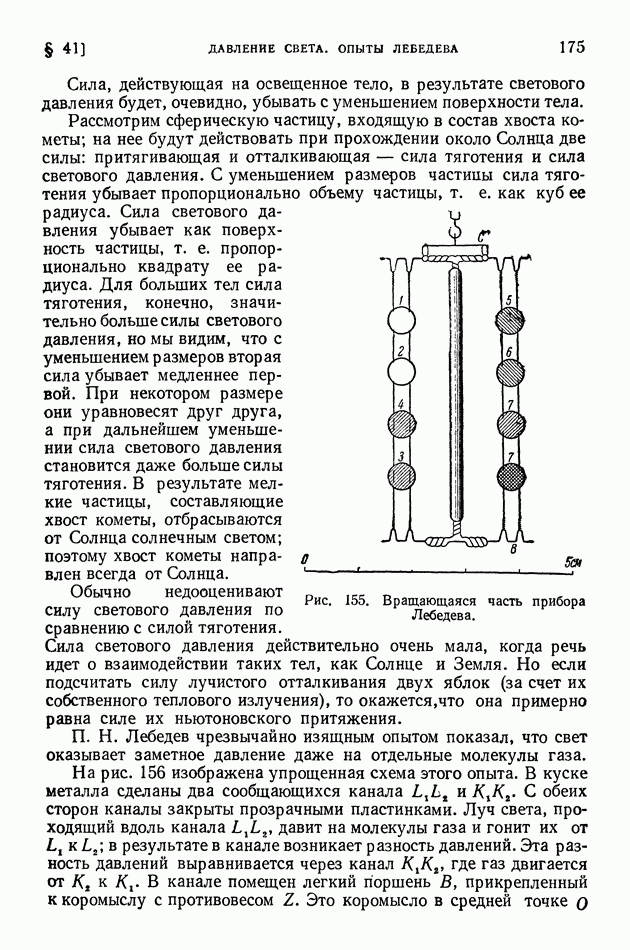
- § 41. Давление света. Опыты Лебедева
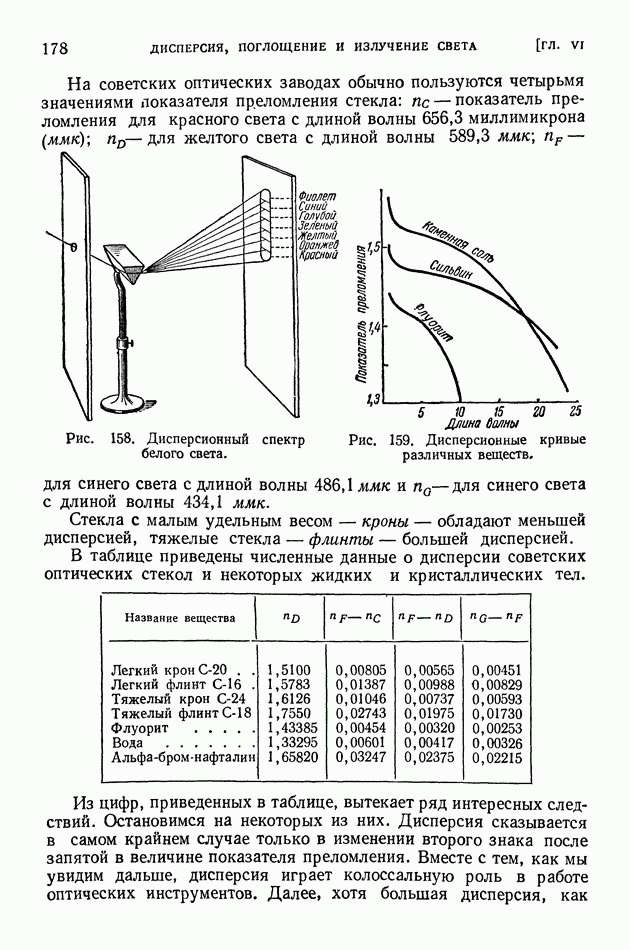
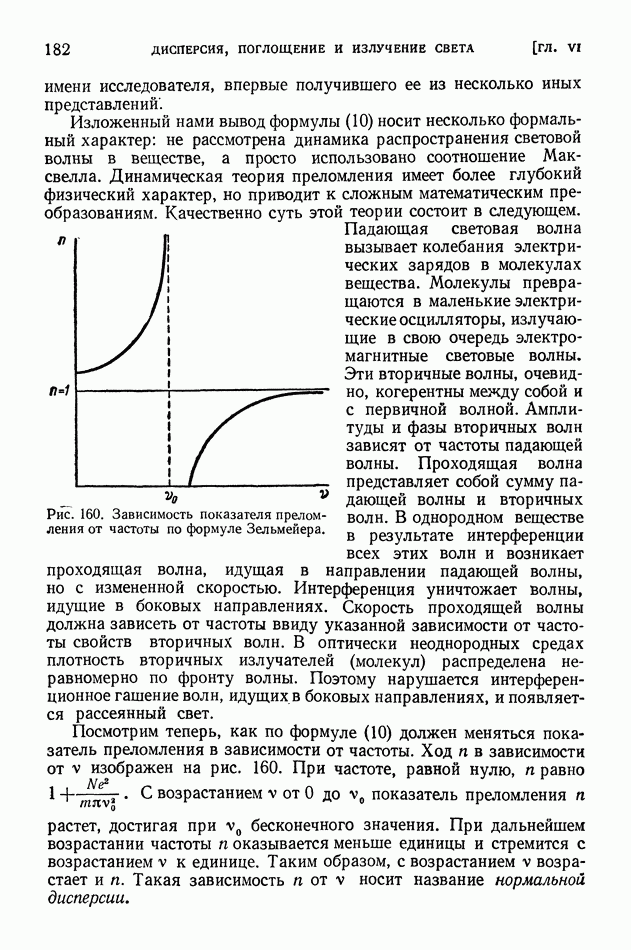
- § 42. Дисперсия. Опыты Ньютона
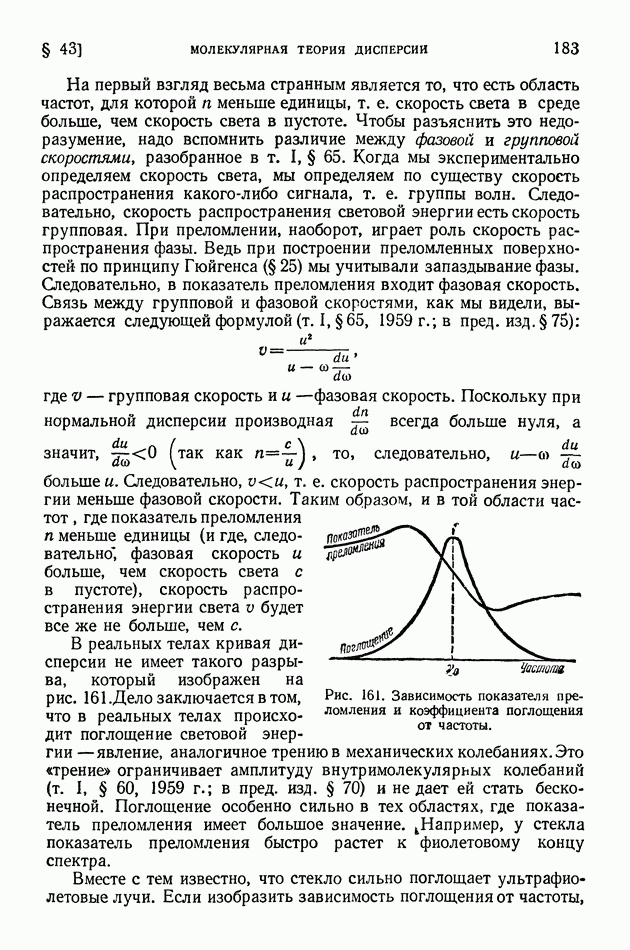
- § 43. Молекулярная теория дисперсии
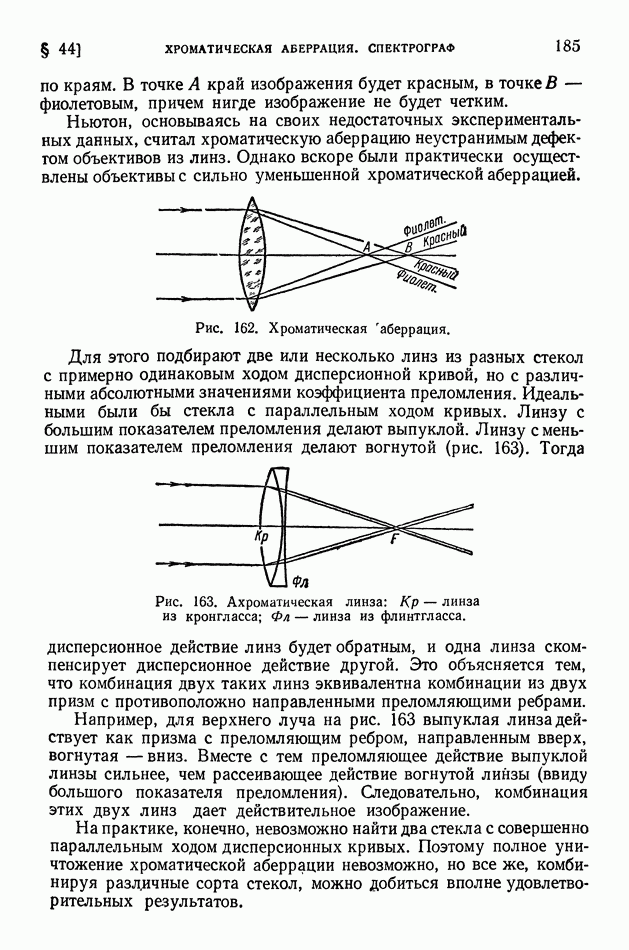
- § 44. Хроматическая аберрация. Спектрограф
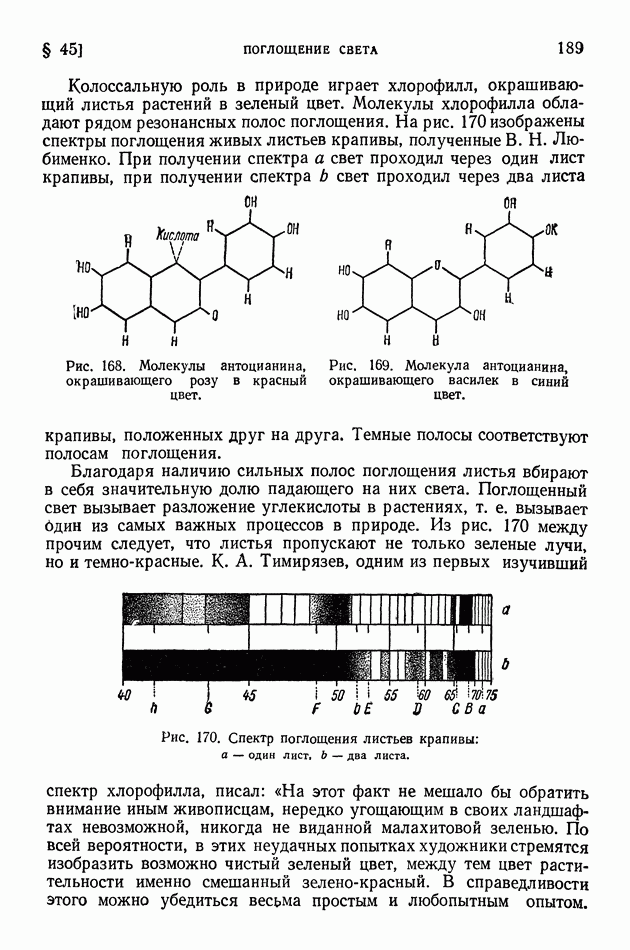
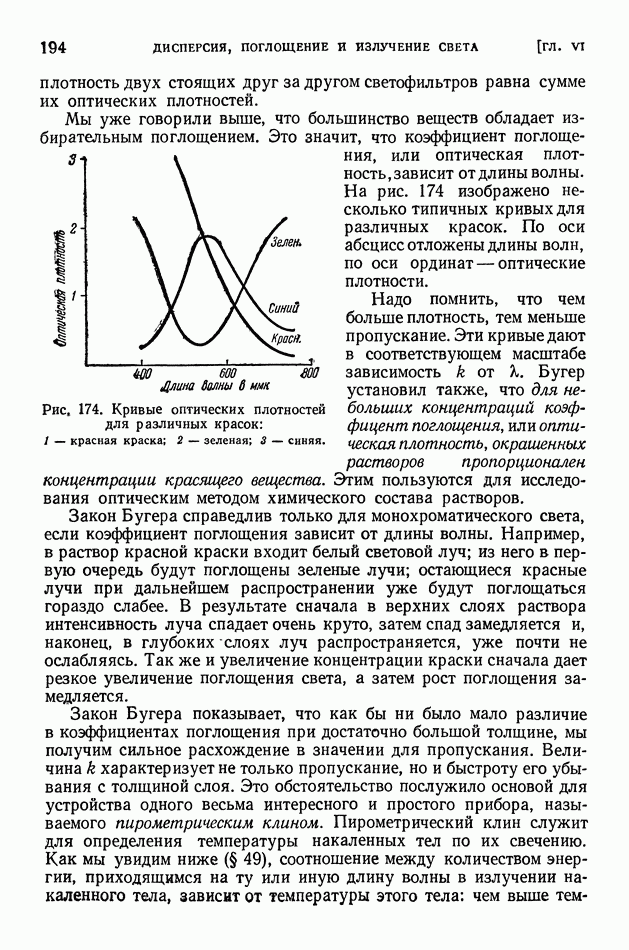
- § 45. Поглощение света
- § 46. Закон Бугера. Опыты Вавилова
- § 47. Атом как элементарный излучатель света
- § 48. Эффект Вавилова — Черенкова
- ГЛАВА VII. ТЕРМОДИНАМИКА ИЗЛУЧЕНИЯ И СВЕТОВОЙ ПОТОК
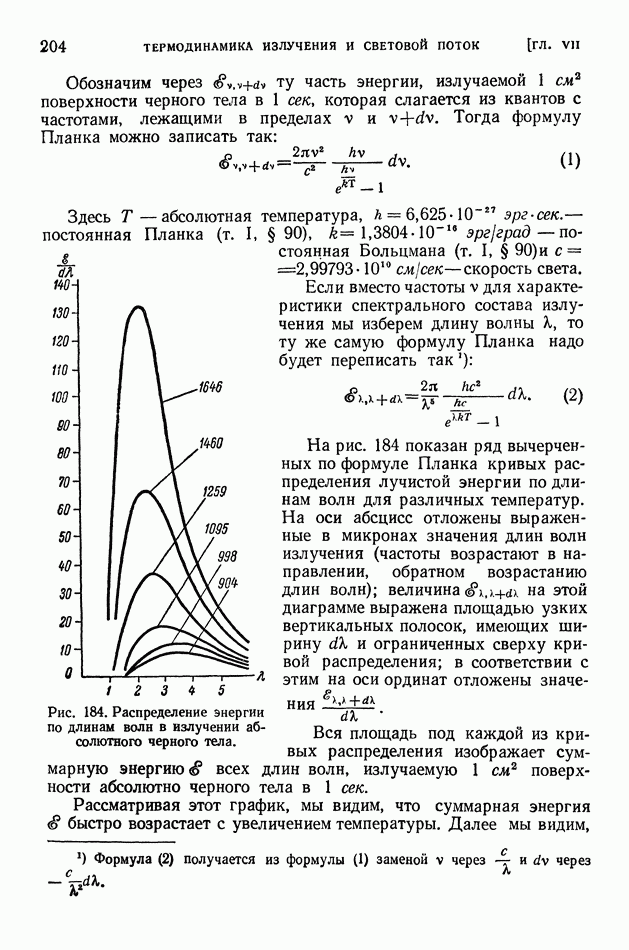
- § 49. Излучение черного тела. Формула Планка. Закон Вина
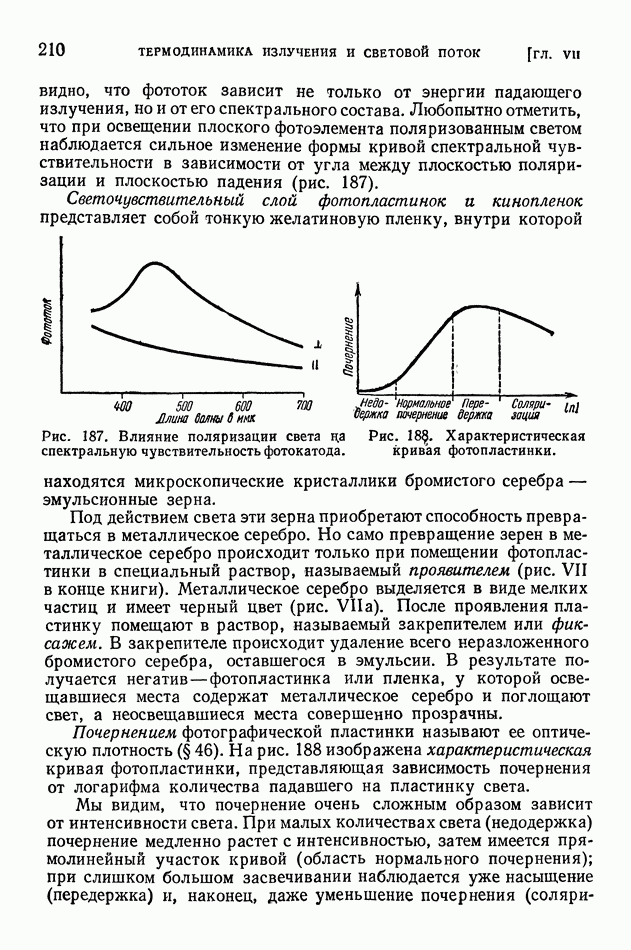
- § 50. Излучение нечерных тел. Законы Кирхгофа
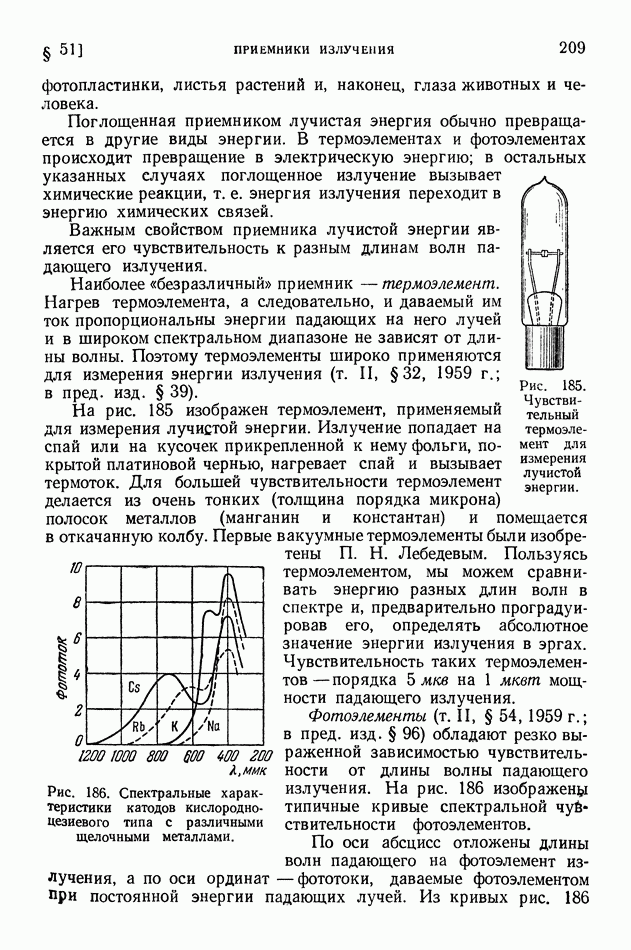
- § 51. Приемники излучения
- § 52. Световые величины и их измерения
- § 53 Температурные излучатели как источники света
- ЧАСТЬ ПЯТАЯ. АТОМНАЯ ФИЗИКА
- ГЛАВА VIII. СТРОЕНИЕ АТОМА И ТЕОРИЯ БОРА
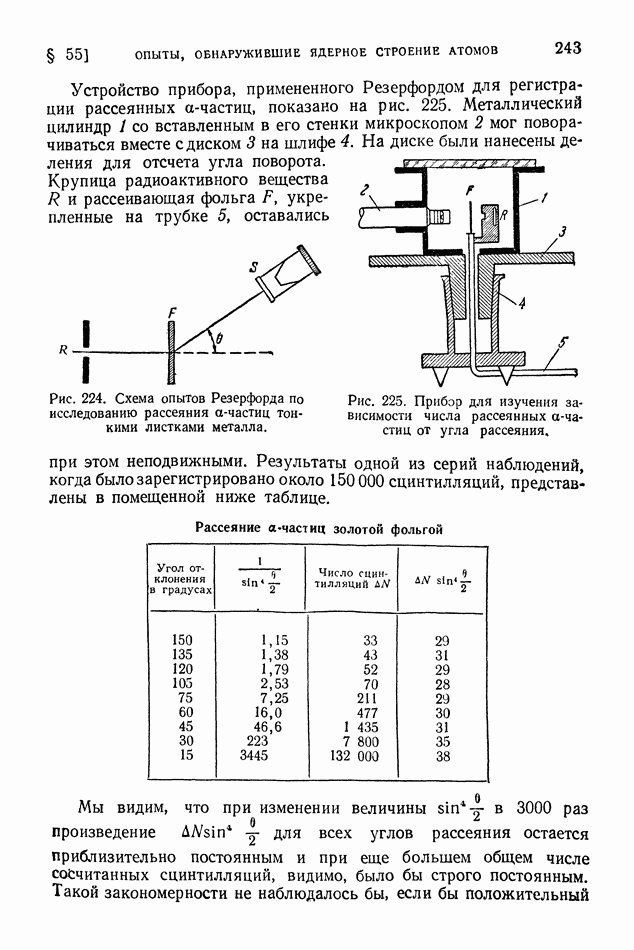
- § 55. Опыты, обнаружившие ядерное строение атомов
- § 56. Противоречие между фактическим строением атомов и выводами классической электродинамики. Строение линейчатых спектров
- § 57. Опытные основания теории квантов в первые годы ее развития
- § 58. Теория Бора. Происхождение спектра водорода
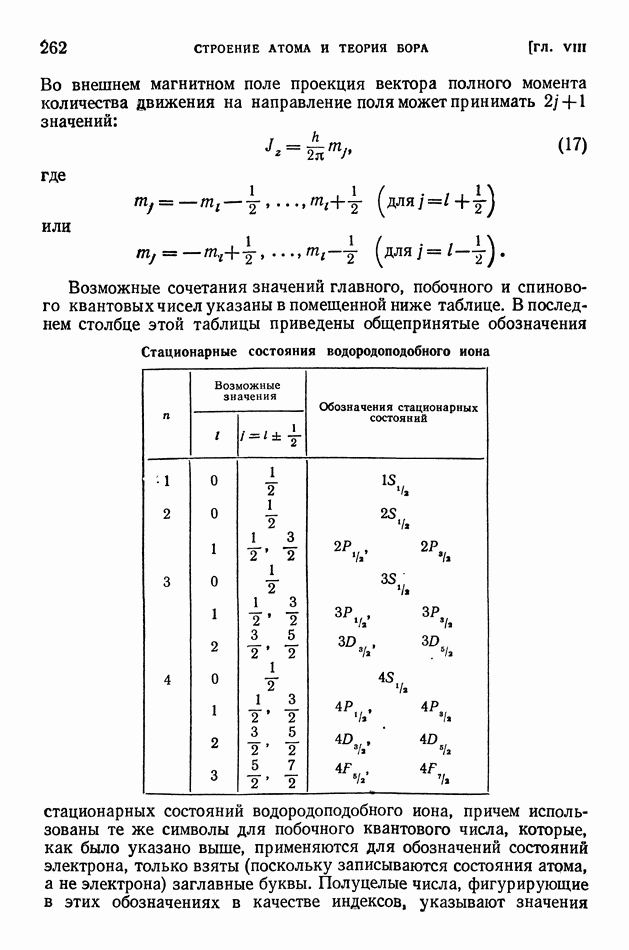
- § 59. Квантовые числа
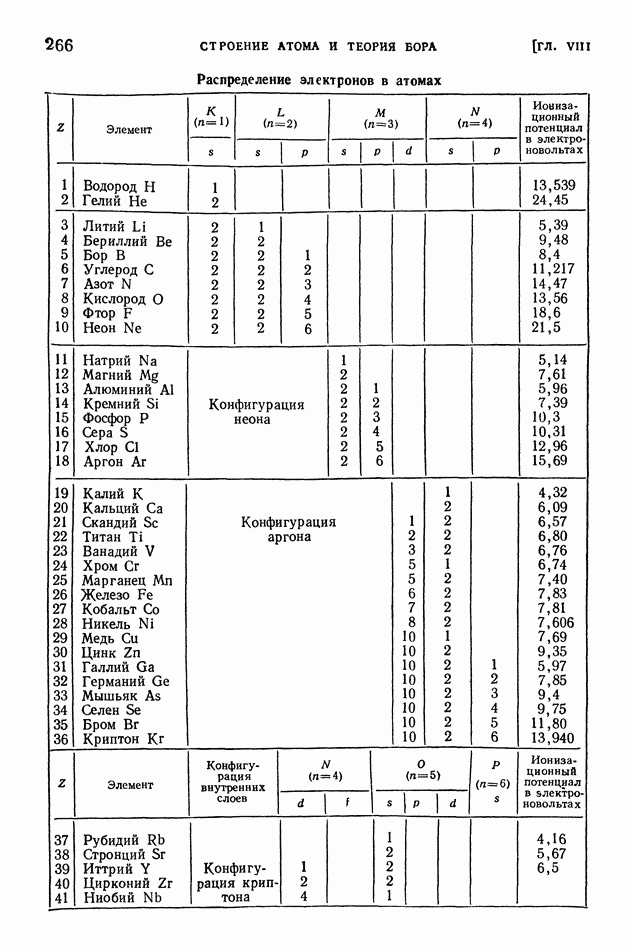
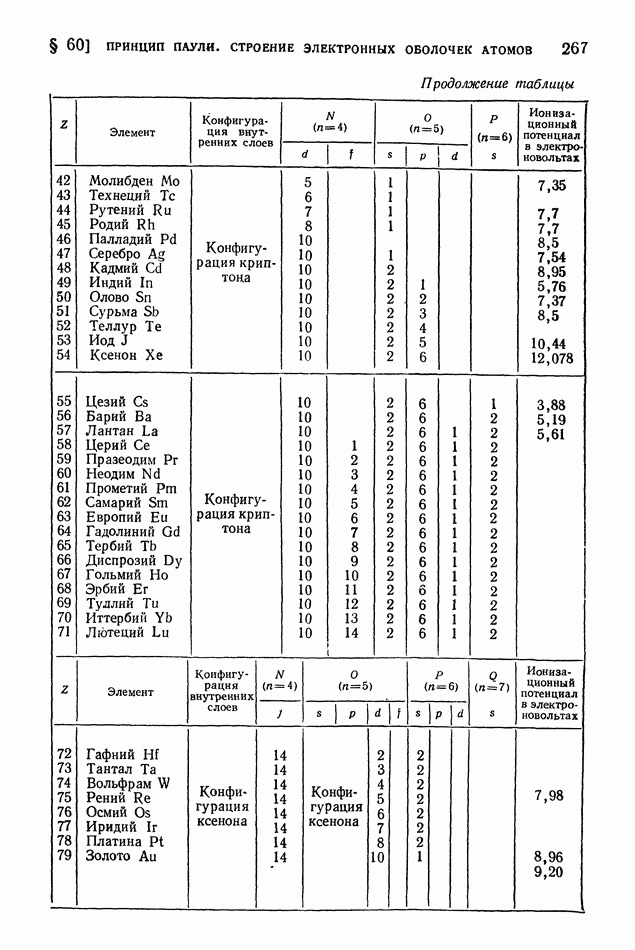
- § 60. Принцип Паули. Строение электронных оболочек атомов
- § 61. Общая картина возникновения спектров
- ГЛАВА IX. ОСНОВЫ КВАНТОВОЙ (ВОЛНОВОЙ) МЕХАНИКИ
- § 62. Волновые свойства частиц. Формула де Бройля. Дифракция электронов
- § 63. Уравнение Шредингера. Просачивание через энергетический барьер. Нулевая энергия
- § 64. Волномеханическая теория атома водорода
- § 65. Соотношение неопределенностей и его разные трактовки
- ГЛАВА X. КВАНТОВАЯ ОПТИКА
- § 66. Развитие квантовой оптики
- § 67. Спектр щелочных металлов. Спин электрона
- § 68. Спектр гелия. Символика спектральных термов
- § 69. Сверхтонкая структура спектральных линий
- § 70. Атом в силовом поле
- § 71. Молекулярные спектры и строение молекул
- § 72. Комбинационное рассеяние света
- § 73. Квантовая картина испускания света атомами и молекулами
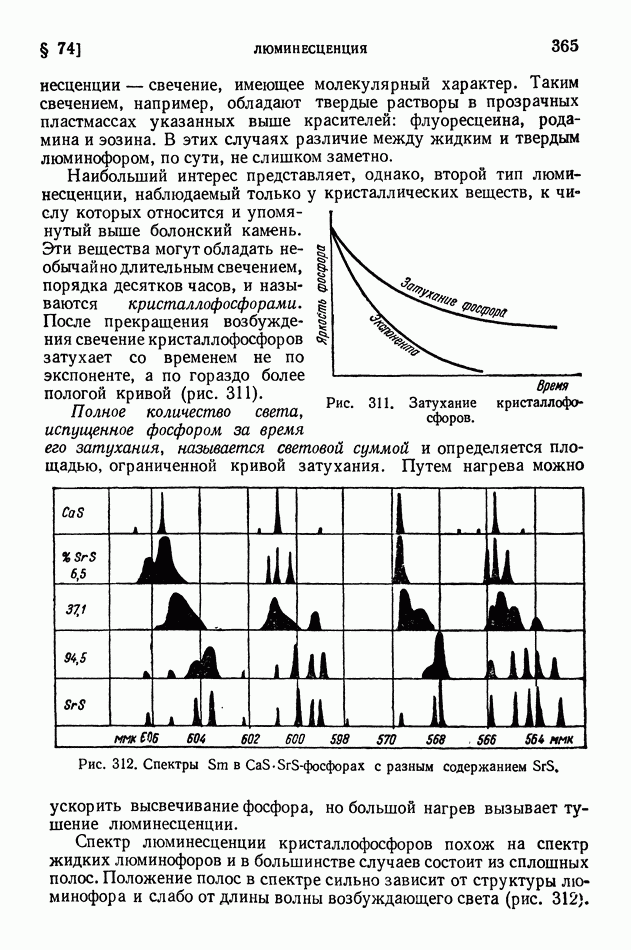
- § 74. Люминесценция
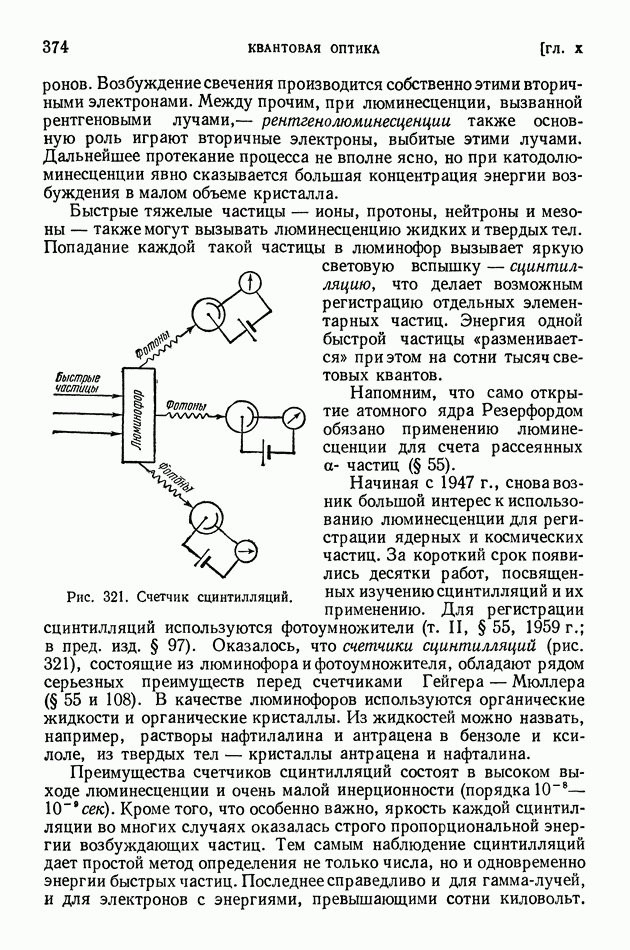
- § 75. Возбуждение люминесценции ударами частиц вещества
- § 76. Применения люминесценции
- § 77. Фотохимические реакции
- ГЛАВА XI. ЗАКОН ПРОПОРЦИОНАЛЬНОСТИ МАССЫ И ЭНЕРГИИ И РЕЛЯТИВИСТСКИЕ СООТНОШЕНИЯ
- § 78. Закон пропорциональности массы и энергии
- § 79. Предварительные замечания о релятивистских эффектах. Зависимость массы от скорости
- § 80. Корпускулярные свойства фотонов. Явление Комптона
- § 81. Вывод закона Эйнштейна сложения скоростей из закона пропорциональности массы и энергии и законов сохранения энергии или количества движения
- § 82. Две трактовки закона пропорциональности массы и энергии и уточнение закона тяготения
- § 83. Красное смещение спектральных линий. Поперечный эффект Доплера
- § 84. Влияние гравитационного поля на скорость света в вакууме и показатель преломления вакуума
- ЧАСТЬ ШЕСТАЯ. ЯДЕРНАЯ ФИЗИКА
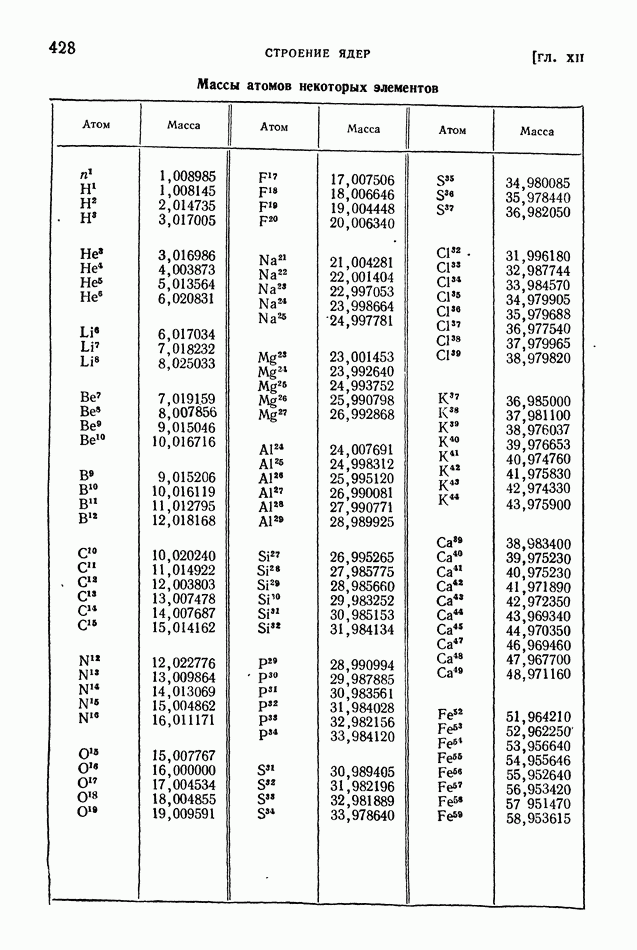
- § 85. Заряд и масса ядра. Масс-спектральный анализ
- § 86. Состав ядер. Изотопы. Атомные единицы массы и энергии
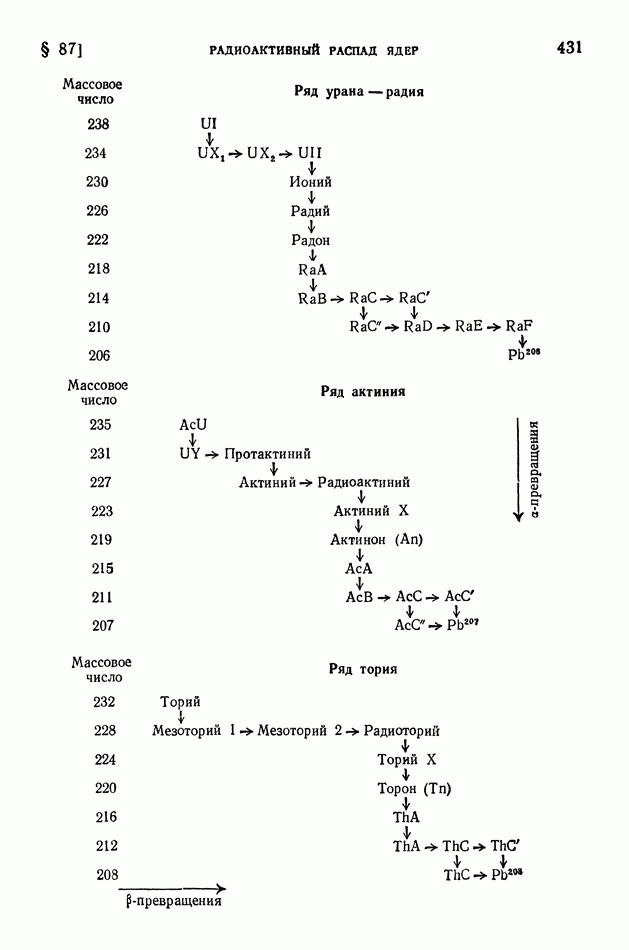
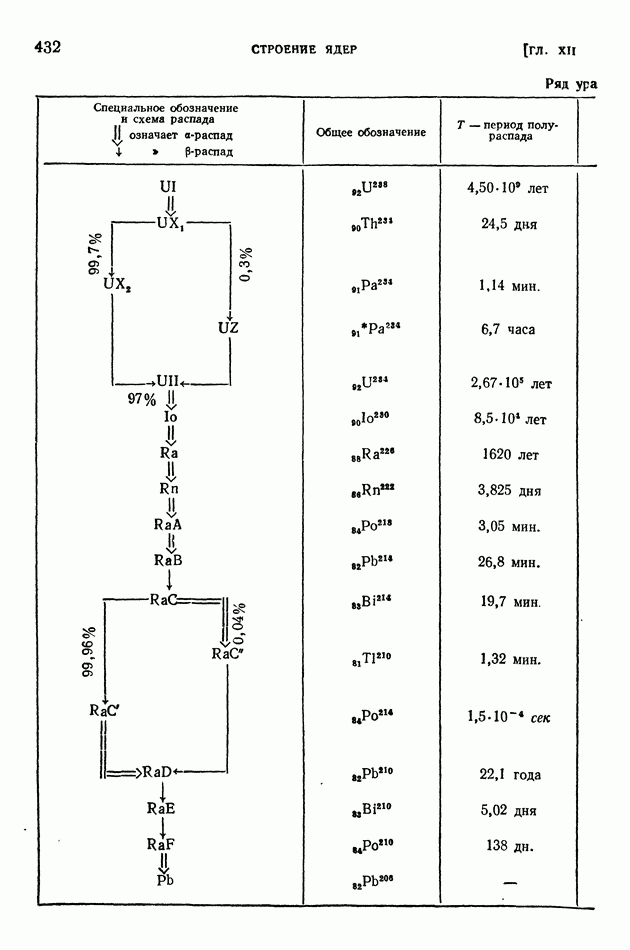
- § 87. Радиоактивный распад ядер. Закон радиоактивного смещения. Изомеры
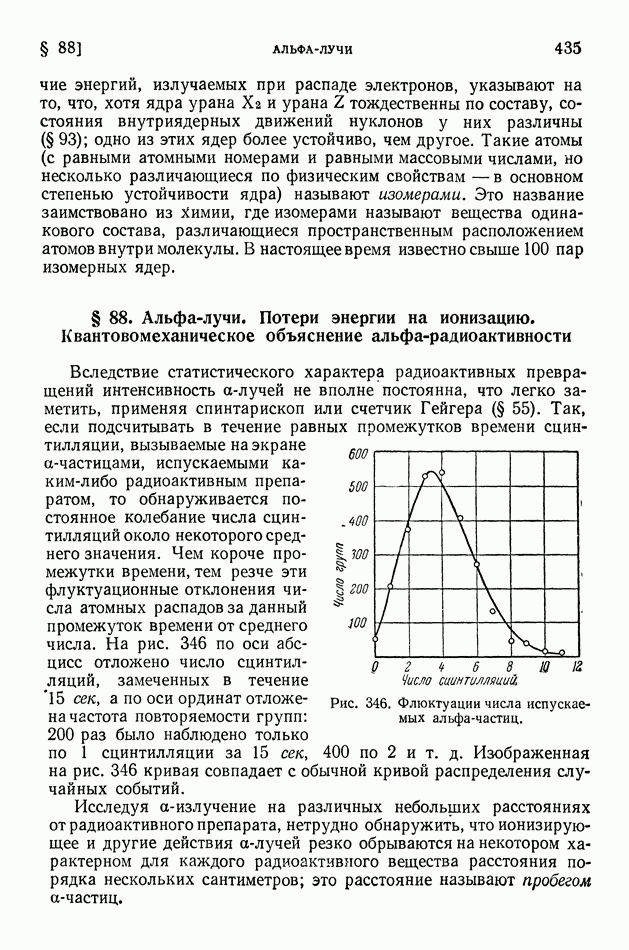
- § 88. Альфа-лучи. Потери энергии на ионизацию. Квантовомеханическое объяснение альфа-радиоактивности
- § 89. Бета- и гамма-лучи
- § 90. Искусственное расщепление ядер. Открытие нейтрона
- § 91. Открытие позитрона. Взаимопревращение фотонов определенной энергии и электронно-позитронных пар
- § 92. Индуцированная позитронная и электронная радиоактивность. Фоторасщепление ядер, K-захват
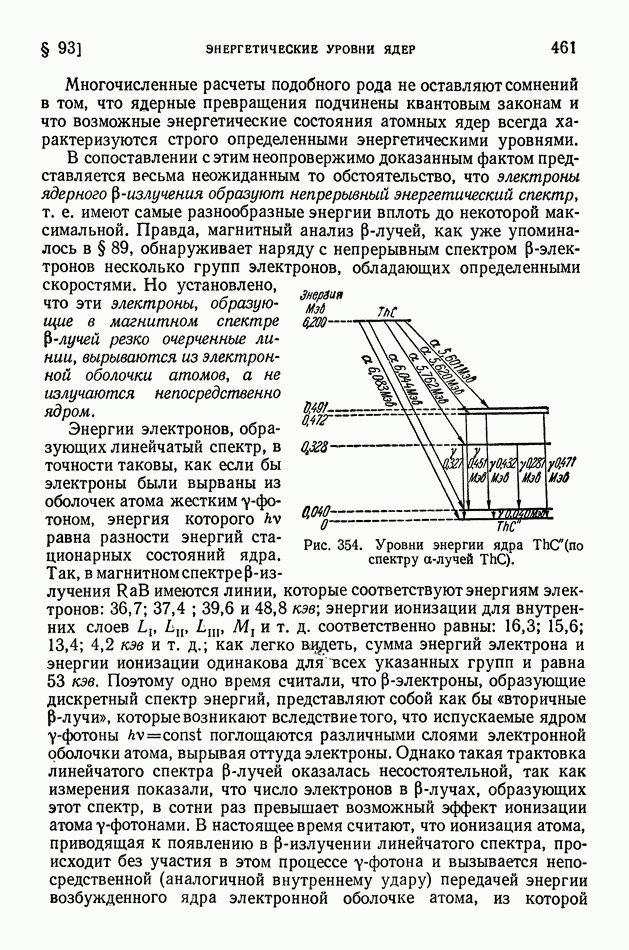
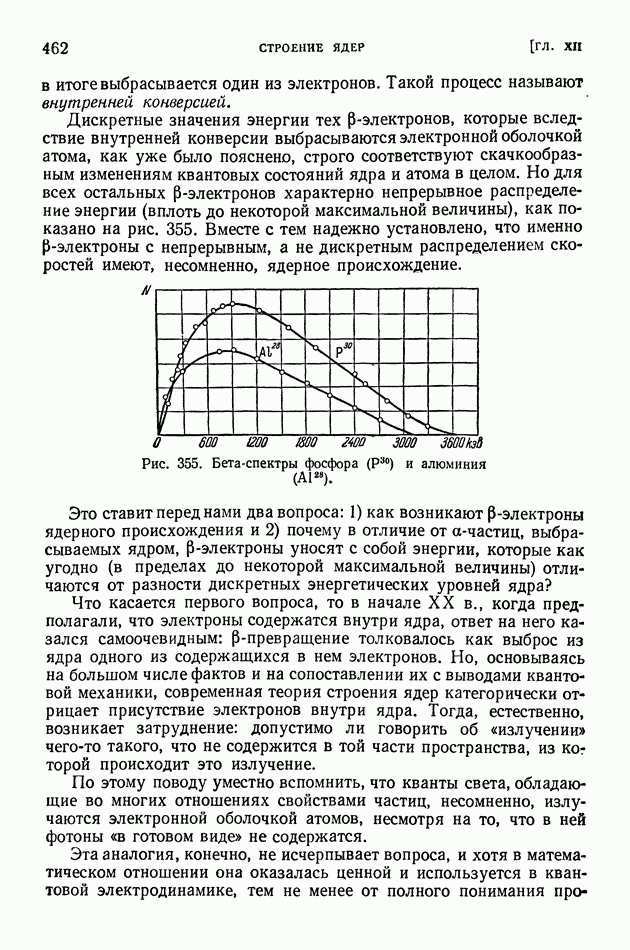
- § 93. Энергетические уровни ядер. Внутренняя конверсия. Нейтрино
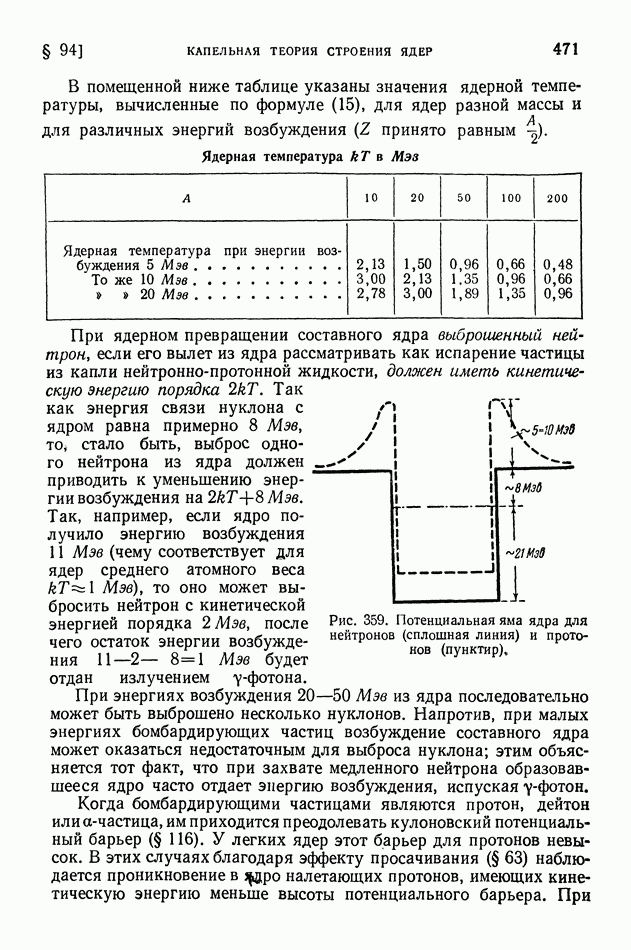
- § 94. Капельная теория строения ядер
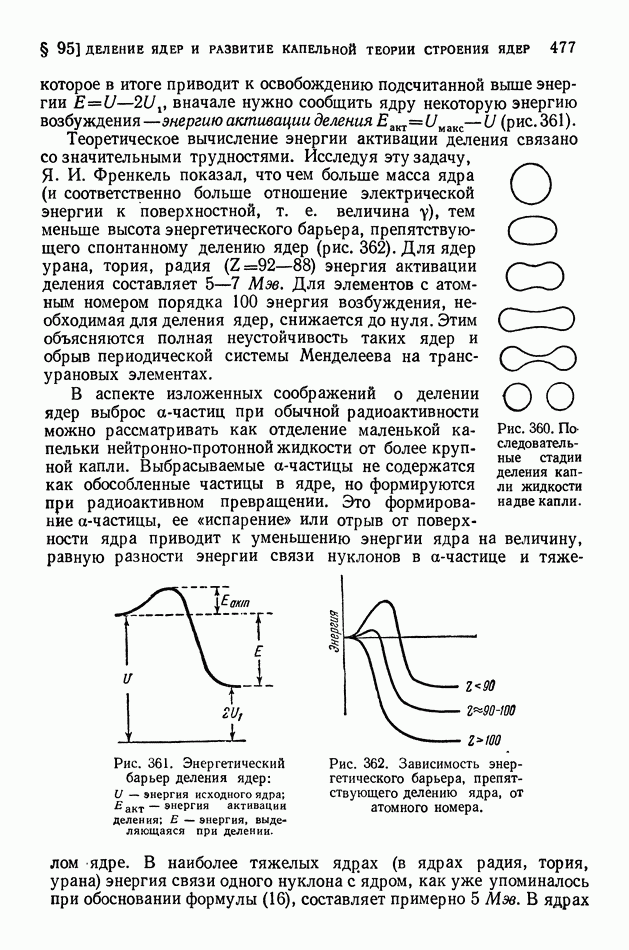
- § 95. Деление ядер и развитие капельной теории строения ядер
- ГЛАВА XIII. КОСМИЧЕСКИЕ ЛУЧИ
- § 96. Методы исследования и первые итоги изучения космических лучей
- § 97. Каскадное образование электронно-позитронных пар в космических лучах. Потери энергии электронами на тормозное излучение
- § 98. «мю»-мезоны. Зависимость времени жизни неустойчивых частиц от скорости движения
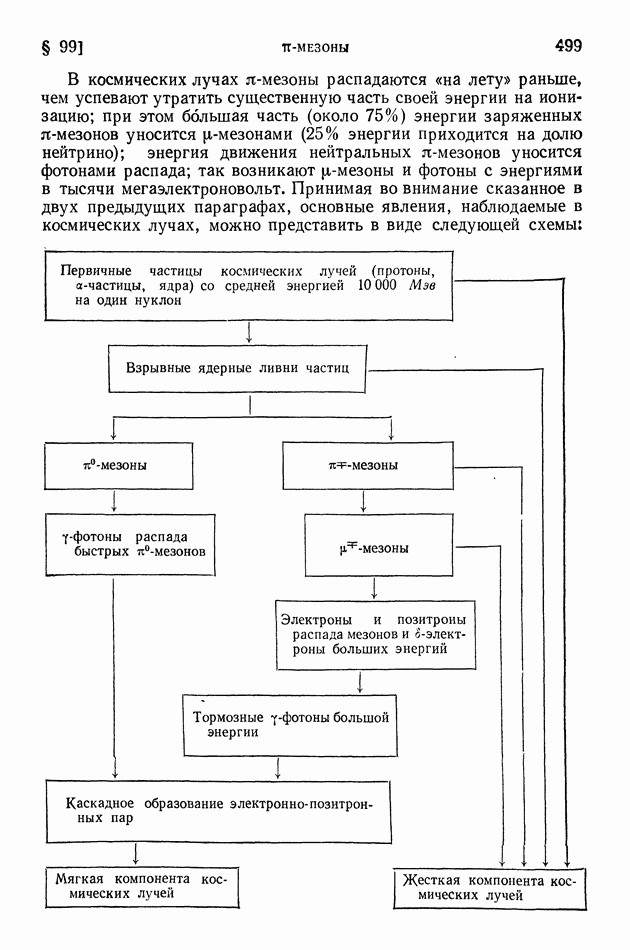
- § 99. «пи»-мезоны
- § 100. Взрывные ядерные ливни и их каскадное развитие в космических лучах
- § 101. Корпускулярный и энергетический спектр космических лучей. Происхождение космического излучения
- ГЛАВА XIV. ЭКСПЕРИМЕНТАЛЬНЫЕ СРЕДСТВА ЯДЕРНОЙ ФИЗИКИ
- § 102. Циклотроны
- § 103. Фазотроны
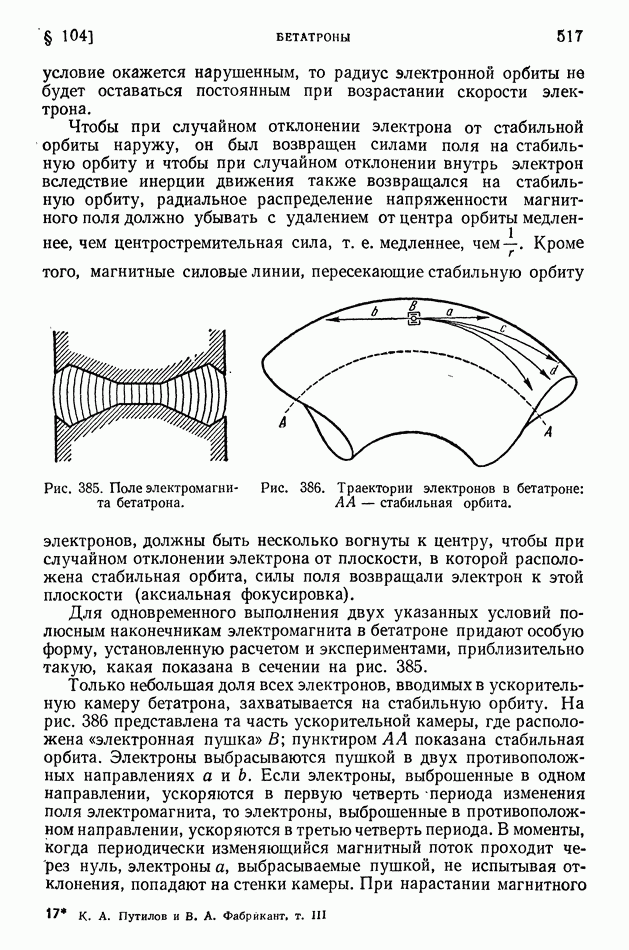
- § 104. Бетатроны
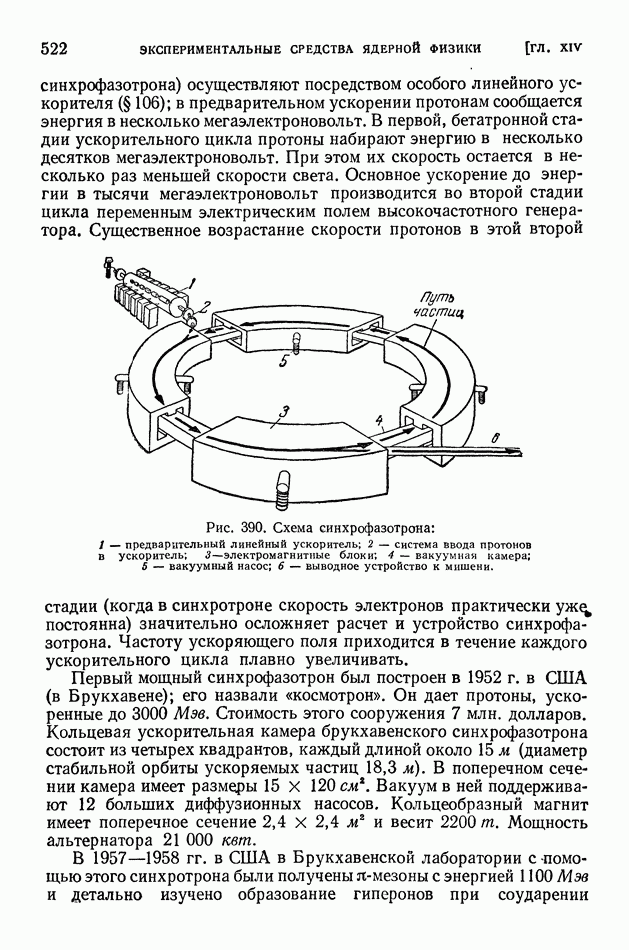
- § 105. Синхротроны и синхрофазотроны
- § 106. Линейные ускорители электронов и ионов
- § 107. Лабораторные источники нейтронов. Замедлители нейтронов в ядерных реакторах
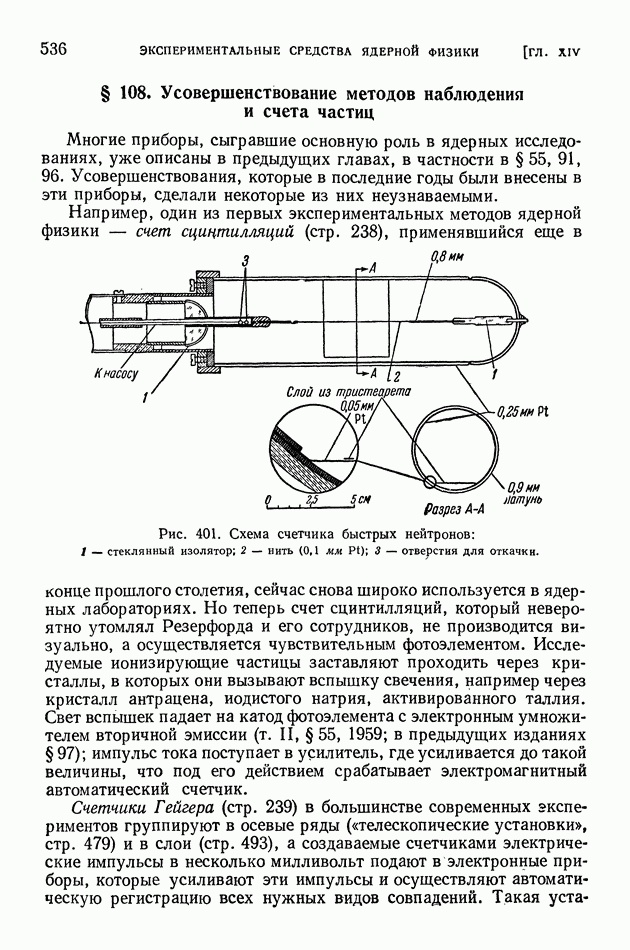
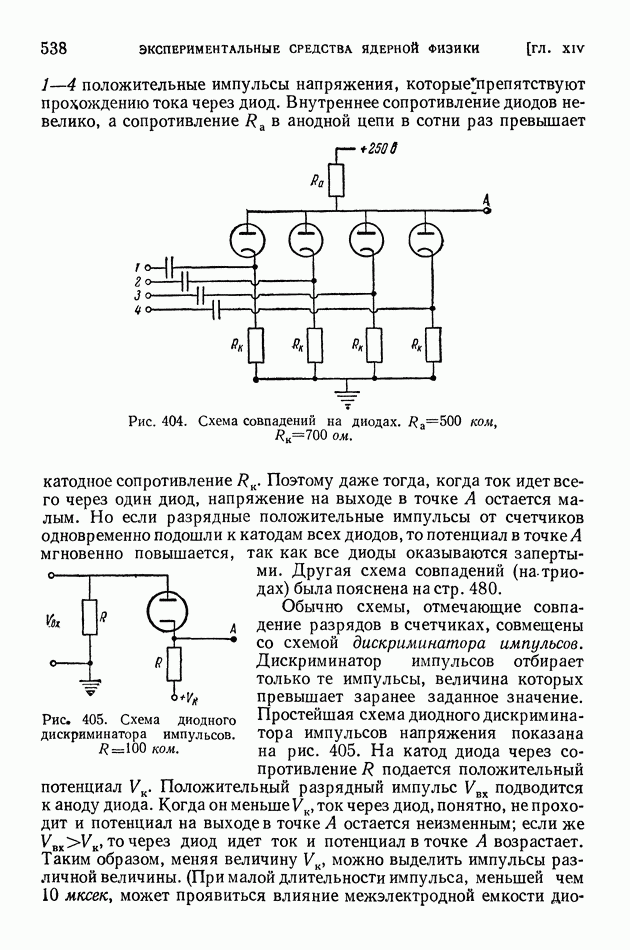
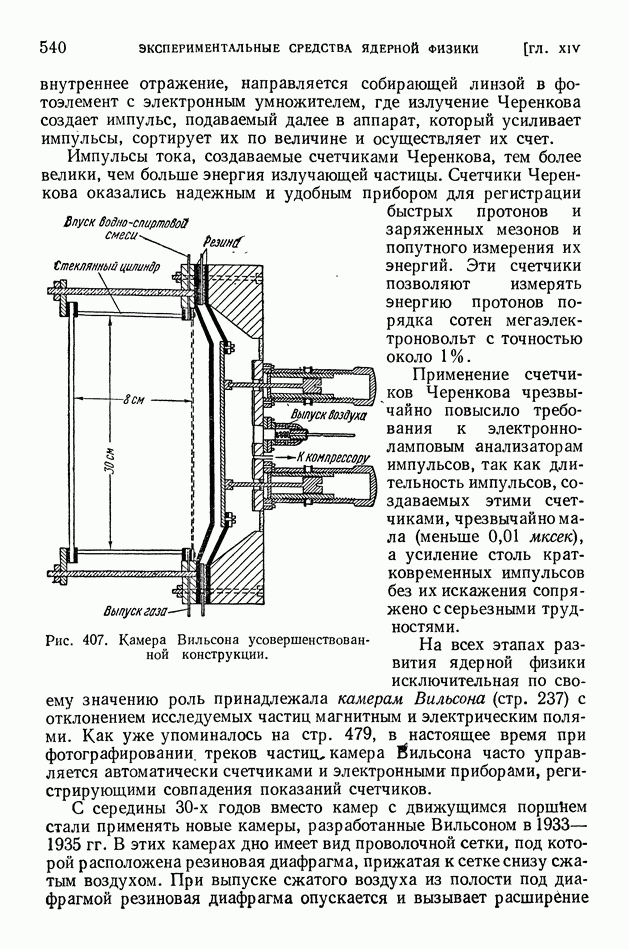
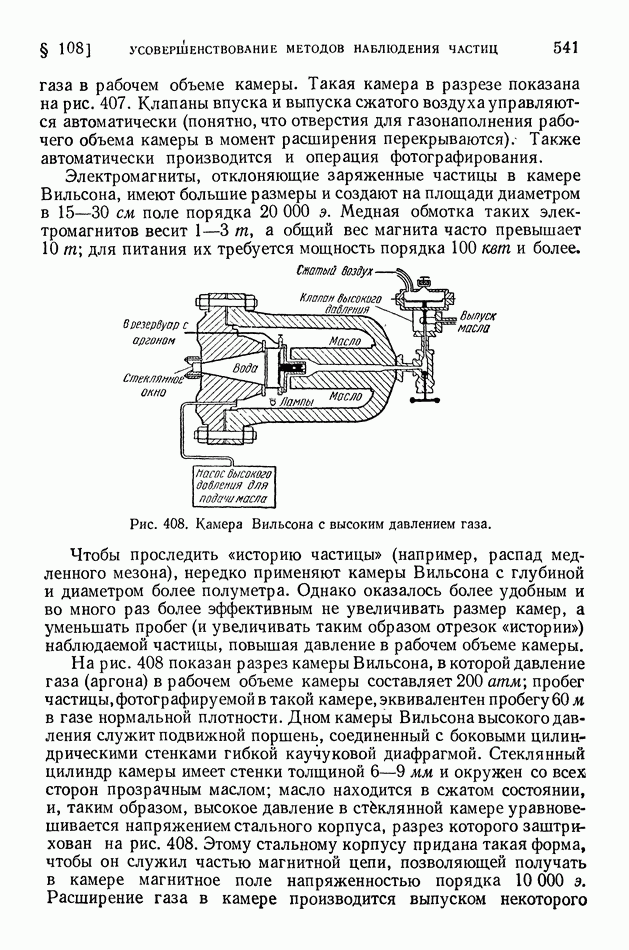
- § 108. Усовершенствование методов наблюдения и счета частиц
- ГЛАВА XV. ЯДЕРНЫЕ РЕАКЦИИ И АТОМНАЯ ЭНЕРГИЯ
- § 109. Основные виды и обозначения ядерных реакций. Конкурирующие процессы в ядерных реакциях
- § 110. Энергетический эффект, энергия возбуждения и порог ядерных реакций
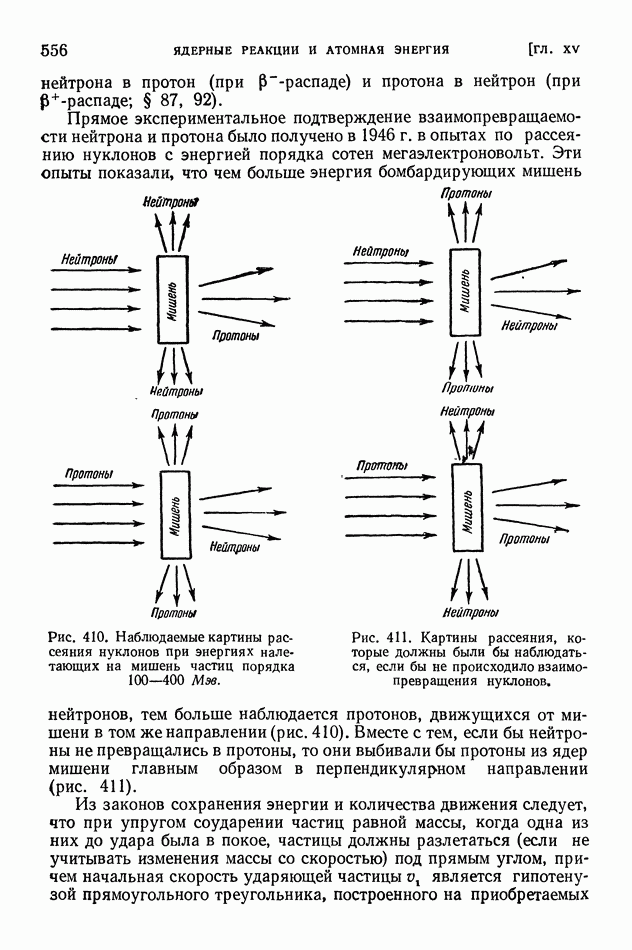
- § 111. Превращения элементарных частиц
- § 112. Ядерные силы
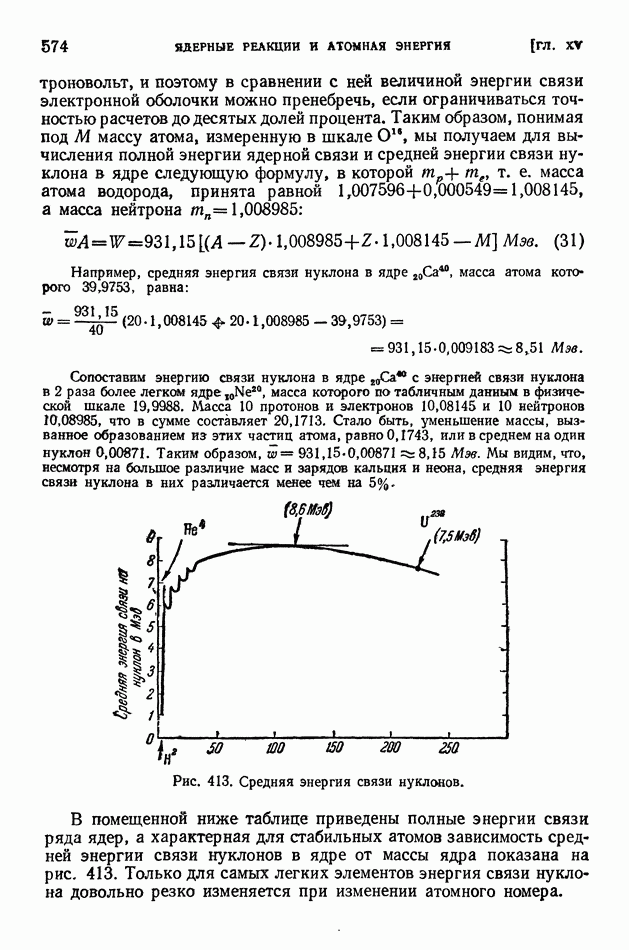
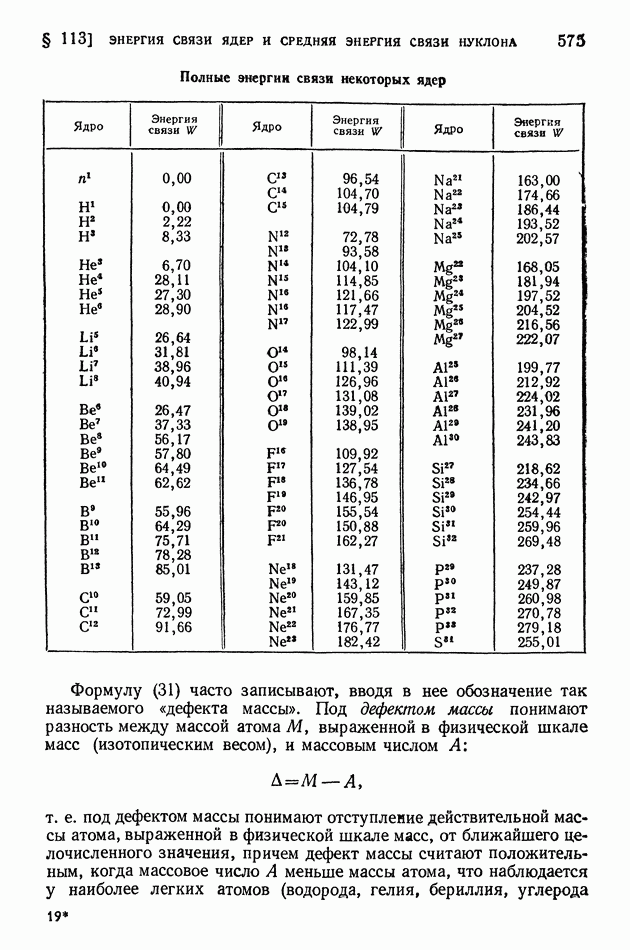
- § 113. Энергия связи ядер и средняя энергия связи нуклона
- § 114. Полуэмпирическая формула для энергии ядерной связи и для атомных энергий и масс
- § 115. Взаимосвязь энергии и строения ядер. Внутриядерное движение нуклонов и нуклонные оболочки. Спины и магнитные моменты ядер
- § 116. Энергия отделения частиц и анализ возможного хода ядерной реакции
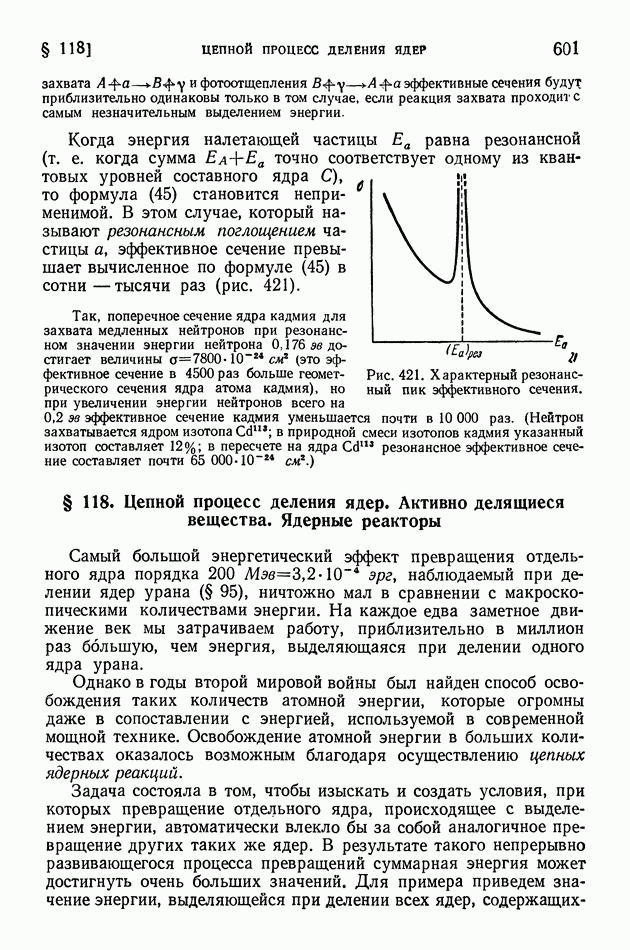
- § 117. Выход продуктов ядерной реакции. Эффективные сечения. Резонансные явления
- § 118. Цепной процесс деления ядер. Активно делящиеся вещества. Ядерные реакторы
- § 119. Термоядерные реакции
- § 120. Применение ядерных реакций
- § 121. Ядерные реакции в звездах