| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
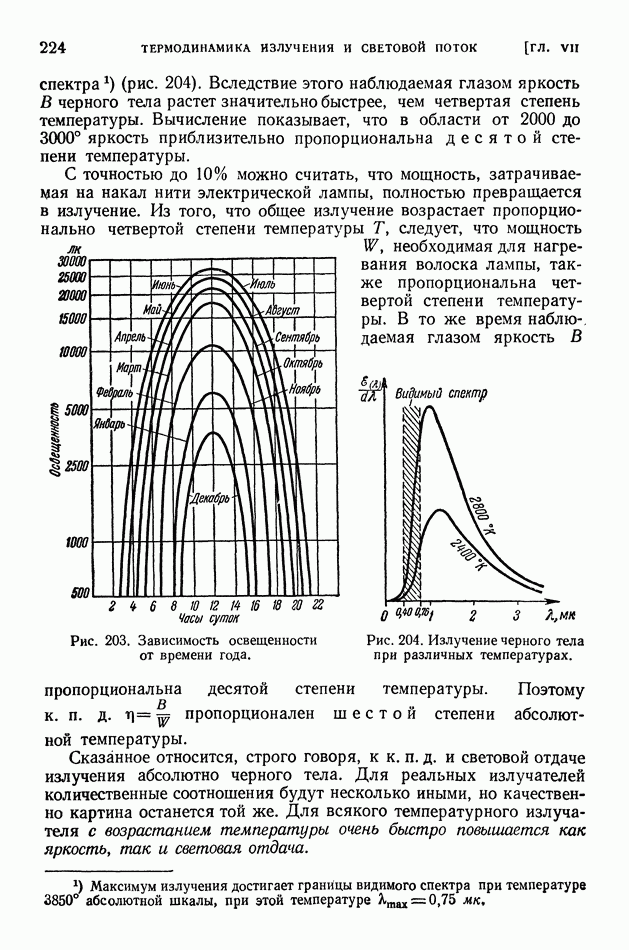
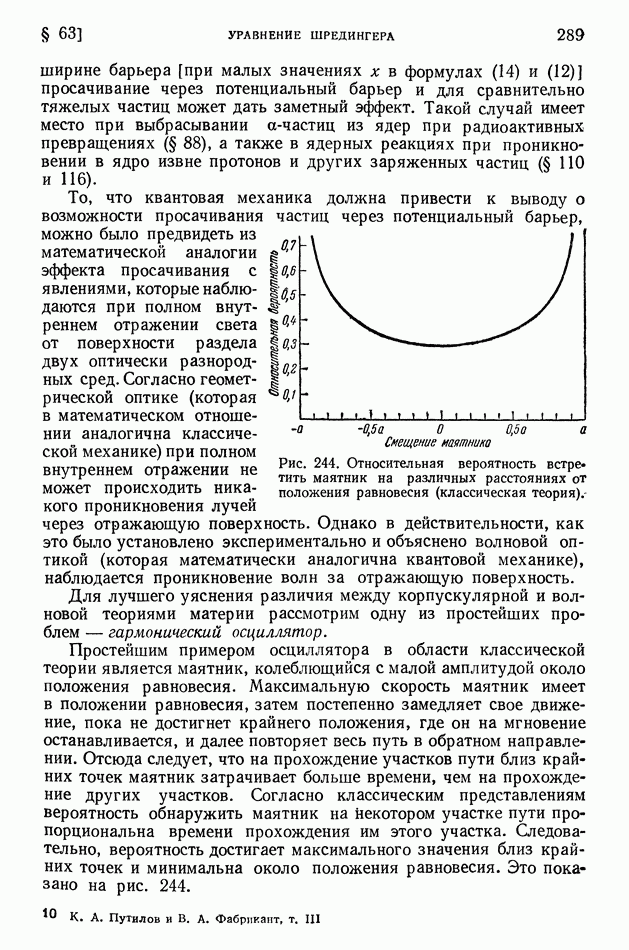
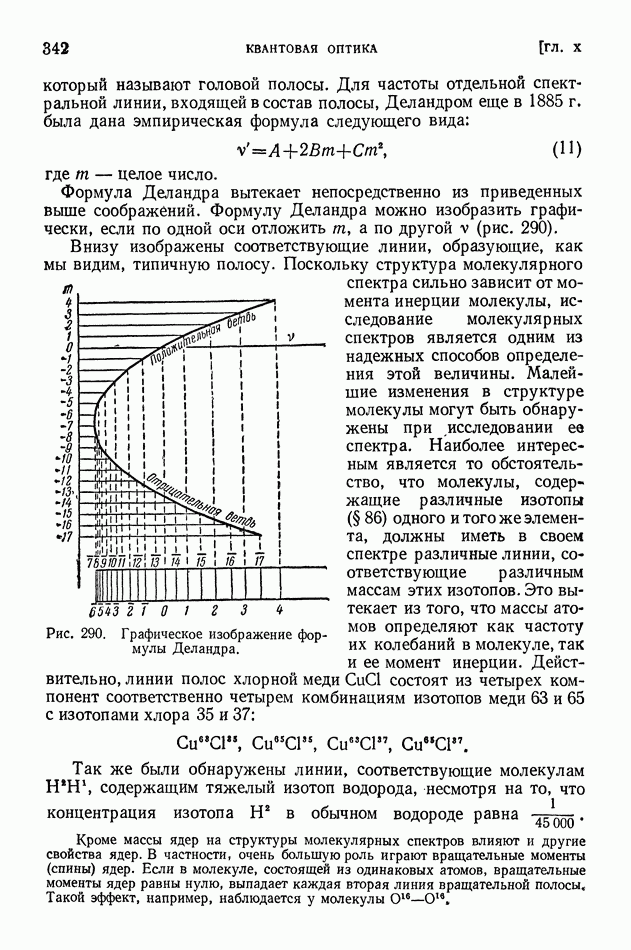
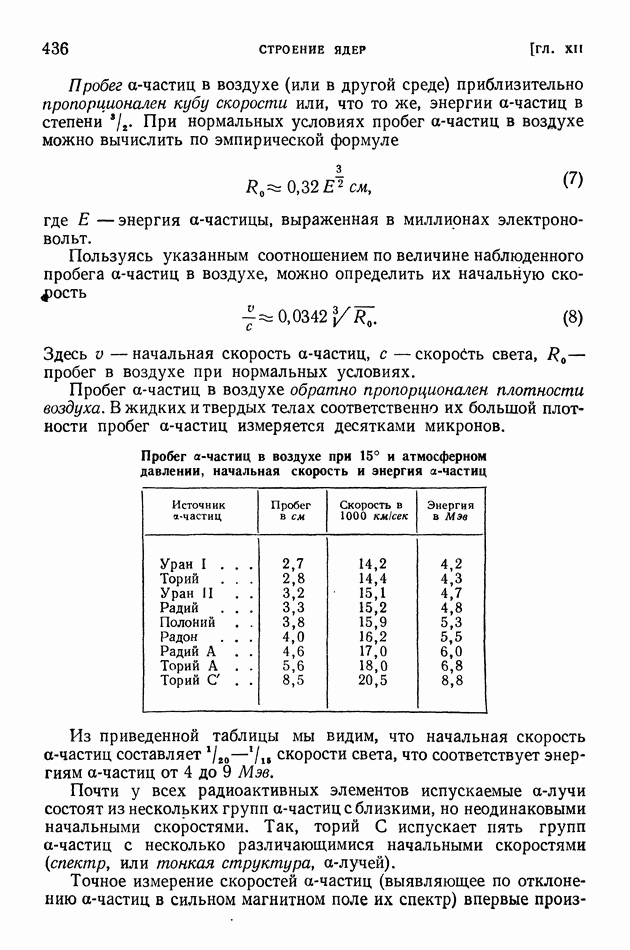
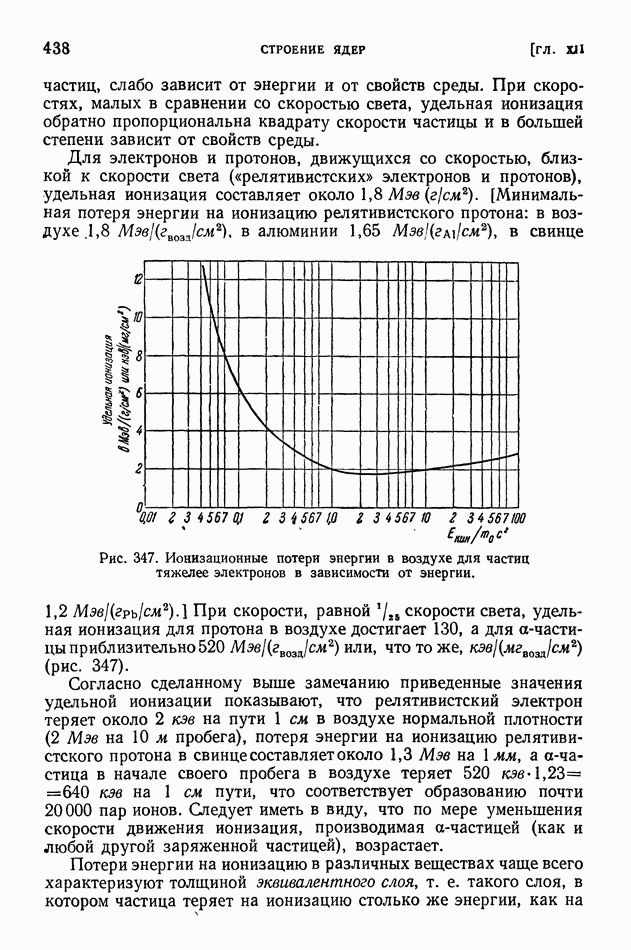
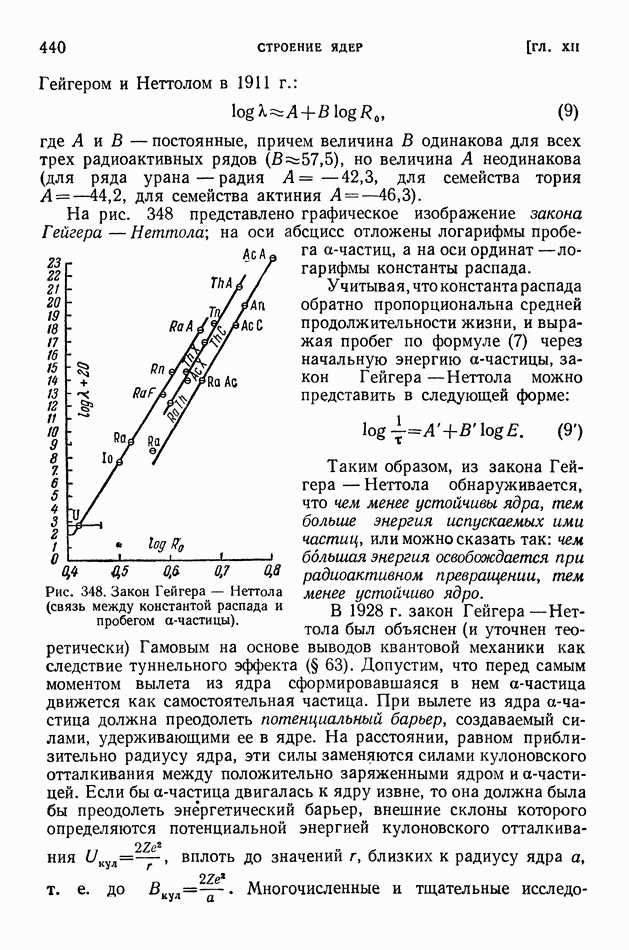
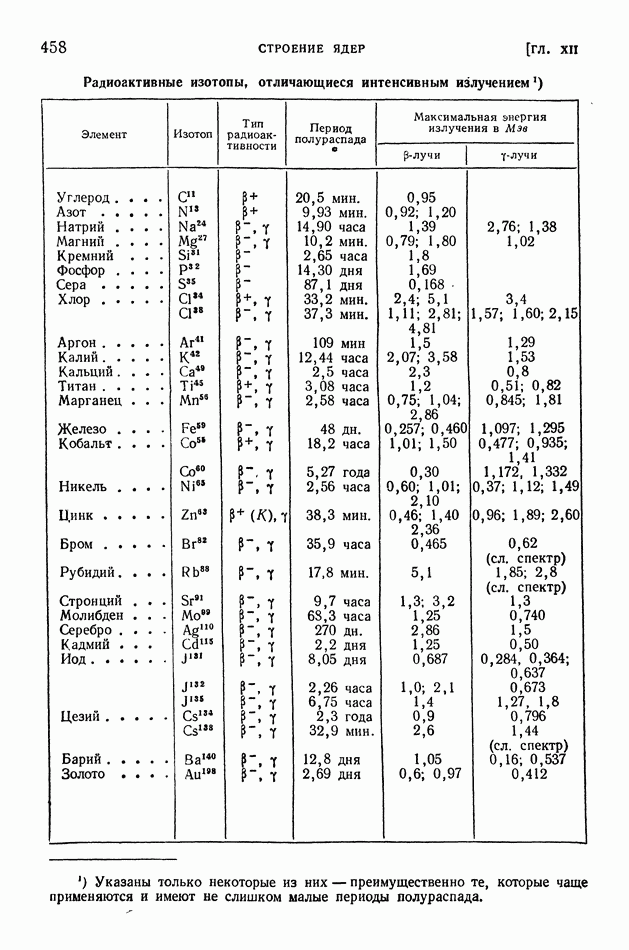
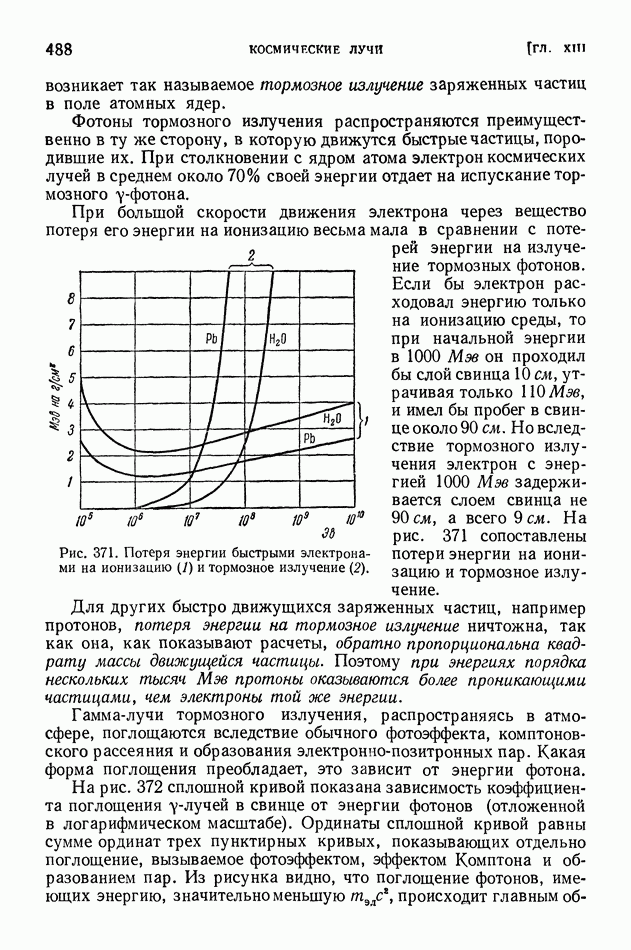
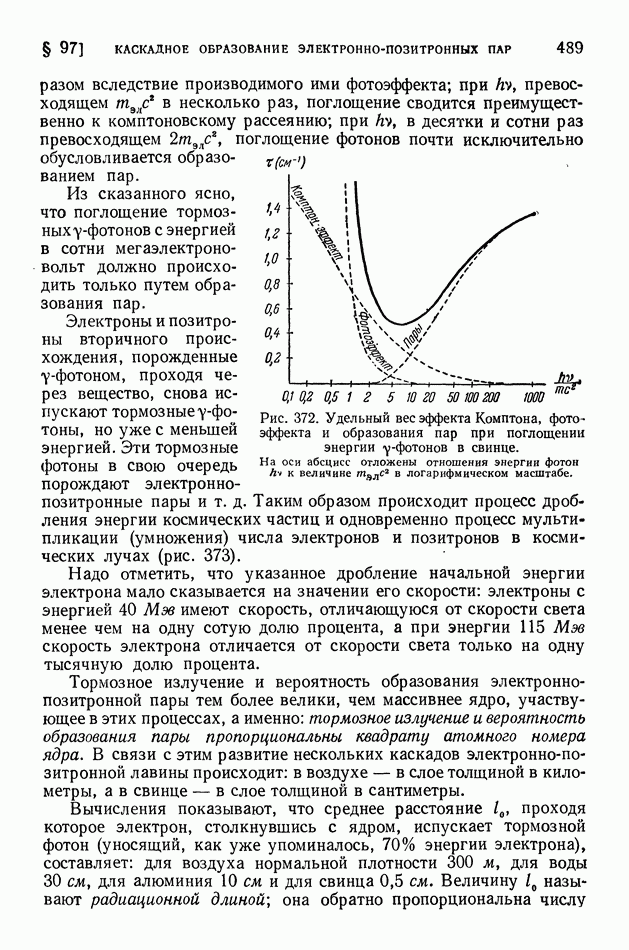
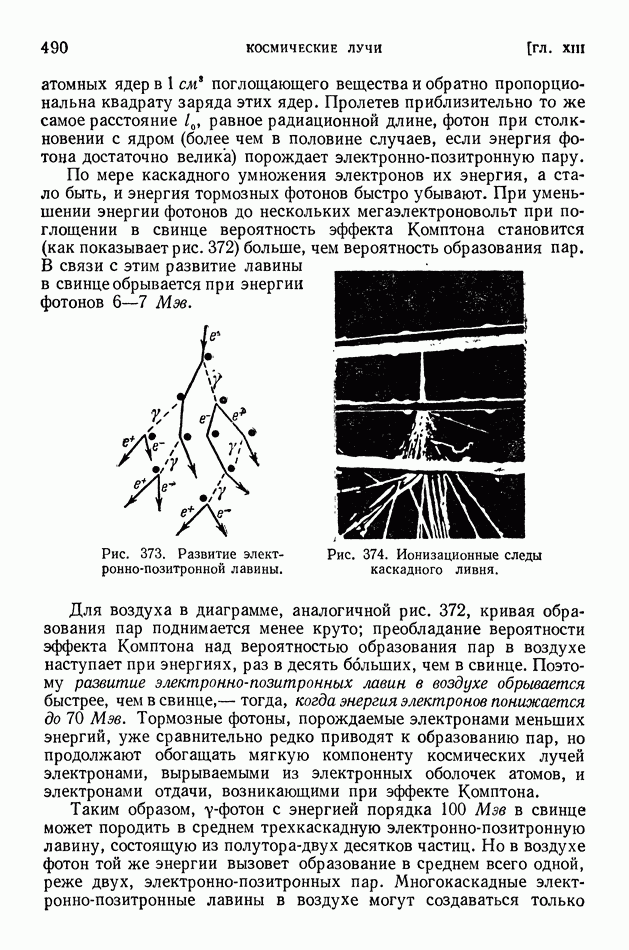
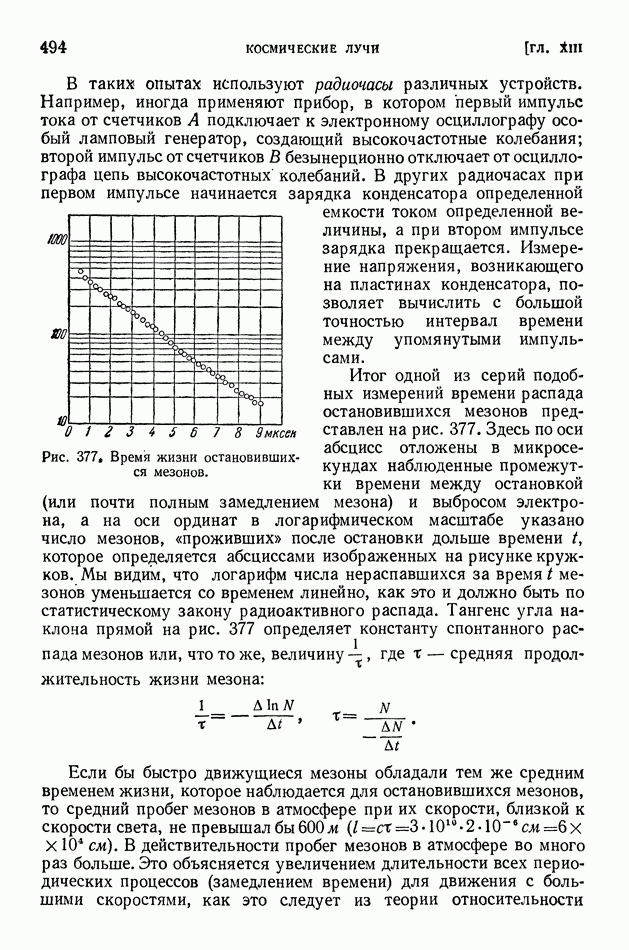
§ 117. Выход продуктов ядерной реакции. Эффективные сечения. Резонансные явления
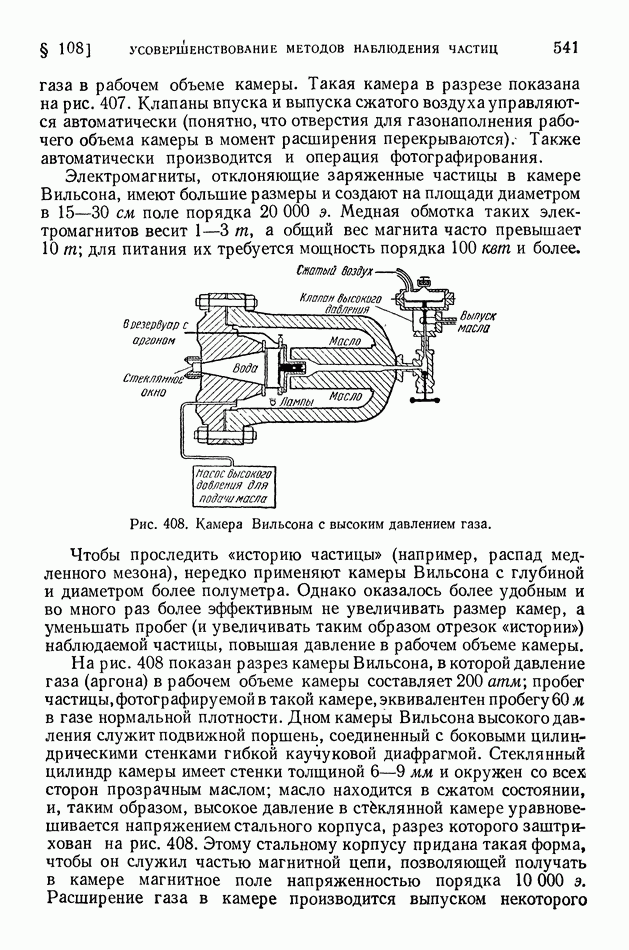
Состав продуктов реакции определяется уравнением реакции, а количество получающихся продуктов реакции (их «выход») зависит: в случае обычных химических процессов — от концентрации и температуры реагирующих веществ, а в ядерных процессах — от числа и энергии налетающих частиц. Чем больше число налетающих частиц, тем большее количество ядер испытывает превращение. Зависимость выхода продуктов реакции от энергии налетающих частиц часто является сложной (для некоторых случаев она проанализирована ниже).
Для характеристики выхода ядерной реакции применяют два способа, которые на первый взгляд кажутся весьма различными, но в действительности связаны друг с другом. Когда облучаемое вещество взято в виде более или менее массивного куска, в котором задерживаются (рассеиваются) практически все налетающие частицы, то для характеристики выхода продуктов реакции указывают процент тех налетающих частиц, которые проникают в ядра и вызывают реакцию.
Например, при облучении куска лития  медленными дейтонами в среднем только один из 108 дейтонов попадает в ядро лития и вызывает его превращение. При облучении куска алюминия
медленными дейтонами в среднем только один из 108 дейтонов попадает в ядро лития и вызывает его превращение. При облучении куска алюминия  альфа-частицами с энергией около
альфа-частицами с энергией около 
только одна из 105 альфа-частиц проникает в ядро и вызывает реакцию  В среднем одно ядерное превращение на
В среднем одно ядерное превращение на  бомбардирующих частиц является характерным выходом для многих ядерных реакций, вызываемых заряженными частицами с энергией, близкой к высоте кулоновского барьера ядра. Для несколько больших энергий налетающей частицы характерен выход реакции: одно превращение на
бомбардирующих частиц является характерным выходом для многих ядерных реакций, вызываемых заряженными частицами с энергией, близкой к высоте кулоновского барьера ядра. Для несколько больших энергий налетающей частицы характерен выход реакции: одно превращение на  бомбардирующих частиц. Когда энергия заряженной налетающей частицы составляет десятые доли высоты кулоновского барьера ядра, наблюдаются выходы реакции; одно превращение на
бомбардирующих частиц. Когда энергия заряженной налетающей частицы составляет десятые доли высоты кулоновского барьера ядра, наблюдаются выходы реакции; одно превращение на  частиц и еще меньшие.
частиц и еще меньшие.
Очень многие реакции, вызываемые нейтронами больших и весьма больших энергий  имеют выход: одно превращение на
имеют выход: одно превращение на  нейтронов. Что касается медленных и тепловых нейтронов, то выходы реакций, вызываемых ими, иногда относительно велики и для разных ядер отличаются нередко в десятки тысяч и даже миллионы раз.
нейтронов. Что касается медленных и тепловых нейтронов, то выходы реакций, вызываемых ими, иногда относительно велики и для разных ядер отличаются нередко в десятки тысяч и даже миллионы раз.
Другой чаще применяемый способ характеристики выхода реакций имеет наибольшую наглядность в случае, когда облучению подвергается настолько тонкий слой вещества, что при воображаемом просвечивании его (в направлении облучения частицами) сечения отдельных ядер не перекрываются (рис. 417). Тогда выход реакции (число ядер, прореагировавших за 1 сек) характеризуют эффективным сечением  это площадь а, которую нужно было бы приписать ядру, чтобы можно было считать, что попадание налетающей частицы в диск площади а обязательно вызывает рассматриваемую ядерную реакцию, а пролетание частицы около ядра вне площади диска а не приводит к реакции.
это площадь а, которую нужно было бы приписать ядру, чтобы можно было считать, что попадание налетающей частицы в диск площади а обязательно вызывает рассматриваемую ядерную реакцию, а пролетание частицы около ядра вне площади диска а не приводит к реакции.

Рис. 417. К пояснению понятия «эффективное сечение ядра».
Если  число ядер в
число ядер в  мишени, то при толщине мишени
мишени, то при толщине мишени  суммарное эффективное сечение ядер на
суммарное эффективное сечение ядер на  мишени равно
мишени равно  Отношение числа частиц, которые вызывают превращение ядер, к общему числу частиц, налетающих на
Отношение числа частиц, которые вызывают превращение ядер, к общему числу частиц, налетающих на  площади мишени, равно, очевидно, отношению
площади мишени, равно, очевидно, отношению  это же отношение определяет вероятность
это же отношение определяет вероятность  что налетающая частица вызовет превращение ядра (или, что то же, выход реакции):
что налетающая частица вызовет превращение ядра (или, что то же, выход реакции):

Пусть плотность потока налетающих частиц есть  и скорость их равна
и скорость их равна  Тогда за 1 сек на
Тогда за 1 сек на  поверхности мишени
поверхности мишени
падает  частиц; их доля
частиц; их доля  вызывает ядерные превращения. Стало быть,
вызывает ядерные превращения. Стало быть,

За единицу эффективного сечения ядер принимают площадь  которую называют барн.
которую называют барн.
Эффективное сечение ядра легко вычисляется из формулы (43) по числу налетающих частиц, вызывающих в среднем одно ядерное превращение в достаточно тонкой мишени (т. е. по величине 
Например, для реакции  при облучении альфа-частицами с энергией около
при облучении альфа-частицами с энергией около  алюминиевой фольги, имеющей вес на каждый квадратный сантиметр
алюминиевой фольги, имеющей вес на каждый квадратный сантиметр  наблюдается одно ядерное превращение на 2 млн. альфа-частиц, т.е.
наблюдается одно ядерное превращение на 2 млн. альфа-частиц, т.е.  Так как масса атома алюминия
Так как масса атома алюминия  то в указанной фольге имеется приблизительно
то в указанной фольге имеется приблизительно  атомов [множитель
атомов [множитель  стало быть,
стало быть,

Для процесса поглощения налетающих частиц ядрами мишени, если через  обозначить интенсивность пучка
обозначить интенсивность пучка  уравнение (44) дает
уравнение (44) дает

и после интегрирования

где  начальная интенсивность пучка налетающих частиц,
начальная интенсивность пучка налетающих частиц,  эффективное сечение поглощения.
эффективное сечение поглощения.
Сопоставляя эту формулу с  § 89, мы видим, что эффективное сечение поглощения, умноженное на число ядер в 1 см (эту величину обозначают
§ 89, мы видим, что эффективное сечение поглощения, умноженное на число ядер в 1 см (эту величину обозначают  и называют микроскопическим сечением поглощения), представляет собой коэффициент поглощения
и называют микроскопическим сечением поглощения), представляет собой коэффициент поглощения  Так как объем грамм-атома, выраженный в см, равен
Так как объем грамм-атома, выраженный в см, равен  где
где  плотность вещества в
плотность вещества в  и А — атомный вес, то
и А — атомный вес, то  а следовательно,
а следовательно,

Величина, обратная макроскопическому сечению поглощения, представляет собой длину свободного пробега налетающей частицы в поглощающем веществе

Соответственно формуле (11) § 89 толщина слоев двукратного и десятикратного ослабления первоначальной интенсивности пучка равна:

Одному и тому же ядру приходится приписывать разные эффективные сечения для различных реакций и для одной и той же реакции при различных энергиях налетающей частицы. Так как при небольших энергиях заряженной налетающей частицы вероятность ее проникновения в ядро невелика  определяется квантовомехаяическим эффектом просачивания частицы через кулоновский барьер ядра), то в этих случаях эффективные сечения ядер обычно составляют только небольшую долю геометрического сечения ядра. Но для реакций, которые вызываются поглощением нейтронов с тепловыми скоростями, эффективные сечения ядер нередко в сотни и тысячи раз превышают геометрическое сечение ядра, что свидетельствует об интенсивном взаимодействии нейтронов с ядрами, в особенности при некоторых, так называемых резонансных значениях энергии нейтрона, которые соответствуют квантовым переходам ядра с одного уровня энергии на другой.
определяется квантовомехаяическим эффектом просачивания частицы через кулоновский барьер ядра), то в этих случаях эффективные сечения ядер обычно составляют только небольшую долю геометрического сечения ядра. Но для реакций, которые вызываются поглощением нейтронов с тепловыми скоростями, эффективные сечения ядер нередко в сотни и тысячи раз превышают геометрическое сечение ядра, что свидетельствует об интенсивном взаимодействии нейтронов с ядрами, в особенности при некоторых, так называемых резонансных значениях энергии нейтрона, которые соответствуют квантовым переходам ядра с одного уровня энергии на другой.
Теоретическое вычисление эффективных сечений для различных ядерных реакций представляет собой довольно сложную кванто-вомеханическую задачу; эта задача с наибольшим успехом решена Брейтом и Вигнером и подробно рассматривается в специальных курсах ядерной физики. В простейших случаях (когда интенсивность ядерной реакции не увеличена резонансным совпадением энергий налетающих частиц с энергиями квантовых переходов составного ядра) для эффективного сечения ядер в реакции  получается формула, которая при некоторых упрощениях приобретает следующий вид:
получается формула, которая при некоторых упрощениях приобретает следующий вид:

здесь  скорости налетающей и выброшенной частиц,
скорости налетающей и выброшенной частиц,  средняя энергия взаимодействия, которая ориентировочно имеет величину порядка глубины потенциальной ямы ядра и
средняя энергия взаимодействия, которая ориентировочно имеет величину порядка глубины потенциальной ямы ядра и  объем ядра; коэффициент Рпрос связан с вероятностью про» сачивания частиц
объем ядра; коэффициент Рпрос связан с вероятностью про» сачивания частиц  через кулоновский барьер и при большой его высоте (для средних и тяжелых ядер) приближенно равен произведению
через кулоновский барьер и при большой его высоте (для средних и тяжелых ядер) приближенно равен произведению  где
где

Если частица а или  нейтрон, то соответственно
нейтрон, то соответственно  или
или
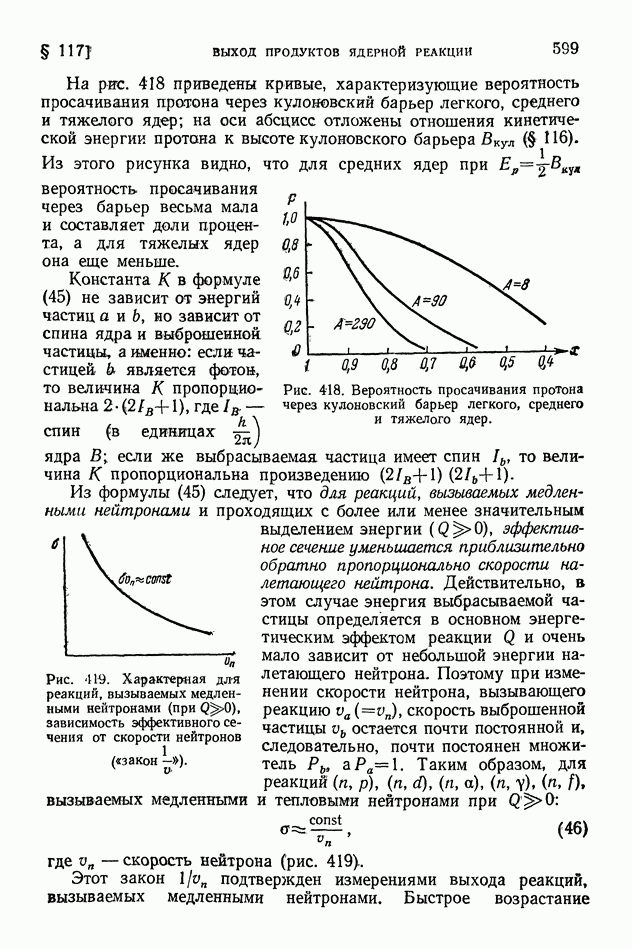
На рис. 418 приведены кривые, характеризующие вероятность просачивания протона через кулоновский барьер легкого, среднего и тяжелого ядер; на оси абсцисс отложены отношения кинетической энергии протона к высоте кулоновского барьера  (§ 116).
(§ 116).
Из этого рисунка видно, что для средних ядер при  вероятность просачивания через барьер весьма мала и составляет доли процента, а для тяжелых ядер она еще меньше.
вероятность просачивания через барьер весьма мала и составляет доли процента, а для тяжелых ядер она еще меньше.

Рис. 418. Вероятность просачивания протона через кулоновский барьер легкого, среднего и тяжелого ядер.
Константа К в формуле (45) не зависит от энергий частиц а  по зависит от спина ядра и выброшенной частицы, а именно: если частицей
по зависит от спина ядра и выброшенной частицы, а именно: если частицей  является фотом, то величина К пропорциональна
является фотом, то величина К пропорциональна  где
где  спин (в единицах
спин (в единицах  ядра
ядра  если же выбрасываемая частица имеет спин
если же выбрасываемая частица имеет спин  то величина К пропорциональна произведению
то величина К пропорциональна произведению 
Из формулы (45) следует, что для реакций, вызываемых медленными нейтронами и проходящих с более или менее значительным выделением энергии  эффективное сечение уменьшается приблизительно обратно пропорционально скорости налетающего нейтрона. Действительно, в этом случае энергия выбрасываемой частицы определяется в основном энергетическим эффектом реакции
эффективное сечение уменьшается приблизительно обратно пропорционально скорости налетающего нейтрона. Действительно, в этом случае энергия выбрасываемой частицы определяется в основном энергетическим эффектом реакции  и очень мало зависит от небольшой энергии налетающего нейтрона. Поэтому при изменении скорости нейтрона, вызывающего реакцию
и очень мало зависит от небольшой энергии налетающего нейтрона. Поэтому при изменении скорости нейтрона, вызывающего реакцию  скорость выброшенной частицы
скорость выброшенной частицы  остается почти постоянной и, следовательно, почти постоянен множитель
остается почти постоянной и, следовательно, почти постоянен множитель  Таким образом, для реакций
Таким образом, для реакций  вызываемых медленными и тепловыми нейтронами при
вызываемых медленными и тепловыми нейтронами при 

где  скорость нейтрона (рис. 419).
скорость нейтрона (рис. 419).
Этот закон  подтвержден измерениями выхода реакций, вызываемых медленными нейтронами. Быстрое возрастание
подтвержден измерениями выхода реакций, вызываемых медленными нейтронами. Быстрое возрастание

Рис. 419. Характерная для реакций, вызываемых медленными нейтронами (при  зависимость эффективного сечения от скорости нейтронов («закон
зависимость эффективного сечения от скорости нейтронов («закон 
эффективного сечения с уменьшением скорости нейтрона можно объяснить тем, что чем медленнее движется нейтрон, тем дольше он остается вблизи встретившегося ему на пути ядра и тем больше вероятность, что он проникнет в это ядро и вызовет его превращение. В соответствии с формулой (44) число ежесекундно превращающихся под действием медленных нейтронов ядер оказывается не зависящим от скорости нейтронов и определяется только плотностью потока нейтронов.
Совершенно иная зависимость эффективного сечения от скорости налетающих частиц получается для реакций, также проходящих со значительным выделением энергии  но вызываемых не нейтронами, а заряженными частицами. В этом случае множитель
но вызываемых не нейтронами, а заряженными частицами. В этом случае множитель  связанный с проницаемостью кулоновского барьера, для налетающей частицы уже не равен единице, а меньше ее; при малых энергиях налетающей частицы множитель
связанный с проницаемостью кулоновского барьера, для налетающей частицы уже не равен единице, а меньше ее; при малых энергиях налетающей частицы множитель  чрезвычайно мал и приближается к единице только при весьма больших ее энергиях. Поэтому для реакций, проходящих со значительным выделением энергии
чрезвычайно мал и приближается к единице только при весьма больших ее энергиях. Поэтому для реакций, проходящих со значительным выделением энергии  и вызываемых заряженными частицами, например для реакций
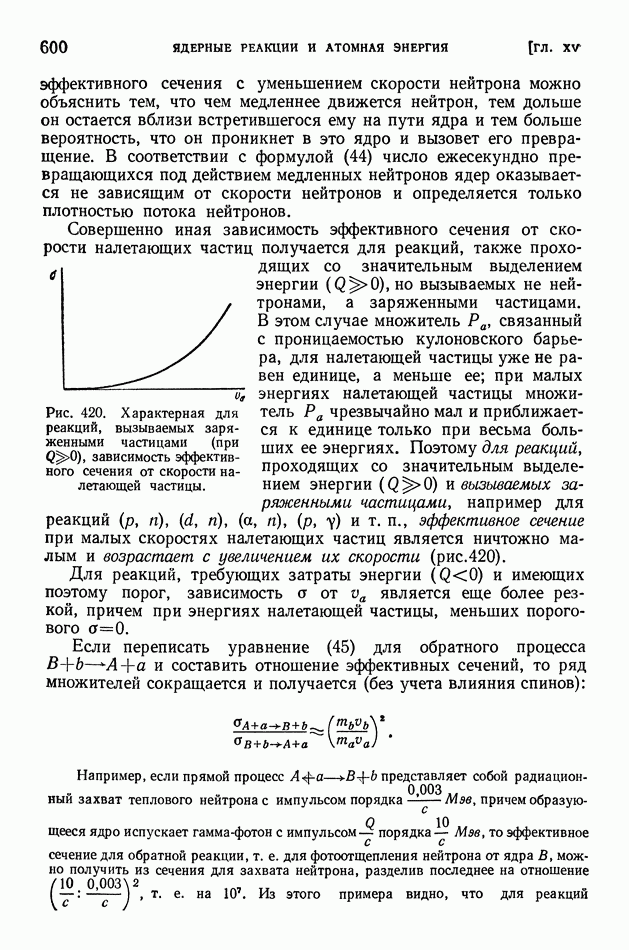
и вызываемых заряженными частицами, например для реакций  и т. п., эффективное сечение при малых скоростях налетающих частиц является ничтожно малым и возрастает с увеличением их скорости (рис. 420).
и т. п., эффективное сечение при малых скоростях налетающих частиц является ничтожно малым и возрастает с увеличением их скорости (рис. 420).

Рис. 420. Характерная для реакций, вызываемых заряженными частицами (при  ), зависимость эффективного сечения от скорости налетающей частицы.
), зависимость эффективного сечения от скорости налетающей частицы.
Для реакций, требующих затраты энергии  и имеющих поэтому порог, зависимость а от
и имеющих поэтому порог, зависимость а от  является еще более резкой, причем при энергиях налетающей частицы, меньших порогового
является еще более резкой, причем при энергиях налетающей частицы, меньших порогового 
Если переписать уравнение (45) для обратного процесса  и составить отношение эффективных сечений, то ряд множителей сокращается и получается (без учета влияния спинов):
и составить отношение эффективных сечений, то ряд множителей сокращается и получается (без учета влияния спинов):

Например, если прямой процесс  представляет собой радиационный захват теплового нейтрона с импульсом порядка
представляет собой радиационный захват теплового нейтрона с импульсом порядка  причем образующееся ядро испускает гамма-фотон с импульсом порядка
причем образующееся ядро испускает гамма-фотон с импульсом порядка  то эффективное сечение для обратной реакции, т. е. для фотоотщепления нейтрона от ядра В, можно получить из сечения для захвата нейтрона, разделив последнее на отношение
то эффективное сечение для обратной реакции, т. е. для фотоотщепления нейтрона от ядра В, можно получить из сечения для захвата нейтрона, разделив последнее на отношение  т. е. на 107. Из этого примера видно, что для реакции
т. е. на 107. Из этого примера видно, что для реакции
захвата А-а—и фотоотщепления В-у—эффективные сечения будут приблизительно одинаковы только в том случае, если реакция захвата проходит с самым незначительным выделением энергии.
Когда энергия налетающей частицы  равна резонансной (т. е. когда сумма
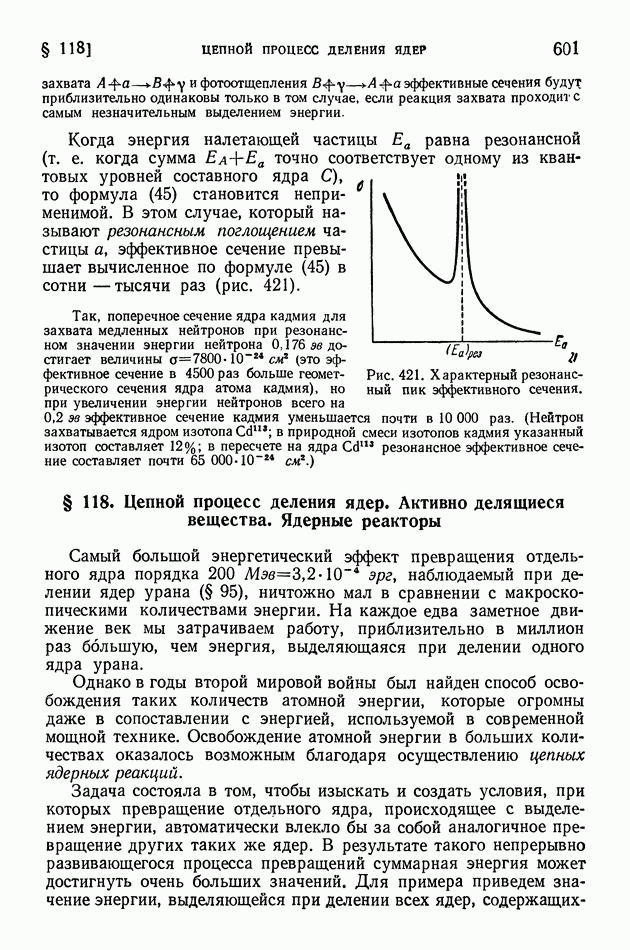
равна резонансной (т. е. когда сумма  точно соответствует одному из квантовых уровней составного ядра С), то формула (45) становится неприменимой. В этом случае, который называют резонансным поглощением частицы а, эффективное сечение превышает вычисленное по формуле (45) в сотни—тысячи раз (рис. 421).
точно соответствует одному из квантовых уровней составного ядра С), то формула (45) становится неприменимой. В этом случае, который называют резонансным поглощением частицы а, эффективное сечение превышает вычисленное по формуле (45) в сотни—тысячи раз (рис. 421).

Рис. 421. Характерный резонансный пик эффективного сечения.
Так, поперечное сечение ядра кадмия для захвата медленных нейтронов при резонансном значении энергии нейтрона 0,176 достигает величины  см (это эффективное сечение в 4500 раз больше геометрического сечения ядра атома кадмия), но при увеличении энергии нейтронов всего на
см (это эффективное сечение в 4500 раз больше геометрического сечения ядра атома кадмия), но при увеличении энергии нейтронов всего на  эффективное сечение кадмия уменьшается почти в 10 000 раз. (Нейтрон захватывается ядром изотопа
эффективное сечение кадмия уменьшается почти в 10 000 раз. (Нейтрон захватывается ядром изотопа  в природной смеси изотопов кадмия указанный изотоп составляет
в природной смеси изотопов кадмия указанный изотоп составляет  в пересчете на ядра
в пересчете на ядра  резонансное эффективное сечение составляет почти
резонансное эффективное сечение составляет почти 
| << Предыдущий параграф | Следующий параграф >> |
- ЧАСТЬ ЧЕТВЕРТАЯ. ОПТИКА
- § 2. Электромагнитная теория света
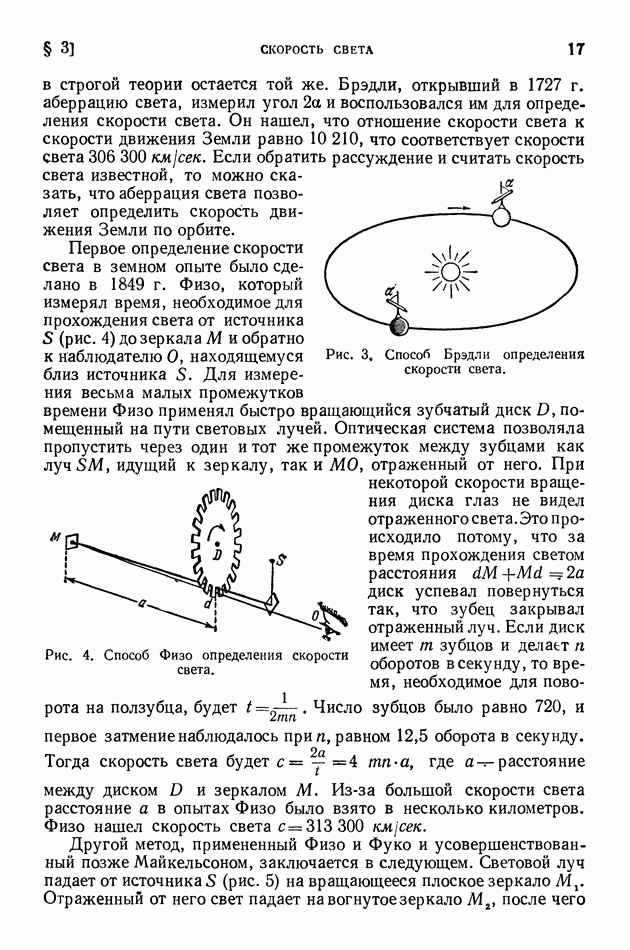
- § 3. Скорость света
- § 4. Опыт Майкельсона
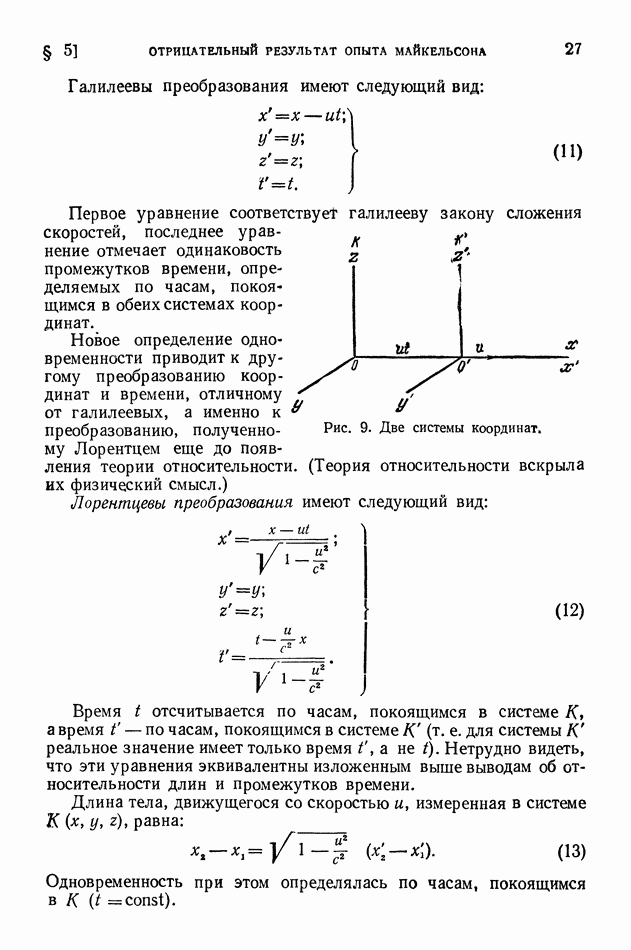
- § 5. Отрицательный результат опыта Майкельсона и теория относительности
- § 6. Некоторые замечания о теории относительности
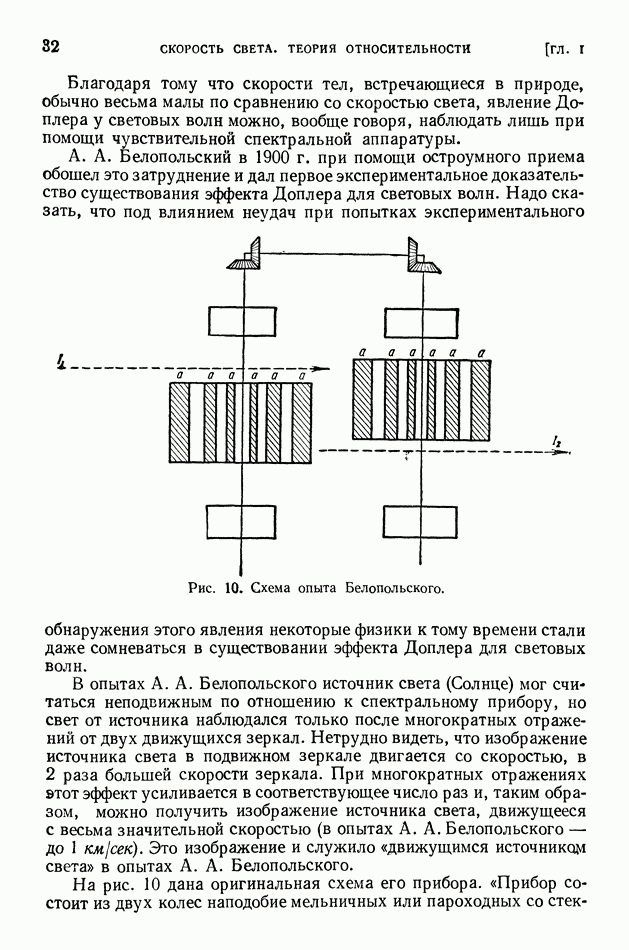
- § 7. Явление Доплера для световых волн
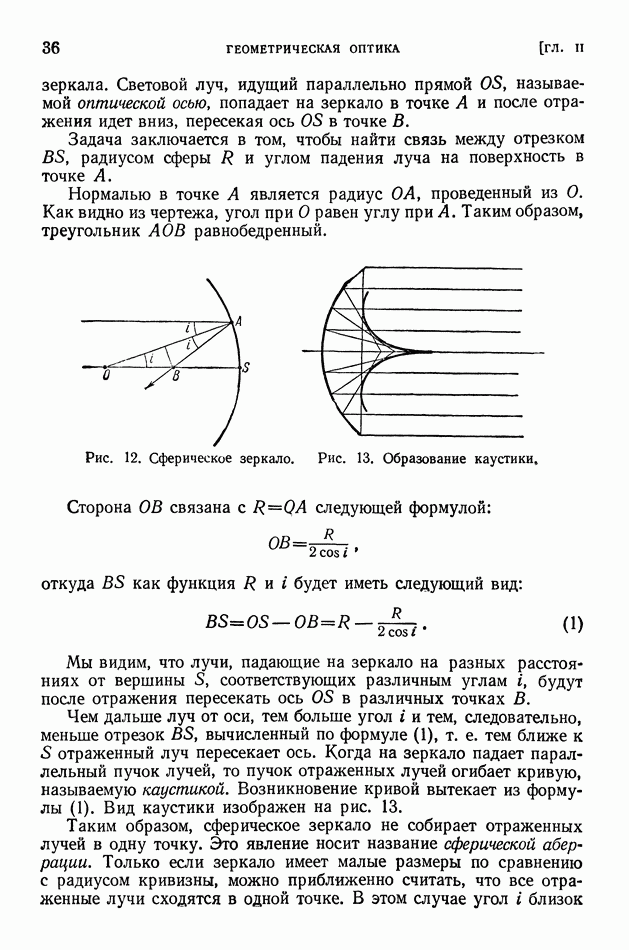
- ГЛАВА II. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- § 8. Законы отражения и преломления света
- § 9. Линза
- § 10. Оптические системы
- § 11. Глаз как оптическая система
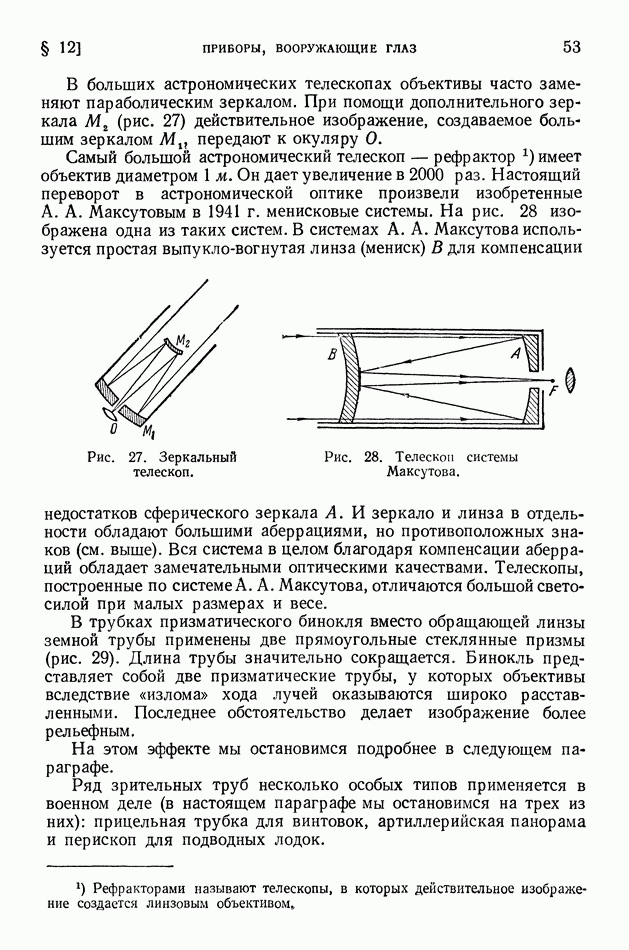
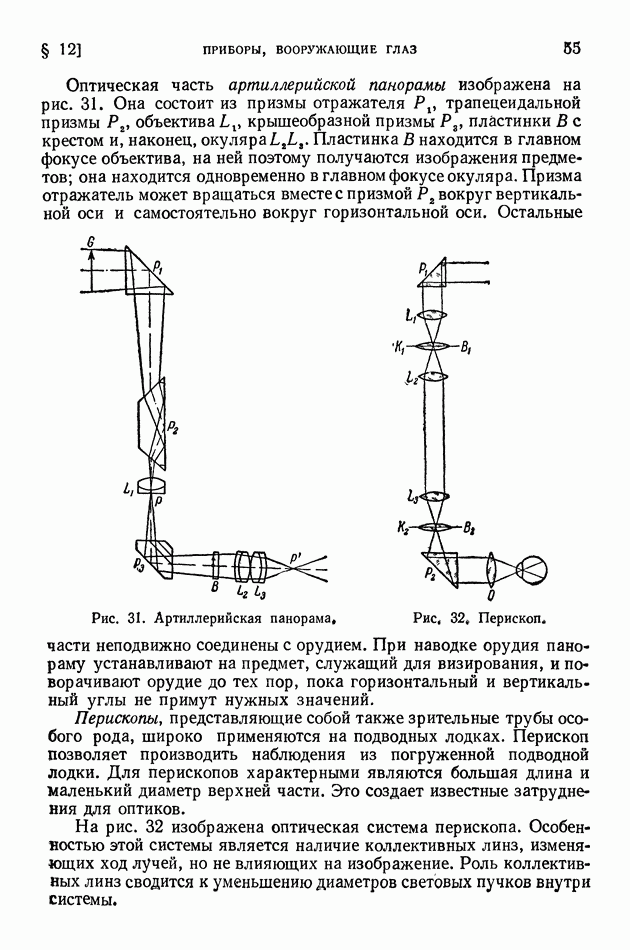
- § 12. Приборы, вооружающие глаз
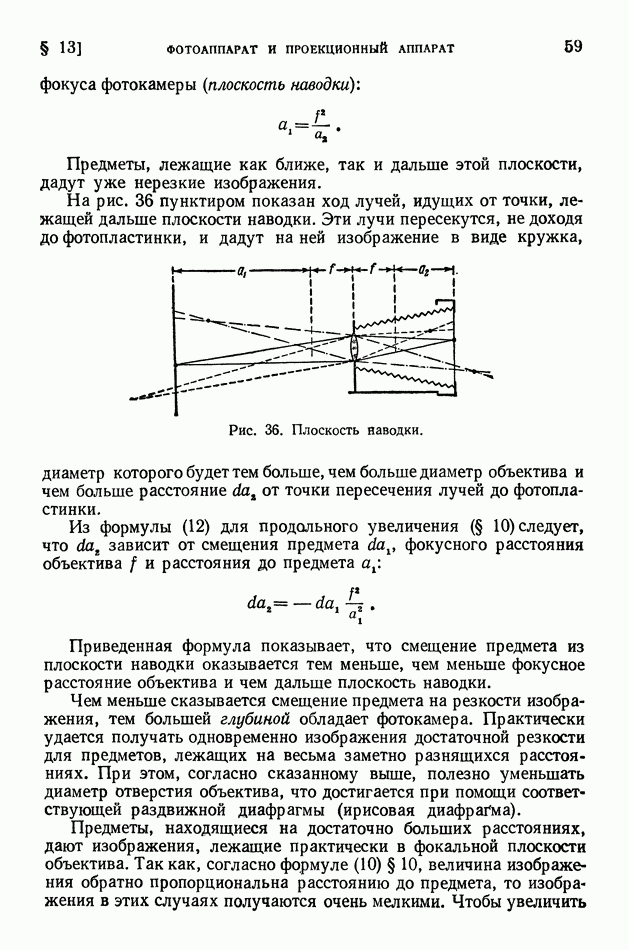
- § 13. Фотоаппарат и проекционный аппарат
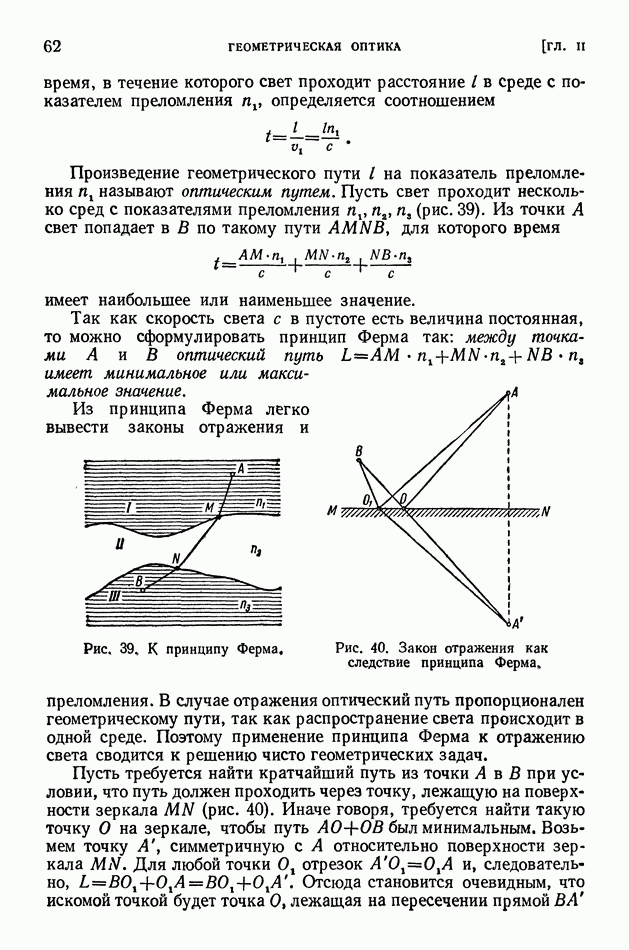
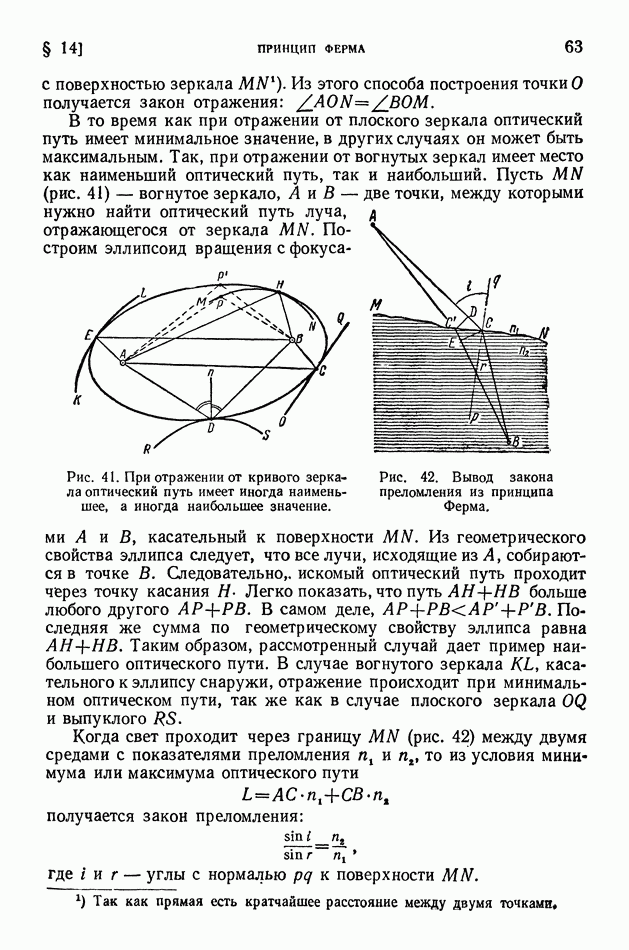
- § 14. Принцип Ферма
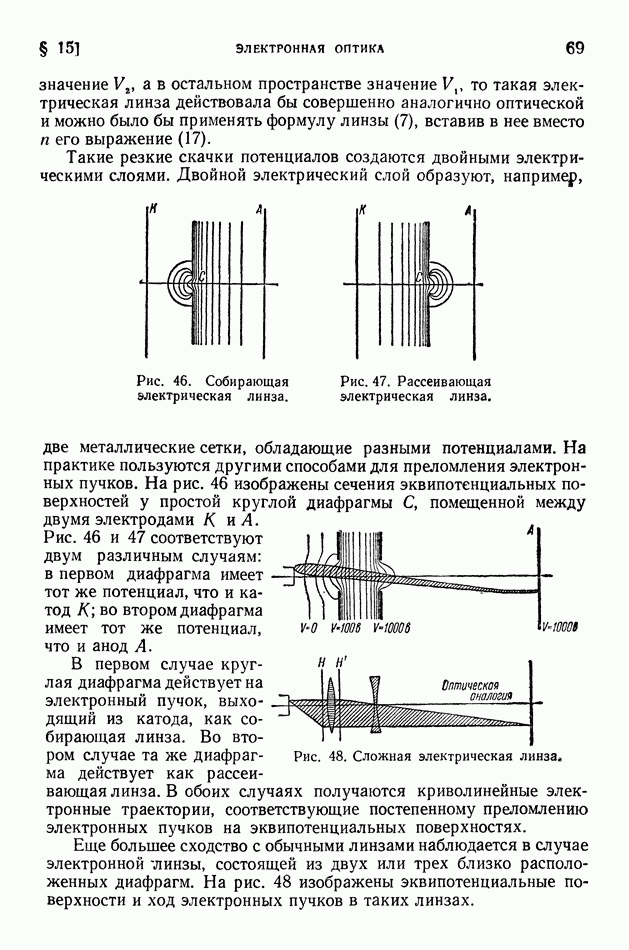
- § 15. Электронная оптика
- ГЛАВА III. ИНТЕРФЕРЕНЦИЯ СВЕТА
- § 16. Принцип суперпозиции. Когерентность
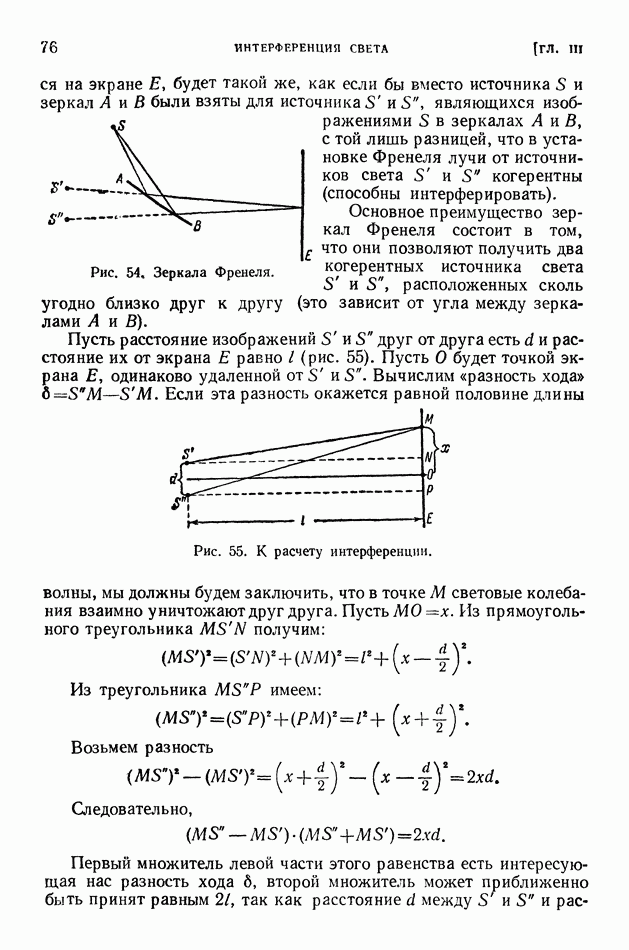
- § 17. Зеркала Френеля
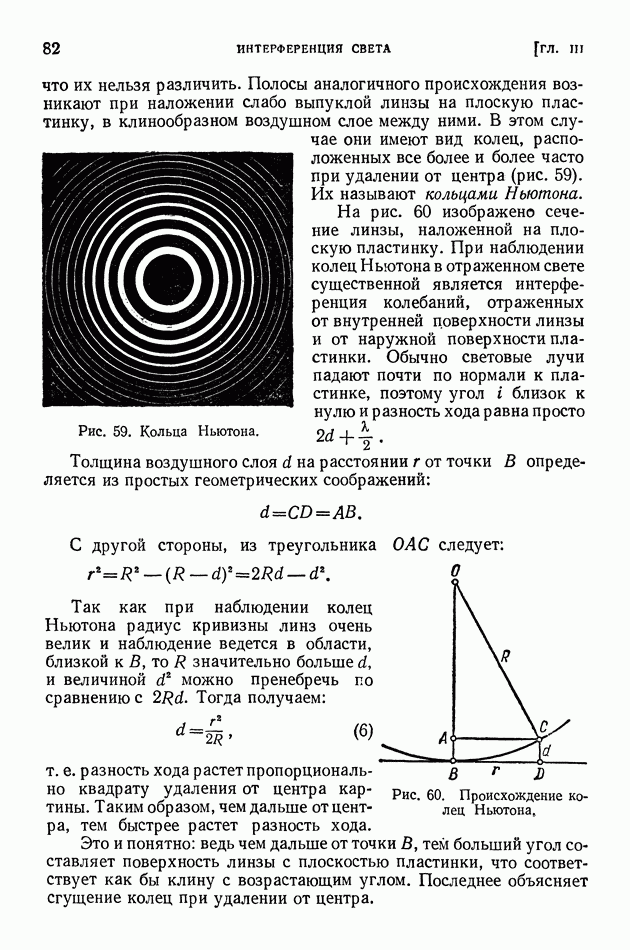
- § 18. Цвета тонких пленок. Полосы равной толщины
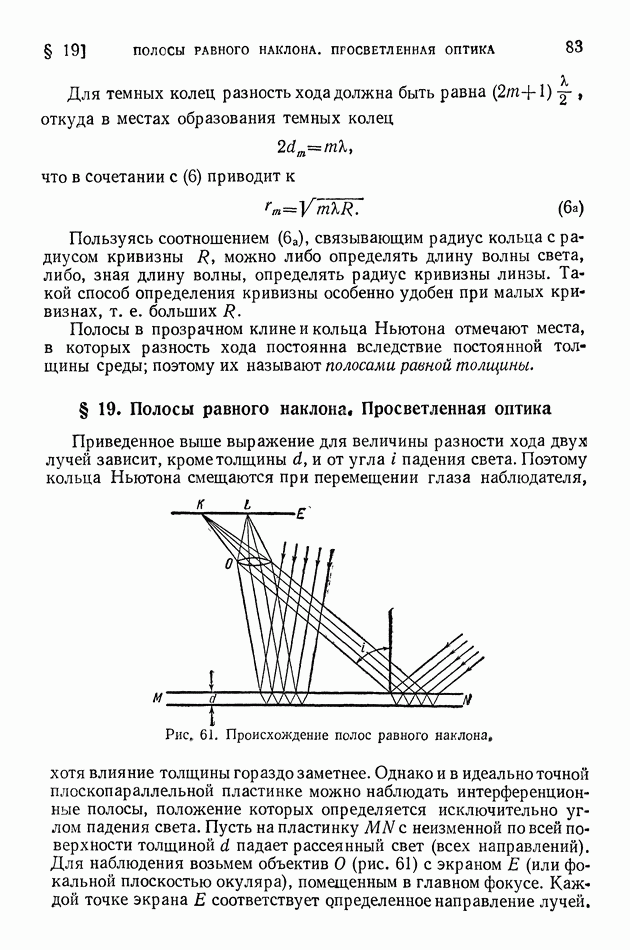
- § 19. Полосы равного наклона. Просветленная оптика
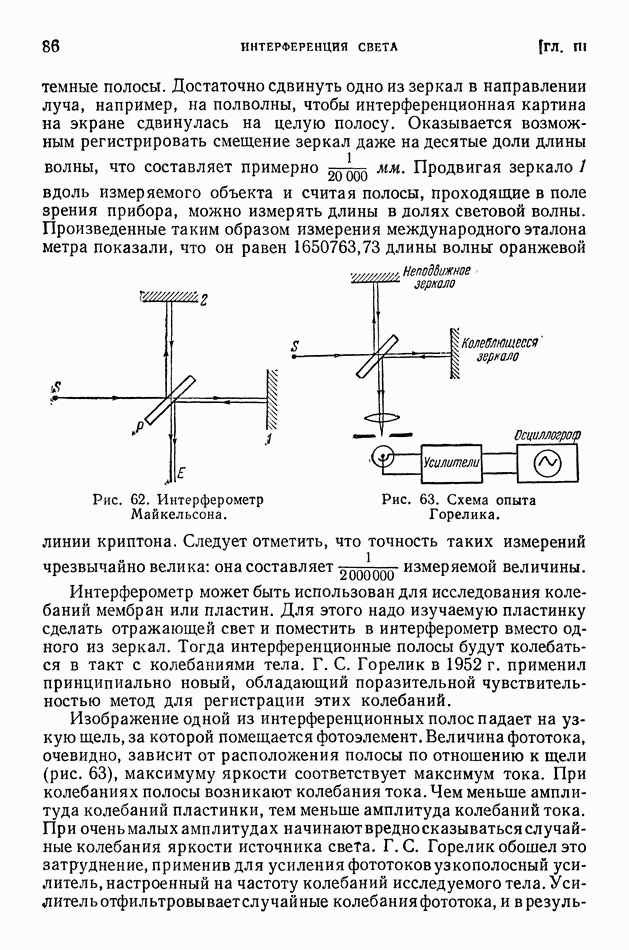
- § 20. Интерферометры
- § 21. Интерференционное измерение технических мер длины
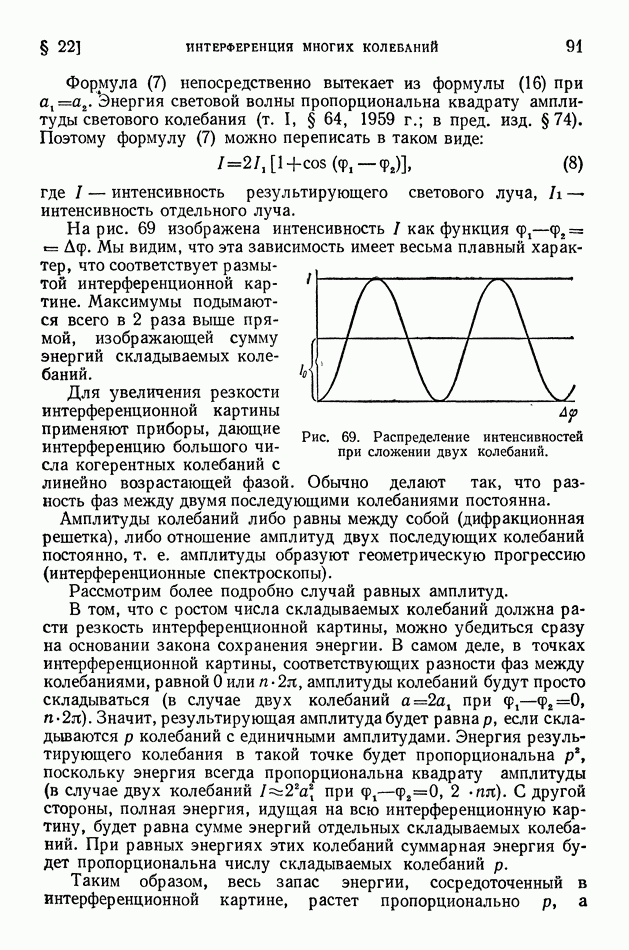
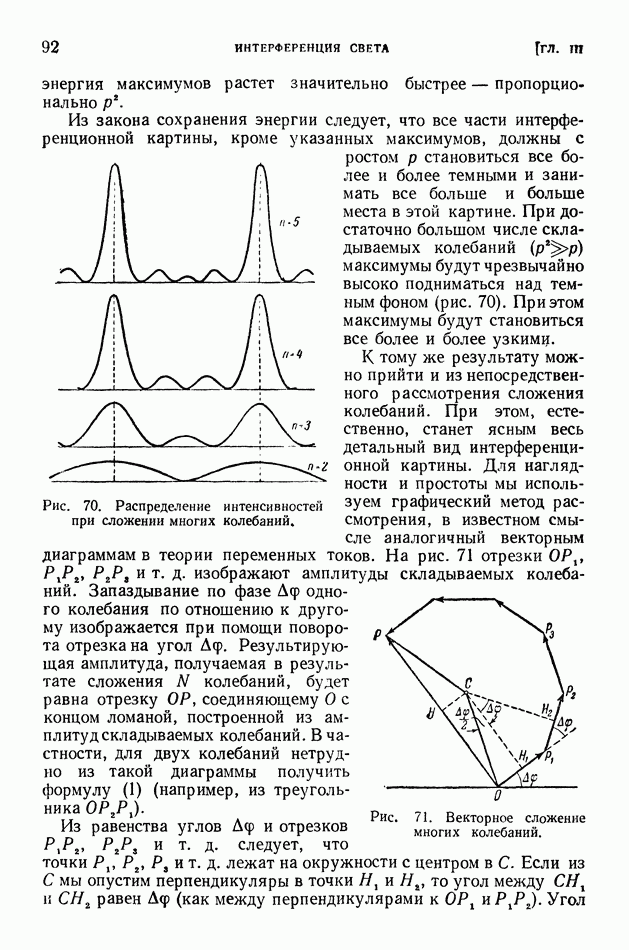
- § 22. Интерференция многих колебаний
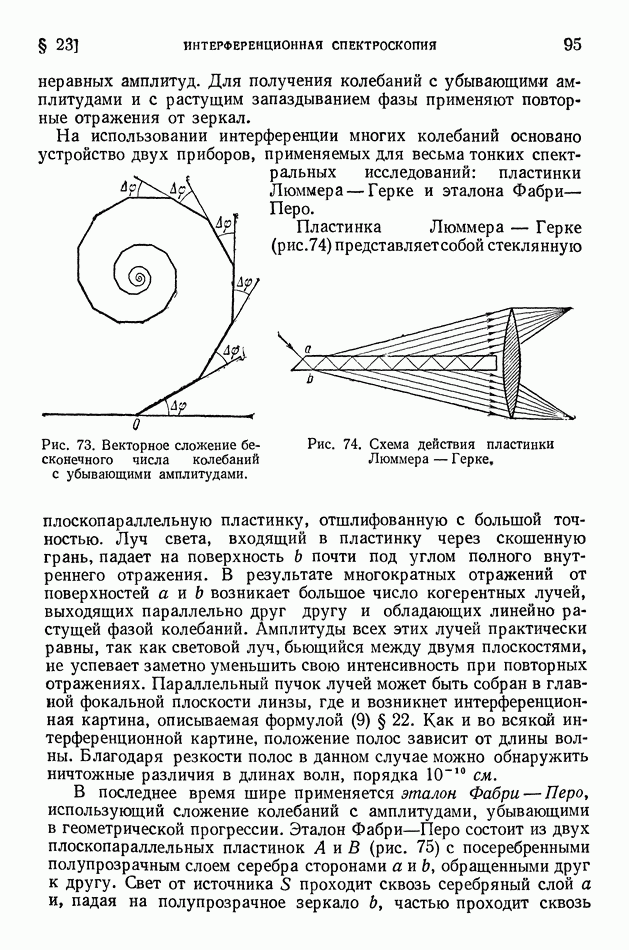
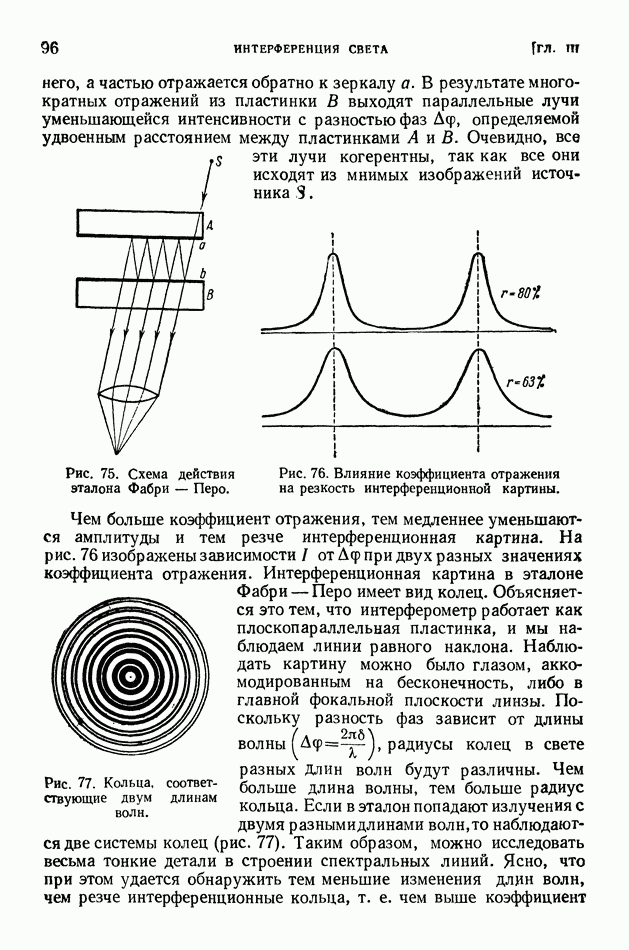
- § 23. Интерференционная спектроскопия
- ГЛАВА IV. ДИФРАКЦИЯ СВЕТА
- § 24. Явление дифракции. Опыт Френеля
- § 25. Принцип Гюйгенса-Френеля
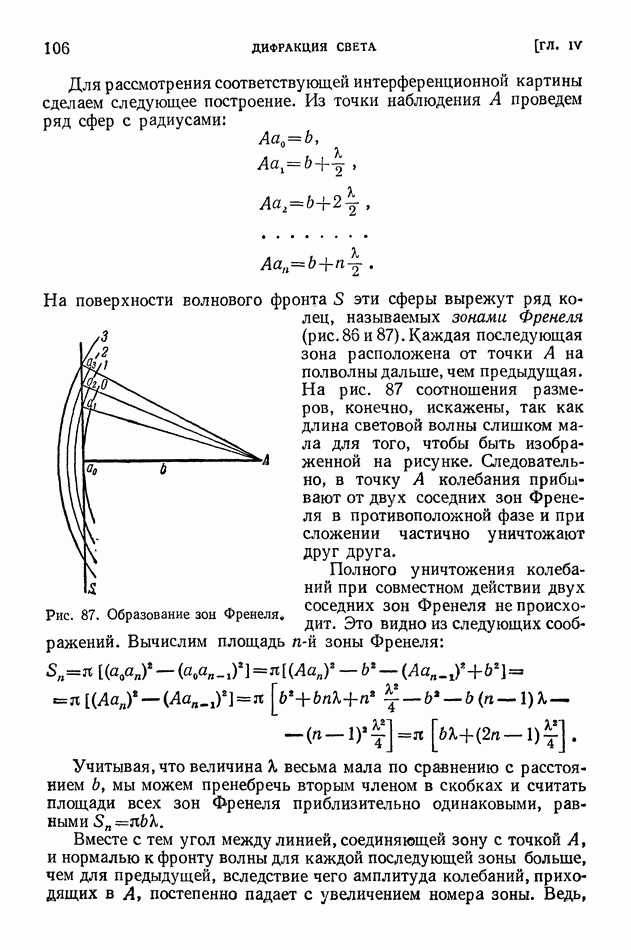
- § 26. Метод зон Френеля
- § 27. Дифракция от узкой щели
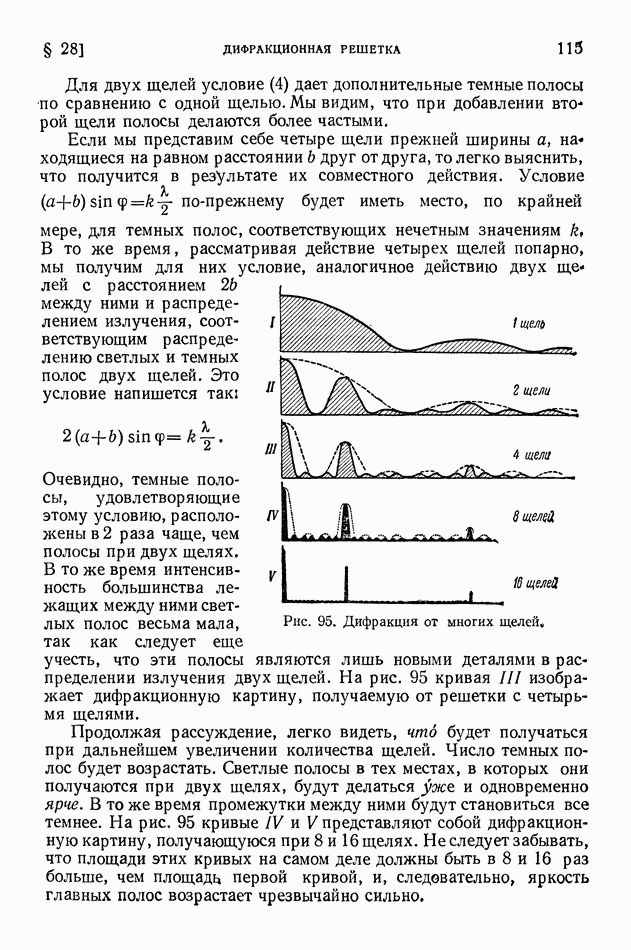
- § 28. Дифракционная решетка
- § 29. Дифракционный спектр. Решетки Роуланда и эшелон Майкельсона
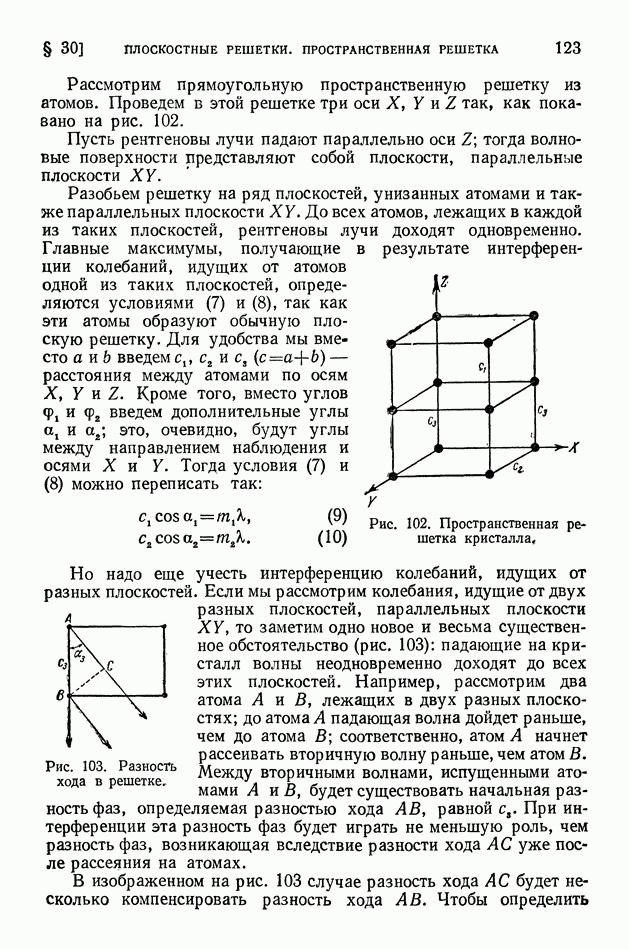
- § 30. Плоскостные решетки. Пространственная решетка
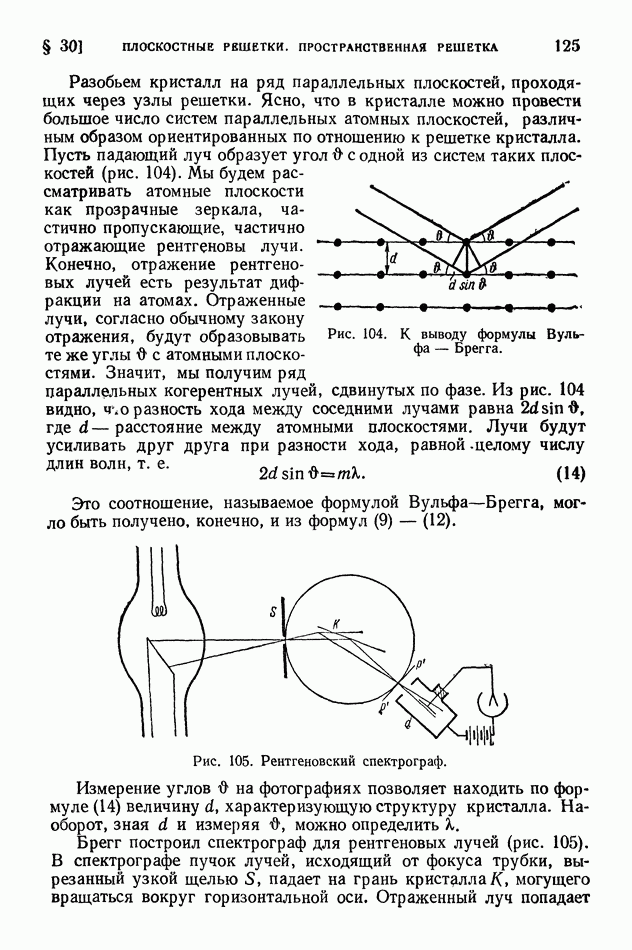
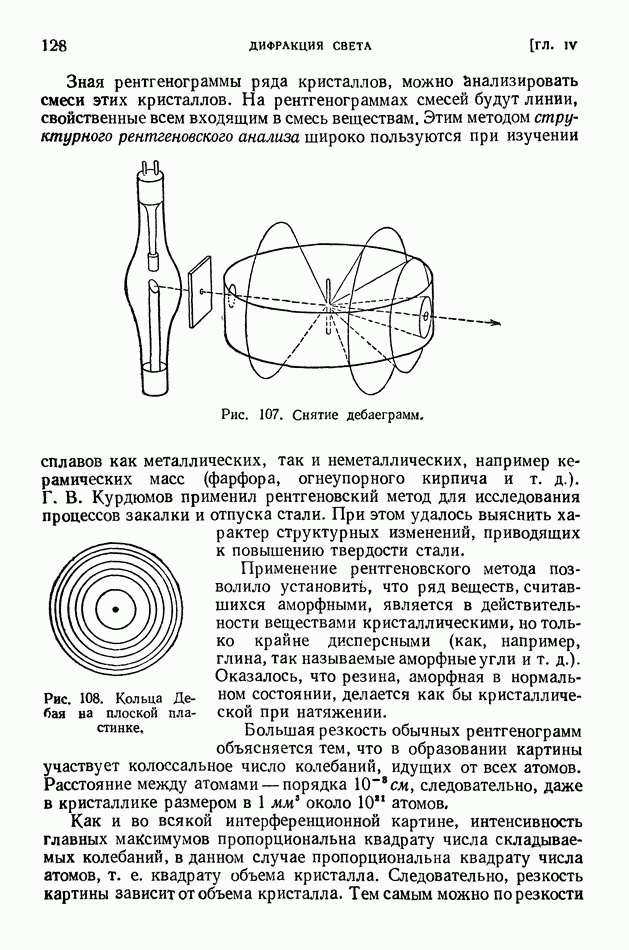
- § 31. Структурный рентгеновский анализ
- § 32. Дифракция света на ультразвуковых волнах
- § 33. Дифракция от мелких частиц
- § 34. Разрешающая способность оптических инструментов. Звездный интерферометр
- ГЛАВА V. ПОЛЯРИЗАЦИЯ СВЕТА
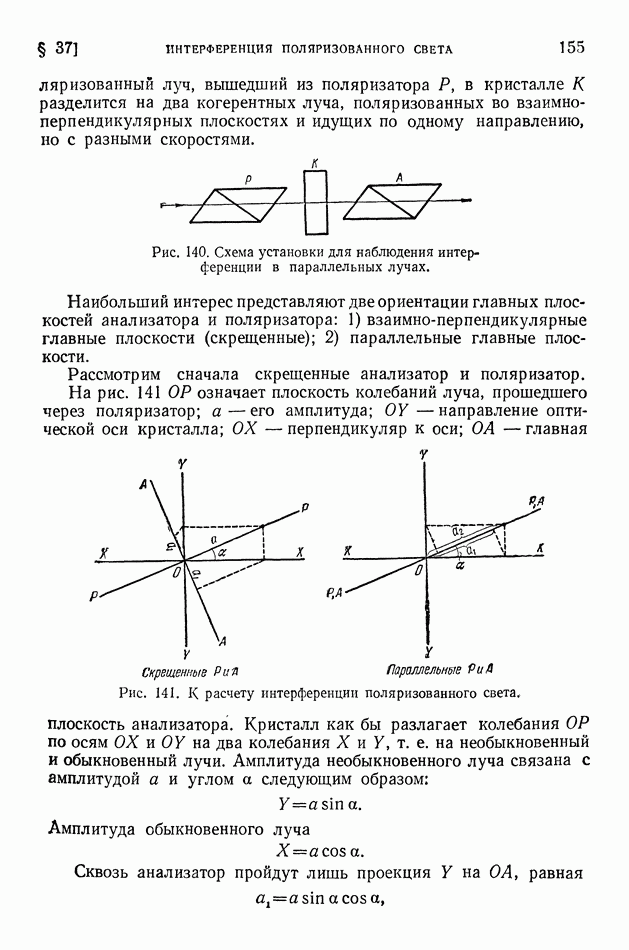
- § 35. Поляризация света
- § 36. Двойное лучепреломление
- § 37. Интерференция поляризованного света
- § 38. Оптический метод исследования упругих натяжений. Эффект Керра
- § 39. Вращение плоскости поляризации. Эллиптическая поляризация
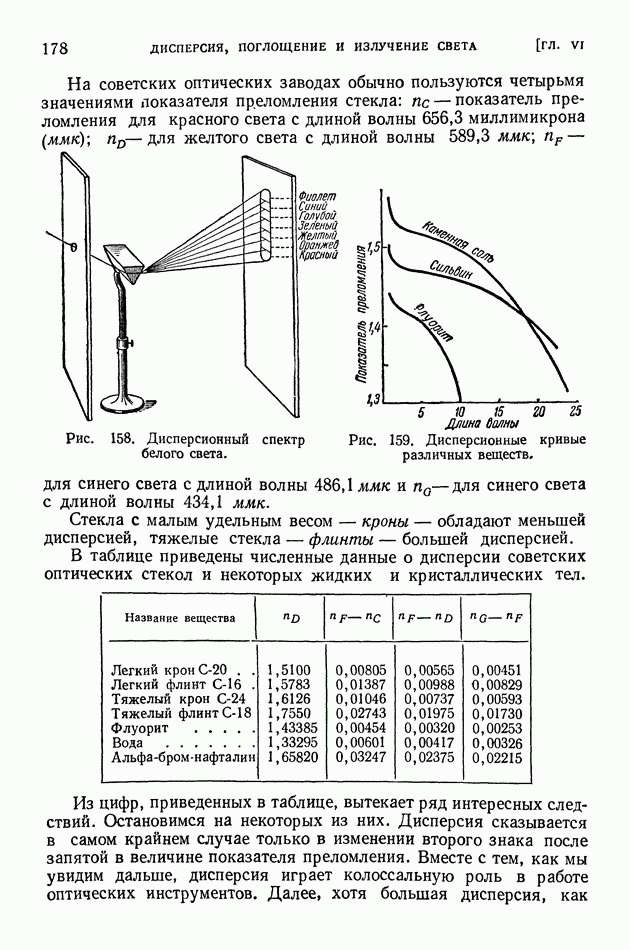
- ГЛАВА VI. ДИСПЕРСИЯ, ПОГЛОЩЕНИЕ И ИЗЛУЧЕНИЕ СВЕТА
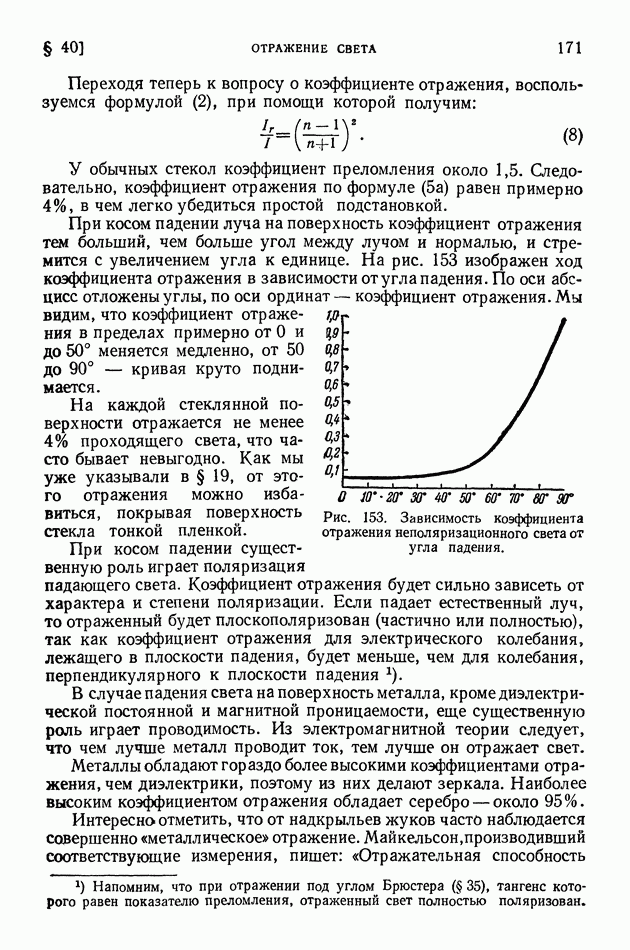
- § 40. Отражение света
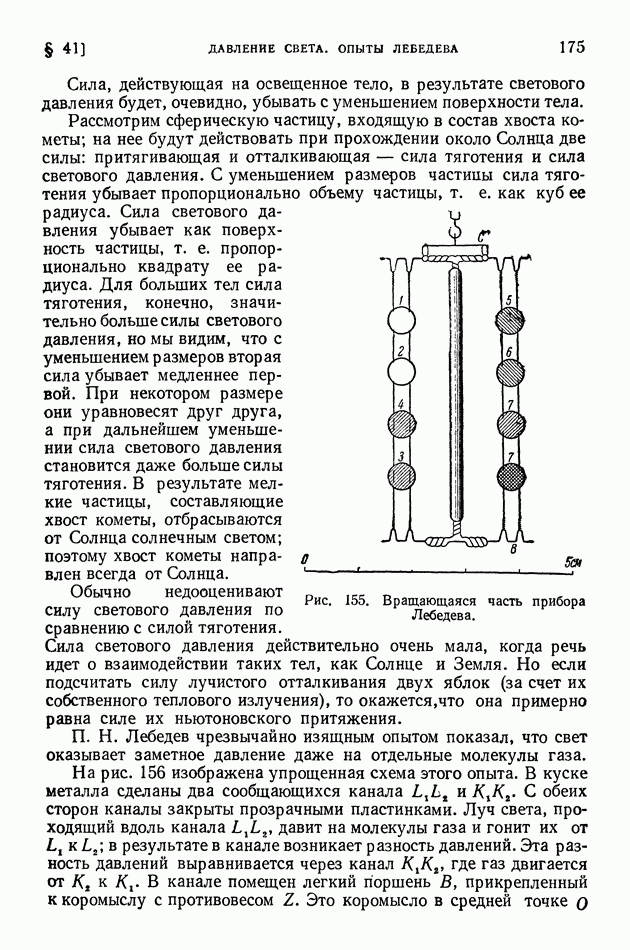
- § 41. Давление света. Опыты Лебедева
- § 42. Дисперсия. Опыты Ньютона
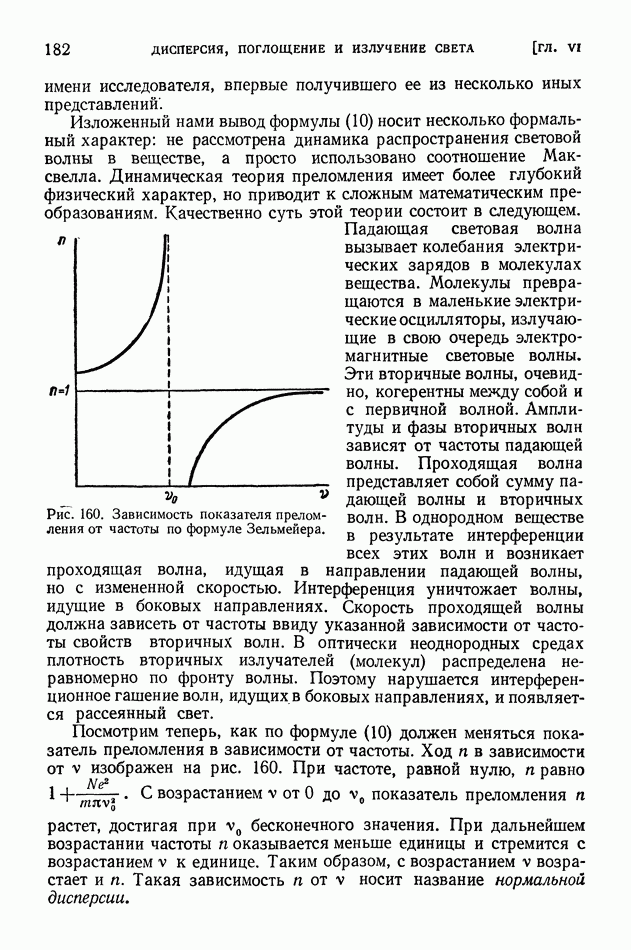
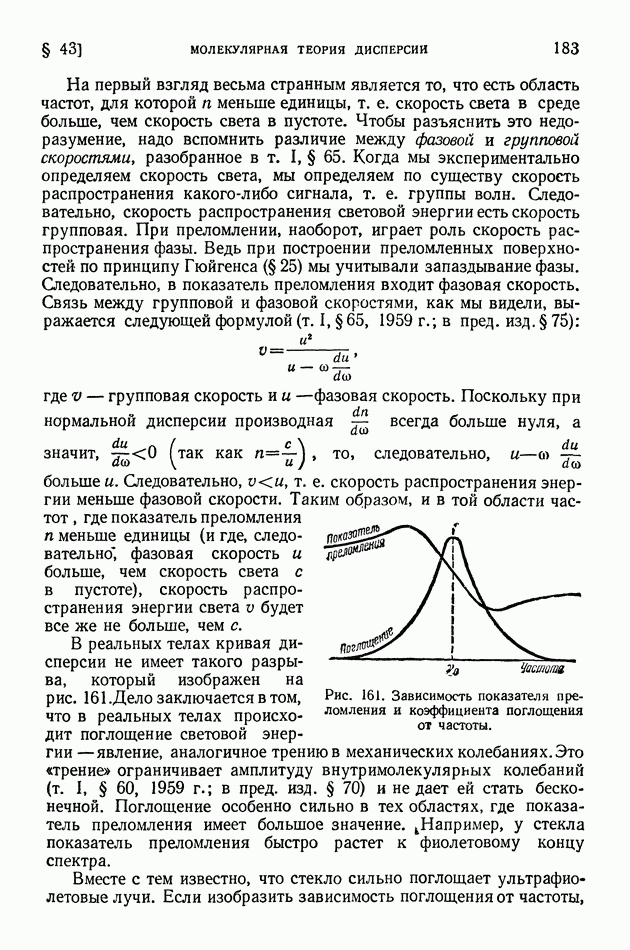
- § 43. Молекулярная теория дисперсии
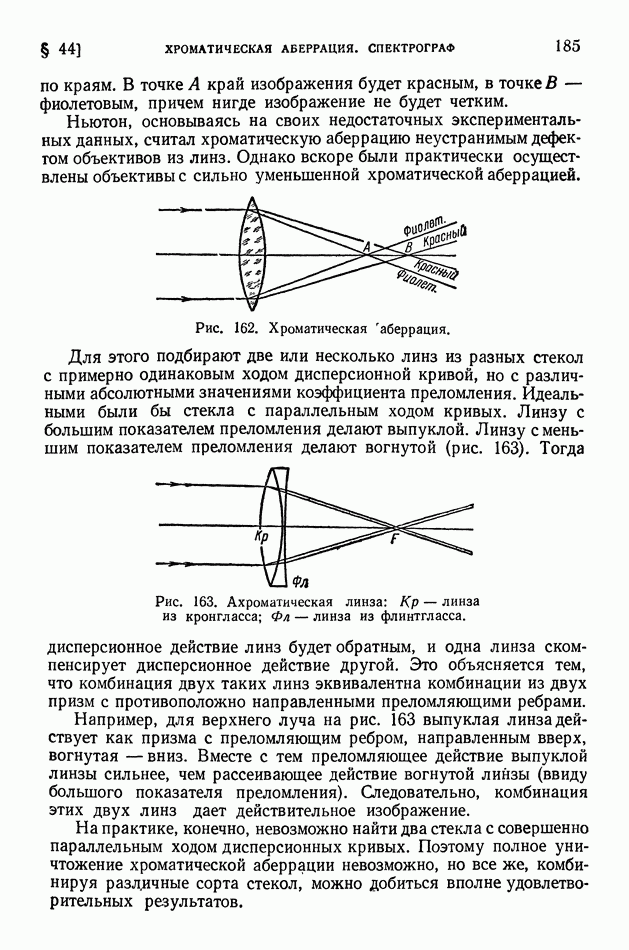
- § 44. Хроматическая аберрация. Спектрограф
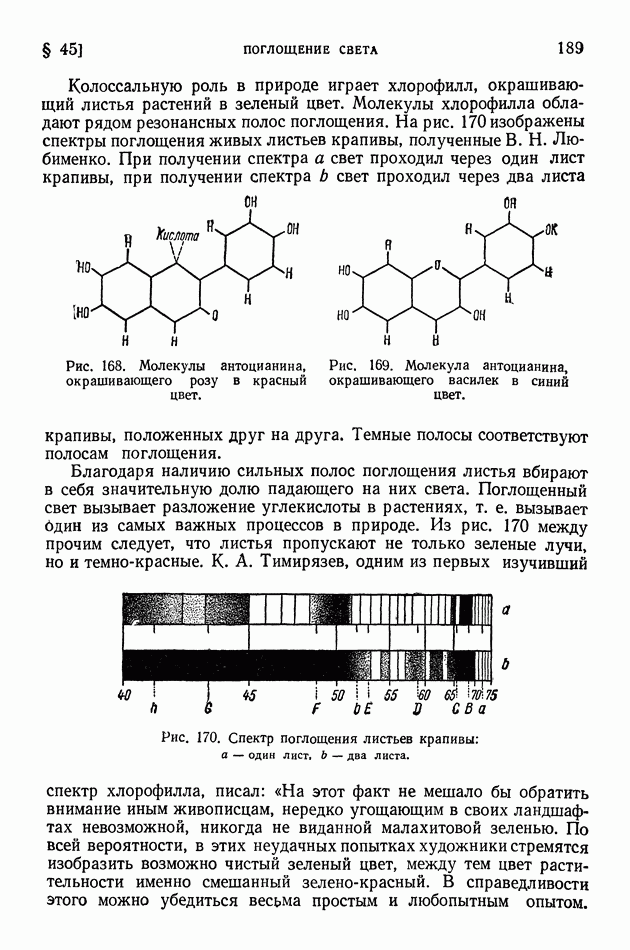
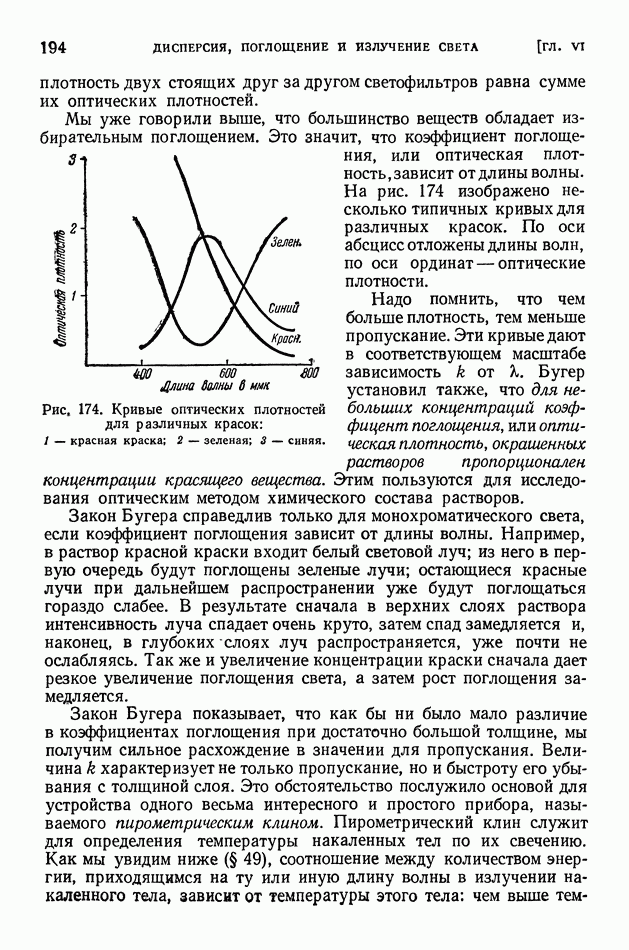
- § 45. Поглощение света
- § 46. Закон Бугера. Опыты Вавилова
- § 47. Атом как элементарный излучатель света
- § 48. Эффект Вавилова — Черенкова
- ГЛАВА VII. ТЕРМОДИНАМИКА ИЗЛУЧЕНИЯ И СВЕТОВОЙ ПОТОК
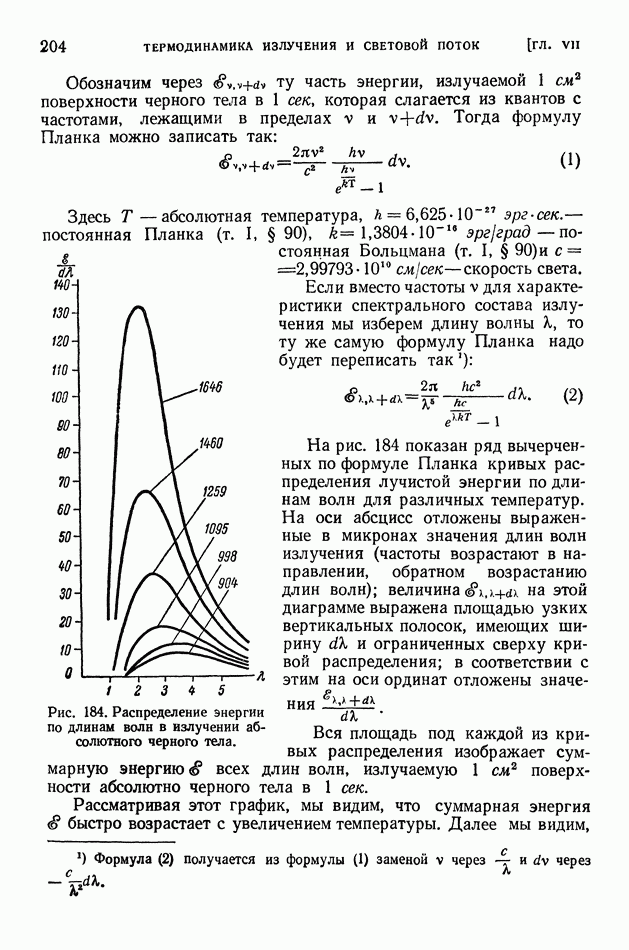
- § 49. Излучение черного тела. Формула Планка. Закон Вина
- § 50. Излучение нечерных тел. Законы Кирхгофа
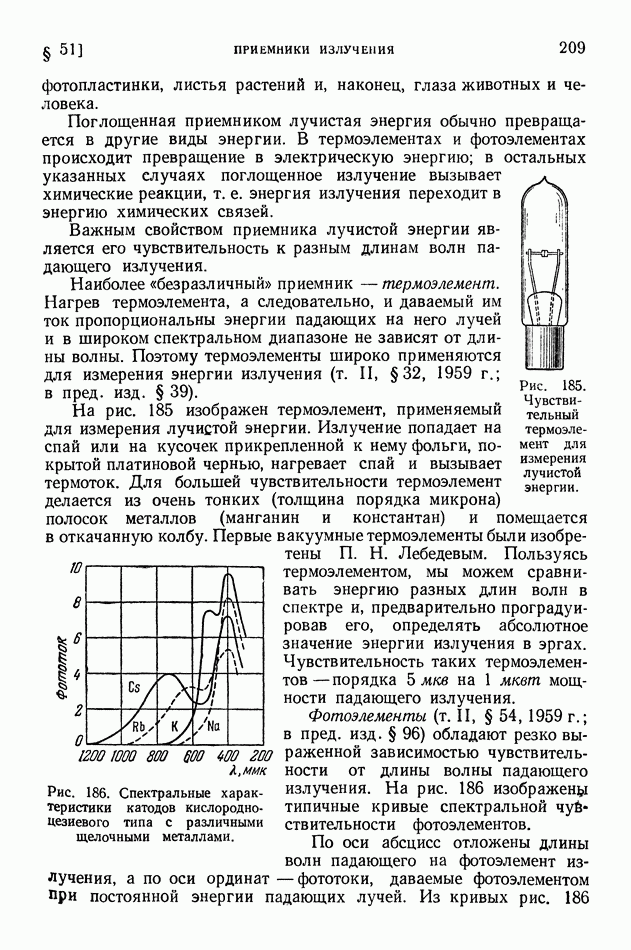
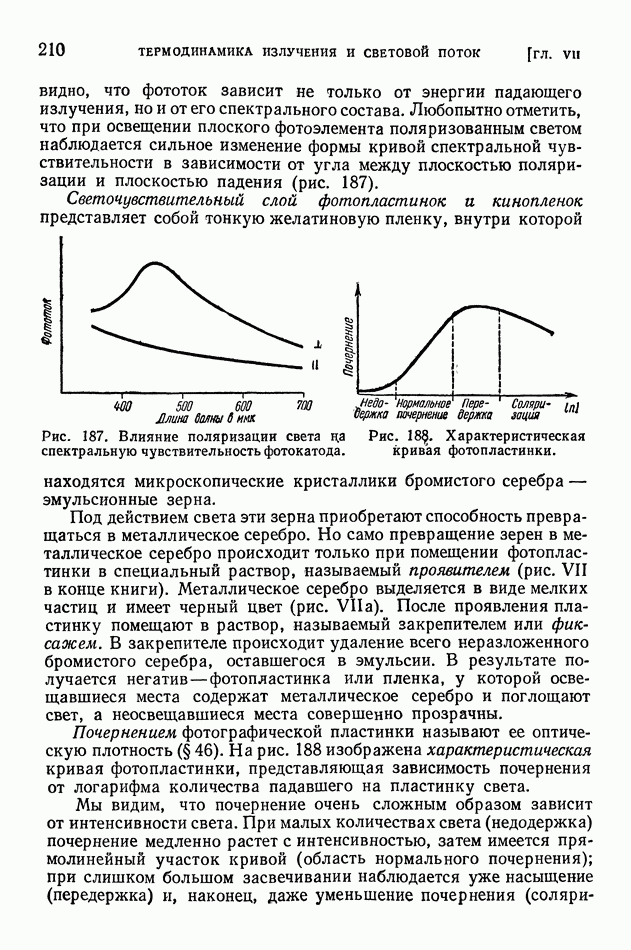
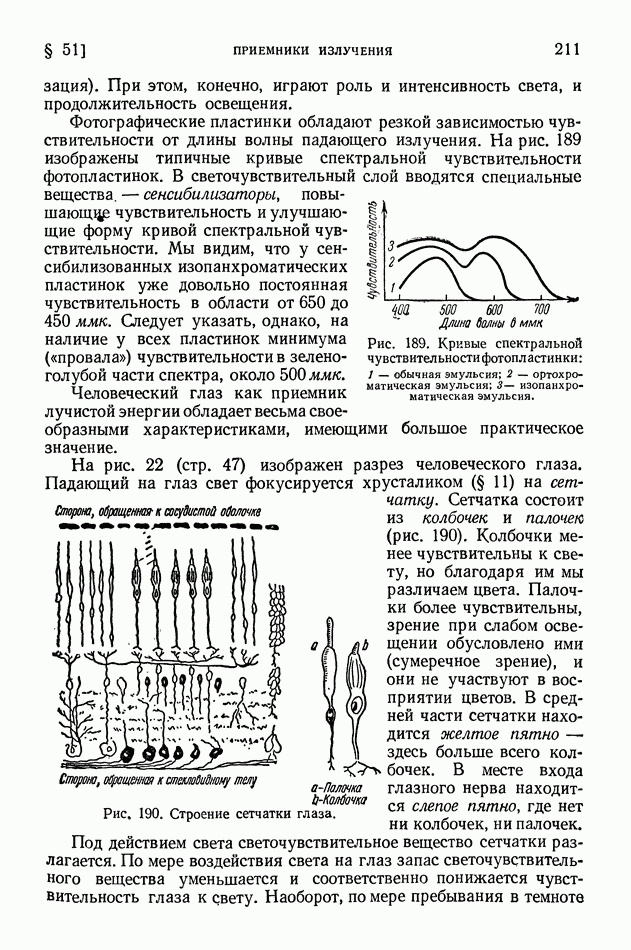
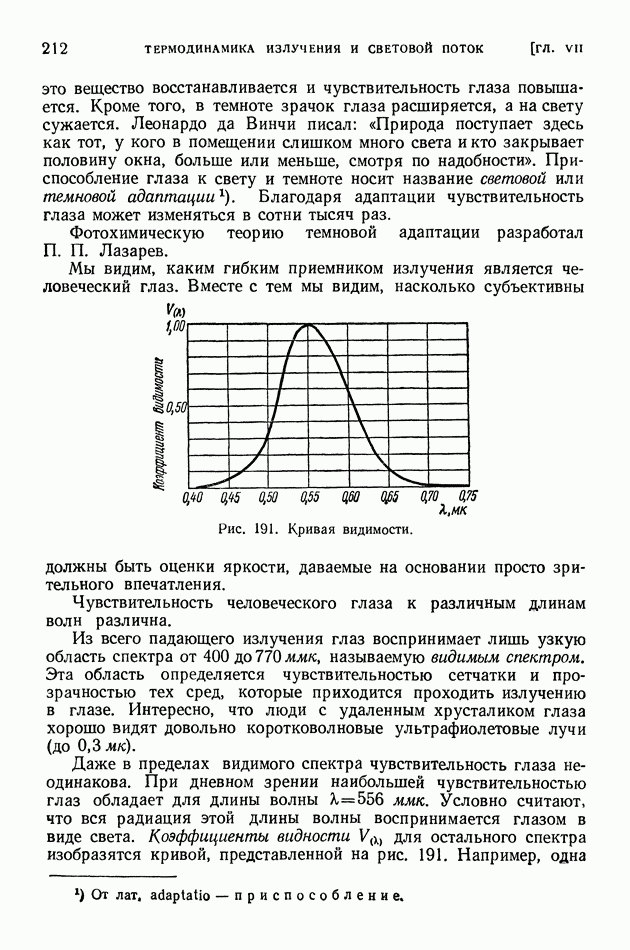
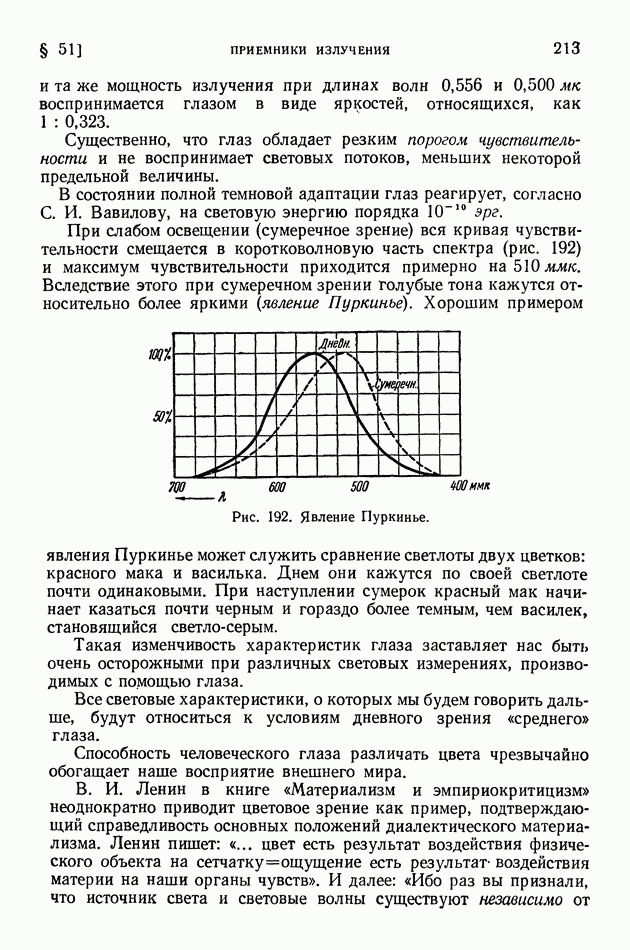
- § 51. Приемники излучения
- § 52. Световые величины и их измерения
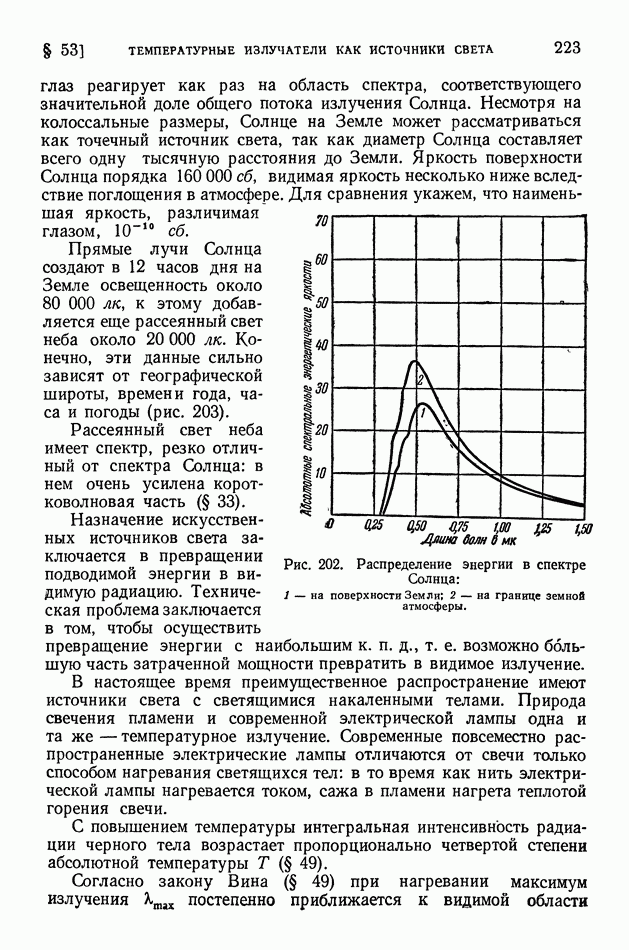
- § 53 Температурные излучатели как источники света
- ЧАСТЬ ПЯТАЯ. АТОМНАЯ ФИЗИКА
- ГЛАВА VIII. СТРОЕНИЕ АТОМА И ТЕОРИЯ БОРА
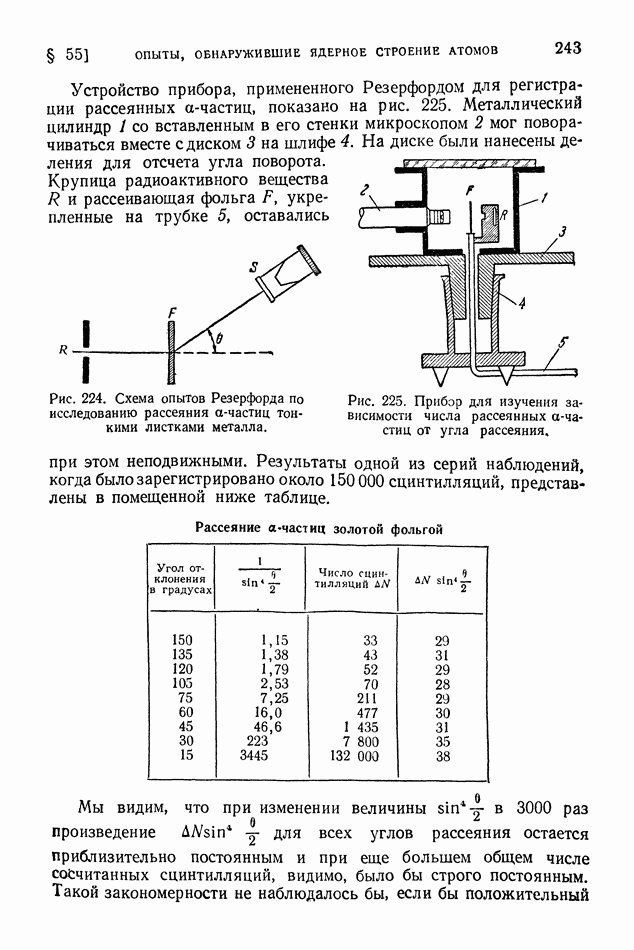
- § 55. Опыты, обнаружившие ядерное строение атомов
- § 56. Противоречие между фактическим строением атомов и выводами классической электродинамики. Строение линейчатых спектров
- § 57. Опытные основания теории квантов в первые годы ее развития
- § 58. Теория Бора. Происхождение спектра водорода
- § 59. Квантовые числа
- § 60. Принцип Паули. Строение электронных оболочек атомов
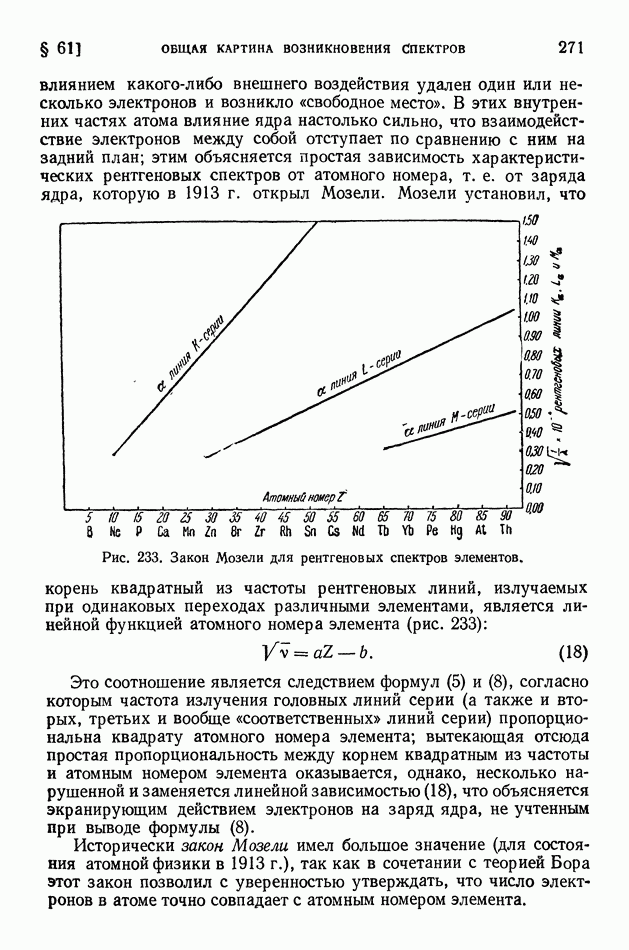
- § 61. Общая картина возникновения спектров
- ГЛАВА IX. ОСНОВЫ КВАНТОВОЙ (ВОЛНОВОЙ) МЕХАНИКИ
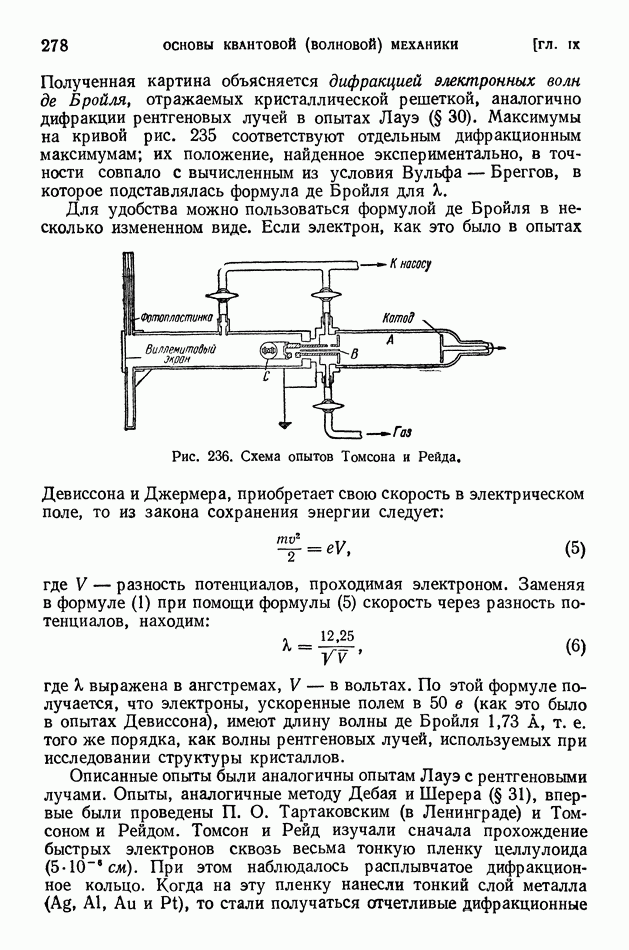
- § 62. Волновые свойства частиц. Формула де Бройля. Дифракция электронов
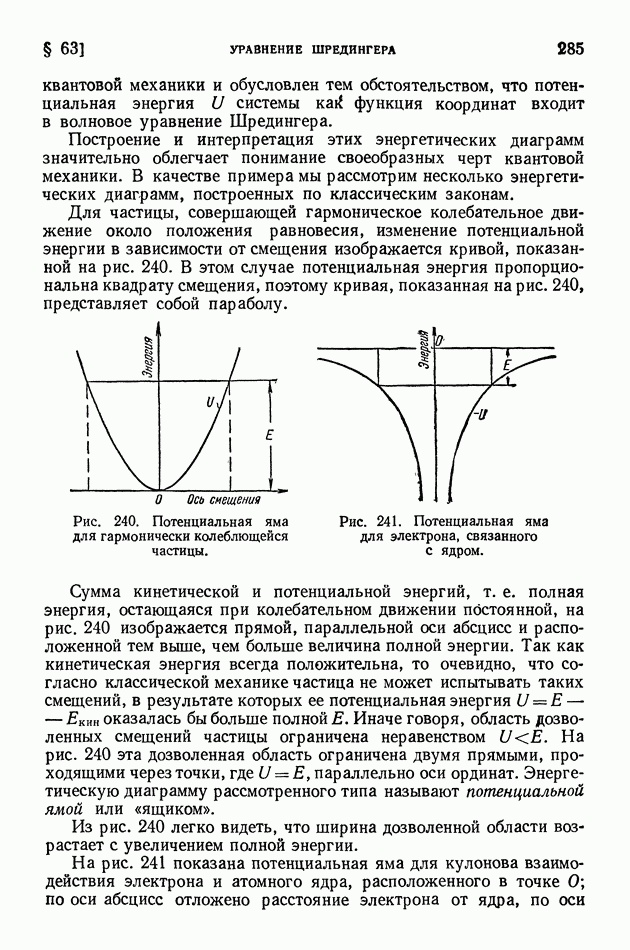
- § 63. Уравнение Шредингера. Просачивание через энергетический барьер. Нулевая энергия
- § 64. Волномеханическая теория атома водорода
- § 65. Соотношение неопределенностей и его разные трактовки
- ГЛАВА X. КВАНТОВАЯ ОПТИКА
- § 66. Развитие квантовой оптики
- § 67. Спектр щелочных металлов. Спин электрона
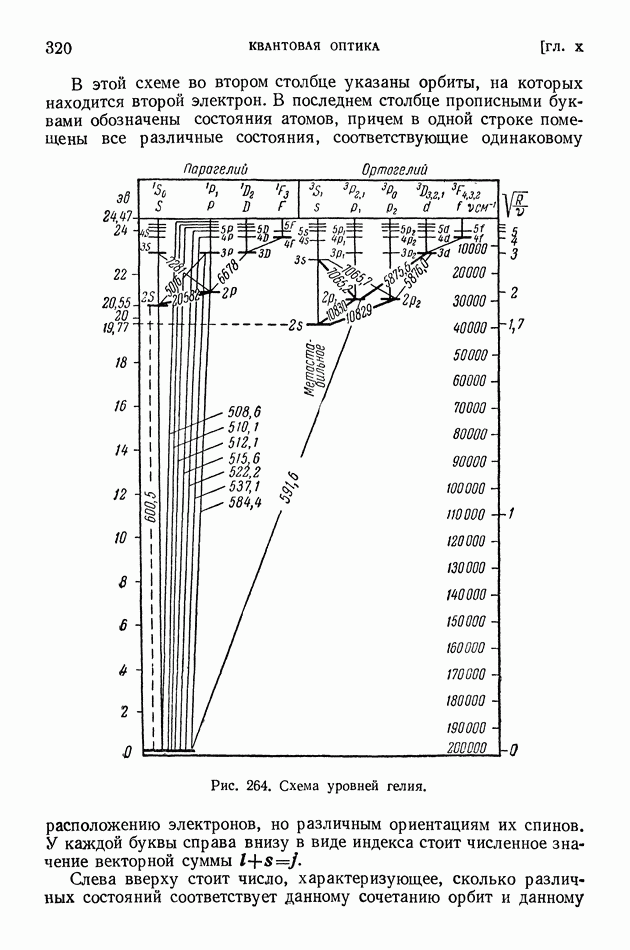
- § 68. Спектр гелия. Символика спектральных термов
- § 69. Сверхтонкая структура спектральных линий
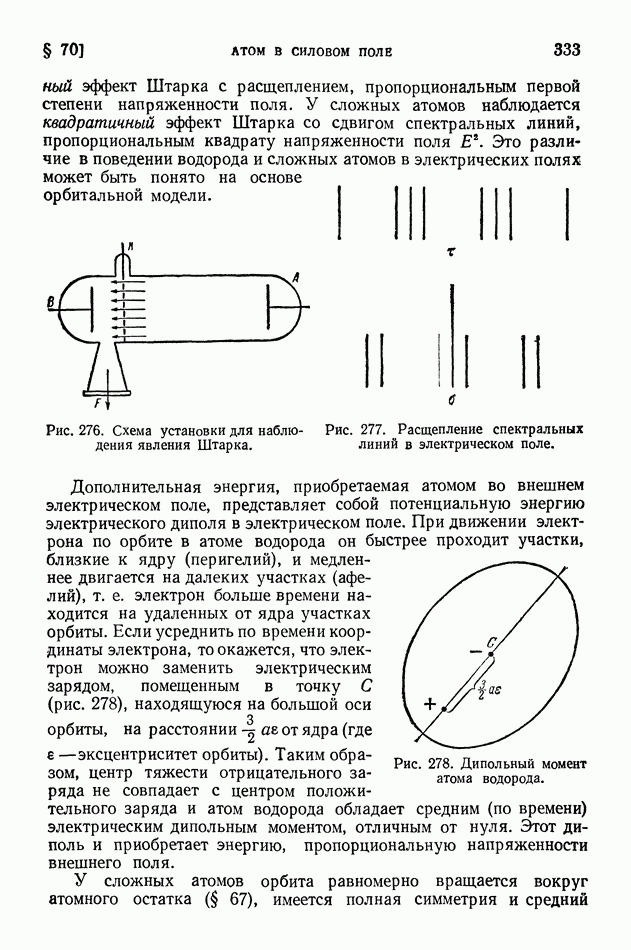
- § 70. Атом в силовом поле
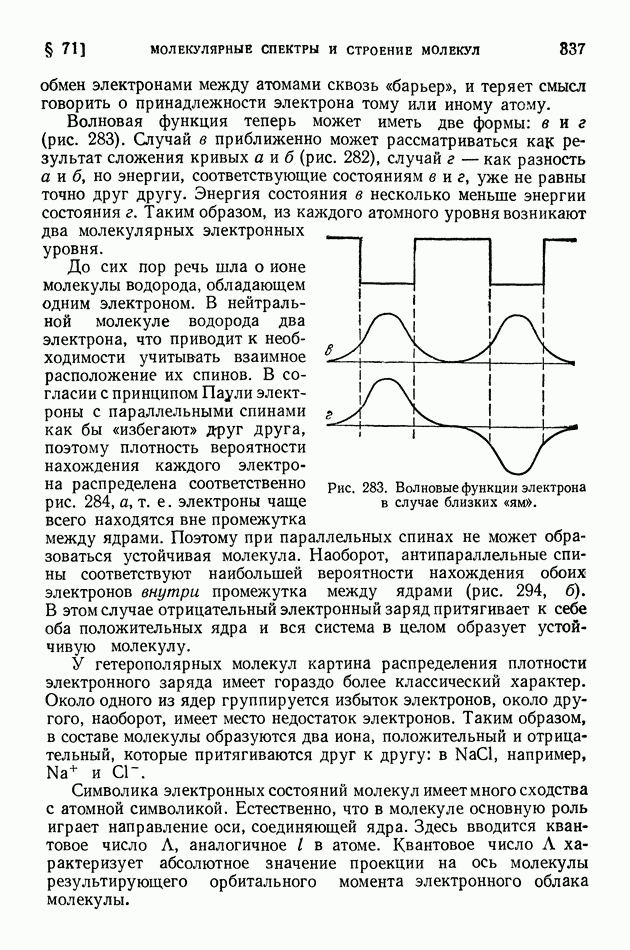
- § 71. Молекулярные спектры и строение молекул
- § 72. Комбинационное рассеяние света
- § 73. Квантовая картина испускания света атомами и молекулами
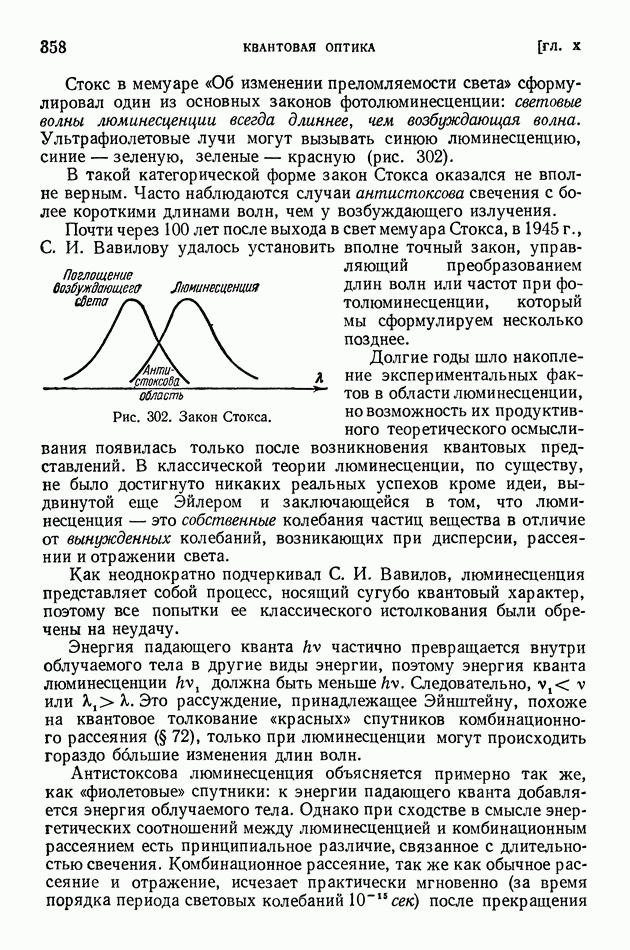
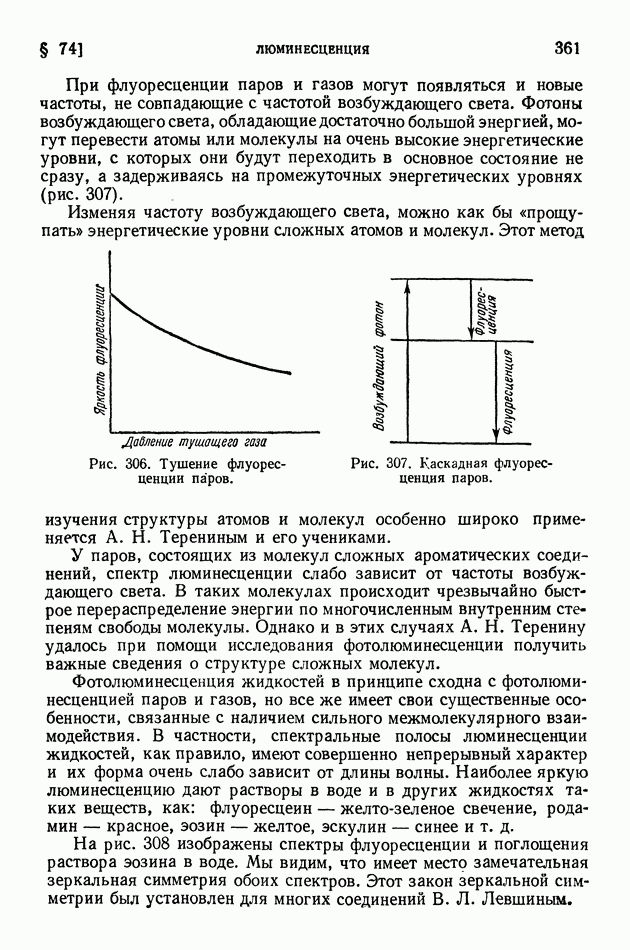
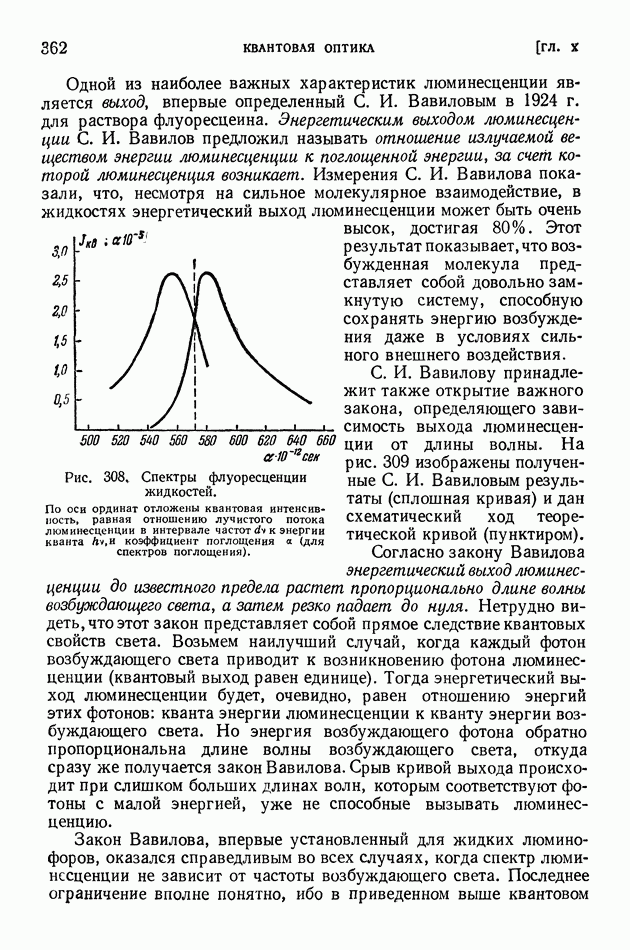
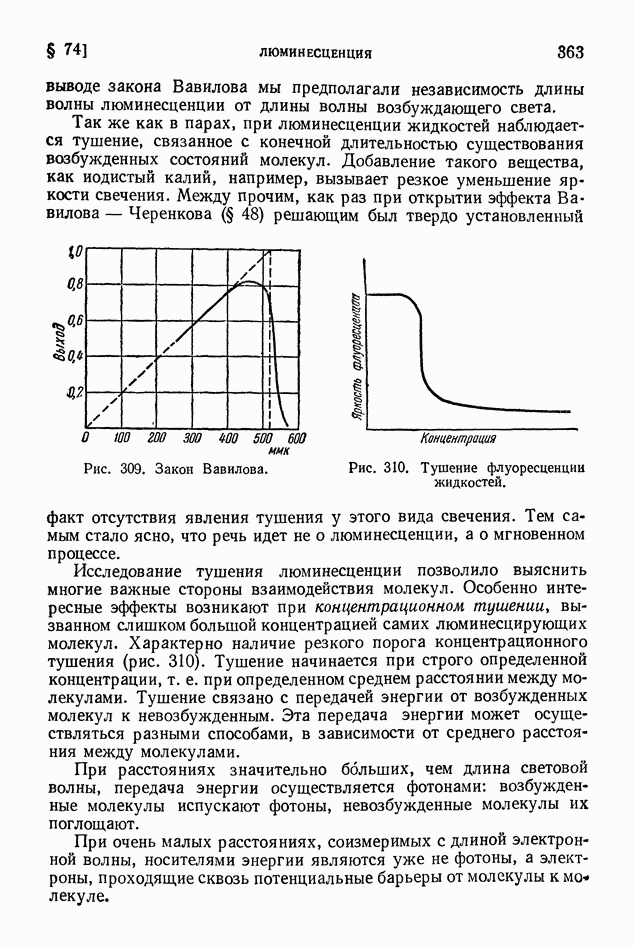
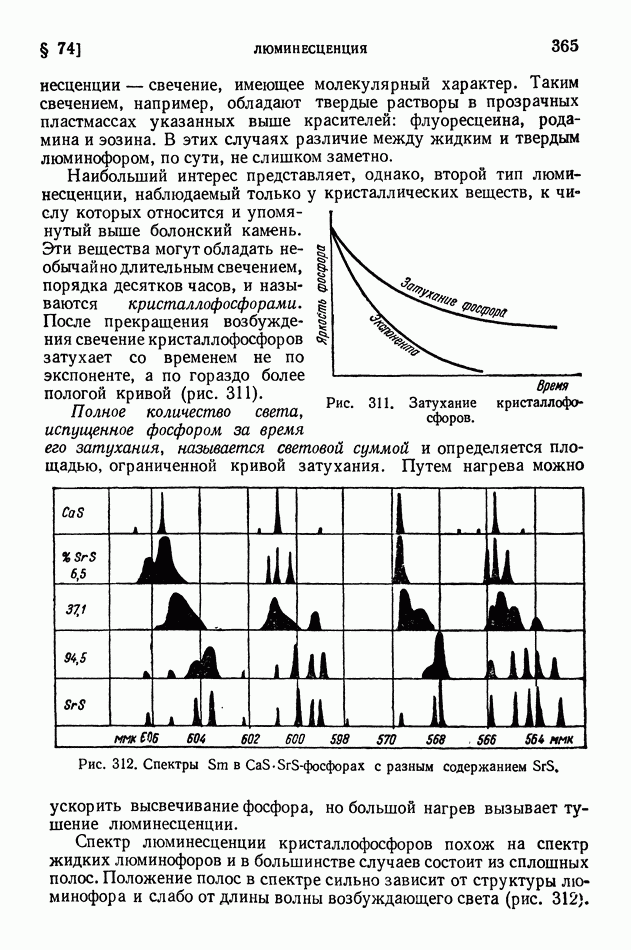
- § 74. Люминесценция
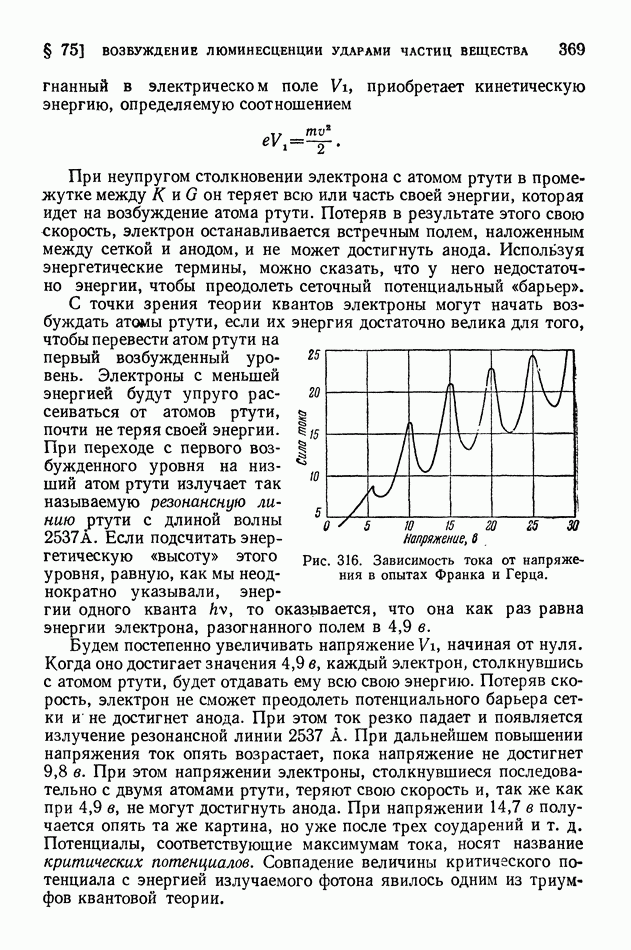
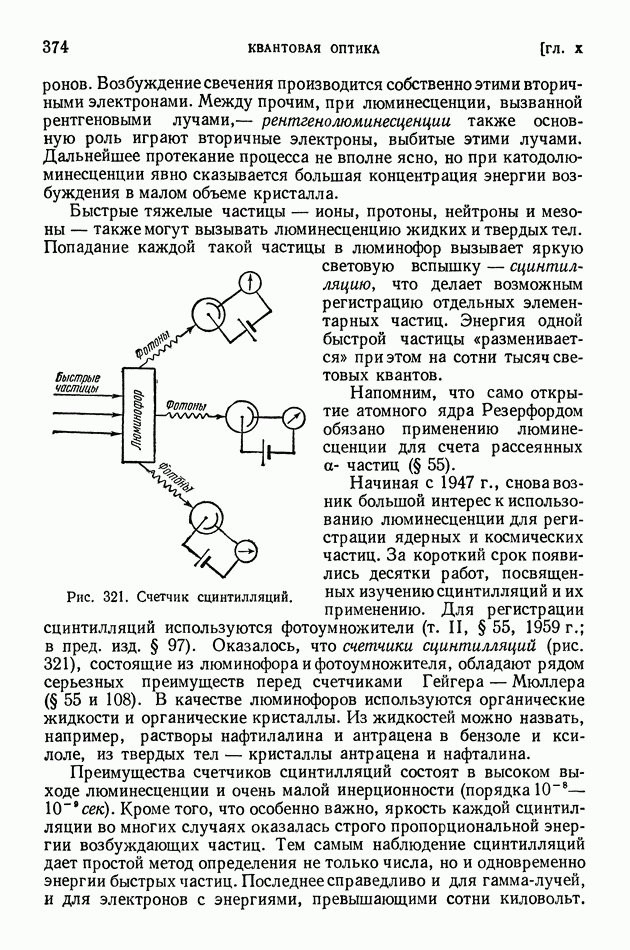
- § 75. Возбуждение люминесценции ударами частиц вещества
- § 76. Применения люминесценции
- § 77. Фотохимические реакции
- ГЛАВА XI. ЗАКОН ПРОПОРЦИОНАЛЬНОСТИ МАССЫ И ЭНЕРГИИ И РЕЛЯТИВИСТСКИЕ СООТНОШЕНИЯ
- § 78. Закон пропорциональности массы и энергии
- § 79. Предварительные замечания о релятивистских эффектах. Зависимость массы от скорости
- § 80. Корпускулярные свойства фотонов. Явление Комптона
- § 81. Вывод закона Эйнштейна сложения скоростей из закона пропорциональности массы и энергии и законов сохранения энергии или количества движения
- § 82. Две трактовки закона пропорциональности массы и энергии и уточнение закона тяготения
- § 83. Красное смещение спектральных линий. Поперечный эффект Доплера
- § 84. Влияние гравитационного поля на скорость света в вакууме и показатель преломления вакуума
- ЧАСТЬ ШЕСТАЯ. ЯДЕРНАЯ ФИЗИКА
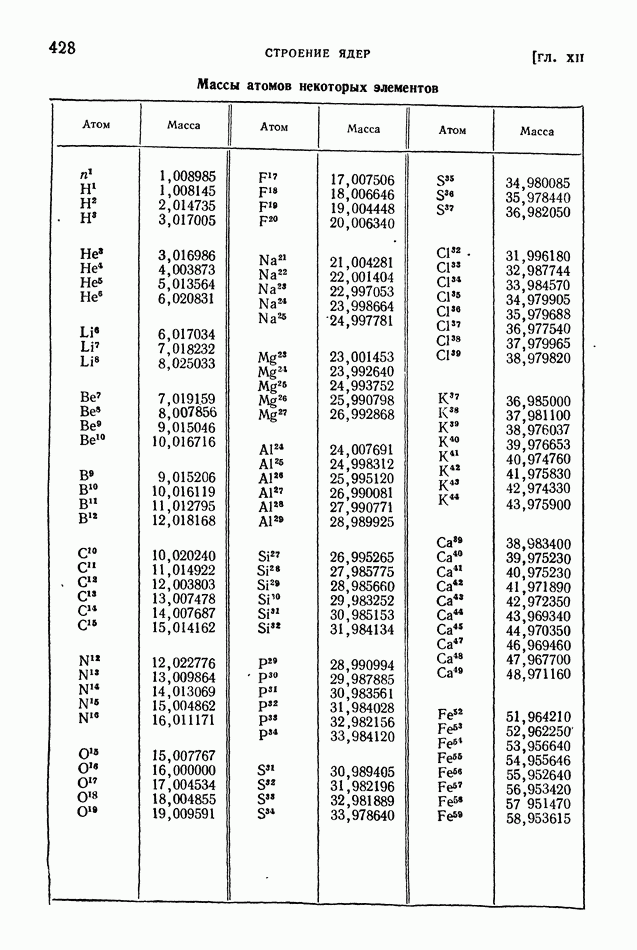
- § 85. Заряд и масса ядра. Масс-спектральный анализ
- § 86. Состав ядер. Изотопы. Атомные единицы массы и энергии
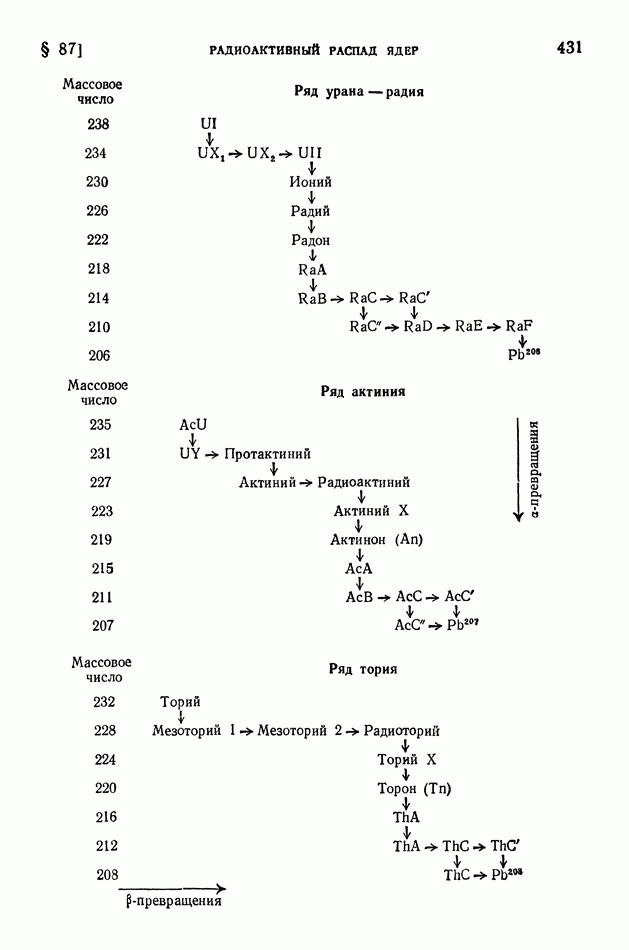
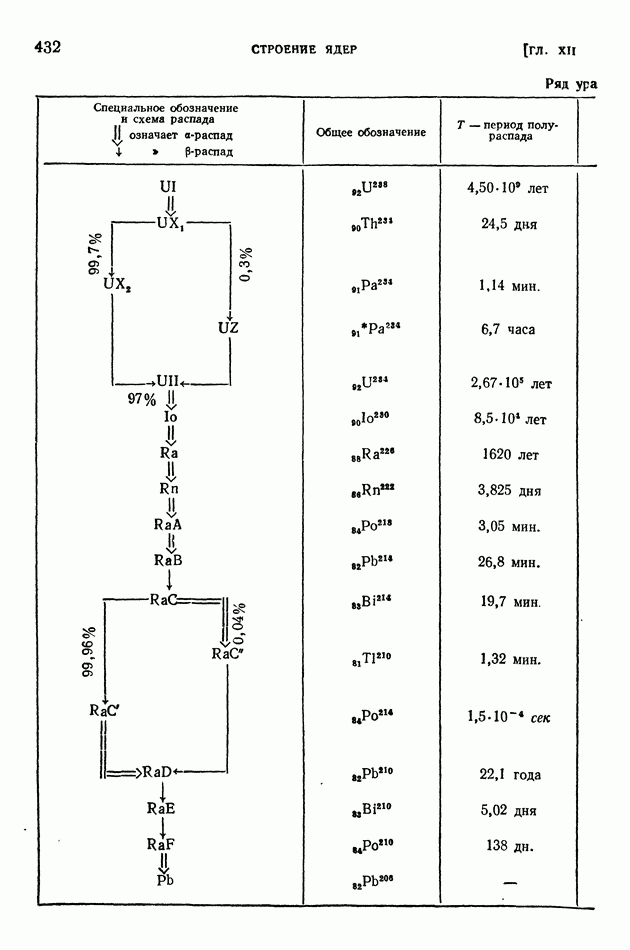
- § 87. Радиоактивный распад ядер. Закон радиоактивного смещения. Изомеры
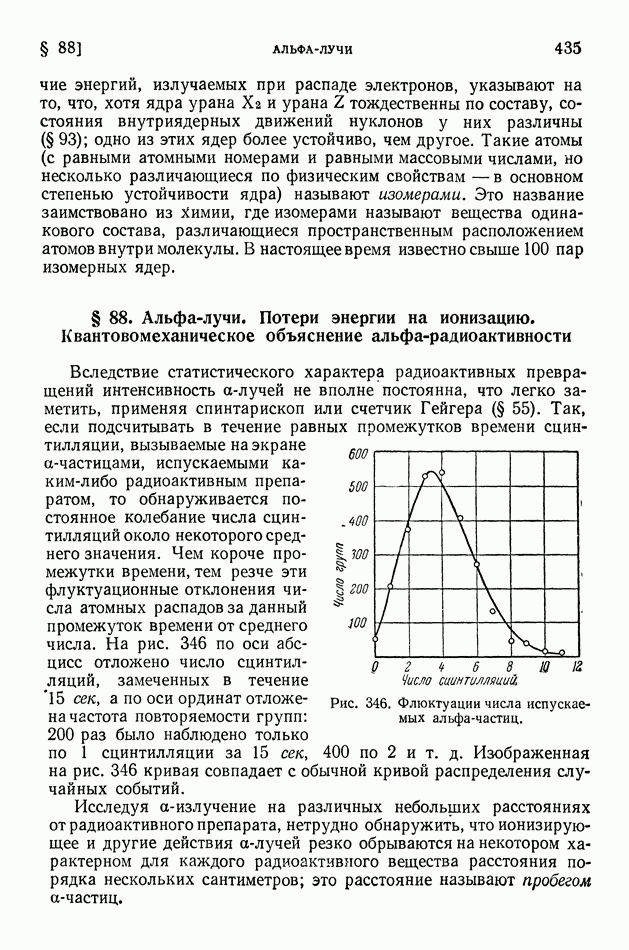
- § 88. Альфа-лучи. Потери энергии на ионизацию. Квантовомеханическое объяснение альфа-радиоактивности
- § 89. Бета- и гамма-лучи
- § 90. Искусственное расщепление ядер. Открытие нейтрона
- § 91. Открытие позитрона. Взаимопревращение фотонов определенной энергии и электронно-позитронных пар
- § 92. Индуцированная позитронная и электронная радиоактивность. Фоторасщепление ядер, K-захват
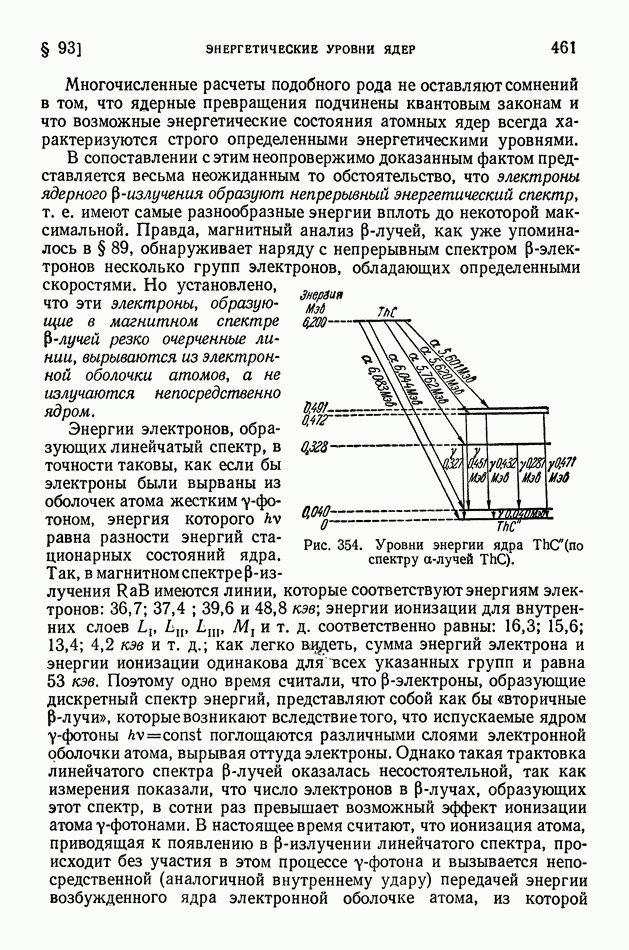
- § 93. Энергетические уровни ядер. Внутренняя конверсия. Нейтрино
- § 94. Капельная теория строения ядер
- § 95. Деление ядер и развитие капельной теории строения ядер
- ГЛАВА XIII. КОСМИЧЕСКИЕ ЛУЧИ
- § 96. Методы исследования и первые итоги изучения космических лучей
- § 97. Каскадное образование электронно-позитронных пар в космических лучах. Потери энергии электронами на тормозное излучение
- § 98. «мю»-мезоны. Зависимость времени жизни неустойчивых частиц от скорости движения
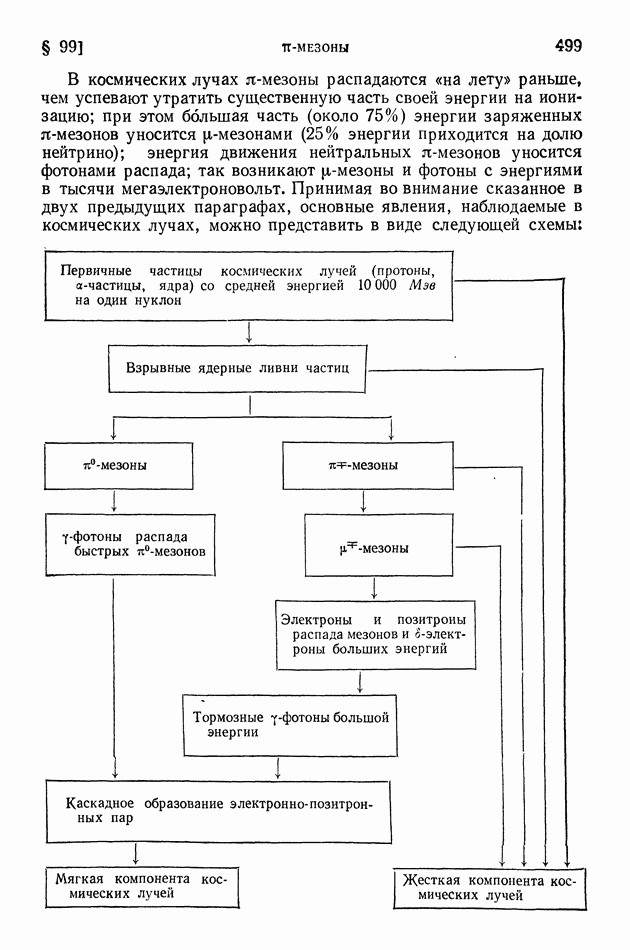
- § 99. «пи»-мезоны
- § 100. Взрывные ядерные ливни и их каскадное развитие в космических лучах
- § 101. Корпускулярный и энергетический спектр космических лучей. Происхождение космического излучения
- ГЛАВА XIV. ЭКСПЕРИМЕНТАЛЬНЫЕ СРЕДСТВА ЯДЕРНОЙ ФИЗИКИ
- § 102. Циклотроны
- § 103. Фазотроны
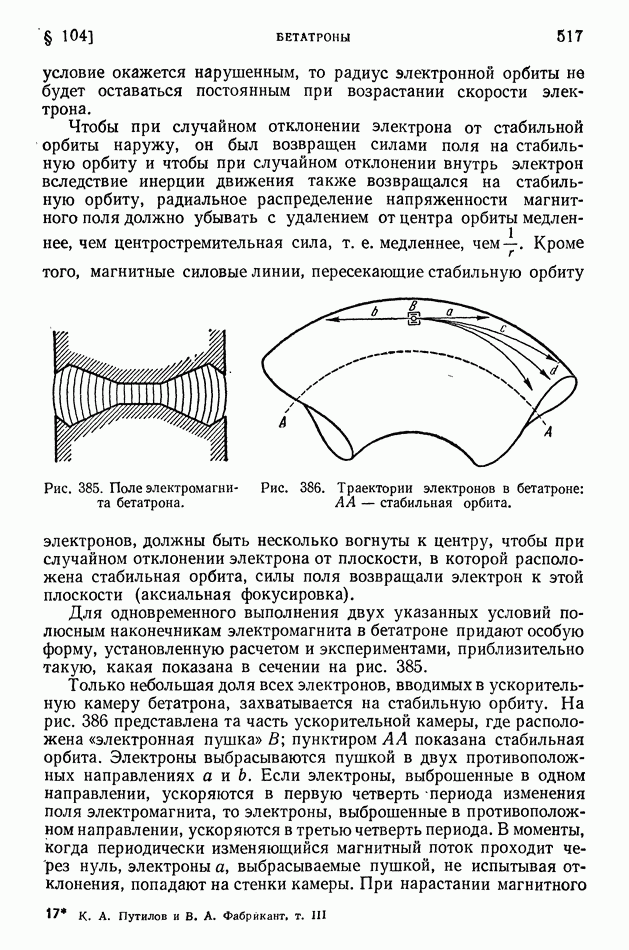
- § 104. Бетатроны
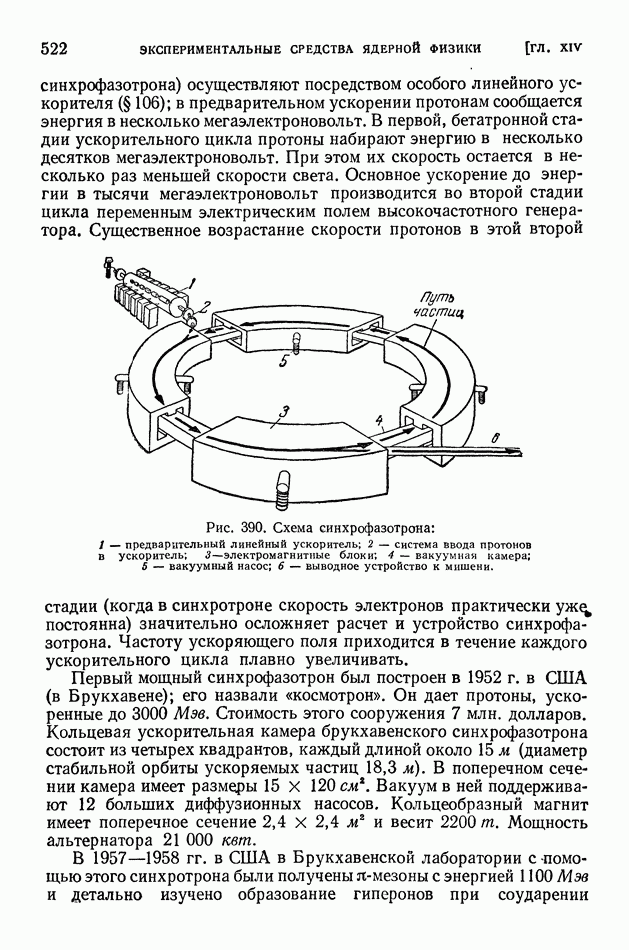
- § 105. Синхротроны и синхрофазотроны
- § 106. Линейные ускорители электронов и ионов
- § 107. Лабораторные источники нейтронов. Замедлители нейтронов в ядерных реакторах
- § 108. Усовершенствование методов наблюдения и счета частиц
- ГЛАВА XV. ЯДЕРНЫЕ РЕАКЦИИ И АТОМНАЯ ЭНЕРГИЯ
- § 109. Основные виды и обозначения ядерных реакций. Конкурирующие процессы в ядерных реакциях
- § 110. Энергетический эффект, энергия возбуждения и порог ядерных реакций
- § 111. Превращения элементарных частиц
- § 112. Ядерные силы
- § 113. Энергия связи ядер и средняя энергия связи нуклона
- § 114. Полуэмпирическая формула для энергии ядерной связи и для атомных энергий и масс
- § 115. Взаимосвязь энергии и строения ядер. Внутриядерное движение нуклонов и нуклонные оболочки. Спины и магнитные моменты ядер
- § 116. Энергия отделения частиц и анализ возможного хода ядерной реакции
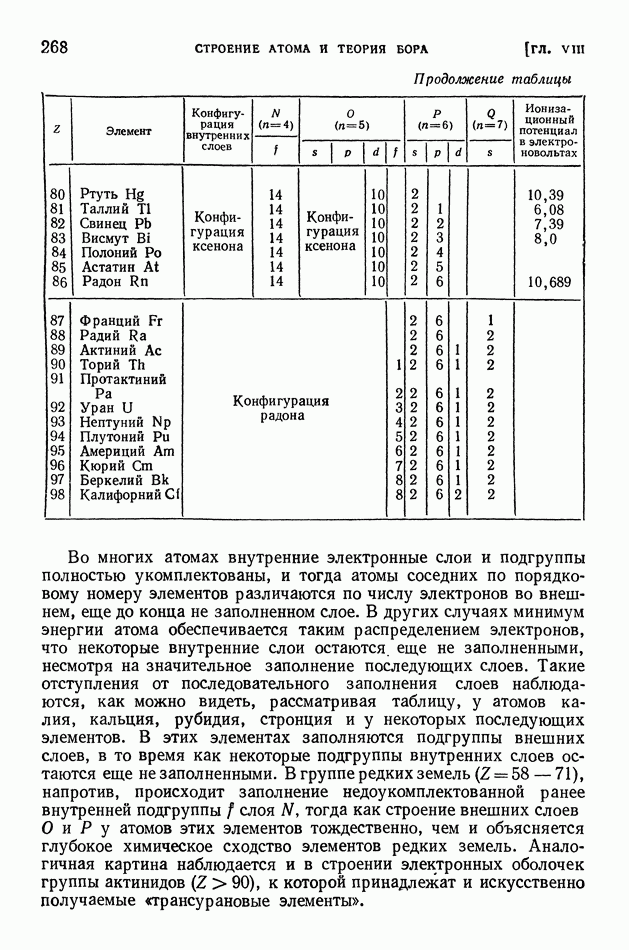
- § 117. Выход продуктов ядерной реакции. Эффективные сечения. Резонансные явления
- § 118. Цепной процесс деления ядер. Активно делящиеся вещества. Ядерные реакторы
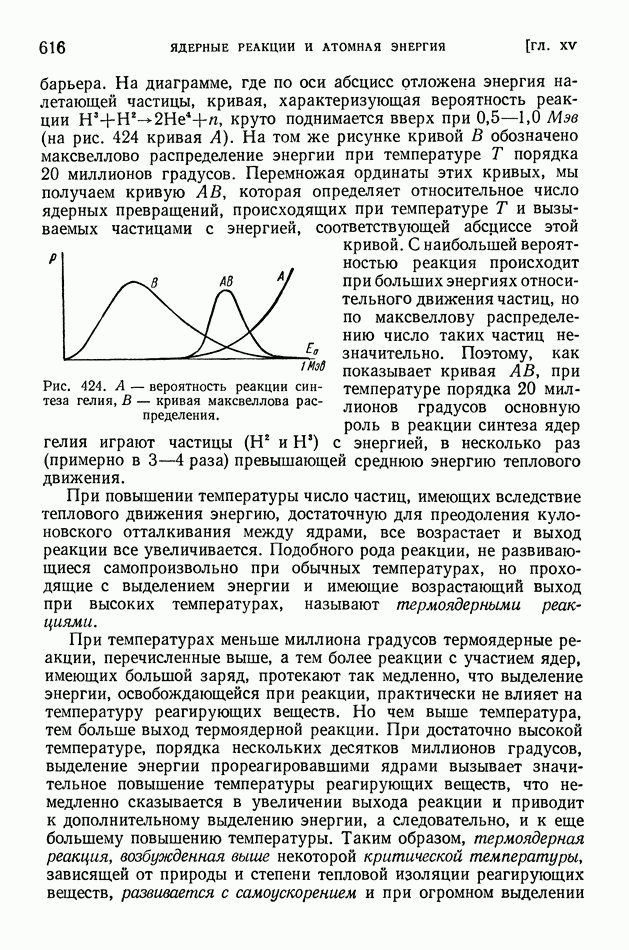
- § 119. Термоядерные реакции
- § 120. Применение ядерных реакций
- § 121. Ядерные реакции в звездах