| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
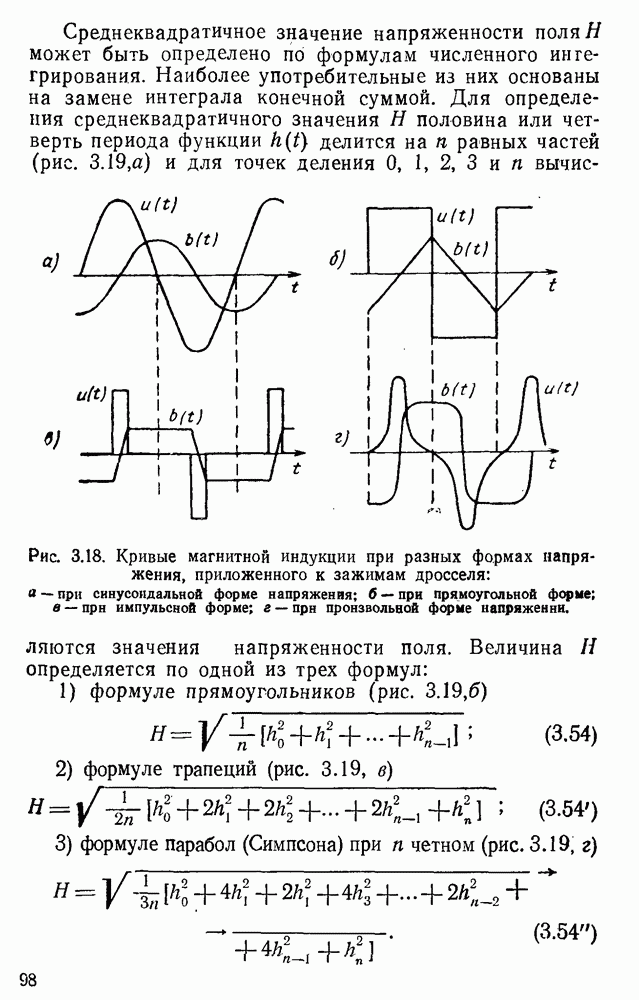
3.4. Аппроксимация кривых намагничивания ферромагнитных сердечников. Относительные единицы. Определение коэффициентов аппроксимации
Для теоретического анализа свойств дросселя нужно иметь аналитические выражения, отображающие свойства его ферромагнитного сердечника. Эти свойства зависят от многих факторов. Поэтому задачу по определению аналитических выражений целесообразно разбить на две отдельные самостоятельные задачи. В первой определим выражение, отображающее свойства сердечников при режиме квазистатичеокого намагничивания; во второй учтем влияние изменения этих свойств при режиме динамического намагничивания. В этом параграфе рассмотрим первую задачу, вторую — в § 3.5.
Свойства ферромагнитного сердечника при квазистатическом режиме намагничивания  в полной мере характеризуются семейством статических (квази-статических) петель гистерезиса. Очевидно, описав эти свойства аналитически, получим возможность выполнять расчеты дросселей аналитическими методами.
в полной мере характеризуются семейством статических (квази-статических) петель гистерезиса. Очевидно, описав эти свойства аналитически, получим возможность выполнять расчеты дросселей аналитическими методами.
Задача аналитического выражения семейств статических петель очень сложная, и поэтому для упрощения ее решения введем понятие о так называемых структурных составляющих петель или, что то же, о кривых намагничивания по реактивным («безгистерезисным»  и активным
и активным  ) процессам. Таие характеристики можно непосредственно получить По семейству гистерезисных петель и затем аппроксимировать. Полученные в результате аналитические выражения, очевидно, могут быть использованы для представления искомых петель.
) процессам. Таие характеристики можно непосредственно получить По семейству гистерезисных петель и затем аппроксимировать. Полученные в результате аналитические выражения, очевидно, могут быть использованы для представления искомых петель.
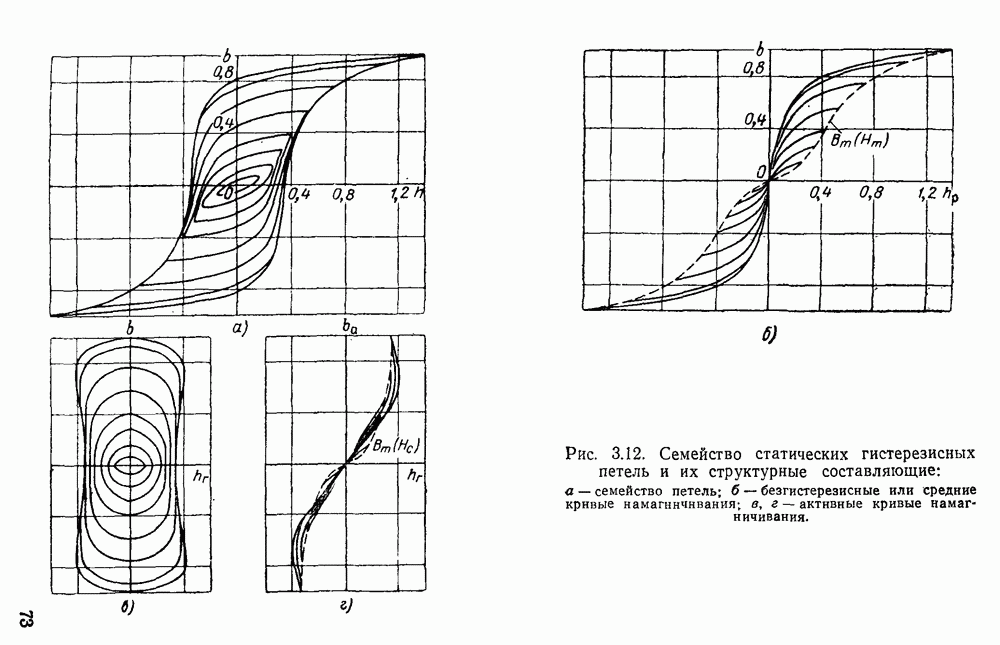
Метод получения структурных составляющих петель сводится, к следующему. По семейству гистерезисных петель (рис. 3.12,а) находятся реактивные (или средние) кривые намагничивания  (на рис.
(на рис.  пунктиром обозначена основная кривая намагничивания). При каждом значении
пунктиром обозначена основная кривая намагничивания). При каждом значении  для соответствующего b средние кривые определяются полусуммой соответствующих значений h петли. Затем можно найти активные кривые намагничивания. Их можно построить в двух координатных системах: в функции
для соответствующего b средние кривые определяются полусуммой соответствующих значений h петли. Затем можно найти активные кривые намагничивания. Их можно построить в двух координатных системах: в функции  (рис. 3.12,в)
(рис. 3.12,в)  функции
функции  (рис. 3.12,г). В первом случае магнитные характеристики имеют петлевой характер; во втором они представляют собой обычные однозначные кривые. Характеристики
(рис. 3.12,г). В первом случае магнитные характеристики имеют петлевой характер; во втором они представляют собой обычные однозначные кривые. Характеристики  определяются значениями напряженности поля, которые нужно добавить к кривой
определяются значениями напряженности поля, которые нужно добавить к кривой  чтобы получить данные самой петли. При получении характеристик
чтобы получить данные самой петли. При получении характеристик  дополнительно нужно воспользоваться нелинейным преобразованием вида
дополнительно нужно воспользоваться нелинейным преобразованием вида

которое дает возможность получить однозначные зависимости  от
от  и, следовательно, упростить задачу их аппроксимирования.
и, следовательно, упростить задачу их аппроксимирования.
Результаты построения структурных составляющих  приведены на рис.
приведены на рис.  и
и  . Здесь и далее
. Здесь и далее  — максимальное значение магнитной индукции при соответствующем циклическом перемагничивании;
— максимальное значение магнитной индукции при соответствующем циклическом перемагничивании;
(см. скан)
Рис. 3.12
 — мгновенное значение магнитной индукции;
— мгновенное значение магнитной индукции;  — мгновенное значение магнитной индукции, преобразованное согласно выражению (3.32);
— мгновенное значение магнитной индукции, преобразованное согласно выражению (3.32);  — мгновенное значение «безгистерезионой» (реактивной) слагающей напряженности поля;
— мгновенное значение «безгистерезионой» (реактивной) слагающей напряженности поля;  — мгновенное значение активной (гистерезисной) слагающей напряженности поля.
— мгновенное значение активной (гистерезисной) слагающей напряженности поля.
Для получения аналитических выражений, отражающих кривые намагничивания, воспользуемся способом аппроксимации. Общую задачу аппроксимации разобьем на две самостоятельные задачи:
— выбор класса функций для аппроксимации кривых намагничивания, т. е. выбор функциональной структуры аппроксимирующего выражения;
— определение коэффициентов аппроксимации, т. е. постоянных, входящих в выражение аппроксимирующей функции.
При выборе класса функций к аппроксимирующему выражению предъявляются следующие требования:
1) функция должна достаточно точно передавать аппроксимируемую характеристику;
2) выражение должно быть простым и удобным для дальнейших исследований;
3) оно должно позволять легко решать задачу относительно желаемой переменной;
4) аппроксимирующее выражение должно быть достаточно универсальным и хорошо отображать варьируемость параметров кривых намагничивания;
5) аналитическое выражение должно обеспечивать простоту решения задач  гармонического анализа;
гармонического анализа;
6) подстановка аналитического выражения в дифференциальное уравнение должна обеспечивать простоту интегрирования.
Желательно также, чтобы аппроксимирующая функция обладала свойством нечетности.
Следует признать, что пока нет такого выражения, которое бы полностью удовлетворяло всем перечисленным требованиям. Предложено лишь много различных аппроксимаций, каждая из которых удовлетворяет отдельным требованиям или их группе.
В большинстве литературных источников выбор выражения обоснован лишь на хорошем совпадении расчетной кривой с аналогичной опытной. В ряде случаев, особенно когда проводится качественный анализ, выбирают простейшие аппроксимации (например, кусочно-линейную и др.).

Рис. 3.13. Зависимость коэффициентов аппроксимации от величины магнитной индукции.
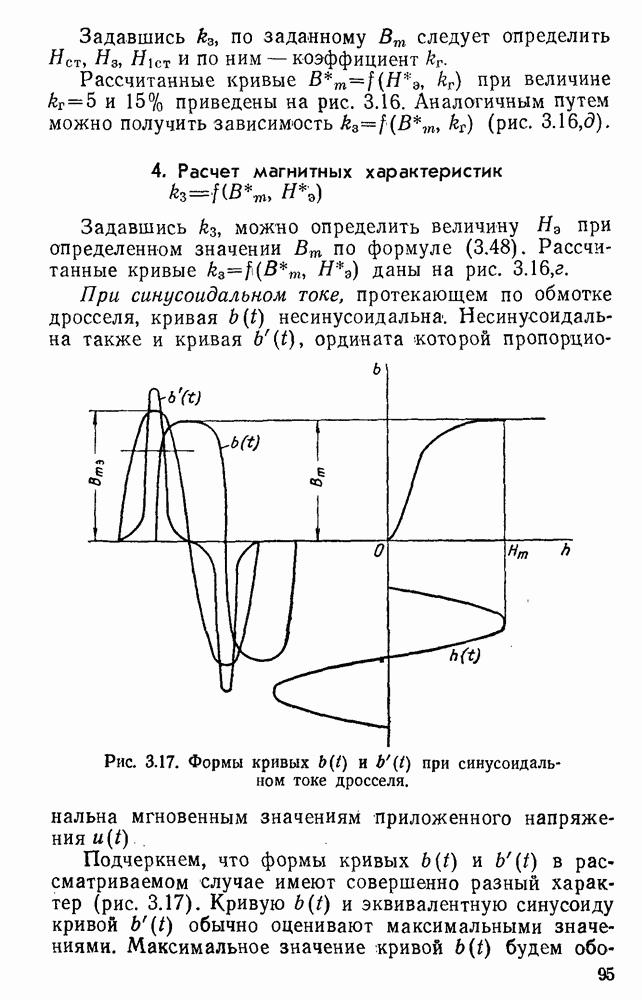
В данной книге для описания «безгистерезисных» или реактивных кривых намагничивания используется гиперболический синус, для описания гистерезисных (или активных) кривых намагничивания — круговой синус. Выбор этих выражений в основном произведен исходя из необходимости обеспечения простоты решения задач гармонического анализа.
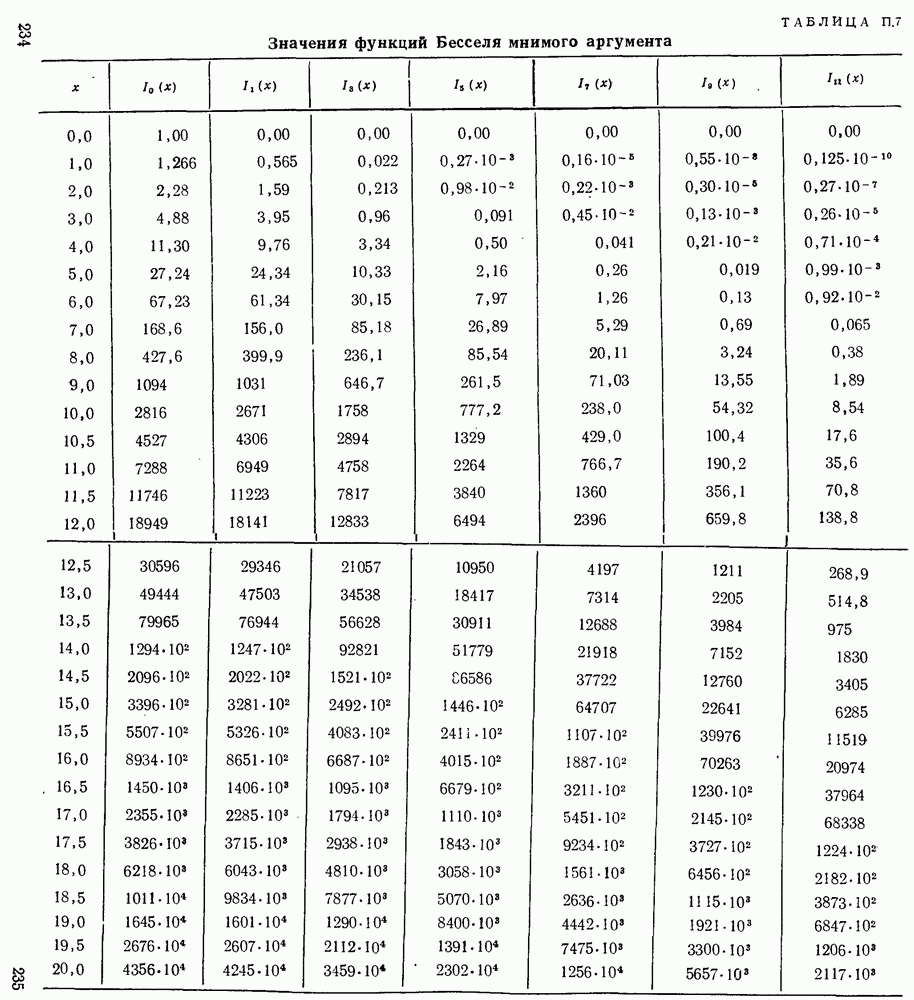
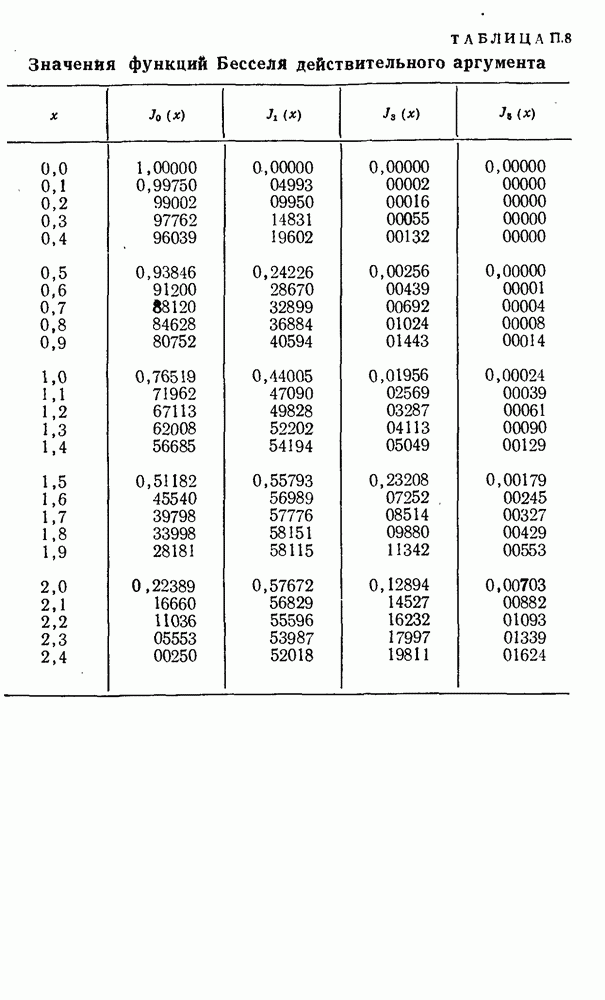
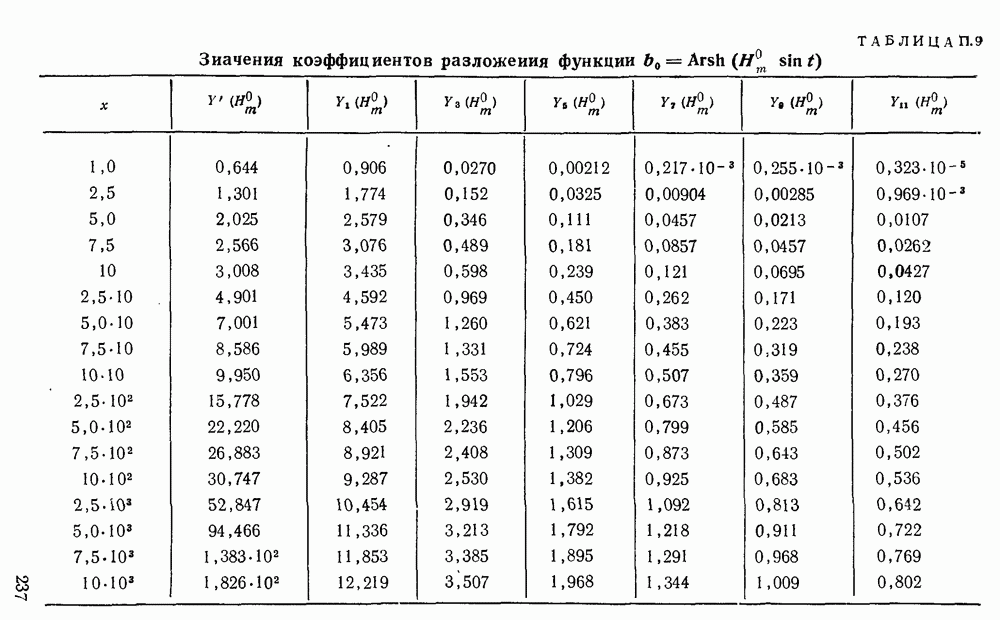
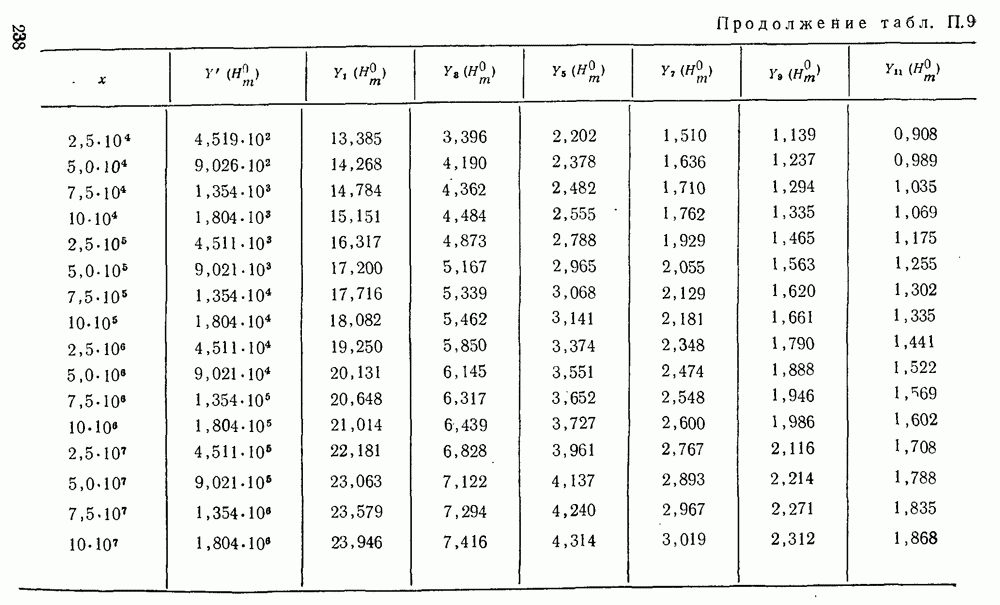
При таком способе аппроксимации анализ «безгистерезисных» (реактивных) процессов легко производится с помощью функций Бесселя от мнимого аргумента, а активных — с помощью функций Бесселя от действительного аргумента.
Семейства реактивных и активных кривых намагничивания при аппроксимации их гиперболическим и круговым синусами имеют следующий вид:

где  — коэффициенты аппроксимации или параметры ферромагнитного сердечника.
— коэффициенты аппроксимации или параметры ферромагнитного сердечника.
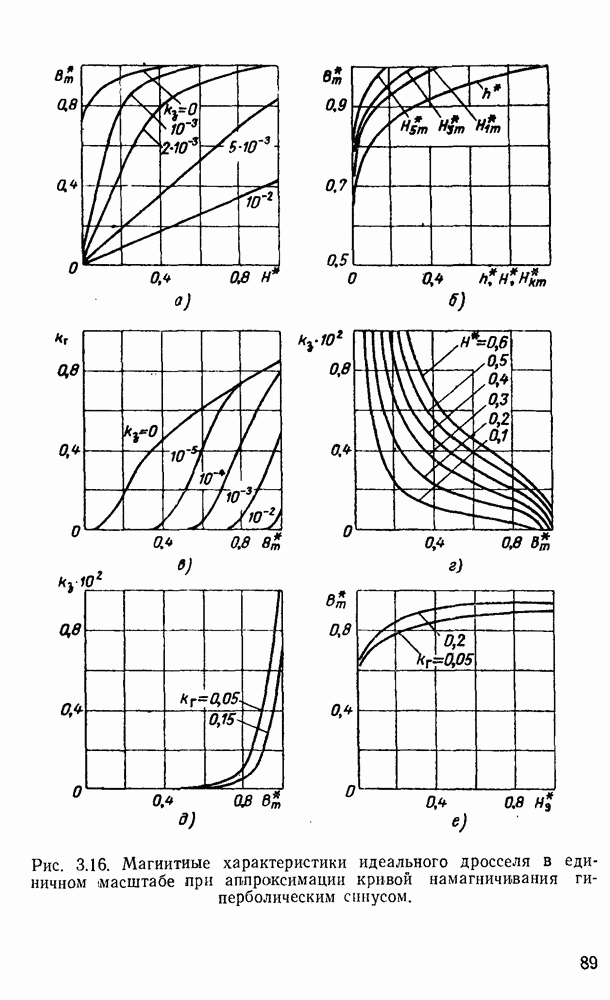
Зависимости этих параметров для семейства петель (рис. 3.12,а) в функции магнитной индукции приведены на рис. 3.13. В общем случае эти коэффициенты являются функцией температуры, внешних упругих напряжений и т. д.
Характерно, что выражения (3.33) и (3.33) совместно позволяют аналитически выразить семейство искомых петель гистерезиса.
Для этого достаточно воспользоваться понятием параллельной схемы замещения магнитной цепи и перейти к выражению  где
где  — значение напряженности поля при квазистатическом режиме намагничивания
— значение напряженности поля при квазистатическом режиме намагничивания  берется знак плюс, при
берется знак плюс, при  — знак минус).
— знак минус).
Для получения петель по этому уравнению нужно при каждом значении  определить связь между
определить связь между  и b за один полный цикл перемагничивания. Подчеркнем, что закон изменения b не оговаривается. Выражение (3.34) инвариантно относительно времени и, следовательно, справедливо при любом (квазистатическом) характере изменения
и b за один полный цикл перемагничивания. Подчеркнем, что закон изменения b не оговаривается. Выражение (3.34) инвариантно относительно времени и, следовательно, справедливо при любом (квазистатическом) характере изменения 
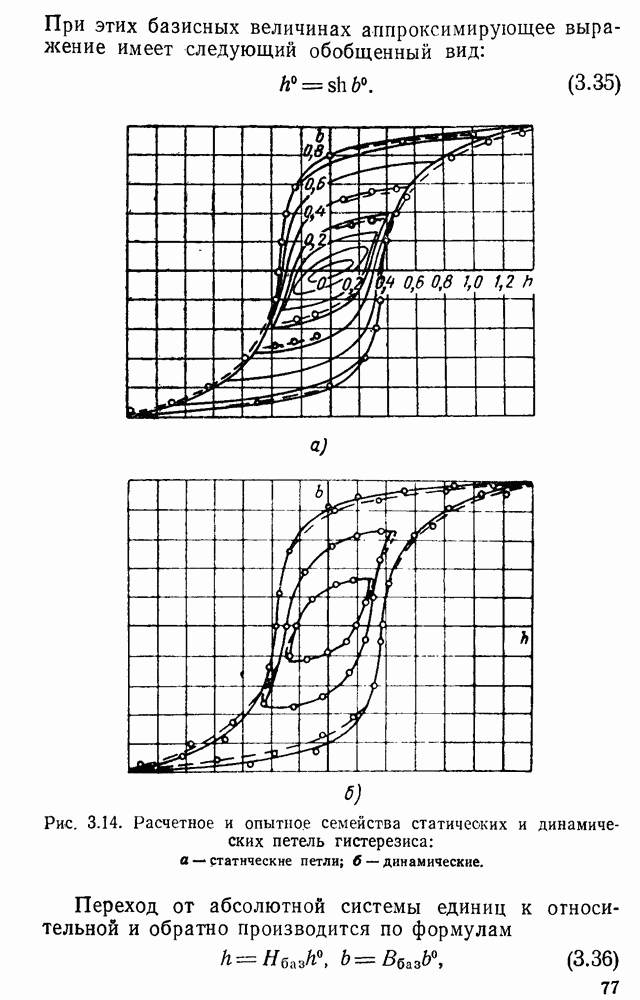
Рассчитанные по уравнению (3.34) семейства статических петель приведены на рис. 3.14,а. Как видим, расчетные петди хорошо согласуются с соответствующими опытными.
При необходимости более точного отражения характера петель в качестве аппроксимирующих выражений семейств кривых следует использовать два гиперболических и соответственно два круговых синуса. При этом, как показано в [72], точность описания гистерезисных петель значительно повышается.
Для дальнейших исследований аппроксимирующие выражения (3.33) и (3.33) удобно представлять в относительных (безразмерных) величинах. При этом можно получить общность результатов анализа. Особенно удобно их использовать при расчетах цепей со сталью без учета гистерезиса, когда можно пренебречь зависимостью параметров ферромагнетика от величины магнитной индукции (при усредненных коэффициентах аппроксимации). Трудоемкие расчеты по решению задач гармонического анализа можно выполнить лишь один раз и в дальнейшем использовать результаты для расчета дросселей.
Примем две системы относительных единиц. При первой системе, применяемой при приближенных расчетах, когда потери в стали можно не учитывать, в качестве базисных величин удобно выбрать

При этих базисных величинах аппроксимирующее выражение имеет следующий обобщенный вид:


Рис. 3.14. Расчетное и опытное семейства статических и динамических петель гистерезиса: а — статические петли; б — динамические.
Переход от абсолютной системы единиц к относительной и обратно производится по формулам

где h, b — мгновенные значения напряженности поля и магнитной индукции;  — то же в относительных безразмерных величинах.
— то же в относительных безразмерных величинах.
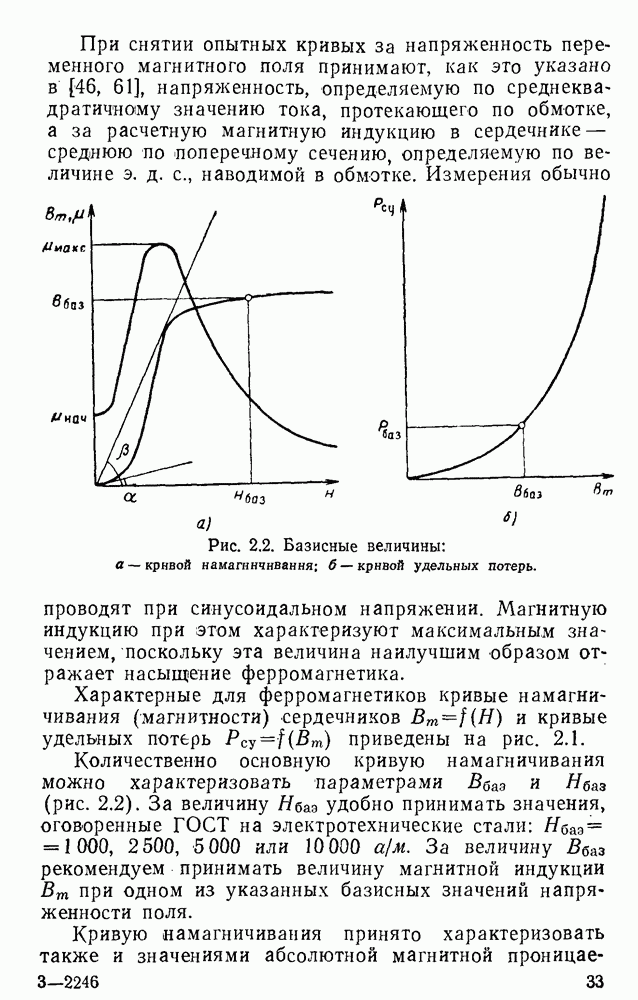
При второй системе относительных единиц кривая намагничивания приводится к единичному масштабу. При этой системе одна из точек кривой намагничивания принимается за базисную  , а координаты всех других точек выражаются относительно этих базисных параметров. В качестве базисных непременно должны быть выбраны такие значения Нбаз и Вбаз, которые находятся в конце рабочего участка кривой намагничивания сердечника. Лишь при таком выборе могут быгь найдены оптимальные значения коэффициентов аппроксимаций, соответствующих нужному рабочему участку. Рабочие участки, или рабочие области, для дросселей с сердечниками из электротехнической стали при аппроксимации реактивных кривых намагничивания следующие: от 0 до 1 000 или до 2 500, 5 000, 10 000, 25 000 а/м.
, а координаты всех других точек выражаются относительно этих базисных параметров. В качестве базисных непременно должны быть выбраны такие значения Нбаз и Вбаз, которые находятся в конце рабочего участка кривой намагничивания сердечника. Лишь при таком выборе могут быгь найдены оптимальные значения коэффициентов аппроксимаций, соответствующих нужному рабочему участку. Рабочие участки, или рабочие области, для дросселей с сердечниками из электротехнической стали при аппроксимации реактивных кривых намагничивания следующие: от 0 до 1 000 или до 2 500, 5 000, 10 000, 25 000 а/м.
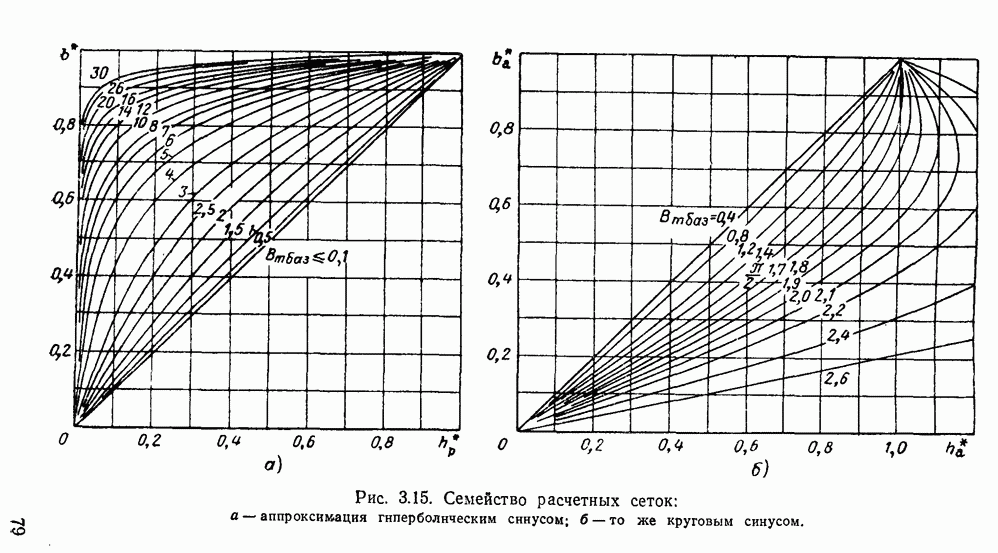
Опишем, как могут быть найдены оптимальные значения коэффициентов аппроксимирующих выражений, наилучшим образом соответствующие рабочему участку какой-либо конкретной кривой намагничивания. Проще всего это сделать, пользуясь полученными нами с помощью ЭЦВМ зависимостями, представленными на рис. 3.15. Зависимости построены по следующим формулам:
при аппроксимации кривой намагничивания гиперболическим синусом

при аппроксимации кривой намагничивания круговым синусом
 (3.37)
(3.37)
где  — показатель нелинейности кривой намагничивания (рис. 3.15).
— показатель нелинейности кривой намагничивания (рис. 3.15).
Способ определения оптимальных коэффициентов аппроксимирующих выражений сводится к следующему. Для базисных значений  кривую намагничивания, подлежащую аппроксимации, следует привести к единичному масштабу и нанести на кальку в том же масштабе, что и кривые сеток (рис. 3.15).
кривую намагничивания, подлежащую аппроксимации, следует привести к единичному масштабу и нанести на кальку в том же масштабе, что и кривые сеток (рис. 3.15).
(см. скан)
Рис. 3.15. Семейство расчетных сеток: а - аппроксимация гиперболическим синусом; б - то же круговым синусом.
Путем совмещения кальки с кривыми сеток подбирается наиболее оптимальная величина показателя нелинейности  .
.
Поиск наивыгоднейшего значения  и коэффициентов
и коэффициентов  можно произвести и аналитически, например методом наименьших квадратов, минимизацией выражения
можно произвести и аналитически, например методом наименьших квадратов, минимизацией выражения

где N — число заданных точек на реальной кривой;  — заданная и аппроксимирующая функции.
— заданная и аппроксимирующая функции.
Оптимальная величина Вдаз находится следующим порядком. Первоначально следует принять  . Из условия необходимости привязки аппроксимирующей зависимости к заданной базисной точке
. Из условия необходимости привязки аппроксимирующей зависимости к заданной базисной точке  можно определить величину коэффициента а и затем по выражению
можно определить величину коэффициента а и затем по выражению  - величину ошибки. По методу прямого спуска [13] путем изменения величины
- величину ошибки. По методу прямого спуска [13] путем изменения величины  можно определить ее оптимальное значение, соответствующее минимуму ошибки.
можно определить ее оптимальное значение, соответствующее минимуму ошибки.
Далее определяются коэффициенты искомой конкретной функции


Нахождение оптимальных значений коэффициентов аппроксимирующего выражения графическим методом лучше всего пояснить на конкретном примере.
Пример. Определить коэффициенты аппроксимации кривой намагничивания сердечника  электротехнической стали
электротехнической стали  при выражении ее гиперболическим синусом.
при выражении ее гиперболическим синусом.
Данные кривой намагничивания приведены в табл. 3.1.
Выберем соответственно данному рабочему участку кривой намагничивания следующую базисную точку:  .
.
В единичном масштабе кривая намагничивания отражается числами, приведенными в табл. 3.2.
Нанесем зависимость  на кальку и совместим кальку с рис. 3.15. Найдем величину
на кальку и совместим кальку с рис. 3.15. Найдем величину  , определяющую степень нелинейности рабочего участка кривой намагничивания:
, определяющую степень нелинейности рабочего участка кривой намагничивания:  .
.
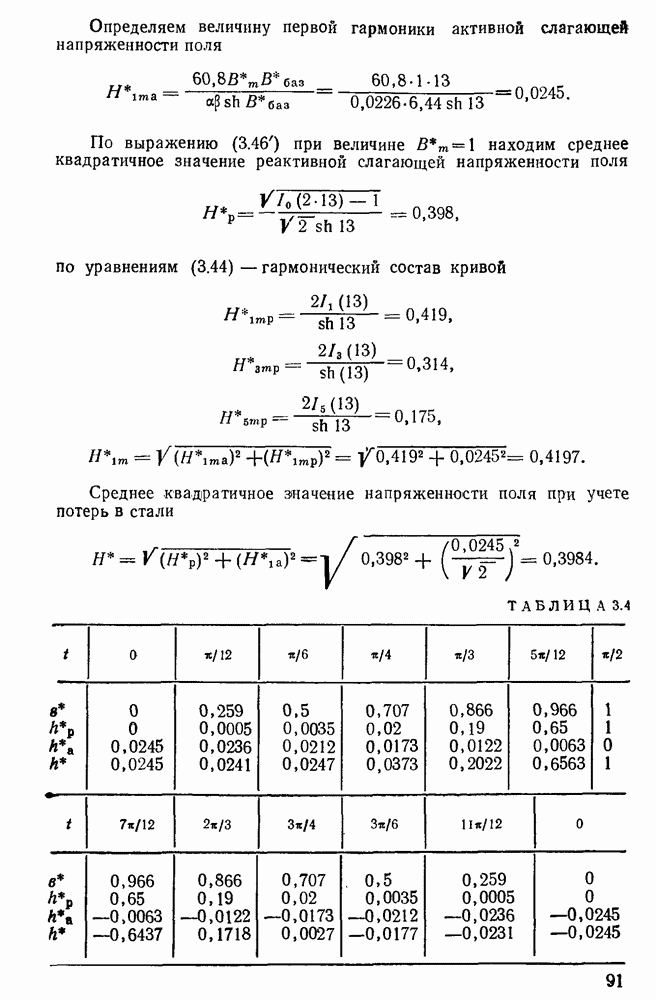
ТАБЛИЦА 3.1

ТАБЛИЦА 3.2

Отсюда коэффициенты аппроксимации

Рабочий участок кривой намагничивания оптимальным образом описывается следующим выражением:

| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- 1. ОСНОВНЫЕ СВЕДЕНИЯ О НЕУПРАВЛЯЕМЫХ ДРОССЕЛЯХ ПЕРЕМЕННОГО ТОКА РАДИОЭЛЕКТРОННОЙ АППАРАТУРЫ
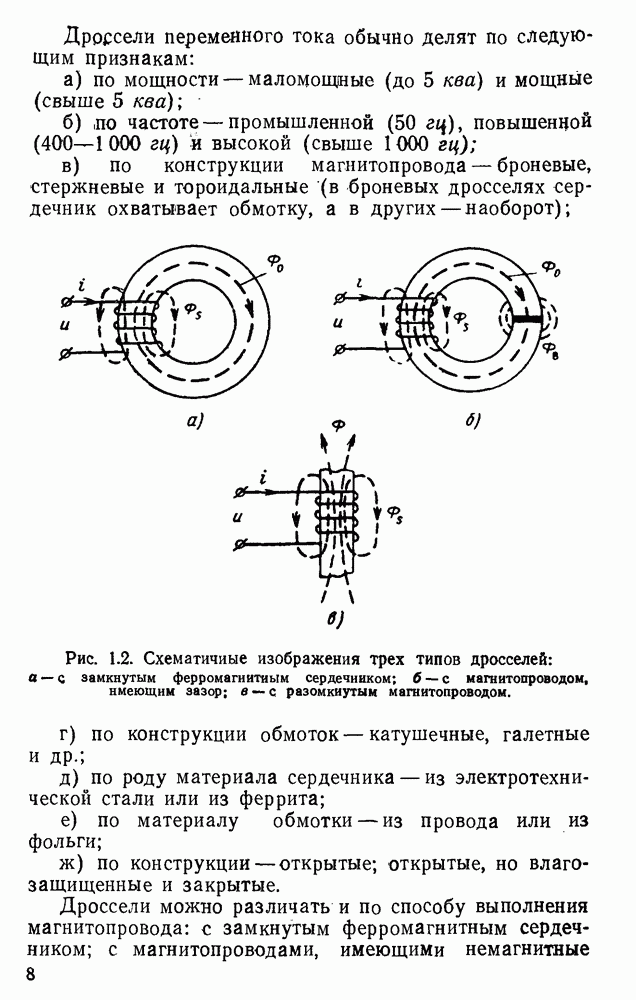
- 1.1. Общие краткие сведения о дросселях. Классификация дросселей
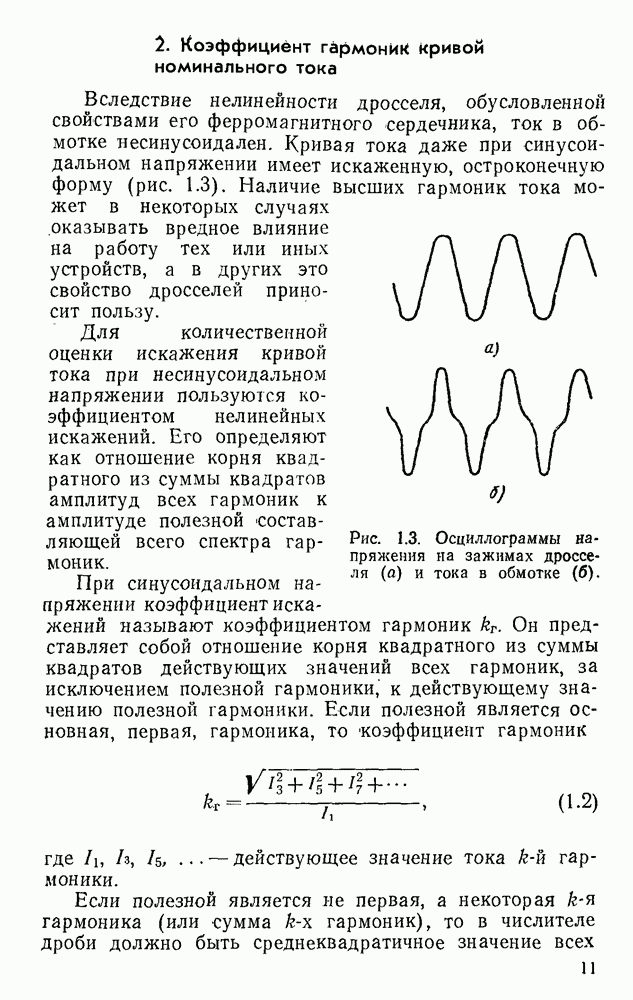
- 1.2. Номинальные параметры нелинейного дросселя
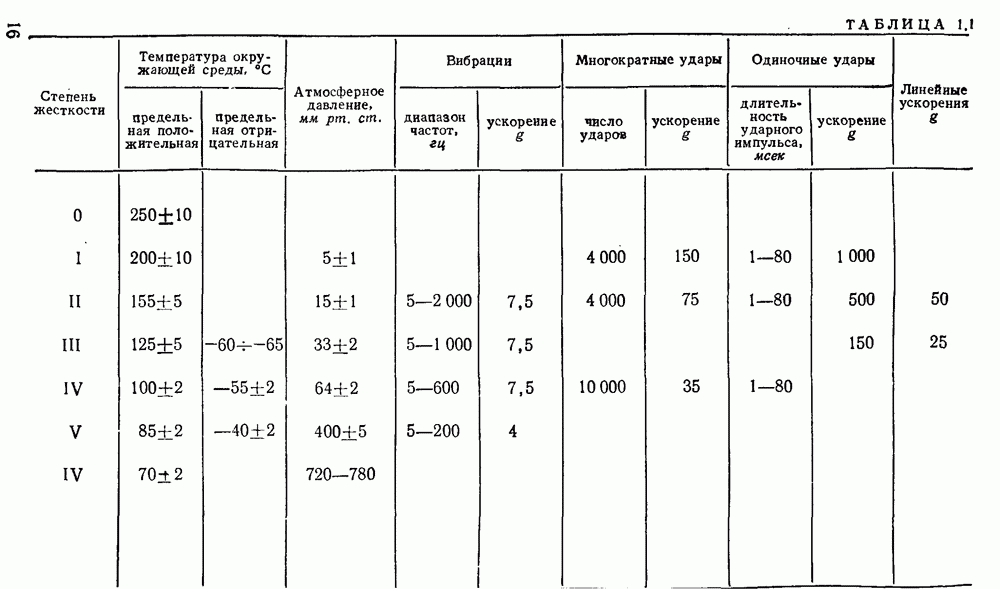
- 1.3. Требования, предъявляемые к дросселям радиоэлектронной аппаратуры. Степени жесткости
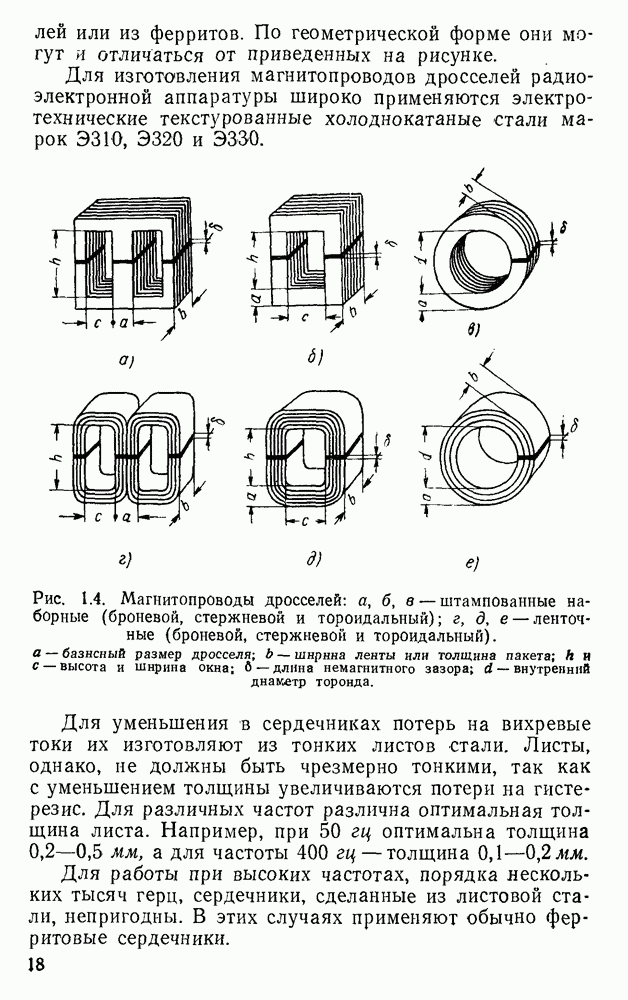
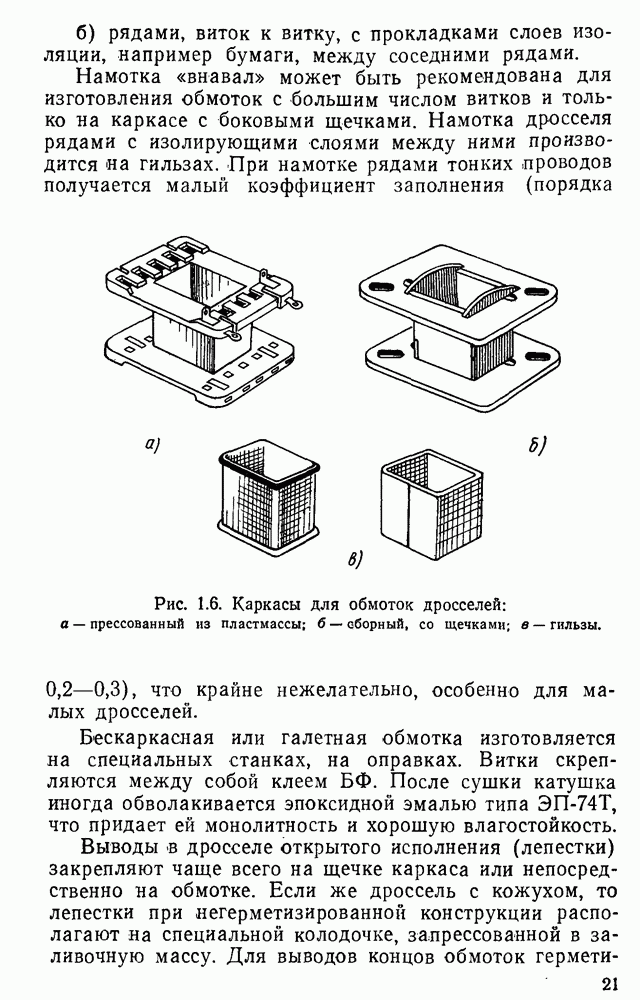
- 1.4. Устройство маломощных дросселей переменного тока
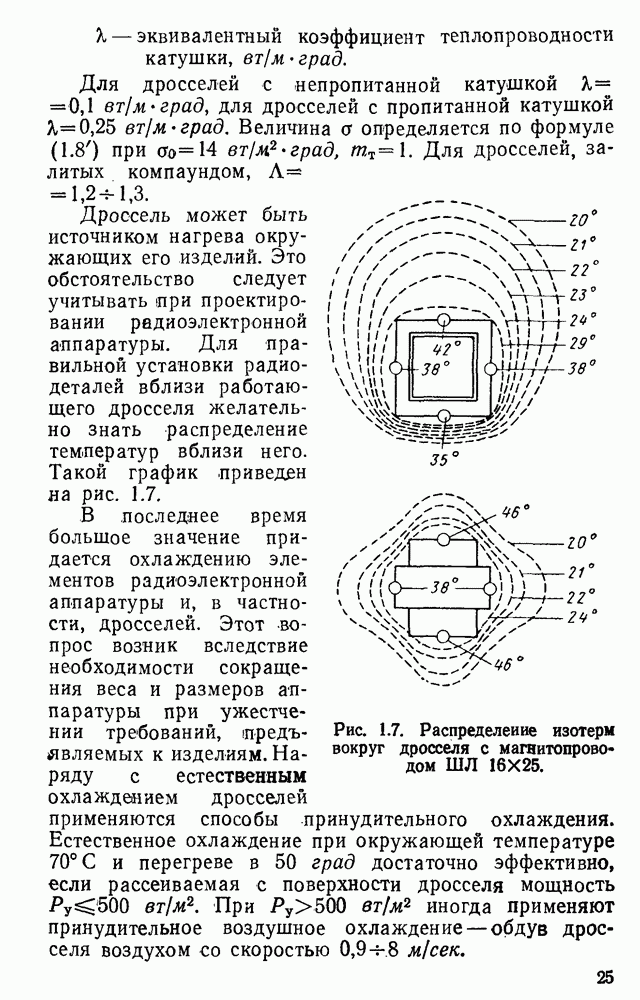
- 1.5. Нагрев и охлаждение дросселей
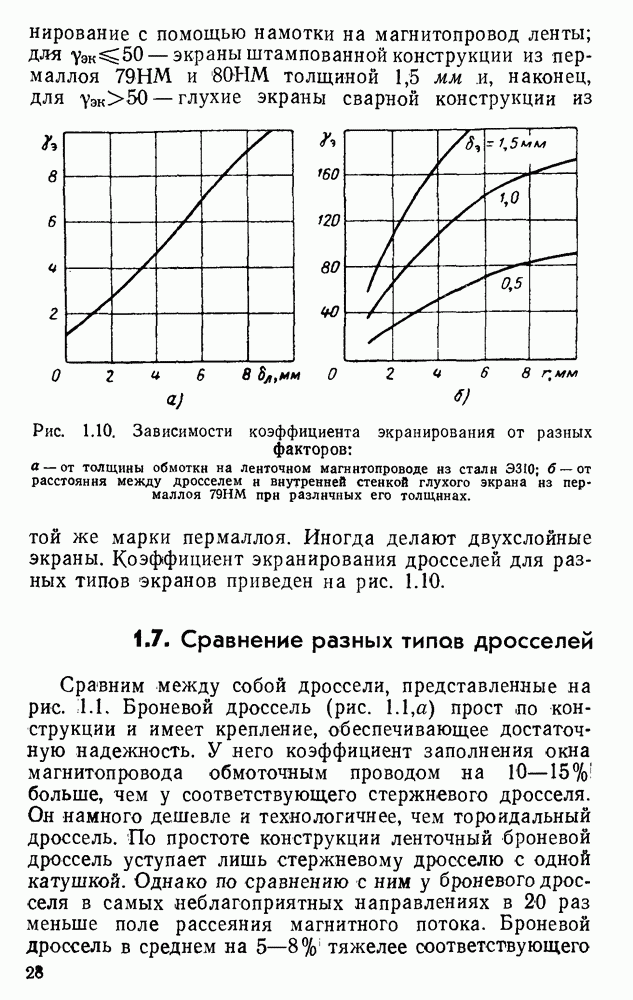
- 1.6. Экранирование дросселей
- 1.7. Сравнение разных типов дросселей
- 2. МАГНИТНЫЕ СВОЙСТВА МАГНИТОПРОВОДОВ ДРОССЕЛЕЙ. ВЫБОР ФЕРРОМАГНЕТИКА
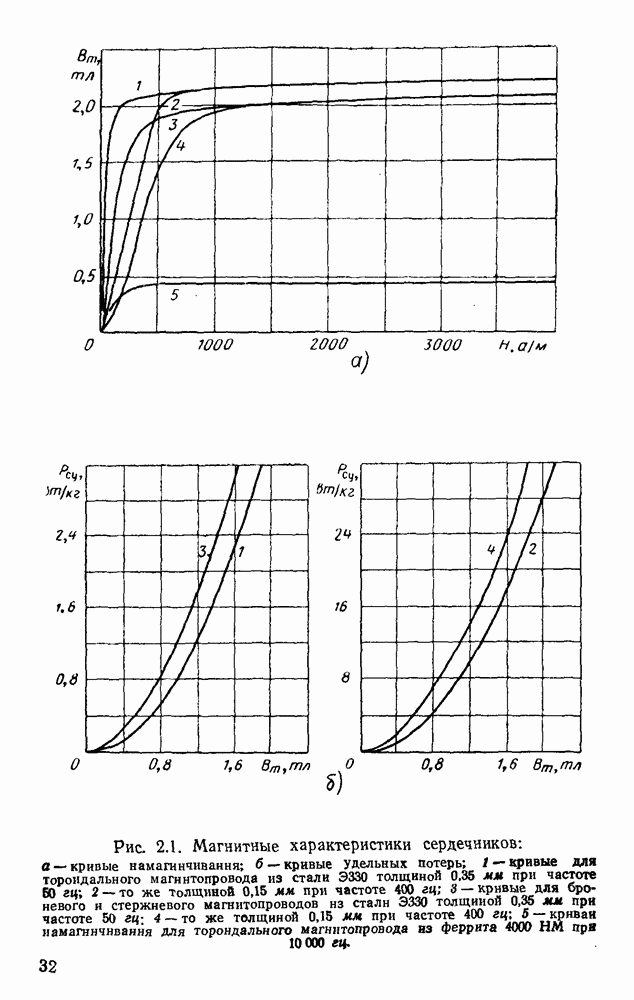
- 2.1. Свойства магнитопроводов дросселей
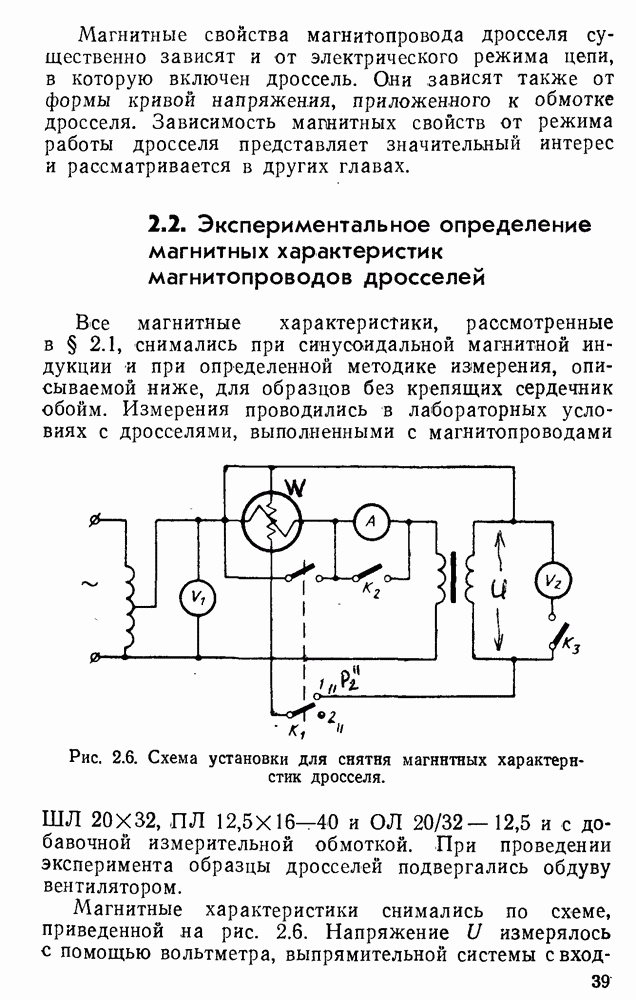
- 2.2. Экспериментальное определение магнитных характеристик магнитопроводов дросселей
- 2.3. Выбор ферромагнетика для сердечника дросселя
- 3. ТЕОРИЯ РАБОТЫ ДРОССЕЛЯ ПЕРЕМЕННОГО ТОКА С НЕЛИНЕЙНЫМ ФЕРРОМАГНИТНЫМ СЕРДЕЧНИКОМ
- 3.2. Связи между электрическими и магнитными величинами в дросселе с нелинейным ферромагнитным сердечником. Эквивалентный дроссель
- 1. Идеальный и идеализированный дроссели без зазора
- 2. Идеальный и идеализированный дроссели с немагнитным зазором
- 3. Реальный дроссель
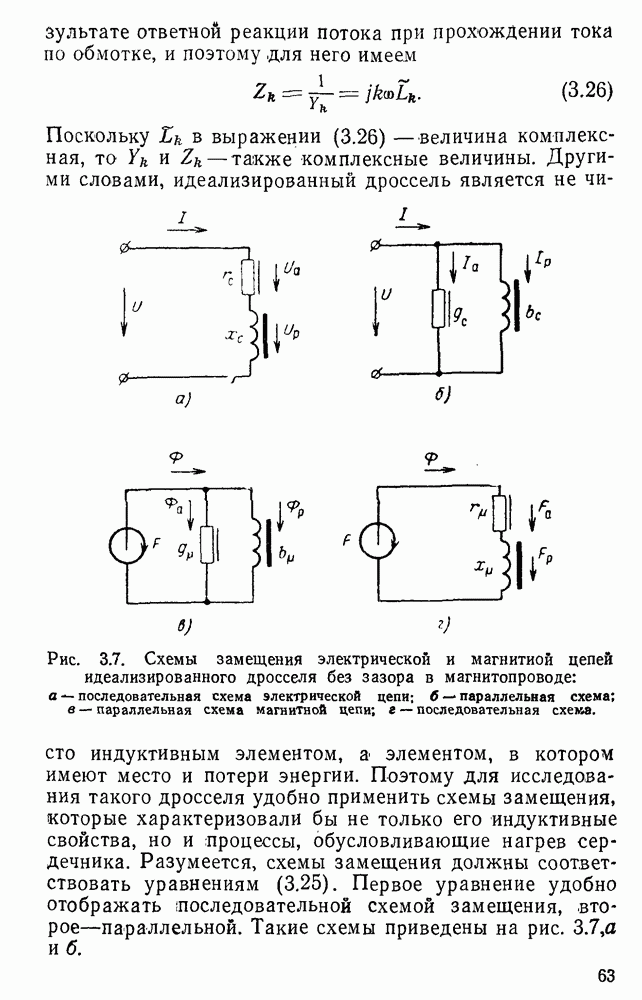
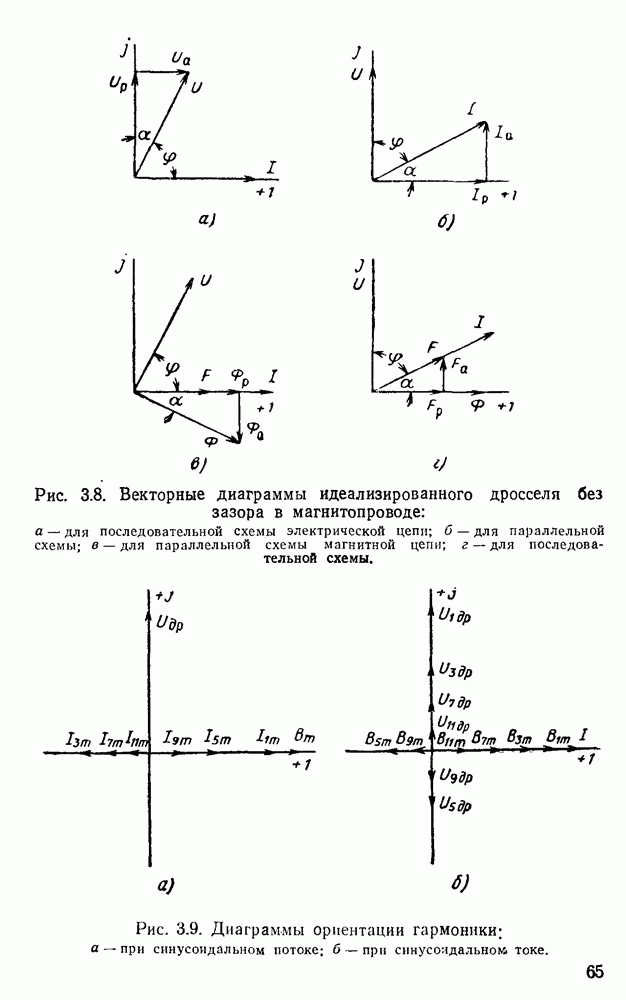
- 3.3. Схемы замещения и векторные диаграммы идеализированного дросселя
- 1. Схемы замещения и векторные диаграммы электрической цепи идеализированного дросселя
- 2. Схемы замещения и векторные диаграммы магнитной цепи идеализированного дросселя
- 3.4. Аппроксимация кривых намагничивания ферромагнитных сердечников. Относительные единицы. Определение коэффициентов аппроксимации
- 3.5. Математическая модель семейства динамических гистерезисных петель. Использование модели для решения задач гармонического анализа
- 1. Определение гармонического состава кривой напряженности поля
- 2. Определение среднеквадратичного значения напряженности поля и потерь в стали
- 3.6. Аналитический расчет магнитных характеристик магнитопроводов идеальных и идеализированных дросселей с зазором
- 3.7. Расчет численными методами магнитных характеристик идеальных и идеализированных дросселей при произвольной форме кривой магнитной индукции
- 3.8. Расчет магнитных характеристик реальных дросселей. Расчет характеристик дросселей, включенных в электрические цепи
- 1. Расчет магнитных характеристик для реального дросселя без рассеяния
- 2. Расчет магнитных характеристик для дросселя, включенного последовательно с активно-индуктивной нагрузкой
- 3.9. Переходные процессы в дросселе
- 3.10. Определение электромагнитного режима и параметров дросселя
- 2. Определение режима и основных характеристик дросселя по комплексной магнитной проницаемости его сердечника
- 4. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПРОЕКТИРОВАНИЯ ДРОССЕЛЕЙ
- 4.1. Общие замечания. Понятие об оптимальных дросселях и их параметрах
- 4.2. Основные уравнения взаимосвязи параметров дросселя и их решение
- 2. Уравнение потерь
- 3. Уравнение теплового режима дросселя
- 4. Уравнения взаимосвязи магнитных параметров дросселя
- 5. Обобщенные уравнения геометрических параметров разных типов и конструкций дросселей
- 6. Технико-экономические показатели дросселей
- 4.3. Определение с помощью ЭЦВМ оптимальных значений соотношений геометрических параметров дросселя. Оптимальные значения соотношений разных типов дросселей
- 4.4. Определение с помощью ЭЦВМ предельных значений параметров дросселей с заданными магнитопроводами
- 4.5. Влияние отдельных факторов на оптимальные значения геометрических соотношений дросселя
- 5. ПРОЕКТИРОВАНИЕ ДРОССЕЛЕЙ
- 5.1. Основные замечания. Техническое задание на проектирование дросселя
- 5.2. Методика проектирования дросселей
- 1. Выбор типа дросселя, марки стали и обмоточного материала
- 2. Выбор типоразмера стандартного сердечника или расчет специального сердечника
- 3. Выбор магнитного режима магнитопровода дросселя
- 4. Расчет длины немагнитного зазора
- 5. Расчет потерь в дросселе
- 6. Определение геометрических параметров дросселя
- 7. Расчет теплового режима дросселя
- 8. Расчет обмоточных данных и междуслойной изоляции
- 9. Расчет катушек дросселя (конструирование обмоток)
- 10. Определение технико-экономических показателей дросселя
- 11. Проверочный расчет дросселя
- 12. Краткая методика расчета дросселя
- 5.3. Примеры проектирования дросселей
- ПРИЛОЖЕНИЯ
- Основные условные обозначения
- Литература