| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6. Технико-экономические показатели дросселей
Основными технико-экономическими показателями дросселя радиоэлектронной аппаратуры (см. § 1.2) являются его удельный вес g, удельный физический и габаритный объем Г и стоимость Ц.
Удельные показатели можно записать в обобщенном виде

где под Э понимается либо вес, либо объем, либо стоимость.
Уравнения (4.4), (4.9) и (4.10) или  с учетом (4.12) и (4.13), а также формул табл. 4.1, позволяют заключить, что основные параметры дросселя определяются его размерами и электромагнитным режимом. Действительно, мощность дросселя при заданном материале и режиме магнитной цепи обусловливается объемом магнитопровода, потери в обмотке при заданной плотности тока [уравнение
с учетом (4.12) и (4.13), а также формул табл. 4.1, позволяют заключить, что основные параметры дросселя определяются его размерами и электромагнитным режимом. Действительно, мощность дросселя при заданном материале и режиме магнитной цепи обусловливается объемом магнитопровода, потери в обмотке при заданной плотности тока [уравнение  ] — суммарным ее объемом, а перегрев зависит от поверхности охлаждения. Резюмируя, можно сказать, что при заданных материалах, тепловом и электромагнитном режимах дроссель должен иметь вполне определенные размеры, а при заданных размерах — вполне определенные параметры.
] — суммарным ее объемом, а перегрев зависит от поверхности охлаждения. Резюмируя, можно сказать, что при заданных материалах, тепловом и электромагнитном режимах дроссель должен иметь вполне определенные размеры, а при заданных размерах — вполне определенные параметры.
Для нахождения размеров дросселя («прямая» задача) нужно прежде всего определить постоянные  рассчитать величину его базисного размера а и величину
рассчитать величину его базисного размера а и величину  характеризующую длину немагнитного зазора б. Напротив, определить электромагнитные параметры дросселя при известных размерах («обратная» задача) — это значит отыскать для него такие величины
характеризующую длину немагнитного зазора б. Напротив, определить электромагнитные параметры дросселя при известных размерах («обратная» задача) — это значит отыскать для него такие величины  которые соответствуют заданным электрическим и тепловым параметрам дросселя. В силу нелинейности уравнений (4.12) и (4.13) обе задачи весьма сложны и практически могут быть решены только методом последовательных приближений.
которые соответствуют заданным электрическим и тепловым параметрам дросселя. В силу нелинейности уравнений (4.12) и (4.13) обе задачи весьма сложны и практически могут быть решены только методом последовательных приближений.
Общий подход к решению обеих задач следующий. Прежде всего необходимо уточнить правомерность технического задания на расчет дросселя, т. е. уточнить необходимое число параметров, которые должны быть получены в результате расчета. Из числа этих параметров нужно задаться теми, которые могут принимать оптимальные значения, например  и v. Оптимальная величина параметра
и v. Оптимальная величина параметра  при расчете дросселя на максимальную добротность должна быть равна единице. Доказательство этого положения дано в конце этого параграфа. При расчете дросселя на заданный перегрев соответствующее значение параметра
при расчете дросселя на максимальную добротность должна быть равна единице. Доказательство этого положения дано в конце этого параграфа. При расчете дросселя на заданный перегрев соответствующее значение параметра  можно найти по формулам, предложенным P. X. Бальяном:
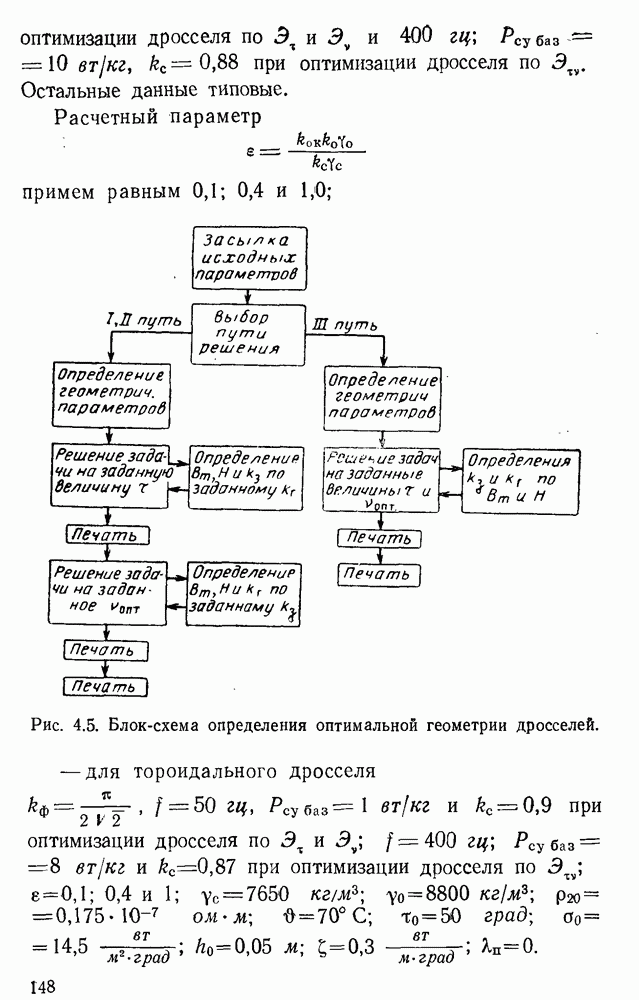
можно найти по формулам, предложенным P. X. Бальяном:

для броневого и стержневого дросселей;

для типовых условий, когда 

для тороидального дросселя.
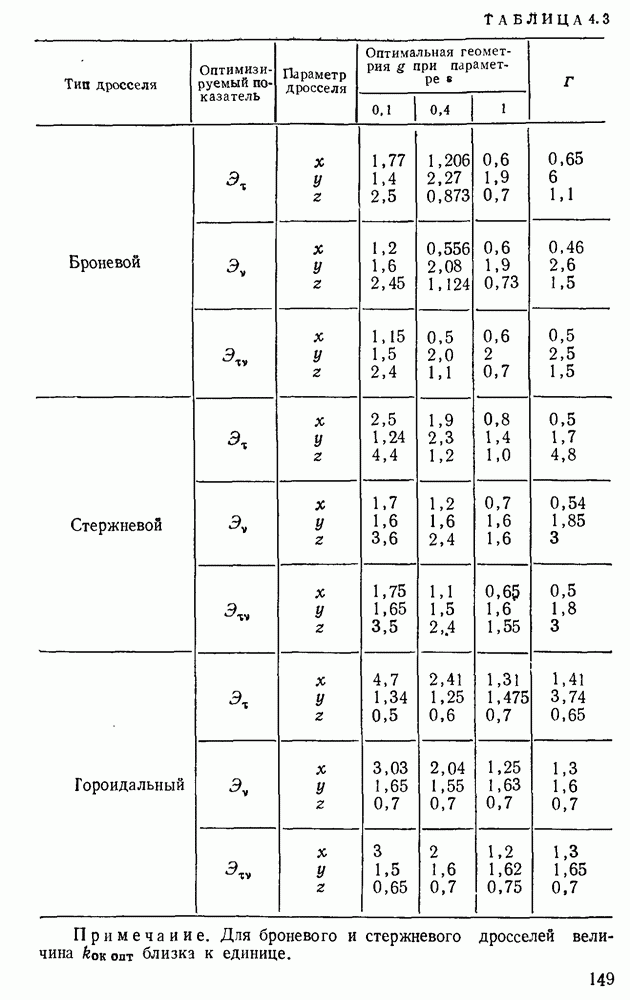
Способ отыскания оптимальных значений параметров  описан в § 4.4.
описан в § 4.4.
Определив параметры дросселя, следует составить необходимое число уравнений. В число таких уравнений обязательно следует включить уравнения (4.12) и (4.13), определяющие взаимосвязь магнитных величин. Далее следует проверить соответствие заданных параметров полученной системе уравнений и задаться величинами необходимых постоянных. Число заданных параметров и установленных значений постоянных непременно должно соответствовать числу уравнений конкретной системы. При соблюдении соответствия можно приступить к решению полученной системы уравнений.
Не имея возможности исследовать решения, соответствующие всем встречающимся в практике вариантам расчетных заданий дросселя, обратимся к решениям лишь тех уравнений, которые соответствуют основным трем вариантам расчетных заданий. Опишем решение уравнений для «прямой» задачи (А) и «обратной» (Б).
A. Расчет дросселя по заданным параметрам («прямая» задача).
Для решения системы уравнений должно быть задано минимально необходимое число основных номинальных параметров дросселя и величины  По ним определяют электромагнитный режим дросселя
По ним определяют электромагнитный режим дросселя  или
или  показатель
показатель  и все линейные и другие
и все линейные и другие  параметры дросселя. Значения
параметры дросселя. Значения  (или
(или  ) должны дать соответствие между найденными геометрическими размерами дросселя и его заданными основными номинальными параметрами.
) должны дать соответствие между найденными геометрическими размерами дросселя и его заданными основными номинальными параметрами.
1) Расчет дросселя по заданным величинам мощности, допустимому коэффициенту гармоник в кривой тока и максимально допустимому перегреву. Величины  и
и  или
или  заданы. Примем какие-либо значения
заданы. Примем какие-либо значения  для параметров дросселя и составим следующую систему уравнений, например для броневого дросселя при
для параметров дросселя и составим следующую систему уравнений, например для броневого дросселя при 

где  и
и  определяются соответственно уравнениями
определяются соответственно уравнениями  .
.
Геометрические величины в уравнениях (4.16) могут быть найдены по формулам табл. 4.1.
(см. скан)
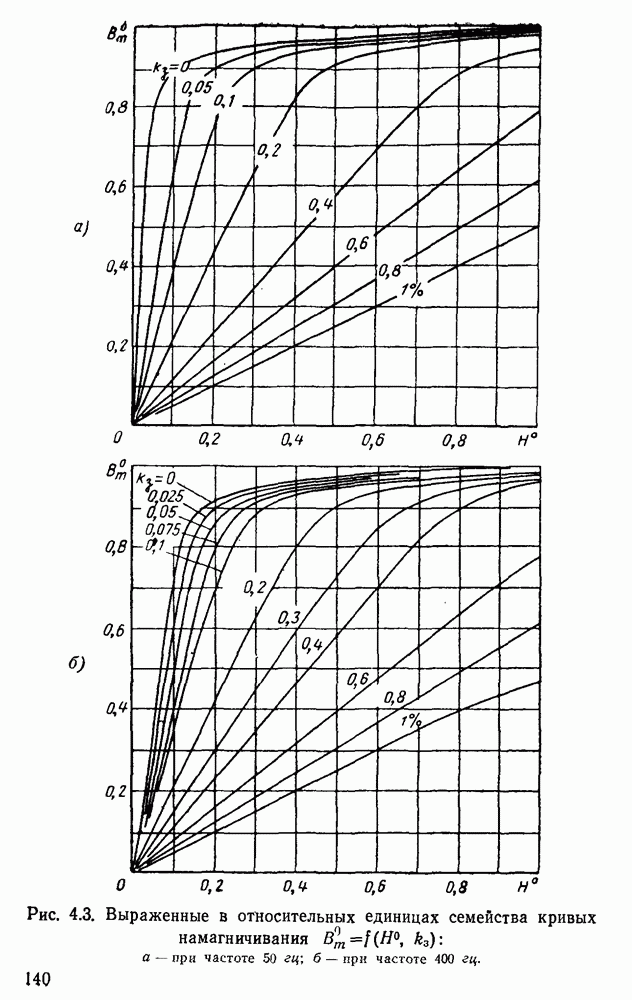
Рис. 4.3. Выраженные в относительных единицах семейства кривых намагничивания  : а — при частоте 50 гц; б — при частоте 400 гц.
: а — при частоте 50 гц; б — при частоте 400 гц.
Зададимся следующими базисными постоянными дросселя:

при  .
.

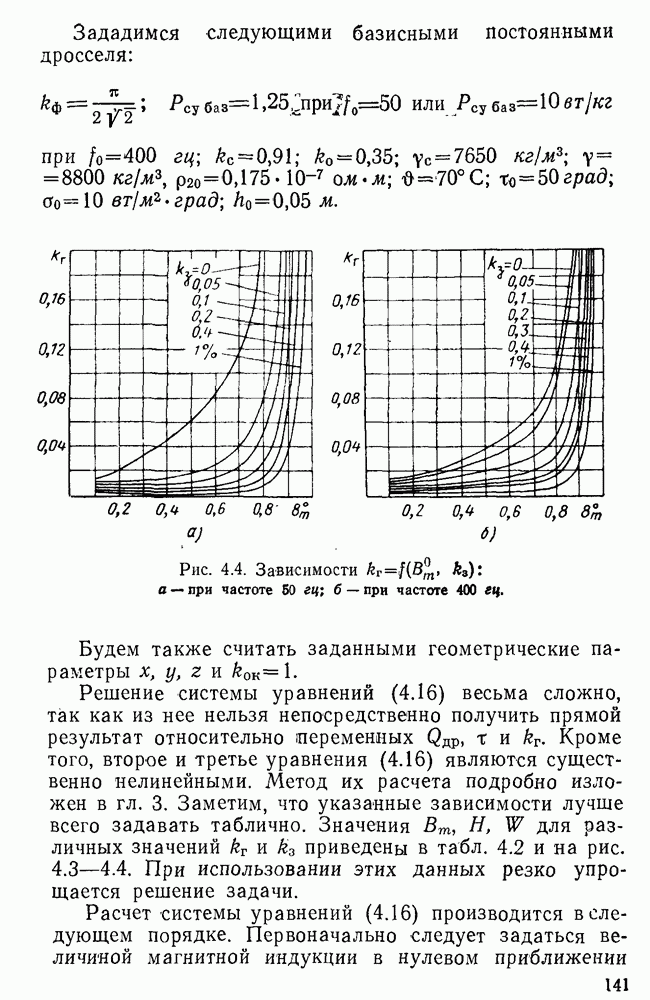
Рис. 4.4. Зависимости  : а — при частоте 50 гц; б — при частоте
: а — при частоте 50 гц; б — при частоте  .
.
Будем также считать заданными геометрические параметры  .
.
Решение системы уравнений (4.16) весьма сложно, так как из нее нельзя непосредственно получить прямой результат относительно переменных  . Кроме того, второе и третье уравнения (4.16) являются существенно нелинейными. Метод их расчета подробно изложен в гл. 3. Заметим, что указанные зависимости лучше всего задавать таблично. Значения
. Кроме того, второе и третье уравнения (4.16) являются существенно нелинейными. Метод их расчета подробно изложен в гл. 3. Заметим, что указанные зависимости лучше всего задавать таблично. Значения  для различных значений
для различных значений  приведены в табл. 4.2 и на рис.
приведены в табл. 4.2 и на рис.  . При использовании этих данных резко упрощается решение задачи.
. При использовании этих данных резко упрощается решение задачи.
Расчет системы уравнений (4.16) производится в следующем порядке. Первоначально следует задаться величиной магнитной индукции в нулевом приближении  (нами рекомендуется величина
(нами рекомендуется величина  ) и определить
) и определить 
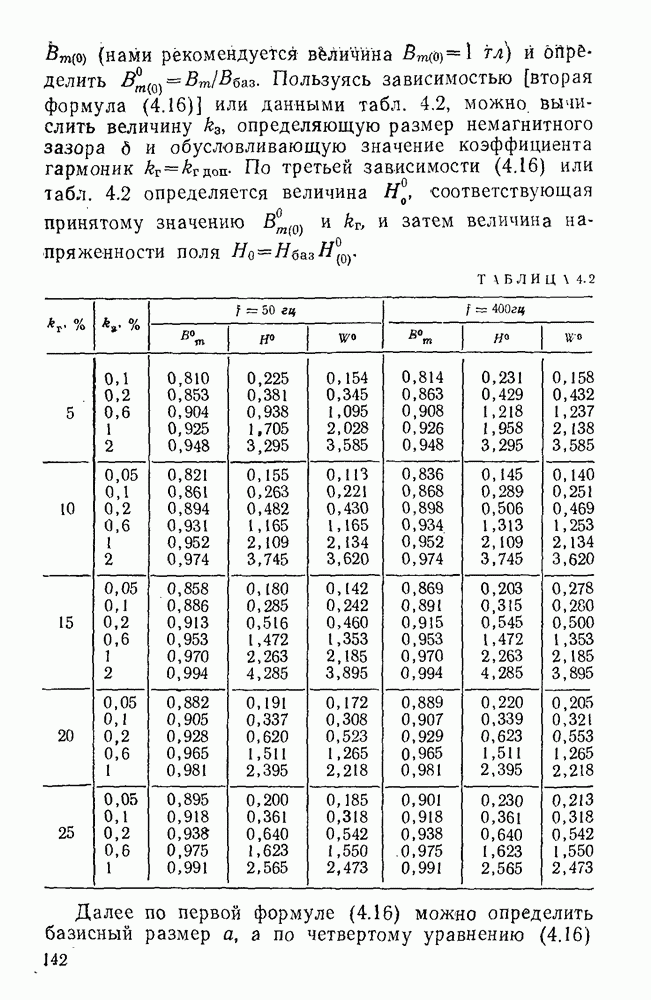
Пользуясь зависимостью [вторая формула (4.16)] или данными табл. 4.2, можно вычислить величину  определяющую размер немагнитного зазора
определяющую размер немагнитного зазора  и обусловливающую значение коэффициента гармоник
и обусловливающую значение коэффициента гармоник  По третьей зависимости (4.16) или табл. 4.2 определяется величина
По третьей зависимости (4.16) или табл. 4.2 определяется величина  соответствующая принятому значению
соответствующая принятому значению  и затем величина напряженности поля
и затем величина напряженности поля  .
.
ТАБЛИЦА 4.2

Далее по первой формуле (4.16) можно определить базисный размер а, а по четвертому уравнению (4.16) или (4.11) - среднеобъемный или соответственно максимальный перегрев обмотки дросселя.
Если (при этом величина  или
или  отличается от заданного значения, расчет повторяется при новом значении
отличается от заданного значения, расчет повторяется при новом значении  но уже в первом приближении. Величина В для каждого из приближений находится по следующей итерационной формуле:
но уже в первом приближении. Величина В для каждого из приближений находится по следующей итерационной формуле:

где  определяется уравнениями (4.16).
определяется уравнениями (4.16).
Расчеты повторяются до сходимости приближений с наперед заданной точностью, т. е. до тех пор, пока величины магнитной индукции и напряженности поля не получат значений, соответствующих заданным значениям допустимого перегрева дросселя. Определив базисный размер дросселей по величинам  можно, пользуясь уравнениями табл. 4.1 и выражениями (4.16), определить все необходимые геометрические и электромагнитные параметры дросселя.
можно, пользуясь уравнениями табл. 4.1 и выражениями (4.16), определить все необходимые геометрические и электромагнитные параметры дросселя.
В заключение расчета проверяется параметр v. Если параметр  то расчет дросселя заканчивается. Если же
то расчет дросселя заканчивается. Если же  то дроссель следует рассчитать при
то дроссель следует рассчитать при  т. е. снять одно из заданных условий, например величину коэффициента гармоник в кривой тока, и произвести расчет дросселя при заданных величинах
т. е. снять одно из заданных условий, например величину коэффициента гармоник в кривой тока, и произвести расчет дросселя при заданных величинах  .
.
2) Расчет дросселя по заданным величинам мощности, коэффициенту гармоник и условию получения максимальной добротности. В этом случае заданы величины  Параметр
Параметр  принимается равным единице и решению подлежит та же система уравнений (4.16).
принимается равным единице и решению подлежит та же система уравнений (4.16).
Решение системы уравнений может быть сделано в том же порядке, что и в пп. 1). Величина магнитной индукции в каждом из приближений в этом случае определяется формулой, аналогичной (4.17), но при заданных величинах  и v. Расчеты повторяются до сходимости приближений по величине
и v. Расчеты повторяются до сходимости приближений по величине  .
.
3) Расчет дросселя по заданным величинам мощности, максимально допустимому перегреву и условиям получения Voht В этом случае заданы  Данный вариант задания наиболее часто встречается при расчете дросселей с относительно высоким уровнем потерь в стали.
Данный вариант задания наиболее часто встречается при расчете дросселей с относительно высоким уровнем потерь в стали.
Напомним, что для получения максимальной добротности v должно быть равно единице, а для получения дросселя с минимальным весом величину  следует определять по формуле (4.15).
следует определять по формуле (4.15).
Уравнения решаются в следующем порядке. Предварительно задавшись величиной  по шестой формуле (4.16) с учетом третьей и первой формул (4.16) и заданного равенства
по шестой формуле (4.16) с учетом третьей и первой формул (4.16) и заданного равенства  определяют базисный размер магнитопровода а; по пятой и седьмой формулам
определяют базисный размер магнитопровода а; по пятой и седьмой формулам  -величину напряженности поля
-величину напряженности поля  ; по четвертой формуле
; по четвертой формуле  -перегрев дросселя Если при этом полученное
-перегрев дросселя Если при этом полученное  отличается от заданного значения, расчет следует повторить при новом значении
отличается от заданного значения, расчет следует повторить при новом значении  и т. д. до сходимости итераций. Далее по третьему уравнению (4.16) или табл. 4.2 определяется величина немагнитного зазора
и т. д. до сходимости итераций. Далее по третьему уравнению (4.16) или табл. 4.2 определяется величина немагнитного зазора  и при помощи второго уравнения (4.16) проверяется неравенство
и при помощи второго уравнения (4.16) проверяется неравенство  При выполнении неравенства по величинам а,
При выполнении неравенства по величинам а,  определяются все необходимые размеры и геометрические параметры дросселя, а по «частным уравнениям (4.16) — все электромагнитные параметры.
определяются все необходимые размеры и геометрические параметры дросселя, а по «частным уравнениям (4.16) — все электромагнитные параметры.
При несоблюдении неравенства  решение следует провести при заданных величинах
решение следует провести при заданных величинах 
Б. Расчет дросселя по заданным размерам его магнитопровода («обратная» задача).
При решении уравнений, соответствующих «обратной» задаче, должны быть заданы все геометрические размеры сердечника и минимальное необходимое число номинальных параметров дросселя. Исследования показывают, что решению подлежит та же система уравнений (4.16) с тем же числом заданных постоянных. Расчетные номинальные параметры те же, что и при решении уравнений прямой задачи, но вместо мощности нужно задаться базисным размером магнитопровода. В результате решения системы уравнений определяется электромагнитный режим дросселя, обусловливающий предельную электромагнитную нагрузку магнитопровода и обмотки и, следовательно, предельную величину мощности дросселя 
Рассмотрим решение основных уравнений, соответствующих трем вариантам заданий.
1) Расчет дросселя по заданным размерам его магнитопровода, допустимому коэффициенту гармоник в кривой тока и максимально допустимому перегреву.
Итак, величины  и
и  заданы. Требуется определить предельную мощность дросселя. Первоначально определяются все геометрические параметры заданного дросселя —
заданы. Требуется определить предельную мощность дросселя. Первоначально определяются все геометрические параметры заданного дросселя —  и др. Затем следует задаться величиной магнитной индукции в нулевом приближении
и др. Затем следует задаться величиной магнитной индукции в нулевом приближении  и по второй формуле (4.16) определить величину
и по второй формуле (4.16) определить величину  обеспечивающую необходимый коэффициент гармоник, а по третьей формуле (4.16) — напряженность поля
обеспечивающую необходимый коэффициент гармоник, а по третьей формуле (4.16) — напряженность поля  . Далее по шестой и седьмой формулам (4.16) определяются потери в сердечнике и обмотке, а по четвертому выражению (4.16) — перегрев дросселя. Расчет производится методом последовательных приближений до сходимости по величине
. Далее по шестой и седьмой формулам (4.16) определяются потери в сердечнике и обмотке, а по четвертому выражению (4.16) — перегрев дросселя. Расчет производится методом последовательных приближений до сходимости по величине  . При выполнении равенства
. При выполнении равенства  пользуясь уравнениями (4.16), можно найти все искомые параметры дросселя:
пользуясь уравнениями (4.16), можно найти все искомые параметры дросселя:  и др.
и др.
В заключение расчета следует проверить величину v, которая должна быть равной или меньшей 
2) Расчет дросселя по заданным размерам его магнитопровода, допустимому коэффициенту гармонике кривой тока и условию получения максимальной добротности. В этом случае заданы размеры магнитопровода  и
и  , а также параметры
, а также параметры  . Решение производится аналогично тому, как и в пп. 1). Величина магнитной индукции при каждом из приближений определяется по формуле (4.17). Расчеты повторяются до тех пор, пока величина v не будет равна
. Решение производится аналогично тому, как и в пп. 1). Величина магнитной индукции при каждом из приближений определяется по формуле (4.17). Расчеты повторяются до тех пор, пока величина v не будет равна 
3) Расчет дросселя по заданным размерам его магнитопровода, максимально допустимому перегреву и условию получения  . В этом случае заданы размеры магнитопровода
. В этом случае заданы размеры магнитопровода  , а также
, а также  и
и  . Весь расчет выполняется без итерации, т. е. решение системы уравнений (4.16) можно получить весьма просто. Для этого по шестому уравнению (4.16) с учетом четвертой формулы (4.16) и равенства потерь в сердечнике и обмотке определяется величина
. Весь расчет выполняется без итерации, т. е. решение системы уравнений (4.16) можно получить весьма просто. Для этого по шестому уравнению (4.16) с учетом четвертой формулы (4.16) и равенства потерь в сердечнике и обмотке определяется величина  а по четвертому уравнению (4.16) — напряженность поля Н. Затем при помощи зависимости
а по четвертому уравнению (4.16) — напряженность поля Н. Затем при помощи зависимости  определяется величина немагнитного зазора
определяется величина немагнитного зазора  дающая соответствующую Н при заданной величине
дающая соответствующую Н при заданной величине 
Далее по первой формуле (4.16) определяется предельная мощность дросселя и при необходимости все другие его параметры и проверяется неравенство  . При невыполнении последнего неравенства расчет дросселя следует провести при заданных величинах
. При невыполнении последнего неравенства расчет дросселя следует провести при заданных величинах  и
и  .
.
Системы уравнений (4.16) для «прямой» и «обратной» задач отдельно для каждого из трех вариантов расчетных заданий проще всего решать с помощью ЭЦВМ.
В заключение обратимся к параметру v — к отношению потерь в магнитопроводе к потерям в обмотке.
При оптимальном значении этого отношения дроссель имеет минимальный вес или же минимальные суммарные потери и, следовательно, максимальную добротность Д. В первом случае величину  можно получить по формулам (4.15); во втором
можно получить по формулам (4.15); во втором  . Докажем это аналитически.
. Докажем это аналитически.
Из уравнений (4.4), (4.8) и восьмой формулы (4.16) можно получить соотношение между мощностью и добротностью

или, исключая величину магнитной индукции,

Как видим, добротность дросселя обусловливается многими величинами и, в частности, геометрией дросселя и величиной v. При фиксированных геометрических соразмерностях дросселя (это условие обеспечивается на каждом шаге при исследовании Э и  ) и при заданных величинах геометрических размеров:
) и при заданных величинах геометрических размеров:

Взяв производную от этого выражения и приравняв ее нулю, получим уравнение

из которого действительно нетрудно подтвердить условие, обеспечивающее максимум добротности в дросселе:

Подчеркнем,  полученное условие можйо реализовать в дросселе только в том случае, когда относительно велики потери в сердечнике. При малых потерях в стали, т. е. когда
полученное условие можйо реализовать в дросселе только в том случае, когда относительно велики потери в сердечнике. При малых потерях в стали, т. е. когда  дроссель имеет минимум технико-экономического показателя при
дроссель имеет минимум технико-экономического показателя при  .
.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- 1. ОСНОВНЫЕ СВЕДЕНИЯ О НЕУПРАВЛЯЕМЫХ ДРОССЕЛЯХ ПЕРЕМЕННОГО ТОКА РАДИОЭЛЕКТРОННОЙ АППАРАТУРЫ
- 1.1. Общие краткие сведения о дросселях. Классификация дросселей
- 1.2. Номинальные параметры нелинейного дросселя
- 1.3. Требования, предъявляемые к дросселям радиоэлектронной аппаратуры. Степени жесткости
- 1.4. Устройство маломощных дросселей переменного тока
- 1.5. Нагрев и охлаждение дросселей
- 1.6. Экранирование дросселей
- 1.7. Сравнение разных типов дросселей
- 2. МАГНИТНЫЕ СВОЙСТВА МАГНИТОПРОВОДОВ ДРОССЕЛЕЙ. ВЫБОР ФЕРРОМАГНЕТИКА
- 2.1. Свойства магнитопроводов дросселей
- 2.2. Экспериментальное определение магнитных характеристик магнитопроводов дросселей
- 2.3. Выбор ферромагнетика для сердечника дросселя
- 3. ТЕОРИЯ РАБОТЫ ДРОССЕЛЯ ПЕРЕМЕННОГО ТОКА С НЕЛИНЕЙНЫМ ФЕРРОМАГНИТНЫМ СЕРДЕЧНИКОМ
- 3.2. Связи между электрическими и магнитными величинами в дросселе с нелинейным ферромагнитным сердечником. Эквивалентный дроссель
- 1. Идеальный и идеализированный дроссели без зазора
- 2. Идеальный и идеализированный дроссели с немагнитным зазором
- 3. Реальный дроссель
- 3.3. Схемы замещения и векторные диаграммы идеализированного дросселя
- 1. Схемы замещения и векторные диаграммы электрической цепи идеализированного дросселя
- 2. Схемы замещения и векторные диаграммы магнитной цепи идеализированного дросселя
- 3.4. Аппроксимация кривых намагничивания ферромагнитных сердечников. Относительные единицы. Определение коэффициентов аппроксимации
- 3.5. Математическая модель семейства динамических гистерезисных петель. Использование модели для решения задач гармонического анализа
- 1. Определение гармонического состава кривой напряженности поля
- 2. Определение среднеквадратичного значения напряженности поля и потерь в стали
- 3.6. Аналитический расчет магнитных характеристик магнитопроводов идеальных и идеализированных дросселей с зазором
- 3.7. Расчет численными методами магнитных характеристик идеальных и идеализированных дросселей при произвольной форме кривой магнитной индукции
- 3.8. Расчет магнитных характеристик реальных дросселей. Расчет характеристик дросселей, включенных в электрические цепи
- 1. Расчет магнитных характеристик для реального дросселя без рассеяния
- 2. Расчет магнитных характеристик для дросселя, включенного последовательно с активно-индуктивной нагрузкой
- 3.9. Переходные процессы в дросселе
- 3.10. Определение электромагнитного режима и параметров дросселя
- 2. Определение режима и основных характеристик дросселя по комплексной магнитной проницаемости его сердечника
- 4. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПРОЕКТИРОВАНИЯ ДРОССЕЛЕЙ
- 4.1. Общие замечания. Понятие об оптимальных дросселях и их параметрах
- 4.2. Основные уравнения взаимосвязи параметров дросселя и их решение
- 2. Уравнение потерь
- 3. Уравнение теплового режима дросселя
- 4. Уравнения взаимосвязи магнитных параметров дросселя
- 5. Обобщенные уравнения геометрических параметров разных типов и конструкций дросселей
- 6. Технико-экономические показатели дросселей
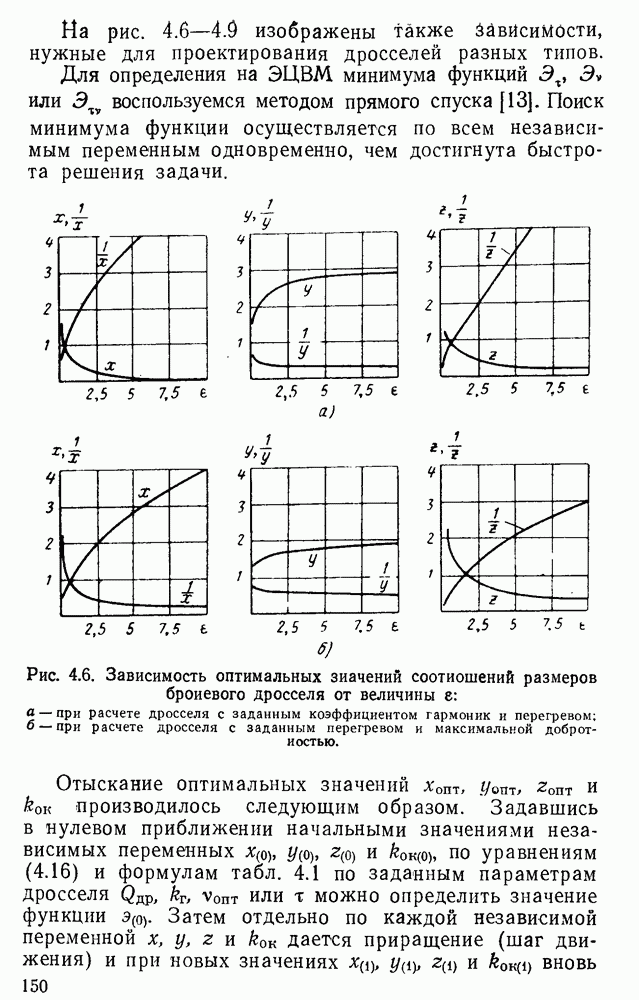
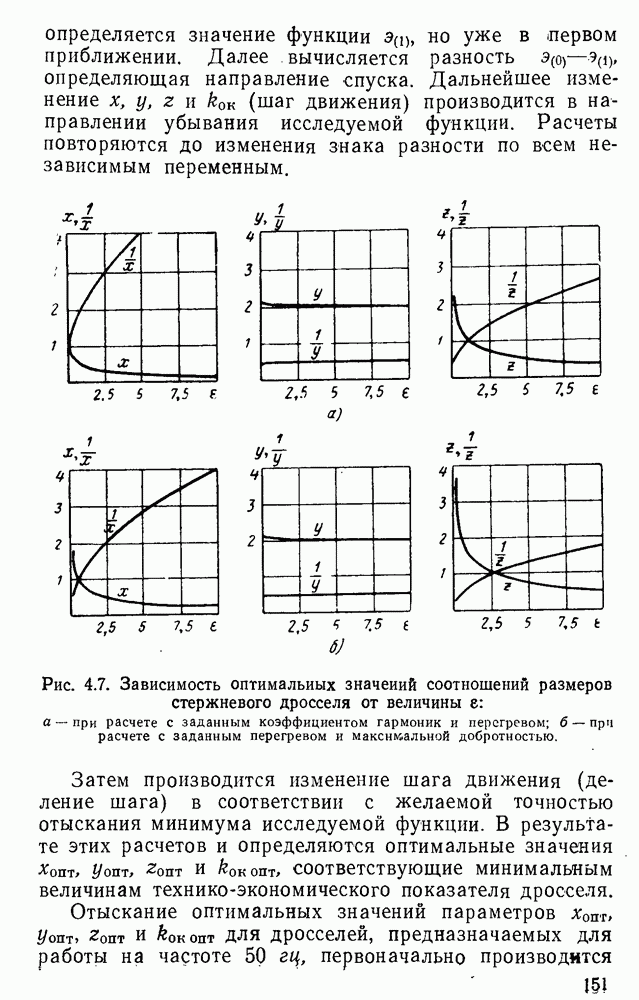
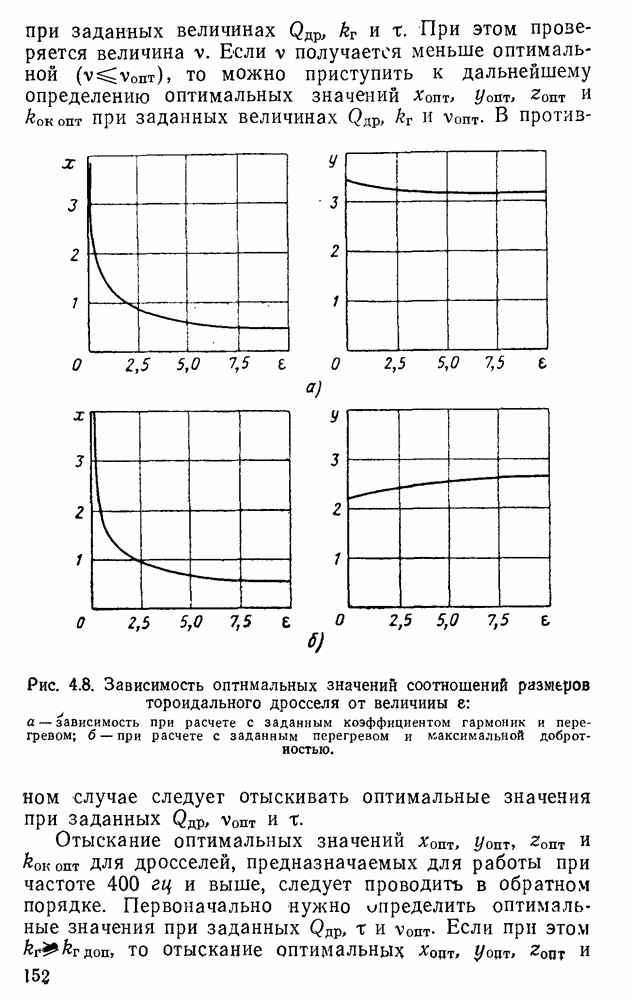
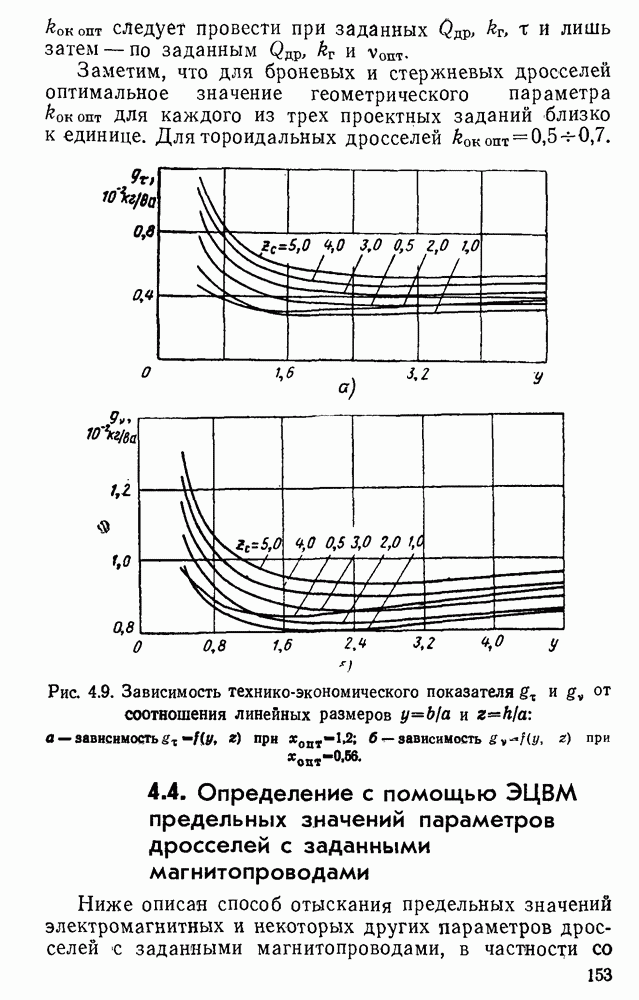
- 4.3. Определение с помощью ЭЦВМ оптимальных значений соотношений геометрических параметров дросселя. Оптимальные значения соотношений разных типов дросселей
- 4.4. Определение с помощью ЭЦВМ предельных значений параметров дросселей с заданными магнитопроводами
- 4.5. Влияние отдельных факторов на оптимальные значения геометрических соотношений дросселя
- 5. ПРОЕКТИРОВАНИЕ ДРОССЕЛЕЙ
- 5.1. Основные замечания. Техническое задание на проектирование дросселя
- 5.2. Методика проектирования дросселей
- 1. Выбор типа дросселя, марки стали и обмоточного материала
- 2. Выбор типоразмера стандартного сердечника или расчет специального сердечника
- 3. Выбор магнитного режима магнитопровода дросселя
- 4. Расчет длины немагнитного зазора
- 5. Расчет потерь в дросселе
- 6. Определение геометрических параметров дросселя
- 7. Расчет теплового режима дросселя
- 8. Расчет обмоточных данных и междуслойной изоляции
- 9. Расчет катушек дросселя (конструирование обмоток)
- 10. Определение технико-экономических показателей дросселя
- 11. Проверочный расчет дросселя
- 12. Краткая методика расчета дросселя
- 5.3. Примеры проектирования дросселей
- ПРИЛОЖЕНИЯ
- Основные условные обозначения
- Литература