| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Определение среднеквадратичного значения напряженности поля и потерь в стали
Разработанная модель дает возможность получить формулы для расчета среднеквадратичного значения напряженности поля Я и удельных потерь в стали 
Для этого нужно воспользоваться известными соотношениями

где  — удельный вес стали.
— удельный вес стали.
Подставляя в (3.45) соответствующие выражения для  а также учитывая (3.44) и (3.44) и известные тригонометрические соотношения
а также учитывая (3.44) и (3.44) и известные тригонометрические соотношения

после интегрирования имеем

Подчеркнем, что полученные формулы являются более обобщенными, чем известные, например из [16]. Так, из (3.46), полагая  можно получить формулу для среднеквадратичного значения
можно получить формулу для среднеквадратичного значения

широко используемую при расчетах цепей со сталью без учета гистерезиса.
С другой стороны, из (3.47) вытекает, как частный случай, известная формула Штейнметца. Действительно, заменяя  рядом Тейлора
рядом Тейлора

и ограничиваясь учетом первого члена ряда, получаем выражение

Введя обозначение

получим формулу для потерь в стали, предложенную Штейнметцом,

где  — удельные потери в сердечнике,
— удельные потери в сердечнике,  .
.
Для дросселей с сердечниками, выполненными из стали  обычно
обычно

и

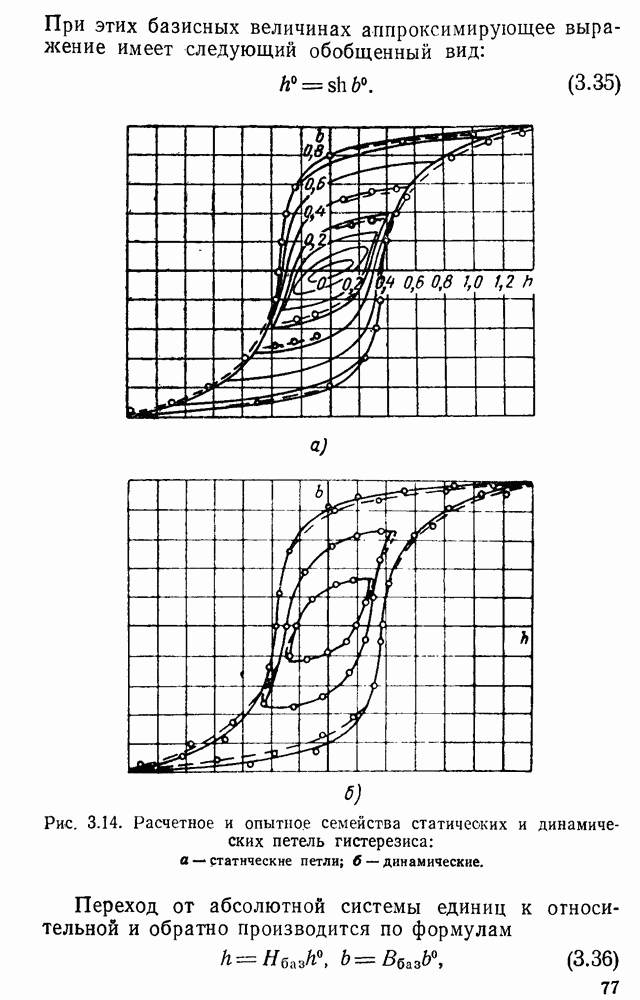
В заключение укажем, что формулы (3.46) и (3.47) дают результаты, хорошо согласующиеся с опытными данными.
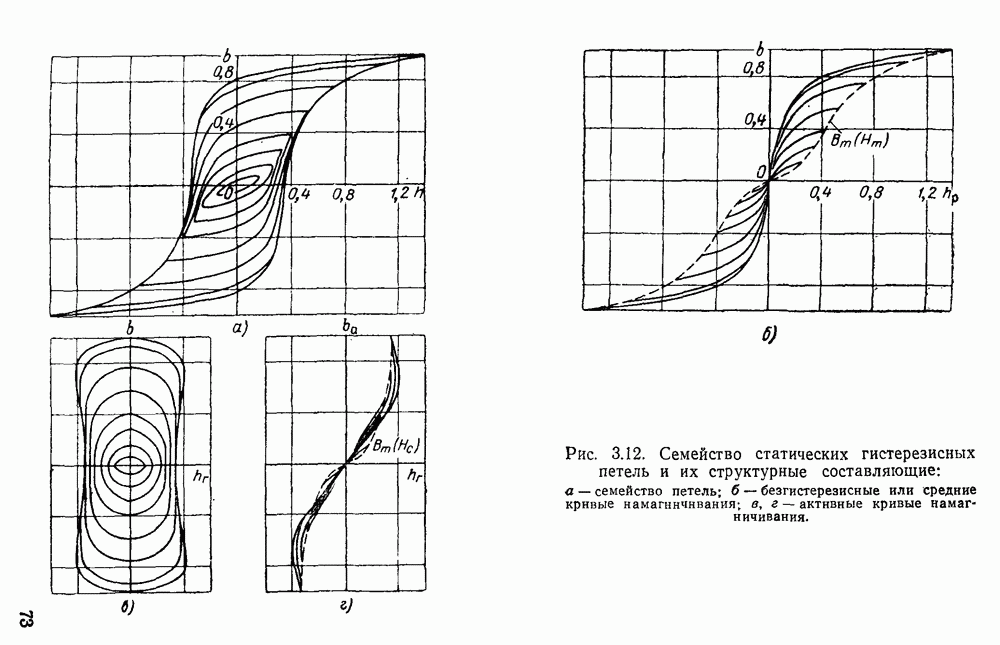
Точность расчетных формул повышается при аппроксимации кривых намагничивания соответственно двумя гиперболическими и двумя круговыми синусами.
Пример 1. Требуется рассчитать магнитную характеристику  при синусоидальной магнитной иидукцни для идеального дросселя без зазора в магнитопроводе и построить ее в единичном масштабе. Кривая намагничивания аппроксимируется гиперболическим синусом с величиной
при синусоидальной магнитной иидукцни для идеального дросселя без зазора в магнитопроводе и построить ее в единичном масштабе. Кривая намагничивания аппроксимируется гиперболическим синусом с величиной  .
.
Полный расчет величины № проведем для  . Для всех других значений Ват приведем лишь готовые результаты.
. Для всех других значений Ват приведем лишь готовые результаты.
Среднеквадратичное значение напряженности поля определяется по формуле (3.46)

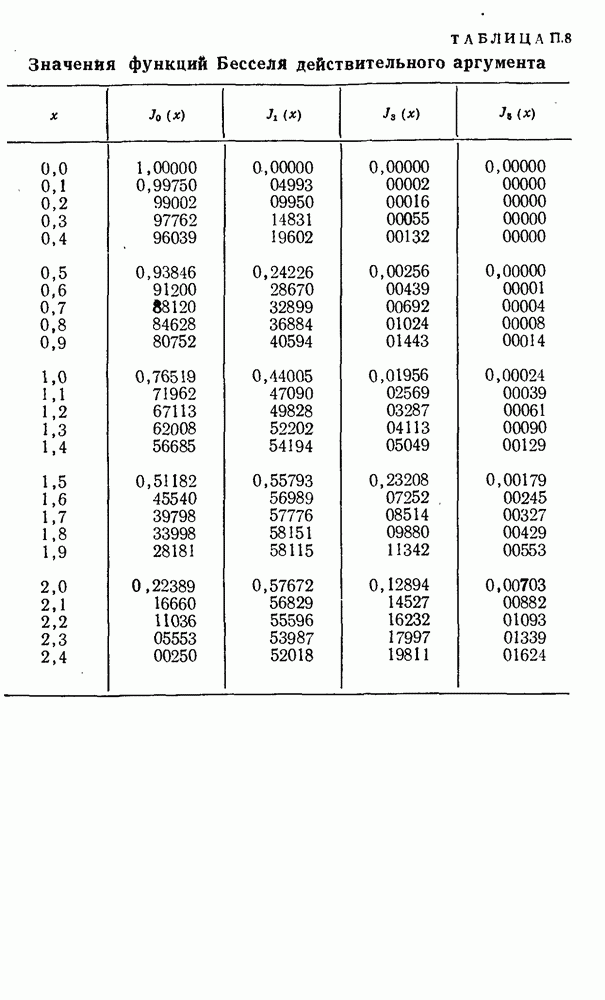
где  (берется по табл.
(берется по табл.  ).
).
Результаты расчетов для всех значений Ват приведены в табл. 3.3.
ТАБЛИЦА 3.3

(см. скан)
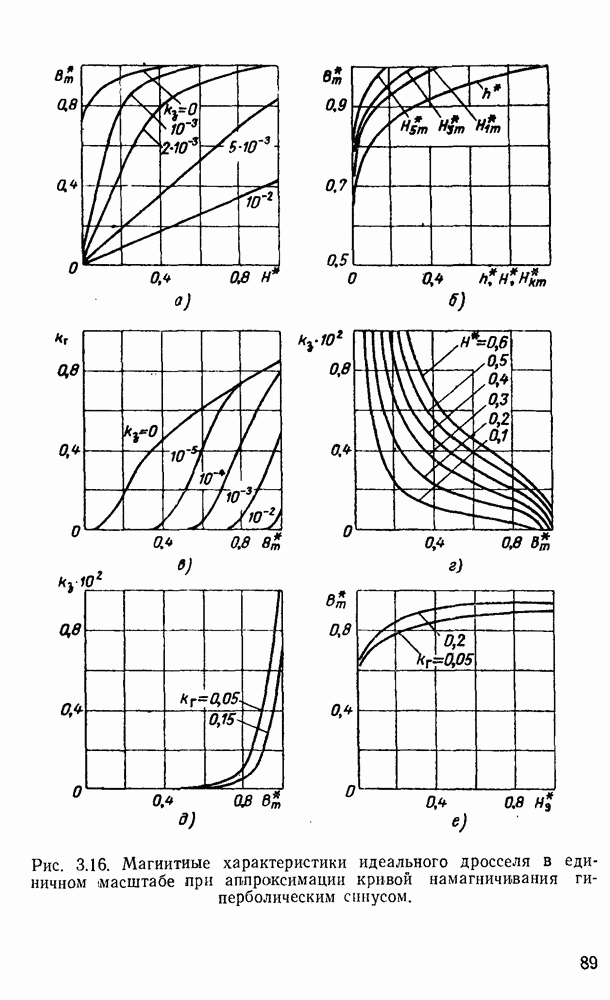
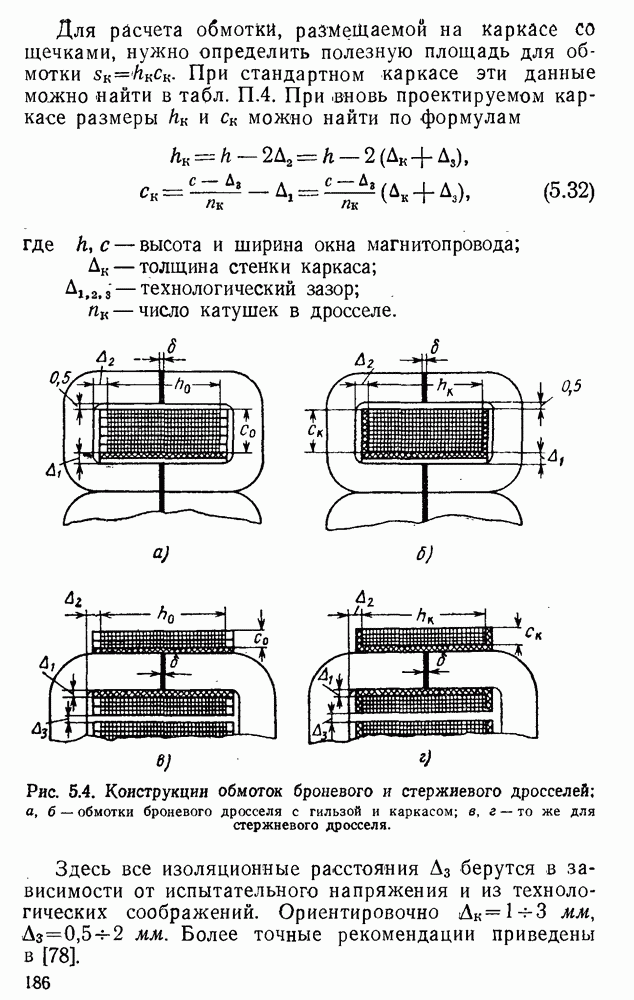
Рис. 3.16. Магнитные характеристики идеального дросселя в единичном масштабе при аппроксимации кривой намагничивания гиперболическим синусом.
Приводя значения  и
и  к единичному масштабу
к единичному масштабу  , получаем значения
, получаем значения  и
и  .
.
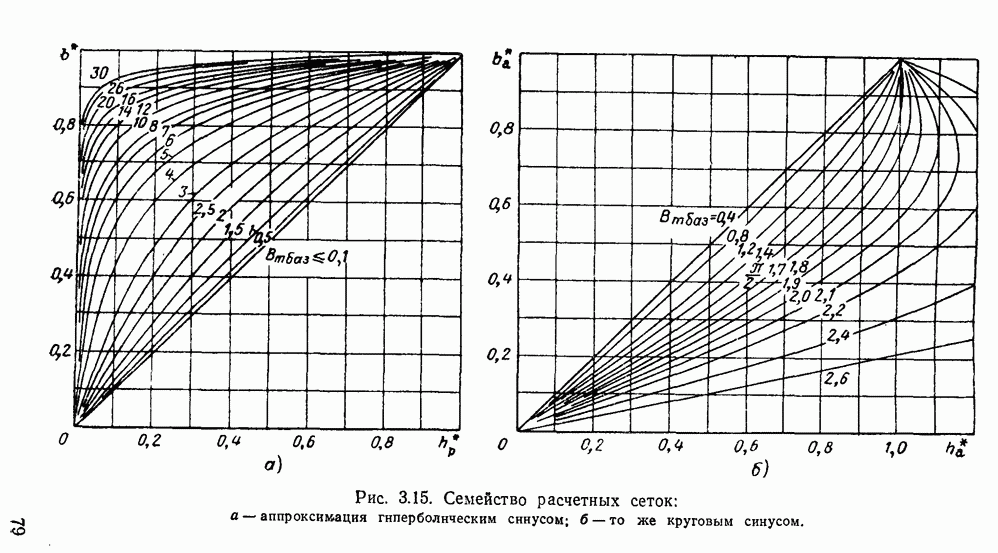
Соответствующая расчетная кривая приведена на рис. 3.16,а (при  ).
).
Пример 2. Требуется рассчитать магнитные характеристики  при синусоидальной магнитной индукции для идеального дросселя без зазора в магнитопроводе и построить их, в единичном масштабе. Кривая намагничивания аппроксимирована гиперболическим синусом с величиной
при синусоидальной магнитной индукции для идеального дросселя без зазора в магнитопроводе и построить их, в единичном масштабе. Кривая намагничивания аппроксимирована гиперболическим синусом с величиной  .
.
Расчет величин  проведем лишь для
проведем лишь для  Величины гармонических составляющих кривой напряженности поля при величине
Величины гармонических составляющих кривой напряженности поля при величине  находим по формулам
находим по формулам 

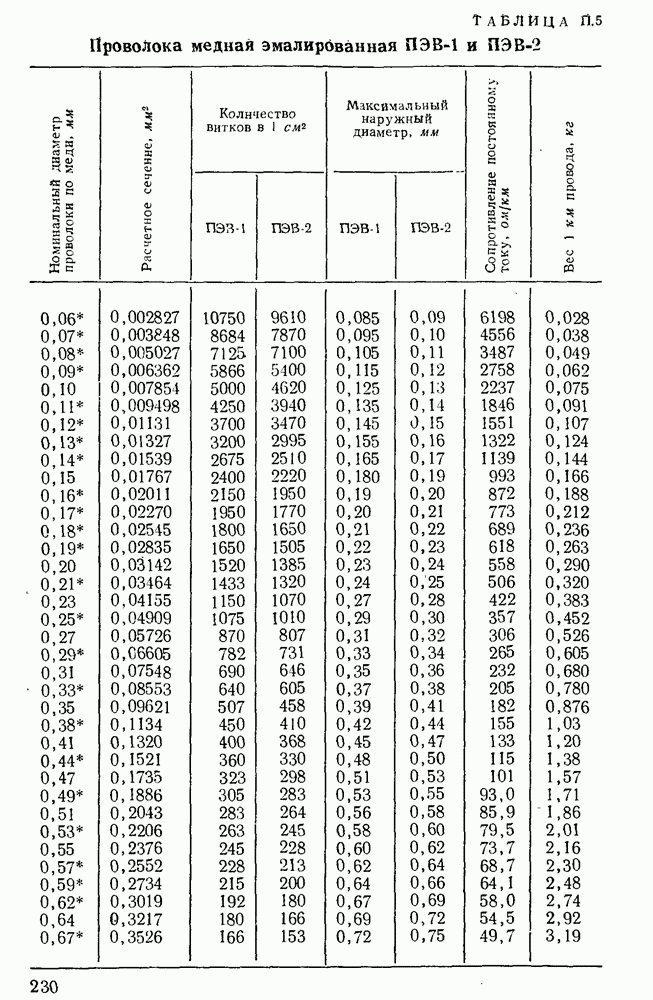
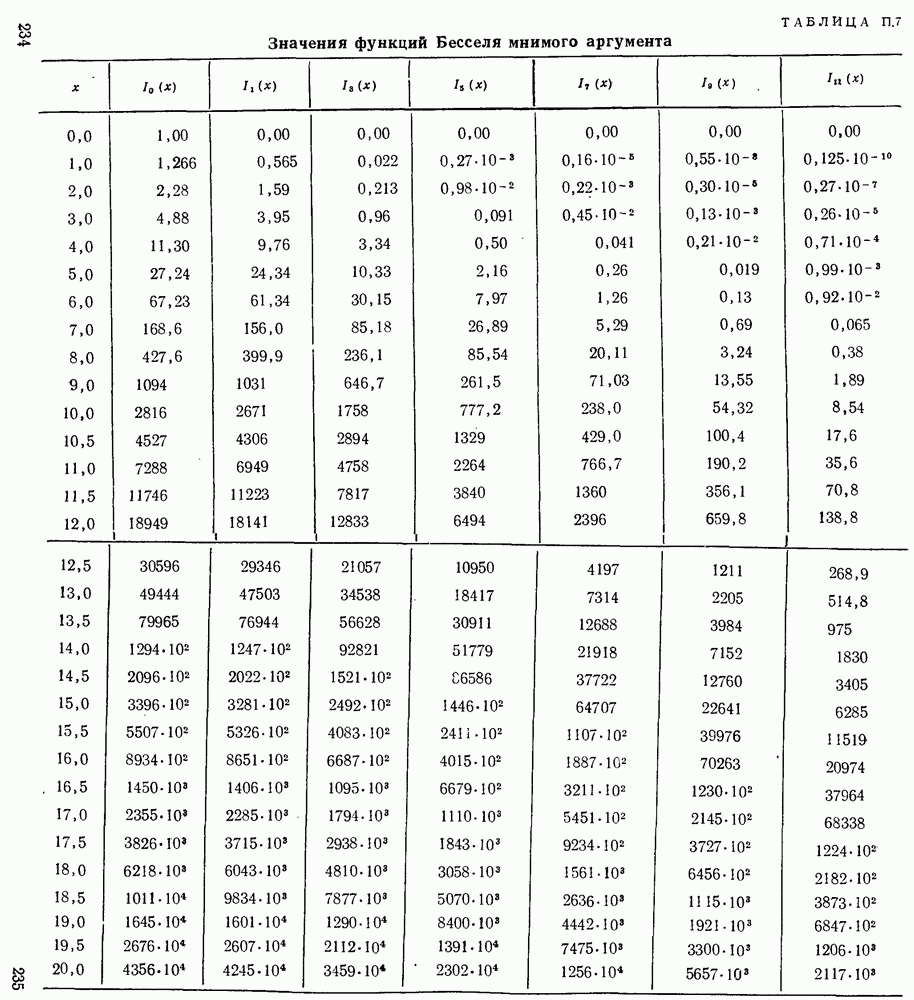
где  — функция Бесселя; функция соответствующего порядка берется по табл.
— функция Бесселя; функция соответствующего порядка берется по табл.  .
.
Коэффициент гармоник кривой напряженности поля при величине  равен
равен

Здесь

где  — функция Бесселя нулевого порядка.
— функция Бесселя нулевого порядка.
Аналогичные расчеты проводятся для всех других значений  Рассчитанные зависимости в единичном масштабе приведены на рис.
Рассчитанные зависимости в единичном масштабе приведены на рис.  .
.
Пример 3. Рассчитаем для идеализированного дросселя без зазора в магнитопроводе напряженность поля и гармонический состав кривой  при значении
при значении  .
.
Активная  и реактивная
и реактивная  слагающие напряженности поля равны
слагающие напряженности поля равны

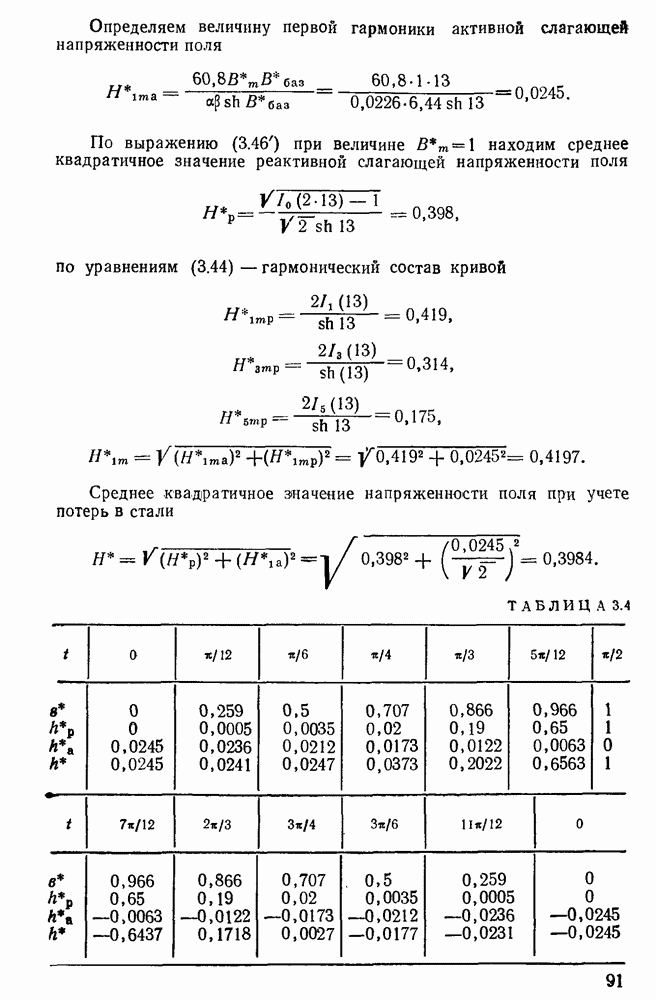
Определяем величину первой гармоники активной слагающей напряженности поля

По выражению (3.46) при величине  находим среднее квадратичное значение реактивной слагающей напряженности поля
находим среднее квадратичное значение реактивной слагающей напряженности поля

по уравнениям (3.44) — гармонический состав кривой

Среднее квадратичное значение напряженности поля при учете потерь в стали

ТАБЛИЦА 3.4

Коэффициент гармоник определим, пользуясь выражением

где

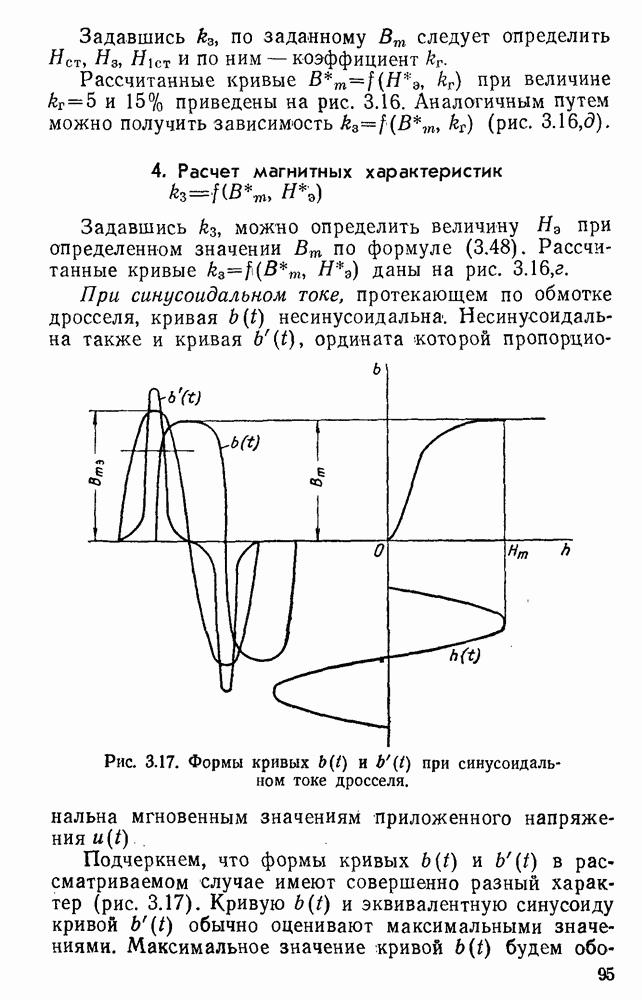
Далее можно найти кривую напряженности поля  и ее активную
и ее активную  и реактивную
и реактивную  слагающие. Результаты расчета сведены в табл. 3.4.
слагающие. Результаты расчета сведены в табл. 3.4.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- 1. ОСНОВНЫЕ СВЕДЕНИЯ О НЕУПРАВЛЯЕМЫХ ДРОССЕЛЯХ ПЕРЕМЕННОГО ТОКА РАДИОЭЛЕКТРОННОЙ АППАРАТУРЫ
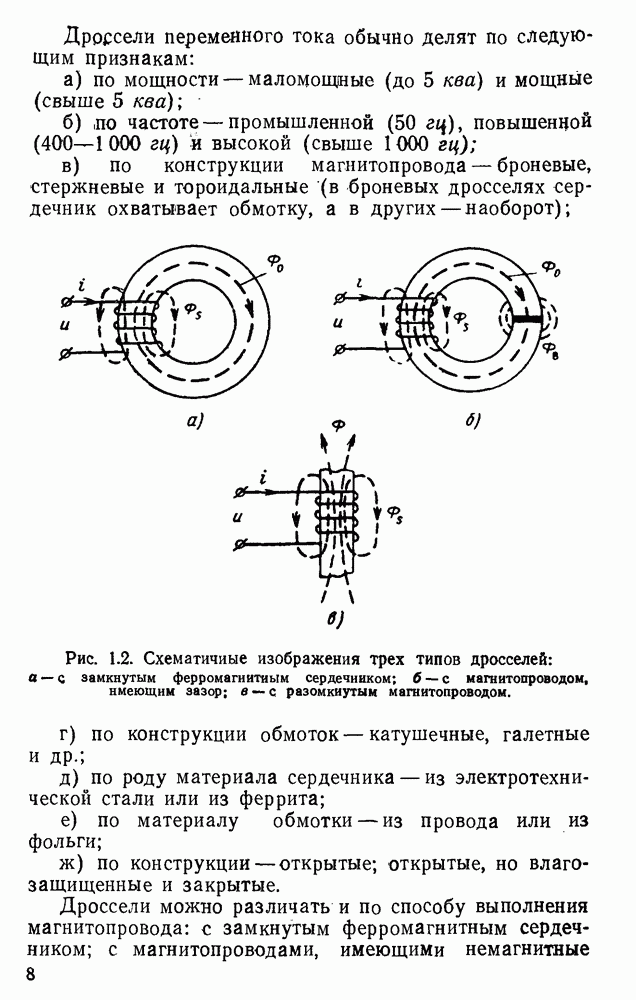
- 1.1. Общие краткие сведения о дросселях. Классификация дросселей
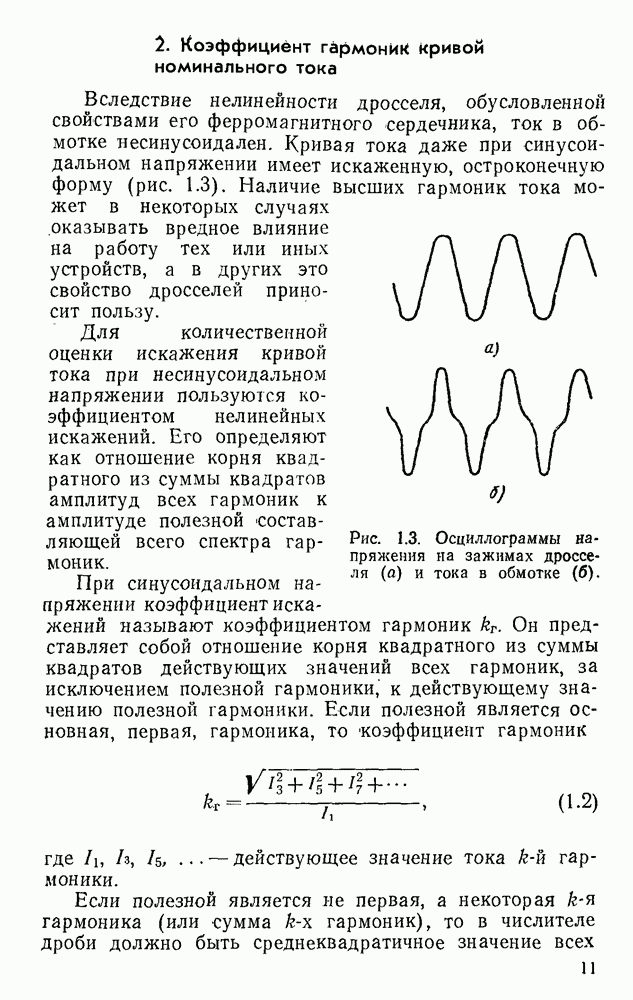
- 1.2. Номинальные параметры нелинейного дросселя
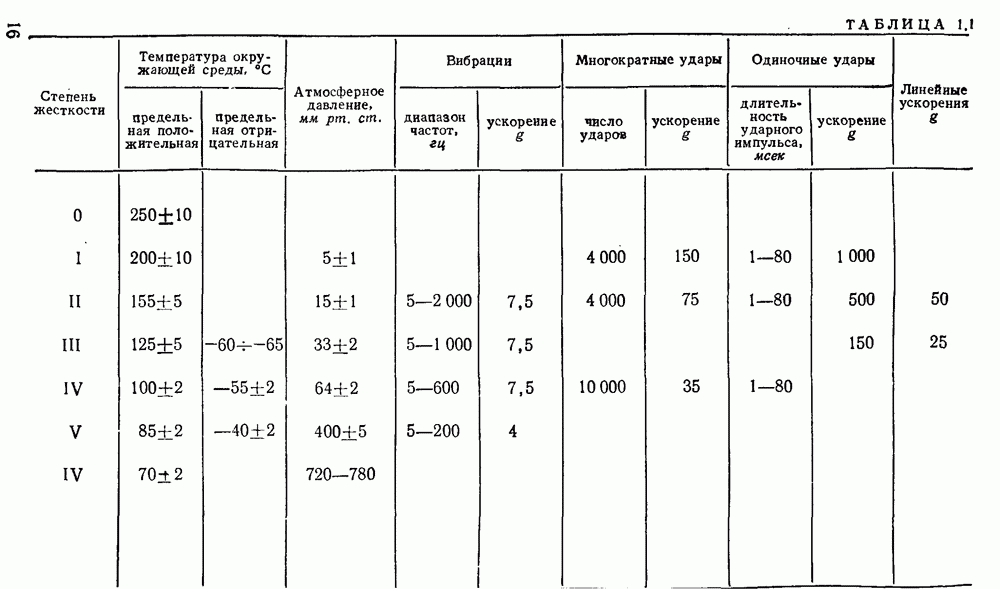
- 1.3. Требования, предъявляемые к дросселям радиоэлектронной аппаратуры. Степени жесткости
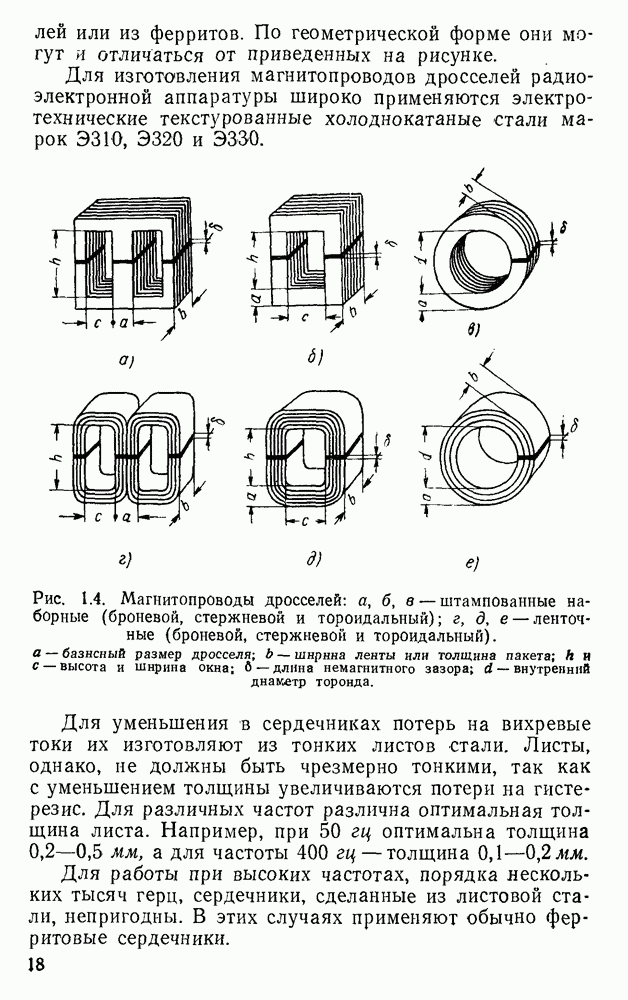
- 1.4. Устройство маломощных дросселей переменного тока
- 1.5. Нагрев и охлаждение дросселей
- 1.6. Экранирование дросселей
- 1.7. Сравнение разных типов дросселей
- 2. МАГНИТНЫЕ СВОЙСТВА МАГНИТОПРОВОДОВ ДРОССЕЛЕЙ. ВЫБОР ФЕРРОМАГНЕТИКА
- 2.1. Свойства магнитопроводов дросселей
- 2.2. Экспериментальное определение магнитных характеристик магнитопроводов дросселей
- 2.3. Выбор ферромагнетика для сердечника дросселя
- 3. ТЕОРИЯ РАБОТЫ ДРОССЕЛЯ ПЕРЕМЕННОГО ТОКА С НЕЛИНЕЙНЫМ ФЕРРОМАГНИТНЫМ СЕРДЕЧНИКОМ
- 3.2. Связи между электрическими и магнитными величинами в дросселе с нелинейным ферромагнитным сердечником. Эквивалентный дроссель
- 1. Идеальный и идеализированный дроссели без зазора
- 2. Идеальный и идеализированный дроссели с немагнитным зазором
- 3. Реальный дроссель
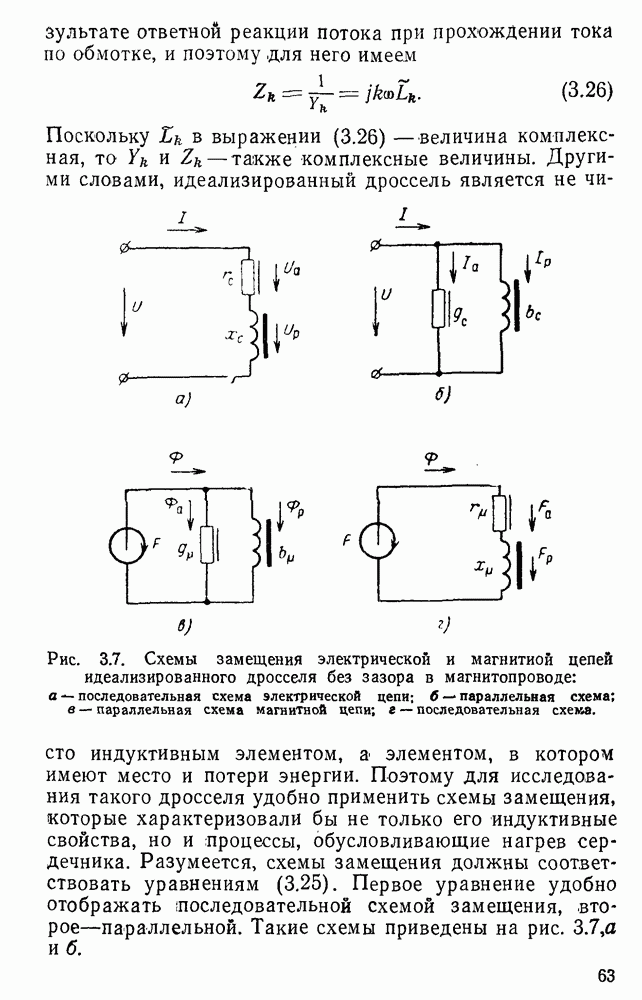
- 3.3. Схемы замещения и векторные диаграммы идеализированного дросселя
- 1. Схемы замещения и векторные диаграммы электрической цепи идеализированного дросселя
- 2. Схемы замещения и векторные диаграммы магнитной цепи идеализированного дросселя
- 3.4. Аппроксимация кривых намагничивания ферромагнитных сердечников. Относительные единицы. Определение коэффициентов аппроксимации
- 3.5. Математическая модель семейства динамических гистерезисных петель. Использование модели для решения задач гармонического анализа
- 1. Определение гармонического состава кривой напряженности поля
- 2. Определение среднеквадратичного значения напряженности поля и потерь в стали
- 3.6. Аналитический расчет магнитных характеристик магнитопроводов идеальных и идеализированных дросселей с зазором
- 3.7. Расчет численными методами магнитных характеристик идеальных и идеализированных дросселей при произвольной форме кривой магнитной индукции
- 3.8. Расчет магнитных характеристик реальных дросселей. Расчет характеристик дросселей, включенных в электрические цепи
- 1. Расчет магнитных характеристик для реального дросселя без рассеяния
- 2. Расчет магнитных характеристик для дросселя, включенного последовательно с активно-индуктивной нагрузкой
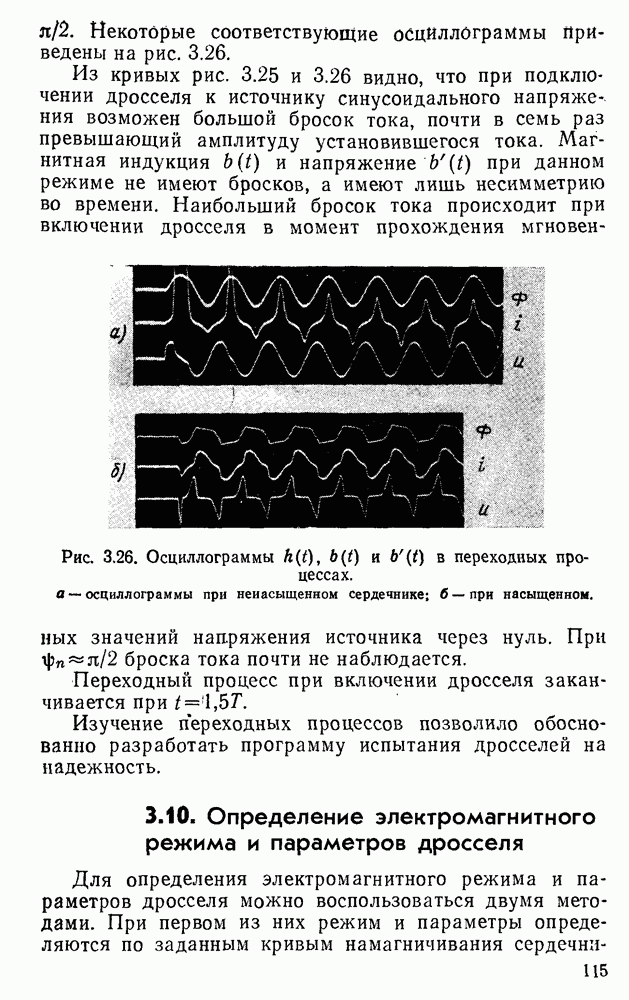
- 3.9. Переходные процессы в дросселе
- 3.10. Определение электромагнитного режима и параметров дросселя
- 2. Определение режима и основных характеристик дросселя по комплексной магнитной проницаемости его сердечника
- 4. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПРОЕКТИРОВАНИЯ ДРОССЕЛЕЙ
- 4.1. Общие замечания. Понятие об оптимальных дросселях и их параметрах
- 4.2. Основные уравнения взаимосвязи параметров дросселя и их решение
- 2. Уравнение потерь
- 3. Уравнение теплового режима дросселя
- 4. Уравнения взаимосвязи магнитных параметров дросселя
- 5. Обобщенные уравнения геометрических параметров разных типов и конструкций дросселей
- 6. Технико-экономические показатели дросселей
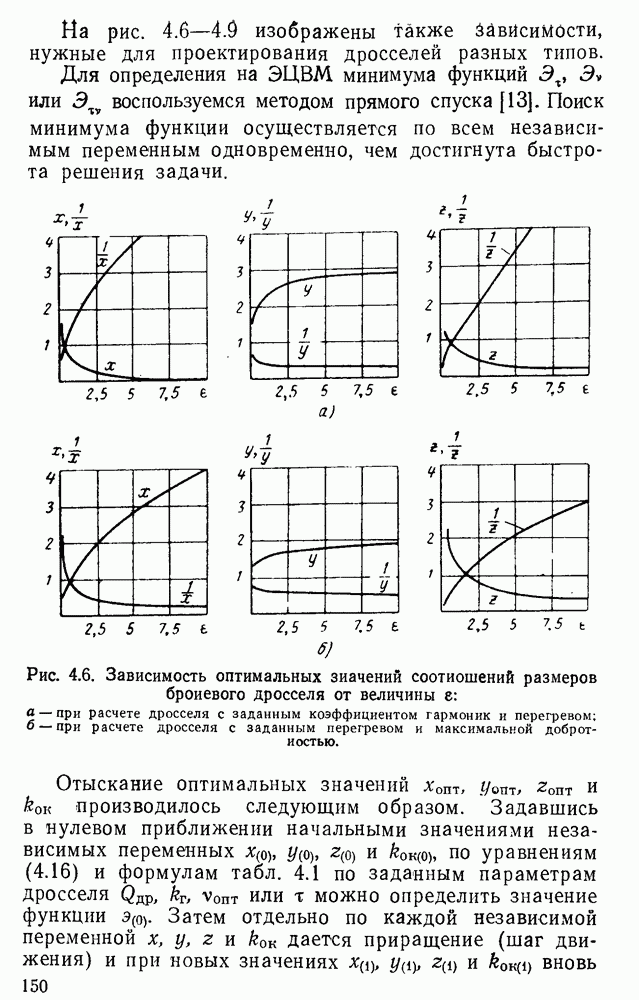
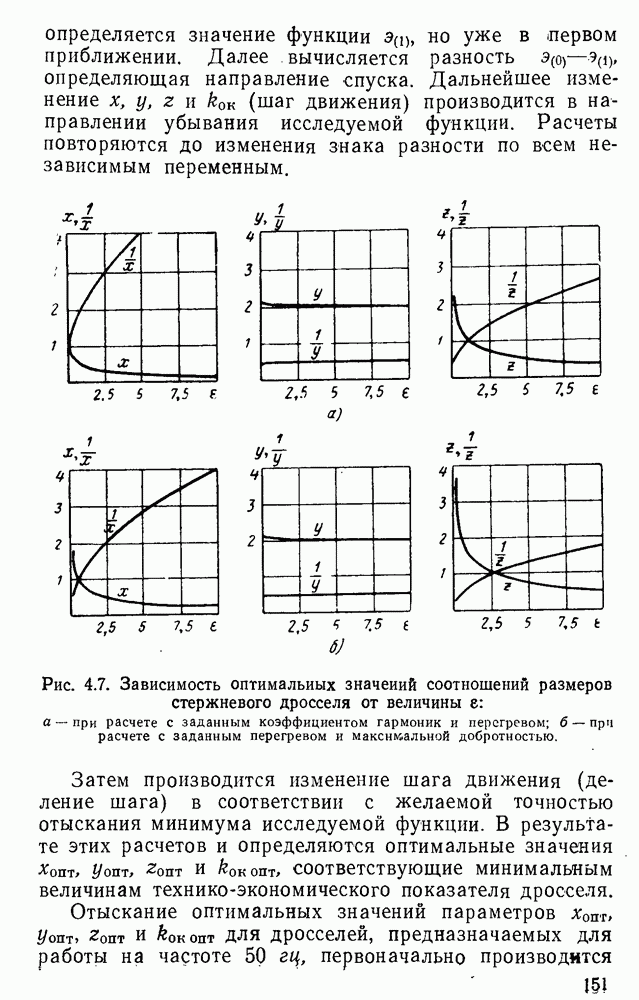
- 4.3. Определение с помощью ЭЦВМ оптимальных значений соотношений геометрических параметров дросселя. Оптимальные значения соотношений разных типов дросселей
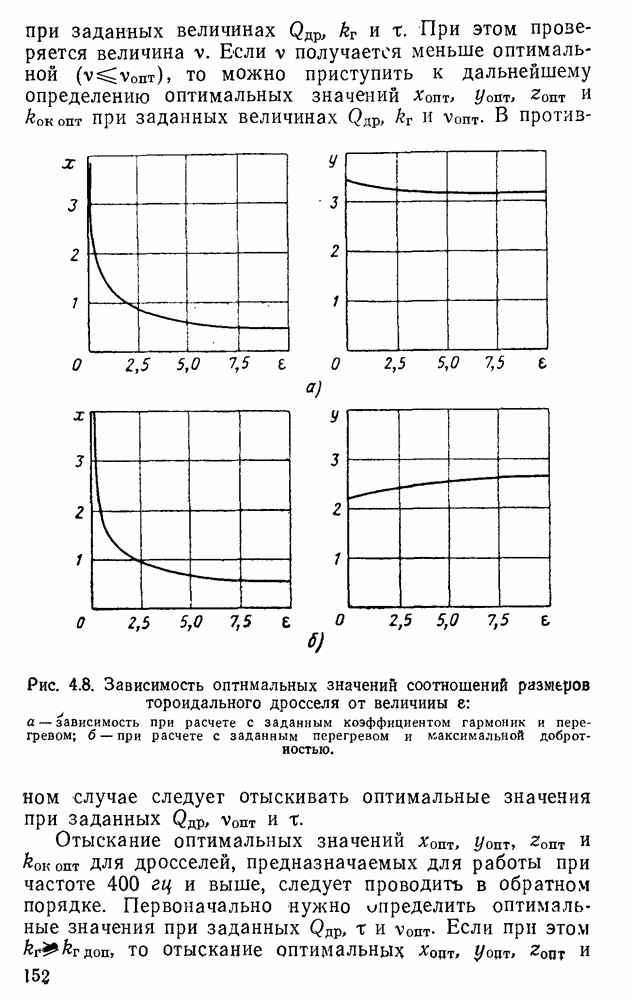
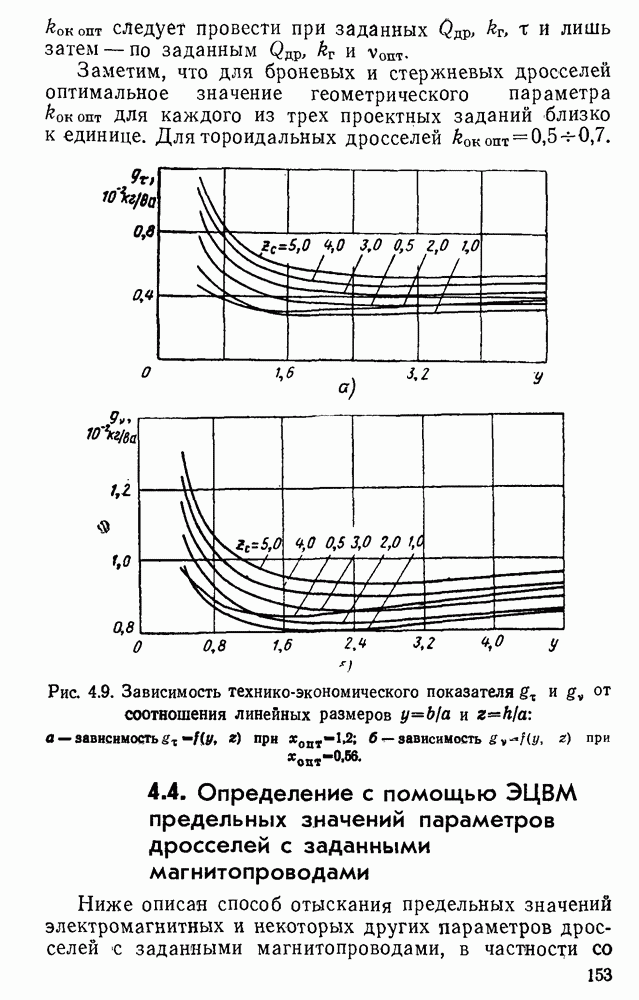
- 4.4. Определение с помощью ЭЦВМ предельных значений параметров дросселей с заданными магнитопроводами
- 4.5. Влияние отдельных факторов на оптимальные значения геометрических соотношений дросселя
- 5. ПРОЕКТИРОВАНИЕ ДРОССЕЛЕЙ
- 5.1. Основные замечания. Техническое задание на проектирование дросселя
- 5.2. Методика проектирования дросселей
- 1. Выбор типа дросселя, марки стали и обмоточного материала
- 2. Выбор типоразмера стандартного сердечника или расчет специального сердечника
- 3. Выбор магнитного режима магнитопровода дросселя
- 4. Расчет длины немагнитного зазора
- 5. Расчет потерь в дросселе
- 6. Определение геометрических параметров дросселя
- 7. Расчет теплового режима дросселя
- 8. Расчет обмоточных данных и междуслойной изоляции
- 9. Расчет катушек дросселя (конструирование обмоток)
- 10. Определение технико-экономических показателей дросселя
- 11. Проверочный расчет дросселя
- 12. Краткая методика расчета дросселя
- 5.3. Примеры проектирования дросселей
- ПРИЛОЖЕНИЯ
- Основные условные обозначения
- Литература