| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.7. Расчет численными методами магнитных характеристик идеальных и идеализированных дросселей при произвольной форме кривой магнитной индукции
Расчет магнитных характеристик в этом случае проще всего производить численными методами. Эти методы, как известно, широко применяются в последнее время в связи с возможностью выполнения расчетов с помощью ЭЦВМ.
Численные методы расчета магнитных характеристик подробно опишем лишь для идеального дросселя без зазора в магнитопроводе. Для идеализированного дросселя и для идеального с зазором дадим лишь блок-схему решения задачи с помощью ЭЦВМ.
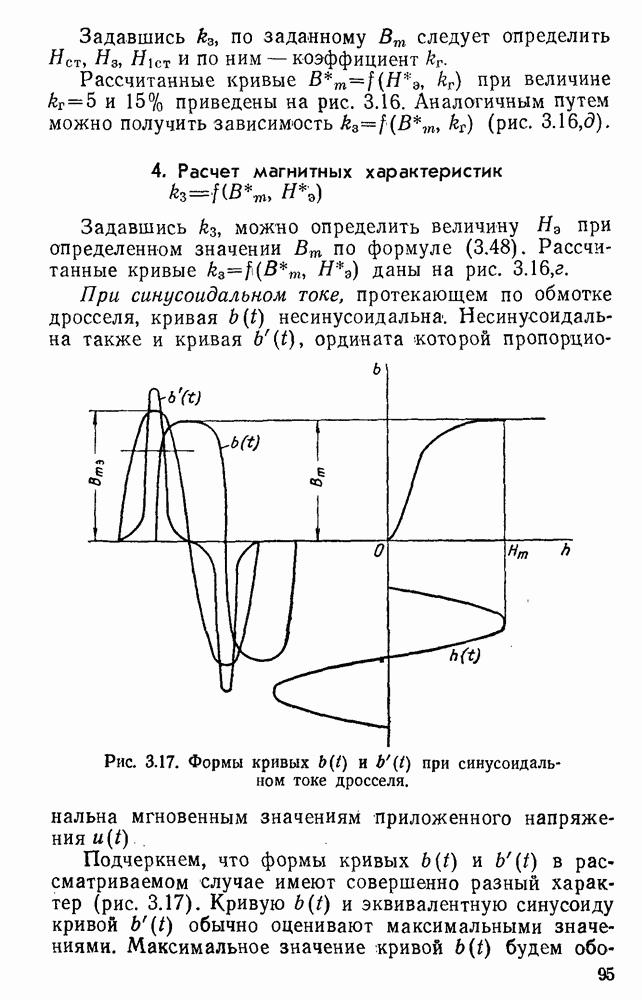
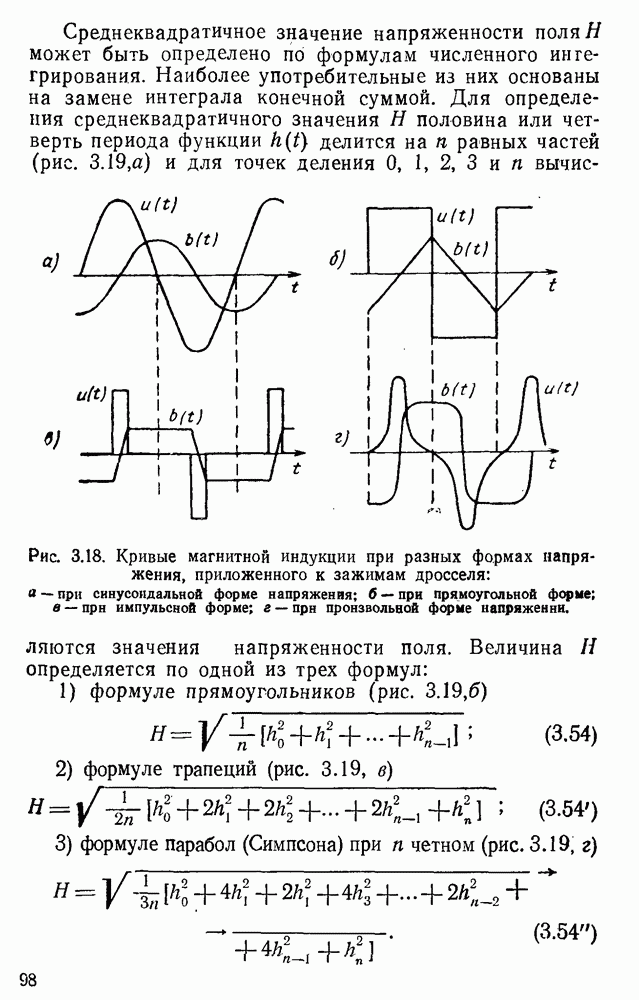
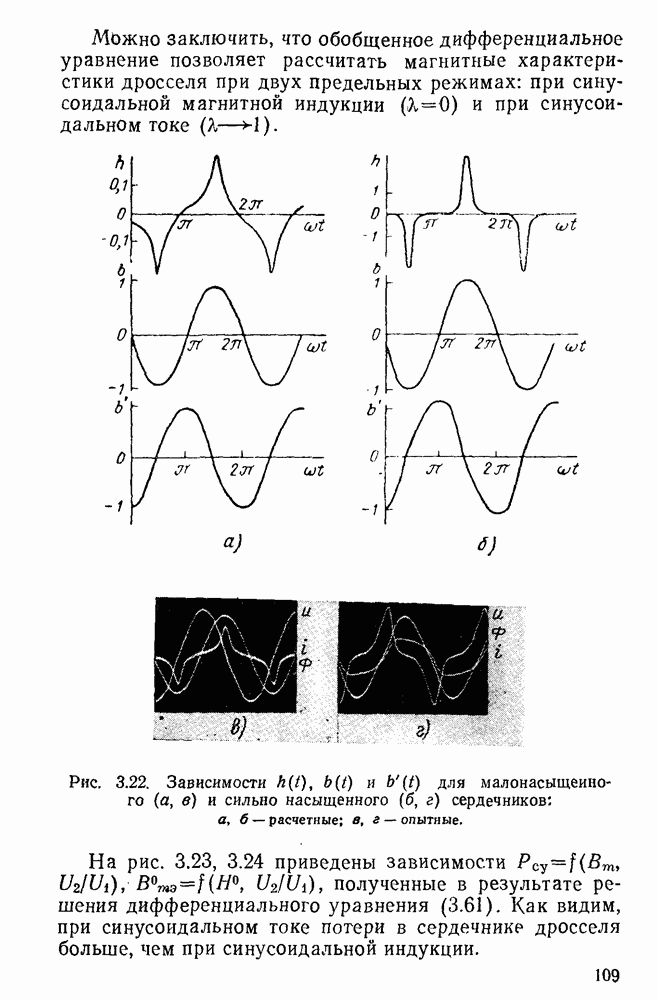
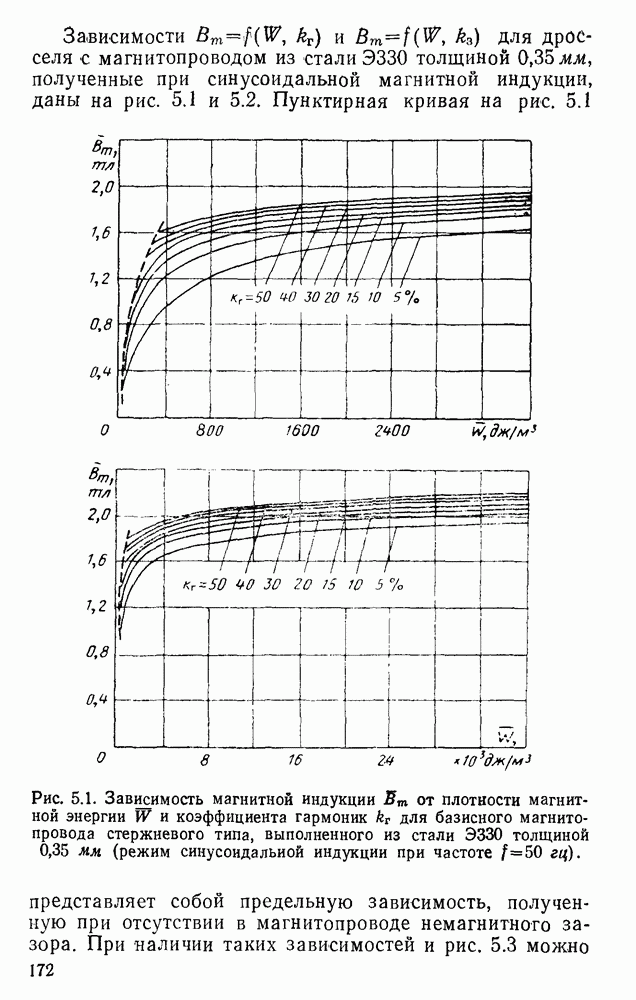
Расчет магнитных характеристик идеального дросселя производится в следующем порядке. Прежде всего по кривой напряжения, приложенного к зажимам дросселя, определяется величина и форма кривой магнитной индукции. Кривая может быть задана как аналитически, так и в виде графика. В первом случае магнитная индукция находится по выражению (3.9), во втором — графическим интегрированием или же с помощью особого прибора — интеграфа. Максимальное значение магнитной индукции определяется при этом по формуле (3.6). Кривые магнитной индукции, рассчитанные для некоторых форм кривой напряжения, приведены на рис. 3.18. По кривой магнитной индукции находится напряженность магнитного поля. Расчет этой кривой производится по зависимостям:

Среднеквадратичное значение напряженности поля Я может быть определено по формулам численного интегрирования. Наиболее употребительные из них основаны на замене интеграла конечной суммой.

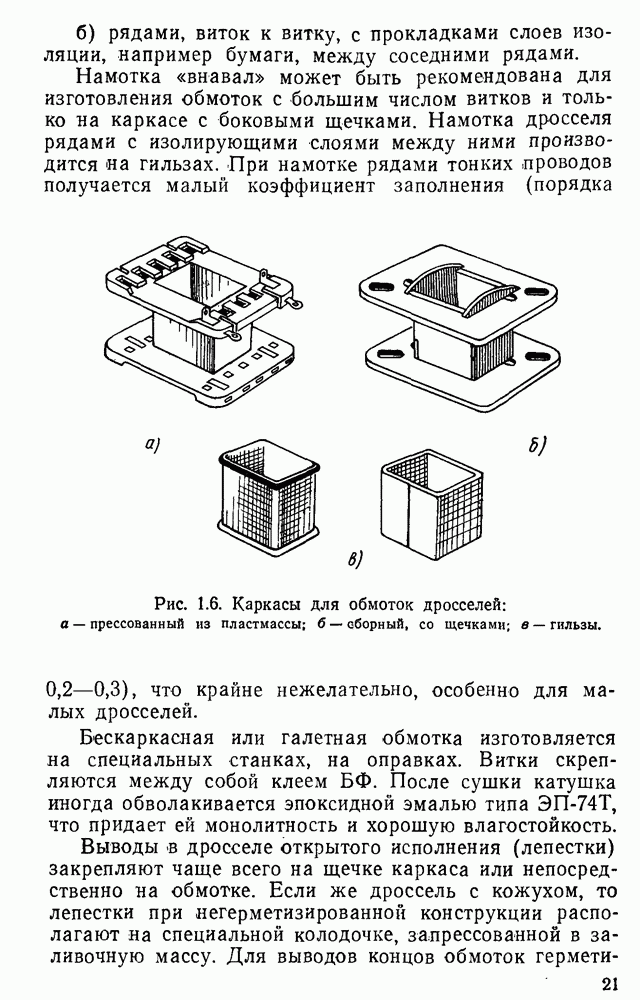
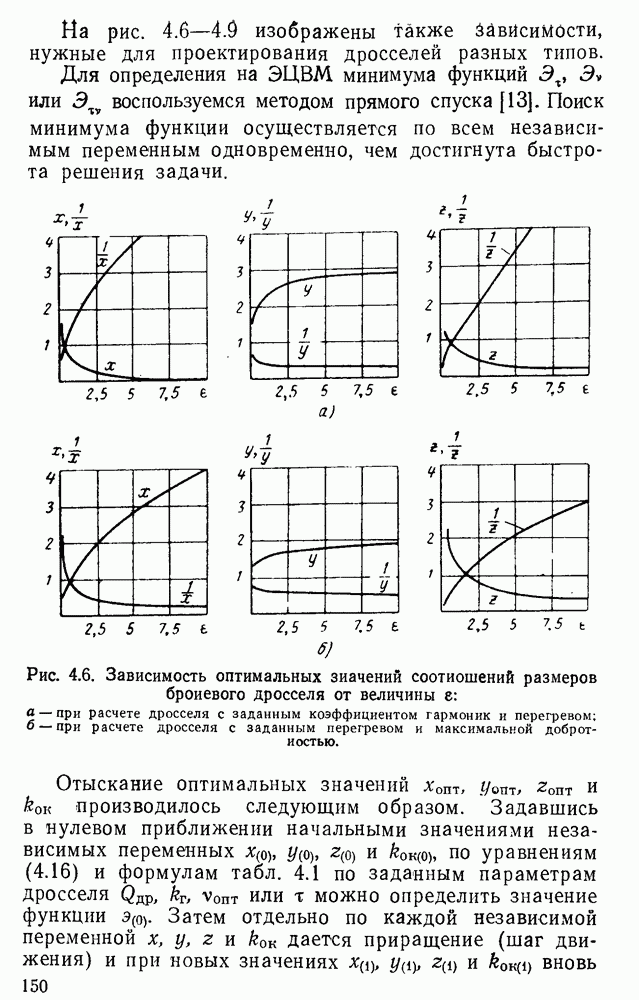
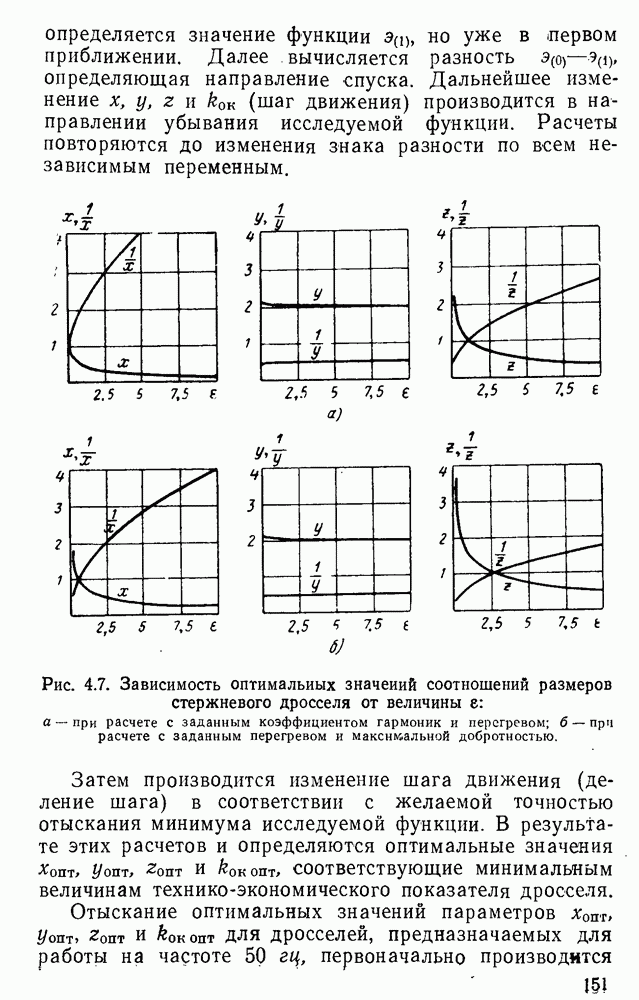
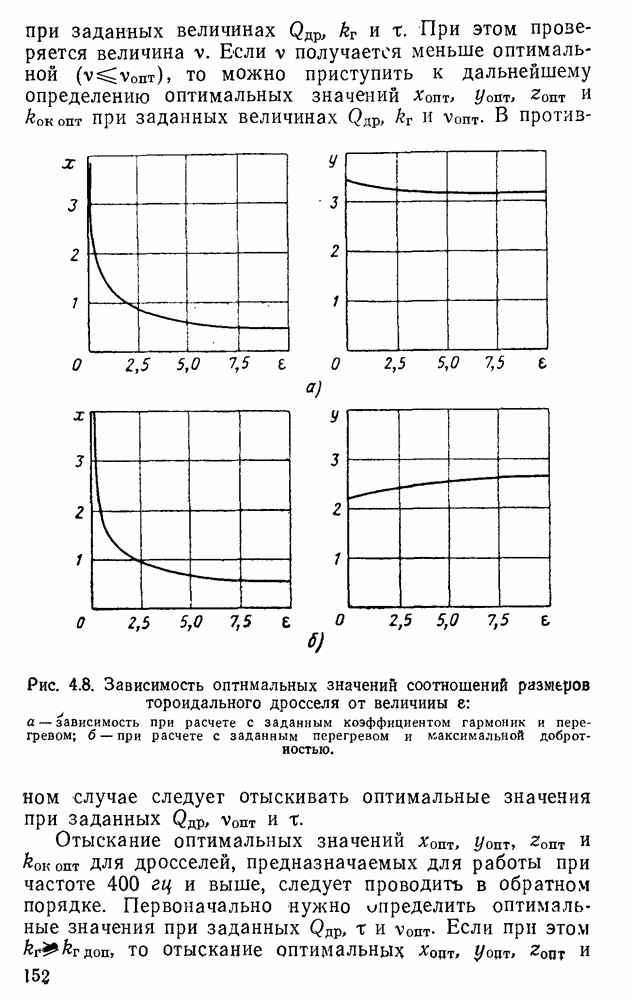
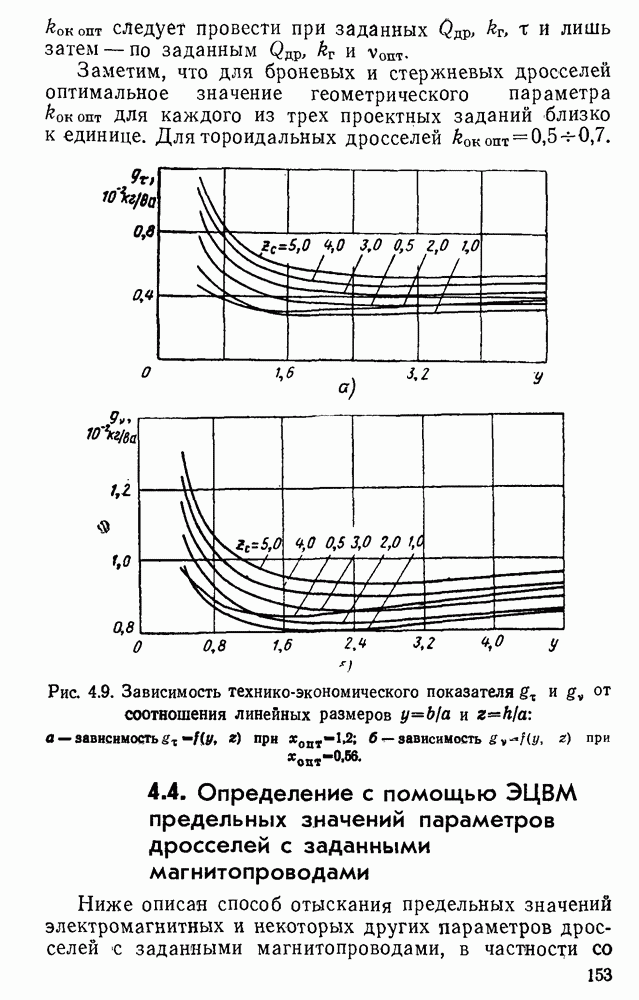
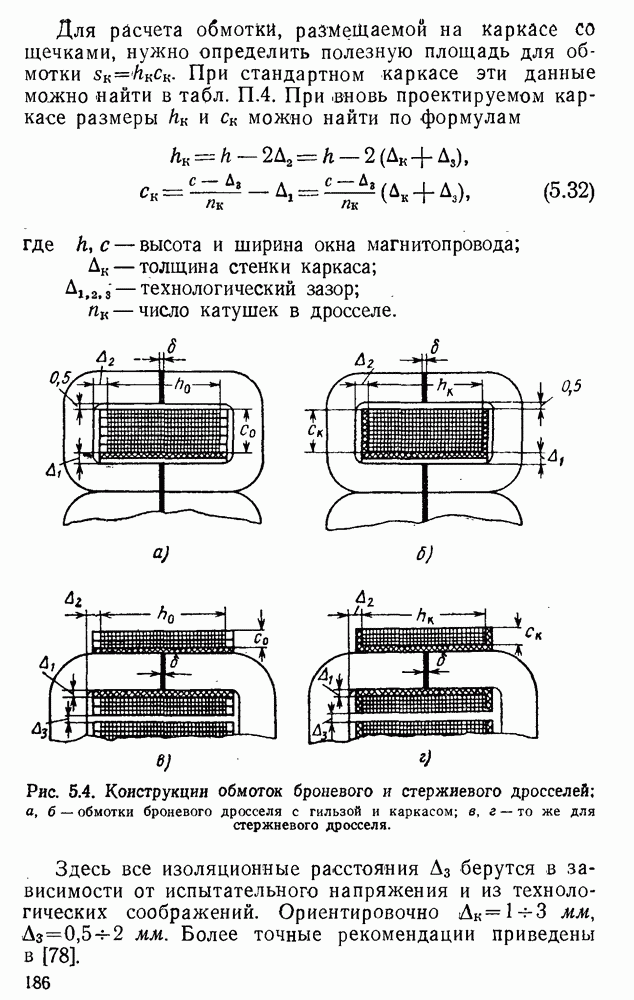
Рис. 3.18. Кривые магнитной индукции при разных формах напряжения, приложенного к зажимам дросселя: а — при синусоидальной форме напряжения; б — при прямоугольной форме; в — при импульсной форме; г — при произвольной форме напряжении.
Для определения среднеквадратичного значения  половина или четверть периода функции
половина или четверть периода функции  делится на n равных частей (рис. 3.19,а) и для точек деления 0, 1, 2, 3 и n вычисляются значения напряженности поля. Величина
делится на n равных частей (рис. 3.19,а) и для точек деления 0, 1, 2, 3 и n вычисляются значения напряженности поля. Величина  определяется по одной из трех формул:
определяется по одной из трех формул:
1) формуле прямоугольников (рис.  )
)

2) формуле трапеций (рис. 3.19, в)

3) формуле парабол (Симпсона) при n четном (рис. 3.19, г)

(см. скан)
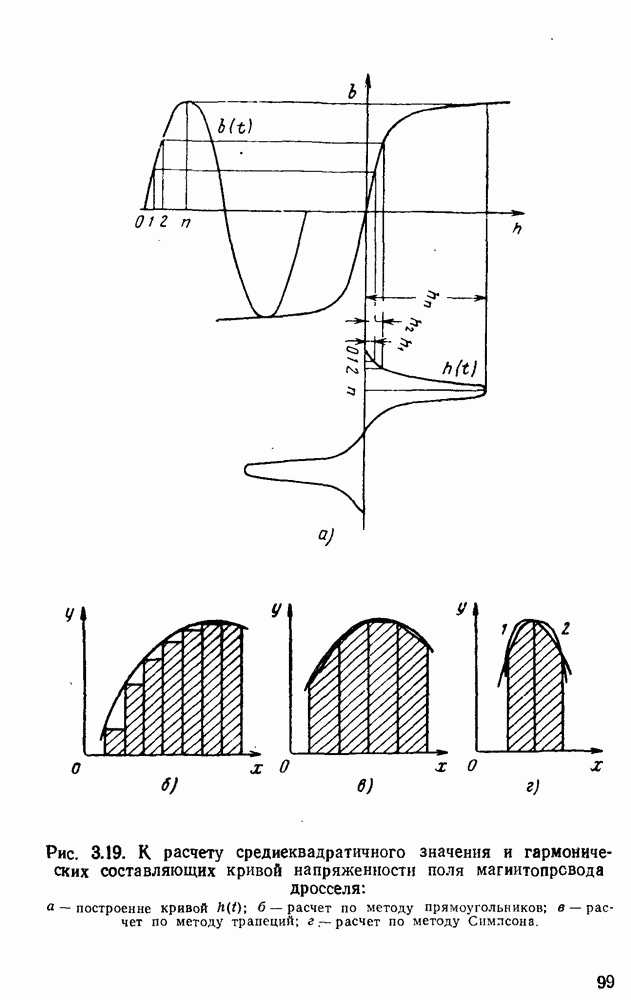
Рис. 3.19. К расчету среднеквадратичного значения и гармонических составляющих кривой напряженности поля магиитопрсвода дросселя: а — построение кривой  б — расчет по методу прямоугольников; в — расчет по методу трапеций; г — расчет по методу Симпсона.
б — расчет по методу прямоугольников; в — расчет по методу трапеций; г — расчет по методу Симпсона.
Все три формулы тем точнее, чем больше n. При одних и тех же n формула трапеций дает большую точность, чем формула прямоугольников, а формула. Симпсона — большую точность, чем формула трапеций. При ручном счете предпочтительнее формула прямоугольников, а при выполнении расчетов на ЭЦВМ лучше пользоваться формулой Симпсона.
Среднеквадратичное значение Н вычисляется следующим образом. Задавшись величиной напряжения на зажимах дросселя и получив величину и форму кривой магнитной индукции, разбивают ее по времени на n равных частей (рис. 3.19,а). При симметричной форме кривой интегрирование возможно делать за половину периода или даже за четверть периода. Для каждого из значений мгновенной индукции при помощи зависимости  определяется мгновенное значение напряженности поля
определяется мгновенное значение напряженности поля  По значениям
По значениям  и т. д. по формуле (3.54), (3.54) или
и т. д. по формуле (3.54), (3.54) или  вычисляется искомое значение напряженности магнитного поля Н. Так, например, для случая, изображенного на рис. 3.19, имеем
вычисляется искомое значение напряженности магнитного поля Н. Так, например, для случая, изображенного на рис. 3.19, имеем

где  — число интервалов разбиения, взятое за четверть периода;
— число интервалов разбиения, взятое за четверть периода;  — величины напряженности поля
— величины напряженности поля  и т. д. соответственно в точках
и т. д. соответственно в точках 
Расчеты повторяются при других значениях  . В результате определяется искомая зависимость
. В результате определяется искомая зависимость  .
.
Разложение кривых  в гармонический ряд можно также выполнить методом численного интегрирования.
в гармонический ряд можно также выполнить методом численного интегрирования.
Среднее значение кривой  или
или  находится по формуле
находится по формуле

Высшие гармоники
 (3.56)
(3.56)
Вычисление интегралов (3.55) и (3.55) также может быть произведено по одному из трех методов:
1) по методу прямоугольников

2) по методу трапеций

3) по методу парабол


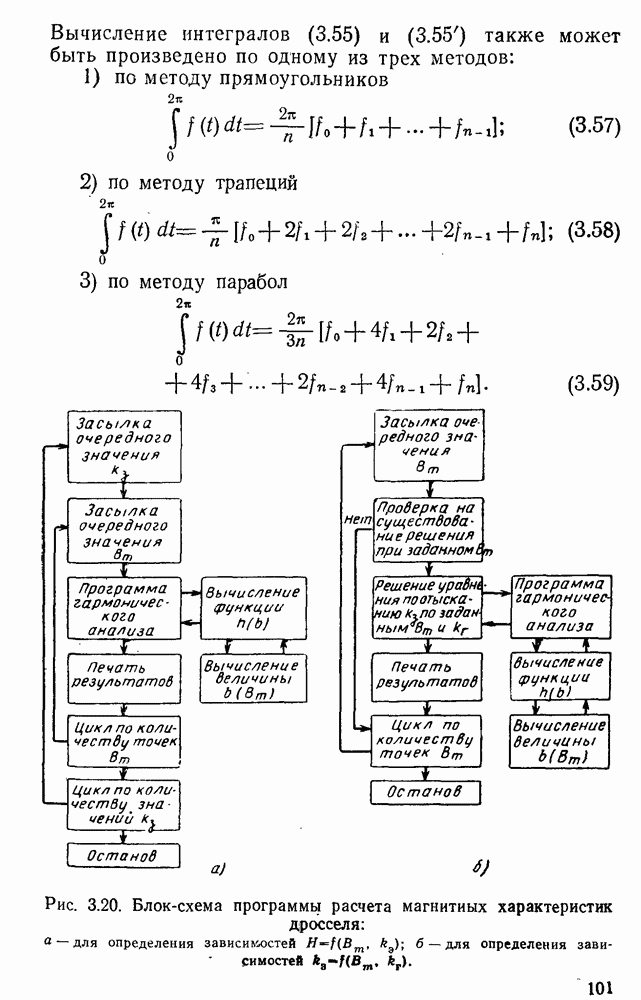
Рис. 3.20. Блок-схема программы расчета магнитных характеристик дросселя: а — для определения зависимостей  ; б — для определения зависимостей
; б — для определения зависимостей 
По известному гармоническому составу кривых, пользуясь формулами (1.2) и (3.8), можно определить коэффициенты, характеризующие несинусоидальность кривых  .
.
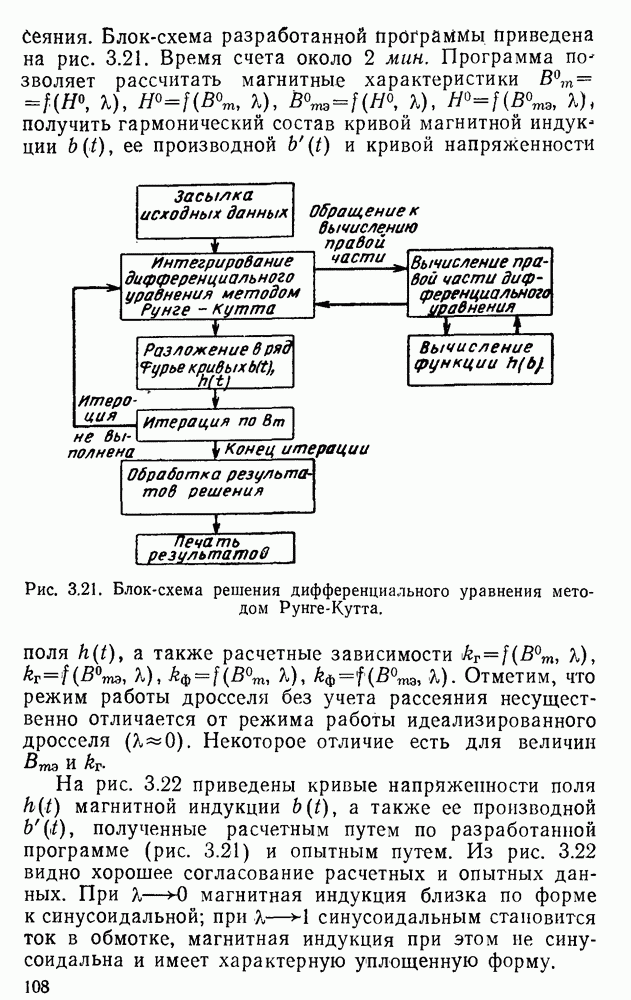
Для расчета магнитных характеристик идеального и идеализированного дросселей нами разработана универсальная программа, позволяющая с помощью ЭЦВМ рассчитать нужные магнитные характеристики при любой форме кривой напряжения на зажимах дросселя. Блок-схема этой программы приведена на рис. 3.20.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- 1. ОСНОВНЫЕ СВЕДЕНИЯ О НЕУПРАВЛЯЕМЫХ ДРОССЕЛЯХ ПЕРЕМЕННОГО ТОКА РАДИОЭЛЕКТРОННОЙ АППАРАТУРЫ
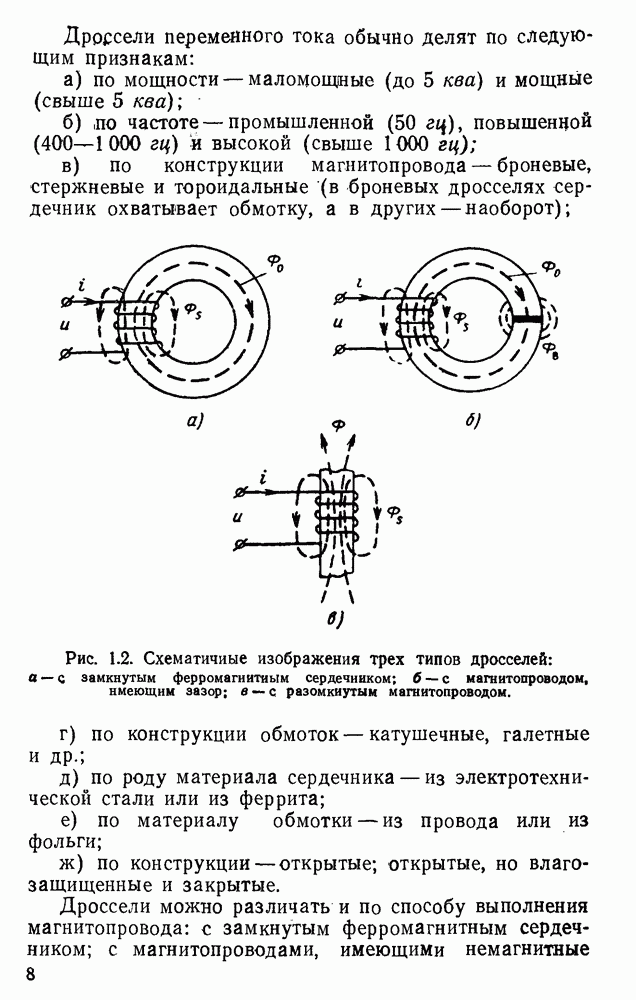
- 1.1. Общие краткие сведения о дросселях. Классификация дросселей
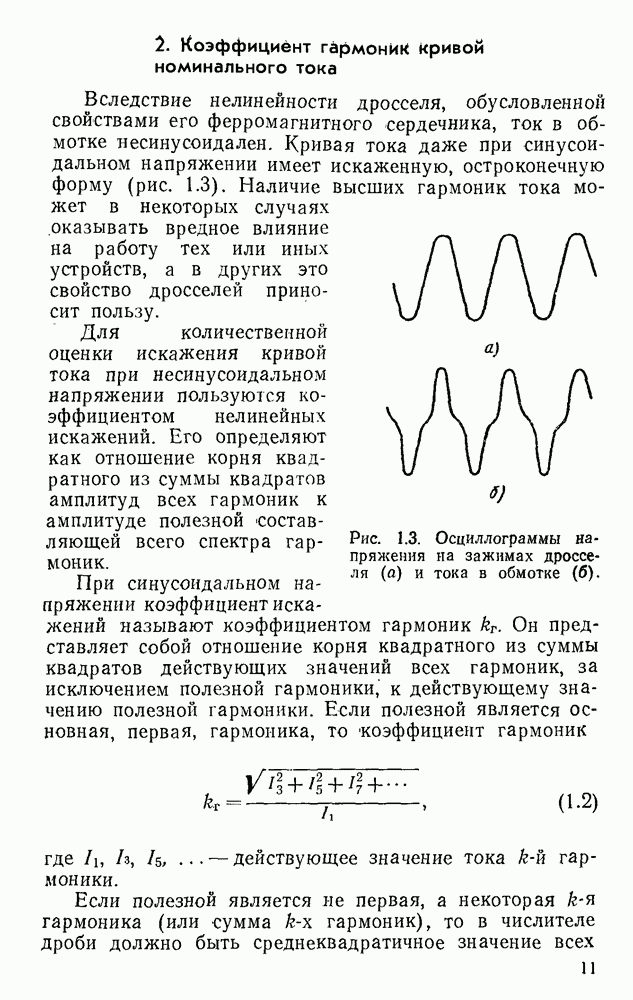
- 1.2. Номинальные параметры нелинейного дросселя
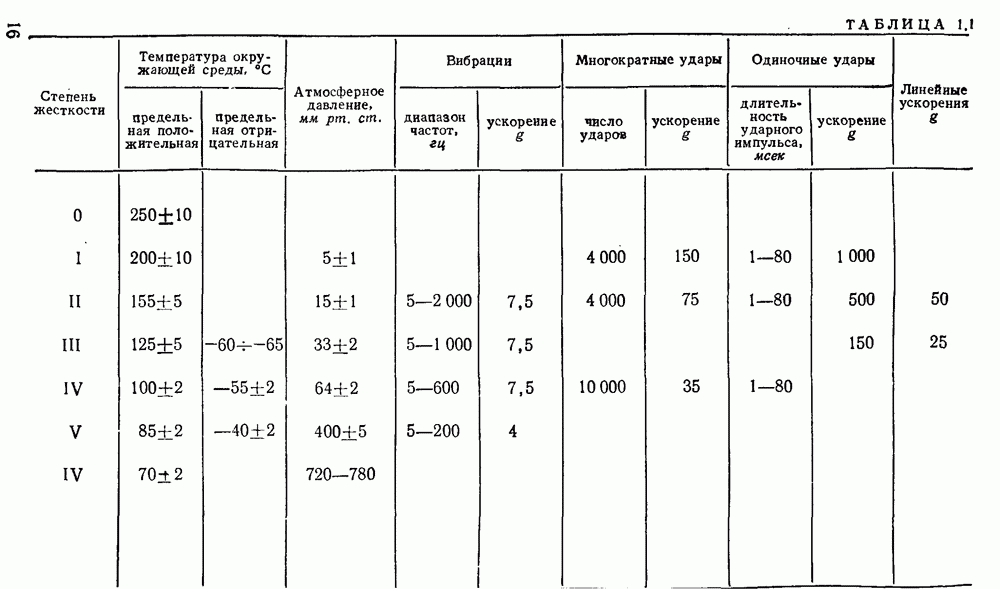
- 1.3. Требования, предъявляемые к дросселям радиоэлектронной аппаратуры. Степени жесткости
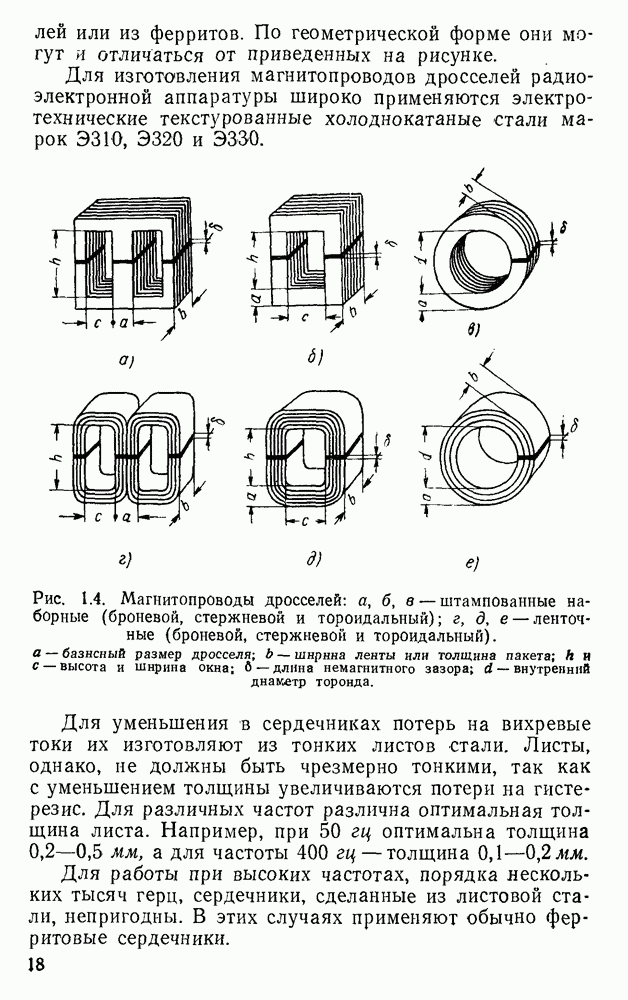
- 1.4. Устройство маломощных дросселей переменного тока
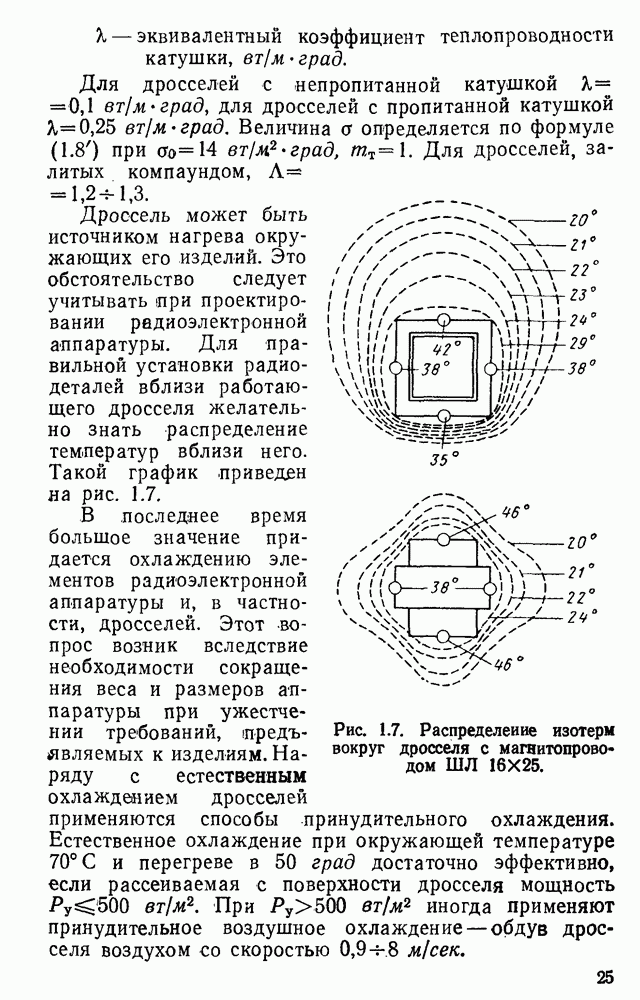
- 1.5. Нагрев и охлаждение дросселей
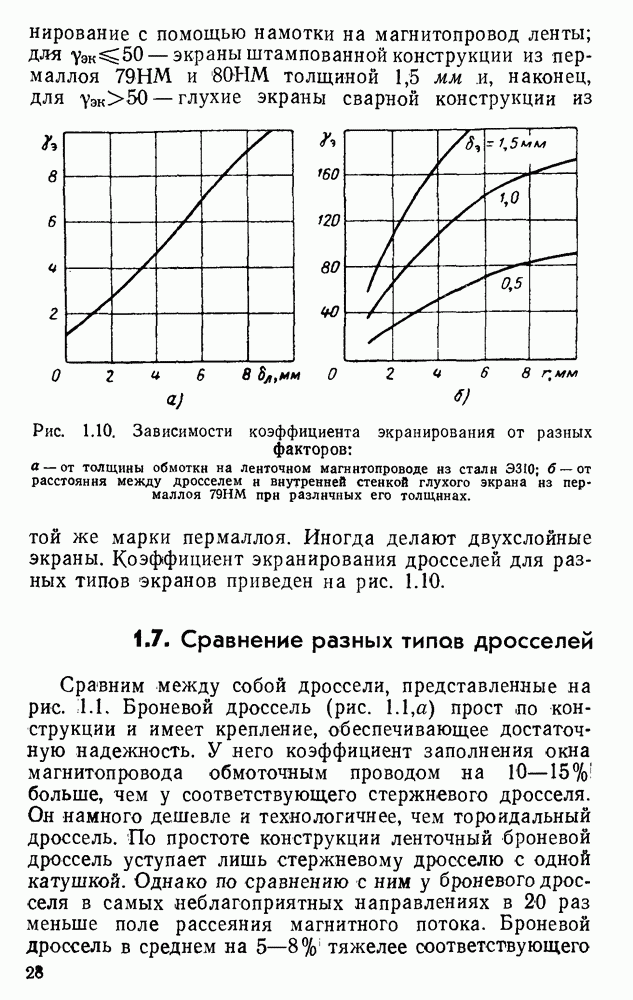
- 1.6. Экранирование дросселей
- 1.7. Сравнение разных типов дросселей
- 2. МАГНИТНЫЕ СВОЙСТВА МАГНИТОПРОВОДОВ ДРОССЕЛЕЙ. ВЫБОР ФЕРРОМАГНЕТИКА
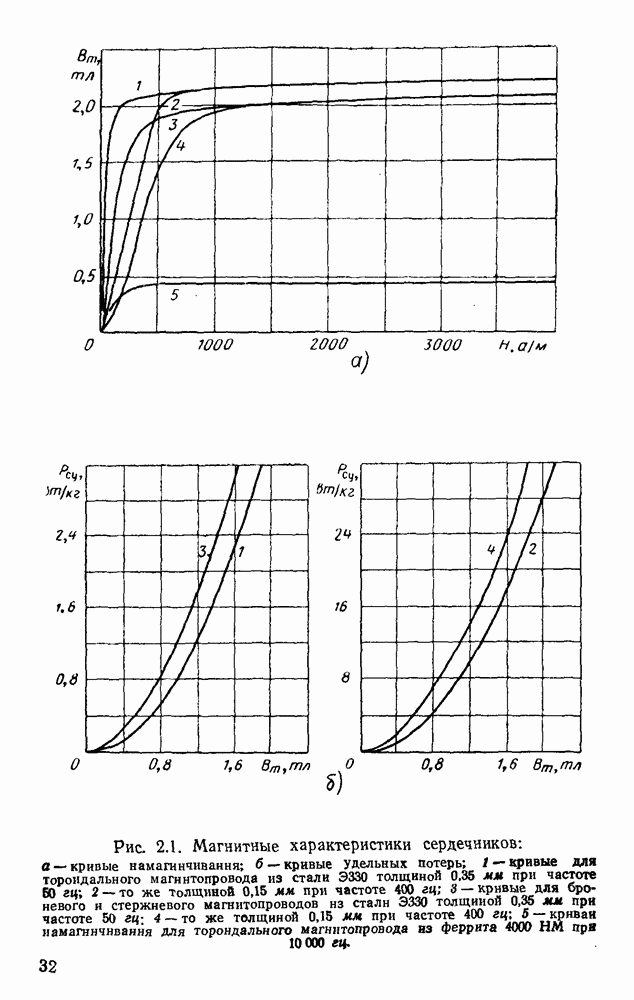
- 2.1. Свойства магнитопроводов дросселей
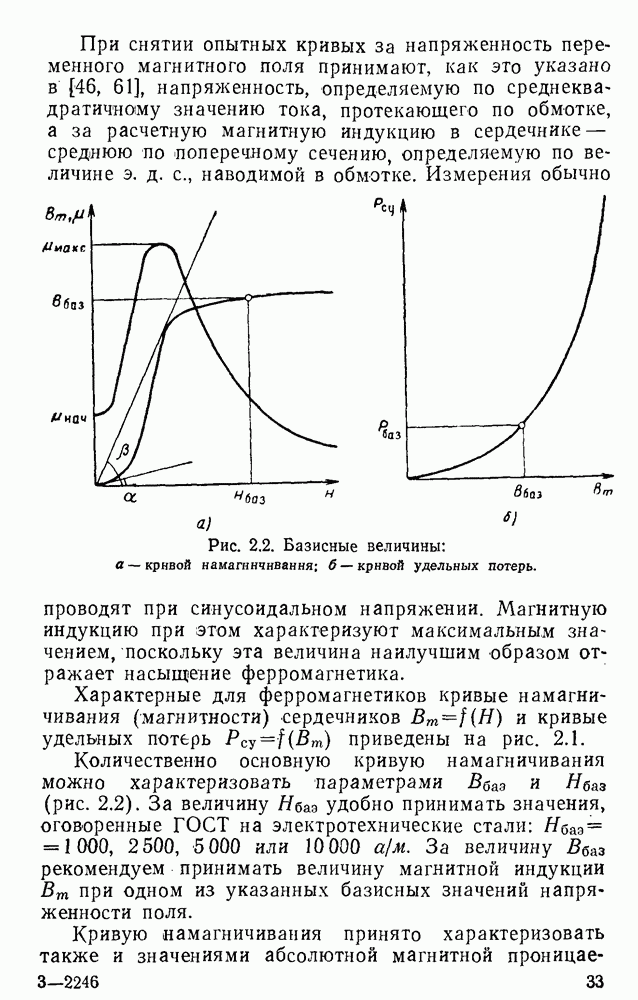
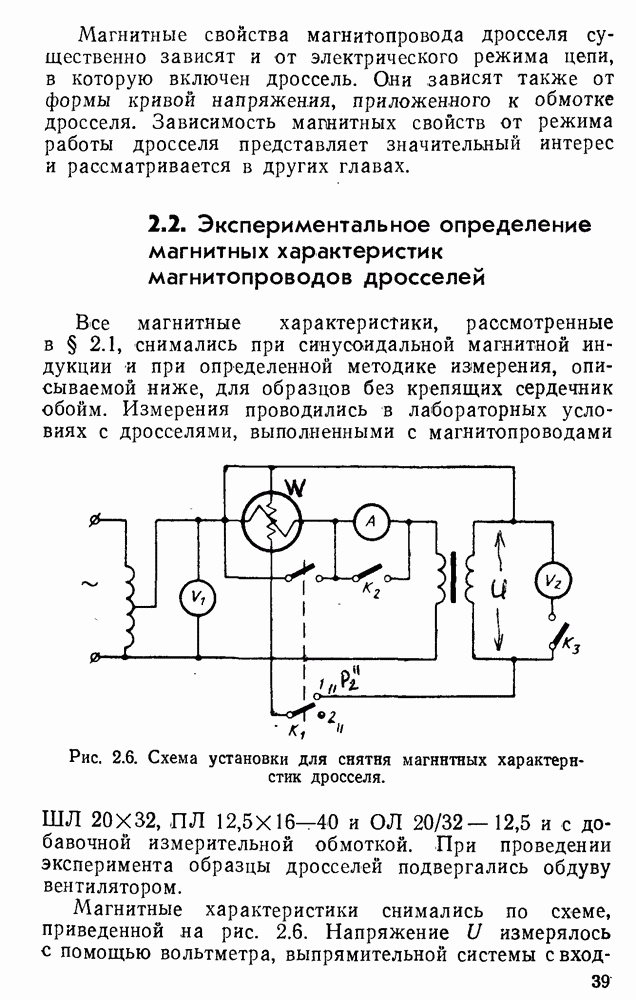
- 2.2. Экспериментальное определение магнитных характеристик магнитопроводов дросселей
- 2.3. Выбор ферромагнетика для сердечника дросселя
- 3. ТЕОРИЯ РАБОТЫ ДРОССЕЛЯ ПЕРЕМЕННОГО ТОКА С НЕЛИНЕЙНЫМ ФЕРРОМАГНИТНЫМ СЕРДЕЧНИКОМ
- 3.2. Связи между электрическими и магнитными величинами в дросселе с нелинейным ферромагнитным сердечником. Эквивалентный дроссель
- 1. Идеальный и идеализированный дроссели без зазора
- 2. Идеальный и идеализированный дроссели с немагнитным зазором
- 3. Реальный дроссель
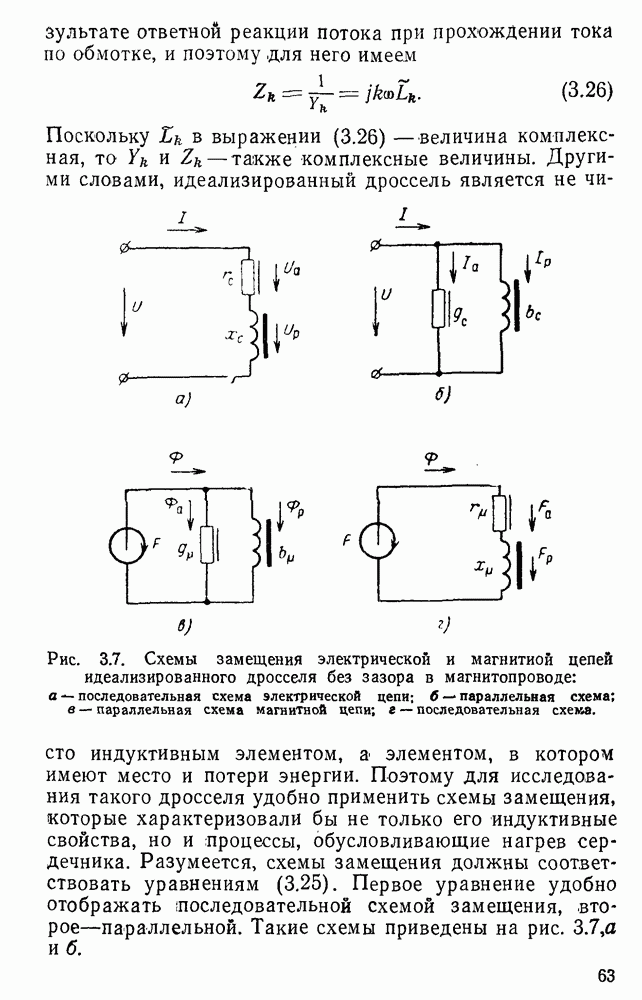
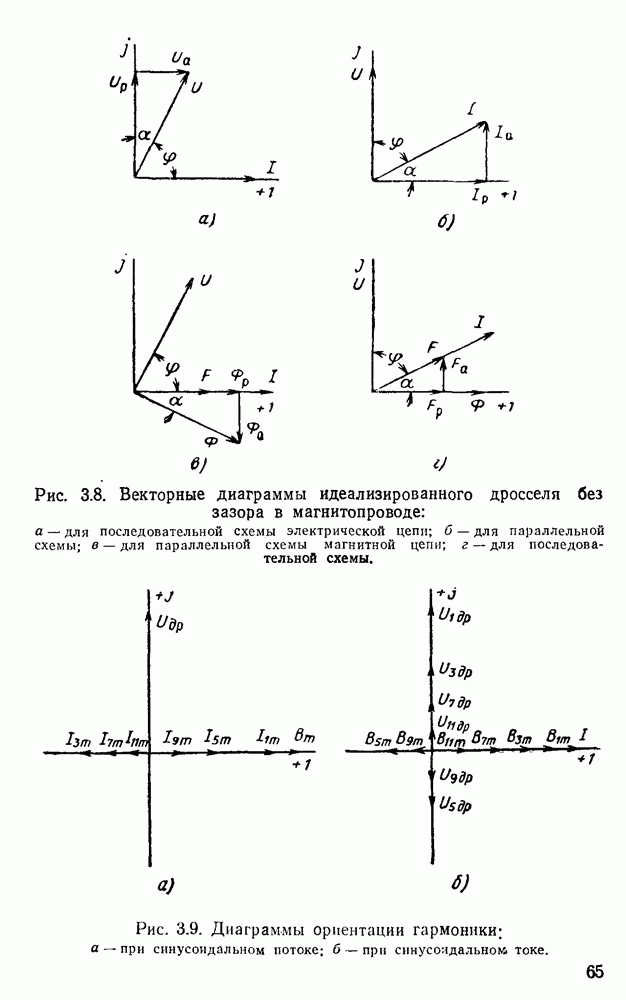
- 3.3. Схемы замещения и векторные диаграммы идеализированного дросселя
- 1. Схемы замещения и векторные диаграммы электрической цепи идеализированного дросселя
- 2. Схемы замещения и векторные диаграммы магнитной цепи идеализированного дросселя
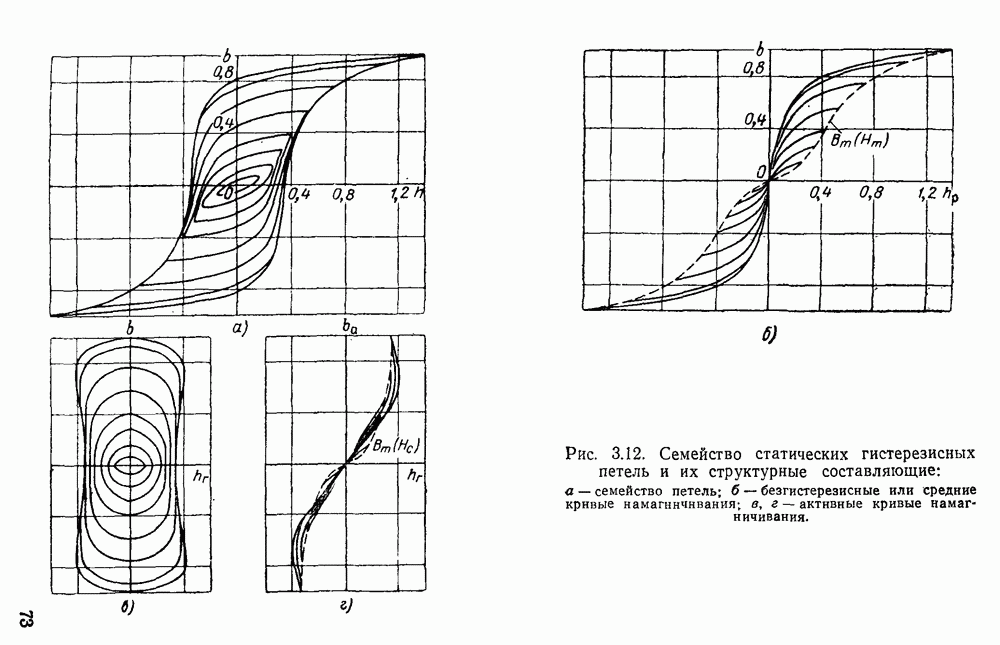
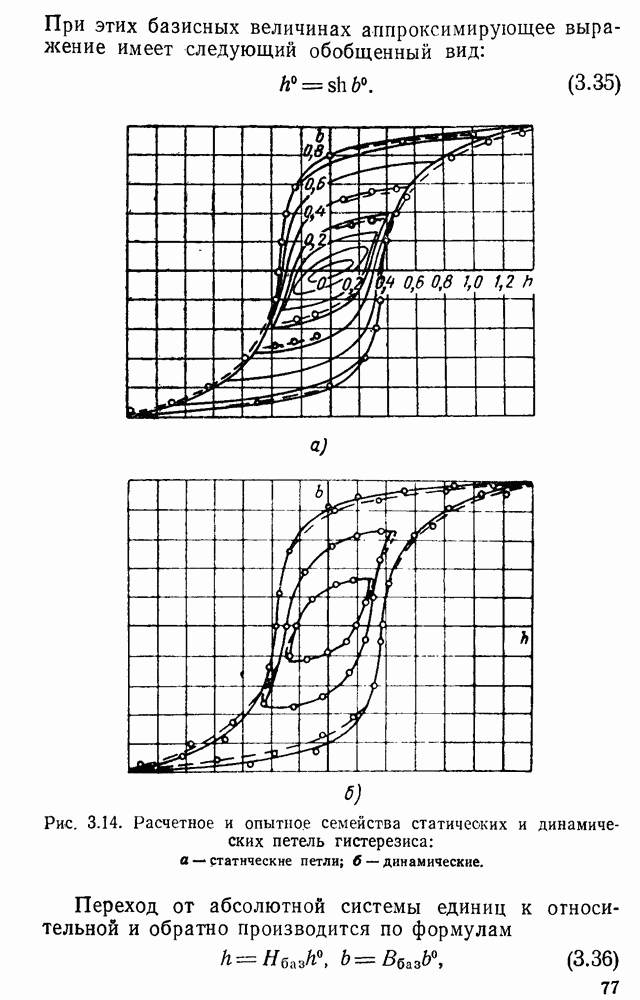
- 3.4. Аппроксимация кривых намагничивания ферромагнитных сердечников. Относительные единицы. Определение коэффициентов аппроксимации
- 3.5. Математическая модель семейства динамических гистерезисных петель. Использование модели для решения задач гармонического анализа
- 1. Определение гармонического состава кривой напряженности поля
- 2. Определение среднеквадратичного значения напряженности поля и потерь в стали
- 3.6. Аналитический расчет магнитных характеристик магнитопроводов идеальных и идеализированных дросселей с зазором
- 3.7. Расчет численными методами магнитных характеристик идеальных и идеализированных дросселей при произвольной форме кривой магнитной индукции
- 3.8. Расчет магнитных характеристик реальных дросселей. Расчет характеристик дросселей, включенных в электрические цепи
- 1. Расчет магнитных характеристик для реального дросселя без рассеяния
- 2. Расчет магнитных характеристик для дросселя, включенного последовательно с активно-индуктивной нагрузкой
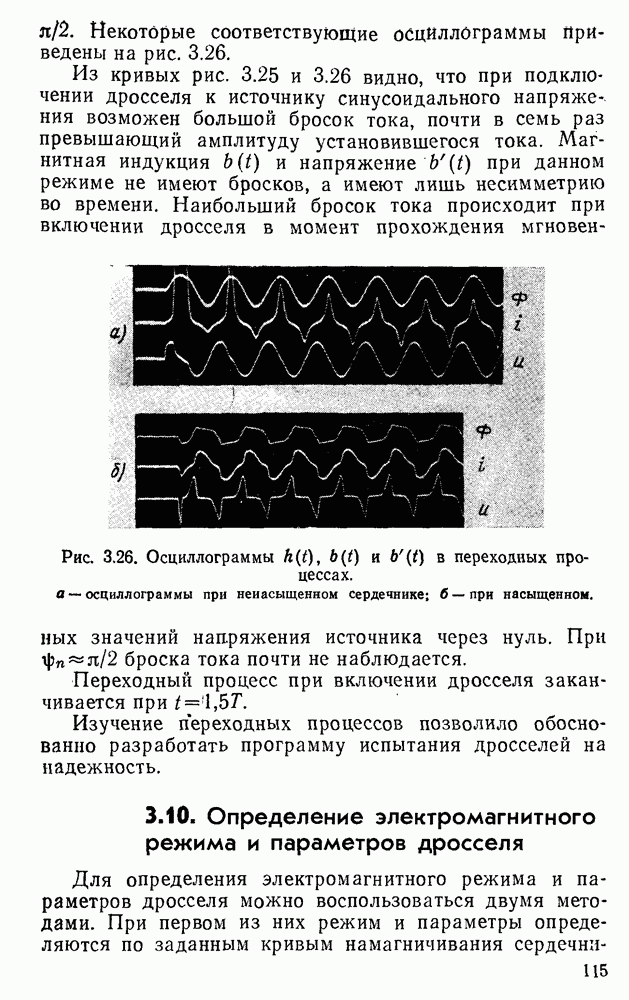
- 3.9. Переходные процессы в дросселе
- 3.10. Определение электромагнитного режима и параметров дросселя
- 2. Определение режима и основных характеристик дросселя по комплексной магнитной проницаемости его сердечника
- 4. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПРОЕКТИРОВАНИЯ ДРОССЕЛЕЙ
- 4.1. Общие замечания. Понятие об оптимальных дросселях и их параметрах
- 4.2. Основные уравнения взаимосвязи параметров дросселя и их решение
- 2. Уравнение потерь
- 3. Уравнение теплового режима дросселя
- 4. Уравнения взаимосвязи магнитных параметров дросселя
- 5. Обобщенные уравнения геометрических параметров разных типов и конструкций дросселей
- 6. Технико-экономические показатели дросселей
- 4.3. Определение с помощью ЭЦВМ оптимальных значений соотношений геометрических параметров дросселя. Оптимальные значения соотношений разных типов дросселей
- 4.4. Определение с помощью ЭЦВМ предельных значений параметров дросселей с заданными магнитопроводами
- 4.5. Влияние отдельных факторов на оптимальные значения геометрических соотношений дросселя
- 5. ПРОЕКТИРОВАНИЕ ДРОССЕЛЕЙ
- 5.1. Основные замечания. Техническое задание на проектирование дросселя
- 5.2. Методика проектирования дросселей
- 1. Выбор типа дросселя, марки стали и обмоточного материала
- 2. Выбор типоразмера стандартного сердечника или расчет специального сердечника
- 3. Выбор магнитного режима магнитопровода дросселя
- 4. Расчет длины немагнитного зазора
- 5. Расчет потерь в дросселе
- 6. Определение геометрических параметров дросселя
- 7. Расчет теплового режима дросселя
- 8. Расчет обмоточных данных и междуслойной изоляции
- 9. Расчет катушек дросселя (конструирование обмоток)
- 10. Определение технико-экономических показателей дросселя
- 11. Проверочный расчет дросселя
- 12. Краткая методика расчета дросселя
- 5.3. Примеры проектирования дросселей
- ПРИЛОЖЕНИЯ
- Основные условные обозначения
- Литература