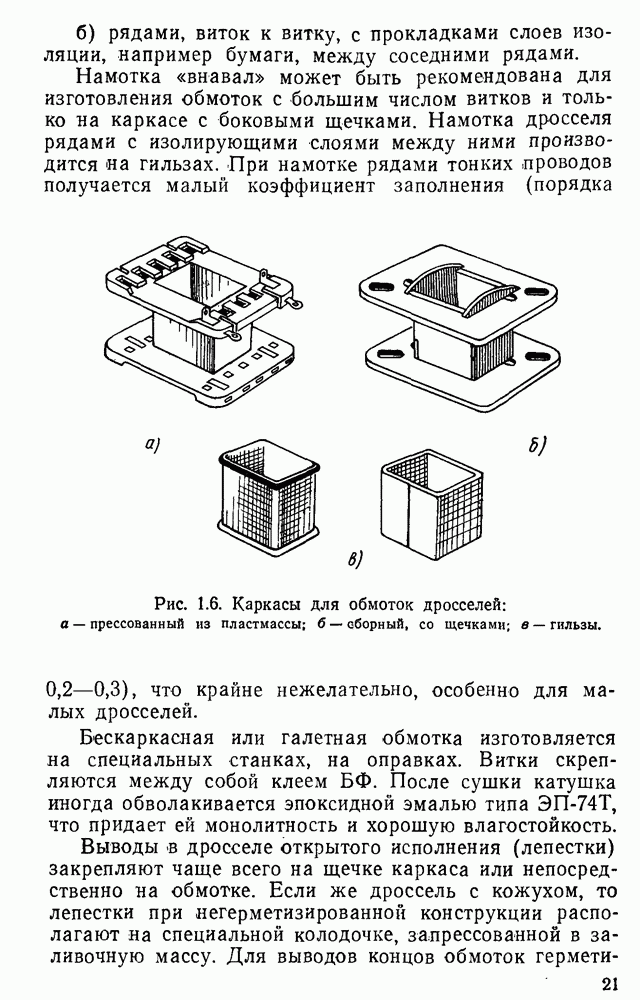
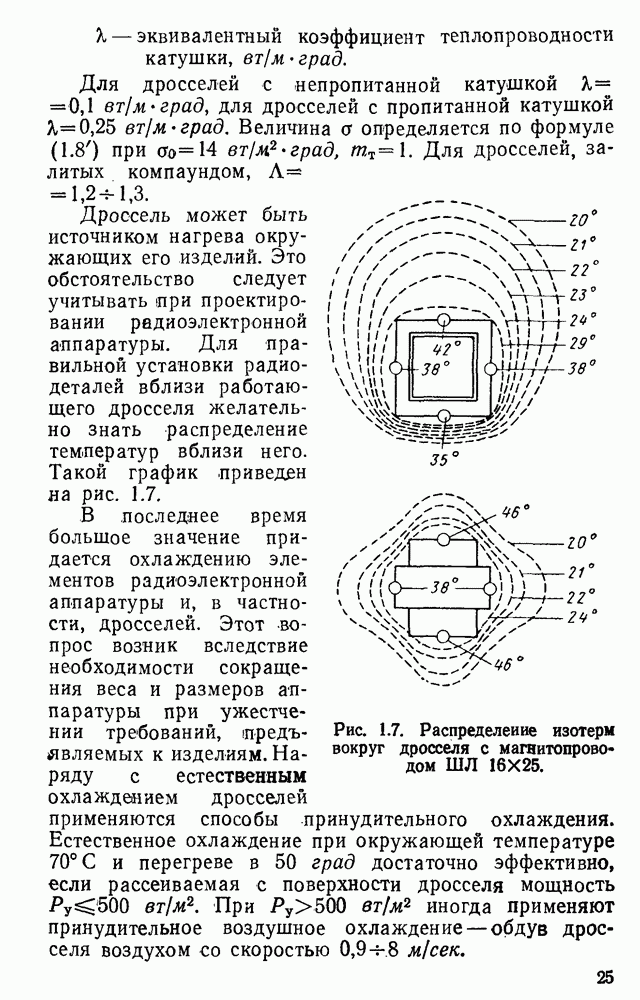
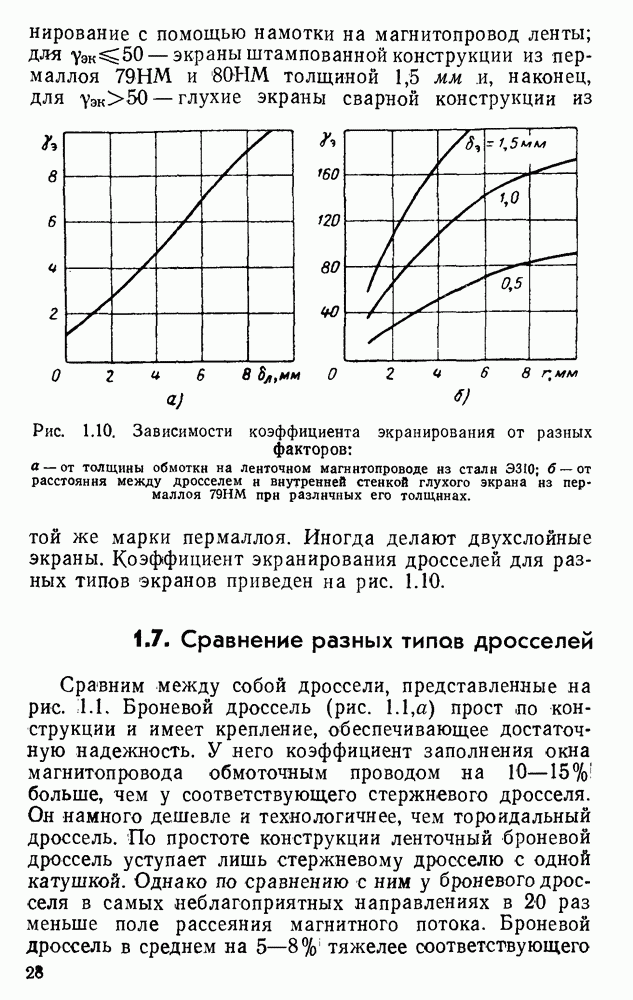
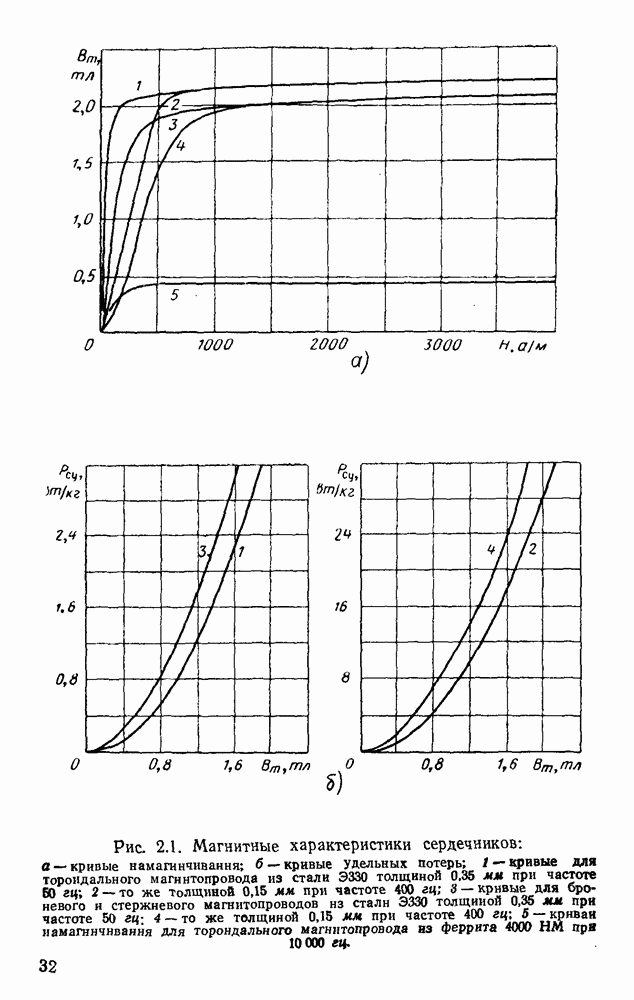
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПРОЕКТИРОВАНИЯ ДРОССЕЛЕЙ
4.1. Общие замечания. Понятие об оптимальных дросселях и их параметрах
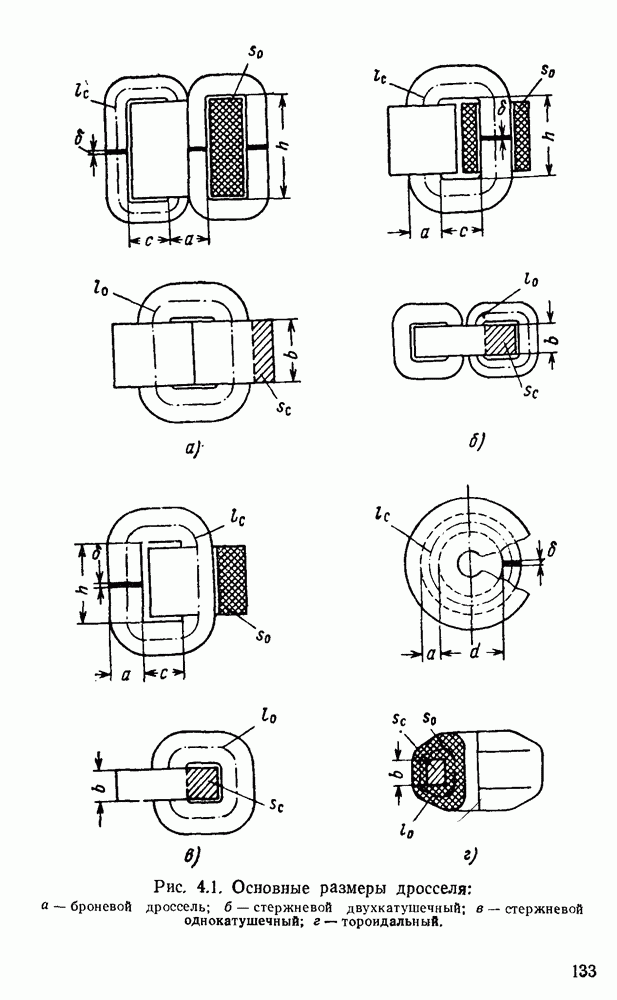
Следует различать Два пути проектирования дросселя: при первом нужно подобрать для дросселя, исходя из его заданных номинальных параметров, стандартный сердечник или определить все размеры нового магнито-провода; при втором — определить значения номинальных параметров дросселя при заданных размерах сердечника, в частности стандартного. Задачу, решаемую в первом случае, будем называть «прямой задачей», во втором — «обратной задачей». Обе задачи имеют много решений. При одних из них технико-экономические показатели спроектированного дросселя относительно лучше, при других — хуже. Обычно нужно проводить отыскание расчетного варианта с наилучшим показателем, т. е. с наименьшим значением технико-экономического параметра — веса, стоимости и т. д. Такой поиск именуют оптимизацией дросселя, а дроссели с наилучшими показателями называют оптимальными. Опыт и анализ показали, что оптимальные дроссели имеют определенные значения для соотношений величин отдельных параметров. Такие значения соотношений также будем называть оптимальными.
Для быстрого решения прямой задачи, в частности для определения размеров нового сердечника, весьма важно заранее знать оптимальные значения соотношений  , так как это сокращает число вариантов расчета. Эти соотношения рассмотрены в § 4.2.
, так как это сокращает число вариантов расчета. Эти соотношения рассмотрены в § 4.2.
Для быстрого решения обратной задачи расчетчику необходимы данные о предельных значениях параметров дросселя, возможных при конкретных сердечниках, в частности стандартных. Оптимальные величины соотношений и нужные для обратной задачи предельные значения параметров легче всего могут быть определены с помощью электронных цифровых вычислительных машин (ЭЦВМ).
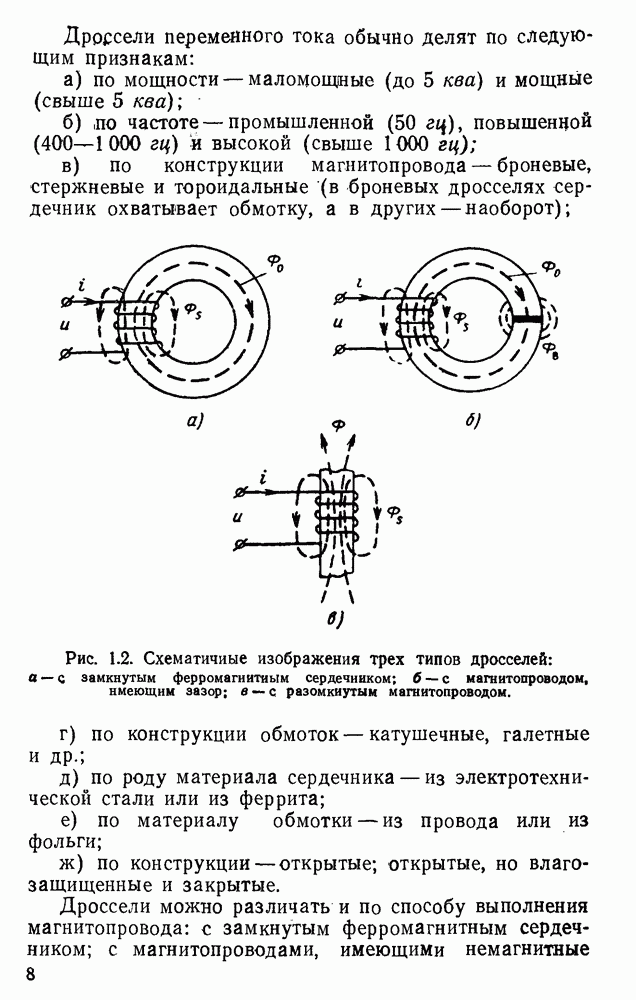
Разъясним некоторые положения, которыми будем пользоваться в дальнейшем. Иногда следует отличать термин «сердечник» от термина «магнитол ровод». В дальнейшем под термином «сердечник» будем понимать только ферромагнитный элемент дросселя, а под термином «магнитопровод» — этот элемент вместе с немагнитным зазором, т. е. всю основную магнитную цепь дросселя. Типовыми условиями работы дросселя следует считать перегрев  , температуру окружающей среды
, температуру окружающей среды  . В этой главе всегда рассматривается дроссель с пропитанной обмоткой, не имеющий специальных теплоотводящих элементов.
. В этой главе всегда рассматривается дроссель с пропитанной обмоткой, не имеющий специальных теплоотводящих элементов.
Определение оптимальных соотношений и предельных значений параметров дросселя основано на решении основных и частных уравнений дросселя, отражающих с учетом нелинейности его ферромагнитного сердечника важнейшие соотношения между его различными геометрическими и электромагнитными параметрами. Исходные уравнения приведены в § 4.2.
Анализ по весу и объему приводится нами только для ленточных броневых дросселей, а материалы, относящиеся к геометрии оптимальных дросселей, — для дросселей всех типов. За недостатком места анализ по стоимости не публикуется.
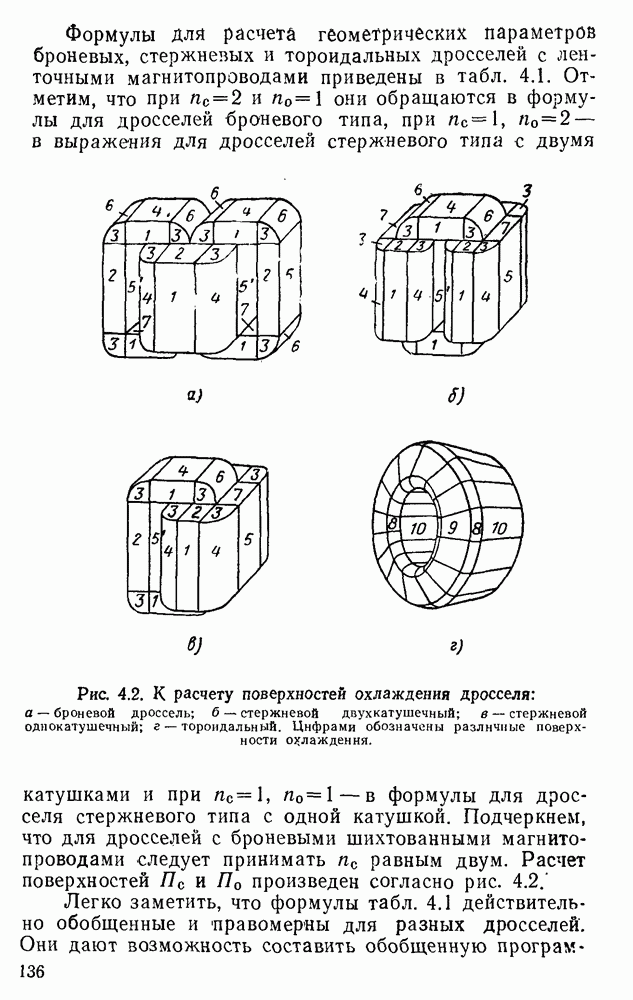
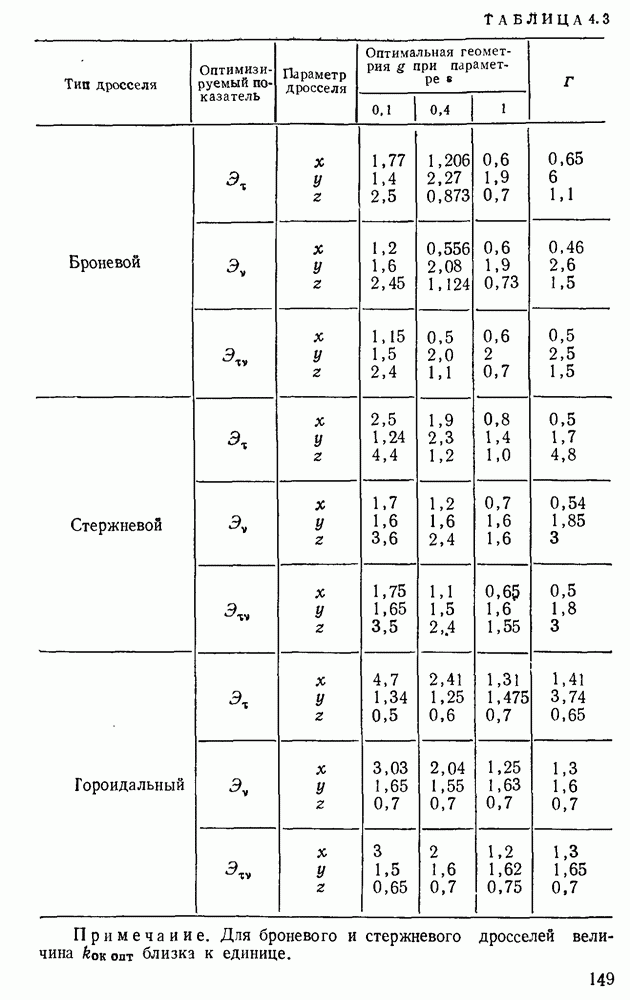
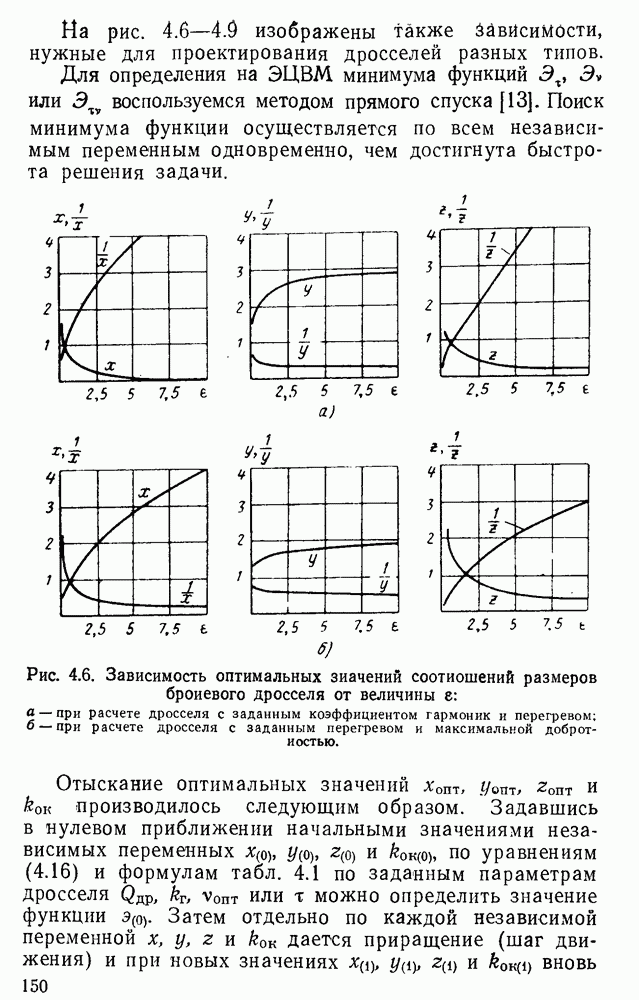
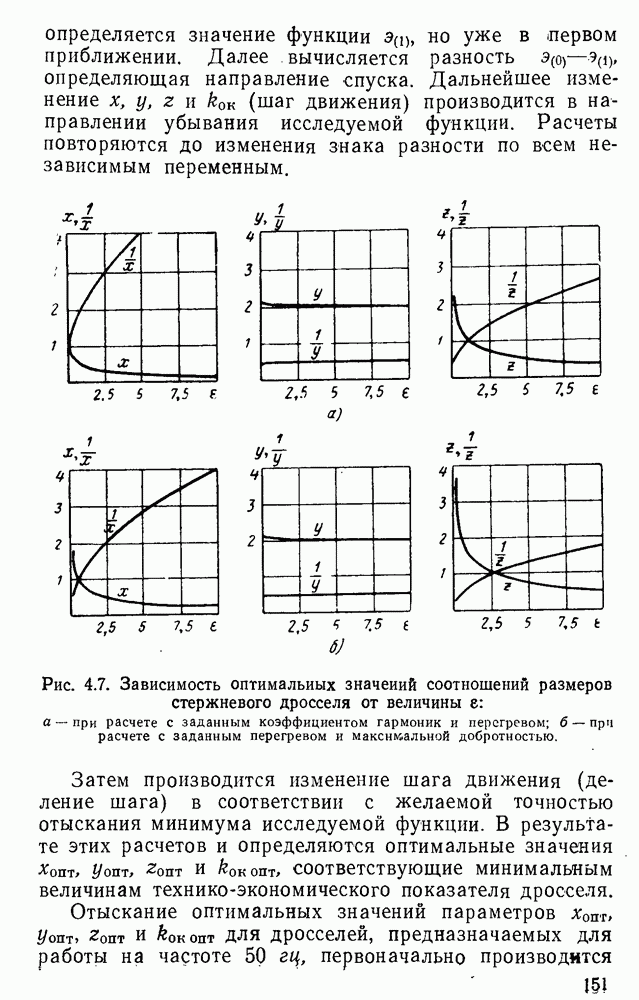
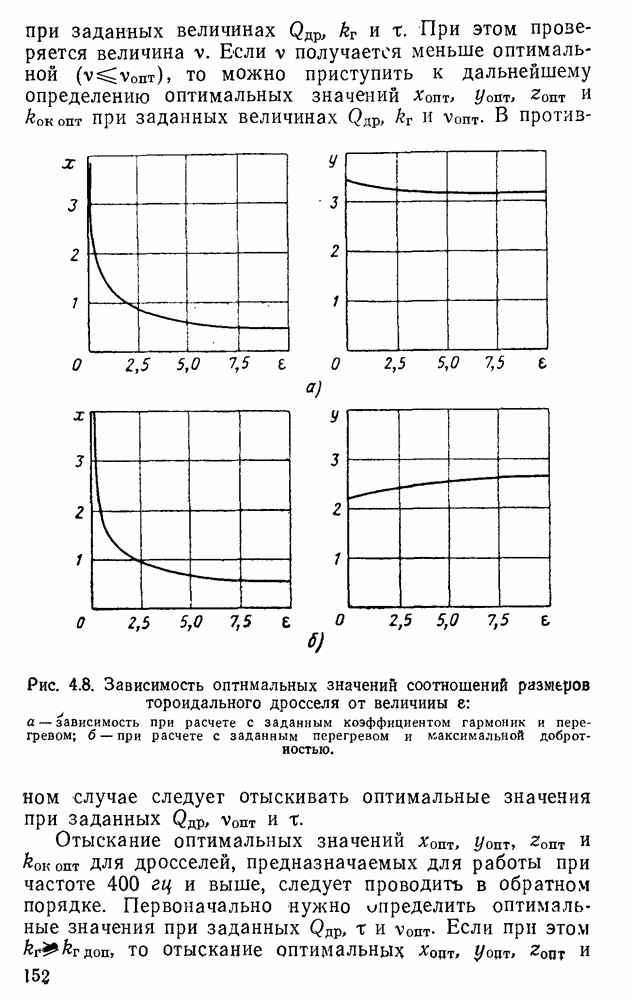
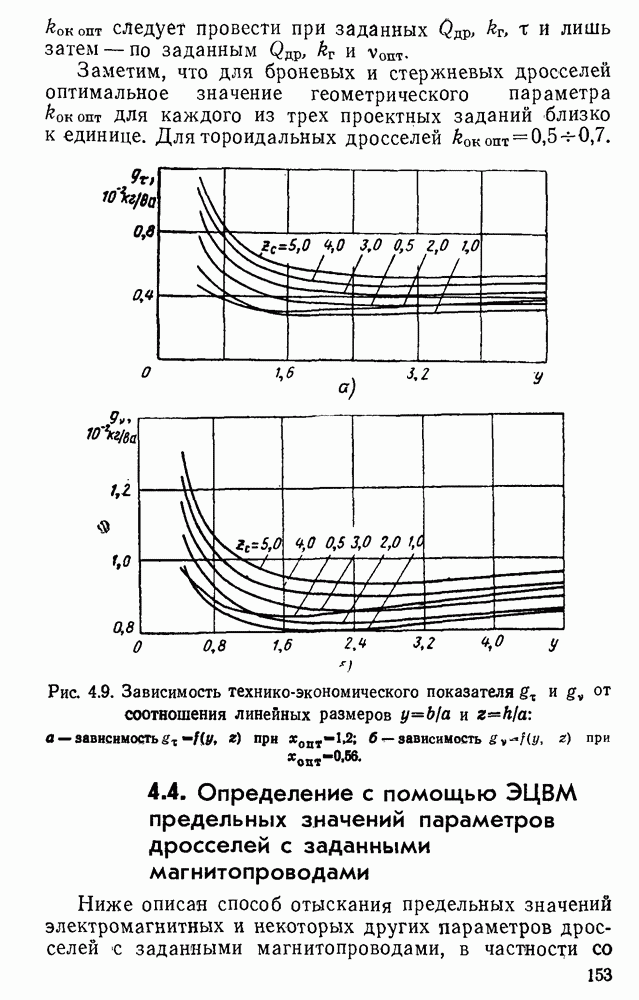
Оптимальные значения соотношений и предельные значения параметров различны для дросселей разных типов. Однако несмотря на то, что дроссели разных типов резко отличаются друг от друга, можно получить обобщенные уравнения геометрических соотношений, правомерные для любых броневых или стержневых дросселей с ленточными сердечниками, и отдельно — для тороидальных ленточных дросселей. Полученные уравнения будут полностью правомерны для тороидальных дросселей с шихтованными сердечниками и с погрешностью. не превышающей 5%, для броневых и стержневых дросселей с шихтованными сердечниками.
Для получения обобщенных уравнений можно использовать некоторые коэффициенты, полностью характеризующие всю конструкцию дросселя, а именно коэффициенты  соответствующие числу отдельных элементарных сердечников и отдельных обмоток проектируемого дросселя, коэффициент
соответствующие числу отдельных элементарных сердечников и отдельных обмоток проектируемого дросселя, коэффициент  равный относительной величине зазора в магнитопроводе, и коэффициент заполнения окна обмоткой
равный относительной величине зазора в магнитопроводе, и коэффициент заполнения окна обмоткой  Для броневого дросселя, имеющего два отдельных сердечника и одну обмотку,
Для броневого дросселя, имеющего два отдельных сердечника и одну обмотку,  для стержневого дросселя
для стержневого дросселя  или
или  ; для тороидального дросселя
; для тороидального дросселя  . Очевидно при
. Очевидно при  уравнения относятся к дросселю с магнитопроводами без зазора, при
уравнения относятся к дросселю с магнитопроводами без зазора, при  — к дросселю с простой сопряженностью сердечника с обмоткой.
— к дросселю с простой сопряженностью сердечника с обмоткой.
Оптимальные значения соотношений и предельные параметры различны и для дросселей одного и того же типа, но рассчитываемых для соответствия разным техническим данным.
Не имея, естественно, возможности привести в этой книге все сведения об оптимальных значениях соотношений и предельных значений параметров, приводим в этой главе лишь данные для дросселей, соответствующих только трем разъясненным ниже вариантам технических заданий. В них задана мощность и частота дросселя.
Выбор в качестве исходного параметра для дальнейших расчетов и исследований, именно мощности, а не номинального тока и индуктивности, обусловлен тем, что мощность является как бы обобщенным параметром, не вызывающим непосредственной необходимости во введении в расчетные уравнения чисел витков, сечений провода и т. д.
Разумеется, в частном случае всегда легко определить мощность, соответствующую току, индуктивности и частоте или, наоборот, при обратной задаче — определить ток и индуктивность, возможные при данном значении мощности.
Перечислим теперь параметры и условия, указываемые в трех отдельных вариантах задания:
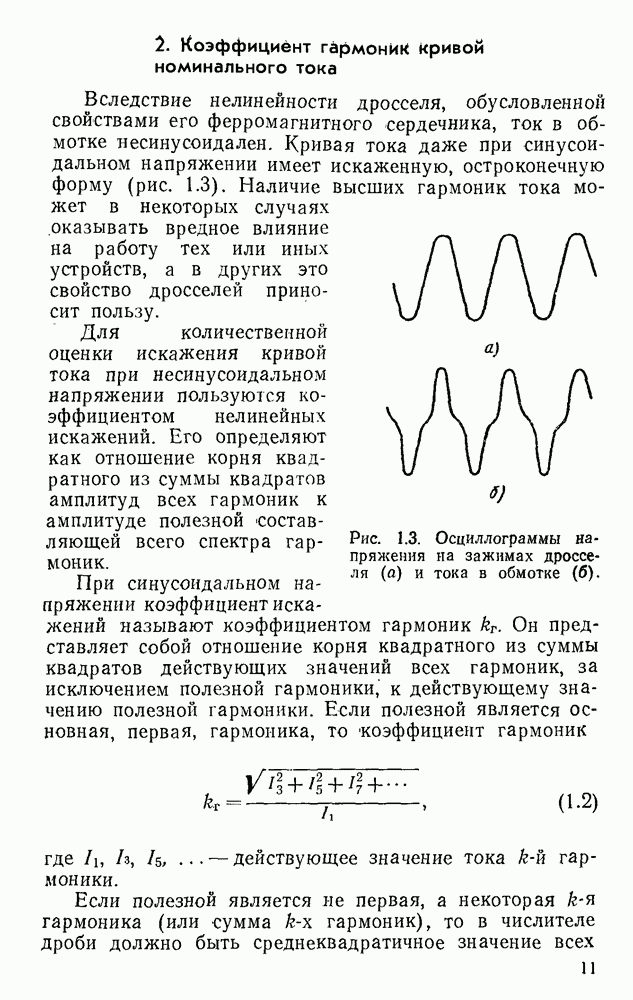
1) предельно допустимые величины коэффициента гармоник тока дросселя и перегрева;
2) предельно допустимая величина коэффициента гармоник и требование максимальной добротности;
3) предельная допустимая величина перегрева и требование оптимальности величины  .
.
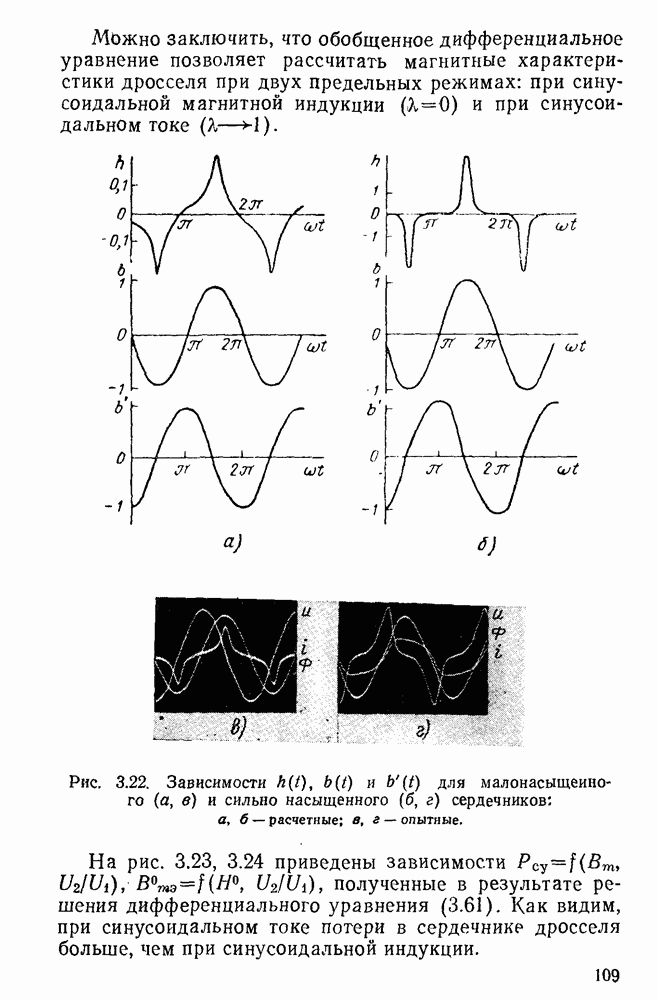
Заметим, что первый и второй варианты задания наиболее часто встречаются при проектировании дросселей малой мощности (до  ), предназначаемых для работы при частоте 50 гц; третий вариант — при проектировании дроссёлей большой мощности, предназначаемых для работы при частоте 50 гц, и преимущественно для всех дросселей, предназначенных для работы при частоте, равной или превышающей 400 гц. Выполнение условия получения максимальной добротности особенно существенно при проектировании дросселей с большими потерями в сердечнике, например при плохом качестве ферромагнетика, при повышенных частотах и др.
), предназначаемых для работы при частоте 50 гц; третий вариант — при проектировании дроссёлей большой мощности, предназначаемых для работы при частоте 50 гц, и преимущественно для всех дросселей, предназначенных для работы при частоте, равной или превышающей 400 гц. Выполнение условия получения максимальной добротности особенно существенно при проектировании дросселей с большими потерями в сердечнике, например при плохом качестве ферромагнетика, при повышенных частотах и др.
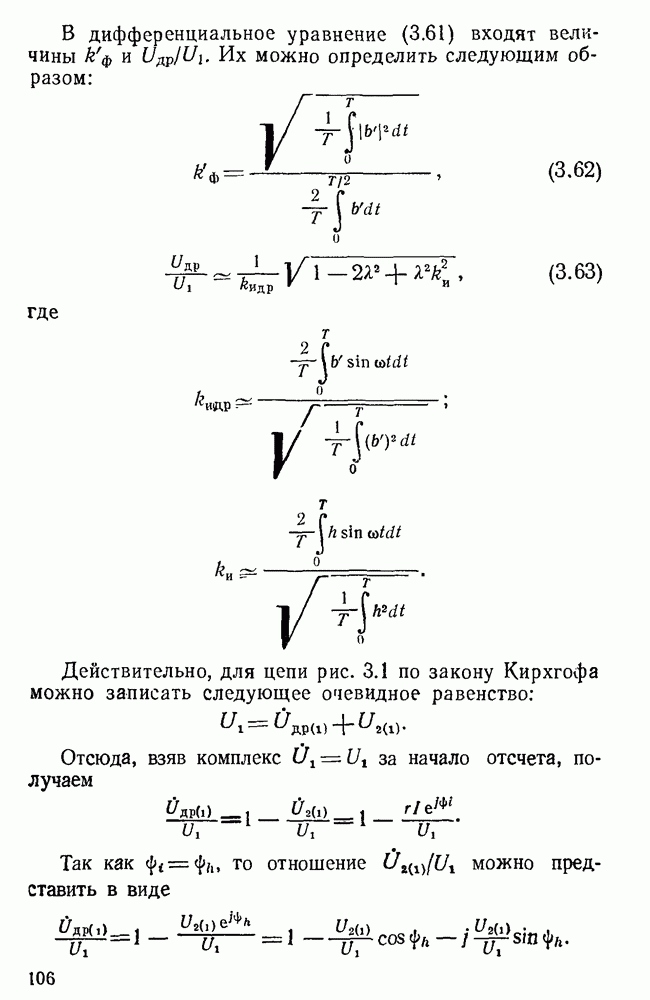
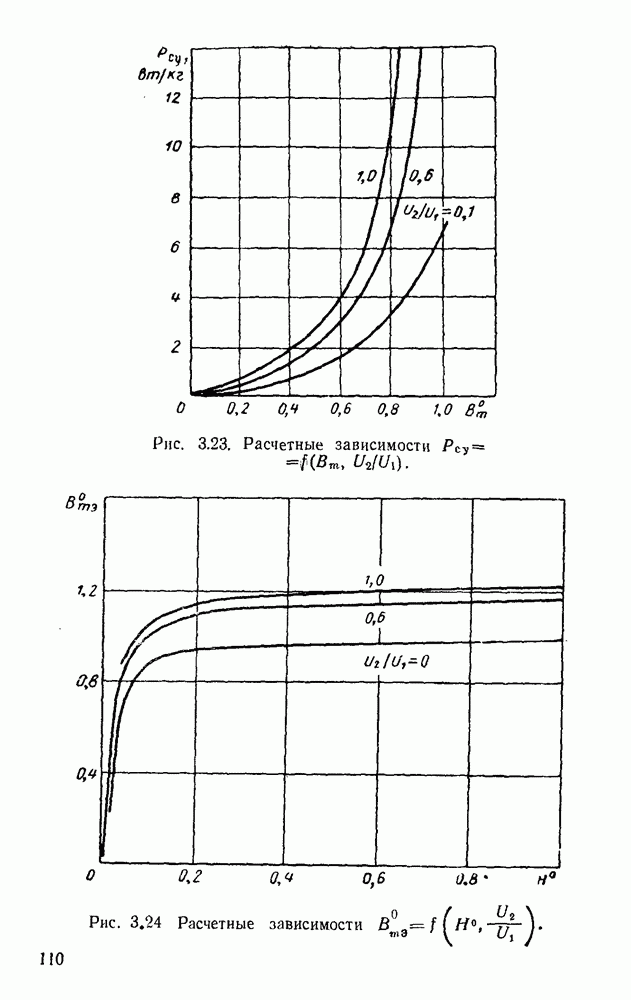
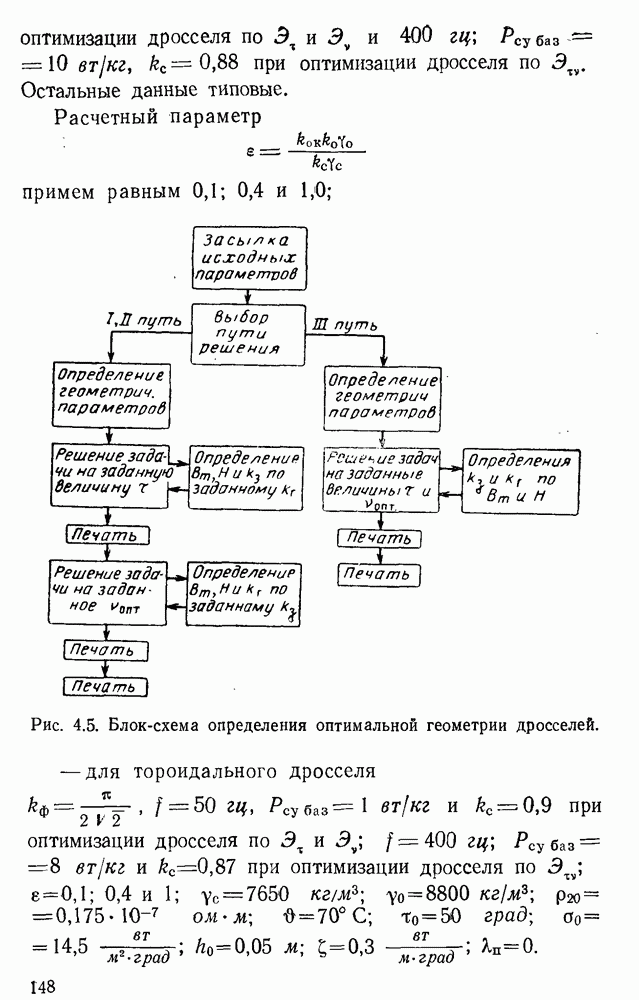
Для отыскания с помощью ЭЦВМ типа  оптимальных значений соотношений и предельных значений параметров у дросселей наименьшего веса или объема нами разработана и использована весьма сложная универсальная программа. Она сложна в основном потому, что решаются частные нелинейные уравнения со многими неизвестными, причем два из уравнений трансцендентны. В отдельных случаях системы уравнений вообще не могут быть решены, так как заданные значения параметров не могут быть получены при данных конкретных свойствах магнитопроводов.
оптимальных значений соотношений и предельных значений параметров у дросселей наименьшего веса или объема нами разработана и использована весьма сложная универсальная программа. Она сложна в основном потому, что решаются частные нелинейные уравнения со многими неизвестными, причем два из уравнений трансцендентны. В отдельных случаях системы уравнений вообще не могут быть решены, так как заданные значения параметров не могут быть получены при данных конкретных свойствах магнитопроводов.
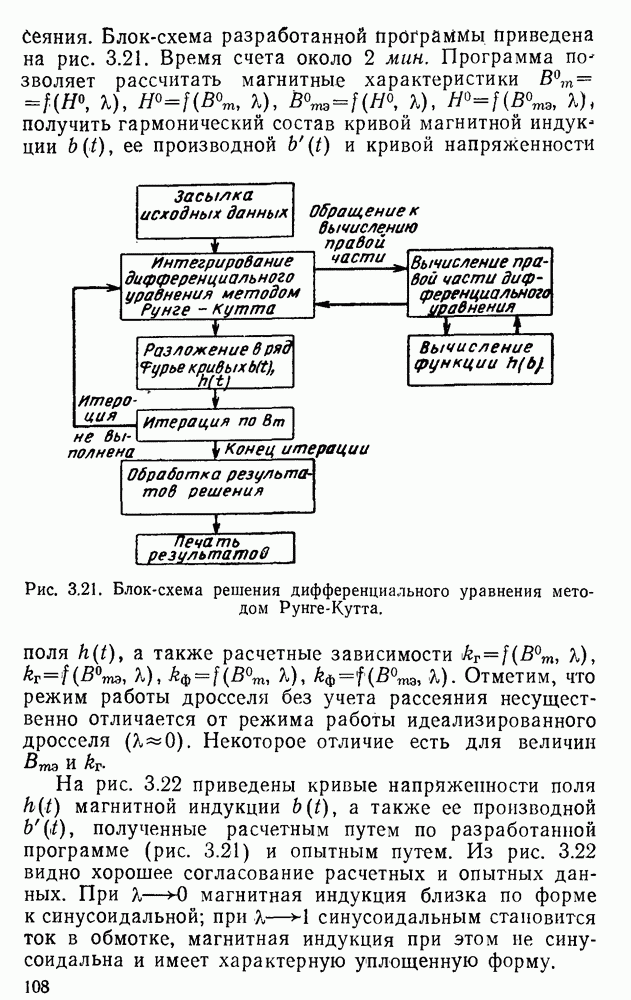
Программа разработана нами с учетом наличия потерь в стали и влияния их на магнитные характеристики и пригодна при любой оговоренной форме кривой магнитной индукции в сердечнике, в частности при синусоидальной. Основное допущение, сделанное при разработке с программы, заключается в том, что принято равенство индукции по всему поперечному сечению сердечника. Программа позволяет находить решения, правильно отражающие работу дросселя как в качестве отдельного изделия, так и в качестве элемента какой-либо конкретной схемы. Блок-схема программы приведена в § 4.3.
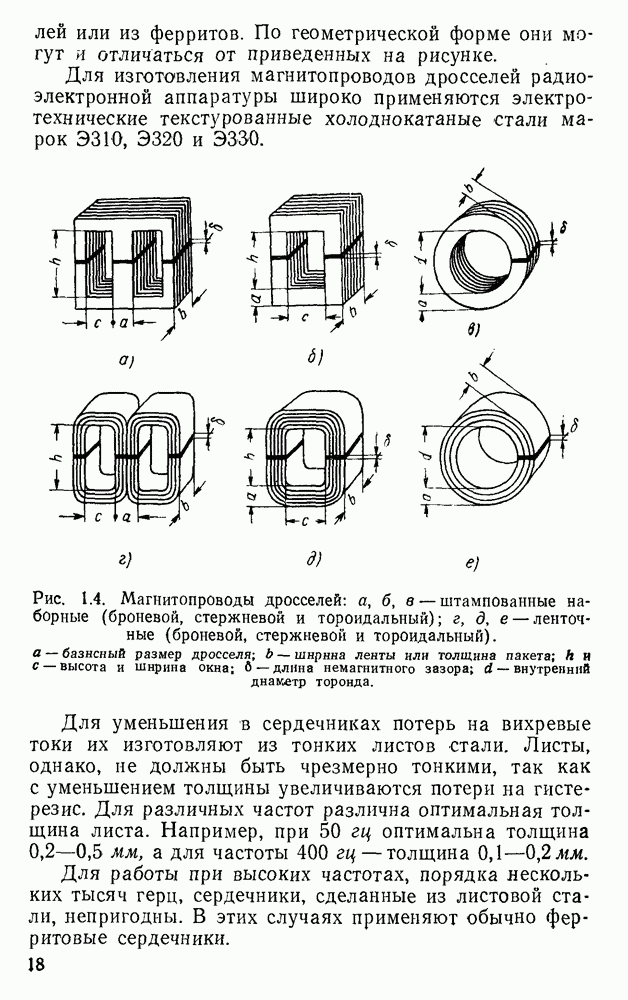
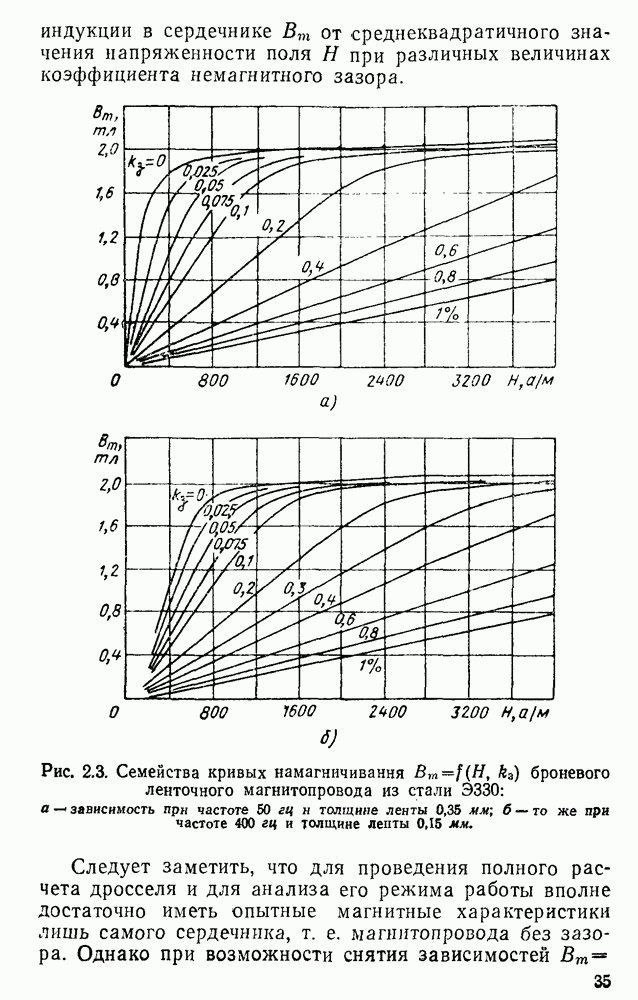
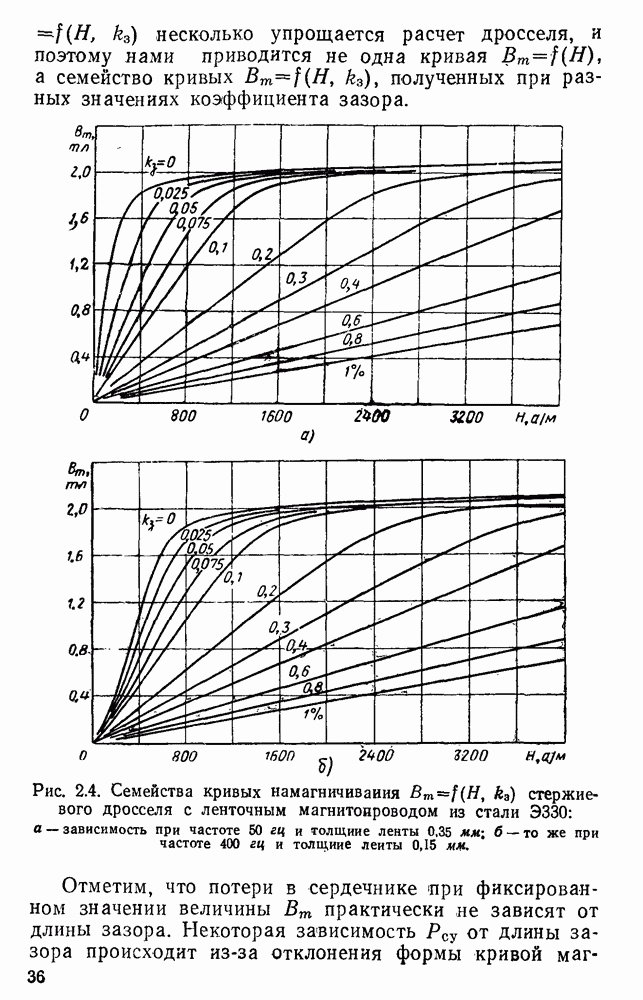
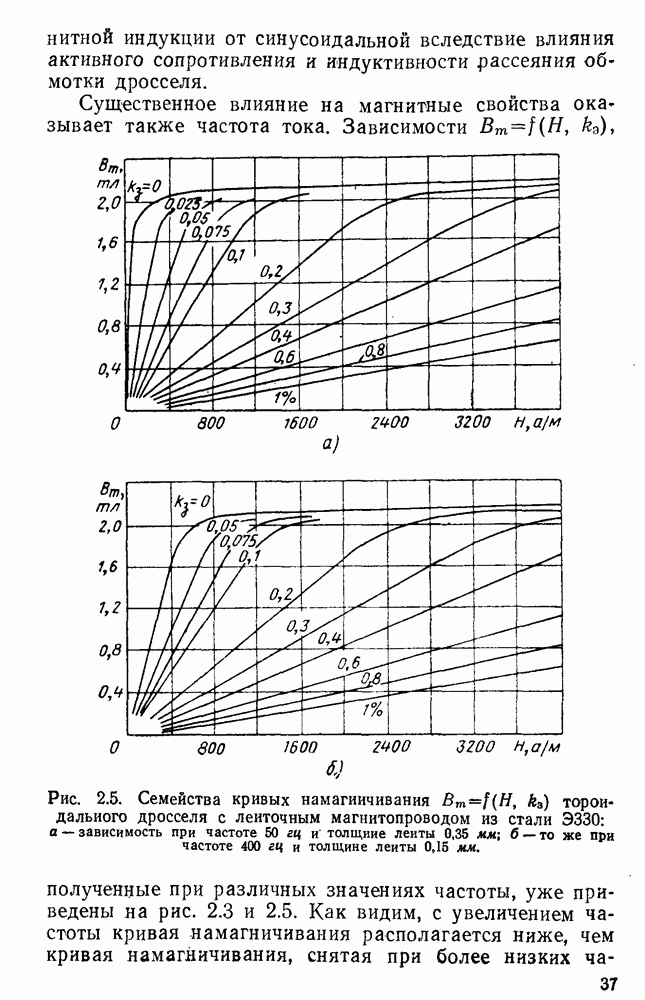
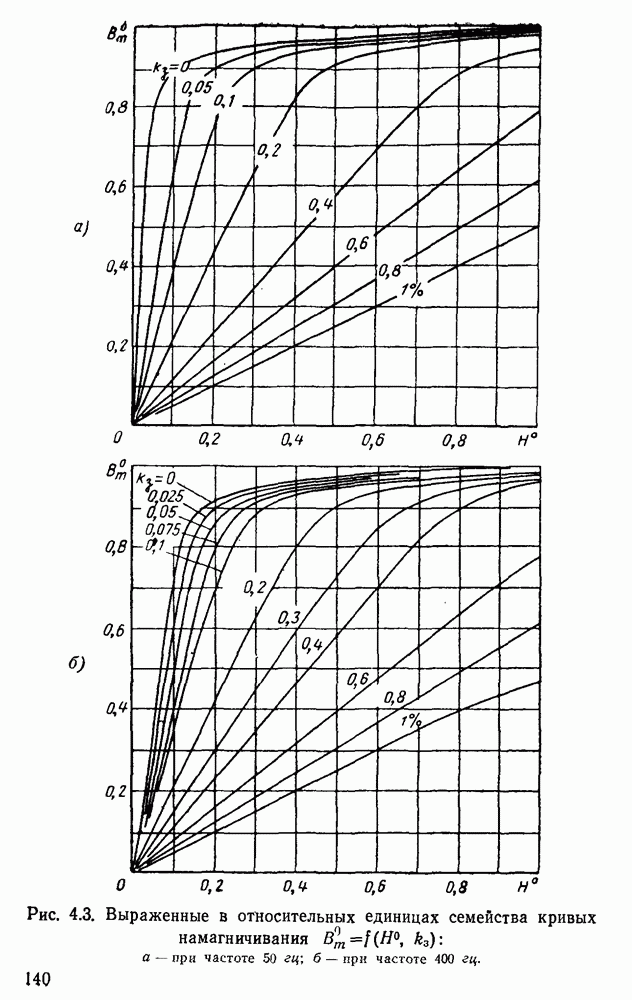
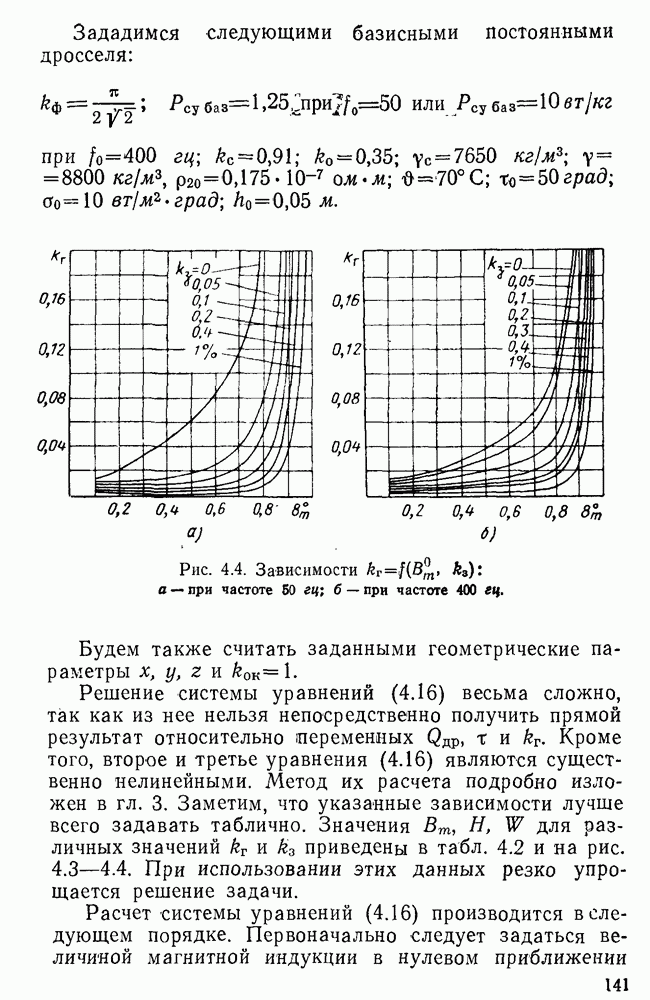
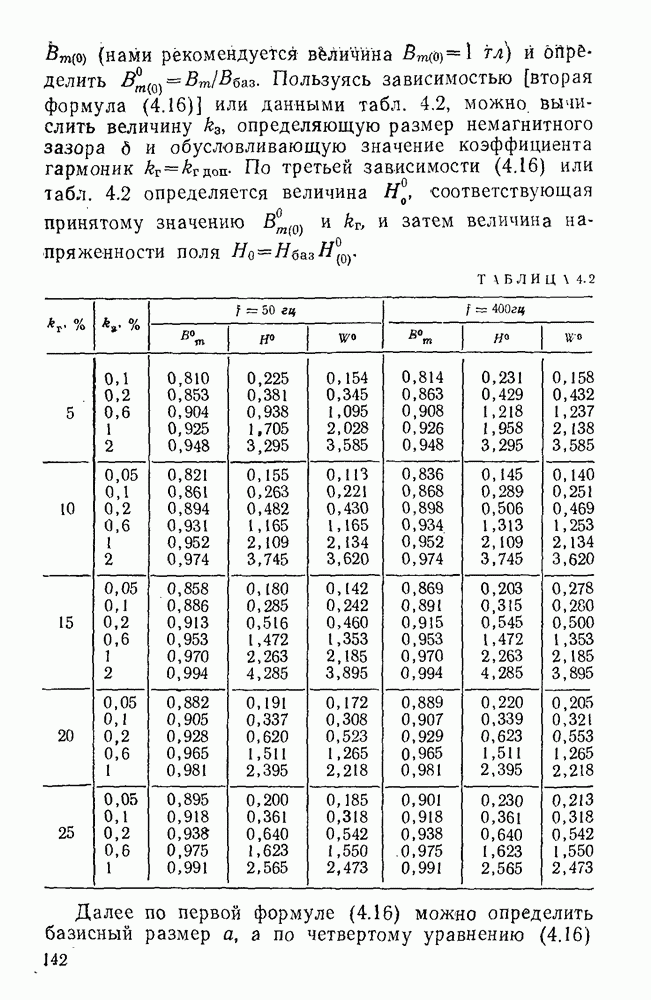
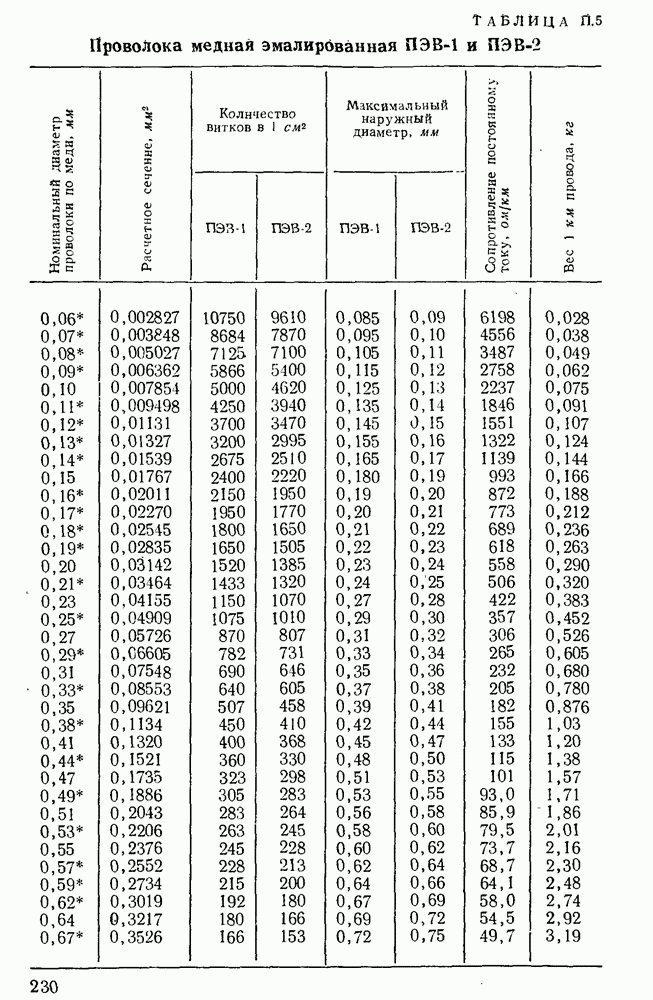
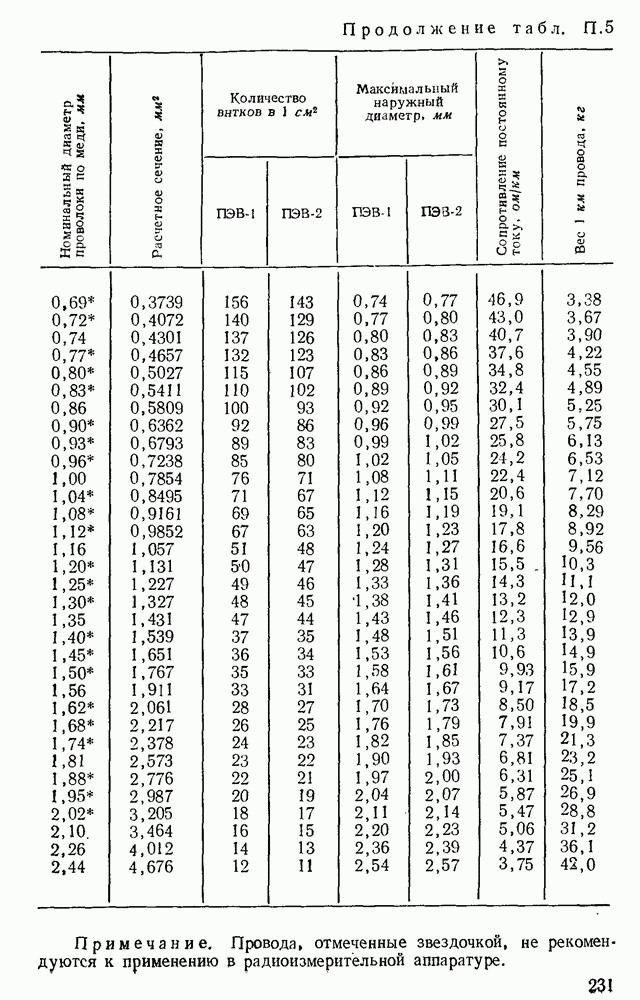
Оптимальные значения соотношений и предельные параметры определены Для дросселей, предназначаемых для работы при частоте 50 или 400 гц и имеющих ленточные сердечники из стали  и обмотку из круглого медного провода. Для дросселей, предназначаемых для работы при частоте 50 гц, принята сталь толщиной 0,35 мм, при 400 гц — толщиной 0,15 мм.
и обмотку из круглого медного провода. Для дросселей, предназначаемых для работы при частоте 50 гц, принята сталь толщиной 0,35 мм, при 400 гц — толщиной 0,15 мм.
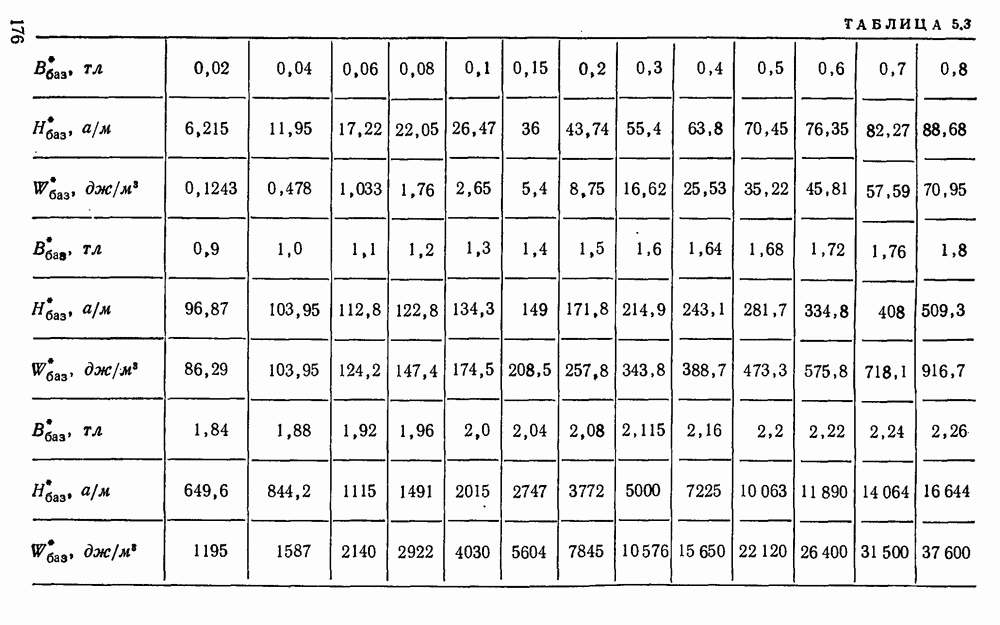
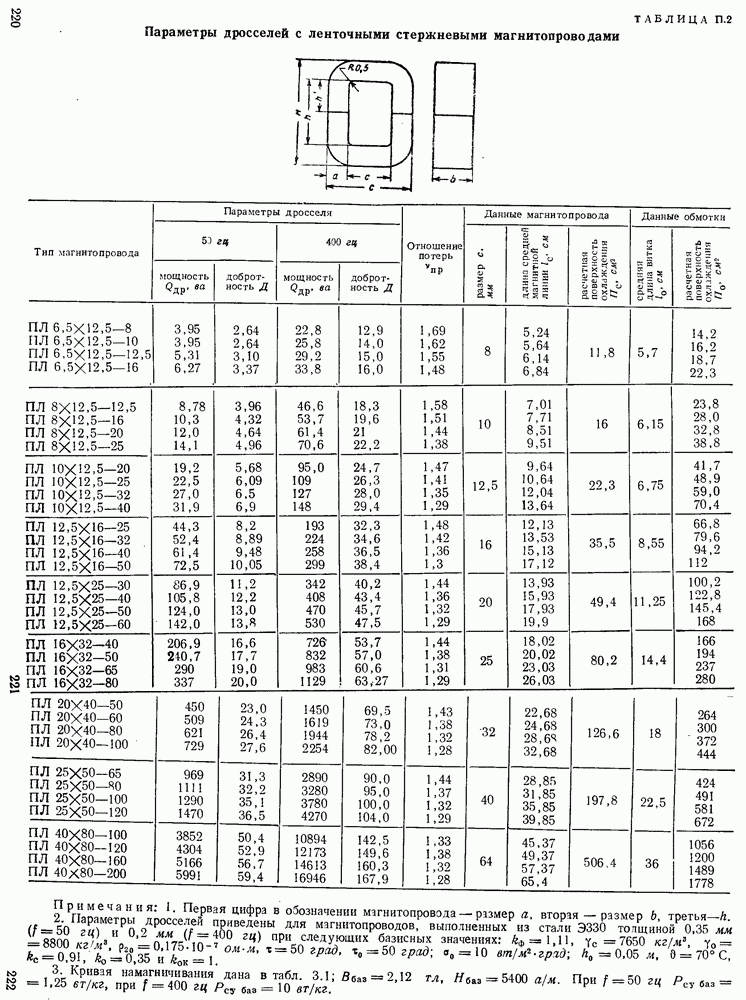
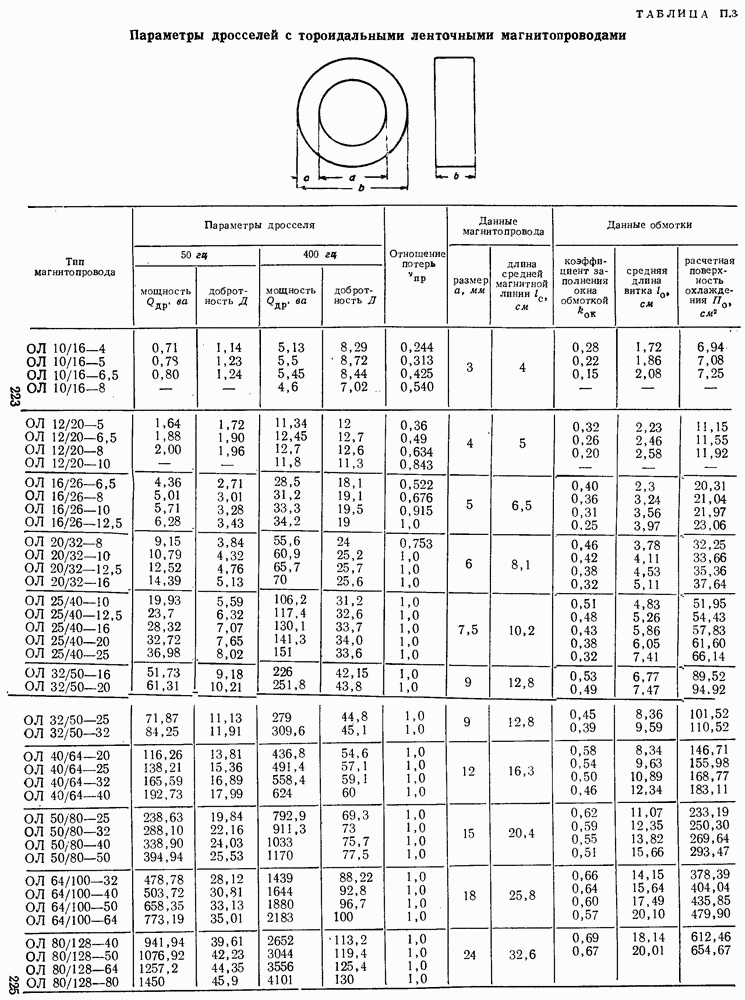
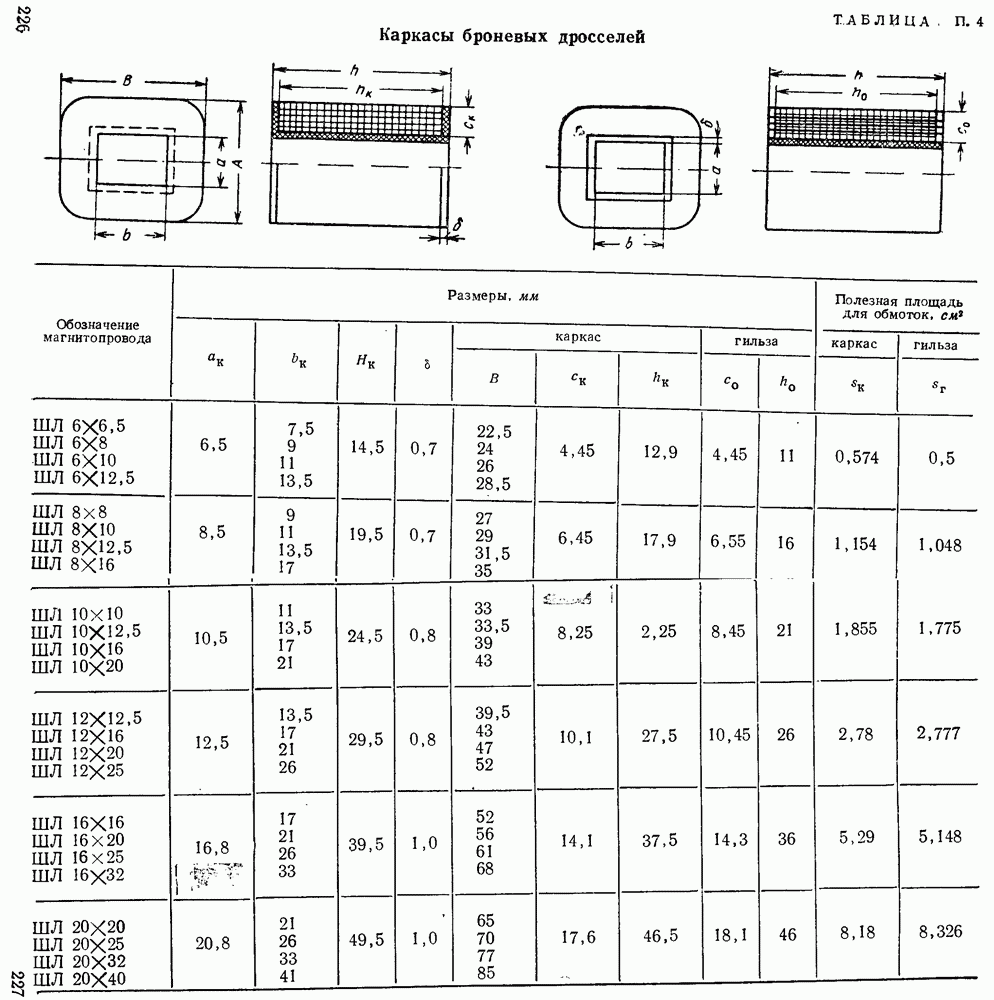
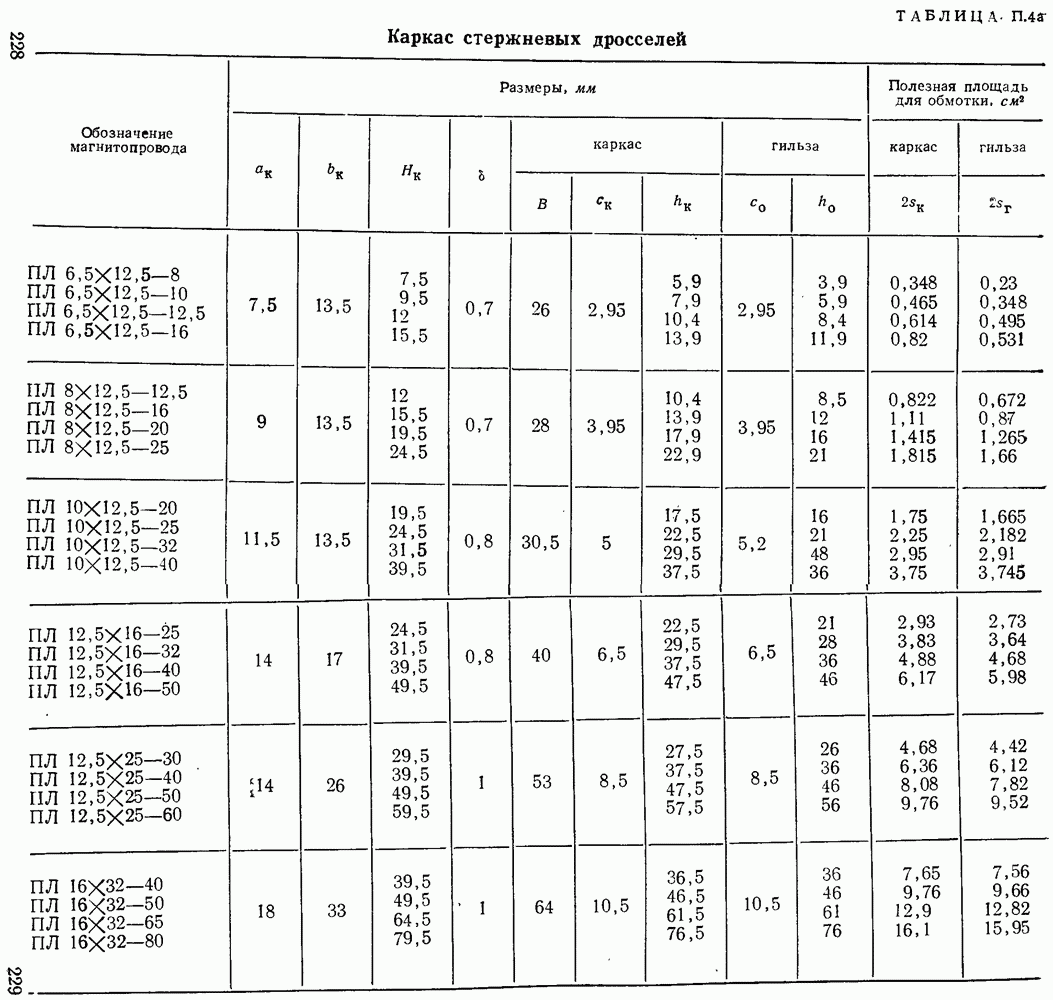
Определенные по разработанной программе с помощью ЭЦВМ оптимальные значения соотношений и предельные параметры дросселей со стандартными сердечниками приведены в табл.  . Полагаем, что конструкторы дросселей будут широко пользоваться сообщаемой полной расчетной информацией о дросселях.
. Полагаем, что конструкторы дросселей будут широко пользоваться сообщаемой полной расчетной информацией о дросселях.
В последующих параграфах этой главы кроме конкретной информации рассматривается решение основных уравнений дросселя, описывается отыскание с помощью ЭЦВМ оптимальных значений соотношений ,и предельных параметров дросселя и рассматривается влияние на них отдельных факторов.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- 1. ОСНОВНЫЕ СВЕДЕНИЯ О НЕУПРАВЛЯЕМЫХ ДРОССЕЛЯХ ПЕРЕМЕННОГО ТОКА РАДИОЭЛЕКТРОННОЙ АППАРАТУРЫ
- 1.1. Общие краткие сведения о дросселях. Классификация дросселей
- 1.2. Номинальные параметры нелинейного дросселя
- 1.3. Требования, предъявляемые к дросселям радиоэлектронной аппаратуры. Степени жесткости
- 1.4. Устройство маломощных дросселей переменного тока
- 1.5. Нагрев и охлаждение дросселей
- 1.6. Экранирование дросселей
- 1.7. Сравнение разных типов дросселей
- 2. МАГНИТНЫЕ СВОЙСТВА МАГНИТОПРОВОДОВ ДРОССЕЛЕЙ. ВЫБОР ФЕРРОМАГНЕТИКА
- 2.1. Свойства магнитопроводов дросселей
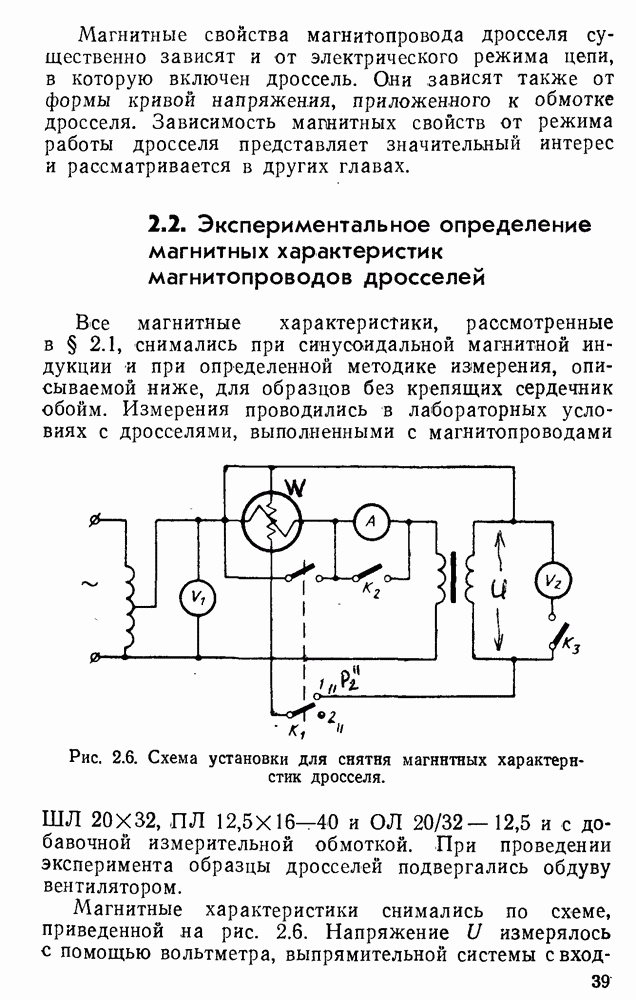
- 2.2. Экспериментальное определение магнитных характеристик магнитопроводов дросселей
- 2.3. Выбор ферромагнетика для сердечника дросселя
- 3. ТЕОРИЯ РАБОТЫ ДРОССЕЛЯ ПЕРЕМЕННОГО ТОКА С НЕЛИНЕЙНЫМ ФЕРРОМАГНИТНЫМ СЕРДЕЧНИКОМ
- 3.2. Связи между электрическими и магнитными величинами в дросселе с нелинейным ферромагнитным сердечником. Эквивалентный дроссель
- 1. Идеальный и идеализированный дроссели без зазора
- 2. Идеальный и идеализированный дроссели с немагнитным зазором
- 3. Реальный дроссель
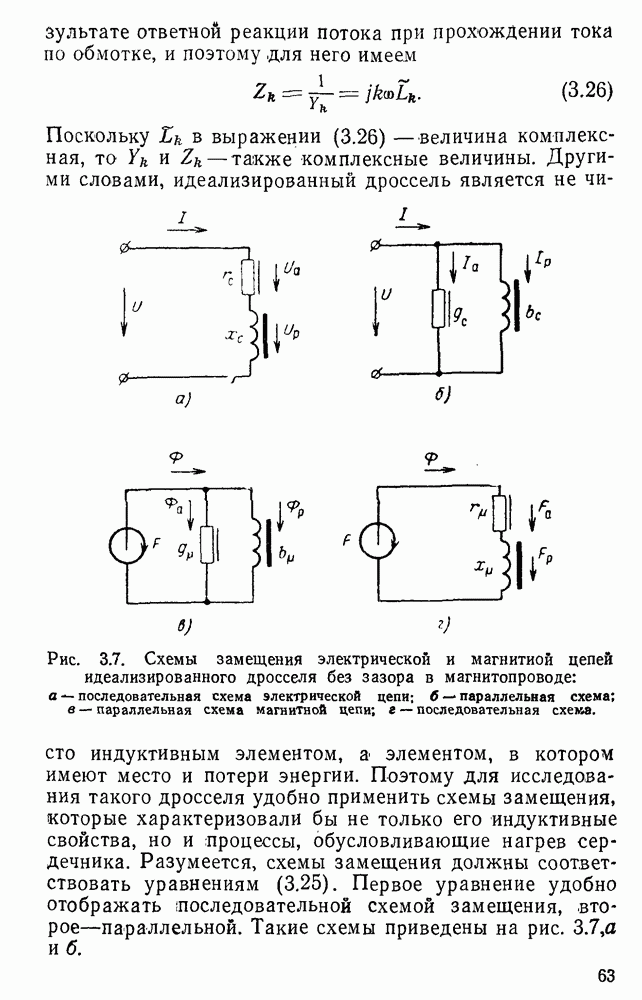
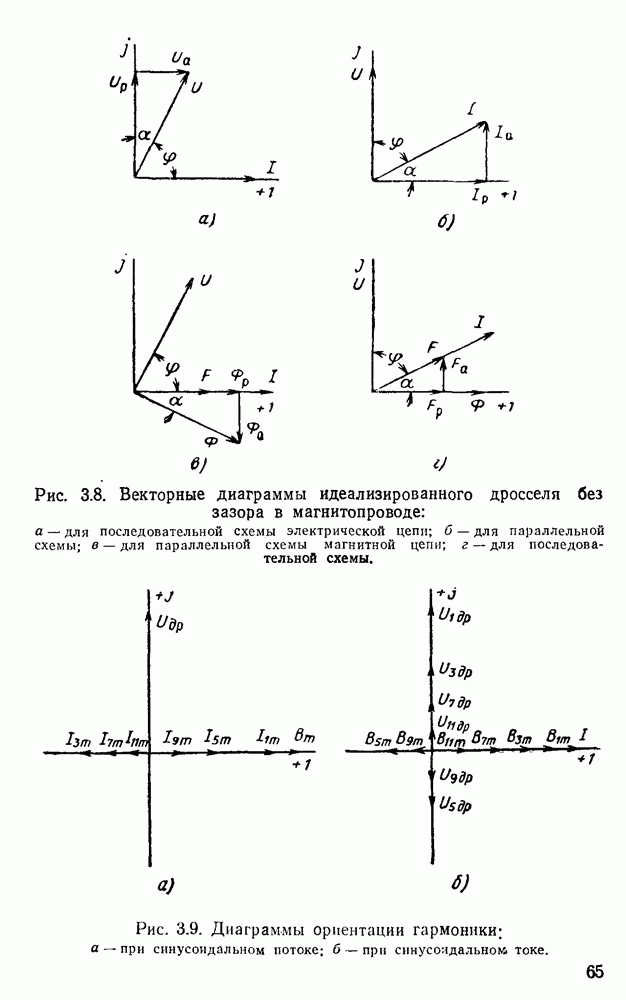
- 3.3. Схемы замещения и векторные диаграммы идеализированного дросселя
- 1. Схемы замещения и векторные диаграммы электрической цепи идеализированного дросселя
- 2. Схемы замещения и векторные диаграммы магнитной цепи идеализированного дросселя
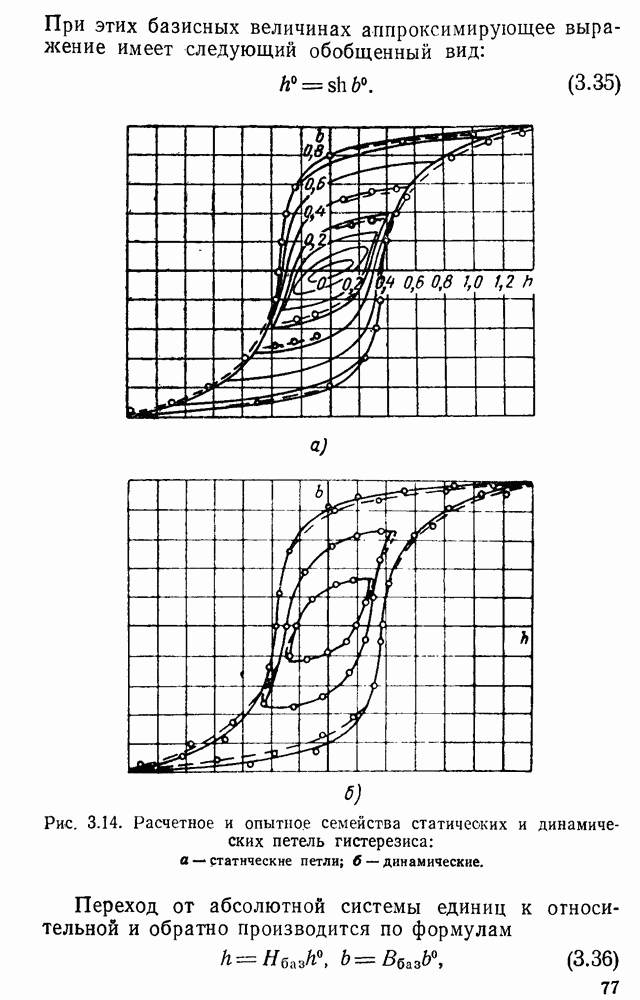
- 3.4. Аппроксимация кривых намагничивания ферромагнитных сердечников. Относительные единицы. Определение коэффициентов аппроксимации
- 3.5. Математическая модель семейства динамических гистерезисных петель. Использование модели для решения задач гармонического анализа
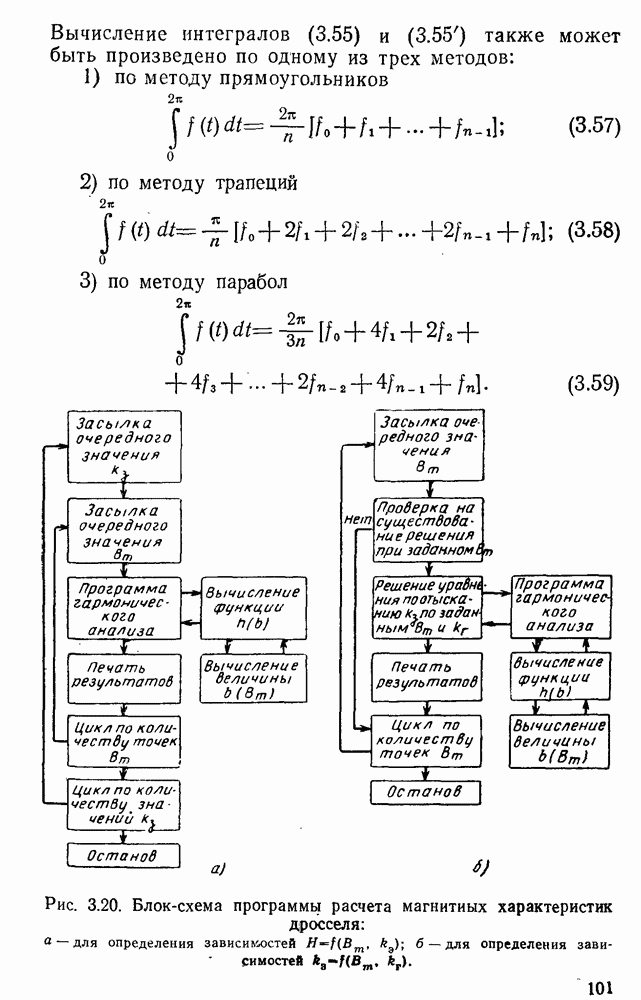
- 1. Определение гармонического состава кривой напряженности поля
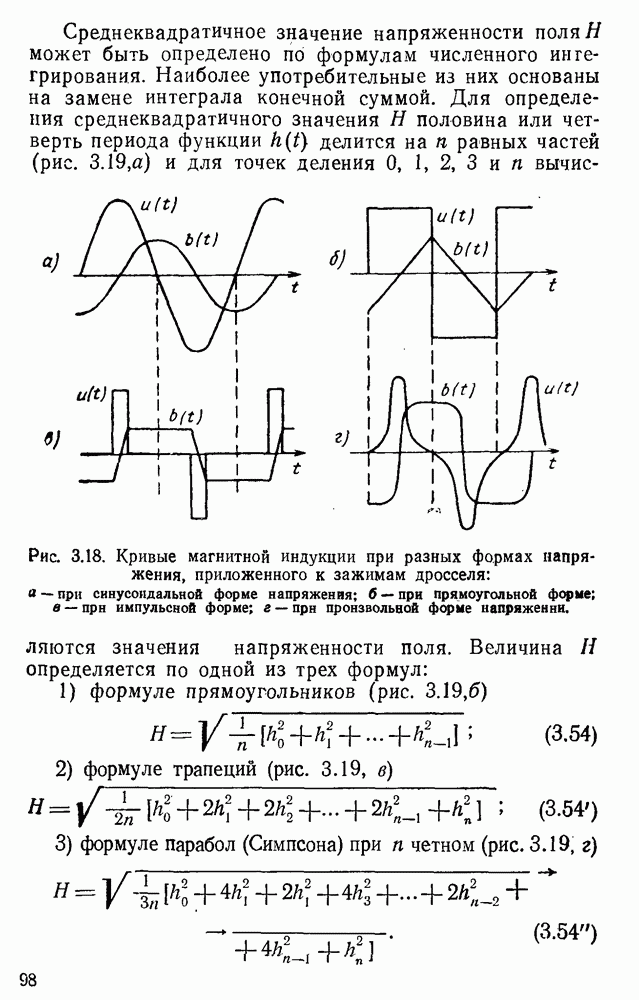
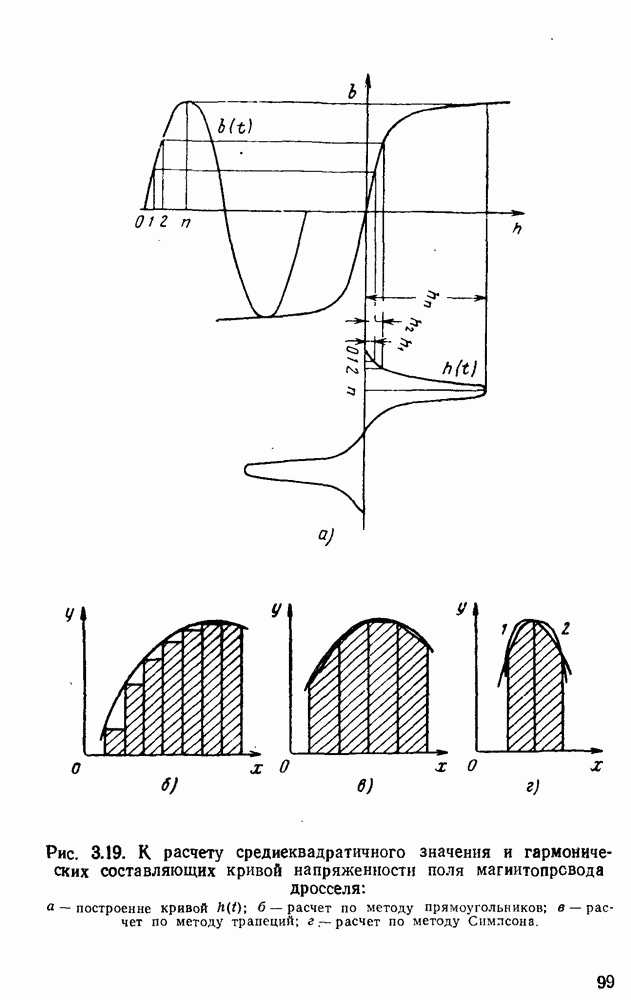
- 2. Определение среднеквадратичного значения напряженности поля и потерь в стали
- 3.6. Аналитический расчет магнитных характеристик магнитопроводов идеальных и идеализированных дросселей с зазором
- 3.7. Расчет численными методами магнитных характеристик идеальных и идеализированных дросселей при произвольной форме кривой магнитной индукции
- 3.8. Расчет магнитных характеристик реальных дросселей. Расчет характеристик дросселей, включенных в электрические цепи
- 1. Расчет магнитных характеристик для реального дросселя без рассеяния
- 2. Расчет магнитных характеристик для дросселя, включенного последовательно с активно-индуктивной нагрузкой
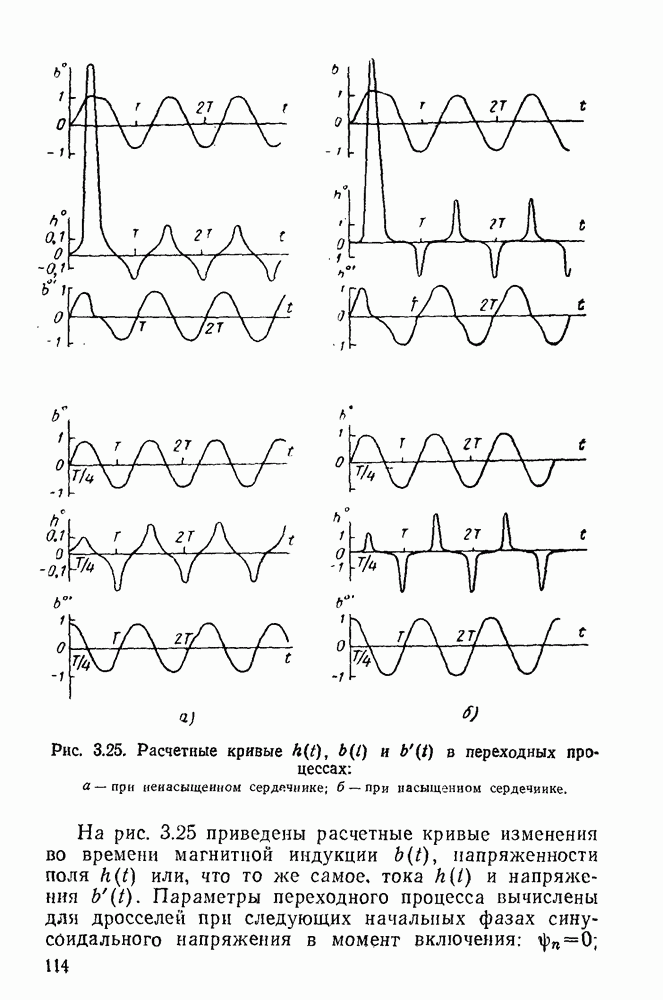
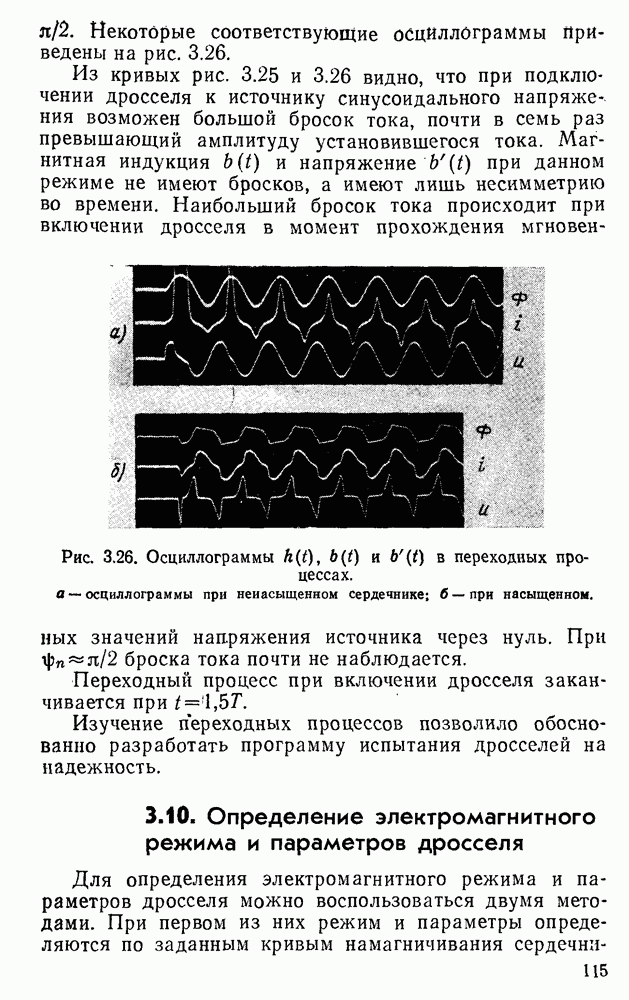
- 3.9. Переходные процессы в дросселе
- 3.10. Определение электромагнитного режима и параметров дросселя
- 2. Определение режима и основных характеристик дросселя по комплексной магнитной проницаемости его сердечника
- 4. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПРОЕКТИРОВАНИЯ ДРОССЕЛЕЙ
- 4.1. Общие замечания. Понятие об оптимальных дросселях и их параметрах
- 4.2. Основные уравнения взаимосвязи параметров дросселя и их решение
- 2. Уравнение потерь
- 3. Уравнение теплового режима дросселя
- 4. Уравнения взаимосвязи магнитных параметров дросселя
- 5. Обобщенные уравнения геометрических параметров разных типов и конструкций дросселей
- 6. Технико-экономические показатели дросселей
- 4.3. Определение с помощью ЭЦВМ оптимальных значений соотношений геометрических параметров дросселя. Оптимальные значения соотношений разных типов дросселей
- 4.4. Определение с помощью ЭЦВМ предельных значений параметров дросселей с заданными магнитопроводами
- 4.5. Влияние отдельных факторов на оптимальные значения геометрических соотношений дросселя
- 5. ПРОЕКТИРОВАНИЕ ДРОССЕЛЕЙ
- 5.1. Основные замечания. Техническое задание на проектирование дросселя
- 5.2. Методика проектирования дросселей
- 1. Выбор типа дросселя, марки стали и обмоточного материала
- 2. Выбор типоразмера стандартного сердечника или расчет специального сердечника
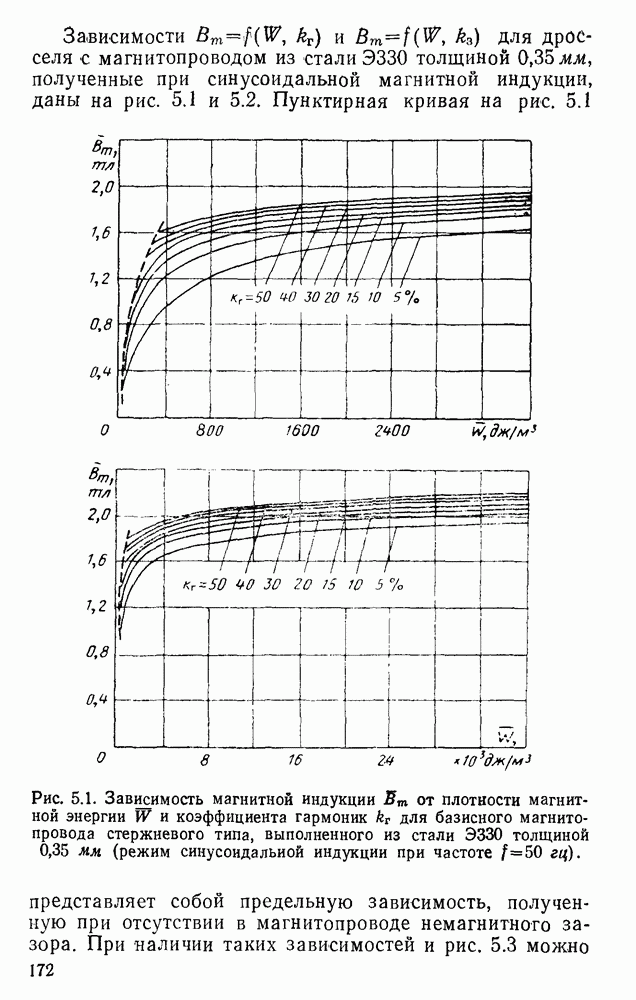
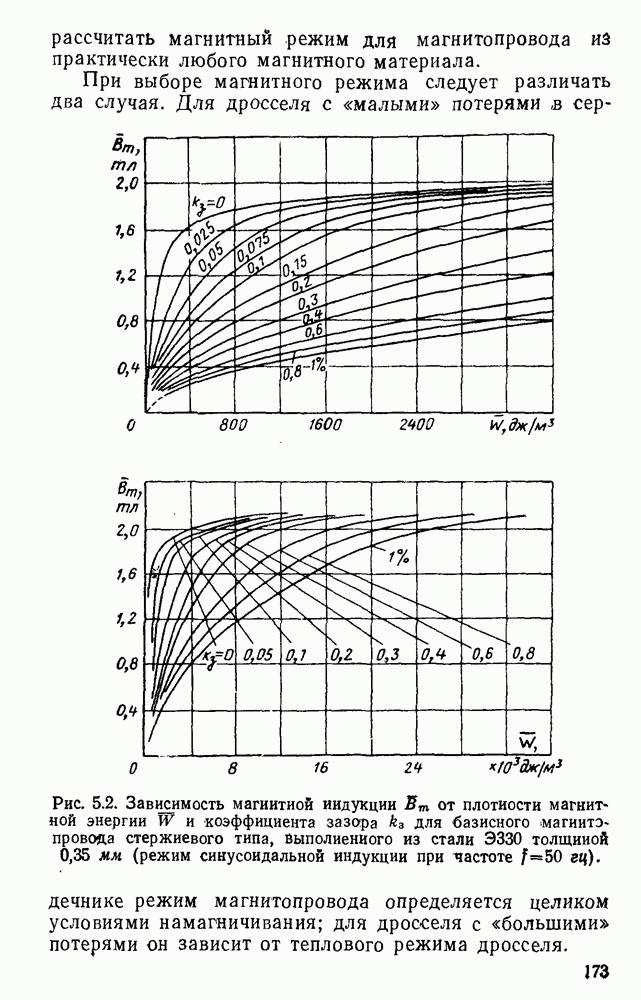
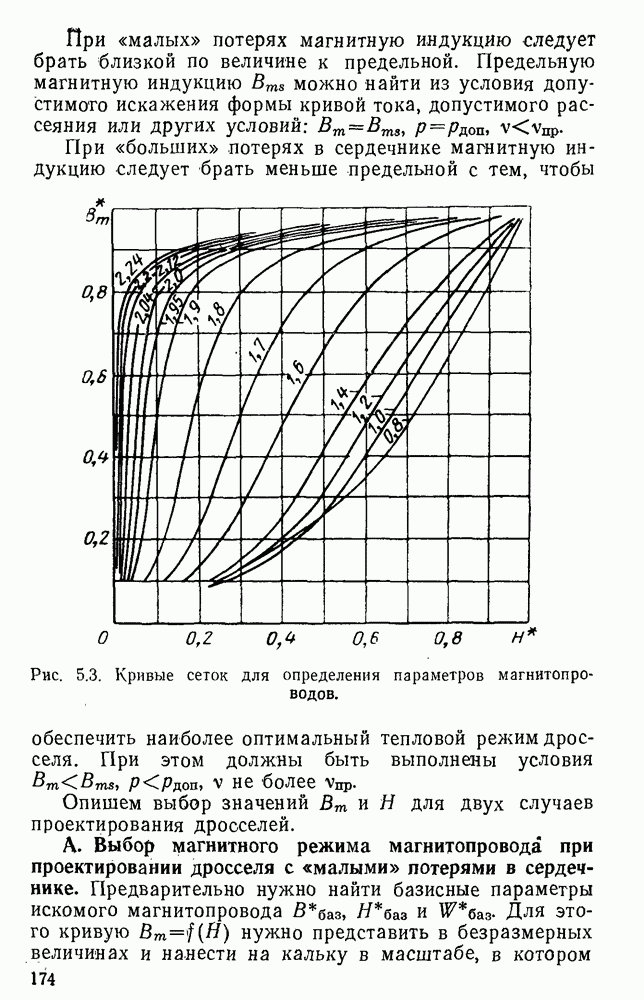
- 3. Выбор магнитного режима магнитопровода дросселя
- 4. Расчет длины немагнитного зазора
- 5. Расчет потерь в дросселе
- 6. Определение геометрических параметров дросселя
- 7. Расчет теплового режима дросселя
- 8. Расчет обмоточных данных и междуслойной изоляции
- 9. Расчет катушек дросселя (конструирование обмоток)
- 10. Определение технико-экономических показателей дросселя
- 11. Проверочный расчет дросселя
- 12. Краткая методика расчета дросселя
- 5.3. Примеры проектирования дросселей
- ПРИЛОЖЕНИЯ
- Основные условные обозначения
- Литература