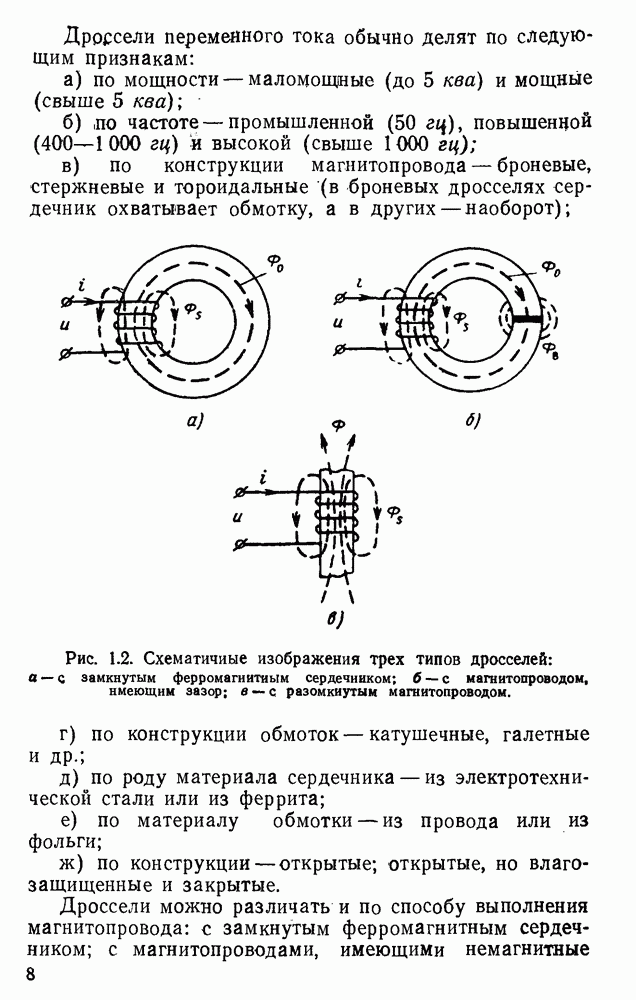
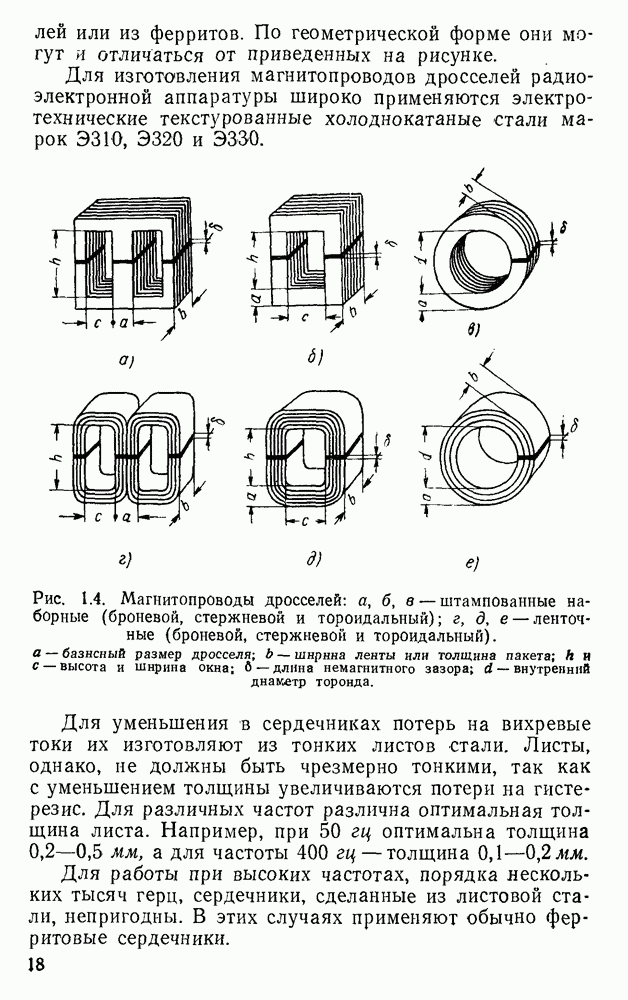
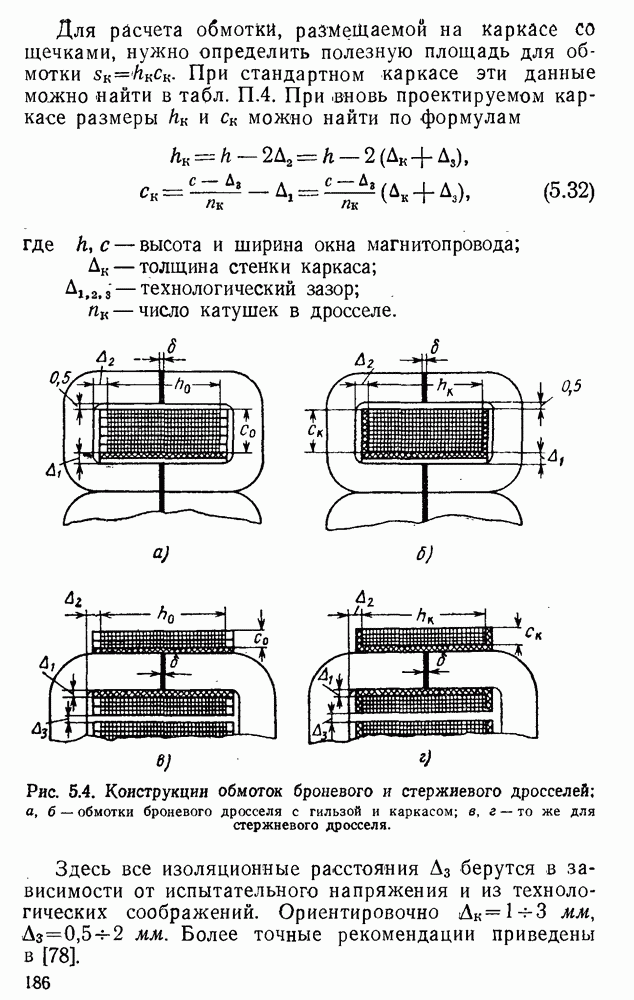
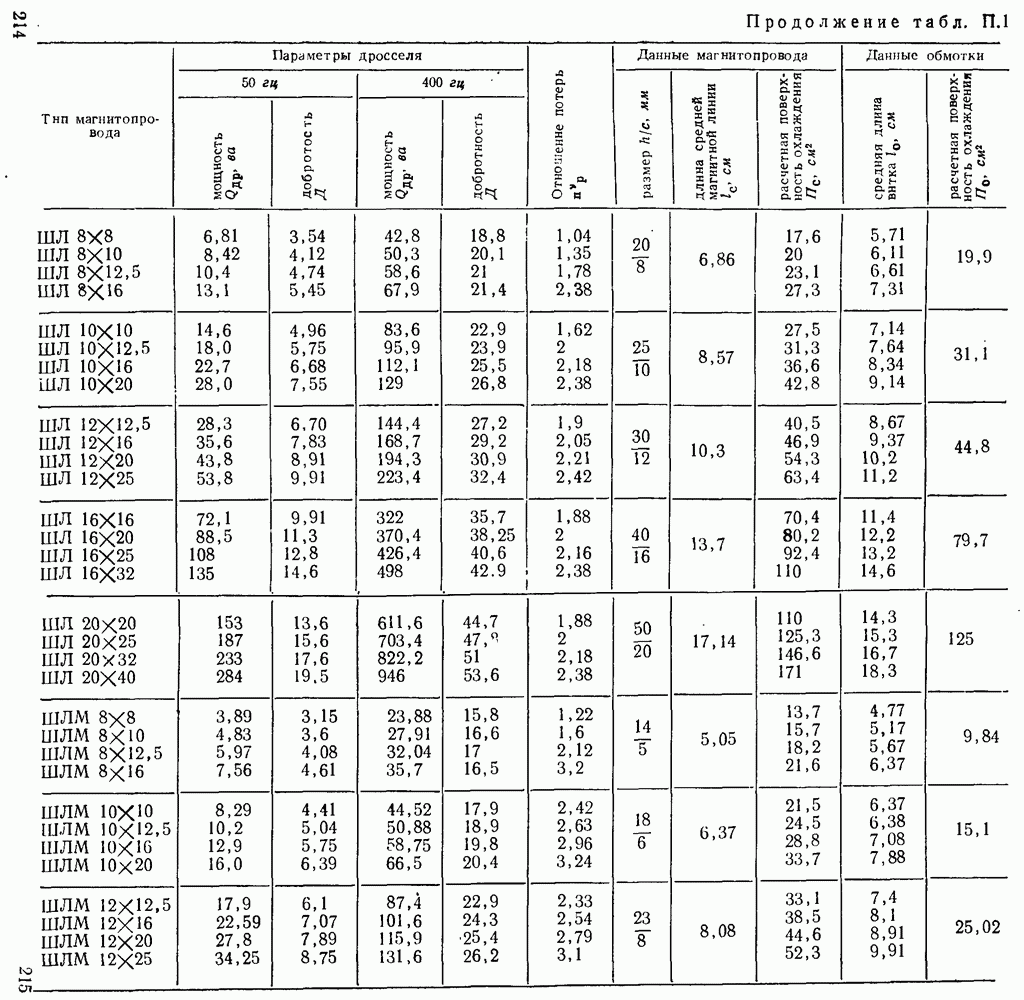
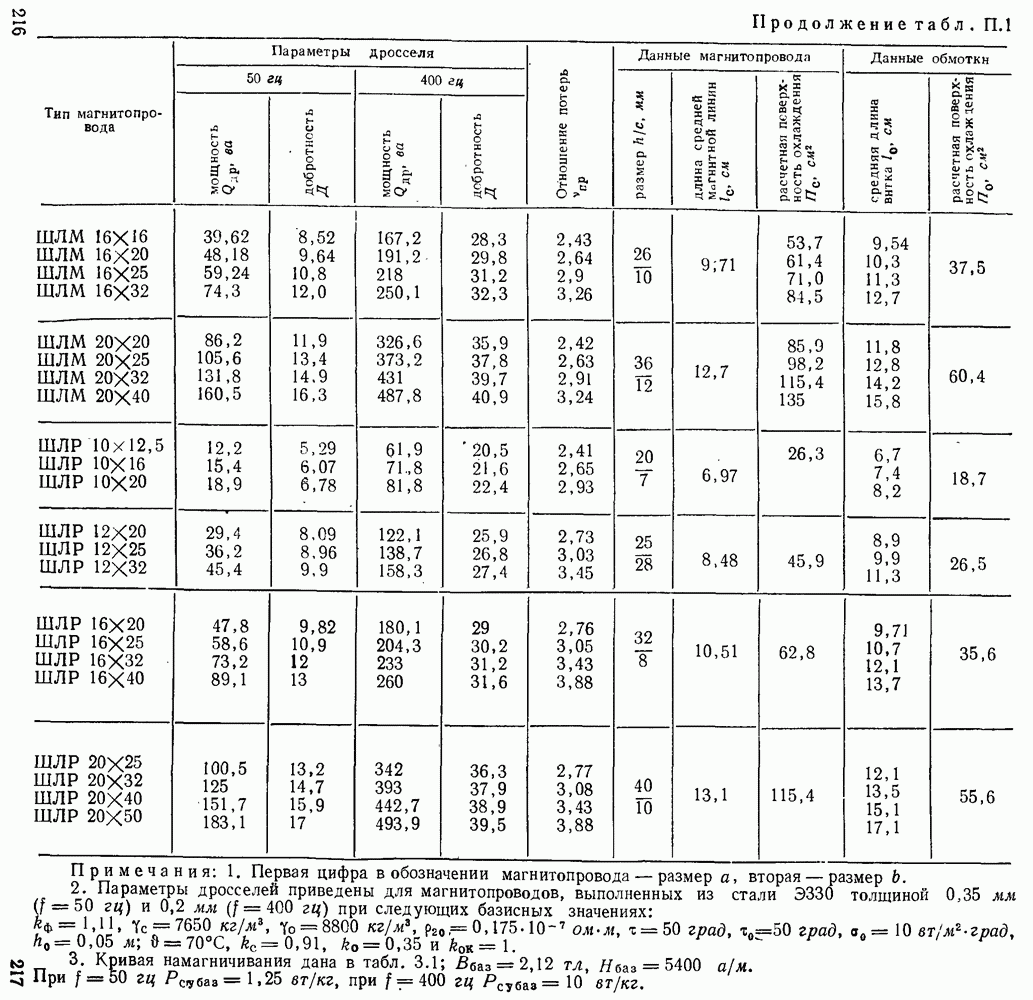
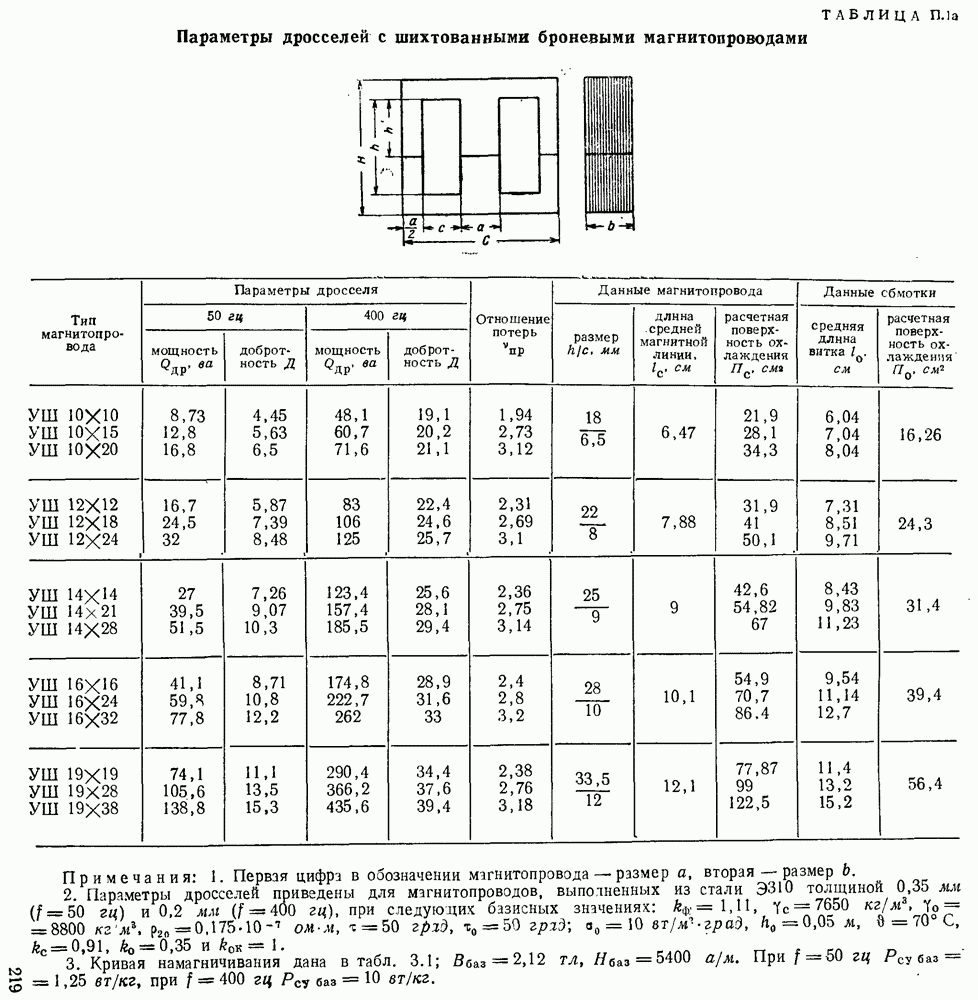
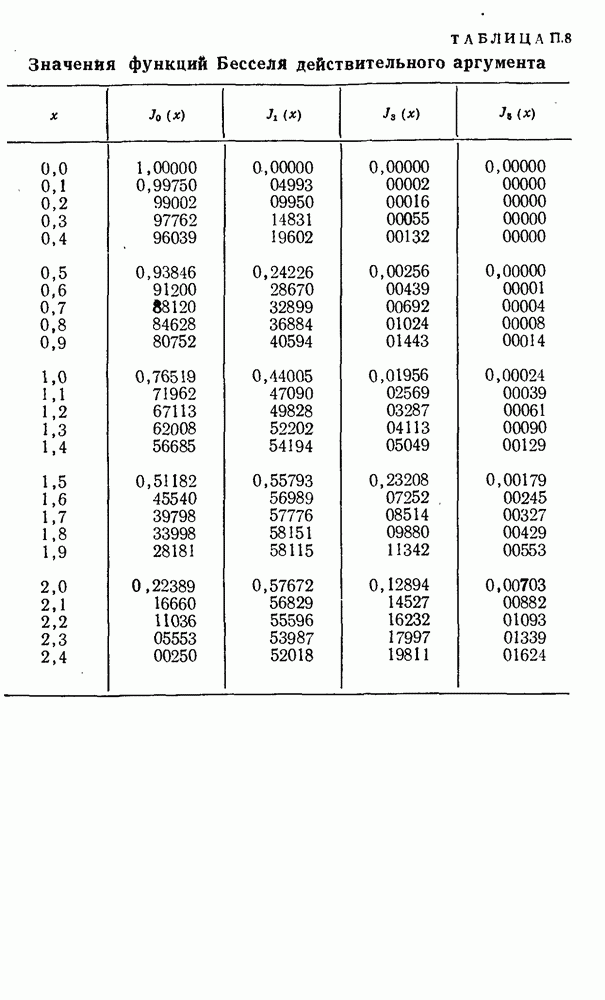
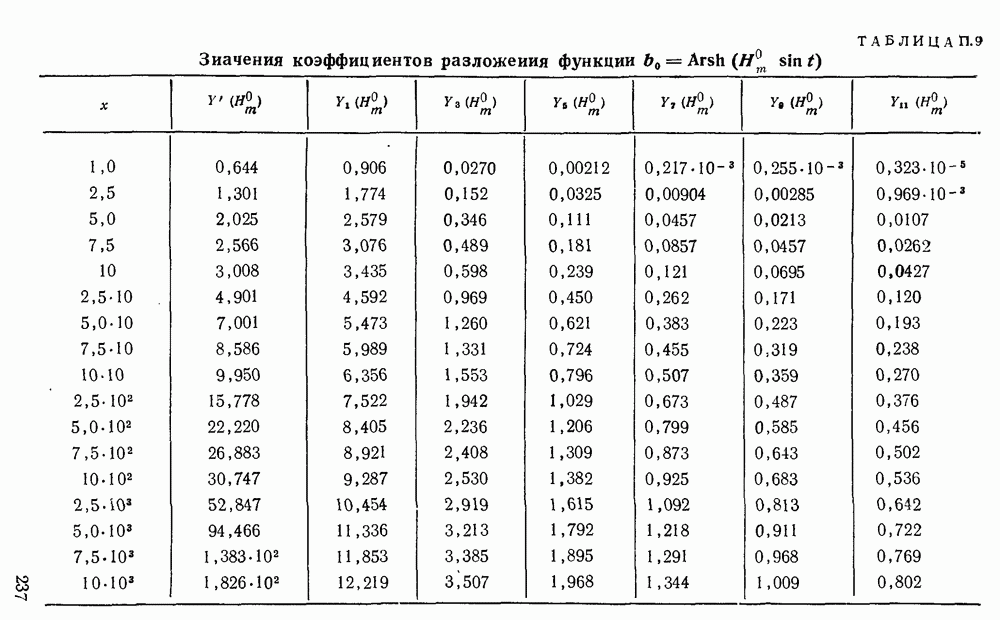
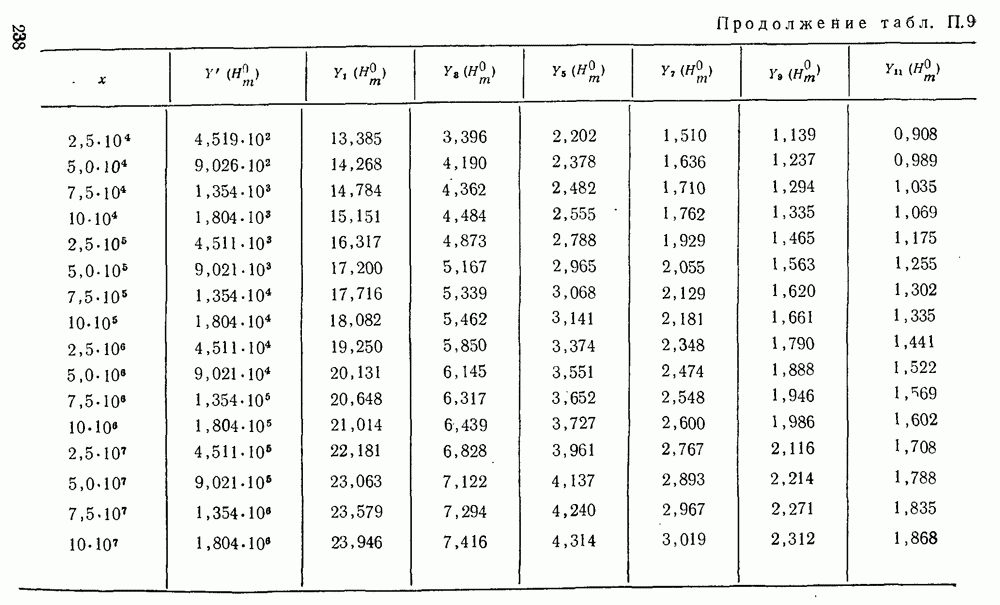
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
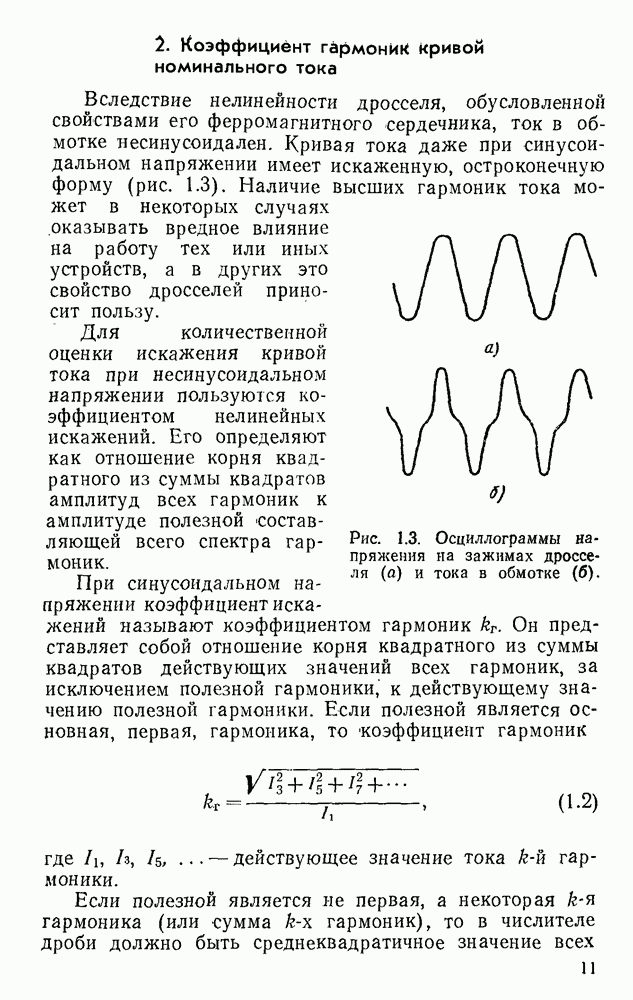
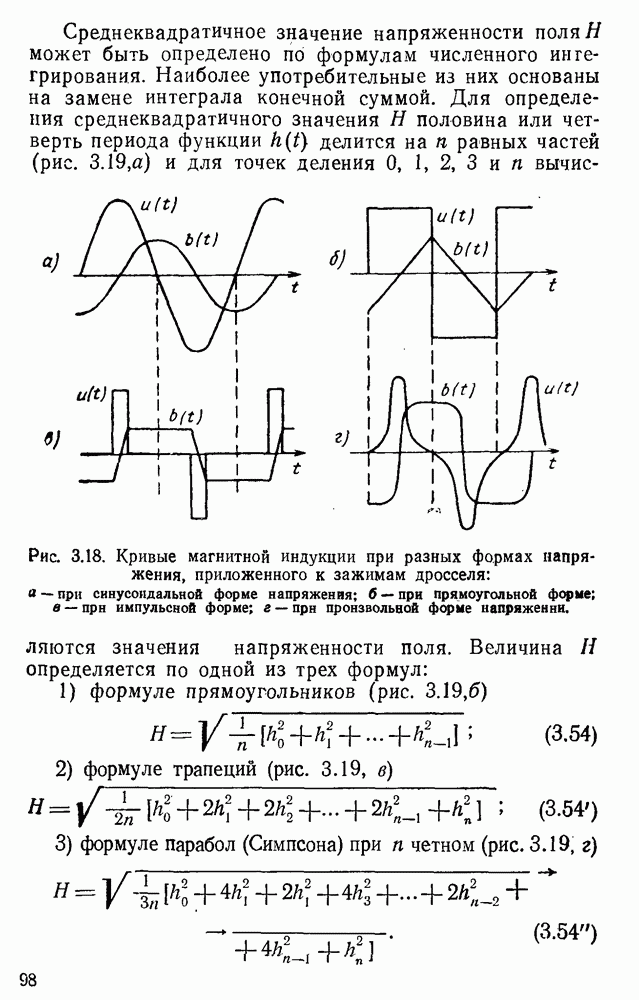
3.5. Математическая модель семейства динамических гистерезисных петель. Использование модели для решения задач гармонического анализа
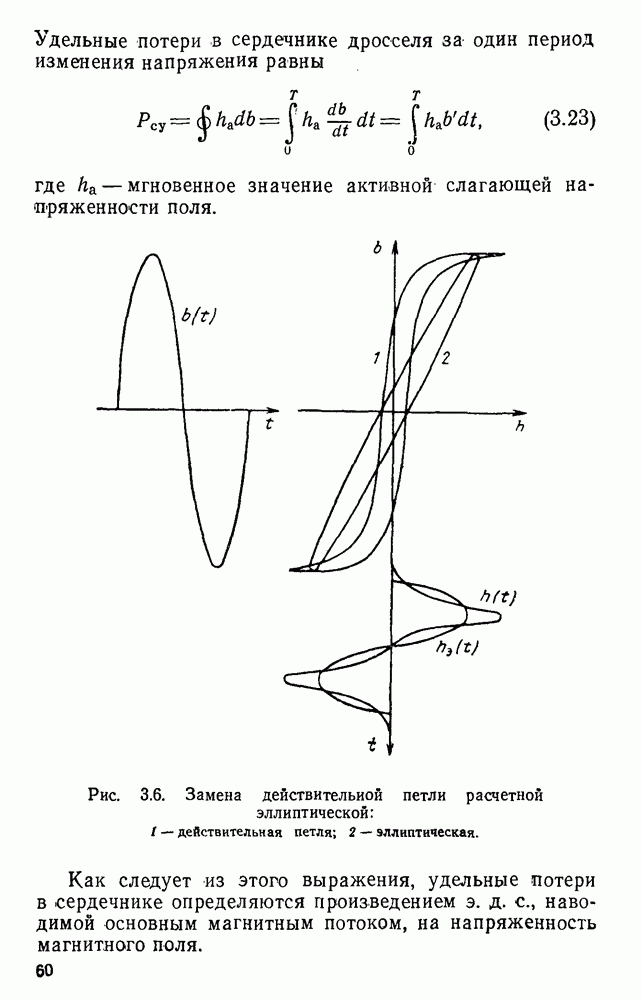
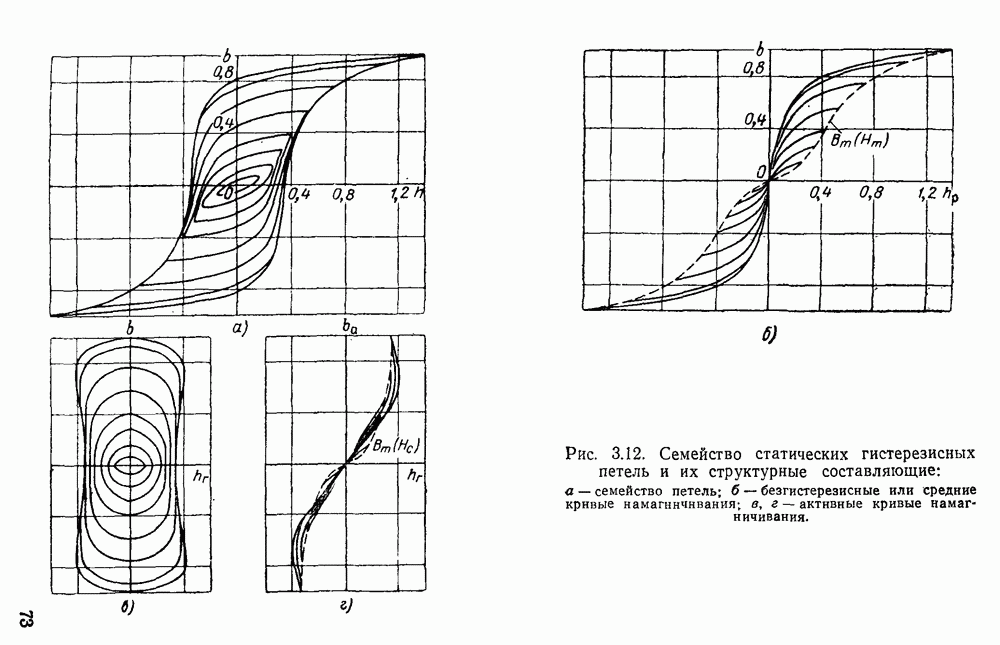
Предложенное в предыдущем параграфе уравнение для выражения семейства статических гистерезисных петель позволяет получить ориентировочную структурную математическую модель для описания семейства динамических петель гистерезиса. Для этого нужно лишь учесть составляющие потерь на вихревые токи 
При установившемся режиме периодического намагничивания математическая модель, выражающая семейство динамических гистерезисных петель, в параметрической форме записи может быть представлена в виде

Здесь  — амплитудное значение
— амплитудное значение  гармоники магнитной индукции;
гармоники магнитной индукции;
 — начальная фаза
— начальная фаза  гармоники;
гармоники;  — максимальное значение кривой несинусоидальной магнитной индукции;
— максимальное значение кривой несинусоидальной магнитной индукции;  — составляющая напряженности поля, обусловленная вихревыми токами;
— составляющая напряженности поля, обусловленная вихревыми токами;  — коэффициент, зависящий от свойств материала ферромагнитного сердечника и от размеров сердечника.
— коэффициент, зависящий от свойств материала ферромагнитного сердечника и от размеров сердечника.
Величина  может быть определена по известной формуле
может быть определена по известной формуле

где  — удельный вес материала;
— удельный вес материала;  — удельные потери на вихревые токи при заданном режиме намагничивания.
— удельные потери на вихревые токи при заданном режиме намагничивания.
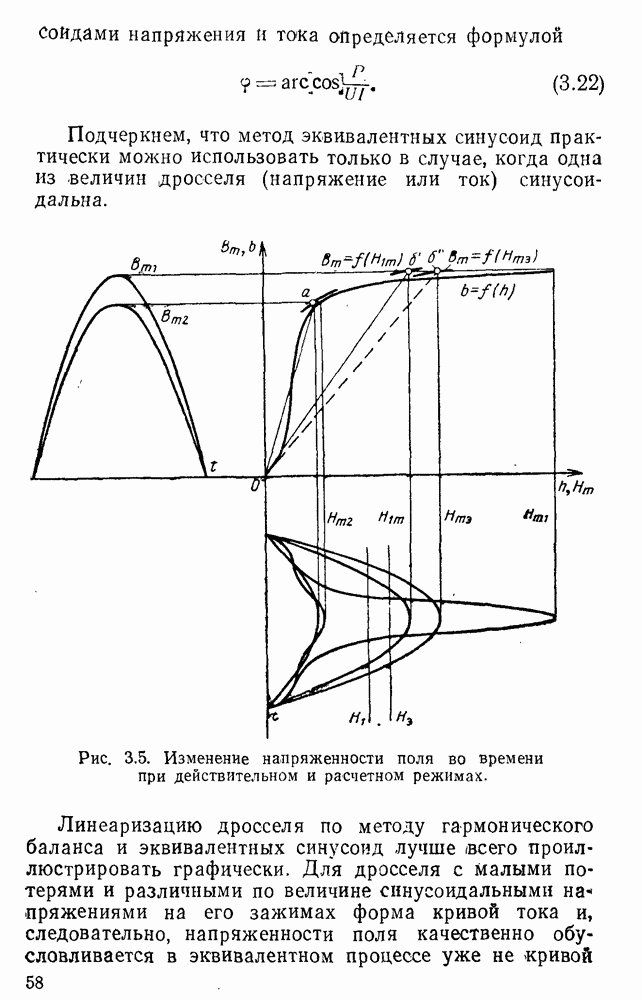
При синусоидальном характере изменения b модель может быть несколько упрощена. Действительно, при  гистерезисная составляющая напряженности поля
гистерезисная составляющая напряженности поля  может быть представлена в виде
может быть представлена в виде

где  — производная от магнитной индукции по времени.
— производная от магнитной индукции по времени.
Сопоставляя полученное выражение с формулой для  можно увидеть, что
можно увидеть, что  обусловливаются производной от магнитной индукции по времени. Отсюда активные процессы ориентировочно можно представить в виде
обусловливаются производной от магнитной индукции по времени. Отсюда активные процессы ориентировочно можно представить в виде

где  — коэффициенты аппроксимации динамической петли гистерезиса.
— коэффициенты аппроксимации динамической петли гистерезиса.

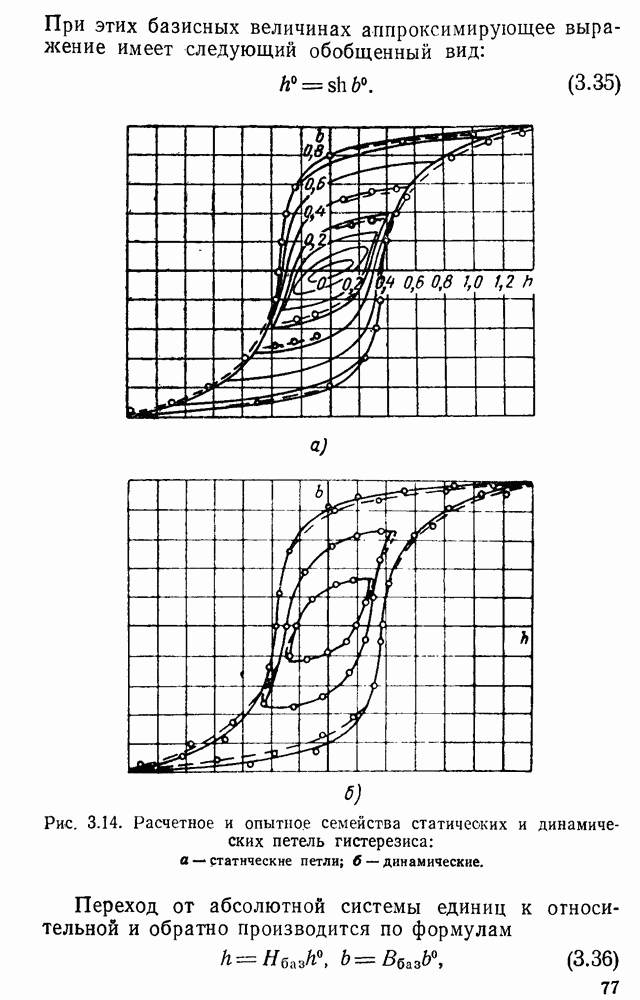
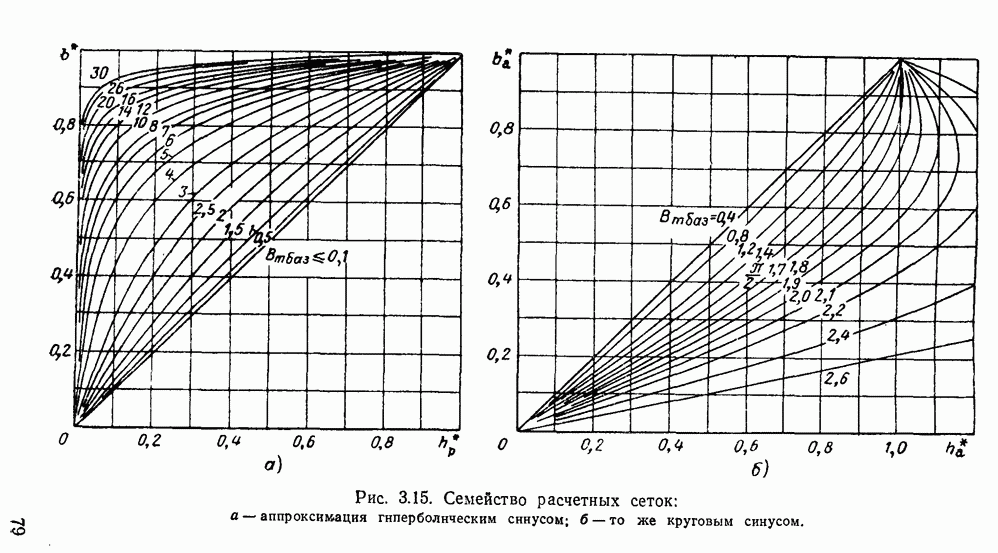
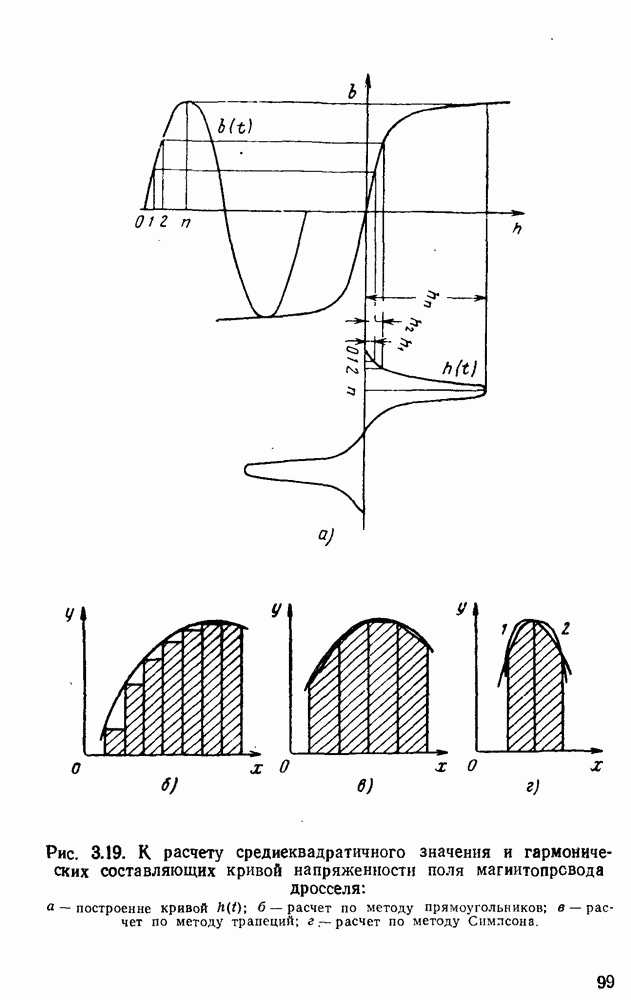
Уравнения гистерезисной петли от величины  при этом имеют вид
при этом имеют вид  Рассчитанные по этим уравнениям гистерезисные петли
Рассчитанные по этим уравнениям гистерезисные петли  даны на рис.
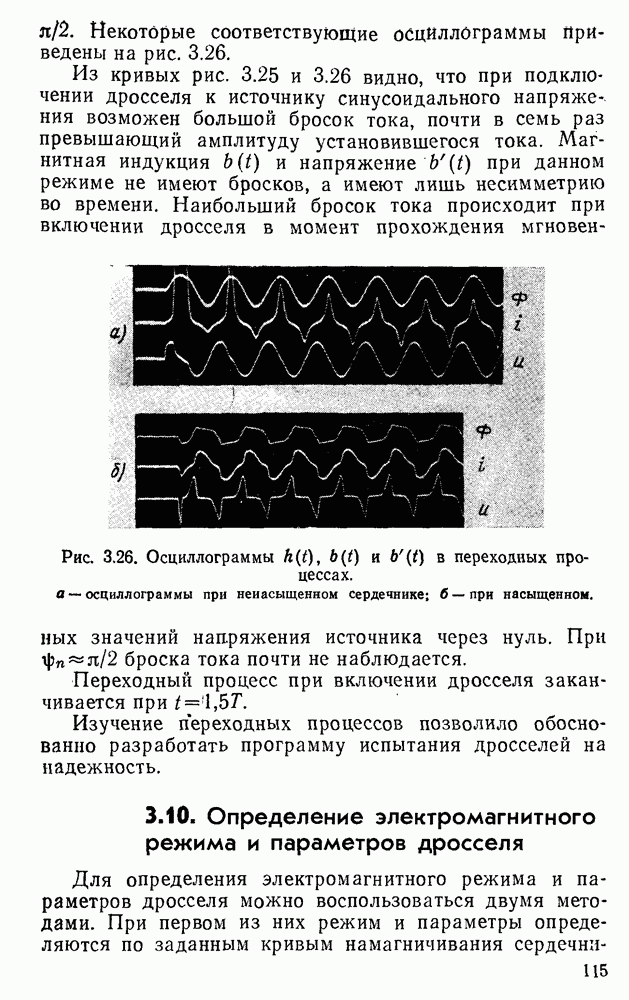
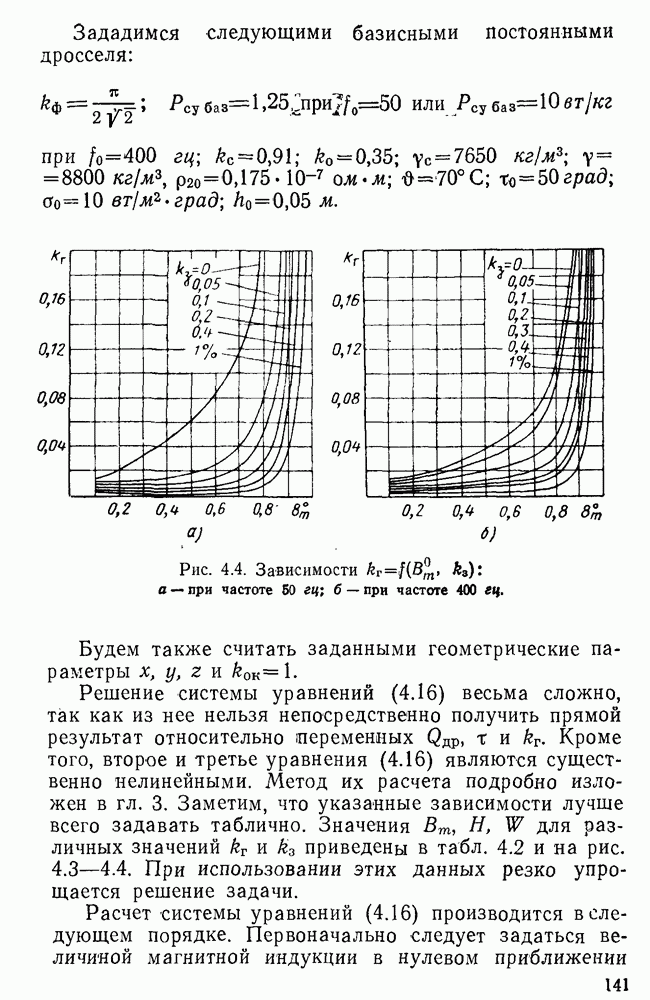
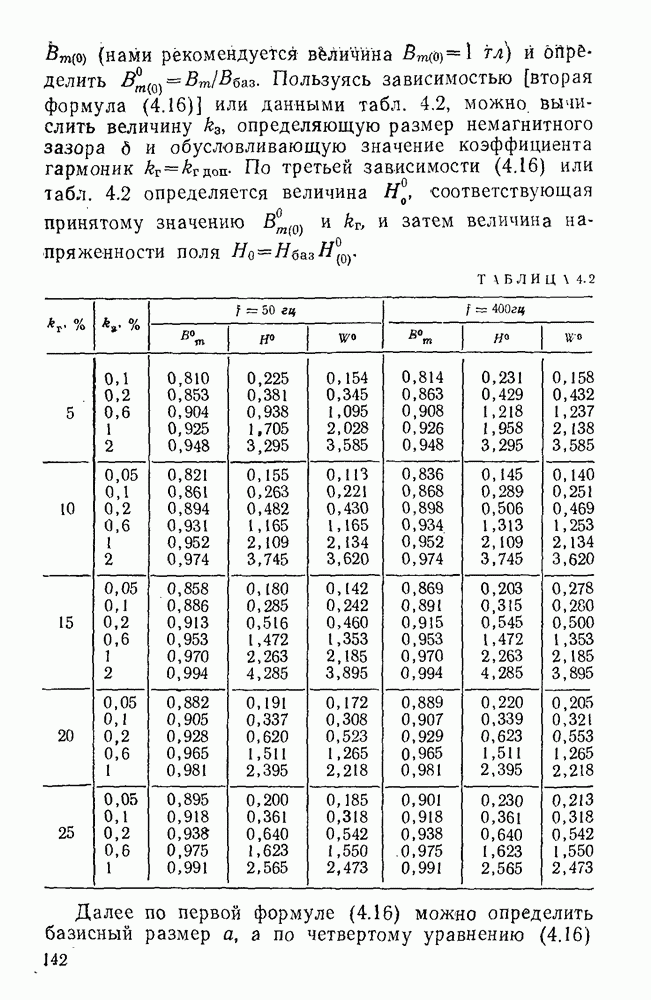
даны на рис.  . Как видим, расчетные петли хорошо согласуются с опытными.
. Как видим, расчетные петли хорошо согласуются с опытными.
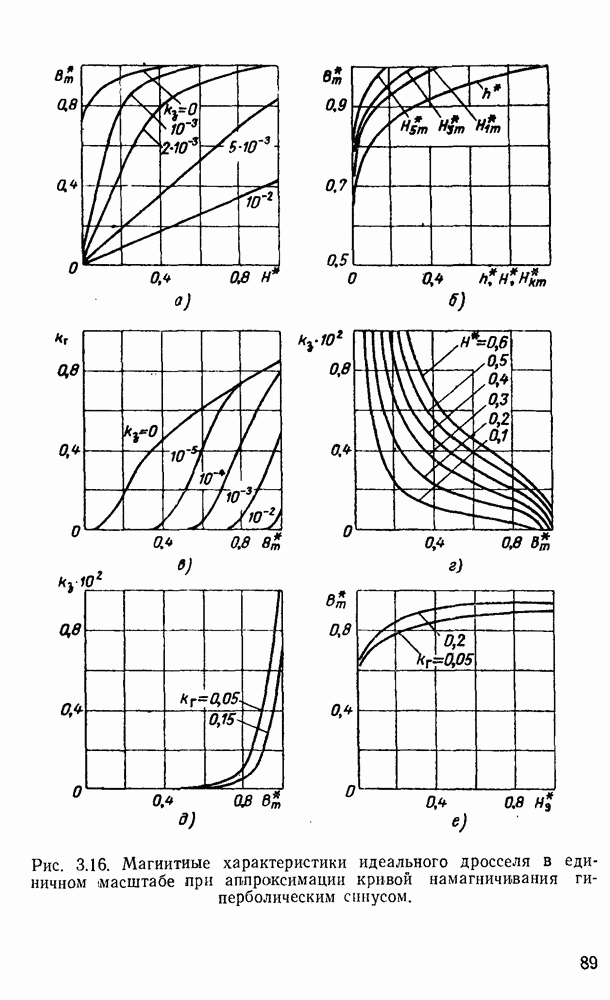
Модели, предлагаемые для выражения процессов намагничивания ферромагнетика, могут быть положены в основу расчета любых цепей с дросселями и при самых различных установившихся режимах. Для этого нужно определить коэффициенты  для всех ожидаемых режимов работы ферромагнетика и затем их аппроксимировать. При этом можно получить петли не только в зависимости от магнитной индукции, как это было показано, но и от других факторов (температуры, частоты тока и т. д.).
для всех ожидаемых режимов работы ферромагнетика и затем их аппроксимировать. При этом можно получить петли не только в зависимости от магнитной индукции, как это было показано, но и от других факторов (температуры, частоты тока и т. д.).
Использование таких моделей, очевидно, приведет к более точным методам расчета дросселей.
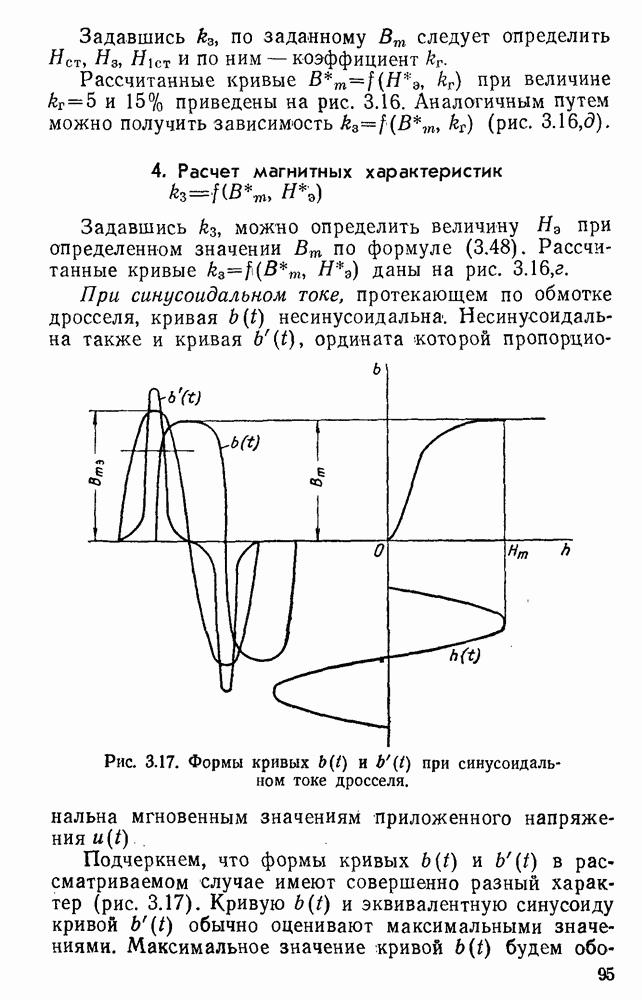
Модель очень удобна для решения задач гармонического анализа. В частности, с помощью этой модели удается аналитическим путем определить гармонический состав кривой напряженности поля, среднеквадратичное значение кривой h и потери в стали.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- 1. ОСНОВНЫЕ СВЕДЕНИЯ О НЕУПРАВЛЯЕМЫХ ДРОССЕЛЯХ ПЕРЕМЕННОГО ТОКА РАДИОЭЛЕКТРОННОЙ АППАРАТУРЫ
- 1.1. Общие краткие сведения о дросселях. Классификация дросселей
- 1.2. Номинальные параметры нелинейного дросселя
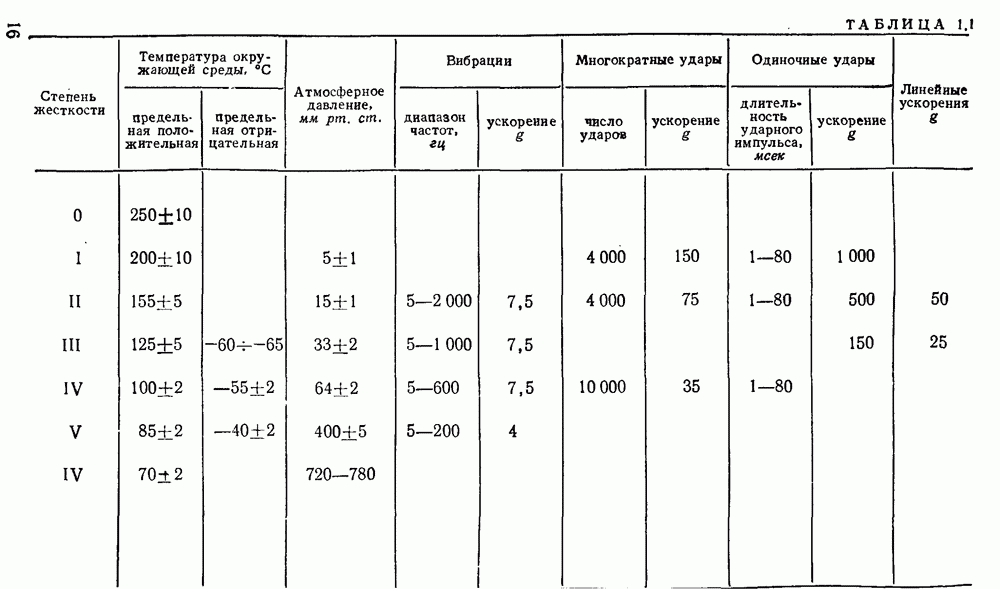
- 1.3. Требования, предъявляемые к дросселям радиоэлектронной аппаратуры. Степени жесткости
- 1.4. Устройство маломощных дросселей переменного тока
- 1.5. Нагрев и охлаждение дросселей
- 1.6. Экранирование дросселей
- 1.7. Сравнение разных типов дросселей
- 2. МАГНИТНЫЕ СВОЙСТВА МАГНИТОПРОВОДОВ ДРОССЕЛЕЙ. ВЫБОР ФЕРРОМАГНЕТИКА
- 2.1. Свойства магнитопроводов дросселей
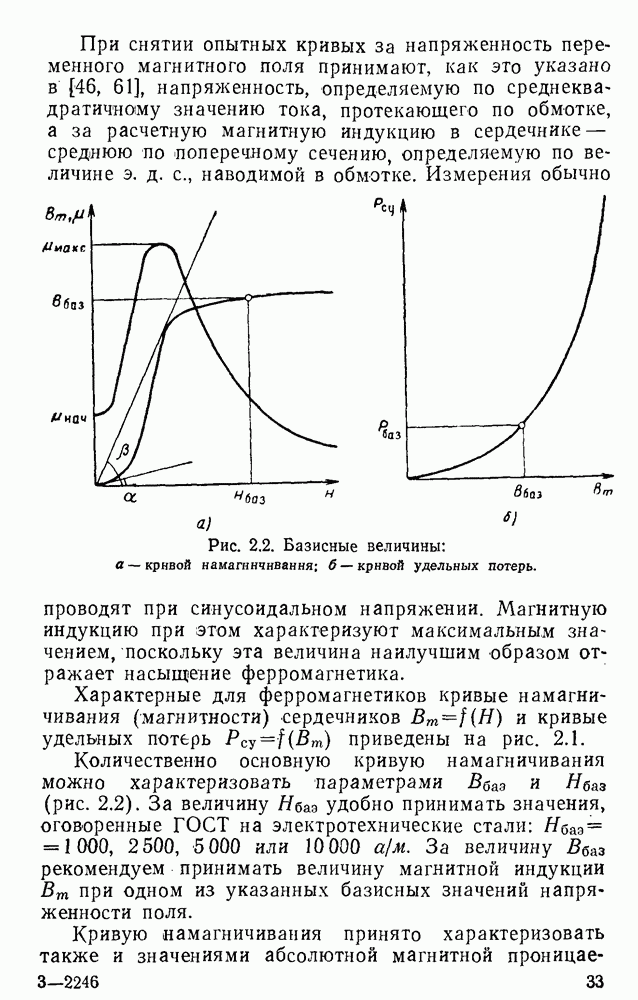
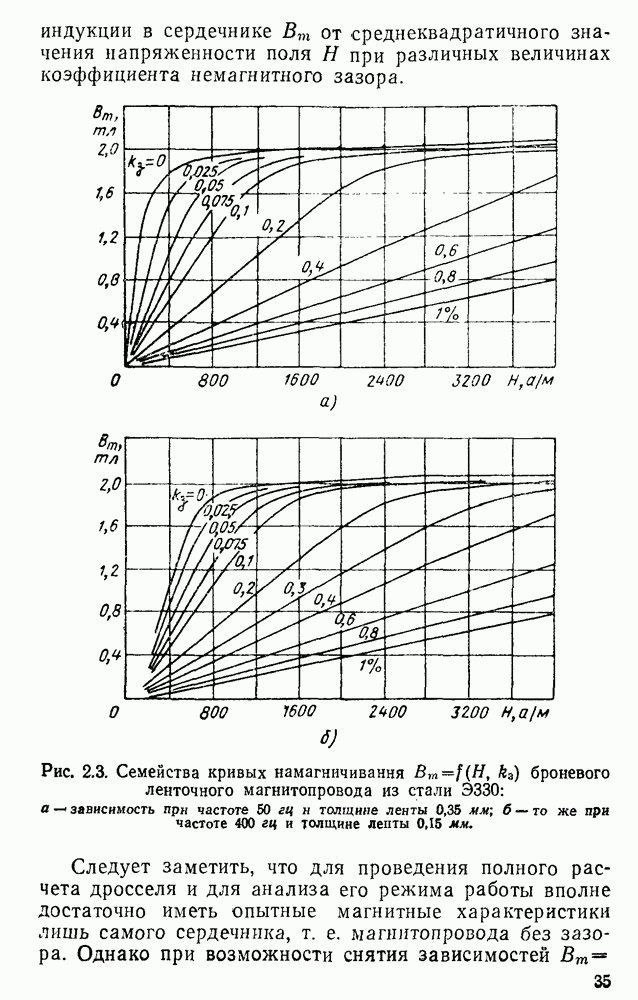
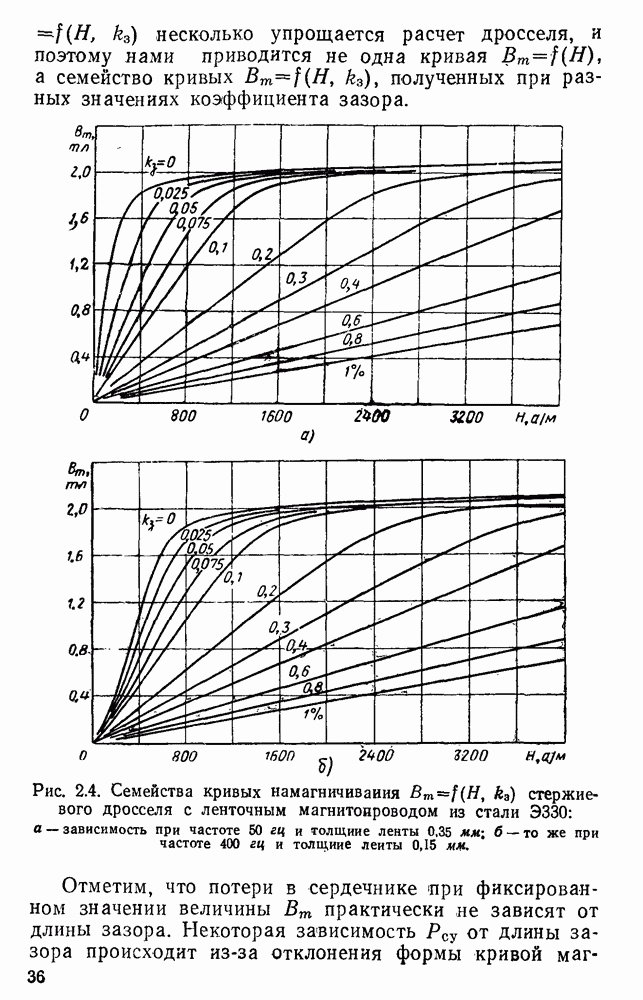
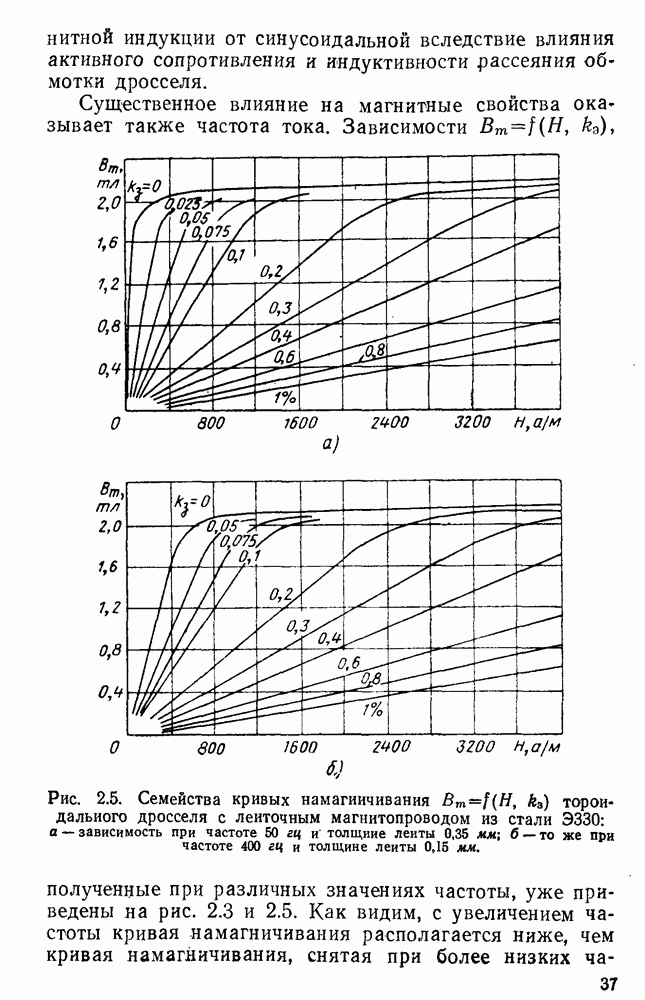
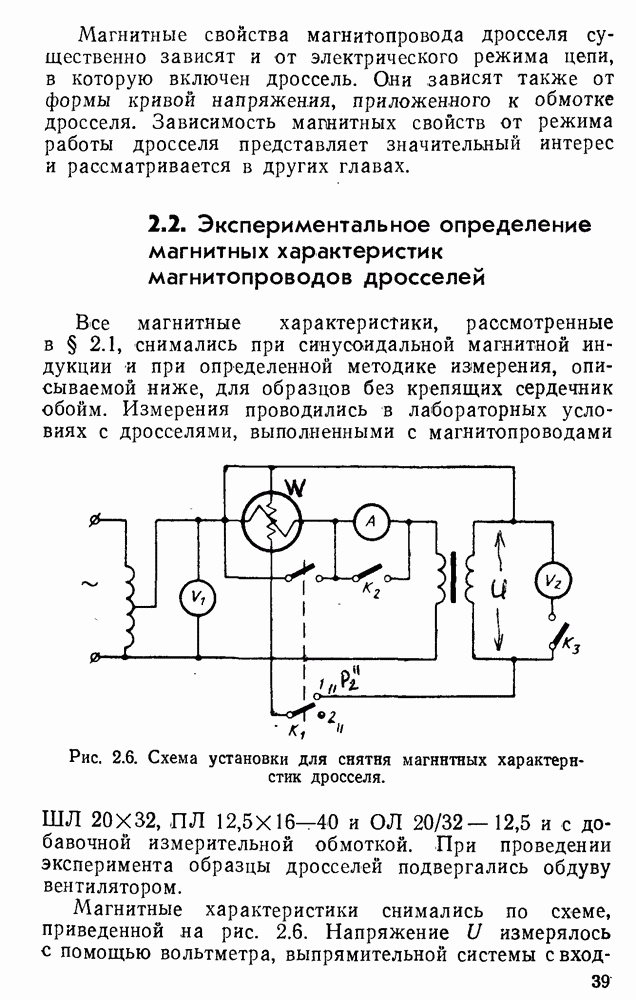
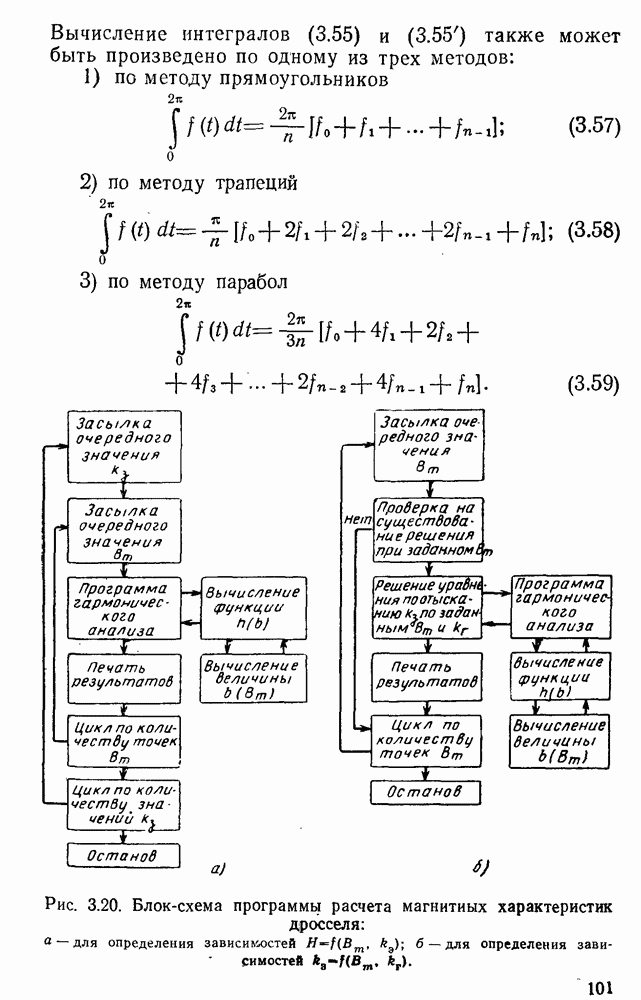
- 2.2. Экспериментальное определение магнитных характеристик магнитопроводов дросселей
- 2.3. Выбор ферромагнетика для сердечника дросселя
- 3. ТЕОРИЯ РАБОТЫ ДРОССЕЛЯ ПЕРЕМЕННОГО ТОКА С НЕЛИНЕЙНЫМ ФЕРРОМАГНИТНЫМ СЕРДЕЧНИКОМ
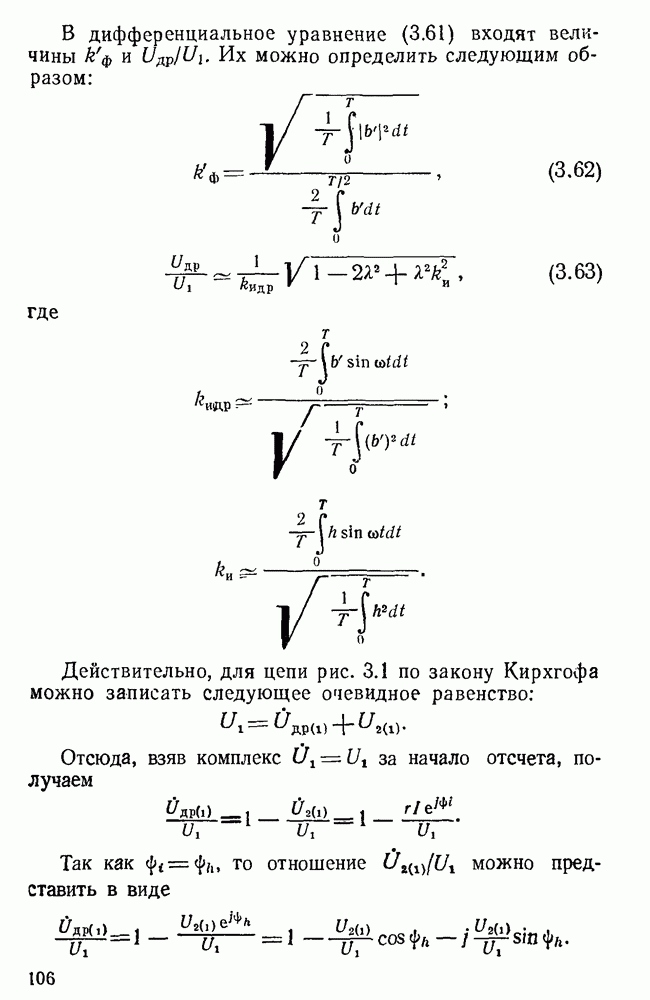
- 3.2. Связи между электрическими и магнитными величинами в дросселе с нелинейным ферромагнитным сердечником. Эквивалентный дроссель
- 1. Идеальный и идеализированный дроссели без зазора
- 2. Идеальный и идеализированный дроссели с немагнитным зазором
- 3. Реальный дроссель
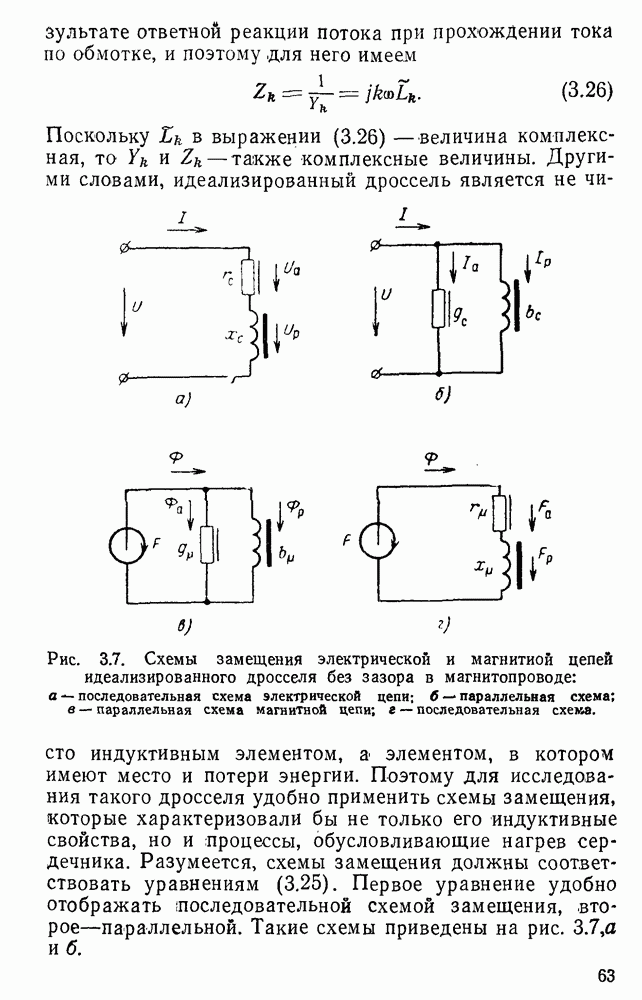
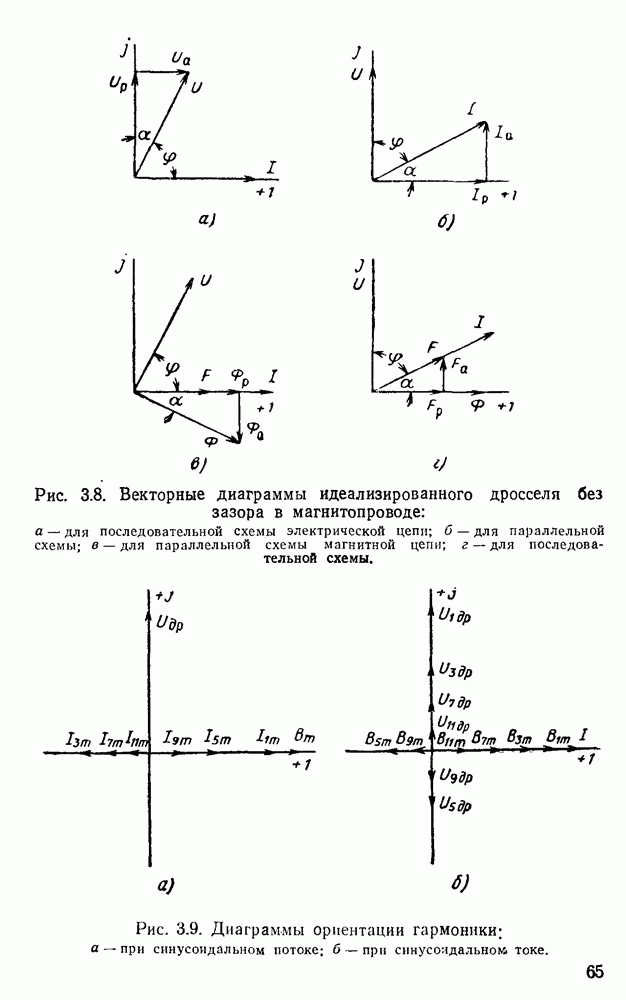
- 3.3. Схемы замещения и векторные диаграммы идеализированного дросселя
- 1. Схемы замещения и векторные диаграммы электрической цепи идеализированного дросселя
- 2. Схемы замещения и векторные диаграммы магнитной цепи идеализированного дросселя
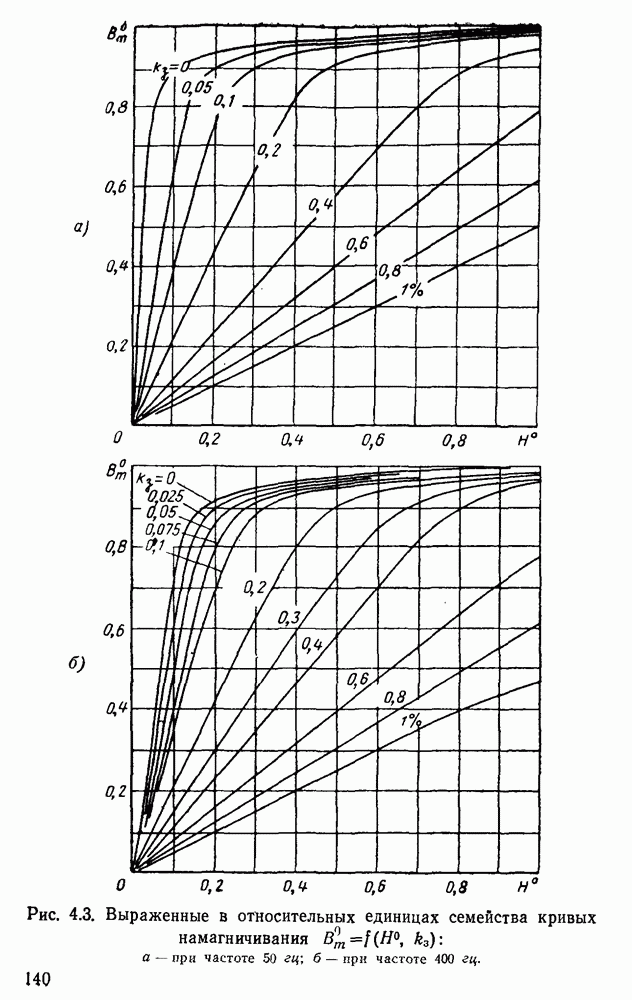
- 3.4. Аппроксимация кривых намагничивания ферромагнитных сердечников. Относительные единицы. Определение коэффициентов аппроксимации
- 3.5. Математическая модель семейства динамических гистерезисных петель. Использование модели для решения задач гармонического анализа
- 1. Определение гармонического состава кривой напряженности поля
- 2. Определение среднеквадратичного значения напряженности поля и потерь в стали
- 3.6. Аналитический расчет магнитных характеристик магнитопроводов идеальных и идеализированных дросселей с зазором
- 3.7. Расчет численными методами магнитных характеристик идеальных и идеализированных дросселей при произвольной форме кривой магнитной индукции
- 3.8. Расчет магнитных характеристик реальных дросселей. Расчет характеристик дросселей, включенных в электрические цепи
- 1. Расчет магнитных характеристик для реального дросселя без рассеяния
- 2. Расчет магнитных характеристик для дросселя, включенного последовательно с активно-индуктивной нагрузкой
- 3.9. Переходные процессы в дросселе
- 3.10. Определение электромагнитного режима и параметров дросселя
- 2. Определение режима и основных характеристик дросселя по комплексной магнитной проницаемости его сердечника
- 4. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПРОЕКТИРОВАНИЯ ДРОССЕЛЕЙ
- 4.1. Общие замечания. Понятие об оптимальных дросселях и их параметрах
- 4.2. Основные уравнения взаимосвязи параметров дросселя и их решение
- 2. Уравнение потерь
- 3. Уравнение теплового режима дросселя
- 4. Уравнения взаимосвязи магнитных параметров дросселя
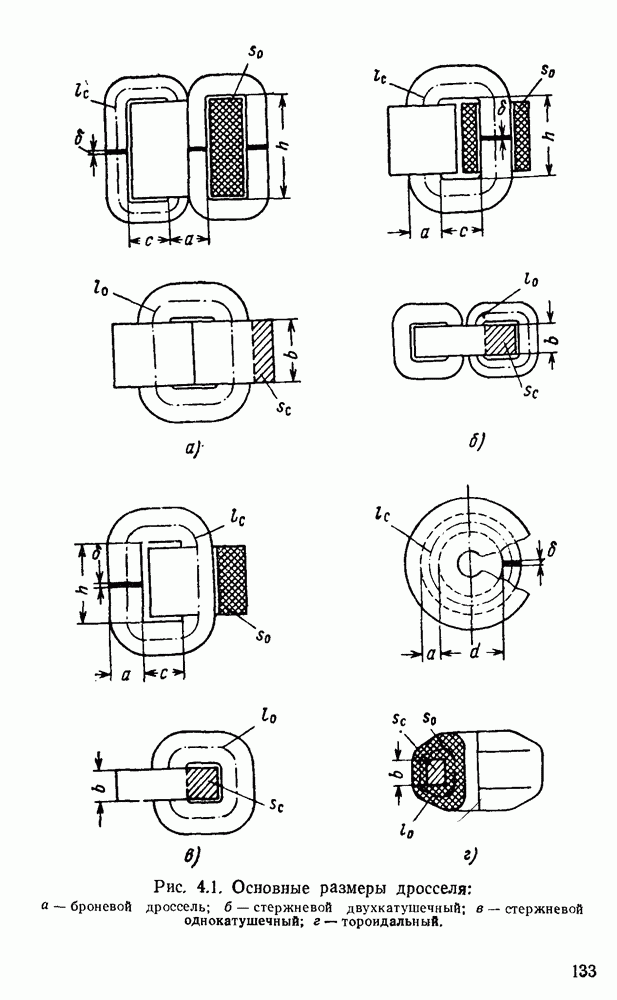
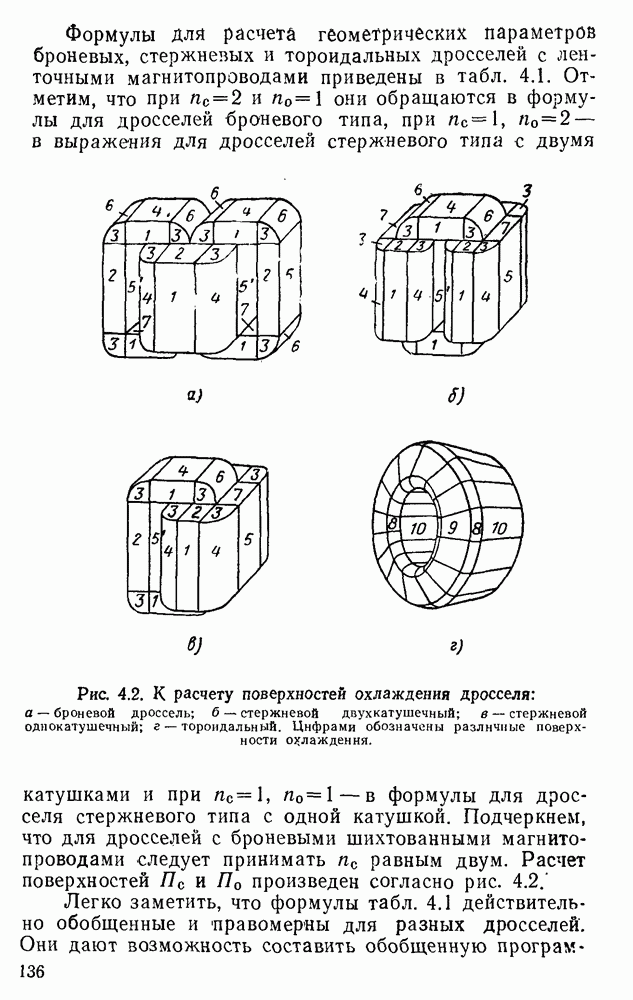
- 5. Обобщенные уравнения геометрических параметров разных типов и конструкций дросселей
- 6. Технико-экономические показатели дросселей
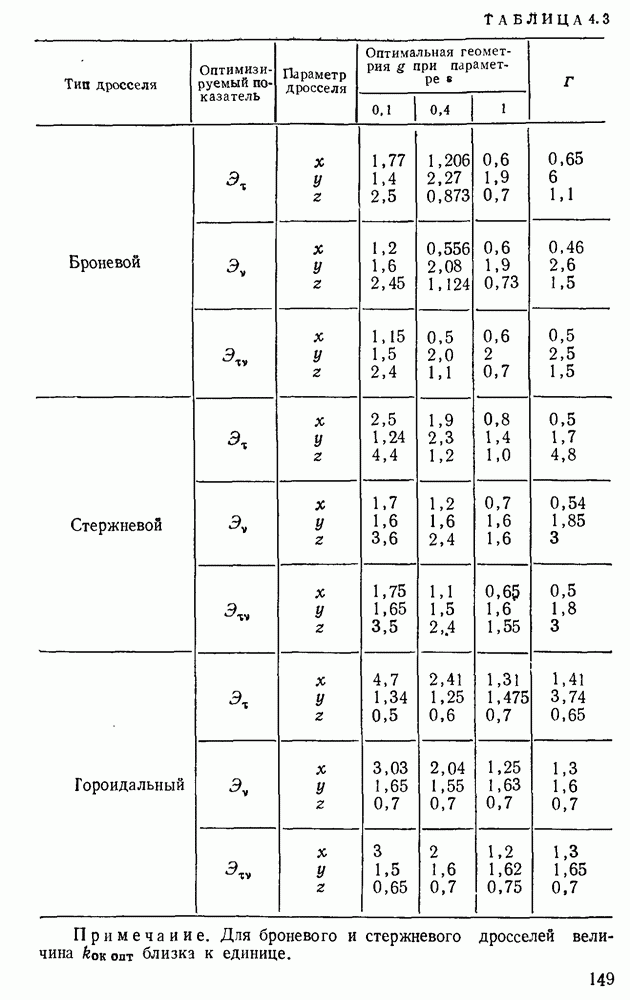
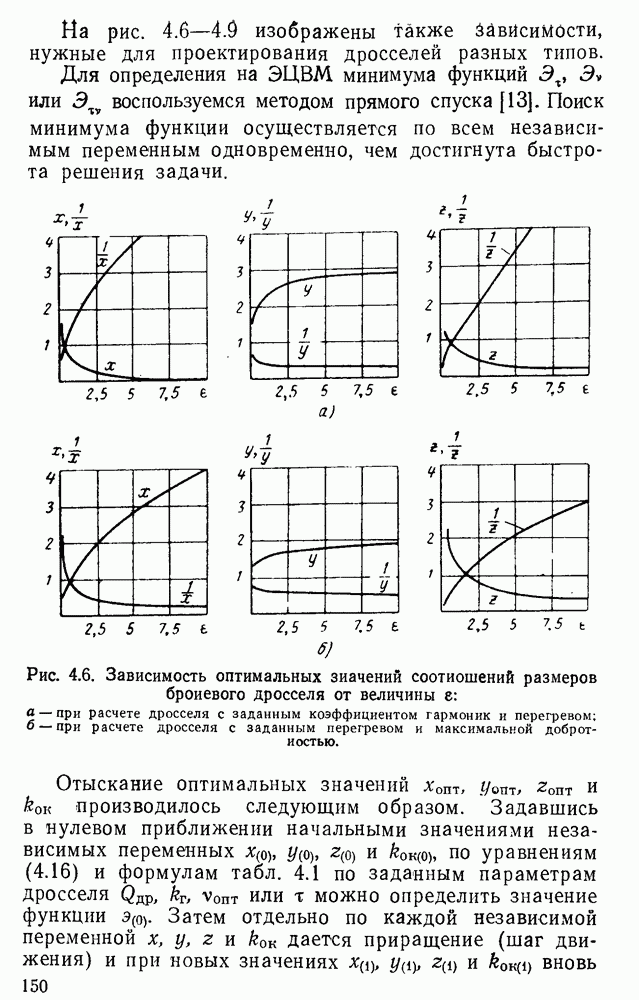
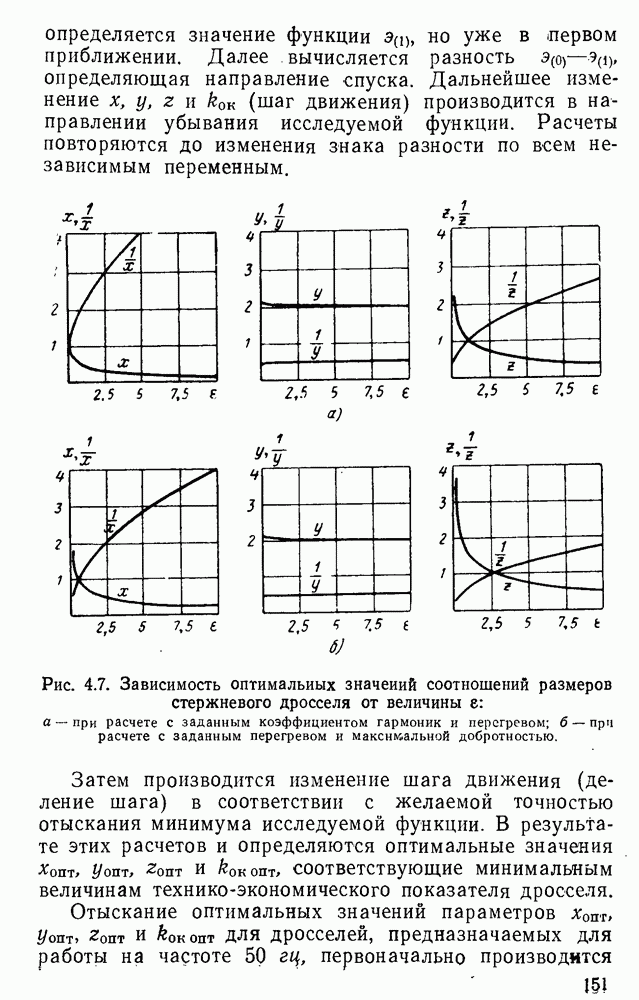
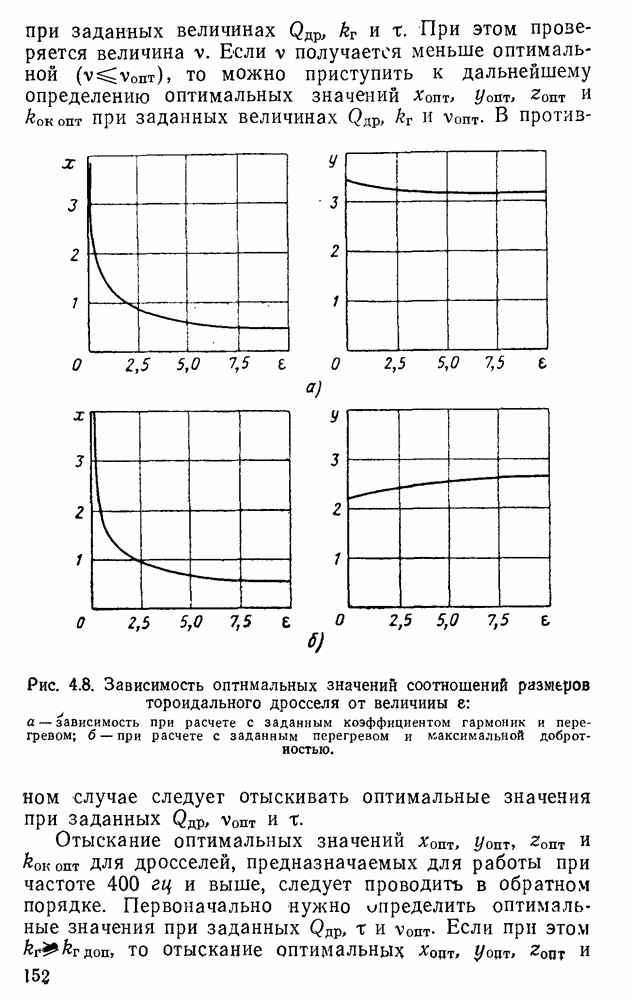
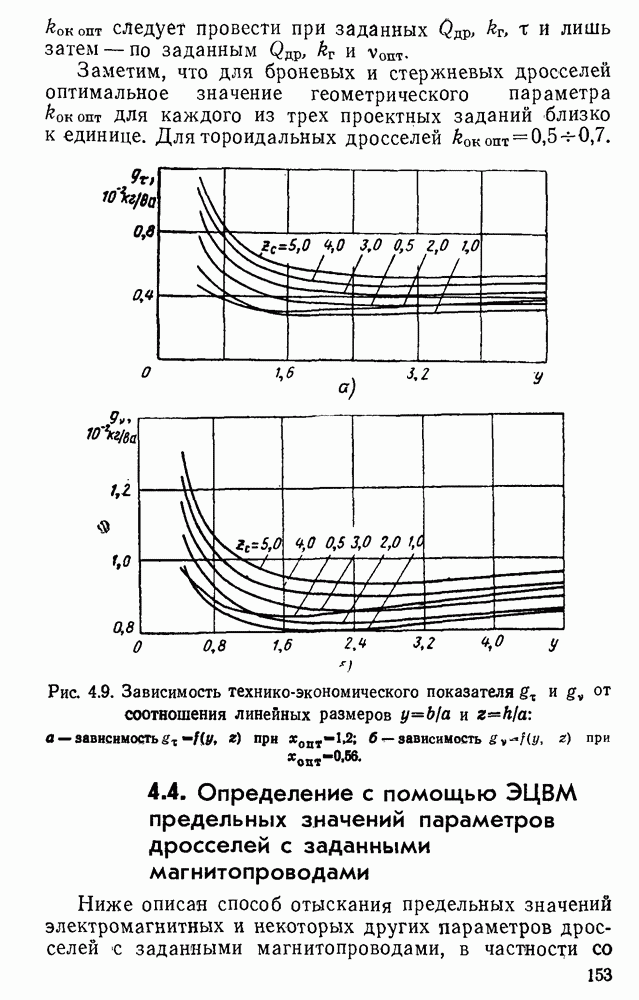
- 4.3. Определение с помощью ЭЦВМ оптимальных значений соотношений геометрических параметров дросселя. Оптимальные значения соотношений разных типов дросселей
- 4.4. Определение с помощью ЭЦВМ предельных значений параметров дросселей с заданными магнитопроводами
- 4.5. Влияние отдельных факторов на оптимальные значения геометрических соотношений дросселя
- 5. ПРОЕКТИРОВАНИЕ ДРОССЕЛЕЙ
- 5.1. Основные замечания. Техническое задание на проектирование дросселя
- 5.2. Методика проектирования дросселей
- 1. Выбор типа дросселя, марки стали и обмоточного материала
- 2. Выбор типоразмера стандартного сердечника или расчет специального сердечника
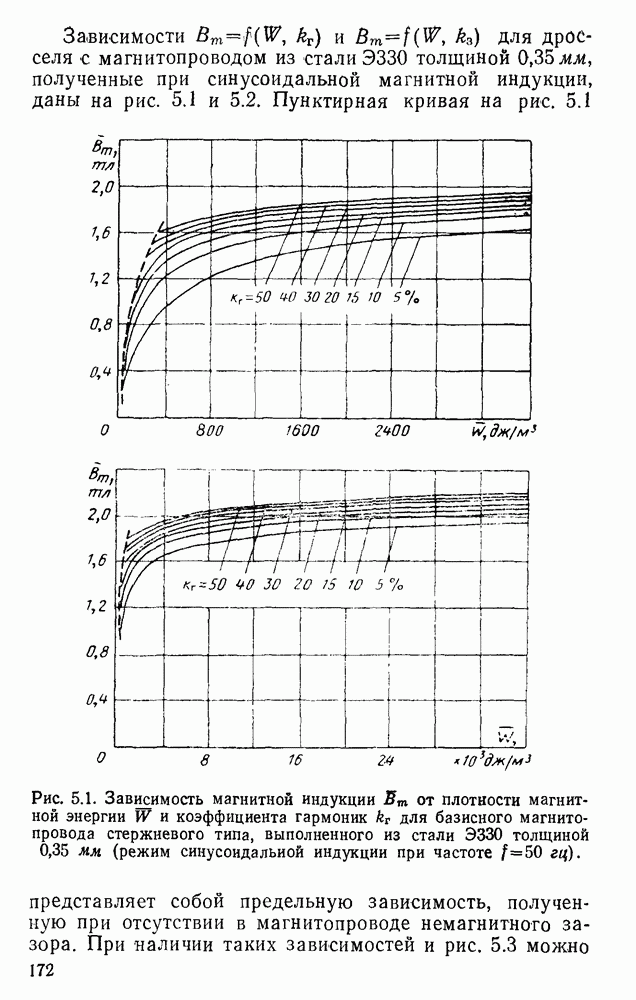
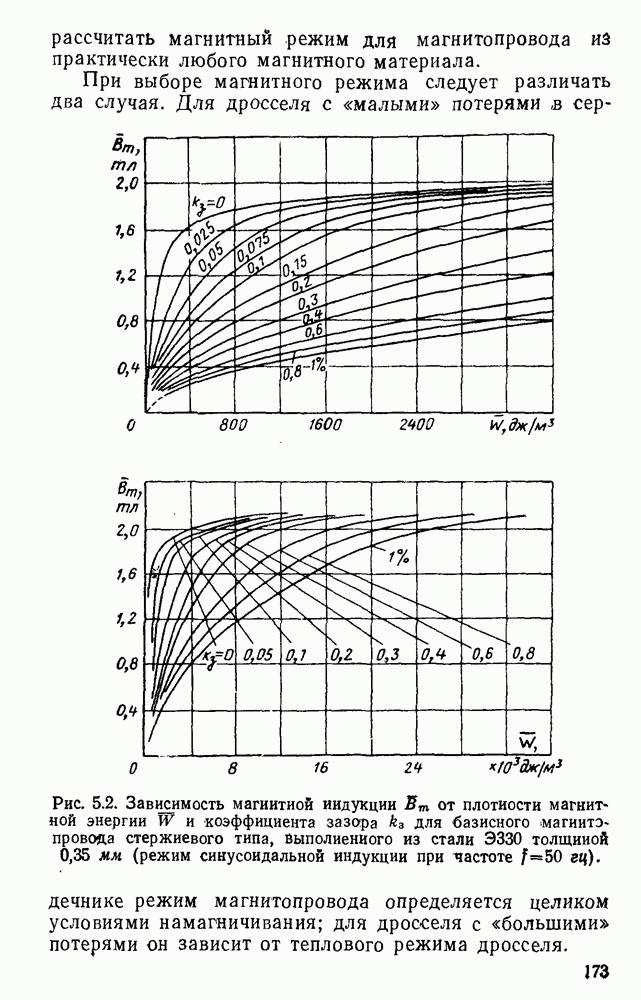
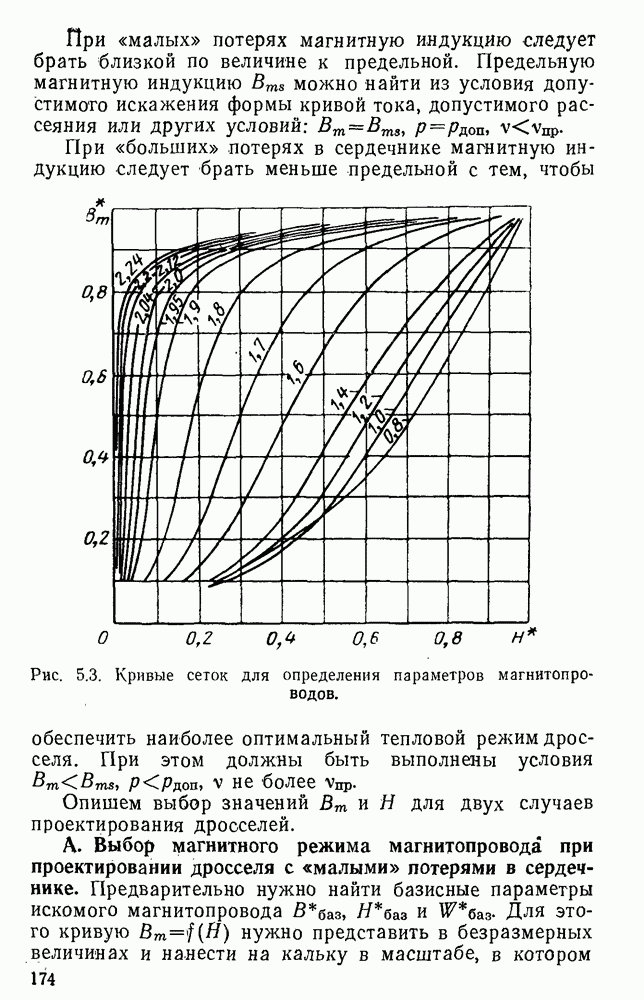
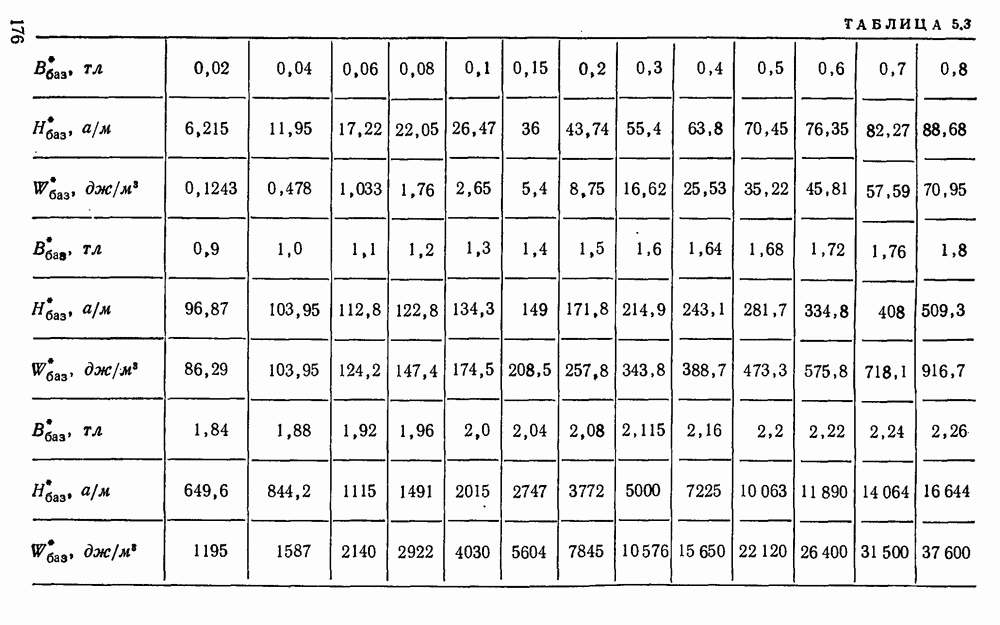
- 3. Выбор магнитного режима магнитопровода дросселя
- 4. Расчет длины немагнитного зазора
- 5. Расчет потерь в дросселе
- 6. Определение геометрических параметров дросселя
- 7. Расчет теплового режима дросселя
- 8. Расчет обмоточных данных и междуслойной изоляции
- 9. Расчет катушек дросселя (конструирование обмоток)
- 10. Определение технико-экономических показателей дросселя
- 11. Проверочный расчет дросселя
- 12. Краткая методика расчета дросселя
- 5.3. Примеры проектирования дросселей
- ПРИЛОЖЕНИЯ
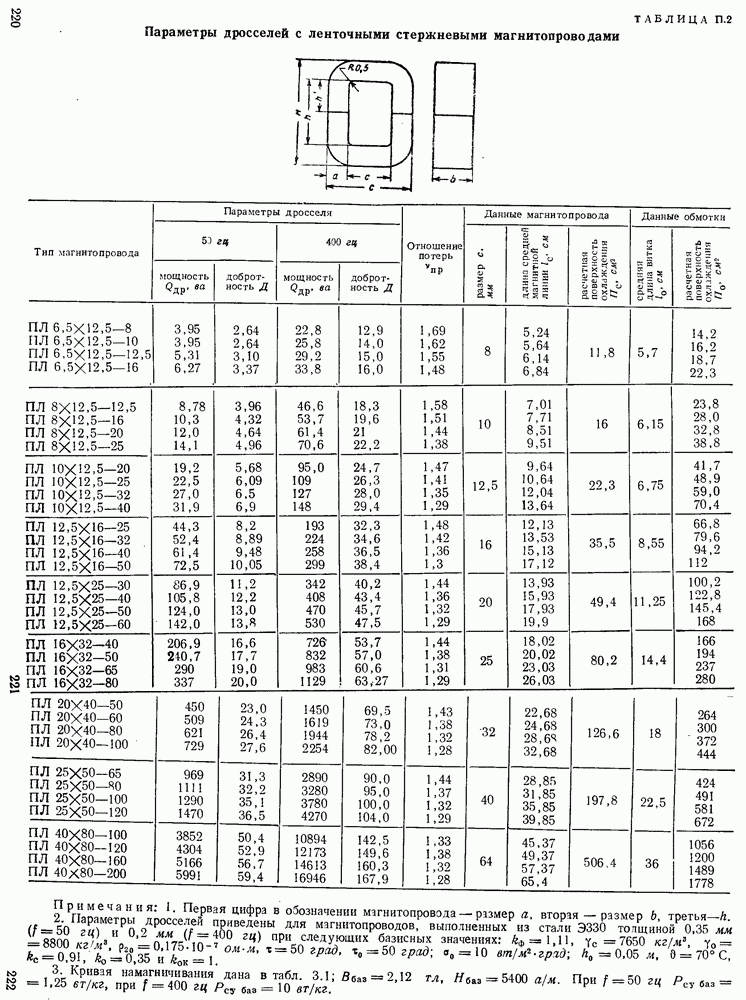
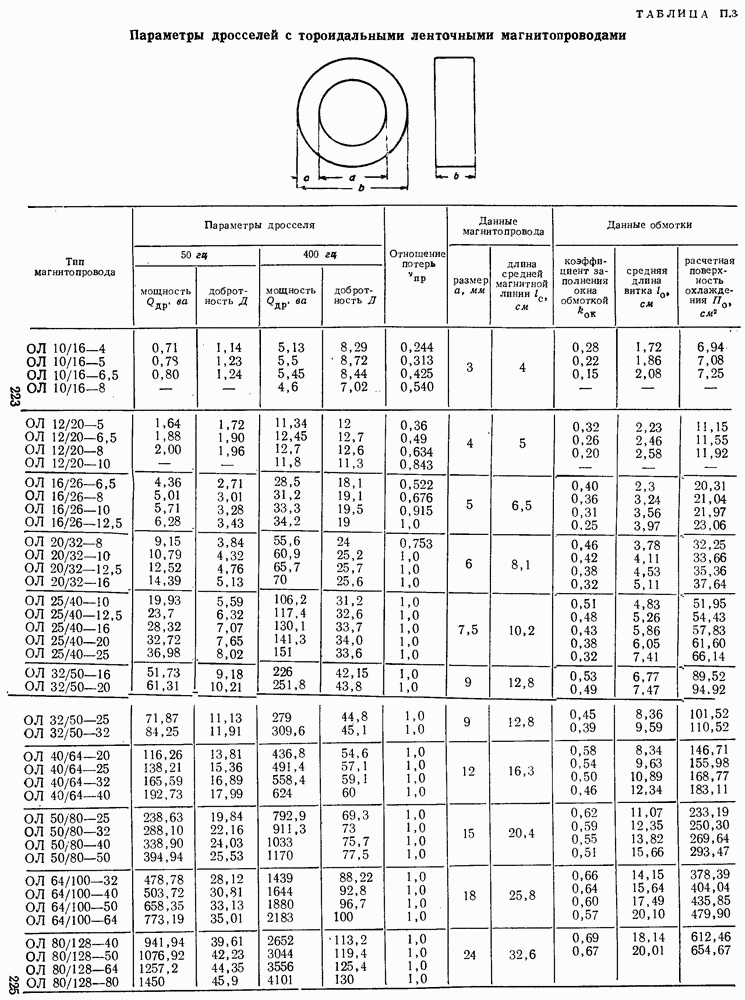
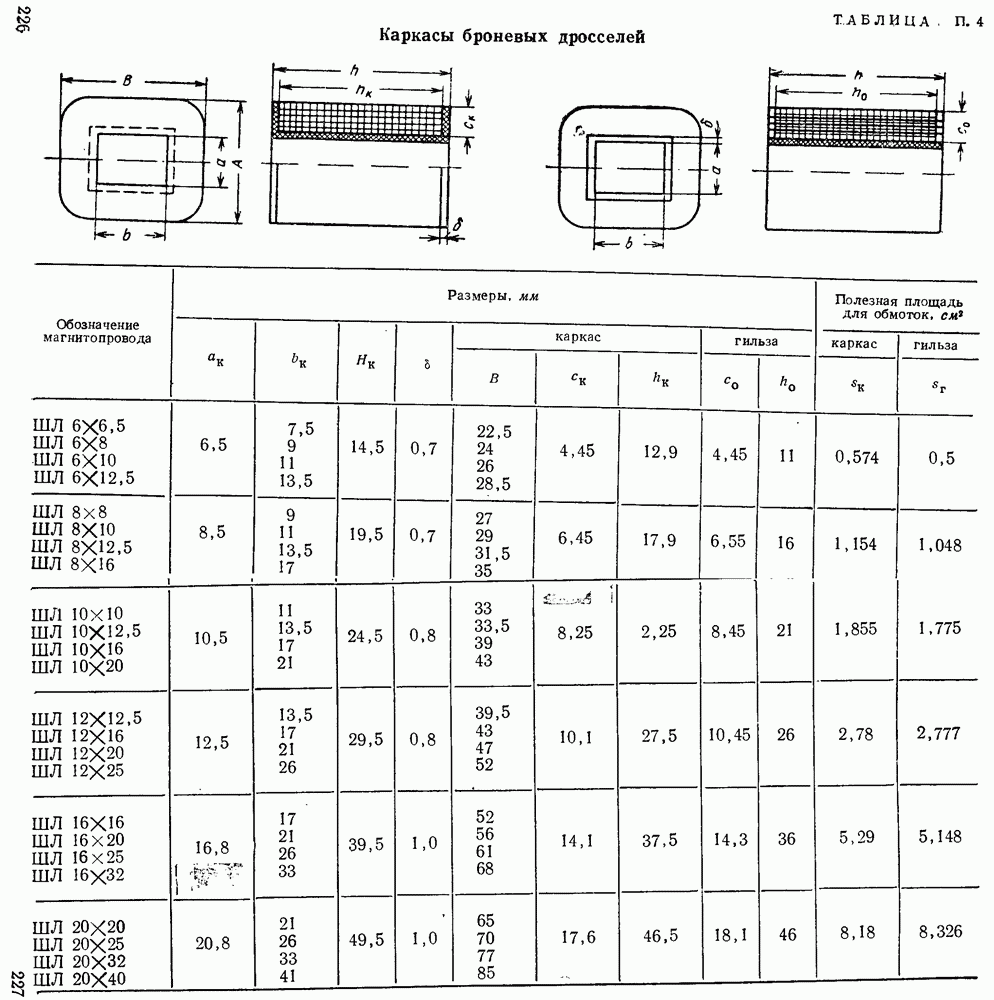
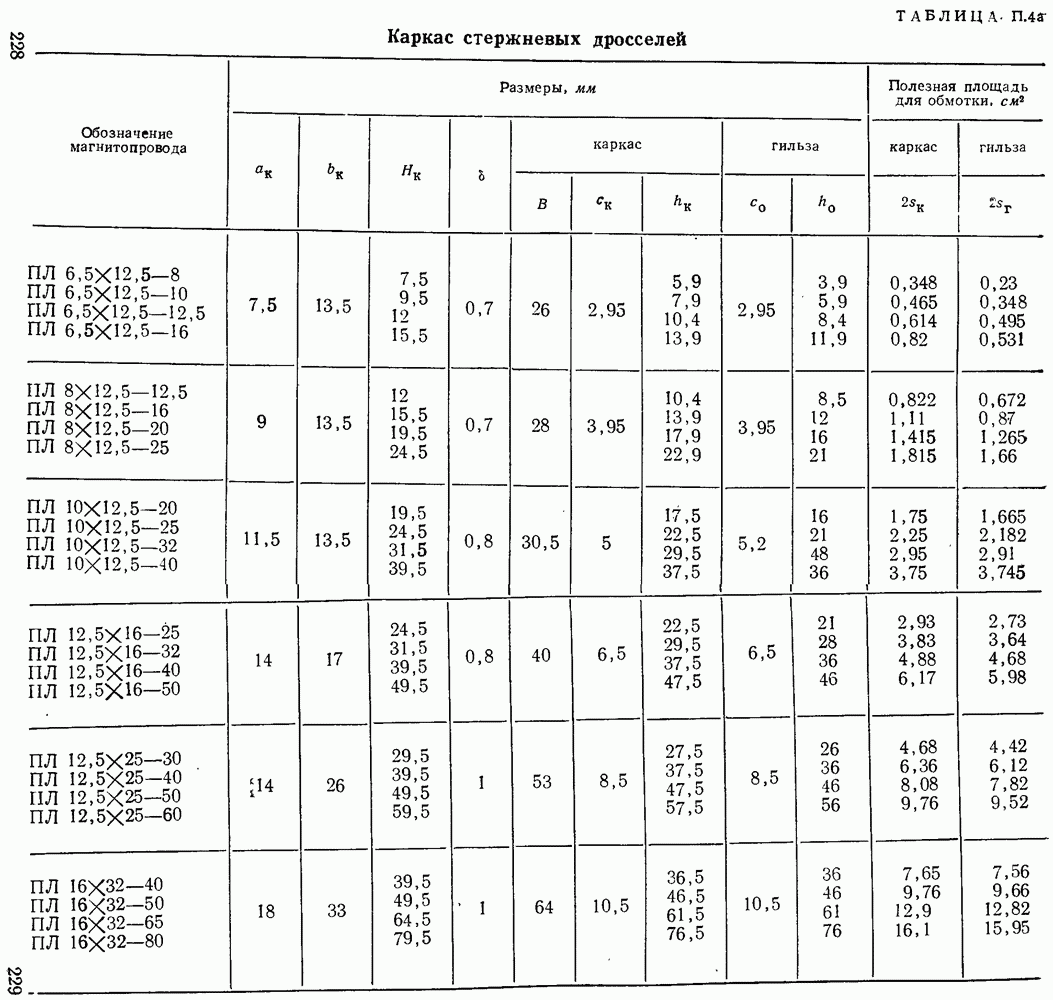
- Основные условные обозначения
- Литература