| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1. Расчет магнитных характеристик для реального дросселя без рассеяния
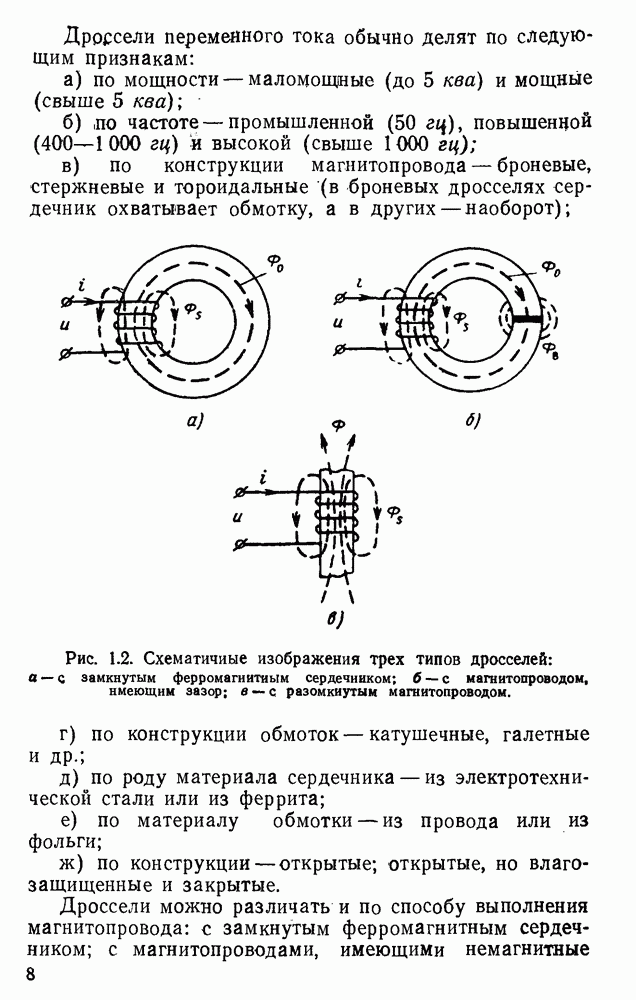
Рассмотрим дифференциальное уравнение для дросселя, питаемого от источника синусоидального напряжения, без учета индуктивности рассеяния обмотки. Такой дроссель, очевидно, может быть представлен схемой, показанной на рис. 3.1.
Для цепи рис. 3.1 можно написать
 (3.60)
(3.60)
Это уравнение для придания общности решения обычно записывают в системе относительных единиц [10]:

где

Здесь  и
и  — выбранные базисные значения магнитной индукции и напряженности поля.
— выбранные базисные значения магнитной индукции и напряженности поля.
Как видим, при введений относительных единиц магнитный поток, напряжение, ток и, наконец, сопротивление обмотки дросселя  заменяются на безразмерные величины
заменяются на безразмерные величины  и таким образом из дифференциального уравнения исключаются такие параметры, как числа витков обмоток w, активное поперечное сечение
и таким образом из дифференциального уравнения исключаются такие параметры, как числа витков обмоток w, активное поперечное сечение  и длина средней магнитной линии сердечника
и длина средней магнитной линии сердечника  частота
частота  а также величины, характеризующие кривую намагничивания
а также величины, характеризующие кривую намагничивания  .
.
Дифференциальное уравнение (3.60) может быть решено, например, методом Рунге-Кутта. Однако в уравнение (3.60) входят величины  обычно неизвестные в начале расчета.
обычно неизвестные в начале расчета.
Гораздо удобнее воспользоваться обобщенным дифференциальным уравнением дросселя, полученным нами и позволяющим рассчитать все необходимые магнитные характеристики. Отметим, что обобщение дифференциального уравнения легко достигается предложенной новой системой относительных единиц. При этой системе коэффициенты в дифференциальном уравнении не зависят от геометрических параметров конкретного дросселя, а являются лишь функцией электромагнитных параметров самого дросселя.
Для получения обобщенного дифференциального уравнения, отображающего в общем виде процессы в нелинейном дросселе, сделаем некоторые преобразования с уравнением (3.60): его второй член умножим и разделим на величину  а правую часть уравнения — на величину
а правую часть уравнения — на величину  . Принимая во внимание очевидные равенства
. Принимая во внимание очевидные равенства

можно после некоторых преобразований получить

где  — коэффициент формы кривой реактивной составляющей напряжения на зажимах дросселя;
— коэффициент формы кривой реактивной составляющей напряжения на зажимах дросселя;
 — коэффициент формы кривой, равный
— коэффициент формы кривой, равный  ,
,  — отношение реактивной составляющей напряжения на зажимах дросселя к напряжению на входе всей цепи;
— отношение реактивной составляющей напряжения на зажимах дросселя к напряжению на входе всей цепи;  параметр дросселя, равный отношению падения напряжения на активном сопротивлении обмотки ко всему напряжению, приложенному к зажимам дросселя.
параметр дросселя, равный отношению падения напряжения на активном сопротивлении обмотки ко всему напряжению, приложенному к зажимам дросселя.
Параметр  имеет непосредственную связь с добротностью дросселя:
имеет непосредственную связь с добротностью дросселя:

 — отношение потерь в сердечнике дросселя к потерям в его обмотке.
— отношение потерь в сердечнике дросселя к потерям в его обмотке.
При известной величине добротности  дросселя параметр
дросселя параметр  имеет вполне определенное значение. И, наоборот, при определенном значении
имеет вполне определенное значение. И, наоборот, при определенном значении  дроссель имеет вполне определенную величину добротности.
дроссель имеет вполне определенную величину добротности.
В дифференциальное уравнение (3.61) не входят такие параметры, как число витков w, сечение магнитопровода  и др., т. е. полученное уравнение — действительно обобщенное. Это позволяет и его решение получить в общем виде, т. е. вне связи с некоторыми конкретными конструктивными параметрами дросселя.
и др., т. е. полученное уравнение — действительно обобщенное. Это позволяет и его решение получить в общем виде, т. е. вне связи с некоторыми конкретными конструктивными параметрами дросселя.
Решение дифференциального уравнения (3.61) приводит к получению нужных магнитных характеристик дросселя:  и др., учитывающих режим работы реального нелинейного дросселя без рассеяния. Расчет таких характеристик производится впервые.
и др., учитывающих режим работы реального нелинейного дросселя без рассеяния. Расчет таких характеристик производится впервые.
Для расчета магнитных характеристик нужны кривые зависимостей активных и реактивных слагающих напряженности магнитного поля от магнитной индукции  Способ получения таких зависимостей приведен в § 3.7. Кривые должны быть аппроксимированы какой-либо конкретной функцией. Поскольку решение дифференциального уравнения (3.61) практически возможно только с помощью ЭЦВМ, для зависимостей
Способ получения таких зависимостей приведен в § 3.7. Кривые должны быть аппроксимированы какой-либо конкретной функцией. Поскольку решение дифференциального уравнения (3.61) практически возможно только с помощью ЭЦВМ, для зависимостей  лучше всего взять сумму гиперболических и соответственно сумму круговых синусов, наиболее точно отображающих реальные кривые намагничивания дросселя.
лучше всего взять сумму гиперболических и соответственно сумму круговых синусов, наиболее точно отображающих реальные кривые намагничивания дросселя.
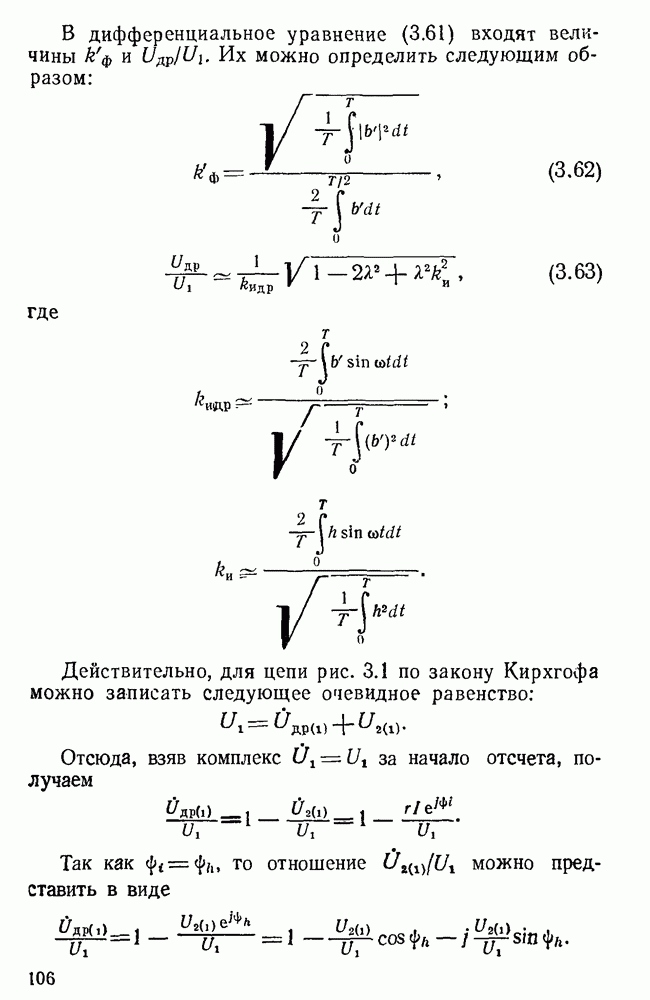
В дифференциальное уравнение (3.61) входят величины  . Их можно определить следующим образом:
. Их можно определить следующим образом:

и

где

Действительно, для цепи рис. 3.1 по закону Кирхгофа можно записать следующее очевидное равенство:

Отсюда, взяв комплекс  за начало отсчета, получаем
за начало отсчета, получаем

Так как  отношение
отношение  можно представить в виде
можно представить в виде

Отсюда модуль величины

Величину фазового угла  можно найти, принимая во внимание следующее обстоятельство. Известно, что при синусоидальном напряжении
можно найти, принимая во внимание следующее обстоятельство. Известно, что при синусоидальном напряжении  мощность на входе дросселя обусловливается только первой гармоникой тока:
мощность на входе дросселя обусловливается только первой гармоникой тока:

Отсюда при принятом начале отсчета, т. е. когда  имеем
имеем

или без учета потерь в стали

Путем подстановки выражения (3.64) в формулу (3.64) легко получить уравнение (3.63).
Как следует из (3.63), в исследуемом дросселе отношение  обусловливается не только отношением
обусловливается не только отношением  , но и коэффициентом искажений форм кривых напряжения на зажимах идеализированного дросселя и тока, протекающего по обмотке. При синусоидальном напряжении
, но и коэффициентом искажений форм кривых напряжения на зажимах идеализированного дросселя и тока, протекающего по обмотке. При синусоидальном напряжении  и токе в обмотке I (линейный дроссель), т. е. при
и токе в обмотке I (линейный дроссель), т. е. при  имеем
имеем

Как видим, уравнение (3.63) справедливо и для линейного дросселя. Другими словами, известное уравнение (3.63) является частным случаем обобщенного уравнения (3.63), правомерного для любого идеализированного дросселя без рассеяния.
Для решения с помощью ЭЦВМ дифференциального уравнения (3.61) нами разработана специальная программа, позволяющая определять методом Рунге-Кутга [13] все необходимые характеристики дросселя без рассеяния.
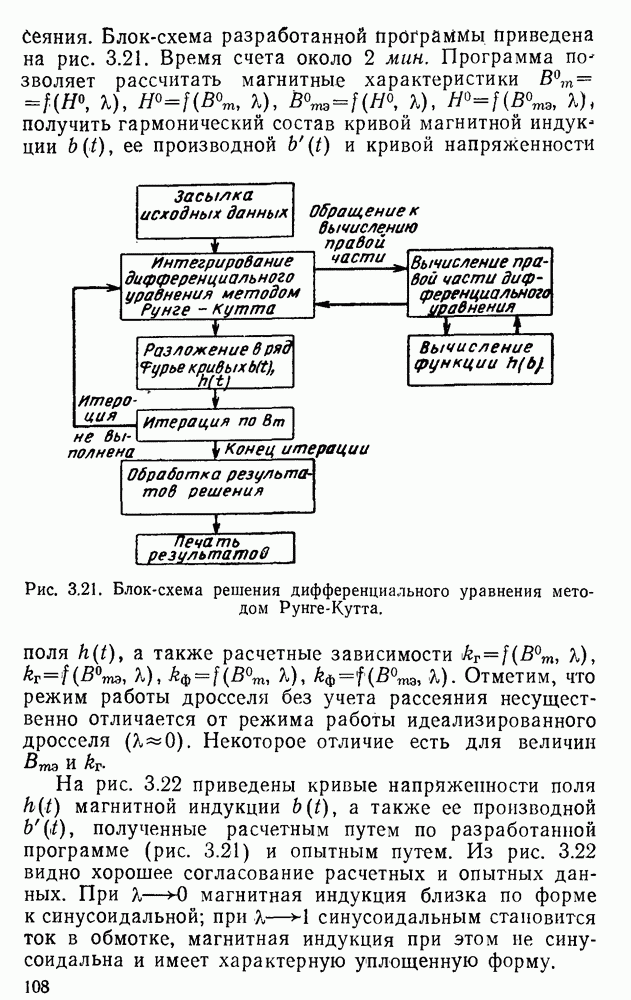
Блок-схема разработанной программы приведена на рис. 3.21. Время счета около 2 мин. Программа по зволяет рассчитать магнитные характеристики  , получить гармонический состав кривой магнитной индукции
, получить гармонический состав кривой магнитной индукции  ее производной
ее производной  и кривой напряженности поля
и кривой напряженности поля  , а также расчетные зависимости
, а также расчетные зависимости  . Отметим, что режим работы дросселя без учета рассеяния несущественно отличается от режима работы идеализированного дросселя
. Отметим, что режим работы дросселя без учета рассеяния несущественно отличается от режима работы идеализированного дросселя  . Некоторое отличие есть для величин
. Некоторое отличие есть для величин 

Рис. 3.21. Блок-схема решения дифференциального уравнения методом Рунге-Кутта.
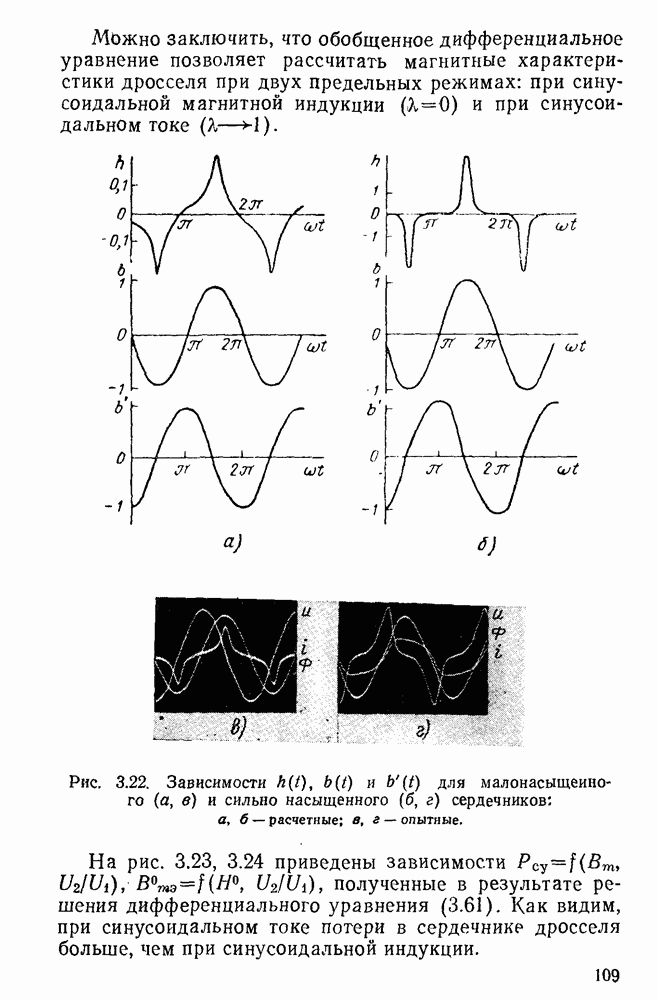
На рис. 3.22 приведены кривые напряженности поля  магнитной индукции
магнитной индукции  а также ее производной
а также ее производной  полученные расчетным путем по разработанной программе (рис. 3.21) и опытным путем. Из рис. 3.22 видно хорошее согласование расчетных и опытных данных. При
полученные расчетным путем по разработанной программе (рис. 3.21) и опытным путем. Из рис. 3.22 видно хорошее согласование расчетных и опытных данных. При  магнитная индукция близка по форме к синусоидальной; при
магнитная индукция близка по форме к синусоидальной; при  синусоидальным становится ток в обмотке, магнитная индукция при этом не синусоидальна и имеет характерную уплощенную форму.
синусоидальным становится ток в обмотке, магнитная индукция при этом не синусоидальна и имеет характерную уплощенную форму.
Можно заключить, что обобщенное дифференциальное уравнение позволяет рассчитать магнитные характеристики дросселя при двух предельных режимах: при синусоидальной магнитной индукции  и при синусоидальном токе
и при синусоидальном токе 

Рис. 3.22. Зависимости  для малонасыщенного
для малонасыщенного  и сильно насыщенного
и сильно насыщенного  сердечников: а, б — расчетные; в, г — опытные.
сердечников: а, б — расчетные; в, г — опытные.
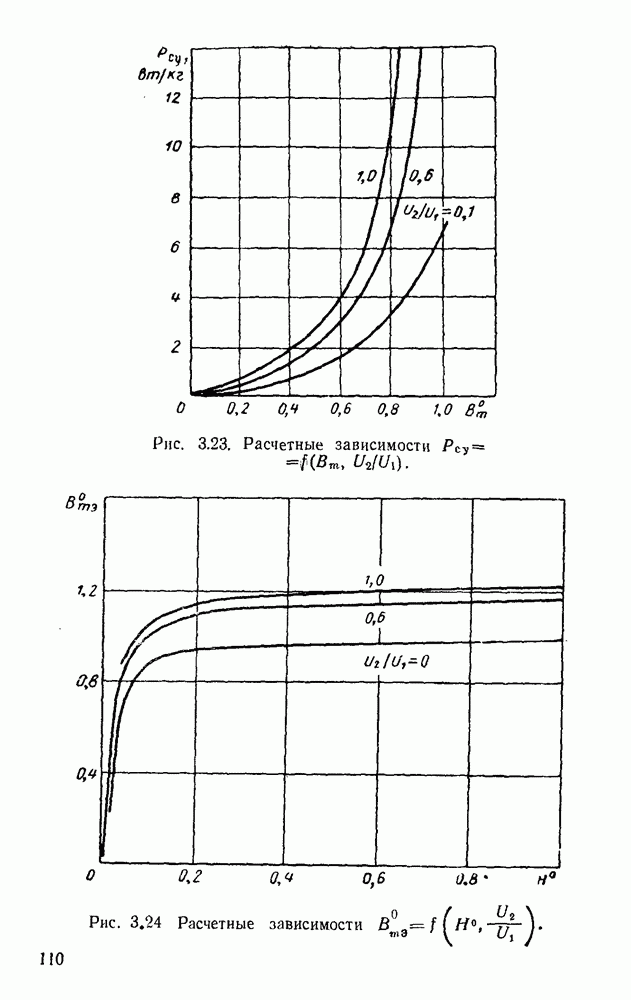
На рис. 3.23, 3.24 приведены зависимости  полученные в результате решения дифференциального уравнения (3.61). Как видим, при синусоидальном токе потери в сердечнике дросселя больше, чем при синусоидальной индукции.
полученные в результате решения дифференциального уравнения (3.61). Как видим, при синусоидальном токе потери в сердечнике дросселя больше, чем при синусоидальной индукции.

Рис. 3.23. Расчетные зависимости 

Рис. 3.24 Расчетные зависимости 
Из рассмотрения рис. 3.23 и 3.24 можно сделать вывод, что при малых  , магнитные характеристики дросселя с учетом активного сопротивления обмотки незначительно отличаются от характеристик идеализированного дросселя и, следовательно, для обычного проектирования правомерно пользование магнитными характеристиками, полученными без учета сопротивления обмотки.
, магнитные характеристики дросселя с учетом активного сопротивления обмотки незначительно отличаются от характеристик идеализированного дросселя и, следовательно, для обычного проектирования правомерно пользование магнитными характеристиками, полученными без учета сопротивления обмотки.
Программа может быть использована также и для решения другой задачи — для определения режима работы идеализированного дросселя, включенного в цепь с активной нагрузкой, например цепь накала радиоламп. Действительно, если во всех уравнениях считать параметр  равным отношению напряжения на активной нагрузке ко входному напряжению цепи, то дифференциальное уравнение будет описывать процессы в идеализированном дросселе, включенном последовательно с активной нагрузкой. Активное сопротивление обмотки реального дросселя для такого рассмотрения должно быть отнесено к сопротивлению нагрузки.
равным отношению напряжения на активной нагрузке ко входному напряжению цепи, то дифференциальное уравнение будет описывать процессы в идеализированном дросселе, включенном последовательно с активной нагрузкой. Активное сопротивление обмотки реального дросселя для такого рассмотрения должно быть отнесено к сопротивлению нагрузки.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- 1. ОСНОВНЫЕ СВЕДЕНИЯ О НЕУПРАВЛЯЕМЫХ ДРОССЕЛЯХ ПЕРЕМЕННОГО ТОКА РАДИОЭЛЕКТРОННОЙ АППАРАТУРЫ
- 1.1. Общие краткие сведения о дросселях. Классификация дросселей
- 1.2. Номинальные параметры нелинейного дросселя
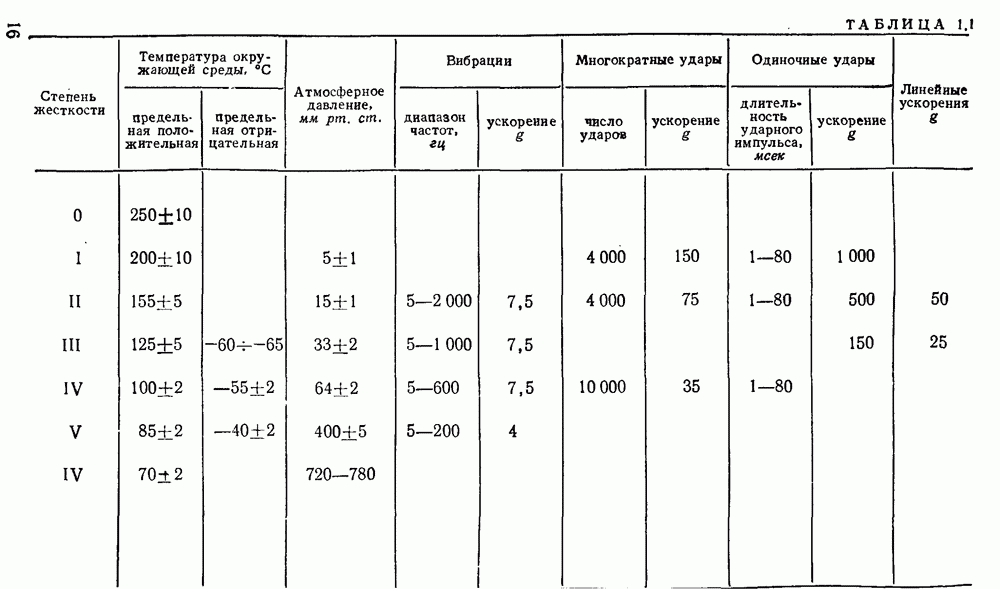
- 1.3. Требования, предъявляемые к дросселям радиоэлектронной аппаратуры. Степени жесткости
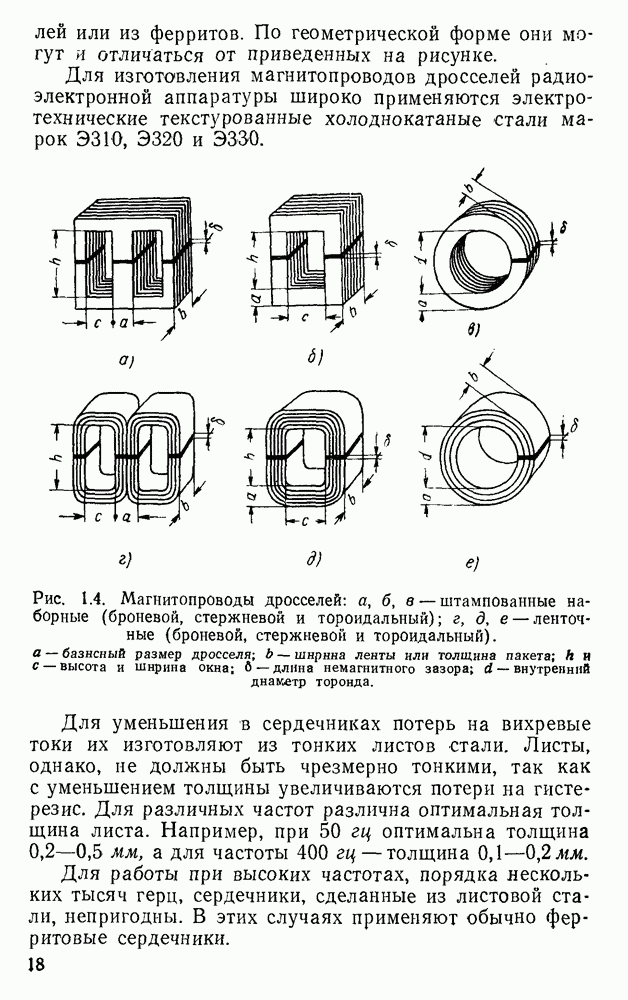
- 1.4. Устройство маломощных дросселей переменного тока
- 1.5. Нагрев и охлаждение дросселей
- 1.6. Экранирование дросселей
- 1.7. Сравнение разных типов дросселей
- 2. МАГНИТНЫЕ СВОЙСТВА МАГНИТОПРОВОДОВ ДРОССЕЛЕЙ. ВЫБОР ФЕРРОМАГНЕТИКА
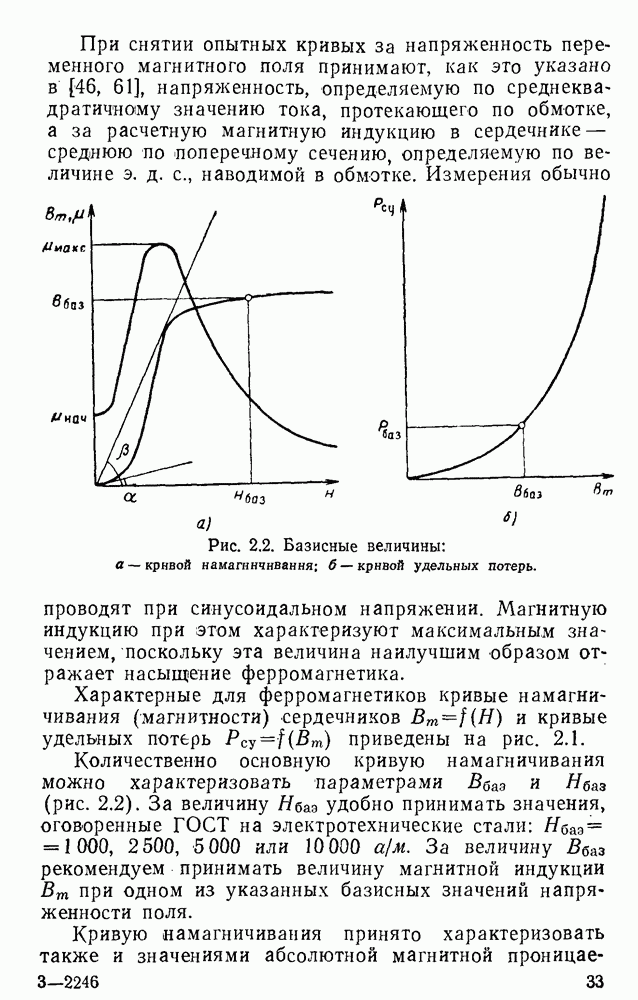
- 2.1. Свойства магнитопроводов дросселей
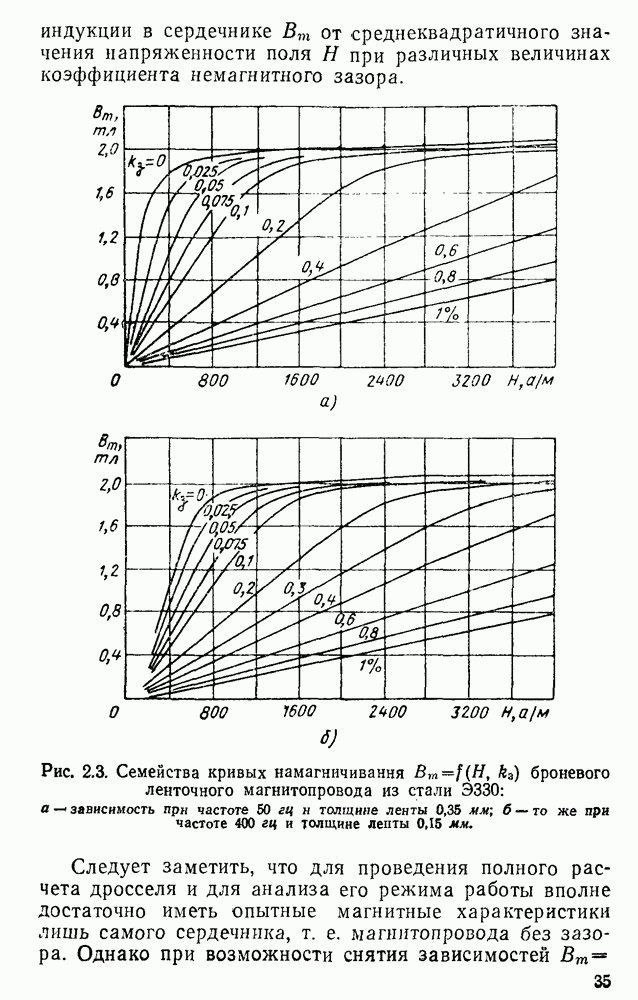
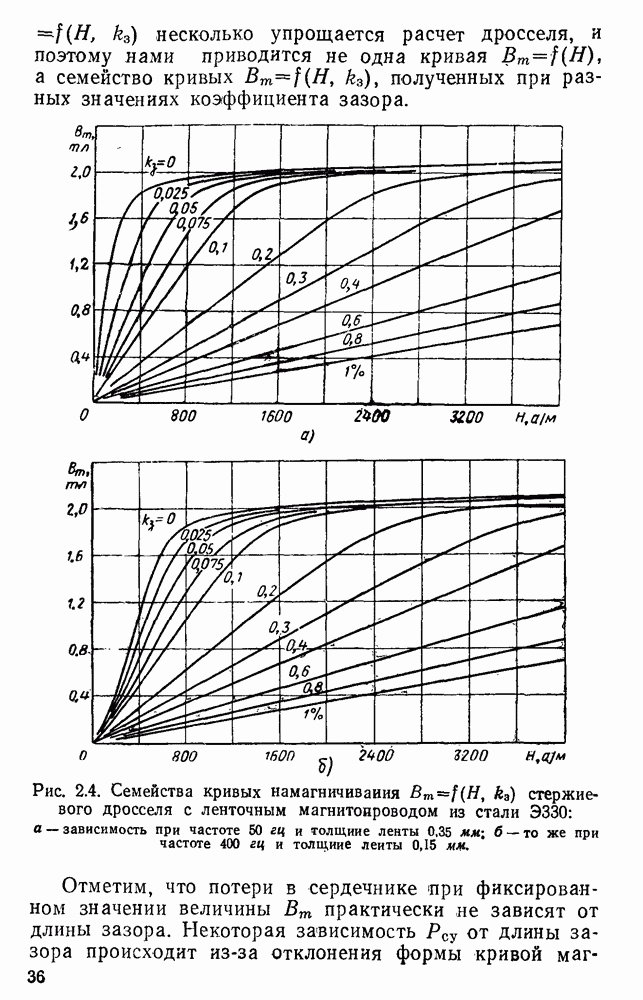
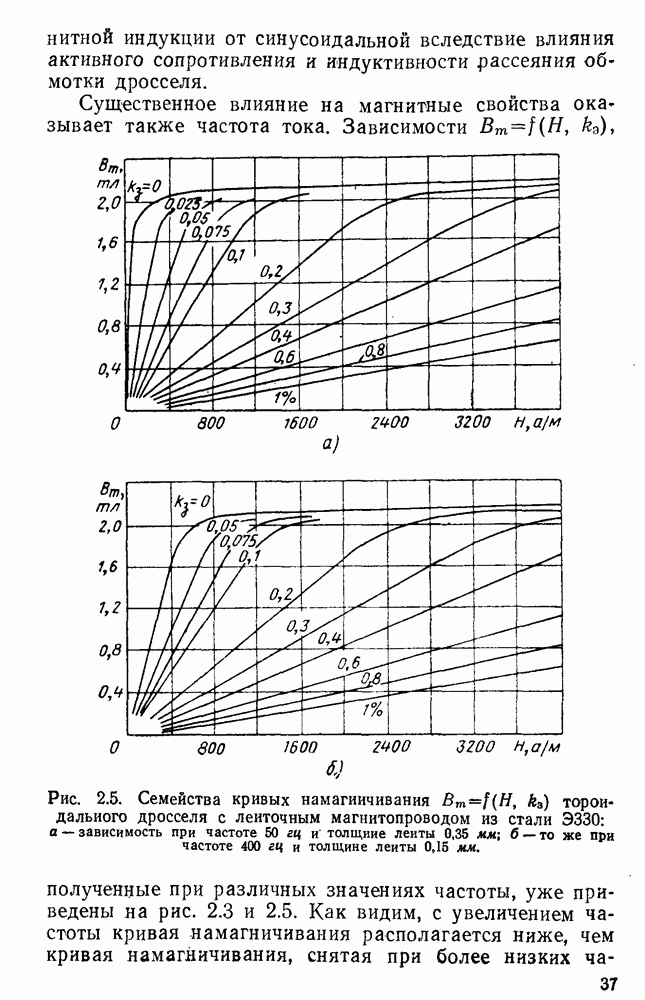
- 2.2. Экспериментальное определение магнитных характеристик магнитопроводов дросселей
- 2.3. Выбор ферромагнетика для сердечника дросселя
- 3. ТЕОРИЯ РАБОТЫ ДРОССЕЛЯ ПЕРЕМЕННОГО ТОКА С НЕЛИНЕЙНЫМ ФЕРРОМАГНИТНЫМ СЕРДЕЧНИКОМ
- 3.2. Связи между электрическими и магнитными величинами в дросселе с нелинейным ферромагнитным сердечником. Эквивалентный дроссель
- 1. Идеальный и идеализированный дроссели без зазора
- 2. Идеальный и идеализированный дроссели с немагнитным зазором
- 3. Реальный дроссель
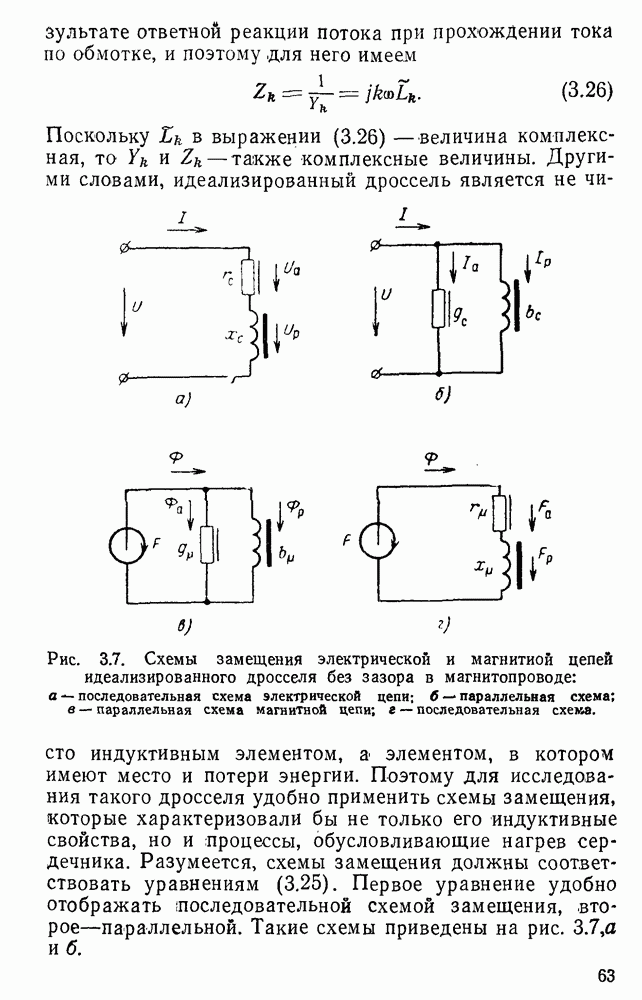
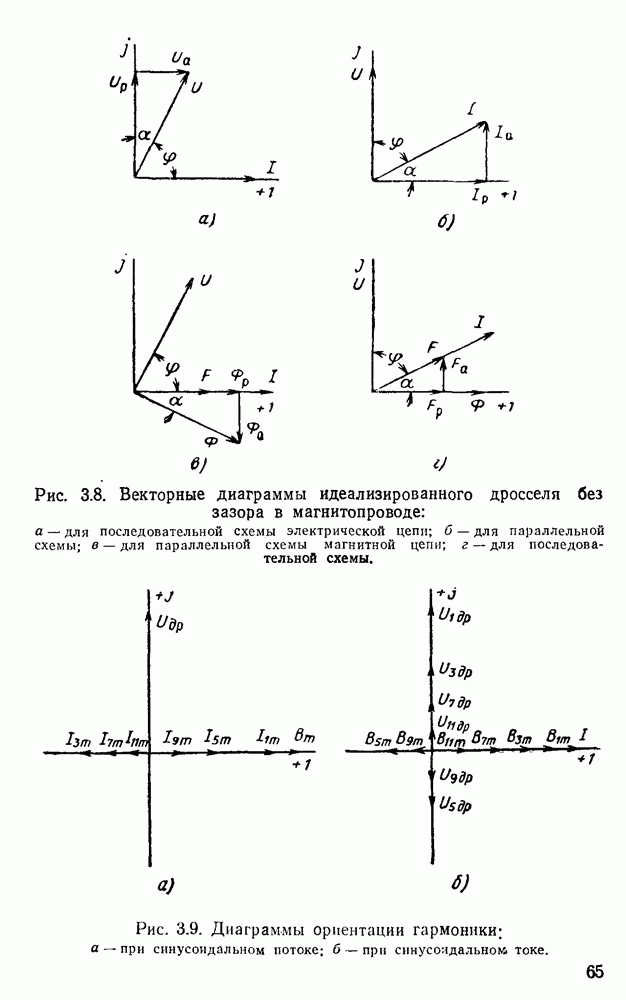
- 3.3. Схемы замещения и векторные диаграммы идеализированного дросселя
- 1. Схемы замещения и векторные диаграммы электрической цепи идеализированного дросселя
- 2. Схемы замещения и векторные диаграммы магнитной цепи идеализированного дросселя
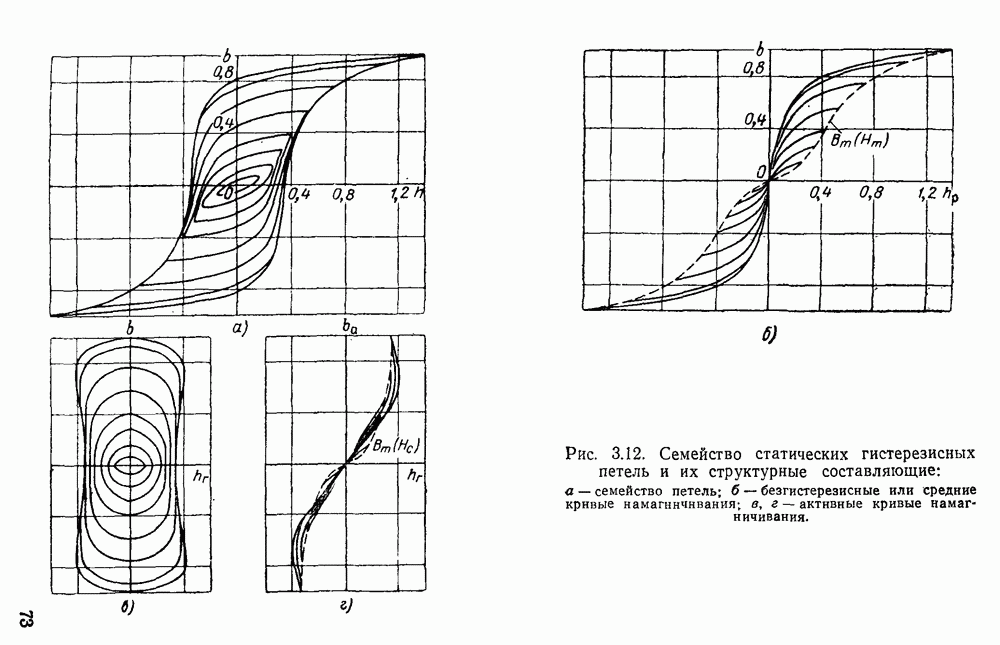
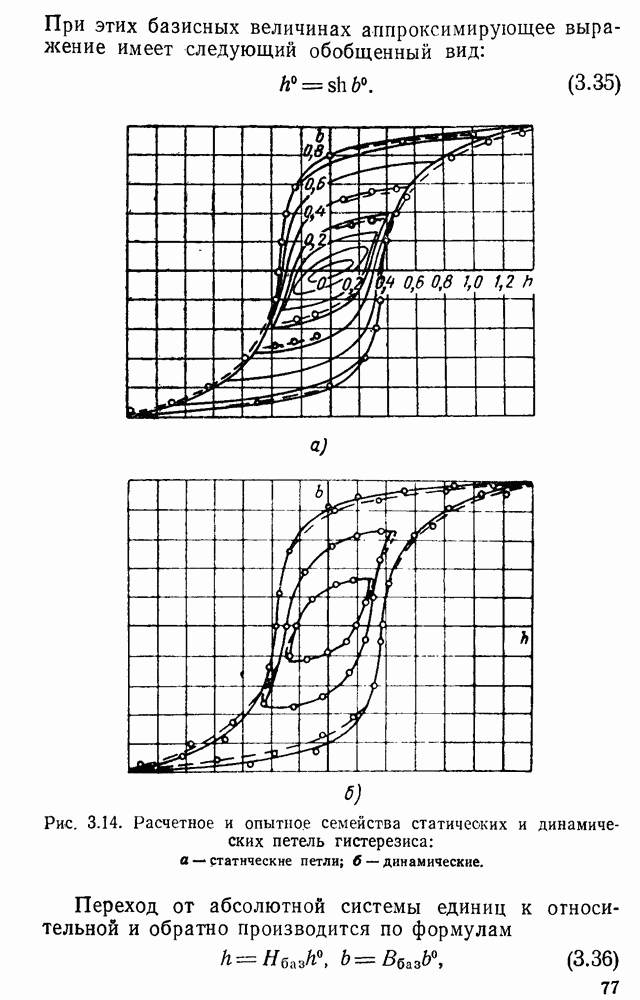
- 3.4. Аппроксимация кривых намагничивания ферромагнитных сердечников. Относительные единицы. Определение коэффициентов аппроксимации
- 3.5. Математическая модель семейства динамических гистерезисных петель. Использование модели для решения задач гармонического анализа
- 1. Определение гармонического состава кривой напряженности поля
- 2. Определение среднеквадратичного значения напряженности поля и потерь в стали
- 3.6. Аналитический расчет магнитных характеристик магнитопроводов идеальных и идеализированных дросселей с зазором
- 3.7. Расчет численными методами магнитных характеристик идеальных и идеализированных дросселей при произвольной форме кривой магнитной индукции
- 3.8. Расчет магнитных характеристик реальных дросселей. Расчет характеристик дросселей, включенных в электрические цепи
- 1. Расчет магнитных характеристик для реального дросселя без рассеяния
- 2. Расчет магнитных характеристик для дросселя, включенного последовательно с активно-индуктивной нагрузкой
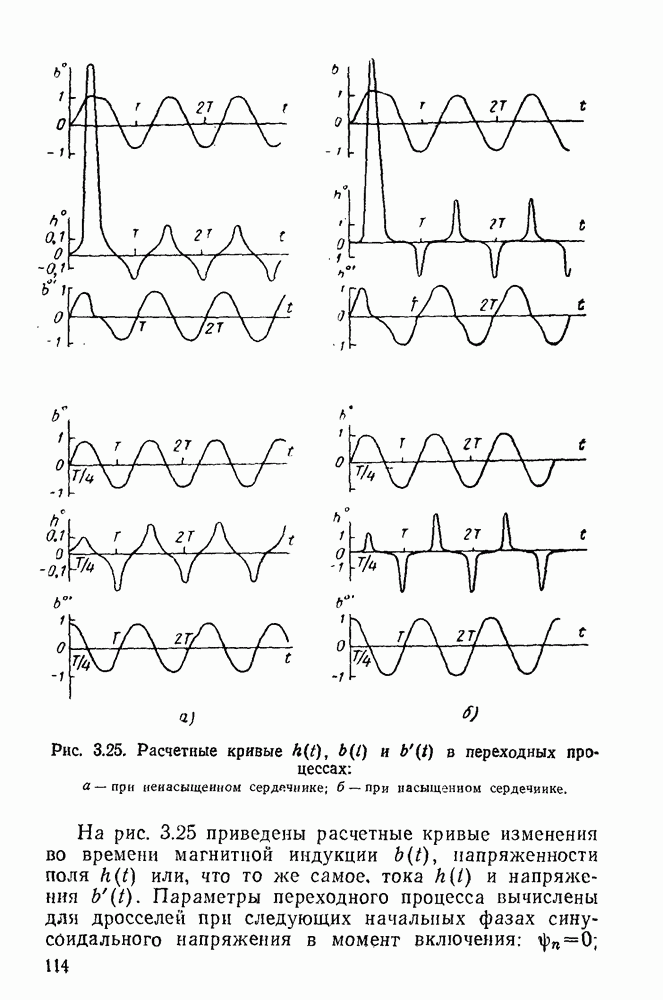
- 3.9. Переходные процессы в дросселе
- 3.10. Определение электромагнитного режима и параметров дросселя
- 2. Определение режима и основных характеристик дросселя по комплексной магнитной проницаемости его сердечника
- 4. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПРОЕКТИРОВАНИЯ ДРОССЕЛЕЙ
- 4.1. Общие замечания. Понятие об оптимальных дросселях и их параметрах
- 4.2. Основные уравнения взаимосвязи параметров дросселя и их решение
- 2. Уравнение потерь
- 3. Уравнение теплового режима дросселя
- 4. Уравнения взаимосвязи магнитных параметров дросселя
- 5. Обобщенные уравнения геометрических параметров разных типов и конструкций дросселей
- 6. Технико-экономические показатели дросселей
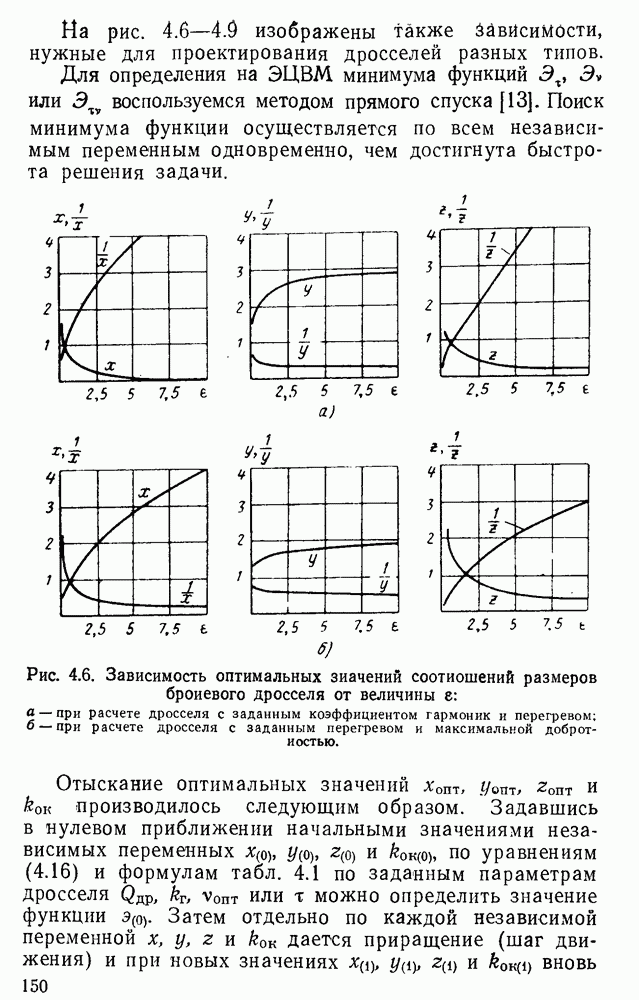
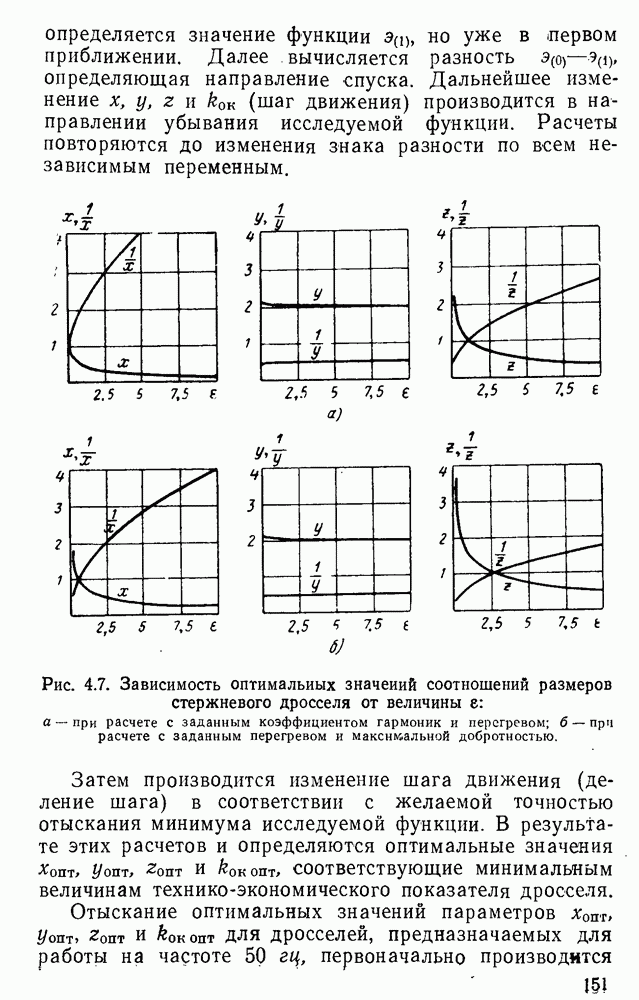
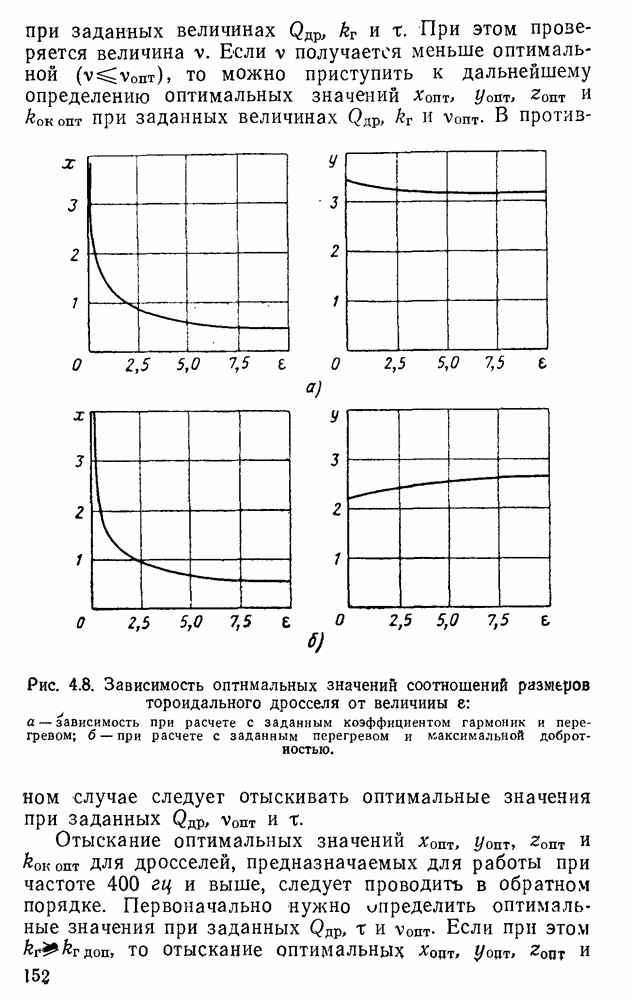
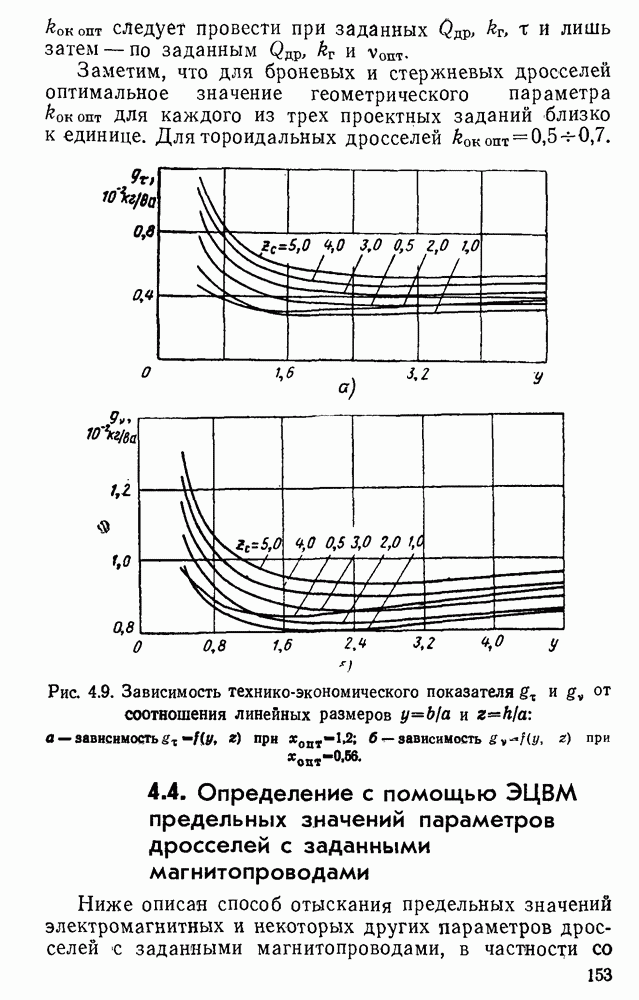
- 4.3. Определение с помощью ЭЦВМ оптимальных значений соотношений геометрических параметров дросселя. Оптимальные значения соотношений разных типов дросселей
- 4.4. Определение с помощью ЭЦВМ предельных значений параметров дросселей с заданными магнитопроводами
- 4.5. Влияние отдельных факторов на оптимальные значения геометрических соотношений дросселя
- 5. ПРОЕКТИРОВАНИЕ ДРОССЕЛЕЙ
- 5.1. Основные замечания. Техническое задание на проектирование дросселя
- 5.2. Методика проектирования дросселей
- 1. Выбор типа дросселя, марки стали и обмоточного материала
- 2. Выбор типоразмера стандартного сердечника или расчет специального сердечника
- 3. Выбор магнитного режима магнитопровода дросселя
- 4. Расчет длины немагнитного зазора
- 5. Расчет потерь в дросселе
- 6. Определение геометрических параметров дросселя
- 7. Расчет теплового режима дросселя
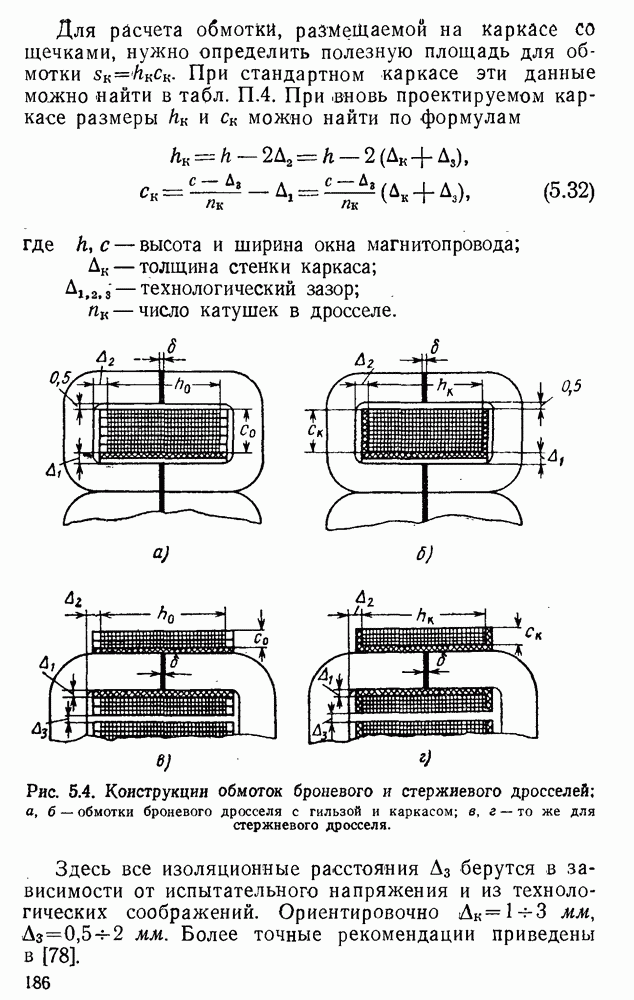
- 8. Расчет обмоточных данных и междуслойной изоляции
- 9. Расчет катушек дросселя (конструирование обмоток)
- 10. Определение технико-экономических показателей дросселя
- 11. Проверочный расчет дросселя
- 12. Краткая методика расчета дросселя
- 5.3. Примеры проектирования дросселей
- ПРИЛОЖЕНИЯ
- Основные условные обозначения
- Литература