| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
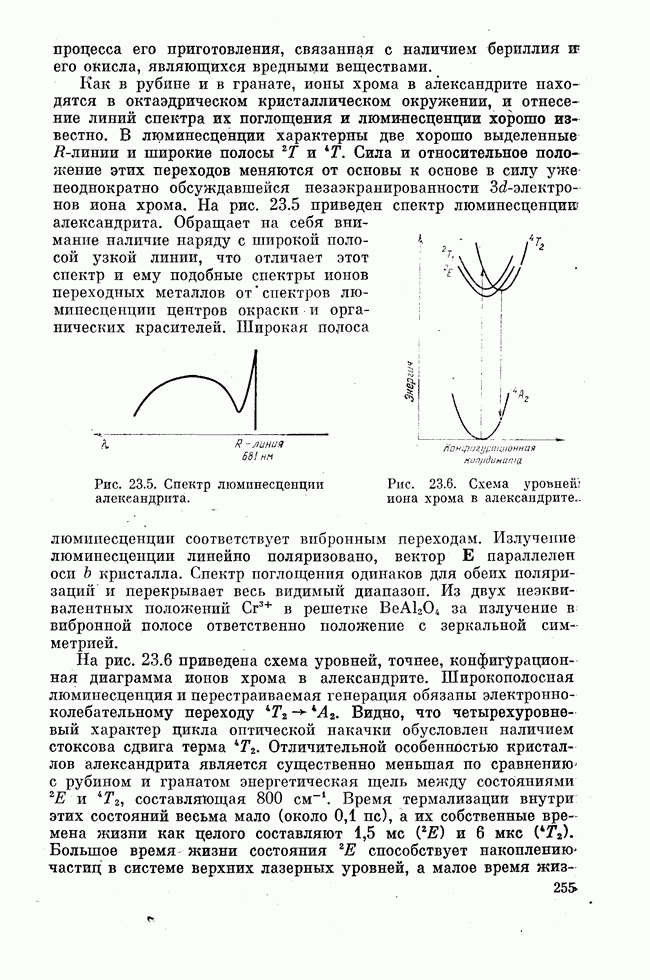
Лекция десятая. НЕУСТОЙЧИВЫЕ РЕЗОНАТОРЫ
Геометро-оптическое рассмотрение. Коэффициент увеличения, потери на излучение. Симметричный резонатор, телескопический резонатор. Эквивалентное число Френеля. Селекция продольных мод. Частотная селекция, пространственная селекция тонкими поглотителями. Дисперсионные резонаторы.
Итак, для неустойчивого резонатора либо произведение

либо произведение

где  . Соответственно неустойчивые резонаторы подразделяются на два класса — резонаторы отрицательной области (10.1) и положительной области (10.2). На диаграмме устойчивости (рис. 9.4) положительная область неустойчивости расположена в первом и третьем квадрантах вне гиперболы
. Соответственно неустойчивые резонаторы подразделяются на два класса — резонаторы отрицательной области (10.1) и положительной области (10.2). На диаграмме устойчивости (рис. 9.4) положительная область неустойчивости расположена в первом и третьем квадрантах вне гиперболы  , отрицательная область неустойчивости — во втором и четвертом квадрантах.
, отрицательная область неустойчивости — во втором и четвертом квадрантах.
Анализ неустойчивых резонаторов может быть достаточно далеко проведен методами геометрической оптики. Дело в том, что в устойчивых резонаторах, где формирование моды в результате многократных отражений волны от зеркал рассматривалось в соответствии с законами дифракции, моды низшего порядка имеют незначительные дифракционные потери. Гауссово поперечное распределение ограничивает размер пятна моды и за край зеркала дифрагирует ничтожная доля энергии. Наличие гауссова распределения определяется фокусирующим действием зеркал в конфигурации устойчивого сферического резонатора. В неустойчивом резонаторе такой фокусировки нет, свет не концентрируется вблизи оси резонатора. И хотя потери, обусловленные выходом излучения за край зеркала, в общем случае всегда можно классифицировать как дифракционные, неустойчивые резонаторы удобно рассматривать с точки зрения геометрической оптики, счптая лучи, выходящие за пределы зеркал, источником геометрических потерь. При этом надо иметь в виду, что геометрические потери в неустойчивых, резонаторах тесно связаны с дифракционными потерями в устойчивых резопаторах и должны совпадать с ними на границе устойчивости.
Пусть числа Френеля зеркал резонатора велики и дифракционными потерями можно пренебречь. В силу отсутствия фокусировки излучения к оси резонатора естественно считать, что зеркала заполнены излучением однородно. Это отличает неустойчивый резонатор от устойчивого. Вместе с тем волновой фронт излучения, задаваемый граничными условиями, налагаемыми сферическими зеркалами, является сферическим. Это объединяет неустойчивые резонаторы с устойчивыми.
Итак, мы считаем, что в геометро-оптическом приближении распределение поля в неустойчивом резонаторе, т. е. его мода, представляет собой суперпозицию двух сферических волн с однородным распределением интенсивности по фронту, исходящих из двух центров, расположенных на оси резонатора. Для выполнения требования замкнутости траектории лучей при полном обходе резонатора излучением эти центры должны являться изображениями друг друга в соответствующих зеркалах. Другими словами, исходящие из одного центра лучи после отражения в зеркале должны переходить в лучи, исходящие из второго центра. В зависимости от расположения центров сферических волн, формирующих моду неустойчивого резонатора, относительно его зеркал реализуются различные тппы неустойчивых резонаторов.

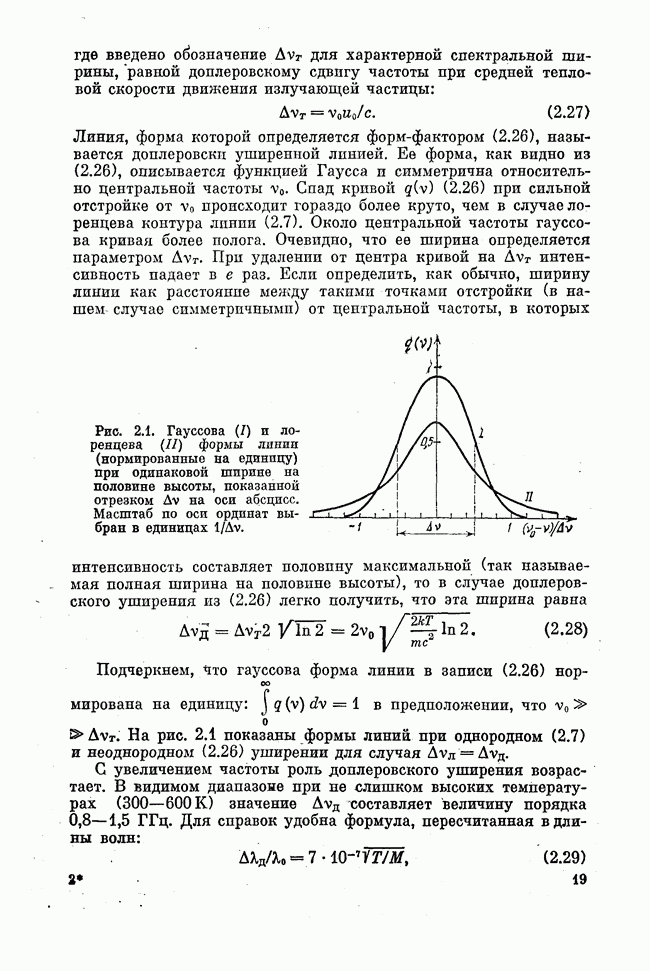
Рис. 10.1. Неустойчивый резонатор: а) общий случай, б) к вычислению величины потерь на излучение за один проход, в) симметричный двухторцовый резонатор.
Вначале рассмотрим геометрию неустойчивого резонатора в общем виде. На рис. 10.1, а показан неустойчивый резонатор, образованный сферическими зеркалами  . Предположим, что волна, уходящая от зеркала
. Предположим, что волна, уходящая от зеркала  является сферической с центром в точке
является сферической с центром в точке  не обязательно совпадающей с центром кривизны пли фокальной точкой этого зеркала. Часть этой волны пройдет мимо зеркала
не обязательно совпадающей с центром кривизны пли фокальной точкой этого зеркала. Часть этой волны пройдет мимо зеркала  часть — отразится. Пусть отраженная сферическая волна исходит из точки
часть — отразится. Пусть отраженная сферическая волна исходит из точки  . Обозначим расстояния от точек
. Обозначим расстояния от точек  до зеркал
до зеркал  соответственно n и
соответственно n и  , а радиусы кривизны зеркал
, а радиусы кривизны зеркал  .
.
Как уже говорилось, точки  должны быть изображениями друг друга в соответствующих сферических зеркалах. Тогда, применяя к попарно сопряженным расстояниям
должны быть изображениями друг друга в соответствующих сферических зеркалах. Тогда, применяя к попарно сопряженным расстояниям  и
и  , а также
, а также  формулу сферического зеркала в параксиальном приближении:
формулу сферического зеркала в параксиальном приближении:

мы получаем уравнения

Совместное решение уравнений (10.4) позволяет найти положение
центров сферических волн, формирующих моду резонатора. Однако более существенно, что величины  и
и  определяют потери резонатора на излучение.
определяют потери резонатора на излучение.
Действительно, проходя резонатор от зеркала к зеркалу и обратно, пучок увеличивает свой поперечный размер в

раз, где  — коэффициенты увеличения при однократном прохождении. Из рис. 10.1, а легко видеть, что
— коэффициенты увеличения при однократном прохождении. Из рис. 10.1, а легко видеть, что

При многократном прохождении резонатора беспредельного увеличения поперечного сечения пучка не происходит в силу конечности поперечного размера зеркал. Часть излучения выходит за край зеркал. Так как размер пятна сферической волны возрастает в  раз и по предположению распределение освещенности зеркал является однородным, то плотность потока излучения в резонаторе уменьшается в
раз и по предположению распределение освещенности зеркал является однородным, то плотность потока излучения в резонаторе уменьшается в  раз. Значение коэффициента увеличения М от размеров зеркал не зависит. Следовательно, полный поток излучения, остающегося в резонаторе, уменьшается в
раз. Значение коэффициента увеличения М от размеров зеркал не зависит. Следовательно, полный поток излучения, остающегося в резонаторе, уменьшается в  раз за время полного обхода резонатора. Это означает, что относительные потери энергии на излучение во внешнее пространство за одни полный обход резонатора составляют
раз за время полного обхода резонатора. Это означает, что относительные потери энергии на излучение во внешнее пространство за одни полный обход резонатора составляют

и определяются значениями  , т. е. конфигурацией резопатора.
, т. е. конфигурацией резопатора.
Рассмотрим этот важный вопрос более подробно. Пусть на зеркало  с площадью поперечного сечения
с площадью поперечного сечения  падает слева расходящаяся сферическая волна с коэффициентом углового увеличения
падает слева расходящаяся сферическая волна с коэффициентом углового увеличения  (рис. 10.1, б). В сечении зеркала
(рис. 10.1, б). В сечении зеркала  поперечный размер этой волны с однородным по предположению распределением интенсивности по сечению составляет
поперечный размер этой волны с однородным по предположению распределением интенсивности по сечению составляет  , где
, где  — радиус левого зеркала
— радиус левого зеркала  Зеркало
Зеркало  отражает в сторону
отражает в сторону  только часть излучения, прпшедшего слева в место его установки. Эта часть составляет
только часть излучения, прпшедшего слева в место его установки. Эта часть составляет

Аналогично зеркало  отражает в сторону зеркала
отражает в сторону зеркала  часть
часть

В результате двух отражений между зеркалами, т. е. в резонаторе, остается часть энергии
 (10.10)
(10.10)
Это означает, что потери на излучение за один полный обход резонатора составляют в соответствии с (10.7)
 (10.11)
(10.11)
и не зависят от размеров зеркал резонатора. Проведенные выше простые выкладки указывают физическую причину этого важного обстоятельства. Дело в том, что уменьшение размеров одного  зеркал приводит к пропорциональному уменьшению углов раствора волн, идущих в обоих направлениях. Следовательно, относительные поперечные размеры (рис. 10.1, б) не изменяются, а значит, остаются неизменными и относительные доли теряемой мощности.
зеркал приводит к пропорциональному уменьшению углов раствора волн, идущих в обоих направлениях. Следовательно, относительные поперечные размеры (рис. 10.1, б) не изменяются, а значит, остаются неизменными и относительные доли теряемой мощности.
Таким образом, вычисление потерь на излучение в неустойчивых резонаторах проводптся методами геометрической оптики. Эти потери называют часто геометрическими или геометро-оптическими. Волновое приближение дает в целом близкую оценку.
Решение уравнений (10.4) в общем случае, хотя и вполне возможное, приводит к громоздким и плохо обозреваемым формулам для  . Рассмотрим более подробно два частных случая. Теоретически нанболее полно исследован симметричный двухторцовый резонатор (рис. 10.1, в). Так как в этом случае
. Рассмотрим более подробно два частных случая. Теоретически нанболее полно исследован симметричный двухторцовый резонатор (рис. 10.1, в). Так как в этом случае  , то
, то  уравнения (10.4) дают
уравнения (10.4) дают
 (10.12)
(10.12)
и соответственно
 (10.13)
(10.13)
Для симметричного резонатора коэффициент увеличения и потери на излучение обычно относят к одному проходу. Именно для этого резонатора наиболее полно проведепо рассмотрение в волновом приближении с помощью интегральных уравнений типа Фокса и Ли и показана разумность геометро-оптического приближения.
Интересной разновидностью неустойчивых резонаторов являются несимметричные конфокальные резонаторы, для которых  . В эту запись радиусы кривизны зеркал входят в алгебраическом смысле, т. е. для выпуклого зеркала радиус кривизны отрицателен. С практической точки зрения наиболее интересен, как правило, односторонний вывод излучения. Поэтому наибольшее распространение получил конфокальный неустойчивый резонатор из вогнутого
. В эту запись радиусы кривизны зеркал входят в алгебраическом смысле, т. е. для выпуклого зеркала радиус кривизны отрицателен. С практической точки зрения наиболее интересен, как правило, односторонний вывод излучения. Поэтому наибольшее распространение получил конфокальный неустойчивый резонатор из вогнутого  выпуклого
выпуклого  зеркал, называемый обычно телескопическим.
зеркал, называемый обычно телескопическим.
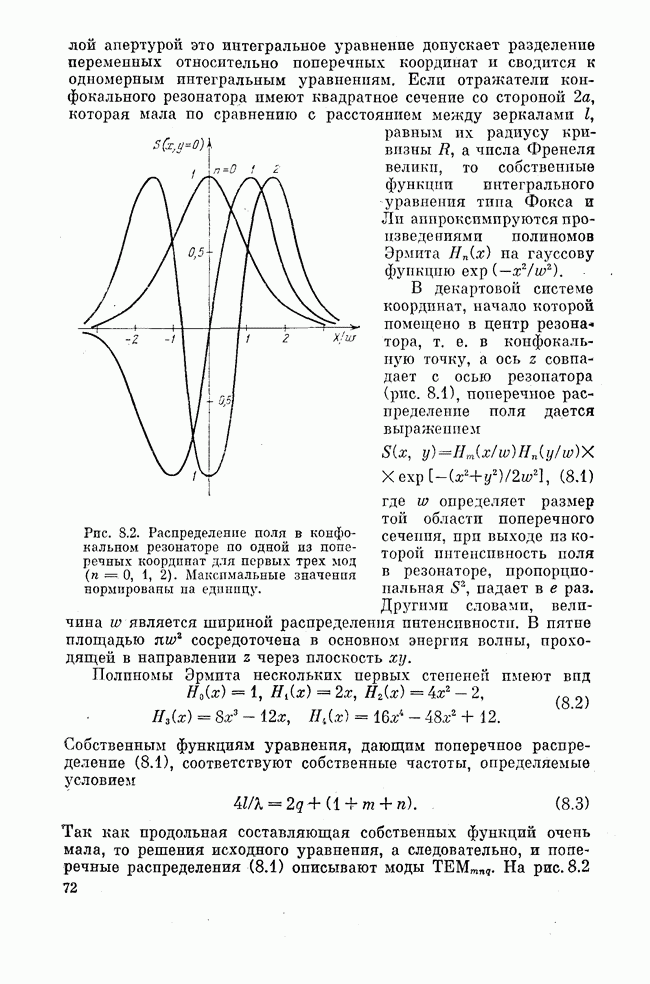
На рис. 10.2, а приведена схема телескопического резонатора. Проведем его геометро-оптический анализ с помощью рис. 10.2, б. В обозначениях этого рисунка уравнения (10.4) принимают вид
 (10.14)
(10.14)
где под  понимаются модули соответствующих
понимаются модули соответствующих
расстояний. Из (10.14) легко получить связь между  :
:

и уравнение для  :
:

При стремлении к конфокальностп  , т. е. в фокальную точку. Колебательная мода резонатора в этом случае является суперпозицией сферической и плоской волн, что и объясняет причину его наименования «телескопический резонатор». Коэффициент увеличения телескопического резонатора равен, как это легко видеть из рис. 10.2,
, т. е. в фокальную точку. Колебательная мода резонатора в этом случае является суперпозицией сферической и плоской волн, что и объясняет причину его наименования «телескопический резонатор». Коэффициент увеличения телескопического резонатора равен, как это легко видеть из рис. 10.2,

а коэффициент связи с внешним пространством составляет

Отметим также, что телескопический резонатор относится к положительной ветви неустойчивых резонаторов, так как прямой расчет показывает, что для этого резонатора произведение  .
.

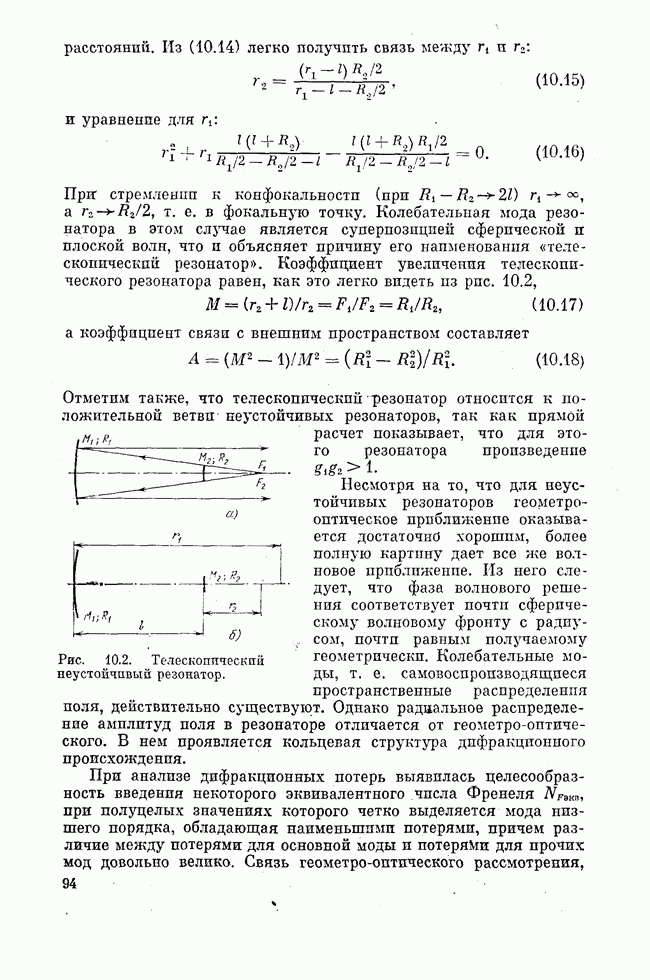
Рис. 10.2. Телескопический неустойчивый резонатор.
Несмотря на то, что для неустойчивых резонаторов геометро-оптическое приближение оказывается достаточно хорошим, более полную картину дает все же волновое приближение. Из него следует, что фаза волнового решения соответствует почти сферическому волновому фронту с радиусом, почти равным получаемому геометрически. Колебательные моды, т. е. самовоспроизводящиеся пространственные распределения поля, действительно существуют. Однако радаальное распределение амплитуд поля в резонаторе отличается от геометро-оптического. В нем проявляется кольцевая структура дифракционного происхождения.
При анализе дифракционных потерь выявилась целесообразность введения некоторого эквивалентного числа Френеля  , при полуцелых значениях которого четко выделяется мода низшего порядка, обладающая наименьшими потерями, причем различие между потерями для основной моды и потерями для прочих мод довольно велико. Связь геометро-оптического рассмотрения,
, при полуцелых значениях которого четко выделяется мода низшего порядка, обладающая наименьшими потерями, причем различие между потерями для основной моды и потерями для прочих мод довольно велико. Связь геометро-оптического рассмотрения,
проведенного выше, с волновым приближением выражается в том; что эквивалентное число Френеля  выражается через геометрический коэффициент увеличения М. В случае симметричного двухторцового резонатора
выражается через геометрический коэффициент увеличения М. В случае симметричного двухторцового резонатора

Для телескопического резонатора
 (10.20)
(10.20)
При полуцелых значениях  , т. е. когда мода низшего порядка хорошо выделяется, ее потери заметно (но не слишком сильно) меньше, чем предсказываемые геометрической оптикой. Разница наиболее заметна при М, лишь незначительно превышающих единицу, и практически несущественна при
, т. е. когда мода низшего порядка хорошо выделяется, ее потери заметно (но не слишком сильно) меньше, чем предсказываемые геометрической оптикой. Разница наиболее заметна при М, лишь незначительно превышающих единицу, и практически несущественна при  , что полностью соответствует картине постепенного перехода из волновой области в геометрическую.
, что полностью соответствует картине постепенного перехода из волновой области в геометрическую.
В заключение рассмотрения неустойчивых резонаторов отметим еще раз их основные достоинства. Прежде всего, это большой объем моды, отсутствие гауссова сжатия распределения поля к оси резонатора. Затем, хорошая селекцпя поперечных мод, связанная с большой величиной геометро-оптических потерь на излучение. Мы, по существу, не затрагивали строгую волновую теорию неустойчивых резонаторов. Но интуитивно ясно, что по природе своей геометро-оптические потери, особенно вблизи границы устойчивости, близки к дифракционным. Следовательно, как это уже говорилось, суммарные потерп в неустойчивых резонаторах спльно зависят от поперечного индекса, что и приводит к селекции мод по этому признаку. Наконец, с практической точки зренпя большим достоинством неустойчивых резонаторов следует считать возможность использования в них только отражательной оптики как для создания резонатора, так и для вывода излучения. Следовательно, можно использовать металлические зеркала, что особенно важно для силовой оптики инфракрасного диапазона.
К числу недостатков неустойчивых резонаторов следует отнести прежде всего их применимость только в случае активных сред с большим усилением. Во многих случаях, хотя далеко не всегда, может быть неудобен тот факт, что поперечное сечение выходного пучка света пмеет форму кольца. Для телескопического резонатора внутренний диаметр кольца равен  , а внешний
, а внешний  , где
, где  — радиус выпуклого зеркала на рис. 10.2, а. Однако в дальней волновой зоне или в фокальной плоскости линзы при фокусировке этого пучка темное пятно исчезает. Существование в поперечном сечении дифракционных колец, наличие которых вытекает из волновой теории неустойчивых резонаторов, обычно не вызывает никаких дополнительных трудностей.
— радиус выпуклого зеркала на рис. 10.2, а. Однако в дальней волновой зоне или в фокальной плоскости линзы при фокусировке этого пучка темное пятно исчезает. Существование в поперечном сечении дифракционных колец, наличие которых вытекает из волновой теории неустойчивых резонаторов, обычно не вызывает никаких дополнительных трудностей.
В заключение наших лекций, посвященных непосредственно резонаторам, целесообразно отметить, что для анализа и расчета оптических систем, резонаторов, линзовых световодов, преобразователей, согласователей гауссовых пучков и т. д. разработаны матричные n диаграммные методы, подробно представленные в справочных изданиях.
Вернемся к вопросу о селекции мод. В нашем предыдущем изложении неоднократно подчеркивалось, что переход к открытым резонаторным системам при резком укорочении длины волны, по сути дела, обусловлен необходимостью резкого разрежения спектра колебании, сгущающегося с ростом частоты пропорционально  . Изложенный выше материал показывает, что в открытых резонаторах это разрежение достигается путем увеличения радиационных потерь нежелательных мод при сохранении низкого уровня потерь желаемых (полезных) тппов колебаний.
. Изложенный выше материал показывает, что в открытых резонаторах это разрежение достигается путем увеличения радиационных потерь нежелательных мод при сохранении низкого уровня потерь желаемых (полезных) тппов колебаний.
Вместе с  в открытых резонаторах, особенно в устойчивых резонаторах, спектр собственных колебаний остается все же слишком богатым с точки зрения требований многих лазерных применений. Методы дальнейшей очистки этого спектра или, иначе говоря, методы улучшения модового состава лазерного излучения получили наименование селекции мод. Все методы селекции мод основаны на уже упомянутой идее увеличения потерь энергии в резонаторе для нежелаемых мод при сохранении высокой добротности резонатора для требуемой моды. При селекции поперечных мод (см. лекцию девятую) используется их различие в поперечной структуре поля. Продольные моды имеют одинаковую поперечную структуру поля, но различаются числом полуволн, укладывающихся между зеркалами резонатора. Следовательно, продольные моды отличаются частотой n расположением узлов стоячей волпы вдоль оси резонатора.
в открытых резонаторах, особенно в устойчивых резонаторах, спектр собственных колебаний остается все же слишком богатым с точки зрения требований многих лазерных применений. Методы дальнейшей очистки этого спектра или, иначе говоря, методы улучшения модового состава лазерного излучения получили наименование селекции мод. Все методы селекции мод основаны на уже упомянутой идее увеличения потерь энергии в резонаторе для нежелаемых мод при сохранении высокой добротности резонатора для требуемой моды. При селекции поперечных мод (см. лекцию девятую) используется их различие в поперечной структуре поля. Продольные моды имеют одинаковую поперечную структуру поля, но различаются числом полуволн, укладывающихся между зеркалами резонатора. Следовательно, продольные моды отличаются частотой n расположением узлов стоячей волпы вдоль оси резонатора.
Наиболее общпй метод селекции продольных мод использует их отличие друг от друга по частоте n поэтому требует введения в резонатор лазера узкополосных дисперсионных элементов. В качестве таких элементов могут быть использованы эталоны Фабри — Перо, призмы n дифракционные решетки, зеркала с частотно зависимыми коэффициентами отражения и т. п.
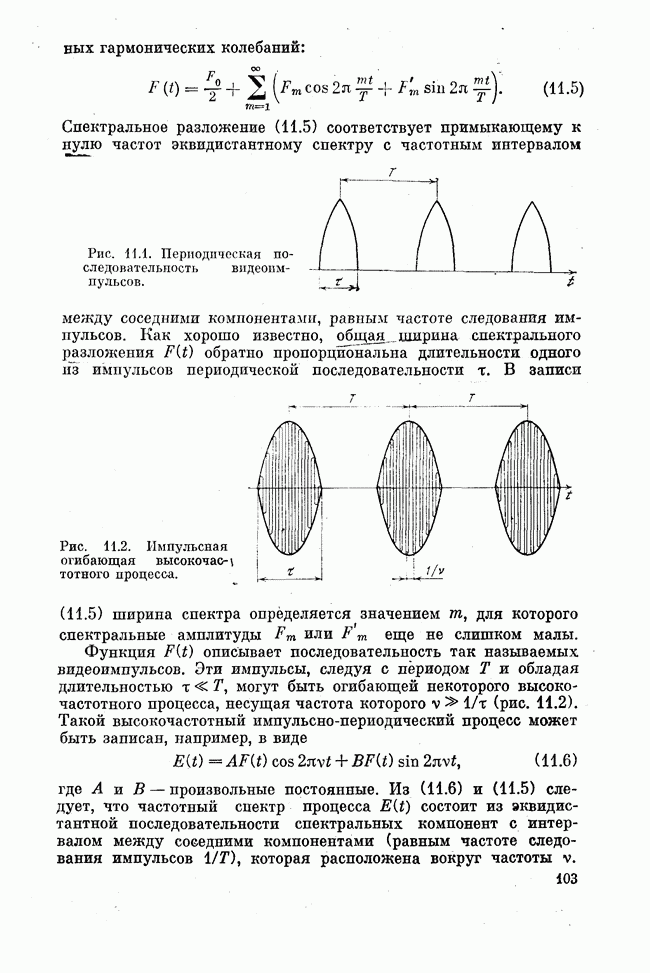
Простейшим является использование для селекции продольных мод частотной зависимости успленпя активного вещества лазера. Межмодовое расстояние для продольных мод составляет (см. формулы (6.14) -(6.17))
 (10.21)
(10.21)
Если расстояние между модами превышает ширину линии усиления:
 (10.22)
(10.22)
а центральные частоты какой-то одной моды и линии усиления близки друг к другу:
 (10.23)
(10.23)
то в лазере возбуждается одномодовая (в смысле продольной моды) и тем самым одночастотная генерация. Частота генерации в этом случае в соответствии с формулой (6.33) определяется настройкой частоты моды на частоту линии и соотношением их добротностей. Этот метод селекции продольных мод может быть успешным в случае газовых лазеров, линии усиления которых достаточно узки. Примером может быть  -лазер низкого давления с шириной линии усиления 60 МГц и длиной резонатора
-лазер низкого давления с шириной линии усиления 60 МГц и длиной резонатора  . Однако в большинстве случаев линии усиления активных сред гораздо шире, и этот метод приводит к неприемлемо коротким резонаторам.
. Однако в большинстве случаев линии усиления активных сред гораздо шире, и этот метод приводит к неприемлемо коротким резонаторам.

Рис. 10.3. Резонатор с дисперсионным зеркалом 
Большое применение нашел метод дисперсионного зеркала. Рассмотрим схему, представленную на рис. 10.3. При  в этом трехзеркальном резонаторе два правых зеркала можно рассматривать как единое зеркало с коэффициентом отражения
в этом трехзеркальном резонаторе два правых зеркала можно рассматривать как единое зеркало с коэффициентом отражения  , зависящим от частоты. Оценить характер зависимости
, зависящим от частоты. Оценить характер зависимости  можно, используя формулу (6.7) для коэффициента пропускания регенерированного эталона Фабри — Перо. При
можно, используя формулу (6.7) для коэффициента пропускания регенерированного эталона Фабри — Перо. При  в приближении плоских волн коэффициент пропускания двух параллельных зеркал с коэффициентами отражения R, разнесенными на расстояние
в приближении плоских волн коэффициент пропускания двух параллельных зеркал с коэффициентами отражения R, разнесенными на расстояние  , составляет в соответствии с (6.7)
, составляет в соответствии с (6.7)
 (10.24)
(10.24)
Тогда коэффициент отражения эквивалентного зеркала  равен
равен

При  величина
величина  обращаемся в нуль, на этих частотах резонатор, образуемый зеркалами
обращаемся в нуль, на этих частотах резонатор, образуемый зеркалами  не имеет добротности, что и приводит к селекции соответствующих продольных мод. Схема, представленная на рис. 10.3, и формула (10.25) не могут претендовать на количественное описание процесса селекции продольных мод введением в резонатор лазера дополнительного дисперсионного элемента. Они приведены здесь лишь для иллюстрации идеи этого метода.
не имеет добротности, что и приводит к селекции соответствующих продольных мод. Схема, представленная на рис. 10.3, и формула (10.25) не могут претендовать на количественное описание процесса селекции продольных мод введением в резонатор лазера дополнительного дисперсионного элемента. Они приведены здесь лишь для иллюстрации идеи этого метода.
На практике используется множество модификаций метода селективного зеркала. При конструировании принимается во внимание необходимость согласования поперечного распределения поля, т. е. согласования мод, во всех резонансных объемах получаемого
таким образом многозеркального резонатора и учитывается взаимное влияние этих парциальных резонаторов.
При селекции продольных мод в принципе может быть использовано различие в продольном распределении поля различных мод. Каждая продольная мода представляет собой стоячую волну. Расстояние между узлами в этих стоячих волнах отличается от моды к моде.
Рассмотрим моду с продольным индексом
 (10.26)
(10.26)
Расстояние между ближайшими к зеркалу узлами мод q и  составляет
составляет

и очень мало. При удалении от зеркала расстояние между узлами нарастает и для узла  моды номер
моды номер  составляет
составляет

что означает, что с узлом  моды совпала пучность
моды совпала пучность  -й моды. Это происходит на расстоянии
-й моды. Это происходит на расстоянии

от зеркала, т. е. в середине резонатора. Но в этой точке находится пучность  2-й моды, узел
2-й моды, узел  3-й, пучность
3-й, пучность  4-й и т. д. Поэтому как-то использовать такое пространственное разнесение узлов и пучностей продольных мод для их эффективной селекции невозможно.
4-й и т. д. Поэтому как-то использовать такое пространственное разнесение узлов и пучностей продольных мод для их эффективной селекции невозможно.
Очевидно, что общее число мод, среди которых надо произвести селекцию, составляет
 (10.30)
(10.30)
Будем считать, что мы ищем способ выделить  моду и что ее центральная частота
моду и что ее центральная частота  совпадает с центральной частотой линии усиления
совпадает с центральной частотой линии усиления  . Тогда номер наиболее далеких продольных мод, от которых желательно избавиться, равен
. Тогда номер наиболее далеких продольных мод, от которых желательно избавиться, равен  . В районе первого узла моды q расстояние между узлами все еще очень мало:
. В районе первого узла моды q расстояние между узлами все еще очень мало:

Номер  узла моды q, который первым совпадает с пучностью моды
узла моды q, который первым совпадает с пучностью моды  определяется уравнением
определяется уравнением

и составляет

Это произойдет на расстоянии
 (10.34)
(10.34)
от зеркала. В этой точке расстояние между узлами ближайших мод в соответствии с (10.27), (10.33), (10.30) и (10.26) равно

что для многих газовых лазеров составляет заметную долю длины волны.
Изложенное подводит к мысли о возможности следующего метода селекции продольных мод.

Рис. 10.4. Дискриминация продольных мод тонким поглотителем. Штриховой линией показана стоячая волна одной из исключаемых мод, сплошной — стоячая волна выделяемой моды (А — частично прозрачная поглощающая пленка).
Поместим в узел номер N желаемой моды q тонкий частично прозрачный поглотитель. Если его толщина много меньше длины волны, то наличие поглотителя в узле, где напряженность электрического поля моды q равна нулю, не вызывает потерь энергии из моды q. Все же остальные моды в этой точке на оси резонатора имеют ненулевую напряженность электрического поля и поэтому будут испытывать потери энергии, что и приведет к их дискриминации (рис. 10.4). Этот метод пространственной селекции продольных мод тонкими поглотителями нашел применение для газовых лазеров, главным образом видимого диапазона. Тонкие частично прозрачные поглотители изготовляются нанесением слоев металла толщиной 1—10 нм на оптически полированные прозрачные подложки.
Ввиду малой оптической стойкости таких пленок их применение ограничено лазерами умеренной мощности.
Введение в резонатор лазера узкополосных дисперсионных элементов позволяет не только проводить селекцию продольных мод, но и в тех случаях, когда линия усиления достаточно широка, а частота настройки дисперсионного элемента управляема, осуществлять перестройку частоты лазерного излучения. Резонаторы с дисперсионными элементами (призмами, дифракционными решетками, эталонами Фабри — Перо), предназначенные для лазеров с перестраиваемой частотой излучения, получили наименование дисперсионных резонаторов. Простейший дисперсионный
резонатор образуется при введении в обычный резонатор призмы (рис. 10.5).

Рис. 10.5. Призменный дисперсионный резонатор.
Брюстера. Дисперсия призмы обычно недостаточна для получения высокой степени монохроматичности и тонкой перестройки частоты излучения. Поэтому широкое распространение нашли более сложные дисперсионные резонаторы (рис. 10.6). В таких резонаторах эталон Фабри — Перо позволяет выделить одну продольную моду, решетка подавляет генерацию на нежелательных

Рис. 10.6. Сложный дисперсионный резонатор: 1 — зеркало, 2 — телескоп, 3 — эталон Фабри — Перо, 4 — решетка.
Для уменьшения потерь при внесении призмы обычно стремятся к тому, чтобы излучение падало на призму под углом максимумах пропускания эталона. Телескоп служит для расширения пучка, исходящего из активной среды, что необходимо для эффективной работы как эталона, так и решетки.
Дисперсионные резонаторы, подобные показанному на рис. 10.6, позволили получить одномодовое по поперечному и продольному индексам излучение, частота которого перестраивается в широком диапазоне.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ЧАСТЬ ПЕРВАЯ. ОСНОВЫ ФИЗИКИ ЛАЗЕРОВ
- Лекция первая. КОЭФФИЦИЕНТЫ ЭЙНШТЕЙНА
- Лекция вторая. ШИРИНА ЛИНИИ
- Лекция третья. УСИЛЕНИЕ
- Лекция четвертая. КОЭФФИЦИЕНТЫ ЭЙНШТЕЙНА И МАТРИЧНЫЙ ЭЛЕМЕНТ ОПЕРАТОРА ПЕРЕХОДА
- Лекция пятая. ЛАЗЕРЫ-УСИЛИТЕЛИ
- Лекция шестая. ГЕНЕРАЦИЯ
- Лекция седьмая. ОТКРЫТЫЕ РЕЗОНАТОРЫ
- Лекция восьмая. ГАУССОВЫ ПУЧКИ
- Лекция девятая. УСТОЙЧИВОСТЬ РЕЗОНАТОРОВ
- Лекция десятая. НЕУСТОЙЧИВЫЕ РЕЗОНАТОРЫ
- Лекция одиннадцатая. СИНХРОНИЗАЦИЯ МОД
- Лекция двенадцатая. ИСТОРИЯ КВАНТОВОЙ ЭЛЕКТРОНИКИ. ОСНОВНЫЕ ФОРМУЛЫ
- ЧАСТЬ ВТОРАЯ. ЛАЗЕРЫ
- Лекция тринадцатая. ГАЗОВЫЕ ЛАЗЕРЫ. ГЕЛИЙ-НЕОНОВЫЙ ЛАЗЕР
- Лекция четырнадцатая. ИОННЫЕ ЛАЗЕРЫ. ЛАЗЕРЫ НА ПАРАХ МЕТАЛЛОВ
- Лекция пятнадцатая. CO2-ЛАЗЕРЫ
- Лекция шестнадцатая. СO2-ЛАЗЕРЫ (продолжение)
- Лекция семнадцатая. ХИМИЧЕСКИЕ ЛАЗЕРЫ
- Лекция восемнадцатая. CO-ЛАЗЕРЫ, ГАЗОВЫЕ ЛАЗЕРЫ НА ЭЛЕКТРОННЫХ ПЕРЕХОДАХ В МОЛЕКУЛАХ
- Лекция девятнадцатая. ВСПОМОГАТЕЛЬНОЕ ИЗЛУЧЕНИЕ НАКАЧКИ В СИСТЕМАХ СО МНОГИМИ УРОВНЯМИ ЭНЕРГИИ
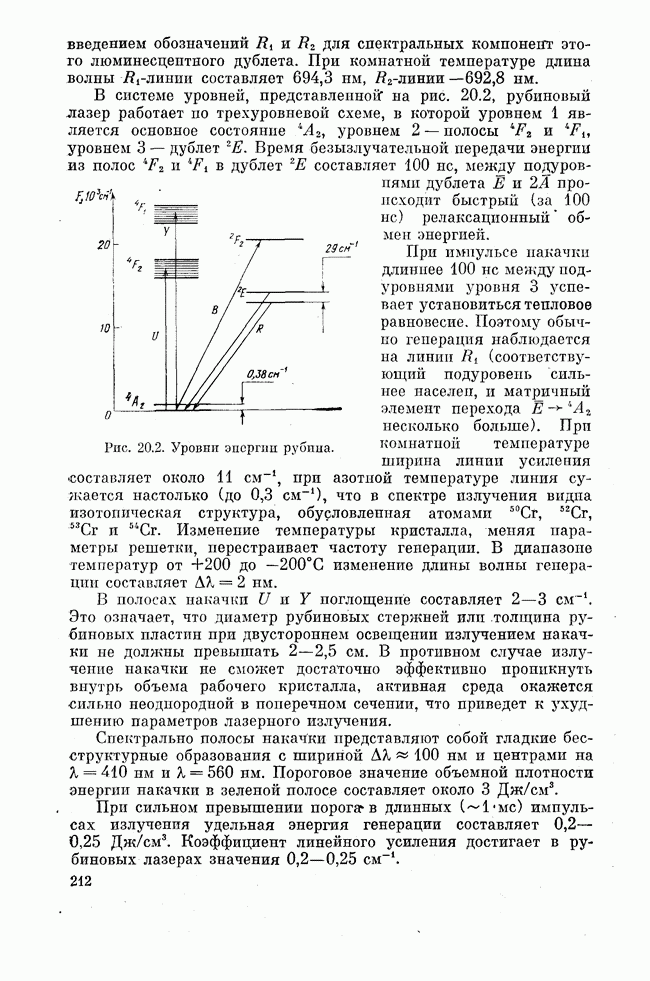
- Лекция двадцатая. РУБИНОВЫЙ И НЕОДИМОВЫЙ ЛАЗЕРЫ
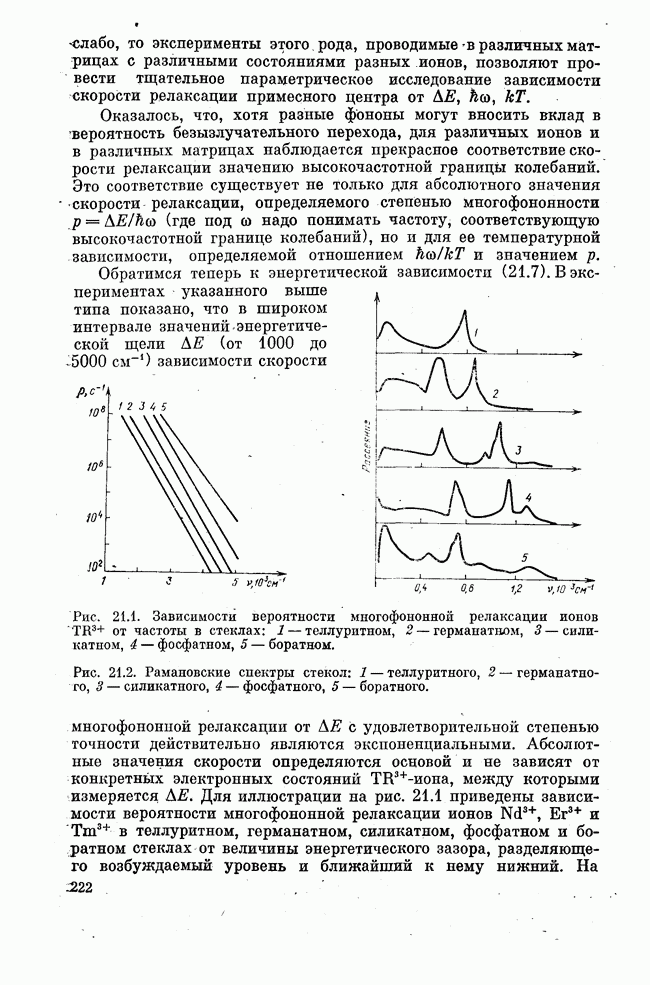
- Лекция двадцать первая. БЕЗЫЗЛУЧАТЕЛЬНАЯ РЕЛАКСАЦИЯ В ТВЕРДОМ ТЕЛЕ
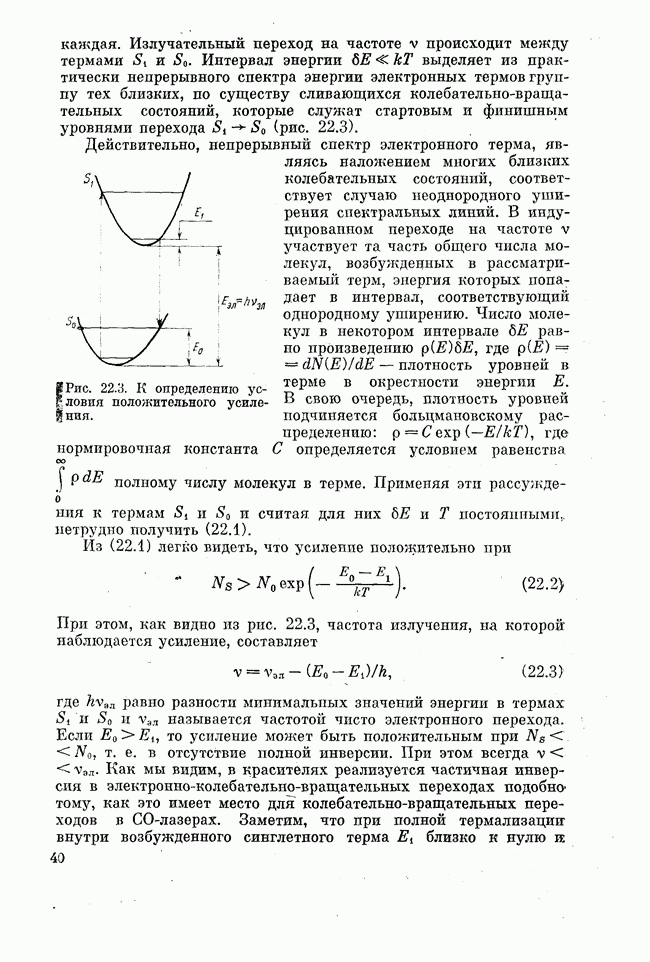
- Лекция двадцать вторая. ЛАЗЕРЫ НА КРАСИТЕЛЯХ
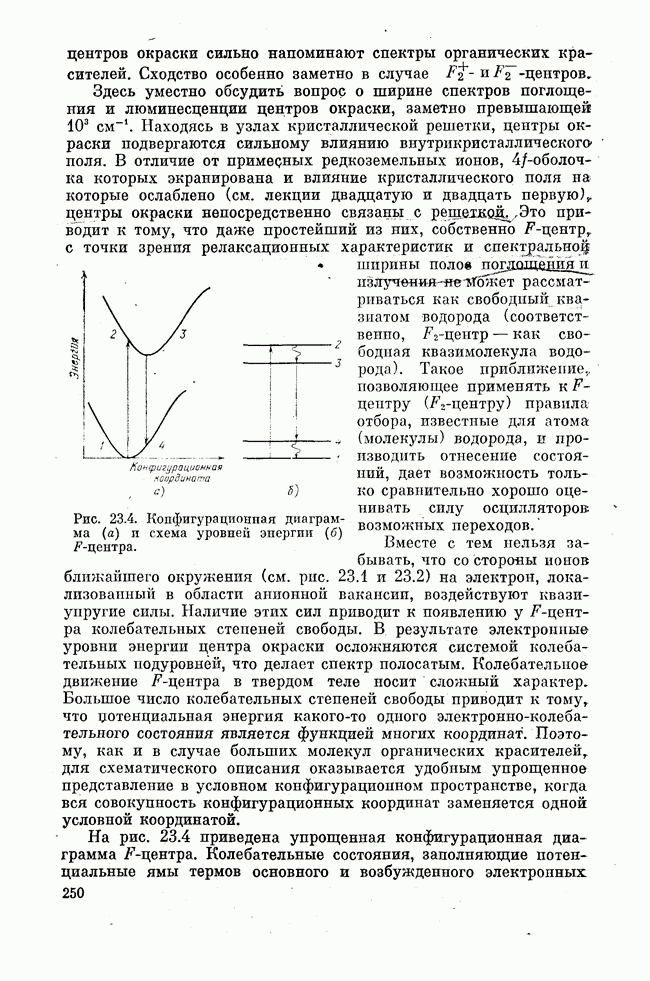
- Лекция двадцать третья. ЛАЗЕРЫ НА ЦЕНТРАХ ОКРАСКИ
- Лекция двадцать четвертая. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ
- Лекция двадцать пятая. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ (продолжение)
- Лекция двадцать шестая. ЛАЗЕРЫ НА СВОБОДНЫХ ЭЛЕКТРОНАХ
- Лекция двадцать седьмая. СЕМНАДЦАТЬ НАИБОЛЕЕ ИЗВЕСТНЫХ ЛАЗЕРОВ
- Заключение. ТЕНДЕНЦИИ РАЗВИТИЯ