| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Лекция вторая. ШИРИНА ЛИНИИ
Соотношение неопределенностей «энергия — время», естественное время жизни, ширина спектра спонтанного излучения. Лоренцева форма линии. Вероятность индуцированных переходов при монохроматическом излучении. Однородное и неоднородное уширения. Гауссова форма линии при доплеровском уширении.
Рассмотрим вопрос о ширине линии излучения (поглощения). До сих пор мы говорили о двух уровнях энергии, замалчивая то обстоятельство, что уровни имеют конечную ширину. Дело в том, что любые процессы, сокращающие время жизни частиц на уровнях, приводят к уширению линий соответствующих переходов.
Действительно, определение энергии состояния должно проводиться за время, не превышающее время жизни в этом состоянии  . А тогда неточность определения энергии в соответствии с соотношением неопределенностей «энергия — время»
. А тогда неточность определения энергии в соответствии с соотношением неопределенностей «энергия — время»
 (2.1)
(2.1)
не может быть меньше  . Неопределенность энергии состояния приводит к неопределенности частоты перехода, равной
. Неопределенность энергии состояния приводит к неопределенности частоты перехода, равной  . Постоянная времени
. Постоянная времени  является мерой времени, необходимого для того, чтобы возбужденная система отдала свою энергию. Значение
является мерой времени, необходимого для того, чтобы возбужденная система отдала свою энергию. Значение  определяется скоростями спонтанного излучения и безызлучательных релаксационных переходов.
определяется скоростями спонтанного излучения и безызлучательных релаксационных переходов.
В отсутствие внешних воздействий спонтанное излучение определяет время жизни состояния. Поэтому наименьшая возможная, так называемая естественная ширина линии  определяется вероятностью спонтанного перехода
определяется вероятностью спонтанного перехода  :
:

Естественная ширина, как правило, существенна только на. очень высоких частотах  и для хорошо разрешенных переходов. Обычно влиянием спонтанного излучения на ширину линии можно пренебречь, так как в реальных условиях релаксационные переходы более эффективно сокращают время жизни.
и для хорошо разрешенных переходов. Обычно влиянием спонтанного излучения на ширину линии можно пренебречь, так как в реальных условиях релаксационные переходы более эффективно сокращают время жизни.
Как уже говорилось, в системах с дискретными уровнями энергии, кроме индуцированных и спонтанных переходов, существенную роль играют релаксационные безызлучательные переходы. Эти переходы возникают в результате взаимодействий квантовой частицы с ее окружением. Механизм процессов этих взаимодействий сильно зависит от вида конкретной системы. Это может быть взаимодействие меясду ионом и решеткой кристалла; это могут быть соударения между молекулами газа или жидкости и т. д. В конечном счете результатом действия релаксационных процессов является обмен энергией между подсистемой рассматриваемых частиц и тепловыми движениями во всей системе в целом, приводящий к термодинамическому равновесию между ними.
Обычно время установления равновесия, время жизни частицы на уровне, обозначается  и называется продольным временем релаксации. Такая терминология отвечает традиции, установившейся при исследовании явлений ядерного магнитного резонанса (ЯМР) и электронного парамагнитного резонанса (ЭПР). Продольная релаксация соответствует движению вектора высокочастотной намагниченности системы частиц вдоль направления внешнего постоянного магнитного поля. Существует еще поперечное время релаксации
и называется продольным временем релаксации. Такая терминология отвечает традиции, установившейся при исследовании явлений ядерного магнитного резонанса (ЯМР) и электронного парамагнитного резонанса (ЭПР). Продольная релаксация соответствует движению вектора высокочастотной намагниченности системы частиц вдоль направления внешнего постоянного магнитного поля. Существует еще поперечное время релаксации  , которое соответствует движению вектора намагниченности в плоскости, перпендикулярной направлению внешнего постоянного поля.
, которое соответствует движению вектора намагниченности в плоскости, перпендикулярной направлению внешнего постоянного поля.
Как правило, нас интересует поведение большой совокупности частиц, электрический или магнитный дипольный момент этой совокупности. Полный момент определяется фазовыми соотношениями между моментами индивидуальных частиц. Пусть в на чальный момент времени все частицы имеют дипольные моменты, осциллирующие синфазно. С течением времени эта синфазность будет нарушаться. Время  является мерой того отрезка времени, в течение которого частицы приобретут случайные по отношению друг к другу фазы.
является мерой того отрезка времени, в течение которого частицы приобретут случайные по отношению друг к другу фазы.
Любой процесс, вносящий вклад во время релаксации  т. е. любой процесс потери энергии частицами, приводит к потере фазы. Следовательно,
т. е. любой процесс потери энергии частицами, приводит к потере фазы. Следовательно,

Но существуют взаимодействия, которые, хотя и не меняют энергию ансамбля частдц, увеличивают степень беспорядка, разрушая фазовые соотношения между составляющими ансамбль частицами. Например, при газокинетических соударениях одна молекула газа совершает переход  , а другая
, а другая  . Система в целом не меняет своей энергии. Но фазовая информация при этом теряется, фазовая память нарушается. Можно считать, что время
. Система в целом не меняет своей энергии. Но фазовая информация при этом теряется, фазовая память нарушается. Можно считать, что время  — это время фазовой памяти или время передачи энергии от частицы к частице по уровню.
— это время фазовой памяти или время передачи энергии от частицы к частице по уровню.
Во всех системах, где существенны взаимодействия частиц друг с другом (спин-спиновые взаимодействия, вообще диполь-дипольные взаимодействия, упругие соударения),  зачастую
зачастую  молекулярных пучках, т. е. когда частицы летят, не соударяясь друг с другом,
молекулярных пучках, т. е. когда частицы летят, не соударяясь друг с другом,  равному, в свою очередь, времени пролета через область взаимодействия с полем излучения. Последнее верно, очевидно, только в случае относительно длинного естественного времени жизни
равному, в свою очередь, времени пролета через область взаимодействия с полем излучения. Последнее верно, очевидно, только в случае относительно длинного естественного времени жизни  .
.
Так как время  является самым коротким временем релаксации, то именно оно и определяет ширину линии перехода
является самым коротким временем релаксации, то именно оно и определяет ширину линии перехода  :
:

В дальнейшем изложении для нас будет более удобным пользоваться обозначением  для времени жизни частицы на уровне и выделять индексом
для времени жизни частицы на уровне и выделять индексом  естественное время жизни (время жизни по отношению к спонтанному излучению)
естественное время жизни (время жизни по отношению к спонтанному излучению)  . Время релаксации, определяющее в том или ином процессе ширину линии перехода, будет обозначаться как
. Время релаксации, определяющее в том или ином процессе ширину линии перехода, будет обозначаться как  .
.
Итак, конечность времени жизни частицы в возбужденном энергетическом состоянии ведет к уширению уровней энергии. Излучение с уширенных уровней приобретает спектральную ширину. Наиболее общим, фундаментальным механизмом, ограничивающим сверху время жизни частицы на возбужденном уровне,
является спонтанное излучение, которое должно, таким образом, иметь спектральную ширину, соответствующего скорости актов спонтанного распада.
Квантовая электродинамика позволяет вычислить спектральное распределение квантов спонтанного излучения, исходящих с уровня шириной

Контур линии спонтанного излучения оказывается имеющим так называемую лоренцеву форму с шириной

Лоренцева форма линии определяется форм-фактором

и имеет вид резонансной кривой с максимумом на частоте  , спадающей до уровня половины пиковой величины при частотах
, спадающей до уровня половины пиковой величины при частотах  . Очевидно, что полная ширина кривой на половине максимальной величины составляет
. Очевидно, что полная ширина кривой на половине максимальной величины составляет  .
.
Если принимать во внимание возможность спонтанного распада не только верхнего из двух рассматриваемых уровней энергии, но и нижнего, когда нижний уровень не является основным, то под  , входящей в формулу (2.7), следует понимать величину, определяемую суммой скоростей распада этих уровней
, входящей в формулу (2.7), следует понимать величину, определяемую суммой скоростей распада этих уровней  :
:

Выражение (2.7) может быть легко получено в классическом приближении.
Уравнение движения осциллирующего диполя с радиационным затуханием сводится к уравнению гармонического осциллятора с вязким трением:

где  — круговая частота колеблющегося электрона в диполе, состоящем из электрона и ядра,
— круговая частота колеблющегося электрона в диполе, состоящем из электрона и ядра,  — классический коэффициент затухания его излучения. Решение этого уравнения хорошо известно:
— классический коэффициент затухания его излучения. Решение этого уравнения хорошо известно:

где  , а С — произвольная амплитуда. Так как интенсивность излучения, испускаемого рассматриваемым лоренцевским осциллятором, пропорциональна квадрату амплитуды колебаний электрона в осцилляторе, то видно, что интенсивность излучения экспоненциально падает во времени с характерным
, а С — произвольная амплитуда. Так как интенсивность излучения, испускаемого рассматриваемым лоренцевским осциллятором, пропорциональна квадрату амплитуды колебаний электрона в осцилляторе, то видно, что интенсивность излучения экспоненциально падает во времени с характерным
временем

Это время представляет собой среднее время жизни возбужденного состояния.
Временной зависимости (2.10) соответствует спектральное распределение  , которое легко получается фурье-преобразованием
, которое легко получается фурье-преобразованием  :
:

При вычислении (2.12) учтено, что (2.10) получено для  . Формула (2.12) дает спектральное распределение амплитуд. Спектральное распределение интенсивности есть квадрат модуля распределения амплитуды. Следовательно,
. Формула (2.12) дает спектральное распределение амплитуд. Спектральное распределение интенсивности есть квадрат модуля распределения амплитуды. Следовательно,

Вводя обозначения  и приняв значение константы
и приняв значение константы  , мы получаем выражение (2.7) для форм-фактора
, мы получаем выражение (2.7) для форм-фактора  .
.
Итак, таковы спектральные свойства спонтанного излучения. Его интенсивность частотно зависима. Следовательно, его вероятность зависит от частоты, имеет некоторую спектральную плотность:

При этом необходимо, чтобы

Отсюда вытекает требование нормировки форм-фактора  :
:

что уже выполнено в записи (2.7) в предположении  .
.
Далее. Мы уже выяснили, что вероятности спонтанного и индуцированного излучений связаны друг с другом. Это было доказано с помощью весьма общих термодинамических соображений. Следовательно, вероятность индуцированного испускания также частотно зависима и имеет спектральную плотность

При этом

Если индуцирующее излучение монохроматично, то

где р — объемная плотность этого излучения, а  — пинцетная дельта-функцня Дирака. Тогда интеграл (2.18) легко берется, и
— пинцетная дельта-функцня Дирака. Тогда интеграл (2.18) легко берется, и

Сокращение времени жизни, приводящее к появлению конечной ширины линии  , уменьшает вероятность индуцированных переходов, вызываемых монохроматическим полем излучения, обратно пропорционально ширине линии.
, уменьшает вероятность индуцированных переходов, вызываемых монохроматическим полем излучения, обратно пропорционально ширине линии.
Уширение линии, обусловленное конечностью времени жизни состояний, связанных рассматриваемым переходом, называется однородным. Каждый атом, находящийся в соответствующем состоянии, излучает при переходе сверху вниз линию с полной шириной  и спектральной формой
и спектральной формой  . Аналогично каждый атом, находящийся в соответствующем нижнем состоянии, поглощает при переходе снизу вверх излучение в спектре с полной шириной
. Аналогично каждый атом, находящийся в соответствующем нижнем состоянии, поглощает при переходе снизу вверх излучение в спектре с полной шириной  и в соответствии со спектральной зависимостью
и в соответствии со спектральной зависимостью  Невозможно приписать какую-либо определенную спектральную компоненту в спектре
Невозможно приписать какую-либо определенную спектральную компоненту в спектре  какому-то определенному атому. При однородном уширении вне зависимости от его природы спектральная зависимость
какому-то определенному атому. При однородном уширении вне зависимости от его природы спектральная зависимость  есть единая спектральная характеристика как одного атома, так и всей совокупности атомов. Изменение этой характеристики, в принципе возможное при том или ином воздействии на ансамбль атомов, происходит одновременно и одинаковым образом для всех атомов ансамбля.
есть единая спектральная характеристика как одного атома, так и всей совокупности атомов. Изменение этой характеристики, в принципе возможное при том или ином воздействии на ансамбль атомов, происходит одновременно и одинаковым образом для всех атомов ансамбля.
Примерами однородного уширения являются естественная ширина линии и столкновительное уширение в газах.
Другое дело — неоднородное уширение. Экспериментально наблюдаемые спектральные линии могут явиться бесструктурной суперпозицией нескольких спектрально неразрешимых однородно уширенных линий. В этих случаях каждая частица излучает или поглощает не в пределах всей экспериментально наблюдаемой линии. Такая спектральная линия называется неоднородно уширенной. Причиной неоднородного уширения может быть любой процесс, приводящий к различию в условиях излучения (поглощения) для части одинаковых атомов исследуемого ансамбля частиц, или наличие в ансамбле атомов с близкими, но различными спектральными свойствами (сверхтонкая структура того или иного вида), однородно уширенные спектральные линии которых перекрываются лишь частично. Термин «неоднородное уширение» возник в спектроскопии ЯМР, в которой уширение этого типа происходило из-за неоднородности внешнего намагничивающего поля в пределах исследуемого образца. Аналогичную природу имеет неоднородное уширение в примесных люминесцентных кристаллах, в которых неоднородность внутрикристаллического электрического поля приводит к различию в величине штарковского
сдвига частоты излучения примесными центрами, расположенными в различных местах кристаллического образца.
Классическим примером неоднородного уширения является доплеровское уширение, характерное для газов при малых давлениях и (или) высоких частотах.
Атомы (молекулы, ионы) газа находятся в тепловом движении. Доплер-эффект первого порядка приводит к смещению частоты излучения частиц, летящих на наблюдателя со скоростью и, на величину  , где
, где  — частота излучения покоящейся частицы,
— частота излучения покоящейся частицы,  — скорость света. Естественное уширение превращает излучение на частоте
— скорость света. Естественное уширение превращает излучение на частоте  в спектральную линию, но это уширение однородно, и частотный сдвиг
в спектральную линию, но это уширение однородно, и частотный сдвиг  испытывает вся линия. Так как частицы газа движутся с различными скоростями, то частотные сдвиги их излучения различны, а суммарная форма линии газа в целом определяется распределением частиц по скоростям. Последнее верно, строго говоря, если естественная ширина линии много уже доплеровских сдвигов частоты, что, как правило, имеет место. Тогда, если обозначить через
испытывает вся линия. Так как частицы газа движутся с различными скоростями, то частотные сдвиги их излучения различны, а суммарная форма линии газа в целом определяется распределением частиц по скоростям. Последнее верно, строго говоря, если естественная ширина линии много уже доплеровских сдвигов частоты, что, как правило, имеет место. Тогда, если обозначить через  функцию распределения частиц по скоростям, форм-фактор доплеровской линии
функцию распределения частиц по скоростям, форм-фактор доплеровской линии  оказывается связанным с
оказывается связанным с  простым соотношением:
простым соотношением:

Далее, наблюдаемая частота равна

Следовательно,  . Отсюда
. Отсюда

При максвелловском распределении частиц по скоростям

где средняя тепловая скорость

Здесь k — постоянная Больцмана, Т — температура газа, m — масса атома (молекулы) газа. Строго говоря, максвелловское распределение справедливо только при тепловом равновесии. Однако отклонение от него обычно незначительно даже для возбужденных (излучающих) частиц. Во всяком случае количественные оценки с помощью максвелловского распределения получаются достаточно надежными. Комбинируя (2.25), (2.24) и (2.23), легко получить  в виде
в виде

где введено обозначение  для характерной спектральной ширины, равной доплеровскому сдвигу частоты при средней тепловой скорости движения излучающей частицы:
для характерной спектральной ширины, равной доплеровскому сдвигу частоты при средней тепловой скорости движения излучающей частицы:

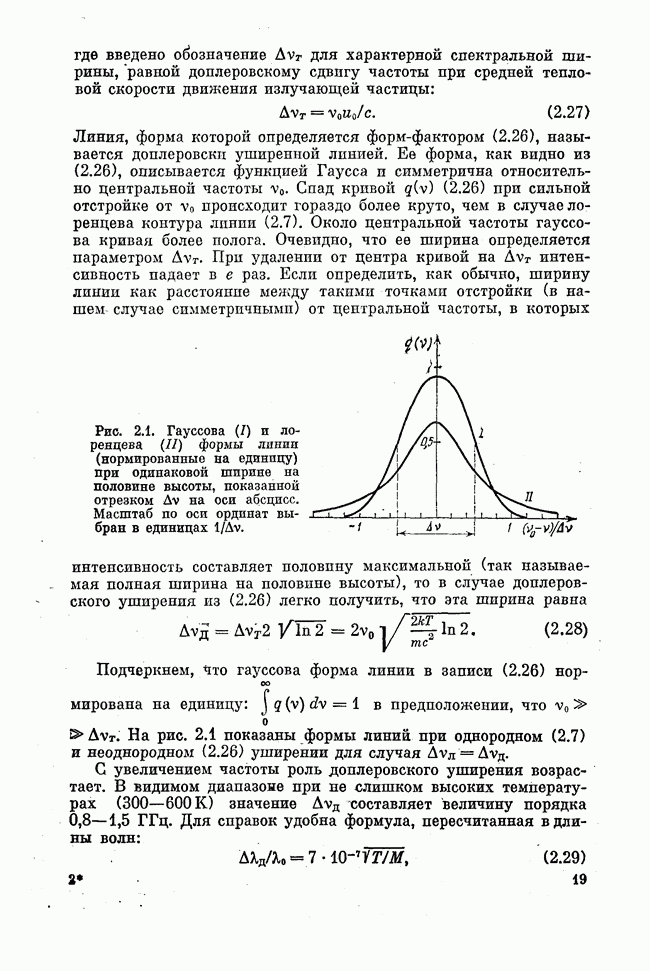
Линия, форма которой определяется форм-фактором (2.26), называется доплеровски уширенной линией. Ее форма, как видно из (2.26), описывается функцией Гаусса и симметрична относительно центральной частоты  . Спад кривой
. Спад кривой  при сильной отстройке от
при сильной отстройке от  происходит гораздо более круто, чем в случае лоренцева контура линии (2.7). Около центральной частоты гауссова кривая более полога. Очевидно, что ее ширина определяется параметром
происходит гораздо более круто, чем в случае лоренцева контура линии (2.7). Около центральной частоты гауссова кривая более полога. Очевидно, что ее ширина определяется параметром  .
.

Рис. 2.1. Гауссова  и лоренцева
и лоренцева  формы линии (нормированные на единицу) при одинаковой ширине на половине высоты, показанной отрезком
формы линии (нормированные на единицу) при одинаковой ширине на половине высоты, показанной отрезком  на оси абсцисс. Масштаб по оси ординат выбран в единицах
на оси абсцисс. Масштаб по оси ординат выбран в единицах  .
.
При удалении от центра кривой на  интенсивность падает в е раз. Если определить, как обычно, ширину линии как расстояние между такими точками отстройки (в нашем случае симметричными) от центральной частоты, в которых интенсивность составляет половину максимальной (так называемая полная ширина на половине высоты), то в случае доплеровского уширения из (2.26) легко получить, что эта ширина равна
интенсивность падает в е раз. Если определить, как обычно, ширину линии как расстояние между такими точками отстройки (в нашем случае симметричными) от центральной частоты, в которых интенсивность составляет половину максимальной (так называемая полная ширина на половине высоты), то в случае доплеровского уширения из (2.26) легко получить, что эта ширина равна

Подчеркнем, что гауссова форма линии в записи (2.26) нормирована на единицу:  в предположении, что
в предположении, что  . На рис. 2.1 показаны формы линий при однородном (2.7) и неоднородном (2.26) уширении для случая
. На рис. 2.1 показаны формы линий при однородном (2.7) и неоднородном (2.26) уширении для случая 
С увеличением частоты роль доплеровского уширения возрастает. В видимом диапазоне при не слишком высоких температурах (300—600 К) значение  составляет величину порядка
составляет величину порядка  . Для справок удобна формула, пересчитанная в длины волн:
. Для справок удобна формула, пересчитанная в длины волн:

где М — относительная молекулярная масса. Так как  , то формуле (2.29), очевидно, эквивалентна запись
, то формуле (2.29), очевидно, эквивалентна запись

Подкоренной характер зависимости  приводит к тому, что для грубых численных оценок
приводит к тому, что для грубых численных оценок  можпо считать в условиях, например, тлеющего газового разряда постоянной величиной, равной
можпо считать в условиях, например, тлеющего газового разряда постоянной величиной, равной  .
.
Забегая несколько вперед, приведем два примера.
Для  -лазера (излучение молекул
-лазера (излучение молекул  при температуре около 400 К на волне около 10 мкм)
при температуре около 400 К на волне около 10 мкм)  составляет 60 МГц, для гелий-неонового лазера (излучение атомов неона при температуре около 400 К на волне 0,63 мкм) доплеровская ширина линии достигает 1,35-1,40 ГГц.
составляет 60 МГц, для гелий-неонового лазера (излучение атомов неона при температуре около 400 К на волне 0,63 мкм) доплеровская ширина линии достигает 1,35-1,40 ГГц.
Вернемся теперь к однородному уширению. Как будет явствовать из дальнейшего изложения, вплоть до очень высоких частот, соответствующих УФ излучению, как правило, естественной шириной линии можно пренебречь. Для газов однородное уширение определяется в реальных условиях столкновительными процессами. В газах среди множества столкновительных процессов существуют соударения такого типа, которые приводят к изменению фазы колебаний возбужденной частицы. В классическом приближении, когда возбужденная частица рассматривается как осциллятор, совершающий колебания с постоянной амплитудой и некоторой определенной фазой, изменение фазы меняет взаимодействие осциллятора с электромагнитным полем. Это изменение носит случайный характер. Если в результате столкновений (одного или нескольких) исходное фазовое соотношение нарушается, то можно считать, что с полем взаимодействует новый осциллятор, а старый исчез. Поэтому среднее время свободного пролета осциллятора между фазосбивающими столкновениями является средним временем жизни частиц газа по отношению к столкновениям этого рода. Это время,  , в соответствии с формулой (2.4) определяет столкновительную ширину линии
, в соответствии с формулой (2.4) определяет столкновительную ширину линии  :
:

Так как газокинетические соударения являются случайным процессом, воздействующим при одном и том же столкновителъном партнере в среднем одинаково на все молекулы (атомы) газа одного сорта, то столкновительное уширение является однородным уширением.
Величина  определяется газокинетическим сечением процесса сбоя фазы при ударе
определяется газокинетическим сечением процесса сбоя фазы при ударе  скоростью теплового движения частиц газа и и плотностью газа n:
скоростью теплового движения частиц газа и и плотностью газа n:

где угловые скобки означают усреднение по скоростям. При простых оценках можно считать, что в (2.32) входит средняя тепловая
скорость  . Вопрос о величине
. Вопрос о величине  требует в каждом конкретном случае отдельного экспериментального исследования.
требует в каждом конкретном случае отдельного экспериментального исследования.
Для квантовой электроники чрезвычайно большое значение имеет обратная пропорциональность  плотности газа. В результате этого столкновительная ширина
плотности газа. В результате этого столкновительная ширина  прямо пропорциональна давлению газа и может достигать заметных величин. Так, для уже упоминавшегося
прямо пропорциональна давлению газа и может достигать заметных величин. Так, для уже упоминавшегося  -лазера крутизна роста ширины линии из-за учащения столкновений с увеличением давления составляет (в зависимости от столкновительного партнера)
-лазера крутизна роста ширины линии из-за учащения столкновений с увеличением давления составляет (в зависимости от столкновительного партнера)  . При суммарном давлении в 10—15 Торр для
. При суммарном давлении в 10—15 Торр для  -лазера однородная столкновительная ширина превышает неоднородную- (доплеровскую).
-лазера однородная столкновительная ширина превышает неоднородную- (доплеровскую).
В заключение этой лекции отметим необходимость принимать в некоторых случаях во внимание так называемую пролетную ширину линии. В спектроскопии атомных (молекулярных) пучков время пролета пучка частиц через область пространства, занятую электромагнитным полем, может быть мало. Очевидно, что среднему времени взаимодействия пучка с полем  соответствует однородное уширение
соответствует однородное уширение

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ЧАСТЬ ПЕРВАЯ. ОСНОВЫ ФИЗИКИ ЛАЗЕРОВ
- Лекция первая. КОЭФФИЦИЕНТЫ ЭЙНШТЕЙНА
- Лекция вторая. ШИРИНА ЛИНИИ
- Лекция третья. УСИЛЕНИЕ
- Лекция четвертая. КОЭФФИЦИЕНТЫ ЭЙНШТЕЙНА И МАТРИЧНЫЙ ЭЛЕМЕНТ ОПЕРАТОРА ПЕРЕХОДА
- Лекция пятая. ЛАЗЕРЫ-УСИЛИТЕЛИ
- Лекция шестая. ГЕНЕРАЦИЯ
- Лекция седьмая. ОТКРЫТЫЕ РЕЗОНАТОРЫ
- Лекция восьмая. ГАУССОВЫ ПУЧКИ
- Лекция девятая. УСТОЙЧИВОСТЬ РЕЗОНАТОРОВ
- Лекция десятая. НЕУСТОЙЧИВЫЕ РЕЗОНАТОРЫ
- Лекция одиннадцатая. СИНХРОНИЗАЦИЯ МОД
- Лекция двенадцатая. ИСТОРИЯ КВАНТОВОЙ ЭЛЕКТРОНИКИ. ОСНОВНЫЕ ФОРМУЛЫ
- ЧАСТЬ ВТОРАЯ. ЛАЗЕРЫ
- Лекция тринадцатая. ГАЗОВЫЕ ЛАЗЕРЫ. ГЕЛИЙ-НЕОНОВЫЙ ЛАЗЕР
- Лекция четырнадцатая. ИОННЫЕ ЛАЗЕРЫ. ЛАЗЕРЫ НА ПАРАХ МЕТАЛЛОВ
- Лекция пятнадцатая. CO2-ЛАЗЕРЫ
- Лекция шестнадцатая. СO2-ЛАЗЕРЫ (продолжение)
- Лекция семнадцатая. ХИМИЧЕСКИЕ ЛАЗЕРЫ
- Лекция восемнадцатая. CO-ЛАЗЕРЫ, ГАЗОВЫЕ ЛАЗЕРЫ НА ЭЛЕКТРОННЫХ ПЕРЕХОДАХ В МОЛЕКУЛАХ
- Лекция девятнадцатая. ВСПОМОГАТЕЛЬНОЕ ИЗЛУЧЕНИЕ НАКАЧКИ В СИСТЕМАХ СО МНОГИМИ УРОВНЯМИ ЭНЕРГИИ
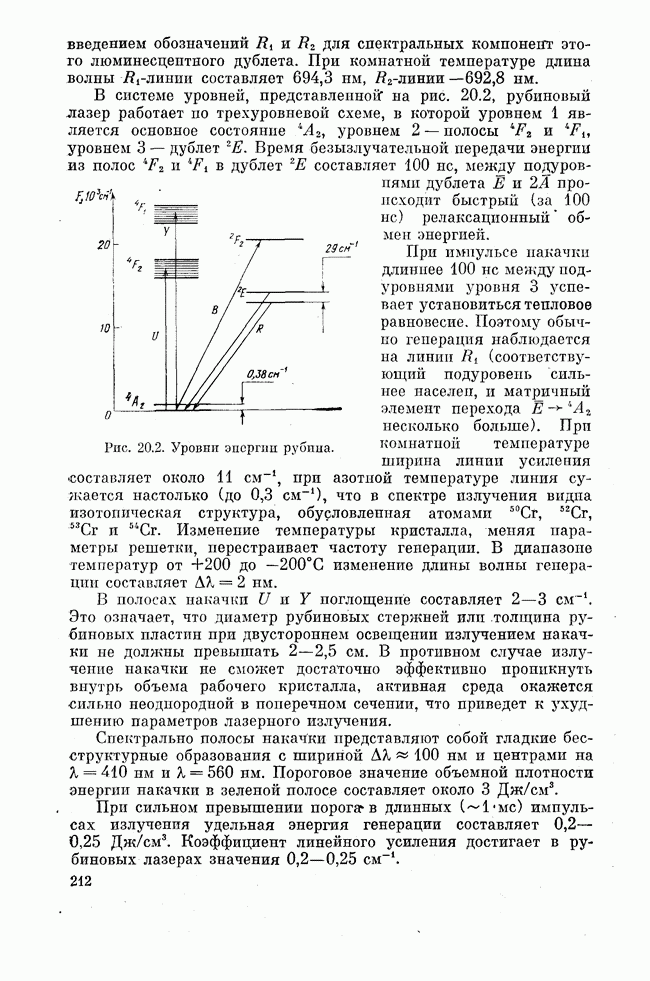
- Лекция двадцатая. РУБИНОВЫЙ И НЕОДИМОВЫЙ ЛАЗЕРЫ
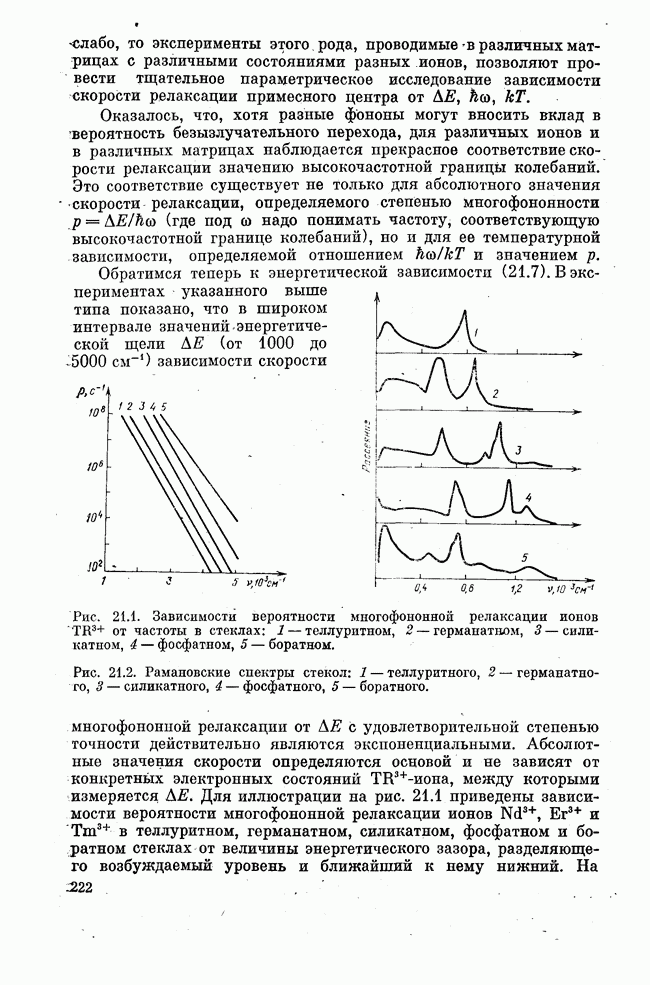
- Лекция двадцать первая. БЕЗЫЗЛУЧАТЕЛЬНАЯ РЕЛАКСАЦИЯ В ТВЕРДОМ ТЕЛЕ
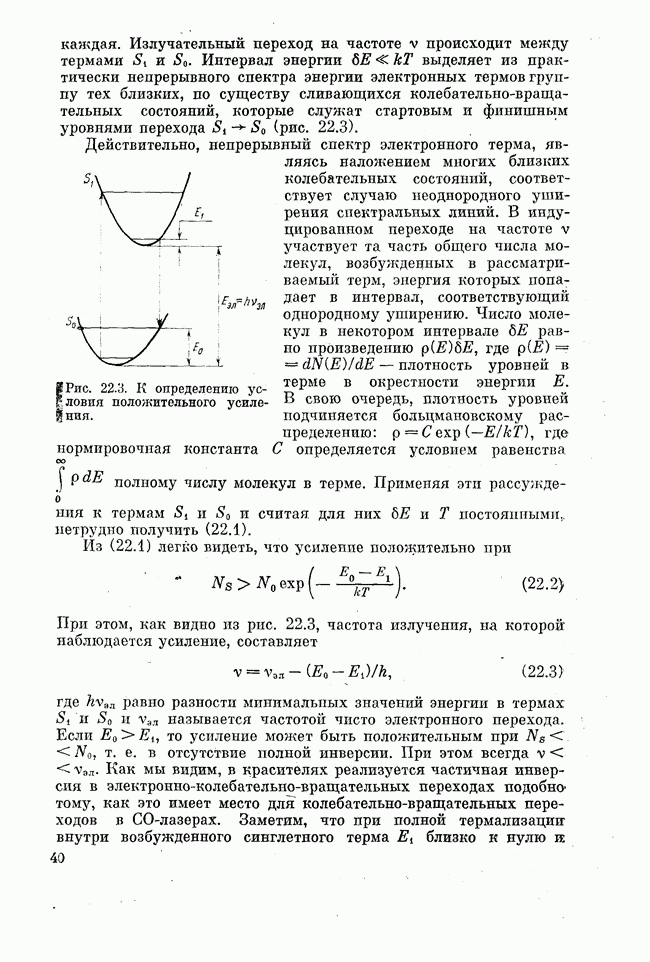
- Лекция двадцать вторая. ЛАЗЕРЫ НА КРАСИТЕЛЯХ
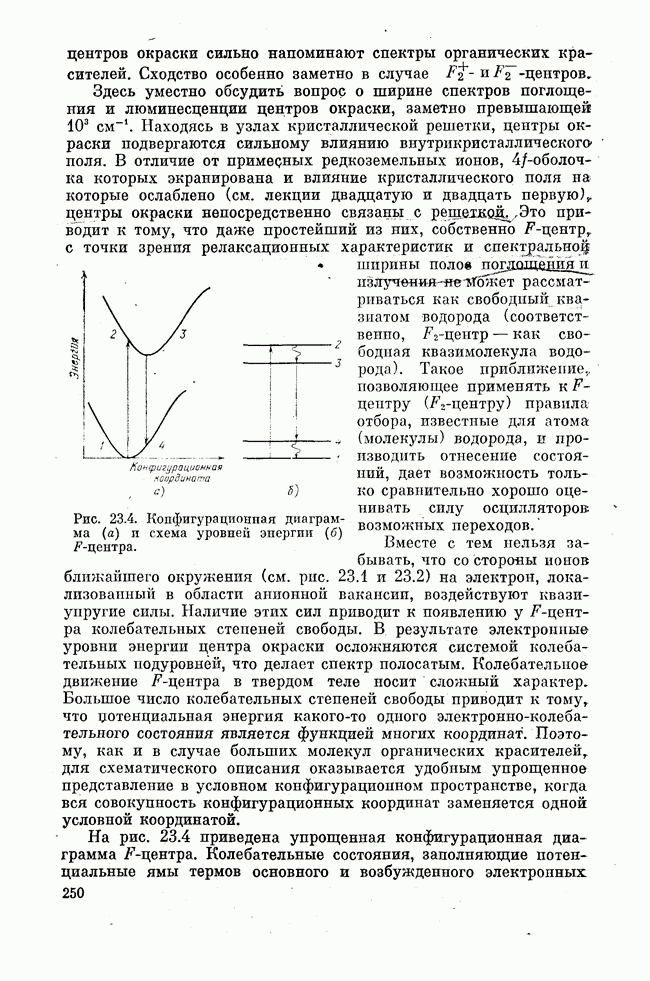
- Лекция двадцать третья. ЛАЗЕРЫ НА ЦЕНТРАХ ОКРАСКИ
- Лекция двадцать четвертая. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ
- Лекция двадцать пятая. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ (продолжение)
- Лекция двадцать шестая. ЛАЗЕРЫ НА СВОБОДНЫХ ЭЛЕКТРОНАХ
- Лекция двадцать седьмая. СЕМНАДЦАТЬ НАИБОЛЕЕ ИЗВЕСТНЫХ ЛАЗЕРОВ
- Заключение. ТЕНДЕНЦИИ РАЗВИТИЯ