| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Лекция шестая. ГЕНЕРАЦИЯ
Открытый резонатор, его добротность. Регенерация резонатора при усилении. Проходной резонаторный усилитель. Отражательный усилитель. Условия самовозбуждения. Условия резонанса. Частота генерации. Максимальная выходная мощность.
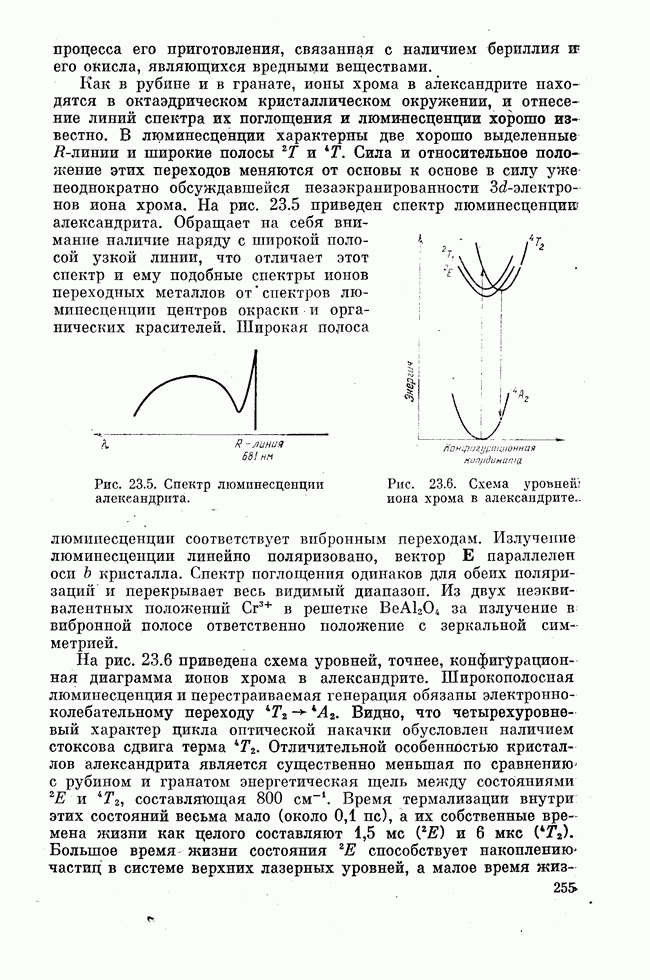
Мы рассмотрели усилитель бегущей волны. Однако взаимодействие усиливаемого излучения и активного вещества может происходить и в режиме стоячей волны. В этом случае излучение. многократно проходит через один и тот же образец вещества, помещенного в объемный резонатор. В радиодиапазоне обычно используются объемные резонаторы, размеры которых сравнимы с длиной возбуждаемой в них волны. Ясно, что для очень коротких волн резонаторы такого типа изготовить невозможно. Поэтому уже для субмиллиметрового (ПК) диапазона вместо резонатора с замкнутым объемом А. М. Прохоровым был предложен открытый резонатор. Размеры такого резонатора много больше, чем длина волны возбуждаемых в нем электромагнитных колебаний. Использование именно такого резонатора в оптике привело к созданию первых лазеров.
В простейшем виде открытый резонатор состоит из двух отражающих параллельных пластин, т. е. зеркал, находящихся на некотором расстоянии  друг от друга. Часто зеркала имеют круглую форму. Диаметр зеркал также много больше длины волны Я, возбуждаемой в резонаторе. Мояшо считать, что между зеркалами возбуждается плоская стоячая волна, если между ними укладывается целое число полуволн. Если размеры зеркал достаточно велики, то дифракционными потерями энергии можно пренебречь. Если, кроме того, пространство между зеркалами заполнено средой без потерь энергии, то добротность резонатора определяется потерями энергии при отражении, т. е., точнее говоря, при идеальных зеркалах потерями энергии на излучение во внешнее пространства через зеркала.
друг от друга. Часто зеркала имеют круглую форму. Диаметр зеркал также много больше длины волны Я, возбуждаемой в резонаторе. Мояшо считать, что между зеркалами возбуждается плоская стоячая волна, если между ними укладывается целое число полуволн. Если размеры зеркал достаточно велики, то дифракционными потерями энергии можно пренебречь. Если, кроме того, пространство между зеркалами заполнено средой без потерь энергии, то добротность резонатора определяется потерями энергии при отражении, т. е., точнее говоря, при идеальных зеркалах потерями энергии на излучение во внешнее пространства через зеркала.
При больших значениях коэффициента отражения R добротность резонатора можно оценить из простых энергетических соображений. Будем считать, что распределение поля в резонаторе близко к чисто стоячей волне. Стоячая волна эквивалентна двум бегущим волнам равной интенсивности, распространяющимся в противоположных направлениях. Пусть поток энергии в каждой из этих бегущих волн равен Р. Тогда при отражении от двух одинаковых зеркал теряется мощность  . Вместе с тем энергия, накопленная в резонаторе, составляет
. Вместе с тем энергия, накопленная в резонаторе, составляет  .
.
Физика колебаний и электроника знают много эквивалентных определений добротности колебательных систем. Наиболее общим из них является энергетическое определение, которое гласит, что  по определению добротность резонатора равна
по определению добротность резонатора равна

При этом

где  . Действие отражающих поверхностей можно рассматривать как увеличение в
. Действие отражающих поверхностей можно рассматривать как увеличение в  раз пути l, проходимого плоской волной в резонаторе.
раз пути l, проходимого плоской волной в резонаторе.
Очевидно, что применительно к теории лазеров требуется более тщательный анализ открытых резонаторов и распределения поля излучения в них. Сейчас для нас важно лишь то, что два параллельных отражающих диска, т. е. два параллельных зеркала, являются резонатором высокой добротности. По существу, открытый дисковый резонатор является хорошо известным в оптике интерферометром Фабри — Перо. Добротность интерферометра, рассматриваемого как резонатор, равна разрешающей силе интерферометра, определяемой как отношение длины волны к ширине интерференционного лепестка 8% на уровне интенсивности, равной половине максимальной. Для проходящего света разрешающая сила интерферометра Фабри — Перо вычислена в курсах оптики. При одинаковых зеркалах

где  характеризует потери энергии при однократном прохождении. При
характеризует потери энергии при однократном прохождении. При  формулы (6.3) и (6.2) совпадают.
формулы (6.3) и (6.2) совпадают.
Если считать, что а обусловлено только резонансными потерями, то при достижении инверсии коэффициент потерь  превращается в коэффициент усиления по мощности в активном веществе за один проход
превращается в коэффициент усиления по мощности в активном веществе за один проход  . В результате резонатор регенерируется, т. е. его добротность возрастает, а полоса пропускания сужается. Мы получаем
. В результате резонатор регенерируется, т. е. его добротность возрастает, а полоса пропускания сужается. Мы получаем

Очевидно, что формула (6.4) справедлива, пока  .
.
Для того чтобы лучше понять, что происходит при регенерации, рассмотрим проходной оптический усилитель с резонатором Фабри — Перо, представляющий собой усилитель бегущей волны, помещенный в резонатор Фабри — Перо. Пусть входной сигнал? падает на левое частично прозрачное зеркало резонатора. Пространство между зеркалами заполнено активной средой. Рассмотрим усиленный сигнал, выходящий из резонатора через правое - частично прозрачное зеркало, идентичное левому. Коэффициент усиления в этой ситуации можно вычислить, производя сложение амплитуд лучей, вышедших из интерферометра после многократных отражений.
При единичной амплитуде входного сигнала поле на выходе определяется суммой

Суммируя в предположении  полученную геометрическую прогрессию, находим комплексный коэффициент усиления напряженности поля
полученную геометрическую прогрессию, находим комплексный коэффициент усиления напряженности поля

Следовательно, коэффициент усиления по мощности

В резонансе, т. е. при 

При  осуществляется режим бегущей волны и
осуществляется режим бегущей волны и  . При
. При  входное излучение не проходит в усилитель и
входное излучение не проходит в усилитель и  . При
. При  нет ни усиления, ни потерь, G приобретает смысл коэффициента передачи эталона Фабри — Перо, в резонансе равного единице. При
нет ни усиления, ни потерь, G приобретает смысл коэффициента передачи эталона Фабри — Перо, в резонансе равного единице. При  коэффициент усиления
коэффициент усиления  . Это означает, что возникает генерация.
. Это означает, что возникает генерация.
Проведенное рассмотрение показывает, как положительная обратная связь приводит к возникновению генерации. Условие

является, по существу, энергетическим условием самовозбуждения. Смысл его прост — потери энергии за один проход должны быть скомпенсированы усилением за этот же проход.
Мы рассмотрели регенерацию проходного резонатора, заполненного активным веществом. Этот усилитель, имеющий одинаковые частично прозрачные зеркала на входе и выходе, при выполнении условия самовозбуждения  становится генератором, одинаково связанным - с внешним пространством с двух противоположных концов. Это не всегда удобно, поэтому лазер-генератор имеет обычно только одно выходное, т. е. частично прозрачное зеркало. Второе его зеркало является глухим, т. е. не пропускающим наружу излучение. В этом случае при наличии инверсии населенностей регенерируется не проходной, а отражательный усилитель, т. е. устройство, коэффициент отражения от которого превышает единицу.
становится генератором, одинаково связанным - с внешним пространством с двух противоположных концов. Это не всегда удобно, поэтому лазер-генератор имеет обычно только одно выходное, т. е. частично прозрачное зеркало. Второе его зеркало является глухим, т. е. не пропускающим наружу излучение. В этом случае при наличии инверсии населенностей регенерируется не проходной, а отражательный усилитель, т. е. устройство, коэффициент отражения от которого превышает единицу.
Суммируя аналогйчно тому, как это делалось для проходного усилителя, амплитуды полей на выходе системы, т. е. амплитуды
полей, претерпевающих многократное отражение от усилителя, находим

Этому соответствует

В резонансе, т. е. при  ,
,

При  усиления нет, при
усиления нет, при  , т. е. осуществляется усиление бегущей волны, дважды проходящей через активное вещество. Генерация наступает при выполнении условия самовозбуждения
, т. е. осуществляется усиление бегущей волны, дважды проходящей через активное вещество. Генерация наступает при выполнении условия самовозбуждения

Можно придумать много различных схем сочетания системы зеркал с активным веществом и для каждой из них получить условие самовозбуждения. Общим для всех из них будет требование того, чтобы усиление в активном веществе за некоторый один эффективный проход излучения через систему зеркал резонатора и активное вещество превышало все потери энергии в резонаторе за тот же один проход. При этом в общий баланс должны быть включены как потери энергии на полезное излучение наружу, так и паразитные потери энергии на рассеяние света, его поглощение и т. п.
Вернемся к резонансным знаменателям формул (6.7) и (6.11). Условие резонанса

эквивалентно хорошо известному условию возникновения стоячей волны (целое число полуволн)

В оптическом диапазоне значение  для открытых резонаторов составляет
для открытых резонаторов составляет  . Это приводит к высокой плотности резонансов, так как расстояние между соседними резонансами составляет
. Это приводит к высокой плотности резонансов, так как расстояние между соседними резонансами составляет

Может случиться, а именно так обстоит дело в большинстве случаев, что инвертируемая резонансная линия шире расстояния между резонансами:

Это приводит к ряду важных особенностей в свойствах соответствующих лазеров, которые будут обсуждены в дальнейшем.
Условие самовозбуждения  или эквивалентные ему дают баланс амплитуд. Однако для возникновения автоколебательного режима необходим также баланс фаз. Резонансные условия типа (6.14) выполняются для излучения той частоты, для которой все фазовые набеги взаимно компенсируются. Следовательно, условие баланса фаз дает значение частоты генерации. Рассмотрим этот вопрос более подробно.
или эквивалентные ему дают баланс амплитуд. Однако для возникновения автоколебательного режима необходим также баланс фаз. Резонансные условия типа (6.14) выполняются для излучения той частоты, для которой все фазовые набеги взаимно компенсируются. Следовательно, условие баланса фаз дает значение частоты генерации. Рассмотрим этот вопрос более подробно.
Дисперсионные свойства активной среды определяют фазовый набег в рабочем веществе. Как хорошо известно, для резонансно поглощающих (усиливающих) сред аномальное поглощение сопровождается аномальной дисперсией. Частотно зависимый фазовый набег обусловлен частотной зависимостью восприимчивости среды. Показатель преломления

где диэлектрическая восприимчивость  записывается в виде
записывается в виде

При малых 

Это приближение эквивалентно приближению малых потерь (усиления) излучения на расстоянии в одну длину волны. Записывая плоскую волну частоты а (длины волны А), распространяющуюся в направлении z, в виде

мы видим, что мнимая часть диэлектрической восприимчивости обусловливает потери (усиление) излучения в веществе, а ее действительная часть — фазовый набег:

Для Определения  существуют хорошо развитые квантовомеханические методы. Мы, однако, воспользуемся снова классической аналогией, уподобляя двухуровневую квантовую систему с конечным временем жизни верхнего уровня классическому осциллятору с трением. Уравнение
существуют хорошо развитые квантовомеханические методы. Мы, однако, воспользуемся снова классической аналогией, уподобляя двухуровневую квантовую систему с конечным временем жизни верхнего уровня классическому осциллятору с трением. Уравнение

имеет, как известно, решение, описывающее вынужденное колебание:

Из определения диэлектрической восприимчивости как коэффициента пропорциональности между дипольиым моментом единицы объема и напряженностью поля следует пропорциональность X вызванному полем смещению  Тогда, записывая
Тогда, записывая  в виде
в виде

где по определению бсол  — отстройка частоты излучения и от центральной частоты линии резонансного перехода сол, и приводя
— отстройка частоты излучения и от центральной частоты линии резонансного перехода сол, и приводя  к виду (6.19), получаем
к виду (6.19), получаем

где В — константа, а  Индивидуальные особенности активной среды удобно учесть, охарактеризовав среду величиной а с помощью соотношений (6.28) и (6.22). Это позволяет исключить константу В и представить фазовый набег в веществе в виде
Индивидуальные особенности активной среды удобно учесть, охарактеризовав среду величиной а с помощью соотношений (6.28) и (6.22). Это позволяет исключить константу В и представить фазовый набег в веществе в виде

где 
Итак, фазовый набег в веществе возникает при отстройке частоты излучения от центра линии. Вещество помещено в резонатор, и на дисперсионной кривой резонатора также происходит фазовый сдвиг. Прохождение излучения через резонатор описывается частотной  функцией передачи резонатора. В рамках одной колебательной моды фазовая характеристика резонатора полностью эквивалентна характеристике одиночного
функцией передачи резонатора. В рамках одной колебательной моды фазовая характеристика резонатора полностью эквивалентна характеристике одиночного  -контура. Как известно, и это легко показать с помощью эквивалентной схемы резонансного фильтра, сдвиг фазы между входным и выходным сигналами может быть представлен в виде
-контура. Как известно, и это легко показать с помощью эквивалентной схемы резонансного фильтра, сдвиг фазы между входным и выходным сигналами может быть представлен в виде

где Q — добротность резонатора, а  — его собственная частота. Вводя по определению
— его собственная частота. Вводя по определению  — отстройку частоты излучения
— отстройку частоты излучения  от
от  и считая ее малой, получаем
и считая ее малой, получаем

где  — ширина полосы пропусканий резонатора (в одной моде). Тогда, приравнивая фазовые сдвиги (6.31) и (6.29), получаем
— ширина полосы пропусканий резонатора (в одной моде). Тогда, приравнивая фазовые сдвиги (6.31) и (6.29), получаем
условие баланса фаз, задающее частоту генерации лазера (мазера).
Отстройки частоты генерации от собственной частоты резонатора и от частоты линии связаны соотношением

где  . Иначе говоря, частота генерации
. Иначе говоря, частота генерации

отличается как от частоты резонатора, так и от частоты линии, если только резонатор не точно настроен на линию  . Только в пределе очень узкой линии или очень высокого усиления
. Только в пределе очень узкой линии или очень высокого усиления  . В пределе очень широкой линии
. В пределе очень широкой линии  частота генерации определяется частотой резонатора. Эти соображения имеют прямое отношение к проблеме квантовых стандартов частоты на основе молекулярных генераторов, с одной стороны, и лазеров с перестраиваемой частотой излучения — с другой.
частота генерации определяется частотой резонатора. Эти соображения имеют прямое отношение к проблеме квантовых стандартов частоты на основе молекулярных генераторов, с одной стороны, и лазеров с перестраиваемой частотой излучения — с другой.
Формула (6.33) была получена А. М. Прохоровым в 1954 г. применительно к аммиачному молекулярному генератору и в несколько иной записи, однако ее общее значение было подчеркнуто еще в те годы. С лазерной точки зрения важно отметить, что в случае широкой линии частота генерации определяется настройкой резонатора. Если линия неоднородно уширена и перекрывает несколько мод резонатора (см. формулу (6.17)), то генерация возникает на нескольких частотах, соответствующих этим модам.
Итак, при регенерации квантового усилителя в процессе обратной связи, возникающей при помещении усилителя в резонатор, происходит его самовозбуждение, т. е. превращение в генератор. Анализ коэффициента усиления регенерированного усилителя позволил определить условие самовозбуждения — найти величину минимального необходимого для генерации коэффициента усиления за один проход (порог самовозбуждения). Анализ фазовых соотношений при самовозбуждении позволил найти частоту генерации. Линейная теория на большее не способна. Амплитуда генерации может быть найдена только с учетом нелинейности процесса усиления, только в" рамках нелинейной теории.
Обратимся теперь к вопросу о выходной мощности лазерных генераторов. Как и в случае квантовых усилителей, определяющую роль здесь играют эффект насыщения и наличие потерь излучения.
Будем рассматривать лазер с одним полностью отражающим (глухим) зеркалом и другим зеркалом, обладающим прозрачностью  (частично прозрачное выходное зеркало). В резонаторе лазера усиливаемое излучение распространяется в активной
(частично прозрачное выходное зеркало). В резонаторе лазера усиливаемое излучение распространяется в активной
среде между зеркалами в виде последовательности нарастающих бегущих волн, предполагаемых плоскими. Напишем уравнения переноса для волн, бегущих слева направо и справа налево:

Здесь интенсивность измеряется в единицах интенсивности насыщения  , а индексы ± отмечают волны, распространяющиеся в противоположных направлениях. Кроме того, принято, что в каждом произвольном сечении z эффект насыщения определяется суммарной усредненной интенсивностью потоков энергии слева направо и справа налево, т. е. пренебрегается влиянием модовой структуры поля излучения в резонаторе на эффект насыщения.
, а индексы ± отмечают волны, распространяющиеся в противоположных направлениях. Кроме того, принято, что в каждом произвольном сечении z эффект насыщения определяется суммарной усредненной интенсивностью потоков энергии слева направо и справа налево, т. е. пренебрегается влиянием модовой структуры поля излучения в резонаторе на эффект насыщения.

Рис. 6.1. Распределение интенсивностей встречных волн в резонаторе лазера длиной l. Слева направо распространяется излучение с интенсивностью  справа палево — с
справа палево — с  итенсивностью
итенсивностью  .
.
Системе уравнений (6.34) соответствует схема, представленная на рис. 6.1. Для значений J на границе  введем обозначения
введем обозначения  . Считаем, кроме того, что
. Считаем, кроме того, что  . Тогда условие стационарности генерации приводит к граничным условиям
. Тогда условие стационарности генерации приводит к граничным условиям

Выходная интенсивность

Теперь поделим уравнения (6.34) друг на друга:

что легко интегрируется:
 (6.38)
(6.38)
Так как при  , то
, то  . Следовательно, уравнения (6.34) имеют интеграл
. Следовательно, уравнения (6.34) имеют интеграл

где  — интенсивность, падающая на правое (глухое) зеркало. Эта интенсивность простым соотношением связана с выходной интенсивностью. Действительно, так как
— интенсивность, падающая на правое (глухое) зеркало. Эта интенсивность простым соотношением связана с выходной интенсивностью. Действительно, так как

то

Таким образом,

Далее  решение идет по следующей схеме. Записываем
решение идет по следующей схеме. Записываем  в виде
в виде  подставляем в первое из уравнений (6.34), опускаем индекс
подставляем в первое из уравнений (6.34), опускаем индекс  и получаем уравнение
и получаем уравнение

которое интегрируется в элементарных функциях.
Интересно видеть, как меняется в силу наличия обратной связи и обратной волны характер члена, определяющего усилепие и насыщение, по сравнению со случаем одной бегущей волны  (см. формулу (5.17)). Сложность записи (6.41) приводит к тому, что решение этого уравнения дается трансцендентным алгебраическим уравнением, плохо обозреваемым и неудобным для анализа.
(см. формулу (5.17)). Сложность записи (6.41) приводит к тому, что решение этого уравнения дается трансцендентным алгебраическим уравнением, плохо обозреваемым и неудобным для анализа.
В частном случае сильного насыщения и большого превышения усиления над потерями 

при 

Так как" длина генератора предполагается бесконечной, это выражение не имеет оптимума по R. Предельная возможная интенсивность составляет

что совпадает, как и следовало ожидать, со случаем усилителя (см. (5.26)).
В противоположном частном случае генератора относительно малой длины  можно считать, что интенсивности волн
можно считать, что интенсивности волн  и нарастают по z линейно. Тогда
и нарастают по z линейно. Тогда  ,
,
и исходные уравнения (6.34) принимают вид

и легко интегрируются.
В результате выходная интенсивность нашего генератора достигает максимального значения
 (6.46)
(6.46)
при оптимальной прозрачности выходного зеркала

Величина оптимальной связи сильнее зависит от коэффициента потерь р, чем максимальная выходная мощность, соответствующая этой связи. При  см и
см и  величина
величина  . Из этого примера видно, какие высокие требования предъявляются к лазерным зеркалам при небольших коэффициентах усиления, характерных, как правило, для газовых лазеров. При такой слабой связи из резонатора лазера выходит только малая доля сконцентрированной в нем интенсивности излучения. Для данных приведенного примера интенсивность излучения, падающего изнутри резонатора на его глухое зеркало, примерно в 20 раз превышает выходную интенсивность (см. формулу (6.40)). При больших усилениях ситуация существенно облегчается.
. Из этого примера видно, какие высокие требования предъявляются к лазерным зеркалам при небольших коэффициентах усиления, характерных, как правило, для газовых лазеров. При такой слабой связи из резонатора лазера выходит только малая доля сконцентрированной в нем интенсивности излучения. Для данных приведенного примера интенсивность излучения, падающего изнутри резонатора на его глухое зеркало, примерно в 20 раз превышает выходную интенсивность (см. формулу (6.40)). При больших усилениях ситуация существенно облегчается.
Заметим, что большая часть лазеров средних мощностей работает в условиях, соответствующих формулам (6.46) и (6.47).
Подчеркнем также еще раз, что, если условия самовозбуждения лазера-генератора (6.9) (или эквивалентная формула (6.13)) были получены из линейной теории, амплитуда (интенсивность) генерации была определена с привлечением нелинейной теории. Этот вывод является частным проявлением общего положения теории колебаний: амплитуда установившихся колебаний в автоколебательной системе при выполнении условий самовозбуждения определяется нелинейной теорией, учитывающей нелинейные эффекты в исходных уравнениях. В квантовой электронике таким нелинейным эффектом является эффект насыщения.
Итак, лазер-генератор при малом  и оптимальной связи излучает интенсивность
и оптимальной связи излучает интенсивность  Это означает, что вся запасенная в активном веществе лазера энергия излучается во внещнее пространство. Этот вывод имеет общее значение. Показать его общность можно, сделав оценку мощности, излучаемой из резонатора лазера во внешнее пространство, в рамках эквивалентной схемы с сосредоточенными постоянными.
Это означает, что вся запасенная в активном веществе лазера энергия излучается во внещнее пространство. Этот вывод имеет общее значение. Показать его общность можно, сделав оценку мощности, излучаемой из резонатора лазера во внешнее пространство, в рамках эквивалентной схемы с сосредоточенными постоянными.
Представим резонатор лазера в виде резонансного RLC-контура (рис. 6.2). Излучающее активное вещество эквивалентно
генератору с э. д. с.  , обладающему внутренним сопротивлением
, обладающему внутренним сопротивлением  и включенному в последовательный колебательный контур
и включенному в последовательный колебательный контур  . Излучение во внешнее пространство представим индуктивной связью контура с согласованной длинной линией. Пусть сопротивление нагрузки длинной линии равно
. Излучение во внешнее пространство представим индуктивной связью контура с согласованной длинной линией. Пусть сопротивление нагрузки длинной линии равно  , взаимная индуктивность петли связи равна М.
, взаимная индуктивность петли связи равна М.
Излучаемая веществом мощность простым соотношением

связана с э. д. с. и внутренним сопротивлением генератора.

Ряс. 6.2. Эквивалентная схема резонатора лазера с излучающим активным веществом.
Эквивалентной схеме (рис. 6.2) на резонансной частоте соответствуют уравнения Кирхгофа

Исключая из уравнений (6.49) ток в резонаторе получаем выражение для тока через нагрузку

где введены обозначения для добротности связи

собственной добротности резонатора

добротности, связанной с внутренним сопротивлением генератора э. д. е.,

Мощность, рассеиваемая в сопротивлении нагрузки, равна

Запись связи выходной мощности с мощностью, генерируемой источником э. д. с. в контуре, через добротности, введенные здесь
соотношениями (6.51) — (6.53), хорошо известными в теории резонансных контуров, но имеющими весьма общий энергетический смысл (см. (6.1)), придает полученному соотношению достаточно общий характер.
Выходная мощность может быть оптимизирована изменением связи с внешним пространством. Формула (6.54) позволяет найти максимальную выходную мощность

которая достигается при оптимальной связи

Когда потерями в резонаторе можно пренебречь  при оптимальной связи вся излучаемая мощность поступает в полезную нагрузку. По существу, петля связи резонатора с линией играет роль трансформатора импедансов, согласующего внутреннее сопротивление источника с сопротивлением полезной нагрузки. В лазерном случае эту роль исполняет частично прозрачное выходное зеркало, согласующее активное вещество резонатора лазера со свободным пространством.
при оптимальной связи вся излучаемая мощность поступает в полезную нагрузку. По существу, петля связи резонатора с линией играет роль трансформатора импедансов, согласующего внутреннее сопротивление источника с сопротивлением полезной нагрузки. В лазерном случае эту роль исполняет частично прозрачное выходное зеркало, согласующее активное вещество резонатора лазера со свободным пространством.
Физически лазерная генерация обусловлена излучением среды с инверсией населенностей. Интенсивность генерации определяется плотностью инверсии населенностей. Для оценок того, что может дать активная среда, особенно в случае мощных лазеров, удобно пользоваться следующими простыми соображениями. Пусть в стационарных условиях скорость создания инверсии составляет А частиц в единичном объеме за единицу времени. Тогда максимально возможная мощность излучения, отнесенная к единице объема, составляет

Это простое соотношение приводит, например, в случае  -лазеров
-лазеров  к такой оценке, что при массовом расходе возбужденного газа
к такой оценке, что при массовом расходе возбужденного газа  максимальная мощность генерации составляет
максимальная мощность генерации составляет  что соответствует мощности 250 кВт при массовом расходе
что соответствует мощности 250 кВт при массовом расходе 
Для импульсных лазеров энергия генерации определяется энергией, накопленной в активном веществе к моменту начала генерации, т. е. инверсией, созданной к моменту начала генерации. Так как генерация прекращается, когда исчезает инверсия, что происходит при уравнивании населенностей верхнего и нижнего лазерных уровней, то инверсии в N частиц соответствует излучение с энергией

Для  -лазера это означает 125 кДж при 1 кг возбужденного
-лазера это означает 125 кДж при 1 кг возбужденного  .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ЧАСТЬ ПЕРВАЯ. ОСНОВЫ ФИЗИКИ ЛАЗЕРОВ
- Лекция первая. КОЭФФИЦИЕНТЫ ЭЙНШТЕЙНА
- Лекция вторая. ШИРИНА ЛИНИИ
- Лекция третья. УСИЛЕНИЕ
- Лекция четвертая. КОЭФФИЦИЕНТЫ ЭЙНШТЕЙНА И МАТРИЧНЫЙ ЭЛЕМЕНТ ОПЕРАТОРА ПЕРЕХОДА
- Лекция пятая. ЛАЗЕРЫ-УСИЛИТЕЛИ
- Лекция шестая. ГЕНЕРАЦИЯ
- Лекция седьмая. ОТКРЫТЫЕ РЕЗОНАТОРЫ
- Лекция восьмая. ГАУССОВЫ ПУЧКИ
- Лекция девятая. УСТОЙЧИВОСТЬ РЕЗОНАТОРОВ
- Лекция десятая. НЕУСТОЙЧИВЫЕ РЕЗОНАТОРЫ
- Лекция одиннадцатая. СИНХРОНИЗАЦИЯ МОД
- Лекция двенадцатая. ИСТОРИЯ КВАНТОВОЙ ЭЛЕКТРОНИКИ. ОСНОВНЫЕ ФОРМУЛЫ
- ЧАСТЬ ВТОРАЯ. ЛАЗЕРЫ
- Лекция тринадцатая. ГАЗОВЫЕ ЛАЗЕРЫ. ГЕЛИЙ-НЕОНОВЫЙ ЛАЗЕР
- Лекция четырнадцатая. ИОННЫЕ ЛАЗЕРЫ. ЛАЗЕРЫ НА ПАРАХ МЕТАЛЛОВ
- Лекция пятнадцатая. CO2-ЛАЗЕРЫ
- Лекция шестнадцатая. СO2-ЛАЗЕРЫ (продолжение)
- Лекция семнадцатая. ХИМИЧЕСКИЕ ЛАЗЕРЫ
- Лекция восемнадцатая. CO-ЛАЗЕРЫ, ГАЗОВЫЕ ЛАЗЕРЫ НА ЭЛЕКТРОННЫХ ПЕРЕХОДАХ В МОЛЕКУЛАХ
- Лекция девятнадцатая. ВСПОМОГАТЕЛЬНОЕ ИЗЛУЧЕНИЕ НАКАЧКИ В СИСТЕМАХ СО МНОГИМИ УРОВНЯМИ ЭНЕРГИИ
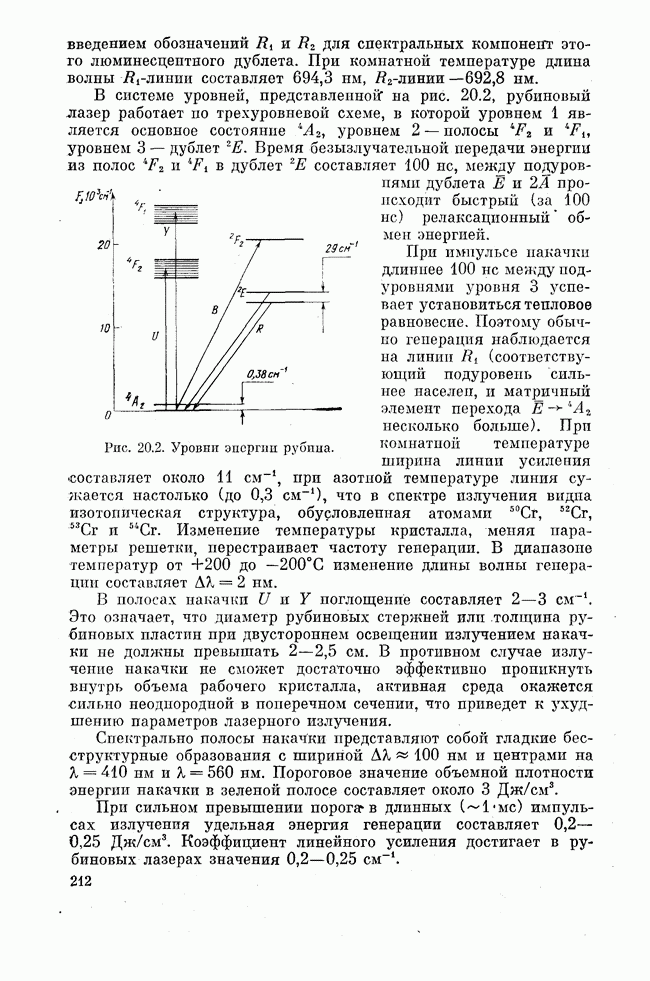
- Лекция двадцатая. РУБИНОВЫЙ И НЕОДИМОВЫЙ ЛАЗЕРЫ
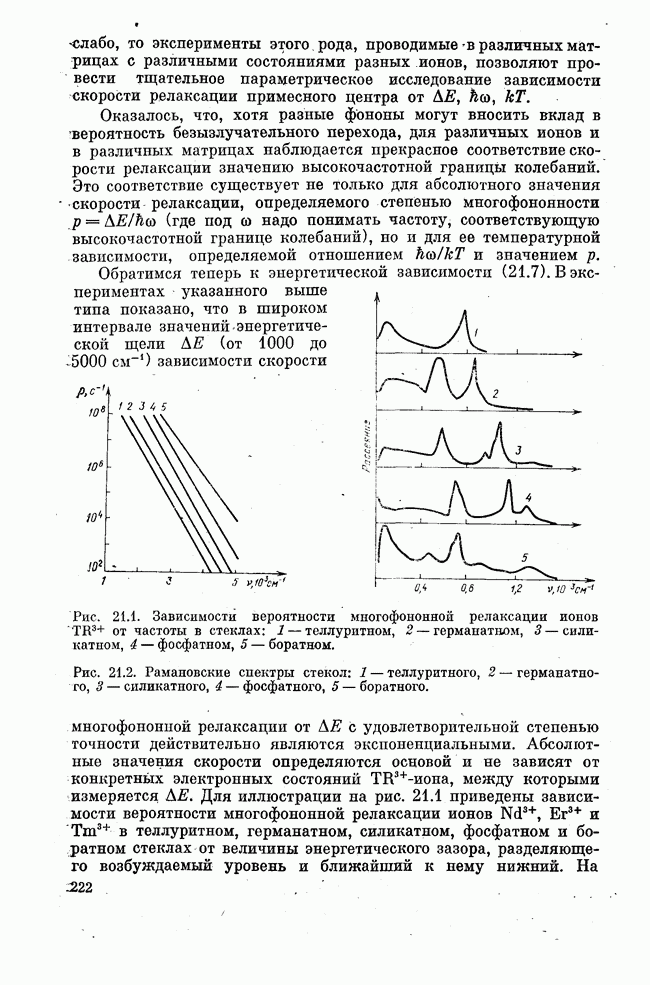
- Лекция двадцать первая. БЕЗЫЗЛУЧАТЕЛЬНАЯ РЕЛАКСАЦИЯ В ТВЕРДОМ ТЕЛЕ
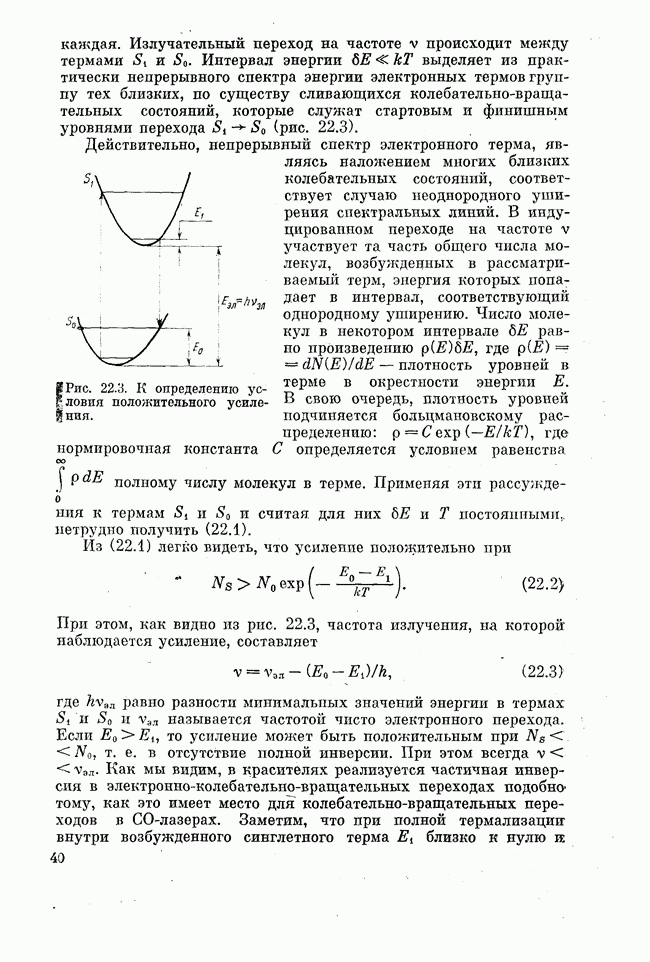
- Лекция двадцать вторая. ЛАЗЕРЫ НА КРАСИТЕЛЯХ
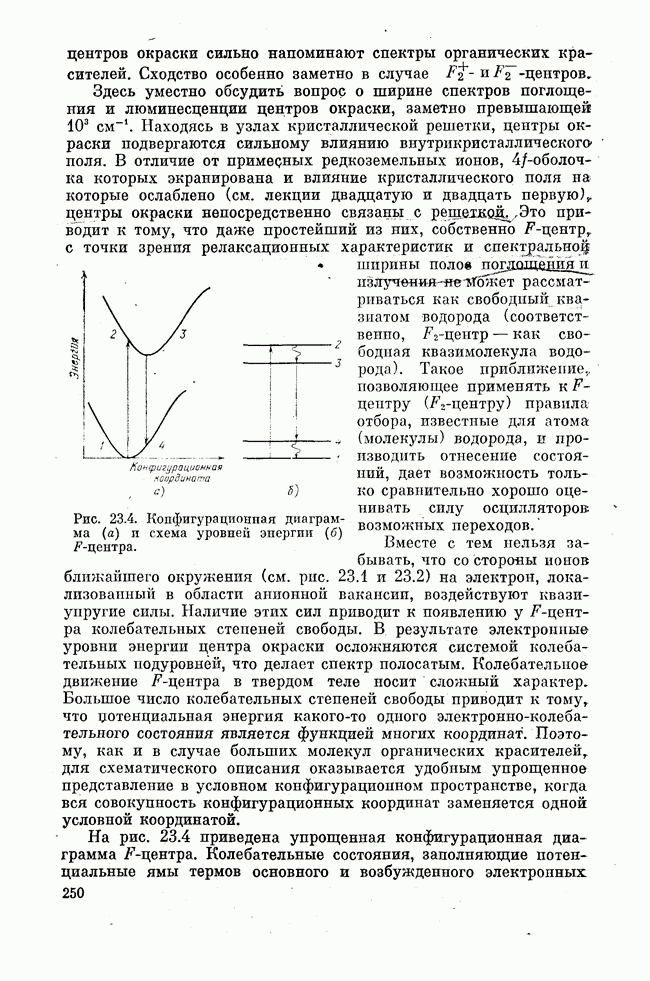
- Лекция двадцать третья. ЛАЗЕРЫ НА ЦЕНТРАХ ОКРАСКИ
- Лекция двадцать четвертая. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ
- Лекция двадцать пятая. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ (продолжение)
- Лекция двадцать шестая. ЛАЗЕРЫ НА СВОБОДНЫХ ЭЛЕКТРОНАХ
- Лекция двадцать седьмая. СЕМНАДЦАТЬ НАИБОЛЕЕ ИЗВЕСТНЫХ ЛАЗЕРОВ
- Заключение. ТЕНДЕНЦИИ РАЗВИТИЯ