Лекция двадцать четвертая. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ

Отличительные особенности полупроводниковых лазеров. Зоны разрешенных состояний. Прямозонные и непрямозонные полупроводники. Рекомбинационное свечение. Уровень Ферми, квазиуровни Ферми. Условие инверсии. Везызлучательная рекомбинация. Внутренний квантовый выход.

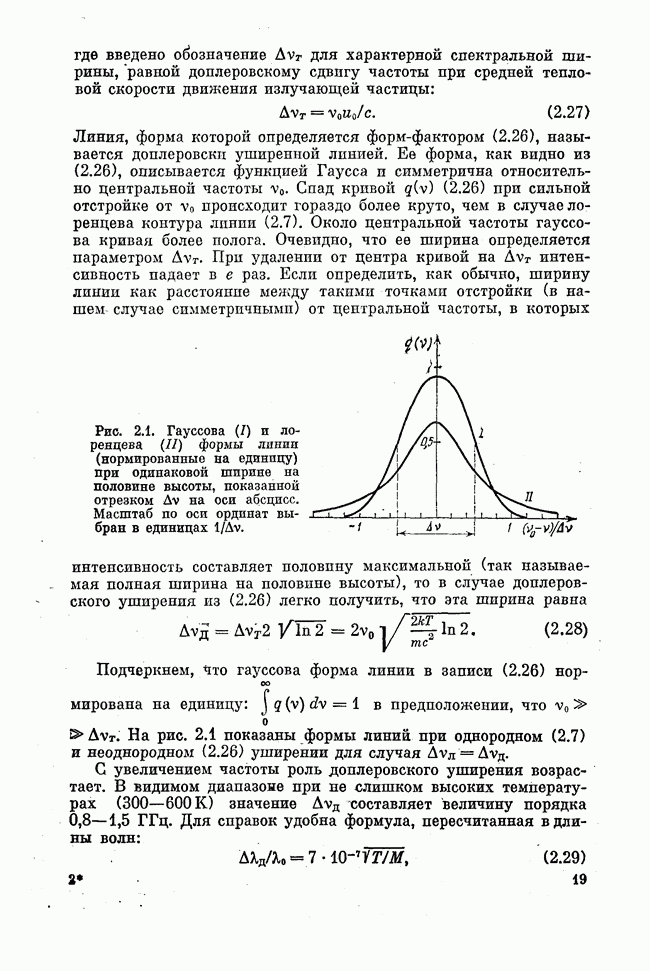
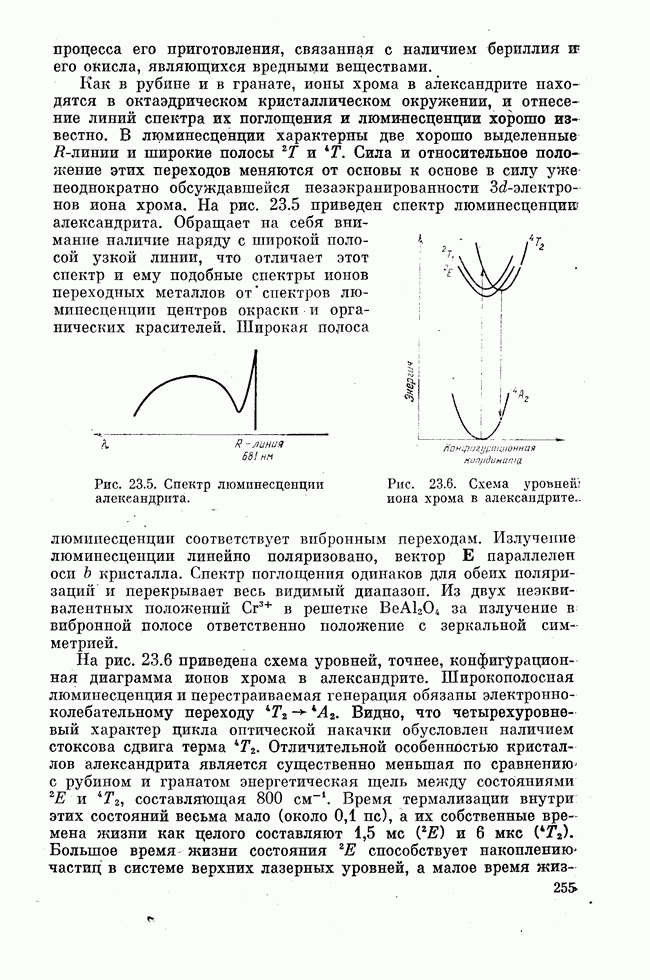
Квантовая электроника является, в основном, электроникой связанных состояний, которым соответствуют дискретные уровни энергии и относительно узкие линии резонансных переходов. Чем более изолирован от внешних воздействий электрон активного центра, тем в большей степени его время жизни в связанном состоянии определяется временем спонтанного распада и тем ближе ширина линии резонансного перехода к предельно узкой. И наоборот, чем больше подвержен внешним воздействиям тот электрон, переходы между связанными состояниями которого рассматриваются как возможные лазерные переходы, тем, вообще говоря, шире соответствующие линии люминесценции и усиления. Примеры хорошо известны. Это уже рассмотренные нами лазеры на красителях, на центрах окраски, александритовый лазер, молекулярные лазеры высокого давления и т. п.

До сих пор мы обсуждали лазеры, активные центры которых характеризуются наличием относительно узких дискретных уровней энергии. Однако получение инверсии возможно и в тех случаях, когда в энергетическом спектре активных центров выделяются широкие энергетические зоны разрешенных состояний, разделенные отчетливо проявляющейся запрещенной зоной. Примером являются полупроводниковые лазеры, рассмотрению которых посвящена эта лекция.

Отличительной особенностью полупроводниковых лазеров является инверсия на переходах между состояниями в электронных энергетических зонах полупроводникового кристалла. Эти энергетические зоны возникают вследствие расщепления уровней

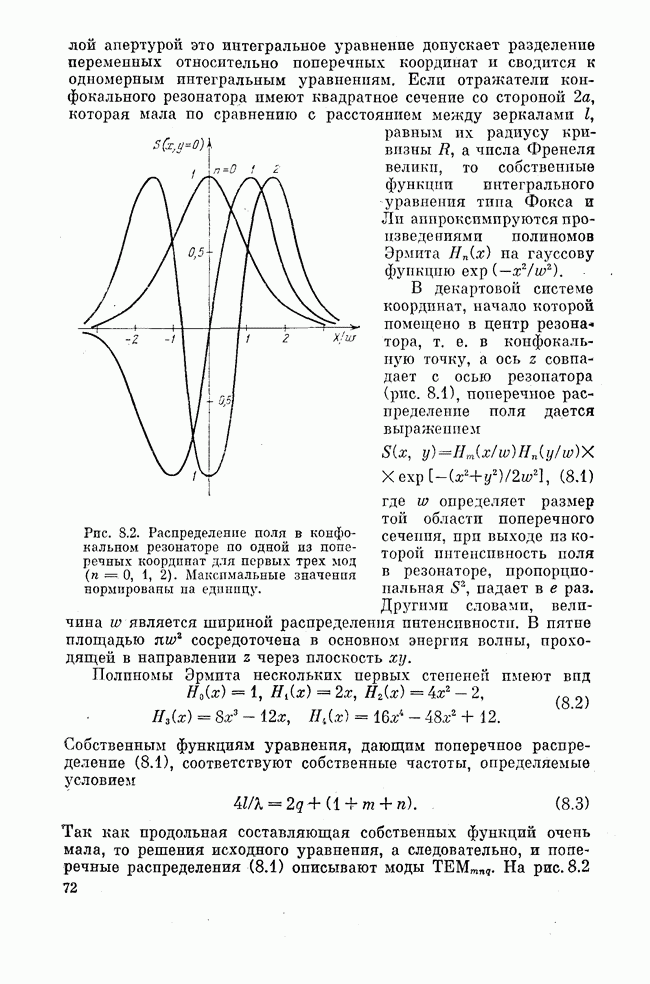
энергии валентных электронов атомов, составляющих кристаллическую решетку кристалла, в сильном периодическом в пространстве внутрикристаллическом поле собственных атомов кристалла. В этом поле индивидуальные атомы теряют свои валентные электроны, локализованность которых исчезает. Другими словами, в сильном периодически поле валентные электроны атомов полупроводникового кристалла обобществляются. Коллективные движения обобществленных электронов в разрешенных энергетических зонах полупроводникового кристалла обеспечивают электропроводность кристалла.

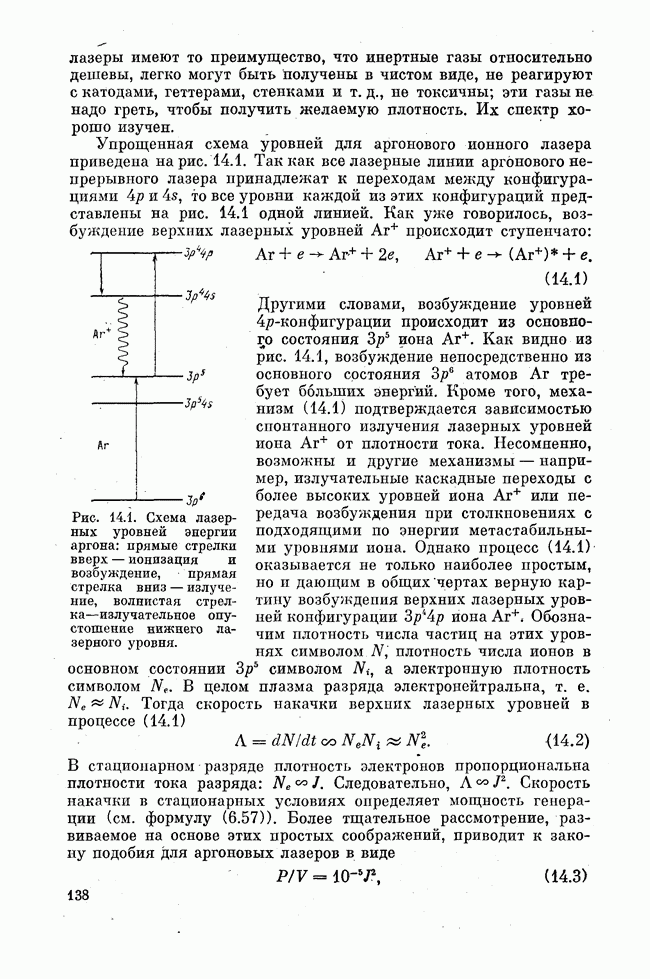
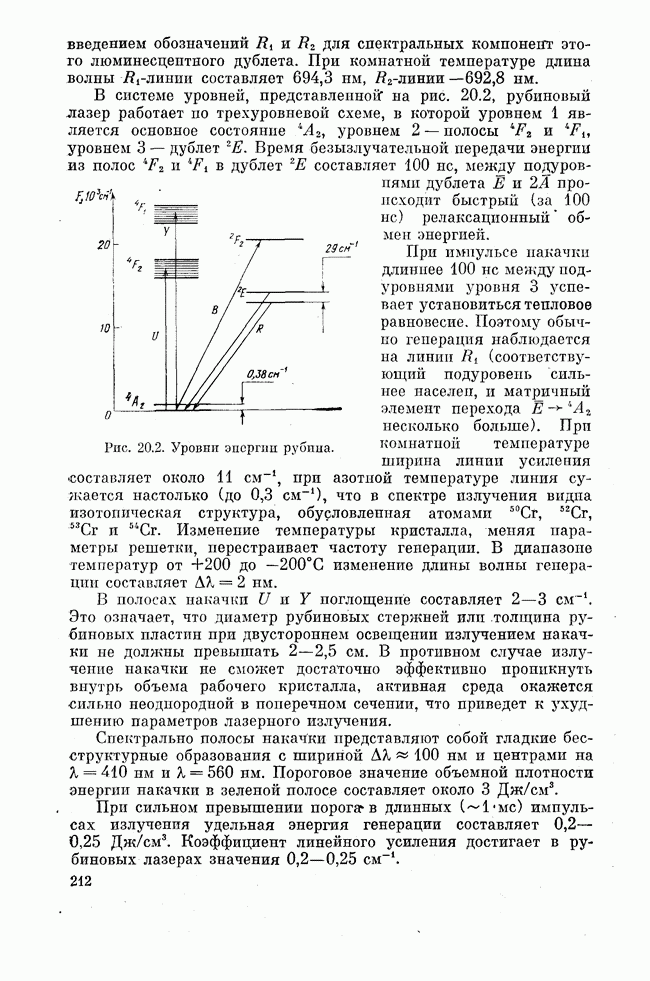
Как известно, носителями тока в полупроводниках являются электроны в зоне проводимости и дырки в валентной зоне. Пусть с помощью какого-либо внешнего воздействия (накачки) созданы избыточные по отношению к равновесным электроны в зоне проводимости n дырки в валентной зоне. Возвращение к равновесию, т. е. рекомбинация избыточных электронов и дырок, может происходить нзлучательно на оптическом переходе зона — зона (рис. 24.1, а).

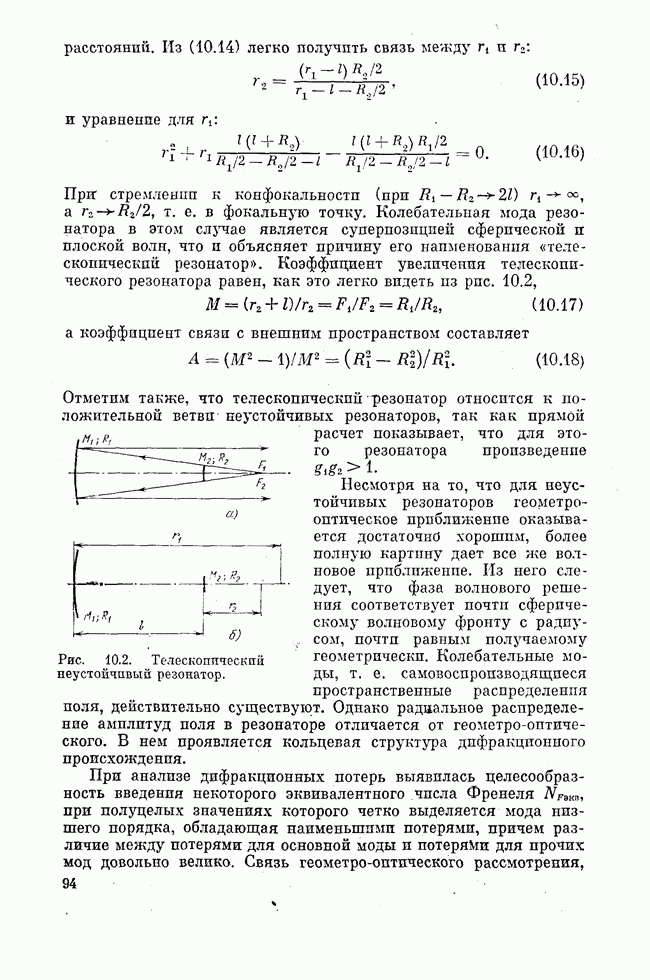
Рис. 24.1. Межзонные оптические переходы в полупроводниках.

Вероятность пзлучательных переходов зона — зона велика, если переходы являются прямыми, т. е. если они могут быть изображены вертикальной прямой на диаграмме, показывающей зависимость энергии Е носителей тока от их квазпимпульса р. Дело в том, что оптические переходы зона — зона завершаются созданием свободных носителей тока. Следовательно, при переходе должен выполняться закон сохранения пмпульса. Ввиду малости импульса фотона это означает, что при переходе квазппмиульс электрона должен остаться неизменным. В случае так называемых прямозонных полупроводников, для которых максимум потенциальной кривой, ограничивающей валентную зону сверху, и минимум потенциальной кривой, ограничивающей зону проводимости снизу, имеют место при одном и том же значении квазинмпульса р (рис. 24.1, б), вертикальные переходы соединяют потолок валентной зоны и дно зоны проводимости, т. е. те части обеих разрешенных зон, которые в первую очередь заселяются избыточными носителями тока. В этом случае переход разрешен, и создание неравновесной заселенности максимально облегчено. Прямозонные полупроводники благоприятны созданию лазеров. В случае непрямозонного полупроводника (рис. 24.1, в) носители тока накапливаются в, состояниях с разными значениями квазиимпульса, вертикальные переходы невозможны

из-за отсутствия рекомбинирующих частиц, а невертикальные (непрямые) переходы сильно запрещены.

Большая вероятность нзлучательных переходов в прямозонных полупроводниках и большая плотность состояний в зонах позволяет получать исключительно высокие значения коэффициентов усиления, превышающие в некоторых особо благоприятных случаях . В лазерах на основе твердых диэлектриков с примесными активными центрами, рассмотренных в предыдущих лекциях и называемых обычно твердотельными лазерами, в отличие от полупроводниковых лазеров используются переходы между дискретными уровнями энергии изолированных ионов. Плотность активных частиц и вероятность переходов в них существенно ниже, поэтому для них характерны значительно меньший коэффициенты усиления и, следовательно, заметно большие линейные размеры активных элементов. Наиболее близки к полупроводниковым лазеры на органических красителях и центрах окраски, для которых в силу интенсивного взаимодействия их активных центров с окружением характерны широкие энергетические зоны, а в силу высокой плотности центров — большие коэффициенты усиления, хотя и не достигающие значений, свойственных полупроводниковым лазерам.

Важным отличием полупроводниковых лазеров от остальных лазеров на конденсированных средах является электропроводность полупроводников, позволяющая осуществлять их накачку электрическим током и тем самым непосредственно преобразовывать электрическую энергию в лазерное излучение.

Таким образом, полупроводниковые лазеры занимают в квантовой электронике особое место, отличаясь от всех прочих лазеров рядом важных особенностей.

С практической точки зрения наиболее существенны следующие достоинства полупроводниковых лазеров:

1. Компактность, обусловленная гигантским коэффициентом усиления в полупроводниках.

2. Еолыной к. п. д., обусловленный высокой эффективностью преобразования подводимой энергии в лазерное излучение при накачке достаточно совершенных полупроводниковых монокристаллов электрическим током.

3. Широкий диапазон длин волн генерации, обусловленный возможностью выбора полупроводникового материала с шириной запрещенной зоны, соответствующей излучению на переходах зона — зона практически в любой точке спектрального интервала от 0,3 до 30 мкм.

4. Плавная перестройка длины волны излучения, обусловленная зависимостью спектрально-оптических свойств полупроводников и прежде всего ширины запрещенной зоны от температуры, давления, магнитного поля и т. п.

5. Малоинерционнорть, обусловленная малостью времен релаксации и практически безынерционностью создания неравновесных

электронов и дырок при накачке электрическим током, приводящая к возможности модуляции излучения изменением тока накачки с частотами, достигающими 10 ГГц.

6. Простота конструкции, обусловленная возможностью накачки постоянным током и приводящая к совместимости полупроводниковых лазеров с интегральными схемами полупроводниковой электроники, устройствами интегральной оптики и волоконных оптических линий связи.

Недостатки полупроводниковых лазеров являются, как это часто бывает, продолжением их достоинств. Малые размеры приводят к низким значениям выходной мощности или энергии. Кроме того, полупроводниковые лазеры, как и все приборы полупроводниковой электроники, чувствительны к перегрузкам (разрушаются при потоках оптического излучения в несколько мегаватт на квадратный сантиметр) и к перегреву, приводящему к резкому повышению порога самовозбуждения и даже к необратимому разрушению при нагреве свыше некоторой характерной для каждого типа лазера температуры.

Лазерная генерация получена при использовании многих различных полупроводниковых материалов, общим числом в несколько десятков. Эти материалы, кроме обычного требования чистоты и монокристаллпчности, доляшы обладать высокой оптической однородностью и малой вероятностью безызлучательной рекомбинации электронов и дырок.

Рассмотрим основной механизм люминесценции полупроводников — излучательную рекомбинацию электронов и дырок.

Рекомбинацией электронов и дырок в полупроводниках называется процесс, приводящий к переходу электрона из зоны проводимости в валентную зону, в результате которого происходит исчезновение пары электрон проводимости — дырка. Рекомбинация всегда означает переход носптеля тока на более низкие уровни энергии — либо в валентную зону, либо на примесный уровень в запрещенной зоне.

При термодинамическом равновесии рекомбинация уравновешивает процесс тепловой генерации носителей, а скорость этих взаимно обратных процессов такова, что их совместное действие приводит к установлению распределения Ферми для электронов и дырок по энергиям.

Известно много механизмов рекомбинации, которые отличаются друг от друга направлением передачи энергии, выделяемой при рекомбинации. Если избыток энергии выделяется в виде кванта излучения, то происходит нзлучательная рекомбинация. Этот элементарный акт генерации света в полупроводниках подобен излучательному распаду возбужденного состояния в системах с дискретным спектром. Возможна также безызлучательная рекомбинация, при которой высвобождающаяся энергия расходуется на возбуждение колебаний кристаллической решетки, т. е. в конечном счете идет на нагрев кристалла. Очевидно, безызлучательная

рекомбинация полностью подобна безызлучательной релаксации энергии возбуждения в системах с дискретным спектром.

При излучательной рекомбинации полное число актов излучения пропорционально произведению пр концентраций электронов (n) и дырок (р). При небольших концентрациях носителей этот канал рекомбинации мало эффективен. При больших концентрациях, превышающих полупроводники становятся эффективными источниками света рекомбинацнонного излучения в относительно узком диапазоне длин волн вблизи края собственного поглощения полупроводника.

Рекомбинационное излучение происходит на переходах зона — зонд (см. рис. 24.1, а). Межзонный характер носит рекомбинационная люминесценция не только в собственных, но и в сильно легированных полупроводниках. В последнем случае энергетический спектр полупроводника вблизи краев запрещенной зоны сильно искажен ввиду того, что при сильном легировании примесные уровни уширены в примесную зону, которая частично или полностью сливается с собственной зоной. При этом энергия квантов рекомбинацнонного излучения может несколько отличаться от номинальной ширины запрещенной зоны легируемого полупроводника. Однако практически для всех процессов излучательной рекомбинации, используемых в полупроводниковых лазерах, характерна близость энергии перехода к энергии запрещенной зоны .

Наличие спонтанной излучательной рекомбинации свидетельствует о возможности создания лазера. Для того чтобы в спектре излучения спонтанной рекомбинации возникло усиление, вынужденное испускание фотонов должно преобладать над их поглощением. Необходимым условием для этого является наличие инверсии населенностей. В полупроводниковых лазерах, следовательно, должна существовать инверсия на переходах излучательной рекомбинации. Рассмотрим условия получения такой инверсии.

Анализ условий достижения инверсии требует знания уровней энергии, сечений их возбуждения, времен релаксации и т. д. При общем рассмотрении такого широкого класса лазерных активных сред, какими являются полупроводники, этот путь нерационален, даже если и возможен. К счастью, достаточно общие термодинамические соображения, учитывающие вместе с те»? специфику статистики электронов в полупроводниках, могут дать общие условия инверсии в этих материалах.

Независимо от конкретного механизма излучательной рекомбинации возникающие при этом фотоны подчиняются общим законам теории излучения. Скорость заполнения фотонами частоты а некоторой радиационной моды объема V составляет

где — число фотонов, имеющихся в моде. Первый член в (24.1) обусловлен спонтанным испусканием, второй соответствует разности скоростей вынужденного испускания и поглощения фотонов. В рассматриваемом случае излучательной рекомбинации в каждом акте испускания фотона одна электронно-дырочная пара исчезает, а в каждом акте поглощения одна такая пара возникаем.

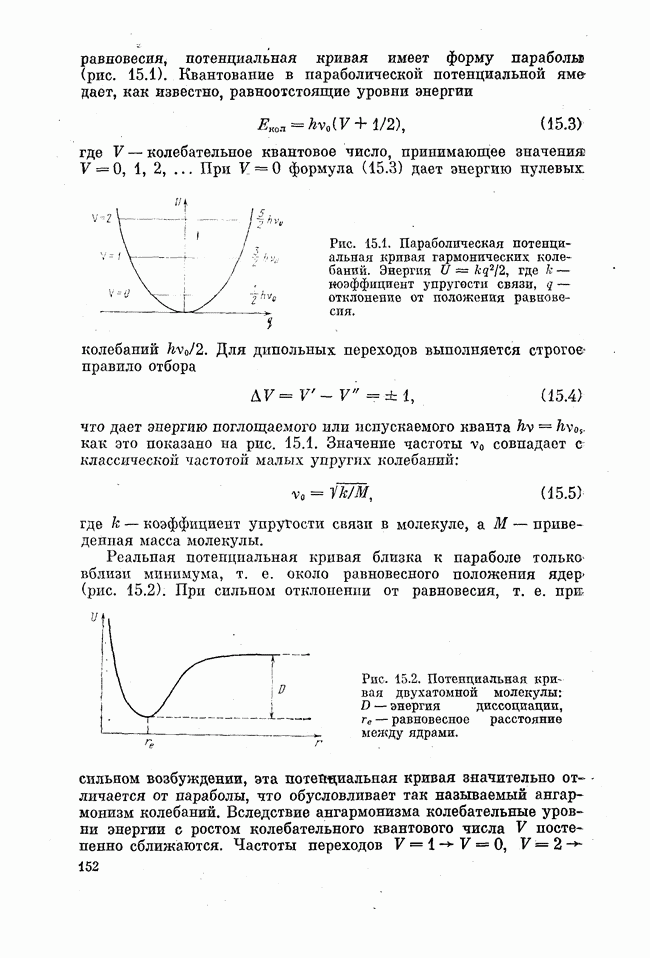
Связь коэффициентов спонтанного А и вынужденного В испусканий можно найти из термодинамических соображений, подобно тому как это делалось в лекции первой. При температуре Т в соответствии со статистикой Бозе — Эйнштейна равновесное число заполнения моды (для двух поляризаций) составляет

При равновесии , следовательно, в силу (24.1) имеем

Дальнейший анализ требует учета специфики полупроводников. Выделим в спектре электронных состояний два уровня с энергиями . Скорость излучательной рекомбинации на переходе пропорциональна произведению концентраций электронов на уровне и дырок на уровне . Электроны, как известно, подчиняются статистике Ферми — Дирака. Вероятность того, что электрон находится в состоянии с энергией Е, задается распределением Ферми

где F — энергия (уровень) Ферми. Вероятность найти на уровне энергии Е дырку равна вероятности того, что этот уровень не здпят электроном, и составляет, следовательно,

Тогда скорость спонтанной рекомбинации, пропорциональная числу электронов на уровне и числу дырок на уровне может быть представлена в виде

где А о — коэффициент пропорциональности.

Аналогично, величина В, определяющая в (24.1) разность скоростей вынужденного излучения и поглощения, составляет

где — коэффициенты пропорциональности. Подставляя эти выражения для А и учитывая равновесные распре-

деления (24.2) и (24.4), мы получаем уравнение

По предположению фотоны с энергией возникают в результате прямозонной излучательной рекомбинации, происходящей между уровнями и значит, . Тогда уравнение (24.8) всегда удовлетворяется, если . Это означает, что

Следовательно, разность между скоростями вынужденного испускания фотонов на переходе зона — зона при излучательной рекомбинации и поглощения фотонов на том же переходе положительна при условии

(24.10)

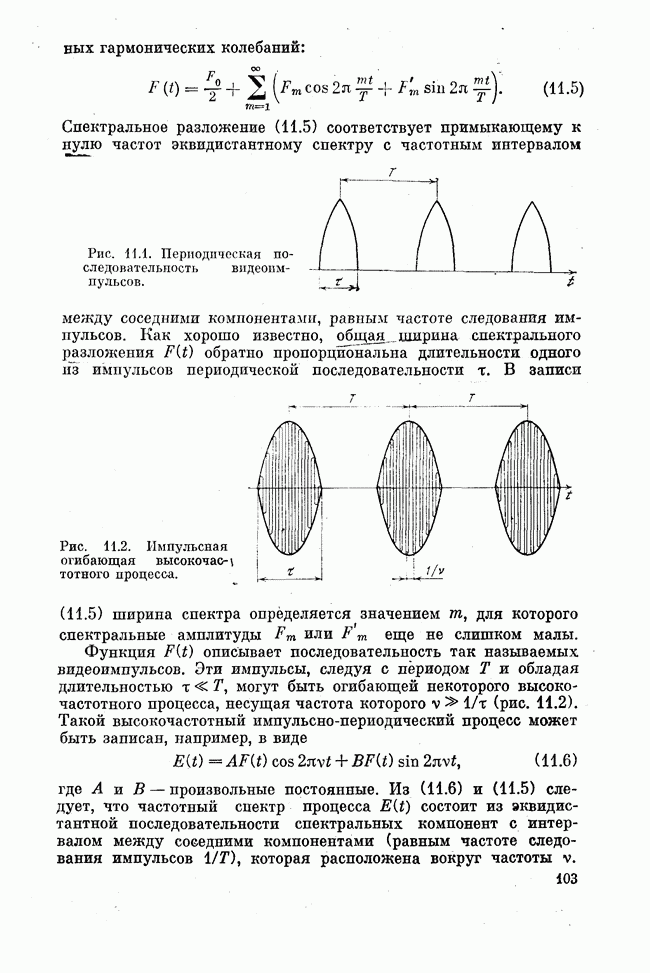
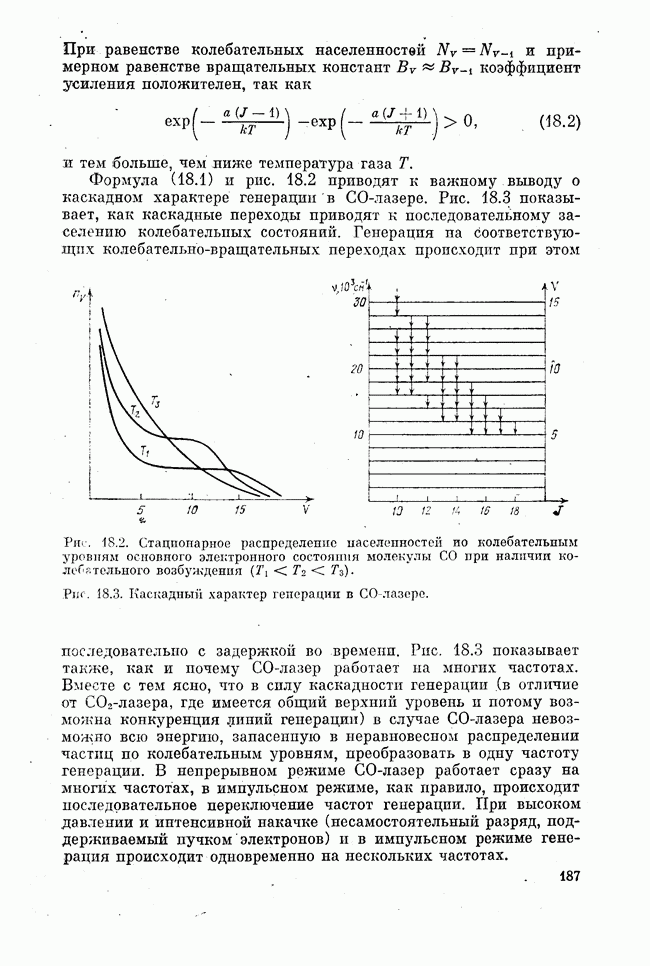
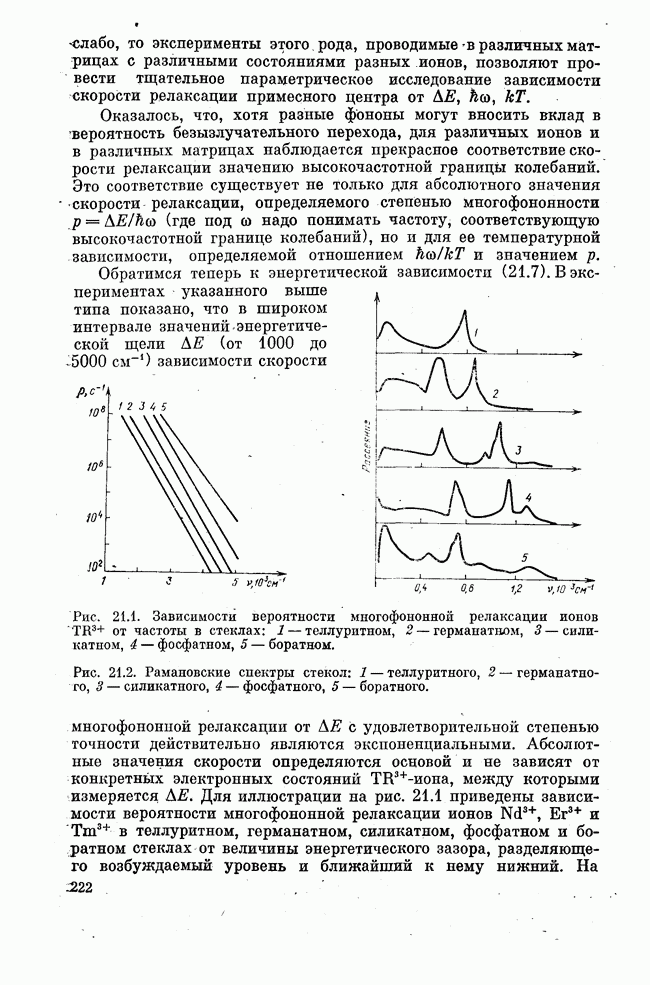
Рис. 24.2. Распределение Ферми (f — уровень Ферми).

Если — распределение Ферми (24.4), представленное на рис. 24.2, то для пары уровней при термодинамическом равновесии это условие не выполняется.

Вспомним теперь, что уровни разделены запрещенной зоной и находятся соответственно в зоне проводимости и в валентной зоне. Неравновесные носители, т. е. неравновесные электроны в зоне проводимости и дырки в валентной зоне, создаваемые каким-то источником накачки, обладают конечными временами жизни в зонах. На протяжении этого времени термодинамическое равновесие не соблюдается, и, следовательно, единого уровня Ферми для всей системы в целом не существует. Однако если в электронном и дырочном газах в отдельности за время, меньшее времени жизни носителей в зонах, устанавливается свое квазиравновесное состояние фермиевского типа, но с одной и той же температурой для всей системы, а равновесие между этими газами отсутствует, то можно ввести так называемые квазиуровни Ферми отдельно для электронов в зоне проводимости и дырок в валентной зоне .

Допустимость введения отдельных квазиравновесных функций распределения для дырок и электронов в валентной зоне и в зоне проводимости соответственно априорно не очевидна. Она

оправдывается тем, что по крайней мере в нескольких полупроводниках время термализации электронов в пределах зоны (0,1 нс) на три-четыре порядка меньше характерного времени межзонной термализации (1—10 нс).

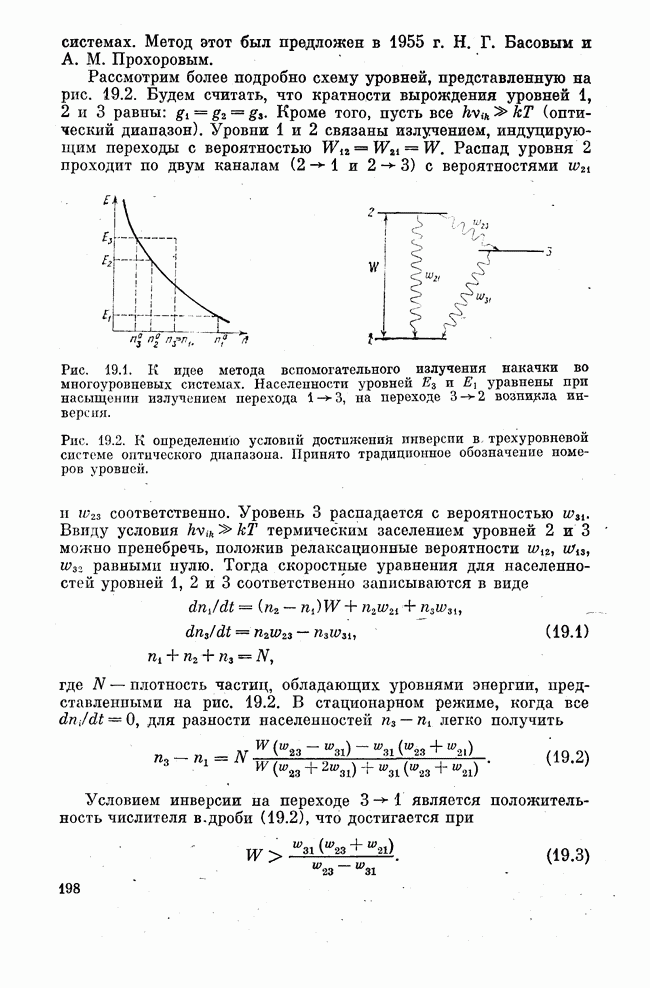
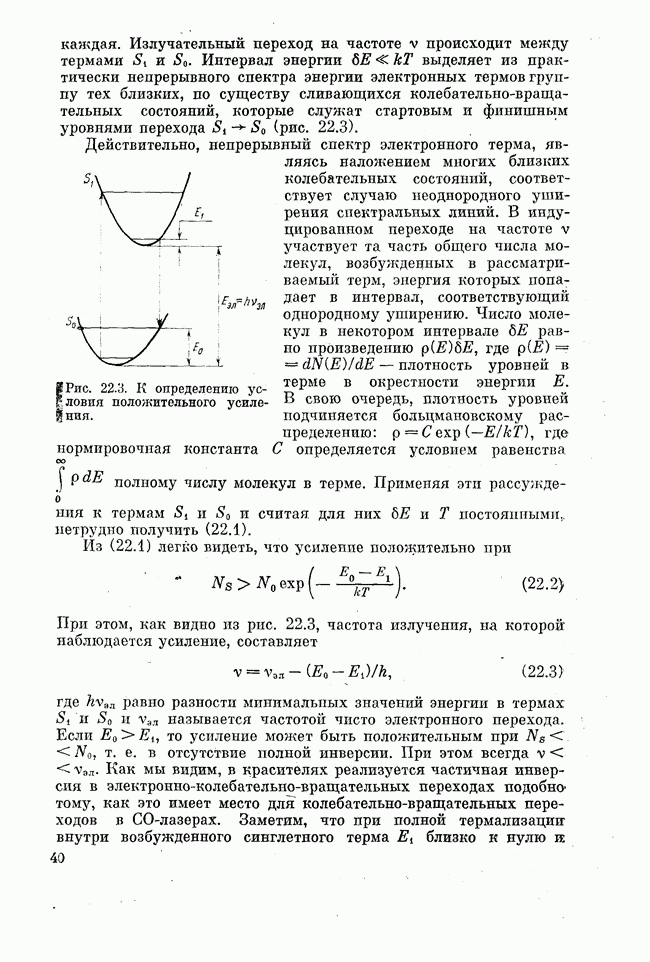
Рис. 24.3. Инверсное распределение электронов в однодолинном полупроводнике.

Вернемся к условию инверсии (24.10). Представив в соответствии с проведенным выше обсуждением в виде

(24.11)

где — квазиуровень Ферми для электронов, a для дырок, из неравенства (24.10) легко получить эквивалентное ему, но более наглядное условие:

(24.12)

Так как минимальное значение равно ширине запрещённой зоны условие инверсии на межзонных переходах приобретает простой вид:

(24.13)

Следовательно, накачка, создающая неравновесность, должна быть достаточно сильной для того, чтобы квазиуровни Ферми оказались внутри соответствующих разрешенных зон энергии. Это означает, что электронный и дырочный газы вырождены, при этом все уровни в валентной зоне с энергией практически полностью незаселены, а все уровни в зоне проводимости с энергией практически полностью заселены электронами (рис. 24.3). Тогда фотоны, энергия которых лежит в интервале

(24.14)

не могут вызвать переходы валентная зона — зона проводимости и поэтому не поглощаются. Обратные переходы зона проводимости — валентная зона возможны. Вынужденная излучательная рекомбинация на этих переходах как раз и создает лазерное излучение. Неравенства (24.14) определяют ширину полосы соответствующего усиления.

Интенсивность излучательной рекомбинации определяется конкретными особенностями зонной структуры полупроводника,

квадратом матричного элемента соответствующего перехода, плотностью рекомбинпрующих пар. Скорость излучательной рекомбинации, т. е. число переходов с излучением в единичном объеме в единицу времени, зависит, очевидно, от тех же факторов. Так как излучательный и безызлучательный каналы рекомбинации параллельны, то результирующая скорость рекомбинации равна сумме скоростей рекомбинаций излучательной и безызлучательной

(24.15)

Очевидно, относительная доля актов излучательной рекомбинации во всем процессе рекомбинации в целом равна отношению соответствующих скоростей . Это же отношение указывает долю всей энергии, заключенной в неравновесных электронах и дырках, которая высвобождается по излучательному каналу рекомбинации. Тем самым мы определили так называемый внутренний квантовый выход излучательной рекомбинации:

Эта величина характеризует качество полупроводникового материала. Правильный выбор легирования и изготовление совершенных кристаллов позволяет получать для многих полупроводниковых материалов значение , приближающееся к 100 %.

Многофотонная безызлучательная рекомбинация на переходе зона — зона маловероятна. Наиболее важным механизмом при невысоких концентрациях носителей является рекомбинация через промежуточные состояния в запрещенной зоне, локализованные около примесей и дефектов. Отметим аналогию рассматриваемого процесса с механизмами безызлучательной релаксации через промежуточные уровни в случае примесных диэлектрических кристаллов (см. лекцию двадцать первую). Роль центров рекомбинации играют многие примеси и дефекты, большая часть которых плохо идентифицирована. Слишком большая концентрация этих центров, возникающая из-за ошибок в технологии, делает полупроводниковый материал непригодным для создания лазерного кристалла.

При повышении концентрации носителей возрастает роль оже-рекомбинации, называемой также ударной рекомбинацией и состоящей в том, что электрон и дырка, рекомбинируя, отдают выделяемую энергию третьему носителю. Этот процесс заметен при больших концентрациях свободных носителей именно потому, что для его реализации требуется столкновение трех носителей. Роль оже-рекомбинации возрастает в узкозонных полупроводниках.

Уравнения, описывающие процессы каскадной и оже-рекомбинаций, нелинейны. Поэтому безызлучательный распад электронно-дырочных пар неэкспоненциален и, строго говоря, не может характеризоваться постоянной времени жизни по отношению и

этому процессу. Для грубой оценки порядка величин скоростей безызлучательной рекомбинации можно пользоваться экспериментально определенными значениями сечений соответствующих процессов. При каскадном процессе сечение захвата на центры рекомбинации может составить . Соответствующий коэффициент рекомбинации заключен в пределах . При концентрации центров рекомбинации это приводит к эффективной скорости рекомбинации . Коэффициент рекомбинации оже-процесса заключен обычно в пределах . При концентрации носителей дает эффективную скорость рекомбинации . Приведенные оценки показывают, что в реальных материалах действительно возможно достижение внутреннего квантового выхода излучательной рекомбинации, приближающегося к 100% (См. формулу (24.16)). Правильное проведение технологического йроцесса выращивания полупроводникового кристалла может исключить неблагоприятное влияние каскадной рекомбинации. Вместе с тем оже-рекомбпнация, скорость которой увеличивается с ростом концентрации как принципиально неустранима.

Итак, при выполнении условия инверсии (24.13) и неравенства Тизл тбезызл в полупроводниковых кристаллах возможно эффективное лазерное излучение.

Применение полупроводниковых кристаллов в квантовой электронике было предложено в 1959 г. Н. Г. Басовым.