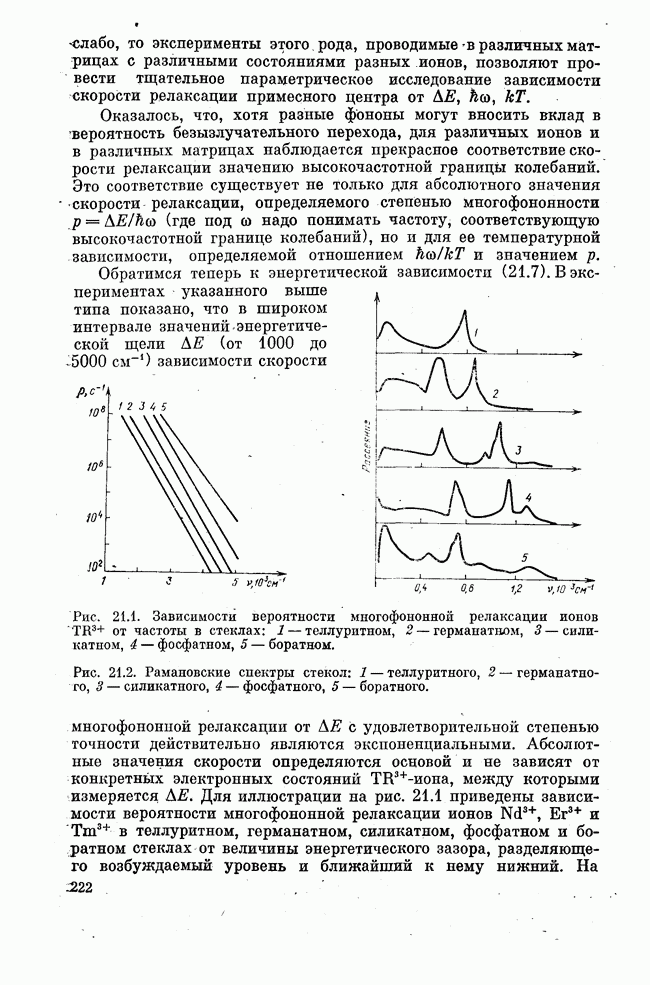
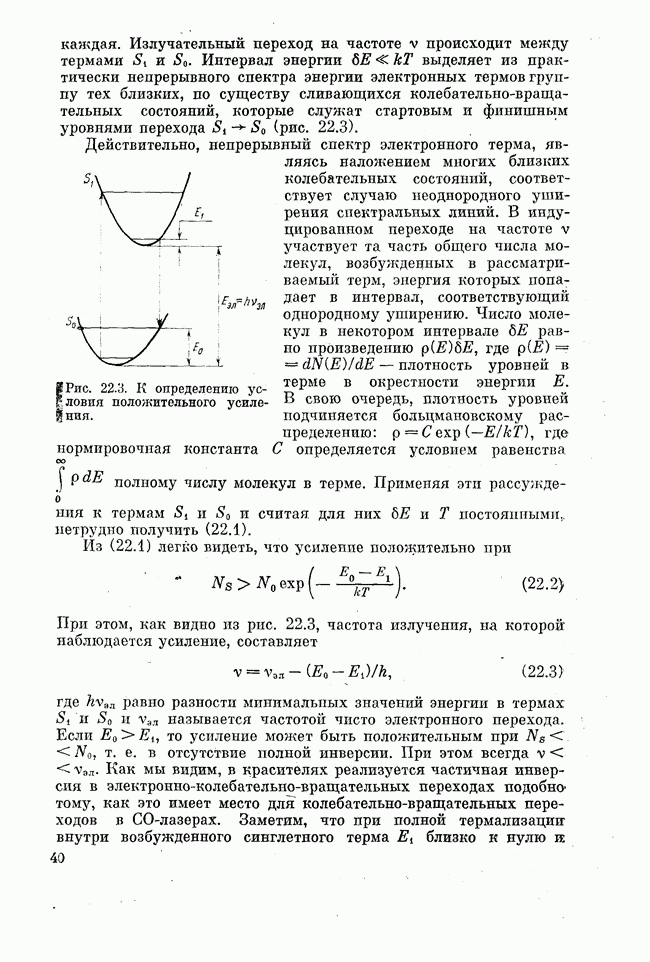
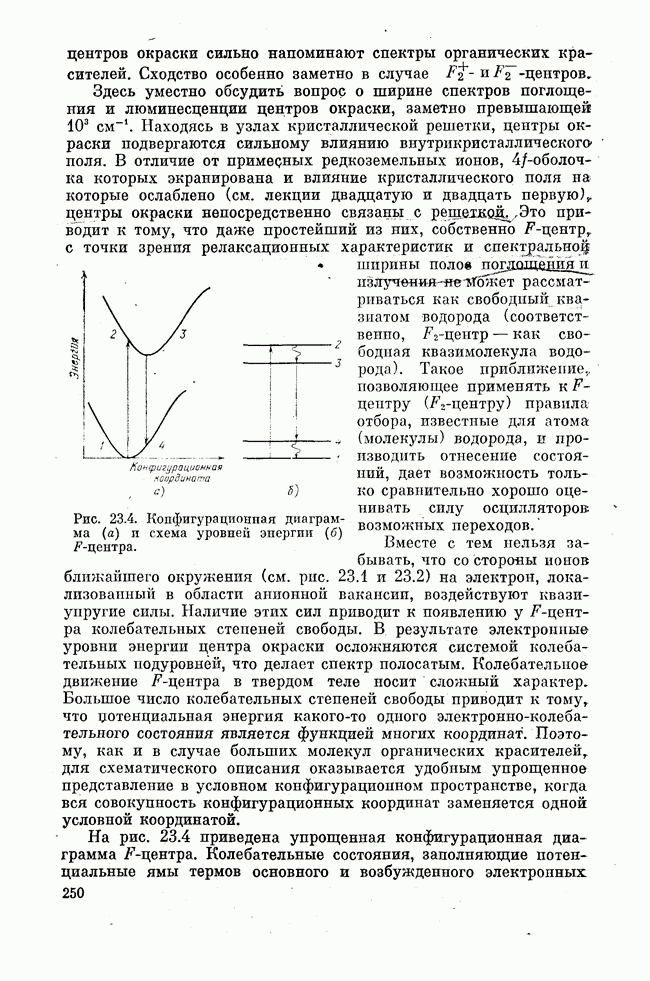
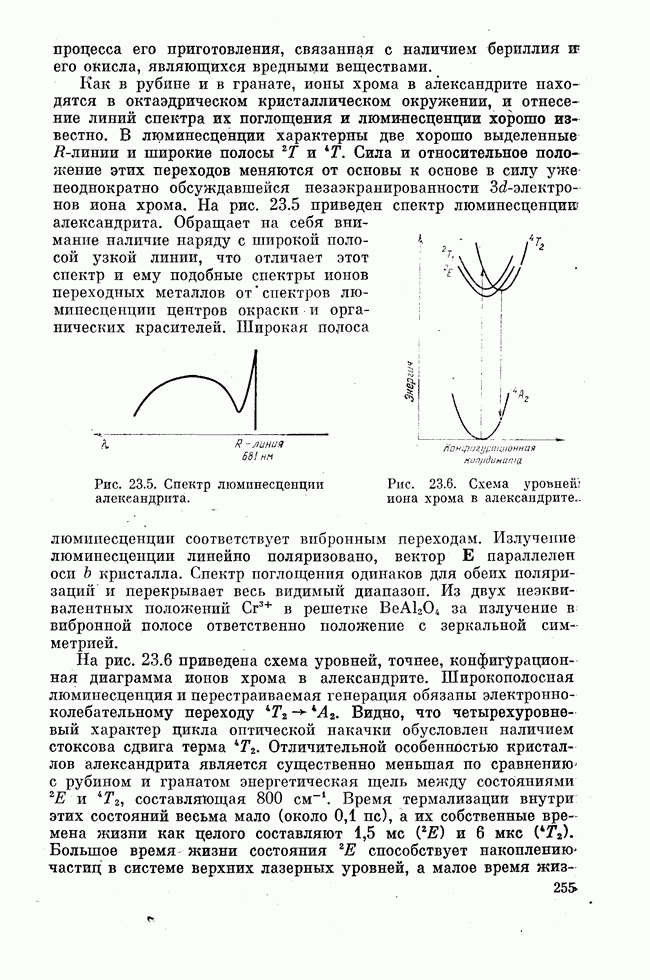
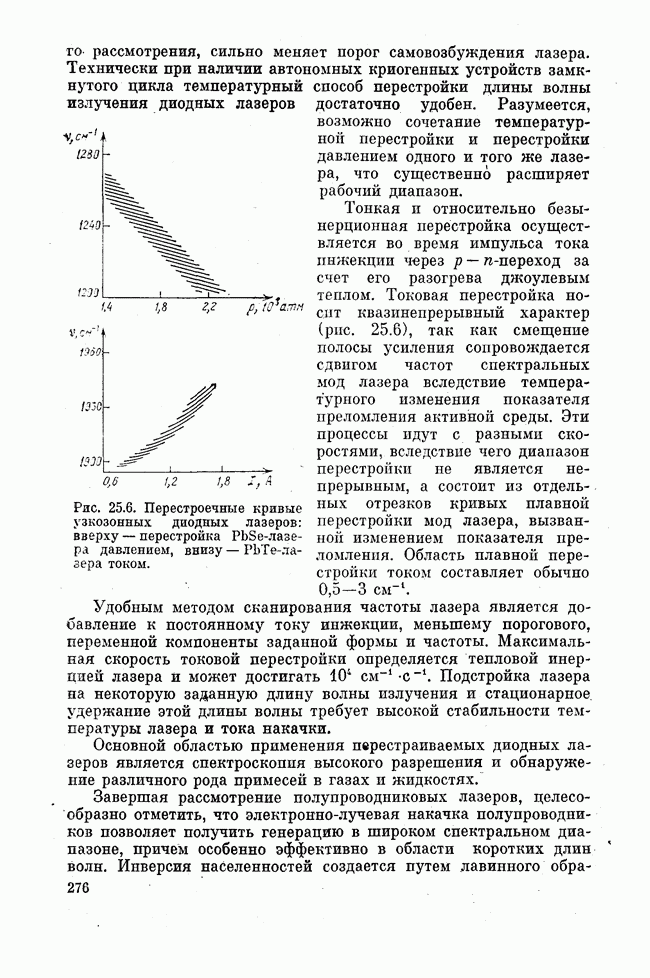
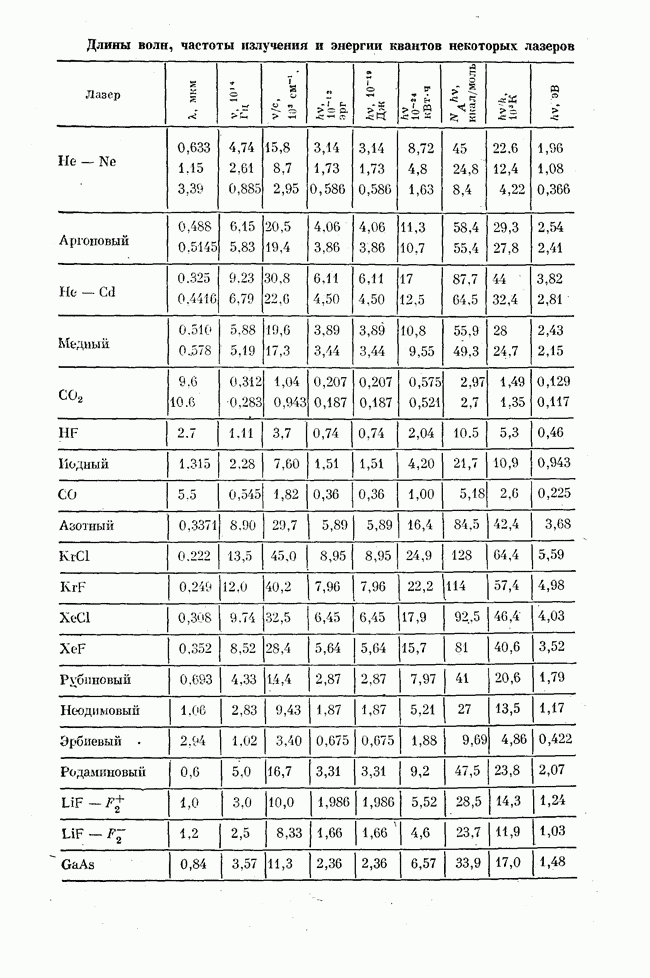
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Лекция пятнадцатая. CO2-ЛАЗЕРЫ
Молекулярные лазеры. Требования к рабочему веществу мощных газовых лазеров с высоким к. п. д. Колебательные спектры молекул. Р-, Q-, R-ветви. Нормальные колебания многоатомных молекул. СО2-лазер, общие сведения. Молекула СO2. Механизм инверсии. Роль азота и гелия. Лазеры с продольной прокачкой. Отпаянные лазеры.
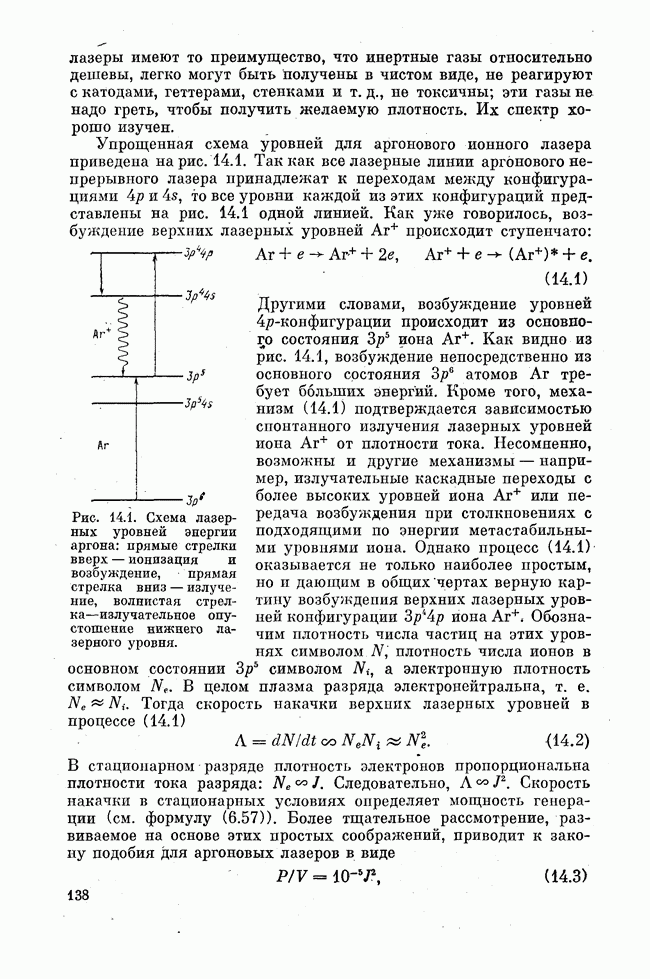
Большое место среди газовых лазеров занимают молекулярные лазеры, т. е. лазеры, активной средой которых являются молекулярные газы. Прежде всего, это связано с тем, что многие, даже весьма тугоплавкие элементы, упругость паров которых в обычных условиях исчезаюзце мала, образуют устойчивые летучие соединения. Молекулярных газов много. Только инертные (благородные)
газы являются устойчивыми атомарными газами, состоящими из химически неактивных атомов. Атомарных газов: мало.
Молекулярные спектры существенно более сложны по сравнению с атомными спектрами. Эта сложность определяется тем, что движение в молекулах носит более сложный характер, чем в. атомах. Наряду с движением электронов относительно ядер атомов, составляющих молекулу, происходит колебательное движение самих ядер около их положений равновесия и вращательное движение всей молекулы как целого. В микромире каждое ограниченное движение квантуется. Поэтому со всеми этими видами движения связаны некие вполне определенные уровни энергии. Переходы между ними дают в видимой и УФ областях полосатые электронные спектры, в ИК области — полосатые колебательные, спектры, в далекой ИК и в микроволновых областях — линейчатые вращательные спектры.
Богатые спектральные возможности молекулярных систем облегчают выбор уровней энергии, подходящих для создания активной среды, многообразие внутренних движений в молекулах облегчает выбор канала релаксации, необходимого для поддержания инверсии.
На этом этапе нашего изложения можно сформулировать ряд: общих требований к рабочему веществу мощных газовых лазеров с высоким к. п. д. По существу эти требования являются обобщением того, что нам уже известно о газовых лазерах.
Прежде всего, верхний рабочий уровень должен иметь сравнительно большое время жизни. Далее, для обеспечения непрерывного режима работы время жизни нижнего уровня должно быть, мало. Но сколько-нибудь высокий к. п. д. может быть обеспечен, если нижний уровень расположен низко, но не слишком низко, чтобы не быть заселенным термически. Следовательно, короткое время жизни нижнего уровня не может быть радиационным. Если учесть возможность пленения излучения, то становится ясно, что радиационное расселение нижнего уровня вообще не должно» привлекаться как механизм опустошения нижнего лазерного уровня, расположенного невысоко над основным состоянием. Значит, нижний уровень должен опустошаться столкновительно. Но столкновения эффективны тогда, когда передаваемая при столкновении энергия не превышает энергию теплового движения. Энергия нижнего лазерного уровня должна превышать энергию теплового движения. Следовательно, столкновительная релаксация: должна расселять нижний лазерный уровень в несколько этапов, через несколько промежуточных уровней, релаксирующих, в свою очередь, столкновительно.
В целом именно молекулы наилучшим образом отвечают всем: этим требованиям.
Прежде чем двинуться дальше, рассмотрим вкратпе молекулярные спектры.
Итак, трем видам движения в молекуле — электронному, колебательному и вращательному — соответствуют три типа квантовых состояний и уровней энергии. Полная энергия молекулы Е имеет определенное значение, соответствующее определенному электронно-колебательно-вращательному состоянию. С хорошей степенью приближения эта энергия может быть представлена как сумма квантованных значений энергии электронного, колебательного и вращательного движений:

Между значениями  существует соотношение
существует соотношение

где  — масса покоя электрона, М — суммарная масса ядер атомов, составляющих молекулу. Обычно
— масса покоя электрона, М — суммарная масса ядер атомов, составляющих молекулу. Обычно  как известно, составляет величину порядка нескольких электрон-вольт, или, что эквивалентно, нескольких единиц
как известно, составляет величину порядка нескольких электрон-вольт, или, что эквивалентно, нескольких единиц  . Тогда
. Тогда  . Различный порядок величин
. Различный порядок величин  связан с относительной медленностью вращения молекулы как целого и движения ядер в молекуле по сравнению с движением электронов, что обусловлено различием движущихся масс. Система уровней молекул состоит, таким образом, из совокупности далеко отстоящих электронных уровней, более близких колебательных уровней и еще более близких вращательных уровней. В каждом электронном состоянии возможны колебания, в каждом колебательном состоянии возможны вращения. Соответствующая энергия как малое возмущение приводит к расщеплению уровней энергии «старшего», т. е. обладающего существенно большей энергией, состояния. Именно это является причиной существования полосатых молекулярных уровней.
связан с относительной медленностью вращения молекулы как целого и движения ядер в молекуле по сравнению с движением электронов, что обусловлено различием движущихся масс. Система уровней молекул состоит, таким образом, из совокупности далеко отстоящих электронных уровней, более близких колебательных уровней и еще более близких вращательных уровней. В каждом электронном состоянии возможны колебания, в каждом колебательном состоянии возможны вращения. Соответствующая энергия как малое возмущение приводит к расщеплению уровней энергии «старшего», т. е. обладающего существенно большей энергией, состояния. Именно это является причиной существования полосатых молекулярных уровней.
Ограничим пока наше рассмотрение молекулярными лазерами ИК диапазона. Им соответствуют колебательные, точнее — колебательно-вращательные спектры. Колебательные уровни энергии получают квантованием колебательной энергии, при этом в первом приближении колебания считаются гармоническими.
Двухатомная молекула, т. е. система с одной колебательной степенью свободы, рассматривается как линейный гармонический осциллятор, а многоатомная молекула — как колебательная система со многими степенями свободы, совершающая малые колебания. Число колебательных степеней свободы равно  в случае молекулы с линейной равновесной конфигурацией и
в случае молекулы с линейной равновесной конфигурацией и  в случае нелинейной молекулы. Здесь N — число атомов в молекуле.
в случае нелинейной молекулы. Здесь N — число атомов в молекуле.
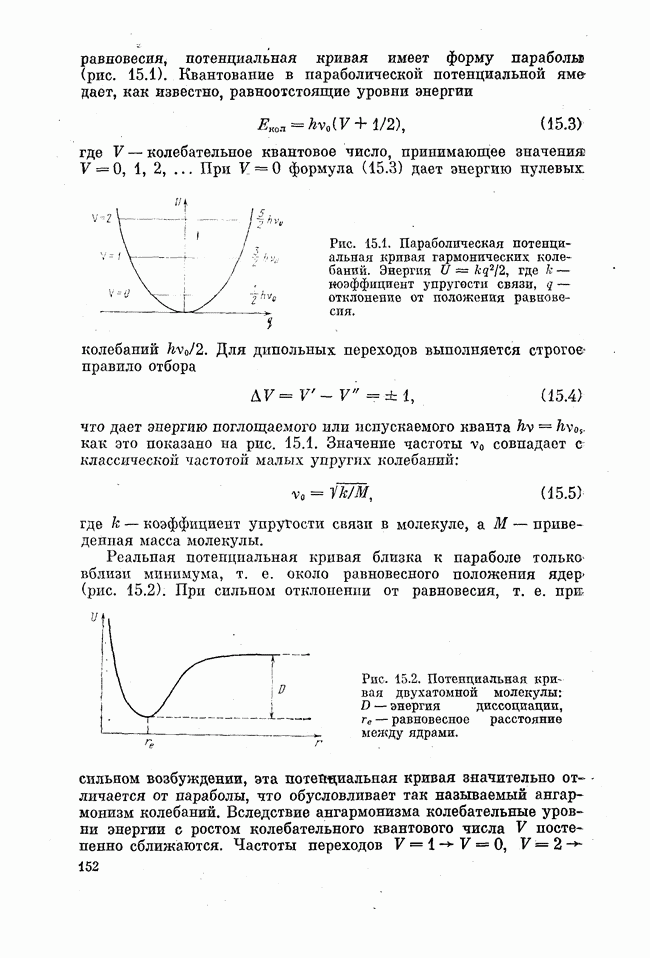
Наиболее прост случай двухатомной молекулы. Для малых гармонических колебаний, когда возвращающая сила носит упругий характер, т. е. пропорциональна отклонению от положения
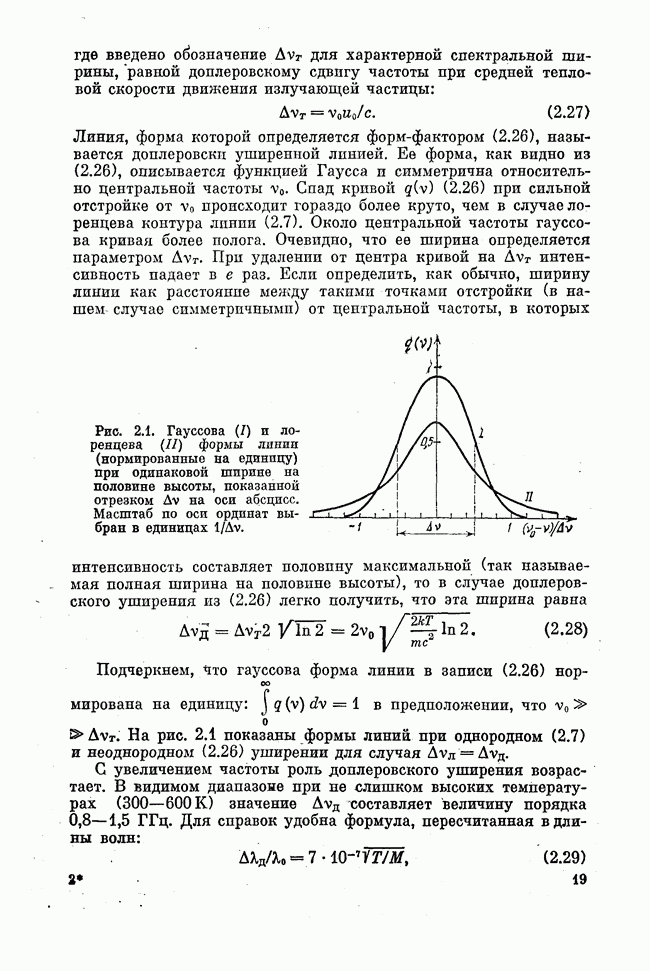
равновесия, потенциальная кривая имеет форму парабольи (рис. 15.1). Квантование в параболической потенциальной яме дает, как известно, равноотстоящие уровни энергии

где V — колебательное квантовое число, принимающее значения  .
.

Рис. 15.1. Параболическая потенциальная кривая гармонических колебаний. Энергия  , где k — коэффициент упругости связи, q — отклонение от положения равновесия.
, где k — коэффициент упругости связи, q — отклонение от положения равновесия.
При  формула (15.3) дает энергию нулевых колебаний
формула (15.3) дает энергию нулевых колебаний  . Для диполъных переходов выполняется строгое правило отбора
. Для диполъных переходов выполняется строгое правило отбора

что дает энергию поглощаемого или испускаемого кванта  как это показано на рис. 15.1. Значение частоты
как это показано на рис. 15.1. Значение частоты  совпадает с классической частотой малых упругих колебаний:
совпадает с классической частотой малых упругих колебаний:

где k — коэффициент упругости связи в молекуле, а М — приведенная масса молекулы.

Рис. 15.2. Потенциальная кривая двухатомной молекулы: D — энергия диссоциации,  — равновесное расстояние между ядрами.
— равновесное расстояние между ядрами.
Реальная потенциальная кривая близка к параболе только вблизи минимума, т. е. около равновесного положения ядер (рис. 15.2). При сильном отклонении от равновесия, т. е. при сильном возбуждении, эта потенциальная кривая значительно отличается от параболы, что обусловливает так называемый ангармонизм колебаний. Вследствие энгармонизма колебательные уровни энергии с ростом колебательного квантового числа V постепенно сближаются. Частоты переходов 
 и т. д. перестают быть равными друг другу. В спектре испускания (поглощения) наряду с переходом «основной частоты
и т. д. перестают быть равными друг другу. В спектре испускания (поглощения) наряду с переходом «основной частоты  появляются обертоны: первый обертон
появляются обертоны: первый обертон  второй обертон
второй обертон  и т. д., интенсивность которых, правда, резко падает с ростом
и т. д., интенсивность которых, правда, резко падает с ростом  . Следовательно, при наличии энгармонизма формула (15.3) и правило отбора (15.4) несправедливы.
. Следовательно, при наличии энгармонизма формула (15.3) и правило отбора (15.4) несправедливы.
В первом приближении замена (15.3) двухчленом

где константа энгармонизма  , довольно хорошо описывает реальную ситуацию. Физически энгармонизм связан с диссоциацией молекулы. По мере увеличения амплитуды колебаний, что является классическим аналогом увеличения колебательного квантового числа F, упругость связи в молекуле падает. Молекула разрыхляется и разрушается. Крутизна правой ветви потенциальной кривой на рис. 15.2 падает. Ее горизонтальный участок соответствует инфинитному движению атомов по отношению друг к другу, т. е. диссоциации.
, довольно хорошо описывает реальную ситуацию. Физически энгармонизм связан с диссоциацией молекулы. По мере увеличения амплитуды колебаний, что является классическим аналогом увеличения колебательного квантового числа F, упругость связи в молекуле падает. Молекула разрыхляется и разрушается. Крутизна правой ветви потенциальной кривой на рис. 15.2 падает. Ее горизонтальный участок соответствует инфинитному движению атомов по отношению друг к другу, т. е. диссоциации.
Легко связать константу энгармонизма  с энергией диссоциации D. Из (15.6) энергия кванта
с энергией диссоциации D. Из (15.6) энергия кванта  перехода с
перехода с  может быть получена в виде
может быть получена в виде

При подходе к порогу диссоциации колебательные уровни сгущаются, энергия кванта стремится к нулю. Это происходит при стремлении колебательного квантового числа V к значению

Подставив это значение в выражение (15.6) для колебательной энергии ангармонического осциллятора, мы получаем максимально возможное значение колебательной энергии этого осциллятора

По определению максимальная колебательная энергия ангармонического осциллятора равна энергии диссоциации соответствующей молекулы:  (см. рис. 15.2). Следовательно,
(см. рис. 15.2). Следовательно,
 (15.10)
(15.10)
Обычно оценка энергии диссоциации по формуле (15.10) с помощью полученных спектроскопически по (15.7) значений  производится с точностью 10—30%. Подчеркнем, однако, что суть явления формула (15.10) отражает верно. Чем больше энергия диссоциации, т. е. чем прочнее молекула, тем точнее она описывается, по крайней мере на нижних уровнях, в приближении гармонического осциллятора.
производится с точностью 10—30%. Подчеркнем, однако, что суть явления формула (15.10) отражает верно. Чем больше энергия диссоциации, т. е. чем прочнее молекула, тем точнее она описывается, по крайней мере на нижних уровнях, в приближении гармонического осциллятора.
Здесь надо вспомнить о том, что, кроме колебательной энергии, существует еще и энергия вращательная. Так как  ,
,
то вращения приводят к расщеплению колебательного уровня на вращательные подуровни. По существу, всегда в ИК спектре молекулы имеется колебательная полоса, обусловленная наличием вращательных уровней энергии. Эти последние находятся квантованием энергии вращения при приближенном рассмотрении молекулы как твердого тела с главными моментами инерции  .
.
Для двухатомной молекулы  (z — ось молекулы), где М — приведенная масса,
(z — ось молекулы), где М — приведенная масса,  — расстояние между ядрами молекулы. Квантование дает
— расстояние между ядрами молекулы. Квантование дает
 (15.11)
(15.11)
где  вращательное квантовое число и
вращательное квантовое число и  — вращательная постоянная. Кратность вырождения вращательного уровня составляет
— вращательная постоянная. Кратность вырождения вращательного уровня составляет  . Все изложенное справедливо и для линейных многоатомных молекул при
. Все изложенное справедливо и для линейных многоатомных молекул при  .
.
Вращательная структура колебательной полосы определяется изменением вращательной энергии при колебательном переходе
 (15.12)
(15.12)
Для динольных переходов выполняется строгое правило отбора:
 (15.13)
(15.13)
что дает так называемые  и R-ветви. По определению в Р-ветви
и R-ветви. По определению в Р-ветви  в
в  -ветви
-ветви  в
в  -ветви
-ветви  . Для линейных молекул существует дополнительный запрет на переход с
. Для линейных молекул существует дополнительный запрет на переход с  и
и  -ветвь отсутствует.
-ветвь отсутствует.
В гармоническом приближении и с учетом правил отбора (15.13) и (15.4) частоты переходов в Р- и  -ветвях в соответствии с (15.3) и (15.11) даются простыми соотношениями:
-ветвях в соответствии с (15.3) и (15.11) даются простыми соотношениями:

где J — вращательное квантовое число стартового подуровня (в поглощении). Из (15.4) и (15.5) видно, что расстояние между соседними линиями колебательно-вращательных переходов в  -ветвях колебательной полосы определяется вращательной постоянной и, составляет
-ветвях колебательной полосы определяется вращательной постоянной и, составляет  .
.
Формулы (15.14) и (15.15) получены в предположении неизменяемости В при колебательном возбуждении. Однако по мере увеличения амплитуды колебаний молекула становится менее жесткой и ее эффективный размер увеличивается. Поэтому вращательная постоянная В обычно несколько уменьшается с ростом колебательного квантового числа V. В Р- и R-ветвях это уменьшение обычно мало заметно, и проявляется оно в спектре  -ветви, частота колебательно-вращательных переходов в которой в соответствии с (15.3), (15.4), (15.11) и (15.13) дается формулой
-ветви, частота колебательно-вращательных переходов в которой в соответствии с (15.3), (15.4), (15.11) и (15.13) дается формулой
 (15.16)
(15.16)
Малая разность значений вращательных постоянных  Для двух соседних по V колебательных состояний V и
Для двух соседних по V колебательных состояний V и  приводит к тому, что
приводит к тому, что  -ветвь много уже Р- и R-ветвей. Как уже отмечалось, кратность вырождения вращательных состояний равна
-ветвь много уже Р- и R-ветвей. Как уже отмечалось, кратность вырождения вращательных состояний равна  . Этот статистический вес необходимо учитывать при определении равновесной населенности вращательного подуровня
. Этот статистический вес необходимо учитывать при определении равновесной населенности вращательного подуровня

Конкуренция предэкспоненциального множителя с экспоненциальной зависимостью приводит к немонотонному характеру заселения состояний с различными при заданной температуре газа. Дифференцирование (15.17) позволяет легко определить, что наиболее населенным является вращательное состояние с вращательным квантовым числом

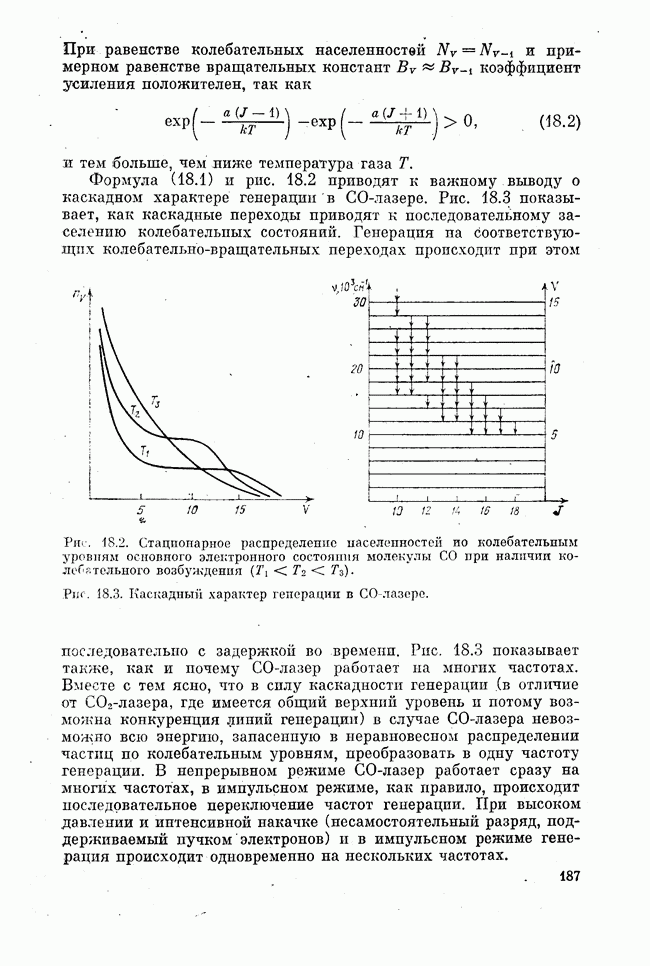
На рис. 15.3 схематически показаны переходы в  и R-ветвях колебательной полосы
и R-ветвях колебательной полосы  в нижней части рисунка приведен спектр этих ветвей, иллюстрирующий изложенное выше.
в нижней части рисунка приведен спектр этих ветвей, иллюстрирующий изложенное выше.

Рис. 15.3. Схема  и R-переходов колебательной полосы
и R-переходов колебательной полосы
Как правило, даяче при сильном нарушении равновесного распределения населенностей колебательных уровней в системе вращательных подуровней очень быстро устанавливается равновесное распределение (15.17). Это обусловлено тем, что вращательное расщепление много меньше  и поэтому в процессе газокинетических соударений молекулы легко передают вращательную энергию друг другу. Другими словами, время вращательной релаксации не превышает времени между газокинетическими столкновениями.
и поэтому в процессе газокинетических соударений молекулы легко передают вращательную энергию друг другу. Другими словами, время вращательной релаксации не превышает времени между газокинетическими столкновениями.
Многоатомная молекула в первом приближении рассматривается как совокупность гармонических осцилляторов. Другими словами, в приближении малых колебаний колебательная энергия молекулы

где r — число колебательных степеней свободы,  — колебательное квантовое число
— колебательное квантовое число  осциллятора, а частота каждого из этих осцилляторов
осциллятора, а частота каждого из этих осцилляторов  называется частотой нормального колебания.
называется частотой нормального колебания.
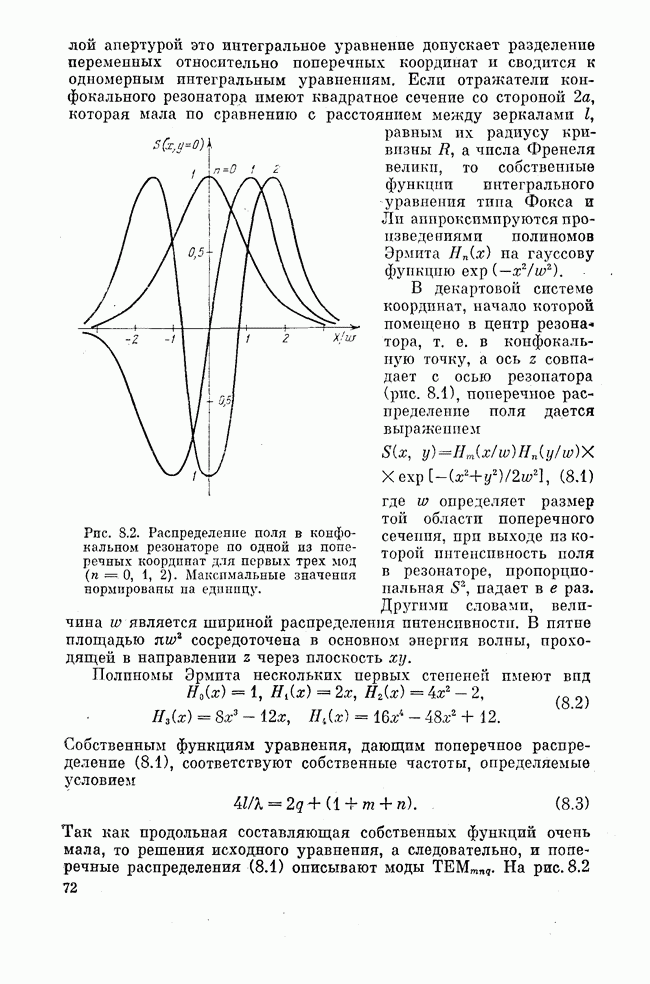
Понятие нормальных колебаний молекул очень существенно для интерпретации молекулярных спектров и выяснения структуры молекул. Как известно из теории колебаний, нормальные колебания — это гармонические собственные колебания, которые могли бы существовать в линейных колебательных системах со многими степенями свободы, если бы в них не происходила диссипация энергии. В каждом нормальном колебании все точки системы колеблются с одной частотой. Число нормальных колебаний равно числу колебательных степеней свободы системы. Все нормальные колебания независимы в том смысле, что, в принципе, можно возбудить только одно из всех возможных нормальных колебаний. Набор частот нормдльных колебаний определяется набором собственных резонансных частот колебательной системы. Аналогия с модами открытых резонаторов очевидна. По существу понятия нормальных колебаний в молекулах и мод в открытых резонаторах тождественны. В последние годы термин «мода» все чаще применяется для описания молекулярных колебаний.
В молекулах наряду с возможностью колебаний всех атомов; часто возникают преимущественные колебания ее отдельных частей, колебания, при которых изменяются длины определенных связей и (или) углы между ними. Знание формы нормальных колебаний (колебательных мод) молекулы позволяет характеризовать движение отдельных частей молекулы относительно друг друга и различать колебания по их локализации. Для наглядности разделяют нормальные колебания молекул на валентные, при которых изменяются длины связей, и деформационные, при которых изменяются углы между связями.
Естественно, что любое допустимое колебательное состояние молекулы является суперпозицией состояний единственного набора  (или
(или  ) подобных нормальных осцилляторов. Типы симметрии колебаний задаются точечной группой симметрии, к которой относится молекула.
) подобных нормальных осцилляторов. Типы симметрии колебаний задаются точечной группой симметрии, к которой относится молекула.
Следует, однако, помнить, что характеристичность нормальных колебаний в многоатомной молекуле падает с ростом колебательного квантового числа V. Тем не менее колебательное состояние молекулы характеризуется набором колебательных квантовых чисел  по всем ее нормальным колебаниям или, как говорят иначе, по всем ее колебательным модам, общее число которых, как мы знаем, равно числу колебательных степеней свободы молекулы.
по всем ее нормальным колебаниям или, как говорят иначе, по всем ее колебательным модам, общее число которых, как мы знаем, равно числу колебательных степеней свободы молекулы.
Моды молекулы обычно обозначаются символами  и т. д. до
и т. д. до  (где
(где  или
или  ). Ангармонизм, обусловленный диссоциацией молекулы, приводит к нарушению правила отбора
). Ангармонизм, обусловленный диссоциацией молекулы, приводит к нарушению правила отбора  и соответственно к появлению в колебательном
и соответственно к появлению в колебательном
спектре молекулы обертонов (гармоник) основных частот. Соответственные состояния обозначаются  и т. д. Радиационные переходы между основным состоянием и вторым, третьим и т. д. возбужденным состоянием той или иной моды происходят на удвоенной, утроенной и т. д. частоте при соответствующем изменении колебательного квантового числа
и т. д. Радиационные переходы между основным состоянием и вторым, третьим и т. д. возбужденным состоянием той или иной моды происходят на удвоенной, утроенной и т. д. частоте при соответствующем изменении колебательного квантового числа  и т. д. Кроме того, в многоатомных молекулах энгармонизм делает возможным появление в колебательном спектре так назывэемых составных частот, возникающих при одновременном изменении двух или более колебательных чисел, т. е. при переходах на так называемые составные колебания. Например, переходу из основного состояния в составное колебание
и т. д. Кроме того, в многоатомных молекулах энгармонизм делает возможным появление в колебательном спектре так назывэемых составных частот, возникающих при одновременном изменении двух или более колебательных чисел, т. е. при переходах на так называемые составные колебания. Например, переходу из основного состояния в составное колебание  соответствуют одновременно
соответствуют одновременно  в состояние
в состояние  — значения
— значения  . Другими словами, ангармонизм разрушэет независимость нормальных колебаний, связывая соответствующие почти гармонические осцилляторы. Отметим здесь, что так как прочность молекулы по разным связям различна, то отличающиеся моды имеют разные энергии диссоциации и соответственно разные константы внутримодового ангэр-, монизмэ.
. Другими словами, ангармонизм разрушэет независимость нормальных колебаний, связывая соответствующие почти гармонические осцилляторы. Отметим здесь, что так как прочность молекулы по разным связям различна, то отличающиеся моды имеют разные энергии диссоциации и соответственно разные константы внутримодового ангэр-, монизмэ.
Возможность колебательных переходов определяется симметрией состояний. Если при каком-то определенном колебании молекулы ее дипольный момент не изменяется, то в дипольном приближении соответствующий переход запрещен. Примером могут служить симметричные валентные колебания молекул, активных в спектрах комбинационного рассеяния и неактивных в ИК спектре поглощения. К их числу относятся все гомоядерные двухатомные молекулы типа симметричной гантели, такие как  и т. п. Колебания такого вида возможны и у многоатомных молекул.
и т. п. Колебания такого вида возможны и у многоатомных молекул.
Наличие нескольких колебательных мод у многоатомных молекул, различие в их частотах и локализэции обеспечивэет существование различных каналов релаксэции энергии возбуждения; при этом релаксация происходит с разной скоростью по разным каналам, что позволяет выбором давления и составэ газовой смеси облегчать условия создания и удержания инверсии населенностей. Кроме того, многомодовость колебательного спектра позволяет разделить каналы возбуждения и генерации, что также облегчает получение лазерной генерации.
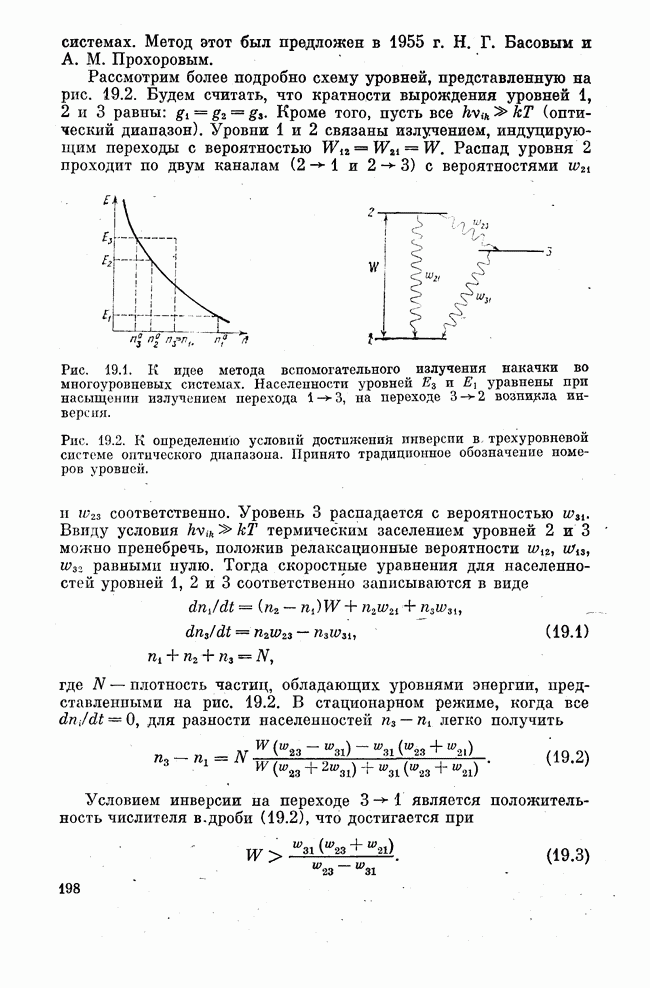
Примером того, как в молекулярных лазерах реализуются требования к рабочему веществу мощных газовых лазеров с высоким к. п. д., является  -лазер.
-лазер.
 -лазер, т. е. лазер, излучающей составляющей активной среды которого является углекислый газ
-лазер, т. е. лазер, излучающей составляющей активной среды которого является углекислый газ  , занимает особое место среди всего многообрэзия существующих лазеров. Этот уникальный лазер отличается прежде всего тем, что для него характерны и большой энергосъем, и высокий к. п. д. В непрерывном режиме получены огромные мощности — в несколько
, занимает особое место среди всего многообрэзия существующих лазеров. Этот уникальный лазер отличается прежде всего тем, что для него характерны и большой энергосъем, и высокий к. п. д. В непрерывном режиме получены огромные мощности — в несколько
десятков киловатт, импульсная мощность достигла уровня в несколько гигаватт, энергия в импульсе измеряется в килоджоулях. К. п. д.  -лазера (порядка 30%) превосходит к. п. д. всех лазеров. Частота следования в импульсно-периодическом режиме может составить несколько килогерц. Длины волн излучения
-лазера (порядка 30%) превосходит к. п. д. всех лазеров. Частота следования в импульсно-периодическом режиме может составить несколько килогерц. Длины волн излучения  -лазера находятся в диапазоне 9—10 мкм (средний ИК диапазон) и попадают в окно прозрачности атмосферы. Поэтому излучение
-лазера находятся в диапазоне 9—10 мкм (средний ИК диапазон) и попадают в окно прозрачности атмосферы. Поэтому излучение  -лазера удобно для интенсивного воздействия на вещество, например в технологических целях. Кроме того, в диапазон длин излучения
-лазера удобно для интенсивного воздействия на вещество, например в технологических целях. Кроме того, в диапазон длин излучения  -лазера попадают резонансные частоты поглощения многих молекул, что делает возможным интенсивное резонансное воздействие лазерного излучения на вещество. При этом следует иметь в виду возможность как дискретной, так и плавной относительно широкодиапазонной перестройки частоты генерации этого лазера, что значительно расширяет его возможности. Добавим к этому, что
-лазера попадают резонансные частоты поглощения многих молекул, что делает возможным интенсивное резонансное воздействие лазерного излучения на вещество. При этом следует иметь в виду возможность как дискретной, так и плавной относительно широкодиапазонной перестройки частоты генерации этого лазера, что значительно расширяет его возможности. Добавим к этому, что  -лазер легко может быть одночастотным.
-лазер легко может быть одночастотным.

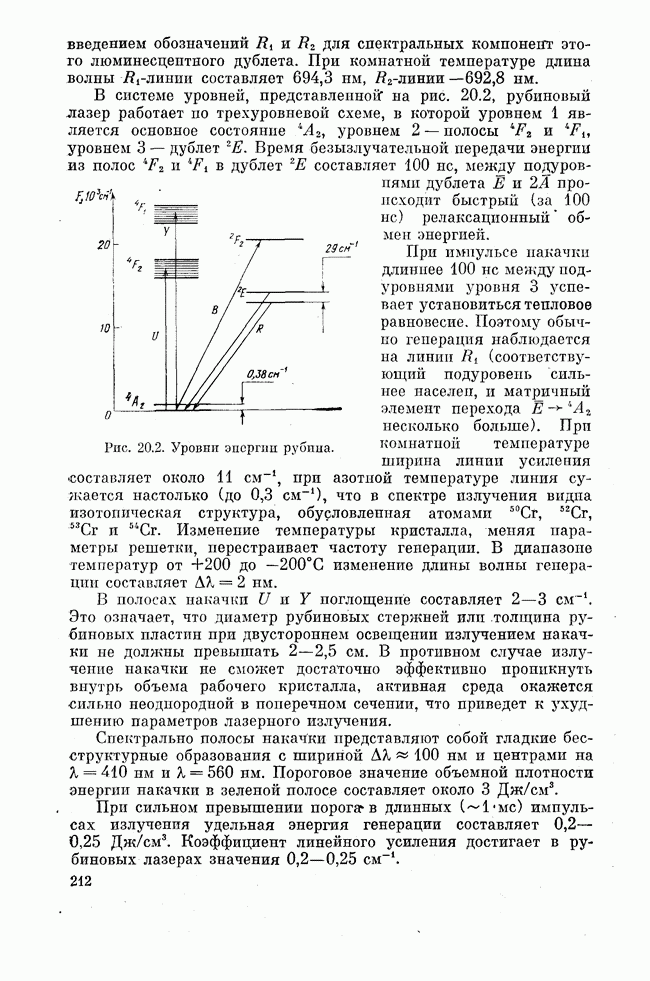
Рис. 15.4. Схема нижних колебательных уровней молекул  в основном электронном состоянии: прямые наклонные стрелки — генерационные переходы, прямая стрелка вверх — возбуждение азота, волнистая горизонтальная стрелка — передача энергии возбуждения от азота к
в основном электронном состоянии: прямые наклонные стрелки — генерационные переходы, прямая стрелка вверх — возбуждение азота, волнистая горизонтальная стрелка — передача энергии возбуждения от азота к  остальные волнистые стрелки — релаксационное опустошение нижних лазерных уровней.
остальные волнистые стрелки — релаксационное опустошение нижних лазерных уровней.
Таким образом, интерес к  -лазерам понятен.
-лазерам понятен.
Молекула  имеет три нормальных колебания — симметричное валентное
имеет три нормальных колебания — симметричное валентное  , деформационное
, деформационное  и несимметричное валентное
и несимметричное валентное  . Деформационное колебание дважды вырождено. Соответственно, заполнение колебательных уровней молекулы
. Деформационное колебание дважды вырождено. Соответственно, заполнение колебательных уровней молекулы  , в том числе не только нормальных частот
, в том числе не только нормальных частот  , но и их обертонов и составных колебаний, определяет тот набор колебательных квантовых чисел
, но и их обертонов и составных колебаний, определяет тот набор колебательных квантовых чисел  который описывает колебательное состояние молекулы. Обозначаются уровни комбинацией квантовых чисел:
который описывает колебательное состояние молекулы. Обозначаются уровни комбинацией квантовых чисел:  . Индекс l вводится из-за вырождения деформационного колебания
. Индекс l вводится из-за вырождения деформационного колебания  . Нам важны нижние колебательные уровни основного электронного состояния, показанные на
. Нам важны нижние колебательные уровни основного электронного состояния, показанные на
рис. 15.4 вместе с условным представлением формы колебаний молекулы  . Случайное совпадение частот колебаний
. Случайное совпадение частот колебаний  в силу резонанса Ферми смешивает эти уровни, и они в кинетических процессах часто выступают как одно состояние. Последнее обстоятельство является очень важным. Нижний лазерный уровень
в силу резонанса Ферми смешивает эти уровни, и они в кинетических процессах часто выступают как одно состояние. Последнее обстоятельство является очень важным. Нижний лазерный уровень  генерационного перехода
генерационного перехода  имеет малое время релаксации в силу сильной связи с деформационным колебанием
имеет малое время релаксации в силу сильной связи с деформационным колебанием  и тем самым с колебанием
и тем самым с колебанием  . Внутри одной. колебательной моды столкновительный обмен энергией в силу малости дефицита энергии происходит очень быстро, практически за одно газокинетическое столкновение. Колебание
. Внутри одной. колебательной моды столкновительный обмен энергией в силу малости дефицита энергии происходит очень быстро, практически за одно газокинетическое столкновение. Колебание  , как и всякое деформационное колебание, имеет большое сечение столкновительной дезактивации. Из простых геометрических соображений очевидно, что сечение неупругого столкновения для валентного колебания, локализующегося вдоль оси молекулы, много меньше, чем для деформационного колебания, которое может быть возбуждено (девозбуждено) частицей, налетающей на молекулу практически под любым углом к ее оси.
, как и всякое деформационное колебание, имеет большое сечение столкновительной дезактивации. Из простых геометрических соображений очевидно, что сечение неупругого столкновения для валентного колебания, локализующегося вдоль оси молекулы, много меньше, чем для деформационного колебания, которое может быть возбуждено (девозбуждено) частицей, налетающей на молекулу практически под любым углом к ее оси.
Если еще учесть случайное совпадение энергии первого колебания молекулы  с уровнем
с уровнем  молекулы
молекулы  , то мы приходим к выводу, что молекула
, то мы приходим к выводу, что молекула  хорошо отвечает требованиям к идеальному газоразрядному лазеру, изложенным в начале этой лекции. Симметричные гомоядерные молекулы азота обладают большим собственным временем жизни в колебательно возбужденном состоянии, легко возбуждаются электронным ударом и охотно отдают энергию возбуждения
хорошо отвечает требованиям к идеальному газоразрядному лазеру, изложенным в начале этой лекции. Симметричные гомоядерные молекулы азота обладают большим собственным временем жизни в колебательно возбужденном состоянии, легко возбуждаются электронным ударом и охотно отдают энергию возбуждения  .
.
В тлеющем электрическом разряде с приведенной напряженностью электрического поля в плазме разряда  при энергии электронов 2—3 эВ (резонасное возбуждение колебаний молекулы
при энергии электронов 2—3 эВ (резонасное возбуждение колебаний молекулы  в диапазоне
в диапазоне  ) и при плотности электронов
) и при плотности электронов  от 40% до 80% молекул азота возбуждены. Сечение возбуждения азота составляет
от 40% до 80% молекул азота возбуждены. Сечение возбуждения азота составляет  . Скорость столкновительной передачи энергии возбуждения от азота к
. Скорость столкновительной передачи энергии возбуждения от азота к  составляет
составляет  . Эта передача энергии идет эффективно между гармониками
. Эта передача энергии идет эффективно между гармониками  молекул
молекул  вплоть до колебания
вплоть до колебания  молекулы
молекулы  Таким образом, в
Таким образом, в  -лазере происходит заселение верхнего лазерного уровня.
-лазере происходит заселение верхнего лазерного уровня.
Что же касается опустошения нижнего лазерного уровня, то оказалось, что первый возбужденный уровень деформационной моды  эффективно релаксирует при столкновениях с атомами
эффективно релаксирует при столкновениях с атомами  . Гелий опустошает уровень
. Гелий опустошает уровень  со скоростью
со скоростью  . При этом уровень
. При этом уровень  моды
моды  гелием практически не затрагивается.
гелием практически не затрагивается.
В итоге мы можем сказать, что цикл лазерной накачки  -лазера в стационарных условиях выглядит следующим образом. Электроны плазмы тлеющего разряда возбуждают молекулы азота,
-лазера в стационарных условиях выглядит следующим образом. Электроны плазмы тлеющего разряда возбуждают молекулы азота,
которые передают энергию возбуждения несимметричному валентному колебанию молекул  , обладающему большим временем жизни и являющемуся верхним лазерным уровнем. Нижним лазерным уровнем обычно является первый возбужденный уровень симметричного валентного колебания, сильно связанный резонансом Ферми с деформационным колебанием и потому быстро релаксирующий вместе с этим колебанием в столкновениях с гелием. Очевидно, что этот же канал релаксации эффективен в случае, когда нижним лазерным уровнем является второй возбужденный уровень деформационной моды. Таким образом,
, обладающему большим временем жизни и являющемуся верхним лазерным уровнем. Нижним лазерным уровнем обычно является первый возбужденный уровень симметричного валентного колебания, сильно связанный резонансом Ферми с деформационным колебанием и потому быстро релаксирующий вместе с этим колебанием в столкновениях с гелием. Очевидно, что этот же канал релаксации эффективен в случае, когда нижним лазерным уровнем является второй возбужденный уровень деформационной моды. Таким образом,  -лазер — это лазер на смеси углекислого газа, азота и гелия, где
-лазер — это лазер на смеси углекислого газа, азота и гелия, где  обеспечивает излучение,
обеспечивает излучение,  накачку верхнего уровня, а Не — опустошение нижнего уровня.
накачку верхнего уровня, а Не — опустошение нижнего уровня.

Рис. 15.5. Цикл накачки  -лазера низкого давления при продольном разряде и медленной продольной прокачке.
-лазера низкого давления при продольном разряде и медленной продольной прокачке.
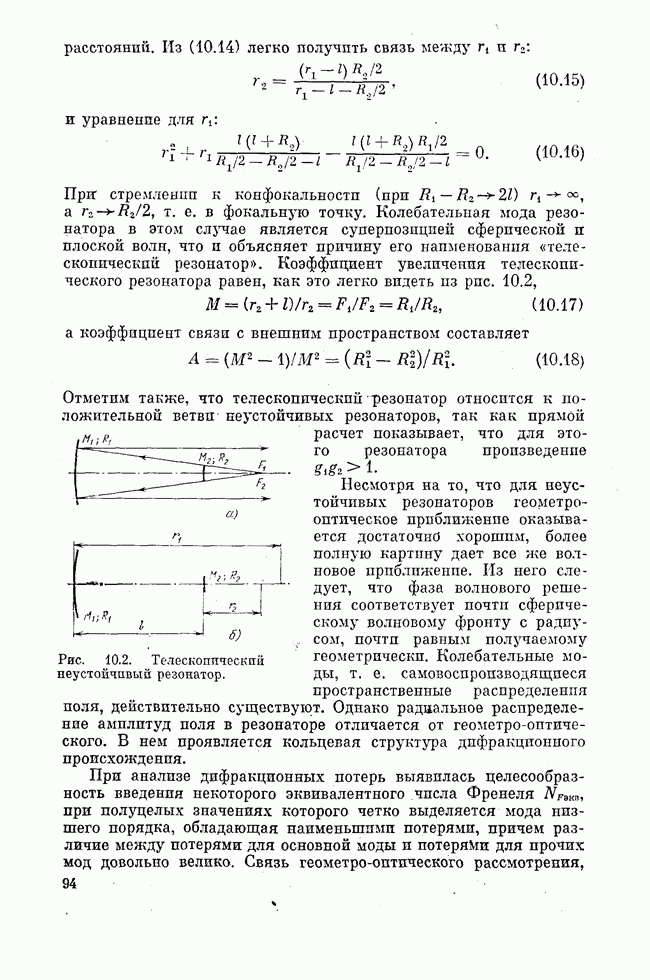
На рис. 15.5 схематически представлен лазерный цикл накачки для конкретного  -лазера. Диаметр разрядной трубки 15 мм, ток разряда 40 мА, приведенная напряженность электрического поля
-лазера. Диаметр разрядной трубки 15 мм, ток разряда 40 мА, приведенная напряженность электрического поля  температура газа на оси трубки 450 К, общее давление газовой смеси 15 Торр, смесь
температура газа на оси трубки 450 К, общее давление газовой смеси 15 Торр, смесь  в отношении
в отношении  . В условиях, близких к показанным на рис. 15.5, коэффициент усиления слабого сигнала составляет 3-4 дБ/м, плотность потока насыщения
. В условиях, близких к показанным на рис. 15.5, коэффициент усиления слабого сигнала составляет 3-4 дБ/м, плотность потока насыщения  , выходная мощность на единицу длины при оптимальной связи
, выходная мощность на единицу длины при оптимальной связи  При длине лазера 200 см (обычное лабораторное устройство) оптимальная прозрачность выходного зеркала составляет
При длине лазера 200 см (обычное лабораторное устройство) оптимальная прозрачность выходного зеркала составляет  .
.
Подчеркнем, что роль гелия не сводится только к опустошению нижнего лазерного уровня. В дополнение к этому гелий облегчает возникновение и поддержание тлеющего разряда. В богатых гелием смесях газов разряд развивается практически так же, как и в чистом гелии, который является классическим объектом плазменных исследований. Кроме того, гелий обладает высокой теплопроводностью, что важно для охлаждения  в зоне разряда. Предотвращение разогрева
в зоне разряда. Предотвращение разогрева  необходимо для того, чтобы избежать термического заселения низко расположенного уровня
необходимо для того, чтобы избежать термического заселения низко расположенного уровня  (см. рис. 15,4). К этому следует добавить, что большое количество
(см. рис. 15,4). К этому следует добавить, что большое количество
гелия в разряде препятствует диссоциации  электронами разряда.
электронами разряда.
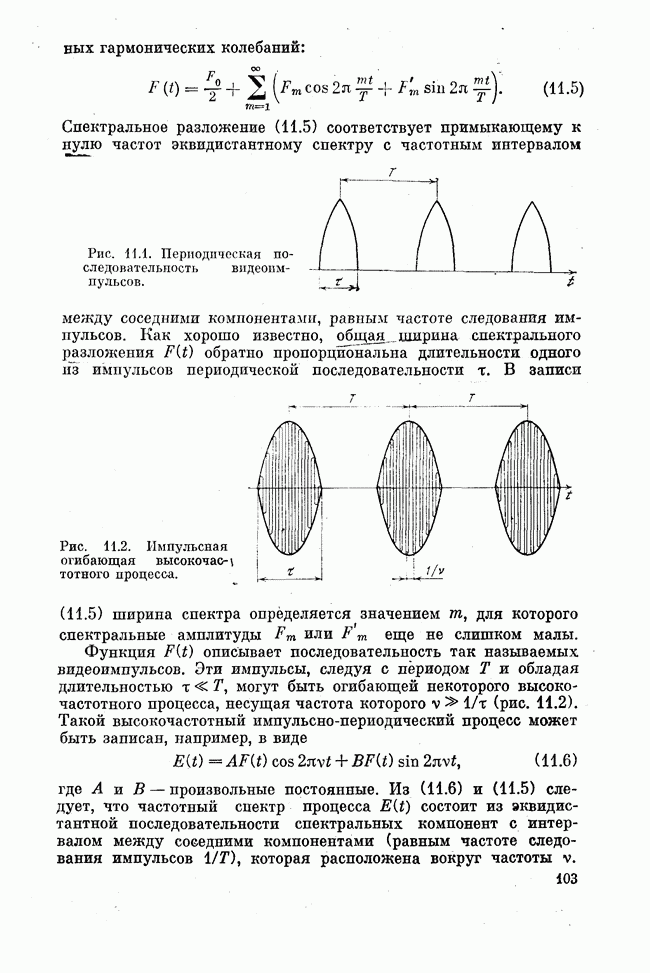
 -лазеры средней мощности (десятки — сотни ватт) конструируются в виде относительно длинных труб с продольным разрядом и продольной прокачкой газа. Типичная конструкция такого лазера показана на рис. 15.6. Продольный разряд наиболее прост в реализации. Необходимо только включить последовательно с разрядом достаточно большое сопротивление, с тем, чтобы ограничить ток разряда и скомпенсировать влияние падающего участка вольт-амперной характеристики разрядного промежутка. Продольная прокачка служит для удаления продуктов диссоциации газовой смеси в разряде. Охлаждение рабочего газа в таких системах происходит за счет диффузии на охлаждаемую снаружи стоику разрядной трубки. Существенной является теплопроводность материала стенки. С этой точки зрения целесообразно применение труб из корундовой
-лазеры средней мощности (десятки — сотни ватт) конструируются в виде относительно длинных труб с продольным разрядом и продольной прокачкой газа. Типичная конструкция такого лазера показана на рис. 15.6. Продольный разряд наиболее прост в реализации. Необходимо только включить последовательно с разрядом достаточно большое сопротивление, с тем, чтобы ограничить ток разряда и скомпенсировать влияние падающего участка вольт-амперной характеристики разрядного промежутка. Продольная прокачка служит для удаления продуктов диссоциации газовой смеси в разряде. Охлаждение рабочего газа в таких системах происходит за счет диффузии на охлаждаемую снаружи стоику разрядной трубки. Существенной является теплопроводность материала стенки. С этой точки зрения целесообразно применение труб из корундовой  или бериллиевон
или бериллиевон  керамик.
керамик.

Рис. 15.6. Схема конструкция  -лазера с продольными разрядом и прокачкой. Охлаждающая вода проходит через катод.
-лазера с продольными разрядом и прокачкой. Охлаждающая вода проходит через катод.
При продольной конфигурации разряда и прокачке максимальная мощность на единицу длины (50-100 Вт/м) не зависит от диаметра газоразрядной трубки. Действительно, при значительном превышении над порогом самовозбуждения лазера излучаемая мощность определяется произведением скорости накачки  объем активной среды V:
объем активной среды V:
 (15.20)
(15.20)
В цилиндрической геометрии  , где l — длина разряда, D — диаметр трубки. Скорость накачки
, где l — длина разряда, D — диаметр трубки. Скорость накачки  определяется произведением плотности молекул в основном состоянии
определяется произведением плотности молекул в основном состоянии  на плотность электронов
на плотность электронов  , сечение возбуждения электронным ударом а и среднюю относительную скорость и:
, сечение возбуждения электронным ударом а и среднюю относительную скорость и:
 (15.21)
(15.21)
Но произведение  имеет смысл плотности тока разряда
имеет смысл плотности тока разряда  следовательно,
следовательно,  . Произведение
. Произведение  дает значение полного тока разряда
дает значение полного тока разряда  , и мы получаем
, и мы получаем
 (15.22)
(15.22)
Так как плотность  пропорциональна полному давлению газовой смеси р, то
пропорциональна полному давлению газовой смеси р, то
 (15.23)
(15.23)
Как мы знаем, произведение тока на давление является важной характеристикой плазменных процессов в длинных трубках. В стационарной плазме тлеющего разряда условия определяются произведением  . Постоянство
. Постоянство  обеспечивает постоянство плазменных условий (см. лекцию тринадцатую). Если для какого-то диаметра фиксировано оптимальное давление, то оптимум сохраняется при сохранении значения произведения
обеспечивает постоянство плазменных условий (см. лекцию тринадцатую). Если для какого-то диаметра фиксировано оптимальное давление, то оптимум сохраняется при сохранении значения произведения  . Следовательно,
. Следовательно,  , а так как
, а так как  , то произведение
, то произведение  .
.
С другой стороны, для СО2-лазера очень важен тепловой режим. Тепловыделение в единичном объеме пропорционально плотности тока J. Теплоотвод в цилиндрической геометрии из центральной части разрядного канала на периферию пропорционален  . Сохранение постоянным некоторого оптимального теплового режима требует постоянства произведения
. Сохранение постоянным некоторого оптимального теплового режима требует постоянства произведения  . Следовательно, произведение
. Следовательно, произведение  является константой, и мы приходим к тому важному выводу, что в оптимальных условиях выходная мощность
является константой, и мы приходим к тому важному выводу, что в оптимальных условиях выходная мощность  -лазера с продольными прокачкой и разрядом пропорциональна только длине лазера:
-лазера с продольными прокачкой и разрядом пропорциональна только длине лазера:
 (15.24)
(15.24)
Напомним, что при проведенном выше анализе мы исключили из рассмотрения наличие нерезонансных потерь по известной формуле  (см. (6.44)), ограничивающей максимальную выходную мощность лазера. В частности, именно поэтому наибольшая выходная мощность, достигнутая в продольной конфигурации, незначительно превышает 1 кВт (суммарная длина разряда
(см. (6.44)), ограничивающей максимальную выходную мощность лазера. В частности, именно поэтому наибольшая выходная мощность, достигнутая в продольной конфигурации, незначительно превышает 1 кВт (суммарная длина разряда  ).
).
Так как прокачка газовой смеси через разрядную трубку обусловлена необходимостью смены газа для удаления продуктов диссоциации  , то добавление в рабочую смесь каких-либо составляющих, способствующих окислению СО в плазме тлеющего разряда до
, то добавление в рабочую смесь каких-либо составляющих, способствующих окислению СО в плазме тлеющего разряда до  позволяет создавать отпаянные
позволяет создавать отпаянные  -лазеры. Такой регенерирующей добавкой обычно служат молекулы воды
-лазеры. Такой регенерирующей добавкой обычно служат молекулы воды  при концентрации меньше 1%. Отпаянные лазеры очень удобны в лабораторном применении, но полученные с их помощью мощности не превышают нескольких десятков ватт.
при концентрации меньше 1%. Отпаянные лазеры очень удобны в лабораторном применении, но полученные с их помощью мощности не превышают нескольких десятков ватт.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ЧАСТЬ ПЕРВАЯ. ОСНОВЫ ФИЗИКИ ЛАЗЕРОВ
- Лекция первая. КОЭФФИЦИЕНТЫ ЭЙНШТЕЙНА
- Лекция вторая. ШИРИНА ЛИНИИ
- Лекция третья. УСИЛЕНИЕ
- Лекция четвертая. КОЭФФИЦИЕНТЫ ЭЙНШТЕЙНА И МАТРИЧНЫЙ ЭЛЕМЕНТ ОПЕРАТОРА ПЕРЕХОДА
- Лекция пятая. ЛАЗЕРЫ-УСИЛИТЕЛИ
- Лекция шестая. ГЕНЕРАЦИЯ
- Лекция седьмая. ОТКРЫТЫЕ РЕЗОНАТОРЫ
- Лекция восьмая. ГАУССОВЫ ПУЧКИ
- Лекция девятая. УСТОЙЧИВОСТЬ РЕЗОНАТОРОВ
- Лекция десятая. НЕУСТОЙЧИВЫЕ РЕЗОНАТОРЫ
- Лекция одиннадцатая. СИНХРОНИЗАЦИЯ МОД
- Лекция двенадцатая. ИСТОРИЯ КВАНТОВОЙ ЭЛЕКТРОНИКИ. ОСНОВНЫЕ ФОРМУЛЫ
- ЧАСТЬ ВТОРАЯ. ЛАЗЕРЫ
- Лекция тринадцатая. ГАЗОВЫЕ ЛАЗЕРЫ. ГЕЛИЙ-НЕОНОВЫЙ ЛАЗЕР
- Лекция четырнадцатая. ИОННЫЕ ЛАЗЕРЫ. ЛАЗЕРЫ НА ПАРАХ МЕТАЛЛОВ
- Лекция пятнадцатая. CO2-ЛАЗЕРЫ
- Лекция шестнадцатая. СO2-ЛАЗЕРЫ (продолжение)
- Лекция семнадцатая. ХИМИЧЕСКИЕ ЛАЗЕРЫ
- Лекция восемнадцатая. CO-ЛАЗЕРЫ, ГАЗОВЫЕ ЛАЗЕРЫ НА ЭЛЕКТРОННЫХ ПЕРЕХОДАХ В МОЛЕКУЛАХ
- Лекция девятнадцатая. ВСПОМОГАТЕЛЬНОЕ ИЗЛУЧЕНИЕ НАКАЧКИ В СИСТЕМАХ СО МНОГИМИ УРОВНЯМИ ЭНЕРГИИ
- Лекция двадцатая. РУБИНОВЫЙ И НЕОДИМОВЫЙ ЛАЗЕРЫ
- Лекция двадцать первая. БЕЗЫЗЛУЧАТЕЛЬНАЯ РЕЛАКСАЦИЯ В ТВЕРДОМ ТЕЛЕ
- Лекция двадцать вторая. ЛАЗЕРЫ НА КРАСИТЕЛЯХ
- Лекция двадцать третья. ЛАЗЕРЫ НА ЦЕНТРАХ ОКРАСКИ
- Лекция двадцать четвертая. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ
- Лекция двадцать пятая. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ (продолжение)
- Лекция двадцать шестая. ЛАЗЕРЫ НА СВОБОДНЫХ ЭЛЕКТРОНАХ
- Лекция двадцать седьмая. СЕМНАДЦАТЬ НАИБОЛЕЕ ИЗВЕСТНЫХ ЛАЗЕРОВ
- Заключение. ТЕНДЕНЦИИ РАЗВИТИЯ