Лекция двадцать первая. БЕЗЫЗЛУЧАТЕЛЬНАЯ РЕЛАКСАЦИЯ В ТВЕРДОМ ТЕЛЕ

Электрон-фононное взаимодействие. Слабая вибронная связь. Вероятность многофононной релаксации. Колебательный спектр матрицы. Максимальная длина волны. Примеры ионов неодима и эрбия. Ион-ионное взаимодействие. Эффективное затухание в системе слабосвязанных осцилляторов. Вероятность переноса энергии от донора к акцептору. Миграция энергии. Выбор оптимальных концентраций. Сенсибилизация.

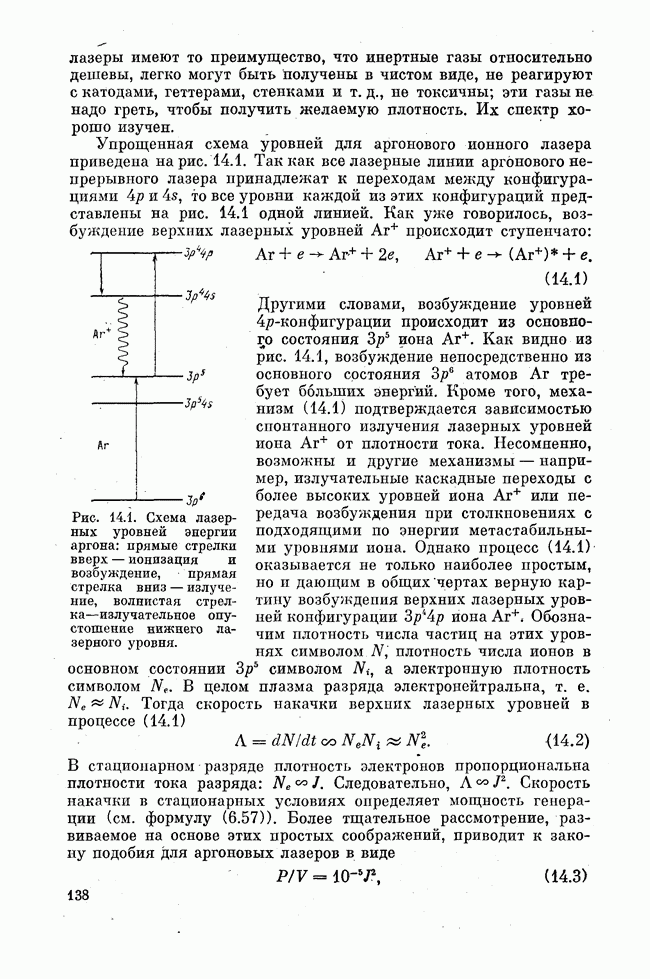
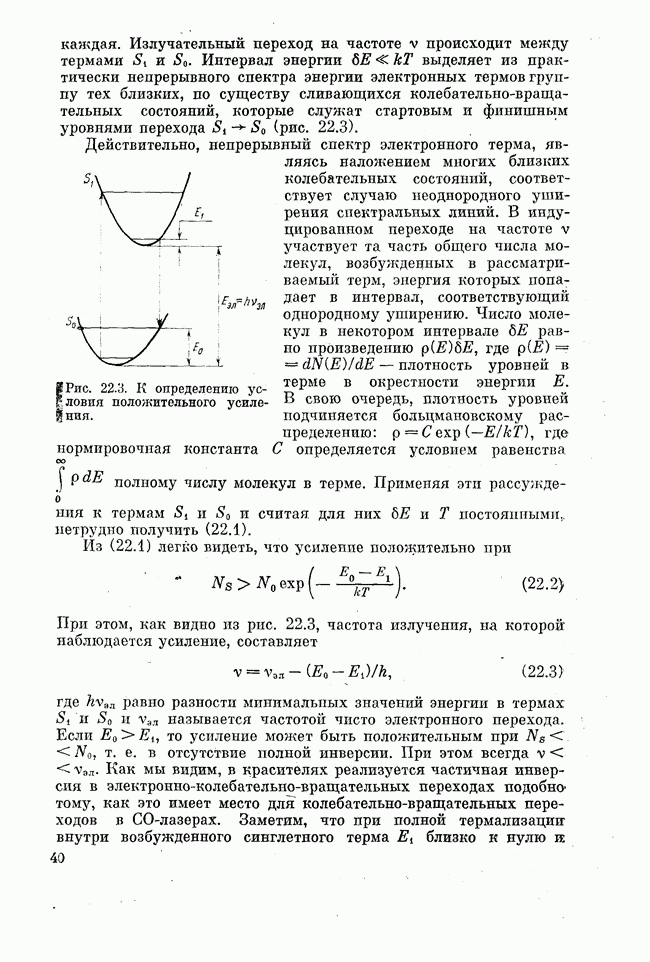
В предыдущем изложении неоднократно отмечалась важная роль, которую играют процессы безызлучательной релаксации при создании инверсии населенностей в лазерах и мазерах. Конкретные проявления и механизмы безызлучательной релаксации различны в разных спектральных интервалах и для разных активных сред квантовой электроники. Особо важную, во многом определяющую роль играют безызлучательные переходы в процессе создания активной среды лазеров на твердом теле (см. лекцию девятнадцатую). Это обстоятельство делает целесообразным несколько более подробное рассмотрение процессов релаксации энергии возбуждения в активных средах твердотельных лазеров в рамках курса лекций по основам квантовой электроники.

Безызлучательные переходы в твердых телах, под которыми в нашем курсе понимаются диэлектрические примесные кристаллы и стекла, определяются взаимодействием двух типов. К первому из них относится электрон-фононное взаимодействие, обусловливающее перенос энергии между различными состояниями одной частицы (одного примесного центра), ко второму — взаимодействие между активными частицами (в нашем случае — ион-ионное взаимодействие), приводящее к переносу энергии между различными примесными центрами.

Рассмотрим вначале электрон-фононное взаимодействие. Общая теория электронно-колебательного взаимодействия в настоящее время весьма далека от завершения. Количественные результаты обычно могут быть получены для двух предельных случаев — сильной и слабой вибронной (т. е. колебательно-электронной) связи. Критерием слабой (или сильной) связи является малость (или немалость) энергии колебательного движения примесного иона по сравнению с энергией колебательного кванта — фонона, равной . 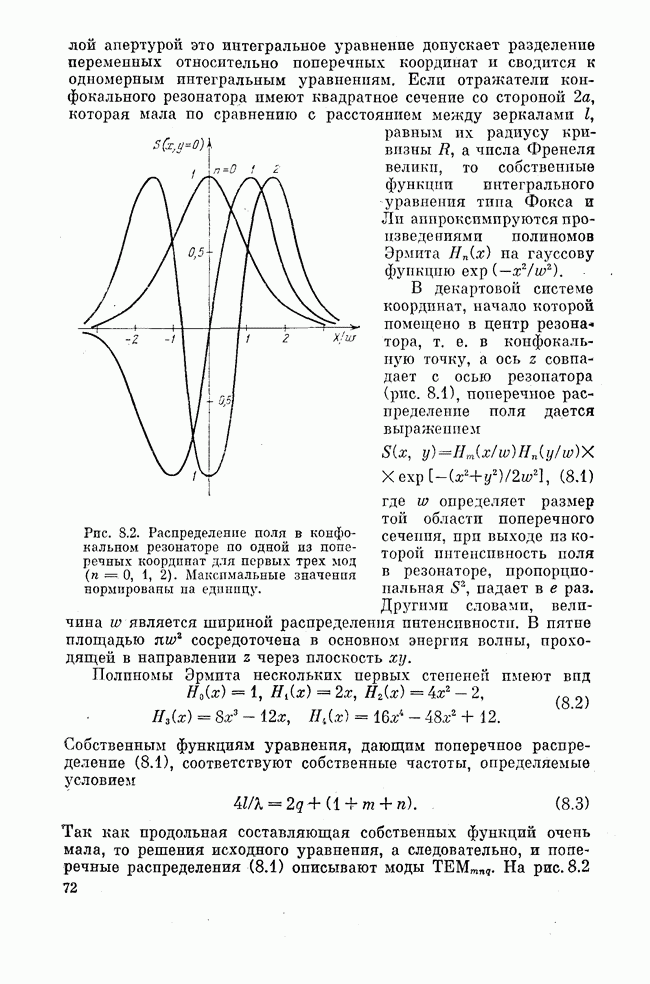Если приведенная масса иона равна М, смещение от положения равновесия составляет , а — частота колебаний, то оценка энергии колебаний дает, как известно, . Безразмерным параметром является отношение малость (немалость) которого определяет обсуждаемые предельные случаи. Большое значение, однако, имеет дипольный момент колеблющегося иона. Его величина пропорциональна смещению из положения равновесия . Поэтому обычно из отношения энергий извлекается корень, и критерий сильной вибронной связи записывается в виде

в то время как обратное неравенство

представляет собой критерий слабой вибронной связи.

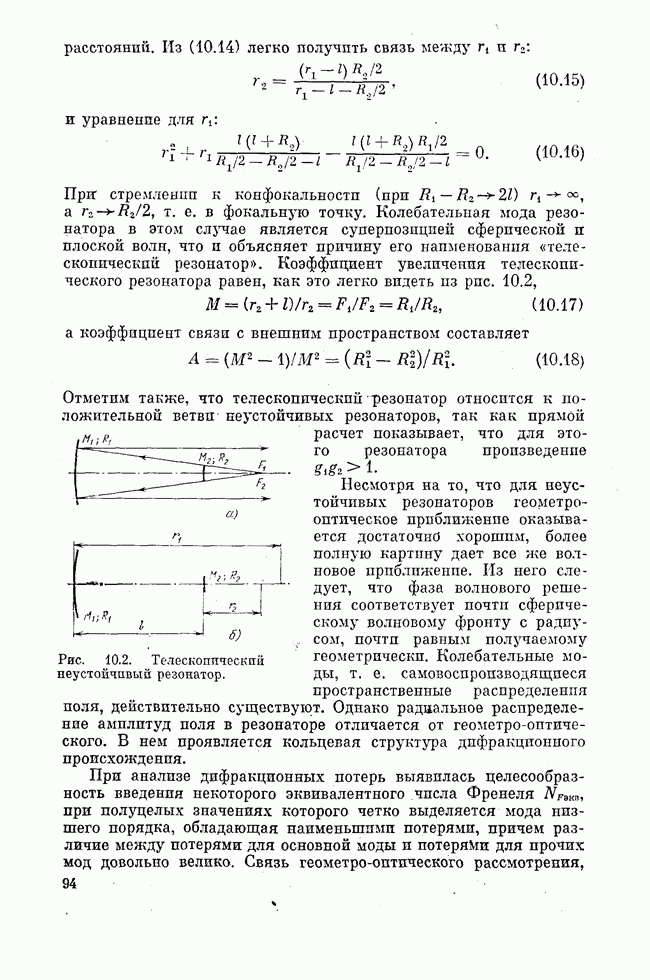
Спектроскопически случаи сильной и слабой вибронной связи проявляются по-разному. В случае сильной связи возникает большой стоксов сдвиг между спектрами. поглощения и излучения, в случае слабой связи стоксов сдвиг практически отсутствует. Для трехвалентных ионов редкоземельных элементов представляющих для нас основной интерес, оптическими являются электроны -оболочки. Будучи экранированной, эта оболочка, как мы знаем, слабо взаимодействует с внутрикристаллическими полями матрицы и тем самым с ее колебаниями. Колебания решетки матрицы слабо воздействуют на потенциальные поверхности электронных термов -оболочки примесного иона. Поэтому возбуждение иона при переходах между электронными состояниями -оболочки не приводит к заметному возбуждению колебаний решетки. Энергия на раскачку колебаний не тратится, а стоксов сдвиг между электронными переходами в спектре поглощения и люминесценции для отсутствует. Следовательно, безызлучательные переходы между электронными срстояниями должны хорошо описываться в приближении слабой вибронной связи, рассмотрением которой мы ограничимся.

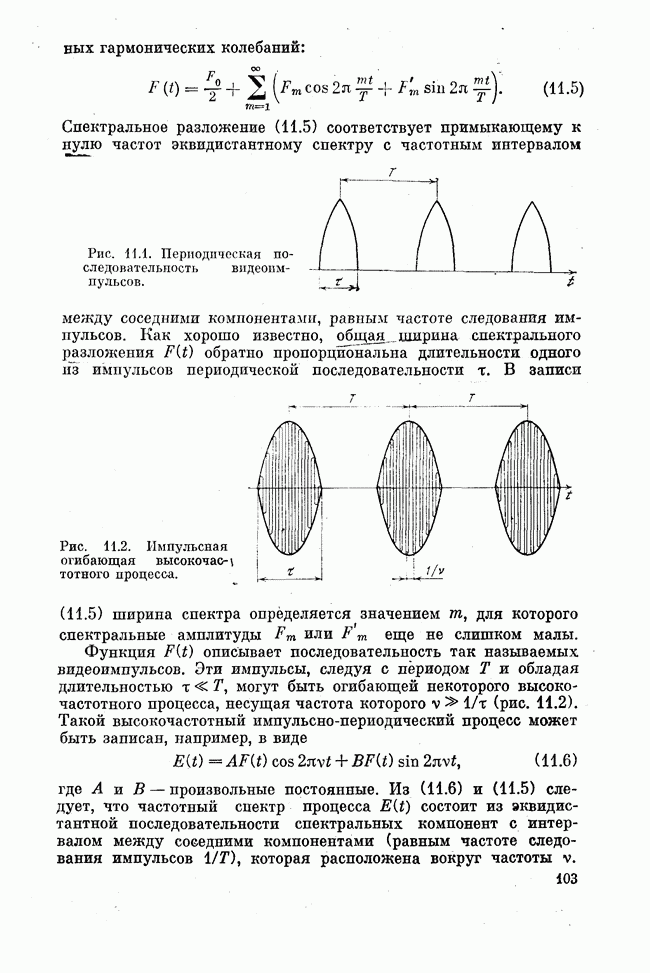
Наиболее общим является Квантовомеханическое рассмотрение, которое должно проводиться с учетом высоких порядков теории возмущений и в нашем случае, для взаимодействия

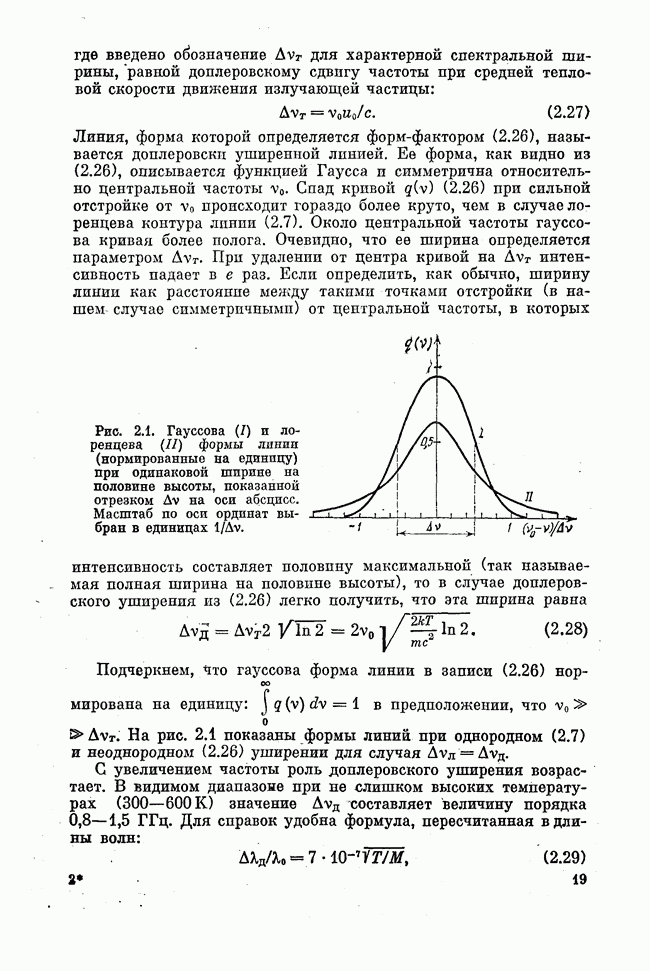
ионов с решеткой, обусловленного модуляцией статического внутрикристаллического поля колебаниями решетки. Так как энергетический зазор между основным и возбужденными состояниями иона велик по сравнению с энергией самого высокочастотного фонона (см. лекцию девятнадцатую), рассматриваемые сейчас безызлучательные переходы носят многофононный характер. Различные модификации теории возмущений дают для вероятности безызлучательной релаксации, идущей с возникновением р фононов при переходе между рассматриваемыми верхним (стартовым) и нижним (финишным) состояниями, крайне громоздкие выражения, включающие в себя волновые функции начального, конечного и всех промежуточных виртуальных состояний, числа фононного заполнения и плотности фононных состояний.

Как правило, необходимая для количественных оценок информация отсутствует. Поэтому обычно используется феноменологическая теория многофононпой релаксации, в которой предполагается, что

а) вероятность многофонного перехода не зависит от характеристик начального и конечного электронных состояний примесного центра;

б) вероятность перехода с испусканием р фононов значительно мепыпе, чем с испусканием фононов:

в) малая величина е является характеристикой основы (а не примесного центра) и не зависит от р;

г) безызлучательиый переход осуществляется с испусканием фононов одинаковой частоты, так что закон сохранения энергии выполняется в виде

Следствием этих предположений является вывод о том, что в процессе многофононного перехода участвуют самые высокоэнергичные, т. е. наиболее высокочастотные фононы колебательного спектра основы. В рамках указанных предположений удается получить простую формулу, дающую зависимость вероятности многофононного перехода от температуры основы Т и энергетического зазора в спектре активной примеси в виде

где

дает температурную зависимость скорости безызлучательных переходов с испусканием р фононов, а

равная при нулевой температуре, дает зависимость

рассматриваемой вероятности от величины энергетической щели . Здесь и — феноменологические константы, характеризующие основу. Как правило, реальная ситуация качественно хорошо описывается в рамках изложенной модели, хотя попытки получения количественной информации о числе и энергии фононов, участвующих в релаксационном процессе, на основе этой модели несостоятельны.

Рассмотрим сначала температурную зависимость релаксации (21.6).

При наличии некоторой избыточной энергии вероятность испускания фонона частоты со пропорциональна числу фононов , имеющихся в фонопной моде частоты со (индуцированное испускание), плюс один (спонтанное испускание):

Заселенность фопонной моды при температуре Т дается распределением Бозе — Эйнштейна

Так как в рассматриваемой модели в единичном акте релаксации предполагается испускание р одинаковых фононов, то вероятность всего процесса в целом пропорциональна что и дает формулу (21.6). Подчеркнем еще раз, что при .

Слабым местом излагаемой модели мпогофононной безызлучательной релаксации является предположение одночастотности (21.4). На самом деле энергетическая щель АЕ перекрывается набором многих фононов с разными частотами и разной степенью миогофопонности в соответствии с особенностями условий возбуждения колебаний в той или иной конкретной основе. Существенную роль здесь играет спектр возможных колебаний, информацию о котором дает, например, комбинационное рассеяние света.

Спектры комбинационного рассеяния (рамановские спектры) кристаллов и. стекол демонстрируют существенные различия в структуре и протяженности фононпых спектров этих материалов. У кристаллов обычно граница высокочастотных колебаний расположена ниже, чем у стекол. Энергия самых высокочастотных фононов, как правило, превышает энергию дебаевских фононов йсов (температура Дебая для лазерных материалов лежит в окрестности 300 К).

Строгого теоретического обоснования формул (21.5) — (21.7) не существует. Поэтому большое значение имеет эксперимент. Обычно экспериментальное исследование проводится путем наблюдения кинетики люминесценции при селективном возбуждении избранного состояния примесного иона , введенного в матрицу, фононный спектр которой должен быть известен. Так как спектр состояний ионов от основы к основе меняется

слабо, то эксперименты этого рода, проводимые в различных матрицах с различными состояниями разных ионов, позволяют провести тщательное параметрическое исследование зависимости скорости релаксации примесного центра от .

Оказалось, что, хотя разные фононы могут вносить вклад в вероятность безызлучательного перехода, для различных ионов и в различных матрицах наблюдается прекрасное соответствие скорости релаксации значению высокочастотной границы колебаний. Это соответствие существует не только для абсолютного значения скорости релаксации, определяемого степенью многофононности (где под надо понимать частоту, соответствующую высокочастотной границе колебаний), но и для ее температурной зависимости, определяемой отношением и значением р.

Обратимся теперь к энергетической зависимости (21.7). В экспериментах указанного выше типа показано, что в широком интервале значений энергетической щели (от 1000 до ) зависимости скорости многофононной релаксации от с удовлетворительной степенью точности действительно являются экспоненциальными.

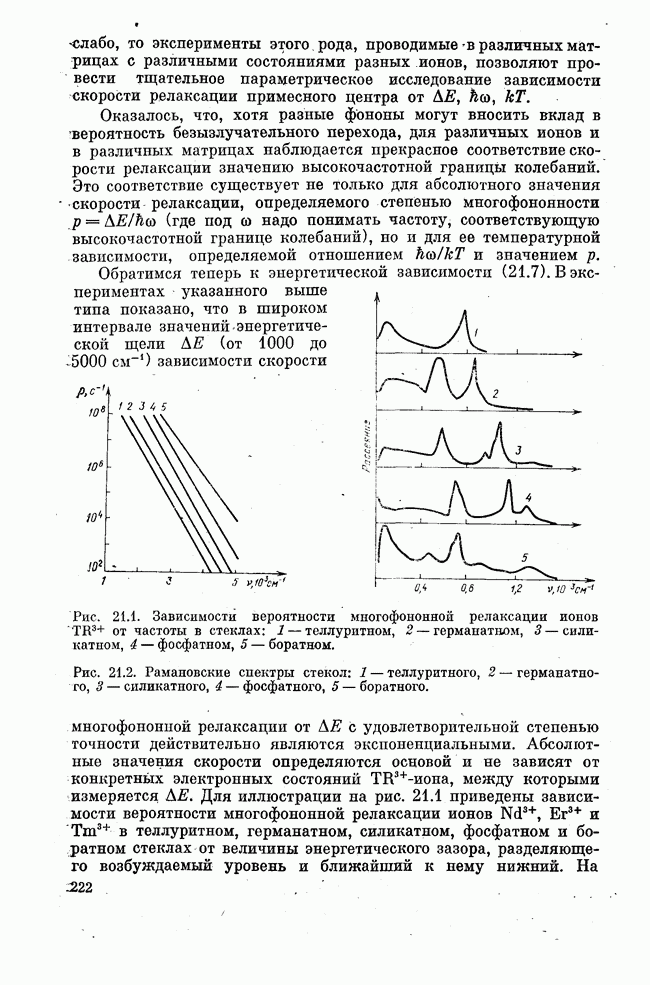
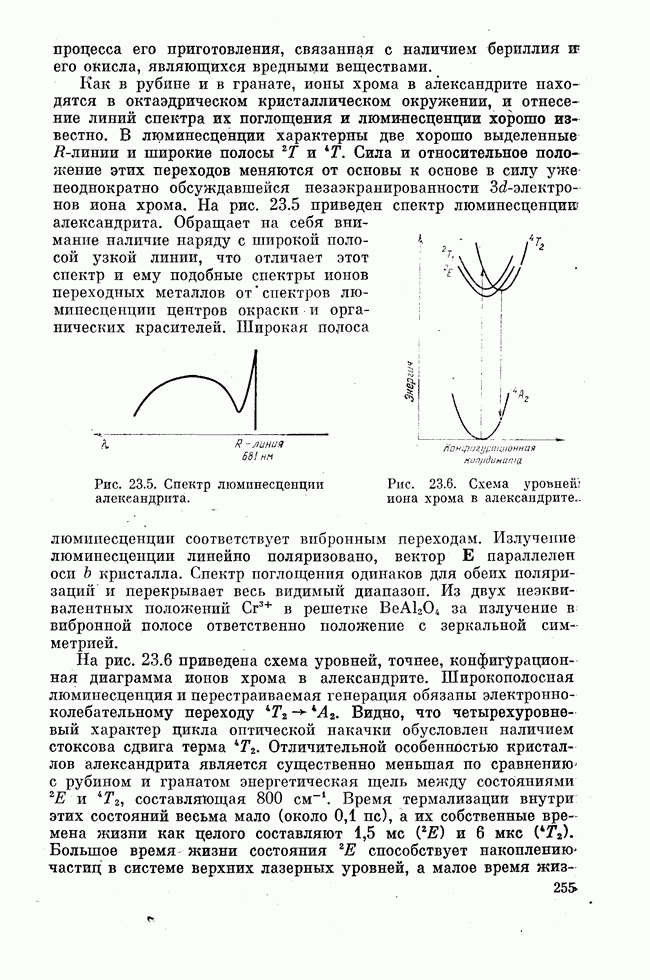
Рис. 21.1. Зависимости вероятности многофононной релаксации ионов от частоты в стеклах: 1 — теллуритном, 2 — германатвом, 3 — силикатном, 4 — фосфатном, 5 — боратном.

Рис. 21.2. Рамановские спектры стекол: 1 — теллуритного, 2 — германатного, 3 — силикатного, 4 — фосфатного, 5 — боратного.

Абсолютные значения скорости определяются основой и не зависят от конкретных электронных состояний , между которыми измеряется . Для иллюстрации на рис. 21.1 приведены зависимости вероятности многофононной релаксации ионов в теллуритном, германатном, силикатном, фосфатном и боратном стеклах от величины энергетического зазора, разделяющего возбуждаемый уровень и ближайший к нему нижний. На

рис. 21.2 приведены рамановские спектры, характеризующие протяженность фононного спектра в тех же стеклах. Легко прослеживается связь между графиками рис. 21.2 и 21.1. Видно, что абсолютные значения вероятности многофононной релаксации являются наименьшими в теллуритном стекле, обладающем наименее протяженным колебательным спектром. Увеличение протяженности фононного спектра ведет к увеличению скорости многофононной релаксации в связи, как это следует из смысла обсуждаемой модели, со снижением степени многофононности р.

Температурно зависимая часть при слабо зависит от р. Сильная зависимость от р, удовлетворяющая предположению (21.3), обусловлена тем, что входящая в (21.7) константа подчиняется неравенству . Обычно , как это можно определить из экспериментальных кривых, подобных приведенным на рис. 21.1.

В целом следует заключить, что. формулы (21.5) — (21.7) правильно отражают характер внутрицентровой безызлучательной электрон-фононной релаксации примесных в диэлектрических кристаллах и стеклах.

Обратимся теперь к важным выводам, которые следуют из изложенного выше механизма внутрицентровой релаксации, формул (21.5) - (21.7) и рис. 21.1, 21.2.

Обсудим прежде всего вопрос о максимально возможной длине волны излучения лазера на твердом теле. Для эффективного создания инверсии необходимо, чтобы скорость безызлучательпой релаксации верхнего лазерного уровня не превышала скорость его радиационного распада (см. лекцию девятнадцатую). Известно, что характерное радиационное время жизни верхнего лазерного уровня составляет примерно 1 мс. Тогда из рис. 21.1 видна невозможность создания лазера с длиной волны» более 2-2,5 мкм на широко применяемых в настоящее время фосфатных и силикатных стеклах, так как при энергетических зазорах менее скорость безызлучательной релаксации в этих матрицах начинает превышать скорость радиационного распада соответствующего верхнего уровня. Вместе с тем на кристаллах, обладающих по сравнению со стеклами, как правило, менее протяженным фононным спектром, возможна генерация и более длинноволнового излучения. Примером может служить генерация на переходе иона , полученная в области 3 мкм в ряде кристаллов . Однако продвижение в область длин волн, превышающих 4 мкм, мало вероятно.

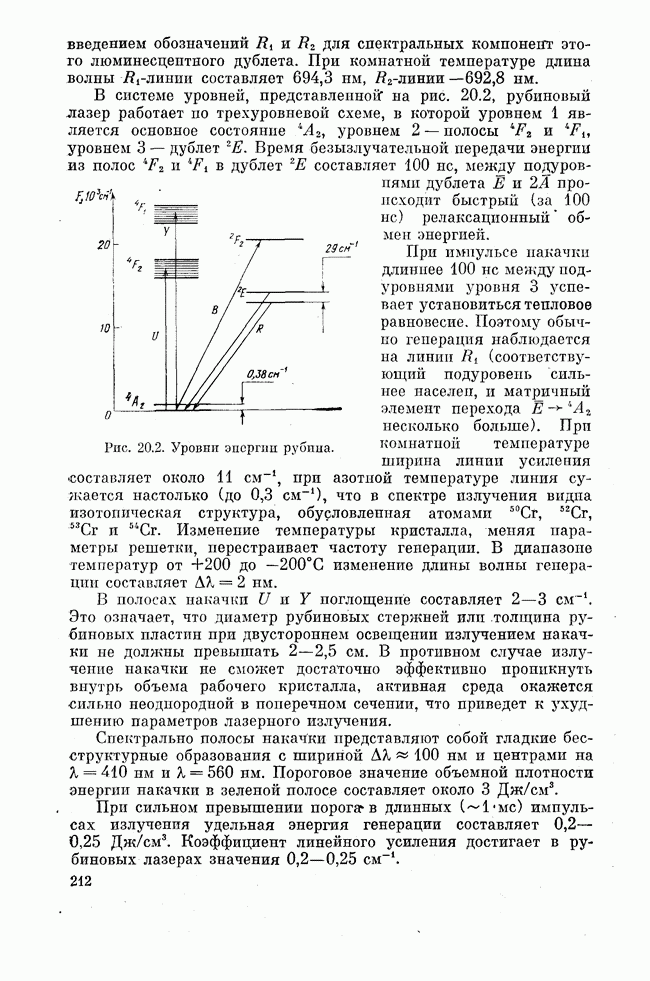
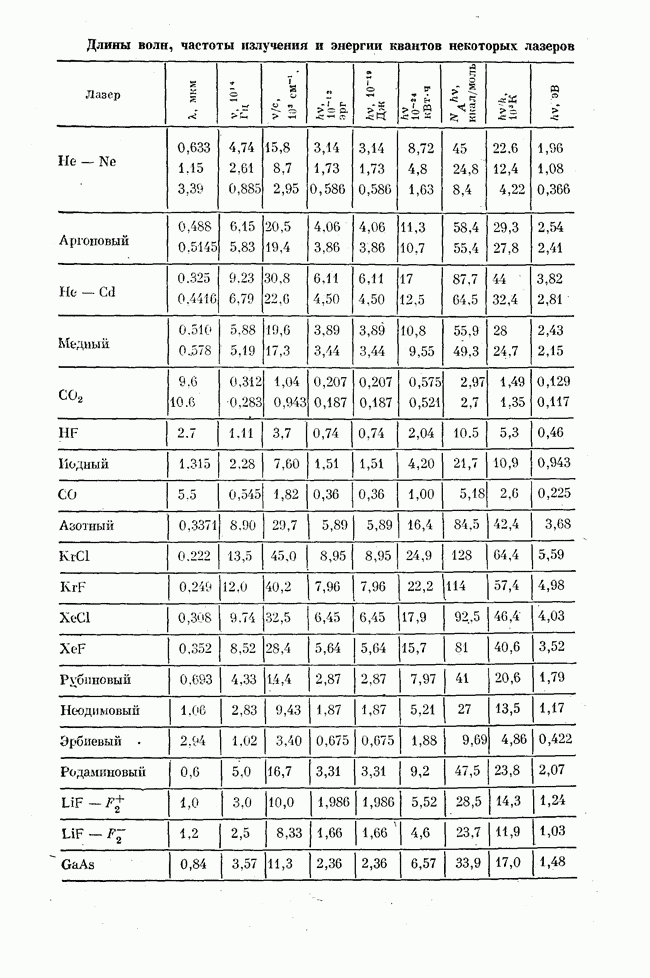
Рассмотрим с точки зрения обсуждаемого процесса многофононной релаксации схему уровней иона неодима (см. рис. 20.3).

Верхний лазерный уровень иона отделен от ближайшего к нему снизу состояния энергетическим зазором . В соответствии с данными рис. 21.1 время многофононной

релаксации оказывается для состояния существенно большим его радиационного времепи жизни. В результате квантовый выход люминесценции верхнего лазерного уровня (в отсутствие концентрационного тушения) близок к 100%.

Финишный лазерный уровень иона неодима лежит выше основного состояния на . Такой зазор в фосфатном и силикатном стеклах обеспечивает время жизни уровня порядка 1 не. Следовательно, режим самоограничения генерации (см. лекцию четырнадцатую) не должен происходить при длительности импульсов, превышающей 1 нс.

Энергетический зазор между верхним лазерным уровнем неодима и основными полосами накачки также не превышает . Следовательно, время безызлучательной релаксации из этих полос в метастабильное состояние лежит в диапазоне 1—10 нс при собственном времени жизни этого уровня . В результате вся энергия возбуждения накапливается в метастабильном состоянии неодима.

Все эти выводы полностью экспериментально подтверждены и составляют физическое обоснование широкого использования попа как активного центра в лазерных кристаллах и стеклах.

Рис. 21.3. Сравнение схем лазерных уровней энергии ионов .

Обратимся теперь к уже упомянутому примеру лазера на переходе иона Упрощенная схема уровней приведена на рис. 21.3 вместе с показанной для сравнения схемой уровней попа неодима. Зазор между финишным лазерным уровнем и основным состоянием составляет около энергия лазерного перехода находится в области . Степень многофопопностн безыдлучательной релаксации по переходам существенно различна. В силу этого время жизни стартового лазерного уровня много меньше, чем финишного уровня и лазер работает в режиме самоограничения, в отличие от рассмотренного выше пеодимового лазера. Полосы поглощения излучения накачки лежат для эрбиевого лазера в области Безызлучательные переходы через довольно значительный, в отличие от неодима, энергетический зазор между полосами накачки и стартовым лазерным уровнем существенно облегчены наличием в. этом зазоре многих уровней, разбивающих зазор на области с малой степенью многофононпости. Приведенные примеры показывают, как проявляются характерные черты внутрицентровой безызлучательной электрон-фононной релаксации примесных в диэлектрических кристаллах

и стеклах в лазерных свойствах соответствующих активных сред.

Рассмотрим теперь ион-ионное взаимодействие. Интерес к процессам переноса энергии между различными примесными центрами обусловлен рядом обстоятельств. Во-первых, с увеличением концентрации примесных ионов, что всегда желательно с целью повышения коэффициента усиления и удельного энергосъема активной среды, возрастает роль процессов переноса энергии в механизмах релаксации энергии, становящихся коллективными. Это, в свою очередь, может определять предельно возможные концентрации примесей в лазерных кристаллах и стеклах. Во-вторых, контролируемое введение в матрицу дополнительных примесей может в процессе последовательных актов переноса энергии и релаксации ускорять передачу энергии из полос поглощения на метастабильные состояния верхних лазерных уровней рабочих примесных центров и (или) ускорять распад их нижних лазерных уровней. В-третьих, присутствие в матрице дополнительных поглощающих ионов, способных эффективно передавать полученную энергию рабочим ионам, существенно повышает энергетическую эффективность активных сред.

Вероятность безызлучательного переноса энергии от донора (D) к акцептору (А), т. е. вероятность процесса типа

при котором возбужденный донор возвращается в основное состояние, а невозбужденный акцептор переходит в возбужденное состояние, при диполь-дипольном взаимодействии частиц D и А, находящихся на расстоянии R друг от друга в среде с показателем преломления и, может быть получена методами кваптовой механики в первом порядке теории возмущений. Однако возможны и классическая интерпретация явления переноса, и классический вывод соответствующего выражения.

В рамках представления о классическом осциллирующем электрическом диполе, уже неоднократно использовавшегося в этих лекциях, рассмотрим два дипольных электронных осциллятора, воздействующих друг на друга своими электромагнитными полями. Система уравнений связанных осцилляторов хорошо известна:

Пусть первый осциллятор соответствует частице D, второй . Пусть также частоты суть величины одного порядка, а связь между осцилляторами мала Наибольший интерес представляет тот случай, когда возбужденное состояние частицы А быстро релаксирует. Это означает, что обратная передача не имеет места. В классической модели этой ситуации соответствует существенно большее затухание второго осциллятора

. Решение системы (21.10) показывает тогда, что в соответствии с обычными положениями теории колебаний наличие связи между осцилляторами увеличивает затухание высокодобротного осциллятора.

Остановимся несколько подробнее на системе уравнений (21.10), хорошо изученной в теории колебаний. Решение этой системы было дано В. Вином еще в конце прошлого века и привело к таким важным понятиям, как собственные (нормальные) частоты колебаний, отличающиеся от парциальных частот в связанных системах со многими колебательными степенями свободы. Относительные амплитуды колебаний на собственных частотах первого и второго осцилляторов системы (21.10) и перекачка энергии из осциллятора в осциллятор определяются не только величиной связи осцилляторов , но и их связанностью и зависят от близости парциальных частот. Понятие связанности осцилляторов было введена Л. И. Мандельштамом при создании общей теории колебаний.

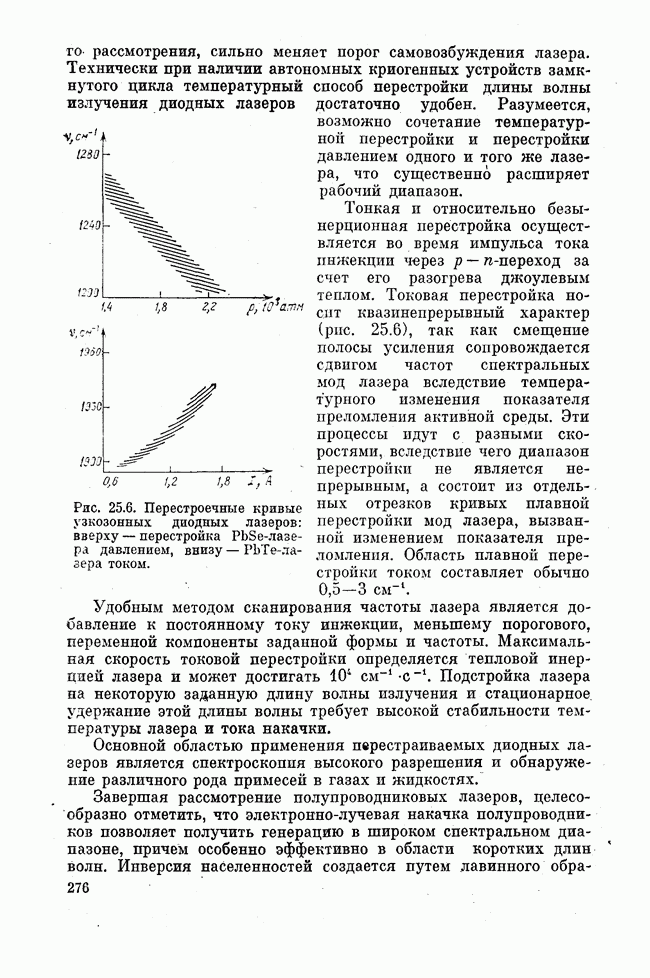
Рис. 21.4. Индуктивно связанные колебательные контуры.

Полное решение системы (21.10) сводится к решению уравнений четвертого порядка и плохо обозримо. Однако в приближении малой связи и малой связанности систему (21.10) легко решить с помощью эквивалентной схемы, представленной на рис. 21.4, уравнениям Кирхгофа которой для гармонических токов частоты со и амплитуд

соответствуют дифференциальные уравнения

(21.12)

Здесь M — взаимная индуктивность, — заряды на конденсаторах , а остальные обозначения ясны из рис. 21.4 (см. также формулы (6.48) — (6.56) и рис. 6.2).

Из (21.11) легко получить выражение для эффективного активного сопротивления некоторого эффективного одиночного контура, образованного системой двух индуктивно связанных RLC-контуров:

Тогда, считая связанность контуров малой и предполагая тем самым наличие в первом осцилляторе только одного гармонического колебания, мы можем соотношением ввести эффективное затухание первого контура при наличии связи со вторым Контуром по аналогии с парциальными коэффициентами затухания соответствующих контуров:

В схеме на рис. 21.4 коэффициенты связи второго контура с первым и первого со вторым составляют соответственно . Уравнения (21.10) и (21.12) отличаются друг от друга видом связи — по координате и ее второй производной соответственно. Эти связи эквивалентны друг другу, если . Для гармонического колебания , получаем тогда условие эквивалентности , что дает .

Рис. 21.5. К определению силы электростатического взаимодействия между двумя диполями.

Учитывая близость и к и считая малой разность мы получаем из (21.14) после тривиальной замены выражение

Рассмотрим, теперь коэффициент связи . Энергию электростатического взаимодействия двух диполей, находящихся на расстоянии R друг от друга, легко определить с помощью рис. 21.5. Дипольные моменты диполей 1 и 2 равны соответственно , где безразмерные множители называемые силами осцилляторов, характеризуют эффективность поляризуемости осцилляторов, образованных оптическим электроном (заряд —е) и ионным остовом (заряд ), разнесенными на расстояния соответственно. Тогда в среде с диэлектрической проницаемостью е энергия взаимодействия диполей равна

(21.16)

и при с точностью до члена порядка составляет

Следовательно, сила, действующая со стороны второго осциллятора на первый, равна

а со стороны первого на второй

Так как в правую часть уравнешш осциллятора в форме (21.10) должны входить вынуждающие силы (где — масса электрона), то очевидно, что

(21.18)

Подчеркнем, что для осциллирующих диполей выполненное выше вычисление справедливо в ближней зоне (при где К — длина волны излучения частоты в рассматриваемой среде).

Сила осциллятора в классической теории дисперсии понимается как доля элементарных осцилляторов, принимающих участие в макроскопической поляризуемости среды на частоте со. При квантовомеханическом рассмотрении силы осцилляторов определяют не как число электронов некоторого типа, а как число виртуальных осцилляторов, принадлежащих электрону, характеризующее эффективность образования диполя, так сказать, степень «дппольности» системы оптический электрон — ионный остов, на рассматриваемой частоте. Квантовая механика позволяет вычислить силу осциллятора заданной электронной системы, которая оказывается равной

(21.19)

где — коэффициент Эйнштейна для спонтанного перехода на частоте . Тогда в нашем случае

и мы получаем

(21.21)

где

Величина 2 в уравнениях (21.10) имеет смысл скорости релаксации интенсивности колебаний осциллятора. Следовательно, величина описывающая аддитивное увеличение скорости релаксации

одного осциллятора за счет потерь энергии в другом осцилляторе, связанном с первым, имеет смысл вероятности переноса энергии от донора к акцептору:

(21.22)

Формула (21.22) для. получена для осцилляторов, находящихся на фиксированных частотах . Но в пределах спектральных линий донора и акцептора частот много. Естественно считать, что форм-факторы линий дают распределение осцилляторов по частотам, или, иначе говоря, вероятность найти осциллятор D или А на той или иной частоте. Тогда вероятность одновременного нахождения донора на частоте и акцептора на частоте есть произведение Вероятность осуществления переноса энергии между ними составляет и определяется как значениями парциальных частот донора и акцептора, так и расстройкой между ними. Следовательно, полная вероятность переноса энергии в процессе дается интегралом по всем частотам и всем значениям расстройки

(21.23)

Так как резонансная кривая линии поглощения (излучения) акцептора значительно шире резонансного множителя то для всех отстроек можно считать, что

Тогда произведение в интегрировании по А не участвует, и мы, используя равенство

получаем окончательно, что

(21.24)

где учтена необходимость усреднения по ориентациям диполей, дающего коэффициент 2/3, и принят во внимание резонансный характер зависимости от частоты произведения , что позволило вынести из-под знака интеграла. Заметим, что

называется интегралом перекрытия.

Формула (21.24) может быть получена, как это уже отмечалось выше, в рамках теории возмущений первого порядка. Тот факт, что в получаемое при квантовомеханическом анализе выражение не входит постоянная Планка h, позволяет проводить классический анализ и вывод этой формулы. Следует подчерк-путь, однако, что запись в виде (21.24) позволяет обобщить результаты, полученные в дипольном приближении, на случай любой мультиполыюсти, учитываемой значениями коэффициентов Эйнштейна и . Все величины, входящие в (21.24), измеримы экспериментально. Так как (где — длина волны среде с показателем преломления ), а коэффициент Эйнштейна А определяет резонансное сечение поглощения (см. (3.19)), то (21.24) можно придать другой вид:

(21.25)

где — ширины линий резонансного поглощения донора и акцептора соответственно.

Итак, скорость переноса энергии от донора к акцептору определяется перекрытием спектров этих частиц и матричными элементами операторов их резонансных переходов. Коэффициенты Эйнштейна характеризуют способность донора и акцептора к взаимодействию, перекрытие спектров обеспечивает возможность этого взаимодействия. Электростатический характер взаимодействия осциллирующих диполей в ближней зоне выражается в сильной (вида ) зависимости скорости переноса от расстояния между ними. Для того чтобы отделить, пространственную зависимость от определяемой свойствами взаимодействующих частиц, в рассмотрение часто соотношением

(21.26)

вводится константа скорости переноса энергии .

Здесь следует отметить, что формула (21.24) описывает взаимодействие в паре донор — акцептор, расположенных на фиксированном расстоянии R. В действительности не приходится говорить о равных и фиксированных расстояниях между взаимодействующими частицами. Их распределение в кристалле, особенно при малом содержании активных центров в матрице, случайно, п. находятся они на различных расстояниях друг от друга. Поэтому макроскопическое описание переноса энергии по каналу требует усреднения по распределению соответствующего распределению расстояний между донорами и акцепторами и вычисляемого по хорошо известным правилам теории вероятности. Заметим, что среднее расстояние между акцепторами составляет где — плотность акцепторов.

В соответствии со сказанным распад доноров во времени оказывается пропорциональным

Для гауссова распределения акцепторов это приводит к зависимости вида

(21.27)

где результате временной ход интенсивности люминесценции доноров имеет вид

(21.28)

где — собственное время жизни доноров. Выражение (21.27) имеет простой физический смысл. Возбуждение каждого из доноров гибнет по экспоненциальному закону , однако для различных взаимодействующих пар различно в силу флуктуаций расстояний R, а сумма экспонент не есть экспонента.

В реальных кристаллах, кроме переноса энергии от доноров к акцепторам (-взаимодействие), играть существенную роль миграция энергии возбуждения в донорной подсистеме (-взаимодействие). Так как природа элементарного акта -взаимодействия та же, что и в случае -взаимодействия, то вероятность соответствующего процесса переноса энергии характеризуется величиной CBD, вводимой аналогично (21.26) соотношением

(21.29)

и определяемой формулами (21.24) или (21.25) с заменой индекса А на D.

Само по себе -взаимодействие не приводит к изменению населенности возбужденного состояния донорной подсистемы. Однако пространственные перемещения возбуждения изменяют эффективные расстояния взаимодействия донорной подсистемы в целом с акцепторной подсистемой. Следовательно, миграция возбуждения по донорной подсистеме влияет на полную скорость распада возбуждения. Это влияние в первом приближении мояет быть учтено введением в показатель экспоненциального распада дополнительного члена, пропорционального скорости миграции . Тогда, в отличие от (21.28), временной ход интенсивности люминесценции доноров характеризуется зависимостью вида

(21.30)

где — плотность доноров. Конкретный

вид функции определяется характером процессов миграции, и его рассмотрение в рамках нашего курса нецелесообразно. Заметим только, что возрастает с ростом

Таким образом, величины и , концентрации доноров и акцепторов определяют скорость гибели энергии возбуждения в коллективе взаимодействующих примесных центров. Проведенное раесмотрение позволяет ответить на вопросы, поставленные выше в начале рассмотрения ион-ионных взаимодействий, и определить оптимальные концентрации примесных центров донорного и акцепторного типов.

Действительно, например, для лазера непрерывного режима, для того чтобы избежать перегрева активной среды, необходимо обеспечить квантовый выход люминесценции, близкий к 100%. Это означает, что в экспоненте (21.30) доминирующим должен быть первый член:

(21.31)

Зная зависимости можно выбрать оптимальные концентрации примесных центров, обеспечивающие выполнение (21.31). Очевидно, что выполнение этого условия только за счет уменьшения нецелесообразно, так как последнее приводит к уменьшению удельного эпергосъема. Отметим, что полезное для рассматриваемого случая уменьшение значений и может быть достигнуто таким выбором матрицы, при котором малы интегралы перекрытия и соответствующие силы осцилляторов. На этом пути созданы новые лазерные среды, например такие, как пептафосфат неодима в которых удалось повысить концентрацию ионов неодима до значений, превышающих т. е. более чем на порядок по сравнению с традиционными лазерными кристаллами и стеклами.

В импульсном режиме характер требований меняется. В этом случае вся энергия возбуждения должна накапливаться верхним лазерным уровнем донорной подсистемы в течение всего импульса возбуяедения. Следовательно, некоторое эффективное время жизни по отношению к распаду (21.30) должно превышать длительность импульса накачки Это означает, в отличие от (21.31), что должно выполняться условие

(21.32)

В качестве примера укаясем литий-лантан-неодимовое фосфатное стекло, в котором концентрация ионов неодима существенно превышает допустимую для обычных лазерных стекол. Выполнение условия (21.32) обеспечено правильным выбором состава стекла.

Вернемся теперь к обсуждению свойств эрбиевого лазера трехмикрометрового диапазона. При рассмотрении электрон-фононной релаксации отмечалось, что время жизни финишного лазерного

уровня существенно превышает время жизни стартового уровня что приводит к режиму самоограничеиия генерации. Введение подходящих акцепторов, например ионов гольмия или тулия, обладающих состояниями, резонансными уровню эрбия, может привести к существенному сокращению времени жизни этого уровня. Если при этом удается изменить смысл неравенства (21.31) для уровня по отношению к собственному времени жизни уровня , т. е. если

(21.33)

то самоограничение генерации не возникает.

Наконец, явление переноса энергии может быть использовано для увеличения населенности верхнего лазерного уровня. Речь идет о хорошо известном явлении сенсибилизации люминесценции, при котором энергия возбуждающего излучения поглощается одними частицами (донорами), а излучается, другими (акцепторами). Естественно, что в этой ситуации именно акцепторы являются рабочей лазерной примесыо. Скорость сенсибилизирующего заселения определяется величинами и . Так как в схеме с сенсибилизацией донор и акцептор отношению к лазерному эффекту меняются местами, то очевидно, что условием эффективного непрерывного режима является условие (21.31), взятое в обратном смысле. В импульсном режиме необходимость накопления энергии акцептором требует превышения скорости передачи энергии не только над скоростью собственного распада донора , но и над скоростью распада акцептора . Если эти условия выполнены, то выигрыш в населенности верхнего лазерного уровня дается отношением

где — спектр излучения накачки, — сечения поглощения в полосах накачки донора и акцептора соответственно, а интегрирование проводится в областях накачки . Такое использование переноса энергии является одним из перспективных направлений твердотельной квантовой электроники.

Проведенное в этой лекции рассмотрение показывает ту важную роль, которую играют процессы безызлучательной релаксации и переноса энергии возбуждения в активных средах твердотельных лазеров.

В заключение подчеркнем еще раз глубокую аналогию, существующую между релаксационными процессами в системе примесных центров твердого тела (электрон-фононное и диполь-дипольное взаимодействия) и столкновительной релаксацией в газах -релаксации),