Лекция девятнадцатая. ВСПОМОГАТЕЛЬНОЕ ИЗЛУЧЕНИЕ НАКАЧКИ В СИСТЕМАХ СО МНОГИМИ УРОВНЯМИ ЭНЕРГИИ

Лазеры на конденсированных средах со многими уровнями энергии. Метод вспомогательного излучения накачки. Трех- и четырехуровневые схемы. Безызлучателъная релаксация в твердом теле. Матрица лазера на твердом теле. Рубин. Электронные конфигурации атомов и ионов переходных групп. Основные состояния трехвалентных ионов хрома и неодима.

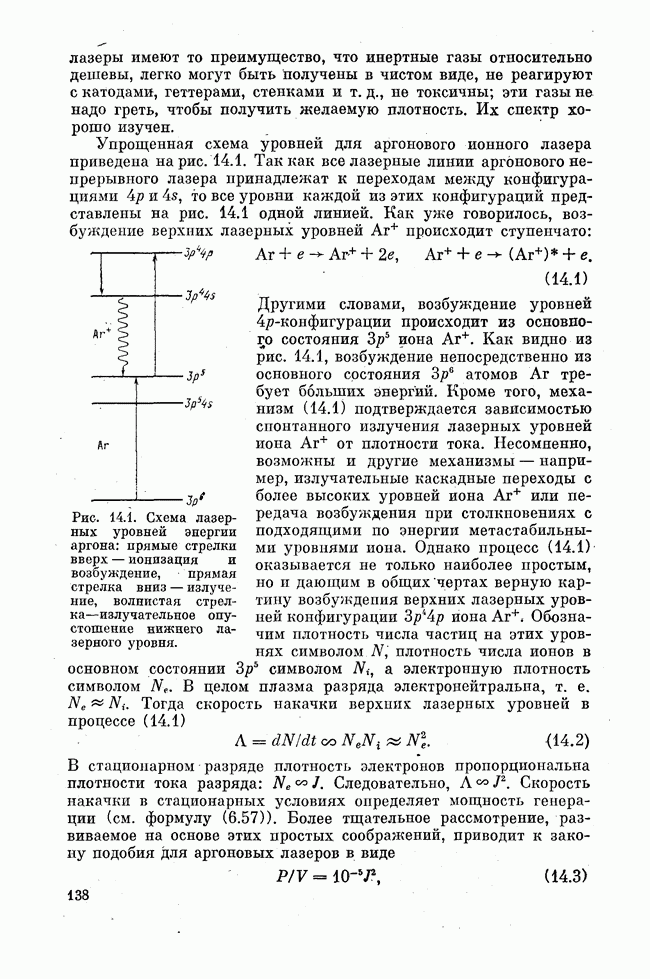
При переходе от газов к конденсированным средам вообще и к твердому телу, в частности прежде всего обращает на себя внимание резкое (в раз) увеличение плотности инверсии. Следовательно, в случае создания активной среды в конденсированной фазе возможна существенно большая плотность инверсии и тем самым большая энергия излучения. Но для твердого тела не представляется возможной реализация всех тех методов создания активной среды, которые характерны для газов (см. лекцию тринадцатую) и которые основаны, по существу, на явлениях переноса зарядов и частиц в среде или организации неравновесных потоков среды.

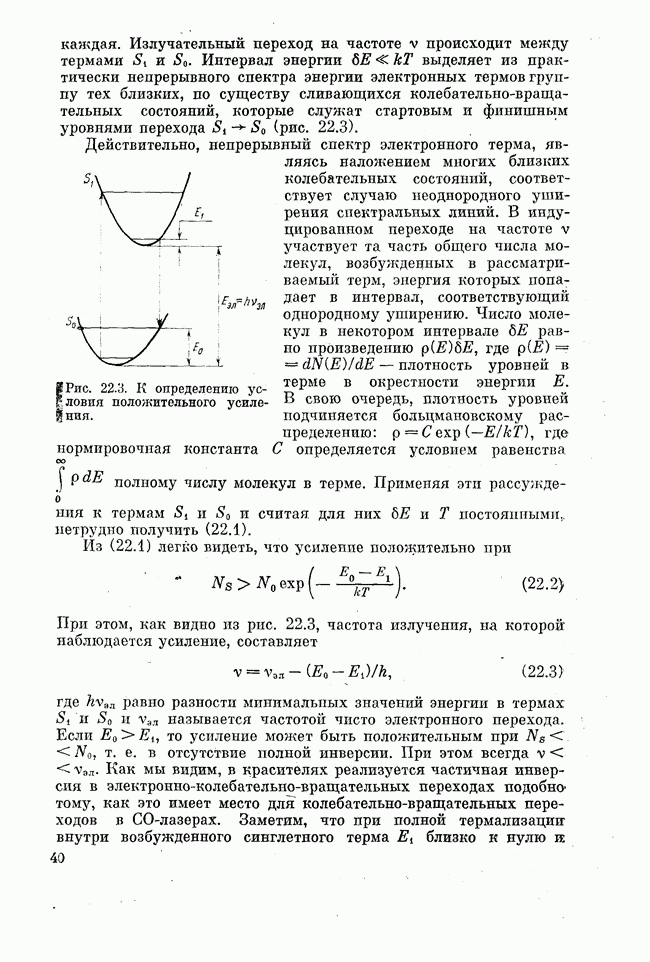
В случае диэлектрика практически единственным способом воздействия на твердое тело, не приводящим к его разрушению, но могущим нарушить термодинамическое равновесие в нем, причем в большом объеме, является облучение тела светом. При наличии проводимости возможно пропускание электрического тока, но об этом — позднее, при рассмотрении полупроводниковых лазеров. Наличие в твердом теле широких полос поглощения приводит к возможности поглощения облучаемым образцом большой энергии при использовании интенсивных источников немонохроматического света. Следовательно, если, вообще говоря, прозрачный диэлектрик содержит некоторые примесные центры, создающие в нем подходящую систему уровней энергии, то инверсия населенностей в этой системе уровней может быть создана только путем поглощения энергии света в ней. При этом принципиальным здесь является наличие по крайней мере трех уровней энергии. Суть дела здесь состоит в следующем.

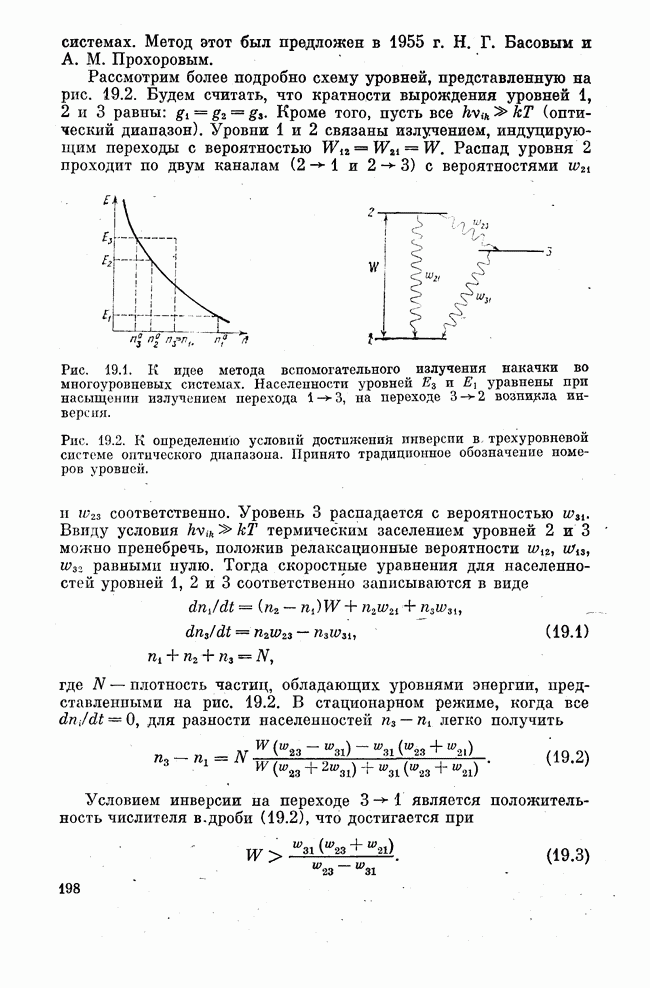
Как мы знаем, достаточно интенсивное резонансное излучение может существенно, вплоть до насыщения, изменять распределение населенностей между уровнями, связанными излучением. Населенность верхнего уровня увеличивается, нижнего — уменьшается. Если на шкале энергий между этими двумя уровнями лежит какой-то третий нерезонансный уровень, то возмояшо возникновение инверсии на переходе, для которого этот уровень является либо верхним, либо нижним. Рис. 19.1 иллюстрирует сказанное, поясняя в упрощенной форме идею метода вспомогательного излучения накачки для создания активной среды во многоуровневых

системах. Метод этот был предложен в 1955 г. Н. Г. Басовым и А. М. Прохоровым.

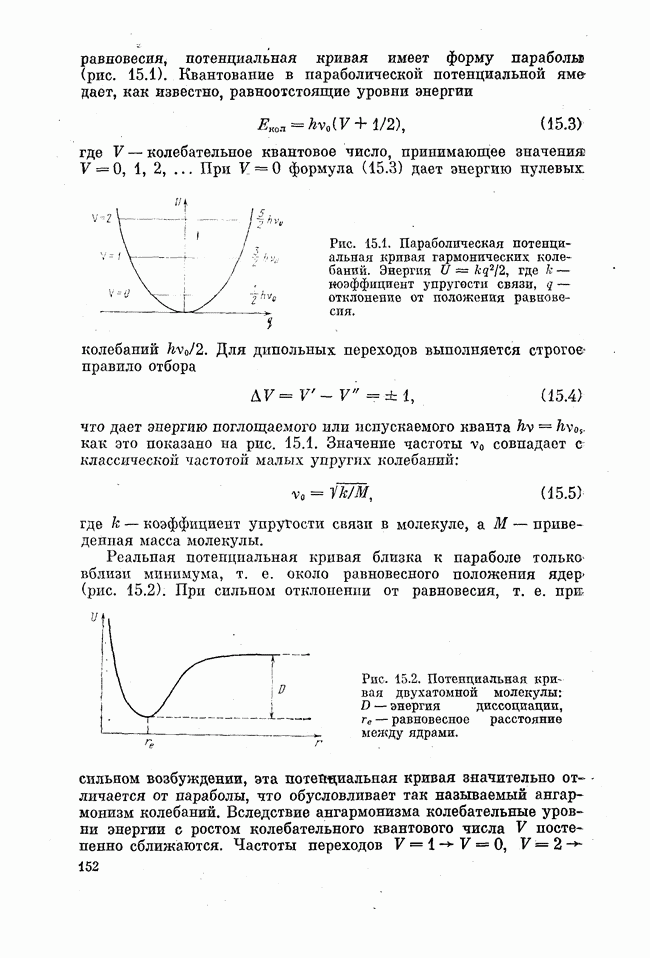
Рассмотрим более подробно схему уровней, представленную на рис. 19.2. Будем считать, что кратности вырождения уровней 1, 2 и 3 равны: . Кроме того, пусть все (оптический диапазон). Уровни 1 и 2 связаны излучением, индуцирующим переходы с вероятностью Распад уровня 2 проходит по двум каналам с вероятностями и соответственно. Уровень 3 распадается с вероятностью

Рис. 19.1, К идее метода вспомогательного излучения накачки во многоуровневых системах. Населенности уровней и уравнены при насыщении излучением перехода на переходе возникла инверсия.

Рис. 19.2. К определению условий достижения инверсии в. трехуровневой системе оптического диапазона. Принято традиционное обозначение номеров уровней.

Ввиду условия термическим заселением уровней 2 и 3 можно пренебречь, положив релаксационные вероятности равными пулю. Тогда скоростные уравнения для населенностей уровней 1, 2 и 3 соответственно записываются в виде

(19.1)

где N — плотность частиц, обладающих уровнями энергии, представленными на рис. 19.2. В стационарном режиме, когда все для разности населенностей легко получить

Условием инверсии на переходе является положительность числителя в дроби (19.2), что достигается при

Выполнение неравенства (19.3) возможно только при

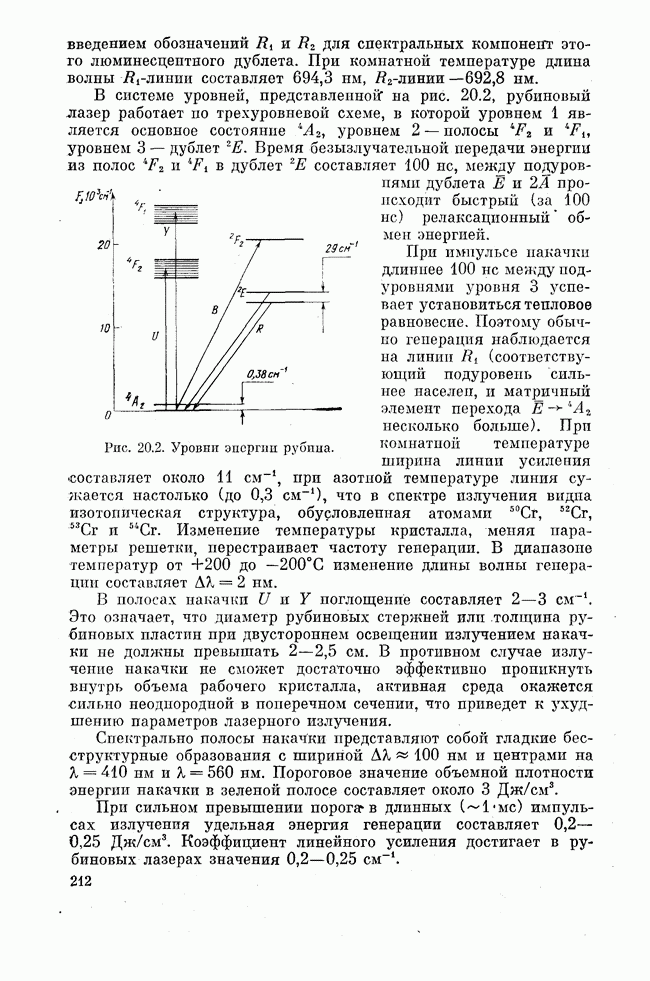
Смысл последнего условия ясен: в процессе безызлучательных переходов верхний уровень должен населяться быстрее, чем опустошаться. Забегая вперед, следует сказать, что схема уровней на рис. 19.2 и скоростные уравнения (19.1) соответствуют рубиновому лазеру. Для рубина уровень 3 является метастабильным, а для вероятностей безызлучательных переходов выполняется неравенство

Тогда условие инверсии приобретает вид

Смысл этого условия прост: если с верхнего непосредственно накачиваемого уровня частицы поступают на метастабильный уровень значительно быстрее, чем стекают с него , то инверсия создается и удерживается, если верхний уровень накачивается быстрее, чем опустошается метастабильный уровень. В этих условиях разность населенностей составляет

и при стремится к N, что, конечно, как правило, не реализуется.

Так как в рассматриваемой трехуровневой схеме инверсия создается по отношению к основному состоянию, то возникает она не сразу после включения накачки. Частицы должны накопиться на метастабильном уровне под действием накачки в течение некоторого конечного времени . Для ответа на вопрос о том, когда разность станет положительной, необходима рассмотреть переходные процессы, т. е. решить систему дифференциальных уравнений (19.1). Не рассматривая общее решение, обратимся к рубиновому лазеру. В этом случае вероятность безызлучательного перехода является наибольшей из всех скоростей процессов, определяющих распределение частиц по уровням энергии 1, 2 и 3. Для рубина не только выполняется условие (19.5), но и при всех разумных интенсивностях накачки

Это означает, что на резонансном уровне 2 частицы не накапливаются, их там нет, так как они сразу же передаются на метастабильный уровень 3. В лазерном цикл накачки, показанном на рис. 19.2, уровень 2 играет роль посредника, передающего энергию возбуждения верхнему лазерному уровню 3, подобно тому как это делает азот в -лазере. Тогда, полагая и, следовательно,

считая мы сводим систему (19.1) к одному уравнению первого порядка:

(19.9)

Отсюда легко получается уравнение для инверсии :

(19.10)

При начальном условии решение этого уравнения имеет вид

что при , как и следовало ожидать, переходит в (19.7). При записи и дальнейшем анализе выражения (19.11) предполагается, что накачка включается в момент t = 0 и остается в дальнейшем неизменной. Временной ход относительной инверсии показан на рис. 19.3.

Рис. 19.3. Временной ход относительной инверсии в трехуровневой схеме при скорости накачки W, включаемой в момент t = 0.

Время просветления рабочего перехода легко определяется из (19.11) приравниванием нулю:

В практически недостижимом случае максимальной инверсии произведение постоянно:

(19.13)

Так как вероятность индуцированных переходов накачки пропорциональна интенсивности накачки, то это произведение определяет максимальную энергию, необходимую для приведения системы в состояние с отрицательным поглощением. В общем случае

Постоянство произведения при больших интенсивностях накачки, когда влиянием всех релаксационных процессов можно пренебречь, имеет простой физический смысл: это произведение Пропорционально энергии, необходимой для перевода всех частиц

из основного состояния на верхний лазерный уровень (см. формулу (19.7) и рис. 19.3).

Целесообразно подчеркнуть еще раз, что необходимость предварительной затраты энергии при создании инверсии населенностей метастабильного уровня по отношению к основному состоянию в оптической трехуровневой системе обусловлена тем, что приходится переводить с уровня 1 через уровень 2 на уровень 3 по крайней мере половину всех частиц. Инверсия в трехуровневой схеме создается по отношению к хорошо заселенному основному состоянию. Поэтому представляют большой интерес схемы, в которых оптическая накачка создает инверсию по отношению к незаселенному термически уровню, как это происходит, например, в газовых лазерах при возбуждении электронным ударом. Это может быть сделано с помощью четырехуровневой системы.

Рис. 19.4 Четырехуровневая схема.

Выпишем скоростные уравнения для населенностей в системе уровней энергии, представленной на рис. 19.4. Будем учитывать безызлучательные переходы, идущие только сверху вниз. Тогда

Рассмотрим условия получения стационарной инверсии на переходе . Подчеркнем, что уравнения (19.15) записаны в предположении отсутствия термического заселения уровня 4 (а тем самым всех остальных более высоко расположенных). Введя обозначение и выполняя несложные алгебраические преобразования, из (19.15) можно получить, что х > 0 при

Это условие инверсии качественно отличается от трехуровневого случая (см. (19.3)) тем, что оно не зависит от W. Коль скоро выполнено неравенство (19.16), всегда . Обычно (ср. с (19.5))

Тогда условие инверсии принимает простой вид:

смысл которого ясен: нижний лазерный уровень должен опустошаться за счет безызлучательных переходов в основное состояние быстрее, чем заселяться переходами с верхнего лазерного уровня. Благоприятное инверсии условие (19.17) означает, что канал безызлучательного заселения верхнего лазерного уровня переходами является наиболее эффективным релаксационным процессом в этой схеме уровней.

Обратимся теперь к вопросу об отсутствии порога по накачке в создании инверсии в четырехуровневой схеме в отличие от трехуровневой. Дело в том, что в скоростных уравнениях (19.15) мы пренебрегли вероятностью безызлучательного заселения нижнего уровня . Но эта величина не равна нулю тождественно. При энергии уровня величина экспоненциально мала по сравнению с (см. формулу (3.25)), но конечна. В отсутствие накачки на уровне 4 есть немного частиц. Они-то и дают порог возникновения инверсии по накачке, тем более низкий, чем сильнее выполняется неравенство . По существу, последнее неравенство является условием применимости проведенного выше рассмотрения и критерием четырехуровневого характера рассматриваемой системы. Нагрев может свести четырехуровневую систему к трехуровневой с соответствующим резким возрастанием порога. Итак, порог возникновения инверсии по накачке мал, когда нижний уровень лазерного перехода расположен выше основного состояния на

(19.19)

В соответствии с проведенным рассмотрением оказывается, что стационарная инверсия в четырехуровневой схеме существенно иначе зависит от интенсивности накачки, чем в случае трехуровневой схемы. Из (19.15) в предположении выполнения условия (19.17) получается, что

Из этой формулы видна пропорциональность инверсии интенсивности накачки при 3, что характерно для реальной ситуации, и очевидно условие инверсии (19.18), не зависящее от интенсивности накачки. Именно это все в целом качественно отличает четырехуровневую схему от трехуровневой (см. (19.7)). При инверсия .

Итак, из рассмотренных примеров видно, как вспомогательное излучение накачки, существенно меняя распределение населенностей между уровнями вспомогательного перехода, приводит к возникновению инверсии населенностей между уровнями, связанными со вспомогательными уровнями безызлучательными переходами. Метод радиационной накачки во многоуровневых системах оказался очень мощным и достаточно общим методом создания активных сред. Мы неоднократно будем к нему обращаться в нашем

дальнейшем изложении. Отметим здесь только, что в квантовой электронике радиодиапазона этот метод успешно применяется для создания усилительных устройств предельно высокой чувствительности (парамагнитные СВЧ мазеры).

Остановимся теперь еще на одном важном обстоятельстве. Во всем нашем рассмотрении метода вспомогательного излучения накачки существенную роль играют вероятности безызлучательных переходов . В лекции второй мы феноменологически ввели понятие безызлучательной релаксации, обусловленной взаимодействием активного центра с окружающей его средой и неотвратимо приводящей неравновесно возбужденный центр к равновесию с окружением. Было отмечено, что конкретный механизм такого взаимодействия сильно зависит от вида рассматриваемой системы. В случае газовых лазеров доминирующим, практически единственным механизмом безызлучательной передачи энергии возбуждения являются газокинетические столкновения. Роль столкновительной передачи энергии была подробно обсуждена в нескольких предыдущих лекциях. В твердом теле столкновения частиц друг с другом исключены. Но остается взаимодействие с фононами, т. е. с колебаниями решетки. Активные центры, обычно ионы, диссипируют свою избыточную энергию в колебательный резервуар кристаллической решетки твердого тела, играющий роль того термостата, в который погружены активные центры. Микромеханизмы взаимодействия центров с фононами различны для различных состояний различных центров в разных кристаллах. Но в грубом приближении суть дела здесь одна: обмен энергией происходит в дипольном взаимодействии того или иного порядка между заданным электронным или электронно-колебательным состоянием активного центра и электрическими диполями, возникающими при колебаниях атомов решетки твердого тела.

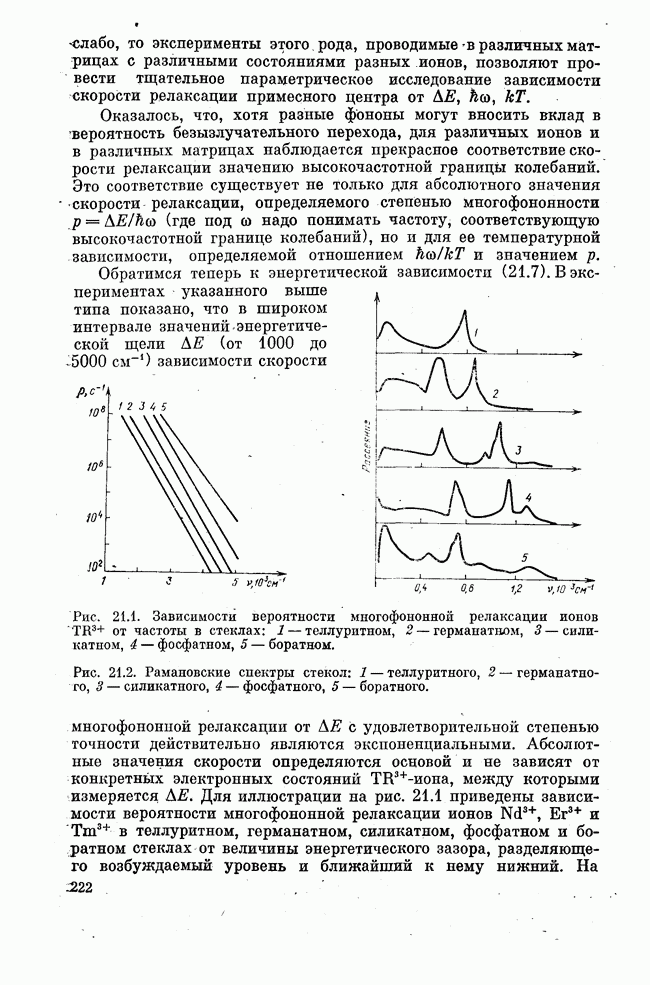
Обычно энергия фононов не превышает . Энергия электронных состояний в десятки раз выше. Поэтому релаксация энергии активных центров в колебания решетки является многофононным процессом, т. е. в единичном акте релаксации рояедается одновременно много фононов. Вероятность такого процесса падает с ростом степени фононности, т. е. отношения энергии релаксирующего состояния к энергии самого высокочастотного из возможных в рассматриваемом твердом теле фонона. (Как известно, частота такого фонона связана с температурой Дебая простым соотношением: .) Это приводит к тому, что, как правило, более высоко расположенные уровни энергии активного центра непосредственно в решетку релаксируют медленнее, чем уровни, расположенные ниже. Как мы знаем, это обстоятельство благоприятно созданию инверсии.

Кроме безызлучательной релаксации энергии примесного центра в колебания решетки, в рассматриваемых выше случаях трех- и четырехуровневых схем, описываемых вероятностями , существенную роль играет, как мы видели, безызлучательная

передача энергии от одного возбужденного уровня одного центра другому возбужденному уровню другого центра ( в тех же случаях). Если дефицит энергии между уровнями мал по сравнению с , то передача энергии происходит эффективно в диполь-дипольном взаимодействии. При наличии заметного дефицита энергии, а именно этот случай сейчас интересен для нас, только бинарное межцентровое диполь-дипольное взаимодействие не может обеспечить эффективную передачу энергии. В процесс передачи вовлекаются фононы как третье «тело». Взаимодействие становится тринарным, и дефицит энергии в процессе многофононной релаксации уходит в колебания решетки, нагревая тем самым твердое тело как целое.

Степень фононности определяется отношением дефицита энергии к энергии принимающих участие в этом процессе фононов. Нас интересует передача энергии с непосредственно возбуждаемого на верхний лазерный уровень. Чем ближе этот уровень к возбуждаемому, тем меньше степень фононности и тем более эффективна передача энергии. Очевидно также, что при этом меньшая доля энергии возбуждения тратится на паразитный нагрев среды. Кроме того, меньшая степень фононности обсуждаемого процесса объясняет, почему в рассмотренных выше случаях вероятность безызлучательной передачи энергии может быть самой большой из всех входящих в уравнения (19.1) и (19.15) вероятностей .

Заметим в заключение, что из проведенного описательного рассмотрения видна глубокая аналогия между процессами безызлучательной релаксации активных центров и передачи энергии возбуждения между ними в твердом теле и при газокинетических столкновениях в газах и плазме.

Обратимся теперь непосредственно к рассмотрению лазеров на твердом теле, или, как их иногда иначе называют, твердотельных лазеров. По сложившейся традиции к ним относят лазеры, активное вещество которых представляет собой твердый диэлектрик — кристалл или стекло, в который как изоморфные примеси введены активные центры. Традиция, как всякая традиция, непоследовательна. Полупроводниковый кристалл является твердым телом в существенно большей степени, чем стекло, — аморфное тело типа переохлажденной жидкости. Тем не менее полупроводниковые лазеры представляют собой отдельный класс. лазерных систем, главным образом в силу специфики накачки их активной среды, а лазеры на твердом теле — это лазеры на диэлектрических кристаллах и стеклах.

Итак, активная среда лазеров на твердом теле — это некая матрица, содержащая активные центры или совокупность центров разного вида как примесь-активатор. Легко сформулировать ряд очевцдных требований к матрицам лазерных активных элементов. Прежде всего, матрица должна легко активироваться, т. е. активная примесь должна легко и однородно входить в матрицу

в регулируемых количествах, не нарушая при этом оптических и механических свойств матрицы. Кроме того, значения вероятностей безызлучательных релаксационных переходов для вводимых в матрицу примесных центров должны быть благоприятны для получения инверсии.

Далее. Матрица должна быть оптически однородной и прозрачной для генерируемого (усиливаемого) излучения и для излучения накачки. В мощных лазерах активная среда подвергается интенсивному лучевому воздействию. Заметпая доля энергии этого воздействия превращается в тепло. Поэтому материал матрицы должен обладать высокой теплопроводностью, матрица должна быть термостойкой и термооптически стойкой, т. е. ее оптические параметры должны возможно более слабо изменяться при нагреве. Очевидным является требование механической, химической стойкости матрицы. Кроме того, матрица дрлжна быть оптически и фотохимически стойкой по отношению к воздействию как можно более интенсивных световых потоков импульсного и непрерывного режимов в спектральных диапазонах излучения накачки и генерации (усиления).

В заключение следует подчеркнуть, что матрица активного элемента лазера на твердом теле должна быть технологичной в изготовлении и оптической обработке.

К настоящему времени осуществлены лазеры более чем на 250 кристаллах и на многих десятках типов стекол.

Замечательным примером является рубиновый лазер — первый лазер, реализованный в 1960 г. Т. Мейманом. Его активным веществом является рубин — твердый раствор . Чистые, т. е. беспримесные кристаллы -модификаций корунда называются лейкосапфиром. Они прозрачны в широком диапазоне длин волн от вакуумного УФ до 5—6 мкм. В бытовом рубине концентрация ионов хрома достигает нескольких процентов, что придает кристаллам красивый глубоконасыщепнып темно красгтый цвет. Лазерные кристаллы содержат около 0,05% ионов — так называемый бледно-розовый рубин. Абсолютная концентрация ионов хрома составляет при этом .

Синтез и рост кристаллов рубина осуществляется обычно методом Вернейля — плавлением порошкообразной пасты в высокотемпературном пламени и последующей кристаллизацией на вращающейся затравке. Разработана технология выращивания больших образцов (диаметром 20-25 мм. длиной 250—300 мм), возможно изготовление плоских и сложнофигуpных образцов большого размера.

Корунд обладает прекрасными механическими, тепловыми, диэлектрическими и оптическими свойствами. Для него характерна высокая теплопроводность — при температурах 300—400 К только на порядок меньшая, чем у металлов, и близкая к металлической теплопроводность при гелиевых температурах. Кристалл «обладает ромбоэдрической симметрией, ось третьего порядка совпадает

с оптической осью кристалла (осью с). Для обыкновенной волны показатель преломления равен 1,769, для необыкновенной 1,760 (-линия натрия).

Применение рубина в квантовой электронике было предложено А. М. Прохоровым в 1956 г. (парамагнитные мазеры — квантовые усилители СВЧ).

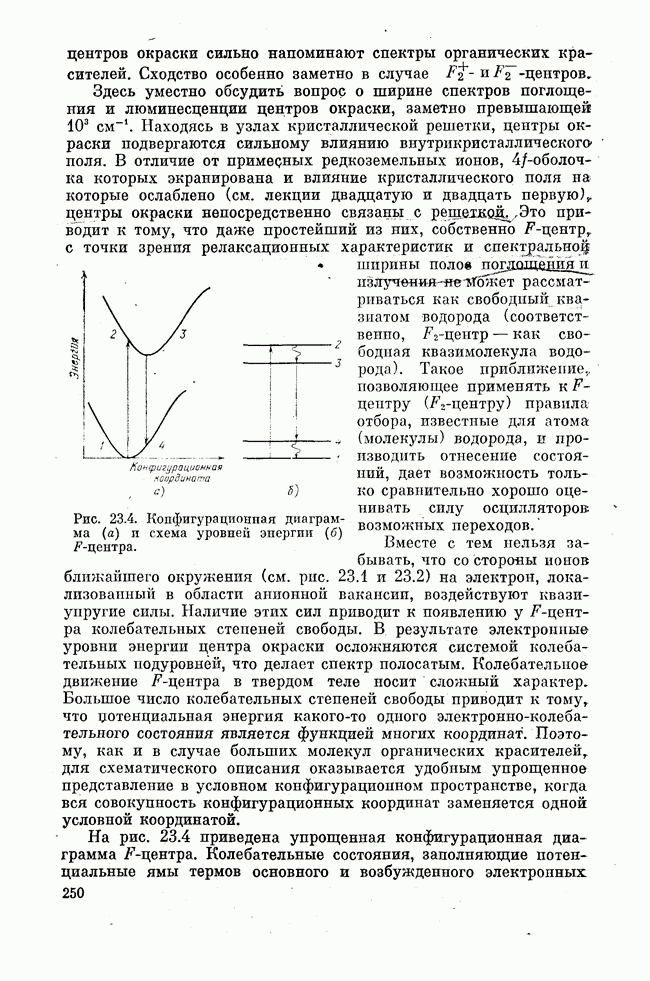
В кристаллах рубина, т. е. хромового корунда, ионы хрома являются активными примесными центрами. В решетке ионы изоморфно замещают ионы , так что они окружены шестью ионами образующими октаэдр. Это ближайшее окта-эдрическое окружение создает сильное электрическое поле, которое существенно влияет на уровень энергии иона . Более удаленные ионы влияют слабее. Таким образом, мы пришли к важному вопросу о спектре примесных ионов в кристаллах.

Активными примесями в кристаллах, используемых в квантовой электронике, являются те или иные ионы элементов переходных групп. Особенностью атомов этих групп является наличие внутренних частично заполненных электронных оболочек. В периодической системе элементов имеется пять переходных групп — группы железа, палладия, редкоземельных элементов, платины и актинидов.

В главных группах элементов заполнение электронных оболочек происходит в строгой последовательности — для каждого главного квантового числа сначала заполняется s-оболочка, затем -оболочка. При заполнении -оболочки этот строгий порядок нарушается. Заполнение -оболочки идет в конкуренции с заполнением -оболочки следующего главного квантового числа, т. е. -оболочка конкурирует с оболочками . В группах железа, палладия, платины заполняются оболочки соответственно. Еще более сложно идет заполнение 4 оболочки редкоземельных атомов, конкурирующей с оболочками

Не выписывая все элементы переходных групп, для иллюстрации приведем электронные конфигурации нескольких элементов; групп железа и группы редких земель:

Примесные кристаллы и стекла, используемые в квантовой электронике, включают в себя примеси тех или иных элементов; не в виде нейтральных атомов, а в виде ионов. При новообразовании электронные конфигурации и состояния ионов переходных, групп строятся не так просто, как в рядах элементов главных групп. Так как для переходных элементов строгая закономерность, заполнения оболочек нарушена, то, вообще говоря, исчезает полное подобие иона последующего элемента атому предыдущего

Рубин, как уже говорилось, — это твердый раствор т. е. в рубин входит трехвалентный ион . Конфигурация нейтрального атома дает для трехвалентного иона хрома конфигурацию . Таким образом, спектр обусловлен тремя -электронами. Здесь целесообразно обсудить важное обстоятельство.

В переходных элементах группы железа заполняется внутренняя оболочка , которая экранируется внешней -оболочкой. Оптические и химические свойства этих элементов в значительной степени определяются застраивающейся -оболочкой и в силу ее экранированности в какой-то мере одинаковы в тех ситуациях, когда с внешним окружением взаимодействует нейтральный атом. Трехвалентные ионы этих атомов теряют экранирующую оболочку. Поэтому спектры этих ионов, изоморфно внедренных в какие-либо кристаллические матрицы, отнюдь не подобны друг другу, отличаются от спектров свободных ионов и различны для одних и тех же ионов, введенных в различные матрицы.

Кардинально другой является ситуация для переходных элементов группы редких земель. Оптические и химические свойства редкоземельных элементов определяются гораздо более глубоко экранированной -оболочкой. Конфигурация атома аргона, входящая символом в приведенные в (19.21) конфигурации переходных элементов атомов группы железа, относительно проста. Она записывается как и не содержит электронов с главными квантовыми чцслами, большими, чем у застраивающейся оболочки и экранирующей ее Это естественно, так как группа железа является первой по порядку возрастания атомного номера переходной группой в таблице Менделеева. Редкоземельным элементам предшествует ксенон. Этот тяжелый атом гораздо более сложен. Его конфигурация содержит, кроме конфигураций всех предшествующих ему атомов благородных газов (гелия, неона, аргона, криптона), также и -электроны и может быть записана в виде . Следовательно, застраивающаяся оболочка элементов группы редких земель экранируется дополнительно двумя и шестью -электронами. Глубокая экранировка -оболочки объясняет близость химических свойств элементов редких земель и подобие их спектров. В трехвалентных ионах редкоземельных элементов -оболочка остается экранированной теми же двумя и шестью -электронами. В результате внешнее воздействие слабо влияет на спектры не только нейтральных атомов, но и ионов элементов этой группы. При внедрении трехвалентных редкоземельных ионов в различные кристаллические матрицы спектры ионов практически не изменяются. Это относится к представляющему для пас большой интерес иону спектр которого обусловлен тремя -электронами

Взаимодействие -электропов иона и -электронов иона с электрическими полями их окружения в матрицах активных

лазерных материалов определяет схему уровней соответствующих лазеров.

Основные состояния свободных ионов определяются правилом Хунда — в заданной электронной конфигурации то состояние имеет наименьшую энергию, для которого реализуется наибольшее из возможных значений суммарного спнна S и наибольшее (из возможных при данном значении S) значение орбитального момента , где k — число электронов в оболочке, заполненной менее чем наполовину. В случае , т. е. трех -электроиов, максимальное значение . Так как , то терм обозначается буквой F. Его мультиплетность . Это означает, что квантовое число может принимать четыре значения от до . Если оболочка заполнена менее чем наполовину, то основное состояние имеет . (В противном случае ) В d-оболочке может быть десять электронов, следовательно, в ионе застраиваемая оболочка заселена менее чем наполовину. Значит, у этого иона в основном состоянии . В результате мы получаем, что основное состояние иона записывается как

(19.22)

Аналогично, ион имеющий три электрона из четырнадцати возможных в застраивающейся в группе редких земель -оболочке, по правилу Хунда в основном состоянии имеет , и его основное состояние записывается как

(19.23)

Однако для твердотельных лазеров основные состояния свободных ионов интересны лишь в той мере, в какой они определяют характер и силу взаимодействия иона с кристаллическими полями содержащей ион матрицы.