| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
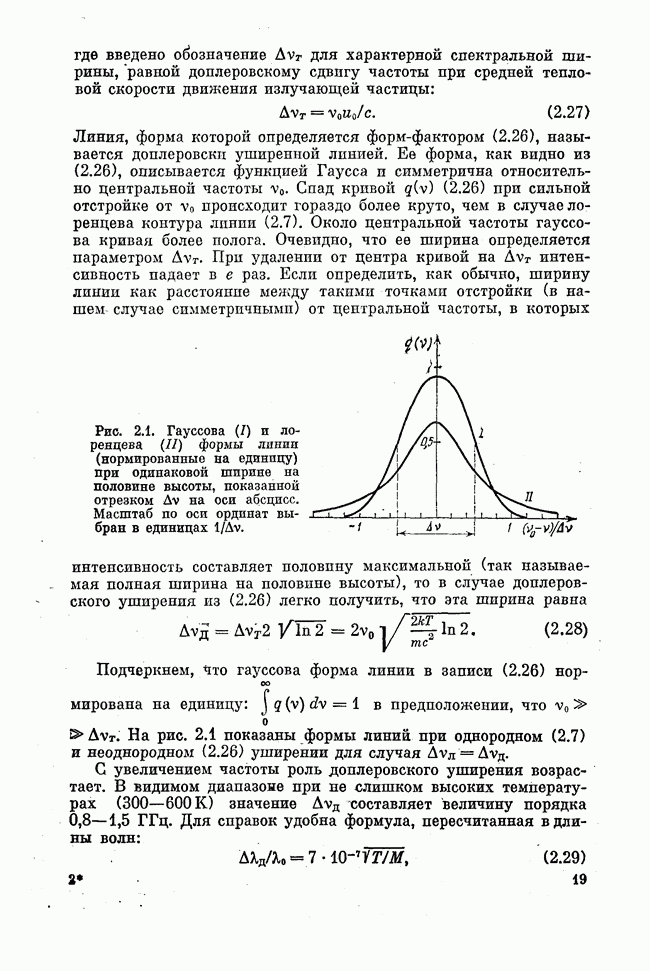
Лекция восьмая. ГАУССОВЫ ПУЧКИ
Конфокальный резонатор. Распределение поля. Гауссовы пучки. Размер пятна. Расходимость излучения. Радиус кривизны волнового фронта. Преобразование гауссовых пучков линзой. Согласование мод резонаторов. Фокусирование гауссовых пучков. Продольный и поперечный размеры фокальной области.
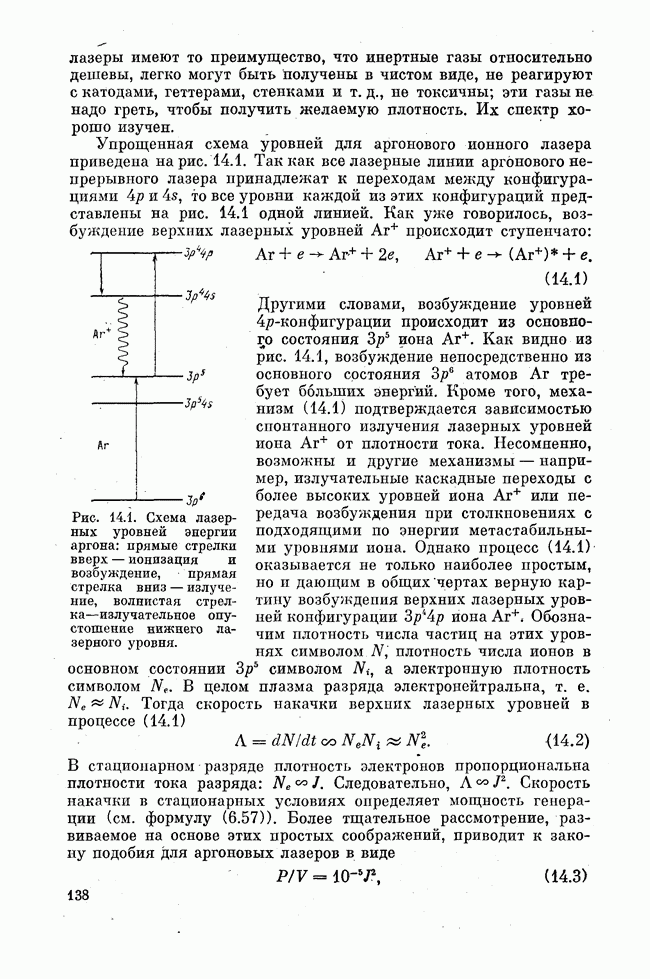
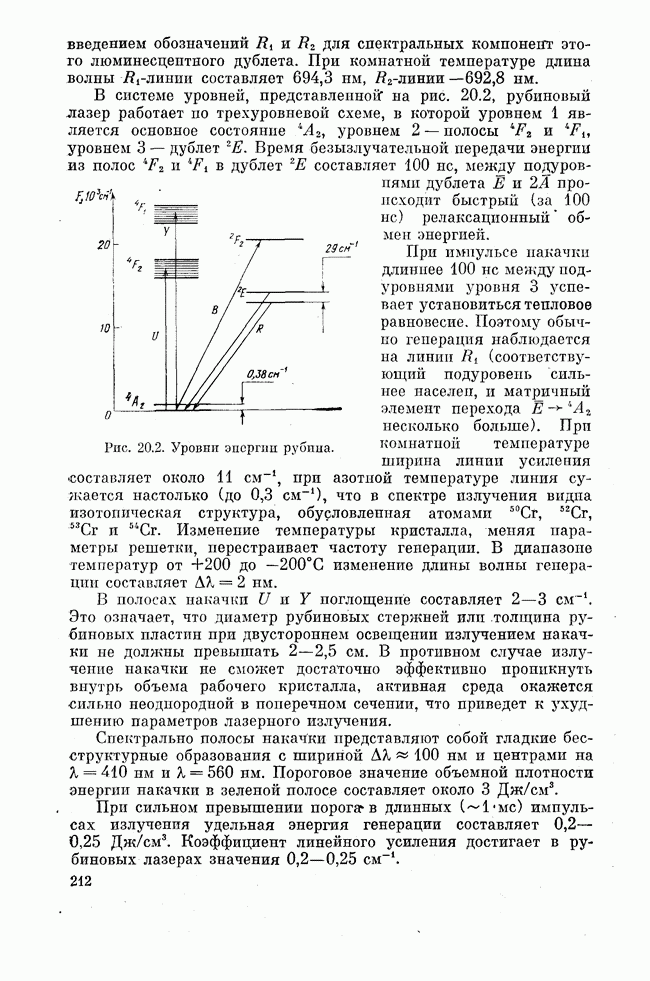
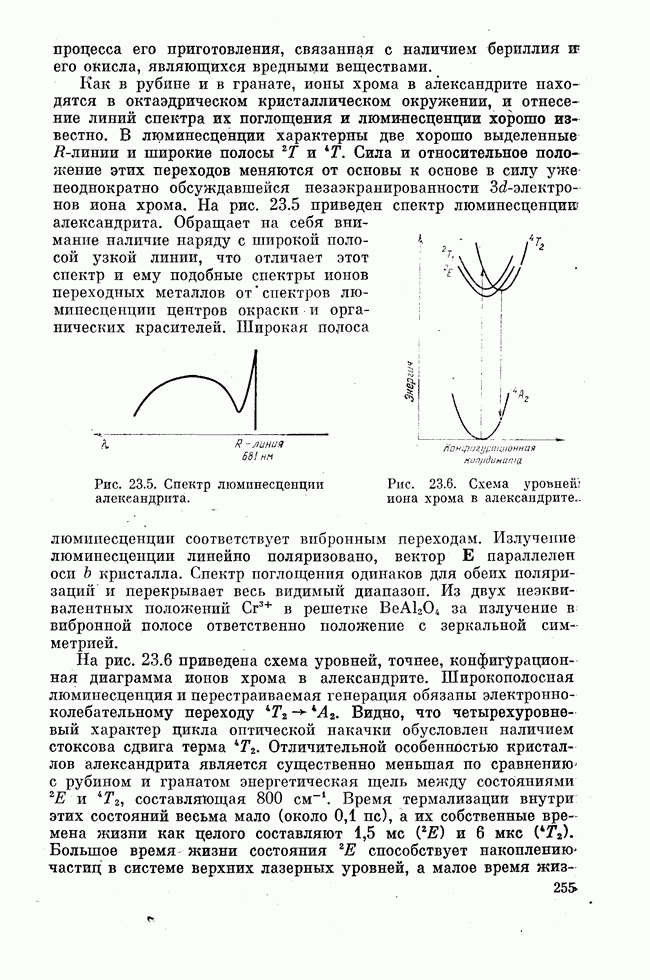
Итак, анализ Фокса и Ли показал, что в открытых структурах типа интерферометров Фабри — Перо существуют характерные колебательные моды. К настоящему времени известно большое число модификаций открытых резонаторов, отличающихся друг от друга конфигурацией и взаимным расположением зеркал. Наибольшей простотой и удобством отличается резонатор, образованный двумя сферическими отражателями с равной кривизной, обращенными вогнутыми поверхностями навстречу друг другу и расположенными на расстоянии радиуса кривизны, равного радиусу сфер, друг от друга. Фокусное расстояние сферического зеркала равно половине его радиуса кривизны.

Рис. 8.1. Схема конфокального резонатора. Плоскость ху перпендикулярна оси z. Конфокальная точка находится в начале координат О.
Поэтому фокусы отражателей совпадают, вследствие чего резонатор называется конфокальным (рис. 8.1). Интерес к конфокальному резонатору обусловлен удобством его юстировки, в отличие от плоскопараллельного резонатора Фабри — Перо не требующей строгой параллельности отражателей друг другу. Необходимо лишь, чтобы ось конфокального резонатора пересекала каждый отражатель достаточно далеко от его края. В противном случае дифракционные потери могут быть слишком большими.
Рассмотрим конфокальный резонатор более подробно. Пусть все размеры резонатора велики по сравнению с длиной волны. Тогда моды резонатора, распределение полей в нем и дифракционные потери можно получить на основе принципа Гюйгенса — Френеля путем решения соответствующего интегрального уравнения. Для сферических зеркал с прямоугольной или круглой
апертурой это интегральное уравнение допускает разделение переменных относительно поперечных координат и сводится к одномерным интегральным уравнениям. Если отражатели конфокального резонатора имеют квадратное сечение со стороной 2а, которая мала по сравнению с расстоянием между зеркалами l, равным их радиусу кривизны R, а числа Френеля велики, то собственные функции интегрального уравнения типа Фокса и Ли аппроксимируются произведениями полиномов Эрмита  на гауссову функцию
на гауссову функцию  .
.

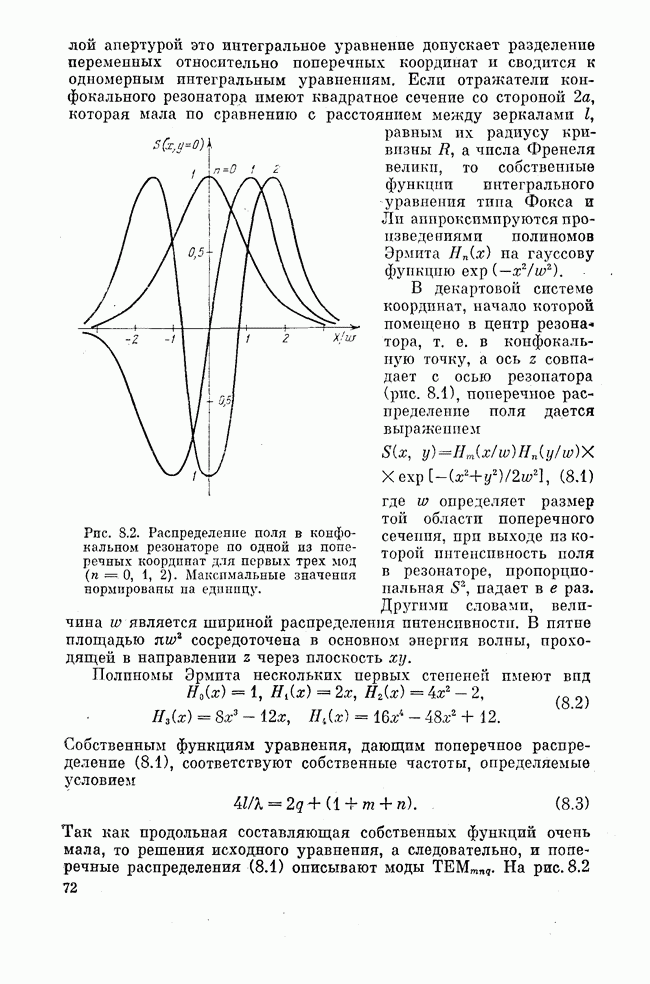
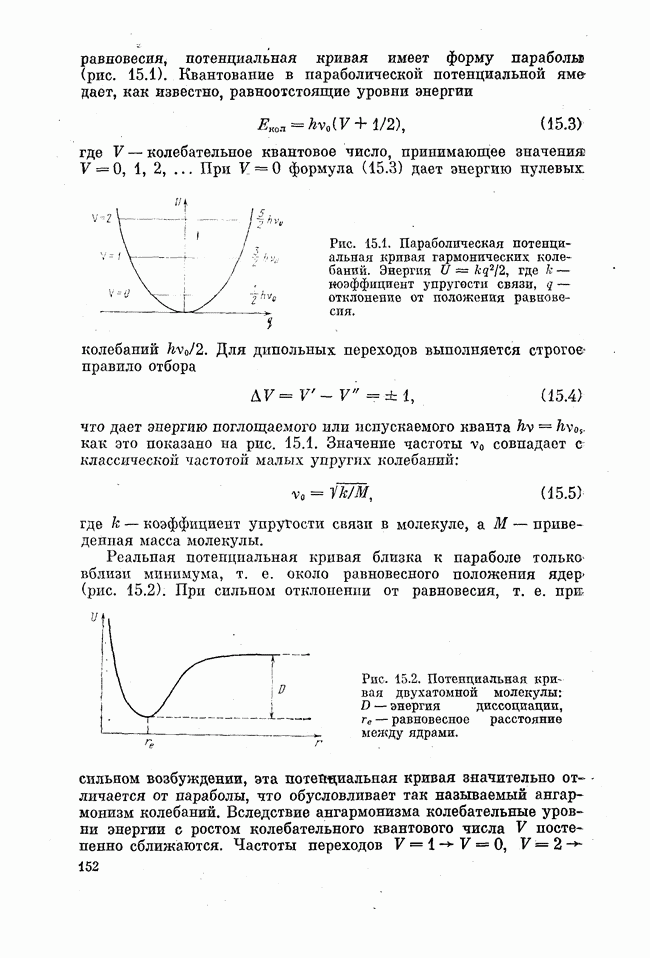
Рис. 8.2. Распределение поля в конфокальном резонаторе по одной из поперечных координат для первых трех мод  Максимальные значения нормированы на единицу.
Максимальные значения нормированы на единицу.
В декартовой системе координат, начало которой помещено в центр резонатора, т. е. в конфокальную точку, а ось z совпадает с осью резонатора (рис. 8.1), поперечное распределение поля дается выражением

где w определяет размер той области поперечного сечения, при выходе из которой интенсивность поля в резонаторе, пропорциональная  падает в е раз. Другими словами, величина w является шириной распределения интенсивности. В пятне площадью
падает в е раз. Другими словами, величина w является шириной распределения интенсивности. В пятне площадью  сосредоточена в основном энергия волны, проходящей в направлении z через плоскость ху.
сосредоточена в основном энергия волны, проходящей в направлении z через плоскость ху.
Полиномы Эрмита нескольких первых степеней имеют вид

Собственным функциям уравнения, дающим поперечное распределение (8.1), соответствуют собственные частоты, определяемые условием

Так как продольная составляющая собственных функций очень мала, то решения исходного уравнения, а следовательно, и поперечные распределения (8.1) описывают моды  . На рис. 8.2
. На рис. 8.2
графически представлены три первые функции Эрмита — Гаусса для одной из поперечных координат, построенные по формуле (8.1) с учетом (8.2). Эти графики наглядно показывают характер изменения поперечного распределения поля с увеличением поперечного индекса n.
Резонансы в конфокальном резонаторе имеют место только для целых значений  . Спектр мод конфокального резонатора вырожден, увеличение
. Спектр мод конфокального резонатора вырожден, увеличение  на две единицы и уменьшение q на единицу дает то же значение частоты. Индексы
на две единицы и уменьшение q на единицу дает то же значение частоты. Индексы  и
и  в обозначении моды
в обозначении моды  относятся к измепепиям поля в направлениях
относятся к измепепиям поля в направлениях  и у n принимают, вообще говоря, значения 0, 1, 2, ..., в то время как индекс q равен числу полуволн, укладывающихся на длине резонатора вдоль оси z.
и у n принимают, вообще говоря, значения 0, 1, 2, ..., в то время как индекс q равен числу полуволн, укладывающихся на длине резонатора вдоль оси z.
Основной является мода  , поперечное распределение поля которой определяется простой гауссовой функцией
, поперечное распределение поля которой определяется простой гауссовой функцией  . Ширина распределения интенсивности меняется вдоль оси z по закону
. Ширина распределения интенсивности меняется вдоль оси z по закону

где  имеет смысл радиуса пучка в фокальной плоскости резонатора, т. е. при
имеет смысл радиуса пучка в фокальной плоскости резонатора, т. е. при  и обычно называется радиусом перетяжки (или радиусом шейки) каустики. Величина
и обычно называется радиусом перетяжки (или радиусом шейки) каустики. Величина  определяется длиной резопатора и составляет
определяется длиной резопатора и составляет

На поверхности зеркала, т. е. при  площадь пятна основной моды, как это видно из (8.4) и (8.5), вдвое больше, чем площадь сечения шейки каустики.
площадь пятна основной моды, как это видно из (8.4) и (8.5), вдвое больше, чем площадь сечения шейки каустики.
Крайне важным является то обстоятельство, что поперечный размер гауссова пучка  не зависит от поперечного размера зеркал 2а. Это является следствием предположений о большой величине числа Френеля
не зависит от поперечного размера зеркал 2а. Это является следствием предположений о большой величине числа Френеля  и малости значения отношения
и малости значения отношения  которые и привели к решению вида (8.1). Так как с учетом (8.5) число Френеля может быть записано в виде
которые и привели к решению вида (8.1). Так как с учетом (8.5) число Френеля может быть записано в виде  требование большого значения этого числа эквивалентно требованию малости площади пятна моды на зеркале
требование большого значения этого числа эквивалентно требованию малости площади пятна моды на зеркале  по сравнению с площадью зеркала.
по сравнению с площадью зеркала.
Решение (8.1) получено для поля внутри резонатора. Но когда одно из зеркал частично прозрачно, как это и бывает в случае активных лазерных резонаторов, то выходящая наружу волна является бегущей волной с поперечным распределением (8.1).
По существу, выделение основной моды активного конфокального резонатора — это способ получения гауссова пучка монохроматического света. Учитывая большое значение и интересные свойства гауссовых пучков, рассмотрим их несколько подробнее.
Пусть некоторая плоскость представляет собой поверхность волнового фронта некоторой монохроматической волны при гауссовом
распределении амплитуды на этом плоском волновом фронте

По принципу Гюйгенса — Френеля исходный волновой фронт создает волну, поле которой определяется интегралом Френеля — Кирхгофа:

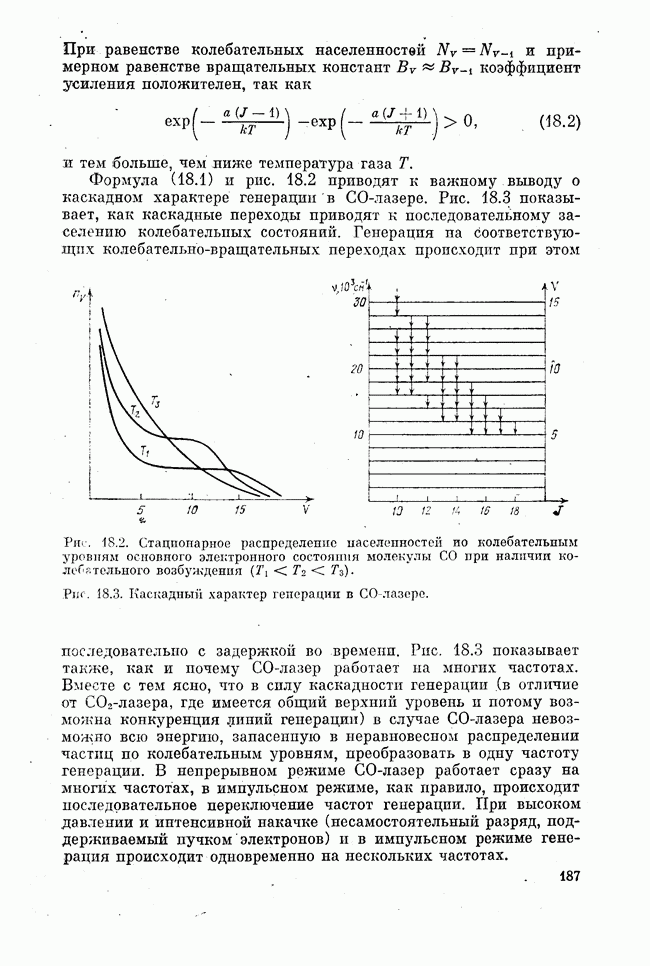
где  , а х, у, z — декартовы координаты, введенные ранее (рис. 8.3). Заменим
, а х, у, z — декартовы координаты, введенные ранее (рис. 8.3). Заменим  на
на  , а в аргументе
, а в аргументе  положим приближенно
положим приближенно  , т. е. в сильно вытянутом прямоугольном треугольнике заменим гипотенузу катетом там, где идет речь об ослаблении амплитуды поля, и учтем пепараллельность z и r там, где речь идет о фазовом набеге волны. Тогда прямое вычисление дает
, т. е. в сильно вытянутом прямоугольном треугольнике заменим гипотенузу катетом там, где идет речь об ослаблении амплитуды поля, и учтем пепараллельность z и r там, где речь идет о фазовом набеге волны. Тогда прямое вычисление дает

где  , а w дается формулой (8.4).
, а w дается формулой (8.4).

Рис. 8.3. К вычислению волнового фронта, создаваемого на расстоянии z плоской волной с гауссовым распределением поля в плоскости z = 0.
В свете рассмотрения, проводившегося в этой и предыдущей лекциях, не вызывает удивления то обстоятельство, что решение  полностью совпадает с основной модой конфокального резонатора
полностью совпадает с основной модой конфокального резонатора  .
.
Поверхность постоянной фазы гауссова пучка, если пренебречь слабой зависимостью а от z, дается уравнением
 (8.9)
(8.9)
При  (что в рамках сделанных с самого начала предположений выполняется всегда) это уравнение задает сферу радиуса R с центром в конфокальной точке. Таким образом, мода
(что в рамках сделанных с самого начала предположений выполняется всегда) это уравнение задает сферу радиуса R с центром в конфокальной точке. Таким образом, мода  конфокального резонатора — это сферическая волна, идущая из центра и обладающая гауссовым распределением интенсивности в плоскости, перпендикулярной направлению распространения. При этом радиус кривизны сферического волнового фронта по мере распространения, меняясь по закону
конфокального резонатора — это сферическая волна, идущая из центра и обладающая гауссовым распределением интенсивности в плоскости, перпендикулярной направлению распространения. При этом радиус кривизны сферического волнового фронта по мере распространения, меняясь по закону

на больших расстояниях от начала координат  совпадает с расстоянием от резонатора до фронта волны:
совпадает с расстоянием от резонатора до фронта волны:  .
.
Это означает, что в дальней зоне волновой фронт гауссова пучка приближается к волновому фронту сферической волны, распространяющейся из точки, расположенной на оси пучка в месте его фокальной перетяжки. При  радиус
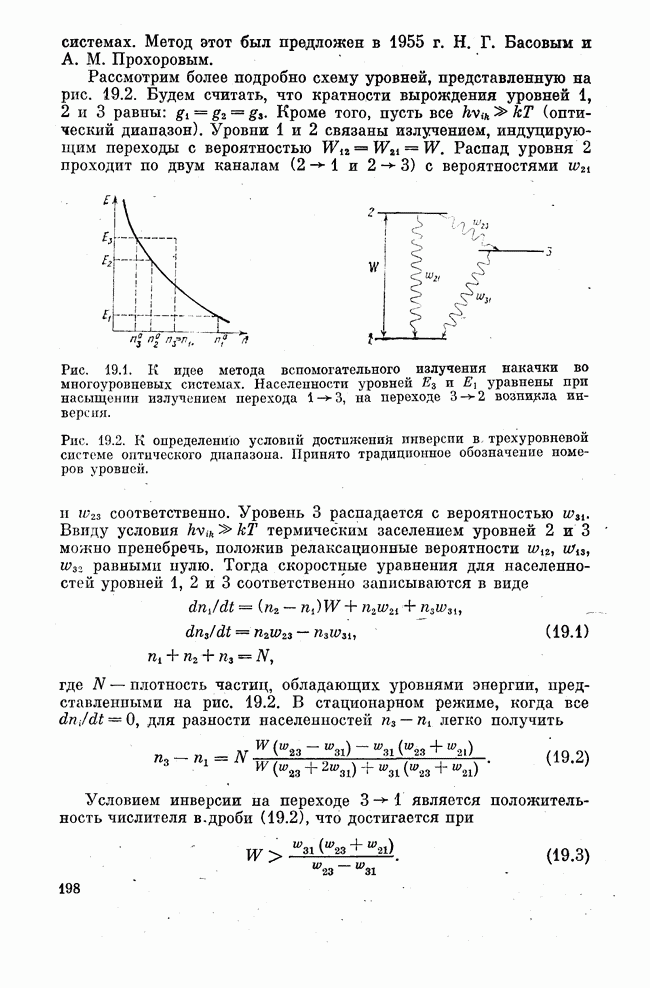
радиус  т. е., как и следовало ожидать, на поверхности зеркала волновой фронт совпадает со сферической поверхностью зеркала. На рис. 8.4 показана огибающая гауссова пучка в резонаторе и волновые фронты.
т. е., как и следовало ожидать, на поверхности зеркала волновой фронт совпадает со сферической поверхностью зеркала. На рис. 8.4 показана огибающая гауссова пучка в резонаторе и волновые фронты.

Рис. 8.4. Огибающая интенсивности гауссова пучка в конфокальном резонаторе и волновые фронты.
Вместе с тем очень важно, что при  . Плоскость симметрии резонатора или, что то же самое, его фокальная плоскость является поверхностью постоянной фазы. Это означает, что в фокальной перетяжке волна является плоской, но пространственно ограниченной эффективным размером
. Плоскость симметрии резонатора или, что то же самое, его фокальная плоскость является поверхностью постоянной фазы. Это означает, что в фокальной перетяжке волна является плоской, но пространственно ограниченной эффективным размером  . Именно этот размер определяет расходимость моды
. Именно этот размер определяет расходимость моды  .
.
Распределение амплитуды по волновому фронту гауссового пучка (8.8) обладает осевой симметрией и шириной w (8.4). На большом расстоянии от резонатора  ширина
ширина  , чему соответствует угловая расходимость
, чему соответствует угловая расходимость
 (8.11а)
(8.11а)
В результате основная часть энергии гауссова пучка сосредоточена в телесном угле
 (8.11б)
(8.11б)
Таким образом, расходимость лазерного излучения в основной моде определяется не поперечным, а продольным размером резонатора лазера. Это является следствием того, что наименьшим эффективным отверстием, на котором происходит дифракция излучения свободно распространяющегося гауссова пучка, является фокальное сечение его каустики. Дифракционная расходимость определяется отношением длины волны  к ширине распределения интенсивности в области перетяжки
к ширине распределения интенсивности в области перетяжки  . В свою очередь, решение интегральных уравнений самосогласованного поля
. В свою очередь, решение интегральных уравнений самосогласованного поля  типа Фокса и Ли приводит в выражению (8.5) для величины
типа Фокса и Ли приводит в выражению (8.5) для величины  .
.
По существу, формула (8.8) оппсывает дифрагированную волну, являющуюся результатом самодифракции гауссова пучка. Дифракционная картина, описываемая формулой (8.8), характеризуется монотонным уменьшением интенсивности при отходе от осевого направления, т. е. полным отсутствием каких-либо осцилляции в яркости дифракционной картины, а также быстрым спаданием интенсивности волны на крыльях распределения. Очевидно, что такой характер имеет дифракция гауссова пучка на любой апертуре, лишь бы размер ее в достаточной мере превышал ширину распределения интенсивности пучка  .
.
Целесообразно отметить, что монотонному характеру дифракционной картины гауссова пучка в радиодиапазоне соответствуют безлепестковые диаграммы направленности приемных и передающих антенн радиолокационных станций или приемных антенн радиотелескопов СВЧ, что достигается спаданием интенсивности облучения на периферийных участках раскрыва антенны, формирующего ее направленность.
Отсутствие осцилляции интенсивности (боковых лепестков) связано с постепенным уменьшением амплитуды поля при удалении от  пучка, а не с конкретным (в нашем случае — гауссовым) законом уменьшения.
пучка, а не с конкретным (в нашем случае — гауссовым) законом уменьшения.
Выражение (8.8) для поля гауссова пучка получено при некотором расположении исходной плоскости  , в которой волновой фронт плоский, а ширина распределения минимальна. Однако вычисления можно повторить, взяв за исходное гауссово распределение в любой иной плоскости, и получить тот же результат. Следовательно, если в каком-то месте пространства некоторый волновой пучок характеризуется сферическим волновым фронтом и гауссовым поперечным распределением амплитуды, то эти свойства сохраняются во всем пространстве. По мере распространения волны изменяется лишь радиус кривизны волнового фронта (8.10) и ширина распределения амплитуды (8.4). Волна этого типа называется гауссовой волной пли гауссовым пучком. Ширина пучка w и радиус кривизны фазового фронта R полностью определяют гауссов пучок в заданной точке на оси его распространения. Изменение знака R означает изменение кривизны фазового фронта на обратную, т. е. превращение расходящегося пучка в сходящийся и наоборот.
, в которой волновой фронт плоский, а ширина распределения минимальна. Однако вычисления можно повторить, взяв за исходное гауссово распределение в любой иной плоскости, и получить тот же результат. Следовательно, если в каком-то месте пространства некоторый волновой пучок характеризуется сферическим волновым фронтом и гауссовым поперечным распределением амплитуды, то эти свойства сохраняются во всем пространстве. По мере распространения волны изменяется лишь радиус кривизны волнового фронта (8.10) и ширина распределения амплитуды (8.4). Волна этого типа называется гауссовой волной пли гауссовым пучком. Ширина пучка w и радиус кривизны фазового фронта R полностью определяют гауссов пучок в заданной точке на оси его распространения. Изменение знака R означает изменение кривизны фазового фронта на обратную, т. е. превращение расходящегося пучка в сходящийся и наоборот.
Так, идеальная тонкая линза преобразует расходящийся гауссов пучок в сходящийся, оставляя его гауссовым. Если поперечные размеры линзы достаточно велики, так что можно пренебречь диафрагмированием пучка на ней, то действие линзы сводится только к изменению кривизны волнового фронта. Как известно из геометрической оптики, идеальная тонкая линза отклоняет все световые лучи, падающие на линзу параллельно ее оптической оси, так, что они пересекают оптическую ось на одном и том же расстоянии от линзы, называемом фокусным расстоянием F. Значит, плоская волна после прохождения линзы становится сферической с радиусом кривизны волнового фронта, равным —F. Следовательно, тонкая линза изменяет кривизну волнового фронта проходящей через линзу волны на величину, равную —  , Тогда радиус кривизны волнового фронта гауссова пучка непосредственно после прохождения линзы определяется соотношением
, Тогда радиус кривизны волнового фронта гауссова пучка непосредственно после прохождения линзы определяется соотношением

где R — радиус волнового фронта непосредственно до прохождения линзы. При достаточно короткофокусной линзе  , т. е. крпвнзна волнового фронта после линзы имеет другой знак, чем до нее, и мы получаем сходящийся гауссов пучок.
, т. е. крпвнзна волнового фронта после линзы имеет другой знак, чем до нее, и мы получаем сходящийся гауссов пучок.
Ввиду важности фокусирования гауссовых пучков в квантовой электронике рассмотрим этот процесс более внимательно.

Рис. 8.5. К вычислению радиуса перетяжки сфокусированного гауссова пучка и расстояния от линзы до перетяжки.
Пусть слева на идеальную линзу с фокусным расстоянием F надает расходящийся гауссов пучок, область перетяжки которого (радиуса  ) находится на расстоянии z от линзы. Радиус кривизны волнового фронта непосредственно до прохожденпя линзы равен R. Кривизна фронта непосредственно после прохожденпя линзы дается формулой (8.12). Ширину пучка в месте нахождения линзы обозначим буквой D. Очевидно, что ширина пучка на линзы одинакова справа и слева (рис. 8.5).
) находится на расстоянии z от линзы. Радиус кривизны волнового фронта непосредственно до прохожденпя линзы равен R. Кривизна фронта непосредственно после прохожденпя линзы дается формулой (8.12). Ширину пучка в месте нахождения линзы обозначим буквой D. Очевидно, что ширина пучка на линзы одинакова справа и слева (рис. 8.5).
Обозначим буквой  искомое расстояние от линзы до той точки на оптической оси линзы, в которой сечение сходящегося пучка минимально и составляет искомую величину Так как пучок после прохождения линзы остается гауссовым, то очевидно, что между величинами
искомое расстояние от линзы до той точки на оптической оси линзы, в которой сечение сходящегося пучка минимально и составляет искомую величину Так как пучок после прохождения линзы остается гауссовым, то очевидно, что между величинами  выполняются соотношения типа (8.4) и (8.10). В результате для
выполняются соотношения типа (8.4) и (8.10). В результате для  мы имеем систему
мы имеем систему
уравнений

которая легко решается. После несложных преобразований получаем

Здесь r дается формулой (8.12), а  в соответствии с (8.4). Полученные соотношения носят достаточно общий характер и позволяют исследовать преобразование одного гауссова пучка в другой, тоже гауссов. Наиболее распространенной является здесь задача согласования полей в двух различных резонаторах.
в соответствии с (8.4). Полученные соотношения носят достаточно общий характер и позволяют исследовать преобразование одного гауссова пучка в другой, тоже гауссов. Наиболее распространенной является здесь задача согласования полей в двух различных резонаторах.
Пусть пассивный резонатор используется как интерферометр Фабри — Перо, например, для исследования спектра излучения лазера, т. е. излучения, выходящего из активного резонатора. Как мы знаем, распределение поля основпой моды конфокального резонатора является гауссовой волной, радиус перетяжки каустики которой определяется длиной резонатора I (см. формулу (8.5)), а радиус кривизны волнового фронта на зеркале — радиусом кривизны зеркала. Поэтому в общем случае моды этих двух резонаторов не совпадают друг с другом. Когда пучок света, соответствующий моде одного резонатора, вводится в другой резонатор и модовые параметры этих резонаторов не согласованы, рассогласование мод приводит к модовому преобразованию. Основная мода лазерного излучепия начинает взаимодействовать с высшими модами пассивного резонатора, возбуялдая в них колебания. При заметной степени перекачки энергии из основной моды активного резонатора возможны серьезные ошибки при исследовании спектральной структуры лазерного излучения. Поэтому важной является возможность преобразования параметров гауссова пучка линзой. Формулы (8.14) и (8.15) позволяют вычислять фокусное расстояние и положение требуемой линзы, зная положение и размеры шейки пучков в обоих резонаторах.
Возвращаясь к важной проблеме фокусирования лазерного излучения, рассмотрим решения (8.14) и (8.15) на большом удалении от перетяжки каустики исходного гауссова пучка, т. е. при  . Применительно к лазерному излучению это соответствует большому расстоянию от резонатора лазера:
. Применительно к лазерному излучению это соответствует большому расстоянию от резонатора лазера:  (см. формулу (8.5)). Пусть также
(см. формулу (8.5)). Пусть также  . Тогда
. Тогда  , и формулы (8.14), (8.15) дают
, и формулы (8.14), (8.15) дают

Таким образом, при большом удалении от перетяжки каустики относительно короткофокусная линза концентрирует исходное излучение гауссова пучка в своей фокальной области, увеличивая его интенсивность в  раз.
раз.
Формально из (8.16) следует, что при  в фокусе линзы получается пятно бесконечно малого радиуса. При этом, однако, пятно на линзе становится бесконечно большим
в фокусе линзы получается пятно бесконечно малого радиуса. При этом, однако, пятно на линзе становится бесконечно большим  что противоречит исходному предположению о том, что линза не диафрагмирует пучок и тем самым не нарушает его гауссовость.
что противоречит исходному предположению о том, что линза не диафрагмирует пучок и тем самым не нарушает его гауссовость.  кое ограничение апертуры гауссова пучка коренным образом меняет характер дифракции, и соответствующий интеграл Френеля — Кирхгофа уже не может быть записан в виде (8.8). Кроме того, и при сохранении гауссовости пучка дифракционные явления накладывают ограничения на величину D.
кое ограничение апертуры гауссова пучка коренным образом меняет характер дифракции, и соответствующий интеграл Френеля — Кирхгофа уже не может быть записан в виде (8.8). Кроме того, и при сохранении гауссовости пучка дифракционные явления накладывают ограничения на величину D.
Угол дифракционной расходимости гауссова пучка составляет  . Это означает, что гауссова волна не мояет быть сфокусирована в пятно радиуса, меньшего
. Это означает, что гауссова волна не мояет быть сфокусирована в пятно радиуса, меньшего  . Из (8.16) вытекает, что
. Из (8.16) вытекает, что  , но
, но  всегда больше
всегда больше  . Так как
. Так как  , то очевидно, что формулы (8.14) -(8.16) верны при условии
, то очевидно, что формулы (8.14) -(8.16) верны при условии

Таким образом, значительная пространственная концентрация энергии основной моды лазерного излучения возможна при фокусировании излучения тонкой линзой, расположенной на большом расстоянии от резонатора лазера  . При этом фокусное расстояние линзы должно быть меньше этого расстояния z, но больше размера пятна на линзе D. В этом случае обсуждаемые условия фокусирования записываются в виде
. При этом фокусное расстояние линзы должно быть меньше этого расстояния z, но больше размера пятна на линзе D. В этом случае обсуждаемые условия фокусирования записываются в виде

п, следовательно, легко выполнимы.
Продольный размер фокальной области, в которой наиболее сильно концентрируется энергия излучения, может быть найден применением формулы (8.4) к сфокусированному излучению. Интенсивность излучения падает в два раза при удалении от точки максимальной концентрации  , где ширина распределения равна
, где ширина распределения равна  на расстояние
на расстояние

При фокусировке излучения на волне 1 мкм в пятно радиусом 10 мкм плотность потока энергии почти постоянна в почти цилиндрической области длиной 1200 мкм.
Подчеркнем, что волновой фронт излучения является плоским точно в фокусе и близок к плоскому во всей рассматриваемой области фокальной перетяжки.
Формулы (8.16) и (8.17) получены для больших 2 из общего решения (8.14) и (8.15). Однако в этом предельном случае они могут быть получены непосредственно. Если z велико, то фокусируемая волна близка к плоской, следовательно, она фокусируется в точке, по определению называемой точкой фокуса. При больших  радиус пятна на линзе при распространении слева направо определяется соотношением
радиус пятна на линзе при распространении слева направо определяется соотношением  , а при распространении справа налево — соотношением
, а при распространении справа налево — соотношением  . Следовательно,
. Следовательно,  .
.
Рассмотрим теперь противоположный частный случай. Поместим перетяжку каустики фокусируемого излучения в передний фокус линзы, т. е. на расстоянии  от плоскости линзы. Исследуем вопрос о том, где сфокусируется гауссов пучок и чему равен в этом случае радиус его повой перетяжки. Подстановка
от плоскости линзы. Исследуем вопрос о том, где сфокусируется гауссов пучок и чему равен в этом случае радиус его повой перетяжки. Подстановка  в формулы (8.4), (8.10) и (8.12) приводит к следующим выражениям для радиуса пятна на линзе и радиуса кривизны волнового фронта непосредственно после линзы:
в формулы (8.4), (8.10) и (8.12) приводит к следующим выражениям для радиуса пятна на линзе и радиуса кривизны волнового фронта непосредственно после линзы:

В свою очередь, подстановка (8.21) в (8.15) дает

При  линза стоит там, где стоит сферическое зеркало эквивалентного конфокального резонатора, формирующего фокусируемый гауссов пучок. Иными словами, если
линза стоит там, где стоит сферическое зеркало эквивалентного конфокального резонатора, формирующего фокусируемый гауссов пучок. Иными словами, если  , то одновременно
, то одновременно  . При
. При  , т. е. на поверхности зеркала, площадь пятна основной моды вдвое превышает площадь сечения перетяжки каустики резонатора (см. (8.4) и (8.5)). Следовательно,
, т. е. на поверхности зеркала, площадь пятна основной моды вдвое превышает площадь сечения перетяжки каустики резонатора (см. (8.4) и (8.5)). Следовательно, 

Таким образом, идеальная тонкая лннза с фокусным расстоянием F преобразует расходящийся гауссов пучок в полностью подобный ему сходящийся пучок, еслп только фокальная перетяжка исходного пучка помещена в фокус линзы. Другими словами, линза сохраняет минимальное сечение гауссова пучка и переводит его  одного своего фокуса в другой, если только именно минимальное сечение помещено с самого начала в фокус линзы.
одного своего фокуса в другой, если только именно минимальное сечение помещено с самого начала в фокус линзы.
Очевидно, что следующая линза с фокусным расстоянием F, помещенная на расстоянии  от предыдущей, преобразует вторичный по отношению к первой линзе гауссов пучок точно таким же образом. Помещая на расстоянии
от предыдущей, преобразует вторичный по отношению к первой линзе гауссов пучок точно таким же образом. Помещая на расстоянии  друг от друга периодическую последовательность одинаковых линз, получаем, таким
друг от друга периодическую последовательность одинаковых линз, получаем, таким
образом, линзовый конфокальный световод, позволяющий передавать на произвольно большое расстояние нерасходящийся в среднем пучок света (рис. 8.6). Траектория волны в конфокальном линзовом световоде представляет периодическую последовательность идентичных сходящихся и расходящихся гауссовых пучков. Распределение поля между линзами полностью подобно распределению поля между зеркалами конфокального резонатора.

Рис. 8.6. Линзовый конфокальный световод (линзы показаны условно вертикальными стрелками).
Естественно, что нормальные моды конфокального линзового световода совпадают с модами конфокального резонатора.
Аналогия между резонаторами и линзовыми световодами достаточно глубока и часто используется для анализа свойств резонаторов разного типа.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ЧАСТЬ ПЕРВАЯ. ОСНОВЫ ФИЗИКИ ЛАЗЕРОВ
- Лекция первая. КОЭФФИЦИЕНТЫ ЭЙНШТЕЙНА
- Лекция вторая. ШИРИНА ЛИНИИ
- Лекция третья. УСИЛЕНИЕ
- Лекция четвертая. КОЭФФИЦИЕНТЫ ЭЙНШТЕЙНА И МАТРИЧНЫЙ ЭЛЕМЕНТ ОПЕРАТОРА ПЕРЕХОДА
- Лекция пятая. ЛАЗЕРЫ-УСИЛИТЕЛИ
- Лекция шестая. ГЕНЕРАЦИЯ
- Лекция седьмая. ОТКРЫТЫЕ РЕЗОНАТОРЫ
- Лекция восьмая. ГАУССОВЫ ПУЧКИ
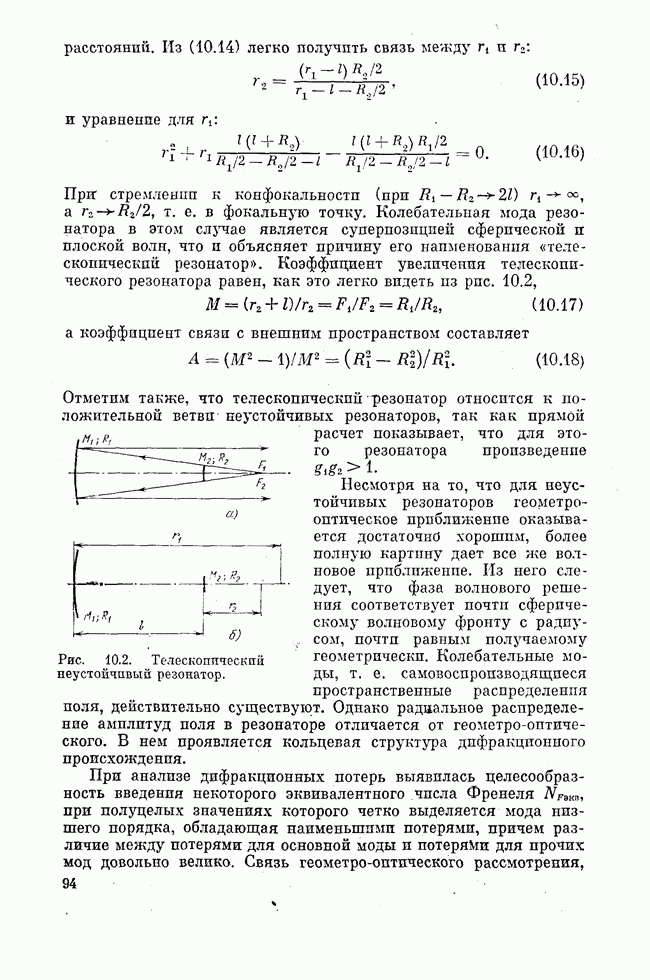
- Лекция девятая. УСТОЙЧИВОСТЬ РЕЗОНАТОРОВ
- Лекция десятая. НЕУСТОЙЧИВЫЕ РЕЗОНАТОРЫ
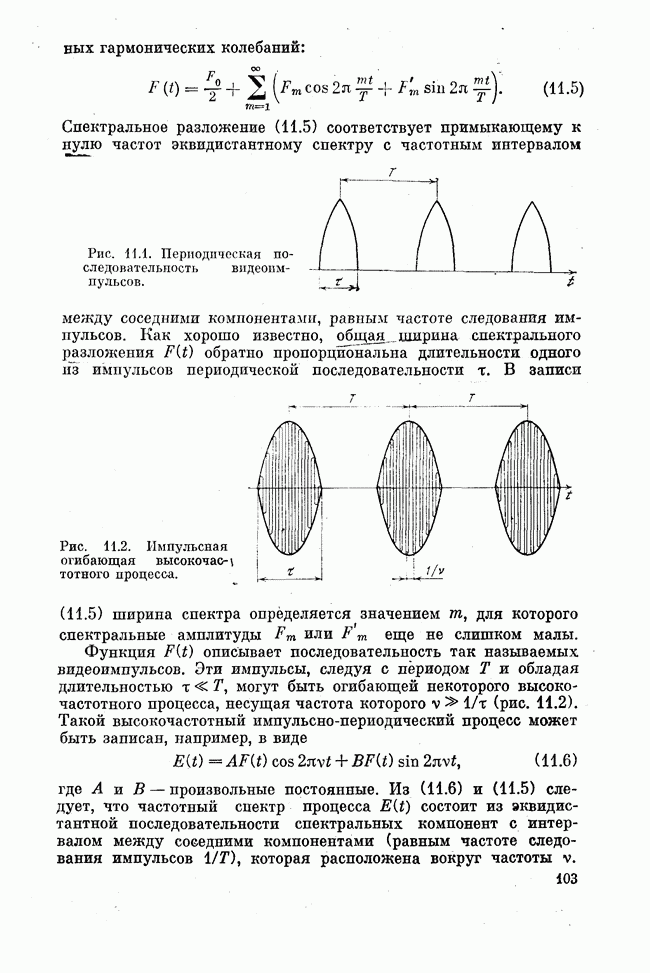
- Лекция одиннадцатая. СИНХРОНИЗАЦИЯ МОД
- Лекция двенадцатая. ИСТОРИЯ КВАНТОВОЙ ЭЛЕКТРОНИКИ. ОСНОВНЫЕ ФОРМУЛЫ
- ЧАСТЬ ВТОРАЯ. ЛАЗЕРЫ
- Лекция тринадцатая. ГАЗОВЫЕ ЛАЗЕРЫ. ГЕЛИЙ-НЕОНОВЫЙ ЛАЗЕР
- Лекция четырнадцатая. ИОННЫЕ ЛАЗЕРЫ. ЛАЗЕРЫ НА ПАРАХ МЕТАЛЛОВ
- Лекция пятнадцатая. CO2-ЛАЗЕРЫ
- Лекция шестнадцатая. СO2-ЛАЗЕРЫ (продолжение)
- Лекция семнадцатая. ХИМИЧЕСКИЕ ЛАЗЕРЫ
- Лекция восемнадцатая. CO-ЛАЗЕРЫ, ГАЗОВЫЕ ЛАЗЕРЫ НА ЭЛЕКТРОННЫХ ПЕРЕХОДАХ В МОЛЕКУЛАХ
- Лекция девятнадцатая. ВСПОМОГАТЕЛЬНОЕ ИЗЛУЧЕНИЕ НАКАЧКИ В СИСТЕМАХ СО МНОГИМИ УРОВНЯМИ ЭНЕРГИИ
- Лекция двадцатая. РУБИНОВЫЙ И НЕОДИМОВЫЙ ЛАЗЕРЫ
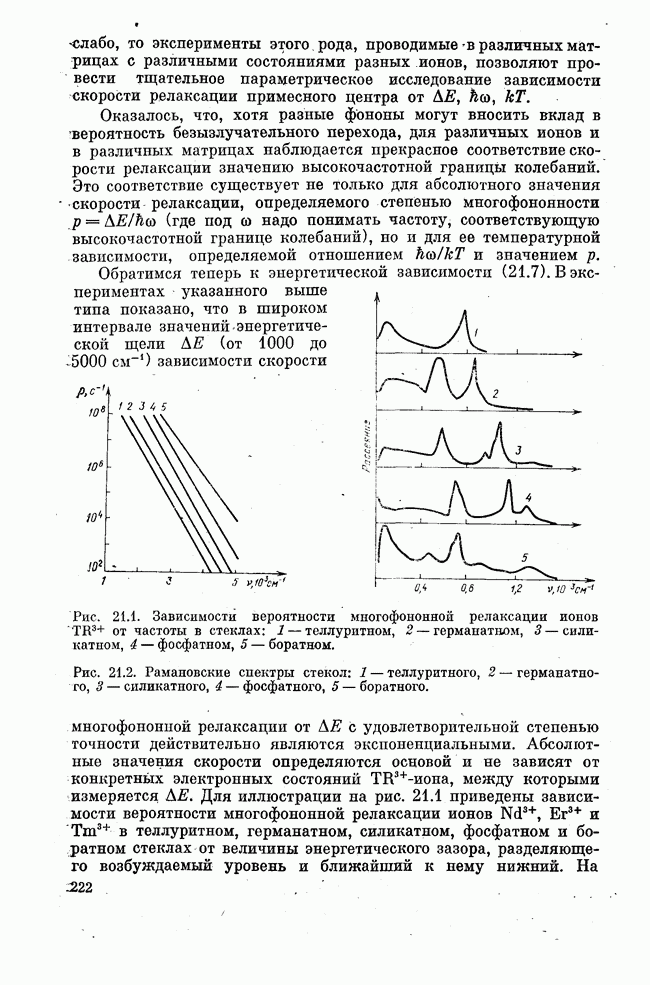
- Лекция двадцать первая. БЕЗЫЗЛУЧАТЕЛЬНАЯ РЕЛАКСАЦИЯ В ТВЕРДОМ ТЕЛЕ
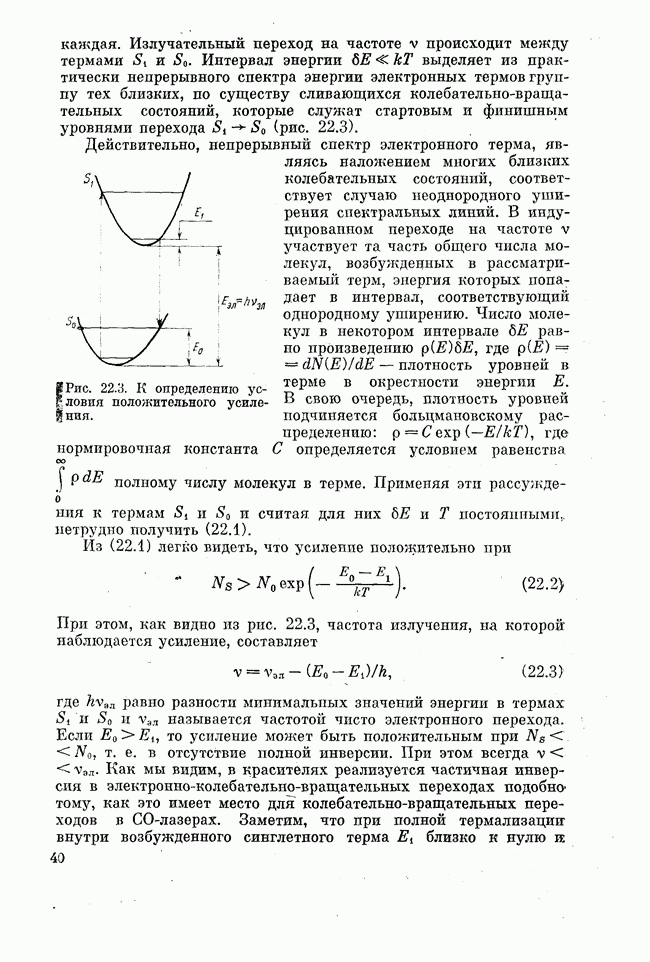
- Лекция двадцать вторая. ЛАЗЕРЫ НА КРАСИТЕЛЯХ
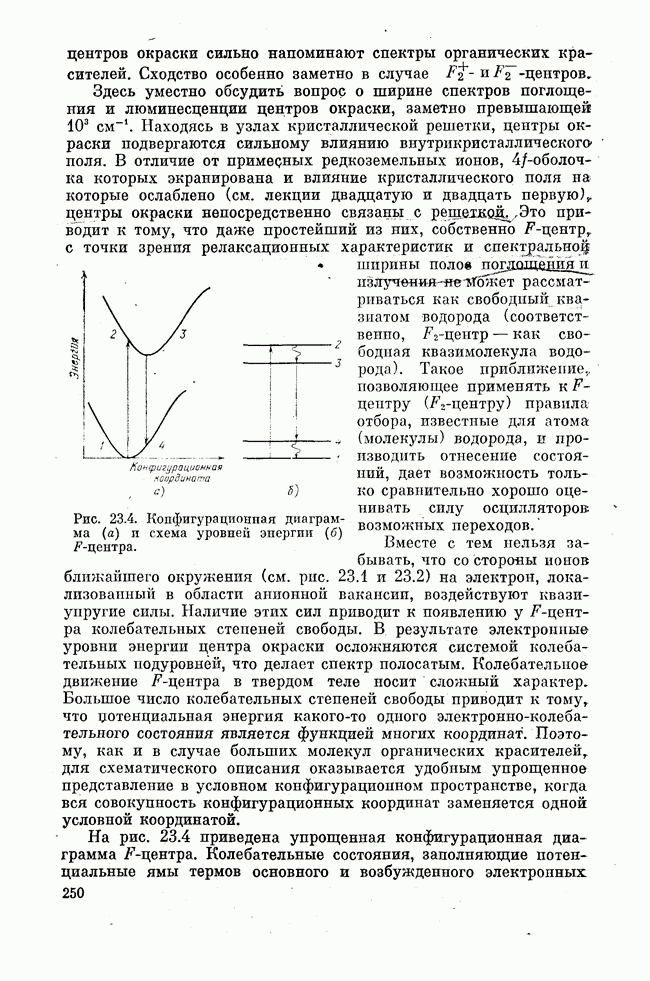
- Лекция двадцать третья. ЛАЗЕРЫ НА ЦЕНТРАХ ОКРАСКИ
- Лекция двадцать четвертая. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ
- Лекция двадцать пятая. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ (продолжение)
- Лекция двадцать шестая. ЛАЗЕРЫ НА СВОБОДНЫХ ЭЛЕКТРОНАХ
- Лекция двадцать седьмая. СЕМНАДЦАТЬ НАИБОЛЕЕ ИЗВЕСТНЫХ ЛАЗЕРОВ
- Заключение. ТЕНДЕНЦИИ РАЗВИТИЯ